Alignment of low-dose X-ray fluorescence tomography images using differential phase contrast

Differential phase contrast images acquired simultaneously with fluorescence images offer a robust method for alignment in low-dose X-ray nanotomography data acquisition.

Abstract

X-ray fluorescence nanotomography provides unprecedented sensitivity for studies of trace metal distributions in whole biological cells. Dose fractionation, in which one acquires very low dose individual projections and then obtains high statistics reconstructions as signal from a voxel is brought together (Hegerl & Hoppe, 1976 ▶), requires accurate alignment of these individual projections so as to correct for rotation stage runout. It is shown here that differential phase contrast at 10.2 keV beam energy offers the potential for accurate cross-correlation alignment of successive projections, by demonstrating that successive low dose, 3 ms per pixel, images acquired at the same specimen position and rotation angle have a narrower and smoother cross-correlation function (1.5 pixels FWHM at 300 nm pixel size) than that obtained from zinc fluorescence images (25 pixels FWHM). The differential phase contrast alignment resolution is thus well below the 700 nm × 500 nm beam spot size used in this demonstration, so that dose fractionation should be possible for reduced-dose, more rapidly acquired, fluorescence nanotomography experiments.

1. X-ray fluorescence nanotomography  

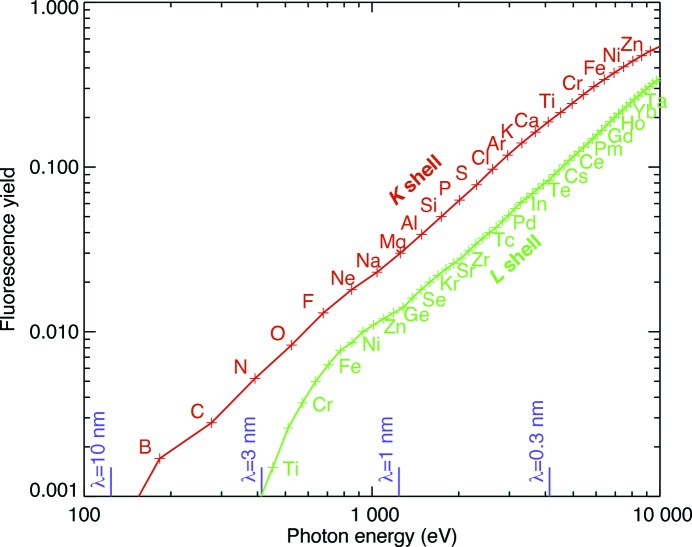
X-ray fluorescence microscopy (XFM) provides the best approach to quantifiably image zinc and other trace metals within whole cells and tissues. The penetrating power of X-rays is well known, allowing one to image many-micrometer-thick specimens in a way that electron microscopes cannot. This penetration can be exploited for element-specific imaging by using incident X-rays to induce the emission of fluorescent X-rays. At atomic numbers greater than about 30, atoms are more likely to respond to X-ray-induced core-level electron vacancies by emitting fluorescent X-rays rather than Auger electrons (see Fig.1 ▶); in electron microprobes, this fluorescent X-ray sits atop a large continuum X-ray background, while in XFM this background is largely absent (there is scattering background, but it is many orders of magnitude lower than the bremsstrahlung background present with electron excitation). By using a single X-ray beam energy above all absorption edges of interest, and using an energy-resolving detector such as a silicon drift diode, one can detect many elements simultaneously in one measurement. These capabilities nicely complement the high spatial resolution capabilities of electron microprobes for studies of thin sections. X-ray fluorescence microscopy also complements the live cell imaging abilities of fluorescence light microscopy, where absolute quantitation of metal content requires exact knowledge of the different binding affinities of fluorophores in all of the cell’s biochemical compartments, fluorophores are available for only a subset of interesting trace metals, and only certain ionic forms of trace metals are visible using fluorophores.

Figure 1.

Many of the biologically relevant trace metals have rather low fluorescence yields, giving rise to poor signal-to-noise in individual projections. Shown here is the fluorescence yield (Krause, 1979 ▶) of several elements plotted as a function of the emission energies. The competing process, Auger electron emission, is not well suited to elemental detection in thick biological specimens because Auger electrons do not escape at their original element-signalling energy except from regions well within 100 nm of the sample’s surface.

While X-ray-induced X-ray fluorescence provides the highest sensitivity and lowest radiation dose for imaging trace elements in micrometer-thick biological specimens (Kirz, 1980 ▶; Sparks, 1980 ▶), it is a low-signal-level process. An X-ray must be absorbed by a trace element atom, a fluorescence X-ray must be emitted, and that photon must be collected by an energy-dispersive detector. Also, until recently most synchrotron X-ray microprobes were operated in a stop–count–move sequence for data collection at each pixel of an image, with per-pixel counting times of ∼1 s and with delays for the micropositioning stage to move to a new position. First demonstrations of X-ray fluorescence nanotomography (de Jonge et al., 2010 ▶) have therefore involved an experiment time of 36 h to collect images over only 24 projection angles, whereas ideally one wishes to have much finer angular spacings (Crowther et al., 1970 ▶). Not only are such images slow to acquire (with high radiation dose imparted to the sample), but aligning low-photon-count images onto a common rotation axis (to correct for position shifts in imperfect rotation stages) would appear to be difficult. As a result, higher resolution applications of X-ray fluorescence nanotomography might seem impractical.

Some of these practical impediments have already been removed. Advances in the response time of energy-dispersive detectors (and in scan acquisition electronics and software) have allowed X-ray microprobes to acquire so-called ‘fly scan’ images with continuous motion during a scan line and per-pixel acquisition times of 1–100 ms (Lombi et al., 2011 ▶); microprobes at the Advanced Photon Source (APS) at Argonne National Laboratory have established routine fly scans down to 1 ms per pixel. However, while this speed-up makes it practical to consider collection of data over finer angular spacings, it does not remove the fundamental problem of low signal level in individual fluorescence images which would make alignment to a common rotation axis even more problematic.

Another difficulty might appear to be poor signal-to-noise level in 3D reconstructions obtained from individual fluorescence images taken with fast per-pixel exposure times. However, Hegerl & Hoppe (1976 ▶) put forward the explanation that dose fractionation overcomes this problem; as stated in the abstract of their paper, A three-dimensional reconstruction requires the same integral dose as a conventional two-dimensional micrograph provided that the level of significance and the resolution are identical. The necessary dose D for one of the K projections in a reconstruction series is, therefore, the integral dose divided by K. Consider a particular voxel in a volumetric reconstruction; to see that the material in this voxel is different from what is in the adjoining voxel, one needs to have determined the number of photons arising (in the fluorescence case) from each voxel. In a two-dimensional image, these photons will all have been collected from one angle, yielding no depth information. In tomography, the information from a voxel will be distributed among specific positions in each of the individual projections, but that information is reorganized into voxels (or, from the point of view of one particular voxel, collected from the set of projections) during the act of tomographic reconstruction. It matters not at all the direction from which different photons were collected into a voxel; what matters is that the total number of photons needed to recognize its contents were obtained. Dose fractionation was originally a controversial concept (see, for example, Hoppe & Hegerl, 1981 ▶), but in fact it has emerged as a necessary condition for the success of modern single-particle electron microscopy methods. In these methods (Nogales & Grigorieff, 2001 ▶), 10⁴–10⁶ individual images of macromolecules are collected, images are sorted by commonality after which they are added to gain statistical significance, and then their projection direction relative to a model of the three-dimensional macromolecule is guessed and a standard tomographic reconstruction is obtained (the sorting, alignment and reconstruction process can be repeated iteratively for refinement). The validity of dose fractionation has also been demonstrated carefully by McEwen et al. (1995 ▶) via the controlled circumstances of simulations; they stated, The simulations verify the basic conclusions of the [dose fractionation] theorem and extend its validity to the experimentally more realistic conditions of high absorption, signal-dependent noise, varying specimen contrast and missing angular range. We therefore see that dose fractionation should allow us to reduce the dose and increase the speed of data collection in X-ray fluorescence tomography; however, while there has been some speculation of its potential (de Jonge & Vogt, 2010 ▶; Lombi et al., 2011 ▶), we are unaware of any work in which dose fractionation has been employed in a systematic and well characterized way in X-ray fluorescence tomography, and application of dose fractionation still requires accurate alignment of low-signal-level fluorescence images onto a common rotation axis.

1.1. Projection alignment using phase contrast  

For biological applications, X-ray fluorescence microscopy systems with energy-resolving fluorescence and total transmission detectors are largely blind to the main constituents of cells: the light elements H, C, N and O. This is because these elements are weakly absorbing and have low fluorescence yield (Fig. 1 ▶). However, phase contrast is significantly stronger than absorption or fluorescence contrast in multi-keV X-ray microscopy of light elements (Schmahl et al., 1994 ▶; Davis et al., 1995 ▶), due to the orders-of-magnitude difference between the real δ and imaginary β parts of the X-ray refractive index of n = 1 − δ − iβ (see, for example, Hornberger et al., 2007 ▶). Phase contrast therefore provides a route to exploiting dose fractionation in X-ray fluorescence nanotomography by providing a stronger signal for alignment of projection images onto a common rotation axis.

Phase contrast can be incorporated into standard data collection in X-ray fluorescence microscopes in a variety of ways. Simple aperturing of the transmission detector provides phase contrast in scanning X-ray microscopy (Kaulich et al., 2002 ▶; Vogt et al., 2004 ▶), while segmented transmission detectors (Feser et al., 2006 ▶; Hornberger et al., 2008 ▶) can be used for differential phase contrast imaging including with quantitative interpretation (Hornberger et al., 2007 ▶, 2008 ▶; de Jonge et al., 2007 ▶, 2008 ▶), and for Zernike phase contrast approaches (Holzner et al., 2010 ▶). For combined phase contrast and fluorescence imaging of specimens with trace metals, phase contrast provides a measure of the specimen mass distribution thus allowing one to measure not just metal content but concentration (Holzner et al., 2010 ▶; Kosior et al., 2012 ▶). In this work, we are using differential phase contrast (DPC).

Cross correlation is a commonly used method for alignment of tomography projections onto a common rotation axis (Koster et al., 1992 ▶; Dierksen et al., 1992 ▶). Almost all rotation stages have some degree of ‘runout’ error, so that the object shifts in some direction transverse to the rotation axis after each rotation. If the rotation angle is small, two projection images a and b of a three-dimensional object will be similar, so that in a cross-correlation image c of

the position of the peak relative to the center of the image can be used to find the transverse position shift in pixels between the two images (here denotes the complex conjugate). We note that improvements in three-dimensional alignment can be obtained by using markers such as gold beads (Penczek et al., 1995 ▶) or iterative re-projection schemes (Winkler & Taylor, 2006 ▶), but cross correlation still represents a more generally applicable and rapidly evaluated alignment method. However, in the case of dose fractionation the low signal level of individual projection images can make their cross-correlation alignment challenging (McEwen et al., 1995 ▶). We propose here that X-ray DPC images, acquired simultaneously with X-ray fluorescence images and with no additional exposure to the specimen, provide a superior signal for image alignment by cross correlation.

2. Experimental demonstration  

In order to demonstrate that simple DPC provides a superior approach for projection alignment in X-ray fluorescence nanotomography, we simultaneously acquired DPC and fluorescence images on a mouse oocyte as part of ongoing studies of the role of zinc in early stage oocyte development (Kim et al., 2010 ▶, 2011 ▶). A metaphase II stage mouse egg in 100 mM NH₄OAc buffer (pH 7.0) was placed inside a 150 µm inner-diameter methyl cellulose capillary (Mager Scientific), and promptly frozen by manual plunge into liquid ethane. The egg and capillary were then loaded at ∼120 K temperature into a turbo-pumped freeze-drying system, and slowly warmed to allow ice to sublimate. This method was used to minimize loss of trace elemental content.

X-ray fluorescence (detected using a Vortex EM from SII Nanotechnology) and segmented transmission [collected by a custom-built segmented silicon drift detector (Hornberger et al., 2008 ▶)] data were acquired simultaneously at 10.2 keV incident photon energy at beamline 2-ID-E at the APS (Fig. 2 ▶), with no extra dose to the specimen beyond what would have been required for fluorescence detection alone. The focused flux was about 5 × 10⁹ photons s⁻¹ in a spot size of about 700 nm × 500 nm using a 320 µm-diameter 80 nm outermost-zone-width zone plate (the larger spot size resulted from accepting a larger fraction of the undulator source phase space to choose flux over resolution; we note that other scanning fluorescence X-ray microscopes at the APS have focused spot sizes below 50 nm). Per-pixel exposure times ranging from 3 to 30 ms were used, with two separate 230 × 230 pixel images acquired at 300 nm pixel size at each exposure time. Full fluorescence spectra were recorded using a SII Vortex energy-dispersive detector to allow for subsequent elemental quantitation by fitting of fluorescence peaks and estimation of scattering backgrounds (Vogt et al., 2003 ▶; Vogt, 2003 ▶); however, for the analysis shown here we used the simpler approach of setting an energy window for each element and integrating the total signal within that window (this simpler approach is consistent with rapid on-line alignment). Segmented transmission detector images were recorded simultaneously, with a shaping amplifier time set to 2 ms for all images (improved signal-to-noise for the longer dwell time images might have been attainable had this been adjusted).

Figure 2.

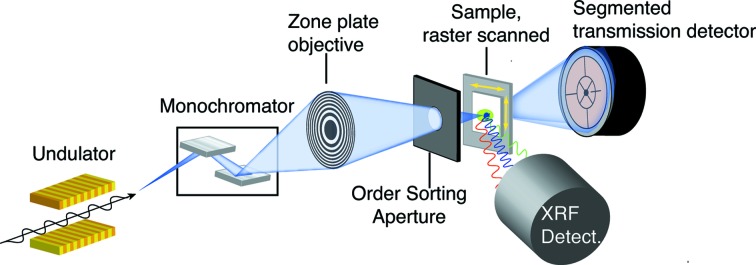
Schematic of the 2-ID-E X-ray fluorescence microprobe instrument at the APS. X-rays from the APS are monochromated, and a Fresnel zone plate is used to produce a small spot through which the sample is scanned. A segmented transmission detector is used to record the signal used to obtain DPC images, and an X-ray fluorescence detector (SII Vortex) is used to collect the X-ray fluorescence spectrum at each pixel. Figure adapted from de Jonge et al. (2010 ▶) and Vogt & Ralle (2012 ▶).

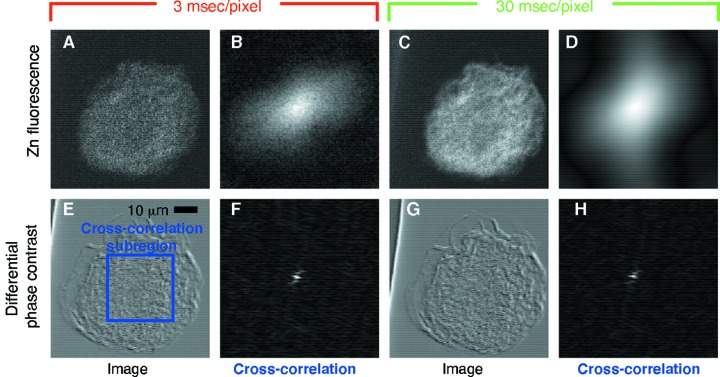
In Fig. 3 ▶ we show a comparison of cross-correlation images between a scan pair taken at the same tilt angle first with 3 ms dwell and then with 30 ms dwell. As a three-dimensional object is rotated, features that would appear to protrude at the periphery from one viewing angle would appear to be internalized in another viewing angle, so that the projected outline of the object might dominate the cross-correlation alignment more than fine internal structure nearer to the rotation axis. Because of this, we chose to examine the cross correlation of a 96 × 96 pixel sub-region (Fig. 3E ▶) within the oocyte, rather than the cross correlation of the entire image field. In addition, by observing no cross-correlation shift between two separately acquired images at the same specimen position and tilt angle, we have ensured that the cross correlation is dominated by specimen features rather than by any noise or artifacts. The sub-region cross-correlation images thus obtained between the pair of zinc fluorescence images at 3 ms dwell (Fig. 3B ▶) and at 30 ms dwell (Fig. 3D ▶) are both rather broad in character, showing lack of a well defined cross-correlation peak; in addition, the 3 ms dwell cross-correlation image is noticeably noisier than the 30 ms dwell image due to poor photon statistics in the real space images (Figs. 3A and 3C ▶, respectively). We also show in Figs. 3E and 3G ▶ the DPC images obtained by a difference over sum operation between detector segments in the upper right quadrant of the detector plane versus segments in the lower left quadrant (Hornberger et al., 2008 ▶). The corresponding sub-region cross-correlation images shown in Figs. 3F ▶ and 3H ▶ are much sharper (especially along the 45° line corresponding to the phase contrast differentiation direction we chose for this work).

Figure 3.

Demonstration of the ability of DPC X-ray images to provide high-accuracy alignment of low-dose X-ray fluorescence images. A freeze-dried oocyte was imaged at APS beamline 2-ID-E using ‘fly scans’ with per-pixel times of 3 ms (images on the left) and 30 ms (images on the right), and both zinc fluorescence images (top) and diagonal DPC images (bottom) were recorded simultaneously. The lack of detail and low signal in the zinc fluorescence projections precludes precise alignment (broad peaks with spurious sub-peaks in cross correlation images B and D), while the diagonal DPC images deliver sharp and low-noise cross-correlation peaks even at 10× reduced X-ray dose (image F).

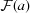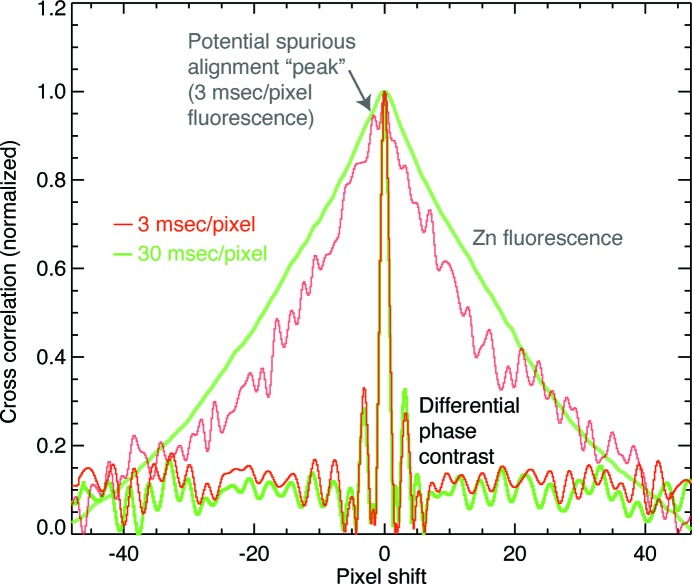
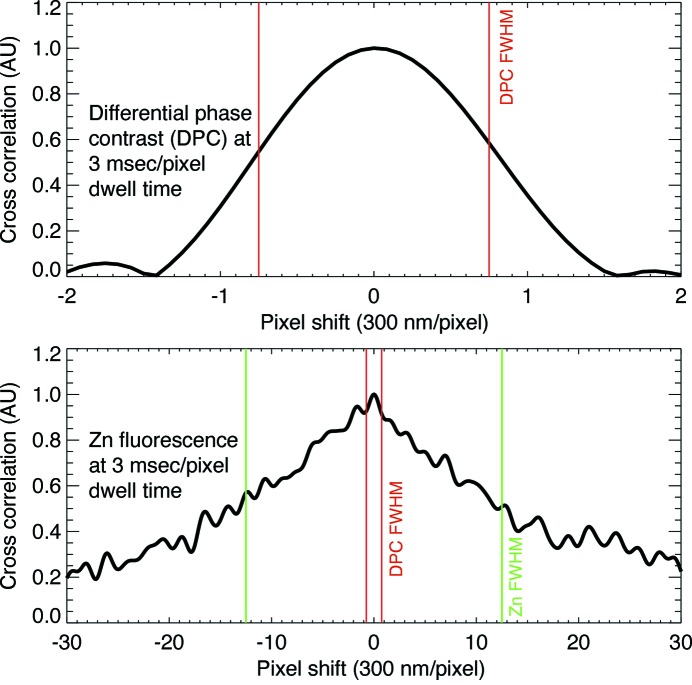
In order to visualize the ability to perform sub-pixel alignment, we calculated the sub-region Fourier transform images and 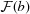[see equation (1)] and then embedded them in a 6× larger array before multiplication and inverse transformation as part of a method for rapid sub-pixel alignment (Guizar-Sicairos et al., 2008 ▶). We then found the position of the cross-correlation peak and extracted horizontal profiles across the peak which are shown in Fig. 4 ▶ for 3 and 30 ms pixel dwell times. With the fluorescence signal, the cross-correlation profile is very broad indicating again a less robust ability to align the low-signal-level fluorescence images, with the 3 ms correlation showing spurious correlations near the center which could lead to erroneous alignment if even shorter dwell times were employed (Fig. 5 ▶). With DPC, the peaks are very narrow indicating a well defined registration between the two images [little difference is seen with increasing exposure time due to the constant shaping time of the analog amplifier in the segmented transmission detector (Hornberger et al., 2008 ▶)]. The DPC peak has a full width at half-maximum (FWHM) size of about 1.5 pixels or 450 nm (as opposed to 25 pixels FWHM for the zinc fluorescence signal), with a regularity that suggests the centroid can be found to be a small fraction of that value corresponding to an alignment accuracy well below the 700 nm × 500 nm beam spot size in this example. We expect a similar trend of DPC cross-correlation alignment errors to be smaller than the beam size to hold in future experiments at higher resolution, potentially providing a pathway for three-dimensional resolution comparable with the resolution in two-dimensional projection images.

Figure 4.

Plots across the cross-correlation images obtained from both zinc fluorescence and differential phase contrast images at per-pixel dwells of 3 and 30 ms. The DPC images show narrower lower-noise cross correlations, especially at lower dose (Fig. 5 ▶). Because the same 2 ms shaping time was used for the segmented transmission detector (Hornberger et al., 2008 ▶) at both dwell times, there is relatively little improvement of the DPC alignment with increased exposure time in this example measurement.

Figure 5.

Cross correlations for 3 ms dwell time images using DPC (top) and zinc fluorescence (bottom). Not only is the cross correlation peak for DPC narrower (as shown with the FWHM marker lines), it is also free of the noise fluctuations present in the zinc fluorescence cross correlation. This makes the DPC signal clearly superior for robust projection alignment, even when low-dose individual fluorescence projections are acquired as part of exploiting dose fractionation (Hegerl & Hoppe, 1976 ▶).

3. Conclusion  

We have demonstrated here that differential phase contrast images can be used for improved alignment of projection images to a common rotation axis in low-dose X-ray fluorescence tomography. This will allow us to fully exploit the dose fractionation theorem (Hegerl & Hoppe, 1976 ▶) by acquiring more projection angles with lower exposure times and thus obtain higher three-dimensional resolution in a reconstructed tomogram (Crowther et al., 1970 ▶; Klug & Crowther, 1972 ▶) than would have resulted from using longer exposure time images over fewer projection angles. That is, for no additional dose, we can in principal obtain higher resolution three-dimensional images. The differential phase contrast images are acquired at the same time as the fluorescence images, so that no additional time or radiaiton dose to the specimen is required. We expect that this will prove to be advantageous in future X-ray fluorescence nanotomography studies.