Abstract
Dolphins and whales use tonal whistles for communication, and it is known that frequency modulation encodes contextual information. An automated mathematical algorithm could characterize the frequency modulation of tonal calls for use with clustering and classification. Most automatic cetacean whistle processing techniques are based on peak or edge detection or require analyst assistance in verifying detections. An alternative paradigm is introduced using techniques of image processing. Frequency information is extracted as ridges in whistle spectrograms. Spectral ridges are the fundamental structure of tonal vocalizations, and ridge detection is a well-established image processing technique, easily applied to vocalization spectrograms. This paradigm is implemented as freely available matlab scripts, coined IPRiT (image processing ridge tracker). Its fidelity in the reconstruction of synthesized whistles is compared to another published whistle detection software package, silbido. Both algorithms are also applied to real-world recordings of bottlenose dolphin (Tursiops trunactus) signature whistles and tested for the ability to identify whistles belonging to different individuals. IPRiT gave higher fidelity and lower false detection than silbido with synthesized whistles, and reconstructed dolphin identity groups from signature whistles, whereas silbido could not. IPRiT appears to be superior to silbido for the extraction of the precise frequency variation of the whistle.
INTRODUCTION
The vocal communication of cetaceans has been the subject of wide ranging research over recent decades, and automated mathematical analysis of vocalizations has long been a desired tool in the research repertoire. The ability to record calls in the wild and then to computerize their processing (either in real time or retrospectively in the laboratory) would greatly reduce time and budgetary burdens as well as reduce potential human observer bias and fatigue. However, existing automatic algorithms have been only partially successful in achieving these aims. Dolphins and whales produce a wide range of tonal and broadband calls; this complicates the challenge of developing automated techniques. In addition, the goals of the automated analysis of cetacean vocalizations need to be clearly specified, as a number of distinct aims exist, and each requires rather different characteristics for a successful algorithm. Automatic analysis of recordings of cetacean vocalizations can be intended to assess wild population parameters such as species identity (Mellinger and Clark, 2000; Gillespie, 2004; Oswald et al., 2007; Roch et al., 2007), population size and presence (Kandia and Stylianou, 2006; Marques et al., 2009), activity, movement, and localization (Thode, 2004) or alternatively to analyze the communication modalities and link them to behavioral observations (Johnson et al., 2009; Henderson et al., 2011).
When the goal of automatic analysis is population assessment, an emphasis is placed on robust detection under conditions of field recordings. The time of occurrence of calls is generally unknown a priori, as is the identity of the species making a particular call. In this case, the emphasis is on high probability of detection of calls and an estimable false positive rate, so that compensation for false detections can be made. For other applications, such as those in which human operators are involved, a low false detection rate is important to prevent user fatigue and subsequent disregarding of true detections. In contrast, when the goal is the characterization of acoustic and other properties of the calls, a greater emphasis is placed on the accuracy of the time-frequency representation, often with recordings in which the onset of the call has already been identified and the focal species is not in doubt.
Many previous works have emphasized the goal of robust detection, but this work is concerned primarily with the latter goal: An accurate trace of whistle vocalizations to further the investigation of the nature and function of tonal vocal communication. Many cetacean species produce stereotyped vocalizations with certain acoustic elements that are repeated at different times and by different individuals. When two or more sub samples of a call are sufficiently similar, they are often coined “syllables” (Kroodsma, 1977) with the implication that the ordering of these vocal elements may represent some non-random process or “syntax.” To test such a hypothesis, it is necessary to identify similar vocal elements and arrive at a definition of the repertoire of syllables for a particular species, which is likely to be cognitively relevant to the communicating animal. This can only be done if vocalizations can be quantified in a consistent and reliable way.
To date, the identification of distinct vocalizations has been performed “by eye” with human observers surmising which vocal elements constitute cognitively distinct groups without any objective evidence that such elements are, in fact, perceived as distinct by the animals in question (e.g., Sayigh et al., 2012). In the absence of indications from behavioral experiments, researchers have to rely on qualitative measures of similarity between elements to arrive at a grouping scheme in which elements labeled as a single syllable are at least similar in some acoustic sense (e.g., Slater and Ince, 1979; Marler, 2004; Bohn et al., 2008; Shapiro et al., 2011; Kershenbaum et al., 2012). A quantitative representation of vocalizations would enable researchers to draw up objective mathematical metrics of similarity, identify acoustically distinct sounds, classify them into groups of presumed behavioral relevance, and then analyze sequences of such syllables for syntactic structure. That is the goal of this work: To produce an automatic extraction algorithm that faithfully encodes and quantifies cetacean vocalizations.
Over the years, many groups have developed automated techniques for the extraction of cetacean whistles from recordings. A variety of techniques have been used, but most have relied on the processing of a three dimensional time-frequency domain representation of the signal, almost always a sequence of short-time discrete Fourier transforms (DFT) in which the signal is represented along dimensions of time, frequency, and power. The particular appeal of processing the signal following a DFT is that it strongly represents the frequency modulation (FM) and harmonic structure of the signal; two features that are considered to be the major characteristics of cetacean tonal whistles (Janik et al., 2006). DFT poorly represents any amplitude modulation (AM) present, but AM appears to play a minor role if at all in encoding information in dolphin whistles (Janik et al., 2006); possibly because AM signals are more prone to degradation during transmission (Van Valkenburg, 1993). AM encoding of information in cetaceans is a relatively neglected field, although some recent work (Ou et al., 2012) has attempted to address this by examining vocalization waveforms before DFT. If we presume that FM of tonal vocalizations is the primary encoding of information in cetacean communication, then accurate tracing of the frequency variation of whistles is vital to represent the vocalizations reliably for further processing.
On a terminological note, it has been common in the literature to refer to a digital representation of the time-frequency variation of a whistle as a “contour.” A more appropriate term is “ridge,” which is a line joining points that are local maxima (we further discuss the geometric nature of ridges in the following text), and we make use of this term in this work, together with the more general term, “frequency profile.”
The first automated techniques for the extraction of frequency profiles from recordings used template matching to a library of known tonal whistle shapes (Mellinger and Clark, 2000). Recently a large number of techniques have been presented (e.g., Madhusudhana et al., 2009; Mellinger et al., 2011; Roch et al., 2011) that extract whistle frequency information by searching for local maxima in the DFT representation and then joining successive maxima in the time domain, such that the connection of two maxima in some way represents a likely causal relationship. In other words, two joined maxima should form sequential points in a true whistle, rather than being arbitrary noise that is coincidentally correlated in time and frequency. Various techniques have been proposed for this including Kalman filtering (Mallawaarachchi, 2008a), heuristic rules (Mellinger et al., 2011), phase tracking (Ioana et al., 2010; Johannson and White 2011), particle filters (Roch et al., 2011; White and Hadley, 2008), and graph-based techniques (Roch et al., 2011). Some of these algorithms produce good detection rates that may be useful in the ecological assessment of cetacean populations (e.g., Marques et al., 2009). However, by taking as their fundamental element the peaks of the DFT spectrum at discrete times, all of these algorithms do not exploit gross shape-based features of the spectrogram. Rather, the information is reconstructed in retrospect connecting temporally adjacent peaks using functions of neighboring peaks that take into account the coherence of the peak patterns but ignore surrounding information that is relevant to a coherent trajectory along a ridge. In fact, the problem of extracting whistle ridges is fundamentally a shape-based application and can be accomplished in a single step using image processing techniques. Images are three dimensional representations (two spatial dimensions and one intensity dimension) just like DFT representations, and tools developed in the fields of artificial vision, pattern recognition, and automatic target recognition can be adapted for the extraction of frequency ridges in cetacean vocalizations. Gillespie (2004) used image processing techniques to analyze right whale calls with an edge detection algorithm. Edge detectors (e.g., Canny, 1986) are two dimensional filters designed to provide high outputs when moving across regions that change from one intensity to another. Ridges in contrast are local maxima separating two regions. Consequently, one might expect algorithms designed to detect ridges to outperform edge detection techniques on cetacean whistles. Similar geometric techniques have been used with some success, such as “active contours” (Lampert and O'Keefe, 2013) or hybrid systems combining image processing and other techniques (e.g., Thode et al., 2012), but they too search for two-dimensional object boundaries and do not necessarily make use of the information available in ridge structures.
In this work, we develop and describe IPRiT, an image processing-based algorithm for the extraction of cetacean whistle ridges, and compare it to an existing automatic extraction algorithm used for whistle detection, silbido (Spanish for whistle), the graph algorithm detector in Roch et al. (2011). We compare the performance of the two algorithms using both synthetic sounds generated by computer and also real-world recordings of dolphin vocalizations.
ALGORITHM
Preprocessing
We performed all the analyses following a DFT. The parameters of the Fourier analysis varied depending on the nature of the recordings; particularly the typical length of the call and the frequency bandwidth. Application of image processing algorithms is likely to be most effective where the resulting DFT representation is “image-like.” The analysis window length and advance/overlap must be set so that the temporal and spectral changes in the whistle allow a representation where relevant fluctuations in the frequency modulation of the whistle are apparent in both the time and frequency domains. This means that the image processing approach would be less able to track fine-grain ridge dynamics for calls with a frequency variation smaller than the DFT bandwidth or very short calls with a large bandwidth (where temporal features may be smaller than one pixel). Although the length and bandwidth of delphinid vocalizations vary widely (e.g., Esch et al., 2009), we restricted ourselves to calls 0.5–3 s long with a fundamental frequency ranging between 2 and 16 kHz. We used a DFT of length 256 with a Hamming window of 3.2 ms and 50% overlap, which, for a 1 s recording at sampling rate 32 000, leads to a spectrogram with 128 pixels on the frequency axis and 640 pixels on the time axis. Following DFT, we took the logarithm of the spectral power, and scaled the spectrogram between 0 and 1.
After generating the spectrogram, we optionally applied a click filter to remove impulsive noise in recordings where the background noise contained echolocation clicks and artifacts. We used a technique based on that of Mallawaarachchi (2008b) by convoluting the spectral image with four 15 × 15 pixel Gaussian kernels with different alignments: Horizontal, vertical, top-left to bottom-right, and bottom-left to top-right. The filtered image is then constructed as
| (1) |
where I is the original image, and subscripts h, v, d1, and d2 each represent the original image convolved by the horizontal, vertical, and two diagonal kernels, respectively. The silbido approach uses a different click suppression algorithm, which we retained when comparing the two implementations.
Rather than applying the subsequent processing to all pixels in the spectrogram, we applied a threshold filter so that processing proceeded only on those regions of the spectrogram with relatively high signal to noise ratio, i.e., where there was high spectral power in the local region. This “interest operator” is commonly used in image processing to remove those regions of an image where a signal is unlikely to exist (Davies, 2004). First, we performed a morphological dilation operation (Dougherty and Lotufo, 2003) on the grayscale image with a flat 4 × 4 pixel structuring element to enlarge those regions of the image with a strong signal. Then we generated a mask to exclude all pixels of the dilated image with a value less than Q standard deviations (σ) above the mean (μ) of the dilated image. Q is a threshold variable that we varied in our analysis of the algorithm performance. Using this technique, the minimum pixel value Pmin= μ + Qσ can be considered an adaptive threshold as the value of Pmin varies with the signal content of the spectrogram, ensuring that sufficient faint pixels are included to allow calculation of the grayscale gradients. Finally, we performed a morphological erosion operation on the mask image using the same structuring element as the previous opening, to return it to its original configuration. Further analysis only made use of those pixels indicated as “interesting” by the mask image.
Ridge extraction
Intuitively, a “ridge” is defined as a watershed between two basins of attraction, but in an intensity image, it can be defined more rigorously as a series of points that comprise local maxima in the direction of the main principal curvature (Lindeberg, 1998). To find these points, we generate first and second derivative maps of the spectral image, using first and second order derivatives of a Gaussian distribution. These maps, ∂T, ∂F, ∂TT, ∂FF, and ∂TF (where T indicates the time axis and F the frequency axis) are constructed using smoothing kernels that reflect the scale of the features we are searching for. Preliminary investigation showed that a smoothing kernel with a standard deviation of one pixel was sufficient for the extraction of whistles because these tend to be rather narrowband signals.
The gradient of the spectrogram intensity shows the direction in which the intensity values increase most quickly. This is not a sufficient condition to define a ridge. On either side of the point, the intensity must be falling (Fig. 1). To determine whether or not points are atop a ridge, one must examine the rate of change. For each pixel falling in an “interesting” region, we calculate the largest magnitude eigenvector E of the Hessian matrix of second derivatives H,
| (2) |
where t and f are the indices of the time and frequency pixels, respectively. The vector E points in the direction of greatest curvature, and the eigenvector's dot product with the gradient is proportional to the cosine between the intensity gradient and the curvature. If the dot product is computed for two points on either side of a ridge, the direction (sign) of the angle changes, and hence at the ridge, the angle will be equal to zero,
| (3) |
This is equivalent to saying that a ridge point occurs for any pixel (t,f) where the major eigenvector Et,f of the Hessian matrix Ht,f is perpendicular to the intensity gradient vector.
Figure 1.
(Color online) Relationship between gradient vectors and a ridge. Notice that the direction of the gradient vectors (arrows) relative to the ridge (heavy line) reverses on either side of the ridge. We use this property to identify the ridge location. Axes are arbitrary, and could represent vertical/horizontal pixels, time/frequency, latitude/longitude, etc.
Calculating the dot product between Et,f and (∂T ∂F)t,f for every pixel in the interest mask, we then track the zero-crossing of this functional by searching the 3 × 3 pixel neighborhood (t ± 1, f ± 1) for a sign change, and interpolating to find the zero-crossing (t*,f*). In the case of multiple zero crossings, the pixel closest to the current pixel is chosen. Tracking ceases when no further zero-crossings exist or when all the zero-crossing pixels in the neighborhood have been flagged as already processed. Tracking then re-commences from the next pixel in the interest mask until all interesting pixels have been exhausted.
Ridge joining
Noise of various forms (ambient, thermal/instrument, aliasing) can cause ridges to become discontinuous in the spectrogram image. The next stage of processing selectively joins ridge tracks where appropriate to form longer continuous ridges. Various algorithms are available for this process. However, to simplify the comparison of our image processing approach with existing techniques, we implemented ridge joining using a heuristic based on that employed in the silbido software, full details of which are given in Roch et al. (2011). Briefly, each ridge is compared with a set of candidate ridges for joining, i.e., those that begin within a time-frequency window of the end of the primary ridge. We used a window of 16 ms and 15 Hz, based on preliminary work with similar data. Each candidate ridge is combined pairwise with the primary ridge and fitted to a family of polynomials of order 1–5. To avoid overfitting, polynomials of order n are rejected for data sets of N points, when N < 3n. If multiple polynomial fits meet this criterion, the one with the lowest residual error is chosen, and the ridges combined to a single ridge. Finally, the ridges are smoothed using two-dimensional Kalman filtering (Mallawaarachchi, 2008a).
METHODS
We compared the existing silbido algorithm to IPRiT using both a synthesized data set and a real-world data set of dolphin signature whistles. We used a synthesized data set as this allowed us to measure the accuracy of the detection precisely because the true frequency profile was known a priori. The real-world data set allowed us to test the performance of the algorithms under more realistic conditions, using a proxy measure of accuracy because the true frequency profile is not known.
Both the silbido algorithm and IPRiT use a form of thresholding to define the region of the spectrogram to be processed. For IPRiT, we varied the interest threshold Q, as described in the preceding text, between 0 and 2. For the silbido algorithm, we varied the “whistle_dB” parameter, which selects peaks based on a signal to noise ratio threshold, between 5 and 9. Although the thresholds for the two algorithms are not directly comparable, the ranges examined represented in both cases very low to very high thresholds. The levels were selected experimentally to show performance at conservative and aggressive detection levels for both algorithms. For both algorithms, we also excluded detections less than 0.1 s in length. Silbido usually defaults to 0.15 s, but this was adjusted to keep both algorithms comparable and to highlight that IPrIT is less likely to string together extraneous peaks on short time scales.
Synthetic data set
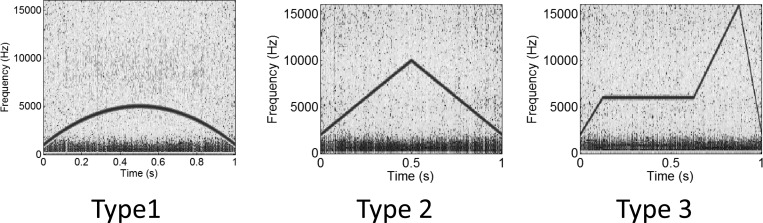
We constructed a synthesized set of whistles having various frequency profiles (Fig. 2): Inverted parabolic, triangular, and complex. Each whistle was 1 s in length and varied in frequency between 2 and 16 kHz. We added noise to the synthesized signals in varying intensities. Noise in underwater recordings is rarely Gaussian white noise (Urick, 1983), and so we introduced into our synthesized whistles noise taken from real-world recordings. We took the first 10 s of silence (i.e., ambient noise without cetacean whistles) from file CVJ.wav, one of the towed-array evaluation files for the 2011 Detection, Classification, and Localization of Marine Mammals Using Passive Acoustic Monitoring workshop from the MobySound database (Mellinger and Clark, 2006) and divided it into ten 1-s samples, which we could add to our synthesized whistles to produce 10 replicates of noisy signal. We repeated this using different noise intensity, by multiplying the noise signal by a factor of 1–100 before addition. This gave us 10 replicates at each noise intensity, for each of three signal types.
Figure 2.
(Color online) Example spectrograms of the three synthetic whistle types, with added noise from real-world recordings.
We then measured ridge extraction fidelity by comparing the contours extracted by each algorithm to the known frequency profile of the synthesized whistle. We defined the following performance metrics: Coverage, false alarm rate, and distance. Coverage is the proportion of the true frequency profile for which a detected ridge is within 4 pixels or 438 Hz. False alarm rate is the proportion of detected ridges that are not within 4 pixels or 438 Hz of the true frequency profile. Distance is the root mean square distance of those detected ridges that are within 4 pixels or 438 Hz of the true frequency profile.
Real-world data set
We used a set of 400 bottlenose dolphin (Tursiops trunactus) signature whistles, 20 recordings of each of 20 animals, as described in Sayigh et al. (2007). These recordings were made during capture-release events in the Sarasota Bay area of Florida, using suction-cup hydrophones, and were between 1.5 and 3.0 s long (mean 2.1 s). Rather than compare the results of the algorithms directly to a “known” true whistle profile, we measured the accuracy of the algorithms indirectly, via their ability to predict biologically relevant findings. Because the frequency modulation in dolphin signature whistles is known to encode individual identity (Sayigh et al., 2007), we used a test of identity reconstruction to quantify the ridge extraction fidelity. An algorithm that accurately extracted the ridges in the signature whistle would be expected to produce a good clustering of whistles into separate groups representing the individual animals that produced them (Kershenbaum et al., 2013). This way, we test extraction fidelity rather than detection. We applied both algorithms to this data set and extracted the longest ridge. We then measured the dissimilarity between each of these 400 ridges (one for each recording) using dynamic time warping (Buck and Tyack, 1993) to produce a 400 × 400 distance matrix. Dynamic time warping measures the minimum difference between two time series when the time axis is allowed to vary freely between samples, and this technique gives an improved measure of similarity especially when salient features may vary in phase or duration. We then used a k-means algorithm to group these whistles into 20 clusters according to similarity. The composition of each cluster could then be compared to the true clustering of dolphin identity. We used normalized mutual information (NMI) (Zhong and Ghosh, 2005) as a measure of cluster purity; producing values near zero for random assignment to clusters and values of unity when each cluster consists of a single individual's signature whistles. Normalized mutual information is defined as
| (4) |
where nc is the number of whistles from dolphin c, nk is the number of whistles in cluster k, nk,c is the number of whistles from dolphin c in cluster k, and N is the total number of whistles. In each case, we compared the algorithm results to a null distribution generated by randomly assigning the 400 whistles to the 20 individual dolphins. We bootstrapped this analysis, excluding a random 20% of whistles on each of 100 repetitions, to generate an error estimate for NMI.
RESULTS
Synthetic data set
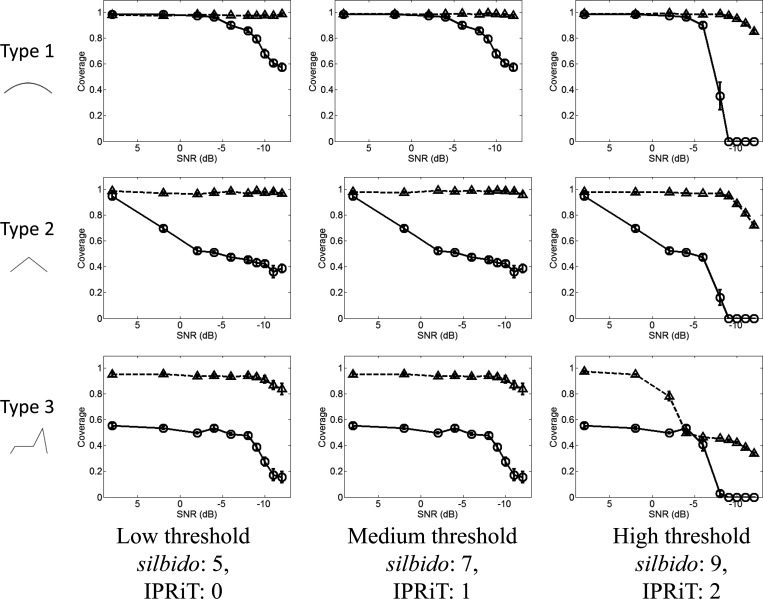
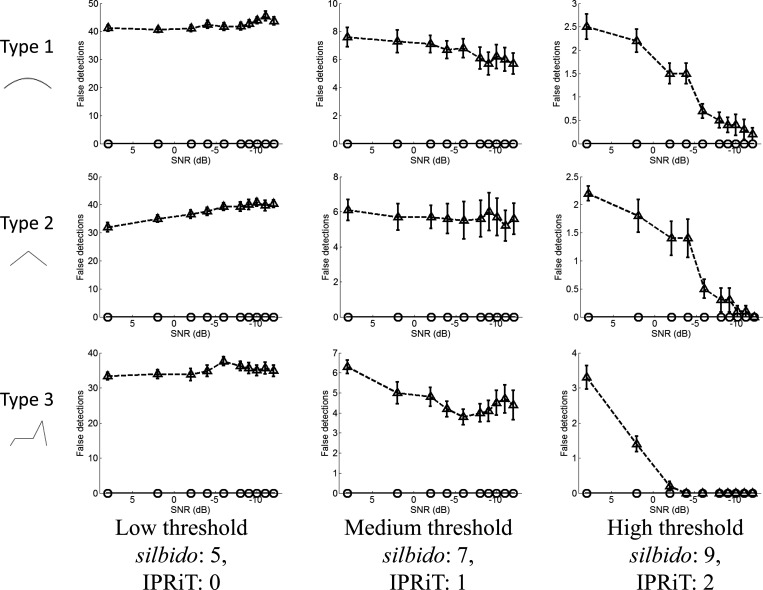
Although silbido gave much better detection than IPRiT for all whistle types, the accuracy of silbido was far lower. Even at high noise levels, silbido maintained detection rates > 50% even at moderate threshold levels. In contrast, in IPRiT, coverage fell sharply at moderate noise levels for all threshold values (Fig. 3). However, silbido is known to produce short spurious detections and the high detection levels of silbido come at the cost of extremely high false alarm rates (Fig. 4). False detections for silbido averaged 10–60 per spectrogram and were high for all noise and threshold levels, although at high thresholds, the number of false detections was lower. The number of false detections in IPRiT was extremely low under all conditions. This is illustrated in Fig. 5, which shows the spectrogram of an example synthetic whistle with added noise and the silbido and IPRiT detections.
Figure 3.
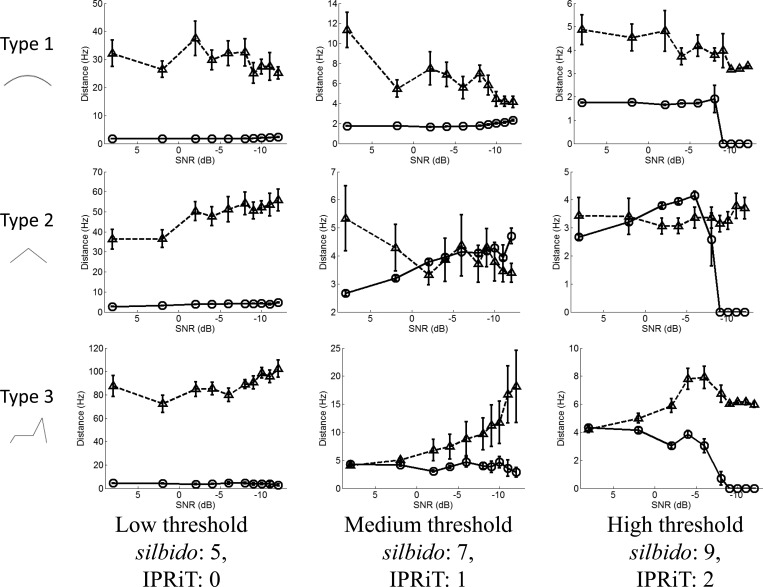
Coverage (y axis) expressed as a proportion detected of the true signal, for varying noise levels (x axis). Rows indicate whistle types 1–3, and columns indicate increasing threshold left to right. Silbido results are indicated by the triangles and broken lines, IPRiT by the circles and solid lines. Error bars indicate standard error.
Figure 4.
Number of false detections per spectrogram (y axis), for varying noise levels (x axis). Rows indicate whistle types 1–3, and columns indicate increasing threshold left to right. silbido results are indicated by the triangles and broken lines, IPRiT by the circles and solid lines. Error bars indicate standard error.
Figure 5.
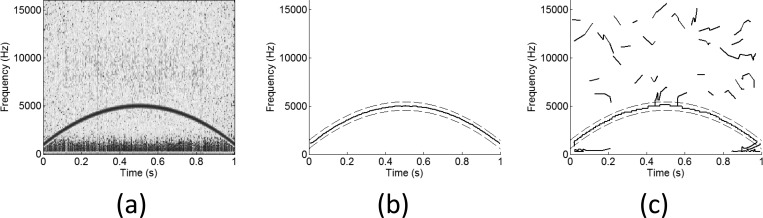
(Color online) Example detections for silbido and IPRiT, using low thresholds. (a) A sample synthesized whistle with low noise. (b) The detections of IPRiT and (c) the detections of silbido. In (b) and (c), the solid line shows the true signal, and the dashed lines indicate the threshold for “true” detection. Notice that both silbido and IPRiT detect the true signal well, but silbido also makes a large number of short false detections.
The fidelity of IPRiT was superior to the silbido algorithm even when excluding false detections. Figure 6 shows the mean distance from the true signal of those detections that were within 438 Hz (approximately four frequency bins) of the true signal. Silbido only gave higher fidelity than IPRiT for the simplest whistle (type 2) and at very low noise levels. At higher thresholds, the fidelity of silbido worsened rapidly as the noise level rose. In the most complex whistle (type 3), the fidelity of IPRiT was significantly better than that of silbido for all parameters.
Figure 6.
Fidelity error (y axis) expressed as the mean distance in hertz of near detections from the true signal for varying noise levels (x axis). Rows indicate whistle types 1–3, and columns indicate increasing threshold left to right. Silbido results are indicated by the triangles and broken lines, IPRiT by the circles and solid lines. Error bars indicate standard error.
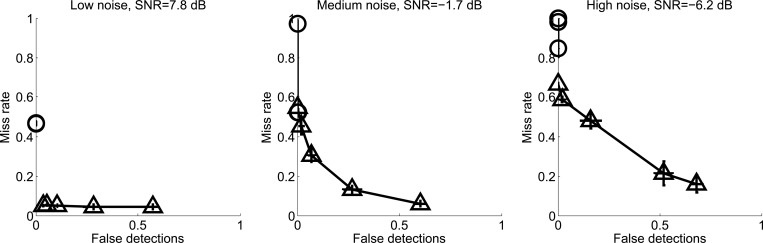
The relative performance of the two algorithms with respect to detection misses (false negative) and false detection (false positive) is best illustrated with “detection error tradeoff” (DET) curves similar to those proposed by Martin et al. (1997) in which the two metrics are plotted against each other for varying threshold. Figure 7 shows DET curves for three noise levels, low, medium, and high. It can be seen that although silbido continues to provide high detection at noise levels when IPRiT detection falls near zero, silbido never results in a level of false detections approaching that of IPRiT for any threshold level.
Figure 7.
Detection error tradeoff curves for synthetic whistles with injected real-world noise, showing false detections against misses, for varying threshold levels. Left panel shows results for low noise (scale factor of an in situ ocean noise source), middle panel for moderate noise, right panel for high noise. Silbido is indicated by the triangles and IPRiT by the circles. Error bars represent standard error.
Real-world data set
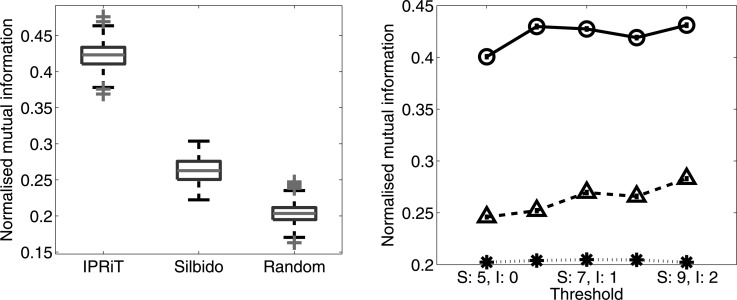
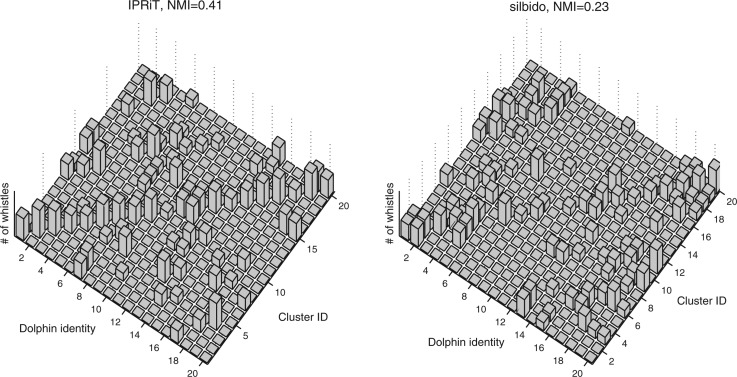
IPRiT gave significantly better results than silbido in clustering the signature whistles according to the dolphin that produced them. For IPRiT, the overall mean normalized mutual information (NMI) was 0.422 ± 0.001 (SE) compared to 0.263 ± 0.001 for silbido, and 0.204 ± 0.001 for the randomized control [Fig. 8a]. The better performance of IPRiT was consistent across all threshold levels [Fig. 8b]. Figure 9 gives a qualitative indication of the success in grouping together ridges from the same individual, by presenting a two-dimensional histogram of true identity vs cluster assignment. NMI measures the unevenness of this two-dimensional histogram, and in the case of perfect clustering, each cluster would contain the whistles of a single dolphin only.
Figure 8.
(Color online) Results of using the two algorithms to cluster dolphin signature whistles. Clustering success is measured as normalized mutual information (y axis), which indicates how well signature whistles analyzed by the two algorithms were assigned to the dolphins that produced them with a value of one indicating perfect clustering. (a) Box plots for the normalized mutual information for the two algorithms and the random control at the lowest threshold. (b) Variation in normalized mutual information with algorithm threshold (silbido varying from 5–9 and IPRiT from 0–2). Silbido is shown as triangles with a broken line, IPRiT as circles with a solid line, and the random control as stars with a dotted line.
Figure 9.
Results of the clustering algorithm, presented as a two-dimensional histogram. The two horizontal axes indicate the true dolphin identity (1–20), vs the cluster number (1–20), and the height of each bar indicates the number of whistles from a particular dolphin assigned to a particular cluster (log scale). If the clustering was perfectly successful, all the whistles would be placed along the diagonal of the matrix. This figure gives a qualitative indication that the clustering of the IPRiT analysis in (a), gives more concentration of the bars along the diagonal than the clustering of the silbido analysis in panel (b). Normalized mutual information (shown above each plot) is a quantification of this distinction.
DISCUSSION
While the silbido algorithm gave good results for detection in the artificial data set, and IPRiT failed to detect whistles at high noise levels, the number of false detections by silbido was very high. The low correlation between noise and false alarm rate is probably due to the detection of a strong impulsive component even at low noise levels, and this may or may not be a problem for detection applications, where further filtering steps may reduce the number of false alarms to a level suitable for human analysis. However, for applications requiring the characterization of whistle shapes, false detections are a serious problem. The poor detection performance of IPRiT is likely not relevant in those communication research applications where recordings are high quality with low noise, such as those taken from suction-cup hydrophones or in an aquarium environment. The overall fidelity of IPRiT was far higher than that of silbido and was maintained at higher noise levels, as long as the algorithm succeeded in detecting the whistle. Examination of the DET curves (Fig. 7) indicates that IPRiT is superior to silbido for applications where accuracy is important. Visual inspection of the ridges extracted by the two algorithms (e.g., Fig. 5) would seem to indicate that the performance of silbido suffers where it joins a number of shorter extractions into a single curve, whereas IPRiT appears to detect longer segments of whistle ridges. This is characteristic of the greater stability of the shape-based approach (IPRiT) compared to the peak-joining approach (silbido).
This is illustrated particularly in the results of the real-world data set, which tests the overall accuracy of the algorithms by applying them to a behavioral test. The results of each algorithm were passed to a clustering process, which grouped the whistles into natural clusters. IPRiT was fairly accurate in allowing the whistles to be clustered into correct groupings according to the dolphin that produced them, whereas the silbido algorithm did not produce results much better than chance (Fig. 8). This result is despite the fact that we selected only the longest ridge from each recording, so that the large number of false detections by silbido cannot by itself explain the poorer clustering result. This strongly indicates that IPRiT is preferable for the detailed analysis of vocalization structure.
Numerous algorithms have been proposed for the automatic analysis of cetacean whistles, and many of them have been used with notable success for the assessment of populations (Kandia and Stylianou, 2006; Marques et al., 2009), and species identification (Oswald et al., 2007; Roch et al., 2007). However, the performance of automated systems is in general limited by a large number of false detections. There is a natural tendency for researchers to develop algorithms based on the analysis of Fourier transformed recordings, i.e., spectrograms, because this analysis presents the frequency modulation information in a very accessible form (visually). This allows developers to use cycles of intuitive trial and error, examining where algorithms pick out useful features and where they fail to perform correctly. However, it is not clear that the spectrographic representation is the optimum one for signal detection. Possibly because of this, most detection algorithms still fall short of the performance required for routine usage. Some researchers have moved away from the spectrographic paradigm for detection (e.g., Ioana et al., 2010; Johansson and White, 2011; Ou et al., 2012), but spectrographic representation undoubtedly provides a parsimonious encoding of the detailed frequency variation. Therefore when the goal is the accurate characterization of the frequency modulation of tonal signals rather than signal detection, there is a clear benefit to extract that information from the Fourier transformed signal. It has been shown (Sayigh et al., 2007) that humans are very accurate in identifying similarities between spectrograms “by eye” and that the results of such manual comparisons are biologically relevant, i.e., humans can correctly assign whistles to the originating individual dolphin. Concluding from this that the visual representation encodes important whistle information reliably and accessibly, we have attempted to access that information through the paradigm of image processing, and our results show that such an algorithm does represent the detailed whistle shape accurately.
We intentionally used recordings of dolphin signature whistles taken during capture-release events and with high signal to noise ratio, rather than open-sea recordings of free-ranging dolphin vocalizations. This is because our goal was to optimize fidelity rather than detection. Our results indicate that the image processing-based approach will not be superior to existing techniques for the detection of calls within large and noisy databases, where robustness and sensitivity are more important than fidelity. Low signal to noise ratio is likely to harm image processing-based detection more than peak finding-based detection (such as silbido), and this is reflected in our results. Similarly, our use of synthesized whistles, while unrealistic for real-world applications, allowed us to provide clear accuracy measures using well-defined truth comparison. Our eventual goal is to use such image processing algorithms to provide statistical descriptions of the different types of vocalizations, or putative syllables, and in many cases, these are recorded under more controlled environments, which more closely approximate the synthetic sounds that we used.
We have made our algorithm publicly available (http://sourceforge.net/projects/iprit/) under the Creative Commons Attribution-ShareAlike (CC BY-SA) license, to allow researchers to assess its utility in their own work. We believe that researchers in the field of animal vocal communication should be aware of the utility of the image processing paradigm, which appears to be highly useful for the accurate automated processing of tonal vocalizations. We are currently applying this technique to applications not just in marine biology but also in the characterization of bird calls and those of terrestrial mammals. We believe that in applications where a visual inspection of a spectrographic representation of a recording provides the best interpretation of the problem at hand, an image processing-based approach to automatic analysis is likely to lead to better results simply because it replicates to an extent the process occurring in the researcher's eye and brain.
ACKNOWLEDGMENTS
We thank Sagi Katz for his suggestions on the implementation of the ridge tracker. This work was supported by the National Institute for Mathematical and Biological Synthesis, an Institute sponsored by the National Science Foundation, the U.S. Department of Homeland Security, and the U.S. Department of Agriculture through NSF Award No. EF-0832858 with additional support from The University of Tennessee, Knoxville. We would like to thank Laela Sayigh, Vincent Janik, Peter Tyack, Carter Esch, Randy Wells, and the Sarasota Dolphin Research Program for help with data collection. We also thank Michael Weise at the Office of Naval Research for support through ONR Award No. N0001411IP20086.
References
- Bohn, K. M., Schmidt-French, B., Ma, S. T., and Pollak, G. D. (2008). “ Syllable acoustics, temporal patterns, and call composition vary with behavioral context in Mexican free-tailed bats,” J. Acoust. Soc. Am. 3, 1838–1848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buck, J. R., and Tyack, P. L. (1993). “ A quantitative measure of similarity for Tursiops truncatus signature whistles,” J. Acoust. Soc. Am. 5, 2497–2506. [DOI] [PubMed] [Google Scholar]
- Canny, J. (1986). “ A computational approach to edge detection,” IEEE Trans. Pattern Anal. Mach. Intell. 6, 679–698. [PubMed] [Google Scholar]
- Davies, E. R. (2004). Machine Vision: Theory, Algorithms, Practicalities, 3rd ed. (Morgan Kaufmann, San Francisco: ), Chap. 4, pp. 102–129. [Google Scholar]
- Dougherty, E. R., and Lotufo, R. A. (2003). Hands-on Morphological Image Processing (SPIE Publications, Bellingham, WA: ). Chap. 2, pp. 25–44. [Google Scholar]
- Esch, H. C., Sayigh, L. S., and Wells, R. S. (2009). “ Quantifying parameters of bottlenose dolphin signature whistles,” Mar. Mamm. Sci. 25, 976–986. 10.1111/j.1748-7692.2009.00289.x [DOI] [Google Scholar]
- Gillespie, D. (2004). “ Detection and classification of right whale calls using an edge detector operating on a smoothed spectrogram,” Can. Acoust. 32, 39–47. [Google Scholar]
- Henderson, E. E., Hildebrand, J. A., and Smith, M. H. (2011). “ Classification of behavior using vocalizations of Pacific white-sided dolphins (Lagenorhynchus obliquidens),” J. Acoust. Soc. Am. 130, 557–567. 10.1121/1.3592213 [DOI] [PubMed] [Google Scholar]
- Ioana, C., Gervaise, C., Stéphan, Y., and Mars, J. I. (2010). “ Analysis of underwater mammal vocalizations using time–frequency-phase tracker,” Appl. Acoust. 11, 1070–1080. [Google Scholar]
- Janik, V. M., Sayigh, L., and Wells, R. (2006). “ Signature whistle shape conveys identity information to bottlenose dolphins,” Proc. Natl. Acad. Sci. U.S.A. 21, 8293–8297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson, A. T., and White, P. R. (2011). “ An adaptive filter-based method for robust, automatic detection and frequency estimation of whistles,” J. Acoust. Soc. Am. 130, 893–903. 10.1121/1.3609117 [DOI] [PubMed] [Google Scholar]
- Johnson, M. P., Aguilar De Soto, N., and Madsen, P. T. (2009). “ Studying the behaviour and sensory ecology of marine mammals using acoustic recording tags: A review,” Mar. Ecol. 395, 55–73. [Google Scholar]
- Kandia, V., and Stylianou, Y. (2006). “ Detection of sperm whale clicks based on the Teager–Kaiser energy operator,” Appl. Acoust. 11, 1144–1163. [Google Scholar]
- Kershenbaum, A., Ilany, A., Blaustein, L., and Geffen, E. (2012). “ Syntactic structure and geographical dialects in the songs of male rock hyraxes,” Proc. R. Soc. London, Ser. B. 1740, 2974–2981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kershenbaum, A., Sayigh, L. S., and Janik, V. M. (2013). “ The encoding of individual identity in dolphin signature whistles: How much information is needed?,” PLoS One 8(10): e77671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kroodsma, D. E. (1977). “ A re-evaluation of song development in the song sparrow,” Anim. Behav. 25, 390–399. 10.1016/0003-3472(77)90013-6 [DOI] [PubMed] [Google Scholar]
- Lampert, T. A., and O'Keefe, S. E. M. (2013). “ On the detection of tracks in spectrogram images,” Pattern Recogn. 5, 1396–1408. [Google Scholar]
- Lindeberg, T. (1998). “ Edge detection and ridge detection with automatic scale selection,” Int. J. Comput. Vision 2, 117–156. [Google Scholar]
- Madhusudhana, S. K., Roch, M. A., Oleson, E. M., Soldevilla, M. S., and Hildebrand, J. A. (2009). “ Blue whale B and D call classification using a frequency domain based robust contour extractor,” in Proceedings of OCEANS 2009 - Europe, pp. 1–7.
- Mallawaarachchi, A. (2008a). “ Spectrogram denoising for the automated extraction of dolphin whistle contours,” Masters of Engineering thesis, National University of Singapore, Chap. 4, pp. 42–48. [Google Scholar]
- Mallawaarachchi, A. (2008b). “ Spectrogram denoising for the automated extraction of dolphin whistle contours,” Masters of Engineering thesis, National University of Singapore, Chap. 3, pp. 30–33. [Google Scholar]
- Marler, P. (2004). “ Science and birdsong: The good old days,” in Nature's Music: The Science of Birdsong (Elsevier, Dordrecht: ), Chap. 1, pp. 1–38. [Google Scholar]
- Marques, T. A., Thomas, L., Ward, J., DiMarzio, N., and Tyack, P. L. (2009). “ Estimating cetacean population density using fixed passive acoustic sensors: An example with Blainville's beaked whales,” J. Acoust. Soc. Am. 125, 1982–1994. 10.1121/1.3089590 [DOI] [PubMed] [Google Scholar]
- Martin, A., Doddington, G., Kamm, T., Ordowski, M., and Przybocki, M. (1997). The DET Curve in Assessment of Detection Task Performance (National Institute of Standards and Technology, Gaithersburg, MD: ), 5 pp. [Google Scholar]
- Mellinger, D. K., and Clark, C. W. (2000). “ Recognizing transient low-frequency whale sounds by spectrogram correlation,” J. Acoust. Soc. Am. 107, 3518–3529. 10.1121/1.429434 [DOI] [PubMed] [Google Scholar]
- Mellinger, D. K., and Clark, C. W. (2006). “ MobySound: A reference archive for studying automatic recognition of marine mammal sounds,” Appl. Acoust. 11, 1226–1242. [Google Scholar]
- Mellinger, D. K., Martin, S. W., Morrissey, R. P., Thomas, L., and Yosco, J. J. (2011). “ A method for detecting whistles, moans, and other frequency contour sounds,” J. Acoust. Soc. Am. 129, 4055–4061. 10.1121/1.3531926 [DOI] [PubMed] [Google Scholar]
- Oswald, J. N., Rankin, S., Barlow, J., and Lammers, M. O. (2007). “ A tool for real-time acoustic species identification of delphinid whistles,” J. Acoust. Soc. Am. 122, 587–595. 10.1121/1.2743157 [DOI] [PubMed] [Google Scholar]
- Ou, H., Au, W. W. L., and Oswald, J. N. (2012). “ A non-spectrogram-correlation method of automatically detecting minke whale boings,” J. Acoust. Soc. Am. 132, EL317–EL322. [DOI] [PubMed] [Google Scholar]
- Roch, M. A., Brandes, T. S., Patel, B., Barkley, Y., Baumann-Pickering, S., and Soldevilla, M. S. (2011). “ Automated extraction of odontocete whistle contours,” J. Acoust. Soc. Am. 130, 2212–2223. 10.1121/1.3624821 [DOI] [PubMed] [Google Scholar]
- Roch, M. A., Soldevilla, M. S., Burtenshaw, J. C., Henderson, E. E., and Hildebrand, J. A. (2007). “ Gaussian mixture model classification of odontocetes in the Southern California Bight and the Gulf of California,” J. Acoust. Soc. Am. 121, 1737–1748. 10.1121/1.2400663 [DOI] [PubMed] [Google Scholar]
- Sayigh, L. S., Esch, H. C., Wells, R. S., and Janik, V. M. (2007). “ Facts about signature whistles of bottlenose dolphins, Tursiops truncatus,” Anim. Behav. 6, 1631–1642. [Google Scholar]
- Sayigh, L., Quick, N., Hastie, G., and Tyack, P. (2012). “ Repeated call types in short-finned pilot whales, Globicephala macrorhynchus,” Mar. Mamm. Sci. 29, 1748–7692. [Google Scholar]
- Shapiro, A. D., Tyack, P. L., and Seneff, S. (2011). “ Comparing call-based versus subunit-based methods for categorizing Norwegian killer whale, Orcinus orca, vocalizations,” Anim. Behav. 81, 377–386. 10.1016/j.anbehav.2010.09.020 [DOI] [Google Scholar]
- Slater, P., and Ince, S. (1979). “ Cultural evolution in chaffinch song,” Behaviour 71, 146–166. 10.1163/156853979X00142 [DOI] [Google Scholar]
- Thode, A. (2004). “ Tracking sperm whale (Physeter macrocephalus) dive profiles using a towed passive acoustic array,” J. Acoust. Soc. Am. 116, 245–253. 10.1121/1.1758972 [DOI] [PubMed] [Google Scholar]
- Thode, A. M., Kim, K. H., Blackwell, S. B., Greene, C. R., Jr., Nations, C. S., McDonald, T. L., and Macrander, A. M. (2012). “ Automated detection and localization of bowhead whale sounds in the presence of seismic airgun surveys,” J. Acoust. Soc. Am., 131, 3726. 10.1121/1.3699247 [DOI] [PubMed] [Google Scholar]
- Urick, R. J. (1983). Principles of Underwater Sound, 3rd ed. (McGraw-Hill, New York: ), Chap. 7, pp. 209–211. [Google Scholar]
- Van Valkenburg, M. E. (1993). Reference Data for Engineers: Radio, Electronics,Computer, and Communications, 8th ed. (Newnes, New York: ), pp. 23–29. [Google Scholar]
- White, P. R., and Hadley, M. L. (2008). “ Introduction to particle filters for tracking applications in the passive acoustic monitoring of cetaceans,” Can. Acoust. 36, 146–152. [Google Scholar]
- Zhong, S., and Ghosh, J. (2005). “ Generative model-based document clustering: A comparative study,” Knowledge Inf. Sys. 3, 374–384. [Google Scholar]