Integrating cognitive and peripheral factors in predicting hearing-aid processing effectiveness

Abstract

Individual factors beyond the audiogram, such as age and cognitive abilities, can influence speech intelligibility and speech quality judgments. This paper develops a neural network framework for combining multiple subject factors into a single model that predicts speech intelligibility and quality for a nonlinear hearing-aid processing strategy. The nonlinear processing approach used in the paper is frequency compression, which is intended to improve the audibility of high-frequency speech sounds by shifting them to lower frequency regions where listeners with high-frequency loss have better hearing thresholds. An ensemble averaging approach is used for the neural network to avoid the problems associated with overfitting. Models are developed for two subject groups, one having nearly normal hearing and the other mild-to-moderate sloping losses.

INTRODUCTION

Perceptual models are often used to predict speech intelligibility and speech quality. In general, these models involve a simplified representation of the auditory periphery combined with the extraction of one or more psychoacoustic or signal-processing features. For example, the speech intelligibility index (SII) (ANSI, 1997) is based on the signal-to-noise ratio (SNR) measured in auditory bands, and takes into account auditory masking within each frequency band and upward spread of masking across frequency bands. Other auditory features have also been used as the bases of speech quality indices. These features include the differences in estimated signal excitation patterns (Thiede et al., 2000; Beerends et al., 2002) and the signal cross-correlation measured in auditory bands (Tan et al., 2004). Changes in the signal envelope modulation measured within auditory bands have also been used to predict speech quality (Huber and Kollmeier, 2006), as well as changes in the time-frequency modulation within and across auditory bands (Kates and Arehart, 2010). Hearing loss, when included in a model, is generally specified by the audiogram (ANSI 1997; Kates and Arehart, 2010).

There is growing evidence, however, that the effect of hearing-aid processing may depend on factors beyond the audiogram (Akeroyd, 2008). Experiments involving linear amplification (Humes, 2002), dynamic-range compression (Lunner, 2003; Gatehouse et al., 2006; Rudner et al., 2009; Cox and Xu, 2010), noise suppression (Lunner et al., 2009; Sarampalis et al., 2009; Ng et al., 2013), and frequency compression (Arehart et al., 2013) all indicate that individual differences in cognitive processing can influence processing benefit. Work in dynamic-range compression (Gatehouse et al. 2006), for example, has shown that listeners with poorer cognition performed better with slow-acting compression while listeners with better cognition performed better with fast-acting compression.

Age has also been shown to be a factor in processing effectiveness. The intelligibility results reported by Arehart et al. (2013) for speech processed using frequency compression showed that both age and working memory were significant factors in explaining listener performance. Age may thus encompass changes in cognitive function beyond working memory and changes in peripheral processing beyond those measured by the audiogram. For example, Schvartz et al. (2008) showed that the ability of older listeners to process distorted speech was related to both working memory and to speed of processing. In addition, temporal processing deficits have been suggested as a factor contributing to age-related problems in understanding noisy speech (Pichora-Fuller et al., 2007; Hopkins and Moore, 2011), and older listeners have been shown to have difficulty in processing temporal envelope information (Grose et al., 2009).

This model presented in this paper describes how peripheral and cognitive factors contribute to the understanding of frequency compressed speech. Frequency compression (Aguilera Muñoz et al., 1999; Simpson et al., 2005; Glista et al., 2009; Alexander, 2013) is intended to improve the audibility of high-frequency speech sounds by shifting them to lower frequency regions where listeners with high-frequency loss have better hearing thresholds. However, frequency compression also introduces nonlinear distortion. The processing modifies the signal spectrum, reduces the spacing between harmonics, alters the signal intensity and envelope within auditory bands, and shifts the trajectories of formant transitions.

Given the large changes to the signal caused by frequency compression, it is possible that cognition may affect the ability of a listener to benefit from the processing. One aspect of cognitive processing is working memory (Daneman and Carpenter, 1980), which involves processing and storage functions. It is hypothesized (Wingfield et al., 2005; McCoy et al., 2005; Francis, 2010; Amichetti et al., 2013; Arehart et al., 2013; Ng et al., 2013) that listening to a degraded speech signal requires a greater allocation of verbal working memory to the recovery of the speech information, leaving fewer resources available to extract the linguistic content. Experimental results indicate that there is a significant relationship between working memory and the intelligibility of speech that has been degraded by peripheral hearing loss (Cevera et al., 2009), additive noise (Pichora-Fuller et al., 1995; Lunner, 2003), spectral modification (Schvartz et al., 2008), dynamic-range compression (Lunner and Sundewall-Thorén, 2007; Foo et al., 2007), and frequency compression (Arehart et al., 2013).

Souza et al. (2013) studied the effects of frequency compression on speech intelligibility and quality for older adults with mild to moderately-severe hearing loss and for a control group of similarly aged adults with nearly normal hearing. They found that listeners with the greatest hearing loss showed the most benefit for the processing, but they also found noticeable variability in the results for listeners with similar degrees of hearing loss. Arehart et al. (2013) further studied these data for the hearing-loss group, looking at the interaction of cognitive ability, age, and hearing loss. Arehart et al. (2013) found that working memory was a significant factor in predicting speech intelligibility, accounting for 29% of the variance in the subject intelligibility scores. The cognitive factor of working memory was measured using the Reading Span Test (RST) (Daneman and Carpenter, 1980; Rönnberg et al., 2008). Combining working memory with age and hearing loss accounted for 47.5% of the variability in the intelligibility scores. However, the interaction of RST and frequency compression benefit may occur only for hearing-impaired listeners; Ellis and Munro (2013) found no significant correlation between RST and speech recognition in a frequency-compression study involving normal-hearing listeners.

There is a challenge in extending perceptual models to include cognitive factors. The traditional models are parametric in nature. The Hearing-Aid Speech Quality Index (HASQI) (Kates and Arehart, 2010) is a good example. The auditory model comprises a filter bank followed by dynamic-range compression, the auditory threshold, extraction of the signal envelope in each band, and conversion to a logarithmic amplitude scale. Changes in the envelope modulation and spectrum are then measured and combined using regression equations. The structure of the model is assumed in advance, and the only free parameters are the regression weights used to combine the different numerical outputs. But it is not clear what model structure should be used when combining peripheral with cognitive measures since the interactions between the different factors may well be nonlinear. Stenfelt and Rönnberg (2009), for example, propose using the output of an auditory model as the input to a cognitive model. They acknowledge, however, that some form of feature extraction is needed to link the two stages of their model, but that the details of the feature extraction are not known.

An alternative to using a parametric modeling approach is to use a statistical model. Such a model makes no assumptions about the underlying model structure and can accommodate nonlinear interactions. The modeling approach investigated in this paper is a neural network (Wasserman, 1989; Beale et al., 2012). The neural network comprises an input layer, one or more hidden layers, and an output layer. The input to each neuron in the hidden and output layers is a weighted sum of the outputs from the previous layer, with the output sum undergoing a nonlinear transformation, termed the activation function. The activation function allows the neural network to produce a complex nonlinear relationship between the input data and the subject responses, thus modeling patterns in the data that a simple linear regression would miss. For example, when predicting the preferred linear amplification from the listener audiogram, a neural network (Kates, 1995) was found to produce a more accurate model than the published NAL-R fitting rule (Byrne and Dillon, 1986) derived from the same data. The goal of the study reported in this paper is to build a neural network model that combines multiple subject factors, and to use the model to predict the effect of frequency compression on intelligibility and quality on an individual basis.

The work presented in this paper tests two hypotheses. The first hypothesis is that intelligibility and quality for speech modified using frequency compression will exhibit a relationship between age, cognitive function, and processing effectiveness and that a neural network model can show these effects. The second hypothesis is that a model of processing effectiveness that incorporates age and measures of cognitive performance will be more accurate than a model that is based exclusively on the auditory periphery.

The remainder of the paper begins with a description of the subjects and the peripheral and cognitive measurements. The potential benefit of incorporating cognitive information into intelligibility and quality models is then explored using mutual information. Mutual information (Kates, 2008b) can measure more complex relationships between a pair of variables than is possible using correlation or linear regression, and an explanation of mutual information is provided. A set of models is constructed using neural networks, and the accuracy and limitations of these models in predicting intelligibility and quality is explored. The paper concludes with a discussion of the potential benefits of using the new models to predict the effects of hearing-aid processing.

DATASET

The models developed in this paper are based on perceptual measures from forty older adults. The measures include the intelligibility scores and quality ratings for frequency-compressed speech reported by Souza et al. (2013) and the working memory data reported by Arehart et al. (2013). In addition, the present analysis includes measures of spectral resolution and speech-in-noise perception.

Listeners

A total of 40 adults took part in the experiments, divided into two groups. The high-loss group consisted of 26 individuals with mild-to-moderate high-frequency loss. The mean age of the individuals in the high-loss group was 74.9 yr, with a range of 62–92 yr. The low-loss group comprised 14 individuals with pure-tone thresholds of 35 dB hearing level (HL) or better through 4 kHz; the average loss in the low-loss group was 12 dB through 3 kHz. The mean age of the individuals in the low-loss group was 66.4 yr, with a range of 60–78 yr. Audiograms for both groups are presented in Souza et al. (2013). Stimuli were presented to one ear, with that ear chosen randomly from subject to subject. All listeners had symmetric losses, spoke English as their first or primary language, and passed the mini-mental status exam (MMSE) (Folstein et al., 1975) with a score of 26 or better.

Spectral ripple threshold

The frequency resolution of each subject was determined using a spectral-ripple detection test (Won et al., 2007). The spectral ripple threshold (SRT) test stimulus consisted of a weighted sum of 800 sinusoidal components spanning the frequency range from 100 to 5000 Hz. The amplitudes of the sinusoids were adjusted so that the resultant spectrum reproduced multiple periods of a full-wave rectified sinusoid on a logarithmic frequency scale. The peak-to-valley ratio of the ripples was fixed at 30 dB. The ripple spectra were then filtered through a shaping filter to approximate the long-term spectrum of speech. To compensate for the individual hearing loss, the filtered ripple stimuli were input at 65 dB sound pressure level (SPL) to a digital filter that provided the NAL-R linear frequency response (Byrne and Dillon, 1986). The mean spectral resolution for the high-loss group was 4.24 ripples/oct with a standard deviation of 1.7 ripples/oct. The mean spectral resolution for the low-loss group was 6.03 ripples/oct with a standard deviation of 1.8 ripples/oct. The groups were significantly different (between-group t₃₈ = 25.31, p < 0.005).

Speech in noise

The ability to understand speech in noise was measured using the QuickSIN (Killion et al., 2004). The QuickSIN uses sentences presented binaurally in a background of four-talker babble. The speech level is held constant and the noise level adjusted to vary the signal-to-noise ratio. Better performance on the QuickSIN has been shown to be correlated with better auditory temporal acuity and with higher working memory ability (Parbery-Clark et al., 2011). The stimuli were presented via insert earphones at a presentation level of 70 dB HL. The mean QuickSIN score for the high-loss group was 4.97 dB, with a standard deviation of 3.44 dB. The mean score for the low-loss group was 2.07 dB, with a standard deviation of 1.45 dB. The QuickSIN scores were significantly different across groups (t₃₈ = 2.81, p = 0.008).

Reading span test

The working memory capacity of the subjects was measured using the RST (Daneman and Carpenter, 1980). In the RST, a sequence of sentences was displayed on a computer screen. Each participant was asked to recall in correct serial order either the first or last words of the sentences. A sample sentence is “The train sang a song.” The participant did not know at the start of the test whether the first or last words would be requested. The scores were based on the total proportion of first or last words correctly recalled, whether or not in correct serial order. The scores ranged from 0.17 to 0.71.

Stimuli

The stimuli for the intelligibility tests consisted of low-context IEEE sentences (Rosenthal, 1969) spoken by a female talker. The stimuli for the quality ratings consisted of two sentences (“Two cats played with yarn,” “She needs an umbrella”) spoken by a female talker (Nilsson et al., 2005). Since all of the results reported in this paper are for a female talker there may be limitations in generalizing to male talkers, although previous results for speech quality (Arehart et al., 2010) did not find a significant effect of talker gender. All of the stimuli were digitized at a 44.1 kHz sampling rate and downsampled to 22.05 kHz to approximate the bandwidth typically found in hearing aids (Kates, 2008a). The sentences were input to the hearing-aid simulation at a level of 65 dB SPL, representing conversational speech. In Arehart et al. (2013) and Souza et al. (2013), the sentences were presented in quiet and in babble noise at several signal-to-noise ratios. The study reported in this paper used only the quiet condition to explore the effects of frequency compression without the confound of noise.

Frequency compression

Frequency compression was implemented using sinusoidal modeling (McAulay and Quatieri, 1986). The signal was divided into a low-frequency and a high-frequency band using a complementary pair of recursive digital five-pole Butterworth filters. Sinusoidal modeling was applied to the high-frequency signal, while the low-frequency signal was used without further modification.

The sinusoidal modeling applied to the high-frequency signal used ten sinusoids. A fast Fourier transform (FFT) analysis was performed on the signal in overlapping 6-ms blocks. For each block, the ten FFT bins corresponding to the highest peaks were selected. The amplitude and phase of each selected peak were preserved while the frequencies were reassigned to lower values. The frequency-compressed output was produced by synthesizing ten sinusoids at the shifted frequencies using the original amplitude and phase values (Quatieri and McAulay, 1986; Aguilera Muñoz et al., 1999). The frequency-compressed high-frequency output was then combined with the original low-frequency signal.

The frequency-compression parameters were chosen to represent the range that might be available in wearable hearing aids. Three frequency compression ratios (1.5:1, 2:1, and 3:1) and three frequency compression cutoff frequencies (1, 1.5, and 2 kHz) were used. In addition, a control condition having no frequency compression was included. The control condition comprised the low-pass and high-pass filters used for the signal band separation; the two bands were recombined after filtering but the sinusoidal modeling in the high-frequency band was bypassed. The filtering of the control condition ensured that all signals had the same group delay as a function of frequency. There were thus a total of ten frequency compression conditions (3 compression ratios × 3 cutoff frequencies, plus the control condition). Following frequency compression, the speech signals were amplified for the individual hearing loss using the National Acoustics Laboratories-Revised (NAL-R) linear prescriptive formula (Byrne and Dillon, 1986).

Stimulus presentation and response tasks

The intelligibility scores and quality ratings presented in this paper are based on the data reported by Souza et al. (2013). A brief summary of the experimental methods is presented here. Testing took place in a double-walled sound booth. The stimuli for each subject were generated on a computer and stored in advance of the experiment. The stimulus files were read out through a sound system comprising a digital-to-analog converter (TDT RX6 or RX8), an attenuator (TDT PA5), and a headphone buffer amplifier (TDT HB7). The sentences were presented monaurally to the listeners through Sennheiser HD 25-1 headphones. Responses were collected using a monitor and computer mouse. The stimulus level prior to NAL-R amplification was 65 dB SPL.

Prior to the intelligibility test, the subjects were presented with a set of practice stimuli. After the practice session, the listeners were presented with 10 sentences for each processing condition. Intelligibility scoring was based on keywords correct (5 per sentence for 50 words per condition per listener).

For the quality ratings, the subjects were presented with the pair of quality sentences for all ten processing conditions, in random order. The same pair of sentences was used for all of the quality conditions to avoid any confounding effects of potential differences in intelligibility. Listeners were instructed to rate the overall sound quality using a rating scale which ranged from 0 (poor sound quality) to 10 (excellent sound quality) (International Telecommunication Union, 2003). The rating scale was implemented with a slider bar that registered responses in 0.05 increments.

MUTUAL INFORMATION

Mutual information (Moddemeijer, 1999; Kates, 2008b) gives the degree to which one variable is related to another. The higher the mutual information, the greater the ability of measurements of one variable to accurately predict the other. Mutual information is a more general concept than correlation. A high degree of correlation requires that the two variables have a linear relationship. A non-linear relationship between two variables will always reduce the correlation because the variables can no longer be represented as shifted and scaled versions of one another. Mutual information, however, only requires that knowledge of one waveform be sufficient to reproduce the other waveform. Non-linear operations, such as taking the square root of a variable, do not reduce the mutual information. Thus mutual information can describe nonlinear dependencies between variables that correlation may miss.

The higher the mutual information between a measured listener characteristic and the subject results, the greater the expected benefit of including the signal or subject characteristic in a model of frequency compression effectiveness. The subject data include the audiogram, the SRT, age, the QuickSIN test, and the RST. The audiogram and SRT measure characteristics of the auditory periphery, age may involve both the periphery and cognitive function, and the QuickSIN, and RST emphasize cognitive characteristics. The relative importance of these peripheral and cognitive features can be determined by computing the mutual information between each of these measurements and the subject responses.

Definition

The mutual information I(x,y) between random variables x and y is given by the entropies H(x), H(y), and H(x,y),

$$I(x;y)=H(x)+H(y)-H(x,y).$$ (1)

The entropy measures the uncertainty or randomness of a random variable. The entropy in bits is given by

$$H(x)=-{\displaystyle \sum _{x}P(x)\hspace{0.17em}{\log }_{2}P(x)},$$ (2)

where P(x) is the probability density function for x and the summation is over all observed values of x. A variable that has a wide range, with a large number of possible states and a low probability of being in any one of them, will have a large entropy. Conversely, a variable that never changes will have an entropy of zero.

For Gaussian distributions, the mutual information is related to the covariance (Moddemeijer, 1999). Assume that random variables x and y are distributed according to a bivariate normal distribution, and that both x and y are zero-mean and have unit variance. The correlation between x and y is given by ρ. The mutual information in bits is then given by

$$I\left(x,y\right)=-\frac{1}{2}\hspace{0.17em}{\log }_2\left(1-{\rho }^2\right),$$ (3)

and the variance of the estimated mutual information $\widehat{I}(x,y)$ in bits squared is approximately

$$\text{Var}\left[\widehat{I}(x,y)\right]={\left[{\log }_2(e)\right]}^2\left[\frac{{\rho }^2}{N}\right],$$ (4)

where N is the number of samples and e is Euler's constant. The mutual information is zero for independent variables (ρ = 0) and approaches infinity for variables that are linearly related (ρ = 1). The variance is inversely proportional to the number of samples used for the estimate and proportional to the square of the correlation.

Uncertainty coefficient

The uncertainty coefficient (Press et al., 2007) is analogous to the correlation coefficient for a linear model. To compute the uncertainty coefficient, the mutual information for variables x and y is divided by the entropy of variable x. An alternative is to divide the mutual information by the average of the entropies of x and y. The uncertainty coefficient ranges from 0 to 1. An uncertainty coefficient value of 0 indicates that the variables are independent, while a value of 1 indicates that knowledge of one variable is sufficient to completely predict the value of the other. An uncertainty coefficient of 0.5 would mean that half of the entropy in bits of one variable can be predicted by measurements of the other variable.

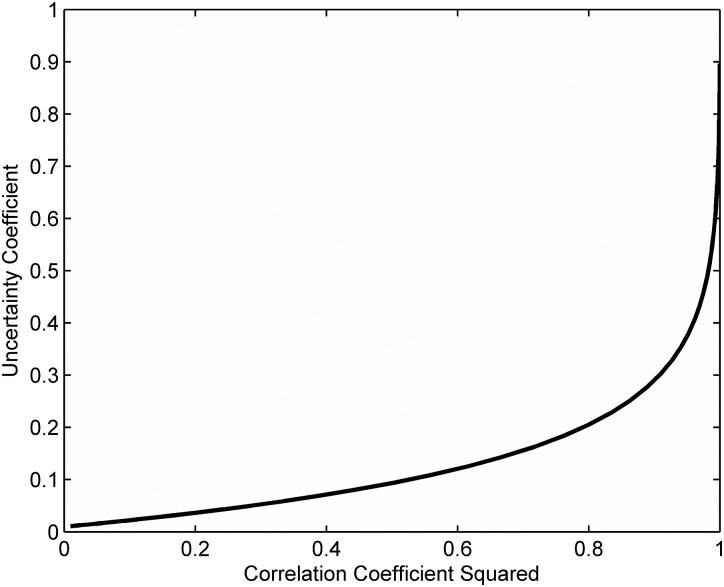
The relationship between the correlation coefficient and the uncertainty coefficient for a pair of Gaussian random variables in plotted in Fig. 1. The plotted values are from a simulation in matlab using 100 000 samples taken from normal distributions for two independent random variables x(n) and q(n). Sequence x(n) was considered to the desired signal and q(n) the interfering noise. Both random variables had zero mean and unit variance. The random variables were combined at different signal-to-noise ratios (SNRs) to give the output y(n), which was then scaled to also have unit variance. The Pearson correlation coefficient r and the uncertainty coefficient between x(n) and y(n) were computed across the range of SNRs. At low values of r² there is an almost linear relationship between the uncertainty coefficient and the correlation coefficient, while at high values of r² the uncertainty coefficient grows much more rapidly.

Figure 1.

Uncertainty coefficient plotted as a function of the square of the Pearson correlation coefficient (r²) for a pair of correlated Gaussian random variables.

Subject scores

The mutual information was computed relating the signal and subject characteristics to the intelligibility scores and quality ratings. The mutual information was calculated using a two-dimensional histogram procedure (Tourassi et al., 2001) with the histogram bin widths selected using Scott's (1979) rule. The calculations were performed separately for the low-loss and high-loss subjects groups and for intelligibility and quality in order to isolate the relative importance of each characteristic for each subject group. The calculations for the low-loss group used 14 subjects × 10 no-noise frequency-compression conditions = 140 data samples, and those for the high-loss group used 26 subjects × 10 no-noise frequency-compression conditions = 260 data samples.

The calculations are summarized in Table TABLE I. in terms of the uncertainty coefficient. The uncertainty coefficient was computed by taking the mutual information in bits between the measured subject or signal characteristic and the subject test results and then dividing by the entropy of the subject results. The average standard deviation of the estimated mutual information (Moddemeijer, 1999), normalized by the entropy of the subject results, is 0.028 for the low-loss group and 0.017 for the high-loss group.

TABLE I.

Uncertainty coefficients between the signal or subject characteristics and the subject scores. The coefficient was computed by taking the mutual information in bits between the subject or signal feature and the subject test results and dividing by the entropy of the subject results. Fcut is the cutoff frequency, FCR is the compression ratio for the frequency compression, ripple is the spectral ripple threshold test (SRT), and RST is the reading span test.

Subject group	Test	Fcut	FCR	Ave. loss	Slope	Ripple	Age	QuickSIN	RST
Low loss	Intel	0.176	0.176	0.091	0.089	0.123	0.135	0.099	0.119
High loss	Intel	0.106	0.065	0.090	0.113	0.102	0.078	0.145	0.093
Low loss	Quality	0.136	0.133	0.078	0.125	0.161	0.142	0.137	0.065
High loss	Quality	0.092	0.121	0.090	0.108	0.071	0.112	0.093	0.070

In Table TABLE I., the frequency compression cutoff frequency (Fcut) and the frequency compression ratio (FCR) describe the stimulus processing. The subject audiograms are summarized in the table by the average loss in dB over the frequencies of 1–4 kHz and slope in dB/oct over 1–4 kHz. It is apparent that both peripheral and cognitive features convey information about the speech intelligibility and quality. The greatest uncertainty coefficient is 0.176 for Fcut and FCR, low-loss intelligibility, while the smallest coefficient is 0.065 for RST, low-loss quality. The processing parameters thus convey the most information about intelligibility for the low-loss group, although SRT, age, and QuickSIN, also make important contributions. For the high-loss group, the QuickSIN conveys the most information about intelligibility, followed by the slope, cutoff frequency, SRT, RST, and average loss. FCR conveys the most information about quality for the high-loss group, followed by age, slope, QuickSIN, cutoff frequency, and average loss.

Looking at the table in terms of the signal characteristics, peripheral loss, and cognitive abilities rather than subject groups, it appears that the processing parameters are relatively more important for the low-loss group than for the high-loss group. The SRT also appears to convey more relative information for the low-loss group than for the high-loss group. The RST appears to convey more information about intelligibility than for quality. Thus the relative importance of the signal, peripheral, and cognitive characteristics varies with the subject group and task.

Relationships among characteristics

In addition to determining the relationship of the signal and subject characteristics to the intelligibility scores and quality ratings, mutual information can also be used to determine the dependency of each characteristic upon the others. The uncertainty coefficient between each pair of features was computed by taking the mutual information in bits between the two features and then dividing by the average of their entropies. The uncertainty coefficients can be interpreted much like correlation coefficients, but are more general since they reflect any functional dependency and not just a linear relationship.

The uncertainty coefficient matrix for the low-loss group is presented in Table TABLE II.. The diagonal elements are all ones, as would be the case for a correlation matrix. The smallest off-diagonal entry is 0.403 which relates age to the RST, and the largest entry is 0.678 which relates age to the QuickSIN. Thus knowing the subject's age is less useful in predicting the RST than in predicting the QuickSIN. Most of the uncertainty coefficients are about 0.5, which indicates a moderate amount of interdependence and which suggests that adding additional variables to the intelligibility and quality models for the low-loss group would not be expected to improve the prediction accuracy.

TABLE II.

Uncertainty coefficient matrix for the signal or subject characteristics for the low-loss group. Each coefficient was computed by taking the mutual information in bits between each pair of features and dividing by the average of their entropies.

	Ave. loss	Slope	Ripple	Age	QuickSIN	RST
Ave. loss	1.000	0.447	0.471	0.438	0.580	0.521
Slope	0.447	1.000	0.483	0.632	0.586	0.471
Ripple	0.471	0.483	1.000	0.474	0.465	0.555
Age	0.438	0.632	0.474	1.000	0.678	0.403
QuickSIN	0.580	0.586	0.465	0.678	1.000	0.514
RST	0.521	0.471	0.555	0.403	0.514	1.000

The uncertainty coefficient matrix for the high-loss group is presented in Table TABLE III.. The smallest off-diagonal entry is 0.240 which relates the RST to the average loss, and the largest entry is 0.489 which relates the audiogram slope to the spectral ripple detection. The uncertainty coefficient between age and RST is 0.315 for the high-loss group, which is lower than the 0.403 for the low-loss group. Overall, the entries for the high-loss group are uniformly lower than for the low-loss group, which indicates more independence between the measured quantities. In particular, the entries in the columns for age and RST are smaller in Table TABLE III. than in Table TABLE II., which suggests that these features would add more information to the intelligibility and quality models for the high-loss group than they would add to the models for the low-loss group.

TABLE III.

Uncertainty coefficient matrix for the signal or subject characteristics for the high-loss group. Each coefficient was computed by taking the mutual information in bits between each pair of features and dividing by the average of their entropies.

	Ave. Loss	Slope	Ripple	Age	QuickSIN	RST
Ave. Loss	1.000	0.329	0.356	0.417	0.343	0.240
Slope	0.329	1.000	0.489	0.421	0.416	0.454
Ripple	0.356	0.489	1.000	0.284	0.404	0.378
Age	0.417	0.421	0.284	1.000	0.361	0.315
QuickSIN	0.343	0.416	0.404	0.361	1.000	0.397
RST	0.240	0.454	0.378	0.315	0.397	1.000

NEURAL NETWORK MODEL

The results from the mutual information analysis suggest that an accurate model of the effects of frequency compression should include cognitive as well as peripheral factors. A neural network (Wasserman, 1989; Beale et al., 2012) was used in the study reported in this paper to build a model to predict the subject intelligibility and quality scores. The neural network model used in this paper comprised an input layer, one hidden layer, and a single neuron as the output layer. The log-sigmoid activation function was used. The number of neurons in the input layer corresponded to the number of input features, and the number of neurons used for the hidden layer increased as the number of input features increased. The neural network was trained to reproduce the either the intelligibility scores or quality ratings. A total of four separate networks were created: low-loss group intelligibility, low-loss group quality, high-loss group intelligibility, and high-loss group quality.

One problem with neural networks is overfitting, in which the network has enough degrees of freedom that it will encode the details of the specific training set rather than generate a general solution (Beale et al., 2012). To avoid the overfitting problem, the ensemble averaging approach of bootstrap aggregation (“Bagging”) was used to average the outputs of several neural networks. A bootstrap is a statistical procedure where multiple partial estimates of a probability distribution are used to estimate the total distribution. Each neural network was trained using a subset comprising 63.2% of the data, randomly selected with replacement (Breiman, 1996); the fraction 0.632 = (1 − e⁻¹) is the statistically optimal bootstrap size (Efron and Tibshirani, 1993). This approach has been shown to give reduced estimator error variance (Kittler, 1998) and provide relative immunity to overfitting (Krogh and Sollich, 1997; Maclin and Opitz, 1997; Domingos, 2000). Any remaining overfitting for a model in the ensemble is in general an advantage and can lead to improved performance of the ensemble taken as a whole (Krogh and Sollich, 1997). Averaging ten neural networks is generally sufficient to get the full benefits in reducing the probability of overfitting (Hansen and Salamon, 1990; Breiman, 1996; Opitz and Maclin, 1999), so ten networks were created and the predictions averaged to produce the final model output.

The simplest neural network model started with the signal features of compression cutoff frequency and frequency compression ratio along with the subject's audiogram. The audiogram was specified as the loss in dB at 0.250, 0.500, 1, 2, 3, 4, 6, and 8 kHz. Five neurons were used in the hidden layer and one neuron in the output layer. Subject characteristics were then added, starting with additional information about the periphery followed by age and then the cognitive information.

The next neural network added the SRT, and the number of neurons in the hidden layer was increased to six. The SRT is an individual bandwidth measure that goes beyond the audiogram but is still peripheral. Subject age was then added. If age was strongly related with working memory, then adding age would provide an improvement in model accuracy but adding the RST score after age would not provide any improvement. Age was followed by the QuickSIN score, which combines peripheral coding of noisy speech with central processing of the signal. The last feature was the RST score, which is purely cognitive since it has no auditory component. As each feature was added, the number of neurons in the hidden layer was increased by 1.

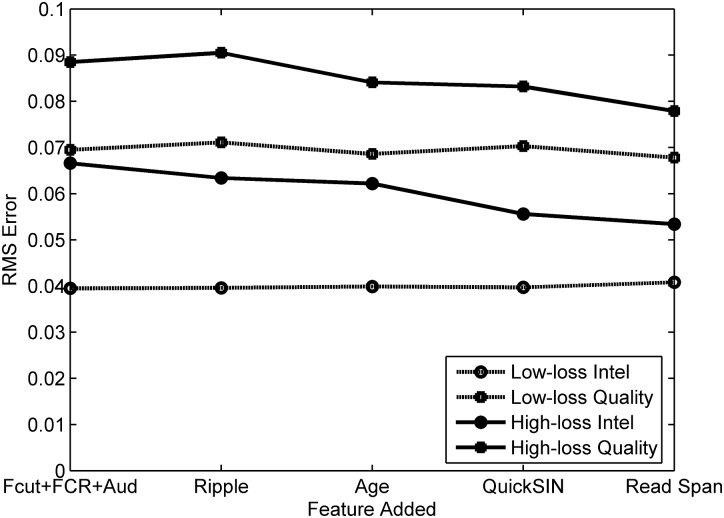
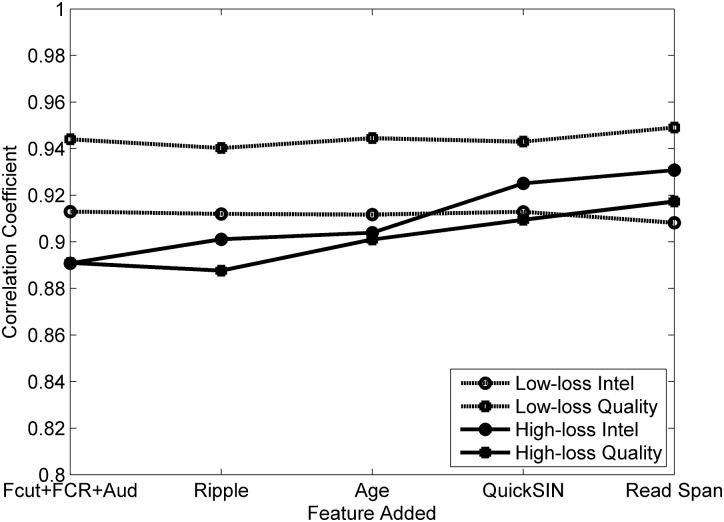
The neural network results are plotted in Figs. 23. The results are averaged across the subjects in each group. The root-mean-squared (RMS) errors between the predicted values and the subject intelligibility or quality results are plotted in Fig. 2. The low-loss group errors are plotted using the open symbols and dashed lines, and the high-loss group errors are plotted using the filled symbols and solid lines. The model results are plotted in Fig. 3 in terms of the Pearson correlation coefficient computed between the predicted values and the subject scores. Improved performance in Fig. 2 is indicated by a reduction in the RMS error, while in Fig. 3 it is shown by an increase in the correlation coefficient.

Figure 2.

RMS error between the neural network prediction and the subject fraction words correct and quality ratings as features are added to the network, computed over the individual subjects and processing conditions.

Figure 3.

Pearson correlation coefficient between the neural network prediction and the subject fraction words correct and quality ratings as features are added to the network, computed over the individual subjects and processing conditions.

The intelligibility predictions for the low-loss group in Fig. 2 show the lowest error, and the performance remains constant even as additional subject data are added. The constant performance indicates that the cognitive measures do not add any useful information about the subjects beyond what is related to the audiogram. A similar effect is observed for the quality predictions for the low-loss group, which also fail to improve as more subject information is incorporated into the neural network. The intelligibility predictions for the high-loss group have a greater error than found for the low-loss group. In contrast to the low-loss group, the error for the intelligibility predictions for the high-loss group decreases as more features are added. The SRT score and subject age each make a small reduction in error when they are added, while including the QuickSIN and RST scores make a more substantial reduction in error. For the high-loss group quality, adding the SRT does not reduce the error, while adding age makes a noticeable improvement. The QuickSIN adds little to what is already conveyed by age, but the RST score reduces the error even further.

In interpreting Figs. 23, it is important to note that the curves show the improvement as a new feature is added. That is, the curves show how much information is added by the feature beyond what the model already has from the previous features. The curves thus show the incremental information added by a feature and not the absolute amount of information that was presented in Table TABLE I.. The incremental increase depends on what has already been incorporated into the model from the previous features. Tables 2, TABLE III. give the uncertainty coefficients between features; adding a feature that has a high uncertainty coefficient with a feature already incorporated into the model would result in only a small incremental improvement in the model accuracy. Changing the order in which the features are added to the model would therefore change the shape of the curve and the incremental improvement associated with each feature, but the ultimate model accuracy for all features included would not change. The order used here was chosen to compare predominantly cognitive to predominantly peripheral effects; the peripheral features were included in the model first and then the cognitive features were added.

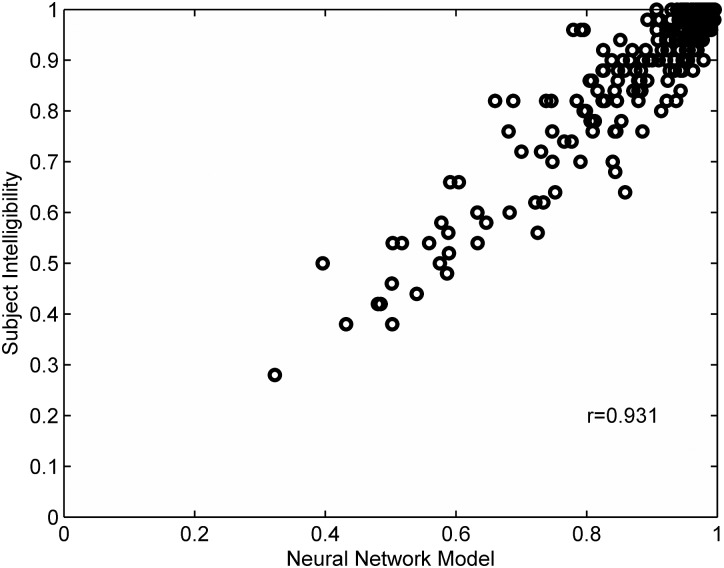
The individual subject intelligibility scores are presented in the scatter plot of Fig. 4 as a function of the neural network prediction for each of the subjects in the high-loss group. Each point represents one subject's observed vs predicted intelligibility for one frequency-compression condition. The Pearson correlation coefficient is 0.931, which on the surface is quite good. However, the points in the figure are clustered in the upper right-hand corner, so the high correlation is really determined by the tail of the distribution for the low intelligibility scores.

Figure 4.

Scatter plot showing the high-loss group subject intelligibility scores plotted as a function of the score predicted by an ensemble of ten neural networks. All features were used in the model.

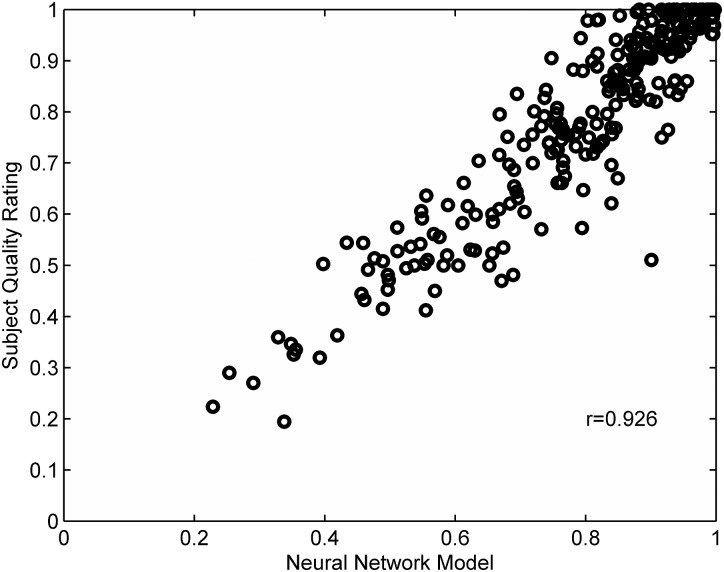
The individual subject quality ratings are presented in the scatter plot of Fig. 5 as a function of the neural network prediction for each of the subjects in the high-loss group. The Pearson correlation coefficient of 0.926 between the observed and predicted values is again quite good. But the quality model results, like the intelligibility results, are clustered in the upper right-hand corner of the plot, so again the high correlation really shows the success in modeling the low ratings.

Figure 5.

Scatter plot showing the high-loss group subject quality ratings plotted as a function of the score predicted by an ensemble of ten neural networks. All features were used in the model.

DISCUSSION

Model results

The results presented in Figs. 23 show different trends for the low-loss as opposed to the high-loss group. In Fig. 3, for example, the correlation coefficient between the low-loss subject intelligibility scores and the model predictions remains essentially constant as more information is added to the model. The correlation coefficient for the high-loss group, on the other hand, increases with additional information, starting at 0.89 and increasing to 0.93. The different trends are consistent with recent studies. The results of Ellis and Munro (2013) showed no relationship between frequency compression and working memory for their group of normal-hearing subjects, while the results of Arehart et al. (2013) showed significant correlations between frequency compression and working memory for their group of hearing-impaired subjects.

The difference in the trends is also consistent with models of cognitive processing that postulate a fixed working memory capacity that is divided among the different tasks being performed (Wingfield et al., 2005; McCoy et al., 2005; Francis, 2010; Amichetti et al., 2013; Arehart et al., 2013; Ng et al., 2013). Francis (2010), for example, used target speech coming from in front of the normal-hearing listeners and interfering speech coming from either in front or to the side, along with a competing visual digit identification task. He found that the proportion of words correctly identified went down and the reaction time went up when the competing visual task was present. Amichetti et al. (2013) had normal-hearing subjects listen to word lists at 25 or 10 dB above auditory threshold. They found that the number of words correctly recalled was reduced for the more difficult listening condition given by the lower presentation level. McCoy et al. (2005) compared older adults with good hearing to an age-matched group that had mild-to-moderate hearing loss. They had the subjects recall the final three words in a running memory task. Both groups had nearly perfect recall of the final word of the three-word sets, but the group with the greater hearing loss could recall fewer of the nonfinal words. Furthermore, brain imaging studies using dual-task paradigms also present evidence for a limited amount of working memory (Bunge et al., 2000) and limited cognitive capacity (Just et al., 2001).

For the low-loss group, it is postulated that adequate working memory is available to process both the distorted speech in the periphery and to allow the extraction of the linguistic content (Stenfelt and Rönnberg, 2009). The high-loss group, on the other hand, is postulated to use more of the available working memory when processing the distorted speech sounds coming from the impaired periphery, leaving fewer resources available to process the linguistic content. The RST measurements add information useful for modeling the high-loss group since the test indicates whether enough working memory is available to process the speech after the cognitive load of processing sounds from the impaired periphery is taken into account. The low-loss group, on the other hand, appears to have enough processing resources available that the limits detected with the RST are not reached in the speech intelligibility task.

The correlation plots for intelligibility also show that the RST adds useful information for the high-loss group beyond that added by age. Including age in the model makes a small improvement over using just the frequency compression parameters and hearing loss, which indicates that age provides some information beyond the audiogram, as found by Schvartz et al. (2008). However, the improvement in the correlation coefficient when the RST is added to a model that already contains age indicates that age does not duplicate the information provided by the RST. This result is also consistent with the data in Table TABLE III., where the uncertainty coefficient between the RST and age was 0.315.

Additional measurements of peripheral or cognitive performance would be expected to lead to improved correlation between the model predictions and the subject results. Hearing-impaired listeners often have reduced temporal processing abilities (Hopkins and Moore, 2007), and this reduction in temporal processing appears not to be correlated with the audiogram (Hopkins and Moore, 2011). Thus a measure of temporal processing abilities could add information not included in the other peripheral measures presented in this paper. Sarampalis et al. (2009) found a significant relationship between the intelligibility of noisy speech and reaction time for a dual task measuring speech intelligibility in conjunction with a competing visual digit identification task, so reaction time measurements may also contribute useful information to a more comprehensive model. McCoy et al. (2005) found that hearing-impaired listeners had more difficulty in recalling words in a running memory task, so a test of short-term memory capacity could be beneficial. Shinn-Cunningham and Best (2008) show that hearing-impaired listeners have more difficulty in directing attention to the sound source of interest in the presence of competing spatially separated sources, so a test of selective attention might also contribute useful information to the model.

The results from the quality model are consistent with the intelligibility results. Adding additional information to the model for the low-loss group does not improve the model accuracy, while adding information to the model for the high-loss group results in a trend in the model accuracy similar to that found for intelligibility. This similarity between quality and intelligibility suggests that quality judgments also depend on the amount of available working memory. One possible explanation is the relationship between intelligibility and quality; when intelligibility is poor, speech quality is related to intelligibility (Preminger and van Tasell, 1995). Thus, for sufficiently degraded speech the quality rating will be reduced due to the reduction in intelligibility, which in turn depends on working memory. A second possibility is that a greater working memory capacity allows the listener to retain more of the sentence in memory while making a quality judgment, thus allowing the listener to react to more regions of the signal that contain distortion.

One would expect to see similar results applying the neural network approach to other forms of signal processing. The neural network combines the selected features to produce a minimum mean-squared error estimate of the subject intelligibility scores or quality ratings. For example, several studies have found a significant relationship between working memory and success in using dynamic-range compression (Lunner, 2003; Gatehouse et al., 2006; Rudner et al., 2009; Cox and Xu, 2010). The statistical significance indicates that a measure of working memory conveys information about the perception of the processed speech, so a model that incorporates a measure of working memory would be expected to be more accurate than a model that leaves it out.

Clinical implications

The neural network models show a high degree of correlation between the model outputs and the average subject intelligibility scores and quality ratings. However, the ultimate objective is predicting the individual reaction to the signal processing and not the group average. The frequency compression conditions that gave the highest intelligibility for the high-loss group are listed in Table TABLE IV., along with the best processing conditions predicted by the neural network. The unprocessed reference condition is indicated by a cutoff frequency of Fcut = 3 kHz and the frequency compression ratio of FCR = 1. The unprocessed condition gave the highest intelligibility for 9 out of the 26 subjects (subjects 1, 2, 4, 6, 7, 9, 13, 14, and 23). The model predicts the best processing condition for only 6 out of the 26 subjects (subjects 4, 11, 15, 18, 20, and 23). If the model were being used for hearing-aid fittings, it would be better at removing inappropriate settings than finding the best setting.

TABLE IV.

Frequency compression conditions giving the highest speech intelligibility and quality for the high-loss subject group in comparison with the condition giving the highest predicted intelligibility or quality using an ensemble of ten neural networks.

	Intelligibility Subject best condition		Intelligibility predicted best condition		Quality Subject best condition		Quality Predicted best condition
Subject	Fcut, kHz	FCR	Fcut, kHz	FCR	Fcut, kHz	FCR	Fcut, kHz	FCR
1	3.0	1.0	1.5	1.5	3.0	1.0	3.0	1.0
2	3.0	1.0	1.5	1.5	3.0	1.0	3.0	1.0
3	2.0	1.5	1.5	1.5	3.0	1.0	3.0	1.0
4	3.0	1.0	3.0	1.0	1.5	1.5	3.0	1.0
5	1.5	2.0	3.0	1.0	3.0	1.0	3.0	1.0
6	3.0	1.0	1.5	1.5	3.0	1.0	3.0	1.0
7	3.0	1.0	1.5	1.5	3.0	1.0	3.0	1.0
8	2.0	3.0	1.5	1.5	3.0	1.0	3.0	1.0
9	3.0	1.0	1.5	1.5	3.0	1.0	3.0	1.0
10	2.0	3.0	3.0	1.0	3.0	1.0	3.0	1.0
11	2.0	1.5	2.0	1.5	3.0	1.0	3.0	1.0
12	2.0	2.0	2.0	1.5	3.0	1.0	3.0	1.0
13	3.0	1.0	2.0	1.5	3.0	1.0	3.0	1.0
14	3.0	1.0	1.5	1.5	3.0	1.0	3.0	1.0
15	1.5	1.5	1.5	1.5	1.5	1.5	3.0	1.0
16	1.5	2.0	1.5	1.5	3.0	1.0	3.0	1.0
17	1.5	2.0	2.0	3.0	2.0	1.5	3.0	1.0
18	1.5	1.5	1.5	1.5	2.0	1.5	3.0	1.0
19	1.0	1.5	2.0	1.5	3.0	1.0	3.0	1.0
20	2.0	1.5	2.0	1.5	3.0	1.0	3.0	1.0
21	2.0	1.5	2.0	3.0	3.0	1.0	3.0	1.0
22	1.5	1.5	1.5	1.5	1.5	1.5	3.0	1.0
23	3.0	1.0	3.0	1.0	3.0	1.0	3.0	1.0
24	2.0	3.0	1.5	1.5	1.5	1.5	3.0	1.0
25	1.5	1.5	2.0	1.5	3.0	1.0	3.0	1.0
26	1.0	1.5	1.5	1.5	3.0	1.0	3.0	1.0

The frequency compression conditions that gave the highest quality ratings for the high-loss group are also listed in Table TABLE IV., along with the best processing conditions predicted by the neural network. The unprocessed condition received the highest quality rating from 20 out of the 26 subjects. The model predicts that the unprocessed condition will give the highest quality for all of the subjects, and thus agrees with these 20 subjects. The prediction, however, conveys no information since it is the same for everyone and it can thus be dispensed with. As was the case for intelligibility, the model is better at identifying the conditions that will be liked least as opposed to those that will receive the highest preference.

The data presented in Table TABLE IV. also show that for many listeners the condition that gave the highest intelligibility differed from the one that gave the highest quality rating. Fewer than half (10 out of 26) of the subjects indicated that the highest intelligibility condition was also the one that gave the best quality. This finding is similar to results for amplification in hearing aids, where the response that gives the highest intelligibility is not necessarily the response that yields the highest listener preference (Punch and Beck, 1980; Souza, 2002).

The most appropriate clinical application of the current modeling approach would be in the initial settings of a frequency-compression hearing aid to improve speech intelligibility. The intelligibility model prediction would provide the recommended starting point for the hearing-aid settings, to be followed by fine-tuning of the processing parameters in the clinic. Even though the intelligibility predictions are imperfect, they would still be better than procedures that ignore the individual variability not described by the audiogram. Additional measurements of listener performance, as outlined in Sec. 5A, would be expected to improve the model accuracy and thus enhance its clinical usefulness.

CONCLUSIONS

This paper has presented a neural network model for predicting the effects of nonlinear signal hearing-aid processing on speech intelligibility and quality. Frequency compression was used as the nonlinear processing example. An ensemble averaging approach was used to avoid the problems associated with overfitting. The model combines peripheral measures of hearing loss with additional subject information and a measure of cognitive ability, and appears to be more accurate than a model that is based on the periphery alone.

The neural network model results show a low RMS error and a high degree of correlation with the subject intelligibility scores and quality ratings when averaged over the low-loss and high-loss subject groups. However, an analysis of the individual high-loss subject data showed that the model was not accurate enough to select the best processing parameters for each subject. The model appears to be better at rejecting inappropriate parameter choices than it is at finding the best fit for each listener. This result is due, in part, to the small differences observed in intelligibility and quality for a large number of the subjects and processing conditions. The neural network modeling framework appears to be effective, however, so an improvement in accuracy would be expected given additional subject information.