Decoding Information in Cell Shape

SUMMARY

Shape is an indicator of cell health. But how is the information in shape decoded? We hypothesize that decoding occurs by modulation of signaling through changes in plasma membrane curvature. Using analytical approaches and numerical simulations, we studied how elongation of cell shape affects plasma membrane signaling. Mathematical analyses reveal transient accumulation of activated receptors at regions of higher curvature with increasing cell eccentricity. This distribution of activated receptors is periodic, following the Mathieu function, and it arises from local imbalance between reaction and diffusion of soluble ligands and receptors in the plane of the membrane. Numerical simulations show that transient microdomains of activated receptors amplify signals to downstream protein kinases. For growth factor receptor pathways, increasing cell eccentricity elevates the levels of activated cytoplasmic Src and nuclear MAPK1,2. These predictions were experimentally validated by changing cellular eccentricity, showing that shape is a locus of retrievable information storage in cells.

INTRODUCTION

Many cellular factors affect spatial dynamics of signaling. The presence of the lipid rafts in plasma membrane (Allen et al., 2007; Lingwood and Simons, 2010; Pike, 2009), cytoskeleton network (Ahmed et al., 2007; Allen et al., 2007; Deshpande et al., 2006; Iglic et al., 2006; Ten Klooster et al., 2006; Lacayo et al., 2007; Lingwood and Simons, 2010; Pike, 2009), scaffolding proteins (Allen et al., 2007; Lingwood and Simons, 2010; McMahon and Gallop, 2005; Pike, 2009; Westphal et al., 2000), and location of intracellular organelles (Ahmed et al., 2007; Campello and Scorrano, 2010; Deshpande et al., 2006; Freche et al., 2011; Iglic et al., 2006; Ten Klooster et al., 2006; Lacayo et al., 2007) all play important roles in controlling the spatial as well as temporal dynamics of signaling. But what about cell shape? It is well established that cell shape is controlled by both physical properties of the plasma membrane and the biochemical reactions involving membrane components and the underlying cytoskeleton, most often the actin filament network (Döbereiner et al., 2004; Dubin-Thaler et al., 2004, 2008; Giannone et al., 2007; Mogilner and Keren, 2009; Xiong et al., 2010). The intracellular signaling network activated by extracellular ligand binding to receptors in plasma membrane utilizes multiple signaling pathways containing small GTPases to regulate the actin cytoskeleton and thus control cell shape (Rangamani et al., 2011). So the shape of cells can be considered as a repository of information that flows through the cell signaling network. Is this information retrievable? If so, what could be the mechanisms of retrieval? These questions, although very fundamental in cell biology, also have translational relevance. For more than 100 years, the field of pathology has had as one of its major foci the observation of cell shape and tissue organization to identify disease states. This is done with precision, albeit in an empirical manner. If we were to understand how information in cell shape can be retrieved and utilized by cells, then there is the possibility that we can identify the mechanisms that relate cell shape to disease states.

The central hypothesis for this study is that cell shape can control signal transduction at the plasma membrane. By doing so, the information stored in cell shape can be retrieved and used to modulate cellular responses to extracellular signals. Such a hypothesis is impossible to answer solely by experimentation, as changing cell shape by plating cells on patterned surfaces affects cytoskeleton organization and dynamics (Ahmed et al., 2007; Allen et al., 2007; Deshpande et al., 2006; Iglic et al., 2006; James et al., 2008; Ten Klooster et al., 2006; Lacayo et al., 2007; Lingwood and Simons, 2010; Pike, 2009) that in turn regulate cell signaling. Hence, a theoretical approach is essential to determine whether cell shape can regulate signal transduction at the plasma membrane.

The fusiform shape is often associated with transformed cells. An early experimental study showed that cell shape controls proliferation (Folkman and Moscona, 1978). These experimental observations, in conjunction with our hypothesis, allowed us to formulate the following question: could the curvature of the plasma membrane result in the spatial gradients of activated signaling components in the plane of the membrane? To answer this question, we used reaction-diffusion formulations with homogeneous initial conditions and analyzed the effect of shape of the boundary on the spatial distribution of activated signaling components in the plane of the plasma membrane and subsequently in the cytoplasm as a function of time. We focused on ellipses as cell shapes because neoplastic transformation leads to cells acquiring a fusiform shape that is close to an ellipsoid (Figure S1 available online) (Campello and Scorrano, 2010; Kim et al., 1999; McMahon and Gallop, 2005). To determine whether cell shape by itself can modulate plasma membrane signal transduction, our mathematical model and numerical simulations did not include cytoskeletal regulation of membrane signaling or the presence of lipid rafts in the membrane. In the following sections, we briefly describe a mathematical model in both two and three dimensions and use it to generate numerical simulations and predictions. We then show that the predictions from the numerical simulations can be observed experimentally.

RESULTS

Mathematical Model for Membrane Gradients of Activated Signaling Components

Consider the following reaction, where A is a component in solution (extracellular or cytoplasmic component) and X is a membrane component. When A binds to X on the membrane, it forms B, which is also a membrane component. This is shown in Figure 1A.

$$A+X\underset{k_{\mathit{off}}}{\overset{k_{\mathit{on}}}{\leftrightharpoons }}B$$ (Equation 1)

Figure 1. Simulations of the Effect of Membrane Curvature on the Transformation of Homogeneous Initial Distribution of Signaling Components to Transient Inhomogeneities in the Membrane and the Cytoplasm.

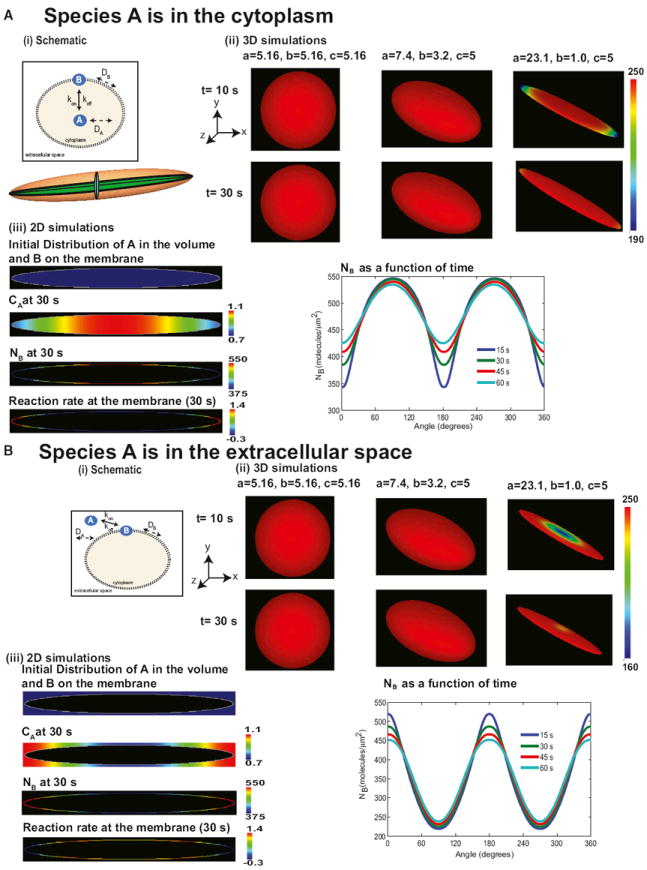
(A) Signaling from the cytoplasm to the membrane. (i) The cytoplasmic component A binds to the plasma membrane to form membrane component B. A is free to diffuse in the cytoplasmic volume, whereas B has lateral mobility in the plane of the membrane. The cartoon below the reaction scheme illustrates that, in an ellipsoid, all 2D cross-sections passing through the center yield ellipses. (ii) Membrane surface distribution of B in 3D at 10 and 30 s in a sphere and two ellipsoids. The needle-shaped cell shows a transient spatial inhomogeneity in the membrane concentration of B. The dimensions of the shapes are shown on the panels. Initial concentration of A in the cytoplasm is 2 μM, and initial distribution of B on the membrane is 0 molecules/μm². The values of a, b, and c are the semiprincipal axes of the ellipsoid and determine its shape. For a sphere, a = b = c = radius of the sphere. (iii) Simulations of the distribution of signaling components in 2D geometry. Shown are the initial distribution of A (2 μM in the cytoplasm) and B (0 molecules/μm²), concentration of A in the cytoplasm at 30 s, molecular density of B on the membrane at 30 s, and reaction rate along the membrane at 30 s, and angular dependence of membrane density of B at different times follows a Mathieu sine function.

(B) Same as in (A) except species A is in the extracellular space. The surface-to-volume relationship is reversed, and this results in a Mathieu cosine function.

See also Figure S1.

In the cytoplasm, A is free to diffuse. X and B are limited to the plasma membrane and are free to diffuse along the plane of the membrane. The dynamics of A in the cytoplasm are governed by

$$\frac{\partial C_A}{\partial t}=D_A{\nabla }^2{C}_A$$ (Equation 2)

where C_A is the concentration of A (in molecules/μm³), and D_A is the diffusion coefficient (μm²/s) of A.

The boundary condition accounts for the balance between diffusive flux and reaction rate at the boundary. This is given by

$$D_A(\mathbf{n}·\nabla C_A)=-k_{\mathit{on}}{C}_A{\mid }_{\partial \mathrm{\Omega }}{N}_X+k_{\mathit{off}}{N}_B$$ (Equation 3)

where k_on, (μm³s⁻¹molecules⁻¹) and k_off are the reaction rate constants (s⁻¹), N_X and N_B are the concentrations of X and B on the membrane, respectively (in molecules/ μm²), n is the unit normal to the membrane at every point along the curve, and C_A∣_∂Ω is the concentration of A at the boundary.

Similarly, membrane components X and B satisfy the following equations

$$\frac{\partial N_X}{\partial t}=D_X{\nabla }^2{N}_X-k_{\mathit{on}}{C}_A{\mid }_{\partial \mathrm{\Omega }}{N}_X+k_{\mathit{off}}{N}_B$$ (Equation 4)

$$\frac{\partial N_B}{\partial t}=D_B{\nabla }^2{N}_B+k_{\mathit{on}}{C}_A{\mid }_{\partial \mathrm{\Omega }}{N}_X-k_{\mathit{off}}{N}_B$$ (Equation 5)

where D_X and D_B are the diffusion coefficients of X and B, respectively. Accordingly, N_X and N_B must satisfy periodic boundary conditions because the domain is closed. We assume that X has a uniform distribution in the membrane initially with a value N_X0 (molecules/μm²), and A has a uniform cytoplasmic distribution of C_A0 (molecules/μm³). Initially, the density of B is zero along the membrane.

We solved the above system of equations for a spherical and ellipsoidal geometry using separation of variables and analyzed the role of curvature in the generation of gradients of N_B in the plane of the membrane. The solution to the system of equations evolves similarly in both coordinates except the final form of the equations.

In many cases, only one surface of the cell is exposed to the stimulus. Therefore, simplification to a two-dimensional (2D) system is reasonable. For further simulations, we used the 2D geometry because it allows us to study the effect of curvature variation along a single axis. However, all results can be readily extended to three-dimensional (3D) models, and although the quantitative behavior of the membrane and cytoplasmic components may vary depending on the eccentricity and size of the ellipsoid, the angle-dependent wave function remains intact. In the case of a first-order reaction, we can obtain analytical solutions to the reaction-diffusion system as Mathieu functions in elliptic coordinates and Bessel functions (Arscott, 1964) in polar coordinates. We only show the final equations in the elliptical coordinates system here, and the complete derivation is in the Supplemental Information.

In elliptical coordinates, the final equations for radial and angular coordinates take the following form:

$$\frac{{\partial }^{2}U}{\partial {\mu }^2}-(I-2\mathit{\omega \; cosh}(2\mu ))U=0$$ (Equation 6)

$$\frac{{\partial }^{2}V}{\partial {\nu }^2}-(I-2\mathit{\omega \; cosh}(2\nu ))V=0$$ (Equation 7)

Here, U(μ) and V(ν) are the radial and angular functions for N_B, respectively; μ is the equivalent of the radius for the ellipse, and μ = μ₀ defines the ellipse; ν is the angle going from 0° to 360°. The quantities l and ω are given as

$$I=\left(a^2{\sinh }^2{\mu }_0+\frac{a^2}{2}\right)\frac{\gamma D_A}{(D_A-D_B)}$$ (Equation 8)

$$\omega =\frac{a^2\gamma D_A}{4(D_A-D_B)}$$ (Equation 9)

where a is the distance between the two foci of an ellipse, and γ is the effective reaction rate in spatial coordinates at the boundary (see Supplemental Information). Equations 6 and 7 are the modified Mathieu and the Mathieu differential equation, respectively (McLachlan, 1947). There is no analogous solution like the m = 0 (see Equation S33) mode for the angular dependence, V(ν). The solution to the Mathieu functions is a series summation of sines and cosines, and it inherently has an angular dependence. The solution to these equations was computed numerically.

Numerical Simulations

Partial differential equations resulting from the reaction diffusion system were solved numerically using the Virtual Cell suite (Loew and Schaff, 2001). The volume component A can be present either in the cytoplasm (Figure 1A) or extracellular space (Figure 1B). In either case, interaction with the membrane depends on the local curvature. Therefore, we conducted simulations for two conditions: (1) when component A is in the cytoplasm (Figure 1A) and (2) when A is in the extracellular space (Figure 1B).

We conducted simulations using 3D geometries. When the volume component A is present in the cytoplasm, there is no spatial variation of membrane component B along the membrane for a sphere. However, as the eccentricity of the ellipsoid increases, the membrane distribution becomes curvature dependent at early times. In this case, the concentration of B is lower at the tip than at the body (Figure 1A, ii). In an ellipsoid, there are surface gradients along all three axes because every cross-section passing through the center of an ellipsoid is an ellipse (see Figure 1A, i, inset).

The system of equations for the 2D reaction-diffusion model was implemented using an elliptical geometry with eccentricity 0.999, and the concentrations of A and B were computed as a function of time (Figure 1A, iii). This geometry was chosen as it is similar in shape of elongated cells characteristics of those that have undergone neoplastic transformation (see Figures S1A–S1C) (Kalluri, 2009; Kalluri and Zeisberg, 2006; Young et al., 2006). At time zero, as per the initial conditions, C_A is homogeneous in the cytoplasm, and N_B is zero on the membrane (Figure 1A, iii). At 30 s, both C_A and N_B demonstrate a concentration gradient (Figure 1A, iii). Furthermore, the reaction flux also shows an angular dependence (Figure 1A, iii). The angular dependence of N_B varies in time during the course of the simulation (Figure 1C, v). The angular dependence of the membrane gradient is a result of the Mathieu functions. In fact, the first mode of the Mathieu sine function shows the same periodicity and qualitative behavior (McLachlan, 1947) as that of the membrane gradient of N_B.

When A is present in the extracellular space, the curvature dependence is reversed (Figure 1B). As expected, a spherical geometry does not exhibit any spatial variation of B along the membrane. As the eccentricity of the ellipsoid increases, the curvature-dependent gradients can be observed transiently (Figure 1B, ii). The membrane gradient exhibits a Mathieu cosine function (Figure 1B, iii). This is because the surface-to-volume relationships are reversed. Therefore, depending on the location of the volume component (cytoplasmic or extracellular), the regions of high curvature (θ = 0) will have minimum or maximum concentration, respectively. We also tested whether the shape of the outer bounding box (similar to extracellular space) would affect the membrane pattern, and we see that, when A is present in the extracellular space (such as a ligand for a membrane bound receptor), the shape of the outer bounding box does not qualitatively affect the nature of the membrane gradient (Figure S1D).

When the reaction pathway is unidirectional toward the membrane—that is, extracellular ligand binding the receptor (Figure 1B) or the intracellular component binding the receptor (Figure 1A)—the effect of curvature is as described by the theoretical analysis. However, when both intracellular and extracellular components bind the membrane-bound receptor, the effect of curvature will depend on the relative rates of reaction and concentrations of the reactions (extracellular species A → membrane species B ← intracellular species C). This effect can be explained by a simulation (Figure S1E) in which both an extracellular and a cytoplasmic component bind simultaneously (within our timescale) to the membrane. Because signal transduction at the cell surface almost always involves near-simultaneous binding of ligand to the receptor on the outer surface and cytoplasmic signaling components on the inner surface, we tested and found that simultaneous binding of cytoplasmic and extracellular components to the membrane can also result in curvature-dependent membrane gradients of B (Figure S1E). Thus, a homogeneous initial distribution can be converted into a signaling microdomain by the curvature of the membrane (i.e., cell shape). In addition to curvature, the directionality of the reactions is also important for curvature-dependent gradients of components restricted to the boundary (i.e., plasma membrane).

Mechanism Underlying Dynamics of Membrane Gradient of Signaling Components

Local Competition between Reaction and Diffusion

What is the physical basis for this differential distribution along the boundary (i.e., the plasma membrane)? The process of free diffusion works toward homogenizing concentration gradients; i.e., Fickian diffusion eliminates concentration gradients over a length scale. On the other hand, chemical reactions are occurring everywhere along the cell membrane, and the local surface-to-volume ratio establishes concentration differences along the membrane. The balance between these two processes is represented by the Thiele modulus (Φ), a dimensionless number. The Thiele modulus is used in chemical engineering to characterize processes that involve reaction diffusion on immobilized surfaces such as catalyst pellets. In those cases, the typical length scale is the size of the catalyst pellet. In the case of elliptical cell shapes, the radius of curvature is the natural choice for length scale. The radius of curvature, R_c, captures how curved the membrane is at any given point and is distinct from the distance from the center of the ellipse to the membrane. The radius of curvature is defined as the radius of the osculating circle that can be drawn at each point along the curve; it is the inverse of curvature. At θ = 0, the ellipse is highly curved, and a small circle (red circle in Figure 2A, inset) will fit in this circle. Hence, R_c is small here.

$${\mathrm{\Phi }}_{\mathit{local}}=R_c\sqrt{\frac{k_{\mathit{on}}}{D_B}}$$ (Equation 10)

Figure 2. Angular Dependence of Local Thiele Modulus in Elliptically Shaped Cells.

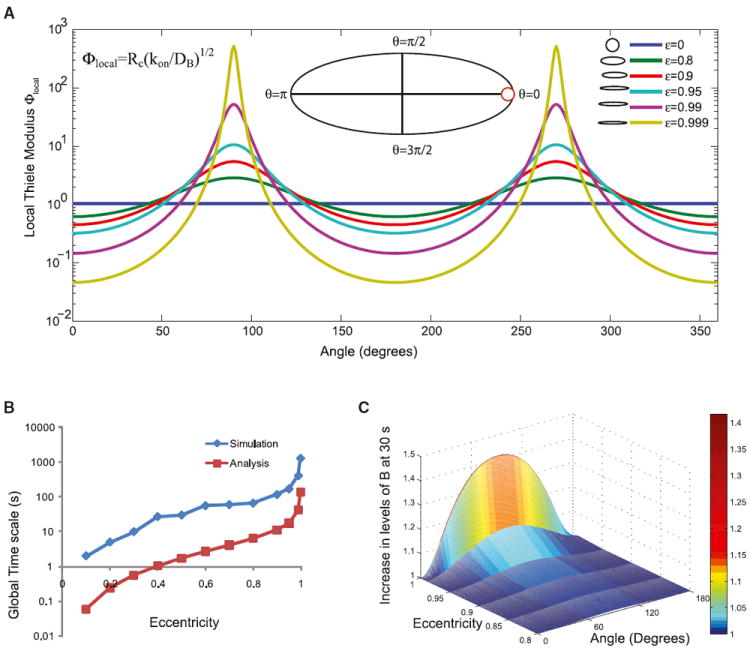
(A) Local Thiele modulus varies along the angle in an ellipse and results in competing reaction and diffusion processes along the membrane. The range of the local Thiele modulus also increases with increasing eccentricity of the ellipse. Inset shows a reference ellipse with the different angles marked. The red circle shows the osculating circle that determines the radius of curvature at the point θ = 0.

(B) The global timescales from analysis and numerical simulations follow similar dependence on eccentricity. Note that the simulation includes the timescale of the reaction, whereas the analysis is based on size and diffusivity alone.

(C) The fold change in component B along the membrane is calculated by normalizing the membrane concentrations by the value of B at θ = 0. The fold change in B depends on the eccentricity of the ellipse, and as the ellipse becomes more elongated (compare ε = 0.9 to ε = 0.999), the fold change in B increases.

The competing processes of reaction and diffusion can be demonstrated by computing the local Thiele modulus (Equation 10 and Figure 2A). At θ = 0, R_c is small, therefore Φ_local is small. Along the circumference of the cell, Φ_local varies from ~0.1, (a diffusion-limited regime) to >1,000 (a reaction-limited regime). Hence, the gradient of A in the cytoplasm follows the membrane gradient because closer to θ = 0, reaction dominates, and closer to θ = π/2, diffusion dominates.

As a result, the local reaction rate along the boundary depends on the local curvature (Figures 1A, iii, and 1B, iii). Consider θ = 0 in Figure 2A; here, the local surface-to-volume ratio is high because curvature is high. Therefore, the contribution of reaction alone (per membrane unit area) is small—more A gets converted to B at the membrane, and there is a depletion of A in the local volume with a minor increase in N_B. In this local region, the process is diffusion limited because the reaction depletes A much faster than diffusion of A from the inside of the cytoplasm. In contrast, at θ = π/2, the distance for A to travel from the center to the membrane is smaller; therefore, the process is less diffusion limited. When A is present in the extracellular space, the surface-to-volume ratio relationships are reversed (more at θ = 0, less at θ = π/2), and this is captured in the volume gradient of A, the membrane gradient of B, and the local reaction rate (Figure 1B).

Global Timescales and Effect of Eccentricity

How do the temporal characteristics of distribution at the boundary (i.e., plasma membrane) arise? The transient membrane inhomogeneities resulting from the shape of the cell are governed by a global timescale that captures the time required for the gradient to be abolished. We estimate the time required for gradient elimination as the difference between diffusion time at the major axis (r₁) and time at the minor axis (r₂) (Equation 11).

$$t=\frac{r_1^2-r_2^2}{4D_A}$$ (Equation 11)

The diffusion-limited “supply vs. demand” causes gradient formation, and thus the difference in diffusion times is a good indicator of the characteristic gradient relaxation time. We compare the computed timescale with the time required to achieve N_B(θ = 0) = N_B(θ = π/2) in the simulations (Figure 2B) and see that the dependence of the timescale on eccentricity is similar. The simulation time includes reaction lifetime and diffusion time, although the analysis is only considering the diffusion.

In the case of a circle, the only acceptable mode of solution is when the mode number m is zero. This gives an exponential decay as the time-dependent solution (Equation S22). In elliptical coordinates, the mode numbers q (Equation S36) are not zero. They capture the different oscillatory patterns of the harmonic solutions of the Mathieu functions. Therefore, there are multiple contributions to the time-dependent solution. Each of these modes contributes to the final solution of the reaction-diffusion equation, and each mode converges to steady state with its own timescale. Areas that are closer to the zero point of the long-lasting modes would converge to steady state earlier than the others. As the eccentricity of the ellipse increases, more modes are required, and the significance of the different time-scales increases. Because relaxation time increases dramatically with eccentricity, cell shape is a key determinant of how long the transient inhomogeneity will last along the membrane.

The increase in the concentration of N_B depends on the eccentricity of the ellipse (Figure 2C). As the eccentricity increases, the curvature range gets wider and the gradient gets steeper. Therefore, even if we start with the same concentration of a biochemical species at all locations, the shape of the cell will dynamically affect the spatial distribution of the activated signaling component in response to a membrane-delimited biochemical signaling event.

Model Predictions

Using our theoretical model, we make the following predictions that may be tested in numerical simulations and experiments. (1) A circular cell shape will have a homogeneous spatial activation of a membrane-bound receptor by a soluble ligand. Spatial distribution of activated receptor depends on the local curvature of the cell membrane. The persistence of a spatial gradient will depend on the relative rates of the reactions. (2) The transient spatial inhomogeneity at the plasma membrane can affect downstream reactions in a biochemical signaling pathway. As a result, there can be transient spatial gradients of the signaling components in the cytoplasm. (3) The effect of local curvature may also be seen in the cell nucleus. If the nucleus is elongated, then signaling interactions at the nuclear membrane will show an increase in activated signaling components in the nucleus.

In testing these predictions by numerical simulations, we had to introduce two additional details to make the simulations realistic: (1) we assumed near-simultaneous binding of agonist to receptor on the outside of the cell and recruitment of the appropriate signaling component from the cytoplasm and (2) inhomogeneous distribution of receptors as the starting condition, based on our observations described below, that receptors are present in higher density at the tips of elliptically patterned cells.

Numerical Simulations and Experimental Testing

GPCR

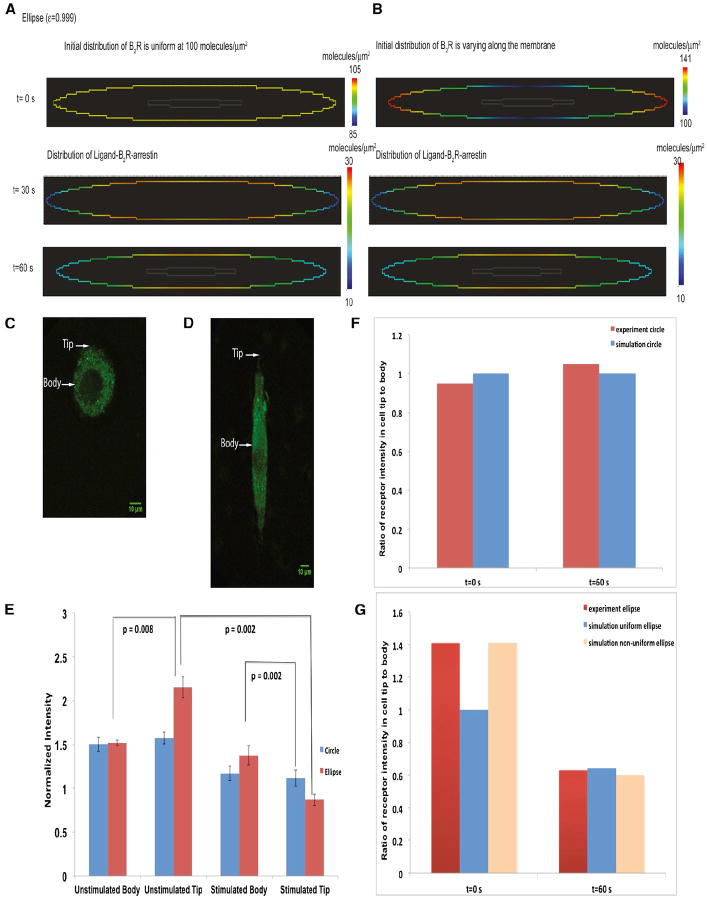
We simulated the distribution of the bradykinin receptor, a G_q/11-coupled receptor in circular and elliptical cells. We chose this receptor type because of the availability of good antibodies that allow us to study the native receptor in the cell. In response to activation by bradykinin, this receptor rapidly recruits β-arrestin (Gera et al., 2011; Philip et al., 2007). The lists of reactions, kinetic parameters, and diffusion coefficients are provided in Tables S1 and S2. As a starting point, we assumed that the initial distribution of the receptor was uniform (Figure 3A). Our simulations showed that, at early times after simulation, the receptors had a curvature-dependent distribution, with higher concentration on the cell body and lower concentration on the tip.

Figure 3. Numerical Simulations and Experiments on the Plasma Membrane Distribution of Bradykinin Receptor in Circular and Elliptical A-10 Cells.

Simulation of the spatial distribution of active bradykinin receptor at 1 min for a uniform initial distribution. The concentration of active bradykinin receptor is higher in the body than in the tips. Please note that this simulation utilizes signaling components binding to the plasma membrane from both the outside (bradykinin) and inside (β-arrestin) of the cell (see Figure S1E).

(A) Simulation of the spatial distribution of active bradykinin receptor at 1 min for a nonuniform initial distribution of the receptor.

(B) Representative circular cell used for analysis. Arrows indicate the region of the plasma membrane where body and tip measurements were taken.

(C) Representative elliptical cell used for analysis. Arrows indicate the region of the plasma membrane where body and tip measurements were taken.

(D) Experiments determining levels of bradykinin receptor in the body or tip of circular and elliptical cells (n = 5). The normalized fluorescence intensity is compared between circular cells and elliptical cells. Data ± SD are shown. p values indicate statistical difference according to Mann-Whitney tests.

(E) Ratio of receptor intensity in cell tip to cell body in circular cells.

(F) Ratio of receptor intensity in cell tip to cell body in elliptical cells.

See also Tables S1 and S2.

To test the predictions of this model, we manipulated cell shape by plating rat aortic smooth muscle A-10 cells on patterned surfaces that were either circular or elliptical. The plating of cells onto elliptical patterns always resulted in more receptors at the tip (Figure 3E). We then tested whether a nonuniform initial distribution (Figure 3B) as seen in the plated cells affected the spatial distribution of the receptor upon activation. We found that a similar curvature-dependent inhomogeneous receptor at early times after agonist addition could be seen, irrespective of the starting distribution (Figure 3B). Although we did not explore the causes of the initial inhomogeneous initial distribution, it is likely that this is related to plating in the presence of serum followed by serum starvation, a protocol that is essential for cells to adhere to the patterned surface. These predictions were tested experimentally in micropatterned A-10 cells (see Experimental Procedures).

The distribution of receptors in elliptical and circular cells is shown in Figures 3C and 3D. Experimental measurements of the receptor distribution in circular cells show that, before and after stimulation, the cells had a uniform distribution of receptors (Figure 3E). Experiments also showed that, in elliptical cells, the distribution of receptors prior to stimulation was nonuniform. The elliptical cells had higher receptor numbers at the tip than in the cell body. This is similar to the initial distribution shown in Figure 3B. One minute after stimulus, the elliptical cells showed a lower concentration of receptors in the tip than in the body (Figure 3E), similar to the predictions from the numerical simulations. We compared the ratio of receptor numbers in the cell tip to the cell body in circular cells (Figure 3F) and elliptical cells (Figure 3G) and found a good match between model predictions and experimental observations.

Growth Factor Receptors

Growth factors such as epidermal growth factor (EGF) and platelet-derived growth factor (PDGF) activate the membrane-bound receptors, which results in downstream recruitment of adaptors such as SHC and the Grb2/Sos complex. Grb2/Sos is an adaptor-guanine nucleotide exchange factor complex for Ras and promotes the exchange of GDP for GTP on Ras leading to MAPK1,2 activation (Asthagiri and Lauffenburger, 2001; Bhalla et al., 2002; Fujioka et al., 2006; Hall, 2005). This pathway has been extensively modeled (Bhalla and Iyengar, 1999; Schoeberl et al., 2002). The complete set of reactions and parameters is presented in Tables S3, S4, and S5. The receptor activation by the ligand (present in the extracellular space) results in a membrane gradient with regions of high curvature having higher concentrations of ligand-bound activated receptor (Figure S1D). However, when the cytoplasmic components such SHC and Grb2/Sos bind the activated receptor, the regions of lower curvature now have a higher active EGFR concentration (Figures 4A and S1E).

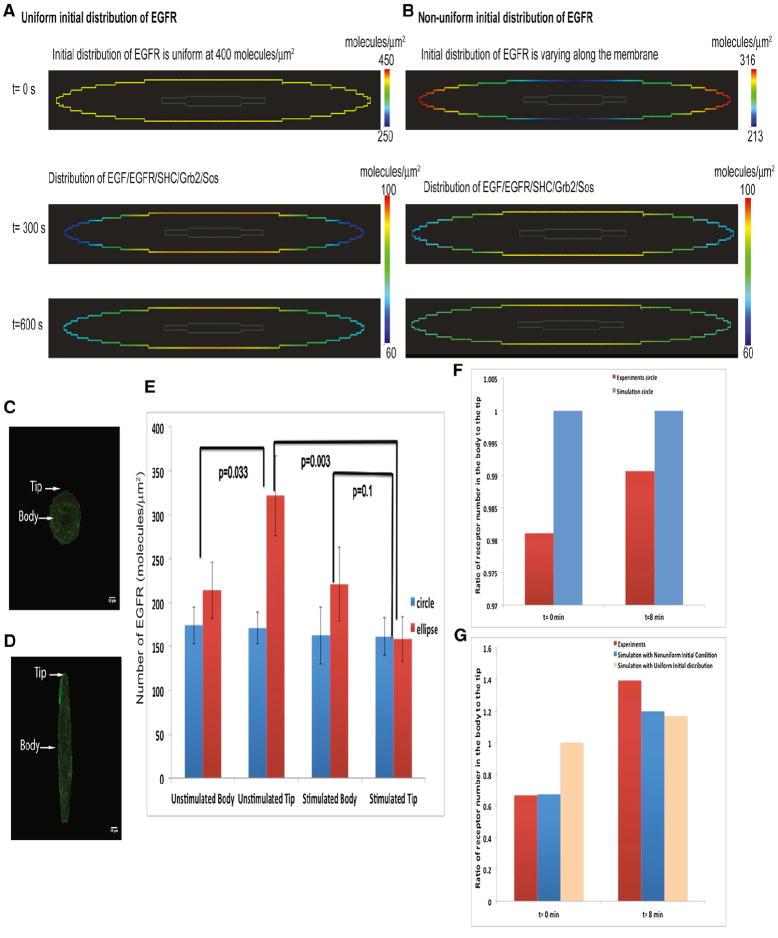
Figure 4. Numerical Simulations and Experiments on the Membrane Distribution of EGFR-eGFP in Circular and Elliptical COS-7 Cells.

(A) Simulation of the spatial distribution of active EGFR-eGFP at 5 and 10 min. The concentration of EGFR is higher in the body than in the tips. Please note that this simulation utilizes signaling components binding to the plasma membrane from both the outside (EGF) and inside (SHC and GRB2) of the cell (see Figure S1E). The initial distribution of EGFR is uniform in this case.

(B) Simulations of the spatial distribution of active EGFR-eGFP at 5 and 10 min. The initial distribution of EGFR is nonuniform in this case. The concentration of EGFR is higher in the body than in the tips.

(C) Representative circular cell transfected with EGFR-eGFP. Arrows indicate the region of the plasma membrane where body and tip measurements were taken.

(D) Representative elliptical cell used for FCS analysis. Arrows indicate the region of the plasma membrane where body and tip measurements were taken.

(E) Experiments determining levels of EGFR-eGFP in the body or tip of elliptical cells (n = 14). Numerical values were extracted from the autocorrelation function fit to fluorescence correlation data for unstimulated data. Cells were measured after 12 hr of serum starvation; for stimulated data, measurements were started immediately after addition of 100 ng/ml EGF and were completed within 8 min. Data ± SD are shown. p values indicate statistical difference according to Mann-Whitney tests.

(F) Ratio of receptor number at the tip to body in simulations and experiment in circular cells.

(G) Ratio of receptor number at the tip to body in simulations and experiment in elliptical cells.

See also Figures S2 and S3 and Tables S3, S4, and S5.

When the initial membrane distribution of EGFR is uniform (Figure 4A), the active receptor shows transient curvature dependence, with higher receptor numbers at the cell body than at the tip. This effect is also observed when the initial distribution of EGFR is nonuniform as shown in Figure 4B. To test our prediction that activated growth factor receptor is in homogeneously distributed in a curvature-dependent manner, we conducted experiments using monkey kidney tissue-derived COS-7 cells that were grown to circular and elliptical shapes using microfabricated surfaces (see Supplemental Information). Most cells fully complied with the induced geometries and took ellipsoidal shapes (Figure S2). These cells were then transfected with EGFR-eGFP, and fluorescence correlation spectroscopy (FCS) was used to quantify receptor dynamics. Unstimulated cells showed a significant difference in the number of molecules (or concentration) between cell tip and body in elliptical cells (Figure 4E). Upon EGF addition to the cell medium, we observed an increased concentration of EGFR at the body and reduced concentration at the tips (Figures 4D and 4E). Circular cells showed no difference in receptor numbers in either control case or upon EGF addition (Figures 4C and 4E). Comparing the ratio of receptor number in the cell tip to cell body (Figures 4F and 4G) shows that the model predictions are validated by the experimental measurements.

Experimentally determined diffusion coefficients of EGFR between the body and the tip in stimulated elliptical cells differed significantly. A similar difference was also seen in tips before and after EGF stimulation (Figure S2E). Hence, we ran a set of simulations varying the diffusion coefficient of EGFR. In the experimentally observed range, we did not see a significant effect of diffusion coefficients on EGFR microdomains (Figure S3A). Because the levels of the transfected EGFR-eGFP are variable, we also ran a set of simulations to determine whether EGFR microdomains varied with overall receptor concentration. No significant effect was found in the experimentally observed range (Figure S3A).

The necessity of binding dynamics for the inhomogeneous distribution was tested by determining the distribution of a constitutively expressed yellow fluorescent protein (YFP)-labeled plasma membrane marker. When we measured the distribution of a YFP-labeled membrane marker (e-YFP-mem, Clontech), which is a doubly palmotiylated fusion protein containing residues 1–20 of GAP-43, no differences were found between circular and elliptical cells (Figures S2F and S2G). Overall, these simulations and experiments validate the first prediction from our mathematical analysis for two different types of membrane receptors.

The curvature-dependent transient gradient of EGFR on the membrane could have functional consequences for MAPK1,2 activation, which regulates gene expression in the nucleus to trigger cellular proliferation. We simulated the EGFR signaling pathway to MAPK1,2 activation and accumulation in the nucleus and explored the consequences of circular versus elliptical shapes. The concentration profiles of active Raf, MEK, and MAPK1,2 in the cytoplasm are greater in the elliptical cell shape than in the circular cell shape (Figure S4). We assumed elongated nuclear geometries in elongated cells because transformed cells have elongated nuclei (Dean et al., 2010).

The simulations show that the spatial distribution of MAPK1,2 in the cytoplasm (Figure 5A) and in the nucleus (Figure 5B) is nearly homogeneous because of the high diffusivity of MAPK in the cytoplasm. Further, average MAPK1,2 concentration in the nucleus and the concentration of MAPK1,2 in the cytoplasm are higher in the ellipse than in the circle (Figure 5C, i and ii). This is because the nuclear shape is elongated in the elliptical cell, which allows for a curvature-dependent reaction flux at the boundary of the cytoplasm-nucleus interface, similar to that at the extracellular space and the plasma membrane. The concentration of activated MAPK1,2 also depends on the eccentricity of the nucleus (Figure S4). In the ellipse, the activation of MAPK1,2 has a steeper initial increase when compared to the circle (Figure S5). The early increase in active MAPK1,2, combined with the increase in time for dissipation of gradient in an ellipse, can have a large impact on cellular decision-making processes even for small increases in the concentration of MAPK1,2. Therefore, transformed cells with the same number of growth factor receptors as normal cells can display enhanced levels of MAPK1,2 in the nucleus.

Figure 5. Levels of Activated MAPK1,2 in the Nucleus of Circular and Elliptical Cells.

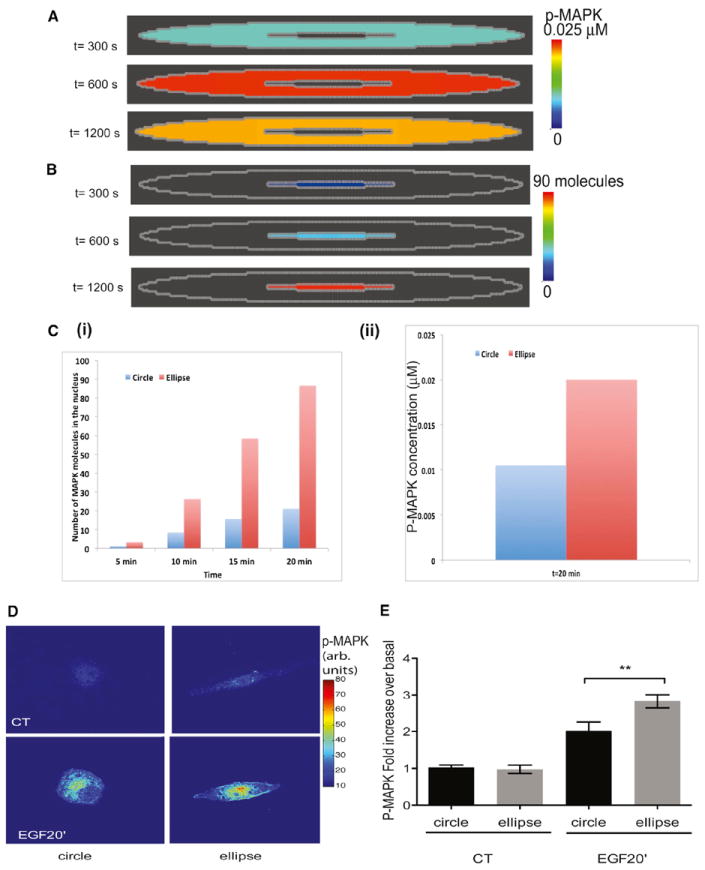
(A) Simulations of the activation of MAPK1,2 in the cytoplasm. The concentration of MAPK1,2 in the cytoplasm follows the kinetics shown in Figure S4—first increasing and then attaining a steady value before decreasing. The spatial distribution of MAPK1,2 in the cytoplasm appears uniform because of the high diffusion coefficient of MAPK1,2 in the cytoplasm. Later time points are shown for comparison with experiments

(B) Simulations of active MAPK1,2 in the nucleus. The concentration of MAPK1,2 increases with time in the nucleus. The spatial distribution of MAPK1,2 in the nucleus appears uniform because of the high diffusion coefficient of active MAPK within the nucleus.

(C) (i) From simulations, the number of molecules of active MAPK1,2 in the nucleus is higher in elliptical cells when compared to the number of active MAPK in circular cells. (ii) The concentration of p-MAPK1,2 in circular and elliptical cells at 20 min is shown from simulations.

(D) Elliptical COS7 cells stimulated with EGF show an enhanced accumulation of phosphor- MAPK. p MAPK1,2 immunostained cells are shown as color-coded grayscale images. Original pseudocolored images are shown in Figure S5.

(E) EGF-treated cells show a higher concentration of p-MAPK1,2 in elliptical cells than in circular cells. Fluorescence intensity ratios of nuclear p-MAPK1,2/MAPK1,2 were plotted as mean ± SEM (n = 15–31; p = 0.0069; one-tailed t test)

See also Figures S4 and S5.

We experimentally tested the prediction that elliptical cells will show higher MAPK1,2 activity in the nucleus as compared to circular cells. Initially, we did this in live-cell imaging experiments. For this, COS-7 cells were transfected with a MAPK1,2 Förster resonance energy transfer (FRET) probe that localizes to the nucleus (Harvey et al., 2008) and were plated on coverslips with microfabricated circular and elliptical wells. The cells were serum starved overnight and then stimulated with EGF, and activated nuclear MAPK1,2 response was measured using FRET. We found that, in elliptical cells, there was an increase in the level of activated MAPK1,2 in the nucleus compared to circular cells (Figure S5). However, these experiments were problematic because the cells transfected with the FRET probe that functions as a de facto dominant negative and plating on the engineered surfaces resulted in a large number of unhealthy cells, leading to variable responses (Figure S5, inset). Hence, we decided to use an immunochemistry approach in which cells plated on microfabricated surfaces were stimulated, fixed, and then stained with phospho-MAPK1,2 antibodies. This approach yielded much more reproducible observations. The nuclei of elongated cells had significantly higher amounts of phosphoto total-MAPK1,2. Representative pseudocolored images are shown in Figure 5D, along with the quantification of the average response in Figure 5E. The original images of the experiment in Figure 5D are in Figure S5. We show that this increase in nuclear MAPK1,2 activation is not due to changes in nuclear area (Figure S5).

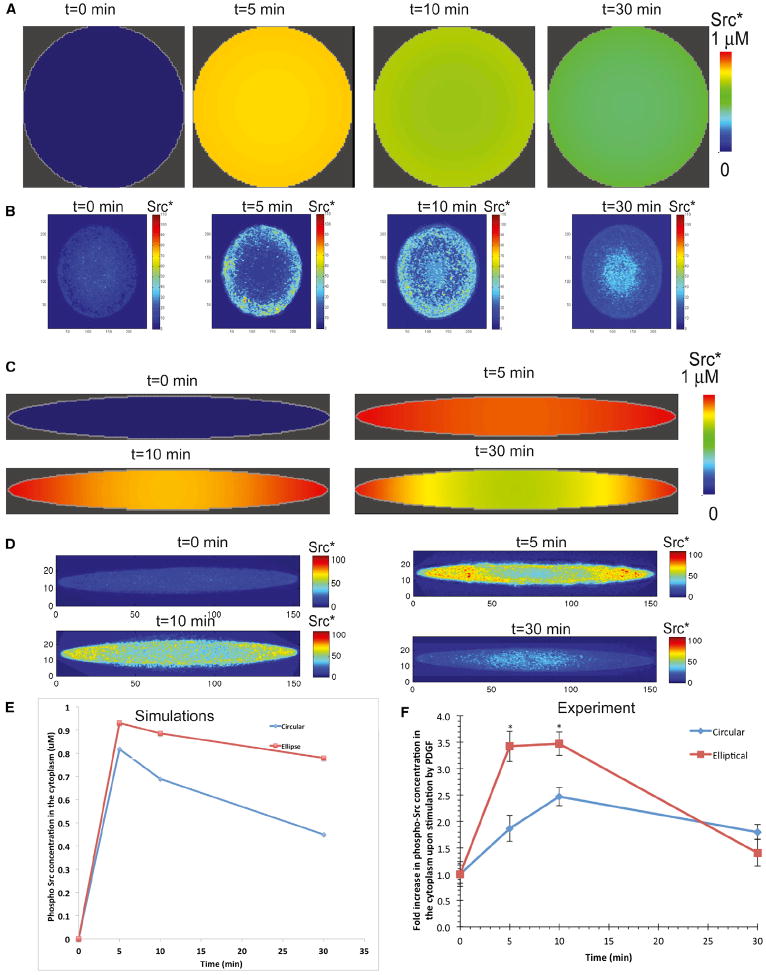
To further establish the general relevance of our findings, we tested our model in another cell type, primary neonatal rat cardiac fibroblasts, where activation of Src is stimulated by the growth factor PDGF. Table S6 shows reactions and various parameters, and experimental time course of p-Src is shown in Figure S6. Whereas circular cells exhibit no spatial variation in Src activation at any time (Figure 6A), elliptical cells generate increased levels of activated Src at the tips where membrane curvature is also higher (Figure 6C).

Figure 6. Levels of PDGF-Activated Phospho-Src in Circle and Elliptically Shaped Cardiac Fibroblasts.

(A) Simulations show that, in circular cells, homogeneous concentration of phospho-Src in the cytoplasm is obtained upon activation of the cells by PDGF.

(B) In experiments, circular cardiac fibroblasts grown in microfabricated grooves (n = 13–19) exhibit nearly uniform activation of Src near the plasma membrane, as measured by quantitative immunofluorescence.

(C) Simulations show that, upon activation, the concentration of phospho-Src leads to a curvature-dependent concentration gradient in the cytoplasm.

(D) In experiments, PDGF-activated phospho-Src in cardiac fibroblasts grown on elliptical cells (n = 12–14) shows a concentration gradient.

(E) Simulations show that phospho-Src in the cytoplasm has a higher concentration in elliptical cells when compared to the concentration of phospho-Src in circular cells.

(F) Summary of experimental data of fold increase of phospho-Src upon PDGF activation for indicated times. Values are means of 12–20 independent cells from two separate experiments and SEM (n = 12–20; *p < 0.001 when comparing ellipses and circles at the same time point; unpaired two-tailed t tests with Bonferroni correction for multiple comparisons).

See also Figure S6 and Table S6.

In order to test these predictions experimentally, primary cardiac fibroblasts were grown on microfabricated surfaces, which resulted in cells with elliptical (eccentricity = 0.99) or circular (eccentricity = 0) shapes. Circular fibroblasts did not exhibit any spatial inhomogeneity of Src activation at any time (Figure 6B); elliptical cells, however, showed a curvature-dependent spatial activation of Src upon stimulation (Figure 6D). This spatial gradient lasted for up to 30 min, demonstrating that the local shape of the cell can induce transient spatial inhomogeneities on the activation of downstream signaling components.

Comparing the concentration of phospho-Src in the cytoplasm shows that elliptical cells have a higher concentration of phospho-Src than circular cells (Figure 6E). This behavior is also observed in experiments, in which elliptical fibroblasts show a higher concentration of phospho-Src when compared to circular cells (Figure 6F). In the case of Src, the cytoplasmic gradient is observed because Src may be associated with endosomal membranes and may not diffuse as fast as MAPK1,2 in the cytoplasm (Kaplan et al., 1992). Thus, the activation of Src through PDGF signaling also shows transient curvature dependence.

DISCUSSION

This study provides evidence that cell shape can play a role in information processing as extracellular signals are transduced to intracellular signals at the plasma membrane. This information-processing capability arises from simple reaction-diffusion kinetics of lateral mobility of proteins in the plane of the membrane and their ability to selectively interact with partners in the aqueous milieu either in the extracellular space, as is the case for receptor agonists, or intracellularly with components in the cytoplasm such as adaptors and exchange factors by receptor tyrosine kinases. Because receptor tyrosine kinases stimulate GTPases such as Rho, Rac, and Cdc42 to affect cell shape and because cell shape can in turn modulate receptor signals flowing through these GTPases, cell shape and growth factor signals can act as a multiscale feedback loop. Such feedback loops could play a role in reinforcing the transformed state, as rate of proliferation can depend on cell shape (Folkman and Moscona, 1978). Although the effects observed at the plasma membrane are small in magnitude, the propagation of these differences along the signaling pathway results in significant changes in downstream effectors such as Src and MAPK such that biologically meaningful effects are likely.

Using a combination of theory, numerical simulations, and experiments, we show that local curvature of the cell can modulate information processing of biochemical signaling pathways. The order of interaction between volume (extracellular and cytoplasmic) and surface (membrane-bound) components also plays an important role in determining the spatial pattern. As shown in Figure 1, in the simple case of one reaction, the resulting spatial gradient can be either Mathieu sine or cosine function. The local competition between reaction and diffusion combined with the reaction direction can lead to a transient inhomogeneity of membrane-bound components resulting solely from cell shapes. This conclusion obtained from our mathematical analyses and numerical simulations illustrates the nonintuitive knowledge of biological mechanisms that can be obtained from theoretical analysis.

The predictions from our model were tested experimentally in different cases. We tested the membrane distribution of receptors for bradykinin and EGF. In both cases, we were able to obtain a good match between the model prediction and the experimental observations. The net result of the curvature-dependent spatial inhomogeneity is that the concentration of downstream cytoplasmic component (MAPK1,2 and Src) is higher in elliptical cells than in circular cells. This observation provides one part of the explanation why cells that have undergone neoplastic transformation can have a higher MAPK activity.

The composition of the plasma membrane is complex, containing regional inhomogeneities in phospholipid and cholesterol concentrations (Eggeling et al., 2009; Lingwood and Simons, 2010) that will alter the lateral mobility of proteins. Additionally, the presence of membrane scaffolds and anchors that connect membrane proteins to the cytoskeleton will also affect lateral mobility. Given these regulatory processes, it would not be possible to fully experimentally decipher what, if any, contribution cell shape alone can make to information processing. The mathematical analyses and numerical simulations shown here clearly demonstrate that the simple physico-chemical properties of the system can enable cell shape to dynamically control information processing as signal flows across the cell-surface membrane. Because cell shape is often the result of prior signaling, in addition to network regulatory motifs such as positive-feedback loops (Bhalla and Iyengar, 1999), cell shape can also be considered a locus of information storage within the cell.

EXPERIMENTAL PROCEDURES

Microfabrication

Circular or elliptical wells were microfabricated with standard photolithography techniques (Qin et al., 2010). Briefly, glass coverslips were cleaned by successive washes in boiling 25% Linbro 7× surfactant and deionized water, nitrogen dried, and treated with oxygen plasma. They were then spin coated with a 500-nm-thick layer of SU-8 2000.5 resist, baked, exposed to UV light on a mask aligner, developed, and rinsed according to the manufacturer’s instructions. The surface area for both elliptical and circular patterns was maintained constant at 2,000 μm². The circular patterns had a diameter of 50 μm. The major axis (r₁) and minor axis (r₂) for elliptical patterns was 134 and 19 μm, respectively.

Diffusion Measurements of EGFR-eGFP in COS-7 Cells

EGFR-eGFP is a kind gift from Dr. Linda Pike (Washington University School of Medicine). Micropatterned coverslips were pretreated with 500 μg/ml Gentamicin (Sigma) and 0.5% Pluronic F127 (Sigma) for 1 hr and washed with distilled water three times. Cells were reverse transfected with Fugene HD using manufacturer’s instructions (Roche Diagnostics). Briefly, EGFR-eGFP and Fugene HD were complexed in a 1:3 μg DNA:μL Fugene ratio and incubated with ~70,000 COS-7 cells in suspension. 36 hr posttransfection, cells were incubated in serum-starving media (DMEM, 0.1% FBS) for 12 hr. At least 1 hr before stimulation, cells were treated with 10 mM NaN₃, 2 mM NaF, and 5 mM 2-deoxy-D-glucose to prevent internalization of EGFR (Liu et al., 2007).

Fluorescence correlation spectroscopy (FCS) measurements were performed on cells expressing EGFR-eGFP using a Zeiss LSM 510 Confocor-2 system equipped with 40× (N.A. 1.2) water immersion objective. eGFP was excited using 488 nm Argon laser, and the focal volume was determined using 10 nM Rhodamine 6G solution (D = 2.8 × 10⁻⁶ cm²/s). The focal volume was focused on either the cell body, which was aligned with the nucleus, or on the cell tip, which was designated as within 5 μm from the apex of the cell shape (Figure S5A). A z axis scan of the cells showed two peaks corresponding to the basolateral and apical membrane populations of EGFR-eGFP (Figure S5B).

The apical peak was chosen for FCS measurements. Each FCS trace was measured for 20 s. EGFR was stimulated using 100 ng/ml of EGF. Measurements were started immediately after EGF addition and were completed within 8 min. Time traces that showed a decrease or increase of intensity were not used for analysis. Autocorrelation functions were analyzed using a two-component, pseudo-2D diffusion model by modifying the 3D fitting routine provided by the Confocor2 software and setting the structural parameter to quasi-infinite: G(τ) = 1 + 1/N{(1+ τ/τ_D)⁻¹[1+ τ(S⁻² τ_D)]^−1/2}, where τ is the correlation time, τ_D is the average time a particle spends in the confocal volume, N is the average number of molecules in the confocal volume, and S is the structural parameter, where S is set to 100 (quasi-infinite) for 2D diffusion. The diffusion coefficient, D, is calculated from the τ_D of a molecule using Einstein relation for diffusion: r² = 4D × τ_D, where r is the radius of the observation volume (Figure S2E). To quantify the number of EGFR-eGFP on the membrane, N was obtained from the fit, which is the average number of receptors in the confocal volume. To determine the concentration of receptors per unit area, N was divided by the area of the beam waist obtained through the calibration of the confocal volume with Rhodamine.

For details on mathematical modeling, simulations using Virtual Cell, the parameters used in the simulations, and standard experimental procedures please see the Supplemental Information.