Abstract
Anatomical contexts (spatial labels) are critical for interpretation of medical imaging content. Numerous approaches have been devised for segmentation, query, and retrieval within the Picture Archive and Communication System (PACS) framework. To date, application-based methods for anatomical localization and tissue classification have yielded the most successful results, but these approaches typically rely upon the availability of standardized imaging sequences. With the ever expanding scope of PACS archives — including multiple imaging modalities, multiple image types within a modality, and multi-site efforts, it is becoming increasingly burdensome to devise a specific method for each data type. To address the challenge of generalizing segmentations from one modality to another, we consider multi-atlas segmentation to transfer label information from labeled T1-weighted MRI data to unlabeled B0 data collected in a diffusion tensor imaging (DTI) experiment. The label transfer approach is fully automated and enables a generalizable cross-modality segmentation method. Herein, we propose a multi-tier multi-atlas segmentation framework for the segmentation of previously unlabeled imaging modalities (e.g., B0 images for DTI analysis). We show that this approach can be used to construct informed structure-wise noise estimates for fractional anisotropy (FA) measurements of DTI. Although this label transfer methodology is demonstrated in the context of quality control of DTI images, the proposed framework is applicable to any application where the segmentation of unlabeled modalities is limited due to the current collection of available atlases.
Keywords: Multi-Atlas Segmentation, PACS-Based Quality Control, Diffusion Tensor Imaging, Fractional Anisotropy
1. INTRODUCTION
Picture Archive and Communication System (PACS) archives are becoming increasingly prevalent for performing large scale analysis of medical images, and, in turn, making powerful clinical inferences about these datasets. Numerous approaches have been devised for segmentation, query, and retrieval within the PACS framework [1, 2]. Yet, these approaches are often highly specialized and limited in their scope of potential applications. With the ever expanding scope of PACS archives — including multiple imaging modalities, multiple image types within a modality, and multi-site efforts, it is becoming increasingly burdensome to devise a specific segmentation method for each data type. As a result, a generalizable framework for performing robust segmentation of wildly varying data has the potential to radically increase the range of potential applications for PACS-based analysis frameworks.
Recently, multi-atlas segmentation models have begun to gain traction as the premier segmentation framework for performing consistent and robust segmentation [3, 4]. While fully-manual techniques suffer from both inter- and intra-rater variability and fully-automated segmentation techniques fail to provide the required robustness, multi-atlas segmentation forms a middle ground between these approaches. In multi-atlas segmentation models, spatial information from an existing dataset (labeled atlases) is transferred to a previously unseen context (target) through a deformable registration. Each atlas provides its own set of labels, creating multiple labeled observations of the target image within the target coordinate system. After performing the deformable registrations, voxelwise label conflicts between the registered atlases are resolved using label fusion [5–7] in order to form a single estimate of the underlying target segmentation. Despite the success of previously proposed multi-atlas segmentation techniques, existing approaches have primarily relied upon using highly consistent and highly controlled datasets (i.e., collected from the same scanner, location, and protocol [3–7]). However, in order for multi-atlas segmentation to be able to be used for clinically relevant applications, the ability to accurately and robustly estimate segmentations for diverse datasets is critical.
In this manuscript, we use multi-atlas segmentation for the robust segmentation of B0 images as part of a quality control framework for Diffusion Tensor Imaging (DTI). DTI is a magnetic resonance (MR) imaging technique that provides contrasts uniquely sensitive to intra-voxel tissue microarchitecture on a scale of tens of microns [8]. DTI has transformed MR neuroimaging studies and has found wide-spread applications in non-invasive assessment of white matter microstructure, reconstruction of major fiber bundles, and mapping of in vivo brain connectivity. Although an invaluable and ubiquitous technique, a DTI experiment is demanding and high quality data is difficult to maintain. The collection of a DTI dataset can consist of up to 90 or more volumes, is aggressive on hardware particularly gradients, and is susceptible to traditional and unique artifacts [9]. Additionally, the processing of DTI data involves mapping data to a logarithmic diffusion model which is well known to induce bias in measured parameters [10]. The documented challenges of producing accurate and biophysically meaningful numbers from a DTI experiment suggest DTI is an important and necessary target for quality analysis evaluation methods. Segmentation methods can significantly bolster automatic quality analysis efforts by enabling the informative projection of statistical parameters across structural regions. In this paper, we provide an inter modality automatic segmentation method for the purposes of creating structurally informed estimates of the noise in fractional anisotropy (FA) estimates.
Unfortunately, existing whole-brain atlases are primarily meant for T1-weighted images, and, as a result, current multi-atlas approaches are limited in their scope of potential applications until the database of potential atlases increases to a broader range of imaging modalities. As a result of this limitation, we propose a multi-tier multi-atlas segmentation framework for the segmentation of previously unseen imaging modalities (e.g., B0 images for DTI analysis). Our multi-atlas approach can be viewed in two distinct steps: (1) we use multi-atlas segmentation in order to construct a collection of B0 atlases, and (2) we use these B0 atlases to perform multi-atlas segmentation of previously unseen DTI images. While we focus on the problem of DTI quality control, the proposed framework could dramatically increase the potential scope of clinically-relevant applications for PACS-based analysis frameworks.
This manuscript is organized in the following manner. First, we provide an overview of our system for constructing intermediate whole-brain B0 atlases. Second, we describe our quality control system for making structurally-informed noise estimates for the estimated FA maps on unseen DTI experiments. Lastly, we provide some brief qualitative and quantitative analysis for the type of information that can be gained using this type of quality analysis system.
2. METHODS AND RESULTS
2.1 Data
Here, we use three distinct datasets in order to perform our analysis. First, we use a collection of T1-weighted atlases that are used for the creation of the B0 atlases. These atlases are part of the Open Access Series of Imaging Studies (OASIS) dataset [11] and were manually labeled by an expert anatomist (courtesy of Neuromorphometrics, Inc. Somerville, MA). For each atlas a collection of 26 labels (including background) were considered: ranging from large structures (e.g., cortical gray matter) to smaller deep brain structures (see Figure 4 for a complete list).
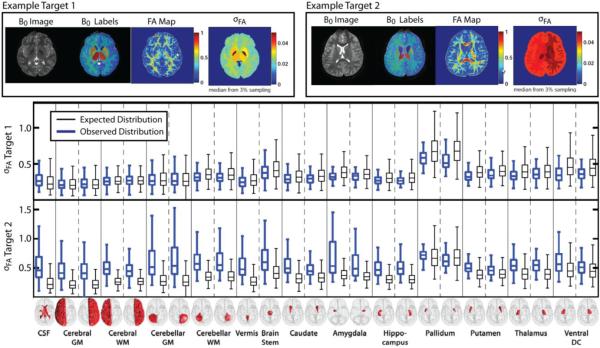
Figure 4.
Example qualitative and quantitative results for the DTI quality analysis framework. Here, two representative subjects are presented. At the top of the figure, the qualitative results are presented. For both target subjects, the B0 image, the B0 segmentation, the estimated voxelwise FA map, and the median structure-wise FA noise estimates are presented using the median value from a wild-bootstrap procedure using 3% of the available voxels for each structure. Lastly, the qualitative results for both target subjects are presented for each subject. For all of the considered structures, the observed distribution of FA values and the expected distribution (from the well-controlled multi-modality dataset) are presented. Note that the observed FA values for the second target subject are significantly different than the expected distribution which indicates the presence of a low-quality DTI dataset.
Second, in order to construct the B0 atlases, we used a collection of data that are part of the Multi-Modal MRI Reproducibility study [12]. Briefly, the study consists of 42 total datasets from 21 subjects, each scanned twice at 3T. Each subject produced both a whole-brain T1-weighted image and DTI image. The T1-weighted images had a voxel resolution of 1.2 × 1.0 × 1.0 mm. The DTI images were acquired with a multi-slice, single-shot, echo planar imaging (EPI) sequence with 32 gradient orientations at a b-value of 700 s/mm2with five signal averages used for the minimally weighted volume. The resulting DTI images consisted of 65 transverse slices with a field-of-view of 212 × 212 mm, reconstructed to 256 × 256 voxels (0.83 × 0.83 × 2 mm). We use the described B0 atlas construction technique in order to provide a whole-brain segmentation of each of the 21 subjects that are part of this dataset.
Lastly, the DTI trial data was collected using echo planar imaging (EPI) on a 3T Philips scanner using an 8 channel head coil. A total of 32 gradient directions were collected using a b-value of 700 s/mm2. The resulting images consisted of 60 transverse slices with a field of view of 212 × 212 × 132 mm, reconstructed to 256 × 256 voxels (0.83 × 0.83 × 2.2 mm).
2.2 Construction of the B0 Atlases
A flowchart demonstrating the creation of the B0 atlases can be seen in Figure 1. The process begins by performing an affine followed by a non-rigid registration (using ART [13]) between the T1 atlases and the provided Multi-Modal T1 subjects. In a recent comparison of several non-rigid registration algorithms [14], ART was shown to be a consistent performer in addition to requiring significant less computation and resources when compared to other non-rigid registration algorithms. After performing these non-rigid registrations, a collection of 15 labeled observations from each subject were created. These labeled observations were then fused using a recently proposed non-local statistical fusion algorithm (Non-Local STAPLE – NLS [5]). Finally, these fused labels were then transferred to the associated B0 image for the same subject using a rigid registration (FSL's FLIRT [15]). This process was then repeated for each of the 21 subjects resulting in 21 intermediate B0 atlases which can then be used for the multi-atlas segmentation of a new, previously unseen DTI target.
Figure 1.
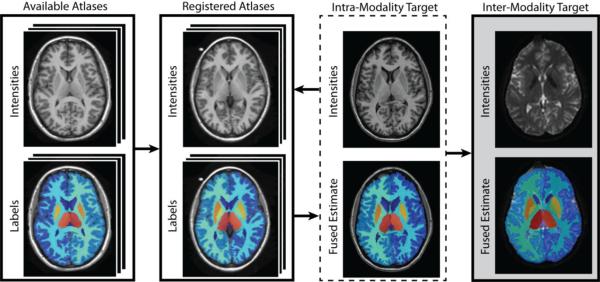
Flowchart demonstrating the B0 atlas construction framework. The process begins by taking a collection of available labeled T1-weighted atlases and performing a non-rigid registration between them and the new, unlabeled, T1-weighted images from a multi-modality dataset. The registered atlases are then fused together (using an existing label fusion algorithm) to form a final estimate for the intra-modality target. Finally, a rigid registration is performed between intra-subject T1-weighted image and the B0 image. A final whole-brain segmentation estimate is then constructed by transferring the labels using the same rigid transformation to the B0 image.
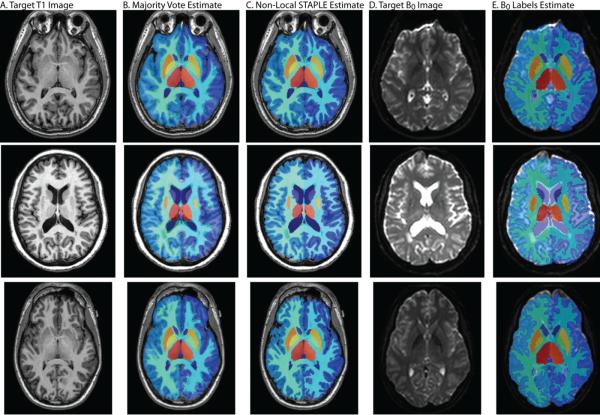
Qualitative results for this process can be seen in Figure 2. Here, we present three representative examples for this atlas creation process. In Figure 1A we present a sample T1-weighted target image from the multi-modal dataset, with associated label estimates from the multi-atlas segmentation process using two different label fusion algorithms: Majority Vote [3] (seen in Figure 2B) and NLS (seen in Figure 2C). Note the clear qualitative improvement provided by NLS over a majority vote, particularly in terms of the quality of estimated cortical gray matter labels. Finally, three representative B0 atlases with their associated label estimates can be seen in Figure 2D and Figure 2E, respectively. Due to the fact that the transfer of these fused labels requires an intra-subject rigid registration, it is expected that the estimated labels would be of a very similar quality to the original T1-weighted labels.
Figure 2.
Example qualitative results from the B0 construction process. Here, three representative target subjects are presented. For each target, the T1-weighted image, the fused labels from a majority vote and the recently proposed Non-Local STAPLE label fusion algorithm are presented. Additionally, the intra-subject B0 image is also presented with the associated final segmentation estimate for this new, previously unseen modality. The B0 segmentation estimate is formed by transferring the Non-Local STAPLE labels via a rigid registration. Note the improvement by Non-Local STAPLE over the standard majority vote based approach.
2.3 PACS-Based DTI Quality Control
Given the provided B0 atlas creation framework, it is now possible to perform multi-atlas segmentation of new, previously unseen, B0 target images that are part of an associated DTI experiment. This multi-atlas segmentation now allows us to make powerful statistical inferences into the relationship between DTI quality analysis and the underlying structure of the image. Here, we use the proposed segmentation framework in order to perform a straightforward, yet powerful inference framework for understanding the local, structure-wise noise in terms of the estimated FA.
An overview of our framework can be seen in Figure 3. The process begins by acquiring a new DTI image using the local PACS-based Vanderbilt Image Processing Enterprise Resource (VIPER). VIPER is an integrated modular quality control system that allows for robust image acquisition using a standard PACS protocol. Once a new DTI image has been acquired, standard DTI processing takes place (e.g., accounting for patient movement via intra-subject rigid registrations) and the FA map is calculated through model fitting procedures for this particular subject. Simultaneously, the pre-computed B0 atlases are used to perform a multi-atlas segmentation of the newly acquired B0 image. The multi-atlas segmentation procedure is identical to the construction of the B0 atlases, where all pairwise registrations are performed using ART and the registered atlases are fused using NLS. Finally, once the FA map and the multi-atlas segmentation of the newly acquired image are performed, local structure-wise noise estimation (i.e., the estimation of σFA) is performed using a bootstrap estimation.
Figure 3.
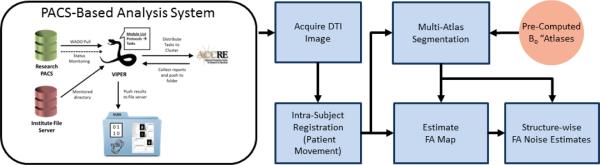
Flowchart demonstrating the PACS-based Diffusion Tensor Imaging quality analysis framework. The framework begins by utilizing a PACS-based framework for acquiring a recently scanned target. Once the DTI image is acquired, standard pre-processing steps are performed for accounting for patient movement via an intra-subject rigid registration. Next, a whole image FA map and the multi-atlas segmentation process (using the pre-computed B0 atlases) are performed simultaneously in order to achieve the pertinent information about the current subject. Finally, structure-wise FA noise estimates are constructed using a wild-bootstrap estimation procedure.
Wild-bootstrap estimation has been adapted for DTI and has recently been demonstrated to produce good estimates of σFA[16], and confidence intervals based upon bootstrap estimates of σFA have been demonstrated to be sensitive to DTI data quality [17]. The premise of bootstrap is that the empirical standard deviation of FA that would be measured if repeated datasets were collected, can be estimated through Monte Carlo simulation of repeated datasets with similar statistical properties as the empirically observed dataset. Measured errors, as determined by the measured versus fitted data, are shuffled and re-added to the fitted data to create new data that is artificially sampled from a population similar to the original measured data. The new data is fit to the diffusion model and a population of FA values is created. This process was repeated for every structure in the multi-atlas segmentation model (using 3% of the total samples per structure) in order to get structure-wise FA noise estimates.
Example results using this DTI quality control framework are shown in Figure 4. Here, we present two representative examples in which meaningful statistical inference can be made about the underlying quality of the DTI data in terms of the structure of the human brain. At the top of Figure 4, visual results for both target images are presented. For each target, the B0 image and labels are presented. Additionally, the estimated FA map, and the median value from the structure-wise noise estimates, σFA, are presented for each structure. Below the qualitative results, quantitative results for each considered structure (from the original T1-weighted atlases) are presented. For both examples, both the observed (blue boxplot) and a canonical (black boxplot) distribution of σFA values are presented. The canonical σFA values are derived from the well-controlled multi-modal dataset that was used to construct the intermediate B0 atlases. These well-controlled results present a representative baseline by which the new DTI datasets can be compared. For the results presented in Figure 4, we show two examples by which largely different inferences can be made. For the example target 1, the structure-wise σFA values are very similar to the expected distribution of noise estimates from the well-controlled dataset. The results for this target are a strong indication that the new, previously unseen, DTI dataset is behaving properly in terms of overall data quality. To contrast, the second example has significantly higher noise. This problem is exhibited both in the qualitative results (top of Figure 4) and the quantitative results (bottom of Figure 4) where the noise estimates are significantly higher than the baseline σFA values estimated from the well-controlled multi-modal dataset.
3. DISCUSSION
The proposed inter-modality analysis framework through multi-atlas segmentation expands the ability of segmentation methods to label a broad range of imaging types present in clinical settings. Herein the segmentation methodology was demonstrated as an integral part of a fully-automated DTI analysis framework intended as a technique for performing large-scale quality control of medical images with only limited user intervention. The key to the implementation of this framework is the development of a technique for constructing intermediate “B0 atlases” without the need for an existing manually labeled dataset of the appropriate modality (Figure 1). Additionally we show that the resulting atlases from this construction framework can be very high quality and not require the need for manual correction or intervention (Figure 2). To demonstrate the potential for this type of framework, we demonstrate a quality control framework for the analysis of DTI images. Here, we use a PACS-based framework to automatically construct a labeled estimate for the B0 image as well as local, structurally-informed noise estimates for the fractional anisotropy of the DTI image (Figure 3). To demonstrate the benefits of this type of approach, we presented both qualitative and quantitative results on two distinct target images that demonstrate the type of inferences that can be made using this analysis framework (Figure 4).
Due to the advancements in multi-atlas segmentation, we can now have confidence in the ability of our approach to construct reasonable atlases from previously unlabeled data and modalities. Herein, we use a very straightforward pairwise registration-based multi-atlas framework for both the construction of the B0 atlases, as well as the segmentation of the new, previously unseen target images. However, in order to implement this on a very large-scale several experiments would have to be performed in order to understand the optimality of the approach. Firstly, we use the non-rigid registration algorithm ART [13]. Significant research would have to take place in order to compare other potential registration algorithms and optimally describe the application at hand (e.g., resource constraints, time constraints, accuracy constraints). For example, if lower quality atlases could be utilized, then it is possible that faster, affine registrations could be used to achieve similar quality control characteristics. Secondly, we use the recently proposed statistical label fusion algorithm, NLS [5]. This approach simultaneously uses rater performance characteristics and the underlying intensity differences between the target and the atlases in order to estimate a globally optimal label estimate. However, this approach can be fairly resource consuming (e.g., 3–4 hours per B0 image). As with the registration approach, less resource consuming approaches could be used (e.g., a majority vote) if lower quality label estimates could be tolerated.
Here, we show how this process can be used for the quality control of DTI images. However, the extension of this technique to other avenues of research (e.g., other MR sequences, MR to computed tomography (CT)) is straightforward and presents fascinating potential. In the end, what we have presented is a fully general framework for analyzing nearly any medical imaging modality or sequence within a PACS-based infrastructure. Today, many PACS archives contain huge numbers of subjects with a wide variety of imaging modalities per subject. As an example, consider a problem where large scale analysis of whole-brain CT images was desired (e.g., for surgical planning purposes). If the proposed model were extended to automatically query the PACS archive for subjects that contain both a whole-brain CT and T1-weighted MRI, then extensive collections of intermediate CT atlases could then be constructed for future analysis of new, previously unseen, patients that have received a whole-brain CT. Additionally, if this query system was taken a step further, it is possible to imagine a PACS-based analysis framework in which huge collections of intermediate atlases are constructed across a wide range of imaging modalities and sequences. In other words, it would be potentially possible to construct intermediate atlases for all imaging modalities in which a single (or collection) of subjects received both the desired modality and a T1-weighted image. The potential for a framework such as this is nearly limitless and would allow for large-scale PACS-based analysis of medical image previously unseen in the research community.
In conclusion, we have demonstrated an expanded application for segmentation methods which enables greater diversity in label transfers and increases the clinical relevance of multi-atlas segmentation. Our method transfers labels from atlases of one image modality (T1-weighted) to a secondary image modality (Bo) for which no atlases exist. The method was incorporated into a fully-automated quality control framework for analysis of acquired DTI images. Our approach requires the (offline) construction of intermediate B0 atlases using a standard pairwise registration multi-atlas segmentation procedure. Using these intermediate B0 atlases, we then show that it is possible to use a PACS-based development environment in order to provide local, structurally-informed, noise estimates for the FA measurements for the quality control of DTI images.
ACKNOWLEDGEMENTS
We would like to acknowledge Michael Esparza for his quality analysis assessment. This research was supported in part by a post-doctoral training grant in image science (T32 EB003817), the Vanderbilt CTSA (UL1 RR024975-01) from NCRR/NIH, and NIH/NINDS 1R21NS064534, 2R01EB006136, 1R03EB012461, R01EB006193.
REFERENCES
- [1].Greenspan H, Pinhas AT. Medical image categorization and retrieval for PACS using the GMM-KL framework. Information Technology in Biomedicine, IEEE Transactions on. 2007;11(2):190–202. doi: 10.1109/titb.2006.874191. [DOI] [PubMed] [Google Scholar]
- [2].Gordon S, Zimmerman G, Greenspan H. Image segmentation of uterine cervix images for indexing in PACS. 2004;298 [Google Scholar]
- [3].Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- [4].Rohlfing T, Russakoff DB, Maurer CR. Performance-based classifier combination in atlas-based image segmentation using expectation-maximization parameter estimation. IEEE Transactions on Medical Imaging. 2004;23(8):983–994. doi: 10.1109/TMI.2004.830803. [DOI] [PubMed] [Google Scholar]
- [5].Asman AJ, Landman BA. Non-Local STAPLE: An Intensity-Driven Multi-Atlas Rater Model. Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2012;7512:417–424. doi: 10.1007/978-3-642-33454-2_53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Transactions on Medical Imaging. 2004;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Sabuncu MR, Yeo BTT, Van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE Transactions on Medical Imaging. 2010;29(10):1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Basser PJ, Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis - a technical review. NMR Biomed. 2002;15(7–8):456–67. doi: 10.1002/nbm.783. [DOI] [PubMed] [Google Scholar]
- [9].Gallichan D, Scholz J, Bartsch A, Behrens TE, Robson MD, Miller KL. Addressing a systematic vibration artifact in diffusion-weighted MRI. Human Brain Mapping. 2010;31(2):193–202. doi: 10.1002/hbm.20856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Jones DK, Basser PJ. Squashing peanuts and smashing pumpkins”: How noise distorts diffusion-weighted MR data. Magnetic Resonance in Medicine. 2004;52(5):979–993. doi: 10.1002/mrm.20283. [DOI] [PubMed] [Google Scholar]
- [11].Marcus DS, Wang TH, Parker J, Csernansky JG, Morris JC, Buckner RL. Open Access Series of Imaging Studies (OASIS): cross-sectional MRI data in young, middle aged, nondemented, and demented older adults. Journal of Cognitive Neuroscience. 2007;19(9):1498–1507. doi: 10.1162/jocn.2007.19.9.1498. [DOI] [PubMed] [Google Scholar]
- [12].Landman BA, Huang AJ, Gifford A, Vikram DS, Lim IAL, Farrell JAD, Bogovic JA, Hua J, Chen M, Jarso S. Multi-Parametric Neuroimaging Reproducibility: A 3T Resource Study. Neuroimage. 2010;54(4):2854–2866. doi: 10.1016/j.neuroimage.2010.11.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Ardekani BA, Braun M, Hutton BF, Kanno I, Iida H. A fully automatic multimodality image registration algorithm. Journal of Computer Assisted Tomography. 1995;19(4):615. doi: 10.1097/00004728-199507000-00022. [DOI] [PubMed] [Google Scholar]
- [14].Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, Christensen GE, Collins DL, Gee J, Hellier P. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. NeuroImage. 2009;46(3):786–802. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Medical Image Analysis. 2001;5(2):143–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- [16].Whitcher B, Tuch DS, Wisco JJ, Sorensen AG, Wang L. Using the wild bootstrap to quantify uncertainty in diffusion tensor imaging. Hum Brain Mapp. 2008;29(3):346–62. doi: 10.1002/hbm.20395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Heim S, Hahn K, Sämann P, Fahrmeir L, Auer D. Assessing DTI data quality using bootstrap analysis. Magnetic Resonance in Medicine. 2004;52(3):582–589. doi: 10.1002/mrm.20169. [DOI] [PubMed] [Google Scholar]