Localization accuracy in single molecule microscopy using electron-multiplying charge-coupled device cameras

Abstract

The electron-multiplying charge-coupled device (EMCCD) is a popular technology for imaging under extremely low light conditions. It has become widely used, for example, in single molecule microscopy experiments where few photons can be detected from the individual molecules of interest. Despite its important role in low light microscopy, however, little has been done in the way of determining how accurately parameters of interest (e.g., location of a single molecule) can be estimated from an image that it produces. Here, we develop the theory for calculating the Fisher information matrix, and hence the Cramer-Rao lower bound-based limit of the accuracy, for estimating parameters from an EMCCD image. An EMCCD operates by amplifying a weak signal that would otherwise be drowned out by the detector’s readout noise as in the case of a conventional charge-coupled device (CCD). The signal amplification is a stochastic electron multiplication process, and is modeled here as a geometrically multiplied branching process. In developing our theory, we also introduce a “noise coefficient” which enables the comparison of the Fisher information of different data models via a scalar quantity. This coefficient importantly allows the selection of the best detector (e.g., EMCCD or CCD), based on factors such as the signal level, and regardless of the specific estimation problem at hand. We apply our theory to the problem of localizing a single molecule, and compare the calculated limits of the localization accuracy with the standard deviations of maximum likelihood location estimates obtained from simulated images of a single molecule.

1. INTRODUCTION

The charge-coupled device (CCD) is a standard image detector with applications in areas as disparate as cellular microscopy and astronomy. However, while its high quantum efficiency renders it the imaging technology of choice in many situations, it is nevertheless unsuitable for imaging under extremely low light conditions. This is primarily due to its measurement noise, which can easily overwhelm the weak signal when few photons are detected from the imaged object. Measurement noise is introduced when the signal is read out from the CCD, and is commonly referred to as the camera’s readout noise.¹

A technology intended as a solution for the readout noise problem under low light conditions is the electron-multiplying charge-coupled device (EMCCD). Similar to a CCD, an EMCCD works by accumulating electrons in proportion to the number of photons it detects. However, it is different in that it can take however many electrons that are accumulated and substantially augment their number via a multiplication process, thereby generating an amplified signal that effectively drowns out the readout noise. The signal amplification is realized by passing the initially accumulated electrons through a gain register consisting of typically several hundred stages. Specifically, electrons are multiplied as each input electron to a given stage generates, with certain probabilities, secondary electrons that are transferred along with the input electron itself to the next stage for further amplification. With such a cascading mechanism, a large number of electrons can be produced at the output of the gain register per initial electron, even when the probabilities with which secondary electrons are generated are usually small (typically 0.01 to 0.02 for one secondary electron per input electron per stage,² and even smaller for multiple secondary electrons per input electron).

Given an image acquired with a CCD or an EMCCD camera, parameters of interest can be estimated that provide useful information about the imaged object. In single molecule microscopy,³ for example, a topic of major interest has been the accurate determination of the location of a fluorescent molecule.^{4, 5} Motivated by this specific estimation problem, we have developed a general framework⁶ for calculating the Fisher information, and hence the Cramer-Rao lower bound,⁷ for the estimation of parameters from an image produced by a microscope. Using this framework, we have derived accuracy limits for estimating the positional coordinates of a single point source^{5, 8} and the distance separating two closely spaced point sources.^{9, 10} These performance measures, however, assume that a CCD is used to acquire the image, and therefore do not apply to images acquired using an EMCCD.

Here, we develop the theory that is needed for deriving the Cramer-Rao lower bound-based limit of the accuracy for estimating a parameter from an EMCCD image. To arrive at the Fisher information for EMCCD data, an expression is required for the probability distribution of the electron count that is obtained from the multiplication process described above. To this end, the stochastic multiplication is modeled as a branching process,¹¹ as others have done in the context of EMCCDs.^{2, 12} However, as opposed to using the typical Bernoulli model where a secondary electron is generated per input electron per stage with probability b, or not generated with probability 1−b, we describe the generation of secondary electrons using a geometric model of multiplication.

Besides deriving a Fisher information expression for EMCCD data, we introduce the notion of a “noise coefficient” which allows the simple comparison of the Fisher information for different data models via a scalar quantity. Using the noise coefficient, we compare the Fisher information for CCD and EMCCD data over a range of expected signal levels. This is an important exercise because electron multiplication is a random process that introduces stochasticity of its own to the data, and should therefore only be used when low signal levels are expected. Comparison using the noise coefficient enables a quantitative determination, based on the expected signal level, of the choice between the CCD and the EMCCD in terms of Fisher information.

The material presented here comprises an important subset of the content of our recent work.¹³ In Section 2, a general result is presented from which the Fisher information expressions for all data models considered in this paper can be obtained. Based on this result, we also define the noise coefficient. In Section 3, a Fisher information expression is presented for data that can be described as the output of a geometrically multiplied branching process with added readout noise. By comparing its corresponding noise coefficient with that for CCD data, we examine the usefulness of electron multiplication as a function of the expected signal level. In Section 4, the theory developed in Sections 2 and 3 for a single signal is generalized for a collection of independent signals which form a CCD or an EMCCD image. This is immediately followed with an example that applies the generalized theory to the problem of localizing a single molecule from an image. Specifically, we calculate the Cramer-Rao lower bound-based limits of the accuracy for estimating the positional coordinates of a point source from a CCD image and an EMCCD image. We also compare the accuracy limits with the results of maximum likelihood estimations performed on simulated image data.

2. THE NOISE COEFFICIENT

We begin with the analysis of the Fisher information content of a scalar random variable that models the data in a single pixel of an EMCCD. Specifically, the signal that is detected is modeled as a Poisson random variable, since photon emission (e.g., by a fluorescent molecule), and hence the detection of those photons by a camera, are typically described as Poisson processes. The actual data in the pixel, however, is a readout noise-corrupted version of the signal that has been stochastically amplified with the intention to drown out the added noise.

Our goal is to calculate the Fisher information matrix pertaining to parameter estimation problems such as the localization of a single molecule from its image. Such estimation problems take on the typical form where the probability distribution of the incident Poisson signal is parameterized by its mean ν. The mean ν, however, is itself a function of the vector θ of parameters (e.g., the positional coordinates of a single molecule) that we want to estimate. We first give an expression for the Fisher information matrix I(θ) of a random variable using this specific parameterization (see our earlier work¹³ for the proof).

Theorem 2.1 Let Z_ν be a continuous (discrete) random variable with probability density (mass) function p_ν, where ν is a scalar parameter. Let ν = ν_θ be a reparameterization of p_ν through the possibly vector-valued parameter θ ∈ Θ, where Θ is the parameter space. We use the notation Z_θ (p_θ) to denote Z_νθ (p_νθ), θ ∈ Θ. Then the Fisher information matrix I(θ) of Z_θ with respect to θ is given by

$$\mathbf{I}(\theta )={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·E\left[{\left(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta }(z))\right)}^2\right].$$ (1)

Note that the scalar expectation term in Eq. 1 is just the Fisher information of the random variable Z_θ with respect to ν_θ.

Two corollaries immediately follow from Theorem 2.1 which pertain to image data acquired under two important scenarios. The first corollary (see our earlier work¹³ for the proof) gives the Fisher information matrix I_P(θ) for the ideal scenario where a Poisson-distributed number of electrons are read out from a camera that introduces no readout noise. This scenario represents the best case wherein a CCD is somehow able to output a pure Poisson signal, and will therefore be used as the benchmark against which practical scenarios are compared. From this point onwards, the function ν_θ will represent the mean of the Poisson signal.

Corollary 2.1 Let Z_θ be a Poisson random variable with mean ν_θ > 0, such that its probability mass function is $p_{\theta ,P}(z)=\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^z}{z!}$, z = 0, 1, …. The Fisher information matrix I_P(θ) of Z_θ is given by

$${\mathbf{I}}_P(\theta )={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·\frac{1}{{\nu }_{\theta }}.$$ (2)

The second corollary (see our earlier work¹³ for the proof) gives the Fisher information matrix I_R(θ) for the practical scenario where readout noise is added to a Poisson-distributed number of electrons when they are read out from a camera. This scenario importantly corresponds to the practical operation of a CCD. As is typically done, this corollary models the readout noise as a Gaussian random variable.

Corollary 2.2 Let Z_θ = V_θ+W, where V_θ is a Poisson random variable with mean ν_θ > 0, and W is a Gaussian random variable with mean η_w and variance ${\sigma }_w^2$. Let V_θ and W be stochastically independent of each other, and let W be not dependent on θ. The probability density function of Z_θ is then the convolution of the Poisson probability mass function with mean ν_θ and the Gaussian probability density function with mean η_w and variance ${\sigma }_w^2$, given by $p_{\theta ,R}(z)=\frac{1}{\sqrt{2\pi }{\sigma }_w}{\displaystyle {\sum }_{j=0}^{\mathrm{\infty }}}\frac{e^{-{\nu }_{\theta }}{\nu }_{\theta }^j}{j!}{e}^{-\frac{1}{2}{(\frac{z-j-{\eta }_w}{{\sigma }_w})}^2}$, z ∈ ℝ. The Fisher information matrix I_R(θ) of Z_θ is given by

$${\mathbf{I}}_R(\theta )={\left(\frac{\partial {\nu }_{\theta }}{\partial \theta }\right)}^T\frac{\partial {\nu }_{\theta }}{\partial \theta }·\left({\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{1}{p_{\theta ,R}(z)}{\left(\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}}{(j-1)!}\right)}^2\mathit{\text{dz}}-1\right).$$ (3)

Note that the probability density function p_θ,R in the above corollary can be found elsewhere.¹

According to Theorem 2.1 and illustrated by Corollaries 2.1 and 2.2, different probability distributions of the random variable Z_θ will produce Fisher information matrices that differ from one another only through the Fisher information of Z_θ with respect to ν_θ (i.e., only through the scalar expectation term of Eq. 1). We therefore propose, for the purpose of comparing the Fisher information of different data models, a “noise coefficient” based on this quantity. Since Eq. 2 gives the Fisher information for the best case scenario of a Poisson signal that is not corrupted by readout noise, we take its scalar expectation term $\frac{1}{{\nu }_{\theta }}$ as the reference, and define the noise coefficient as follows.

Definition 2.1 Let Z_θ be a continuous (discrete) random variable with probability density (mass) function p_θ. Let p_θ be parameterized by θ through the mean ν_θ > 0 of a Poisson-distributed random variable. Then the noise coefficient (with respect to ν_θ) of Z_θ, denoted by α, is given by

$$\alpha ={\nu }_{\theta }·E\left[{\left(\frac{\partial }{\partial {\nu }_{\theta }}\text{ln}(p_{\theta }(z))\right)}^2\right].$$ (4)

The noise coefficient of Eq. 4 is simply the ratio of the Fisher information of Z_θ to that of the ideal, uncorrupted Poisson signal, both with respect to ν_θ. It is a nonnegative scalar, and the larger its value, the higher the amount of information the random variable Z_θ contains about the parameter vector θ. Using the noise coefficient, the Fisher information matrix I(θ) of a random variable Z_θ that falls within the confines of Definition 2.1 can be expressed as I(θ) = α · I_P(θ), where I_P(θ) is the matrix of Eq. 2.

For the ideal scenario of Corollary 2.1 where the data is the pure Poisson signal, the noise coefficient is trivially ${\alpha }_P={\nu }_{\theta }·\frac{1}{{\nu }_{\theta }}=1$. For the practical scenario of Corollary 2.2 where Gaussian readout noise is added to the Poisson signal, the noise coefficient α_R is just

$${\alpha }_R={\nu }_{\theta }·\left({\displaystyle \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}}\frac{1}{p_{\theta ,R}(z)}{\left(\frac{e^{-{\nu }_{\theta }}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=1}^{\mathrm{\infty }}}\frac{{\nu }_{\theta }^{j-1}{e}^{-\frac{1}{2}{\left(\frac{z-j-{\eta }_w}{{\sigma }_w}\right)}^2}}{(j-1)!}\right)}^2\mathit{\text{dz}}-1\right),$$ (5)

and the Fisher information matrix I_R(θ) of Eq. 3 can be written as I_R(θ) = α_R · I_P(θ).

The results presented thus far, and the result to be presented in Section 3, entail data that can be described as a Poisson signal with mean ν_θ that may have been stochastically amplified by some random function M before potentially being corrupted by some additive readout noise W. Since neither the stochasticity introduced by the multiplication nor the readout noise is dependent on θ, they contribute no additional information about θ. The noise coefficient α for these data models can therefore be expected to be at most 1 (i.e., at most α_P), and we state this result formally in the following theorem (see our earlier work¹³ for the proof).

Theorem 2.2 Let Θ be a parameter space and let Z_θ = M(V_θ) + W, θ ∈ Θ, where V_θ is a Poisson random variable with mean ν_θ > 0, M is a random function, and W is a scalar-valued random variable. We assume that V_θ, M, and W are stochastically independent. Then, for the noise coefficient α of Z_θ, 0 ≤ α ≤ 1.

3. GEOMETRIC SIGNAL MULTIPLICATION

As stated in Section 1, we model electron multiplication in an EMCCD pixel as a branching process¹¹ that is geometrically multiplied. Specifically, the branching process is one where an initial Poisson-distributed number of signal electrons are fed into a series of stages, and where in each stage, an input electron generates a total of k electrons, including itself, according to the zero modified geometric distribution¹⁴ defined as follows.

Definition 3.1 A zero modified geometric distribution is a probability distribution (p_k)_k=0,1,… given by

$$p_k=\{\begin{array}{cc}a,\hfill & k=0,\hfill \\ (1-a)(1-b)b^{k-1},\hfill & k=1,2,\dots ,\hfill \end{array}$$ (6)

where 0 ≤ a < 1 and 0 ≤ b < 1.

It is easily verified that the zero modified geometric distribution has mean $m=\frac{1-a}{1-b}\text{ and variance }{\sigma }^2=\frac{(1-a)(b+a)}{{(1-b)}^2}$. Importantly, it has a probability generating function of linear fractional form, a special property which allows the probability distribution of the number of electrons X_N,θ at the output of an N-stage branching process with a zero modified geometric model of multiplication to be specified explicitly without recursion.¹¹ Moreover, Definition 3.1 shows that the zero modified geometric distribution allows the possibility of obtaining zero or more electrons per input electron per stage (including the input electron itself). This makes it suitable for modeling signal amplification in an EMCCD, since electron loss mechanisms may exist during the multiplication, and since it is possible that more than one secondary electron is generated per input electron per stage.¹² By setting the parameter a = 0, the zero modified geometric distribution of Eq. 6 reduces to the standard geometric distribution p_k = (1 − b)b^k−1, k = 1,2,…, with mean $m=\frac{1}{1-b}\text{ and variance }{\sigma }^2=\frac{b}{{(1-b)}^2}$. While the more general zero modified geometric distribution will be used in the next theorem, the standard geometric distribution will be assumed for all subsequent illustrations.

Using the theory of probability generating functions, a probability mass function was previously derived¹³ for the number of electrons X_N,θ at the output of an N-stage branching process with an initial Poisson-distributed number of electrons and a zero modified geometric model of multiplication. Since we model the data Z_θ in a given pixel of an EMCCD as the sum of X_N,θ and a Gaussian random variable W representing the readout noise, the probability density function of Z_θ is the convolution of the probability mass function of X_N,θ and a Gaussian probability density function. The following Theorem gives this density function and the corresponding noise coefficient and Fisher information matrix.

Theorem 3.1 Let Z_θ = X_N,θ + W, where X_N,θ, N ∈ {0, 1, …}, is the number of particles at the output of an N-stage branching process with an initial Poisson-distributed particle count with mean ν_θ > 0 and a zero modified geometric model of multiplication, and W is a Gaussian random variable with mean η_w and variance ${\sigma }_w^2$. Let X_N,θ and W be stochastically independent, and let W be not dependent on θ.

1. The probability density function of Z_θ is, for z ∈ ℝ,

   $$p_{\theta ,\mathit{\text{GeomR}}}(z)=\frac{e^{-{\nu }_{\theta }\frac{A}{B}}}{\sqrt{2\pi }{\sigma }_w}\left[e^{-{\left(\frac{z-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}+{\displaystyle \sum _{l=1}^{\mathrm{\infty }}}{e}^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}{\displaystyle \sum _{j=0}^{l-1}}\frac{\left(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array}\right)C^{l-1-j}{(D{\nu }_{\theta })}^{j+1}}{(j+1)!B^{j+l+1}}\right],$$ (7)

   where A = (1 − a)(m − 1)m^N, B = b(m^N − 1)m + (1 − a)(m − 1), C = b(m^N − 1)m, D = m^N(1 − a)²(m − 1)², $m=\frac{1-a}{1-b}\ne 1,\mathit{\text{ and }}\left(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array}\right)$ denotes “l − 1 choose j”.
2. The noise coefficient corresponding to p_θ,GeomR is

   $${\alpha }_{\mathit{\text{GeomR}}}={\nu }_{\theta }·\left({\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}\frac{D^2{e}^{-2{\nu }_{\theta }\frac{A}{B}}}{p_{\theta ,\mathit{\text{GeomR}}}(z)}{\left({\displaystyle \sum _{l=1}^{\mathrm{\infty }}}\frac{e^{-{\left(\frac{z-l-{\eta }_w}{\sqrt{2}{\sigma }_w}\right)}^2}}{\sqrt{2\pi }{\sigma }_w}{\displaystyle \sum _{j=0}^{l-1}}\frac{\left(\begin{array}{c}\hfill l-1\hfill \\ \hfill j\hfill \end{array}\right)C^{l-1-j}}{j!B^{j+l+1}{(D{\nu }_{\theta })}^{-j}}\right)}^2\mathit{\text{dz}}-\frac{A^2}{B^2}\right),$$ (8)

   and the Fisher information matrix of Z_θ is I_GeomR(θ) = α_GeomR · I_P(θ), where I_P(θ) is as given in Eq. 2.

The term m^N in Eqs. 7 and 8 is called the mean gain, and is the average number of electrons at the output of the multiplication process given a single initial electron.

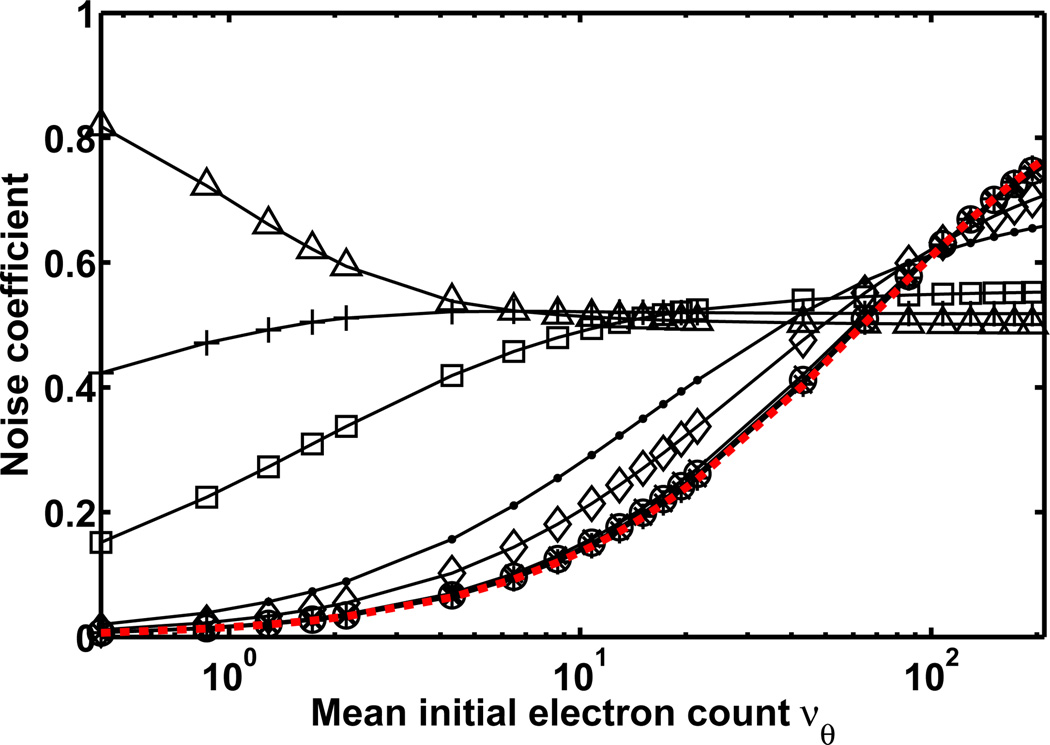
To demonstrate a comparison of the Fisher information of different data models using the noise coefficient, Fig. 1 plots, as a function of the mean ν_θ of the initial Poisson electron count, the noise coefficient α_R of Eq. 5, and the noise coefficient α_GeomR of Eq. 8 for different mean gain values and with a = 0 for standard geometric multiplication. In accordance with Theorem 2.2, the plot shows that α_R and α_GeomR take on values between 0 and 1 for any value of ν_θ. The Fisher information matrices I_R(θ) and I_GeomR(θ) are therefore, as expected, no greater than I_P(θ) of the ideal scenario of Corollary 2.1.

Figure 1.

Noise coefficient α_R of Eq. 5 and noise coefficient α_GeomR of Eq. 8 plotted as a function of the mean ν_θ of the signal, which ranges in value from 0.43 to 194.19 electrons. Noise coefficient α_R (red curve) corresponds to the scenario of a Poisson signal that is corrupted by readout noise, and noise coefficient α_GeomR (black curves with markers) corresponds to the scenario of a Poisson signal that is amplified by multiplication and subsequently corrupted by readout noise. In the case of α_GeomR, the signal is amplified through N = 536 stages (as in the gain register of a CCD97 chip, E2V Technologies, Chelmsford, UK) of standard geometric multiplication (i.e., a = 0 in Eq. 8), and the different curves correspond to mean gain values of m^N = 1.01 (*), 1.03 (○), 1.06 (×), 1.31 (◊), 1.71 (·), 4.98 (□), 14.49 (+), and 1015.46 (Δ). For both α_R and α_GeomR, the readout noise is Gaussian with mean η_w = 0 e⁻ and standard deviation σ_w = 8 e⁻.

The figure further shows, for the set of mean gain values used, that α_GeomR is greater than α_R for ν_θ values of up to roughly 60 electrons. In this range of ν_θ values, a higher mean gain generally yields a larger α_GeomR. Beyond roughly ν_θ = 60 electrons, however, α_GeomR starts to become smaller than α_R in order of decreasing mean gain. By roughly ν_θ = 130 electrons, multiplication with any of the mean gain values yields an α_GeomR that is less than α_R. Figure 1 thus demonstrates that electron multiplication is beneficial when the expected signal level is relatively low (or equivalently, when the readout noise level is relatively significant). When the expected signal level is relatively high such that the readout noise level is already insignificant in comparison, multiplication has the undesirable net effect of introducing additional stochasticity to the data. Though these observations are generally known, we have demonstrated them quantitatively as a function of the expected signal level, and from the perspective of Fisher information.

4. GENERALIZATION TO AN IMAGE

The theory we have developed in the previous sections applies to a single pixel of a CCD-based detector. By making the reasonable assumption that the data in different pixels of an image are independent measurements, however, the Fisher information matrix for an image is just the sum of the Fisher information matrices for its pixels. For an image of K pixels, the Fisher information matrix can thus be written as ${\mathbf{I}}_{\mathit{\text{im}}}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_k(\theta )={\displaystyle {\sum }_{k=1}^K}{\alpha }_k·{\mathbf{I}}_{P,k}(\theta )$, where the notation is as before and the subscript k denotes quantity for the k^th pixel. It follows that for an ideal K-pixel image of uncorrupted Poisson signals, (i.e., α_k = 1 for k = 1, …, K), the Fisher information matrix is just ${\mathbf{I}}_{\mathit{\text{im}},P}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_{P,k}(\theta )$. Using these expressions, we give an inequality (see our earlier work¹³ for the proof) which relates I_im(θ) for a practical image to I_im,P(θ) for its corresponding ideal image.

Theorem 4.1 Let ${\mathbf{I}}_{\mathit{\text{im}}}(\theta )={\displaystyle {\sum }_{k=1}^K}{\alpha }_k·{\mathbf{I}}_{P,k}(\theta ),\mathit{\text{ and let }}{\mathbf{I}}_{\mathit{\text{im}},P}(\theta )={\displaystyle {\sum }_{k=1}^K}{\mathbf{I}}_{P,k}(\theta )$. Let α_min and α_max denote, respectively, the smallest and the largest elements in the sequence (α_k)_{k = 1, …, K}. Then we have

$${\alpha }_{\mathit{\text{min}}}·{\mathbf{I}}_{\mathit{\text{im}},P}(\theta )\le {\mathbf{I}}_{\mathit{\text{im}}}(\theta )\le {\alpha }_{\mathit{\text{max}}}·{\mathbf{I}}_{\mathit{\text{im}},P}(\theta ).$$

Theorem 4.1 can be used to assess how close a practical image is to its corresponding ideal image in terms of Fisher information content. It will be used in the example that follows.

To conclude this paper, we apply our theory to the localization of a fluorescent molecule. We consider the estimation of the location of an in-focus point source (i.e., a single molecule) from its image as observed through a fluorescence microscope and detected by a CCD or an EMCCD camera. For this problem, the mean of the Poisson-distributed electron count at the k^th pixel of the camera due to detected photons can be shown to be⁶

$${\nu }_{\theta ,k}=\frac{N_{\mathit{\text{photon}}}}{M^2}{\displaystyle {\int }_{C_k}}q(x/M-x_0,y/M-y_0)\mathit{\text{dxdy}}+{\beta }_k,$$ (9)

where N_photon is the expected number of photons from the point source that are detected at the detector plane, x₀ and y₀ are the x and y coordinates of the point source in the object space where it resides, M is the magnification of the microscope, C_k is the region in the detector plane occupied by the pixel, and β_k is the expected number of background photons (i.e., photons from anything other than the point source) detected at the pixel, which is assumed to be Poisson-distributed and independent of the number of photons detected from the point source. The function q is referred to as an image function,⁶ and describes the image at unit magnification of a point source that is located at the origin of the object space coordinate system. Here, we assume the image of our point source to be given by the classical Airy point spread function,¹⁵ and q can thus be written as⁶

$$q(x,y)=\frac{J_1^2\left(\frac{2\pi n_a}{\lambda }\sqrt{x^2+y^2}\right)}{\pi (x^2+y^2)},(x,y)\in {ℝ}^2,$$

where n_a is the numerical aperture of the objective lens, λ is the wavelength of the photons detected from the point source, and J₁ is the first order Bessel function of the first kind.

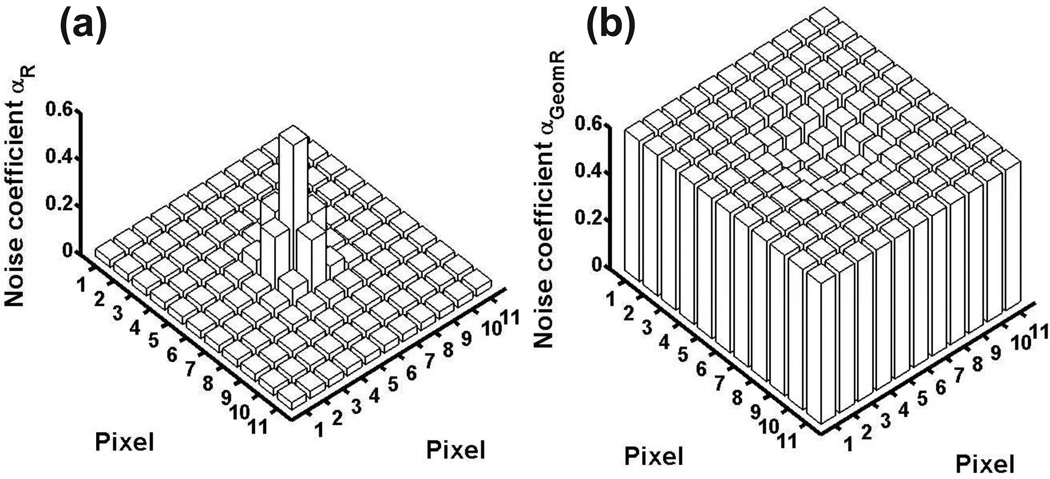
Using Eq. 9 and the point source attributes and imaging parameters given in Fig. 2, the mean initial electron counts in the pixels of an 11-by-11 pixel image were calculated. Using these values, the noise coefficients for the ideal, the CCD, and the EMCCD data models were then computed. By definition, the noise coefficient α_P of the ideal Poisson data scenario is trivially 1 for every pixel of the image. For the CCD and the EMCCD scenarios, their noise coefficient profiles are plotted in Fig. 2. Shown in part (a) of the figure, α_R (Eq. 5) for the pixels of the CCD scenario exhibits a relatively wide range of values from 0.031 to 0.579. By Theorem 4.1, this implies that the Fisher information for this scenario is somewhere between 3% and 58% of that for the ideal scenario. In contrast, and shown in Fig. 2(b), α_GeomR (Eq. 8) for the pixels of the EMCCD scenario exhibits a much narrower range of values from 0.502 to 0.597. Therefore, a much tighter bound can be obtained for the Fisher information in this case using Theorem 4.1, which indicates that the information content is somewhere between 50% and 60% of that for the ideal scenario. Note that the relatively large minimum α_GeomR of 0.502 represents a significant increase in the information content of all but the center pixel due to the high mean gain multiplication. The center pixel has by far the highest signal level, and actually has an α_GeomR that is smaller than α_R. This reiterates the idea that EMCCD amplification is most beneficial when the signal level is low, and is minimally useful or even harmful when the signal level is high.

Figure 2.

Noise coefficient (α_R for (a), α_GeomR for (b)) profile for (a) a CCD image and (b) an EMCCD image of an in-focus point source. The point source is assumed to emit photons of wavelength λ = 520 nm, which are collected by an objective lens with magnification M = 100 and numerical aperture n_a = 1.4. The image of the point source is given by the Airy point spread function, and is centered on an 11-by-11 array of 16 µm by 16 µm pixels (i.e., x₀ = y₀ = 880 nm, assuming the upper left corner of the pixel array is (0, 0)). The expected number of photons detected from the point source is set to N_photon = 200. The expected number of background photons is set to β_k = 2 for every pixel k. In (a), readout noise with mean η_w = 0 e⁻ and standard deviation σ_w = 8 e⁻ is assumed for every pixel. In (b), the standard deviation is higher at σ_w = 24 e⁻, and standard geometric multiplication with a mean gain of m⁵³⁶ = 900 is assumed.

To demonstrate what the noise coefficient profiles of Figs. 2(a) and 2(b) translate to in terms of parameter estimation accuracy, the Cramer-Rao lower bound-based limits of the accuracy for localizing the point source were calculated for all three data scenarios. Specifically, by defining the coordinates of the point source as the unknown parameters to be estimated (i.e., by defining θ = (x₀, y₀)), the limits of accuracy were obtained as $\sqrt{{[{\mathbf{I}}_{\mathit{\text{im}}}^{-1}(\theta )]}_{11}}\text{ for }{x}_0\text{ and }\sqrt{{[{\mathbf{I}}_{\mathit{\text{im}}}^{-1}(\theta )]}_{22}}$ for y₀, where I_im(θ) was calculated for each data scenario using its respective noise coefficient profile. Since the accuracy limit is identical for x₀ and y₀ due to the symmetry of the image as defined, it is simply referred to as the limit of the localization accuracy in Table 1. As shown in this table, the best accuracy limit of 7.48 nm, as expected, belongs to the ideal scenario of Poisson data. In sharp contrast and worse by more than a factor of two, the poorest accuracy limit of 16.41 nm belongs to the CCD scenario due to the corruption of the Poisson signals by the camera readout noise. However, demonstrating the effect of using high mean gain electron multiplication to drown out the readout noise, the table shows that a significantly improved accuracy limit of 10.47 nm is obtained for the EMCCD scenario.

Table 1.

Limits of the localization accuracy and results of maximum likelihood estimations using simulated images.

Data model	Number of x0 estimates	True x0 (nm)	Mean of x0 estimates (nm)	Limit of the localization accuracy (nm)	Standard deviation of x0 estimates (nm)
Ideal	1000	880	880.17	7.48	7.56
CCD	995a	880	880.03	16.41	16.30
EMCCD	1000	880	879.74	10.47	10.47

^aFive outlier estimates which place the center of the point source’s image outside the pixel array have been excluded.

Additionally, Table 1 shows, for each data scenario, the mean and standard deviation of the x₀ estimates produced by maximum likelihood estimations performed on 1000 simulated images of the point source. For each data scenario, the mean of the estimates is very close to the true value of x₀, and the standard deviation of the estimates closely recovers the corresponding limit of the localization accuracy. These results suggest that the maximum likelihood estimator is able to achieve the Cramer-Rao lower bound. Details pertaining to the generation of the simulated images and the implementation of the maximum likelihood estimator for each data scenario are as described in our earlier work.¹³