NONUNIFORM FOURIER TRANSFORMS FOR RIGID-BODY AND MULTI-DIMENSIONAL ROTATIONAL CORRELATIONS

Abstract

The task of evaluating correlations is central to computational structural biology. The rigid-body correlation problem seeks the rigid-body transformation (R, t), R ∈ SO(3), t ∈ ℝ³ that maximizes the correlation between a pair of input scalar-valued functions representing molecular structures. Exhaustive solutions to the rigid-body correlation problem take advantage of the fast Fourier transform to achieve a speedup either with respect to the sought translation or rotation. We present PFcorr, a new exhaustive solution, based on the non-equispaced SO(3) Fourier transform, to the rigid-body correlation problem; unlike previous solutions, ours achieves a combination of translational and rotational speedups without requiring equispaced grids. PFcorr can be straightforwardly applied to a variety of problems in protein structure prediction and refinement that involve correlations under rigid-body motions of the protein. Additionally, we show how it applies, along with an appropriate flexibility model, to analogs of the above problems in which the flexibility of the protein is relevant.

1. Introduction

Structural interactions between proteins are responsible for their functions as building blocks in our cells. In order to understand protein interactions, it is essential to determine the three-dimensional structure of the participating protein or smaller protein subunits. Based on the analysis of data obtained via X-ray crystallography, NMR spectroscopy or Electron Microscopy (EM), the structure of proteins can be evaluated. Typical tasks in protein structure evaluation include molecular replacement to identify protein crystal structures [39], protein-protein docking to calculate the structure of newly-formed protein complexes [19] or protein match and fit to refine low resolution maps of proteins by replacement of known atomic structures [53].

One common aspect of these tasks is an optimization problem. The solution space is the set of motions and transformations the molecules or groups of atoms can undergo, while the objective function evaluates the quality of the complex with respect to the task. The vast variety of approaches to this problem differ in the choice of the solution space, description of the molecules or molecular subunits, the way the solution space is searched, and the metric used to evaluate the quality of the complexes.

In this paper we address the optimization problem by a fast Fourier-based evaluation of correlations over three dimensional rigid-body motion, i.e., given a pair of functions, we find the rigid-body transformation such that the overlap of the two functions is maximized. The primary contribution of this work is PFcorr, a Fourier-based approach to solve multi-dimensional rotational correlation problems. PFcorr addresses two major deficiencies/drawbacks in prior Fourier-based approaches; we discuss these drawbacks in the following section, which also provides a brief overview of present work in this area. Section 3 provides necessary mathematical preliminaries to compute rigid-body correlations, which are described in detail in Section 4. We continue by giving a practical description of a matching/correlation procedure which can be used as a step-by-step guideline using PFcorr. This includes sampling considerations and numerical results. In Section 5, we apply PFcorr to the complementary problem of flexible multi-dimensional correlations, which takes into account the flexibility of proteins in solvent (see Figure 1.1). We solve the flexible correlation problem with a suitable parametrization of the space of flexible motions of the protein, after which each element of that space is just a rigid entity, conducive to rigid-body correlations.

Fig. 1.1.

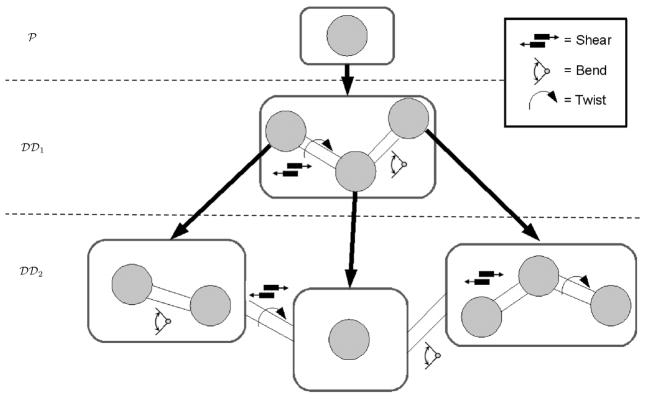
Domain-based flexible fitting as a sample application of the flexible correlation algorithm using PFcorr. The Figure chose an example of a domain decomposition with 3 hierarchical levels. The protein crystal structure is decomposed into domains at level 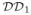according to a chosen criterion. The domains of 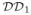are consecutively decomposed into domains at level 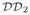. The motions between pairs of domains of 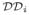can be specified in a motion graph. They imply a set of rigid-body transformations with respect to the domains.

2. Related and prior work

Solving optimization problems for protein structure interpretation reduces to a correlation based scoring and search over a space of relative transformations. The objective function in general is highly non-convex, possessing several local maxima and minima. The vast number of existing solutions to the rigid-body correlation problem can be distinguished by a few basic approaches. Feature-based methods compute and correlate reduced representations of proteins. An early example of a feature-based approach is the method of vector quantization [54], in which sets of vectors are used to represent molecules. A similar approach is geometric hashing [23], whereby critical features are hashed into a table of values, and a score—related to the correlation score—measures the match between the participating proteins for a particular relative orientation. Feature-based approaches, used in docking [40] and fitting [50], result in improved performance due to the reduced search space, at the possible expense of poor resolution scaling.

Iterative approaches vary in sophistication, ranging from a simple version of steepest ascent [30] to more powerful techniques such as Powell optimization [51]. Most such approaches result in locally optimal solutions that, depending on the initial guess, may or may not be close to the globally optimal correlation. They are thus usually used in conjunction with an exhaustive approach that provides the requisite initial guess.

Exhaustive or Fourier-based approaches exploit the fact that it is beneficial if the computation of the objective function can be done relatively fast or if the search space is restricted. In these approaches the proteins are treated as rigid bodies. The automated search of all possible motions, i.e., translations and rotations to maximize the overlap between both structures is the main task of these programs. This is done by evaluating a correlation integral with respect to the motions using Fast Fourier transforms. Fourier based methods combine an accurate and exhaustive search with reduced computational cost, and have thus proven quite popular as a search scheme, see, e.g. [3, 7, 16, 26, 31, 37, 52, 57]. Many, if not most, existing Fourier-based docking algorithms use a regular discrete three-dimensional cartesian grid onto which the molecules are projected. The correlation score of these discretised and suitably weighted structures serves as the objective function for the optimization problem. The correlation score between pairs of grid cells is computed via fast Fourier transforms, thus implicitly searching over the three dimensional space of translations. The remaining rotational degrees of freedom however need to be incorporated into a global search. Such an approach has been first published by [19] in 1992. Since then, this approach has been adapted and improved many times. An overview of these translational grid-based FFT search schemes can be found in [9]. In recent approaches, the equispaced grid has been replaced with a non-equispaced Cartesian one, as in [3], or a polar one, as in [10, 13, 38, 44]. Fast translational matching exploits the fact that for each rotation, the objective function is a correlation integral, and can be computed by fast Fourier transforms. On the other hand, the space of rotations is still subject to exhaustive search.

While the optimal matching solution exists in a highly localized region of relative translations, the range of relative rotations varies widely for each translation. The disparity between size and sampling density of translational and rotational search spaces motivates this work. We present a fast rotational correlation matching that extends the methods of [38] and [44], which use spherical harmonic functions and classical orthogonal polynomials to model molecular shapes. We employ algorithms to compute the fast Fourier transform on the rotation group to solve the matching problem. In this work, instead of correlating functions defined on the unit cube, we use functions defined on ℝ³ but split into ℝ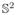⁺ × . We exploit the fact that correlations of functions defined on 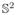can be computed by means of Fourier transforms on the rotation group. This enables efficient computation of the objective function over rotational degrees of freedom instead of translational degrees of freedom.

A three-dimensional translation can be expressed as a translation along the z-axis followed by two rotations, one about the y-axis and one about the z-axis. Hence, it has two rotational degrees of freedom and one translational. Combining this in a motion, we have five rotation angles that describe a motion and one absolute value of a translation along one axis. If we are able to speed up the computation for the rotations by correlating functions on the sphere, we get an improved complexity for five of the six degrees of freedom instead of the previous three. This approach has been suggested in [21] for protein fitting and can also be found in [10].

The essential mathematical tool used in this work for protein fitting is the fast calculation of the discrete Fourier transform on the rotation group SO(3). An implementation of such an algorithm can be found in [34]. For completeness, we also mention the related work of [15] and [6]. The paper of [15] uses representation theory of the rotation group for approaching optimization problems in the cryoEM setting, as we do. However the nature of our optimization problem is fundamentally different than theirs. The paper of [6] develops discrete Fourier transforms on the motion group SE(3), and applies it to topics ranging from workspace density of robotic manipulators to conformational statistics of macromolecules. This is quite different to our use of the fast discrete Fourier transform on the rotation group SO(3), to provide an efficient solution to our optimization problem.

Current exhaustive techniques suffer from two main drawbacks. The first drawback relates to local refinement. Depending as they do on the equispaced FFT, exhaustive techniques cannot be gracefully used to refine existing solutions. Say we wish to improve a matching pose, obtained using a translational FFT speedup with a certain grid size. If we redo the experiment with half the grid length of the previous computation, the three dimensional FFT becomes eight times as expensive, but more importantly, it spends much of its time at points on the new grid already excluded by the initial experiment. A similar argument applies to rotational speedups; in both these approaches, the concept of a local refinement is largely absent.

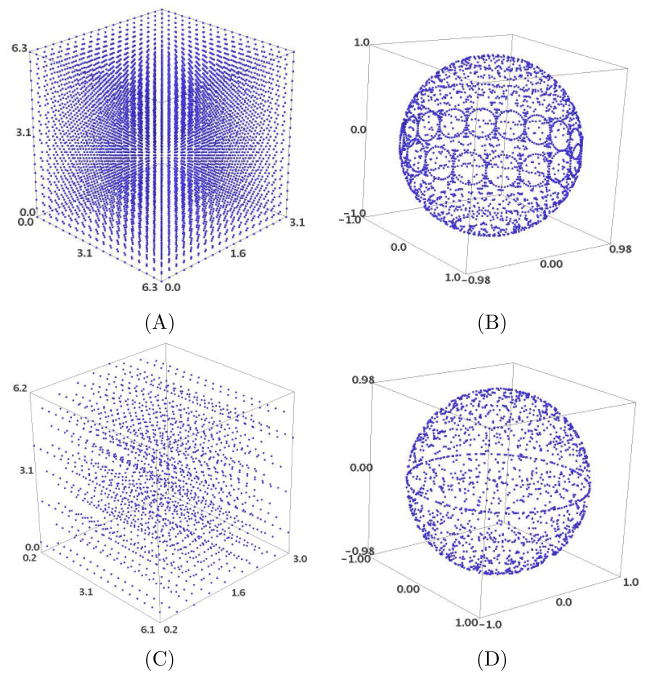
A second drawback relates to the question of uniform sampling in rotational space. While sampling in translational space is straightforward, involving Cartesian grids with uniform, possibly differing grid-sizes in each independent direction, the notions of uniformity and direction do not translate easily to the rotational space SO(3). In particular, equispaced Euler angular grids do not result in equispaced SO(3) samples as is illustrated in Figure 2.1. Due to this, rotational FFT-based techniques are destined to oversample certain regions of SO(3) while leaving others wholly unexamined.

Fig. 2.1.

(A) A uniform grid with respect to three Euler Angles grid with angular resolution 20° in each angle leads to (B) a non-uniform sampling of SO(3), with very high angular resolution in certain regions and holes in certain others. By contrast, (C) a highly non-uniform Euler angular grid leads to (D) a more uniform sampling of SO(3). (C) and (D) were obtained by the techniques in [28]; they contain fewer samples, exhibit a separation very close to the required angular resolution of 20°, and are highly uniform with respect to suitable metrics on SO(3). We discuss sampling on SO(3) in Section 4.1.

2.1. Proteins and flexibility

One main point of criticism of rigid-body fitting methods is that proteins undergo conformational changes during the induced fit, i.e., they not only move with respect to each other but also deform, shear or bend. Flexibility often involves movements between large rigid parts of the protein, called domains, flexible loops on the molecular surface and large side chain at active sites. A commonly used method to deal with flexibility is using multi-copying approaches or multi-term potentials. Due to the vastness of the space of flexible motions, protein flexibility can be practically dealt with by (A) conducting all-atomistic local searches, as in the case of molecular dynamical algorithms [17, 18, 24, 42, 43], (B) Building a coarse-grained representation of the protein, also known as a domain decomposition [1, 11, 33, 41], or (C) A combination of the strategies in (A) and (B) [47, 48, 59].

Domain-based approaches have so far lacked a search scheme that takes advantage of the translational or rotational speedups that FFT-based approaches can afford. This has to do with the issue of focusing: in uniform FFT-based techniques, there is no way to restrict the search space to a small area of interest that can be occupied by a single domain rather than the entire protein. By contrast, searching over the entire space for each domain is both time-consuming and results in spurious and geometrically implausible false positives, and sifting through these grows rapidly inefficient as the number of domains increases. This is also why domain-based flexibility algorithms such as those in [46, 47, 48] prefer Monte-Carlo-based or steepest-ascent-based search schemes.

2.2. Our contributions

We address the drawbacks mentioned in Section 2 with a pair of rotationally exhaustive, non-equispaced techniques to compute rigid-body correlations. The resulting family of techniques, which we call PFcorr, has the following properties:

• Sampling robust. The technique is capable of efficiently computing correlations over arbitrary samples of rigid body motions ℝ³ × SO(3).

• Compatible. It can be used along with existing equispaced FFT-based techniques.

• General. It unifies the rotationally-exhaustive paradigms in [12, 22, 36, 38].

PFcorr thus provides an alternative to existing rigid-body correlation techniques.

The second half of this work presents an algorithm that uses PFcorr to explore correlations in multi-domain search spaces. The non-uniformity inherent to PFcorr implies that these correlations can be focused in a specific subset of ℝ³ ×SO(3), while its exhaustive nature guarantees that it is not sensitive to local optima. We believe that the above properties, along with its speed, make PFcorr a realistic and in many ways preferable alternative to existing correlation search schemes.

One of the two halves of PFcorr depends on looking up certain matrices describing the influence of a translation on the obtained series expansions. The high complexity of computing these matrix entries means that they often have to be precomputed and stored. We outline an efficient algorithm, based on polynomial update rules, that, while not obviating the need for precomputation and storage, has nevertheless a lower complexity than existing algorithms.

Finally, this work also aims to be a self-contained overview of correlation techniques that depend on expressing the input scalar valued functions in terms of rotationally invariant bases. In particular, we prove all relevant properties inherent to our mathematical framework.

3. Background

In this Section we give some necessary definitions and background information needed for the PFcorr algorithms. Note that we defer most multi-line proofs to the Appendix.

Let A, B: ℝ³ ↦ ℂ be a pair of scalar-valued functions. We define the rigid-body correlation problem as follows.

Definition 3.1

For two functions A: ℝ³ ↦ ℂ and B : ℝ³ ↦ ℂ we define

$$C({\mathbf{R}}_i,{\mathbf{t}}_j)={\int }_{{\mathbb{R}}^3}A(\mathbf{x})B({\mathbf{R}}_i\mathbf{x}+{\mathbf{t}}_j)d\mathbf{x},i\in \{1,\dots ,N_{\mathit{rot}}\},j\in \{1,\dots ,N_{\mathit{trans}}\}$$ (3.1)

as the rigid-body correlation between A and B for a given set S = {(R_i, t_j)}, R_i ∈ SO(3), t_j ∈ ℝ³ of rigid-body motions. The rigid-body correlation problem is to maximize C(R_i, t_j) over the set S.

The rigid-body correlation problem is a non-convex geometric optimization problem. The several problem domains in computational biology to which it applies can be distinguished by their choice of A and B. In protein-protein docking, for instance, A and B are affinity functions that represent a relevant property, such as shape or electrostatics, of the underlying protein; in protein-density map fitting, A is a blurred representation of the atoms of the protein, while B is the density map itself.

The objective function (3.1) can be efficiently calculated by expanding it in a series of orthogonal basis functions. The starting point of this approach is a coordinate transform of vectors x ∈ ℝ³ from Cartesian to spherical coordinates. The inner product of two square-integrable functions f, g : ℝ³ ↦ ℂ parameterized in spherical coordinates is given by

$$\langle f,g\rangle ={\int }_{{\mathbb{R}}^{+}}{\int }_{{\mathbb{S}}^2}f(r\mathbf{u})\overline{g(r\mathbf{u})}{r}^2\text{d}\mathbf{u}\text{d}r.$$ (3.2)

We now consider the orthogonal bases for the two components of the product space separately. Let ξ ∈ 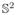and let (ϕ, θ) ∈ [0, 2π) × [0, π] be its coordinates. For any l ∈ ℕ₀ and m = −l, … l the spherical harmonics of degree l are defined as

$$Y_l^m(\xi )=\sqrt{\frac{2l+1}{4\pi }}{P}_l^{\mid m\mid }(cos\theta ){\text{e}}^{\text{i}m\phi }$$

where $P_l^m:[-1,1]\to \mathbb{R}$ are associated Legendre polynomials, cf. [45], that arise as the derivatives of ordinary Legendre polynomials P_l(x).

The spherical harmonics satisfy the orthogonality relation

$${\int }_{{\mathbb{S}}^2}{Y}_l^m(\xi )\overline{Y_{l^{\prime }}^{m^{\prime }}(\xi )}\text{d}\xi ={\delta }_{{ll}^{\prime }}{\delta }_{{mm}^{\prime }}.$$ (3.3)

Secondly, we employ a weighted version of the Laguerre polynomials denoted by $R_k^l(r)$. These functions have been used to describe the radial part of the orbitals of hydrogenic atoms and are also known as radial wavefunctions, see [2, pp. 368 3] for general informations. In [36] these functions have been employed in the context of six-dimensional rigid-body docking.

Definition 3.2

For $r\in {\mathbb{R}}_0^{+}$, l, k ∈ ℕ₀, k > l, the weighted Laguerre polynomials $R_k^l:{\mathbb{R}}^{+}\to \mathbb{R}$ are given by

$$R_k^l(r)=\sqrt{\frac{2(k-l-1)!}{\mathrm{\Gamma }(k+\frac{1}{2})}}{\text{e}}^{-\frac{r^2}{2}}{r}^l{L}_{k-l-1}^{l+\frac{1}{2}}(r^2)$$

using the Laguerre polynomials $L_k^l$, see [45]. For $r\in {\mathbb{R}}_0^{+}$, l, k ∈ ℕ₀, k > l, the functions $R_k^l(r)$ satisfy

$${\int }_0^{\infty }{R}_k^l(r)R_n^l(r)r^2\text{d}r={\delta }_{k,n}.$$ (3.4)

Based on the previous orthogonality relations (3.3) and (3.4), we see that the functions $R_k^l(r)Y_l^m(\mathbf{u})$ for k, l ∈ ℕ, k > l ≥ |m| are orthonormal with respect to the inner product from (3.2). This follows immediately by

$$\begin{array}{l}\langle R_k^l(r)Y_l^m(\mathbf{u}),R_{k^{\prime }}^{l^{\prime }}(r)Y_{l^{\prime }}^{m^{\prime }}(\mathbf{u})\rangle ={\int }_0^{\infty }{R}_k^l(r)R_{k^{\prime }}^{l^{\prime }}(r)r^2\text{d}r{\int }_{{\mathbb{S}}^2}{Y}_l^m(\mathbf{u})\overline{Y_{l^{\prime }}^{m^{\prime }}(\mathbf{u})}\text{d}\mathbf{u}\\ ={\delta }_{k,k^{\prime }}{\delta }_{l,l^{\prime }}{\delta }_{m,m^{\prime }}.\end{array}$$ (3.5)

Moreover, these products of functions constitute an orthogonal basis of the space of square-integrable functions on ℝ³. Therefore, we find a unique series expansion of the two given functions A(x) and B(x) in terms of these functions as

$$A(\mathit{x})=A(r\mathbf{u})=\sum _{k=1}^{\infty }\sum _{l=0}^{k-1}\sum _{m=-l}^l{\widehat{a}}_{\mathit{klm}}{R}_k^l(r)Y_l^m(\mathbf{u})$$ (3.6)

with coefficients

$${\widehat{a}}_{\mathit{klm}}={\int }_0^{\infty }{\int }_{{\mathbb{S}}^2}A(r\mathbf{u})\overline{R_k^l(r)Y_l^m(\mathbf{u})}{r}^2\text{d}\mathbf{u}\text{d}r,$$ (3.7)

and analogously for B(x).

Typically the initial data for A(x) and B(x) will be obtained by an EM or read in from a database as an atomic structure in terms of a collection of atoms and charges. Either way the methods only provide a finite number of samples of the unknown functions A and B. Hence the integral (3.7) will be approximated by a suitable quadrature rule. In PFcorr we use a combination of the Clenshaw-Curtis formula for the spherical part cf. [8, pp. 86] and a Gauss-Legendre formula for the radial part cf. [8, pp. 222]. Alternatives to such deterministically sampled quadrature schemes are quasi Monte-Carlo methods or Monte-Carlo methods. Since this is not the focus of this work we omit further details on quadrature and merely comment on the error induced by step.

Lemma 3.3

Let A : ℝ³ ↦ ℂ be a complex scalar-valued, 2-Lipschitz continuous function with finite support on the domain Ω ⊂ ℝ³. For a given spherical grid with maximum grid-diameter h¹, for small h the coefficients â_klm can be computed with an error E = Ch|Ω| for a constant C ∈ ℝ.

3.1. Multi-basis framework

As a first step in solving the rigid-body correlation problem in Equation 3.1, A and B are represented in terms of orthogonal basis functions. PFcorr offers two distinct choices of how to proceed.

1. Mixed bases. The standard approach uses the expansion (3.6) and approximates it by

   $$A_L(\mathit{x})=A_L(r\mathbf{u})=\sum _{k=1}^L\sum _{l=0}^{k-1}\sum _{m=-l}^l{\widehat{a}}_{\mathit{klm}}{R}_k^l(r)Y_l^m(\mathbf{u}),$$ (3.8)

   and analogously for B_L(x). For convenience, we shall omit the subscript L from now on.

2. Pure spherical basis. This slightly modified approach following [22] and [12], divides the three dimensional space into discrete spherical slices and uses only a spherical basis expansion in terms of spherical harmonics on each slice with fixed radius r. The pure spherical representation of a scalar valued function A : ℝ³ ↦ ℂ for a given radial coordinate r is given by

   $$A_r(\mathbf{u})=\underset{L\to \infty }{lim}\sum _{l=0}^L\sum _{m=-l}^l{\widehat{a}}_{lm}(r)Y_l^m(\mathbf{u})$$ (3.9)
   with coefficients

   $${\widehat{a}}_{lm}(r)={\int }_{{\mathbb{S}}^2}{A}_r(\mathbf{u})\overline{Y_l^m(\mathbf{u})}\text{d}\mathbf{u},$$ (3.10)

   where A_r(u) = A(r, u).

The next step in solving the rigid-body correlation problem from Definition 3.1 involves applying a motion to the functions A and B. We assume that A and B are rigid bodies, and restrict the motion to rotations and translations in three-dimensional space.

3.2. Rotating basis expansions of scalar-valued functions

We shall now examine how a function expanded as in (3.8) behaves under the application of a rotation. We conveniently employ the representation property of spherical harmonics stating for arbitrary rotations R ∈ SO(3) that

$$Y_l^n({\mathit{R}}^T\mathit{u})=\sum _{m=-l}^l{Y}_l^m(\mathit{u})D_l^{mn}(\mathit{R}),\text{for}\mid m\mid \le l,\mathit{u}\in {\mathbb{S}}^2.$$ (3.11)

where $D_l^{mn}(\mathbf{R})$ is a Wigner-D function [49].

The Wigner-D functions $D_l^{m,n}$ with degree l and orders m, n with max{|m|, |n|} ≤ l are given by the explicit expression

$$D_l^{m,n}(\alpha ,\beta ,\gamma )={\text{e}}^{-\text{i}m\alpha }{d}_l^{m,n}(cos\beta ){\text{e}}^{-\text{i}n\gamma }$$

where α, γ ∈ [0, 2π) and β ∈ [0, π] are the Euler angle decomposition of a rotation R ∈ SO(3) and $d_l^{m,n}$ are the Wigner-d functions

$$d_l^{m,n}(x)=\epsilon {\left(\frac{s!(s+\mu +\nu )!}{(s+\mu )!(s+\nu )!}\right)}^{1/2}{2}^{-\frac{\mu +\nu }{2}}{(1-x)}^{\frac{\mu }{2}}{(1+x)}^{\frac{\nu }{2}}{P}_{l-L_{\ast }}^{(\mu ,\nu )}(x),$$ (3.12)

$P_{l-L_{\ast }}^{(\mu ,\nu )}(x)$ are the Jacobi polynomials and

$$\begin{array}{ll}\mu =\mid n-m\mid ,\hfill & \nu =\mid n+m\mid ,\hfill \\ L_{\ast }=max\{\mid m\mid ,\mid n\mid \},\hfill & s=l-L_{\ast },\hfill \end{array}\epsilon =\{\begin{array}{ll}1,\hfill & \text{if}m>n,\hfill \\ {(-1)}^{n-m},\hfill & \text{if}m\le n.\hfill \end{array}$$

Note that $d_l^{m,n}$ is a polynomial of degree l if m + n is even. Otherwise, it is a polynomial of degree l − 1 times a factor of (1 − x²)^1/2.

By virtue of (3.11), applying an arbitrary rotation R ∈ SO(3) to the given function A(x) will yield

$$A({\mathit{R}}^T\mathit{x})=A(r{\mathit{R}}^T\mathit{u})=\sum _{k=1}^{\infty }\sum _{l=0}^{k-1}\sum _{m,n=-l}^l{\widehat{a}}_{\mathit{kln}}{D}_l^{mn}(\mathbf{R})R_k^l(r)Y_l^m(\mathbf{u}).$$

Note that the rotation does not affect the radial parts of the function as a rotation preserves distance. Hence, a similar result holds for the radial-basis independent coefficients â_lm.

Lemma 3.4

Given two functions A : ℝ³ ↦ ℂ and B : ℝ³ ↦ ℂ expanded in terms of a mixed basis as given in (3.8) the pure rotational correlation can be obtained by evaluating

$$C(\mathbf{R})=\sum _{k=1}^L\sum _{l=0}^{k-1}\sum _{m=-l}^l\sum _{m^{\prime }=-l}^l{(-1)}^m{\widehat{a}}_{kl-m}{\widehat{b}}_{{\mathit{klm}}^{\prime }}{D}_l^{m,m^{\prime }}(\mathbf{R})$$ (3.13)

for arbitrary choices of R ∈ SO(3). This is a direct result from using the orthogonality property (3.5) with the basis expansions of A(x) and B(R^Tx) in

$$C(\mathbf{R})={\int }_{\mathbb{R}\times {\mathbb{S}}^2}\sum _{\mathit{klm}}{\widehat{a}}_{\mathit{klm}}{R}_k^l(r)Y_l^m(\mathbf{u})\sum _{k^{\prime }{l}^{\prime }{m}^{\prime }{m}^{″}}\overline{{\widehat{b}}_{k^{\prime }{l}^{\prime }{m}^{\prime }}}{R}_{k^{\prime }}^{l^{\prime }}(r)\overline{D_l^{m^{″},m^{\prime }}(\mathbf{R})Y_{l^{\prime }}^{m^{″}}(\mathbf{u})}{r}^2\mathit{drd}\mathbf{u}.$$

Lemma 3.5

Given two functions A : ℝ³ ↦ ℂ and B : ℝ³ ↦ ℂ expanded in terms of a pure spherical basis as given in (3.9) the pure rotational correlation can be obtained by evaluating

$$C(\mathbf{R})=\sum _{l=0}^L\sum _{m=-l}^l\sum _{m^{\prime }=-l}^l{(-1)}^m{(-1)}^{m^{\prime }}{D}_l^{m,m^{\prime }}(\mathbf{R}){\int }_{{\mathbb{R}}^{+}}{\widehat{a}}_{l-m}(r)\overline{{\widehat{b}}_{l-m^{\prime }}}(r)r^{2}dr$$ (3.14)

for arbitrary choices of R ∈ SO(3).

3.3. Fourier Transforms on the rotation group SO(3)

To efficiently calculated the correlations (3.13), (3.13), we will use the Fast SO(3) Fourier Transform. For details on the algorithm we refer the reader to [34]. Here we simply outline the basic idea and show how it can be applied to compute our scoring function.

The space of square integrable functions in SO(3) is denoted L² (SO(3)) and defined via the standard inner product

$$\langle f,g\rangle ={\int }_0^{2\pi }{\int }_0^{\pi }{\int }_0^{2\pi }f(\alpha ,\beta ,\gamma )\overline{g(\alpha ,\beta ,\gamma )}sin\beta \text{d}\gamma \text{d}\beta \text{d}\alpha .$$

A convenient orthogonal basis for L²(SO(3)) are the Wigner-D functions $D_l^{m,n}(\mathit{R})$ which satisfy the orthogonality condition

$$\langle D_l^{m,n},D_{l^{\prime }}^{m^{\prime },n^{\prime }}\rangle =\frac{8{\pi }^2}{2l+1}{\delta }_{l,l^{\prime }}{\delta }_{m,m^{\prime }}{\delta }_{n,n^{\prime }}.$$

Definition 3.6 (NDSOFT)

The nonequispaced discrete SO(3) Fourier transform (NDSOFT) is defined as the evaluation of the sums

$$f({\alpha }_q,{\beta }_q,{\gamma }_q)=\sum _{l=0}^L\sum _{m=-l}^l\sum _{n=-l}^l{\widehat{f}}_l^{m,n}{\stackrel{\sim }{D}}_l^{m,n}({\alpha }_q,{\beta }_q,{\gamma }_q),q=1,2,\dots ,Q,$$ (3.15)

for given Fourier coefficients ${\widehat{f}}_l^{m,n}$ and nodes (α_q, β_q, γ_q).

We outline our strategy for the fast approximate algorithm, a detailed description of this algorithm, called the nonequispaced fast Fourier transform (NFSOFT) can be found in [34]. We can rearrange (3.15) to

$$f(\alpha ,\beta ,\gamma )=\sum _{m=-L}^L\sum _{n=-L}^L{\text{e}}^{-\text{i}m\alpha }{\text{e}}^{-\text{i}n\gamma }\sum _{l=L_{\ast }}^L{\widehat{f}}_l^{m,n}{d}_l^{m,n}(cos\beta ).$$

We can then calculate new coefficients ${\overline{f}}_l^{m,n}$ from the coefficients ${\widehat{f}}_l^{m,n}$ in (L³ log² L) arithmetic operations to rewrite the inner most sum for m, n = −L, …, L using the Chebyshev polynomials of first kind T_l(x),

$$\sum _{l=L_{\ast }}^L{\widehat{f}}_l^{m,n}{d}_l^{m,n}(cos\beta )=\sum _{l=0}^{L-\chi }{\stackrel{\sim }{f}}_l^{m,n}{(1-x^2)}^{\chi /2}{T}_l(x),$$ (3.16)

where χ = [m + n odd]. We are now able to replace the Chebyshev polynomials of first kind with complex exponentials,

$$\sum _{l=0}^{L-\chi }{\stackrel{\sim }{f}}_l^{m,n}{(1-x^2)}^{\chi /2}{T}_l(x)=\sum _{l=-L}^L{\widehat{g}}_l^{m,n}{\text{e}}^{-\text{i}l\beta },m,n=-L,\dots ,L.$$

We can compute the coefficients ${\widehat{g}}_l^{m,n}$ from the coefficients ${\overline{f}}_l^{m,n}$ with (L³) arithmetic operations. The obtained form is now ready to be inserted into (3.15) to become

$$f(\alpha ,\beta ,\gamma )=\sum _{l=-L}^L\sum _{m=-L}^L\sum _{n=-L}^L{\widehat{g}}_l^{m,n}{\text{e}}^{-\text{i}m\alpha }{\text{e}}^{-\text{i}l\beta }{\text{e}}^{-\text{i}n\gamma }.$$ (3.17)

This is a plain three-dimensional Fourier sum and we can use the NFFT algorithm to evaluate it with (L³ log L + Q) operations, where Q is the number of nodes at which we evaluate the function; see [35]. Hence, the application of a NFSOFT results in (L³ log² L + Q) operations.

4. Rigid-body correlations

Although not immediately apparent, the idea of exploiting the rotational invariance of the spherical harmonics that serve as basis functions in the Fourier expansion of a functions in L²( 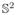) has some advantages over translation-invariant Fourier expansion in [3, 7].

The key idea is to first express the three-dimensional translation in terms of two rotations and a translation in one dimension. Hence, this translation will have two rotational degrees of freedom and one translational. A three dimensional translation t ∈ ℝ³ of a object can be uniquely expressed as t = r R_Z(ϕ)R_Y (θ)e_z for ϕ ∈ [0, 2π), θ ∈ [0, π] and r ∈ ℝ⁺ where e_z = (0, 0, 1)^T. Combining, this with the three independent rotation parameters of the object, we have five rotation angles that describe a motion and one absolute value of a translation along one axis. Consequently, are able to speed up the computation for the rotations by spherical Fourier transforms and obtain an improved complexity for five of the six degrees of freedom of rigid-body correlations instead of the previous three. For U = R_Z(ϕ)R_Y (θ), we have

$$\begin{array}{l}C(\mathit{R},\mathit{t})=C(\stackrel{\sim }{\mathit{R}},\mathit{U}{z\mathit{e}}_z)={\int }_{{\mathbb{R}}^3}A(\mathit{x})B(\mathit{Rx}-\mathit{U}{z\mathit{e}}_z)\text{d}\mathit{x}\\ ={\int }_{{\mathbb{R}}^3}A({\mathit{U}}^T\mathit{x})B(\stackrel{\sim }{\mathit{R}}\mathit{x}-{z\mathit{e}}_z)\text{d}\mathit{x},\end{array}$$ (4.1)

with R̃ = U^TR. A similar approach has been previously suggested in [21] for protein matching. Here we will focus on its efficient computation. A schematic depiction can be found in Figure 4.1.

Fig. 4.1.

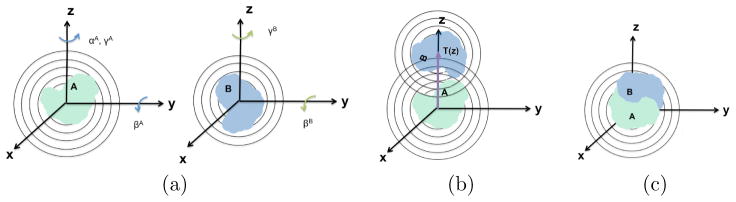
Schematic of the rigid-body correlation search scheme introduced in this work. Here A, B are two complex or real scalar-valued functions. In (a) the initial positions of A and B are given in different coordinate frames. Both functions are rotated. A is manipulated by a three-dimensional rotation, B only by a two dimensional rotation. In (b) A and B are translated to share the same origin. A set of a translation along the z-axis is searched until the best arrangement (c) is found.

After having considered the effects of rotations, it remains for us to examine the effect of the single one dimensional translation, say along the z-axis. In spherical coordinates a translation of the vector x about ze_z is given by x – ze_z = r_zu_z with $r_z=\sqrt{r^2+2\mathit{rz}cos\theta +z^2}$ and ${\mathit{u}}_z=(arccos\left(\frac{r}{r_z}sin\theta \right),\varphi )$. We point out that the longitudal angle ϕ does not change during a translation along the z-axis. The effect of a translation along the z-axis on the ℝ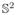⁺ × basis functions can be expressed in terms of translation matrix (T-matrix) elements $T_{jh,kl}^n(z)$ as described in [36] as

$$R_k^l(r_z)Y_l^n({\mathit{u}}_z)=\sum _{k^{\prime }=0}^{\infty }\sum _{l^{\prime }=0}^{k^{\prime }-1}{T}_{k^{\prime }{l}^{\prime },kl}^n(z)R_{k^{\prime }}^{l^{\prime }}(r)Y_{l^{\prime }}^n(\mathbf{u}).$$ (4.2)

Note that the T-Matrices apply only to mixed basis expansions (3.8); for pure spherical basis expansions, the coefficients â_lm for each radial slice with radius r have to be recomputed after each translation t ∈ ℝ³.

These translation coefficients are expressed as

$$T_{k^{\prime }{l}^{\prime },kl}^n(z)={\text{e}}^{-z^2/4\lambda }\sum _{m=\mid l-l^{\prime }\mid }^{l+l^{\prime }}{A}_m^{{ll}^{\prime }\mid n\mid }\sum _{j=0}^{k-l+k^{\prime }-l^{\prime }-2}{C}_j^{kl,k^{\prime }{l}^{\prime }}M!{(z^2/4\lambda )}^{m/2}{L}_M^{(m+1/2)}(z^2/4\lambda ),$$ (4.3)

where

$$\begin{array}{l}M=j+\frac{l+l^{\prime }-m}{2},C_j^{k^{\prime }{l}^{\prime },kl}=\sum _{j=0}^{k-l-1}\sum _{j^{\prime }=0}^{k^{\prime }-l^{\prime }-1}{\delta }_{n,j+j^{\prime }}{X}_{\mathit{klj}}{X}_{k^{\prime }{l}^{\prime }{j}^{\prime }},\\ X_{\mathit{klj}}={\left[\frac{(k-l-1)!{(1/2)}_k}{2}\right]}^{1/2}\frac{{(-1)}^{k-l-j-1}}{j!(k-l-j-1)!{(1/2)}_{l+j+1}},\\ A_m^{l^{\prime }l\mid n\mid }={(-1)}^{(m+l^{\prime }-l)/2+n}(2m+1){[(2l^{\prime }+1)(2l+1)]}^{1/2}\left(\begin{array}{ccc}{l}^{\prime }& l& m\\ 0& 0& 0\end{array}\right)\left(\begin{array}{ccc}{l}^{\prime }& l& m\\ n& -n& 0\end{array}\right).\end{array}$$

Moreover $\left(\begin{array}{ccc}a& b& c\\ \alpha & \beta & \gamma \end{array}\right)$ denotes the Wigner 3-j symbol and (·)_m is the Pochhammer symbol.

Directly computing T-Matrix entries in Equation 4.3 for fixed k, l, k′, l′, m takes (L³N_t) steps, where N_t is the number of translations in one dimension. The overall complexity is thus L⁵· (L³N_t) = (L⁸N_t). An important contribution of the PFcorr algorithm is the fast and efficient computation of the T-Matrix entries in (L⁷+L⁶N_t) steps. Details of this speedup can be found in the Appendix.

Having collected all the ingredients we state the following important Theorem.

Theorem 4.1

For a fixed cut-off degree L ∈ ℕ₀ and two given functions

$$A(r\mathbf{u})=\sum _{k=1}^L\sum _{l=0}^{k-1}\sum _{m=-l}^l{\widehat{a}}_{\mathit{klm}}{R}_k^l(r)Y_l^m(\mathbf{u}),B(r\mathbf{u})=\sum _{k=1}^L\sum _{l=0}^{k-1}\sum _{m=-l}^l{\widehat{b}}_{\mathit{klm}}{R}_k^l(r)Y_l^m(\mathbf{u})$$

the objective function (3.1) can be evaluated by computing

$$C(\mathit{R},\mathit{t})=C(\mathit{R},\mathit{U}{z\mathit{e}}_z)=\sum _{k,k^{\prime }=1}^L\sum _{l=0}^{k-1}\sum _{l^{\prime }=0}^{k^{\prime }-1}\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}\sum _{m=-l}^l\sum _{n=-min(l,l^{\prime })}^{min(l,l^{\prime })}{(-1)}^n{\widehat{a}}_{k^{\prime }{l}^{\prime }m}{\widehat{b}}_{\mathit{klm}}\times D_h^{-{nm}^{\prime }}(\mathbf{R})D_l^{nm}(\mathbf{U})T_{k^{\prime }{l}^{\prime },kl}^n(z)$$

for arbitrary choices of R ∈ SO(3) and t ∈ ℝ³. Its proof can be found in the Appendix.

Following an observation in [12], it is not as efficient to use the pure spherical basis expansions to express a general rigid-body correlation. Instead, Equation 3.14 is used along with a scan of the translational degrees of freedom, in which the basis coefficients are recomputed for each distinct t ∈ ℝ³. Hence we omit mentioning the case of pure spherical expansions here.

We conclude this section with some notes on the complexity of the evaluation of the introduced expansions. If we use the NFSOFT [34] to compute Equations (3.13) then the pure rotational correlation in Lemma 3.4 can be computed in $\mathcal{O}(L^4+N_{\mathbf{R}}^3)$ steps using the following recipe, where N_R is the number of distinct rotation angles per rotational degree of freedom, i.e., per Euler angle.

Recipe 1

Evaluate

$$C(\mathbf{R})=\sum _{k=1}^L\sum _{l=0}^{k-1}\sum _{m=-l}^l\sum _{n=-l}^l{(-1)}^m{\widehat{a}}_{kl-m}{\widehat{b}}_{\mathit{kln}}{D}_l^{m,n}(\mathbf{R})$$ (4.4)

for $N_{\mathbf{R}}^3$ different choices of Euler angles.

1. Rearrange the multiple summations such that the sum over k becomes the innermost sum.

2. Compute

   $${\widehat{f}}_{\mathit{lmn}}-\sum _{k=l+1}^L{(-1)}^m{\widehat{a}}_{kl-m}{\widehat{b}}_{\mathit{kln}}$$

   in (L⁴) steps.

3. Use the SO(3) Fourier transform to compute the remaining sums

   $$C(\mathbf{R})=\sum _{l=0}^{L-1}\sum _{m=-l}^l\sum _{n=-l}^l{\widehat{f}}_{\mathit{lmn}}{D}_l^{mn}(\mathit{R})$$

   in $\mathcal{O}(L^3{log}^{2}L+N_{\mathbf{R}}^3)$ steps, where N_R is the number of unique Euler angles per rotation axis.

In a similar fashion, the pure rotational correlation in Lemma 3.5 can be computed in (L³ log² L+N_R + L³I) steps where I is the complexity of computing the integral ∫_R⁺â(r)b̂(r)r²dr for a given pair of scalar-valued functions â, b̂: ℝ⁺ ↦ ℂ. Since there are (L³) integrals ∫_ℝ⁺â(r) b̂(r)r²dr we get the aforementioned complexity.

Let us now consider general rigid-body motion. The general rigid-body correlation in Theorem 4.1 can be computed in $\mathcal{O}(L^6+L^4{N}_{\mathbf{R}}^2+N_{\mathbf{R}}^5)N_t$ steps using the outlined a way to speed up computations of the translation matrix entries (4.3) and the NFSOFT, where $N_{\mathbf{R}}^3$ and $N_{\mathbf{R}}^2$ are the number of rotations of A and B respectively, and N_t is the number of one-dimensional translations. The computation is performed according to the following recipe.

Recipe 2

Evaluate

$$C(\mathit{R},\mathit{t})=C(\mathit{R},\mathit{U}{z\mathit{e}}_z)=\sum _{k,k^{\prime }=1}^L\sum _{l=0}^{k-1}\sum _{l^{\prime }=0}^{k^{\prime }-1}\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}\sum _{m=-l}^l\sum _{n=-min(l,l^{\prime })}^{min(l,l^{\prime })}{(-1)}^n{\widehat{a}}_{k^{\prime }{l}^{\prime }{m}^{\prime }}{\widehat{b}}_{\mathit{klm}}\times D_h^{-{nm}^{\prime }}(\mathbf{R})D_l^{nm}(\mathbf{U})T_{k^{\prime }{l}^{\prime },kl}^n(z)$$

for N_R different choices of R and N_t different choices of one-dimensional translations z ∈ ℝ

1. Compute

   $${\widehat{c}}_{{\mathit{kll}}^{\prime }}^{m^{\prime }n}=\sum _{k^{\prime }=l^{\prime }+1}^L{\mathbf{1}}_{\mid n\mid \le l^{\prime }}{\widehat{b}}_{k^{\prime }{l}^{\prime }{m}^{\prime }}{T}_{k^{\prime }{l}^{\prime },kl}^n(z)$$

   in (L⁶) steps.

2. Compute

   $${\stackrel{\sim }{c}}_{kl}^n=\sum _{l^{\prime }=0}^{L-1}\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}{\widehat{c}}_{{\mathit{kll}}^{\prime }}^{m^{\prime }n}{D}_{l^{\prime }}^{-n,m^{\prime }}(\mathbf{U})$$

   using a modification of the NFSOFT in $\mathcal{O}(L^{5}logL+N_{\mathbf{R}}^2{L}^3)$ steps.

3. Compute

   $$c_l^{mn}=\sum _{k=l+1}^L{(-1)}^n{\widehat{a}}_{\mathit{klm}}{\stackrel{\sim }{c}}_{kl}^n.$$
4. Compute

   $$C(\mathit{R},\mathit{U}{z\mathit{e}}_z)=\sum _{l=0}^{L-1}\sum _{m=-l}^l\sum _{n=-l}^l{c}_l^{mn}{D}_l^{n,m}({\mathbf{R}}^A)$$

   using the standard NFSOFT [34] in $\mathcal{O}(N_{\mathbf{R}}^2(L^4+L^{3}logL+N_{\mathbf{R}}^3))$ steps.

Hence, the overall cost is $\mathcal{O}(L^6+L^{5}logL+N_{\mathbf{R}}^2(L^3+L^4)+N_{\mathbf{R}}^2{N}_{\mathbf{R}}^3)N_t$, i.e., $\mathcal{O}(L^6+L^4{N}_{\mathbf{R}}^2+N_{\mathbf{R}}^5)N_t$.

With these recipes established, we now outline algorithms to perform fast rigid-body correlations given a pair of scalar-valued functions as input. Algorithm 1 uses the mixed basis, while Algorithm 2 uses the pure spherical harmonic basis.

Algorithm 1.

Fast Rotational Correlation with mixed radial/spherical basis functions

Algorithm 2.

Fast Rotational Correlations with pure spherical harmonic basis functions

4.1. Rigid-body correlations: numerical results and discussion

There are three sources of error in PFcorr. The first is the expansion error, i.e., the error induced by truncating the basis expansion at a finite value of L. The second is the representation error, i.e., the error induced in numerically integrating the coefficients in Equation (3.7). The third is the NFFT error, i.e., the error induced by approximating the exponential sums by the NFFT.

Following [12, 36, 38], the first two sources of error can be respectively mitigated by choosing an expansion degree between 20 ≤ L ≤ 25, and using a single-point quadrature rule. We provide further evidence in Section 4.2 of the former assertion.

The NFFT approximates exponential sums with a kernel basis expansion, providing a choice of several kernels, and several parameters govern the actual error of the expansion. In our implementation, we choose the Gaussian kernel with an oversampling factor of 3, see [35], resulting in the errors in Table 4.1. On more information about the error of the NFFT and the NFSOFT we refer to [35] and [34], respectively. Note that, in solutions to the correlation problem, the absolute value of the correlation is less important than the value relative to other rigid-body rotations, i.e., the ability of the search scheme to discriminate between two different rigid-body motions. A measure of this ability is presented in Section 4.2 in the context of sampling arbitrary subsets of the motion group SE(3).

Table 4.1.

(A) Relative errors between the directly computed correlation and the correlation as computed by Recipes 1 and 2 for two real-valued functions A, B: ℝ³ → ℝ at varying expansion degrees over 500 randomly-generated rigid-body rotations. For L > 12, the direct correlation is exceedingly slow to compute therefore the relative error is omitted here. (B) The maximum complex value of the correlation score as a different error measure. Note that we used real valued input functions, and hence this table demonstrates the numerical error due to cut-offs. The above experiments were conducted with mixed bases; similar results hold for pure spherical bases, as the speedup scheme for these bases is the same as that used for Recipe 1.

(A)
L	Recipe 1	Recipe 2
4	1.93e-5	1.26e-4
6	1.37e-5	1.44e-4
8	1.61e-5	1.22e-4
10	1.61e-5	1.34e-4
12	1.72e-5	1.32e-4

(B)
L	Recipe 1	Recipe 2
4	1.71e-10	1.84e-10
6	1.53e-10	1.76e-10
8	1.72e-10	1.71e-10
10	1.77e-10	1.85e-10
12	1.41e-10	1.81e-10

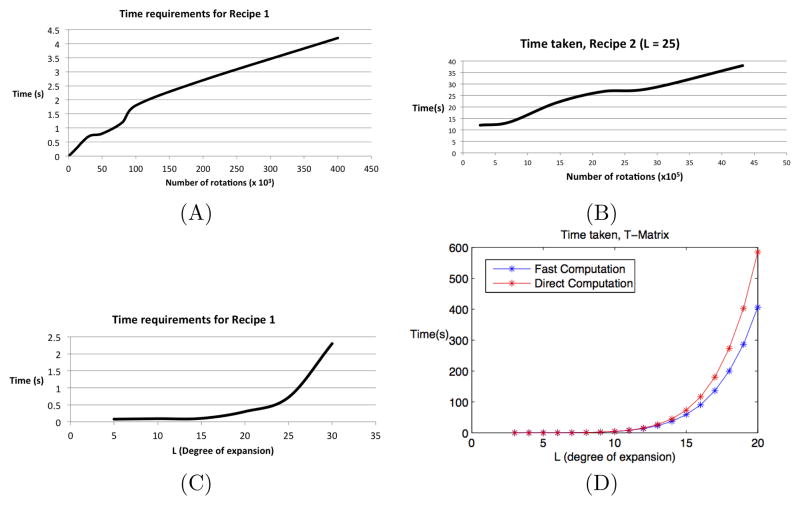
We provide timing information in Figure 4.2. All timing information is from a single-threaded, dual core Macbook Pro at 2.3 GhZ with 8GB of RAM. For Recipe 1, we see that linear scaling with respect to the number of rotations and the quartic scaling with respect to expansion degree as predicted are reproduced by the implementation. For Recipe 2, the scaling with respect to expansion degree is not very important, as typically L⁶, the leading expansion term, is much less than L⁴N_RB, which, for practical correlation problems, is in turn less than the product of the number of rotations N_RA N_RB. We hence examine how Recipe 2 scales with respect to the product N_RA N_RB; Figure 4.2(C), shows that the scaling is linear, as expected.

Fig. 4.2.

Time taken by each of the algorithms in Section 4. (A) Time requirements of the algorithms from Recipe 1 as a function of the number of rotations at fixed degree L = 25. Note that in Recipe 1 we search over three rotational degrees of freedom. (B) Time requirements of the algorithms from Recipe 2 as a function of the number of rotations at fixed degree L = 25. Note that in Recipe 2 we search over five rotational degrees of freedom. (B) Time requirements of the algorithms from Recipe 1 as a function of the maximum degree of the series expansion L at a fixed number of 30.000 rotations. (D) Time requirements of the T-Matrix computation as a function of the maximum degree of the series expansion L for the direct computation and the speedup.

For the T-Matrix computation (Figure 4.2(D)), a dramatic speedup with respect to the direct algorithm is observed in L ≥ 10 regime, where the L⁷ v/s L⁸ scaling is apparent. However, for typical values of L (see following paragraph), the computation times are still too slow to be usable in the inner loop of any Fourier-based correlation approach, including our own. Like prior work that uses the T-Matrix (See the introduction for an overview), we thus prefer to precompute and store T-Matrix entries for given values of z and λ (See Equation 4.3).

From a practical standpoint, our rigid-body correlation search is seen to be a viable, if somewhat slower, alternative to existing rigid-body correlation search techniques. Most of the degradation in performance is due to the NFFT, which uses, in its implementation, an oversampled FFT to enable the non-uniformity inherent to it. Following [38], we choose L to typically lie between 20 and 25, in which case typical run times for an exhaustive correlation involving about 1.5 · 10⁷ distinct rigid-body samples lie between 2 and 3 minutes. We also note that, other than the argument in Section 4.2, there is no reason to prefer the non-uniformity inherent to PFcorr and, if performance is a concern, each of the steps involving the NFFT can be replaced by the equispaced FFT.

4.2. Sampling arbitrary subsets of the motion group SE(3); addressing the drawbacks of existing techniques

The main advantage of PFcorr is in sampling arbitrary (finite) subsets of the space of rigid body motion in three dimensions SE(3) = ℝ³ × SO(3). In our implementation (See Figure 4.3 for an example of its use in rigid-body fitting), this is as simple as specifying a set of rigid-body motions on which correlations are to be performed. By contrast, all prior techniques require an equispaced angular grid for rotational search, a property that results in a highly non-uniform search of the space of rotations (See Drawback 2 in the introduction). For exhaustive correlations between a pair of scalar-valued functions, one typically employs uniform sampling of the space of rotations SO(3). As we mention in the introduction, most of the uncertainty in the rigid-body correlation problem lies in the space of rigid-body rotations, and it is thus more important to sample this space exhaustively. There are several existing techniques that, given an angular sampling criterion, provide a set of samples that are uniform with respect to accepted metrics of uniformity [14, 28, 55]. We use the approach from [28], in which the metrics of local separation and global coverage compete to provide a set of highly uniform samples in SO(3). See also Figure 2.1.

Fig. 4.3.

An example of a rigid-body fitting exercise. Here an atomic structure of the Rotavirus subunit is fit into a segmented 3D EM map. (A) Atomic structure of the rotavirus (PDB ID 1QHDa [27]). (B) Bilaterally smoothed rotavirus subunit segmented from EMD 1461 [58] at 3.8 Å using the techniques in [56]. (C) The atomic structure is placed into the 3D EM map subunit using the algorithms in PFcorr.

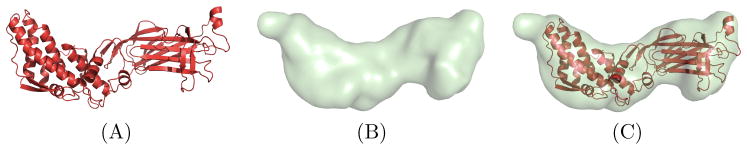
The ability to sample and correlate over arbitrary subsets of SE(3) is only useful if, at any expansion degree, the fineness of the rotational sampling does not exceed the accuracy with which â_klm and b̂_klm represent A and B respectively (See Equation (3.7)). Such a scenario would give rise to correlations that are so close to each other as to be essentially indistinguishable, and would result in a set of correlations clustered around the average correlation. To measure this tendency, we compute the Z-score $z=\frac{x-\mu }{\sigma }$, a measure of the distance of each individual correlation from the average. The results, in Figure 4.4, indicate that the top-ranking Z-score increases with increase in degree, as expected, leveling off at L ≥ 20, where the error due to floating-point calculations begins to rival the error due to representation, and that even at very low expansion degrees, the top-ranking Z-score is 3 standard deviations from the mean, indicating a very high confidence. Figure 4.4 also presents another argument as to why the regime 20 ≤ L ≤ 25 is best, as the latter provides a balance between the errors of representation and floating-point computation. For additional information on the Z-score measure see e.g. [32].

Fig. 4.4.

Average top-ranking Z-Scores for Recipe 1 at varying degrees. The rotational sampling fineness is fixed at 8° per Euler angle.

5. Flexible correlations: main results

We present an algorithm (Algorithm 3) for domain-based protein matching. This algorithm, given as input

1. A protein ,

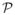2. A hierarchical domain decomposition, defined in Section 5.1, of ,

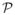3. A scalar-valued function B: ℝ³ ↦ ℝ representing a stationary target, and,

4. A scalar-valued representation A of ,

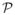produces as output the optimal correlation between A and B under rigid-body motions of the domains of 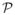. Algorithm 3 makes use of the ability of PFcorr to uniformly sample arbitrary subsets of ℝ³ × SO(3).

5.1. Domain-based protein flexibility framework

We assume a generic framework for domain-based protein flexibility. This framework consists of ideas from domain-decomposition of proteins that have existed in various forms over the past decade (see especially [25]), as well as a set of techniques, described, for instance, in [4], to assign motions to each of these domains.

Let a protein crystal structure 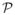comprise a set of atoms. Designate a subset of 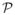as a domain D. A domain decomposition of 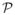is a set 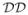= {D_i}, 1 ≤ i ≤ n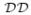, where D_i is a domain. A hierarchical domain decomposition 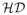= { 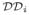}, 1 ≤ i ≤ n 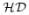is a set of domain decompositions 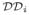such that each domain in 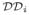is a subdomain of some domain in 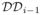(See, for example, [5]). For each 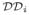of the hierarchical domain decomposition 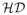, a motion graph MG specifying relative motions between domains of 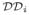can be specified. The motion graph consists of a set of edges F_ij, called flexors, between pairs of domains i, j that undergo relative motion. The geometric properties of each flexor imply a set of rigid-body transformations ( ${\mathbf{R}}_{i,j}^k,{\mathbf{t}}_{i,j}^k$), k ∈ {1 … N_T} applied to D_j relative to D_i [4].

Algorithm 3.

Greedy multi-domain matching

5.2. Algorithm for flexible matching

Algorithm 3 applies to a particular domain decomposition of 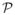, i.e, it applies to a particular index in the hierarchical domain decomposition of 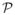. It uses the ability of PFcorr to sample arbitrary subsets of SE(3) to match representations of domains A_i ∈ A to a target scalar-valued function B: ℝ³ ↦ ℝ. Note by contrast that a classic equispaced Fourier-based correlation scheme would not be able to perform the tasks in Algorithm 3 without also producing several results that do not belong to the chosen subset of SE(3). This focusing property enables PFcorr to combine the merits of both local and global optimization schemes in the following sense. The algorithm is local in that it is restricted to the chosen subset of SE(3), but global in that it samples that subset exhaustively. It thus combines the speed of a local search without being sensitive, as local search algorithms are, to local optima.

6. Conclusion

We have presented PFcorr, a non-uniform correlation search scheme. PFcorr displays the following properties: (A) It is sampling robust, making searches over arbitrary subsets of SE(3) efficient while retaining the capabilities of classical exhaustive Fourier-based search schemes, (B) It is compatible with existing equispaced FFT-based techniques, in the sense that its non-equispaced nature is desirable but not necessary, and (C) Its algorithms extend to the rotationally exhaustive paradigms in [12, 22, 36, 38]. We have also presented an algorithm to compute translation matrix entries for SO(3) that achieves a better scaling than existing direct algorithms. Finally, we have presented an algorithm for multi-dimensional flexible correlations that leverages the sampling robustness of PFcorr. PFcorr applies to several fields within computational biology, including, most notably, molecular fitting and docking, where the above properties make it a natural and efficient tool for correlation-amenable search. A link to download PFcorr can be found at http://www.ices.utexas.edu/CVC/software/.

Appendix

Here we give additional details on the mathematical background of the used algorithms.

T-Matrices Computation

The translation coefficients $T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }(z)·exp(z^2/4\lambda )$ are polynomials of degree

$$max(n+2M)=max(n+2(j+\frac{l+l^{\prime }-k}{2}))=max(2j+l+l^{\prime })=2k-l+2k^{\prime }-l^{\prime }-4.$$

Let d = 2k − l + 2k′ − l′ − 4, n = min(p, l + l′) − s and $i=\frac{p-n}{2}$ Then Equation (4.3) can be arranged to obtain

$$T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }(z)exp(z^2/4\lambda )=\sum _{p=0}^{2k-l+2k^{\prime }-l^{\prime }-4}{\alpha }_p·z^p$$

where

$${\alpha }_p=\sum _{s=0}^{min(p,l+l^{\prime })-\mid l-l^{\prime }\mid }{A}_n^{{ll}^{\prime }\mid m\mid }\sum _{j=max(i-\frac{l+l^{\prime }-n}{2},0)}^{k-l+k^{\prime }-l^{\prime }-2}{C}_j^{k,l,k^{\prime }{l}^{\prime }}M!\frac{{(1/2)}_{M+n+1}}{(M-i)!{(1/2)}_{n+i+1}}·\frac{1}{{(-4\lambda )}^{i}i!},$$

and s is even if and only if d is even.

The coefficients α_p can be computed for all p in (L³) steps. For fixed k, l, k′, l′, m, the T-Matrix polynomial can be computed in (LN_t). The complexity for fixed k, l, k′, l′, m is hence (L³ +LN_t), resulting in an overall complexity of (L⁸ + L⁶N_t).

A polynomial can be evaluated at a set of equispaced arguments with (L) multiplications. Applying Nuttall’s update rule for polynomials [29] reduces these multiplications to additions without altering the number of operations required. This affords a small speedup.

T-Matrices Computation Speedup

If $A_n^{{ll}^{\prime }\mid m\mid }$ is precomputed for all m, the other terms in Equation (4.3) have to be calculated only once for fixed k, l, k′, l′. In the first step, we compute

$$b_n:=\sum _{j=0}^{k-l+k^{\prime }-l^{\prime }-2}{C}_j^{kl,k^{\prime }{l}^{\prime }}M!exp(-z^2/4\lambda ){(z^2/4\lambda )}^{n/2}{L}_M^{(n+1/2)}(z^2/4\lambda )$$

for all m and fixed n, l, n′, l′. The summation over j and the computation of $L_M^{n+1/2}$ each takes (L) steps, implying a complexity of (L²) for each b_n, and a complexity for all m of (L³).

In the second step we compute the T-Matrix entries $T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }={\displaystyle \sum _{n=\mid l-l^{\prime }\mid }^{l+l^{\prime }}}{b}_n·A_n^{{ll}^{\prime }\mid m\mid }$.

Since the above calculation has to be done for all k, l, k′, l′ and for N_t translations, the overall complexity for $T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }$ is now (L⁷N_t), instead of (L⁸).

Computation of the coefficients $C_j^{kl,k^{\prime }{l}^{\prime }}$ can also be sped up. Only these coefficients and the boundary of the innermost sum depend on k and k′. If k and k′ are switched, the boundary of the sum does not change, so for switched k and k′ only the value $C_j^{kl,k^{\prime }{l}^{\prime }}$ changes. In the first step

$$l(z^2/4\lambda ):=L_M^{(n+1/2)}(z^2/4\lambda )$$

is computed for all j, n, l, l′. In the second step

$$t_{kl,k^{\prime }{l}^{\prime }}:=\sum _{j=0}^{k-l+k^{\prime }-l^{\prime }-2}{C}_j^{kl,k^{\prime }{l}^{\prime }}M!exp(-z^2/4\lambda ){(z^2/4\lambda )}^{n/2}l(z^2/4\lambda )$$

and t_k′l,kl′ respectively are computed. In the third step

$$T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }=\sum _{n=\mid l-l^{\prime }\mid }^{l+l^{\prime }}{A}_n^{{ll}^{\prime }\mid m\mid }·t_{kl,k^{\prime }{l}^{\prime }}$$

and $T_{{kl}^{\prime },k^{\prime }l}^{\mid m\mid }$ respectively are computed.

Moreover, the symmetry property [36] $T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }={(-1)}^{l-l^{\prime }}{T}_{kl,k^{\prime }{l}^{\prime }}^{\mid m\mid }$ implies $T_{{kl}^{\prime },k^{\prime }l}^{\mid m\mid }={(-1)}^{l-l^{\prime }}{T}_{k^{\prime }l,{kl}^{\prime }}^{\mid m\mid }$. Hence, the dynamic programming approach above allows us to calculate $T_{kl,k^{\prime }{l}^{\prime }}^{\mid m\mid },T_{{kl}^{\prime },k^{\prime }l}^{\mid m\mid }$ and $T_{k^{\prime }l,{kl}^{\prime }}^{\mid m\mid }$ by calculating $T_{k^{\prime }{l}^{\prime },kl}^{\mid m\mid }$.

The complexity of the approach of representing the T -coefficients as a polynomial can be reduced by using the speed-up by dynamic programming as explained above. To achieve the reduction in the complexity we consider the calculation of α_p. Instead of computing α_p directly, first

$$b_s^p:=\frac{1}{{(-4\lambda )}^i·i!{(1/2)}_{n+i+1}}\sum _{j=max(i-\frac{l+l^{\prime }-n}{2},0)}^{k-l+k^{\prime }-l^{\prime }-2}{C}_j^{k,l,k^{\prime }{l}^{\prime }}M!\frac{{(1/2)}_{M+n+1}}{(M-i)!}$$

is precomputed. Due to the summation and the parameters s and p, this computation has the complexity (L³) Afterwards the α_p

$${\alpha }_p=\sum _{s=0}^{min(p,l+l^{\prime })-\mid l-l^{\prime }\mid }{A}_n^{{ll}^{\prime }\mid m\mid }·b_s^p$$

are computed This has the complexity (L²), implying a complexity of (L³) for the precomputation of α_p for all m. The total computation of the α_p for all m is hence (L³ + L³) = (L³).

The subsequent computation of

$$T_{{kl}^{\prime },k^{\prime }l}^{\mid m\mid }exp(z^2/4\lambda )=\sum _{p=0}^{2k-l+2k^{\prime }-l^{\prime }-4}{\alpha }_p·z^p$$

is for fixed k, l, k′, l′, m and all m is (L²N_t). Therefore the overall complexity for fixed k, l, k′, l′ and all m is (L³ + L²N_t). Thus, for all k, l, k′, l′ the complexity is (L⁴) (L³ + L²N_t) = (L⁷ + L⁶N_t).

Proof of Lemma 3.3

Let Ω be subdivided in N grid-cells Ω_i with centers x_i, volume V_i and diameter d_i. The approximation error in the ith grid-cell is given by

$$E_i=\left|{\int }_{{\mathrm{\Omega }}_i}A(\mathbf{x})d\mathbf{x}-A({\mathbf{x}}_i)V_i\right|=\left|{\int }_{{\mathrm{\Omega }}_i}A(\mathbf{x})-A({\mathbf{x}}_i)\text{d}\mathbf{x}\right|.$$

Expanding A(x) in a Taylor series about x_i, we get

$$E_i=\left|{\int }_{{\mathrm{\Omega }}_i}{(\mathbf{x}-{\mathbf{x}}_i)}^{\text{T}}\nabla A({\mathbf{x}}_i)+\mathcal{O}({\left|\right|\mathbf{x}-{\mathbf{x}}_i\left|\right|}^2)\text{d}\mathbf{x}\right|\le \left|{\int }_{{\mathrm{\Omega }}_i}c·d_i\text{d}\mathbf{x}\right|\le c·d_i·V_i.$$

for some constant c, due to A(x) being 2-Lipschitz continous on Ω. Thus the error across all grid cells is the sum $E={\displaystyle \sum _{\forall i}}{E}_i\le c\underset{\forall i}{max}{d}_i\mid \mathrm{\Omega }\mid$. Since the maximum diameter of the grid-cells is proportional to the grid fineness h, we have E ≤ Ch|Ω| for a fixed constant C.

Proof of Theorem 4.1

Consider a rotation R ∈ SO(3) that is applied to the molecule A. By the representation property of spherical harmonics 3.11 the affinity function becomes

$$A({\mathit{R}}^T\mathit{x})=A(r{\mathit{R}}^T\mathit{u})=\sum _{k=1}^{\infty }\sum _{l=0}^{k-1}\sum _{m,n=-l}^l{\widehat{a}}_{\mathit{klm}}{D}_l^{nm}(\mathbf{R})R_k^l(r)Y_l^n(\mathbf{u}).$$

The molecule B will be rotated by U = R_Z (ϕ)R_Y (θ) and translated by the vector (0, 0, z)^T. Using (4.2), this yields the series expansion

$$\begin{array}{l}B(\mathit{Ux}-{z\mathit{e}}_z)=B(r_z{({\mathit{U}}^T\mathit{u})}_z)=\sum _{k=1}^{\infty }\sum _{l=0}^{k-1}\sum _{m,n=-l}^l{\widehat{b}}_{\mathit{klm}}{D}_l^{nm}(\mathbf{U})R_k^l(r_z)Y_l^n({\mathbf{u}}_z)\\ =\sum _{k=1}^{\infty }\sum _{l=0}^{k-1}\sum _{m,n=-l}^l\sum _{k^{\prime }=0}^{\infty }\sum _{l^{\prime }=0}^{k^{\prime }-1}{\widehat{b}}_{\mathit{klm}}{D}_l^{nm}(\mathbf{U})T_{k^{\prime }{l}^{\prime },kl}^n(z)R_{k^{\prime }}^{l^{\prime }}(r)Y_{l^{\prime }}^n(\mathit{u}).\end{array}$$

After inserting both of the above expansions of the affinity functions into the correlation integral (4.1), we are now able to use the orthonormality property

$$\langle R_k^l(r)Y_l^m(\mathbf{u}),R_{k^{\prime }}^{l^{\prime }}(r)Y_{l^{\prime }}^{m^{\prime }}(\mathit{u})\rangle ={\delta }_{k,k^{\prime }}{\delta }_{l,l^{\prime }}{\delta }_{m,m^{\prime }}$$

to simplify the correlation integral to

$$\begin{array}{l}C(\mathit{R},\mathit{U}{z\mathit{e}}_z)={\int }_{{\mathbb{R}}^3}A({\mathit{R}}^T\mathit{x})B({\mathit{U}}^T\mathit{x}-{z\mathit{e}}_z)\text{d}\mathit{x}\\ =\sum _{k,k^{\prime },k^{″}=1}^{\infty }\sum _{l^{″}=0}^{k^{″}-1}\sum _{m^{\prime },n^{\prime }=-l^{″}}^{l^{″}}\sum _{l=0}^{k-1}\sum _{m,n=-l}^l\sum _{l^{\prime }=0}^{k^{\prime }-1}{(-1)}^{n^{\prime }}{\widehat{a}}_{k^{″}{l}^{″}{m}^{\prime }}{D}_{l^{″}}^{n^{\prime }{m}^{\prime }}(\mathbf{R})\times {\widehat{b}}_{\mathit{klm}}{D}_l^{nm}(\mathbf{U})T_{k^{\prime }{l}^{\prime },kl}^n(z){\delta }_{k^{\prime },k^{″}}{\delta }_{l^{\prime },l^{″}}{\delta }_{n,-n^{\prime }}\\ =\sum _{k,k^{\prime }=1}^{\infty }\sum _{l=0}^{k-1}\sum _{l^{\prime }=0}^{k^{\prime }-1}\sum _{m^{\prime }=-l^{\prime }}^{l^{\prime }}\sum _{m=-l}^l\sum _{n=-min(l,l^{\prime })}^{min(l,l^{\prime })}{(-1)}^n{\widehat{a}}_{k^{\prime }{l}^{\prime }{m}^{\prime }}{\widehat{b}}_{\mathit{klm}}\times D_{l^{\prime }}^{-{nm}^{\prime }}(\mathbf{R})D_l^{nm}(\mathbf{U})T_{k^{\prime }{l}^{\prime },kl}^n(z).\end{array}$$

If we now approximate the infinite sums by sums with a certain maximum degree L we obtain the formula from Theorem 4.1.