Exploring the three-dimensional organization of genomes: interpreting chromatin interaction data

Abstract

How DNA is organized in three dimensions inside the cell nucleus and how that affects the ways in which cells access, read and interpret genetic information are among the longest standing questions in cell biology. Using newly developed molecular, genomic, and computational approaches based on the chromosome conformation capture technology (such as 3C, 4C, 5C and Hi-C) the spatial organization of genomes is being explored at unprecedented resolution. Interpreting the increasingly large chromatin interaction datasets is now posing novel challenges. Here we describe several types of statistical and computational approaches that have recently been developed to analyze chromatin interaction data.

Introduction

Chromosomes are some of the most complex molecular entities in the cell: the molecular composition of the chromatin fiber is highly diverse along its length and the fiber is intricately folded in three dimensions. Tremendous efforts are being devoted to mapping the local structure of chromatin by analyzing the complement of DNA-associated proteins and their modifications along chromosomes. Such studies allow identification of genomic locations of genes and regulatory elements that are active in a given cell type and they have started to uncover comprehensive sets of functional elements of the human genome and the genomes of several model organisms (e.g. ^1–3). Only over the last decade have a series of molecular and genomic approaches been developed that can be used to study three-dimensional chromosome folding at increasing resolution and throughput; these methods are all based on Chromosome Conformation Capture (3C). These methods allow the determination of the frequency with which any pair of loci in the genome is in close enough physical proximity (probably in the range of 10–100 nm) to become cross-linked ^4,5 (Box 1).

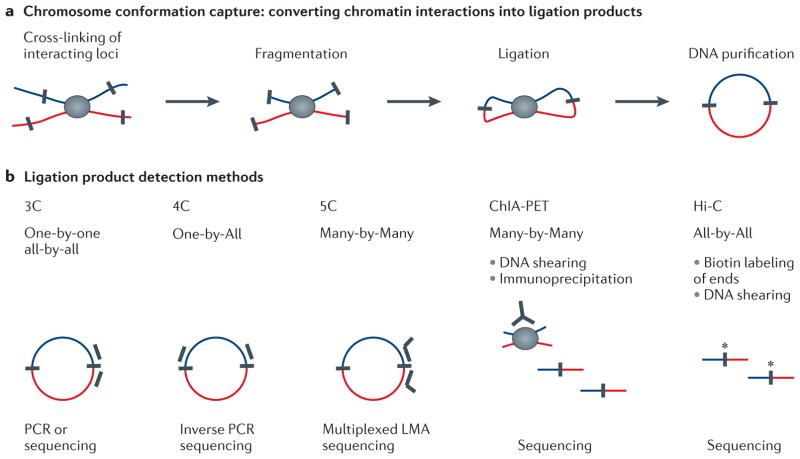
Box 1. 3C-based methods.

In 3C-based methods (top panel), cells are crosslinked with formaldehyde to covalently link chromatin segments that are in close spatial proximity. Next, chromatin is fragmented by restriction digestion or sonication. Crosslinked fragments are then ligated to form unique hybrid DNA molecules. Finally, the DNA is purified and analyzed. The different 3C based methods only differ in the way hybrid DNA molecules, each corresponding to an interaction event of a pair of loci, are detected and quantified (bottom panel). In classical 3C experiments single ligation products are detected by PCR one at the time using locus-specific primers. Given that 3C can be laborious, most 3C analysis typically cover only tens to several hundred Kb. 4C (“circular 3C” or “3C-on-Chip”) uses inverse PCR to generate genome-wide interaction profiles for single loci ^48,106,107, while 5C combines 3C with hybrid capture approaches to identify up to millions of interactions in parallel between two large sets of loci, e.g. between a set of promoters and a set of distal regulatory elements ^46,108,109. 4C approaches are genome-wide, but anchored on a single locus. 5C analyses typically involve two sets of hundreds to thousands of restriction fragments to interrogate up to millions of long-range interactions that can cover up tens Mb that can be contiguous or scattered over loci of interest throughout the genome, The Hi-C method was the first unbiased and genome-wide adaptation of 3C and includes a unique step where after restriction digestion the staggered DNA ends are filled in with biotinylated nucleotides ⁶⁴. This facilitates selective purification of ligation junctions that are then directly sequenced. Hi-C provides a true all-by-all genome-wide interaction map, but the resolution of this map depends on the depth of sequencing. When several hundred million read pairs are obtained, as is currently routine, chromatin interactions in the mouse or human genome can be detected at 100 Kb resolution.

Other 3C variants have recently been described that differ in molecular details, but that all generate comprehensive and genome-wide interaction maps ^28,47,57,75. Interestingly, technology development has now gone full circle back to 3C: the classical 3C method is no longer only used for analyzing interactions one at the time by PCR, but is now also used for genome-wide interaction mapping as the resulting complete 3C DNA ligation mixture can be directly sequenced on modern deep-sequencing platforms ⁵⁷. Finally, a variety of approaches combine 3C with chromatin immunoprecipitation to enrich for chromatin interactions between loci bound by specific proteins of interest ^110,111. For instance the ChIA-PET method allows for genome-wide analysis of long-range interactions between sites bound by a protein of interest. Because ChIA-PET data represents a selected sub-set of interactions that occur in the genome, the three analysis approaches described in this article cannot directly be applied to this datatype.

These 3C-based methods are starting to generate vast amounts of genome-wide interaction data. Here we briefly describe the main experimental approaches and then describe in more depth recently developed analytical, computational and modeling approaches for analysis of comprehensive chromatin interaction datasets. We discuss three emerging approaches to analyze 3C-based datasets. The first approach simply aims to identify pairs or sets of loci that interact more frequently than otherwise expected, which points to chromatin looping or specific co-location events. Analysis of groups of preferentially interacting loci has been used to identify higher order chromosomal domains. The other two approaches – restraint-based modeling and approaches that model chromatin as a polymer - use all interaction data, including baseline and non-specific interactions, to build ensembles of spatial models of chromosomes. 3D models can then be used to identify higher order structural features and DNA elements involved in organizing chromosomes, to estimate chromatin dynamics within one cell as well as cell-to-cell variability in folding. We discuss how the application of these approaches is starting to uncover principles that determine the spatial organization of chromosomes, to reveal novel layers of chromatin structure and to relate these structures to gene expression and regulation.

Studying chromosome organization

Insights from imaging

When chromosomes are observed in living cells they can appear highly variable between cells ^6,7, which could be interpreted as reflecting a general lack of organization. However, detailed studies using a variety of improved imaging techniques have revealed several organizational principles of chromosomes at the scale of the whole nucleus ⁷. First, in interphase cells of many organisms, chromosomes do not readily mix but instead occupy their own separate territories ⁸. Second, where chromosome territories touch, they can form areas in which intermingling occurs, providing opportunities for potentially functional interactions between loci located on different chromosomes ⁹. Third, transcription does not occur diffusely throughout the nucleus but happens at sub-nuclear sites enriched in RNA polymerase II and other components of the transcription and RNA processing machinery ^10–12. This implies that actively transcribed genes tend to co-localize, possibly in specific groups related to their transcriptional regulators ¹³. Finally, transcriptionally inactive segments of the genome also tend to associate with each other and often can be found localized at the nuclear periphery ¹⁴, around nucleoli ^15,16 or, in Drosophila, at sub-nuclear structures such as polycomb bodies ^17–19. These observations point to a spatially and functionally compartmentalized nucleus, where sub-nuclear positioning of loci is correlated with gene expression.

3C-based technologies

Imaging approaches do not readily allow a comprehensive analysis of the three-dimensional folding of complete genomes, or determination of the organization of entire chromosomes within their territories at Kb resolution. To overcome these limitations, approaches based on 3C have been developed that enable the mapping of chromosome folding at sufficient resolution to observe individual genes and regulatory elements, and at a genome-wide scale ^4,5. The rationale of 3C-based approaches is that when a sufficient number of pair-wise interaction frequencies are determined for a genomic region, chromosome or whole genome, one can infer its three-dimensional arrangement. 3C-based methods have been extensively reviewed and discussed elsewhere ^5,20–22 and are summarized in Box 1.

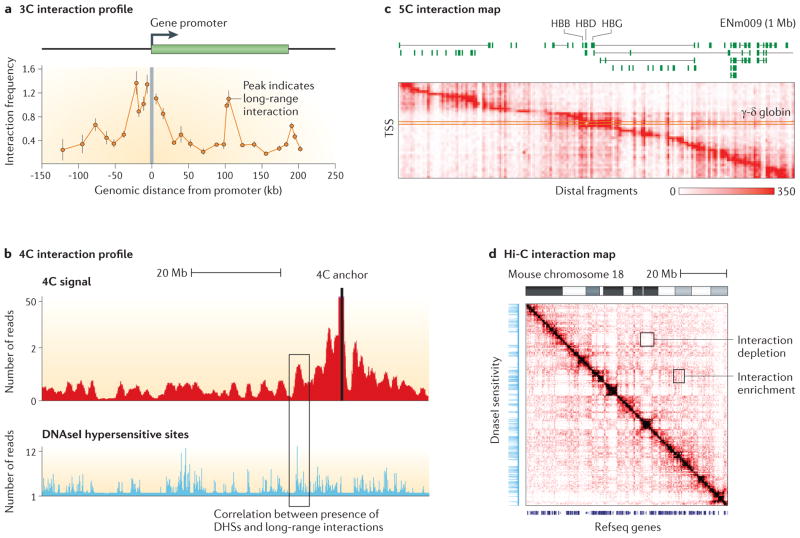
3C and 4C generate single interaction profiles for individual loci. For instance, 3C typically yields a long-range interaction profile of a selected gene promoter, or other genomic element of interest vs. surrounding chromatin (Fig. 2A), whereas 4C generates a genome-wide interaction profile for a single locus (Fig. 2B). These datasets can be represented as single tracks that can be plotted along the genome, and compared to other genomic features such as DNAseI hypersensitive sites (hallmarks of gene regulatory elements, ²³) or genes. 5C and Hi-C methods are not anchored on a single locus of interest, but instead generate matrices of interaction frequencies that can be represented as two-dimensional heatmaps, with genomic positions along the two axes (Fig 2C and 2D).

Figure 2. Examples of 3C, 4C, 5C and Hi-C datasets.

A. 3C data for the CFTR gene in Caco2 cells ³⁴, B. 4C data (simulated from data from Zhang et al. ¹¹²). C. An example of a 5C interaction map for the ENm009 region in K562 cells ⁴⁶. Each row represents an interaction profile of a transcription start site (TSS) across the 1 Mb region on human chromosome 11 that contains the beta-globin locus. D. Hi-C from Zhang et al. ¹¹². 3C and 4C data are linear profiles along chromosomes and can be directly compared to other genomic tracks such as DNAseI sensitivity. 5C and Hi-C data are often represented as two-dimensional heatmaps. Other genomic features, such as positions of genes or the location of DNAseI hypersensitive sites, can be displayed along the axes for visual analysis of chromosome structural features. DNAse I data from the laboratory of Dr. Stamaoryannopoulos ¹¹⁴.

Interpreting chromatin interaction data

Before analyzing chromatin interaction data it is important to carefully consider what 3C-based assays capture (Fig. 1). These methods report on the frequency in the cell population by which two loci are in close spatial proximity, but they do not distinguish functional from non-functional associations, nor do they reveal the mechanisms that led to their co-localization. Close spatial proximity can be the result of direct and specific contacts between two loci, mediated by protein complexes that bind them, or can be the result of indirect co-localization of pairs of loci to the same sub-nuclear structure such as the nuclear lamina, nucleolus or transcription factory etc. In addition, co-localization in a given cell can be a non-specific result of the packing and folding of the chromatin fiber as determined by other (nearby) specific long-range interactions or other constraints, or can be due to random (non-specific) collisions in the crowded nucleus. Further, one of the defining features of chromosomes is that they are very long and flexible chromatin fibers. This feature - the polymer nature of chromosomes - also determines to a significant extent the frequency with which pairs of loci interact even in the absence of any specific higher-order structures ^24,25.

Figure 1. Processes leading to close spatial proximity of loci.

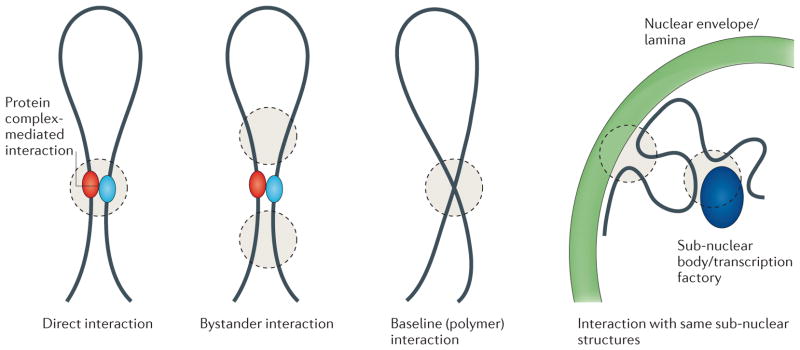
3C-based technologies capture loci that are in close spatial proximity. Various biologically and structurally distinct examples are shown in which loci are in close spatial proximity. Analysis and interpretation of 3C data sets needs to take these different scenarios in consideration.

Finally, the precise three-dimensional path of a chromatin fiber is highly variable even between otherwise identical cells, and locally (up to a Mb or so) dynamic within cells ^26,27. This explains why comprehensive chromatin interaction datasets typically show that a locus has some non-zero probability to interact with almost any other locus in the genome, though this probability of course varies widely reflecting the overall non-random conformation of the genome ^24,25,28,29. Each instance of a chromatin interaction, or ligation product, that is detected represents an interaction involving a pair of loci in a single cell in the population. Thus, 3C interaction frequency data represent the fraction of cells in which pairs of loci are in close spatial proximity at the time the cells are fixed and the data can only be understood when genome folding displays enormous cell-to-cell heterogeneity (^28,29, and see below). These considerations highlight the complex nature of comprehensive chromatin interaction datasets: the data represent the sum of interactions across a large cell population, and in each cell chromosome conformation is determined by many different constraints that act on the chromatin fiber.

Currently, the challenge of analyzing chromosome conformation is shifting from developing experimental approaches for generating increasingly comprehensive and quantitative datasets to building analytical tools to interpret the interaction data. The first approach we consider is used to identify point-by-point looping interactions, e.g. between promoters and gene regulatory elements.

Linking regulatory elements to target genes

Identifying looping interactions

In genomes of metazoa each gene is surrounded by large numbers of elements ^1–3 and a major question is what principles determine which elements regulate any given gene at a given time. From detailed analyses of single genes over the last decade, and more comprehensive genome-wide studies reported more recently, the main mechanism by which regulatory elements communicate with their cognate target genes is through chromatin looping, which brings elements that are widely spaced in the linear genome in close spatial proximity ^30,31.

In many single-locus studies classical 3C is used to quantify interaction frequencies between an element of interest, e.g. a promoter, and flanking chromatin extending up to hundreds of Kb (see example in Fig. 2A). Analysis of such “anchored” interaction profiles can then point to distal loci that interact with the anchor locus more frequently than expected, pointing to a looping interaction (e.g. ^4,32–34). In general, it has been found that interaction frequencies exponentially decay with increasing genomic distance. In many studies looping interactions are inferred when a local peak is observed on top of the overall decaying baseline of interactions ³⁵. Most single locus 3C analyses are qualitative in nature, and simple visual inspection of interaction profiles is used to identify peaks in interaction frequencies. Comparison of interaction profiles obtained in different cells or under different conditions can then provide further support, including statistical quantitative support, of the looping interaction when the long-range contact is condition or cell type specific. Fig. 2A shows a typical example of such looping interaction analysis of the CFTR locus ³⁴.

Examples of looping at specific loci

One of the best-studied examples is the long-range interaction between the Locus Control Region (LCR) and the set of distal beta-globin genes located 40–80 Kb away. 3C studies in mouse and human detected prominent interactions between these elements in globin expressing cells, and these interactions were significantly less frequent in cells that do not express these genes, e.g. in brain ^32,36. These interactions are mediated by specific transcription factors, including EKLF1 and GATA1 that bind the LCR and the gene promoters ^37,38. Further, the looping interaction directly stimulates transcription by facilitating recruitment and phosphorylation of RNA polymerase II ³⁹. Looping has been found in many other cases. For instance for the alpha-globin genes ⁴⁰, the CFTR gene ^33,34, the interleukin gene cluster ⁴¹, the myc gene ^42,43, the MHC-II genes ⁴⁴, yeast silent mating type loci HML and HMR ⁴⁵ etc.; and across a range of species including human, mouse, flies, yeast, and plants. Thus, chromatin looping constitutes a common mechanism by which gene regulatory elements control genes over large genomic distances.

Comprehensive analysis of looping

Analysing looping with 5C

5C has allowed more comprehensive analysis of chromatin looping for large numbers of genes by measuring many anchored interaction profiles in parallel (Fig. 2C). For example, in a recent study interaction profiles for over 600 gene promoters were mapped in three human cell lines and at the resolution of single restriction fragments (~4 Kb) ⁴⁶. The baseline of interaction frequencies could be estimated from the entire dataset by assuming that the large majority of interrogated interactions were not specific looping interactions. This led to an estimate for the baseline interaction frequency for each genomic distance (Fig. 3A). Looping interactions were then identified by detection of signals that are significantly higher than this baseline, at a chosen p-value and false discovery rate. This approach provides more statistically rigorous analysis of identifying significant peaks on top of this baseline, compared to classical 3C single gene studies. A similar analysis was used for identification of sets of significant interactions in the yeast genome ⁴⁷. These approaches can identify pairs of loci that interact more frequently than expected, but they are limited by the models and assumptions that are used to define the expected interaction frequencies. Another limitation is that interactions frequencies are obtained in arbitrary units and thus the real interaction frequency in the examined cell population (the percentage of cells in which the loci interact) remains unknown and can be quite low as shown by fluorescence in situ hybridization (e.g. ^45,48,49), which makes it difficult to assess the functional role of these interactions in any given cell (see ⁵⁰ for more considerations on this issue).

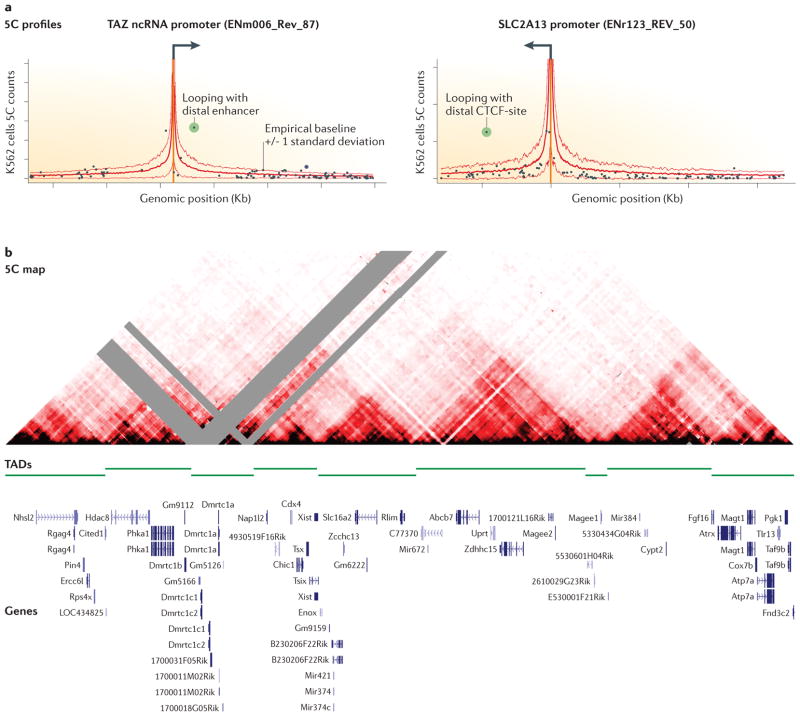
Figure 3. Chromatin looping interactions and topological association domains.

A. Examples of long-range interaction profiles in the human genome as determined by 5C (data from ⁴⁶). The orange vertical bar indicates the position of the gene promoters, the solid red line indicates the empirically estimated level of baseline interactions (thin red lines indicate baseline plus/minus one standard deviation). The presence of a looping interaction is inferred when a pair of loci interact statistically more frequently than expected based on the baseline frequency. The green data points represent significant looping interactions. B. A dense 5C interaction map of a 4.5 Mb region on the mouse X chromosome containing the X-chromosome inactivation center (data from ⁵⁸). In red is the interaction frequency between pairs of loci, grey represents missing data due to low mappability. The interaction map is cut in half at the diagonal to facilitate alignment with genomic features. Visual inspection reveals the presence of triangles, which correspond to regions (topologically associating domains, TADs) in which loci interact frequently with each other. Loci located in different TADs do not interaction frequently. TAD boundaries have been determined by computationally determining the asymmetry between up- and down stream interactions around them ⁵⁹.

Insights into looping landscapes

Despite its limitations, comprehensive looping analyses are now starting to reveal common principles of long-range interactions involved in gene expression. Sanyal et al. ⁴⁶ identified thousands of significant long-range looping interactions between gene promoters and distal loci, reinforcing the notion that many if not all gene promoters engage with distal elements through looping. Analysis of this large set of looping interactions identified important general concepts of long-range gene regulation, and also countered some long-held ideas. First, many of the looping events are cell type-specific interactions between active gene promoters and distal elements resembling active enhancers, consistent with a role of these chromosome structures in gene activation. Second, one abundant class of long-range interactions involves promoters looping to sites bound by the insulator protein CTCF. The role of this class of looping interactions in gene regulation is not fully understood, but a general architectural role seems likely ^31,51,52. Third, regulatory elements are often assumed to regulate the nearest gene, even though previous genetic studies have provided examples where this is not the case ⁵³. However, looping interactions often skip one or more genes, suggesting that the linear arrangement of genes and elements is a relatively poor predictor of their functional and structural interactions. Finally, relationships between genes and regulatory elements are far from exclusive: genes can interact with multiple distal elements, and elements can interact with multiple genes. Computational predictions based on correlations between gene activity and activity of distal elements across panels of cell lines also led to the prediction that genes are regulated by multiple distal elements ^54–56.

In addition, it was found that the average pattern of looping interactions around promoters is asymmetric: promoters interact with distal elements that can be located up-or downstream of the transcription start site, but looping interactions are most frequently observed with elements located around ~120 Kb upstream. Why the looping landscapes of promoters display this asymmetry is not clear, but it may point to some form of directionality in the mechanism by which transcriptional looping interactions are formed.

From these studies a picture emerges of chromosomes as highly complex three-dimensional networks driven by long-range interactions. This view raises many new questions related to the processes that determine the specificity of gene-element interactions, the proteins that mediate them, and how these looping interactions contribute to gene regulation.

Topologically associating domains

Methods, including 5C and Hi-C, that map all interactions in a genomic region of interest or in complete genomes in an unbiased fashion can be analyzed in various ways to identify structural features of chromosomes. One prominent feature of metazoan genomes is the formation of various types of chromosomal domains (Box 2, ⁵⁰). Studies using these approaches for Drosophila, mouse and human chromosomes have recently discovered that chromosomes are composed of discrete Topologically Associating Domains (TADs) (Fig. 3B), which can be hundreds of kilobases in size ^57–60. Visual inspection of a high-resolution 5C interaction map of a 4.5 Mb region encompassing the mouse X-chromosome inactivation centre revealed a series of large structural domains ⁵⁸. Loci located within these TADs tend to frequently interact with each other, but they interact much less frequently with loci located outside their domain. This feature enabled researchers to identify TADs throughout the human and mouse genomes by analyzing lower resolution, but genome-wide, Hi-C interaction maps in combination with a hidden Markov Model approach ⁵⁹. This analysis showed that TADs are universal building blocks of chromosomes ⁵⁹; the human and mouse genomes are each composed of over 2,000 TADs covering over 90% of the genome.

Box 2. Genome compartments.

Inter- and intra-chromosomal interaction maps for mammalian genomes ^28,64,112 have revealed a pattern of interactions that can be approximated by two compartments -A and B – that alternate along chromosomes and have a characteristic size of about 5Mb each. A-compartments preferentially interact with other A-compartments throughout the genome (Fig. 5). Similarly, B-compartments associate with other B-compartments. Compartment signal can be quantified by eigenvector expansion of the interaction map ^64,112,113. The A/B compartment signal is not simply biphasic (representing just two states), but rather continuous ¹¹³ and correlates with indicators of transcriptional activity such as DNA accessibility, gene density, replication timing, GC content and several histone marks, suggesting that A-compartments are largely euchromatic, transcriptional active regions.

TADs are distinct from the larger A- and B-compartments. First, analysis of embryonic stem cells, brain tissue and fibroblasts suggests that the majority, but not all, of TADs are tissue-invariant ^58,59, whereas A- and B compartments are tissue-specific domains of active and inactive chromatin that are correlated with cell type-specific gene expression patterns ⁶⁴. Second, A- and B- compartments are large (often several Mb) and form an alternating pattern of active and inactive domains along chromosomes. In contrast, TADs are smaller (median around 400–500 Kb), can be active or inactive, and adjacent TADs are not necessarily of opposite chromatin status. Thus, it seems that TADs are hard-wired features of chromosomes, and groups of adjacent TADs can organize in A- and B- compartments (see ⁵⁰ for a more extensive discussion).

TADs are defined by genetically encoded boundary elements. This was demonstrated directly by deletion of a boundary between two TADs in the X-chromosome inactivation centre ⁵⁸, which led to partial fusion of the two flanking TADs. The two TADs did not fully merge, suggesting that a new boundary was activated. Further, genome-wide analysis of boundary regions indicated that they are enriched in CTCF-bound loci, although CTCF also frequently binds sites within TADs. This suggests that at least some CTCF-bound elements may indeed act as boundary elements, as has long been hypothesized ^51,61. However, CTCF-bound sites are certainly not the only genomic elements enriched near TAD boundaries ^59,60, and the mechanisms that establish TAD boundaries are still undefined.

The existence of TADs also suggests constraints on which looping interactions between genes and distal regulatory elements can occur. It is tempting to speculate that looping interactions would be limited to elements located within the same TAD. Indeed, an initial analysis in the mouse genome suggests that enhancer-promoter interactions are particularly frequent within TADs ⁵⁶. If correct, this would point to a major role for TADs in regulation of gene expression by limiting genes to only a certain set of distal regulatory elements. Consistent with this idea, analysis of the TADs in the X-chromosome inactivation centre showed that genes within the same TAD tend to be coordinately expressed during cell differentiation ⁵⁸, possibly because they share the same set of gene regulatory elements. The presence of TADs could provide a chromatin structural explanation for the long-standing observation that groups of neighboring genes are often correlated in expression across cell types ^62,63.

Building 3D models of chromatin

Several analytical approaches are being developed that use comprehensive interaction datasets - not only those interactions that occur significantly more frequently than expected - to generate ensembles of 3D conformations of loci, chromosomes or whole genomes. These 3D representations can lead to identification of higher order features of chromosome conformation, such as formation of globular domains, chromosome territories etc., and may help to identify the sequence elements and processes involved in folding.

3D modeling approaches can be divided in roughly two types of methods. In the first approach – discussed in this section - a chromatin interaction dataset is used to derive a population-averaged 3D conformation. In the second approach (discussed below), chromatin interaction data is analyzed in statistical terms of polymer ensembles.

Restraint-based 3D model building

Comprehensive interaction maps reflect the population-averaged co-location frequencies of loci, which tend to be inversely related to average spatial distance (e.g. ^45,58,59,64). Interaction frequencies, or average spatial distances inferred from them, can therefore be used as restraints to build 3D models that place loci in relative 3D space in a way that is most consistent with their interaction probabilities ⁶⁵. In this context, restraints refer to forces in the modeling that are applied to pairs of loci that will position them according to their average spatial distance as inferred from their interaction frequency. Such approaches aim at finding 3D models of chromatin by treating them as a computational optimization problem. Therefore, optimal 3D models of genomic domains or genomes can be generated by minimizing a scoring function proportional to the violation of the imposed spatial restraints.

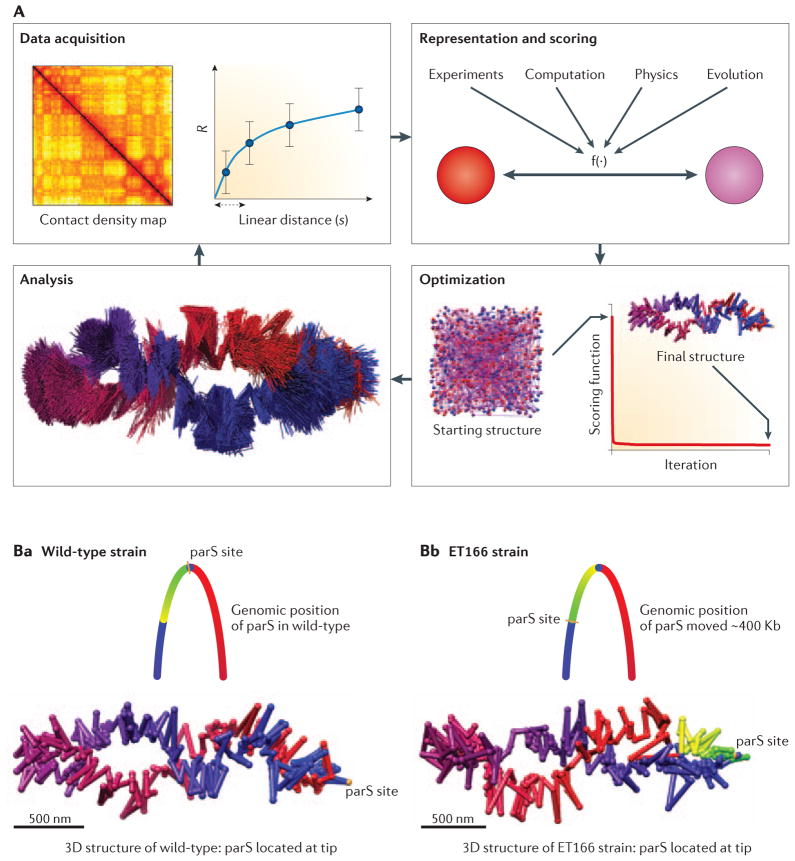
Generally, such 3D modeling follows an iterative process that cycles over four stages: information gathering (experiments), model representation and scoring, model optimization, and model analysis (Fig. 4A). After experimental chromatin interaction or distance data is obtained (usually by light microscopy or 3C-based methods) a genomic domain is then represented as a string of particles and spatial restraints between them ⁶⁶. Such representation needs to be adequate to the resolution of the input experimental data so that the use of the available information makes an exhaustive search of the 3D conformational space computationally feasible. For instance, the depth of DNA sequencing and size of the genomic region will determine the maximal resolution at which models can be built; the region is divided into the smallest particles that each still have sufficient long-range interaction data. For 5C datasets one can use each restriction fragment as a particle, whereas for genome-wide datasets one often uses larger bins, e.g. 1 Mb for the human genome or 10–30 Kb for the smaller genome of yeast. Next, it is necessary to determine a scoring function that will affect the spatial restraints between the particles. To this end, the experimental observations about the genomic domain or genome need to be translated into measurable relationships between the particles. The functional forms of restraints may be diverse to accommodate the integration of diverse sets of experimental observations, e.g. real average distances between some of the loci as determined by light microscopy. Once the system is represented at the appropriate scale and the relationships between the particles are formulated based on the observations, the final structure of the modeled object is obtained by minimizing the scoring function. That is, simultaneously reducing the violations of all imposed restraints. The resulting algorithmically optimal models can be refined and further analyzed using additional experimental observations that were not used during model building.

Figure 4. 3D modeling of genomes and genomic domains.

A. Iterative and integrative process for model building. The iterative process consists of data acquisition, model representation and scoring, model optimization, and model analysis. B. 3D model of the wild-type Caulobacter genome highlighting the position of the parS site located at the tip of the elliptical 3D structure of the genome. C. 3D model of the ET166 strain where the parS site has been moved ~400Kb of its original locus (indicated in the schematic diagram of the genome). In the 3D structure of genome of the ET166 strain the parS site are found at the tip of the structure again, which required a genome-wide rotation. The 3D models of Caulobacter are described in ⁷². Models in panels A, B and C are reproduced from ⁷², with permission.

Restraint-based modeling of genomic regions

A pioneer implementation of restraint-based 3D modeling of a genomic domain was the spatial analysis of the human Igh locus using distance measurements obtained by light microscopic imaging of a set of 12 positions across the locus ⁶⁷. The resulting images were integrated with computational simulations to propose that the Igh locus is organized into compartments containing clusters of loops separated by linkers. Another study used a conceptually similar approach, but with 5C data, for analysis of the 3D organization of the human HoxA gene cluster ⁶⁸. The models indicated that the chromatin conformation of the HoxA cluster changes during cell differentiation ⁶⁸. Also, 5C interaction maps for the human α-globin region were used to build 3D models with the Integrative Modeling Platform ⁶⁹. The models demonstrated that long-range interactions among sets of widely spaced active functional elements are sufficient to drive folding of local chromatin domains into compact globular states ^70,71. It is tempting to suggest that these globular conformations are related to TADs. The models also confirmed that the α-globin genes were in close spatial proximity to their cognate long-range acting enhancers, as has been discovered from analysis of pairs of loci that interact more frequently than expected (as described above, ⁴⁶). Importantly, the formation of globular domains could not readily be inferred from analysis of only significant pair-wise looping interactions and thus highlights how 3D model building helps to gain insights into higher order chromosome structures beyond the formation of chromatin loops.

Restraint-based modeling of genomes

With the availability of high-resolution interaction maps for entire genomes, the first genome-wide three-dimensional models were built based on the same principles of data integration used previously to study genomic domains. The 3D structure of the Caulobacter crescentus genome was determined by combining genome-wide 5C chromatin interaction data, live-cell imaging, and computational modeling ⁷². The resulting models illustrated that the bacterial genome is ellipsoidal with periodically arranged arms. The ellipsoidal structure predicted that specific cis-regulatory elements must be located at the tips of the arms and further analyses showed that parS sequence elements have a role in chromosome folding ^72–74 (Figure 4B). This work provided one of the first examples where structural analysis directly led to the identification of DNA elements involved in chromosome folding, and suggests that structure-function studies, as more typically done for proteins, may be feasible for whole chromosomes.

3D models have also been generated for several eukaryotic genomes, including the fission and budding yeast genomes ^29,47,75,76 and, at a much lower resolution, the human genome ²⁸. The first budding yeast 3D genome model was a coarse-grained static snapshot of the genome, but it recapitulated the known features of its organization into a Rabl configuration and identified additional features such clustering of origins of early replication and tRNA genes ⁴⁷. A 3D model for the fission yeast genome was built using a genome-wide chromatin interaction dataset ⁷⁵ and showed a global genome organization that is similar to budding yeast, with prominent centromere clustering. Interestingly, the model revealed statistically significant interactions among highly expressed functionally related genes, which may be reminiscent of the formation of transcription foci in the nuclei of mammalian cells ²⁹. These models all confirmed previously described characteristics of the yeast nucleus as observed in microscopic studies ^77,78 but, importantly, they demonstrated that a relatively small set of spatial constraints is sufficient to yield a highly organized genome architecture ²⁹. A model of the human genome at low-resolution based on a genome-wide chromatin interaction dataset ²⁸ and statistical analysis showed that non-specific inter-chromosomal interactions are consistent with known architectural features.

Structural models of chromatin provide the opportunity to place linear annotations of the genome, such as positions of genes and gene regulatory elements, into a 3D context. Therefore, further developments in 3D model building will help to define the various levels of chromosome organization (including looping events, globules or TADs and higher order compartments), to pinpoint sequence elements that determine these structures, and to place widely spaced genomic loci in a spatial context that can reveal potentially functional long-range relationships.

Polymer approaches

Although restraint-based modeling has proven informative for analyzing relatively stable chromosomal domains, such as looped domains, polymer approaches provide insight into statistical organizational features of folding states of chromosomes, their cell-to-cell variability, and their dynamics within one cell. The application of polymer physics to chromosome research has a long history. Early works addressed such questions as the organization of interphase chromosomes, mechanisms of mitotic condensation, roles of topological constrains and DNA supercoiling ^79–86. Other studies have used simulations of polymer rings to suggest that chromosomal territories can be formed due to topological constraints that prevent mixing ⁸⁷ of individual chromosomes ^88–90. Polymer simulations are also being used to investigate how location of chromosomes can be influenced by properties of the chromatin fiber, its local folding and specific interactions between chromosomes ^88,91,92.

The equilibrium globule state

Several studies have sought to find a polymer model of interphase chromosomes that is consistent with FISH data on spatial distances between loci as a function of their genomic distances ^79,81,83. These studies considered equilibrium states of a homopolymer such as a self-avoiding chain in a good solvent (known as a swollen coil), a non-interacting chain (known as an ideal chain) and a polymer in a poor solvent or that is externally confined (known as an equilibrium globule). These studies demonstrated that a confined polymer (i.e. an equilibrium globule) is consistent with the observed increase in spatial separation with genomic distance for loci up to 5–10Mb apart ⁷⁹ and an independence of the spatial distance from genomic distance for more genomically distant loci ⁸¹. Some recent studies that explain the same phenomena using more complex models of polymer condensation ^93–95 nevertheless lead to a state that is strikingly similar to the equilibrium globule.

The equilibrium globule is known to emerge upon slow polymer condensation and equilibrate irrespective of exact mechanisms of condensation: confinement into a chromosomal territory ⁹⁴, condensation by pairwise interactions ⁹³ or action of crosslinking molecules ⁹⁵. While the equilibrium globule is not the only possible model of compact polymer organization (see below), large cell-to-cell variations in spatial distances measured by FISH make it hard to differentiate between various models ⁹⁶.

Interpretation of interaction data using polymer physics

With the emergence of 3C methods, approaches of polymer physics are being used to rationalize measured probabilities of spatial interactions ^4,64,97,98. Measured contact frequencies are used to determine and characterize the ensemble of chromatin conformations. The first question to be asked is whether conformations of a chromosomal locus are all similar to each other, like conformations of a single protein folded into native structure, or as diverse as conformations of a random polymer coil. HiC data show a lack of specific contacts among loci >1Mb apart, whereas specific interactions are detected at smaller scales (for example, TADs and loops between genes and regulatory elements generally involve loci separated by <1Mb). The absence of reproducible contacts at larger length scales makes higher order chromosome conformations very different from conformations of a single folded protein, suggesting that chromatin at large scales (>1Mb) can be better characterized as a statistical ensemble of diverse conformations, likely reflecting differences between individual cells, that collectively possess some specific statistical, spatial or topological properties.

Contact probability and genomic distance: the fractal globule

Interactions within single chromosomal arms exhibit a striking 100-fold decrease of the contact probability P with genomic distance s, making it the most prominent feature of intra-chromosomal interactions. Hi-C data for non-synchronized human cells⁶⁴ show three regimes each exhibiting a power-law decline in the contact probability P(s) ~ s^α (Fig. 5B) but with different powers: firstly, a shallow decline α ≈ −0.7 for s<0.7Mb corresponding to TADs ⁵⁸; secondly, a steeper decline of the contact probability α ≈ −1 for 0.7Mb < s <10Mb corresponding to some globular organization of chromatin; and thirdly a shallow decline at distance s >10Mb, but at these distances the interaction frequencies are very low so the statistics are not robust.

Figure 5. Large-scale features of genome folding.

A Whole-genome map of relative contact probabilities obtained by Hi-C (normalized by ICE ¹¹³). Insets show two most prominent features: intra-chromosomal decline of the contact probability; and a compartment pattern of interactions observed inter- and intra-chromosomally. B Contact probability P(s) as a function of genomic separation s. The mean contact probability for each separation is shown by the blue line, with the distribution shown by 75%-quantiles in light blue. Pink line show P(s)~s⁻¹ scaling. Two characteristics regimes corresponding to TADs (<0.7Mb) and the fractal globule (between 0.7 and 7Mb) are labeled. C (Top) Polymer model of the fractal globule of 10Mb (one monomer representing 2 nucleosomes) with 1Mb region shown in blue, illustrating its compactness within the globule. The same region in the equilibrium globule (bottom) is delocalized.

Polymer models can be used to build conformational ensembles that can give rise to P(s) ~ s⁻¹ contact probability scaling. In these simulations, chromatin is represented by a 10-nm fiber with one monomer corresponding to 2–5 nucleosomes ⁶⁴. A 10Mb region is modeled by thousands of monomers that have excluded volume, are connected into a polymer chain, and are subject of external forces and constraints. The folding and dynamics of the fiber is simulated by Monte Carlo or Brownian dynamics - a standard simulation technique in which each monomer experiences forces acting on it, including random Brownian fluctuations, and moves in response to these forces. An ensemble of obtained conformations is used to calculate a map of contact frequency and its features, e.g. P(s), are compared to those of experimental Hi-C maps.

Simulations and theory demonstrated that the P(s) ~ s⁻¹ scaling observed in Hi-C for 0.7–10Mb range is inconsistent with the equilibrium states (i.e. conformational ensembles) of a homopolymer such as the ideal chain, the swollen coil and the equilibrium globule. A non-equilibrium state called the fractal globule, conjectured in 1988 ⁹⁹, was simulated and found to recapitulate P(s) ~ s⁻¹ contact probability ^64,100. These simulations studied condensation of a chromatin fiber of 4–16Mb which was represented by a polymer chain of N=4,000–32,000 monomers. Such long chains are essential to capture statistical properties of polymers.

The fractal globule, which emerges as a result of polymer condensation during which topological constraints prevent knotting and equilibration of the polymer, has a number of important properties. First, dense and uniform packing of chromatin at the scale of <10Mb is consistent with observed chromatin globules of about 1 μm in diameter¹⁰¹ (assuming a realistic 5–10% chromatin volume density). Second, the unknotted conformation of the fractal globules (which is not a feature of equilibrium globules) allows easy opening and closing or translocation of chromosomal regions over large distances in the nucleus ^102,103. Third, dense packing of sub-chains in the fractal globule implies that continuous regions of the genome (in the size range 1–10Mb) are folded into local blobs rather than being spread in the nuclear volume. That is, regions that are close along the genome sequence are also close in space, consistent with other observations ¹⁰⁴. One of the limitations of the original fractal globule model is that the fractal globule is formed during condensation, rather than de-condensation of the chromatin from mitotic chromosomes. However, it has been demonstrated that a similar organization could emerge when several initially condensed chromosomes were allowed to de-condense into the nuclear volume ⁹⁰. Rosa et al have suggested that topological interactions between chromosomes prevent their mixing and equilibration during biologically relevant time scales. The fractal globule state can also emerge as an equilibrium state of a polymer ring in a melt of other such rings ⁸⁹, where rings model stable chromatin loops. What unites all these models is a central role of topological constrains in “crumpling” interphase chromatin.

Another study that aimed to explain the scaling of Hi-C contact probability used an equilibrium homopolymer model and suggested that the fractal globule emerges in equilibrium, at the transition between the open and condensed states ⁹⁵. This result, however, contradicts well-known facts in polymer physics ¹⁰⁵, and is likely a result of a poor statistics due to very short chains (N=512) used in simulations.

Connections of the fractal globule conformation to much smaller TADs and much larger chromosomal territories and compartments are yet to be established. It also remains to be seen whether the fractal globule is susceptible to slow “melting” over long times or due to activity of topoisomerase II enzymes, or whether specific biological mechanisms are responsible for its maintenance.

Future perspective

In the coming years we can expect a wealth of chromatin interaction data to become available. With expected further increases in sequencing capacity and reduction in cost, chromatin interaction maps will become available for even the largest genomes at increasing resolution. Analyzing these datasets will become the major challenge, requiring new developments in bioinformatics, computational biology and biophysics. The approaches described here are only a starting point, and we envision a rapid expansion in efforts to explore the three dimensional folding of chromosomes and the effects on the biology of genomes. Further improvements in both experimental and computational data analysis approaches will facilitate addressing several important questions that the field of genome regulation is currently grappling with. For instance, most 3C-based studies do not directly allow measurement of the dynamics and cell-to-cell variation in chromosome folding and thus it is currently largely unknown how stable looping interactions and chromatin domains are within individual cells or how stochastic they are between cells. Further, the relative contributions of genomic sequence and transcriptional activity in establishing the compartmentalized architecture of chromosomes are yet to be determined. The roles of lamina association, direct or mediated co-localization of transcribed regions and other molecular mechanisms shaping activity-associated organization of the nucleus need to be established. Finally, we still know little about how chromosome structure changes during development, upon perturbation (e.g. as cells respond to signals) and how chromosomes fold and unfold during the cell cycle. With the rapid technological developments in this field we may get some answers to these questions in the years ahead.