Age-related Changes in Human Peripapillary Scleral Strain

Abstract

To test the hypothesis that mechanical strain in the posterior human sclera is altered with age, twenty pairs of normal eyes from human donors aged 20 to 90 years old were inflation tested within 48 hours post mortem. The intact posterior scleral shells were pressurized from 5 to 45 mmHg while the full-field three-dimensional displacements of the scleral surface were measured using laser speckle interferometry. The full strain tensor of the outer scleral surface was calculated directly from the displacement field. Mean maximum principal (tensile) strain was computed for eight circumferential sectors (45° wide) within the peripapillary and mid-peripheral regions surrounding the optic nerve head (ONH). To estimate the age-related changes in scleral strain, results were fit using a functional mixed effects model that accounts for intra-donor variability and spatial autocorrelation.

Mechanical tensile strain in the peripapillary sclera is significantly higher than the strain in the sclera farther away from the ONH. Overall, strains in the peripapillary sclera decrease significantly with age. Sectorially, peripapillary scleral tensile strains in the nasal sectors are significantly higher than the temporal sectors at younger ages, but the sectorial strain pattern reverses with age, and the temporal sectors exhibited the highest tensile strains in the elderly.

Overall, peripapillary scleral structural stiffness increases significantly with age. The sectorial pattern of peripapillary scleral strain reverses with age, which may predispose adjacent regions of the lamina cribrosa to biomechanical insult. The pattern and age-related changes in sectorial peripapillary scleral strain closely match those seen in disk hemorrhages and neuroretinal rim area measurement change rates reported in previous studies of normal human subjects.

1. Introduction

The mechanism of damage to the retinal ganglion cell axons in glaucoma is not well understood, but it is hypothesized that intraocular pressure-driven biomechanics of the optic nerve head (ONH) and peripapillary sclera play a role (Sigal et al. 2005; Burgoyne and Downs. 2008). The preponderance of evidence indicates that glaucomatous damage to retinal ganglion cell axons occurs at the ONH, a structure through which the axons pass out of the eye on their path to the brain. Evidence also suggests that the ONH is particularly susceptible to the effects of intraocular pressure (IOP), as it is less resistant to IOP-related mechanical stress than the other regions of the ocular coats (Roberts et al. 2010). The sclera surrounds the ONH, and transmits IOP-related forces and deformations to the ONH at the scleral canal wall. Hence, scleral biomechanics are inseparably intertwined with ONH biomechanics (Sigal et al. 2011).

While race, family history, ocular perfusion pressure, and refractive status have been shown to be risk factors in open angle glaucoma, age is the only risk factor other than IOP that is independently associated with the onset and progression of glaucoma across all of the major prospective clinical trials conducted over the past twenty years (Drance et al. 2001; Kass et al. 2002; The AGIS Investigators 2002; Leske et al. 2004; EGPS Group 2007). In addition to data from prospective trials in glaucoma and ocular hypertension, every population-based survey conducted to date has demonstrated a strong relationship between the prevalence of glaucoma with advancing age (Rudnicka et al. 2006), despite there being little change in IOP with age (Leske et al. 1997; Weih et al. 2001). Furthermore, while normal tension glaucoma is not uncommon within elderly populations (Chumbley and Brubaker 1976; Levene 1980), it is not seen in children or young adults other than in a few isolated case reports (Geijssen 1991). These findings indicate that the aged ONH becomes increasingly vulnerable to glaucomatous injury at similar levels of IOP.

As with any solid structure, the degree of local deformation (strain) experienced by the ONH under a given level of stress is dependent upon its 3D architecture and material properties (Bellezza et al. 2000; Downs et al. 2003; Sigal et al. 2005; Girard et al. 2011). A variety of age-related changes in the ONH and scleral connective tissues may affect ONH compliance (Morrison et al. 1989; Hernandez et al. 1989; Albon et al. 1995; Bailey et al. 1998; Albon et al. 2007; Girard et al. 2009). Thus, variation in ONH anatomy and material properties that occur with aging may account for the increased susceptibility to IOP-induced glaucomatous injury in the elderly.

Sigal and colleagues determined that variations in scleral thickness, radius of the eye, laminar stiffness, and scleral thickness have the greatest influence on the biomechanical response of the ONH using computational models based on axisymmetric idealized geometries (Sigal et al. 2004). A follow up study using more accurate estimates of the ranges of laminar and scleral material properties indicates that laminar structural stiffness also plays a prominent role in determining laminar biomechanics (Sigal et al. 2011). In a computational study, Norman and colleagues (2011) showed that the peripapillary sclera adjacent to the ONH is a particularly important factor in laminar biomechanics. Grytz et al. (2011) showed that the collagen architecture of the peripapillary sclera and the lamina cribrosa have a significant impact on the IOP-induced deformation response of the lamina cribrosa using computational modeling. These studies demonstrate that variation in both the material properties and geometries of the sclera and lamina, which combine to govern the overall structural stiffness of the posterior pole, are important determinants of the mechanical environment in the ONH.

In spite of the importance of the sclera in determining ONH biomechanics, surprisingly few studies have been designed to accurately assess the sclera's mechanical behavior in human eyes, especially as they change with age. Studies have shown that the sclera of various species has nonlinear (Woo et al. 1972; Girard et al. 2009) (stiffens as it stretches) and anisotropic elastic properties (Sigal et al. 2004) (resists deformation more in certain directions), stiffens with age (Avetisov et al. 1983; Sigal et al. 2004), and remodels in response to chronic elevated IOP exposure (Downs et al. 2005; Girard et al. 2011). Eilaghi and coworkers (Eilaghi et al. 2010a; Eilaghi et al. 2010b) confirmed the nonlinear behavior of the stress-strain relationship in human sclera using planar biaxial testing of small scleral patches excised near the ONH, although there was large variability among donors that resulted in a wide range of reported material properties. Geraghty and coworkers (2012) recently reported significant age-related stiffening in the anterior sclera based on uniaxial testing of scleral strips in tension, but they did not see any significant differences in the posterior sclera. A recent study by Coudrillier and colleagues (2012) reported significant collagen stiffening in the human sclera with age, but their estimates of age-related changes were based upon a customized model of collagen stiffness derived from experimental inflation data over the entire peripapillary and mid-peripheral regions, rather than calculated directly from the experimental displacement measurements themselves for sectors around the ONH. Glaucoma is a disease of focal axonal damage in the ONH, so focal strain in the surrounding peripapillary sclera may prove important. None of these studies report the changes in sectorial peripapillary scleral strain with age in human eyes for physiologic loading conditions.

The principal aim of this work was to assess age-related changes in IOP-induced mechanical strain in the posterior human sclera for both the peripapillary and mid-peripheral regions using mechanical inflation tests. Regional variations in peripapillary strains could contribute to the focal structural and functional defects typically seen in glaucoma patients and changes in scleral strains with age could explain some of the increased susceptibility of the elderly to the disease. This study was designed to test the hypothesis that aging alters the sectorial patterns of peripapillary and mid-peripheral scleral strain measured in human donor eyes. The results of these studies will serve as important inputs for future biomechanical modeling studies of the ONH and aging, and also provide accurate strain ranges for in vitro studies of the response of scleral cells to mechanical deformation. In addition, quantification of scleral strain via post-processing of clinical images may prove useful as an eye-specific assessment of biomechanical risk factors in glaucoma.

2. Materials and Methods

2.1. Human Donor Specimens

Twenty pairs of eyes from normal human donors were obtained from the Lions Eye Bank of Oregon in Portland, Oregon and the Alabama Eye Bank in Birmingham, Alabama. Donor eyes were deemed normal by next-of-kin questionnaire; donors with a history of glaucoma, severe myopia, or diabetes were excluded. All specimens were stored in isotonic saline at 4°C immediately after enucleation and tested within 48 hours post mortem as follows. Of the twenty pairs of human donor eyes used in this study, 19 pairs from donors aged 20 to 90 years old (average age of 52.8, 12 Males, 8 Females) were used in a statistical analysis to estimate the change in scleral strain with age. Scleral strains from one pair of eyes from a newborn donor (age 0 years old) were used post hoc to qualitatively assess the appropriateness of the regression function for estimating the age-related strain change at the lower extreme of the age range. Strain data from ten pairs of eyes from elderly donors were published in a previous report focused on regional and sectorial strain variation (Fazio et al. 2012b). For this study, we combine those data from elderly donors with ten more pairs of eyes from young donors to study age-related changes in the human scleral strain within the peripapillary and mid-peripheral regions of the posterior pole.

2.2. Inflation Testing, B-spline Based Displacement Fitting, Mechanical Strain Calculations

The custom scleral inflation testing apparatus and general protocol used in this work has been described in previous studies (Girard et al. 2009; Fazio et al. 2012b). Briefly, the scleral inflation testing apparatus consists of a clamping stage that allows the posterior third of the eye to be sealed and pressurized while preventing non-inflation induced motion. A sealed chamber with a silica window was fitted atop the clamping stage, which allows the inflation testing to be performed with the specimen immersed in physiologic phosphate buffered saline solution (PBS) while measuring displacements optically through the window. Each eye was preconditioned using 20 pressurization cycles from 5 mmHg to a maximum of 30 mmHg at a rate of 5 mmHg per second, and then allowed to recover for 15 minutes. Each eye was then pressurized from 5 to 45 mmHg in small steps of 0.01 to 0.2 mmHg using an automated system with computer feedback control, while scleral surface displacements were recorded using a commercial laser speckle interferometer (ESPI; Q-100, Dantec Dynamics A/S, Denmark). After each pressure step, displacements were allowed to reach equilibrium before they were recorded, and pressure step size was carefully controlled via computer feedback during the testing protocol to ensure displacement steps of similar size. A starting pressure of zero could not be used since the posterior scleral shell does not maintain its shape at that pressure. So, we began testing at an internal pressure of 5 mmHg, which was assumed to be a zero load condition for the purposes of strain calculation. As in our previous studies (Girard et al. 2009; Fazio et al. 2012b) all pressure testing was performed at room temperature.

Following inflation testing, the shape of each eye was acquired using a 3D digitizer with a nominal resolution of ∼0.2 mm (MicroScribe G2X, Immersion, San Jose, CA). Three-dimensional coordinates of ∼2500 points on the outer surface of the posterior sclera were acquired while the shell was pressurized with PBS at 10 mmHg instead of the reference pressure of 5 mmHg because the sclera is more rigid at 10 mmHg and hence was considerably more resistant to undesired indentions of the digitizer tip. This does not affect the strain calculations, as small deformation theory dictates that the strains as calculated in Eq. 2 are independent from the initial specimen shape. A customized B-spline fitting system was used for obtaining continuous and differentiable analytical functions that define the three-dimensional displacement field over 2/3 of the posterior hemisphere of the eye as described previously (Fazio et al. 2012b). Using the same functional form to describe specimen shape and displacement allows direct surface deformation analysis and local strain calculation without any intermediate finite element or analytical modeling and the associated limitations of their inherent assumptions.

Speckle pattern interferometry is a measurement technique based on the principle that a rough surface illuminated with a coherent light beam creates a distribution of light spots, i.e., a speckle field, randomly distributed in space. Interference between the speckle field generated by the illuminated surface with a reference field generates a light intensity distribution that is functionally dependent on the surface deformation. By analyzing this light interference, one can reconstruct the surface displacement field in three dimensions at nanometer resolution.

In a recent study, we assessed the uncertainty of our ESPI displacement measurement system. Mean displacement measurement uncertainty was ±16 nm at the 95% confidence level (Fazio et al. 2012a), which demonstrates that ESPI possesses extremely high spatial resolution and low measurement uncertainty (measurement error) when used for measuring deformations in immersed spheroid pressure vessels.

The IOP-induced displacement field was measured using ESPI for each eye as described above, then processed to calculate the engineering strain tensor for the outer surface of each eye as described in our previous report (Fazio et al. 2012b). Briefly, mechanical strain was computed as follows:

ESPI displacements in Cartesian space were filtered and fit to continuous, differentiable, analytical functions U(θ,φ) = {u_θ(θ,φ), u_φ(θ,φ), u_r(θ,φ)} (meridional, circumferential, and radial displacement, respectively), which defines the displacement field over the domain defined by the meridional $\mathbf{[}\theta ,0,\frac{\pi }{2}\mathbf{]}$ and circumferential [φ, 0, 2π] angles. For the outer surface of each eye, five (ε_θθ, ε_θφ, ε_φφ, ε_rφ, ε_rθ) out of 9 components of the full strain tensor (Eq. 1) were computed by direct mathematical differentiation of the analytical displacement functions (Eq. 2); three components ε_φθ, ε_θr, and ε_φr, were computed by strain compatibility equations, and the final component, ε_rr, was numerically computed by assuming tissue incompressibility, thereby imposing det[ε +I] = 1 (where I is the Identity Matrix). In agreement with small deformation theory, calculated strains are independent from the initial or deformed specimen shapes. When these components are calculated with respect to a spherical reference system (Eq. 2) the radius of the sphere comes into play, but the relative errors are miniscule for even relatively large errors in the estimate of the sphere radius.

$$\text{Strain Tensor}=\mathit{\varepsilon }(\theta ,\phi )=\left\{\begin{array}{ccc}{\varepsilon }_{\theta \theta }& {\varepsilon }_{\theta \phi }& {\varepsilon }_{\theta r}\\ {\varepsilon }_{\phi \theta }& {\varepsilon }_{\phi \phi }& {\varepsilon }_{cr}\\ {\varepsilon }_{r\theta }& {\varepsilon }_{rc}& {\varepsilon }_{rr}\end{array}\right\}$$ (1)

$$\text{where}\{\begin{array}{c}{\varepsilon }_{\theta \theta }=\frac{1}{r}(\frac{\partial u_{\theta }}{\partial \theta }+u_r)\hfill \\ {\varepsilon }_{\phi \phi }=\frac{1}{r\sin \theta }(\frac{\partial u\phi }{\partial \phi }+u_r\sin \theta +u_{\theta }\cos \theta )\hfill \\ {\varepsilon }_{\theta \phi }=\frac{1}{2r}(\frac{1}{\sin \theta }\frac{\partial u_{\theta }}{\partial \phi }+\frac{\partial u_{\phi }}{\partial \theta }-u_{\phi }\cot \theta )\hfill \\ {\varepsilon }_{r\theta }=\frac{1}{2}(\frac{1}{r}\frac{\partial u_r}{\partial \theta }+\frac{\partial u\theta }{\partial r}-\frac{u\theta }{r})\hfill \\ {\varepsilon }_{r\phi }=\frac{1}{2}(\frac{1}{r\sin \theta }\frac{\partial u_r}{\partial \phi }+\frac{\partial u\phi }{\partial r}-\frac{u\phi }{r})\hfill \end{array}$$ (2)

Maximum principal tensile strain (ε_I, Eq. 3) was computed over the entire scleral surface by computing eigenvalues of the full strain tensor:

$${\mathit{\varepsilon }}^{\mathit{\text{Eig}}}=\left\{\begin{array}{ccc}{\varepsilon }_I& 0& 0\\ 0& {\varepsilon }_{\mathit{\text{II}}}& 0\\ 0& 0& {\varepsilon }_{\mathit{\text{III}}}\end{array}\right\}$$ (3)

A recent study by Tang and colleagues showed that variation of the meridional and circumferential components of displacement in the radial direction within the outermost layer of the scleral shell is minimal (Tang and Liu 2012). So, meridional and circumferential displacement variation in the radial direction, $\frac{\partial u_{\theta }}{\partial r}(\theta ,\phi )$ and $\frac{\partial u_{\phi }}{\partial r}(\theta ,\phi )$ in Eq. 2, respectively, were assumed to be zero in the infinitesimally thin outer layer of the scleral shell. This assumption cannot be used through the full thickness of the sclera because there is considerable variation of the tangential displacement components in the radial direction (Tang and Liu 2012). This assumption, together with tissue incompressibility assumption, and analysis of strain sensitivity to noise were quantified and reported in the last paragraph of this section.

2.3. Regionalization and Strain Sampling

The data analysis focused on measurements of the mean maximum principal (tensile) strain taken on a 200 × 200 equally spaced grid of meridional (θ) and circumferential (φ) angles across a region of the scleral surface including both the peripapillary and mid-peripheral regions surrounding the ONH. The peripapillary region was defined as a ∼10 degree-wide-band adjacent to the ONH (approximately 2.2 mm wide) and the adjacent mid-peripheral region was defined for each eye such that it had the same surface area as the peripapillary region. Previous studies have shown that the peripapillary sclera adjacent to the ONH is a particularly important factor in laminar biomechanics (Norman et al. 2011; Grytz et al. 2011) so we focused our measurements in this region. For tabulation of mean sectorial strains with age, mean maximum principal (tensile) strain was computed for eight circumferential sectors (45° wide) of equal surface area within both the peripapillary and mid-peripheral regions surrounding the ONH.

2.4. Statistical Analysis

Strain values were modelled using Bayesian wavelet-based functional mixed models (Morris and Carroll 2006), an extension of linear mixed models designed to handle complex functional and quantitative image data. The age effect was modelled using an exponential function (see below). In preliminary analyses we also considered linear age effects, but Akaike Information Criterion (AIC) tests found the exponential model was a better fit for the data, and the maximum likelihood was achieved by using 110 years of age for the asymptotic value of the exponential function. The model was fit using a Bayesian approach assuming non-informative vague prior distributions for the regression coefficients, with a Markov Chain Monte Carlo procedure yielding posterior samples for all model parameters. We chose the functional mixed modelling approach because it can model the maximum principal strain data on the entire meridional and circumferential grid while accounting for the correlations within each eye in a flexible way. Improperly accounting for spatial autocorrelation can result in erroneously low p-values (type I error), so the Bayesian approach we used is more conservative than less flexible statistical approaches that are typically available in software packages. Statistical modeling and inference details are given below.

While we modelled maximum principal strain continuously on the scleral surface, we also computed aggregate summaries of strain and its relationship with age within eight circumferential sectors (45° wide) of equal surface area in both the peripapillary and mid-peripheral regions surrounding the ONH. Our Markov Chain Monte Carlo procedure produced posterior samples for these quantities, from which we computed posterior means, standard errors, and credible intervals for intercept a and age effect b continuously for (θ,φ), both regionally and sectorially. To assess statistical significance of the age effects, we computed P = 2*min{Prob(b>0|Y), Prob(b<0|Y)} for the age effect b for each section within the two considered regions. Note that given non-informative vague priors for the regression coefficients, this measure is approximately equivalent to the p-value for a two-sided test of the null hypothesis that b=0. The details of our statistical modeling approach are as follows.

Let Y_ij(θ,φ) be the mean maximal principal (tensile) strain for eye j (j=1, left eye, j=2, right eye) from subject i at meridional angle θ and circumferential angle φ. The functional mixed model we fit was:

$$Y_{\mathit{\text{ij}}}(\theta ,\phi )=a(\theta ,\phi )+b(\theta ,\phi )\ast exp\{{\mathit{\text{age}}}_i/({\mathit{\text{age}}}_i-110\left)\right\}+u_i(\theta ,\phi )+e_{\mathit{\text{ij}}}(\theta ,\phi ),$$ (4)

where a(θ,φ) and b(θ,φ) are the intercept and age coefficient, u_i(θ,φ) are random effect functions, and e_ij(θ,φ) are residual error functions. A Bayesian wavelet domain modelling approach (Morris et al. 2011) was used to fit model (Eq. 4). This approach allows the method to model a(θ,φ) and b(θ,φ) continuously while adaptively borrowing strength from nearby measurements, and automatically accounting for local covariance structure (spatial autocorrelation) across (θ, φ) in the random effects and residual error variance in a flexible way.

2.5. Error Assessments and Sensitivity Analysis

Two pairs of eyes (one from a young, and one an old donor) were used to assess the impact of our assumptions of tissue incompressibility and zero variation of the in-plane displacement components in the radial direction at the outer surface of the sclera. We also assessed the sensitivity of the reported strains to random displacement measurement noise.

2.5.1. Tissue incompressibility Assumption

Assuming scleral incompressibility basically assumes that there is a negligible volume change in the tissue following mechanical deformation. Sclera is mechanically anisotropic, hyperelastic, and inhomogeneous, so true validation of the incompressibility assumption under real mechanical conditions is impractical. In order to estimate the impact of our incompressibility assumption on the reported strain values, we considered a simplified case of homogeneous, isotropic sclera (same Poisson's ratio in any direction) subject to equibiaxial in-plane tensional deformation (ε_θ = ε_φ); equibiaxial deformation maximized the sensitivity of the radial contraction to a variation of the Poisson's ratio. Under these conditions, out-of-plane (radial) contraction would be 0.5 times the magnitude of the in-plane deformation $(-\frac{{\varepsilon }_{\phi }}{{\varepsilon }_r}=-\frac{{\varepsilon }_{\theta }}{{\varepsilon }_r}=0.5)$. If this simplified sclera was compressible (assume a Poisson's ratio of 0.45), the out-of-plane contraction (ε_r) would be reduced by 10%. Therefore, we assessed the impact of tissue compressibility by imposing a 15% decrease in ε_r (the only component in our method affected by this assumption) and quantified the absolute variation of the sectorial mean maximum principal strain. On average we observed a 1.58% relative change in strain when assuming scleral incompressibility versus assuming a reasonable value for scleral compressibility.

2.5.2. Assumption of negligible variation of in-plane displacement components in the radial direction

To assess the dependency of the strain computation reported in this paper we also computed maximum principal strain using only the components of the strain tensor ε_θθ, ε_φφ, ε_θφ (in-plane components); these components of the strain tensor can be directly calculated from the displacements without any underlying assumptions.

Maximum principal strains computed with the approximated full 3D tensor are slightly different in absolute value from those computed with the 2D, in-plane strain components only, but both the sectorial pattern and age-related variations are very similar (see Results section).

2.5.3. Sensitivity of Strain to Random Displacement Measurement Noise

To quantify the impact of random noise on the strain, we added random displacement noise of −5 to 5 μm to the raw displacement components at pressure levels from 10 to 45 mmHg at each 5 mmHg step. The resulting relative difference in sectorial mean maximum principal strain was 1.66%, which demonstrates the robustness of our customized B-spline fitting method to noise. A graphical representation of the assessment of error due to random displacement measurement noise is shown in Figure 1, where we compare the b-spline surface fitting of the original data (blue) to that including +5 μm of simulated random noise (red). The fitting methodology we used is effectively insensitive to random noise, even for noise magnitudes much larger than would be expected for our experimental setup.

Fig. 1.

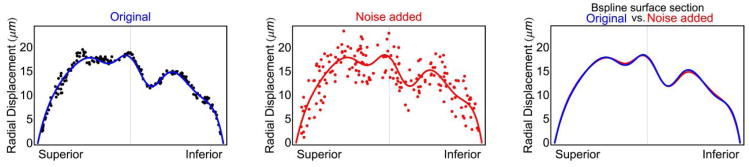
Superior-inferior section through the b-spline surface fitting of both the original measurement data (blue) and the original data with ±5 μm of random displacement noise added.

2.5.4. Interactions

The aforementioned estimates of potential error were calculated independently, but the highest total error can be achieved by combining all three potential sources of error. Considering all possible combinations, the maximum relative error in sectorial mean maximum principal strain was 3.77%, which is negligible given the differences we report in the Results section below.

3. Results

3.1. Strain Variation in the Posterior Pole

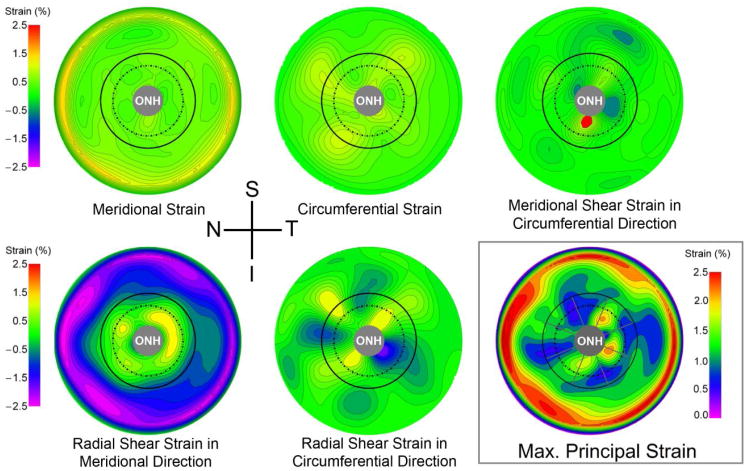
Contour maps of the measured strain components and the maximum principal (tensile) strain for a representative human scleral specimen are presented in Figure 2. Strain values are particularly pronounced in the peripheral sclera near the clamp (Figure 2). The nature of inflation testing of quasi-spherical specimens requires that the radial displacement component (u_r) is zero at the clamp ring where the sclera is constrained, which forces a steep gradient in the radial displacements near the clamp and induces a large radial shear strain in the meridional direction (Figure 2). Also, shear strain is particularly pronounced around the ONH due to the mechanical discontinuity caused by the presence of the relatively compliant ONH within a stiffer posterior scleral shell. As a result, the outer boundary of the mid-peripheral region was located sufficiently distant from the clamping ring in this study to ensure that clamp-induced shear deformation was negligible.

Fig. 2.

Contour plots showing the five unique components of the strain tensor and the analytically derived maximum principal (tensile) strain for an IOP elevation from 5 to 45 mmHg in a representative human eye in right eye configuration. The boundaries of the peripapillary and mid-peripheral regions surrounding the ONH are shown by the solid and dashed lines on the lower right plot, respectively, and the boundaries of the 45-degree-wide sectors are shown with radial gray lines. The spatial complexity and steep gradients of the strain around the ONH (3.3 mm in diameter in this eye) indicate that only techniques with extremely high spatial resolution and displacement measurement accuracy are appropriate for displacement and strain calculation in scleral shells subjected to inflation testing

3.2. Regional Differences in Maximum Principal Strain

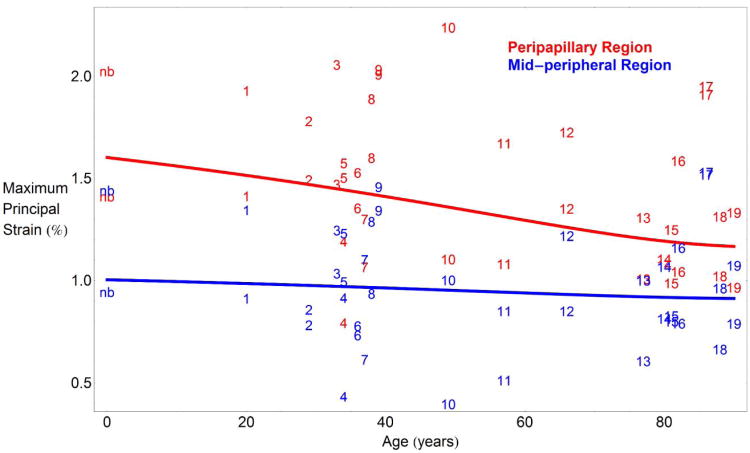
Average maximum principal strain significantly decreased with age in the peripapillary region, from 1.54% at 20 years old to 1.32% at 90 years old (P<0.001; Figure 3). Interestingly, the mid-peripheral sclera did not exhibit a significant change in average strain level with age (P=0.16; Figure 3). Across all ages, strain in the peripapillary region adjacent to the ONH was significantly higher than strain in the mid-peripheral region for a 40 mmHg IOP elevation (P<0.001; Figure 3).

Fig. 3.

Average regional maximum principal strain versus age for a pressure elevation of 40 mmHg. Overall regional mean maximum principal strain in the peripapillary region significantly decreases with age (P<0.001), while mid-peripheral strain did not exhibit a significant change with age (P=0.16). Maximum principal (tensile) strain was significantly higher in the peripapillary region (red line) than in the mid-peripheral region (blue line) at all ages (P<0.001). Mean maximum principal strain values for the peripapillary (red numbers) and mid-peripheral (blue numbers) regions of each eye are labeled by donor number, which were assigned in ascending order by donor age (higher numbers indicate higher age). Strain data from the newborn donor (nb) is included in the plot but not in the statistical analysis used to estimate the plotted curves, and it matches the statistical estimates of scleral strain at age 0 years

3.3. Sectorial Differences in Tensile Strain by Age

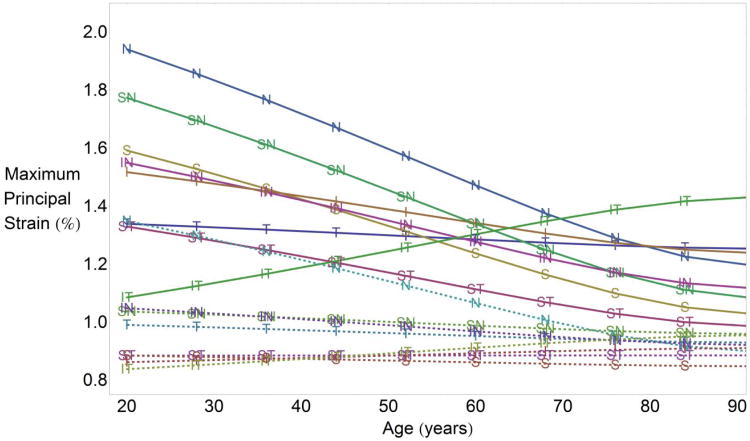
Strain changes with age sectorially in both the peripapillary region (solid lines) and mid-peripheral regions of the sclera (dashed lines) as shown in Figure 4. Six of the eight sectors in the peripapillary region showed significant stiffening with age (P<0.034 for all sectors, Table 1), while the inferotemporal sector showed a significant softening with age (P<0.001, Table 1). In the mid-peripheral region further from the ONH, only the nasal sector showed a significant stiffening (strain decrease) with age (P=<0.001, Table 1). Table 1 lists the fitting function and estimates of the coefficients necessary to calculate the sectorial tensile strain in both regions as a function of age.

Fig. 4.

Sectorial strain change by age for sectors in the peripapillary region (solid lines) and mid-peripheral region (dashed lines) for a pressure elevation of 40 mmHg. Maximum principal strain changed significantly with age in 7 of 8 sectors in the peripapillary region (P<0.05 for all, except the T sector), while only one sector (N) in the mid-peripheral region showed significant change with age. While the peripapillary region stiffened significantly overall and in 6 of 8 sectors with age, the inferotemporal sector softened significantly. S, superior; I, inferior, N, nasal; T, temporal

Table 1.

Coefficient estimates, standard errors, and posterior probabilities (P) for the age-related strain change coefficient b of the non-linear regression function for maximum principal (tensile) strain, aggregated within sectors in the peripapillary and mid-peripheral regions. Due to the exponential formulation of the aging function, the coefficient a estimates the strain value in each sector at an age of 110 years old. Strains can be estimated at any age using the function at the top of the table and the listed coefficient estimates. Note that P is equivalent to the standard p-value for a two-sided test of the null hypothesis that b=0.

Predicted Maximum Principal Strain = a + b*e(age/(age-110)) (Mean values over Sectors of the Peripapillary and Mid-peripheral Regions)
Peripapillary Region	a		b
Sector	Estimate	Std. Error	Estimate	Std. Error	P
Temporal	1.2523	0.09	0.1078	0.1892	0.57
Superotemporal	0.9825	0.0759	0.433	0.1628	0.004*
Superior	1.0227	0.0885	0.71	0.1886	0.002*
Superonasal	1.0765	0.0725	0.8697	0.153	<0.001*
Nasal	1.1884	0.0751	0.939	0.1574	<0.001*
Inferonasal	1.1125	0.0894	0.5452	0.1919	<0.001*
Inferior	1.2357	0.0708	0.351	0.1518	0.034*
Inferotemporal	1.4337	0.0682	−0 4357	0.1459	<0.001*
Mid-peripheral Region	a		b
Sector	Estimate	Std. Error	Estimate	Std. Error	P
Temporal	0.9286	0.0677	0.0771	0.1427	0.602
Superotemporal	08849	0.0489	−0.0007	0.1069	0.976
Superior	0.8472	0.0621	0.0464	0.1318	0.734
Superonasal	0.9582	0.0575	0.0979	0.1234	0.438
Nasal	0.8945	0.0601	0.5673	0.1287	<0.001*
Inferonasal	0.9196	0.0703	0.1601	0.1489	0.304
Inferior	0.9108	0.0526	−0.0611	0.1132	0.578
Inferotemporal	0.9559	0.05	−0.1476	0.1088	0.17

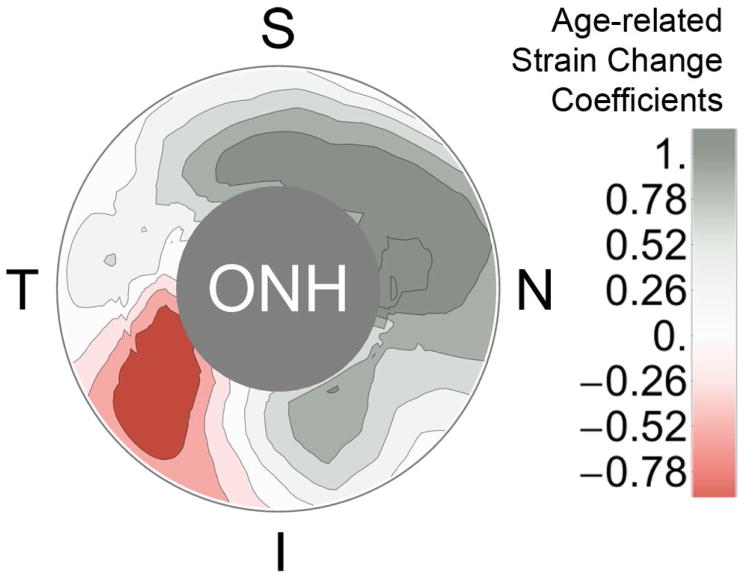
Local age-related strain change rate (b coefficients in Table 1) for the peripapllary scleral region are graphically represented in Figure 5, which shows the variabilty in the age-related change in scleral mechanical response.

Fig. 5.

Contour map of the age-related strain change coefficients of the nonlinear regression function (b coefficients in Table 1) for the peripapllary scleral region. Negative values of the strain change coefficient indicate a local increase in scleral compliance with age, while positive values indicate local scleral stiffening with age. Age was significantly associated with peripapillary scleral strain in all but the temporal sector (P<0.05). S, superior; I, inferior; N, nasal; T, temporal; ONH, optic nerve head

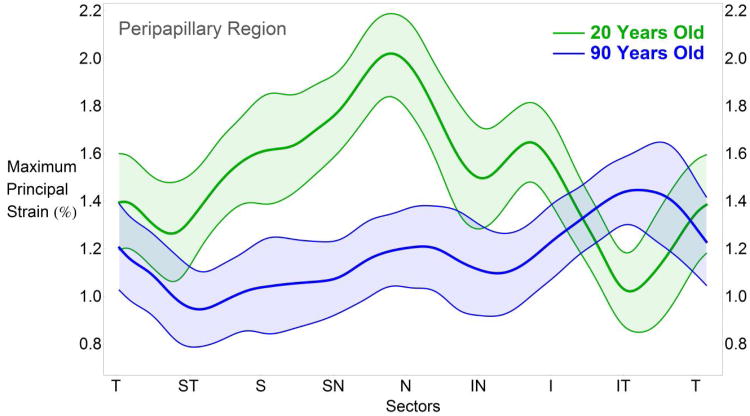
Sectorial differences in maximum principal scleral strain calculated at the two extremes of the age-range of the donors in this study (20 and 90 years old) are presented in Figure 6 for sectors of the peripapillary region only. At 20 years old, tensile strains in the nasal sectors are significantly higher than the temporal sectors. The sectorial strain pattern reverses with age, and the temporal sectors exhibit the highest tensile strains as subjects get older. The age-related changes in tensile strain by sector and region can be calculated using the function and coefficient estimates given in Table 1.

Fig. 6.

TSNIT plot of the estimated mean maximum principal strain at 45 mmHg (assuming zero deformation at 5 mmHg and a 40 mmHg IOP elevation) in the peripapillary region, as predicted by the statistical model for 20 and 90 years old. The 95% credible intervals of the estimated means of strain values are indicated by the color-shaded areas around each curve. On average, the nasal sectors exhibit the highest strains when humans are young, but that reverses with age such that the temporal sectors exhibit the highest strains in the elderly. Sectorial strain variability decreases with age due to the gradual overall stiffening of the sclera with age. T, temporal; S, superior; N, nasal; I, inferior

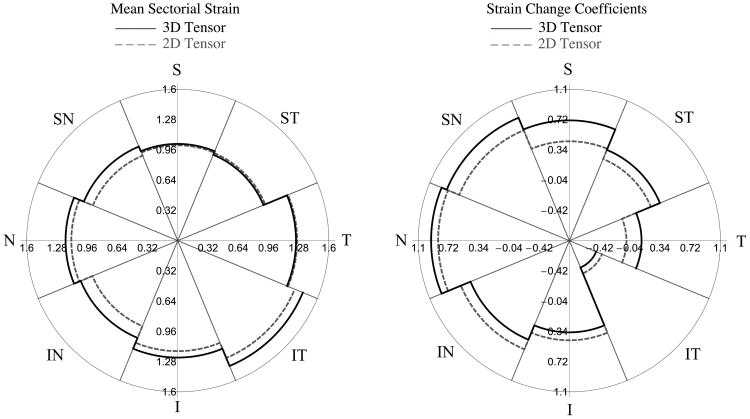
As briefly introduced in the methods section above, we investigated the sensitivity of the maximum principal strain values to the assumptions used in the definition of the 3D strain tensor. Fig. 7 shows a comparison between the mean sectorial maximum principal strain (a coefficients in Table 1) and the strain change coefficient (b coefficients in Table 1) obtained using the approximated 3D strain tensor formulation and the directly calculated 2D strain tensor with the in-plane components only (ε_θθ, ε_φφ, ε_θφ). This highlights that the assumptions underlying the 3D strain tensor calculation did not affect the sectorial variability or age-related changes reported in this study.

Fig. 7.

Mean sectorial maximum principal strains (Left) and age-related strain change coefficients (Right) obtained by computing the maximum principal strain with the approximated 3D strain tensor shown in Eq. 2 (thick lines) and a partial 2D strain tensor with the in-plane strain components only (dashed lines). Mean sectorial strains and age-related strain change were slightly different, but the sectorial pattern and variation with age were effectively identical using both the 3D and 2D calculations.

4. Discussion

The main finding of this work is that mechanical strain in human peripapillary sclera significantly changes with age within 7 of 8 sectors around the ONH. Only one sector of the mid-peripheral sclera exhibited a significant change in the strain level with age. Across all ages, strain in the peripapillary region adjacent to the ONH was significantly higher than strain in the mid-peripheral region. The sectorial pattern of peripapillary scleral strain pattern changes significantly with age; maximum strains are seen in the nasal and minimum in the inferotemporal quadrants in young donors, while the maximum strains were found in the inferotemporal and the minimum in the nasal quadrants in the elderly donors. Also, while scleral strains generally decrease in the peripapillary region with age, the sectorial variability in the strains also decreases with age (Fig. 4), but the statistical significance of this was not assessed.

This work should be viewed with several limitations in mind, which have been described in detail in our previous reports (Fazio et al. 2012a; Fazio et al. 2012b). Briefly, there is error in the displacement measurement at the outer edge of the specimen due to ESPI phase map reconstruction difficulties. We positioned the ONH and peripapillary sclera at the center (apex) of the posterior scleral specimen and analyzed strains in a relatively narrow band around the ONH to avoid these edge effects. Under these conditions, our ESPI system has a measurement uncertainty of ±16 nm (Fazio et al. 2012a) and possesses sufficient measurement precision and spatial resolution to capture the local scleral deformation changes between sectors within the peripapillary and mid-peripheral sclera, as well as the small but significant changes in the sector deformations with age.

We assumed that the sclera is incompressible to calculate one of the nine strain tensor components necessary for our analyses, as described in detail in our previous report (Fazio et al. 2012b). This assumption affects only one of the nine strain tensor components used to calculate maximum principal strain, so no significant errors are expected to be dependent of this assumption.

We computed strain values in the sclera assuming zero-strain state at 5 mmHg IOP, so the strain values we reported are lower than the true strain. We used an initial 5 mmHg pressure reference to avoid the geometric nonlinearities that would invalidate analytical computation of the strain tensor from the displacement field.

The Coudrillier study also reported a significant age-related stiffening of the mid-peripheral sclera (Coudrillier et al. (2012), which does not agree with our findings. A possible explanation of this discrepancy is that Coudrillier and coworkers did not include a spatial autocorrelation structure in their statistical analysis that accounts for the correlation and inter-dependence of the deformations measured at adjacent points on the sclera. The sclera is mechanically continuous, and hence each point on the tissue deforms in a manner consistent with the deformations of neighboring points. Disregarding the spatial autocorrelation of the scleral displacement measurements leads to a bias in the estimated parameters and results in erroneously small p-values (type I error) (Dormann et al. 2007; Dormann 2007), which may explain the differences in the results reported herein and the previously published work.

We also performed scleral inflation testing at room temperature because the ESPI displacement measurement system we used is so sensitive that thermal convection currents in heated PBS induce measurement errors. Regional and sectorial strain variations we report should not be affected by testing temperature because all specimens were tested under identical conditions. Since all specimens were treated identically, age-related changes in the regional and sectorial strains that are the focus of this report should be unaffected by these factors.

We assumed that the donor eyes were normal without confirming normality through an ophthalmic exam performed while the patient was living. This could prove crucial for studies on cellular activity or neural tissues, or those that are designed to detect differences due to treatments or disease states such as glaucoma. However, there are relatively few conditions or diseases that are likely to significantly impact scleral biomechanics for ostensibly normal eyes, and these were broadly excluded based on next-of-kin questionnaire.

This study is the first to report sectorial age-related changes in peripapillary and mid-peripheral scleral strain in human eyes subjected to inflation testing. The analysis of strain used herein accounts for scleral thickness, shape, loading, boundary conditions, and local structural discontinuities intrinsically. Hence, direct strain calculation of scleral shells subjected to inflation testing allows the study of the mechanical response of the peripapillary sclera under physiologically mimetic conditions, which minimizes the differences between the true biomechanical behavior of the tissue in vivo and the experiment-specific testing conditions. In particular, our approach allows for analysis of the structural stiffness of the peripapillary sclera acting in concert with the contained ONH, and not as a standalone tissue, e.g., biaxial testing of excised patches of sclera (Eilaghi et al. 2010b) or uniaxial testing of scleral strips (Geraghty et al. 2012). Testing hypotheses concerning age-, race-, or disease-related changes in scleral biomechanics greatly benefits from this approach, and the optimized ESPI technique we developed, coupled with inflation testing of the intact posterior scleral shell, allows scleral strain analyses that are not possible with other measurement methods. We demonstrated and extensively discussed (Fazio et al. 2012a) the necessity of using displacement measurement techniques with extremely high spatial and measurement resolution to capture the small, localized strain variations around the ONH, as well as the small but significant deformation changes with age (Fazio et al. 2012b).

The direct differentiation of analytical functions describing the continuous scleral displacement field allows direct calculation of the scleral strain tensor, which avoids the intermediate computational methods and their limiting assumptions that are typically required to estimate strain from experimental displacement data. The direct approach used in this study requires no underlying assumptions other than tissue incompressibility, which only affects one of the nine strain components used to calculate our main output variable (maximum principal strain) and is reasonable given that sclera is composed of 70% water.

A recent study on age-related changes scleral strain (Coudrillier et al. 2012) reported significant decreases in meridional and circumferential strain with age in human posterior scleral shells. While our results agree with their general conclusions, their digital image correlation (DIC)-based strain calculations yield shear strains that are one-tenth the magnitude of the circumferential and meridional strains, which does not agree with the large magnitude shear strains we report (Figure 2). Furthermore, the computational approach used to calculate scleral stiffnesses in the aforementioned study assumes that all six shear components of the strain tensor are negligible, which is clearly a questionable assumption given the large shear strains we observed. Figure 2 shows that the shear strain components are the largest and most rapidly changing components of the strain tensor in the sclera, especially in the peripapillary and mid-peripheral regions that influence the biomechanical environment of the ONH. Correlation-based displacement measurement techniques such as DIC (Schreier et al. 2000; Bornert et al. 2009) are constrained by a compromise between spatial resolution and displacement measurement uncertainty, because increasing the spatial resolution (lowering pixel subset size) increases the measurement uncertainty (Robert 2007). Speckle-based interferometry techniques such as the ESPI method used in this work are more suitable for assessing small, localized strain variations since displacement measurement resolution is decoupled from spatial resolution because each pixel performs as a stand-alone interferometer and can measure displacements with a ±16 nm accuracy (Fazio et al. 2012a). The shear components of the scleral strain tensor represent the difference in local displacement components along orthogonal directions. Hence, the differences between the large in-plane shear strain we report and the small values observed by Coudrillier et al. (2012) likely arise from the inability of the DIC technique used in that study to discern the small localized changes in the orthogonal displacement components necessary to capture shear strains.

The detailed regional and sectorial distributions of scleral strain are important, as they inform us about the strains that scleral tissues and the resident cells actually experience when IOP is elevated, both acutely and chronically. We measured scleral tensile strains that were significantly higher in the peripapillary sclera compared to the adjacent mid-peripheral sclera across all ages.

Sectorial and regional variations in peripapillary strains could contribute to the focal structural and functional defects typically seen in glaucoma, a disease that is associated with advancing age. Hence, this study was designed to test the hypothesis that regional and sectorial localized variations in peripapillary scleral strain change significantly with age. The values and age-related dependence of the sectorial and regional scleral strain reported herein can serve as benchmarks for validation of future computational models as well as define the appropriate strain ranges for applying mechanical deformations to scleral cells and tissues in vitro.

A similar pattern of sectorial and regional variation in tensile strain was found in all eyes, but some eyes exhibited much higher strains overall than others (sectorial strain range: 0.758% - 3.63%). This wide range of strain between sectors of different eyes may relate to variations in scleral thickness, ONH biomechanics, and/or the distribution of collagen, elastin, and crosslink density. Furthermore, the sclera is a living tissue that may remodel and grow in response to different stimuli including IOP-induced mechanical strain (Girard et al. 2011) and the variation in strain might relate to different IOP loading and remodeling histories of each eye.

The high strains we observed in the inferotemporal sector may be due to local differences in ONH morphology, scleral thickness, and/or material properties, as this sector corresponds to the site of fetal fissure closure during scleral development. See, Chauhan, and colleagues showed that the inferotemporal sectors exhibited the highest neuroretinal rim area measurement change rate with age and the nasal sectors exhibited the lowest rate in their normal control cohort (See et al. 2009). It is interesting that in normal donor eyes, the pattern of age-related change in peripapillary scleral strain shown in Figure 5 and the overall pattern of strain magnitude seen in Figure 4 also match this pattern. This suggests the possibility that the age-related increase in peripapillary scleral strain in the inferotemporal sector could be an age-related risk factor for focal progressive loss of retinal ganglion cell axons, or that underlying scleral strain is changing the measurement reference in these sectors. In addition, Healey and colleagues showed that the incidence of optic disk hemorrhage is significantly higher in the inferotemporal sector in normal subjects (Healey et al. 1998). This study also showed that the odds ratio of DH increases significantly with age in normal subjects (odds ratio = 2.2 per decade). Two other studies have shown that disk hemorrhage incidence is highest in the inferotemporal sectors and lowest in the nasal sectors in cohorts of normal subjects (Airaksinen et al. 1981) of glaucoma suspects with normal disk appearance (Yamamoto et al. 2004). While we have not demonstrated a causative link between disk hemorrhage and the sectorial peripapillary scleral strain changes reported herein, it is interesting that sectorial disk hemorrhage incidence follows the same sectorial pattern and age-related susceptibility we observed for the age-related strain changes shown in Table 1 and Figures 4 and 5.

Mechanical tensile strain in the peripapillary sclera is a direct measure of the stretch to which the scleral fibroblasts, extracellular matrix, and penetrating vasculature are exposed. While we do not fully understand the extent to which peripapillary scleral strain is transmitted to the ONH and lamina cribrosa or how laminar strain induces axonal damage, it is plausible that high regional peripapillary strains induce high strains in the adjacent lamina cribrosa, which damages the contained axons in that area through a variety of mechanisms. Given that the sectorial pattern and age-related susceptibility to both disk hemorrhages and neuroretinal rim area loss closely matches the age-related sectorial changes in peripapillary scleral strain, it is also plausible that increasing peripapillary scleral strain increases the risk of disk hemorrhages and focal retinal ganglion cell axon loss. Further work should be done to elucidate the mechanistic relationships between local peripapillary scleral strains, laminar strains, and focal retinal ganglion cell axon damage.