Significance
The properties of proteins are in principle determined by interactions among all of their residues, but for practical reasons, phylogenetic analyses assume that residues change independently. We experimentally investigate the extent to which the effects of individual mutations on protein stability change as other residues diverge. We find that mutational effects on stability are highly conserved, with relatively little interdependence. Of course, mutations can still interact in other ways to affect protein function in a nonindependent manner. Nonetheless, our results suggest that the preference of a position for specific amino acids tends to be well conserved during the evolution of protein homologs with similar structures and functions.
Keywords: heterotachy, consensus design, substitution models
Abstract
Protein stability and folding are the result of cooperative interactions among many residues, yet phylogenetic approaches assume that sites are independent. This discrepancy has engendered concerns about large evolutionary shifts in mutational effects that might confound phylogenetic approaches. Here we experimentally investigate this issue by introducing the same mutations into a set of diverged homologs of the influenza nucleoprotein and measuring the effects on stability. We find that mutational effects on stability are largely conserved across the homologs. We reach qualitatively similar conclusions when we simulate protein evolution with molecular-mechanics force fields. Our results do not mean that proteins evolve without epistasis, which can still arise even when mutational stability effects are conserved. However, our findings indicate that large evolutionary shifts in mutational effects on stability are rare, at least among homologs with similar structures and functions. We suggest that properly describing the clearly observable and highly conserved amino acid preferences at individual sites is likely to be far more important for phylogenetic analyses than accounting for rare shifts in amino acid propensities due to site covariation.
Most biological proteins stably fold to a well-defined native structure (1). Stable folding to the native structure is typically essential for a protein to perform its evolutionarily selected function. Stability and folding are the result of highly cooperative interactions among a protein’s constituent amino acids (1). Therefore, evolutionary selection at a site in a protein acts on properties that in principle are determined by interactions of that site with every other position in the sequence.
However, phylogenetic approaches assume that protein sites evolve independently. This assumption has historically been justified primarily by pragmatic considerations. If substitution models are site independent, then the evolution of each site is mathematically described by a 20 × 20 matrix, with entries corresponding to all amino acid interchanges at that site. On the other hand, if each site depends upon all other sites, then the evolution of a protein of length L is mathematically described by a 20L × 20L matrix, with entries corresponding to all interchanges among the 20L sequences. Even for a small protein of length L = 100, the number of entries in such a matrix vastly exceeds the number of atoms in the universe, which poses severe computational challenges.
The fact that sites are not actually independent at the physicochemical level has provoked concern about the use of site-independent substitution models (2–5). Pollock et al. (2) have used computer simulations to suggest that there are widespread evolutionary shifts in mutational effects, where for instance a mutation is destabilizing in one homolog but stabilizing in another homolog due to interactions with other covarying sites. They have argued that such evolutionary shifts in mutational effects on stability have profound implications for phylogenetic modeling (2).
However, are such evolutionary shifts really of sufficient prevalence and magnitude to require a radical rethinking of approaches used to model protein evolution? The standard way to address this question has been to simulate or analyze protein sequences, using some computational force field that predicts the stability of different variants (2–5). Unfortunately, there is no good a priori reason to believe that the force fields themselves authentically represent interactions among sites. Even state-of-the-art force fields are at best modestly accurate at predicting mutational effects (6, 7). Furthermore, all tractable force fields approximate the true multibody quantum–mechanical interactions among protein sites in terms of pairwise interactions (8–10).
Here we experimentally assess the extent to which mutational effects on stability change during protein evolution. We introduce the same mutations into a series of homologs and measure the effects on stability. We find that the effects of individual mutations on stability are largely conserved even when homologs differ at as many as 28% of sites. Our results do not imply an absence of all forms of epistasis (interactions among sites) during protein evolution. Epistasis at the level of function and fitness can arise even if stability is fully site independent due to counterbalancing stabilizing and destabilizing mutations (11, 12), and stability is only one mechanism of epistasis (13, 14). However, for reasons that we discuss below, these other forms of epistasis seem less likely to cause pervasive shifts in substitution patterns that would seriously confound phylogenetic approaches. However, our experiments do highlight the existence of strong and largely conserved preferences for certain amino acids at specific sites. We therefore suggest that the use and further development of phylogenetic approaches (15–24) that account for these clearly observable site-specific but largely site-independent preferences is of far greater practical importance than accounting for rare evolutionary shifts in site preferences.
Results
Analysis of Mutational Effects in a Set of Homologs.
We introduced the same mutations into a set of homologs of the nucleoprotein (NP) of influenza A virus. NP is a 498-residue protein that serves as a scaffold for viral RNA during replication, transcription, and genome packaging (25). Crystal structures of several NPs have been solved (26–28), and all fold to similar mostly alpha-helical conformations. NP multimerizes, but we have developed a protocol for purifying monomeric NP and measuring its stability (11).
As the reference protein for our study, we chose the NP of a recent human H3N2 strain, A/Brisbane/10/2007. We then selected NPs from three increasingly diverged strains: the human H3N2 strain A/Aichi/2/1968, the human 2009 H1N1 pandemic strain A/California/4/2009, and the bat strain A/little yellow-shouldered bat/Guatemala/164/2009. Fig. 1A shows the relationship among these NPs. Brisbane/2007, Aichi/1968, and California/2009 NPs are descended from a close predecessor of the 1918 pandemic virus. The bat/2009 NP is highly diverged from all other known strains (29). Influenza genes evolve primarily through point mutations with little or no recombination (30) and few insertions or deletions. As a result, the homologs align without gaps across their 498-residue lengths with the exception of a single amino acid deletion in the bat/2009 NP (SI Discussion).
Fig. 1.
The homologs and mutations examined in this study. (A) Phylogenetic tree of the four NP homologs, constructed using the Goldman–Yang codon model. (B) The blue spheres show the sites of the six experimentally studied mutations and their identities in each homolog. The red sticks show all other sites that differ between each homolog and Brisbane/2007. The crystal structure is PDB 2IQH.
We selected six mutations based on our previous experimental work on naturally occurring mutations to NP (11). When named with respect to the identity in Brisbane/2007, these mutations are A280V, G384R, I186V, V239M, L259S, and H334N. Based on our previous work (11), we expected that in Brisbane/2007, the first two mutations would be stabilizing, the next two would have little effect, and the last two would be destabilizing. Fig. 1B shows the mutations in the NP structure, as well as the wild-type identities in each homolog. Fig. 1B also shows all other sites that differ between Brisbane/2007 and the other homologs. The protein-sequence identities of the homologs with Brisbane/2007 range from 94% to 72%. The number of substitutions that occurred during divergence of the homologs is not an observable quantity. However, inferences made using PAML (31) with two common substitution models (32, 33) suggest that the most distant pair diverged via 200- to 300-amino-acid substitutions (Table S1).
Experimentally Measured Mutational Effects on Stability Are Largely Conserved.
We cloned and purified histidine-tagged variants of each homolog. Fig. S1 shows that all variants exhibited similar circular dichroism (CD) spectra with the classical alpha-helical minima near 208 and 222 nm (34), suggesting that all variants retained the alpha-helical NP structure (26–28). The only variant that we could not purify was bat/2009 with L259S; we suspect that this variant is too destabilized to yield folded protein (Fig. S2). All variants were free of nucleic acid except for a few bat/2009 variants that retained absorbance at 260 nm relative to 280 nm despite extensive nuclease treatment (Table S2).
We monitored the thermal denaturation by CD (Fig. S1). All variants unfolded with a single cooperative transition, although a few bat/2009 variants exhibited sloping baselines (Fig. S1), possibly due to contaminating nucleic acids (35). Thermal denaturation of NP is irreversible (11), so we cannot determine changes in thermodynamic stability (ΔΔG values). However, we can determine nonequilibrium melting temperatures (Tm) at a constant thermal scan rate (Table S2). We report the effect of a mutation as the change in Tm (ΔTm). For example, the ΔTm for G384R is the Tm of variant R384 minus the Tm of variant G384; a positive ΔTm indicates that the mutation is stabilizing.
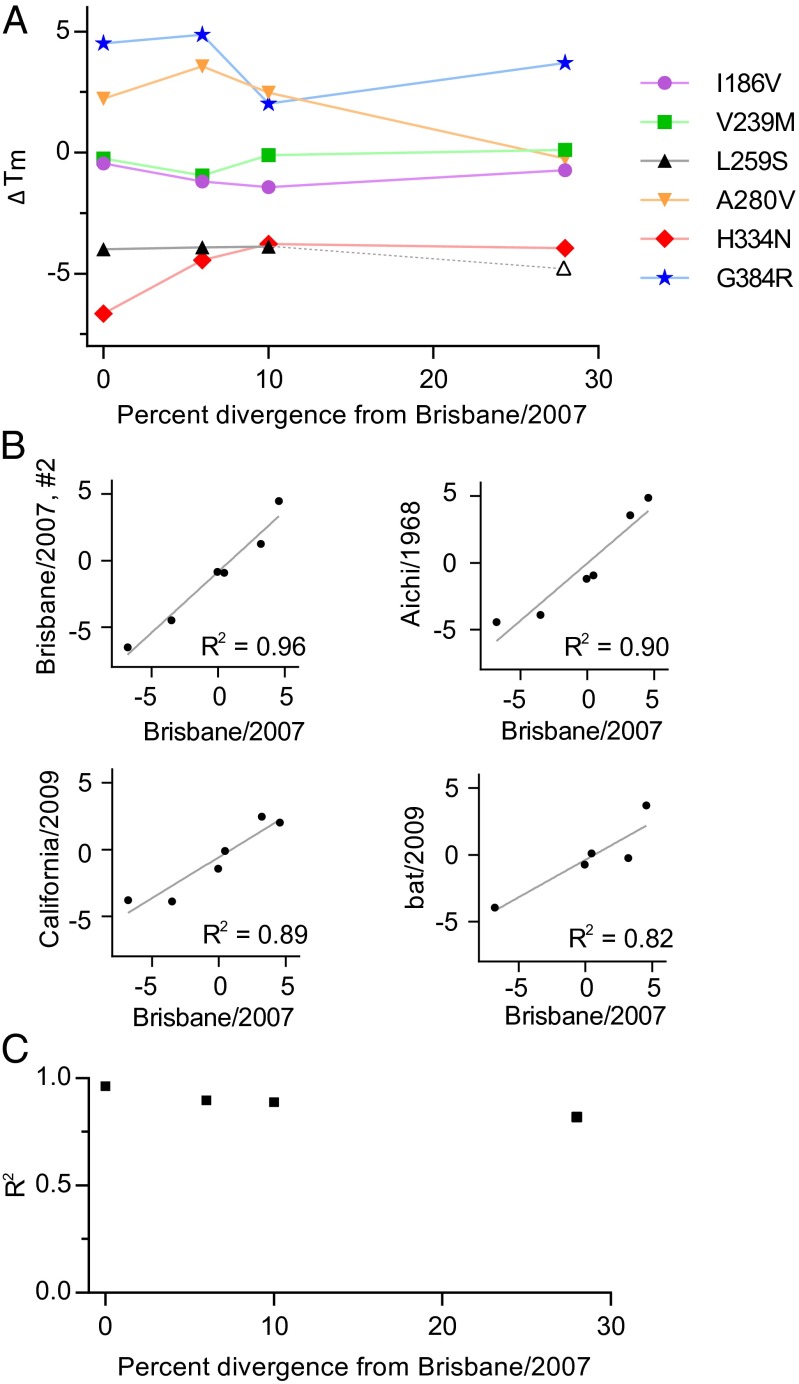
Fig. 2A shows ΔTm values for all homologs. The mutational effects on stability are quite conserved. The two strongly destabilizing mutations in Brisbane/2007 (H334N and L259S) are destabilizing in all homologs tested (we are unable to purify bat/2009 with L259S; Fig. S2). The two mutations with only slight effects on Brisbane/2007 (I186V and V239M) also only have small effects in other homologs. Of the two stabilizing mutations in Brisbane/2007, G384R is also stabilizing in the other homologs, whereas A280V is stabilizing in Aichi/1968 and California/2009 but has little effect on bat/2009. Therefore, examination of six mutations in four homologs identifies only a single substantial shift in a mutation’s effect on stability.
Fig. 2.
Experimentally measured mutational effects on stability are similar in all homologs. (A) The difference in melting temperature (ΔTm in °C) caused by the indicated single-site change in each homolog versus the protein-sequence divergence of that homolog from Brisbane/2007. We were unable to purify bat/2009 with L259S, so an open symbol shows the hypothetical ΔTm if this variant had a Tm equal to the least stable NP that we successfully purified (typically highly destabilized proteins are hard to purify). (B) The correlation between ΔTm values for the single-site changes for two replicates of Brisbane/2007 and then between the first Brisbane/2007 replicate and the other homologs. (C) The squared Pearson correlation (R2) between the stability effects as a function of sequence divergence. The R2 for bat/2009 does not include L259S. For bat/2009, ΔTmG384R = ΔTmH384R − ΔTmH384G.
To examine whether mutational effects become increasingly different as sequences diverge, we plotted the correlations between ΔTm values in the different homologs (Fig. 2 B and C). The correlation between two replicates of Brisbane/2007 is high (R2 = 0.96) and provides a measure of the experimental error. The correlation does gradually decline with increasing sequence divergence, falling to 0.89 in California/2009 (90% identity) and 0.82 in bat/2009 (72% identity). Note however that this last correlation is calculated on a reduced dataset because we were unable to purify bat/2009 with L259S; if our inability to purify this variant is construed as evidence of destabilization, then the actual correlation may be higher. In addition, the differences in correlation coefficients may not be meaningful given the small number of data points (SI Discussion). However, Fig. 2 B and C clearly indicate that mutational effects on stability are similar even in homologs diverged to 72% identity.
Simulated Mutational Effects on Stability Are Largely Conserved.
In our experiments we can only examine a limited number of homologs. Pollock et al. (2) used computer simulations to argue for evolutionary shifts in mutational effects on stability. Such simulations allow the analysis to be extended to an arbitrary number of homologs, with the caveat that the simulation force field may not accurately represent the true effects of mutations in a real protein.
We followed the simulation methodology of Pollock et al. (2). We began with the sequence of an NP that has been previously crystallized (26). At each generation, a random mutation was introduced into the sequence, and a force field was used to predict the stability of the parent and mutant proteins. Fitness was computed as the fraction of molecules with that stability that would be folded at equilibrium, allowing us to assign a selection coefficient. The mutation was retained with a probability proportional to its fixation probability assuming a population size of 103 (36). This process parallels real evolution, and the sequences diverge as more mutations are retained.
We performed simulations using two force fields. The first is FoldX (37), a sophisticated force field designed to predict mutational effects on protein stability. The second is the Miyazawa–Jernigan force field (38), the simple pairwise potential used by Pollock et al. (2). For both force fields, we first “equilibrated” the initial sequence by evolving it until its stability had become roughly constant before collecting statistics about how mutational effects changed as the sequences evolved.
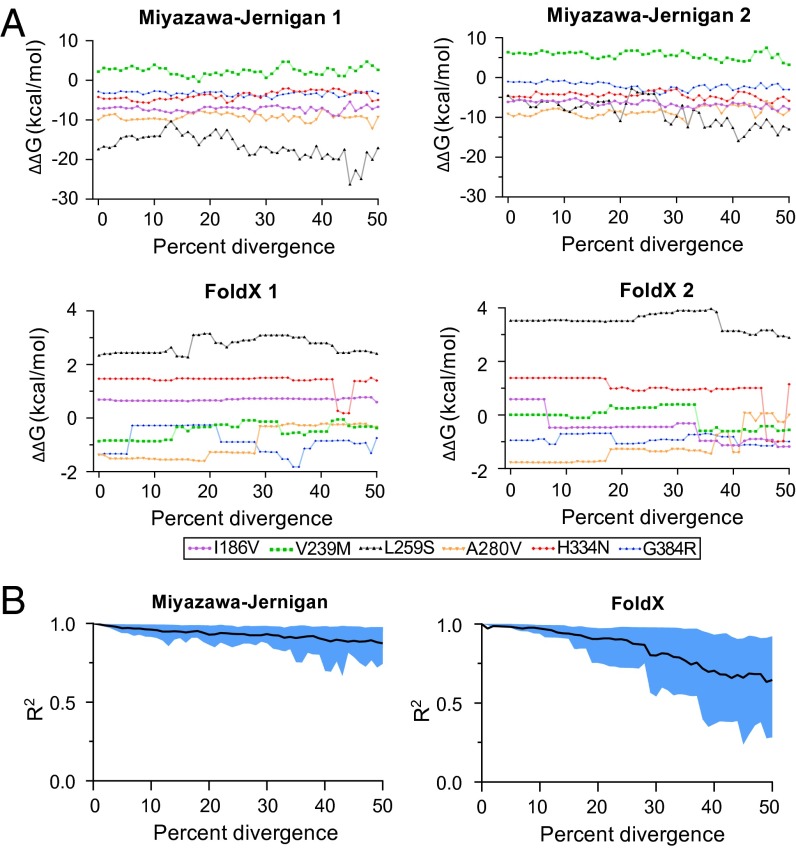
Fig. 3 shows simulations displayed to parallel the experimental data in Fig. 2. The overall trends with respect to conservation of the mutational effects are similar to those observed experimentally. Although there is some variation between the simulated replicates (evolution is stochastic), mutational effects on stability change only slowly as the sequences diverge, and remain substantially correlated even at 50% divergence. Pollock et al. (2) present changes in mutational effects as a function of the number of substitutions, whereas Figs. 2 and 3 show these effects as a function of sequence divergence. The number of substitutions is not an observable quantity for real homologs and so cannot be plotted in Fig. 2 (although it can be inferred, Table S1), but the number of substitutions can be monitored during simulations. We therefore performed additional simulations and plotted the results as functions of both divergence and number of substitutions (Figs. S3–S5). The number of substitutions required to reach 50% divergence in simulated evolution differs between the force fields (400–500 for FoldX, 2,000–3,000 for Miyazawa-Jernigan; Figs. S3–S5), but in all cases, there are only small shifts in mutational effects at these levels of divergence. Note that the number of substitutions in our Miyazawa–Jernigan simulations exceeds that in nearly all of the simulations by Pollock et al. (2).
Fig. 3.
Predicted mutational effects after simulating NP evolution using the FoldX or Miyazawa–Jernigan force field. (A) Mutational effects as a function of protein-sequence divergence for two replicates of simulated evolution with the Miyazawa–Jernigan or FoldX force field. (B) Correlation between the effects in the original parent and the simulated homologs at different levels of sequence divergence. Plots show the mean (black line) and 10–90% interval of the correlation between the effects in the original parent and homologs for many replicates of simulated evolution with the Miyazawa–Jernigan (50 replicates) or FoldX (20 replicates) force field. Additional replicates and plots where the x axis is the number of substitutions are in Figs. S3–S5.
A difference in simulation methodology explains much of the discrepancy between our results and those of Pollock et al. In many of their simulations, Pollock et al. (2) constrain a destabilizing substitution to remain fixed during evolution, and then monitor the effect of reverting this substitution as the rest of the sequence evolves. In contrast, in our simulations (and in real evolution), there are no such constraints – destabilizing mutations can be alleviated by reversion in addition to changes at other sites. When we perform additional simulations in which we constrain destabilizing substitutions as done by Pollock et al., we do observe evolutionary shifts in the effect of reverting the constrained destabilizing substitution as the protein relaxes to accommodate the forcibly fixed substitution (Fig. 4 and Figs. S6 and S7).
Fig. 4.
In simulations, making a destabilizing substitution and constraining it to remain fixed during subsequent evolution leads to a shift in the substitution’s effect on stability. Each plot shows the stability effect of reverting the initially destabilizing substitution listed in the plot title as a function of the amount of subsequent evolution. Reversion of the destabilizing mutation is initially stabilizing (ΔΔG << 0) but becomes less so, especially when evolution is simulated with the Miyazawa–Jernigan force field. Each line in a plot shows a different independent replicate: 10 per plot for Miyazawa–Jernigan and 5 for FoldX. These simulations parallel those used by Pollock et al. (2) to argue for an evolutionary shift in mutational effects on stability. However, real evolution does not include artificial constraints forcing destabilizing substitutions to remain fixed, and in practice we observe that destabilizing substitutions often revert (Figs. 1 and 5). Additional plots and plots where the x axis is number of substitutions are in Figs. S6 and S7.
Destabilizing Substitutions Often Revert During Real Evolution.
The contrasting results of the simulations in Figs. 3 and 4 suggest that the extent of evolutionary shifts in mutational effects depends on the long-term fate of destabilizing substitutions: if they revert then mutational effects will be largely conserved, whereas if they are constrained to remain fixed then there may be evolutionary shifts as the protein evolves to accommodate the initial destabilization. What is the typical fate of destabilizing substitutions in real proteins? A simple inspection of NP’s evolution provides a straightforward answer: destabilizing substitutions often revert. Four of the six mutations that we experimentally characterized have large effects on stability, which in all cases are conserved among Brisbane/2007, Aichi/1968, and California/2009. Fig. 5A shows the inferred identities at these sites superimposed on a phylogenetic tree (bat/2009 is a more diverged homolog for which there is no intermediate evolutionary information; Fig. 1A). Although the destabilizing mutations H334N and L259S transiently fix, both later revert (Fig. 5A). We have previously detailed the evolutionary dynamics of counterbalancing stabilizing and destabilizing mutations of this NP lineage (11). The schematic in Fig. 5B integrates those dynamics with the current finding that mutational effects on stability are largely conserved. After destabilizing mutations fix, they do not gradually lose their destabilizing properties due to an evolutionary shift in their effect; rather, they simply eventually revert.
Fig. 5.
Destabilizing mutations only fix occasionally during actual evolution and then tend to revert. (A) At the four sites where mutations are experimentally characterized to have large effects on stability, most influenza variants have the more stable amino acid (green) rather than the less stable one (red). Shown are NP phylogenetic trees colored according to the amino acid with the highest posterior probability. (B) Schematic of the mode of evolution suggested by our results. When destabilizing mutations fix, they tend to revert; we see little evidence of evolutionary shifts that alter the fact that the initial mutation is destabilizing.
Discussion
We have found that the effects of mutations on stability are largely conserved during protein evolution, at least for NP homologs up to 30% sequence divergence. Of course, mutational effects do shift to some degree (witness A280V in bat/2009 versus the other homologs; Fig. 2A), but large shifts appear to be rare. So, whereas we concur with Pollock et al. (2) that evolutionary shifts in mutational effects on stability can in principle occur, we doubt that such shifts are of sufficient prevalence and magnitude to have profound implications for phylogenetic modeling of homologs with similar structures and functions. Our findings are consistent with the experimental work of Fersht and coworkers (39), who found independent and additive effects on stability among the 17 substitutions separating two RNase homologs of 85% sequence identity, with no indication that one mutation altered the stability effect of another.
More extensive but less direct experimental evidence for the conservation of mutational effects on stability comes from “consensus design,” a highly effective engineering strategy for enhancing stability that has been applied to a wide range of proteins (40–42). In this strategy, residues are simply mutated to their consensus identities in an alignment of often quite distant homologs. Consensus design would fail if mutational effects on stability were frequently context dependent—its success is a testament to the fact that stability effects are mostly conserved, leading most homologs to have the most stabilizing identity at any given site as illustrated in Fig. 5B.
Of course, substantial shifts in mutational effects on stability could be pervasive at much higher levels of sequence divergence than we have explored here. However, we are unaware of any direct supporting evidence for this idea. In rare cases—such as the fixation of a destabilizing but highly adaptive substitution—real evolution may involve scenarios that correspond to Pollock et al.’s constraint that a destabilizing substitution remains fixed for all subsequent evolution, but Figs. 1 and 5 indicate that this is certainly not the norm for NP. Such scenarios could be more common among highly diverged proteins that no longer share similar structures or functions.
Our results do not imply a lack of epistasis at the level of function or fitness. Counterbalancing stabilizing and destabilizing mutations can still have epistatic effects on function in the absence of shifts in stability effects due to the sigmoidal relationship between function and stability (11, 43). For instance, we have previously shown that three of the mutations characterized here are deleterious in some NP homologs because they are excessively destabilizing (11). However, these same mutations were fixed in other homologs, and this fixation did not involve any underlying evolutionary shift that rendered the mutations nondestabilizing—instead, the destabilizing mutations were simply counterbalanced by independent stabilizing mutations (11). Whereas such epistasis between counterbalancing mutations can cause transient fluctuations in the rate of substitution (44), it does not drive systematic shifts in substitution patterns. Rather, the underlying preferences of sites for specific stabilizing residues is well conserved, explaining why mutations to consensus amino acids tend to stabilize proteins (40–42) and why a mutation’s effect on stability is correlated with its rate of fixation (45).
A limitation is that our study focused only on stability; particularly in active sites, epistasis can be mediated by properties other than stability, and can involve specific interactions that do cause evolutionary shifts in site preferences (13, 14, 46). However, in most cases, mutations coupled to the active site probably contribute only a small amount to the sequence divergence (47, 48) that is analyzed in phylogenetics.
Overall, the conservation of mutational effects on stability supports the approximate validity of site-independent substitution models in most phylogenetic contexts. However, even if sites are completely independent, an incorrect substitution model can lead to erroneous inferences (24), and our results do not inspire confidence in commonly used substitution models, which typically assume a single set of equilibrium amino acid frequencies for all sites. For instance, in our experiments, H is consistently more stabilizing than N at site 334, and R is consistently more stabilizing than G at site 384; yet the stationary state of the Jones-Taylor-Thornton (JTT) matrix (32) implies that at equilibrium, N will always be more common than H, and G will always be more common than R.
We therefore believe that recent progress in developing models that allow for different equilibrium frequencies at different sites is highly promising. Such models use various approaches: sites can be preassigned equilibrium frequencies based on structural features (21–23), or modeling with force fields (19, 20), sites can be allowed to choose among a predefined set of equilibrium frequencies (17, 18), or the equilibrium frequencies can themselves be inferred (15, 16). Some of these models have been implemented in phylogenetic inference software, and by statistical metrics they improve performance (15–18). Interestingly, for phylogenetic purposes, models that extract site-specific equilibrium frequencies from sequence data have proven more useful than those that use structure-based assignments or force fields (15–18). Our experimental results suggest that site preferences do have a biophysical basis—we therefore suspect that the relatively poorer performance of biophysically inspired models is due to the inadequacy of current force fields (6, 7) rather than a lack of fundamental connection between protein biophysics and evolution.
Overall, our work provides a mechanistic justification for the use of site-specific but site-independent evolutionary models: proteins possess highly conserved preferences for certain amino acids at specific sites. The use and further development of evolutionary models that capture these preferences will help reconcile phylogenetic inference with the experimental observations that we have reported here.
Materials and Methods
Protein Purification and Denaturation.
NP variants were purified as in ref. 11. All variants had deletion of residues 2–7, the mutation R416A, and a C-terminal 6-His tag. Stability measurements were performed as in ref. 11 using a scan rate 2 °C/min. All variants were denatured at 5 μM except for the bat/2009 variants, which could only be purified at lower yield. These variants were denatured at 4 μM based on the absorbance at 280 nM, although the actual concentration for some variants may have been lower, due to confounding signal from nucleic-acid contamination (Table S2).
Phylogenetic Trees.
Fig. 1A shows a maximum-likelihood tree constructed using codonPhyML (49) with the Goldman–Yang substitution model (50) with kappa and a single omega value estimated by maximum-likelihood and with CF3 × 4 equilibrium frequencies (51). The tree was rendered with FigTree.
Fig. 5A shows maximum clade credibility trees constructed using date-stamped sequences and a strict molecular clock in BEAST (52) using the JTT (32) substitution model. The trees were rendered using FigTree, and branches are colored according to the identity of the residue with the highest posterior probability at the descendent node.
Simulations.
The simulated evolution follows ref. 2 using a population size of 103. The protein sequence was mapped onto a single chain from Protein Data Bank (PDB) 2IQH using A/WSN/33 NP as an initial sequence. The Miyazawa–Jernigan potential (38) was applied as in ref. 2, with the unfolded state represented by 55 diverse structures obtained from PDBselect (53) and weighted to NU = 10265, corresponding to 3.4 conformations per residue for the 498-residue protein. For this potential, the evolution was equilibrated for 2,000 accepted mutations, at which point the stability had stabilized at approximately −6 kcal/mol. For FoldX (37), the predicted absolute stabilities were scaled by subtracting the stability of the initial PDB structure. Mutations were modeled and stabilities computed using the “BuildModel” and “Stability” commands. FoldX simulations were equilibrated for 100 accepted mutations.
Supplementary Material
Acknowledgments
We thank Jeff Thorne and an anonymous reviewer for helpful comments. This research was supported by Grant R01GM102198 from the National Institute of General Medical Sciences of the National Institutes of Health.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. A.J.R. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1314781111/-/DCSupplemental.
References
- 1.Anfinsen CB. Principles that govern the folding of protein chains. Science. 1973;181(4096):223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 2.Pollock DD, Thiltgen G, Goldstein RA. Amino acid coevolution induces an evolutionary Stokes shift. Proc Natl Acad Sci USA. 2012;109(21):E1352–E1359. doi: 10.1073/pnas.1120084109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rodrigue N, Philippe H, Lartillot N. Assessing site-interdependent phylogenetic models of sequence evolution. Mol Biol Evol. 2006;23(9):1762–1775. doi: 10.1093/molbev/msl041. [DOI] [PubMed] [Google Scholar]
- 4.Choi SC, Hobolth A, Robinson DM, Kishino H, Thorne JL. Quantifying the impact of protein tertiary structure on molecular evolution. Mol Biol Evol. 2007;24(8):1769–1782. doi: 10.1093/molbev/msm097. [DOI] [PubMed] [Google Scholar]
- 5.Nasrallah CA, Mathews DH, Huelsenbeck JP. Quantifying the impact of dependent evolution among sites in phylogenetic inference. Syst Biol. 2011;60(1):60–73. doi: 10.1093/sysbio/syq074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Potapov V, Cohen M, Schreiber G. Assessing computational methods for predicting protein stability upon mutation: Good on average but not in the details. Protein Eng Des Sel. 2009;22(9):553–560. doi: 10.1093/protein/gzp030. [DOI] [PubMed] [Google Scholar]
- 7.Kellogg EH, Leaver-Fay A, Baker D. Role of conformational sampling in computing mutation-induced changes in protein structure and stability. Proteins. 2011;79(3):830–838. doi: 10.1002/prot.22921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Elrod MJ, Saykally RJ. Many-body effects in intermolecular forces. Chem Rev. 1994;94(7):1975–1997. doi: 10.1021/cr00031a010. [DOI] [PubMed] [Google Scholar]
- 9.van der Vaart A, Bursulaya BD, Brooks CL, Merz KM. Are many-body effects important in protein folding? J Phys Chem B. 2000;104(40):9554–9563. [Google Scholar]
- 10.Ejtehadi MR, Avall SP, Plotkin SS. Three-body interactions improve the prediction of rate and mechanism in protein folding models. Proc Natl Acad Sci USA. 2004;101(42):15088–15093. doi: 10.1073/pnas.0403486101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gong LI, Suchard MA, Bloom JD. Stability-mediated epistasis constrains the evolution of an influenza protein. Elife. 2013;2:e00631. doi: 10.7554/eLife.00631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.DePristo MA, Weinreich DM, Hartl DL. Missense meanderings in sequence space: A biophysical view of protein evolution. Nat Rev Genet. 2005;6(9):678–687. doi: 10.1038/nrg1672. [DOI] [PubMed] [Google Scholar]
- 13.Bridgham JT, Ortlund EA, Thornton JW. An epistatic ratchet constrains the direction of glucocorticoid receptor evolution. Nature. 2009;461(7263):515–519. doi: 10.1038/nature08249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Harms MJ, et al. Biophysical mechanisms for large-effect mutations in the evolution of steroid hormone receptors. Proc Natl Acad Sci USA. 2013;110(28):11475–11480. doi: 10.1073/pnas.1303930110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lartillot N, Philippe H. A Bayesian mixture model for across-site heterogeneities in the amino-acid replacement process. Mol Biol Evol. 2004;21(6):1095–1109. doi: 10.1093/molbev/msh112. [DOI] [PubMed] [Google Scholar]
- 16.Lartillot N, Rodrigue N, Stubbs D, Richer J. PhyloBayes MPI: Phylogenetic reconstruction with infinite mixtures of profiles in a parallel environment. Syst Biol. 2013;62(4):611–615. doi: 10.1093/sysbio/syt022. [DOI] [PubMed] [Google Scholar]
- 17.Le SQ, Lartillot N, Gascuel O. Phylogenetic mixture models for proteins. Philos Trans R Soc Lond B Biol Sci. 2008;363(1512):3965–3976. doi: 10.1098/rstb.2008.0180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wang HC, Li K, Susko E, Roger AJ. A class frequency mixture model that adjusts for site-specific amino acid frequencies and improves inference of protein phylogeny. BMC Evol Biol. 2008;8:331. doi: 10.1186/1471-2148-8-331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Parisi G, Echave J. Structural constraints and emergence of sequence patterns in protein evolution. Mol Biol Evol. 2001;18(5):750–756. doi: 10.1093/oxfordjournals.molbev.a003857. [DOI] [PubMed] [Google Scholar]
- 20.Fornasari MS, Parisi G, Echave J. Site-specific amino acid replacement matrices from structurally constrained protein evolution simulations. Mol Biol Evol. 2002;19(3):352–356. doi: 10.1093/oxfordjournals.molbev.a004089. [DOI] [PubMed] [Google Scholar]
- 21.Koshi JM, Goldstein RA. Models of natural mutations including site heterogeneity. Proteins. 1998;32(3):289–295. [PubMed] [Google Scholar]
- 22.Goldman N, Thorne JL, Jones DT. Assessing the impact of secondary structure and solvent accessibility on protein evolution. Genetics. 1998;149(1):445–458. doi: 10.1093/genetics/149.1.445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thorne JL, Goldman N, Jones DT. Combining protein evolution and secondary structure. Mol Biol Evol. 1996;13(5):666–673. doi: 10.1093/oxfordjournals.molbev.a025627. [DOI] [PubMed] [Google Scholar]
- 24.Halpern AL, Bruno WJ. Evolutionary distances for protein-coding sequences: Modeling site-specific residue frequencies. Mol Biol Evol. 1998;15(7):910–917. doi: 10.1093/oxfordjournals.molbev.a025995. [DOI] [PubMed] [Google Scholar]
- 25.Portela A, Digard P. The influenza virus nucleoprotein: A multifunctional RNA-binding protein pivotal to virus replication. J Gen Virol. 2002;83(Pt 4):723–734. doi: 10.1099/0022-1317-83-4-723. [DOI] [PubMed] [Google Scholar]
- 26.Ye Q, Krug RM, Tao YJ. The mechanism by which influenza A virus nucleoprotein forms oligomers and binds RNA. Nature. 2006;444(7122):1078–1082. doi: 10.1038/nature05379. [DOI] [PubMed] [Google Scholar]
- 27.Ng AK, et al. Structure of the influenza virus A H5N1 nucleoprotein: Implications for RNA binding, oligomerization, and vaccine design. FASEB J. 2008;22(10):3638–3647. doi: 10.1096/fj.08-112110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ye Q, et al. Biochemical and structural evidence in support of a coherent model for the formation of the double-helical influenza A virus ribonucleoprotein. MBio. 2012;4(1):e00467–e12. doi: 10.1128/mBio.00467-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tong S, et al. A distinct lineage of influenza A virus from bats. Proc Natl Acad Sci USA. 2012;109(11):4269–4274. doi: 10.1073/pnas.1116200109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Boni MF, Zhou Y, Taubenberger JK, Holmes EC. Homologous recombination is very rare or absent in human influenza A virus. J Virol. 2008;82(10):4807–4811. doi: 10.1128/JVI.02683-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Yang Z. PAML 4: Phylogenetic analysis by maximum likelihood. Mol Biol Evol. 2007;24(8):1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
- 32.Jones DT, Taylor WR, Thornton JM. The rapid generation of mutation data matrices from protein sequences. Comput Appl Biosci. 1992;8(3):275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- 33.Whelan S, Goldman N. A general empirical model of protein evolution derived from multiple protein families using a maximum-likelihood approach. Mol Biol Evol. 2001;18(5):691–699. doi: 10.1093/oxfordjournals.molbev.a003851. [DOI] [PubMed] [Google Scholar]
- 34.Manavalan P, Johnson WC. Sensitivity of circular-dichroism to protein tertiary structure class. Nature. 1983;305(5937):831–832. [Google Scholar]
- 35.Kypr J, Kejnovská I, Renciuk D, Vorlícková M. Circular dichroism and conformational polymorphism of DNA. Nucleic Acids Res. 2009;37(6):1713–1725. doi: 10.1093/nar/gkp026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kimura M. On the probability of fixation of mutant genes in a population. Genetics. 1962;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Guerois R, Nielsen JE, Serrano L. Predicting changes in the stability of proteins and protein complexes: A study of more than 1000 mutations. J Mol Biol. 2002;320(2):369–387. doi: 10.1016/S0022-2836(02)00442-4. [DOI] [PubMed] [Google Scholar]
- 38.Miyazawa S, Jernigan RL. Estimation of effective interresidue contact energies from protein crystal-structures: Quasi-chemical approximation. Macromolecules. 1985;18(3):534–552. [Google Scholar]
- 39.Serrano L, Day AG, Fersht AR. Step-wise mutation of barnase to binase. A procedure for engineering increased stability of proteins and an experimental analysis of the evolution of protein stability. J Mol Biol. 1993;233(2):305–312. doi: 10.1006/jmbi.1993.1508. [DOI] [PubMed] [Google Scholar]
- 40.Steipe B, Schiller B, Plückthun A, Steinbacher S. Sequence statistics reliably predict stabilizing mutations in a protein domain. J Mol Biol. 1994;240(3):188–192. doi: 10.1006/jmbi.1994.1434. [DOI] [PubMed] [Google Scholar]
- 41.Lehmann M, et al. The consensus concept for thermostability engineering of proteins: Further proof of concept. Protein Eng. 2002;15(5):403–411. doi: 10.1093/protein/15.5.403. [DOI] [PubMed] [Google Scholar]
- 42.Amin N, et al. Construction of stabilized proteins by combinatorial consensus mutagenesis. Protein Eng Des Sel. 2004;17(11):787–793. doi: 10.1093/protein/gzh091. [DOI] [PubMed] [Google Scholar]
- 43.Taverna DM, Goldstein RA. Why are proteins marginally stable? Proteins. 2002;46(1):105–109. doi: 10.1002/prot.10016. [DOI] [PubMed] [Google Scholar]
- 44.Bloom JD, Raval A, Wilke CO. Thermodynamics of neutral protein evolution. Genetics. 2007;175(1):255–266. doi: 10.1534/genetics.106.061754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Bloom JD, Glassman MJ. Inferring stabilizing mutations from protein phylogenies: Application to influenza hemagglutinin. PLOS Comput Biol. 2009;5(4):e1000349. doi: 10.1371/journal.pcbi.1000349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lunzer M, Golding GB, Dean AM. Pervasive cryptic epistasis in molecular evolution. PLoS Genet. 2010;6(10):e1001162. doi: 10.1371/journal.pgen.1001162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.King JL, Jukes TH. Non-Darwinian evolution. Science. 1969;164(3881):788–798. doi: 10.1126/science.164.3881.788. [DOI] [PubMed] [Google Scholar]
- 48.Kimura M. Evolutionary rate at the molecular level. Nature. 1968;217(5129):624–626. doi: 10.1038/217624a0. [DOI] [PubMed] [Google Scholar]
- 49.Gil M, Zanetti MS, Zoller S, Anisimova M. CodonPhyML: Fast maximum likelihood phylogeny estimation under codon substitution models. Mol Biol Evol. 2013;30(6):1270–1280. doi: 10.1093/molbev/mst034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Goldman N, Yang Z. A codon-based model of nucleotide substitution for protein-coding DNA sequences. Mol Biol Evol. 1994;11(5):725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
- 51.Kosakovsky Pond S, Delport W, Muse SV, Scheffler K. Correcting the bias of empirical frequency parameter estimators in codon models. PLoS ONE. 2010;5(7):e11230. doi: 10.1371/journal.pone.0011230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Drummond AJ, Rambaut A. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol Biol. 2007;7:214. doi: 10.1186/1471-2148-7-214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Griep S, Hobohm U. PDBselect 1992-2009 and PDBfilter-select. Nucleic Acids Res. 2010;38(Database issue):D318–D319. doi: 10.1093/nar/gkp786. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.