A theory for how sensorimotor skills are learned and retained in noisy and nonstationary neural circuits

Significance

The synaptic trace theory of memory posits that the brain retains information through learning-induced changes in synaptic connections. Once consolidated, a memory is embodied through its fixed trace. For the case of motor memories, e.g., learning how to ride a bicycle, we propose a slight variation on this theme. Because there are so many different ways for the motor system to accomplish the same task goal, motor memories are defined not by fixed patterns of synaptic connections, but rather by nonstationary patterns that fluctuate coherently while still generating the same fixed input–output mapping. This mechanism provides a noisy sensorimotor system with enough flexibility so that motor learning can occur rapidly with respect to new memories without overwriting older memories.

Abstract

During the process of skill learning, synaptic connections in our brains are modified to form motor memories of learned sensorimotor acts. The more plastic the adult brain is, the easier it is to learn new skills or adapt to neurological injury. However, if the brain is too plastic and the pattern of synaptic connectivity is constantly changing, new memories will overwrite old memories, and learning becomes unstable. This trade-off is known as the stability–plasticity dilemma. Here a theory of sensorimotor learning and memory is developed whereby synaptic strengths are perpetually fluctuating without causing instability in motor memory recall, as long as the underlying neural networks are sufficiently noisy and massively redundant. The theory implies two distinct stages of learning—preasymptotic and postasymptotic—because once the error drops to a level comparable to that of the noise-induced error, further error reduction requires altered network dynamics. A key behavioral prediction derived from this analysis is tested in a visuomotor adaptation experiment, and the resultant learning curves are modeled with a nonstationary neural network. Next, the theory is used to model two-photon microscopy data that show, in animals, high rates of dendritic spine turnover, even in the absence of overt behavioral learning. Finally, the theory predicts enhanced task selectivity in the responses of individual motor cortical neurons as the level of task expertise increases. From these considerations, a unique interpretation of sensorimotor memory is proposed—memories are defined not by fixed patterns of synaptic weights but, rather, by nonstationary synaptic patterns that fluctuate coherently.

Sensorimotor skill learning, like other types of learning, occurs through the general mechanism of experience-dependent synaptic plasticity (1, 2). As we learn a new skill (such as a tennis stroke) through extensive practice, synapses in our brain are modified to form a lasting motor memory of that skill. However, if synapses are overly pliable and in a state of perpetual flux, memories may not stabilize properly as new learning can overwrite previous learning. Thus, for any distributed learning system, there is inherent tension between the competing requirements of stability and plasticity (3): Synapses must be sufficiently plastic to support the formation of new memories, while changing in a manner that preserves the traces of old memories. The specific learning mechanisms by which these contradictory constraints are simultaneously fulfilled are one of neuroscience’s great mysteries.

The inescapability of the stability–plasticity dilemma, as faced by any distributed learning system, is shown in the cartoon neural network in Fig. 1A. Suppose that the input pattern of [0.6, 0.4] must be transformed into the activation pattern [0.5, 0.7] at the output layer. Given the initial connectivity of the network, the input transforms to the incorrect output [0.8, 0.2]. Through practice and a learning mechanism, the weights are adapted to produce the correct output, and the new synaptic pattern materially embodies the learned memory “trace”. This conceptual framework suffices for explaining memory formation, when a single learned pairing is viewed in isolation. However, what if these nodes are part of a larger network required to learn many different distributed and overlapping input–output pairings at different times across multiple timescales? How can a previously learned synaptic trace persevere, in a recoverable fashion, when the network is continuously confronted by a stream of intermingled (and often nonunique) input–output maps arriving in no predictable order?

Fig. 1.

Neural networks. (A) Stability–plasticity dilemma. See text for details. (B) The gold and green lines correspond to all solutions in weight space (i.e., a manifold) for skills and . The manifolds are “blurry” because the presence of feedback precludes the need for an exact feed-forward solution. Point P denotes the intersections of these manifolds (and α is the intersection angle). The untrained network exhibits a starting configuration, S, and through the practice/performance of the different skills, the network approaches P. Three learning steps are illustrated. (C) A schematic phase portrait of network behavior as a function of learning rate and noise level. Our network exhibits a high level of irreducible noise (blue “x”), which forces the network into a high learning rate. (D) An example of ill-conditioned oscillatory behavior. Gray lines denote level curves of the error function, and the black lines denote the trajectory in weight space.

Here a theory is proposed to resolve this dilemma for the case of sensorimotor skill learning. It first assumes that synapses are perpetually modified at rapid rates. This facet of the theory ensures the “upside” of plasticity, i.e., a capacity for rapid sensorimotor learning and the behavioral flexibility that follows. To examine the “downside” of plasticity (i.e., instability), these highly adaptive synapses are embedded in a conventional artificial neural network for learning multiple skills over different timescales. As expected, performance is unstable at high learning rates. However, when high noise levels and massive redundancy are also incorporated—two features of biological sensorimotor systems expected to exert a destabilizing influence—the process of motor memory formation is, surprisingly, stabilized. The discovery that massively parallel networks can function in this atypical parameter regime leads to a class of “hyperplastic” networks that exhibit the following unique properties: (i) weights that change continuously even in the absence of overt error reduction, (ii) a critical postasymptotic phase of learning that is required for memory permanence given network nonstationarity, and (iii) a tendency to segregate the internal representations used in well-rehearsed skills. The distinctive learning dynamics of hyperplastic networks are postulated as a unifying principle that may bridge the cellular and behavioral domains of skill learning.

Theoretical Framework

A Neural Network Approach.

Artificial neural networks (4) are layers of processing units connected by adaptive weights that convert input vectors to output vectors through specific rules of information flow (Fig. S1). Through use of an error signal and a learning algorithm for weight adaptation, a neural network can be trained to learn an arbitrary functional mapping through repeated exposure to instances of the mapping (the desired input–output pairings). Feed-forward, multilayer perceptrons with gradient descent learning are used for the simulations shown, not because such networks accurately capture the details of brain function, but because they serve as an analytically tractable and well-studied connectionist system capable of illustrating general principles of learning with distributed computing elements. The use of additional network variants and learning algorithms is described in SI Methods.

Within a neural network framework, a sensorimotor skill can be represented as a functional association between a movement intention expressed as a vector in task space, , and a corresponding vector of motor activation commands, , designed to produce the target movement intention. To learn a set of sensorimotor skills, the network must simultaneously learn multiple associations in the form of a nonlinear functional map (5, 6),

where the superscript denotes an individual skill. In general, the vectors and are high dimensional and functions of time.

Solution Manifolds in Weight Space.

The adaptable parameters of a neural network are the values of the weights. In the network of Fig. S1, where a layer of three nodes fully connects to a layer of four nodes that fully connects to a layer of two nodes, there are a total of 20 (3 × 4 + 4 × 2) weights. A given configuration of the network can be considered as a point, , in a 20-dimensional weight space, and each such point corresponds to a function, : or . Suppose the network is required to learn two skills, and . Mathematically, this means the network must be configured to meet two constraints:

A collection of points in weight space that satisfy a desired constraint is called a solution manifold. In Fig. 1B, we plot two schematic solution manifolds, one for skill and the other for skill . All points on the manifold embody network configurations that fulfill the first constraint, whereas points on the manifold satisfy the second constraint. Starting from a point, S, in weight space, the network must dynamically evolve, through training, to a point, P, where the two manifolds intersect. The learning process can be geometrically envisioned as follows (Fig. 1B). Every time skill is practiced, the system moves from its current location in weight space toward the manifold along the connecting perpendicular (trial-by-trial learning). The magnitude of the displacement depends on the size of the learning rate and the error. The same procedure holds true every time skill is practiced. Although this geometric formulation oversimplifies actual learning algorithms (e.g., the gradient of the error function is not necessarily perpendicular to the manifold), it embodies the key features.

A critical point about neural networks is that they are redundant—that is, many different weight configurations embody the same functional mapping. Learning algorithms are designed merely to obtain a solution (not a particular solution). Because the sensorimotor system is massively redundant at all levels from neurons to muscles (see below), a neural network model should also be highly redundant (many more hidden nodes are used than are required to accomplish the task). In essence, the system should be so underconstrained that a given weight can assume a wide range of values and still be part of a solution set. Thus, the solution manifolds, represented by lines, are actually high-dimensional curved surfaces, and the intersection of two solution manifolds, depicted by a point, is also a high-dimensional submanifold. Exactly what is meant by “high-dimensional” is discussed in SI Results.

Network Features.

Below we identify three features inherent to biological nervous systems as multijoint controllers that distinguish them from artificial neural networks used, for example, to solve problems in pattern recognition or data mining.

Noisy.

Neurons are noisy (7, 8). They are noisy signal processors; their synapses are noisy signal transducers; synaptic change is a noisy morphological process. The noise level relative to the signal may be high (9). Our simulations included all three possible noise sources ranging from low levels to extremely high levels: up to 30% of the signal for nodes/weights and 400% for weight changes (Methods). These noise levels far surpass the levels that are usually included in neural networks.

Redundant.

Biological motor systems are massively redundant—the system contains many more degrees of freedom than are necessary to accomplish the task (10). Redundancy applies throughout the system, as there are excess numbers of cortical neurons, spinal neurons, muscles, joints, etc. Two different types of redundancy exist—external system redundancy and internal system redundancy—depending upon whether the redundancy applies to an observable behavioral variable (external) or an unobservable state variable (internal). See SI Discussion for examples. Our focus is on internal system redundancy, although all manners of both types of redundancy coexist.

Reliant on feedback.

Biological motor systems rely on feedback from multiple sensory/proprioceptive modalities, as well as corollary discharge, for online self-correction. Feed-forward commands are inherently imperfect due, in part, to corruption by internal noise sources, and feedback signals help to compensate. The manifolds in Fig. 1B are correspondingly fuzzy to depict a buffer zone providing tolerance for imprecision in the feed-forward command (this “cloud” extends in all directions in weight space). Feedback mechanisms also serve as a natural source for generating teaching signals by which to train the system (11, 12).

Three additional assumptions that could apply to any network are also incorporated.

Hyperplasticity.

This assumption qualitatively characterizes the learning rate of the system as high: Even when sensorimotor errors are relatively small, synapses are hypothesized to undergo significant changes. In the gradient descent learning algorithm used in our simulations, weight changes range from 15% to 50% of the gradient (not the typical 1% used for these types of networks) (Methods). Hyperplasticity and high noise levels distinguish our network from other stochastic gradient methods in that the weights remain highly malleable at all stages of the learning process.

Trial-by-trial learning.

After each instance of practicing/performing a sensorimotor act, synapses are altered to reduce the experienced error. This assumption, standard for neural networks, is supported by the rapid error reduction observed in sensorimotor adaptation experiments (13, 14) and the autocorrelation of errors seen during unperturbed movements (15).

Equivalence of Internally Redundant Solutions.

In dynamical systems theory, it has long been known that different combinations of system parameters can lead to the same output behavior. This point has been explicitly made for the crustacean pyloric circuit (16). For connectionist learning systems, network configurations can exhibit different patterns of synaptic weights, yet as long as inputs map correctly to outputs, all solutions are equally valid.

By incorporating these features—most critically, the dual assumptions of hyperplasticity and high noise levels—we construct a unique type of neural network for understanding the processes of biological motor memory formation and retention.

Results

Solution Space of Viable Networks.

Our analysis focuses on network properties as a function of two parameters: learning rate and noise level. For every network variant (number of nodes, input–output mapping, choice of transfer function, etc.) (Methods), these two critical parameters were systematically varied. The resulting network behavior was characterized according to the following three criteria: (i) convergence, (ii) performance threshold, and (iii) conditionability. The convergence criterion requires that the network error converges, rather than diverges, with increasing trial number. The performance threshold criterion requires that the average error, at asymptote, falls below a desired threshold value. The conditionability criterion requires that convergent solutions are well behaved (i.e., not ill-conditioned).

For the simulations that were run, a typical phase portrait of network response is schematized in Fig. 1C. The dashed black line denotes a boundary of convergence. When the step size is too large, because the learning rate or noise level (or a combination of both) is too high, the system diverges as if it were a control system operating with too high a feedback gain (17). The solid line is the performance threshold—that is, the level set (or isocontour) of learning rates and noise levels that exactly meets the minimum performance requirements (all points above the line satisfy this constraint). Its exact shape, as well as the exact shape of the boundary of convergence, depends on the specific network architecture, learning rule, problem to be solved, etc. However, the performance threshold must slope upward at low learning rates: If the noise is increased, the learning rate must be increased to compensate for the noise, while still maintaining the same level of performance. It must also tend toward verticality at the point where the noise level is so high that no boost in learning rate can produce the desired performance.

Divergence is not the only type of instability exhibited by connectionist systems. If the learning rate is too high, the error oscillates at asymptote instead of smoothly converging, i.e., the “cross-stitching” effect (18) shown in Fig. 1D. This problem of network ill-conditioning (19) arises when the error function is characterized by sharply different slopes for different directions in weight space (numerically assessed from the eigenvalues of the Hessian matrix). Geometrically, ill-conditioning can be envisioned as long, narrow valleys of the error surface that induce unproductive oscillatory behavior. Noise mitigates the problem by providing the network with the capacity to “escape” from such ravines, thereby enabling a network to operate at higher learning rates without producing oscillations in the error at asymptote. As a result, if a minimum performance threshold is specified with regard to a network being properly conditioned, it slopes upward like the dotted line in Fig. 1C—all points below this line will satisfy the constraint. A more detailed explanation of how an increased noise level enables a network to avoid cross-stitching is contained in SI Results. Here we note that examples of the exploratory benefits of noise are found in the concepts of simulated annealing (20), reinforcement learning (21), and other stochastic learning methods (22).

Hyperplastic and Noisy Networks.

The shaded area in Fig. 1C represents the region in parameter space fulfilling all three criteria above. The first result of this work is that all network variants admitted solutions in regions of the parameter space where the learning rate and the noise level were both “high”. Here, a high learning rate is characterized as ranging between 15% and 50% of the gradient. At these learning rates, if the noise in the system is dropped to zero, the network becomes ill-conditioned or divergent. High noise levels typically range from 10% to 30% for the nodes/weights and from 200% to 400% for the weight changes. At these noise levels, a significant drop in the learning rate leads to high network error or divergence. Clearly, then, high learning rates and high noise levels reciprocally interact to restore network functionality where the effect of a large value of either parameter alone is otherwise deleterious.

Our theory posits a high level of irreducible noise in biological systems (the blue “x” in Fig. 1C), and this noise level forces the network to assume a high learning rate to satisfy the performance threshold criterion. Such networks are termed hyperplastic and noisy. The rest of the paper investigates the attributes of these networks compared with conventional neural networks, i.e., those with a low learning rate and no noise. Our ultimate conclusion is that the combination of high learning rates and high noise levels imbues biological sensorimotor systems with many of their distinctive properties. To our knowledge, hyperplastic and noisy networks signify an entirely unique construction, presumably because for most application purposes, it would not make sense to willfully inject extremely high noise levels into a system.

Adaptive Weights That Never Stop Adapting.

The key result observed during the simulation of hyperplastic and noisy networks is that simple error-based learning gives rise to a permanently nonstationary network: The weights are perpetually in flux, regardless of whether or not overt learning is taking place at the behavioral level. Consider the performance of a highly stereotyped skill with little or no behavioral variability. As the skill is performed, system noise generates random perturbations in the feed-forward command signals. Because the skill is well learned, task deviations as a result of these perturbations will be relatively small, so that feedback can largely compensate for their effect during performance. After performance, the system automatically attempts to reduce its own feedback-compensated errors via its usual learning mechanisms of weight adaptation, so that on the next trial there is no feed-forward error, assuming that there is no noise. Of course, there is always noise. In essence, the network adapts its structure to accommodate the noise it experienced on its last trial, even when feedback prevents the presence of behavioral error: Learning of some kind is always taking place. Critical to this conception of learning is the notion that some level of feedback control is always operative in biological motor systems, even during the performance of highly practiced and skilled movements (in contrast to robotics where, absent external perturbations, canonical movements can be precisely and repeatedly executed using feed-forward commands alone). This assumption is supported by findings that precise movements require online visual (23) and proprioceptive (24) feedback.

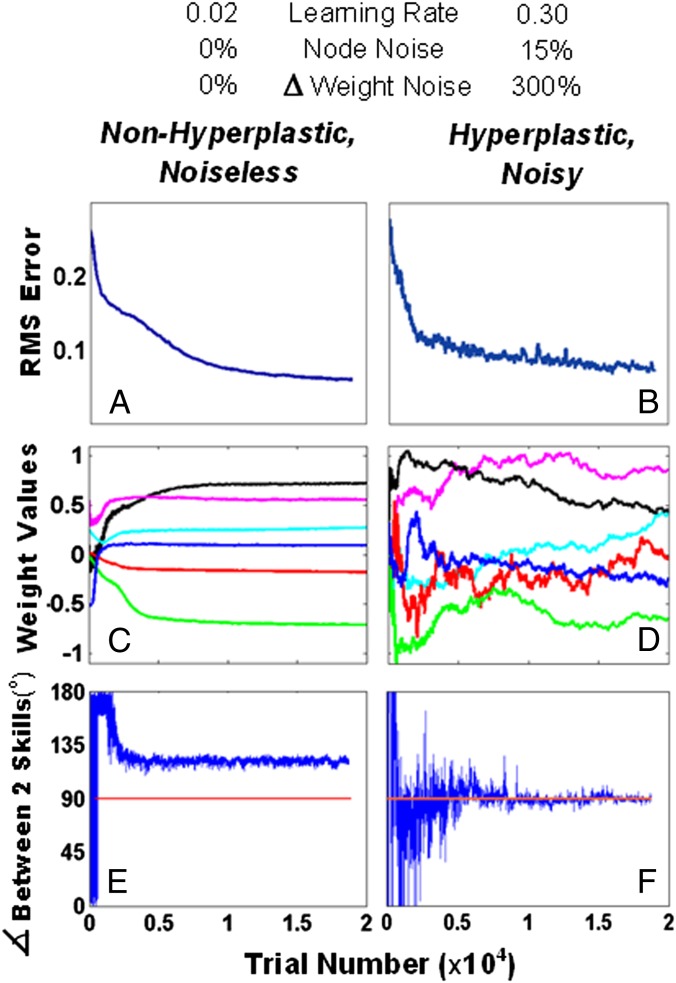
If the theory is viewed from a graphical perspective, a skill has been learned when the network configuration lies at or near a point in weight space contained on the corresponding solution manifold. If the skill is then repeatedly practiced, noise-induced learning will move the weight configuration of the network toward, by definition, some point on the high-dimensional solution manifold. Given the randomness of the noise and the flexibility afforded by massive redundancy, the place in weight space where the network ends up is not necessarily the same place where it started; i.e., the weight configuration of the network randomly wanders in the neighborhood of a large null space of solutions. Fig. 2 illustrates this point for two artificial neural networks that learn to perform a function approximation task (a simulation of center–out arm reaches in eight directions—SI Methods). The network architectures and learning rules are identical. The difference is that one network is hyperplastic and noisy, whereas the other has a low learning rate and no noise. Although the networks achieve similar levels of performance (Fig. 2 A and B), the temporal profiles of the weights differ radically: The weights in the hyperplastic, noisy network (Fig. 2D) are always changing, even after performance asymptotes. The weight changes are driven by random noise but are not wholly random, as lying on a solution manifold represents a strong constraint for the population of weights as a whole.

Fig. 2.

Comparison of network performance between a nonhyperplastic, noiseless network and a hyperplastic, noisy network. The values of key parameters distinguishing the two are displayed at the top. (A and B) The total error approaches a similar value for both network types, albeit slightly lower for the noiseless network. (C and D) The time course of six weights taken from all three network layers. (E and F) The “angle” (Methods) between two specific skills is plotted across trials. This angle approaches in the hyperplastic network.

The idea that experience-dependent synaptic change is always taking place at high rates, even in adulthood, comports with a growing body of evidence attesting to the remarkable degree of plasticity inherent in the vertebrate central nervous system. This evidence includes cellular operant conditioning studies showing that the firing rates of individual neurons are significantly modulated (50–500%) on the timescale of minutes (25), single-cell recording studies showing rapid in-session changes in motor cortical activity during adaptation tasks and continued postasymptotic activity changes (26, 27), and recent two-photon microscopy studies revealing that dendritic spines and axonal boutons continuously sprout and retract (see Dendritic Spine Fluctuation). However well motivated, though, the hyperplasticity assumption still seems to lead to a functional paradox: How can a perpetually nonstationary network stably retain previous learning? Hyperplasticity appears well suited only to explain the “plasticity” half of the “stability–plasticity” dilemma, leaving unexplained the stability of long-term memories. Here we propose a resolution to this dilemma, and a metaphor for the answer can be drawn from statistical thermodynamics in the concept of a dynamical equilibrium: A closed liquid–vapor system held at thermal equilibrium maintains constant thermal properties even as individual molecules are rapidly transitioning across different physical states of matter. Similarly, a learned skill need not entail a fixed configuration of synapses within a sensorimotor network (28). Individual synapses can rise and fall as long as the network is properly balanced on a global scale. How is this global balance achieved and what form does it take?

The Orthogonal Manifold Theory.

Consider Fig. 1B again. Learning skill slightly unlearns skill . Geometrically, the reason for this “interference” is that a movement of along the perpendicular of the manifold leads to a movement of away from the perpendicular of the manifold. Suppose the network is configured at a point in weight space where the manifolds are orthogonal to one another: . The learning of does not unlearn —there is no interference. More generally, suppose a network is configured at or near a point of intersection between two solution manifolds. What condition ensures that the network remains configured at or near such an intersection point, despite the network’s nonstationarity, during continued practice of the two skills? The answer is that the normal vectors to the manifolds must be perpendicular at the intersection point.

Weight space is high dimensional and manifolds are curved, so the condition of noninterference must be phrased generally in differential-geometric terms. If a network is configured near an intersection point of solution manifolds and , the skills will not interfere with each other when the weight change induced by the error in practicing is guaranteed to be parallel to the local tangent plane of the manifold and vice versa. Specifically, let the network be represented as and suppose the network is configured near an intersection point so that and . The weight change experienced after practicing/performing skill , denoted as , depends on the specific learning rule used. For this weight change to avoid generating increased error in the subsequent practice/performance of skill , it must be contained within the local tangent plane of skill ,

where is the gradient of the error of the network function, f, taken with respect to the current weight vector, and the superscript means evaluated at .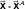

This new condition allows us to formulate sensorimotor skill learning as more than a function approximation problem. Suppose that a biological learning system must learn n patterns, with the ith pattern denoted 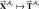, and the network itself is represented as the function f: . Then full learning is said to have occurred when the network configuration lies within a manifold in weight space such that any point contained within that manifold, called , fulfills the following two conditions:

i) Static equilibrium.

This is the standard definition of associative learning cast as a function approximation problem: Points in weight space exist such that each input pattern is mapped to its corresponding output pattern, meaning that the overall error is small. The network starts at a random configuration in weight space and, through use of a learning rule, moves to such a point.

ii) Dynamic equilibrium.

For learning to be maintained given the perpetual nonstationarity of the weights, the network configuration must arrive at a region in weight space such that the skills in a skill set fulfill the orthogonality constraint: The movement in weight space induced by practicing a given skill is roughly orthogonal to the gradient of all other skills. Because the inner product between the error gradient and the weight change trivially goes to zero if the magnitude of the weight change goes to zero (as naturally happens in noiseless neural networks), the inner product must be divided by the norm of the weight change. Condition ii must hold generally for any noisy learning system, regardless of network architecture or choice of learning rule. For a standard feed-forward neural network with gradient-descent learning, we show the neurophysiological consequences of this condition in Neurophysiological Consequences of Orthogonality.

What guarantees that a dynamic equilibrium will be reached or approached when the only mechanism for weight change is simple gradient descent? First, it must be established that orthogonal intersections exist, which can be done if the dimensionality of weight space is sufficiently large. Simple calculations on the number of synaptic connections within real neural circuits suggest that more than enough redundancy exists (SI Results). Given the existence of orthogonal solutions, the network is guaranteed to move toward them with sufficient practice because weight change is proportional to error, and for networks whose weights never settle, orthogonal solutions minimize error across a skill set. This fact is illustrated in Fig. 3A, where the network is configured near the orthogonal intersection of two solution manifolds. When skill is practiced and subsequent movement of the configuration in weight space takes place, the deterministic movement component projects in the direction of the gradient of , which is locally parallel to the manifold of skill . Thus, the error in skill does not, on average, increase through practice of skill (Fig. 3A and SI Results). In contrast, when learning has concluded for a noiseless network with a low learning rate, the intersection angles are immaterial, because—regardless of local geometry—the error is already minimized and the weights have stabilized.

Fig. 3.

Stages of learning. (A) This schematic shows a single practice trial of skill during the late stage of learning of both skill and skill when the network is near an orthogonal intersection. The black circle represents the network configuration at the start of the trial, and the dotted lines denote movement from performing skill . The black dotted line represents the deterministic movement component resulting from error reduction in the direction of the gradient, i.e., perpendicular to the manifold. The red dotted lines represent potential displacements due to noise in the weight change process itself: displacements that can occur both in the direction of the gradient and perpendicular to the gradient. Because of orthogonality, the configuration does not, on average, move away from the manifold (minimal interference). (B) In early learning, the network configuration approaches an intersection point of the manifolds of desired skills. (C) In late learning, the network explores the space of intersections, tending toward solutions that fulfill the orthogonality constraint.

It is important to realize that, for hyperplastic and noisy networks, the path of convergence to orthogonal solutions is probabilistic, not deterministic. The system is not designed to specifically seek out orthogonal intersections over nonorthogonal intersections. Rather, by always acting to reduce error, the network statistically gravitates (with sufficient practice) to regions of weight space where the desired constraint of Eq. 3 is fulfilled. A loose analogy for this process is found in the concept of a biased random walk: On a given trial, a step can occur in any direction, yet movement in the long run always takes place in the direction of bias. For hyperplastic and noisy networks, the mechanism of convergence is somewhat inverted. The system constantly steps through weight space with an average step size that is a function of the intersection angles of the solution manifolds, so that displacement is minimized when the solutions are orthogonal. Thus, the constraint of Eq. 3 acts something like an attractor because once the network enters, through exploration, a region of orthogonality, its tendency to leave is minimized. Unlike a conventional attractor, there is no mechanism to specifically pull the network inside, only a tendency to prevent it from leaving. For this reason, extensive repetition is required after behavioral asymptote to attain an orthogonal solution.

Fig. 2F plots an example of how the angle of intersection between a single pair of solution manifolds tends toward after extended practice, despite wild fluctuations in the “intersection” angle at the beginning. [The concept of an intersection angle is ill-defined early in practice when error is high because an intersection point, by definition, requires low error (SI Methods).] This tendency of moving toward orthogonality is found for all possible pairs of solution manifolds (Fig. S2). As network redundancy is decreased (SI Methods), the tendency toward orthogonalization is reduced and the time course of convergence lengthened. For a nonhyperplastic and noiseless network, the angle of intersection quickly settles at an arbitrary nonorthogonal value (Fig. 2E).

A Geometric Interpretation of Skill Learning.

The condition of dynamic equilibrium leads to a geometric interpretation of skill learning. For a set of multiple skills, practice eventually drives the weight configuration to a location in weight space where the gradients of the solution manifolds are mutually orthogonal, so that each skill is insulated from noise-induced weight changes that result from the practice/performance of other skills. Convergence to this end goal occurs through a two-stage process: (i) The system approaches an intersection area of the solution manifolds, and (ii) the system moves along the intersection area toward a more desirable (i.e., orthogonal) solution. These stages are now characterized further.

In the early or preasymptotic stage of learning (stage I), the network is driven toward a weight configuration where the solution manifolds for the different skills intersect. At this point in the process, individual learning trials act, on average, to appreciably reduce the considerable distance between the current weight configuration and the solution manifold of the practiced skill (Fig. 3B). What matters most during stage I learning are the global metric properties of the solution manifolds—specifically, the distance from the current weight configuration to the closest region of intersection.

Once behavioral asymptote has been reached, however, the network dynamics change. It becomes difficult to move any closer to a solution manifold because of the effects of noise and hyperplasticity, which together induce “jumps” in weight space of comparable magnitude to the distance from the manifold. At this point, a late or postasymptotic learning stage (stage II) commences, whereby significant error reduction occurs not from positioning the network closer to a solution manifold, but from moving the network toward locations within a region of intersection where the solution manifolds more closely approach orthogonality (Fig. 3C). The strong stochastic component to the weight change process ensures that the network will take steps in the “wrong” direction, i.e., away from an orthogonal intersection. Nonetheless, as the simulations show, after asymptote the weight configuration migrates, on balance, along the intersection manifold from regions far from orthogonality to regions close to orthogonality. What matters most during stage II learning is the local geometry of the intersecting solution manifolds. The two learning stages exist as emergent network properties, not built-in assumptions, because only the single mechanism of trial-by-trial error reduction drives learning.

If skills are naturally orthogonal because they engage distinctly different skeletomuscular machinery—such as threading a needle vs. kicking a field goal, for which skills nonoverlapping neural circuits are engaged—stage II learning is not necessary, because each skill will automatically be stable with respect to the practice/performance of the other skill. However, if the skills share many of the same skeletomuscular requirements—for example, a slice backhand and a backhand volley—the manifolds of the skills will not be orthogonal at the initial intersection point, and orthogonality can be attained only through extensive practice.

A Reversal of Learning Transfer—Prediction and Experiment.

This two-stage geometric formulation of learning gives rise to a clear prediction: In the case of highly similar skills, a reversal of learning transfer will occur across the two stages. Consider a highly similar skill pair (by which is meant that the sensorimotor requirements of the two skills overlap significantly). Because of the shared sensorimotor structure, the solution manifolds will occupy similar regions of weight space. Thus, as stage I learning begins from a distant starting point in weight space, movement toward one manifold brings the network closer to the other manifold: Learning transfers. This prediction is common to all learning models. However, as learning continues after asymptote, our model makes a very distinct prediction. In the initial region of manifold intersection, the intersection angle between the manifolds is expected to be highly acute, once again because of the shared sensorimotor structure. Thus, during the onset of stage II learning, the two skills will interfere with each other, as noise-induced weight changes of one skill displace the network from the solution manifold of the other skill. The sensorimotor similarity that facilitates transfer during early learning ends up creating interference during late learning when high levels of expertise are sought.

We tested this prediction of transfer reversal, using a target reaching task performed under the visuomotor perturbation of a cursor rotation (29). Subjects learn to control an onscreen computer cursor with a robotic manipulandum (Fig. 4A), while direction of handle movement is dissociated from direction of cursor movement by a rotation of . Subjects move to two neighboring targets only—D₁ and D₂ in Fig. 4B—so that the two movement tasks are highly similar. First, we investigated transfer during stage I learning. The results replicated the well-established finding (SI Methods) that de novo learning of the visuomotor rotation to either D₁ or D₂ in isolation transfers significantly to the other target.

Fig. 4.

Reversal of learning transfer for the visuomotor rotation task. (A) Robotic manipulandum controlling onscreen cursor. (B) Two targets are used. (C) The order of target presentation for the experiment is displayed. There are eight targets in a cycle, and each cycle contains either D₂ only or a pseudorandom mixture of D₁ and D₂ (except for cycles 34 and 98). (D) The black and blue points denote the error for movements to target D₁ (shown with SE), whereas gray points denote movements to target D₂ (error bars omitted). Individual trial movement data are shown instead of cycle averages for cycles 34 and 98. (E) Simulation results for the same experiment are shown. Because the model includes high noise levels, 1,000 simulation results are averaged. (F) The angle between the two skill manifolds is plotted over time after asymptote is reached. The model reproduces the data through an increase in the orthogonality of the two skills as interleaved practice occurs beyond asymptote.

Next, we tested the more distinct prediction that during the onset of stage II learning, movements to D₁ and D₂ will interfere with one another. Fig. 4C outlines the protocol, and Fig. 4D and Fig. S3 show the data. After an initial period of practicing D₁ and D₂ in alternation so that behavioral asymptote is just reached (stage II onset), subjects repeat movement D₂ by itself 120 times (15 cycles). Performance of movement D₁ is then briefly assessed after the extended practice of D₂. There is a huge jump in error for movement D₁ from 10.8° at cycle 18 to 23.3° during the first movement of cycle 34 (Fig. 4D and Fig. S3). Although this initial rise in error (an increase of 12.5°) is highly significant (P < 0.00001, n = 12), it fades quickly (back down to 11.0° after four movements). Thus, the extended practice of D₂ generates a temporary increase in error for D₁ after the two skills were learned in tandem just to asymptote. This increase in error cannot be attributed to a surprise or novelty effect because subjects were explicitly informed of the upcoming change in target sequence (SI Methods).

After cycle 34, both movements are practiced in a pseudorandom fashion for 48 cycles (192 movements to each target). Then movement D₂ is again practiced, by itself, 120 times from cycle 82 to cycle 97. When performance in movement D₁ is assessed this time, the error no longer jumps significantly: The error for movement D₁ at cycle 82 is 8.6°, compared with 9.7° during the first movement of cycle 98 (Fig. 4D and Fig. S3). Thus, practicing one skill repeatedly can actually unlearn a similar skill if asymptote has just been reached. Once the skills have been repetitively practiced in tandem after asymptote, such disruption does not occur. These observations are simulated with good results, using a hyperplastic, noisy network (Fig. 4E). Fig. 4F illustrates that motor memory “stabilization” occurs within the model because the two solution manifolds become orthogonal during the extended period of mixed practice after asymptote. A noiseless distributed network cannot replicate this result because once the error reaches asymptote, the network configuration remains static (Fig. 2C), and the error never jumps. Finally, the model predicts that the transfer reversal effect will increase in magnitude as the two skills are made more similar, because the orientations of the two solution manifolds within the initial region of intersection correspondingly become more similar.

We liken this phenomenon to the striking asymmetric transfer observed in sports science studies (30), whereby the backhand of a skilled tennis player who has never played squash will transfer positively to a squash backhand, even though—at the same time—continued practice of the squash backhand is well known to negatively impact the expert tennis stroke. Asymmetric transfer is one of many heuristics emanating from the sports science/kinesiology communities (e.g., variability of practice effect, rapid deadaptation, warm-up decrement, etc.) that form the basis of our current pedagogy on skill instruction (30) and are codified by the invocation of hyperplastic and noisy networks (31).

Dendritic Spine Fluctuation

Neurophysiological support for the model would consist of direct experimental evidence showing that synaptic weights fluctuate significantly in mature animals, even when behavioral learning has reached asymptote with little or no behavioral error. Here, we examine the existing cellular imaging data on dendritic spine turnover and address the question of whether the model can be used to simulate these data.

Standard neural networks represent the aggregate connection strength by which one neuron (or neural population) affects the firing rate of another neuron (or neural population) with a single continuous-valued weight (e.g., 0.57). In real neural circuits, neurons are interconnected through a multitude of synapses, each of which links (in most cases) a single axonal bouton to a single dendritic spine. The overall synaptic input convergent upon an individual neuron can therefore be modulated by (i) altering the efficacy of existing synapses (such as long-term potentiation or depression), (ii) adding and/or removing boutons/spines without global remodeling of axonal and dendritic arbors, or (iii) larger-scale remodeling of axonal or dendritic arbors as happens during development. From an experimental standpoint, it is difficult to establish the occurrence of i. However, with the advent of two-photon microscopy for bioimaging (32), it is now possible to observe within the cerebral cortices of behaving animals the turnover of dendritic spines and larger-scale restructuring of axonal and dendritic arbors. Numerous studies from multiple laboratories have produced detailed observations on dendritic structures as they vary on timescales from hours to days over a variety of behavioral conditions for adult behaving animals (33–36). These studies largely agree on the following three findings:

• Significant large-scale remodeling of axonal and dendritic arbors does not appear to take place in adult animals even under conditions of behavioral manipulation and learning.

• Under conditions that are conducive to adaptation/learning (such as the alteration of sensory input or the learning of a novel motor task), significant turnover occurs within the population of dendritic spines on the timescale of hours to days.

• Even under control conditions when no overt learning takes place, there is still a fairly significant baseline level of dendritic spine turnover.

The first observation reinforces the understanding that the basic skeletal outline for global synaptic connectivity within neural circuits is laid down during development and likely not modified significantly thereafter. The second observation affirms the widely held hypothesis that experience-dependent plasticity—including the growth and retraction of dendritic spines—underlies the adaptive formation of new memories in response to novel environmental conditions. The third observation, however, is intuitively puzzling for some of the same reasons discussed in the Introduction. Why should dendritic spines come in and out of existence even when there is no overt learning? Will perpetual synaptic flux destabilize a learning system and erase old memories?

A pair of recent two-photon microscopy studies looked at the addition and subtraction of dendritic spines in the primary motor cortices of mice while the mice learned a new motor task (35, 36). Fig. 5A shows the key result from ref. 36. After 2 d of training on a new motor task, roughly 8% of the total population of observable dendritic spines are newly formed (and a comparable percentage of existing spines have been removed). Presumably, the development of these spines has something to do with the adaptive reorganization of the relevant cortical circuits to better perform the behavioral task. However, even in the case of control mice where no overt learning takes place, there is still significant dendritic spine turnover: After 2 d, over 3% of the spines have been newly formed. These results typify the two-photon microscopy data in adult mice across a variety of perceptual manipulations and motor adaptations. Although the exact numbers depend on the specific preparation and task, after 2 d of learning somewhere between 8% and 12% of the dendritic spines are newly formed in the treatment group, whereas 3–5% of the dendritic spines are newly formed in the control group. It is a remarkable, although unexplained, finding that the baseline level of dendritic spine turnover consistently comprises 30–50% of the learning-induced turnover.

Fig. 5.

Turnover in dendritic spines. (A) Data from Yang et al. (36). (B) Simulated turnover in dendritic spines (relative to t = 0). As skill learning commences in the novel learning condition, the dendritic spines appear and disappear fairly rapidly, with roughly 8% of the spines newly formed after 100 trials. After behavioral asymptote is reached (the “A” in B), the rate of turnover slows down. In the simple repetition condition, the dendritic spine turnover is slower at the outset but still significant. Note that after asymptote is reached, the rates across the two conditions become comparable.

To simulate the basic paradigm of refs. 35 and 36, we modify our neural network simulations of visuomotor adaptation such that each pair of interconnected neurons is linked by a huge number of potential dendritic spines. Specifically, an aggregate connection strength between two neurons is represented by the percentage of activation of a pool of 10,000 potential excitatory synapses and a pool of 10,000 potential inhibitory synapses (neurons are typically believed to make roughly 10,000 synaptic connections). These synapses are considered to be binary valued, either 1 or 0 (i.e., active or inactive), so that this model does not incorporate changes in synaptic efficacy (SI Methods). A dendritic spine, once created, is active; if not active, it is removed. With this formalism in place, the same gradient descent learning scheme can be implemented, only now a weight change entails the creation/removal of a certain number of excitatory/inhibitory synapses (and, correspondingly, a weight value entails the current activation/deactivation of a certain percentage of excitatory/inhibitory synapses). As before, we run the simulations in a nonhyperplastic, noiseless mode and a hyperplastic, noisy mode.

Fig. 5B shows a simulation run for the hyperplastic, noisy network. The percentage of new dendritic spines is plotted vs. the number of trials of practicing/performing a motor task (visuomotor adaptation). There are two different conditions. In the “novel learning” condition, the subject has not been exposed to a visuomotor perturbation and must learn it. In the “simple repetition” condition, the subject has already learned the visuomotor perturbation to asymptote and merely continues repeating trials. This condition resembles a control condition because no new learning is taking place. The basic phenomenon revealed in the two-photon microscopy literature is captured. After 100 trials, roughly 8% of the dendritic spines are new in the novel learning condition. This percentage continues to increase even after behavioral asymptote is reached (the “A” in Fig. 5B), although at a significantly slower rate. In the simple repetition condition, just under 3% of the spines are new after 100 trials, and this percentage, too, continues to increase, albeit at a slower rate.

Clearly, these simulations are not perfectly analogous to the paradigms used in refs. 35 and 36, and a variety of simplifications are necessarily made (SI Methods) that preclude a quantitative comparison with the data. Nonetheless, from a qualitative standpoint, hyperplastic and noisy networks robustly capture the central features of these (and other) two-photon microscopy studies in a parameter-independent fashion—that is, for all combinations of simulation parameters (SI Methods), the following results always held for this type of network:

• Dendritic spine turnover in the novel learning condition varies between 5% and 20% after the first 100 trials.

• The percentage of new dendritic spines arising after 100–200 trials in the simple repetition condition constitutes between 15% and 45% of the percentage of new spines arising in the novel learning condition for an equivalent number of trials.

Just as significantly, the nonhyperplastic, noiseless network fails to reproduce either of these phenomena under any parameter setting, as illustrated in Fig. S4. In the novel learning condition, the spines turn over at a much lower rate and on a much longer timescale compared with the hyperplastic, noisy network (thousands of trials are required to achieve 2% new spine growth). More tellingly, in the simple repetition condition, the percentage of spine turnover remains essentially at 0% the entire time, an expected result given that neural networks usually “freeze” a system’s parameters once an acceptable solution has been reached for a fixed learning problem.

Neurophysiological Consequences of Orthogonality.

If the orthogonality constraint does constitute a fundamental organizing principle of the central nervous system, how are its consequences reflected in activity patterns of single neurons? The answer is that orthogonality leads to the development of specialized neural representations embodied, in part, by sharpened neural tuning curves. To deduce this result, one must evaluate the orthogonality constraint for a specific learning rule, error function, and network architecture. Here we assume gradient descent learning, a quadratic error function, and a purely feed-forward multilayer perceptron (see SI Discussion for other assumptions).

From Eq. 1 and gradient descent learning, orthogonality is quantified by (i) computing the gradient of the network error function with respect to all of the weights for each skill separately, (ii) taking the inner product of these gradients for each skill pair, and (iii) summing these inner products. The gradient of the error function can be decomposed and simplified into an expression involving the gradients of the activity of individual output nodes (Eq. S3). In the presence of noise, the entire summand goes to zero when each of the following terms goes to zero (SI Results),

where the gradient means that individual output node activity is differentiated with respect to every weight in the network (i and j index skills, and k denotes output node). At this point, the modularity of feed-forward neural networks can be exploited by dividing an arbitrarily large multilayer network into pairs of successive layers connected by a corresponding weight matrix (SI Results). Given this hierarchical decomposition of network structure into modules, the inner product of Eq. 4 can be recast as the module-by-module sum of inner products involving only the partial derivatives of output node activity taken with respect to the corresponding weight matrices (SI Results). By computing this quantity across all pairs of skills, we gain insight into how each module of a feed-forward network contributes to the overall measure of orthogonality.

Unfortunately, this formulation of orthogonality is still not useful because no obvious empirical method exists for measuring the values of individual weights. The network quantities most accessible to measurement are the nodal activities. Thus, if the vector of partial derivatives with respect to weights can be alternatively expressed in terms of nodal activations, then the orthogonality constraint can be cast into an interpretable form. Fig. 6A depicts a network module. R neurons in layer I feed forward to S neurons in layer II, 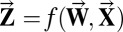is the activation of neuron r in layer I, w_rs is an individual term of the weight matrix W that connects neurons in layer I to neurons in layer II, is the neural activation function, is the total input to neuron s in layer II, u_s is the activation of neuron s in layer II, and is the derivative of output node with respect to u_s. The contribution to network orthogonality made by this module can be written as (see SI Results for complete derivation)

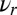where is the gradient of the output node with respect to , the vector of inputs into layer II, during performance of skill . Neural activations, such as , are measurable through standard physiological techniques, and the quantity is conceivably measurable through a combination of current injection and multisite recording. The left-hand side of Eq. 5 will tend toward zero when the product of the two terms tends to zero, as happens when one or both of the following conditions are satisfied:

• i) The inner product of the neural activity vectors arising in layer I across any pair of skills tends to zero. Because activities are taken to be positive only, this condition corresponds directly to representations that do not overlap within that layer. If two activity patterns do not overlap, then the two skills use separate sets of weights in transmitting signals from layer I to layer II (Fig. 6A), meaning that changing a weight in W alters the downstream activity for one skill but yields no net change in downstream activity for the other skill.

• ii) The inner product of the change in activity of an output node with respect to the vector of input activity at layer II tends to zero across all skill pairs. This condition is harder to interpret intuitively. Basically, it means that the network has reconfigured itself to exhibit an internal structure that decouples, across skills, the output effects of changing the inputs to the layer, so that weight changes that impact an output for one skill exert no influence on any outputs for the other skills.

Fig. 6.

(A) Two layers of a feed-forward network with associated signals (arrow denotes direction of information flow). See text for definition of terms. (B) A simulation of sharpening of a tuning curve (to movement direction) for a model neuron. The black curve represents a neuron’s tuning in the hyperplastic, noisy network when the learning curve has begun to asymptote. The gray curve represents the same neuron’s tuning curve 20,000 trials later. Although network performance improves minimally over this span, the tuning curve sharpens noticeably. For the hyperplastic, noisy network, the tuning curves of 35% of the model neurons sharpened by at least 10%.

During training, a hyperplastic noisy network will generally increase its orthogonality by reducing the value of both inner products in Eq. 5. Condition i indicates that a tendency toward task specificity of neural activity—as reflected through sharpened neural tuning curves—is a strong neurophysiological prediction that follows directly from the orthogonality constraint. A simulation of the phenomenon for tuning to movement direction in the center–out task is shown in Fig. 6B. In a hyperplastic, noisy network, the neuron’s tuning curve becomes significantly sharper after extensive postasymptotic training, despite the absence of specific sharpening mechanisms, e.g., a recurrent feedback architecture of lateral on-center excitation and off-surround inhibition (37). Intuitively, the idea of enhanced neural selectivity makes sense. An effective way to insulate one skill from the noise of other skills is to segregate—as much as possible—the cell subpopulations responsible for each skill, so that the system autonomously acts to reduce the overlap of its own internal representations. Even if the activity of neurons overlaps significantly across different skills, orthogonality can still be achieved through fulfillment of condition ii. Finally, we note that in more realistic neural networks with feedback across layers and recurrence within a layer, Eq. 5 could not be cast into such a simple form, and the extent to which the same consequences would be expected in more realistic neural networks is considered in SI Discussion.

Discussion

All existing paradigms of biological memory posit the storage of information through the formation and retention of a “synaptic trace”—that is, a novel pattern of synaptic connectivity imprinted through experience. Because these synaptic memory traces are embedded within the context of distributed neural circuits, they can be degraded or interfered with through a variety of means (e.g., damage to the circuit). Nonetheless, current doctrine asserts that the essence of a memory is embodied in the degree to which the constitutive integrity of its original synaptic trace remains intact; ideally, a synaptic trace will remain unaltered from its original conception. Here we argue that, for the case of motor memories, the pattern of synaptic connectivity is perpetually nonstationary and that our view of motor memory formation must be accordingly modified. Mnemonic permanence is to be found not at the level of synaptic structure but, more so, in the patterns of neural activity thereby elicited. With each neuron connecting, on average, to 10,000 other neurons, the nervous system is highly redundant so that a given pattern of neural activity can be actualized by many different patterns of synaptic connectivity. According to our theory, all such solutions are equivalent and, as a result of hyperplasticity and high noise levels, they are randomly interchanged through continued practice of the corresponding motor skill.

The full power of redundancy in driving a hyperplastic system to explore its underlying solution space was understated in the analysis of this paper, because a motor goal was represented as an invariant activation pattern across a set of output neurons (analogous to neurons in the motor cortex). This formulation takes into account only internal redundancy, whereas external redundancies are ignored. If the ultimate objective of a motor act is more broadly construed as accomplishing a task in the environment (38), then additional redundancies arise from motor cortical neurons to spinal motoneurons, from spinal motoneurons to muscle activations, and from muscle activations to joint degrees of freedom to end-effector and task degrees of freedom. These additional redundancies further enhance the flexibility of the system in achieving a desired task goal and may further reduce the identifiable invariance of a motor memory to little more than a circuit-wide configuration that yields the correct input–output mapping.

The hypothesized link between the degree of neural tuning and the level of behavioral expertise potentially resolves one of the most puzzling aspects of motor neurophysiology. Decades of studies have reported a bewildering multiplicity of movement parameters, both high level and low level (e.g., muscle activations, joint torques, hand position, movement direction, movement velocity, movement curvature, serial order, etc.), all prominently represented throughout the motor cortices (39, 40). However, surely the motor system need not—and from a computational efficiency perspective should not (41)—explicitly represent all aspects of the motor behaviors it can perform. A resolution to this paradox lies in the way the experiments are conducted. To test for the representation of a specific movement parameter, a nonhuman primate is deliberately overtrained in behaviors that vary widely across the dimension(s) in which that movement parameter is measured. Regardless of whether or not the movement parameter was recognizably encoded before training, the cortex reorganizes (according to the theory) through training to segregate the neural representations of the practiced behaviors. Thus, the parameter’s heightened saliency in neural response may emerge circularly from the experimental design, with neural representation reflecting, in part, the statistical structure of affordances present in the prevailing environment. If true, neural response properties before a period of intensive behavioral training lasting months or years may be very different from those observed afterward (see SI Discussion for examples).

On the surface, this notion of constant network recalibration may appear inconsistent with the known permanence of certain motor memories even in the absence of practice: One never forgets how to ride a bicycle. However, these two ideas are easily reconciled by considering the level of intrinsic interference between the memorized skill and other routinely performed tasks. If a finely tuned skill exhibits little sensorimotor overlap with common tasks, then the skill will tend to persevere over time, degrading slowly. If, however, the skill’s sensorimotor overlap with daily activity is significant, then routine tasks will interfere with skill maintenance, and performance will be degraded more rapidly (just as practice of D₂ disrupted D₁ in the experiment above). See SI Results for a more detailed analysis of the mnemonic permanence of bicycle riding and other skills, and see SI Discussion for how hyperplastic and noisy networks may even be consistent with declarative memory.

The key hypothesis of the model—and the one likely to generate the most controversy—is hyperplasticity. What, exactly, does it mean for a network to be hyperplastic and how can hyperplasticity be inferred? A quantitative definition is not straightforward, because system-level in vivo learning rates cannot be determined experimentally and, even if they could, the numerical threshold for hyperplasticity varies according to network architecture, input preprocessing, output postprocessing, and other factors (SI Discussion). These caveats aside, five operational definitions of hyperplasticity are provided in SI Results, along with a distinction between developmental plasticity and adult hyperplasticity.

Methods

Two different types of methods are used in this paper: neural network modeling (including the basic effect, simulations of the psychophysical results, and simulations of dendritic spine turnover) and motor psychophysics. The neural network modeling adheres to standard connectionist practices with the exception of using hyperplastic learning rates and high noise levels. See SI Methods for a detailed exposition of all methods. The mathematical derivations are contained in SI Results.