The visual system's intrinsic bias and knowledge of size mediate perceived size and location in the dark

Abstract

Dimly lit targets in the dark are perceived as located about an implicit slanted surface that delineates the visual system's intrinsic bias (Ooi, Wu, & He, 2001). If the intrinsic bias reflects our internal model of visual space – as proposed here – its influence should extend beyond target localization. Our first two experiments demonstrated that the intrinsic bias also influences perceived target size. We employed a size-matching task and an action task to measure the perceived size of a dimly lit target at various locations in the dark. Then using the size distance invariance hypothesis along with the accurately perceived target angular declination, we converted the perceived sizes to locations. We found that the derived locations from the size judgment tasks can be fitted by slanted curves that resemble the intrinsic bias profile from judged target locations. Our third experiment revealed that armed with the explicit knowledge of target size, perceived target locations in the dark follow an intrinsic bias-like profile that is slightly shifted farther from the observer than the profile obtained without knowledge of target size, i.e., slightly more veridical. Altogether, we showed that the intrinsic bias serves as an internal model, or memory, of ground surface layouts when the visual system cannot rely on external depth information. This memory/model can also be weakly influenced by top-down knowledge.

Introduction

A blindfolded observer in the full-cue environment can walk accurately to a previously viewed target located on a continuous ground surface (see Loomis, Da Silva, Philbeck, & Fukusima, 1996 for a review). This remarkable spatial ability can be taken as proof of our fitness in the terrestrial environment (Gibson, 1950, 1979; Sedgwick, 1986). According to the ground theory of space perception, the visual system capitalizes on the ground surface, which often extends continuously from one's feet to the far horizon, as a reference frame for space perception (Gibson, 1950, 1979; He, B. Wu, Ooi, Yarbrough, & J. Wu, 2004; Ooi & He, 2007; Sedgwick, 1986; Sinai, Ooi, & He, 1998). The ground theory of space perception has received significant support from empirical findings over the past two decades (e.g., Bian & Andersen, 2011; Bian, Braunstein, & Andersen, 2005, 2006; Feria, Braunstein, & Andersen, 2003; He et al., 2004; McCarley & He, 2000, 2001; Meng & Sedgwick, 2001, 2002; Ni, Braunstein, & Andersen, 2007; Ooi, B. Wu, & He, 2001, 2006; Ooi & He, 2007; Ozkan & Braunstein, 2010; Philbeck & Loomis, 1997; Sinai, et al., 1998; B. Wu, He, & Ooi, 2004, 2007a&b; J. Wu, He, & Ooi, 2005, 2008). For example, Sinai et al. (1998) discovered that the observer makes accurate egocentric distance judgment when the ground surface is continuous, but becomes inaccurate when the ground surface is discontinuous due to a gap in the ground or an abrupt change in the ground's texture gradient. Clearly, studying how the visual system represents the ground surface holds a key to understanding space perception in the intermediate distance range.

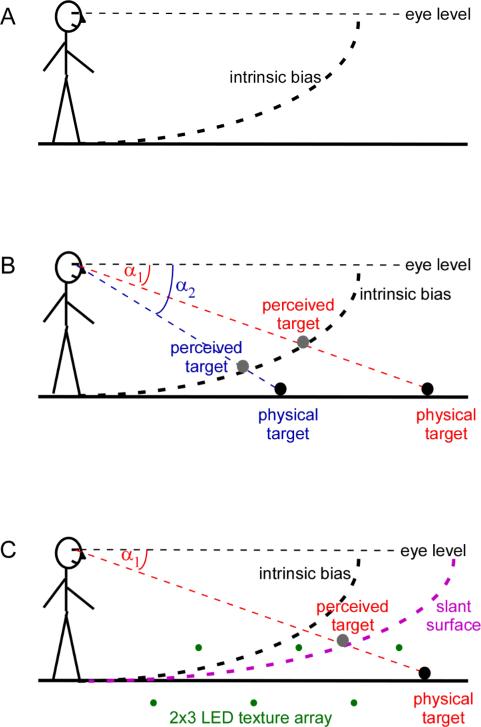
We have proposed that the visual system relies on the external depth information in the visual scene and its internal default, which we call the “intrinsic bias”, to construct a global ground surface representation for space perception (He et al., 2004; Ooi et al., 2001, 2006; Ooi & He, 2007; Wu et al., 2007b). The intrinsic bias is in the form of an implicit slant/curved surface with its far-end approaching the frontoparallel plane (figure 1A). It acts like a representation of the ground surface when the physical ground surface is not visible in the dark (Ooi et al., 2001, 2006). As illustrated in figure 1B, a dimly-lit target on the non-visible ground surface in an otherwise dark room is perceived at the intersection between the eye-to-target projection line and an implicit curved surface (the intrinsic bias). Also, owing to the default (intrinsic bias), the perceived distance of a dimly-lit target in the dark increases as the angular declination of the dimly-lit target decreases (α₁<α₂) (Ooi et al., 2001, 2006; Philbeck & Loomis, 1997).

Figure 1.

Influence of intrinsic bias on space perception in the dark and reduced-cue environments. (A) The intrinsic bias takes the form of an implicit slant/curved surface and it acts like a representation of the ground surface when the physical ground surface is not visible in the dark. (B) A dimly-lit target on the non-visible ground surface in the dark is perceived at the intersection between the eye-to-target projection line and the intrinsic bias. The perceived distance of the dimly-lit target increases as the angular declination of the dimly-lit target (α₁<α₂) decreases. (C) The dimly-lit target in a reduced cue environment is located on an implicit slanted surface that is less slanted than the intrinsic bias.

Normally, the intrinsic bias does not contribute much to ground surface representation when there is adequate depth information on the ground surface. Its contribution becomes significant when the depth information is insufficient in a reduced-cue environment. For example, when the only depth information is derived from an array of LED light spots that are placed on the floor in an otherwise dark room, the observer judges a dimly-lit target located on the level ground as nearer and above the ground. Specifically, the target appears to be located on an implicit slanted surface (figure 1C) that is less slanted than the intrinsic bias measured without extrinsic depth cues (Wu, He & Ooi, 2006). This implicit slanted surface can be taken as the visual system's representation of the ground surface, which is derived from the integration of the intrinsic bias and the relatively weak texture information of the LED light array on the floor (Aznar-Casanova, Keil, Moreno, & Supèr, 2011; Wu et al., 2007b).

The intrinsic bias can also influence the representation of the ground surface in a well-lighted environment if the depth information on the ground surface is not optimal (Feria et al., 2003; He et al., 2004; Sinai et al., 1998; Wu et al., 2004, 2007a). For example, when there exists a texture boundary between the near and far ground surfaces, the far ground surface is represented as slanted with its far end slanted upward. The slant is similar in trend, though lesser in magnitude, than the intrinsic bias (Wu et al., 2007a). We have also shown that the intrinsic bias causes the underestimation of exocentric depth in the well-lighted full cue environment (Ooi & He, 2007; B Wu et al, 2004; J Wu et al, 2008). For example, using a task similar to Gilinsky (1951), we measured perceived exocentric depth on the horizontal ground in the full environment and found a foreshortening of perceived exocentric depth (Ooi & He, 2007). Importantly, our data analysis showed that the judged depth can be fitted well by a function that assumes the horizontal ground surface has a constant slant error due to the influence of the intrinsic bias (Gilinsky, 1951; Ooi & He, 2007).

Owing to its overriding influence, the intrinsic bias can be considered as an essential component of the visual system's internal model (memory) that integrates with external depth information to create our perceptual space (Ooi et al., 2006; Wu et al., 2007b). Furthermore, we propose that the outcome of the internal model is a perceptual space that affects other kinds of space judgments. [In a way, our concept of the intrinsic bias significantly expands on the original idea of the specific distance tendency (Gogel & Tietz, 1973), which is mainly concerned with the perceived egocentric distance of a target in the reduced cue environment.] Working on this assumption, we previously conducted two experiments using respectively, an action task and a perceptual-matching task, to measure the perceived egocentric distance and shape/slant of an L-shaped target in the dark (Ooi et al., 2006). The first experiment, which was similar to an earlier study by Ooi et al. (2001), measured the judged location of a dimly-lit target in the dark by using a blind walking-gesturing paradigm. The blind walking-gesturing task is an adaptation of the blind walking paradigm (Giudice, Klatzky, Bennett, & Loomis, 2012; Loomis, Da Silva, Fujita, & Fukusima, 1992, 1996; Ooi et al., 2001, 2006; Ooi & He, 2006; Philbeck, O'Leary, & Lew, 2004; Philbeck, Woods, Arthur, & Todd, 2008; Rieser, Ashmead, Talor, & Youngquist, 1990; Sinai et al., 1998; Thompson, Dilda, & Creem-Regehr, 2007; Thomson, 1983; Wraga, Creem, & Proffitt, 2000). The task requires the observer to gesture the remembered target height after walking blindly to the remembered distance. We found that the judged target location (x, y) derived from the walked distance (x) and gestured height (y) could be fitted by a slanted curve (the intrinsic bias). The second experiment had the observer perceptually match the length of a fluorescent L-shaped target on the level floor to its width in the dark. This allowed us to obtain the ratio of the judged (perceived) aspect ratio to the physical aspect ratio of the L-shaped target (RAR) (Loomis & Philbeck, 1999; Loomis, Philbeck, & Zahorik, 2002). From the RAR, we derived the perceived optical slant of the L-shaped target using a trigonometric relationship (Ooi et al., 2006; Wu et al., 2004). We found that the L-shaped target was perceived as a slanted surface that reclined on the intrinsic bias derived from the first experiment. These findings thus reveal that the intrinsic bias contributes significantly both to the perceived target location and shape/slant in the dark.

Clearly, the findings of Ooi et al. (2006) lend more weight to the hypothesis that the intrinsic bias is part of the visual system's internal model for space perception. To further this hypothesis, the first two experiments in this paper investigated the influence of the intrinsic bias on the perceived metric size (size, hereafter) of a dimly-lit target in the dark. We adopted an approach similar to Gogel, Loomis, Newman and Sharkey (1985), who used size judgment and head-motion judgment protocols to derive target distances. They found a significant correlation between the two judgments.

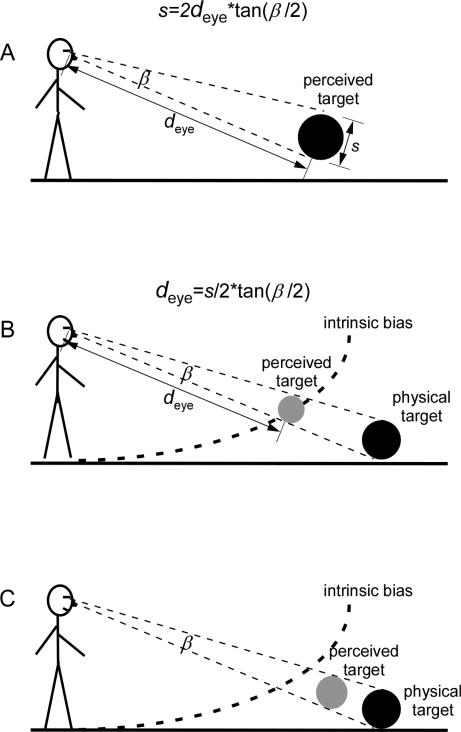
Our first two experiments measure the perceived sizes of dimly-lit targets in the dark at various locations in the intermediate distance range. According to the well-known size-distance invariance hypothesis (SDIH) (Gilinsky, 1951; Kilpatrick & Ittelson, 1953; Schlosberg, 1950), the perceived size of a target is proportional to the perceived target distance. As illustrated in figure 2A, we have the equation,

$$s=2{d_{eye}}^{\ast }\tan (\beta ∕2)$$ (1)

where s and d_eye are the perceived size (diameter) and perceived eye-to-target distance, respectively, and β is the physical angular size of the dimly-lit target that is often assumed to be accurately represented. From equation (1), we can also estimate d_eye from s. Therefore, by measuring s in the dark, we can derive d_eye, which allows us to estimate the perceived target location (figure 2B). Should the intrinsic bias contribute to size perception in the dark, the estimated location will be found about the curved profile of the intrinsic bias as depicted in figure 2B.

Figure 2.

Relationship between perceived distance and perceived size. (A) The well-known size-distance invariance hypothesis (SDIH) states that the perceived size (s) of a target is proportional to the perceived target distance (d_eye). (B) To estimate the perceived target location in the dark, we can derive the perceived eye-to-target distance (d_eye) by measuring the perceived target size (s). Should the intrinsic bias contribute to size perception in the dark, the estimated location will be found about the curved profile of the intrinsic bias. (C) If the knowledge of target size can affect space perception, the perceived target location will deviate from the intrinsic bias that is revealed without the knowledge of target size.

Our third experiment investigates the interaction between the intrinsic bias and knowledge of size on distance judgment in the dark. This investigation was motivated by the observation that the size of a familiar object can affect its apparent distance (see Epstein, 1961). Arguably, the observer could use either the presumed size, or the informed size, of a dimly-lit target in the dark to estimate its distance according to the SDIH (figure 2A). It should be noted that previous studies from our laboratory used dimly-lit targets with a constant angular size and variable metric sizes that were devoid of the familiar size information. Moreover, we did not inform the observers of the actual target sizes (Ooi et al., 2001, 2006). Therefore, the perceived locations in our previous studies were determined by the intrinsic bias rather than the knowledge of target size.

Here, we propose that the knowledge of target size can also affect space perception in the dark (figure 2C). It has been shown that distance information inferred from the knowledge of size (top-down) is weighted by the visual system to determine the responses to distance (e.g., Gogel, 1981; Gogel & Da Silva, 1987; Hastorf, 1950; Predebon, Wenderoth, & Curthoys, 1974). Thus, we predict that for Experiment 3, armed with the knowledge of target size, the profile of judged target locations in the dark will deviate away from those measured without the top-down knowledge of size.

Preliminary reports of this work have been presented in an abstract form (Zhou, He, & Ooi, 2010).

Experiment 1: Size judgment in the dark reveals an intrinsic bias (perceptual matching task)

To reveal whether the intrinsic bias influences size perception in the dark, we used a perceptual size-matching task to measure the judged size (s) of a dimly-lit target at various locations (Holway & Boring, 1941). This allows us to estimate the perceived eye-to-target distance, d_eye=s/2*tan(β/2). Then by relating d_eye (polar coordinates) to the angular declination of the target [perceived angular declination (α) of a dimly-lit target in the dark is accurate], we can derive the judged target location (Ooi et al., 2001, 2006). We predict that the judged target locations will cluster about an implicit slanted curve (profile) resembling the intrinsic bias.

Method

Observers

Eight observers (age = 27.8±1.6 years old; eye height = 158.94 ± 3.79 cm) who were naïve to the purpose of the study participated in all three experiments. All observers had normal, or corrected-to-normal, visual acuity (at least 20/20). They all passed the Keystone Screening test and had at least 20 arc sec stereoacuity. Informed consent was obtained from the observers before commencing the experiment.

Design

The observer's task was to match the size of a matching target that was placed at the eye level from a 1-m viewing distance to a dimly-lit test target at one of eight predetermined locations (below the eye level) in the dark (see cartoon in figure 3). Since observers were likely to make small overestimation errors in perceiving the distance of the matching target at 1-m (Ooi et al, 2006), they might perceive the size of the matching target as larger than its actual size. This means that the matched size of the test target might be smaller than the true perceived size of the test target by a constant ratio, which might lead to a small but constant effect on the estimated distance.

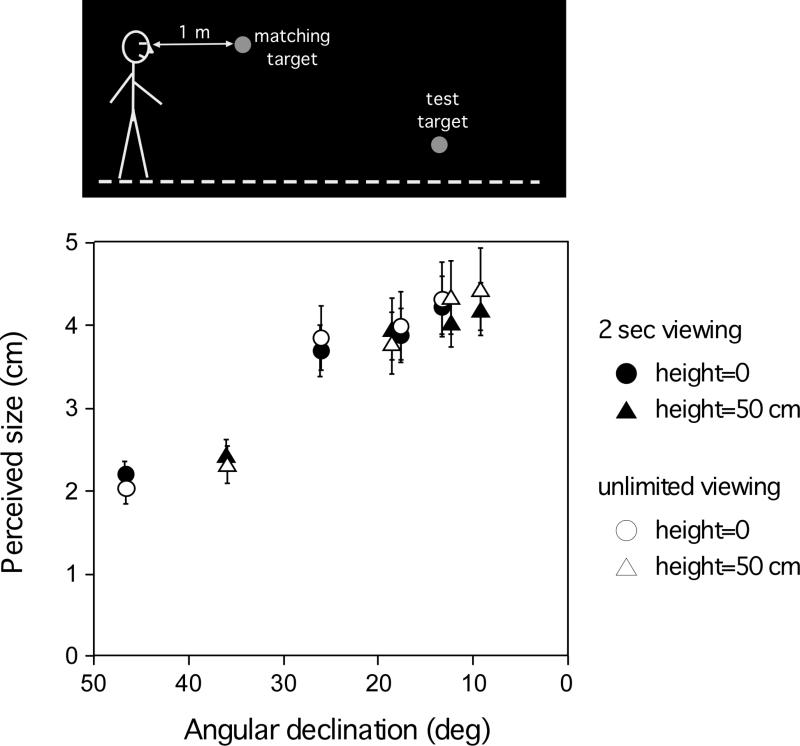
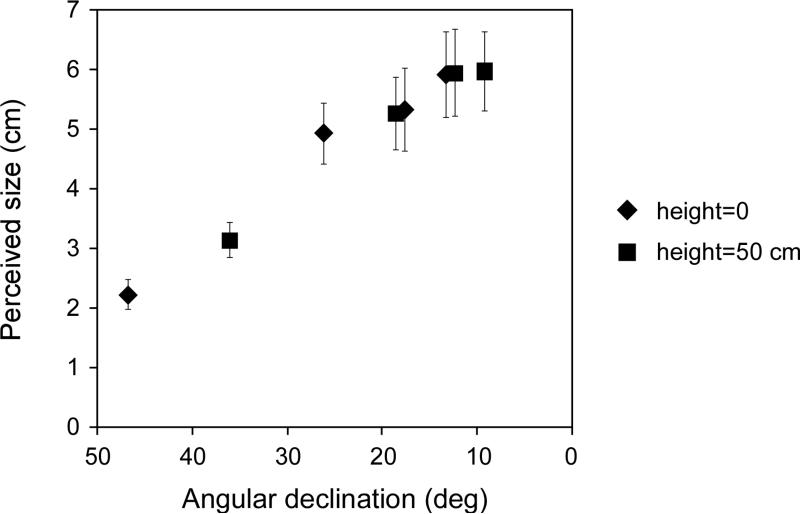
Figure 3.

Experiment 1: Perceived target size from the perceptual matching task as a function of angular declination. The top cartoon illustrates the test setting in the dark. The graph shows that the matched target size increases significantly as the angular declination decreases. The data from the two target heights (on the floor and 50 cm above the floor) overlap, indicating that angular declination, rather than target height, determines the perceived target size in the dark. The matched sizes are similar in the two viewing conditions.

We used a within subject design with three independent variables (viewing duration, distance and height of the test target). The two viewing duration conditions tested were the 2-sec and unlimited viewing conditions. In the 2-sec viewing condition, the observer had to respond after viewing the test target for 2-sec. Whereas in the unlimited viewing duration, the observer was allowed unlimited time to view the test target before performing the perceptual size matching task. [The reason for testing the 2-sec stimulus duration was to reveal if a relatively short viewing time was sufficient to make size estimation.] The 8 target locations comprised all possible combinations of 4 distances (1.5, 3.25, 5 and 6.75m) and 2 heights (0m and 0.5m above the floor). Each test location was measured 4 times. Half a group of observers was tested in the 2-sec viewing condition on the first day and the unlimited viewing condition on the second day, while the other half was tested in the reverse order.

Stimuli

The test and matching targets had the same luminance (0.06 cd/m²) and flicker frequency (5 Hz) and were controlled by a computer. The test target was constructed by placing a green LED in the center of a ping-pong ball and encasing the ball in a small opaque box with an adjustable iris-diaphragm aperture. In this way, the test target always subtended a constant angular size of 0.75 deg when measured at the eye level at all viewing distances. The matching target was constructed by placing a green LED at the center of a spherical lampshade. The front (opening) of the lampshade was covered with a piece of white diffusing paper to ensure even illumination. An iris-diaphragm aperture was attached to the front of the white paper to allow for adjustment of the target size (diameter) during the experiment. In this and the next two experiments, the targets were viewed binocularly in an otherwise completely dark room whose layout and dimension were unknown to the observer.

Procedure

At the start of the experiment, the observer was informed of the viewing condition (2-sec or unlimited duration). He/she was then led in blindfold from a fully illuminated break room to an adjacent waiting area (1.60 × 1.88 m) housed within the test room with carpeted floor. The waiting area was illuminated with a tungsten lamp and located at one end of the test room (9.00 × 1.88 m). While in the waiting area, the observer sat on a chair facing the wall in an opposite direction from the test area and removed his/her blindfold.

To begin a trial, the experimenter stood next to the matching target in the test area and shook a guidance rope that was tied to the opposite walls of the room, to signal to the observer that the trial could begin. Upon feeling the vibration of the rope, the observer turned off the tungsten lamp to put the test room in total darkness. He/she then stood up from the chair and turned around to make his/her way to the designated observation position (starting point) with the help of the guidance rope. At the starting point, he/she verbally indicated that he/she was ready for the trial for the experimenter to switch on the test target.

In the unlimited viewing condition, the observer viewed the test target until he/she felt ready to perform the perceptual matching task, where he/she had to set the size of the matching target to the remembered size of the test target. The observer then asked the experimenter to switch off the test target and switch on the matching target, and instructed the experimenter to increase (adjust) the size of the matching target (from a small size of roughly 0.1 cm in diameter) until it matched the remembered size of the test target. (The matching target was always adjusted from small to big size. This precautionary measure was taken to prevent a possible interference from a large afterimage had the matching target been adjusted from big to small. Keeping the luminance low also minimized the possibility of inducing afterimages.) The observer was told that he/she could ask the experimenter to switch on the test target (after switching off the matching target) for repeated viewing if he/she so desired. However, such a repeated viewing strategy was not permitted in the 2-sec viewing condition. In either viewing condition, once the observer was satisfied with the size setting of the matching target, he/she verbally asked the experimenter to turn off the matching target to end the trial.

The observer then turned around to walk to the chair at the waiting area with the help of the guidance rope. He/she sat on the chair, switched on the tungsten lamp and waited for the experimenter to prepare for the next trial. The observer was not given any feedback regarding his/her performance. Before the formal data collection, the observer received several practice trials to ensure that he/she was comfortable performing the test procedure. During the entire test session (and for Experiments 2 and 3 as well), music was played aloud to prevent possible acoustic cues from indicating the location of the test target, particularly when the experimenter was setting up the target condition after each trial.

Results

Figure 3 plots the mean matched size as a function of the angular declination, respectively, for the 2-sec and unlimited viewing conditions. The matched size increases significantly as the angular declination decreases, as revealed by a two-way analysis of variance (ANOVA) with repeated measures and the Greenhouse–Geisser correction. The statistics for the floor condition is F(1.17, 8.16)=57.70, p=0.000, η²=0.39 and for the 0.5m height condition is F(1.26, 8.84)=47.82, p=0.000, η²=0.42. Furthermore, for the targets with angular declinations between 10 and 20 deg, the data points with similar angular declinations but the two different target heights overlap (circles and triangles), indicating that the perceived size in the dark is determined by the angular declination. This dovetails with our previous findings showing that judged target distance in the dark is determined by the angular declination (Ooi et al, 2001). Figure 3 also demonstrates that the matched sizes are similar in the two viewing duration conditions. A 2-way ANOVA with repeated measures fails to reveal a significant difference; for the floor condition: F(1, 7)=0.02, p=0.902, η²=1; for the 0.5m height condition: F(1, 7)=0.05, p=0.824, η²=1.

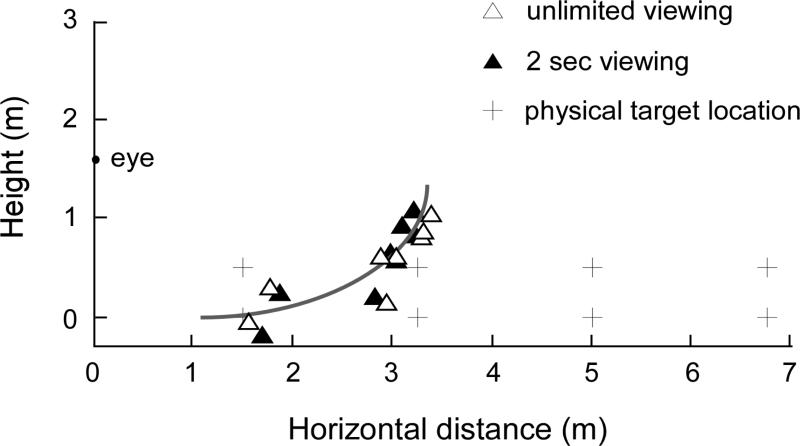
We next transformed the average matched size (s_m) to the perceived eye-to-target distance (d_eye) using the relationship, d_eye=s_m/tan(β/2). With the derived d_eye and the physical angular declination (α) (polar coordinate with the origin at the average eye position on the y-axis), we plot in figure 4 the derived judged target locations for both conditions (filled triangles: 2-sec viewing; open triangles: unlimited viewing). Clearly, the derived judged locations are deviated from the physical target locations represented by the plus symbols. Instead, as predicted, the data exhibit a bias to fall along an implicit curved surface, i.e., the intrinsic bias. This finding resembles those previously found by our laboratory when we measured judged target locations in the dark (Ooi et al., 2001, 2006). Experiment 2 below further strengthens this finding by having the same observers performed size and location judgments simultaneously in the same trial.

Figure 4.

Experiment 1: Derived judged location from the matched target size. We transformed the matched target size (s_m) to perceived eye-to-target distance (d_eye) using the relationship, d_eye=s_m/tan(β/2). The derived judged target location is plotted with the derived d_eye and the physical angular declination (α) (polar coordinate with the origin at the average eye position on the y-axis). The derived judged locations (triangle symbols) are deviated from the physical target locations (plus symbols) and fall instead along an implicit curved surface (the intrinsic bias).

Experiment 2: Size and location judgments measured simultaneously with an action task (blind walk-and-gesture-height-and-size task)

To simultaneously measure the size and location judgments in the same trial, we developed a new task that we call “blind walk-and-gesture-height-and-size”. Essentially, this task is an extension of the blind walking-gesturing paradigm (Ooi et al., 2001, 2006) that is used to measure judged location. As the name of the new task suggests, the observer had to walk blindly to the perceived (remembered) target location, then gesture the perceived height of the target, and indicate the size of the target. The observer gestured the target height with his/her left hand (as the right hand held the guidance rope), and used his/her left thumb and index finger to indicate the size (diameter) of the target. By doing so, we can determine the judged target location based on: (i) the walked distance and gestured height, and (ii) the perceived d_eye using the same relationship as in Experiment 1 [d_eye=s_g/tan(β/2)], where s_g is the gestured target size. We predict that the judged target locations from the action-based performance in this experiment will also be constrained by the intrinsic bias of the visual system.

Method

Design

We used a within subject design with two independent variables, namely, the distance (1.5, 3.25, 5.0, and 6.75m) and height (0, 0.5m above the floor, and at the eye level) of the target. Each location was tested 3 times. The experiment (30 test trials) was completed in a single session.

Stimuli

The observers were tested in the same test environment as in Experiment 1. The same dimly-lit test target (0.06 cd/m², 5 Hz and 2 sec viewing duration) was used in the experiment. However, the angular size of the test target was now 0.85 deg.

Procedure

Before the proper experiment, the observer practiced the blind walking-gesturing task in a bright hallway without any feedback, for the purpose of familiarization in performing the task (Ooi et al, 2001). The observer also received a training session to learn to reliably report the perceived target size (diameter) by using the tips of his/her left thumb and index finger to indicate the target length. A black cardboard pasted with an array of 15 white paper discs of various diameters (1-15 cm) was hung on the wall at a viewing distance of 1 m from the observer. The center of the disc array coincided with the observer's eye level. The experimenter randomly pointed to a disc for the observer to judge for about 2 sec. After which, the observer closed his/her eyes and gestured with his left thumb and index finger the remembered length (diameter) of the disc. The observer then opened his/her eyes to compare the indicated disc length with the real disc for feedback. A typical training session consisted of about one hundred trials, which led to a reasonably accurate and reliable performance.

During the proper test session, and as in Experiment 1, the observer was blindfolded and led by the experimenter from the break room to the waiting area within the test room. A trial began with the experimenter shaking the guidance rope. The observer switched off the tungsten lamp, stood up from the chair, and walked to the starting point (observation position). He/she stood facing the test room and verbally indicated his/her readiness. Thereupon, the experimenter switched on the dimly-lit test target that flickered at 5 Hz for 2 sec. The observer judged the target's location and size, and then pulled a blindfold over his/her eyes, and verbally signaled to the experimenter that he/she was ready to walk. The experimenter immediately removed the target to free up the space for the observer to walk unobstructed and shook the guidance rope, signaling to the observer to begin walking. The observer then walked without hesitation to the remembered target location as he/she held on to the guidance rope with the right hand for safety. Upon reaching the remembered target location, the observer used his/her left hand to indicate the remembered target height and also gestured the remembered target length with his/her left thumb and index finger. Following this, the observer verbally signaled to the experimenter to mark his/her feet location on the floor, measure the gestured height of the left hand, and the length between the left thumb and index finger. The observer then walked back to the waiting area with the aid of the guidance rope and switched on the lamp next to the chair. While facing the wall opposite the test area, he/she removed the blindfold and sat on the chair to wait for the next trial. Meanwhile, the experimenter set up the next target condition. Throughout the experiment, the observer received no feedback regarding his/her performance and music was played aloud.

Results and discussion

Figure 5 depicts the mean judged size as a function of angular declination. The judged sizes from both target heights (floor and 0.5 m) transcribe the same curve, and they increase as the angular declination decreases. This is confirmed by an analysis of one-way ANOVA with repeated measures and the Greenhouse–Geisser correction, F(1.60, 11.22)=21.24, p=0.000, η²=0.23. This trend is similar to that obtained with the perceptual size matching task in Experiment 1 (figure 3).

Figure 5.

Experiment 2: Judged target size from the blind walk-gesture-height-size task as a function of angular declination. The judged sizes from both target heights transcribe the same curve and increase as the angular declination decreases. This trend is similar to that obtained with the perceptual size matching task in Experiment 1 (figure 3).

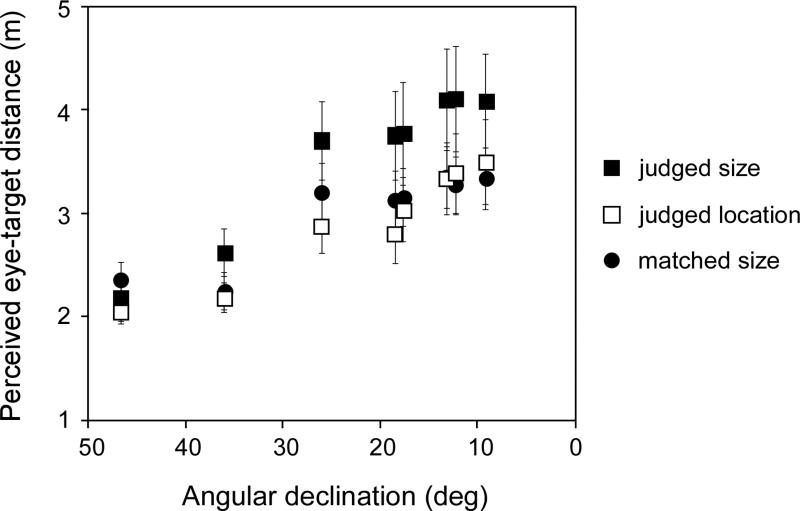
We transformed the judged size (s_g) to d_eye, as in Experiment 1, and plotted the data in figure 6 (filled square). We also calculated d_eye based on the judged target location using the formula, d²_eye =d²_w+(H-h_g)², where d_w and h_g are the walked horizontal distance and gestured height, respectively, and H is the eye height. These derived data are represented by the open square symbols in figure 6. Additionally, we also included the d_eye data from the perceptual size matching judgments of Experiment 1 (filled circles) in figure 6. For clarity, we plotted the judged locations of targets on the floor and 0.5m above the floor with the same symbols since they overlap. Overall, there is a general trend where the perceived d_eye increases as the angular declination decreases. Consistent with this, a 2-way ANOVA with repeated measures and the Greenhouse–Geisser correction reveal a significant main effect of angular declination, F(1.51, 12.81)=25.83, p=0.000; η²=0.22. The perceived d_eye based on s_g from the blind walk-gesture size task (filled squares) appears longer than those based on the judged location from the blind walk-gesture height task (open square) and the perceptual matching task s_m (filled circles). We speculate this could be due to a difference in spatial scaling when judging target size using perceptual vs. action tasks. Nevertheless, statistical analysis (2-way ANOVA with repeated measures and the Greenhouse–Geisser correction) fails to reveal a reliable difference between the two d_eye measures derived from the two types of size judgment tasks and the d_eye from the blind walk-gesture task; main effect of judgment type, F(1.89, 13.20)=2.37, p=0.130, η²=0.943; interaction effect between angular declination and measurement types, F(2.77, 19.41)=2.16, p=0.129; η²=0.20. Importantly, the data from all three types of measurements reveal the same trend (default tendency). This indicates that the intrinsic bias of the visual system plays a large role in determining the perception of size and location in the dark. We also calculated the Pearson Product-Moment Correlations (r) between the d_eye measures from the various tasks based on each observer's judgments. We found r=0.54 (p<0.000, df=62) between the gestured size and matched size, and r=0.70 (p<0.000, df=62) between the walked distance and gestured size.

Figure 6.

Experiment 2: Using the perceived eye-to-target distance (d_eye) as a function of angular declination for comparison among the three different measures from Experiments 1 and 2. First, we transformed the gestured target size (s_g) from Experiment 2 to d_eye (filled square). Second, we calculated d_eye based on the judged target location from Experiment 2 using the formula, d²_eye =d²_w+(H-h_g)², where d_w and h_g are the walked horizontal distance and gestured height, respectively, and H is the eye height (open square). The d_eye data from the perceptual size matching judgments of Experiment 1 are represented by filled circles. Overall, the perceived d_eye increases as the angular declination decreases. The perceived d_eye based on s_g from the blind walk-gesture size task (filled squares) appears longer than those based on the judged location from the blind walk-gesture height task (open square) and the perceptual matching task s_m (filled circles).

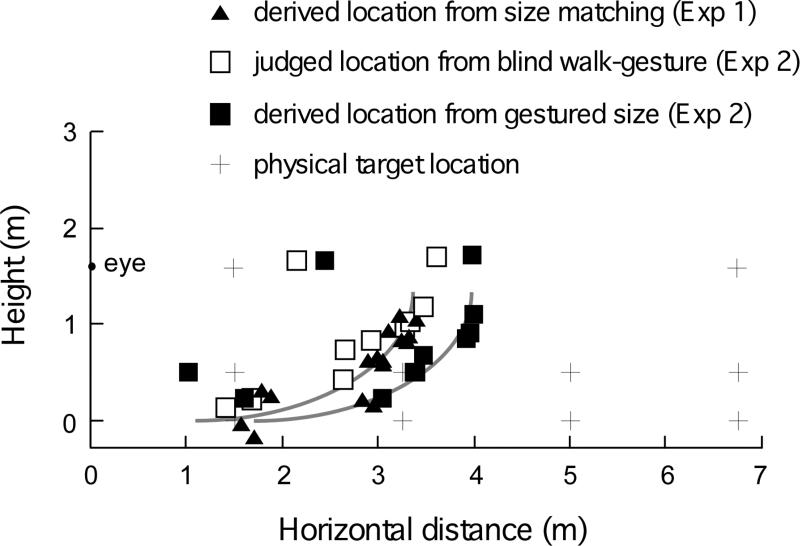
To more directly demonstrate the role of the intrinsic bias, we plot in figure 7 the judged target locations from the blind walk-gesture height task, the derived target locations from the blind walk-gesture size task (s_g) of the current experiment and from the perceptual size matching task (s_m) of Experiment 1. Clearly, the judged locations (open square) and derived locations from the perceptual size matching task of Experiment 1 (filled triangle) cluster together and could be well fitted by the same curve taken from figure 4. The derived locations from the blind walk-gesture size task (filled square) shift rightward, and are also fitted by the same slanted curve. This rightward shift reflects the difference in spatial scaling owing to the different tasks (figure 6). Nevertheless, the data points obtained from the different tasks form a profile that is fitted with the same slanted curve, which is characteristic of the intrinsic bias.

Figure 7.

Experiment 2: Comparing measured and derived judged locations. The graph plots the judged target locations from the blind walk-gesture height task, the derived target locations from the blind walk-gesture size task (s_g) of Experiment 2 and from the perceptual size matching task (s_m) of Experiment 1. The judged locations (open square) and derived locations from the perceptual size matching task of Experiment 1 (filled triangle) cluster together and is well fitted by the same intrinsic bias profile taken from figure 4. The derived locations from the blind walk-gesture size task (filled square) are also fitted by the intrinsic bias profile when shifted rightward.

In the above analysis, we converted both the s_m and s_g to d_eye according to Equation (1), d_eye=s/2*tan(β/2), that is based on the SDIH and assumption of veridical representation of the angular size of the target (β). The outcomes, plotted in figure 6, show that the three sets of data are quite close. However, several studies in the past showed that their empirical data do not conform well to the equation (figure 2a) (e.g., see Gogel & Da Silva, 1987). For example, some data are better fitted by the equation, d_eye=k*s/2*tan(β’/2), where k is a constant and β’ differs from the physical β. It is likely the deviation of the empirical data from Equation (1) in some instances is caused by the fact that perceptual space varies somewhat when the observer engages in different types of perceptual tasks, which require attention to select different visual information. Specifically, that the measured d_eye and s do not follow Equation (1) in the full cue condition is in part due to the size and distance judgment tasks requiring visual attention to select different information from the target and its surrounding environment (ground surface). Whereas attention is more directly focused on the target since there is no distracting visual information in the dark.

It has been shown that the attention selection process can affect the judged egocentric distance and judged length of the target in the full cue condition (Creem-Regehr, Willemsen, Gooch, & Thompson, 2005; Gogel & Tietz, 1977; He et al., 2004; B. Wu et al., 2004; J. Wu et al., 2008). For example, B. Wu et al. (2004) found that egocentric distance is underestimated when the observer only has a limited access to the local ground surface surrounding the target. J. Wu et al. (2008) also found that the length of a rod (in depth) is judged as shorter if the observer attends predominantly to the rod on the ground, than if he/she expands the visual sampling to a larger ground surface area. Indeed, it is very likely that in the everyday task of judging the size of an object on the ground, one often pays more attention to the target without sampling the entire ground surface beyond the vicinity of the target. As a result, the ground surface representation becomes less accurate in comparison to that when one has to judge the target's egocentric distance. In the latter task, when one needs to judge egocentric distance to perform the blind walking task, one often expands one's attention globally from the near to far (up to the target) region of the ground surface. These considerations thus suggest that judged size and distance measurements result in two different outcomes of ground surface representation, and therefore, it is reasonable that their relationship deviates from Equation (1). However, the impact of the selection process on space perception becomes less significant in the current study where the ground surface is not visible in the dark. In fact, the dark environment causes the visual system to rely on the retinal image of the dimly-lit target and the intrinsic bias to judge both size and distance. This may explain why our data from the size and location judgments are quite close.

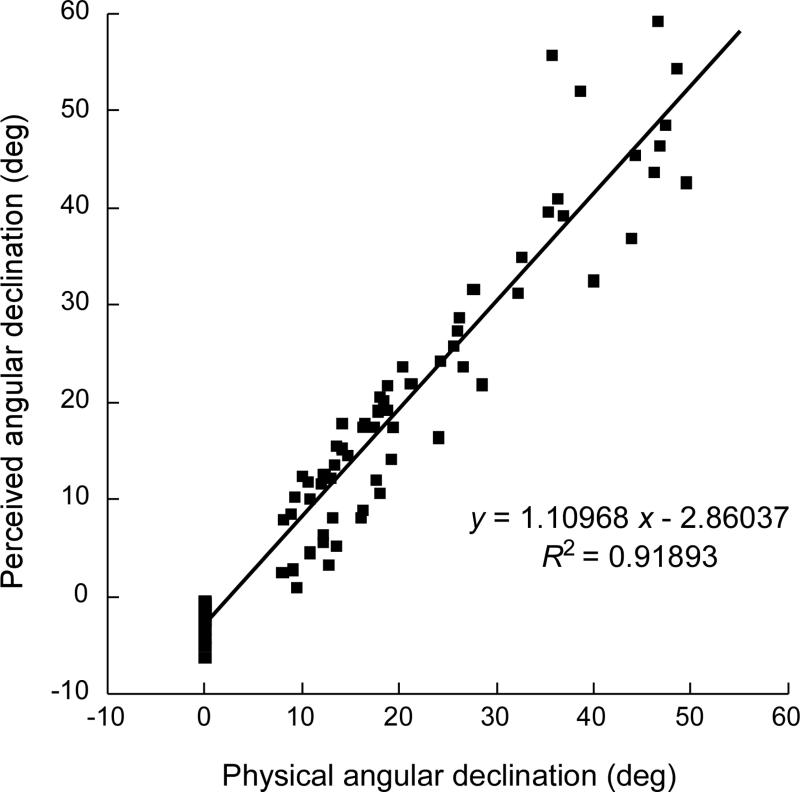
Finally, we plotted each observer's average judged angular declination at each target location (based on the blind walk-gesture height task) as a function of the physical angular declination of the target in figure 8. Clearly, they can be fitted well by a regression line with a slope close to unity (y=1.11x-2.86, R²=0.919). This confirms that observers accurately perceive the angular declination in the dark (Ooi et al., 2001, 2006).

Figure 8.

Experiment 2: Physical versus perceived angular declination. We correlated each observer's average judged angular declination at each target location (based on the blind walk-gesture height task) with the physical angular declination of the target. The regression line has a slope close to unity suggesting that the observers accurately perceived the angular declination.

Experiment 3: The explicit knowledge of target size and the intrinsic bias affect space perception in the dark

While the intrinsic bias largely influences size perception in the dark when the available visual information is minimal, other factors can also affect perceived size. Here, we examined the influence of explicit knowledge on judged target size in the dark. Since we are testing in the dark, we predict that the distance information derived from the explicit knowledge of target size (familiar size cue) along with the intrinsic bias determine the final perceived target size, and hence, the perceived target location. We measured the observer's judged target location using the blind walking-gesturing task in a same-angular-size condition and a same-physical-size condition. In the latter condition, the observer knew the actual physical size of the target.

Method

Design

We used a within subject design with three independent variables (target size conditions, distance and height of the test target). The two target size conditions (same-angular-size and same-physical-size) were tested in two separate sessions over two days. Half a group of observers were tested first in the same-angular-size condition (session 1), followed by the same-physical-size condition (session 2). The other half of the group was tested in the reverse order. In session 1 (same-angular-size condition), the angular size of the target was kept at 0.21 deg and the observer was informed that the physical size of the target would not be the same. In session 2 (same-physical-size condition), the observer was shown a white paper disc with the same size as the test target (2.5 cm), and informed that the target size would remain at the same size as that of the paper disc. Effectively, the smallest angular size of the target in the same-physical-size condition was about 0.21 deg when the target was placed at a distance of 6.75m. Overall, the angular size of the target used in the same-physical-size condition was either larger than, or equal to, the angular size of the target used in the same-angular-size condition (0.21 deg). Additionally, in session 2, unbeknownst to the observer, we randomly interspersed catch trials with two targets of different sizes (1.4 or 4.45 cm).

For each condition, four target distances (1.5, 3.25, 5 and 6.75 m) and three target heights (0, 0.5 m and eye height) were tested. The targets used in the catch trials for the same-physical-size condition were located at the eye height and two distances (5.0 and 8.9m, respectively, subtending 0.16 and 0.29 deg in angular size). Each test location and catch trial location was tested three times.

Stimuli

Other than the various target sizes reported above, the target's design was the same as that in Experiment 1 (0.16 cd/m², 5 Hz). The 2 sec target duration was employed.

Procedure

We follow the same test procedure as in Experiment 2 but with two exceptions. We asked the observers to perform the blind walking-gesturing task, instead of the blind walk-and-gesture-height-and-size task. We also informed the observers of the size of the target (fixed or variable physical size).

Results and discussion

Figure 9 reveals the judged target locations from the same-angular-size (filled circle) and the same-physical-size (open circle) conditions. The data from each condition cluster about an implicit slanted curve, suggesting that the perceived locations are largely determined by the intrinsic bias. This finding is notable because until now, our studies have always used targets of the same angular size. Here, we demonstrate that even when the angular size changed as the target of the same physical size was located to a different distance, the data point can be fitted by a slanted curve.

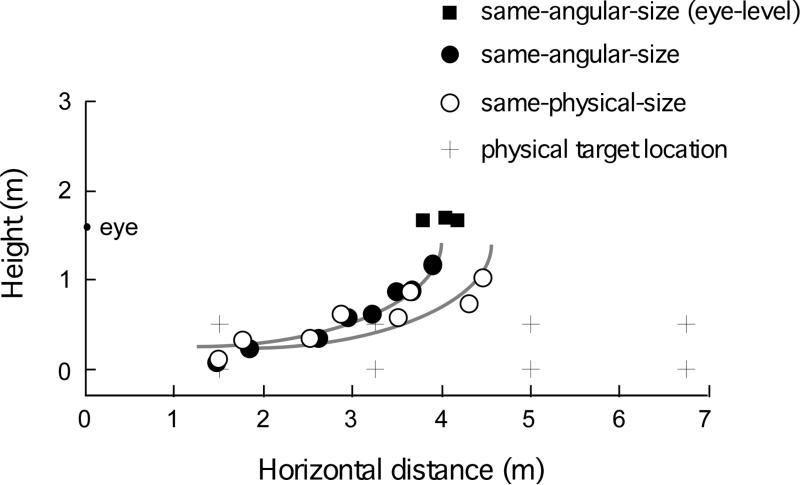
Figure 9.

Experiment 3: Judged target locations from the blind walking-gesturing task. Generally, the data from the same-angular-size (filled circle) and same-physical-size (open circle) conditions cluster about an implicit slanted curve, suggesting that the perceived locations are largely determined by the intrinsic bias. However, a closer comparison between the two conditions reveals that the data from the same-physical-size condition (open circle) are shifted rightward, due to the far targets being perceived as farther than those in the same-angular-size condition (filled circle). This indicates the impact of explicit knowledge of target size (figure 2c). The filled squares from the left to right represent the data from the same-angular-size condition where the targets were placed at the eye level and at distances, 3.25, 5.0, and 6.75m, respectively.

A comparison between the same-angular-size and same-physical-size conditions reveals that the data from the same-physical-size condition are shifted rightward, due to the far targets in this condition being perceived as farther than those in the same-angular-size condition. The near targets in both conditions are judged at roughly similar locations. Our finding at the near distance has some resemblance to Mershon and Gogel (1975)'s study, which also did not show the effect of familiar size on visually perceived distance in an illuminated small rectangular room (34.3 × 55.9 × 62.2 cm).

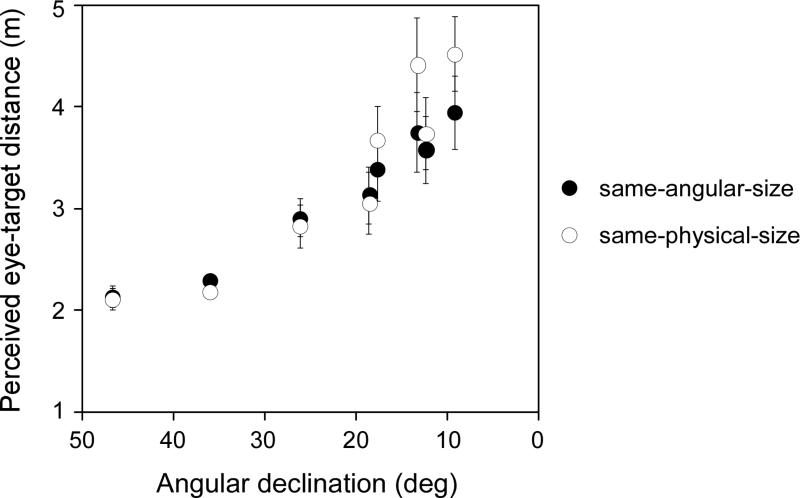
For the far target that is located beyond the near space, i.e., a target with a small angular declination, the explicit knowledge of the target size exerts a greater impact on judged location. This is likely caused by the lack of reliable near depth information and the relatively large variance (uncertainty) of distance specified by the intrinsic bias when the target's angular declination is small (far distance). For a more quantitative description of the effect of size knowledge, we derived the perceived eye-to-target distance (d_eye) from the formula, d²_eye=d²_w+(H-h_g)², where d_w and h_g are, respectively, the walked horizontal distance and gestured height and H is the eye height. Figure 10 plots d_eye as a function of the physical angular declination (α) of the target for both conditions (filled circles: same-angular-size; open circles: same-physical-size). Clearly, d_eye increases as α decreases. This is confirmed by a 2-way ANOVA with repeated measures and the Greenhouse–Geisser correction that reveal a significant main effect of α, F(2.28, 15.96)=35.84, p=0.000, η²=0.28. Notably, d_eye is significantly longer (farther) in the same-physical-size condition than in the same-angular-size condition and their difference increases as α decreases; main effect of test condition, F(1, 7)=5.78, p=0.047, η²=1; interaction effect (angular declination × test condition), F(3.30, 23.08)=4.65, p=0.009, η²=0.41. Nevertheless, the graph also demonstrates that the effect of familiar size on distance perception does not appear robust. If the visual system could fully utilize familiar size to determine the target distance, the perceived distance would be veridical. But in actuality, the perceived d_eye in the same-physical-size condition is far shorter than the physical d_eye (figure 9).

Figure 10.

Experiment 3: Derived perceived eye-to-target distance. We derived the perceived eye-to-target distance (d_eye) from the formula, d²_eye=d²_w+(H-h_g)², where d_w and h_g are, respectively, the walked horizontal distance and gestured height and H is the eye height. The graph plots d_eye as a function of the physical angular declination (α) of the target for both conditions (filled circles: same-angular-size; open circles: same-physical-size). Clearly, d_eye increases as α decreases and is longer (farther) in the same-physical-size condition than in the same-angular-size condition, and their difference increases as the angular declination decreases.

One might note that in the same-physical-size condition, the angular size of the target at the far distance is smaller than that at the near distance. Consequently, is it possible that even without the explicit knowledge of the target's physical size, our observers’ distance judgments were simply affected by the difference in the target's angular size? For example, when one compares the filled circles in figure 10 (Experiment 3) with the open squares in figure 6 (Experiment 2), one can note the data represented by the filled circles are moderately larger in judged eye-to-target distances [Main effect of angular size of the target: F(1, 7)=4.74, p=0.066, η²=1; Main effect of angular declination: F(1,63, 11.43)=27.09, p=0.000, η²=0.23 (Greenhouse–Geisser correction); Interaction effect: for the 0.5m height condition: F(3.89, 27.26)=1.83, p=0.153, η²=0.56; A 2-way ANOVA with repeated measures]. This could be due to the smaller angular size of the target in Experiment 3 (0.21 deg) than in Experiment 2 (0.85 deg) (e.g., Gajewski et al, 2010). Nevertheless, this moderate effect of the target's angular size may not be sufficient to override the influence of the explicit knowledge of the physical target size for two reasons. First, the target with the smallest angular size in the same-physical-size condition in Experiment 3 was located at 6.75m (and 0.5m above the floor). At this distance, its angular size was the same as that of the target in the same-angular-size condition (0.21 deg). Yet, the judged distance at this location (6.75m, 0.5m) in the same-physical-size condition was longer than that in the same-angular-size condition. Second, for the remaining test locations, the angular size of the target used in the same-angular-size condition was smaller than the angular size of the target used in the same-physical-size condition. However, we did not find the judged distance to be longer in the same-angular-size condition.

We also analyzed the perceived angular declination (α) of the targets in the two conditions (figure not shown) and found that they overlap [t(63)=0.47, p=0.64]. This indicates that the knowledge of size does not influence the perceived angular declination. Furthermore, we obtained the regression lines between the perceived and physical angular declinations for both test conditions with the least squares method [same-angular-size: y=1.05x-1.67, R²=0.88; same-physical-size: y=1.02x-1.33, R²=0.89]. We found the slopes in both conditions are close to unity. This finding is similar to those of Experiment 2 and of the previous findings from our laboratory (Ooi et al., 2001, 2006; J Wu et al, 2005).

We have consistently observed that the judged angular declination derived from the blind walking-gesturing tasks is largely veridical. This occurs in the dark environment (Ooi et al., 2001, 2006; J Wu et al, 2005), in the reduced cue condition with sparse texture background in an otherwise dark environment (J. Wu et al, 2006), and in the full cue environment (Ooi & He, 2006). A similar finding is obtained using the modified blind walking-gesturing task wherein the observer used a rod to point to the perceived target location (Guidice et al, 2012; Zhou et al, 2012). It should be emphasized that in the above-mentioned studies, the judged angular declination was derived from action-based tasks that required the observers to judge the target's location. The angular declination finding from these action-based tasks differ from the finding based on the verbal report task (e.g., Durgin & Li, 2011).

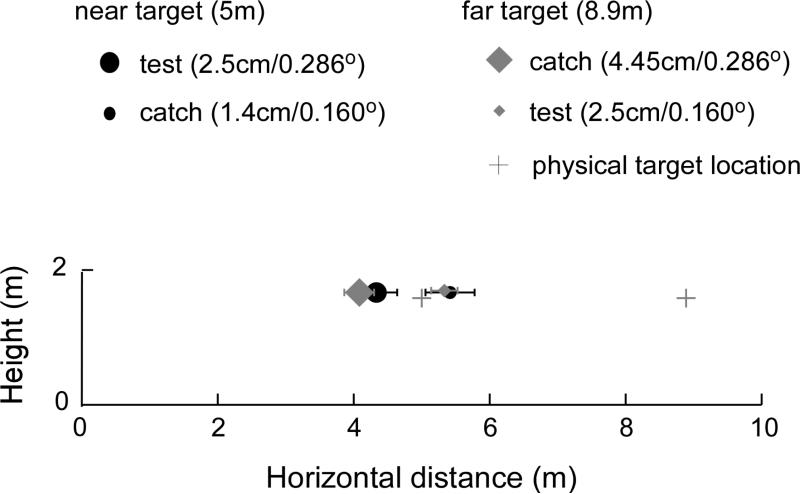
Finally, for the data in the same-physical-size condition, we compared the performance in the catch trials with those from the test trials at the same target distance and eye level. For the near target distance of 5.0 m, the target sizes were 2.5 cm (0.29 deg) and 1.4 cm (0.16 deg), respectively, in the test and catch trials. For the far target distance of 8.9 m, the target sizes were 2.5 cm (0.16 deg) and 4.45 cm (0.29 deg), respectively, in the test and catch trials. (Recall that we purposely misinformed the observers of the two sizes of the targets in the catch trials. They were told that all targets in the condition were 2.5 cm.) The average judged locations plotted in figure 11 show distance underestimation for both the test and catch targets. Also revealing, is that the two targets with the same angular size are perceived at the same distance despite the difference in their physical distances. Targets with the smaller angular size (0.16 deg) are perceived as farther. We suggest an explanation for this is related to our manipulation of the observer's knowledge. That is, with the explicit instruction that all targets had the same size (2.5 cm), the observer then relied on the angular size cue to judge the target distance in accordance with the SDIH. Specifically, with d_eye=s/2*tan(β/2) and s being constant, d_eye only depends on β. Intuitively, the observer might have assumed that when the physical size of the target was the same, seeing the target with a smaller retinal image size indicated that the target was farther away.

Figure 11.

Experiment 3: Catch-trials in the same-physical-size condition. The graph compares the average judged locations in the catch trials with those from the test trials at the same target distance and eye level. Distances are underestimated with both the test and catch targets. Furthermore, catch and test targets with the same angular size are perceived at the same distance despite the difference in their physical distances (and physical sizes), with targets having the smaller angular size being perceived as farther. This reveals the effect of angular size on perceived distance.

General Discussion

Previous investigations from our laboratory have found that perceived surface shape/slant as well as egocentric distance in the dark are largely determined by the visual system's intrinsic bias (Ooi et al., 2001, 2006). In this paper, we capitalized on the well-known relationship between perceived size and egocentric distance as predicted by the SDIH (see Epstein, 1961; Gogel and Da Silva, 1987; Sedgwick, 1986) to reveal that the visual system's intrinsic bias largely influences space perception of size and distance in the dark. In addition, we showed in our third experiment that space perception in the dark can also be moderately affected by the knowledge of object size. Together, our findings support the notion that the intrinsic bias is a special state of the visual system's internal model that constructs perceptual space based on the ground surface representation. There is a considerable wealth of empirical evidence showing that the ground surface representation is often used as the reference frame for space perception in the intermediate distance range. In particular, varying the configurations of the ground surface, or the relationship between the observer and the ground surface can alter space perception (e.g., Feria, et al., 2003; He et al., 2004; Mark, 1987; Meng & Sedgwick, 2001, 2002; Ooi et al., 2007; Sinai et al., 1998; Wu et al., 2004, 2007b). Furthermore, it has been shown that our visual system is more efficient in representing the ground-like surface than the ceiling-like surface, wherein less depth foreshortening is observed on the ground-like surface (Bian & Andersen, 2011; Bian et al., 2006). No doubt, these findings provide support for J. J. Gibson's ground theory of space perception.

Delving into a computational-based explanation of space perception, He and Ooi (2000) proposed that the visual system uses a Quasi-2D coding strategy. With this strategy, the visual system employs the large background surface, rather than the 3D Cartesian coordinate, as a reference frame to code object locations. Effectively, by employing the large background surface, whether it be a plane (2D) or curved surface (quasi-2D) as a space reference frame, the visual system needs only two, not three, coordinates to locate an object on the surface. Thus, adopting the Quasi-2D coding strategy allows the brain to reduce the cost of coding object locations in 3D. This is possible given that most objects that we frequently interact with in our ecological environment (terrestrial) are located on, or supported by, a large background surface. These surfaces, such as the ground surface, provide ample reliable depth information (e.g., texture gradients) (Gibson, 1950; Sedgwick, 1986). Indeed, the preference to use a quasi-2D strategy is found in other visual psychophysical observations related to motion, attention deployment, binocular depth perception, memory, and visual search (e.g., Bian et al., 2006; Gillam, Sedgwick, & Marlow, 2011; Glennerster & McKee, 1999; Hayman, Verriotis, Jovalekic, Fenton, & Jeffery, 2011; He & Nakayama, 1994, 1995; He & Ooi, 2000; Madison, Thompson, Kersten, Shirley, & Smits, 2001; McCarley & He, 2000, 2001; Ni et al., 2007). In space perception, when the ground surface is not visible in the dark, the visual system does not simply assign a random 3-D Cartesian coordinate to the dimly-lit target. Rather, in accordance with the Quasi-2D coding strategy, it defaults to the intrinsic bias that functions like the ground surface representation for the dimly-lit target to rest upon (Ooi et al., 2001, 2006).

The intrinsic bias possibly originates from one's past experience with the statistical properties of the natural scenes, where humans, animate and inanimate objects are either directly, or indirectly, supported by the ground (Gibson, 1979; McCarley & He, 2000; Sedgwick, 1986). Consequently, when the ground is not visible, the visual system capitalizes on the intrinsic bias to act as a reference frame for an “educated” guess of the target's location (Ooi et al, 2001; Yang & Purves, 2003; Zhou et al, 2012). The utility of the intrinsic bias may extend beyond scene representation of visual stimuli. One possibility to be investigated is whether it serves as a framework from which memory-based scene representations can be built.

Along this line of thinking, we speculate that at the phenomenological level, our visual space often appears as an empty space enclosed by large surfaces comprising the sky and ground surface. It is this empty space that constitutes our phenomenological space, and perhaps, gives rise to the concept of space. In this regard, the visual system's intrinsic bias affords us the impression or awareness of the empty space around us when no visual information is available (e.g., in the dark). This suggests that our perceptual space is the outcome of the visual system's internal model, or memory, of the external world that relies heavily on assumptions or ideas/knowledge (Kant, 1787/1963).

Arguably, lawful geometrical relationships such as the SDIH are assumptions or ideas/knowledge adopted by the visual system for space representation. They can be used by the visual system not only for constructing the ground surface representation (reference frame), but also for localizing objects within the perceptual space (using the relative positions between the objects and the reference frame). Observance of the lawful geometrical relationships by the visual system helps to ensure that objects appear stable within the perceptual space. These conjectures, however, are occasionally challenged by empirical observations where the space judgment data do not exactly follow the geometrical laws.

For example, the SDIH has been questioned because various empirical studies showed that the judged distance and size of the target did not follow the quantitative prediction of the SDIH (e.g., Gogel & Da Silva, 1987; Kilpatrick & Ittelson, 1953). Furthermore, our current Experiment 2 (figure 6) reveals that the perceived eye-to-target distances based on the judged locations (open squares) do not coincide with those derived from the gestured sizes (filled squares). Nonetheless, these findings to the contrary may not necessarily discount the SDIH when we take the following reasoning into consideration. Namely, perceptual judgments are determined by both the perceptual (visual) representation operation and response operation. This raises the possibility that experimental studies that reported non-conformity with the SDIH could be traced to the idiosyncrasy of the response operation. Notably, the perceptual process underlying the task of judging target location (egocentric task) in our Experiment 2 differs from the one underlying the task of judging size (exocentric task) (e.g., Loomis et al, 1996; Loomis & Philbeck, 2008). This suggests that the difference between the open and filled squares in figure 6 could be attributed to the two underlying response processes (hand gesturing and walking) that have different spatial scales.

In addition, the two perceptual processes underlying egocentric and exocentric tasks also differ in their operations for selecting information. Our laboratory has previously shown that the accuracy of the global ground surface representation (i.e., perceptual space) depends on how the visual attention system selects the depth information on the ground surface (He et al, 2004; Wu et al, 2004; Wu J et al, 2008). For example, judged target distance (D_c) with the blind walking (egocentric) task is mainly accurate when the visual attention system samples a large ground surface area extending from the feet to the target for global surface representation (He et al, 2004; B Wu et al, 2004; J Wu et al, 2008). But when asked to judge the size (S) or local depth of the target (exocentric task), the observer often focuses attention more on the target and the local ground area immediately surrounding the target. Doing so prevents the visual system from accurately representing the global ground surface. As a result, this would lead to an inaccurate coding of egocentric distance (D_i). In theory, the relationship between S and D_i should be determined by SDIH if both egocentric and exocentric tasks were performed in the same experiment. In reality, however, one usually measures S in one experiment (task), and measures judged egocentric distance in a different experiment using tasks such as blind walking (leading to D_c, which is more veridical). In this case, it is reasonable that S and D_c do not strictly obey the SDIH. The abovementioned factor of selection of depth information on the ground surface can also be used to explain why the data obtained in the dark (no visible ground surface) fit the SDIH better than those obtained in the light (Wu J. et al, 2008).

Admittedly, while our finding is qualitatively consistent with the SDIH, it is uncertain whether the perceptual space is precisely dictated by the SDIH. However, there is a persuasive argument for the visual system to adopt the SDIH, as well as other lawful geometrical relationships, to construct the perceptual space. This is because the main function of the perceptual space is to guide and direct motor actions in the real 3-D environment, which follow the lawful geometrical relationships. By adopting compatible spatial coding mechanisms for the perceptual space and the motor system (action space), the brain can achieve better efficiency (Fitts & Deininger, 1954).