Abstract
Closed-loop insulin delivery continues to be one of most promising strategies for achieving near-normal control of blood glucose levels in individuals with diabetes. Of the many components that need to work well for the artificial pancreas to be advanced into routine use, the algorithm used to calculate insulin delivery has received a substantial amount of attention. Most of that attention has focused on the relative merits of proportional-integral-derivative versus model-predictive control. A meta-analysis of the clinical data obtained in studies performed to date with these approaches is conducted here, with the objective of determining if there is a trend for one approach to be performing better than the other approach. Challenges associated with implementing each approach are reviewed with the objective of determining how these approaches might be improved. Results of the meta-analysis, which focused predominantly on the breakfast meal response, suggest that to date, the two approaches have performed similarly. However, uncontrolled variables among the various studies, and the possibility that future improvements could still be effected in either approach, limit the validity of this conclusion. It is suggested that a more detailed examination of the challenges associated with implementing each approach be conducted.
Keywords: artificial pancreas, closed-loop insulin delivery, continuous glucose monitoring, continuous subcutaneous insulin infusion
Introduction
The development of a closed-loop insulin delivery system linking continuous glucose sensors with insulin pumps is widely acknowledged as one of the most promising strategies for achieving near-normal control of blood glucose levels in individuals with type 1 diabetes. Achieving what would be an artificial β-cell will require a substantial effort from individuals with diverse backgrounds. Research into many of the components requires specialized knowledge and often attracts individuals with similar backgrounds. An exception is the insulin delivery algorithm, which often attracts engineers who are trained in modeling and control systems but have little or no medical training, and clinicians who are trained in managing diabetes but have no formal training in modeling or control theory. The latter will often lack the background to evaluate theoretical arguments put forth by engineers as to why a particular control algorithm should or should not be used for calculating insulin delivery. In the cases where engineers disagree, the question for the clinician is how to make an informed choice about competing narratives.
This article presents one-half of an ongoing debate regarding the relative merits of model-predictive control (MPC) versus proportional-integral-derivative (PID) control. Only the arguments favoring PID control are presented; however, a companion article outlining the arguments favoring MPC has been prepared by my colleague Dr. Wayne Bequette1 and appears in this issue of Journal of Diabetes Science and Technology. We both agree that PID and MPC should both be considered as approaches rather than as specific algorithms. This article will focus on the PID algorithms I have developed with my colleagues.2–8 This version did not originate as a “PID” algorithm per se,9 but rather as a model of β-cell insulin secretion,10,11 referred to as “physiologic insulin delivery.” It was, however, first implemented2 using only the proportional, integral, and derivative terms needed to fit the β-cell response to a hyperglycemic clamp.12 Although it was later modified to include terms emulating cephalic-phase insulin release3 and the effect of insulin per se to inhibit insulin release,4 the term “PID” in this article can be taken to mean “proportional integral derivative.”
Returning to the question of how an individual without training in control theory might make an informed choice regarding competing control algorithms, the question is not as straightforward as might appear on initial reading. The obvious answer is with a prospective randomized clinical trial that will compare the two approaches; however, as both PID and MPC algorithms come in multiple flavors, such a trial would necessarily need to focus on a specific MPC algorithm and a specific PID algorithm. For the comparison to be meaningful, each algorithm would need to be optimized to achieve the same a priori agreed-upon outcomes. Optimizing control algorithms is not a straightforward engineering task and it is unlikely there will be agreement as to which clinical outcomes should be used to assess performance. There is little agreement on what an ideal meal response should look like or how to factor in the use of supplemental carbohydrate to prevent hypoglycemia, or the use of open-loop meal boluses to prevent postprandial hyperglycemia, when comparing algorithms.
Review of Available Clinical Data
A comparison of the first studies using the Medtronic PID algorithm (Figure 1A) with the initial reports of MPC (Figure 1B; data extracted from published reports using FindGraph version 2.281, Uniphiz Lab) shows that good control can be achieved with either approach. Throughout this article, the focus will be on breakfast, as this tends to be the most difficult meal to control. Controllers that perform well during breakfast can be expected to perform well during other meals and during nighttime when no meals are consumed. The breakfast response with the Medtronic PID algorithm improved as modifications to the algorithm were introduced in the first three studies. Peak postprandial glucose levels declined from ~250 to 180 mg/dl, and levels 3–4 h postprandial became more stable. Meal responses obtained with MPC by teams comprising investigators at the University of Virginia and Padova and at Boston University and Massachusetts General Hospital13–16 (Figure 1B) generally showed the peak breakfast response to be similar to the initial PID study2. Still, comparing meal responses across studies can be confounded by differences in meal size, and averaging data inevitably results in peak postprandial values lower than the average of individual peak values. To investigate this further, the mean and standard deviation of individual breakfast meal responses were extracted from the published data (Figure 1C) and normalized to meal size (Figure 1D; results shown as mean and 95% confidence interval). From this analysis, significant differences in the peak response can be observed among the studies, but given the variability among the studies, it is hard to argue a clear advantage with either approach.
Figure 1.
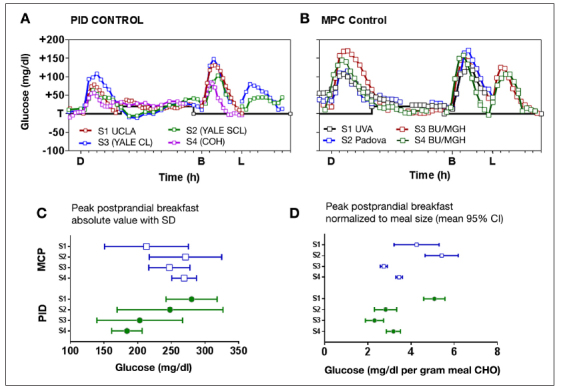
Comparison of initial PID and MPC studies. (A) PID study 1 conducted at University of California, Los Angeles without meal bolus;2 studies 2 and 3 conducted at Yale with (semi-closed loop) and without (closed loop) one-third meal bolus (randomized);3 and study 4 conducted at City of Hope with fixed meal bolus (2 U).4 (B) Model-predictive control study 1 conducted at University of Virginia,13 study 2 conducted in Padova,14 and studies 315 and 4 16 conducted at Boston University/Massachusetts General Hospital. Breakfast size in study 4 is assumed to be the same as in study 3, as per-day carbohydrate load was reported without delineating separate amounts by meal.16 (C) Mean and standard deviation of individual breakfast meals shown in (A) and (B). (D) Mean and 95% confidence interval normalized to meal carbohydrate amount. UCLA, University of California, Los Angeles; CL, closed loop; SCL, semi-closed loop; COH, City of Hope; S1, study1; S2, study 2; S3, study 3; S4, study 4; UVA, University of Virginia; BU/MGH, Boston University/Massachusetts General Hospital; SD, standard deviation; CI, confidence interval; CHO, carbohydrate.
In addition to meal size, there are other uncontrolled factors in the analysis of Figure 1, one is the fat content in individual meals. With PID control, high-fat dinners have been shown to result in substantially elevated meal responses compared with low-fat dinners with identical carbohydrate content (Figure 2A, green versus blue curves, both obtained with PID control)5. This might be explained by an effect of free fatty acids to inhibit insulin’s ability to suppress hepatic glucose output,17 but irrespective of the mechanism, the result suggests that normalizing meal responses to the size of the carbohydrate load is a less-than-perfect approach to comparing meal responses. Absent a correction for carbohydrate or fat content, the dinner response with PID control5 was lower in this study than the dinner response obtained by Russell and coauthors16 with MPC (black line), and the reverse was true during breakfast.
Figure 2.
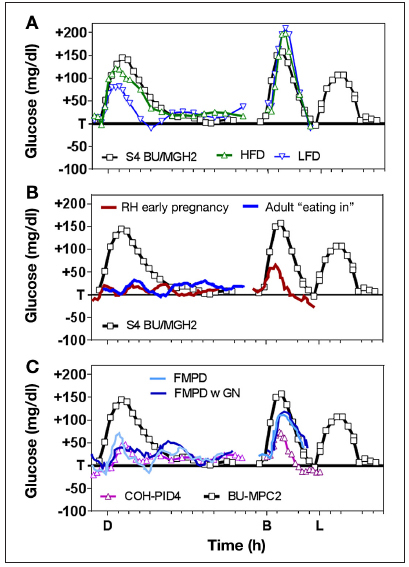
(A) Effect of fat content in closed-loop PID meal response5(high-fat dinner shown in green curve, with low-fat dinner with identical carbohydrate shown in blue) together with response obtained with MPC in a study by Russell and coauthors16 without use of meal boluses (black curve). (B) Same MPC curve from the study by Russell and coauthors16 shown in panel A (black line) together with MPC curves obtained from studies performed by Hovorka and coauthors18,19 with open-loop meal boluses. (C) Use of glucagon in closed-loop control fading memory proportional derivative control with and without glucagon20 (blue and light blue lines) with PID control obtained with insulin feedback4 and MPC results without meal bolus.16S4, study 4; BU/MGH, Boston University/Massachusetts General Hospital; HFD, high-fat dinner; LFD, low-fat dinner; FMPD, fading memory proportional derivative; GN, glucagon; COH, City of Hope; D, dinner; B, breakfast; L, lunch.
At best, the data argue a definitive answer as to which of these specific MPC and PID algorithms has the better meal response will require a properly controlled prospective randomized study.
Although not a comparison of PID versus MPC per se, Figure 2B highlights two additional issues related to the comparison of meal responses. All the data in the panel are from MPC studies—the green curve being from the same study by Russell and coauthors16 shown in Figure 2A (repeated from Figure 1B) and the red and blue curves from studies performed by Hovorka and coauthors.18,19 The first issue is how to compare two “closed-loop” algorithms in which one of the algorithms relies on a meal announcement with an open-loop meal bolus. The second, less obvious issue is how to decide which meal response is better—one that that goes up and down or one that remains flat. A flat meal response can be obtained with a sufficiently high premeal insulin bolus; however, as insulin has both metabolic and mitogenic effects,10 it is not clear that the “optimal” response is the same as the smallest response. We originally argued that the optimal meal response should emulate the response obtained in a normal, glucose-tolerant subject consuming the identical meal10—the comparative group in the 2006 study of PID control2—but the idea has gained little traction among advocates of MPC who tend to favor optimization of predefined mathematical cost functions.
Confounding comparisons of different control approaches is the use of glucagon to prevent or correct hypoglycemia. The group at Boston University/Massachusetts General Hospital has advocated the use of glucagon throughout development of their MPC algorithm,15,16 whereas the PID algorithm developed at Medtronic,2–4 and variations evaluated at Boston Children’s Hospital/Joslin Diabetes Center,5,6 have been developed for use with insulin alone. The use of glucagon is not strictly speaking an MPC versus PID question, as glucagon can be used with PID control. Castle and coauthors20 included glucagon in their fading memory proportional derivative controller (Figure 2C, blue and light blue lines, with PID and MPC results from previous panels included for reference), albeit the fading memory proportional derivative algorithm does not— as is evident in the name—include integral action. A discussion of the benefit of integral action is deferred until later in this report. Here, it is noted only that the use of glucagon does not ensure prevention of hypoglycemia and that repeated use might not be tolerated by all subjects. Generally, the hypoglycemic incidence rate with PID control has gone down as the meal response has improved, with studies by Weinzimer and coauthors21,22 on the use of PID with insulin feedback (PIDIFB) and the use of PIDIFB with or without pramlintide showing zero incidences in what are admittedly small studies.
A number of clinical studies using approaches that do not fall into either PID or MPC categories have appeared in the literature. These include the nighttime-only results obtained by Phillip and coauthors23 using MD-Logic (a type of fuzzy-logic control) and results obtained by Breton and coauthors24 comparing what the authors refer to as standard control-to-range (sCTR) and enhanced control-to-range (eCTR)—the latter being modified to include an MPC component. While a complete discussion of the relative advantages and disadvantages of controlling to a range versus controlling to a target is beyond the scope of this article, as is any theoretical discussion of fuzzy logic, the results obtained with the approaches are included for completeness. Figure 3A shows the glucose interquartile ranges (IQRs) obtained with MD-Logic23 (red-shaded area), eCTR24 (gray-shaded area), and PIDIFB4 (magenta-shaded area).
Figure 3.
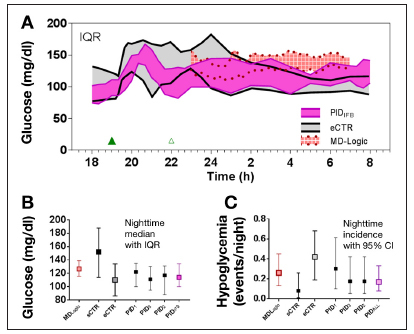
(A) Median and IQR range for dinner and nighttime control effected with PIDIFB algorithm4 superimposed with median and IQR for the enhance control to range eCTR study performed by Breton and coauthors24 and MD-Logic nighttime-only study performed by Phillip and coauthors.23 (B) Median and IQR for nighttime glucose values reported in the MD-Logic study by Phillip and coauthors.23 (C) Standard control-to-range versus eCTR study performed by Breton and coauthors.24 CI, confidence interval.
The results obtained with MD-Logic23 in particular represent a seminal advance in the quest to achieve closed-loop control in that they were obtained outside of the clinic. Further, while the results are for nighttime only, a nighttime-only controller is widely believed to be a more realistic goal for the first closed-loop device to be made widely available. Nonetheless, the nighttime results were not better than the nighttime results obtained with the initial PID controller modified with insulin feedback (PIDIFB).4 The IQR of glucose values was higher (Figure 3A) as was the reported incidence of hypoglycemia (7 events in 27 nights with MD-Logic versus 0 events in 9 nights of control with PIDIFB,4 or 6 events in 35 nights if the first three PID studies2–4 shown in Figure 1 are combined). While the sCTR algorithm24 had the lowest incidence of nighttime hypoglycemia (Figure 3C), the rate was achieved at the expense of having the highest nighttime glucose IQR (Figure 3B). The eCTR algorithm reduced the nighttime glucose IQR24 but did so with a nighttime incidence of hypoglycemia more than twice that observed with MD-Logic23 or the first three PID studies combined.2–4
A comparison of the dinner glucose response with eCTR algorithm24 with that obtained with PIDIFB4 shows that the eCTR also had an upper IQR well above that obtained with PIDIFB despite the two studies having comparable carbohydrate loads (1.08 ± 0.24 g/kg body weight for eCTR versus a median of 59.5 g with a range of 35–103 g for PID; body mass index but not body weight is reported in Reference 24). Here, the reader should only consider the responses between hours 19 and 22, as the eCTR protocol included a snack at hour 22 and the PIDIFB protocol did not. Still, considering the initial 3 h of the meal, and the fact that eCTR had more than twice the nighttime incidence of hypoglycemia during the night following dinner, it is hard to justify any statement as to the superiority of MPC over PID. Finally, while meal responses were not reported in the study using MD-Logic (fuzzy logic), a study using a fuzzy logic controller has reported on meals.25 The study with meals (30 g breakfast and 60 g lunch)25 reported 10 subjects being enrolled, with 7 completing and 2 subjects being discontinued due to hypoglycemia. Average glucose levels were 165 mg/dl.
Although it is difficult to compare the meal response in this latter fuzzy-logic study25 with that obtained with any of the PID studies given the substantial difference in meal sizes, it is interesting to note that control was achieved without meal announcement. This is interesting insofar many investigators have concluded that meals cannot be controlled without open-loop bolus despite the fact that the initial 2006 PID study2 did not include meal announcement and showed peak meal responses that were generally within 15–25 mg/dl of those observed in normal glucose-tolerant subjects who consumed the identical diet.2 While Weinzimer coauthors21,22 showed the peak response obtained with PID could be improved by giving one-third the normal meal bolus 15 min in advance of the meal, the reliance on meal boluses has steadily declined in subsequent PID studies.4,5,6 The first report of PIDIFB used only a small fixed bolus (2 U for all meals; Figure 3C).4 This was later reduced to an even smaller bolus related to the subject’s total daily dose of insulin (0.5, 1.0, and 1.5 U in subjects using <15, 15–30, and >30 U)5 and then eliminated altogether in a study in children less than seven years old.6 The study in children less than seven years old argued specifically that the bolus should not be given in children for safety reasons, as children may not always consume the anticipated carbohydrates. Arguably, investigators should approach this issue with equipoise until a definitive study demonstrates that an adequate meal response cannot be obtained without the meal bolus and until the disadvantages of including the bolus are fully considered.
Use of Metabolic Models to Compare Control Algorithms
Still another approach to comparing control algorithms is to use model simulations. Model-based comparisons are inherently attractive in that everything other than variable of interest can be controlled, the number of simulations can be large, and any outcome of interest can be precisely calculated. Simulations can also be performed without putting patients at risk. The Food and Drug Administration has approved a simulator for replacing animal studies in preclinical investigational device exemptions,26 and the simulator has shown several model-based control algorithms to outperform PID.27, 28 Of the two studies showing poor PID performance,27, 28 one showed substantial overnight hyperglycemia with PID (Figure 4A, individual subject data28) and one showed substantial hypoglycemia, with the average minimum glucose of 54 mg/dl (Figure 4B, 100 subjects with 1000 simulations27). However, in using a model to compare MPC to PID control, it is critically important to understand how the model used for simulation differs from the model used for control and—this should go without saying—how the PID controller used in the simulation was configured. It is equally important to note that numerous models capable of simulating closed-loop control have been proposed29–31 and that each model can be expected to produce a different answer as to whether PID control or MPC is the preferred control approach. These issues are addressed in the following paragraphs, beginning first with the choice of simulation model.
Figure 4.
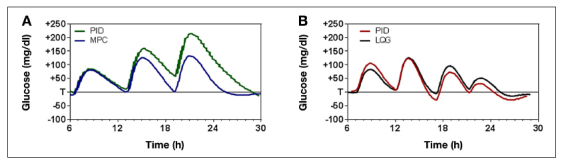
Use of model simulation to compare PID to model-based algorithms (A) PID versus MPC per se28 and (B) PID versus linear-quadratic-Gaussian control.27 LQG, linear quadratic Gaussian.
Differences in simulation models relate primarily to the number of differential equations used to describe the glucose and insulin kinetics (model order), how intraday and interday variability in insulin requirement is characterized, and whether or not the model was developed from data obtained in individuals with type 1 or type 2 diabetes.32,33 Generally, advocates of MPC have favored the use of high-order models for simulation and low-order models for the MPC algorithm, arguing that the inconsistency in model order approximates the differences that might be observed between a patient and a model. However, differences that arise from a difference in model order are not guaranteed to reflect differences between human and model or achieve statistical significance when assessing differences in ability to describe clinical data (F-test comparing sum square errors). This is particularly true when the high-order simulation model includes “near unobservable” terms. Most engineers will be familiar with the technical definition of observability as it relates to pole-zero cancellations;9 clinicians reading this report can simply take the phrase to refer to model components that do change the insulin pharmacokinetic (PK)/pharmacodynamic (PD) curve by a clinically significant amount. Figure 5 shows an example of a near unobservable higher-order model effect that results in differences that are unlikely to be considered clinically significant. In the example, a low-order two-compartment model is fit to the higher-order model insulin PK curve taken from one of the subjects used in evaluating PID control with the University of Virginia model. The curve is taken from a simulation study conducted at the U.S. Department of Defense.26 While the difference between the low- and high-order model does result in statistically significant residuals (p < 0.001 by runs test) and is technically observable, it is unlikely that the difference is clinically or control relevant.
Figure 5.
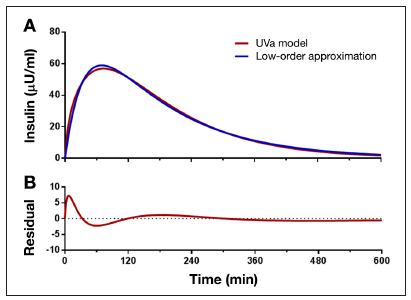
(A) Differences between model used for simulation (red curve) and model used for control (blue curve) assuming University of Virginia simulation model and low second-order model used for control (blue curve). (B) Residual runs analysis indicating statisticaly significant residuals that may or may not be clinically or control relevant (see text). UVa, University of Virginia.
Although differences in model order can generate difference between the model used for simulation and the model used for control, an alternative method to introduce differences is to have the simulation model include time-varying model parameters, as was done in the model used as an aid in developing the Medtronic PID algorithm.33 Time-varying model parameters are necessary when describing individuals with type 1 diabetes using pumps to manage their glucose levels, as the majority of these subjects use different basal rates during the day, and there is substantial anecdotal evidence that the basal rates that work on one day may not work on another day. Generally, changes in the required basal rate reflect changes in model parameters related to insulin sensitivity or endogenous glucose production,32,33 and sudden changes in either can present a substantial challenge to both the MPC and PID control approaches. This is particularly so during periods where the subject is initially at target glucose and stable (rate of glucose change equal zero) and the basal requirement decreases, as it is during these times that the risk of hypoglycemia is greatest. Importantly, the only indication available to either algorithm that the basal requirement has decreased will be when glucose levels begin to decline. Understanding the differences in how an MPC versus a PID controller responds to such a challenge is critical to making an informed choice as to which algorithm is preferred.
The main challenge for an MPC controller is to identify the model parameters responsible for the decrease in basal requirement while at the same using those parameters to effect control. Generally, MPC algorithms use recursive least squares (RLS) to identify the parameters responsible for the change in insulin requirement. Control engineers should be familiar with the RLS algorithm; clinicians reading this commentary can simply consider the algorithm to be an efficient approach for obtaining the same parameters that would be obtained from regular least squares approach. Important points to consider are that, once the model parameters change, the algorithm will require at least as many new data points as there are model parameters and that, in practice, substantially more points are needed to keep the estimates from being overly sensitive to measurement error. As more points are added to the identification, a forgetting factor is needed to minimize the effect of earlier points (reflecting conditions before the change). This increases the time needed to converge on the new parameter values, reflecting need for less insulin. Optimal parameter identification requires glucose values and insulin values to be constantly changing—so called persistent excitation34—which decreases sensitivity to measurement noise. However, persistently changing glucose level is counter to the objectives of the control.
In contrast, PID control relies primarily on derivative action to suspend delivery once the initial fall in glucose from target is detected and on integral windup protection to prevent further insulin delivery until the risk of hypoglycemia subsides. Again, engineers reading this report should be familiar with integral windup protection; clinicians reading the report can simply consider the algorithm to be analogous to insulin-on-board calculations used to prevent overbolusing. The challenge for the PID controller is to assess when the initial fall in glucose is sufficient to warrant suspending the pump when the risk of rebound hyperglycemia is sufficient to justify restarting it and what basal rate should be used once restarted.
Returning to the question of how model simulations might be used to compare MPC and PID control, I would argue that simulations can be invaluable. For an MPC algorithm, simulations can characterize how fast the algorithm can identify changes in model parameters and determine the impact of using model parameters that have not converged to their new values on predictions of future glucose values as well as the impact of errors in calculating insulin delivery from those predictions. For PID control, simulations can be used to assess how reliable the derivative is at suspending insulin delivery, how effective the integral windup protection algorithms are in preventing rebound hyperglycemia, and whether an appropriate new basal rate is established. However, for the simulations to be of value, the simulator needs to include time-varying parameters. Moreover, any comparison of PID and MPC needs to state what model parameters will change and how fast the changes will occur. Generally, simulations in which the parameters change slowly favor MPC, whereas simulations with parameters that change rapidly favor PID control. With slowly changing parameters, RLS is able to track the parameters with sufficient accuracy to effect control based on the estimated parameter values. With rapidly changing parameters, the derivative action within a PID controller is more likely to rapidly suspend delivery in response to a rapid decrease in glucose or deliver insulin in response to a rapid unanticipated increase. Ideally, the simulations should include parameter changes that result in prolonged changes in the underlying basal requirement, as this can be used to confirm that the control algorithm can re-establish target without error. The integral component of the PID controller can be assured of re-establishing target glucose levels at whatever basal rate is required, provided the rate does not exceed the maximum rate the pump can deliver.
The last statement represents what is likely the single most compelling reason that, “Despite all the progress in advanced control, the PID remains the most popular controller.”35 This phrase is taken verbatim from a report by the IEEE Control Systems Society, “The Impact of Control Technology,” in which the authors go on to note, “A remarkable property of a controller with integral action is that it gives the correct steady state, if a steady state exists, even for nonlinear processes.”35 I would add that this is true irrespective of the choice of parameters used to define the relative contribution of the proportional, integral, and derivative components (control gain Kp; U/h per mg/dl above target; integration time TI in minutes, and derivative time TD, also in minutes). For the clinician reading this report, parameter TI can be taken to affect how long it will take to achieve target, and parameter TD can be taken to affect how well the PID algorithm compensates delay in the insulin PK/PD curve. Although it is true that steady state target will be achieved irrespective of the values chosen for Kp, TI, and TD, the values will affect other aspects of the control performance such as meal excursions, incidence of nighttime hypoglycemia, and, most importantly, stability. Thus, any comparison of PID versus MPC—simulation or clinical—needs to state how the parameters were obtained. Comparisons in which the PID controller is poorly configured are inherently flawed and counterproductive to the goal of achieving closed-loop control.
As indicated earlier, the choice of parameter TI affects how long it may take to achieve target. Combining the proportional and integral components of a PID algorithm allows the user to set a desired rate of glucose change as the difference from target divided by TI. Higher values of TI will increase the time needed to normalize glucose but reduce the likelihood of hypoglycemia. The choice of TD affects how the PID compensates for delay. Generally, combining the proportional and derivative components allows any one delay in the PK/PD response to be perfectly compensated by choosing the derivative time equal to that delay. Using all three terms together makes tuning more complicated, but the principle is the same—integration time affects how long it takes to respond to changes in basal requirement and derivative time affects how well the algorithm adjusts for PK/PD delay. While it is true that combining proportional and derivative components can only effect perfect compensation for one PK/PD delay, modifications to the algorithm such as insulin feedback can limit the impact of all delays in the PK/PD response.36 Thus the often-stated argument made by advocates of MPC that PID control cannot address delay whereas MPC can is simply untrue and counterproductive. There are multiple mechanisms for compensating for delay when using PID; neither MPC nor PID can make the delays disappear.
How are the PID parameters chosen? Typically, PID parameters are obtained empirically in much the same way as open-loop basal rates, carbohydrate-to-insulin ratios, and other open-loop parameters are chosen. This is not optimal. A detailed discussion of how the optimal tuning might be achieved is beyond the scope of this article; however, it is noted here that optimization is typically done with the aid of a model. Virtually all standard textbooks on control theory contain multiple problems in which a model of the system to be controlled is provided and the student is asked to design a PID controller to achieve specified criteria. This returns us to the question of what the appropriate model is. It is inevitable that a poor choice of model will result in poor PID performance.
Summary
Superimposing and/or placing side-by-side the clinical results obtained with the MPC and PID approaches studied to date shows no evidence of MPC being superior to PID control. Results of simulation studies showing superiority are based on simulation models that lack interday and intraday variability in insulin requirement. Arguments presented here favoring PID control point to a better meal response and a lower incidence of nighttime hypoglycemia. These arguments are independent of arguments that PID control reproduces what the β-cell naturally does, although modeling the β-cell may still be a viable approach for optimizing control.11 Although there are challenges with changing the delivery site from the portal vein to a subcutaneous site, the clinical results achieved to date with PID control have improved as changes in the algorithm have been effected to meet those challenges. Conversely, the limitations related to MPC are rarely addressed by advocates of the algorithm. Specifically, what happens when the predicted future glucose values are based on parameters that are rapidly changing or change in the timeframe used in the prediction horizon? PID studies conducted to date have not used optimal PID parameters and it is unreasonable to expect the results obtained with the empirically derived values to be the best results that can be achieved.
Response to Comments Raised by Dr. Bequette
During the preparation of the MPC versus PID debate papers, Dr. Bequette and I exchanged preliminary versions of our paper and discussed format. We agree on many points; however, a “debate” in which the two sides agree on everything is not interesting. What do the authors disagree on? Dr. Bequette comments that simulation studies performed to date have included both model “parameter uncertainty” and “structure uncertainty.” While true, I would counter that the structural uncertainty likely introduced errors that were neither clinically nor control relevant. Having the blue line be the “model used for control” in Figure 5 and the red line be the “model used for simulation” is a meaningless structural uncertainty. Moreover, the “parameter uncertainty” introduced was a one-time-only event, meaning the parameters could easily be identified during breakfast on Monday and then used to control lunch on Monday. The real-challenge with “parameter uncertainty” only occurs when the uncertainty is repeatedly introduced, i.e., if the parameters for lunch on Monday are not the same as for breakfast on Monday or if the parameters for breakfast on Tuesday are not the same as the parameters for breakfast on Monday. Still another disagreement is the statement put forth by my colleague that “the advanced control approach most commonly used in industry is model predictive control.”1 It is difficult to reconcile this with the statement by Åström and coauthors that, “Despite all the progress in advanced control, the PID remains the most popular controller.”35 Dr. Bequette and I have had numerous discussions on this point, and we agree that 90–95% of controllers used in industry are in fact PID. Dr. Bequette’s statement is true if the qualifier “advanced” is taken to mean “non-PID.” I agree that, of the 5–10% of non-PID loops, most are likely MPC but would disagree that PID is limited to non-advanced problems. I would argue that real-world complex control problems are routinely addressed by PID control and put forth as evidence patent literature describing complex problems such as spacecraft maneuvering (U.S. Patent 8352101) and missile control (US Patent 8436283) that use PID control. A close look at such patents suggests that the engineers have chosen PID control not because they are unfamiliar with the putative advantages of MPC, but because they are familiar with the disadvantages of the approach.
Conclusion
Although the objective of this debate article was to argue the merits of PID control over MPC, the clinical data available to date indicate that both approaches work and that the debate would do well to include even more approaches. What is needed are fewer broadly sweeping statements about the putative weakness of any one approach and more constructive debate about the strengths and weakness inherent in all approaches. To this end, I thank my opponent in this debate, Dr. Bequette, for the many thoughtful discussions on the relative merits of the MPC and PID approaches in particular.
Glossary
- (eCTR)
enhanced control-to-range
- (IQR)
interquartile range
- (MPC)
model-predictive control
- (PID)
proportional integral derivative
- (PD)
pharmacodynamic
- (PIDIFB)
proportional integral derivative with insulin feedback
- (PK)
pharmacokinetic
- (RLS)
recursive least squares
- (sCTR)
standard control-to-range
Funding
Garry Steil is supported by a grant from the JDRF (1–2011–581, Closed-Loop Control Utilizing Model-Based PK/PD Compensation).
Disclosures
Garry Steil serves on the medical advisory board for BD. No BD devices were used in the conduct of this study. Dr. Steil is a former employee of Medtronic MiniMed and is presently an investigator on a study for which Medtronic MiniMed provides devices.
References
- 1.Bequette BW. Algorithms for a closed-loop artificial pancreas: the case for model predictive control. J Diabetes Sci Technol. 2013;7(6):1632–1643. doi: 10.1177/193229681300700624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Steil GM, Rebrin K, Darwin C, Hariri F, Saad MF. Feasibility of automating insulin delivery for the treatment of type 1 diabetes. Diabetes. 2006;55(12):3344–3350. doi: 10.2337/db06-0419. [DOI] [PubMed] [Google Scholar]
- 3.Weinzimer SA, Steil GM, Swan KL, Dziura J, Kurtz N, Tamborlane WV. Fully automated closed-loop insulin delivery versus semiautomated hybrid control in pediatric patients with type 1 diabetes using an artificial pancreas. Diabetes Care. 2008;31(5):934–939. doi: 10.2337/dc07-1967. [DOI] [PubMed] [Google Scholar]
- 4.Steil GM, Palerm CC, Kurtz N, Voskanyan G, Roy A, Paz S, Kandeel FR. The effect of insulin feedback on closed loop glucose control. J Clin Endocrinol Metab. 2011;96(5):1402–1408. doi: 10.1210/jc.2010-2578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wolpert HA, Atakov-Castillo A, Smith SA, Steil GM. Dietary fat acutely increases glucose concentrations and insulin requirements in patients with type 1 diabetes: implications for carbohydrate-based bolus dose calculation and intensive diabetes management. Diabetes Care. 2013;36(4):810–816. doi: 10.2337/dc12-0092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Dauber A, Corcia L, Safer J, Agus MS, Einis S, Steil GM. Closed-loop insulin therapy improves glycemic control in children aged <7 years: a randomized controlled trial. Diabetes Care. 2013;36(2):222–227. doi: 10.2337/dc12-1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wintergerst KA, Deiss D, Buckingham B, Cantwell M, Kache S, Agarwal S, Wilson DM, Steil G. Glucose control in pediatric intensive care unit patients using an insulin-glucose algorithm. Diabetes Technol Ther. 2007;9(3):211–222. doi: 10.1089/dia.2006.0031. [DOI] [PubMed] [Google Scholar]
- 8.Agus MS, Steil GM, Wypij D, Costello JM, Laussen PC, Langer M, Alexander JL, Scoppettuolo LA, Pigula FA, Charpie JR, Ohye RG, Gaies MG. SPECS Study Investigators. Tight glycemic control versus standard care after pediatric cardiac surgery. N Engl J Med. 2012;367(13):1208–1219. doi: 10.1056/NEJMoa1206044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ogata K. 4th. Englewood Clifs: Prentice Hall; 2002. Modern control engineering. [Google Scholar]
- 10.Steil GM, Panteleon AE, Rebrin K. Closed-loop insulin delivery-the path to physiological glucose control. Adv Drug Deliv Rev. 2004;56(2):125–144. doi: 10.1016/j.addr.2003.08.011. [DOI] [PubMed] [Google Scholar]
- 11.Steil GM, Grodsky GM. The artificial pancreas: is it important to understand how the β cell controls blood glucose? J Diabetes Sci Technol. 2013;7(5):1359–1369. doi: 10.1177/193229681300700528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Steil GM, Rebrin K, Janowski R, Darwin C, Saad MF. Modeling beta-cell insulin secretion--implications for closed-loop glucose homeostasis. Diabetes Technol Ther. 2003;5(6):953–964. doi: 10.1089/152091503322640999. [DOI] [PubMed] [Google Scholar]
- 13.Clarke WL, Anderson S, Breton M, Patek S, Kashmer L, Kovatchev B. Closed-loop artificial pancreas using subcutaneous glucose sensing and insulin delivery and a model predictive control algorithm: the Virginia experience. J Diabetes Sci Technol. 2009;3(5):1031–1038. doi: 10.1177/193229680900300506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bruttomesso D, Farret A, Costa S, Marescotti MC, Vettore M, Avogaro A, Tiengo A, Dalla Man C, Place J, Facchinetti A, Guerra S, Magni L, De Nicolao G, Cobelli C, Renard E, Maran A. Closed-loop artificial pancreas using subcutaneous glucose sensing and insulin delivery and a model predictive control algorithm: preliminary studies in Padova and Montpellier. J Diabetes Sci Technol. 2009;3(5):1014–1021. doi: 10.1177/193229680900300504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.El-Khatib FH, Russell SJ, Nathan DM, Sutherlin RG, Damiano ER. A bihormonal closed-loop artificial pancreas for type 1 diabetes. Sci Transl Med. 2010;2(27):27ra27. doi: 10.1126/scitranslmed.3000619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Russell SJ, El-Khatib FH, Nathan DM, Magyar KL, Jiang J, Damiano ER. Blood glucose control in type 1 diabetes with a bihormonal bionic endocrine pancreas. Diabetes Care. 2012;35(11):2148–2155. doi: 10.2337/dc12-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rebrin K, Steil GM, Mittelman SD, Bergman RN. Causal linkage between insulin suppression of lipolysis and suppression of liver glucose output in dogs. J Clin Invest. 1996;98(3):741–749. doi: 10.1172/JCI118846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Murphy HR, Elleri D, Allen JM, Harris J, Simmons D, Rayman G, Temple R, Dunger DB, Haidar A, Nodale M, Wilinska ME, Hovorka R. Closed-loop insulin delivery during pregnancy complicated by type 1 diabetes. Diabetes Care. 2011;34(2):406–411. doi: 10.2337/dc10-1796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hovorka R, Kumareswaran K, Harris J, Allen JM, Elleri D, Xing D, Kollman C, Nodale M, Murphy HR, Dunger DB, Amiel SA, Heller SR, Wilinska ME, Evans ML. Overnight closed loop insulin delivery (artificial pancreas) in adults with type 1 diabetes: crossover randomised controlled studies. BMJ. 2011;342:d1855. doi: 10.1136/bmj.d1855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Castle JR, Engle JM, El Youssef J, Massoud RG, Yuen KC, Kagan R, Ward WK. Novel use of glucagon in a closed-loop system for prevention of hypoglycemia in type 1 diabetes. Diabetes Care. 2010;33(6):1282–1287. doi: 10.2337/dc09-2254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ruiz JL, Sherr JL, Cengiz E, Carria L, Roy A, Voskanyan G, Tamborlane WV, Weinzimer SA. Effect of insulin feedback on closed-loop glucose control: a crossover study. J Diabetes Sci Technol. 2012;6(5):1123–1130. doi: 10.1177/193229681200600517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Weinzimer SA, Sherr JL, Cengiz E, Kim G, Ruiz JL, Carria L, Voskanyan G, Roy A, Tamborlane WV. Effect of pramlintide on prandial glycemic excursions during closed-loop control in adolescents and young adults with type 1 diabetes. Diabetes Care. 2012;35(10):1994–1999. doi: 10.2337/dc12-0330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Phillip M, Battelino T, Atlas E, Kordonouri O, Bratina N, Miller S, Biester T, Stefanija MA, Muller I, Nimri R, Danne T. Nocturnal glucose control with an artificial pancreas at a diabetes camp. N Engl J Med. 2013;368(9):824–833. doi: 10.1056/NEJMoa1206881. [DOI] [PubMed] [Google Scholar]
- 24.Breton M, Farret A, Bruttomesso D, Anderson S, Magni L, Patek S, Dalla Man C, Place J, Demartini S, Del Favero S, Tofanin C, Hughes-Karvetski C, Dassau E, Zisser H, Doyle FJ, 3rd, De Nicolao G, Avogaro A, Cobelli C, Renard E, Kovatchev B. International Artificial Pancreas Study Group. Fully integrated artificial pancreas in type 1 diabetes: modular closed-loop glucose control maintains near normoglycemia. Diabetes. 2012;61(9):2230–2237. doi: 10.2337/db11-1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mauseth R, Hirsch IB, Bollyky J, Kircher R, Matheson D, Sanda S, Greenbaum C. Use of a “fuzzy logic” controller in a closed-loop artificial pancreas. Diabetes Technol Ther. 2013;15(8):628–633. doi: 10.1089/dia.2013.0036. [DOI] [PubMed] [Google Scholar]
- 26.Laxminarayan S, Reifman J, Steil GM. Use of a food and drug administration-approved type 1 diabetes mellitus simulator to evaluate and optimize a proportional-integral-derivative controller. J Diabetes Sci Technol. 2012;6(6):1401–1412. doi: 10.1177/193229681200600621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Patek SD, Breton MD, Chen Y, Solomon C, Kovatchev B. Linear quadratic gaussian-based closed-loop control of type 1 diabetes. J Diabetes Sci Technol. 2007;1(6):834–841. doi: 10.1901/jaba.2007.1-834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Magni L, Raimondo DM, Bossi L, Man CD, De Nicolao G, Kovatchev B, Cobelli C. Model predictive control of type 1 diabetes: an in silico trial. J Diabetes Sci Technol. 2007;1(6):804–812. doi: 10.1177/193229680700100603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Steil GM, Clark B, Kanderian S, Rebrin K. Modeling insulin action for development of a closed-loop artificial pancreas. Diabetes Technol Ther. 2005;7(1):94–108. doi: 10.1089/dia.2005.7.94. [DOI] [PubMed] [Google Scholar]
- 30.Steil GM, Reifman J. Mathematical modeling research to support the development of automated insulin-delivery systems. J Diabetes Sci Technol. 2009;3(2):388–395. doi: 10.1177/193229680900300223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Steil GM, Hipszer B, Reifman J. Update on mathematical modeling research to support the development of automated insulin delivery systems. J Diabetes Sci Technol. 2010;4(3):759–769. doi: 10.1177/193229681000400334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kanderian SS, Weinzimer S, Voskanyan G, Steil GM. Identification of intraday metabolic profiles during closed-loop glucose control in individuals with type 1 diabetes. J Diabetes Sci Technol. 2009;3(5):1047–1057. doi: 10.1177/193229680900300508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kanderian SS, Weinzimer SA, Steil GM. The identifiable virtual patient model: comparison of simulation and clinical closed-loop study results. J Diabetes Sci Technol. 2012;6(2):371–379. doi: 10.1177/193229681200600223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Norton JP. Mineola: Dover Publications; 2009. An introduction to identification. [Google Scholar]
- 35.Åström KJ, Hägglund T. Auto-tuners for PID controllers. In: Samad T, Annaswamy AM, editors. The impact of control technology. IEEE Control Systems Society; 2011. [Google Scholar]
- 36.Kanderian S, Steil G. Apparatus and method for controling insulin infusion with state varible feedback. Patent publication number US2007/0173761


