Quantitative characterization of electron detectors for transmission electron microscopy

Abstract

A new generation of direct electron detectors for transmission electron microscopy (TEM) promises significant improvement over previous detectors in terms of their modulation transfer function (MTF) and detective quantum efficiency (DQE). However, the performance of these new detectors needs to be carefully monitored in order to optimize imaging conditions and check for degradation over time. We have developed an easy-to-use software tool, FindDQE, to measure MTF and DQE of electron detectors using images of a microscope’s built-in beam stop. Using this software, we have determined the DQE curves of four direct electron detectors currently available: the Gatan K2 Summit, the FEI Falcon I and II, and the Direct Electron DE-12, under a variety of total dose and dose rate conditions. We have additionally measured the curves for the Gatan US4000 and TVIPS F416 scintillator-based cameras. We compare the results from our new method with published curves.

Introduction

Transmission electron microscopy (TEM) can be used to obtain images of thin samples at atomic resolution. To preserve the high-resolution contrast, images have traditionally been recorded using photographic film. Film combines relatively high sensitivity with a large active area, both of which are particularly important when working with beam-sensitive specimens, such as biological material (Grigorieff and Harrison, 2011). Images recorded from these samples suffer from low signal-to-noise ratio (SNR) due to the small total dose (20 – 30 electrons/Ų) that must be used; many images must be averaged to suppress the noise and amplify the signal, i.e. the structure of the specimen. Single-particle electron cryo-microscopy (cryo-EM) can yield structures of biological materials at resolutions higher than 4 Å, which can be interpreted by atomic models. Such near-atomic resolution structures have been determined for highly symmetric viruses and chaperonins (e.g. Wolf et al., 2010, Sachse et al., 2007, Liu et al., 2010), while medium-resolution has been achieved with smaller, lower symmetry particles, providing insights into their secondary structure. Automated collection of large datasets (Mastronarde, 2005, Suloway et al., 2005) and computational methods to sort out structural heterogeneity (Penczek et al., 2006, Simonetti et al., 2008, Scheres, 2010, Orlova and Saibil, 2010, Frank et al., 2012, Lyumkis et al., 2013), have greatly contributed towards these recent improvements, as have improvements in instrumentation, especially the use of field emission guns in modern high-resolution TEMs.

Detectors have been a limiting factor in achieving high resolution with cryo-EM. Although photographic film has desirable properties as a detector, data collection cannot easily be automated. Until recently, the only electronic detectors that could be used with automation incorporated scintillators. Scintillator based-detectors turn incident electrons into light, which is then detected by a CCD or CMOS chip (Faruqi and Henderson, 2007). The small area and relatively low sensitivity of these detectors makes them suboptimal for low-dose cryo-EM. A new type of detector, the direct electron detector (DED), bypasses scintillators and offers significantly improved sensitivity and output SNR (McMullan et al., 2009a). Detector performance can be evaluated quantitatively using the detective quantum efficiency (DQE), which measures how much noise a detector adds to a recorded image. Apart from a higher DQE, the current CMOS-based DEDs also allow the recording of movies at frame rates of 10s to 100s of frames per second, which is sufficient to correct for beam-induced sample movement, enhancing high-resolution contrast (Brilot et al., 2012, Campbell et al., 2012, Li et al., 2013a, Bai et al., 2013).

The performance of DEDs varies with dose rate and beam energy, and can degrade over time due to beam damage. Quantitative evaluation of detector performance is therefore also useful to determine optimal imaging parameters and detector lifetime. We have developed a software tool to easily and quantitatively evaluate detector performance, using images of the beam stop of an electron microscope. In this work, we have applied this method to the current generation of DEDs, as well as to high-performance CCDs, and we present their DQEs together for comparison.

Theory

Detective quantum efficiency

Electron detectors can be characterized qualitatively by observing Thon rings (Thon, 1966) calculated from micrographs of carbon film. The visible oscillations in the pattern indicate the approximate frequency to which signal is discernible (Bammes et al., 2011, Milazzo et al., 2011). A more quantitative description of detector performance is provided by the DQE. The DQE can be calculated from the modulation transfer function (MTF) of the detector and the noise power spectrum (NPS) of the output image. The MTF measures the response of an imaging system in the frequency domain. In other words, it describes how much contrast is transferred from the object to the image at each resolution:

$$\mathrm{M}\mathrm{T}\mathrm{F}(\mathrm{\omega })=\frac{\text{Modulation}{(\mathrm{\omega })}_{\text{out}}}{\text{Modulation}{(\mathrm{\omega })}_{i\mathrm{n}}}={\left(\frac{I{(\mathrm{\omega })}_{\text{max}}-I{(\mathrm{\omega })}_{\text{min}}}{I{(\mathrm{\omega })}_{\text{max}}+I{(\mathrm{\omega })}_{\text{min}}}\right)}_{\text{out}}/{\left(\frac{I{(\mathrm{\omega })}_{\text{max}}-I{(\mathrm{\omega })}_{\text{min}}}{I{(\mathrm{\omega })}_{\text{max}}+I{(\mathrm{\omega })}_{\text{min}}}\right)}_{\text{in}}=\sqrt{\frac{P{(\mathrm{\omega })}_{\text{out}}}{P{(\mathrm{\omega })}_{\text{in}}}}$$ (1)

where ω denotes spatial frequency, I_min and I_max are the minimum and maximum intensities of a sinusoidal test pattern with frequency ω, P is its power, and the subscripts “in” and “out” refer to the image before and after its detection, respectively. The MTF can also be defined as the Fourier transform of the point spread function (PSF):

$$\mathrm{M}\mathrm{T}\mathrm{F}(\mathrm{\omega })=\mathrm{F}\mathrm{T}(\mathrm{P}\mathrm{S}\mathrm{F}(r))$$ (2)

where r is the real space coordinate. The PSF is the blurring kernel of the detector:

$${\text{Image}}_{\text{out}}=\mathrm{P}\mathrm{S}\mathrm{F}\otimes {\text{Image}}_{\text{in}}$$ (3)

where ⊗ indicates convolution. In Fourier space, this becomes

$$\mathrm{F}\mathrm{T}({\text{Image}}_{\text{out}})=\mathrm{M}\mathrm{T}\mathrm{F}·\mathrm{F}\mathrm{T}({\text{Image}}_{\text{in}})$$ (4)

The DQE is the ratio of input to output SNR (ratio of signal and noise variance):

$$\mathrm{D}\mathrm{Q}\mathrm{E}(\mathrm{\omega })=\frac{\mathrm{S}\mathrm{N}\mathrm{R}{(\mathrm{\omega })}_{\text{out}}}{\mathrm{S}\mathrm{N}\mathrm{R}{(\mathrm{\omega })}_{\text{in}}}$$ (5)

The DQE thus describes how the detector degrades the SNR, or how efficiently it detects an electron (the original name for DQE was ‘useful quantum efficiency’ (Rose, 1946)). Because cryo-EM of beam-sensitive specimens is concerned with minimizing electron dose, the DQE, which takes into account the efficiency of each electron, is a more informative quantity than the MTF.

The DQE can also be calculated from the MTF and NPS (see Shaw, 1978, and references therein):

$$\mathrm{D}\mathrm{Q}\mathrm{E}(\mathrm{\omega })=\frac{n_{\text{out}}^2·\mathrm{M}\mathrm{T}{\mathrm{F}}^2(\mathrm{\omega })}{n_{\text{in}}·\mathrm{N}\mathrm{P}\mathrm{S}(\mathrm{\omega })}$$ (6)

where n_out is the average signal of the output image (with no sample or test object inserted), and n_in is the input electron dose.

The MTF of a detector usually declines monotonically with increasing frequency. This is because detectors are not point samplers; they are made up of pixels of finite size. Assuming square pixels, the ideal detector’s MTF will be a two-dimensional sinc function that arises from the Fourier transform of the corresponding PSF with a width of one pixel (Eq. (2)). The MTF of such a detector thus declines to 0.64 at Nyquist frequency. For an ideal detector NPS(ω) = const (Grob et al., 2013); setting n_out and n_in to unity, we can use Eq. (6) to write for the DQE of an ideal pixel detector:

$$\mathrm{D}\mathrm{Q}\mathrm{E}(\mathrm{\omega })=\text{sin}{\mathrm{c}}^2(\pi \mathrm{\omega }/2)$$ (7)

which falls to 0.41 at Nyquist frequency.

Determining the MTF

The MTF can be calculated from the PSF, which can be obtained from observing single electron events (Ghadimi et al., 2011). However, not all detectors are sufficiently sensitive to allow these measurements. It is also possible to use holographic fringes from a thin crystal in order to create a periodic test pattern from which the MTF can be calculated (McLeod and Malac, 2013); however, this is experimentally intensive. The PSF can also be measured using the knife-edge method. In this method, a straight-edged test object is placed in the microscope. The edge spread function (ESF), the one-dimensional profile normal to the edge, is measured, and differentiated to give the line spread function (LSF). The LSF is the radial average of the PSF, and is Fourier transformed to yield the MTF (Samei et al., 1998, Meyer and Kirkland, 2000). The knife-edge method has been used extensively, but has the major disadvantage of requiring a microscopically straight-edged test object to be inserted into the microscope.

We have implemented a method for measuring the DQE that uses the silhouette of a beam stop (Broek et al., 2012). This implementation should allow TEM users to easily evaluate installed detectors and obtain quantitative DQE measurements. The silhouette method is based on estimating the input image before detection by converting the detected image into a black-and-white image using a threshold value that separates pixels within the silhouette of the beam stop from pixels outside it. In order to simulate the effects of aliasing, the output image is up-sampled four times using bilinear interpolation and then thresholded to generate the black-and-white beam stop image. A blurring kernel is applied to this image to simulate the MTF before pixel integration, and pixel integration is then performed by replacing each group of 4 × 4 pixels with the pixel average:

$${\text{Image}}_{\text{sim}}(r)=\text{DOWN}(\mathrm{F}{\mathrm{T}}^{-1}[\text{kernel}·\mathrm{F}\mathrm{T}(\mathrm{T}\mathrm{H}[\mathrm{U}\mathrm{P}({\text{Image}}_{\text{out}}(r))])])$$ (8)

Here, the UP and DOWN operations refer to the up-sampling and pixel integration (down-sampling), respectively, and TH refers to the thresholding operation. The detector MTF is found by modifying the blurring kernel to minimize the squared difference Δ between simulated and measured output image:

$$\mathrm{\Delta }={({\text{Image}}_{\text{out}}-{\text{Image}}_{\text{sim}})}^2$$ (9)

(the difference is calculated as the sum of pair-wise pixel differences). The detector MTF is calculated by multiplying this blurring kernel with a sinc function to account for the effects of pixel integration (the DOWN operation in EQ. (8)). The blurring kernel is written as the sum of five Gaussian functions (McMullan et al., 2009a):

$$\text{kernel}(\mathrm{\omega })=\sum _{i=1}^5{W}_i·e^{-\frac{{\mathrm{\omega }}^2}{2{{\mathrm{\sigma }}_i}^2}}$$ (10)

where W_i are the weights of the Gaussians and σ_i specify their widths. Minimization of Δ (Eq. (9)) is achieved by varying W_i and σ_i.

MTF of a counting detector

The MTF at zero-frequency, MTF(0), is conventionally set to 1. However, we (see below) and others have found that the hard-coded algorithm of the K2 Summit counting detector depresses low-frequency modulation relative to modulation at higher frequencies, especially at higher dose rates (Li et al., 2013a,b). This is due to so-called coincidence loss (Li et al., 2013b) - the suppression of counts that occur too close in time and space to already registered counts. The suppression leads to a loss of counts, with a lost “image” that has a low-frequency correlation with the registered (output) image. We therefore decided to account for the lost counts by lowering the MTF at low resolution, effectively allowing MTF(0) values smaller than 1. Alternatively, the lost counts could also have been accounted for by a depression of the signal. We model the counting detector MTF as a product of two terms, MTF_l, and MTF_d. The first represents the MTF of the detector when used with a vanishingly low dose rate, while the second term represents an additional modulation of the detected signal due to lost counts when using a dose rate d. Both terms are frequency-dependent. MTF_d is assumed to be 1 for all frequencies at vanishingly low dose rates, giving MTF = MTF_l, i.e. MTF_l is equivalent to the MTF of a non-counting detector.

For counting detectors that are not affected by lost counts, NPS_l (α) = const. This is due to the counting mode which assigns detected electrons to single pixels. A flat NPS is indeed observed for counting detectors at very low dose rates (see Results). According to our model, reduction of power at low frequencies relative to higher frequencies is due to MTF_d:

$$\mathrm{N}\mathrm{P}\mathrm{S}(\mathrm{\omega })=\mathrm{N}\mathrm{P}{\mathrm{S}}_l(\mathrm{\omega })·\mathrm{M}\mathrm{T}{\mathrm{F}}_d^2(\mathrm{\omega })/\mathrm{M}\mathrm{T}{\mathrm{F}}_d^2(0)=\mathrm{M}\mathrm{T}{\mathrm{F}}_d^2(\mathrm{\omega })/\mathrm{M}\mathrm{T}{\mathrm{F}}_d^2(0)$$ (11)

Therefore, apart from a scaling factor, MTF_d can be calculated directly from the observed NPS. The NPS of the K2 Summit counting detector operating in its “super-resolution” mode has been modeled using a sinc² function (Li et al., 2013b). The sinc² function models the depressed NPS at low resolution; however it leads to some discrepancies between model and observed NPS at higher resolution (see Fig. 3A in Li et al., 2013b). Since the details of the algorithm actually implemented in the K2 camera are not publically available, we have explored different functions to model the NPS of the K2 camera operating both in super-resolution and simple counting modes. For super-resolution images, the NPS can be modeled more closely by

$$f_{\text{sin}\mathrm{c}}(\mathrm{\omega })=[s_1-{s_2}^{*}\text{sin}\mathrm{c}(s_3\mathrm{\omega })]e^{-s_4^2{\mathrm{\varpi }}^2}$$ (12)

(Fig. 1A) where s_i are the parameters to be found in the fit. For images recorded in simple counting mode, a logistic function achieves a good fit:

$$f_{\text{logistic}}(\mathrm{\omega })=\frac{s_1}{1+\text{exp}((s_2-\mathrm{\omega })/s_3)}+s_4$$ (13)

(Fig. 1B). Eq. (12) and (13) represent heuristic descriptions of the observed NPS. A more detailed model for power spectra from counting detectors may be derived with the knowledge of the algorithms employed to identify counts and to determine the centroids of the detected counts in super-resolution imaging. Using the appropriate fit f, MTF_d is then calculated as

$$\mathrm{M}\mathrm{T}{\mathrm{F}}_d(\mathrm{\omega })=\sqrt{\frac{f(\mathrm{\omega })}{\text{max}f}}$$ (14)

The scaling by $\sqrt{\text{max}f}$ ensures that MTF_d is never greater than 1. Due to the observed attenuation of the NPS at low frequencies, the maximum of f will generally occur at Nyquist frequency, resulting in MTF_d (0) < 1 (see Results). This, in turn, will lead to a decrease in the DQE at low frequencies (Eq. (6)).

Figure 3.

DQE of detectors at 200 kV. The DEDs outperform scintillator-based detectors. The dose rates used were: K2 Summit in super-resolution mode – 4 electrons/pixel/second (this value refers to physical pixels); K2 Summit in simple counting mode – 3 electrons/pixel/second; DE-12 – 13 electrons/pixel/second with a frame rate of 25 frames/second; Falcon I – 6 electrons/pixel/second; F416 – 50 electrons/pixel/second; US4000 – 40 electrons/pixel/second.

Figure 1.

Modeling of the noise power spectra of the K2 Summit detector operating in counting mode. A. NPS and sinc function fit (Eq. (12)) of an image recorded using the super-resolution mode of the detector. B. NPS and logistic function fit (Eq. (13)) of an image recorded using the simple counting mode.

Methods

Data collection

Images were recorded on several cameras: Falcon I and II (FEI), US4000 (Gatan), F416 (TVIPS), and DE-12 (Direct Electron), mounted on FEI Tecnai F20 microscopes; K2 Summit (Gatan), mounted on an FEI Tecnai F30 microscope; an additional Falcon I camera, mounted on an FEI Titan Krios microscope for comparison with the images recorded on the Tecnai F20. The Falcon I camera and Titan Krios microscope are part of a shared facility at the Janelia Farm Research Campus of the Howard Hughes Medical Institute. The shared facility is being used extensively and therefore allowed us to assess the degradation of the detector with total dose received (see Results). As test objects we used both the built-in microscope beam stops and 0.5 mm gold or platinum wires inserted at the beam stop position. The total dose in each image was about 50 electrons/pixel. The dose and the dose rate were measured using the microscopes’ fluorescent screen and manufacturers’ calibrations for the detectors, which were verified with a Faraday cup.

Estimation of the noise power spectrum

The NPS is sensitive to spurious features in recorded images that can be introduced, for example with a poor gain correction that is typically applied to an image recorded with an electronic detector. We monitored such image artifacts and reduced them to a minimum or eliminated them through careful operation of camera and microscope. We also implemented a feature in FindDQE that allows analysis of pairs of images. Provided the errors made in successively recorded images are similar, their influence on the NPS can be reduced if the NPS is calculated from the difference of these two images. The NPS calculated from the difference image must be divided by 2 to arrive at a NPS that is equivalent to that calculated from a single image.

Implementation

FindDQE is implemented in Fortran 90. Data processing was conducted on a Linux desktop workstation; processing of a 4096 × 4096 pixel image required approximately one hour of CPU time using an Intel Xeon X5365 3.00GHz CPU. To run FindDQE the input image has to be provided in MRC format (Crowther et al., 1996) together with either the gain conversion factor of the camera or the total electron dose used. Additional options allow the user to specify a second, flat field image to aid in NPS calculation (see below); indicate whether the image was taken in a program that divides counts in 16-bit images by 2 (such as SerialEM (Mastronarde, 2005)); and change the percentage of the NPS that is interpolated at low resolution.

Source code and executable Linux binary files are available for download from the author’s website (http://grigoriefflab.janelia.org/software).

Results

Performance of the silhouette method

The major advantage of the silhouette method over the more traditional knife-edge method is that it does not rely on a particular shape of test object. In Fig. 2A, we present the DQE curves measured for the Falcon detector using four different test objects: two different beam stops, a piece of 0.5 mm gold wire inserted at the beam stop position, and a piece of 0.5 mm platinum wire inserted at the same location. Fig. 2B–D show the images of three of the objects. The silhouette method returns essentially the same DQE whether a straight piece of wire or a more unevenly shaped beam stop is used. Based on the variance between these measurements, we estimate the error in the DQE measured by FindDQE to be 10%.

Figure 2.

Effect of beam stop shape on DQE. A. The DQE of the Falcon detector at 200 kV, using three different shapes of beam stop. The platinum wire images were taken at dose rates of 10 (blue line) and 3 electrons/pixel/second (purple line); the gold wire image and Brandeis pointer image used 6 electrons/pixel/second; the Janelia pointer image used 20 electrons/pixel/second, and was taken with a Falcon I detector mounted on a Titan Krios microscope located at the Janelia Farm Research Campus. B. Image of 0.5 mm diameter platinum wire inserted at beam stop position. C. Image of 0.5 mm gold wire inserted at beam stop position D. Image of the beam stop installed on a FEI TF20. The images in panels B – D were recorded using a Falcon I detector.

Comparison of scintillator-based detectors and DEDs

Fig. 3 shows the DQE curves for the US4000, F416, DE-12, Falcon I, Falcon II, and K2 Summit detectors for 200 keV electrons. The x-axis is the fraction of Nyquist frequency, i.e., 1 = 1/2p where p is the pixel size of the detector. Detector pixel sizes and dimensions are listed in Table 1. Table 2 summarizes our results, for 200 and 300 keV, giving key values of the DQE at 0, 0.5 and full Nyquist frequency for each detector and comparing the measurements with published values, where available.

Table 1.

Detector dimensions and pixel sizes.

Detector	Pixel Size (µm)	Pixel Dimensions
US4000	15	4080 × 4080
TVIPS F416	15.6	4096 × 4096
Falcon I	15	4096 × 4096
Falcon II	15	4096 × 4096
DE-12	6	4096 × 3072
K2 Summit	5	3840 × 3712

Table 2.

Summary of key DQE values and comparison to some previously published results. The estimated error of the FindDQE values is 10%. Published results for the US4000 and K2 Summit were found on the Gatan website (http://www.gatan.com/products/digital_imaging/products/K2/dqe.php). Published values for the K2 Summit camera varied between May and October 2013: we compare the values for 200 and 300 keV obtained in simple counting mode (no super-resolution) with those published on May 23, 2013. The remaining values were taken from the Gatan we page on October 23, 2013. The published values for the DE-12 camera were taken from the Direct Electron website (http://www.directelectron.com/cameras/de/performance/) on October 23, 2013.

Detector	Fraction of Nyquist	DQE (FindDQE)	Detector	Fraction of Nyquist	DQE (FindDQE)	DQE (published)
US4000 (120 keV)	0	0.47	US4000 (200 keV)	0	0.37	0.48
	0.5	0.20		0.5	0.11	0.11
	1	0.01		1	0.02	0.02
F416 (120 keV)	0	0.62	DE-12 (200 keV)	0	0.45	0.47
	0.5	0.32		0.5	0.37	0.35
	1	0.05		1	0.12	0.13
F416 (200 keV)	0	0.52	K2 Counting (200 keV)	0	0.75	0.82
	0.5	0.15		0.5	0.47	0.56
	1	0.07		1	0.15	0.13
Falcon I (120 keV)	0	0.76	K2 Counting (300 keV)	0	0.81	0.94
	0.5	0.18		0.5	0.54	0.55
	1	0.11		1	0.18	0.18
Falcon I (200 keV)	0	0.47	K2 Super-res. (200 keV)	0	0.79	0.84
	0.5	0.23		0.5	0.46	0.54
	1	0.09		1	0.22	0.20
Falcon I (300 keV)	0	0.50	K2 Super-res. (300 keV)	0	0.76	0.76
	0.5	0.36		0.5	0.55	0.55
	1	0.12		1	0.31	0.23
Falcon II (200 keV)	0	0.43
	0.5	0.32
	1	0.09

The US4000 detector has the lowest DQE at all resolutions, whereas the K2 Summit detector, in super-resolution mode, has the highest. The DE-12 performs almost as well as the K2 Summit at high frequencies, but falls short at lower frequencies. The Falcon I and II have lower DQEs at all frequencies than the other two DEDs; they are better than the F416 at high frequencies but not at low frequencies. One reason for the lower performance of the Falcon I detector is the thicker substrate of the detector chip which leads to backscattered electrons that produce additional noise (McMullan et al., 2009b). The detector chips built into the K2 Summit, DE-12, and Falcon II were backthinned to reduce noise and improve DQE.

Effect of beam energy on DQE

Electron energy is an important parameter determining the DQE of a detector. We measured the response of three different detectors (Falcon I, F416, and K2 Summit) using different beam energies (Fig. 4). In agreement with previous measurements (McMullan et al., 2009a), the MTF for non-counting devices shows a significant drop at low resolution (Fig. 4A, B) due to the scattering of electrons within the sensitive layer, leading to detector counts being generated up to tens of µm from the initial point of incidence (McMullan et al., 2009a). The distance traveled by scattering electrons within the sensitive layer increases with electron energy, leading to drops in the MTF over a narrowing range at lower resolution. However, at higher energies, electrons have a smaller scattering cross-section. They therefore generate fewer counts (deposit less energy) in a detector, as they are less likely to scatter. This lowers the overall DQE (Meyer and Kirkland, 1998) which is visible especially at low resolution (Fig. 4D, E). The situation is different for the K2 Summit, which was used in counting mode. MTF and DQE (Fig. 4C, F) are essentially unchanged between 200 and 300 keV, presumably because electrons at either energy generate sufficient signal to be reliably registered by the counting algorithm implemented in the K2 Summit.

Figure 4.

Effect of beam energy on Falcon I, F416 and K2 Summit MTF and DQE. Higher voltage leads to a faster drop in MTF at low resolution for both Falcon I and F416, due to scattering within a larger radius from the point of incidence of an electron. Smaller scattering cross-sections at higher voltage also decrease the DQE at lower resolution. MTF and DQE for the K2 Summit are essentially unchanged between 200 and 300 keV, presumably because electrons at either energy generate sufficient signal to be reliably registered by the counting algorithm implemented in the K2 Summit. The dose rates used were: Falcon I – 20 electrons/pixel/second; F416 – 50 electrons/pixel/second; K2 Summit in counting mode – 3 electrons/pixel/second.

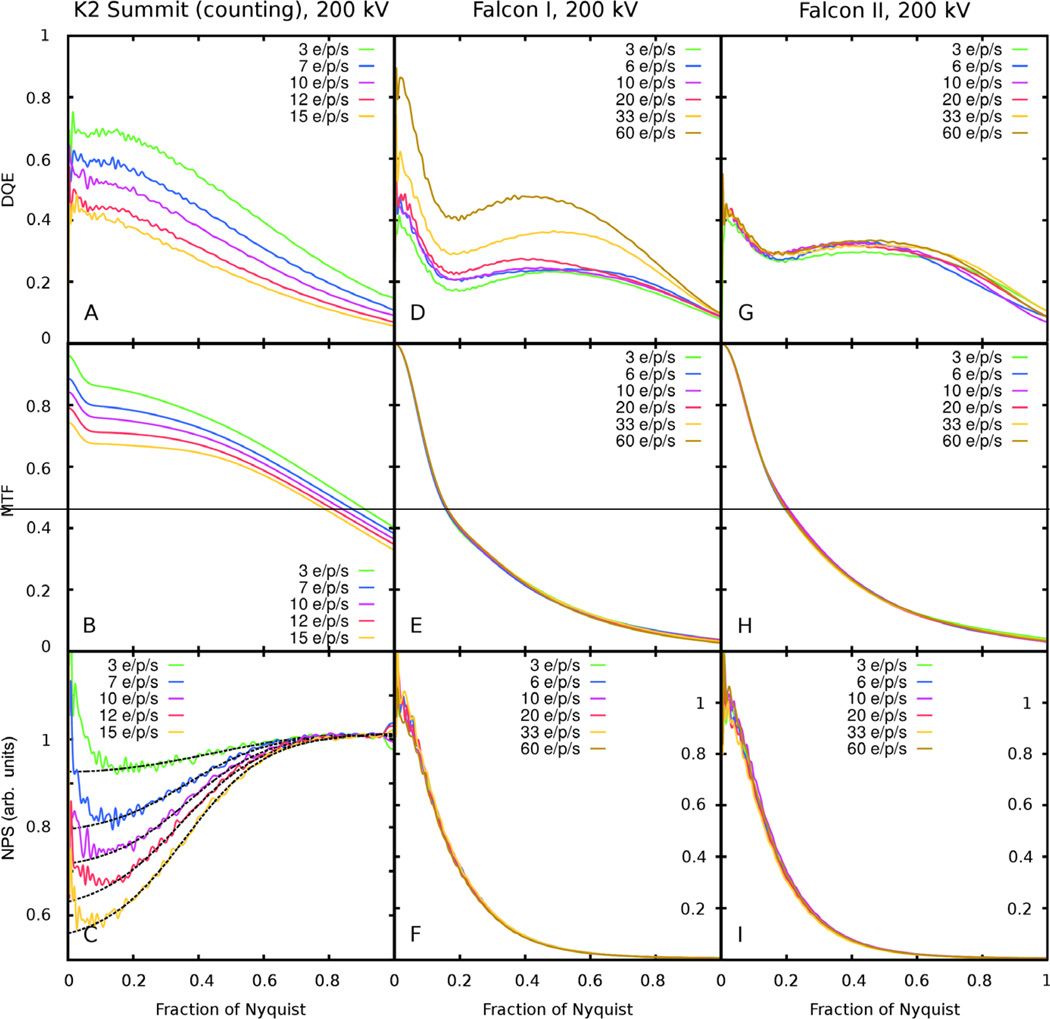
Effect of dose rate on direct electron detectors

The dose rates can affect detector performance when an image is recorded “frame-wise”, i.e. the final image is the result of a summation of individual frames recorded as a movie spanning the duration of the exposure (Brilot et al., 2012, Campbell et al., 2012, Li et al., 2013a,b, Bai et al., 2013). Existing DEDs record images frame-wise even if movies are not requested by the user because an incident electron typically generates hundreds of counts in a pixel. If the counts are not read out in short intervals the pixels will become saturated. In a counting device, such as the K2 Summit, an additional requirement is the avoidance of two or more electrons hitting the detector in close proximity and short succession (Li et al., 2013b). A counting detector will therefore have to operate with a frame rate of several hundred frames/second to enable dose rates that allow recording of images with exposure times of a few seconds, rather than hours.

We studied the detector performance of the K2 Summit, Falcon I and Falcon II detectors at different dose rates, including dose rates that noticeably degrade detector performance. Fig. 5A – C shows DQE, MTF, and normalized NPS (NPS/NPS(0)) for the K2 Summit operating in simple counting mode (no super-resolution) and used with dose rates of 3–15 electrons/pixel/second. The DQE decreases with increasing dose rate, especially at low frequencies. This is a consequence of changes in both the NPS and the MTF. At high dose rates, the counting algorithm fails to register more electrons than at lower dose rates, resulting in a depressed NPS and MTF at low frequency (as discussed in the Theory section). The small increase visible in the NPS at very low frequency (approximately 0–0.05 Nyquist) likely reflects residual unevenness in the flat field that may be due, for example, to small errors in gain correction.

Figure 5.

Response of DEDs to increasing dose rate. The K2 Summit (counting mode) DQE decreases with dose rate. B. The K2 Summit MTF also decreases with dose rate and, as a consequence of lost counts at higher dose rates does not reach 1 at low frequencies (see text). C. The K2 Summit normalized NPS increases with dose rate towards higher resolution, again reflecting missed counts. The Falcon I DQE shows an apparent increase with dose rate due to a non-linear response of the detector at higher dose rates. E, F. The Falcon I MTF and the normalized NPS do not change with dose rate. G, H, I. The Falcon II DQE, MTF, and normalized NPS do not change with dose rate.

Measured DQE, MTF, and normalized NPS curves for dose rates of 3–60 electrons/pixel/second for the Falcon I are shown in Fig. 5D–F, and for the Falcon II in Fig. 5G–I, respectively. At first glance, the DQE of the Falcon I appears to increase with increasing dose rate. However, this is likely an artifact produced by saturated pixels (see above). Fig. 5E and F show that both the MTF and the normalized NPS of the Falcon I remain approximately unchanged with dose rate. We found that, instead, the standard deviation of the noise decreases with increasing dose rate, despite the unchanged total dose (50 electrons/pixel), as shown in Fig. 6. This can be explained with the nonlinear response of the detector resulting from saturated pixels. The artifactual decrease of the noise at higher dose rates leads the observed inflation of the DQE. The DQE, MTF, and NPS of the Falcon II appear to be essentially dose-rate independent, even when a relatively high dose rate of 60 electrons/pixel/second is used (Fig. 5G–I).

Figure 6.

Falcon I response at high dose rates. The standard deviation of counts observed in flat field images with increasing dose rate decreases with increasing dose rate, although the total dose applied (50 electrons/pixel) remained constant. This may reflect nonlinearity in the sensor element response due to saturation. The dose rates are displayed on a log scale for ease of viewing.

Effect of total lifetime dose on direct electron detectors

DEDs are built to withstand the high-energy electron radiation of a typical cryo-EM experiment. However, the electronic components inside a CMOS chip may be damaged over time as a result of energy deposited during inelastic scattering events. We were able to document the performance at two time points of one of the direct detectors tested here. Fig. 7 shows two DQE curves of the Falcon I detector mounted on the Titan Krios at the Janelia Farm Research Campus. The Janelia facility is used regularly for 24-hour data collection, five days a week; therefore, a fairly large total lifetime dose accumulates over only a few months. One DQE curve was calculated using data recorded when the detector had received a total lifetime dose of about 5 million electrons/pixel while the second curve shows the DQE at a total dose of about 35 million electrons/pixel. The two curves agree with each other within their estimated error, suggesting that a total dose of 35 million electrons/pixel can easily be tolerated by this camera. Other cameras might exhibit different tolerances; further experiments are needed for a more systematic evaluation of radiation damage to DEDs.

Figure 7.

Comparison of DQE curves calculated for the Falcon I camera after exposure to total lifetime doses of 5 million and 35 million electrons/pixel. The data was collected at 300 keV and with a dose rate of 20 electrons/pixel/second. The DQE curve for the lower total dose exhibits slightly increased values at high resolution. This may be due to a somewhat uneven illumination of the detector.

Discussion

We present here a software tool to measure the DQE of electron detectors for TEM from images of the microscope’s built-in beam stop, making DQE measurements easily accessible to users. We evaluated a range of detectors: three DEDs currently available, a CMOS scintillator-based camera, and a CCD scintillator-based camera. Our measurements are in good agreement with previous assessments and manufacturer's specifications. The estimated 10% error in the DQE measurements allows users to optimize data collection protocols (e.g. dose rate), monitor detector performance over time, and compare different detectors. Table 2 shows that DEDs have higher DQEs than scintillator-based detectors; the K2 Summit in super-resolution mode has the highest DQE overall.

DQE measurements obtained by FindDQE can be affected by imaging artifacts that can be introduced, for example, by a damaged detector, or by an improperly applied or poor gain correction. These spurious features can alter the apparent MTF and, with it, DQE. It is therefore good practice to carefully monitor image quality, for example by inspecting the Fourier transform, and to record a new gain reference before DQE evaluation. In the case of the K2 Summit operated in super-resolution mode it was difficult to obtain images that were completely free of artifactual features, which can readily be detected in Fourier transforms (see Fig. 8). Depending on the nature of these features, DQE measurements can be inflated or depressed. The origin of these features is not entirely clear but may be related to camera software issues that are still being addressed by the manufacturer.

Figure 8.

Spurious features in images collected using the K2 Summit detector in super-resolution mode. A. Flat field image recorded at 200 keV. B. Fourier transform of the image in A, showing a vertical line originating that indicates image artifacts. The dose rate used was 4 electrons/pixel/second (same beam and exposure time as for the pointer image used to calculate the DQE curve in Fig. 2).

Another factor affecting the performance of FindDQE is the total dose of the test image. At a dose significantly lower than 50 electrons/pixel, fitting of the MTF is affected by image noise. It is therefore important to accumulate a sufficient average dose/pixel for reliable DQE measurements.

Previous studies have found that the DQE at zero Nyquist frequency, DQE(0), is difficult to measure directly (McMullan et al., 2009a). The lowest frequency components of the NPS are represented by only a small number of Fourier terms, making measurements unreliable due to noise. However, DQE(0) is an important quantity because it indicates the percentage of the electrons that are detected. To estimate DQE(0) we calculate an average value of the NPS between 0.02 and 0.03 Nyquist frequency and use this value with Eq. (6) to calculate DQE(0). In addition the NPS is smoothed using a cubic spline function to suppress noise in the calculation of the DQE curve.

Our results show that the DQE(0) values and low to mid frequency DQEs of the Falcon I and K2 Summit detectors are greatly affected by dose rate. The K2 counting algorithm can miss counts when two detection events fall too close together; it can also register spurious events due to electron scattering at large distances from the point of incidence. The Falcon sensor elements appear to saturate at high dose rate; this causes a decrease in the standard deviation of the noise and an artificially increased DQE. It is therefore important that these new devices are used with an appropriately low dose rate to take advantage of their full potential. Our results suggest that a maximum dose rate of about 20 electrons/pixel/second or lower be used for the Falcon I and a dose rate lower than about 5 electrons/pixel/second for the K2 Summit detector when operated in counting mode.

DEDs hold great promise for the future of high-resolution cryo-EM. High-resolution structures of proteins imaged with direct detectors have already been published (Bai et al., 2013, Li et al., 2013a) using smaller datasets compared to what was needed previously to obtain similar results. FindDQE should help users optimize their imaging systems for further success.