Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2013 May 3;117(23):12258–12265. doi: 10.1021/jp4041106

Exploiting the Synergy of Powder X-ray Diffraction and Solid-State NMR Spectroscopy in Structure Determination of Organic Molecular Solids

Dmytro V Dudenko †,‡, P Andrew Williams †, Colan E Hughes †, Oleg N Antzutkin ‡,§, Sitaram P Velaga ∥, Steven P Brown ‡, Kenneth D M Harris †,*
PMCID: PMC3876745  PMID: 24386493

Abstract

graphic file with name jp-2013-041106_0009.jpg

We report a strategy for structure determination of organic materials in which complete solid-state nuclear magnetic resonance (NMR) spectral data is utilized within the context of structure determination from powder X-ray diffraction (XRD) data. Following determination of the crystal structure from powder XRD data, first-principles density functional theory-based techniques within the GIPAW approach are exploited to calculate the solid-state NMR data for the structure, followed by careful scrutiny of the agreement with experimental solid-state NMR data. The successful application of this approach is demonstrated by structure determination of the 1:1 cocrystal of indomethacin and nicotinamide. The 1H and 13C chemical shifts calculated for the crystal structure determined from the powder XRD data are in excellent agreement with those measured experimentally, notably including the two-dimensional correlation of 1H and 13C chemical shifts for directly bonded 13C–1H moieties. The key feature of this combined approach is that the quality of the structure determined is assessed both against experimental powder XRD data and against experimental solid-state NMR data, thus providing a very robust validation of the veracity of the structure.

1. Introduction

In general, in order to understand and rationalize the physicochemical properties of crystalline solids, an essential prerequisite is to establish the structural properties of the material of interest. As a consequence, the development of new and improved strategies for determining the structural properties of crystalline materials has the potential to make significant impact across the broad range of fields within the physical sciences in which knowledge of crystal structure is required. Although single-crystal X-ray diffraction (XRD) is the most powerful and routine technique for determining the structural properties of crystalline solids, the requirement for a single-crystal specimen of appropriate size and quality imposes a limitation on the scope of this technique. Indeed, many crystalline solids exist only as microcrystalline powders and are therefore not suitable for investigation by single-crystal XRD. To establish the structural properties of such materials, the most direct approach is to use powder XRD, although it is important to emphasize that carrying out structure determination from powder XRD data is significantly more challenging than from single-crystal XRD data. However, the opportunities in this regard have improved significantly in recent years as a consequence of progress in the development of new data analysis techniques1−9 (such as the direct-space strategy for structure solution, which has made a particularly significant impact in the case of structure determination of organic molecular solids from powder XRD data).

In order to allow the methodology for structure determination from powder XRD data to be extended to cases of increasing structural complexity, we are interested in exploring opportunities to introduce information derived from other experimental and/or computational techniques within the structure determination process. In this regard, given the complementary nature of powder XRD and solid-state nuclear magnetic resonance (NMR) spectroscopy as techniques for probing the structural properties of solids, there is considerable potential to include an assessment of solid-state NMR data at appropriate stages within the structure determination process. In the context of structure determination of organic molecular solids from powder XRD data, solid-state NMR has so far been used only in a rather peripheral manner,10 by providing insights on specific structural aspects that either assist in setting up the correct structural model for a direct-space structure solution calculation or help in validating the final structure obtained from Rietveld refinement (examples of the insights obtained from NMR data include the number of independent molecules in the asymmetric unit, the tautomeric form of the molecule, the existence of specific interactions, the existence of disorder, and the values of specific interatomic distances). There is considerable scope for solid-state NMR and powder XRD to be used more closely in tandem, particularly by developing combined approaches that exploit the enhanced information content of two-dimensional solid-state NMR spectra as well as the power of first-principles computational techniques, notably the GIPAW (Gauge Including Projector Augmented Wave) approach,11−13 that allow solid-state NMR spectra to be predicted reliably from a crystal structure. Clearly, the opportunity to carry out such calculations for crystal structures generated in the context of structure determination from powder XRD data, together with an assessment of the quality of agreement between calculated and experimental solid-state NMR data, would provide a powerful and robust assessment of the veracity and quality of the crystal structure.

In the present article, we report a combined approach of this type and demonstrate the successful application of this approach for structure determination of the 1:1 cocrystal containing indomethacin (denoted IND; Scheme 1) and nicotinamide (denoted NIC; Scheme 1). Structure determination of this material, which is of relevance in pharmaceutical research,14−17 was carried out directly from powder XRD data using the direct-space strategy for structure solution followed by Rietveld refinement. For the fully refined crystal structure, the isotropic 1H and 13C NMR chemical shifts were calculated under periodic boundary conditions by the GIPAW method based on density functional theory (DFT) employing a plane-wave basis set and pseudopotentials. The calculated chemical shifts are found to be in excellent agreement with the corresponding chemical shifts measured experimentally by solid-state NMR,18 yielding a robust confirmation of the structure determined from the powder XRD data.

Scheme 1. Molecular Structures of (a) Indomethacin (IND) and (b) Nicotinamide (NIC).

Scheme 1

Open in a new tab

2. Experimental Section

A polycrystalline sample of the IND–NIC cocrystal was prepared using the method described previously.18 The powder XRD pattern of this material was recorded at 294 K on a Bruker D8 instrument using Ge-monochromated CuKα1 radiation and operating in transmission mode with a foil type sample holder (data collection time ca. 39.5 h). Experimental solid-state NMR data for the IND–NIC cocrystal have been reported previously,18 comprising two-dimensional 1H double quantum and 14N–1H and 1H–13C heteronuclear MAS NMR spectra recorded at 1H Larmor frequencies of 500 and 850 MHz. The isotropic 1H and 13C NMR chemical shifts determined in this previous study were used as the experimental NMR data in the present work.

The powder XRD pattern of the IND–NIC cocrystal was indexed using the ITO19 code in the program CRYSFIRE,20 giving the following unit cell with monoclinic metric symmetry: a = 27.38 Å, b = 5.02 Å, c = 17.19 Å, β = 97.4° (V = 2343.1 Å3). Given the volume of this unit cell and consideration of density, the number of formula units in the unit cell was assigned as Z = 4. From systematic absences, the space group was assigned as P21/a (corresponding to Z′ = 1). Profile fitting using the Le Bail method,21 implemented in the program GSAS,22 gave a good quality of fit (Rwp = 1.53%, Rp = 1.16%). The refined unit cell and profile parameters obtained in the Le Bail fitting procedure were used in the subsequent structure solution calculation.

Structure solution was carried out using the direct-space genetic algorithm (GA) technique23−26 incorporated in the program EAGER.27−32 In the GA structure solution calculation, the IND molecule was defined by a total of 11 structural variables (three positional variables, three orientational variables, and five torsion-angle variables), and the NIC molecule was defined by a total of seven structural variables (three positional variables, three orientational variables, and one torsion-angle variable). Each GA structure solution calculation involved the evolution of 100 generations for a population of 100 structures, with 10 mating operations and 50 mutation operations carried out per generation. In total, 16 independent GA calculations were carried out, with the same good-quality structure solution obtained in 12 cases.

The best structure solution was used as the initial structural model for Rietveld refinement, which was carried out using the GSAS program.22 Standard restraints were applied to bond lengths and bond angles, planar restraints were applied to aromatic rings, and a single isotropic displacement parameter was refined for each molecule, with the value for the hydrogen atoms fixed at 1.2 times the value for the non-hydrogen atoms. Preferred orientation was taken into account using the March–Dollase function.33,34 The known crystal structure of pure IND was included as a second phase in the refinement, as an impurity amount of this phase was present in the sample of the IND–NIC cocrystal used in the present work.

DFT calculations were carried out using CASTEP (Accelrys, San Diego, CA)35 Academic Release version 6.0.1, which implements DFT within a generalized gradient approximation and the plane-wave pseudopotential approach. All calculations used the Perdew–Burke–Ernzerhof exchange-correlation functional36 with ultrasoft pseudopotentials37 and a basis set cutoff energy of 700 eV. The crystal structure of IND–NIC determined from the powder XRD data was used as the starting structure for geometry optimization, in which the positions of all 56 atoms in the asymmetric unit were relaxed, the unit cell was fixed, the space group symmetry (P21/a) was preserved, and periodic boundary conditions were applied.

The NMR chemical shift calculations (carried out on the geometry optimized structure) employed the GIPAW method11−13 to determine the shielding tensor for each nucleus in the crystal structure. The calculations used a plane-wave basis set with a maximum cutoff energy of 700 eV, with integrals taken over the Brillouin zone by using a Monkhorst–Pack grid of minimum sample spacing 0.1 × 2π Å–1. To compare the results directly with experimentally measured isotropic chemical shifts, the following conversion was used: δiso = σref – σiso, where σiso is the absolute isotropic shielding value generated from the CASTEP calculation. The reference shieldings were established by considering the mean value of the experimental isotropic chemical shifts and the mean value of the calculated shieldings,13,38 giving σref values of 167.3 ppm for 13C and 30.9 ppm for 1H.

3. Results and Discussion

3.1. Structure Determination from Powder XRD Data

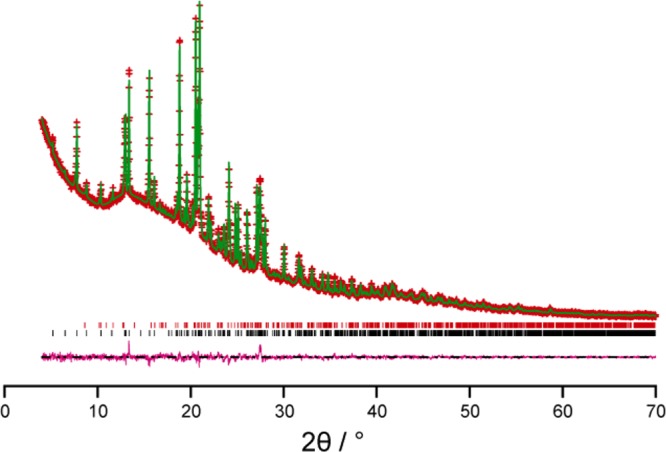
The crystal structure of IND–NIC was determined in the present work directly from powder XRD data, employing the direct-space genetic algorithm technique for structure solution followed by Rietveld refinement. Full details of the methodology and strategy are given in the Experimental section. The final Rietveld refinement gave an excellent fit to the powder XRD data (Rwp = 1.85%, Rp = 1.37%; Figure 1) with the following refined parameters: a = 27.3847(10) Å, b = 5.01906(16) Å, c = 17.1935(6) Å, β = 97.3103(20)°; V = 2343.96(21) Å3 (space group, P21/a; 2θ range, 4 to 70°; 3867 profile points; 238 refined variables). As now discussed, the crystal structure was validated by assessing the level of agreement between DFT-calculated solid-state 1H and 13C NMR data and the corresponding experimental solid-state 1H and 13C NMR data.

Figure 1.

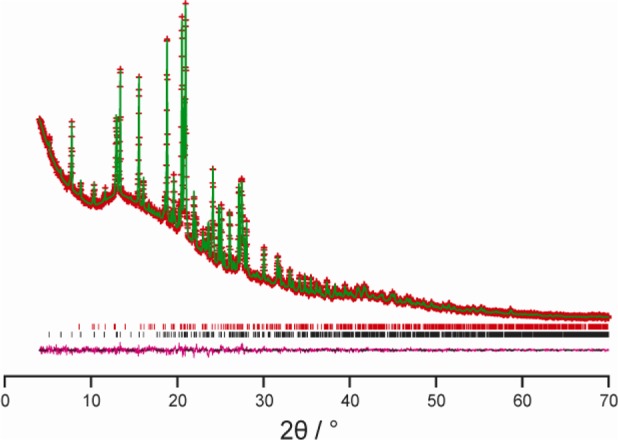
Figure 1

Open in a new tab

Final Rietveld refinement for the IND–NIC cocrystal, showing the experimental (red + marks), calculated (green solid line), and difference (purple lower line) powder XRD profiles. Tick marks indicate peak positions (black represents the IND–NIC cocrystal, and red represents an impurity of the pure phase of IND).

3.2. Structure Validation from Consideration of Solid-State 1H and 13C NMR Data

Geometry optimization of the crystal structure of IND–NIC using CASTEP (see Experimental section for details), starting from the crystal structure determined from powder XRD data, leads to only very minor shifts in atomic positions [Figure 2; for non-hydrogen atoms, the mean atomic displacement is 0.077 Å, and the largest displacement is 0.14 Å], confirming that the crystal structure determined from the powder XRD data lies very close to an energy minimum for this system. As a further indication of the close similarity of the DFT-optimized structure and the final refined structure from the powder XRD data, the fit of the optimized structure to the powder XRD data was assessed by taking the optimized structure as a fixed structural model in a Rietveld refinement calculation (with only the nonstructural parameters refined). As shown in Figure 3, this calculation reveals that the DFT-optimized structure gives an excellent quality of fit to the experimental powder XRD data (Rwp = 1.99%, Rp = 1.48%).

Figure 2.

Figure 2

Open in a new tab

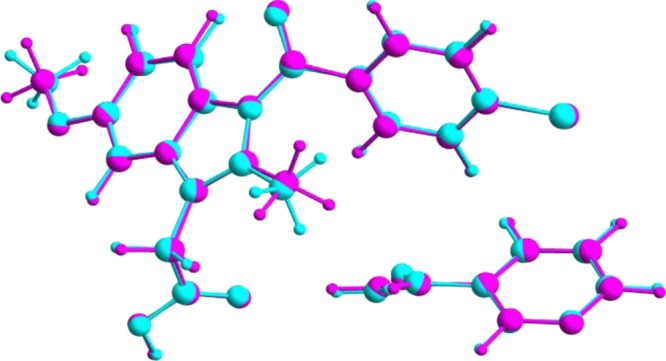
Overlay (viewed along the b-axis) of the asymmetric unit in the crystal structure of IND–NIC determined from powder XRD data (cyan) and the asymmetric unit in the relaxed crystal structure resulting from the DFT geometry optimization calculation using CASTEP (magenta).

Figure 3.

Figure 3

Open in a new tab

Rietveld refinement taking the DFT-optimized structure of IND–NIC as a fixed structural model, with only the nonstructural parameters refined. The experimental (red + marks), calculated (green solid line), and difference (purple lower line) powder XRD profiles are shown. Tick marks indicate peak positions (black represents the IND–NIC cocrystal, and red represents an impurity of the pure phase of IND).

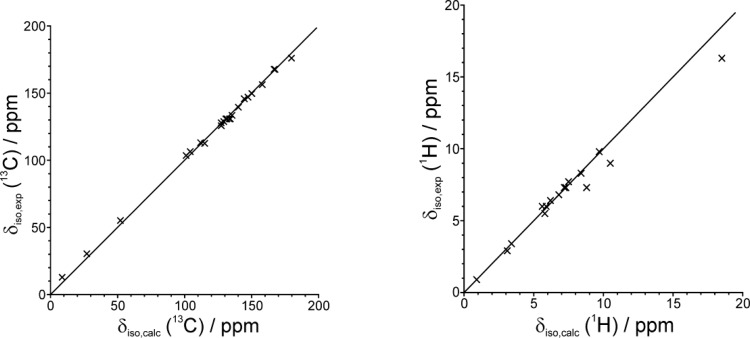
It is well established that GIPAW calculations reliably reproduce experimental NMR chemical shifts for cases with known crystal structures determined from single-crystal XRD, with agreement typically better than ±0.3 ppm for 1H and ±3 ppm for 13C chemical shifts.38−51 Thus, comparison of chemical shifts calculated using the GIPAW method for the crystal structure of IND–NIC determined here from powder XRD data represents a robust and independent validation of the structure. Indeed, the 1H and 13C NMR chemical shifts calculated for the geometry optimized structure are in excellent agreement (see Figure 4 and Table 1) with the corresponding experimental solid-state NMR data published previously18 (the slightly poorer agreement in the 1H chemical shifts for the three hydrogen-bonded protons is discussed below).

Figure 4.

Figure 4

Open in a new tab

Comparison of experimental and calculated (GIPAW) values of the isotropic 13C and 1H chemical shifts for IND–NIC. The comparatively poorer agreement in the 1H chemical shifts for the three hydrogen-bonded protons is discussed in the text.

Table 1. Calculated and Experimental 1H and 13C Chemical Shifts for the IND–NIC Cocrystal.

IND 1H(σiso) 13C(σiso) 1H(δiso)a 13C(δiso)b 1H(δiso,exp) 13C(δiso,exp)
1   31.9   135.4   133.5
2   52.3   115.0   112.6
3   36.6   130.7   130.8
4 24.1 66.2 6.8 101.1 6.8 103.6
5   9.4   157.9   156.3
6 25.1 63.1 5.8 104.2 5.5 106.5
7 23.6 55.4 7.3 111.9 7.3 113.1
8   38.1   129.2   128.8
9 27.5 140.3 3.4 27.0 3.4 30.4
10   –12.4   179.7   176.0
11 27.8 115.2 3.1 52.1 2.9 55.2
12 30.0 158.7 0.9 8.6 0.9 12.9
13   –0.1   167.4   167.7
14   33.9   133.4   130.8
15c 25.3 38.1 5.6 129.2 6.0 128.8
16c 23.7 36.2 7.2 131.1 7.3 130.8
17c   22.9   144.4   146.0
18c 25.0 40.0 5.9 127.3 6.0 127.9
19 24.7 35.7 6.2 131.6 6.4 130.8
OH 12.4   18.5   16.3  
NIC 1H(σiso) 13C(σiso) 1H(δiso)a 13C(δiso)b 1H(δiso,exp) 13C(δiso,exp)
1 21.2 20.1 9.7 147.2 9.8 147.0
2   33.2   134.1   130.8
3 23.4 27.2 7.5 140.1 7.7 139.5
4 22.5 39.9 8.4 127.4 8.3 125.8
5 21.2 17.2 9.7 150.1 9.8 149.7
6   0.6   166.7   167.7
NH2ad 20.4   10.5   9.0  
NH2be 22.1   8.8   7.3  
Open in a new tab
a

δiso = −(σiso – σref), with σref = 30.9 ppm for 1H.

b

δiso = −(σiso – σref), with σref = 167.3 ppm for 13C.

c

Reassignments compared to those stated in Table S1 of ref (18).

d

The H atom forming the N–H···O hydrogen bond between NIC(1) and NIC(3) [in the structure determined from powder XRD: N···O, 2.95 Å; N–H···O, 170.6°].

e

The H atom forming the N–H···O hydrogen bond between NIC(1) and IND(1) [[in the structure determined from powder XRD: N···O, 2.99 Å; N–H···O, 163.5°].

In addition to the good agreement between experimental and calculated chemical shifts considered separately for the isotropic 1H and 13C chemical shifts (as shown in Figure 4), an even more robust test is to consider the two-dimensional 1H and 13C NMR chemical shift correlations for directly bonded CH, CH2, and CH3 moieties, for which excellent agreement between experimental and calculated data is again achieved (Figure 5). Specifically, for the aromatic CH resonances, very good reproduction of the experimental two-dimensional 1H–13C correlation spectrum is obtained. In particular, the mean and highest differences between experimental and calculated chemical shifts are as follows: for 1H, 0.4 ppm (mean), 2.2 ppm (highest); for 13C, 1.6 ppm (mean), 4.3 ppm (highest).

Figure 5.

Figure 5

Open in a new tab

Calculated (GIPAW) 1H and 13C chemical shifts (red crosses) for directly bonded CH, CH2, and CH3 moieties in the IND–NIC cocrystal overlaid on the experimental 1H–13C correlation NMR spectrum (as presented in ref (18)).

Considering Figure 4, the only significant differences arise in the case of the 1H chemical shifts for the OH group of IND (exptl, 16.3 ppm; calcd, 18.5 ppm) and for the two 1H environments in the NH2 group of NIC (exptl, 9.0 and 7.3 ppm; calcd, 10.5 and 8.8 ppm). However, we note that the difference (1.7 ppm) between the experimental 1H chemical shifts of the two NH2 protons is exactly reproduced by the calculation. The observation that the experimental 1H chemical shift is ca. 2 ppm lower than the calculated value in these cases is a consequence of the known temperature dependence of 1H chemical shifts of hydrogen-bonded protons43,47,52 and the well-established fact50,53,54 that geometry optimization yields a static hydrogen-bonded structure, whereas the actual structure probed experimentally at ambient temperature is flexible/dynamic. As a consequence, geometry optimization produces a structure with stronger hydrogen bonding and hence higher 1H chemical shifts. We note that improved agreement between the experimental and calculated 1H chemical shifts for these groups may be expected to result from the use of molecular dynamics simulation techniques50,55 as a further assessment of the veracity of the final refined crystal structure.

3.3. Discussion of Crystal Structure of IND–NIC

In the crystal structure of IND–NIC (Figure 6a), the molecules form a helical hydrogen-bonded motif that follows the 21 screw axis (parallel to the b-axis) and is constructed from an alternating arrangement of IND and NIC molecules: NIC(1)···IND(1)···NIC(2)···IND(2)···NIC(3)···IND(3). The repeat unit comprises one molecule of each type [e.g., NIC(1)···IND(1) in the above designation]. Thus, NIC(1)···IND(1) and NIC(2)···IND(2) are related to each other by the 21 screw operation, whereas NIC(1)···IND(1) and NIC(3)···IND(3) are related by the unit cell translation along the b-axis. Within the helical hydrogen-bonded chain, the NIC(1)···IND(1) interaction is an N–H···O hydrogen bond (N···O, 2.99 Å; N–H···O, 163.5°) involving an N–H bond of NIC as the donor and the O=C oxygen of the carboxylic acid group of IND as the acceptor, and the IND(1)···NIC(2) interaction is an O–H···N hydrogen bond (O···N, 2.63 Å; O–H···N, 173.7°) involving the O–H bond of the carboxylic acid group of IND as the donor and the nitrogen atom in the heterocyclic ring of NIC as the acceptor (all hydrogen-bond geometries quoted here refer to the experimental structure determined from powder XRD data). In addition, alternate NIC molecules along the helical chain [i.e., those related by the unit cell translation along the b-axis, such as NIC(1) and NIC(3)] are linked by an N–H···O hydrogen bond (N···O, 2.95 Å; N–H···O, 170.6°), giving rise to a linear hydrogen-bonded motif that runs parallel to the b-axis (Figure 6b).

Figure 6.

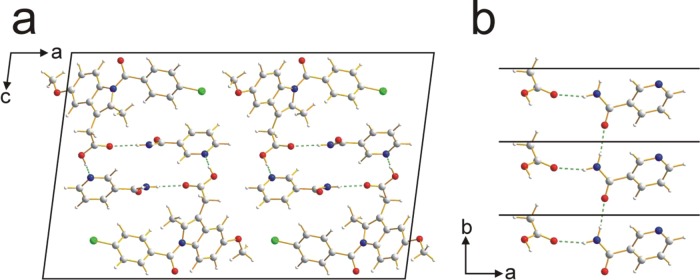
Figure 6

Open in a new tab

(a) Crystal structure of the IND–NIC cocrystal viewed along the b-axis. (b) Part of the crystal structure, viewed along the c-axis, illustrating the linear hydrogen-bonded chain, running parallel to the b-axis, involving the amide groups of NIC molecules (black lines denote the unit cell repeat along the b-axis; the −CH2CO2H moieties of IND molecules are also shown, illustrating the additional hydrogen bonding involving the amide group of NIC). In both panels, hydrogen bonds are indicated by green dashed lines.

The hydrogen bonding observed in the crystal structure of IND–NIC verifies previous insights deduced from a comprehensive solid-state NMR study of this material.18 In particular, the solid-state NMR study identified the strong O–H···N hydrogen bond discussed above, together with a weak C–H···O=C interaction involving an aromatic C–H bond of the same molecule of NIC and the O=C oxygen of the same carboxylic acid group of IND. This C–H···O=C interaction (C···O, 3.16 Å; C–H···O, 129.8°) is also identified in the crystal structure reported here, although, as it is geometrically far from optimal, we refrain from ascribing it as a significant hydrogen bond.41,44

4. Concluding Remarks

In conclusion, we emphasize that the approach developed in the present article for using complete solid-state NMR spectral data within the context of structure determination from powder XRD data allows the quality of the crystal structure determined from the powder XRD data to be assessed and validated both against the experimental powder XRD data (in the Rietveld refinement) and against the experimental solid-state NMR data (in the subsequent comparison of calculated and experimental chemical shifts). As a consequence, this approach provides a stringent and robust assessment of the validity and quality of the refined crystal structure, particularly when the two-dimensional correlation of 1H and 13C chemical shifts for directly bonded 13C–1H moieties is included in the assessment.

While the combined approach employed in the present work represents the first example of the use of ab initio structure determination of an organic molecular solid from powder XRD data followed by rigorous assessment of the refined structure against complete solid-state 1H and 13C NMR spectral data, we note that DFT-calculated solid-state NMR data have been used in various manifestations within the process of structure determination of other types of solid materials from powder XRD data. Examples include a number of strategies for the structure determination of inorganic framework structures57,58 and hybrid organic–inorganic materials,59 as well as for elucidating specific structural details (in particular, hydrogen-bonding arrangements) for materials of mineralogical interest.60,61 In addition, DFT-based chemical shift calculations have been employed successfully to augment the process of structure determination of an organic polymer from wide-angle X-ray and wide-angle neutron diffraction techniques.62 We also note that, in proof of principle investigations,51,63 comparison between GIPAW calculations and experimental solid-state 1H NMR data has been employed within crystal structure prediction studies for small organic molecules; although demonstrated only in the case of known structures (determined previously by XRD), the work has shown that assessment of the solid-state NMR data provides a viable approach for selecting the correct structure from among those generated by the crystal structure prediction algorithm.

While techniques for successfully determining the crystal structures of organic materials directly from powder XRD data have been in use for almost 20 years, it is the much more recent advances56 in the methodology for first-principles calculation of solid-state NMR data from known crystal structures that has now created the opportunity to propose and demonstrate our combined approach in which the refined crystal structure is scrutinized against complete solid-state 1H and 13C NMR spectral data. We anticipate that this combined approach will be utilized extensively in the future and may play an important role in enabling the application of powder XRD methodology to be extended to tackle increasingly complex structural problems.

Acknowledgments

We are grateful to EPSRC (postdoctoral funding for D.V.D.) for financial support under EPSRC Award EP/J010510/1 (Collaborative Computational Project for NMR Crystallography, CCP–NC). Helpful discussions within the CCP–NC project, in particular with Paul Hodgkinson and Jonathan Yates, are acknowledged. We acknowledge the use of previously published solid-state NMR results,18 including data recorded at the UK 850 MHz Solid-State NMR Facility, which was funded by EPSRC and BBSRC as well as the University of Warwick including via part funding through Birmingham Science City Advanced Materials Projects 1 and 2 supported by Advantage West Midlands (AWM) and the European Regional Development Fund (ERDF). EAGER calculations were performed on the Advanced Research Computing @ Cardiff (ARCCA) HPC cluster Raven. CASTEP calculations were performed on the University of Warwick Centre for Scientific Computing cluster. We are grateful to Accelrys for providing the Materials Studio Interface for NMR calculations.

Supporting Information Available

Crystallographic information (cif) file for the crystal structure determined from powder XRD data, cif file for the crystal structure after geometry optimization using CASTEP, tabulations of experimental and calculated 1H and 13C chemical shifts and other calculated solid-state NMR data, and the input files for CASTEP calculations (both geometry optimization and calculations of solid-state NMR data). This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

jp4041106_si_001.pdf (130.7KB, pdf)
jp4041106_si_002.cif (13.2KB, cif)
jp4041106_si_003.cif (2.6KB, cif)
jp4041106_si_004.pdf (89KB, pdf)

References

  1. Harris K. D. M.; Tremayne M.; Lightfoot P.; Bruce P. G. Crystal Structure Determination from Powder Diffraction Data by Monte Carlo Methods. J. Am. Chem. Soc. 1994, 116, 3543–3547. [Google Scholar]
  2. Langford J. I.; Louër D. Powder Diffraction. Rep. Prog. Phys. 1996, 59, 131–234. [Google Scholar]
  3. Elizabé L.; Kariuki B. M.; Harris K. D. M.; Tremayne M.; Epple M.; Thomas J. M. Topochemical Rationalization of the Solid-State Polymerization Reaction of Sodium Chloroacetate: Structure Determination from Powder Diffraction Data by the Monte Carlo Method. J. Phys. Chem. B 1997, 101, 8827–8831. [Google Scholar]
  4. Harris K. D. M.; Tremayne M.; Kariuki B. M. Contemporary Advances in the Use of Powder X-ray Diffraction for Structure Determination. Angew. Chem., Int. Ed. 2001, 40, 1626–1651. [DOI] [PubMed] [Google Scholar]
  5. David W. I. F., Shankland K., McCusker L. B., Baerlocher C., Eds. Structure Determination from Powder Diffraction Data; IUCr/OUP: Oxford, U.K., 2002. [Google Scholar]
  6. Martinetto P.; Terech P.; Grand A.; Ramasseul R.; Dooryhee E.; Anne M. Molecular Structure of a d-Homoandrostanyl Steroid Derivative: Single Crystal and Powder Diffraction Analyses. J. Phys. Chem. B 2006, 110, 15127–15133. [DOI] [PubMed] [Google Scholar]
  7. Zhou Z.; Siegler V.; Cheung E. Y.; Habershon S.; Harris K. D. M.; Johnston R. L. Advantages of a Redefinition of Variable-Space in Direct-Space Structure Solution from Powder X-ray Diffraction Data. ChemPhysChem 2007, 8, 650–653. [DOI] [PubMed] [Google Scholar]
  8. David W. I. F.; Shankland K. Structure Determination from Powder Diffraction Data. Acta Crystallogr., Sect. A: Found. Crystallogr. 2008, 64, 52–64. [DOI] [PubMed] [Google Scholar]
  9. Fujii K.; Uekusa H.; Itoda N.; Hasegawa G.; Yonemochi E.; Terada K.; Pan Z.; Harris K. D. M. Physicochemical Understanding of Polymorphism and Solid-State Dehydration/Rehydration Processes for the Pharmaceutical Material Acrinol, by ab Initio Powder X-ray Diffraction Analysis and Other Techniques. J. Phys. Chem. C 2010, 114, 580–586. [Google Scholar]
  10. Harris K. D. M.; Xu M. In NMR Crystallography; Harris R. K., Wasylishen R., Duer M. J., Eds.; Wiley: Chichester, U.K., 2009; pp 275–287. [Google Scholar]
  11. Pickard C. J.; Mauri F. All-Electron Magnetic Response with Pseudopotentials: NMR Chemical Shifts. Phys. Rev. B 2001, 63, 245101. [Google Scholar]
  12. Yates J. R.; Pickard C. J.; Mauri F. Calculation of NMR Chemical Shifts for Extended Systems using Ultrasoft Pseudopotentials. Phys. Rev. B 2007, 76, 024401. [Google Scholar]
  13. Harris R. K.; Hodgkinson P.; Pickard C. J.; Yates J. R.; Zorin V. Chemical Shift Computations on a Crystallographic Basis: Some Reflections and Comments. Magn. Reson. Chem. 2007, 45, S174–S186. [DOI] [PubMed] [Google Scholar]
  14. Alhalaweh A.; Velaga S. P. Formation of Cocrystals from Stoichiometric Solutions of Incongruently Saturating Systems by Spray Drying. Cryst. Growth Des. 2010, 10, 3302–3305. [Google Scholar]
  15. Alhalaweh A.; Sokolowski A.; Rodriguez-Hornedo N.; Velaga S. P. Solubility Behavior and Solution Chemistry of Indomethacin Cocrystals in Organic Solvents. Cryst. Growth Des. 2011, 11, 3923–3929. [Google Scholar]
  16. Alhalaweh A.; Arora K. K.; Suryanarayanan R.; Velaga S. P.. Crystallization Behavior of Melt-Quenched Indomethacin Cocrystals; AAPS: Washington, D.C., 2011. [Google Scholar]
  17. Bogdanova S.; Sidzhakova D.; Karaivanova V.; Georgieva S. Aspects of the Interactions Between Indomethacin and Nicotinamide in Solid Dispersions. Int. J. Pharm. 1998, 163, 1–10. [Google Scholar]
  18. Maruyoshi K.; Iuga D.; Antzutkin O. N.; Alhalaweh A.; Velaga S. P.; Brown S. P. Identifying the Intermolecular Hydrogen-Bonding Supramolecular Synthons in an Indomethacin-Nicotinamide Cocrystal by Solid-State NMR. Chem. Commun. 2012, 48, 10844–10846. [DOI] [PubMed] [Google Scholar]
  19. Visser J. W. A Fully Automatic Program for Finding Unit Cell from Powder Data. J. Appl. Crystallogr. 1969, 2, 89–95. [Google Scholar]
  20. Shirley R.The CRYSFIRE System for Automatic Powder Indexing: User’s Manual; The Lattice Press: Guildford, U.K., 1999. [Google Scholar]
  21. Le Bail A.; Duroy H.; Fourquet J. L. Ab initio Structure Determination of LiSbWO6 by X-ray Powder Diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar]
  22. Larson A. C.; Von Dreele R. B.. Los Alamos National Laboratory Report, LAUR 86-748, 2004.
  23. Kariuki B. M.; Serrano-González H.; Johnston R. L.; Harris K. D. M. The Application of a Genetic Algorithm for Solving Crystal Structures from Powder Diffraction Data. Chem. Phys. Lett. 1997, 280, 189–195. [Google Scholar]
  24. Turner G. W.; Tedesco E.; Harris K. D. M.; Johnston R. L.; Kariuki B. M. Implementation of Lamarckian Concepts in a Genetic Algorithm for Structure Solution from Powder Diffraction Data. Chem. Phys. Lett. 2000, 321, 183–190. [Google Scholar]
  25. Habershon S.; Harris K. D. M.; Johnston R. L. Development of a Multipopulation Parallel Genetic Algorithm for Structure Solution from Powder Diffraction Data. J. Comput. Chem. 2003, 24, 1766–1774. [DOI] [PubMed] [Google Scholar]
  26. Habershon S.; Cheung E. Y.; Harris K. D. M.; Johnston R. L. An Efficient Algorithm for Calculating Whole-Profile Functions in Crystal Structure Solution from Powder Diffraction Data. Chem. Phys. Lett. 2004, 390, 394–398. [Google Scholar]
  27. Harris K. D. M. Powder Diffraction Crystallography of Molecular Solids. Top. Curr. Chem. 2012, 315, 133–177. [DOI] [PubMed] [Google Scholar]
  28. Miao P.; Robinson A. W.; Palmer R. E.; Kariuki B. M.; Harris K. D. M. Structural Properties of Self-Organized Organo-Silicon Macromolecular Films Investigated by Scanning Tunneling Microscopy and X-ray Diffraction. J. Phys. Chem. B 2000, 104, 1285–1291. [Google Scholar]
  29. Albesa-Jové D.; Kariuki B. M.; Kitchin S. J.; Grice L.; Cheung E. Y.; Harris K. D. M. Challenges in Direct-Space Structure Determination from Powder Diffraction Data: A Molecular Material with Four Independent Molecules in the Asymmetric Unit. ChemPhysChem 2004, 5, 414–418. [DOI] [PubMed] [Google Scholar]
  30. Guo F.; Harris K. D. M. Structural Understanding of a Molecular Material That Is Accessed Only by a Solid-State Desolvation Process: The Scope of Modern Powder X-ray Diffraction Techniques. J. Am. Chem. Soc. 2005, 127, 7314–7315. [DOI] [PubMed] [Google Scholar]
  31. Pan Z.; Xu M.; Cheung E. Y.; Harris K. D. M.; Constable E. C.; Housecroft C. E. Understanding the Structural Properties of a Dendrimeric Material Directly from Powder X-ray Diffraction Data. J. Phys. Chem. B 2006, 110, 11620–11623. [DOI] [PubMed] [Google Scholar]
  32. Guo F.; Martí-Rujas J.; Pan Z.; Hughes C. E.; Harris K. D. M. Direct Structural Understanding of a Topochemical Solid State Photopolymerization Reaction. J. Phys. Chem. C 2008, 112, 19793–19796. [Google Scholar]
  33. March A. Mathematische Theorie der Regelung nach der Korngestalt bei affiner Deformation. Z. Kristallogr. 1932, 81, 285–297. [Google Scholar]
  34. Dollase W. A. Correction of Intensities for Preferred Orientation in Powder Diffractometry: Application of the March Model. J. Appl. Crystallogr. 1986, 19, 267–272. [Google Scholar]
  35. Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. J.; Refson K.; Payne M. C. First Principles Methods Using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar]
  36. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
  37. Vanderbilt D. Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism. Phys. Rev. B 1990, 41, 7892–7895. [DOI] [PubMed] [Google Scholar]
  38. Webber A. L.; Emsley L.; Claramunt R. M.; Brown S. P. NMR Crystallography of Campho[2,3-c]pyrazole (Z′ = 6): Combining High-Resolution 1H–13C Solid-State MAS NMR Spectroscopy and GIPAW Chemical-Shift Calculations. J. Phys. Chem. A 2010, 114, 10435–10442. [DOI] [PubMed] [Google Scholar]
  39. Harris R. K.; Ghi P. Y.; Puschmann H.; Apperley D. C.; Griesser U. J.; Hammond R. B.; Ma C. Y.; Roberts K. J.; Pearce G. J.; Yates J. R.; Pickard C. J. Structural Studies of the Polymorphs of Carbamazepine, Its Dihydrate and Two Solvates. Org. Process Res. Dev. 2005, 9, 902–910. [Google Scholar]
  40. Yates J. R.; Dobbins S. E.; Pickard C. J.; Mauri F.; Ghi P. Y.; Harris R. K. A Combined First Principles Computational and Solid-State NMR Study of a Molecular Crystal: Flurbiprofen. Phys. Chem. Chem. Phys. 2005, 7, 1402–1407. [DOI] [PubMed] [Google Scholar]
  41. Yates J. R.; Pham T. N.; Pickard C. J.; Mauri F.; Amado A. M.; Gil A. M.; Brown S. P. An Investigation of Weak CH···O Hydrogen Bonds in Maltose Anomers by a Combination of Calculation and Experimental Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2005, 127, 10216–10220. [DOI] [PubMed] [Google Scholar]
  42. Mifsud N.; Elena B.; Pickard C. J.; Lesage A.; Emsley L. Assigning Powders to Crystal Structures by High-Resolution 1H–1H Double Quantum and 1H–13C J-INEPT Solid-State NMR Spectroscopy and First Principles Computation. A Case Study of Penicillin G. Phys. Chem. Chem. Phys. 2006, 8, 3418–3422. [DOI] [PubMed] [Google Scholar]
  43. Pickard C. J.; Salager E.; Pintacuda G.; Elena B.; Emsley L. Resolving Structures from Powders by NMR Crystallography Using Combined Proton Spin Diffusion and Plane Wave DFT Calculations. J. Am. Chem. Soc. 2007, 129, 8932–8933. [DOI] [PubMed] [Google Scholar]
  44. Uldry A. C.; Griffin J. M.; Yates J. R.; Perez-Torralba M.; Maria M. D. S.; Webber A. L.; Beaumont M. L. L.; Samoson A.; Claramunt R. M.; Pickard C. J.; Brown S. P. Quantifying Weak Hydrogen Bonding in Uracil and 4-Cyano-4′-ethynylbiphenyl: A Combined Computational and Experimental Investigation of NMR Chemical Shifts in the Solid State. J. Am. Chem. Soc. 2008, 130, 945–954. [DOI] [PubMed] [Google Scholar]
  45. Salager E.; Stein R. S.; Pickard C. J.; Elena B.; Emsley L. Powder NMR Crystallography of Thymol. Phys. Chem. Chem. Phys. 2009, 11, 2610–2621. [DOI] [PubMed] [Google Scholar]
  46. Harris R. K.; Hodgkinson P.; Zorin V.; Dumez J. N.; Elena-Herrmann B.; Emsley L.; Salager E.; Stein R. S. Computation and NMR Crystallography of Terbutaline Sulfate. Magn. Reson. Chem. 2010, 48, S103–S112. [DOI] [PubMed] [Google Scholar]
  47. Webber A. L.; Elena B.; Griffin J. M.; Yates J. R.; Pham T. N.; Mauri F.; Pickard C. J.; Gil A. M.; Stein R.; Lesage A.; Emsley L.; Brown S. P. Complete 1H Resonance Assignment of β-Maltose from 1H–1H DQ-SQ CRAMPS and 1H (DQ-DUMBO)-13C SQ Refocused INEPT 2D Solid-state NMR Spectra and First Principles GIPAW Calculations. Phys. Chem. Chem. Phys. 2010, 12, 6970–6983. [DOI] [PubMed] [Google Scholar]
  48. Bradley J. P.; Velaga S. P.; Antzutkin O. N.; Brown S. P. Probing Intermolecular Crystal Packing in γ-Indomethacin by High-Resolution 1H Solid-State NMR Spectroscopy. Cryst. Growth Des. 2011, 11, 3463–3471. [Google Scholar]
  49. Webber A. L.; Masiero S.; Pieraccini S.; Burley J. C.; Tatton A. S.; Iuga D.; Pham T. N.; Spada G.; Brown S. P. Identifying Guanosine Self Assembly at Natural Abundance by High-Resolution 1H and 13C Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2011, 133, 19777–19795. [DOI] [PubMed] [Google Scholar]
  50. Mafra L.; Santos S. M.; Siegel R.; Alves I.; Paz F. A. A.; Dudenko D.; Spiess H. W. Packing Interactions in Hydrated and Anhydrous Forms of the Antibiotic Ciprofloxacin: A Solid-State NMR, X-ray Diffraction and Computer Simulation Study. J. Am. Chem. Soc. 2012, 134, 71–74. [DOI] [PubMed] [Google Scholar]
  51. In this context, it is relevant to note that a simple comparison of experimental and calculated 1H chemical shifts has been used successfully by Salager et al. to identify the correct structure (determined previously from single-crystal XRD) from the 23 most reasonable structures generated from a crystal structure prediction approach for thymol. See the following paper:Salager E.; Day G. M.; Stein R. S.; Pickard C. J.; Elena B.; Emsley L. Powder Crystallography by Combined Crystal Structure Prediction and High-Resolution 1H Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2010, 132, 2564–2566. [DOI] [PubMed] [Google Scholar]
  52. Brown S. P.; Zhu X. X.; Saalwachter K.; Spiess H. W. An Investigation of the Hydrogen-Bonding Structure in Bilirubin by 1H Double-Quantum Magic-Angle Spinning Solid-State NMR Spectroscopy. J. Am. Chem. Soc. 2001, 123, 4275–4285. [DOI] [PubMed] [Google Scholar]
  53. Dumez J. N.; Pickard C. J. Calculation of NMR Chemical Shifts in Organic Solids: Accounting for Motional Effects. J. Chem. Phys. 2009, 130, 104701. [DOI] [PubMed] [Google Scholar]
  54. de Gortari I.; Portella G.; Salvatella X.; Bajaj V. S.; van der Wel P. C. A.; Yates J. R.; Segall M. D.; Pickard C. J.; Payne M. C.; Vendruscolo M. Time Averaging of NMR Chemical Shifts in the MLF Peptide in the Solid State. J. Am. Chem. Soc. 2010, 132, 5993–6000. [DOI] [PubMed] [Google Scholar]
  55. Hansen M. R.; Graf R.; Sekharan S.; Sebastiani D. Columnar Packing Motifs of Functionalized Perylene Derivatives: Local Molecular Order Despite Long-Range Disorder. J. Am. Chem. Soc. 2009, 131, 5251–5256. [DOI] [PubMed] [Google Scholar]
  56. Bonhomme C.; Gervais C.; Babonneau F.; Coelho C.; Pourpoint F.; Azais T.; Ashbrook S. E.; Griffin J. M.; Yates J. R.; Mauri F.; Pickard C. J. First-Principles Calculation of NMR Parameters Using the Gauge Including Projector Augmented Wave Method: A Chemist’s Point of View. Chem. Rev. 2012, 112, 5733–5779. [DOI] [PubMed] [Google Scholar]
  57. Brouwer D. H.; Moudrakovski I. L.; Darton R. J.; Morris R. E. Comparing Quantum-Chemical Calculation Methods for Structural Investigation of Zeolite Crystal Structures by Solid-State NMR Spectroscopy. Magn. Reson. Chem. 2010, 48, S113–S121. [DOI] [PubMed] [Google Scholar]
  58. Brouwer D. H. Structure Solution of Network Materials by Solid-State NMR without Knowledge of the Crystallographic Space Group. Solid State Nucl. Magn. Reson. 2013, 51–52, 37–45. [DOI] [PubMed] [Google Scholar]
  59. Martineau C.; Cadiau A.; Bouchevreau B.; Senker J.; Taulelle F.; Adil K. SMARTER Crystallography of the Fluorinated Inorganic-Organic Compound Zn3Al2F12.[HAmTAZ]6. Dalton Trans. 2012, 41, 6232–6241. [DOI] [PubMed] [Google Scholar]
  60. Zhou B.; Michaelis V. K.; Pan Y. M.; Yao Y. F.; Tait K. T.; Hyde B. C.; Wren J. E. C.; Sherriff B. L.; Kroeker S. Crystal Structure Refinements of Borate Dimorphs Inderite and Kurnakovite Using 11B and 25Mg Nuclear Magnetic Resonance and DFT Calculations. Am. Mineral. 2012, 97, 1858–1865. [Google Scholar]
  61. Davies E.; Duer M. J.; Ashbrook S. E.; Griffin J. M. Applications of NMR Crystallography to Problems in Biomineralization: Refinement of the Crystal Structure and 31P Solid-State NMR Spectral Assignment of Octacalcium Phosphate. J. Am. Chem. Soc. 2012, 134, 12508–12515. [DOI] [PubMed] [Google Scholar]
  62. Pawlak T.; Jaworska M.; Potrzebowski M. J. NMR Crystallography of α-Poly(l-lactide). Phys. Chem. Chem. Phys. 2013, 15, 3137–3145. [DOI] [PubMed] [Google Scholar]
  63. Baias M.; Widdifield C. M.; Dumez J.-N.; Thompson H. P. G.; Cooper T. G.; Salager E.; Bassil S.; Stein R. S.; Lesage A.; Day G. M.; Emsley L. Powder Crystallography of Pharmaceutical Materials by Combined Crystal Structure Prediction and Solid-State 1H NMR Spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 8069–8080. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp4041106_si_001.pdf (130.7KB, pdf)
jp4041106_si_002.cif (13.2KB, cif)
jp4041106_si_003.cif (2.6KB, cif)
jp4041106_si_004.pdf (89KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES