Abstract
Hubel and Wiesel‘s 1962 paper, “Receptive fields, binocular interaction and functional architecture in the cat“s visual cortex” reported several important discoveries: orientation columns, the distinct structures of simple and complex receptive fields, and binocular integration. But perhaps the paper‘s greatest influence came from the concept of functional architecture (the complex relationship between in vivo physiology and the spatial arrangement of neurons) and several models of functionally specific connectivity. They thus identified two distinct concepts, topographic specificity and functional specificity, which together with cell-type specificity constitute the major determinants of cortical connectivity. Orientation columns are iconic examples of topographic specificity, whereby axons within a column connect with cells of a single orientation preference. Hubel and Wiesel also saw the need for functional specificity at a finer scale, in their model of thalamic inputs to simple cells, verified in the 1990s. The difficult but potentially more important question of intracortical functional specificity is only now becoming tractable with new experimental techniques.
Functional architecture
It is useful to approach the topic of synaptic connections in the cortex by considering three distinct types of specificity: topographic specificity (where you are), cell-type specificity (who you are), and functional specificity (what you do; Lee and Reid, 2011). Recent technical advances have accelerated progress in understanding cell-type and, to a lesser extent, functional specificity, but it is useful to begin with the better understood topic of cortical topography, or functional architecture. Building upon the revolutionary findings of Vernon Mountcastle, who in 1957 proposed that narrow vertical columns of neurons are the fundamental unit in cortical processing (Mountcastle, 1957), Hubel and Wiesel introduced the term ‘functional architecture’ in 1962 to describe the relationship between anatomy and physiology in cortical circuits. A common textbook description of functional architecture is that receptive fields in a cortical column are all extremely similar. Instead, Hubel and Wiesel gave a more nuanced treatment of functional architecture in the visual cortex. They proposed that a cortical column can be very homogeneous for some receptive-field attributes, loosely organized for others, and even completely disorganized in yet other respects. One aspect of functional architecture in the cat visual cortex, the orientation column, is indeed monolithic: “It can be concluded that the striate cortex is divided into discrete regions within which the cells have a common receptivefield axis orientation.” But the second aspect, ocular dominance, is more loosely organized in columns: “While cells of different ocular dominance were present within single columns, there were nevertheless indications of some grouping.” Ocular dominance columns were later found to be clearer and more distinct in the monkey (Hubel and Wiesel, 1968). Finally, they found that retinotopic organization of within a column is disorganized, so that “at this microscopic level the retinotopic representation no longer strictly holds.”
As Hubel and Wiesel pointed out, the fine-scale functional architecture of visual cortex, with its homogeneous orientation selectivity and disorganized retinotopy, might play an important role in information processing.
“At first sight it would seem necessary to imagine a highly intricate tangle of interconnexions in order to link cells with common axis orientations while keeping those with different orientations functionally separated.... The cells of each aggregate have common axis orientations and the staggering in the positions of the simple fields is roughly what is required to account for the size of most of the complex fields.”
It is crucially important to emphasize that Hubel and Wiesel did not intend functional architecture to be synonymous with the existence of distinct columns for orientation selectivity. It was instead a general construct to help understand the relationship between function and anatomy. The term functional architecture might be used to express simple ideas: neurons with the same preferred orientation clump together. But it also encompassed more complex ideas: a precise map for orientation combined with an imprecise map for retinotopy might help in the construction of complex receptive fields. Taken more generally, the concept of functional architecture provided a framework for linking the anatomy of a cortical circuit with the physiological transformations performed by that circuit. But the exact relationship between functional architecture, neural connections, and the physiological function of individual cells could only be speculated upon in 1962. Hubel and Wiesel could put forward their hierarchical models of simple and complex receptive fields in the cat (Fig. 1), but these models were presented as conjecture: simple cells might create orientation selectivity by adding synaptic signals from LGN cells whose receptive fields line up in a row; complex cells might generalize orientation selectivity by adding synaptic signals from simple cells tuned to a single orientation. But only recently is it becoming possible to study the detailed interrelationships between physiology and wiring diagrams at the single-cell level, a line of inquiry that has been given a new name, functional connectomics (a term that would have made Hubel and Wiesel shudder in 1962).
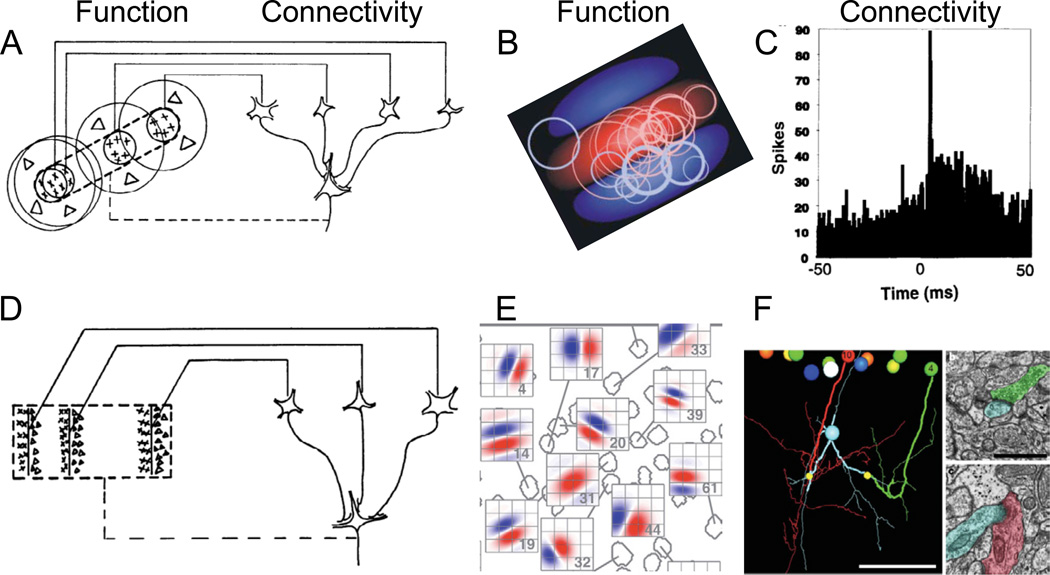
Figure 1. Hubel and Wiesel’s receptive-field models and some strategies for testing them.
(A) Hubel and Wiesel‘s simple-cell model. The simple cell receives convergent input from multiple LGN cells (Connectivity) whose receptive fields (Function) are of the same sign (in this example, on-center) and are aligned in visual space. As a result, the simple cell has a receptive field with an elongated on subregion (indicated by the interrupted lines in the receptive-field diagram) flanked by two off subregions. From Hubel and Wiesel (1962). (B,C) Experimental proof for the model from Reid and Alonso (1995). (B) Summary diagram showing the relationship between the receptive fields (Function) of monosynaptically connected pairs of neurons. Receptive field of each simple cell was transformed into a typical receptive field, shown with a central on subregion (red) flanked by two off subregions (blue). The circles indicate the relative size, sign and locations of the receptive fields of monosynaptically connected LGN cells. (C) Example of a ‘monosynaptic” cross-correlation between an LGN cell and a simple cell (Connectivity). Note the sharp peak at +4 msec, indicating in increase in the probability that the cortical cell fired 4 msec after LGN firing. (D) Hubel and Wiesel‘s complex cell model. (E, F) A theoretical example of how the model might be examined. (E) Simple receptive fields can be mapped with two-photon calcium imaging. Receptive field diagrams (red = on subregion, blue = off subregion) corresponding to different cells (gray outlines) in mouse visual cortex (Bonin et al., 2011). (F) Example of functional connectomics, from a different study of excitatory inputs onto inhibitory neurons (Bock et al., 2011). The axons of a group of neurons with different orientation tunings (coded by different colors) were reconstructed. Axons of vertically and horizontally tuned neurons (red and green) descend and make synapses (small yellow balls) onto dendrites of an inhibitory interneuron (cyan). Insets: electron micrographs showing the synapses onto the inhibitory neuron from cell 4 (b) and cell 10 (c) with corresponding colors overlaid.
Functional connectomics of cortical circuits
The term connectomics has been used in several different ways since it first appeared seven years ago. As originally defined by Sporns and colleagues (2005), it is “a comprehensive structural description of the network of elements and connections forming the human brain,” which could be considered either at a “macroscale [of] brain regions and pathways” or a “microscale [of] single neurons and synapses.” On the one hand, there is the network of brain areas, as in the Human Brain Connectome Project, in which MRI is used to trace projection pathways (Van Essen et al., 2012). But there is also the field of synaptic networks between individual neurons, which is typified by the use of large-scale EM to study local networks (Lichtman and Sanes, 2008).
Another potential source of confusion is that the word itself implies comprehensiveness, but it has also been used to describe studies of networks that are only sparsely reconstructed (Seung, 2011). It would therefore be useful to have a word that denotes the less exalted study of neural connectivity with modern tools. But in the modern biology, very few “-ologies” are being coined, while a new “-omics” appears almost every month. So we are left with the term connectomics, a term that exemplifies the long-term aspirations of a field, but which for now can also refer to rapidly improving anatomical methods for studying neural connections.
Functional connectomics is a more specific term that describes studies of neuronal networks in which physiological measurements help us understand connections, and vice versa (Seung, 2011). As such, it captures the ideas in the following quote from Hubel and Wiesel‘s 1962 paper:
“At present we have no direct evidence on how the cortex transforms the incoming visual information. Ideally, one should determine the properties of a cortical cell, and then examine one by one the receptive fields of all the afferents projecting upon that cell. In the lateral geniculate, where one can, in effect, record simultaneously from a cell and one of its afferents, a beginning has already been made in this direction (Hubel & Wiesel, 1961).”
But in 1962, to study the cortex in this manner was virtually unimaginable, due to technical limitations:
“In a structure as complex as the cortex the techniques available would seem hopelessly inadequate for such an approach. Here we must rely on less direct evidence to suggest possible mechanisms for explaining the transformations that we find.”
Fortunately, in the ensuing 50 years the techniques for measuring neural activity and for tracing synaptic connections have advanced considerably
Cell types and the architecture of cortical circuits
From work over the past 25 years, primarily from cortical slices in vitro, we now have a detailed understanding of the overall architecture of cortical circuits: cell types and their laminar organization, dendritic and axonal morphology, and the outlines of a wiring diagram. The cellular biophysics of cortical neurons has been correlated to different cell types with great specificity (Sugino et al., 2006, Nelson et al., 2006). The connections between neurons have also been well characterized with an increasing emphasis on the relationship between connectivity, cell types, and anatomy. There are now many examples of stereotyped connections between different neuronal types— excitatory neurons synapse onto the cell bodies of inhibitory neurons but avoid excitatory somata, chandelier cells form synapses exclusively onto the axon initial segments of pyramidal cells, and gap junctions are made between inhibitory neurons of a single class (reviewed in Brown and Hestrin, 2009). Of course, the question of what defines a cortical cell type has not been settled (Nelson et al., 2006; Ascoli et al., 2007). In particular, when might differences in the functional properties of neurons, or their patterns of connections, turn out to be related to unidentified distinctions between cell classes or patterns of gene expression?
A great simplifying assumption has been that neurons of a given class are all equivalent. In this case, the only thing we need to know about a neuron is its class and anatomical location, for instance a pyramidal cell at the bottom of layer 2/3 in primary visual cortex, and the anatomical extent of its dendrites and axons. If this were the case, we would only need to know the generic structure of the microcircuit, plus the range of in vivo functional properties of the afferents that impinge upon the circuit, to begin modeling its in vivo physiology.
A corollary of this assumption—that cortical neurons of a given class are identical— is that connections between neurons are non-specific. The clearest formulation of this idea has become known as Peters‘ Rule (Braitenberg and Schüz, 1989): “The distribution of synapses from various origins... on the dendritic tree of any one neuron reflect[s] simply the availability of those presynaptic elements in the tissue... Conversely, the postsynaptic partners of any axonal tree would simply reflect the distribution of the postsynaptic elements.” Although this point of view was quite influential, it is becoming increasingly clear that connections between cortical neurons are far from random. Instead, there are several lines of evidence showing that connections between cortical neurons can be highly specific, both because of cell-type-specific connections as well as other, more poorly understood factors (Yoshimura et al., 2005; Song et al., 2005; Perin et al., 2011).
Structure in neuronal networks: three types of specificity
In order to discuss structure in a cortical network, it is useful to consider three broad classes of specificity: topographic specificity, cell-type specificity, and functional specificity (Lee and Reid, 2011). Topographic specificity is seen, for instance, when axons respect a laminar boundary or a functional map, such as for retinotopy or preferred orientation (Mooser et al., 2004). If Peters‘ rule holds, then topographic specificity alone specifies the wiring diagram. Cell-type specificity, as discussed above, describes cases in which an axon has tropism for a given class of neurons found amidst a mixed local population. Functional specificity can be defined as any form of synaptic specificity that cannot be explained by axonal and dendritic topography, cell types, or perhaps even gene expression, but instead must relate to the physiology of the pre- and postsynaptic cells. A more accurate term might therefore be local functional connectivity, or even local epigenetic specificity. The three types of specificity are of course not perfectly delineated; they nonetheless serve as useful abstractions until we have a better understanding of molecular and activity-dependent influences on neuronal connectivity.
The LGN is a particularly well-studied example in which topographic specificity plays some role, but functional specificity comes to dominate the local wiring diagram. The retinal input to the thalamus is one of the classic models for the segregation of inputs into both eye-specific layers and retinotopic maps. But even after topographic segregation of axonal arbors is complete, midway through development, there is further synaptic refinement (Tavazoie and Reid, 2000; Chen and Regehr, 2000). At the end of development there is a very specific network in which multiple overlapping axons make synaptic contact onto distinct and very specific targets. This was demonstrated in a serial-section EM study (Hamos et al., 1987) that 25 years later remains the clearest anatomical illustration of functional specificity in central circuits. As discussed below, and as elaborated in an extraordinary review of the relationship between connectivity and visual function (Cleland, 1986), the mature wiring diagram between retina and LGN must have a crystalline underlying structure based on the geometric tiling of retinal receptive fields. The relationship between cortical wiring and visual function, however, is far more complicated.
Hubel and Wiesel’s Models of Functional Connectivity
The generation of orientation-selective visual responses in the cortex is one of the classic problems in visual neuroscience. Neurons in the visual thalamus (the lateral geniculate nucleus, or LGN) respond relatively indiscriminately to stimuli of different orientations, while their postsynaptic targets in the cortex can be exquisitely selective. In the first of their two models of function and connectivity, Hubel and Wiesel outlined how precise connections between thalamus and cortex could generate the orientation-selective responses of cortical simple cells (Fig. 1A). In the most famous figure of the 1962 paper, they proposed that LGN cells whose receptive fields were arranged in a row converge onto a simple cell whose receptive field was elongated with the same orientation (fig. 1A).
As it turned out, this class of model could be proven with 20th century electrophysiology. In the 1990s, evidence for this model accumulated (Chapman et al., 1991, Reid and Alonso 1995; Ferster et al., 1996; Priebe and Ferster, 2012). Two lines of evidence gave strong indirect support to the model without needing to examine individual connections from thalamus to cortex. First, Chapman and colleagues silenced the cortex so that action potentials from individual thalamic axons could be recorded. They found that in the ferret, LGN axons that projected to a single column had receptive fields that lined up in a row (Chapman et al., 1991; see Jin et al., 2011). Ferster and colleagues examined the same question from the standpoint of a single neuron rather than a single column (Ferster et al., 1996). They found that in the cat, the orientation selectivity of a cortical neuron did not change when the cortex was silenced: thus the orientation selectivity of the thalamic input alone matched that of the neuron when it was embedded in the functioning circuit. To examine the functional logic of individual connections between a pair of neurons, however, it was necessary to study their receptive fields and connections a pair at a time, as Hubel and Wiesel suggested. In the 1960s, this was possible within the LGN (Hubel and Wiesel 1961), but later it became possible for the thalamocortical projection with the technique of cross-correlation (see below; Tanaka, 1983; Reid and Alonso, 1995).
The second model (for complex cells, Fig. 1D) addressed the much more difficult problem of how intracortical circuitry might transform sensory information. Although some progress with this model has been made with conventional electrophysiology (Alonso and Martinez, 1998). In Hubel and Wiesel‘s complex cell model (Fig. 1D) a difficult problem, of receiving inputs from simple cells with one preferred orientation, was solved by the orientation column. It was transformed from a problem that might require intracortical local functional connectivity, to one that was solved by topography. To quote the key passage again: “At first sight it would seem necessary to imagine a highly intricate tangle of interconnexions in order to link cells with common axis orientations…. [but] gathered together in discrete columns are the very cells we require to be interconnected in our scheme.” Without orientation columns, in the mouse, it is necessary to imagine this “highly intricate tangle of interconnexions”, a phrase that can serve as perhaps the best definition of functional specificity.
Hubel and Wiesel‘s simple-cell model (Fig. 1A) relies on functional specificity. To first approximation, in the cat visual cortex the axons of on-center and off-center LGN cells are intermingled in layer 4 (but see Jin et al., 2011). Therefore, the precise arrangement of receptive fields of on or off-center LGN inputs to a single simple cell cannot be explained simply by a random sampling of local thalamocortical axons (unless the number of LGN afferents to a simple cell are assumed to be unrealistically low, Ringach, 2003). Their complex-cell model (Fig. 1D), however, relies primarily on topographic specificity. Because of the functional architecture of the cat, in which orientation is homogeneous in a column but receptive fields are spatially scattered, complex cells can be built by indiscriminate pooling of local simple cells. This fundamental difference between the two models has posed some difficulty in thinking about them. In particular, the existence of functional architecture confounds the two potential mechanisms of topographic specificity and functional specificity.
For instance, in two species there is strong evidence that topographic specificity, rather than (local) functional specificity, can help account for the generation of orientation specificity. In the ferret, as noted above, the LGN cells projecting to a single column have receptive fields that line up in a row whose orientation matches that of the local cortical neurons (Chapman et al., 1991). Thus cortical orientation selectivity can be achieved by non-specific summation of the locally available afferents. In the tree shrew there is a similar arrangement, except it is caused by anisotropic intracortical projection of axons. In the tree shrew, layer 4 neurons are not orientation-selective, so orientation selectivity is generated first in layer 2/3, but otherwise the arrangement is similar to the ferret. Unlike in the ferret, however, the spatial elongation of the afferent connections was demonstrated anatomically, rather than physiologically. Using a clever combination of optical imaging and anterograde axonal tracing, Fitzpatrick and colleagues (Mooser et al. 2004) demonstrated an orientation-specific arrangement of layer 4 afferents to layer 2/3. As in the ferret, the receptive fields of the afferents line up in a row retinotopically, so that orientation selectivity could be generated with indiscriminate pooling by layer 2/3 neurons of their local afferents. By the definitions of the terms (above), this is an example of topographic specificity rather than local functional specificity.
Because functional architecture can often make it difficult to differentiate topographic from functional specificity, it is fortunate therefore that two of the currently favored species for visual physiology, rats and mice, do not have functional architecture for orientation selectivity (Ohki et al., 2005; Fig 2A). Instead, cells that respond to different orientations are completely intermingled, as are cells that have different configurations of their simple receptive fields (Bonin et al., 2010). Thus, almost by definition, any specificity of wiring that underlies receptive field properties must either be due to some combination of cell-type and functional specificity (Fig. 2B,C). For many reasons, the mouse is not the best model for understanding human vision, of course. But the mouse visual cortex is proving to be an excellent model for studying general principles of cortical computation.
Figure 2. Models of function and connectivity in rodent visual cortex.
(A) Map of orientation selectivity from mouse visual cortex, with examples of spatial receptive fields from another experiment. Note that vertically oriented cells are interspersed with horizontally oriented cells. (B) Model of like-to-like recurrent connectivity within layer 2/3, as was found with calcium imaging and correlated slice physiology (Ko et al., 2011), but has not been confirmed anatomically. (C) Model of like-to-like feedforward connections from layer 4 to layer 2/3, which has not yet been demonstrated.
Functional connectivity inferred from correlation studies
Before the advent of modern anatomical and physiological techniques for demonstrating synaptic connections, cross-correlation studies provided the best tool for inferring a synaptic connection between two neurons studied in vivo (Perkel et al., 1967). If one neuron has a synaptic connection with another, the connection can be demonstrated by an increase in the firing probability of the postsynaptic cell, several milliseconds after the presynaptic cell fires. Because correlation is not causation, however, only under special circumstances can an actual synaptic connection be inferred rigorously. One example is in a strong feedforward pathway, such as the retina to the thalamus (Cleland et al., 1971; Mastronarde, 1987; Usrey et al., 1998), or the thalamus to the cortex (Tanaka, 1983; Reid and Alonso, 1995; Reid, 2001).
Cross-correlation analysis was highly effective in deciphering the functional logic of thalamocortical connections in the visual system (Fig 1B,C; Reid and Alonso, 1995; Alonso et al., 2001; Reid et al., 2001), as well as in the somatosensory (Bruno and Simons, 2002; Swadlow, 1995; Swadlow and Gusev, 2002; See Alonso and Swadlow, 2005) and auditory systems (Miller et al., 2001). Due to the difficulty of recording from more than a handful of neurons at a time (Alonso et al, 2001), this approach was still a long way from Hubel and Wiesel‘s dream of recording from “all the afferents projecting upon that cell”; the number of thalamic afferents to a simple cell is at least 30 (Alonso et al., 2001), and that the number of cortico-cortical afferents is in the thousands.
Further, it is important to emphasize that both the model itself and the supporting data did not exclude a role for intracortical connections in determining the response properties of simple cells (see Priebe and Ferster 2012 in this issue). It is therefore unfortunate that cross-correlation analysis cannot reliably detect weak connections within the cortex (except in the special case of strong feedforward connections, see Alonso and Martinez, 1998). Instead, studies of the functional logic of intracortical circuitry had to wait for 21st century approaches that combine optical physiology with network analysis (Fig. 1E,F; Bock et al., 2011; Ko et al., 2011). These new approaches hold the promise to achieve complete functional and structural imaging of cortical circuits, so that functional relationships in the network can be examined in principle for any pair of neurons.
Specificity: a substrate for sensory computations, or for information storage?
Before reviewing new methods for examining synaptic connections, it is useful to consider two complementary ways of thinking about connectivity. First, the wiring diagram can be thought of as the substrate of a local computation. In this view, the information delivered by afferent inputs is routed and recombined to yield a different representation of this information—the output—that is relayed to other local circuits. Alternatively, the network can be thought of as storing information (Chklovskii et al., 2004), such as in an associative memory. The quintessential examples of these two viewpoints are the visual cortex and the hippocampus. The visual cortex has been described as performing receptive field transformations that are best computed by a series of precisely wired feedforward networks (Hubel and Wiesel, 1962), although this view has been controversial from the beginning. The hippocampus, on the other hand, has been described as a learning machine that makes associations between its complex inputs by strengthening some connections and weakening others. The details of how this learning results in the storage of specific memories are not always specified, but it is widely accepted that plasticity results in the long-term storage of information.
It is ironic that the two fields, sensory processing in neocortical networks vs. information storage in recurrent hippocampal networks, have had such different biases. In the network for which we have far more information about input/output transformations in vivo—information processing in neocortical networks—the idea of functional specificity has not often been championed. Until recently, connections between cortical neurons (excitatory neurons in particular) were often presumed to be random, or at most having topographic (Braitenberg and Schüz, 1998) or cell-type specificity.
The inverse problem, of reading out the information stored in connections, is one that has received even less attention. In one scenario, it has been proposed that a temporal sequence in the firing of neurons can be predicted by analyzing the graph of their interconnections (Seung, 2009). Alternatively, it is likely that the spatial relations in a sensory map can be inferred from the connections in a network. In the LGN, as in the cortex (Hubel and Wiesel, 1962), there is a coarse grain retinotopic map at the scale of hundreds of µm to several mm, but the map breaks down at the scale smaller than 100 µm. Nonetheless physiological information about the location of receptive fields can be examined so that nearby neurons can be placed in a precise retinotopic map (as in Alonso et al., 2001). The hope is that the wiring diagram can also be used to perform the same sorting operation, to yield spatial information about receptive fields without any functional measurements. This idea was first proposed by Cleland (1986) for the simple and highly structured wiring diagram from retina to LGN, but it is very likely to hold for other wiring diagrams based on retinotopic relations, such as Hubel and Wiesel‘s 1962 model of the simple cell. A major goal of functional connectomics should be to test this conjecture: to examine not only whether function can predict connectivity, but also whether connectivity can predict function.
New tools for microscale connectomics
At minimum, synaptic circuit reconstruction requires several things: the ability to recognize a synapse and the ability to assign the pre- and postsynaptic neurons that form the synapse. Recently, there has been a great expansion in the tools for reconstruction of circuits in the nervous system. Currently, in vivo functional imaging can be combined with at least three different methods for examining connections in a. First, there is slice physiology which, when correlated with in vivo calcium imaging, can be used to examine the probability that neurons of a given functional type, for instance of with the same preferred orientation, are synaptically connected (Ko et al., 2011). Second, there is transsynaptic tracing with replication-incompetent (G-deleted) rabies, which in one variant can label only neurons that are presynaptic to a single target neuron (Wickersham et al., 2007). When combined with in vivo calcium imaging, this technique holds the promise to fulfill the dream of Hubel and Wiesel to “examine one by one the receptive fields of all the afferents projecting upon that cell.” Despite the conceptual simplicity of the technique, it has proven difficult so far to apply routinely, principally because it requires the delivery of multiple genes to a single target neuron in vivo.
Slice physiology is an ideal technique to study the interconnections between neurons; but it is currently limited to tens of connections in a given experiment. The single-cell version of G-deleted rabies may allow hundreds of connections to be examined, but all from the vantage point of one post-synaptic cell. In the long run, serial-section electron microscopy has the potential to examine the thousands of connections between neurons that may be necessary to understand the functional logic of a cortical circuit (Fig. 1F).
Serial-section EM has long been a powerful method for analyzing the dense neuropil of the central nervous system. But except for the simplest nervous systems (White et al., 1987), it has been poorly suited for studying extended circuits, with a few notable exceptions (for instance Sterling 1983; Hamos et al., 1987). The major drawback in the method is one of scale. Although serial-section microscopy was well developed in the 1960s, and began to be computerized as early as the 1970s (Ware and LoPresti, 1975), computers were too slow and storage too expensive for very large-scale reconstructions.
In order to collect three-dimensional, nanoscale data from a circuit that spans hundreds of micrometers, terabytes of data are required, a scale that has only become tractable in recent years (Anderson et al., 2011; Bock et al., 2011; Briggman et al., 2011). Because of the technical hurdles needed to collect and annotate EM data sets of this size, it has taken some time for the first research studies since the original demonstration of ultrastructural reconstructions at the circuit scale (Denk and Horstmann, 2004; Bock et al., 2011; Briggman et al., 2011; Anderson et al., 2011). At present, however, large-scale EM data collection is now being performed in a number of laboratories. The greatest challenge in the coming years for EM circuit reconstruction will not be data collection, but image segmentation (Jain et al., 2010). Nonetheless, even a partial annotation of data sets will allow fundamental questions in functional connectomics to be addressed (Bock et al., 2011; Briggman et al., 2011; Seung, 2011).
Toward complete functional and structural imaging: some questions
In the coming years, neuroscience will have complete data sets that will rival those of genetics and structural biology. In the age of complete genomes and protein structures solved at atomic resolution, it‘s important to recall that these structures were first solved either in pieces or at lower resolution. It is possible to imagine the structural and functional imaging of a complete local cortical circuit, which in the mouse is encompassed by roughly a quarter of a cubic millimeter: 1 mm spans the full depth of cortex, from pia to white matter, while 500×500 µm spans the local dendritic and axonal arbors of neurons in the center of the volume. In this volume are roughly 25,000 neurons and 2.5×108 synapses. Like structural biology, complete functional imaging is a goal that is being successively approximated by better techniques for data collection.
Two-photon functional imaging is increasing in bandwidth and temporal resolution so it is easy to extrapolate to the day when every cell in a circuit can be monitored physiologically, and potentially many of the synapses as well (Chen et al., 2011). There exist several methods for recording from the full depth of the cortex (Mittmann et al., 2011; Chia and Levene, 2009). Genetically encoded calcium indicators are constantly improving, so that measurements can be achieved at increasing bandwidth and high signal-to-noise ratios (Tian et al., 2009). Further, chronic imaging from a circuit is becoming increasingly robust, so that activity can be monitored for many hours over the course of weeks (Andermann et al., 2010).
Electron microscopy techniques are improving so that it is likely that the data can be collected at the scale of local cortical circuits, with data sets increasing from tens of terabytes (Bock et al., 2011; Briggman et al., 2011; Anderson et al., 2011) to hundreds of terabytes. The task of segmenting and annotating of these data, however, poses the greatest challenge to for this emerging field (Jain et al., 2009). While it is possible to collect a data set that has hundreds of millions of connections, current approaches in segmentation and annotation limit us to examine only thousands of connections in a reasonable amount of time. Nonetheless, it is an unprecedented opportunity that one can collect such large data sets, which can best thought of as an anatomical cortical slice— similar to an in vitro slice—that can be endlessly queried for synaptic connections as computational techniques improve. A physiological slice experiment would be considered hugely successful if 100 connections could be probed. For the time being, the promise of examining many thousands of connections is the unique province of large-scale electron microscopy.
Beyond the refinement of techniques that are already extremely powerful, the field needs further refinement of questions about functional connectomics. For fifty years, Hubel and Wiesel‘s examples of visual cortical receptive fields remained perhaps the only wellknown models of how individual connections in the cerebral cortex might underlie information processing in a local circuit. Now that the dream to analyze the “highly intricate tangle of interconnexions” is coming true—with slice recordings, viral tracing, or large-scale EM—it is time to formulate new questions.
Are there geometric regularities in the axonal and dendritic arbors, or are they randomly arranged with respect to each other? One example is the arrangement of apical dendrites into fascicles (Peters and Kara, 1987). To the extent that new patterns are found (Kozloski et al., 2001), what are the functional correlates of these patterns?
Are there geometrical regularities in the individual connections neurons make with each other? For instance, are synapses with particular functional properties clustered on a dendrite, as is predicted in some models (Mel, 1993; see Kleindienst et al., 2011), or are they scattered at random throughout the dendritic arbor (Chen et al., 2011)?
Are there regularities in the connection matrix between neurons? As the connections in a circuit become increasingly densely sampled, it will become possible to examine regularities in the wiring diagram, such as cliques of neurons that are densely connected within a clique, but not between cliques (Yoshimura et al., 2005; Song et al., 2005; Perin et al., 2011). While functional measures might help understand these sub-circuits, the ability to identify them anatomically, independent of function, will be a major advance.
Most importantly, what are the key determinants of the probability of connections between neurons? Geometric relationships between neurons of course affect the probability of connections (Stepanyants and Chklovskii, 2005), as do cell-type identities (Brown and Hestrin, 2009). But we are almost completely ignorant of functional specificity in cortical circuits. It is important to emphasize that this is not one question, but many questions. Hubel and Wiesel‘s models of simple and complex cells offer two archetypal examples involving feedforward connections (Fig. 2C), but now it is possible to imagine many different types. For instance, which of the following excitatory pathways in a cortical circuit are related to in vivo functional properties: recurrent excitatory connections within a layer (Ko et al., 2011; Fig 2B), feedback connections between layers, or excitatory inputs to inhibitory neurons (Bock et al., 2011)?
It is perhaps surprising that we still do not know the answers to these simple questions, fifty years after Hubel and Wiesel‘s groundbreaking work. It is heartening, however, that new approaches hold the promise to answer them, and in the coming years to inspire new questions that we have not yet considered.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alonso JM, Martinez LM. Functional connectivity between simple cells and complex cells in cat striate cortex. Nat. Neurosci. 1998;1:395–403. doi: 10.1038/1609. [DOI] [PubMed] [Google Scholar]
- Alonso JM, Usrey WM, Reid RC. Rules of connectivity between geniculate cells and simple cells in cat primary visual cortex. J Neurosci. 2001;21:4002–4015. doi: 10.1523/JNEUROSCI.21-11-04002.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alonso JM, Swadlow HA. Thalamocortical specificity and the synthesis of sensory cortical receptive fields. J Neurophysiol. 2005;94:26–32. doi: 10.1152/jn.01281.2004. [DOI] [PubMed] [Google Scholar]
- Andermann ML, Kerlin AM, Reid RC. Chronic cellular imaging of mouse visual cortex during operant behavior and passive viewing. Front. Cell. Neurosci. 2010;4:3. doi: 10.3389/fncel.2010.00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson JR, Jones BW, Watt CB, Shaw MV, Yang J-H, DeMill D, Lauritzen JS, Lin Y, Rapp KD, Mastronarde D, et al. Exploring the retinal connectome. Mol Vis. 2011;17:355–379. [PMC free article] [PubMed] [Google Scholar]
- Ascoli GA, Alonso-Nanclares L, Anderson SA, Barrionuevo G, Benavides-Piccione R, Burkhalter A, Buzsaki G, Cauli B, Defelipe J, Fairen A, et al. Petilla Interneuron Nomenclature Group. Petilla terminology: nomenclature of features of GABAergic interneurons of the cerebral cortex. Nat. Rev. Neurosci. 2008;9:557–568. doi: 10.1038/nrn2402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bock DD, Lee WC, Kerlin AM, Andermann ML, Hood G, Wetzel W, Yurgenson S, Soucy ER, Kim HS, Reid RC. Network anatomy and in vivo physiology of visual cortical neurons. Nature. 2011;471:177–182. doi: 10.1038/nature09802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonin V, Histed MH, Yurgenson S, Reid RC. Local diversity and fine-scale organization of receptive fields in mouse visual cortex. J Neurosci. 2011;31:18506–18521. doi: 10.1523/JNEUROSCI.2974-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braitenberg V, Schüz A. Cortex: Statistics and geometry of neuronal connectivity. 2nd ed. Berlin, New York: Springer; 1998. [Google Scholar]
- Brown SP, Hestrin S. Cell-type identity: a key to unlocking the function of neocortical circuits. Curr Opin Neurobiol. 2009;19:415–421. doi: 10.1016/j.conb.2009.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Briggman KL, Helmstaedter M, Denk W. Wiring specificity in the direction-selectivity circuit of the retina. Nature. 2011;471:183–188. doi: 10.1038/nature09818. [DOI] [PubMed] [Google Scholar]
- Bruno RM, Simons DJ. Feedforward mechanisms of excitatory and inhibitory cortical receptive fields. J. Neurosci. 2002;22:10966–10975. doi: 10.1523/JNEUROSCI.22-24-10966.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapman B, Zahs KR, Stryker MP. Relation of cortical cell orientation selectivity to alignment of receptive fields of the geniculocortical afferents that arborize within a single orientation column in ferret visual cortex. J Neurosci. 1991;11:1347–1358. doi: 10.1523/JNEUROSCI.11-05-01347.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Leischner U, Rochefort NL, Nelken I, Konnerth A. Functional mapping of single spines in cortical neurons in vivo. Nature. 2011;475:501–505. doi: 10.1038/nature10193. [DOI] [PubMed] [Google Scholar]
- Chen C, Regehr WG. Developmental remodeling of the retinogeniculate synapse. Neuron. 2000;28:955–966. doi: 10.1016/s0896-6273(00)00166-5. [DOI] [PubMed] [Google Scholar]
- Chklovskii DB, Mel BW, Svoboda K. Cortical rewiring and information storage. Nature. 2004;431:782–788. doi: 10.1038/nature03012. [DOI] [PubMed] [Google Scholar]
- Cleland BG, Dubin MW, Levick WR. Simultaneous recording of input and output of lateral geniculate neurones. Nature - New Biology. 1971;231:191–192. doi: 10.1038/newbio231191a0. [DOI] [PubMed] [Google Scholar]
- Cleland BG. The dorsal lateral geniculate nucleus of the cat. In: Pettigrew JD, Sanderson KS, Levick WR, editors. Visual Neuroscience. London: Cambridge University Press; 1986. pp. 111–120. [Google Scholar]
- Denk W, Horstmann H. Serial block-face scanning electron microscopy to reconstruct three-dimensional tissue nanostructure. PLoS Biol. 2004;2:e329. doi: 10.1371/journal.pbio.0020329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferster D, Chung S, Wheat H. Orientation selectivity of thalamic input to simple cells of cat visual cortex. Nature. 1996;380:249–252. doi: 10.1038/380249a0. [DOI] [PubMed] [Google Scholar]
- Hamos JE, Van Horn SC, Raczkowski D, Sherman SM. Synaptic circuits involving an individual retinogeniculate axon in the cat. J. Comp. Neurol. 1987;259:165–192. doi: 10.1002/cne.902590202. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Integrative action in the cat's lateral geniculate body. J. Physiol. (London) 1961;155:385–398. doi: 10.1113/jphysiol.1961.sp006635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat‘s visual cortex. J Physiol (Lond) 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain V, Seung HS, Turaga SC. Machines that learn to segment images: A crucial technology for connectomics. Curr. Opin. Neurobiol. 2010;20:653–666. doi: 10.1016/j.conb.2010.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J, Wang Y, Swadlow HA, Alonso JM. Population receptive fields of ON and OFF thalamic inputs to an orientation column in visual cortex. Nat Neurosci. 2011;14:232–238. doi: 10.1038/nn.2729. [DOI] [PubMed] [Google Scholar]
- Kleindienst T, Winnubst J, Roth-Alpermann C, Bonhoeffer T, Lohmann C. Activity-dependent clustering of functional synaptic inputs on developing hippocampal dendrites. Neuron. 2011;72:1012–1024. doi: 10.1016/j.neuron.2011.10.015. [DOI] [PubMed] [Google Scholar]
- Ko H, Hofer SB, Pichler B, Buchanan KA, Sjostrom PJ, Mrsic-Flogel TD. Functional specificity of local synaptic connections in neocortical networks. Nature. 2011;473:87–91. doi: 10.1038/nature09880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozloski J, Hamzei-Sichani F, Yuste R. Stereotyped position of local synaptic targets in neocortex. Science. 2001;293:868–872. doi: 10.1126/science.293.5531.868. [DOI] [PubMed] [Google Scholar]
- Lee WC, Reid RC. Specificity and randomness: structure-function relationships in neural circuits. Curr Opin Neurobiol. 2011;21:801–807. doi: 10.1016/j.conb.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chia TH, Levene MJ. Microprisms for in vivo multilayer cortical imaging. J. Neurophysiol. 2009;102:1310–1314. doi: 10.1152/jn.91208.2008. [DOI] [PubMed] [Google Scholar]
- Lichtman JW, Sanes JR. Ome sweet ome: what can the genome tell us about the connectome? Curr. Opin. Neurobiol. 2008;18:346–353. doi: 10.1016/j.conb.2008.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mastronarde DN. Two classes of single-input X-cells in cat lateral geniculate nucleus II Retinal inputs and the generation of receptive-field properties. J. Neurophysiol. 1987;57:381–413. doi: 10.1152/jn.1987.57.2.381. [DOI] [PubMed] [Google Scholar]
- Mel BW. Synaptic integration in an excitable dendritic tree. J. Neurophysiol. 1993;70:1086–1101. doi: 10.1152/jn.1993.70.3.1086. [DOI] [PubMed] [Google Scholar]
- Miller LM, Escabi MA, Read HL, Schreiner CE. Functional convergence of response properties in the auditory thalamocortical system. Neuron. 2001;32:151–160. doi: 10.1016/s0896-6273(01)00445-7. [DOI] [PubMed] [Google Scholar]
- Mittmann W, Wallace DJ, Czubayko U, Herb JT, Schaefer AT, Looger LL, Denk W, Kerr JN. Two-photon calcium imaging of evoked activity from L5 somatosensory neurons in vivo. Nat Neurosci. 2011;14:1089–1093. doi: 10.1038/nn.2879. [DOI] [PubMed] [Google Scholar]
- Mountcastle V. Modality and topographic properties of single neurons of cat somatosensory cortex. J. Neurophysiol. 1957;20:408–434. doi: 10.1152/jn.1957.20.4.408. [DOI] [PubMed] [Google Scholar]
- Nelson SB, Sugino K, Hempel CM. The problem of neuronal cell types: a physiological genomics approach. Trends Neurosci. 2006;29:339–345. doi: 10.1016/j.tins.2006.05.004. [DOI] [PubMed] [Google Scholar]
- Ohki K, Chung S, Ch'ng YH, Kara P, Reid RC. Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature. 2005;433:597–603. doi: 10.1038/nature03274. [DOI] [PubMed] [Google Scholar]
- Perkel DH, Gerstein GL, Moore GP. Neuronal spike trains and stochastic point processes II Simultaneous spike trains. Biophys. J. 1967;7:419–440. doi: 10.1016/S0006-3495(67)86597-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perin R, Berger TK, Markram H. A synaptic organizing principle for cortical neuronal groups. Proc. Natl. Acad. Sci. USA. 2011;108:5419–5424. doi: 10.1073/pnas.1016051108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peters A, Kara DA. The neuronal composition of area 17 of rat visual cortex. IV. The organization of pyramidal cells. J. Comp. Neurol. 1987;260:573–590. doi: 10.1002/cne.902600410. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Ferster D. Mechanisms of neuronal computation in mammalian visual cortex. Neuron. 2012 doi: 10.1016/j.neuron.2012.06.011. this issue. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid RC, Alonso JM. Specificity of monosynaptic connections from thalamus to visual cortex. Nature. 1995;378:281–284. doi: 10.1038/378281a0. [DOI] [PubMed] [Google Scholar]
- Reid RC, Alonso JM, Usrey WM. Integration of thalamic inputs to cat primary visual cortex. In: Payne BR, Peters A, editors. The cat primary visual cortex. San Diego: Academic Press; 2001. pp. 319–342. [Google Scholar]
- Reid RC. Divergence and reconvergence: multielectrode analysis of feedforward connections in the visual system. Prog. Brain. Res. 2001;130:141–154. doi: 10.1016/s0079-6123(01)30010-9. [DOI] [PubMed] [Google Scholar]
- Seung HS. Towards functional connectomics. Nature. 2011;471:170–172. doi: 10.1038/471170a. [DOI] [PubMed] [Google Scholar]
- Seung HS. Reading. the book of memory: sparse sampling versus dense mapping of connectomes. Neuron. 2009;62:17–29. doi: 10.1016/j.neuron.2009.03.020. [DOI] [PubMed] [Google Scholar]
- Sherman SM, Guillery RW. On the actions that one nerve cell can have on another: distinguishing “drivers” from “modulators”. Proc. Natl. Acad. Sci. USA. 1998;95:7121–7126. doi: 10.1073/pnas.95.12.7121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Sjostrom PJ, Reigl M, Nelson S, Chklovskii DB. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3:e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Kötter R. The Human Connectome: A structural description of the human brain. PLoS Comput Biol. 2005;1:e42. doi: 10.1371/journal.pcbi.0010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stepanyants A, Chklovskii DB. Neurogeometry and potential synaptic connectivity. Trends Neurosci. 2005;28:387–394. doi: 10.1016/j.tins.2005.05.006. [DOI] [PubMed] [Google Scholar]
- Sterling P. Microcircuitry of the cat retina. Annu Rev Neurosci. 1983;6:149–185. doi: 10.1146/annurev.ne.06.030183.001053. [DOI] [PubMed] [Google Scholar]
- Sugino K, Hempel CM, Miller MN, Hattox AM, Shapiro P, Wu C, Huang ZJ, Nelson SB. Molecular taxonomy of major neuronal classes in the adult mouse forebrain. Nat. Neurosci. 2006;9:99–107. doi: 10.1038/nn1618. [DOI] [PubMed] [Google Scholar]
- Swadlow HA. Influence of VPM afferents on putative inhibitory interneurons in S1 of the awake rabbit: evidence from cross-correlation, microstimulation, and latencies to peripheral sensory stimulation. J Neurophysiol. 1995;73:1584–1599. doi: 10.1152/jn.1995.73.4.1584. [DOI] [PubMed] [Google Scholar]
- Swadlow HA, Gusev AG. Receptive-field construction in cortical inhibitory interneurons. Nat Neurosci. 2002;5:403–404. doi: 10.1038/nn847. [DOI] [PubMed] [Google Scholar]
- Tanaka K. Cross-correlation analysis of geniculostriate neuronal relationships in cats. J Neurophysiol. 1983;49:1303–1318. doi: 10.1152/jn.1983.49.6.1303. [DOI] [PubMed] [Google Scholar]
- Tavazoie SF, Reid RC. Diverse receptive fields in the lateral geniculate nucleus during thlamocortical development. Nat. Neurosci. 2000;3:608–616. doi: 10.1038/75786. [DOI] [PubMed] [Google Scholar]
- Tian L, Hires SA, Mao T, Huber D, Chiappe ME, Chalasani SH, Petreanu L, Akerboom J, McKinney SA, Schreiter ER, et al. Imaging neural activity in worms, flies and mice with improved GCaMP calcium indicators. Nat. Methods. 2009;6:875–881. doi: 10.1038/nmeth.1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usrey WM, Reppas JB, Reid RC. Paired-spike interactions and synaptic efficacy of retinal inputs to the thalamus. Nature. 1998;395:384–387. doi: 10.1038/26487. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K, Auerbach E, Barch D, Behrens TE, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss SW, et al. The Human Connectome Project: A data acquisition perspective. Neuroimage. 2012 Feb 17; doi: 10.1016/j.neuroimage.2012.02.018. Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ware RW, LoPresti V. Three-dimensional reconstruction from serial sections. Int. Rev. Cytology. 1975;40:325–440. doi: 10.1016/s0074-7696(08)60956-0. [DOI] [PubMed] [Google Scholar]
- Wickersham IR, Lyon DC, Barnard RJ, Mori T, Finke S, Conzelmann KK, Young JA, Callaway EM. Monosynaptic restriction of transsynaptic tracing from single, genetically targeted neurons. Neuron. 2007b;53:639–647. doi: 10.1016/j.neuron.2007.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White JG, Southgate E, Thomson JN, Brenner S. The structure of the nervous system of the nematode Caenorhabditis elegans . Philos Trans. R. Soc. Lond. B. 1986;314:1–340. doi: 10.1098/rstb.1986.0056. [DOI] [PubMed] [Google Scholar]
- Yoshimura Y, Dantzker JL, Callaway EM. Excitatory cortical neurons form fine-scale functional networks. Nature. 2005;433:868–873. doi: 10.1038/nature03252. [DOI] [PubMed] [Google Scholar]