Control time reduction using virtual source projection for treating a leg sarcoma with nonlinear perfusion

Abstract

Purpose

Blood perfusion is a well-known factor that complicates accurate control of heating during hyperthermia treatments of cancer. Since blood perfusion varies as a function of time, temperature and location, determination of appropriate power deposition pattern from multiple antenna array Hyperthermia systems and heterogeneous tissues is a difficult control problem. Therefore, we investigate the applicability of a real-time eigenvalue model reduction (virtual source - VS) reduced-order controller for hyperthermic treatments of tissue with nonlinearly varying perfusion.

Methods

We impose a piecewise linear approximation to a set of heat pulses, each consisting of a 1-min heat-up, followed by a 2-min cool-down. The controller is designed for feedback from magnetic resonance temperature images (MRTI) obtained after each iteration of heat pulses to adjust the projected optimal setting of antenna phase and magnitude for selective tumor heating. Simulated temperature patterns with additive Gaussian noise with a standard deviation of 1.0°C and zero mean were used as a surrogate for MRTI. Robustness tests were conducted numerically for a patient's right leg placed at the middle of a water bolus surrounded by a 10-antenna applicator driven at 150 MHz. Robustness tests included added discrepancies in perfusion, electrical and thermal properties, and patient model simplifications.

Results

The controller improved selective tumor heating after an average of 4-9 iterative adjustments of power and phase, and fulfilled satisfactory therapeutic outcomes with approximately 75% of tumor volumes heated to temperatures >43°C while maintaining about 93% of healthy tissue volume < 41°C. Adequate sarcoma heating was realized by using only 2 to 3 VSs rather than a much larger number of control signals for all 10 antennas, which reduced the convergence time to only 4 to 9% of the original value.

Conclusions

Using a piecewise linear approximation to a set of heat pulses in a VS reduced-order controller, the proposed algorithm greatly improves the efficiency of hyperthermic treatment of leg sarcomas while accommodating practical nonlinear variation of tissue properties such as perfusion.

1. Introduction

The therapeutic outcome of hyperthermia is known to be significantly affected by blood perfusion ^[1], which is usually a nonlinear function of temperature ^[2]. A controller that works for constant perfusion is not guaranteed to converge for nonlinear perfusion cases. Moreover, theoretically the required steering and re-focusing time for a feedback controller to selectively heat the tumor is proportional to the square of the number of the antennas ^[3]. Heating during this period is ineffective, and this time expenditure could be intolerably long, for systems with a large number of antennas. Quantitatively, it would require 432 minutes for a BSD-2000 Sigma-Eye 3-ring 12-paired antenna array, if each single learning-iteration takes 3 minutes. These problems are addressed in literature ^{[4] [5] [3]}. However, in general, those controllers still require M² steps for model identification when M antennas are used. Recently, Cheng et. al. ^[6] developed a model reduction method using virtual source (VS) approach that was validated by steady state temperature optimization when perfusion is either constant or nonlinearly varying. Therefore, we were motivated to design a real-time reduced-order feedback controller incorporating this model-reduction method for a hyperthermic treatment with nonlinear blood perfusion.

2. Methods

2.1. Nonlinear blood perfusion models for tissues and tumor

The hyperthermia community commonly incorporates the Pennes bio-heat transfer equations ^[7] with some empirically curve-fitted perfusion relations ^[8] to simulate the bio-heat transfer process.

$$\rho \cdot C_t\cdot \frac{\partial T}{\partial t}=\nabla •(k\cdot \nabla T)-w_b\left(T\right)\cdot C_b\cdot (T-T_b)+Q$$ <1>

One such fitted perfusion model was developed using a half-Gaussian curve to fit Song's experiment results ^[2] to mimic blood vessel dilation to dissipate excessive heat. The following curve was employed to simulate this phenomenon ^{[9] [5] [6]}.

$$w_{\mathrm{tissue}}=\{\begin{array}{l}{w}_{\mathrm{tissue},1}+w_{\mathrm{tissue},2}\cdot \exp \left(\frac{-{(T-T_{\mathrm{crit},\mathrm{tissue}})}^2}{s_{\mathrm{tissue}}}\right)\\ w_{\mathrm{tissue},1}+w_{\mathrm{tissue},2},T>T_{\mathrm{crit},\mathrm{tissue}}\end{array},T\le T_{\mathrm{crit},\mathrm{tissue}}$$ <2.1>

For tumor perfusion dynamics, some experimental studies ^{[10] [2]} reported that tumor perfusion tends to decrease with increase of temperature beyond a certain critical temperature, probably because tumor vessels are more sensitive to temperature and thus are damaged as temperature increases beyond a mild hyperthermic range ^[11]. Therefore we have chosen to mimic perfusion dynamics in tumor by a decreasing half-Gaussian curve.

$$w_{\mathrm{tumor}}=\{\begin{array}{l}{w}_{\mathrm{tumor},1}+w_{\mathrm{tumor},2}\cdot \left(1-\exp \left(\frac{-{(T-T_{\mathrm{crit},\mathrm{tumor}})}^2}{s_{\mathrm{tumor}}}\right)\right)\\ w_{\mathrm{tumor},1},T>T_{\mathrm{crit},\mathrm{tumor}}\end{array},T\le T_{\mathrm{crit},\mathrm{tumor}}$$ <2.2>

2.2. The design of the proposed feedback controller

A minimum-norm least-squares-errors-based (MNLSE) feedback algorithm ^[3] is incorporated with a model-reduction of VS for steady state temperature optimization ^[6]; therefore, the feedback correction is limited to a smaller VS subspace at each iteration. This way, we can potentially shorten the lengthy M²-step model-identification process (M-antenna applicator) by using a smaller number of N (< M) virtual antennas in fewer steps of N² (≪M².) Then, a reduced-order VS feedback controller was developed to operate in this reduced subspace. The VS feedback controller starts from an initial assumption of the reduced patient model, which is then iteratively updated using thermal imaging feedback. Accordingly, the system matrices defining the patient model are updated, and the power is adjusted based on the difference between the thermal images and expected temperature distribution at each iterative session. Concurrent with this update, the temperature distribution is steered to maximize heating at the target location.

2.3. Setup for numerical validation

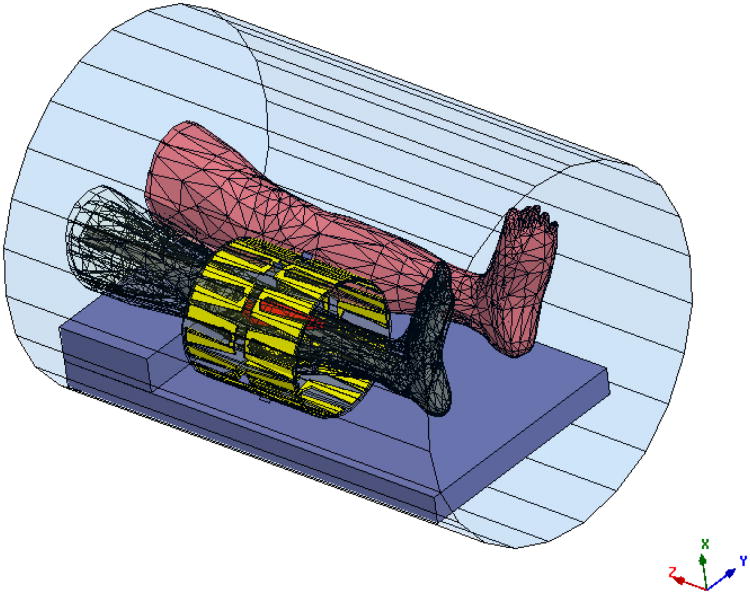
The feasibility and robustness of the proposed VS-based reduced-order feedback controller was numerically investigated on a human lower leg dataset heated in a 10-antenna mini annular phased array (MAPA) applicator. The MAPA is coherently driven at 150 MHz. For impedance matching and thermal cooling, the antennas are coupled to the patient via a bolus filled with de-ionized water. Numerical patient and applicator models were constructed as shown in Fig. 1 and then imported into the electromagnetic simulator-HFSS (Ansoft Corporation (Pittsburgh, PA)).

Figure 1.

Electromagnetic segmentation model of the leg as derived from patient CT scan showing meshes for anatomical structures (the red object is tumor) inside 10-antenna cylindrical array. The whole system sits inside the MRI bore. The antennas are evenly separated by 36° around a cylindrical surface of diameter = 23 cm and length =24 cm. The tumor is in the upper right position, next to the upper portion of the tibia, and occupies a volume of about 138.59 cm³. The size of the tumor is 18 cm × 5.65 cm (maximum width).

The corresponding power deposition patterns generated by these EM fields were used as source terms for an in-house finite difference temperature solver. A uniform temperature of 37°C was used as the initial and boundary condition. Tissue property values used were adapted from literature ^{[12] [13] [14] [15] [16]} and are summarized in Table 1. Parameters for the nonlinearly varying tissue perfusion are given in Table-2.

Table-1. Nominal Property Values (assumed for 150 MHz).

	Relative electric permittivity, εR, $${\epsilon }_R=\frac{\epsilon }{{\epsilon }_0}$$	Electrical conductivity, σ (S/m)	Density, ρ (kg/m3)	Specific heat, Ct (J/kg/°K)	Thermal conductivity, k (W/m/°C)	Blood perfusion, wb (kg/m3/s)
Blood	-	-	-	3770	-	-
Bone cortical	14.4	0.07	1700	1300	2.3	0.0
Bone marrow	6.1	0.024	1700	1300	0.58	0.1
Fat	5.8	0.037	900	2987	0.33	1.1
Muscle	62.2	0.727	1050	3639	0.50	3.6
Tumor	68	0.9	1050	3639	0.50	1.8
Water	78	0.002	996	4178	0.61	-

Permittivity of vacuum, ε₀ = 8.854*10⁻¹² Farad/m and permeability of vacuum, μ₀ = 4*π*10⁻⁷ Henry/m. The permeabilities of all tissues were assumed to be equal to that of vacuum.

Table-2. Parameter Values For Nonlinear Perfusion Models.

	Perfusion in Normal Condition	Perfusion Increase	Threshold Temperature	Saturation Parameter
	w1	w2	Tcrit	s
Fat	0.77	0.66	45	12
Muscle	0.90	5.40	45	12
Tumor	0.90	1.80	43	12

2.4. Feasibility studies

A set of practical perturbations to these assumed initial tissue properties were used to validate the controller robustness. Specifically, we simulated the robustness of the controller to variations in electrical and thermal property values, including blood perfusion, which can vary significantly between different patients and tissue sites ^{[12] [13] [14]}. The deviations in the initial model investigated in this work are listed in Table 3.

Table-3. Property Deviations for Lower Leg Tissues.

	Relative electric permittivity, εR, $${\epsilon }_R=\frac{\epsilon }{{\epsilon }_0}$$	Electrical conductivity, σ (S/m)	Density, ρ (kg/m3)	Specific heat, (J/kg/°K)	Thermal Ct conductivity (W/m/°C)	Blood perfusion, k wb (kg/m3/s)
Blood	-	-	-	+50%	-	-
Bone cortical	+50%	−50%	−50%	+50%	+50%	+0.0%
Bone marrow	+50%	+50%	−50%	−50%	−50%	+50%
Fat	+50%	−50%	+50%	−50%	−50%	+50%
Muscle	−50%	−50%	-50%	+50%	+50%	−50%
Tumor	−50%	+50%	+50%	−50%	−50%	+50%

Also, we used the simplified model preserving exact patient leg and tumor geometry of that in Fig. 1, but assuming all property values are the same as pure muscle, except those in the tumor ^[3]. Treatment preparation is greatly simplified if the proposed algorithm remains robust to this easy-to-build simplified model. Moreover, MRTI comes with unavoidable measurement noise, and therefore Gaussian white noise with a standard deviation (STD) of 1.0°C was added to the simulated temperature patterns from the MRTI to determine robustness of the controller in the presence of noise.

In this study, the following numerical simulations were performed for a lower leg tumor model with nonlinear variation of perfusion: the reduced-order approximate tumor model with piecewise constant perfusion was reconstructed within the reduced subspace spanned by the first 2 to 5 VS basis vectors of the three variants: 1) lower leg model, 2) lower leg model with property deviations as given in Table 3, and 3) pure-muscle lower leg model with property deviations.

3. Results and Discussion

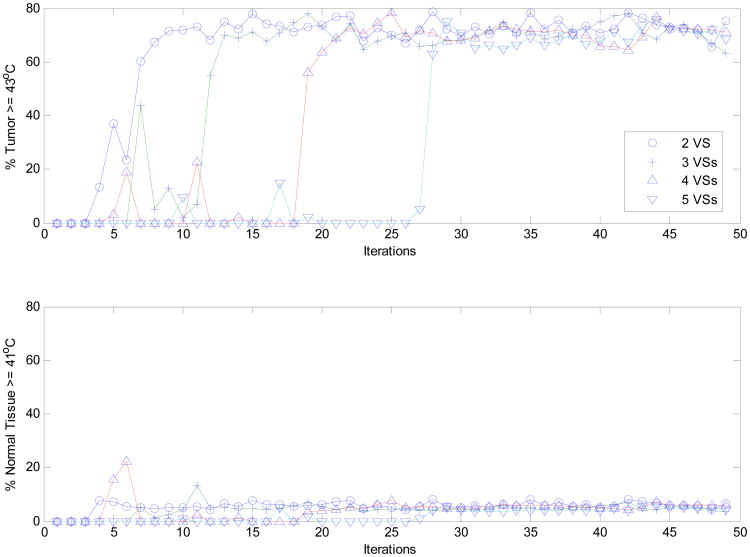
The proposed real-time MRTI-guided VS reduced-order feedback controller accomplished successful selective tumor heating, even when patient blood perfusion values change nonlinearly with temperature as shown in Figs 3-5. Fig. 4 shows that an optimal heating vector was achieved by iterative feedback refinement producing a steady state heating distribution with ∼75% of the tumor volume heated to > 41 °C, accompanied by only ∼7% of the healthy volume > 41 °C. This steady state condition was reached in ∼N² steps, when the first N VS basis vectors from the initial erroneous model were used. Moreover, as illustrated in Fig. 5, the heating vector at each correction step was iteratively adjusted by the proposed controller, based on the MNLSE synthesized approximate linear model spanned by the first 2-5 VS basis vectors (determined by initial standard or erroneous models). This controlled correction is seen to converge.

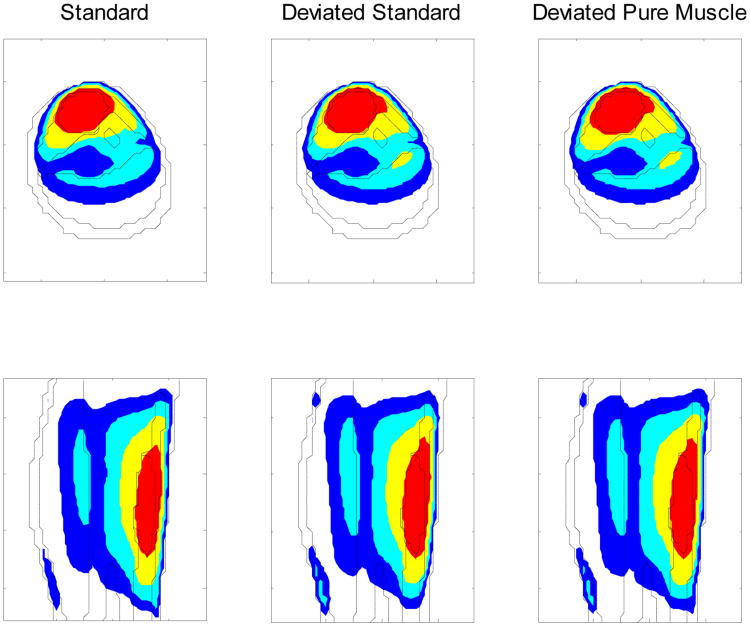
Figure 3.

Temperature distributions in axial and sagittal views of lower leg sarcoma patient at the 49^th iteration, for an initial driving vector corresponding to the minimum eigenvector of the approximate model, with piecewise constant perfusion, constructed by the reduced subspaces spanned by the first 4 virtual source basis vectors of different models (labeled above) with (linear) constant perfusion. The temperatures were determined from bio-heat transfer equations with nonlinear temperature-dependent perfusion (tumor perfusion rapidly decreases with temperature.) The outermost ring is fat, within which is the muscle region. The larger irregular object on the topside of the muscle region is tumor, and the two smaller irregular objects at the center are bone. The colored regions are: red for ≥ 43°C, yellow for ≥ 41°C, light blue for ≥ 40°C and blue for ≥ 39°C.

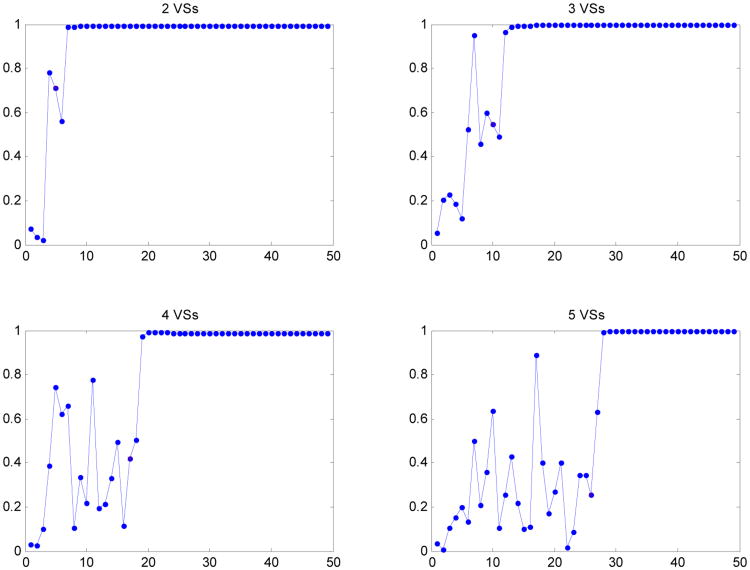
Figure 5.

The dot product at each feedback iteration step between the heating vectors of the pure-muscle lower leg model with deviated tissue properties and nonlinear temperature-dependent perfusion models to the maximum eigenvector of the standard model with constant perfusion, when the first heating vector was obtained from minimum eigenvector of the approximate deviated pure-muscle lower leg model constructed by the reduced subspaces spanned by the first 2 to 5 virtual source basis vectors.

Figure 4.

The percentage of heated tumor volume (T ≥ 43°C) and normal tissues (T ≥ 41°C), when initial driving vector is the minimum eigenvector of the linear model constructed by the reduced subspaces spanned by the first 2 to 5 orthonormal virtual sources of the deviated pure-muscle lower leg models with constant perfusion. The temperatures were determined from the bio-heat transfer equations with nonlinear temperature-dependent perfusion. Note, in determining the heated normal tissue volume, those in the vicinity of target tumor within 1.0 cm around were not considered due to the unavoidable diffusive nature of thermal dissipation.

As is evident from the numerical simulations, the proposed controller successfully accomplishes satisfactory therapeutic outcomes. The reduced-order controller also reduces the convergence time for the simulated lower-leg sarcoma hyperthermia treatment in a 10-antenna array to only 4-9% of the time required without the virtual source model reduction approach.

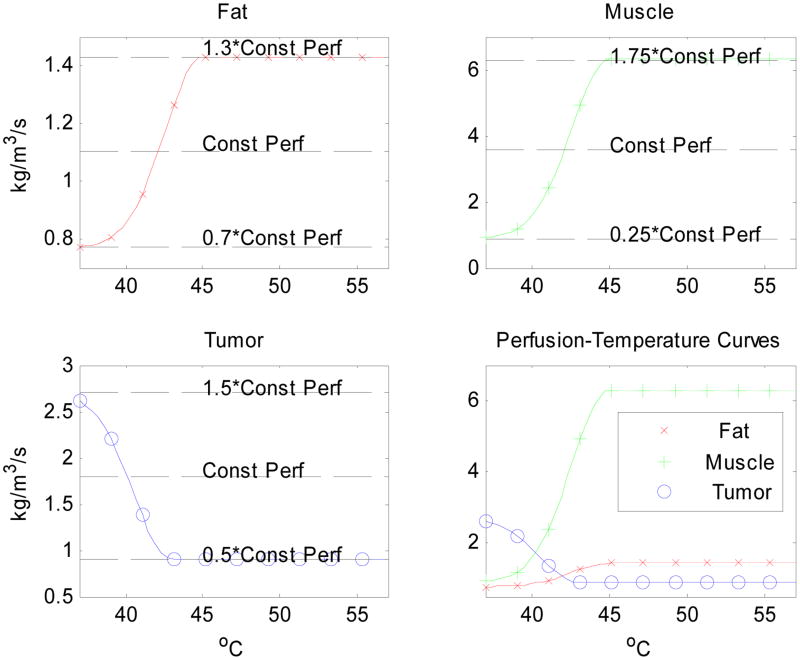
Figure 2.

Curves modeling perfusion-temperature relations in fat, muscle and tumor, attempting to mimic the trend observed in Song's experimental data. Here we assume a decreasing tumor perfusion with temperature. In developing these functions, we assumed that perfusion increases with temperature in fat and muscle, ranging from 30% below to 30% above the constant perfusion value of fat, plus and minus 75% for muscle in Table 1. However, a decreasing perfusion was assumed for tumor, ranging from 50% below to 50% above the constant perfusion value in Table 1.