Monoplane Stereoscopic Imaging Method for Inverse Geometry X-ray Fluoroscopy

Abstract

Scanning Beam Digital X-ray (SBDX) is a low-dose inverse geometry fluoroscopic system for cardiac interventional procedures. The system performs x-ray tomosynthesis at multiple planes in each frame period and combines the tomosynthetic images into a projection-like composite image for fluoroscopic display. We present a novel method of stereoscopic imaging using SBDX, in which two slightly offset projection-like images are reconstructed from the same scan data by utilizing raw data from two different detector regions. To confirm the accuracy of the 3D information contained in the stereoscopic projections, a phantom of known geometry containing high contrast steel spheres was imaged, and the spheres were localized in 3D using a previously described stereoscopic localization method. After registering the localized spheres to the phantom geometry, the 3D residual RMS errors were between 0.81 and 1.93 mm, depending on the stereoscopic geometry. To demonstrate visualization capabilities, a cardiac RF ablation catheter was imaged with the tip oriented towards the detector. When viewed as a stereoscopic red/cyan anaglyph, the true orientation (towards vs. away) could be resolved, whereas the device orientation was ambiguous in conventional 2D projection images. This stereoscopic imaging method could be implemented in real time to provide live 3D visualization and device guidance for cardiovascular interventions using a single gantry and data acquired through normal, low-dose SBDX imaging.

1. INTRODUCTION

X-ray fluoroscopy (XRF) is the primary image guidance method for cardiovascular interventions due to its high spatial and temporal resolution and ease of use. However the projection process of XRF compresses all of the features in the 3D imaging volume into a single 2D image, eliminating information about the relative position of anatomy and devices along the direction of the projection (i.e. depth information). Recent interventional therapies such as RF ablation for cardiac arrhythmias¹ and transendocardial therapeutic injections² require precise device guidance within cardiac chambers, where they can be freely manipulated in 3D. Visualization of device depth and orientation may improve the accuracy and efficiency of these procedures.

An additional x-ray view allows the operator to better determine the depth or orientation of an object. Biplane XRF typically uses two orthogonal views from which the operator can mentally reconstruct a 3D representation of the field of view. If the two views are only slightly different instead of orthogonal, they can be presented as a single, 3D stereoscopic image.^{3, 4} Each eye sees a different view, and the brain interprets the disparity between object positions, or parallax, in the two views as depth.⁵ The single, 3D display can convey depth information to the user in way that is as intuitive as normal binocular human vision.

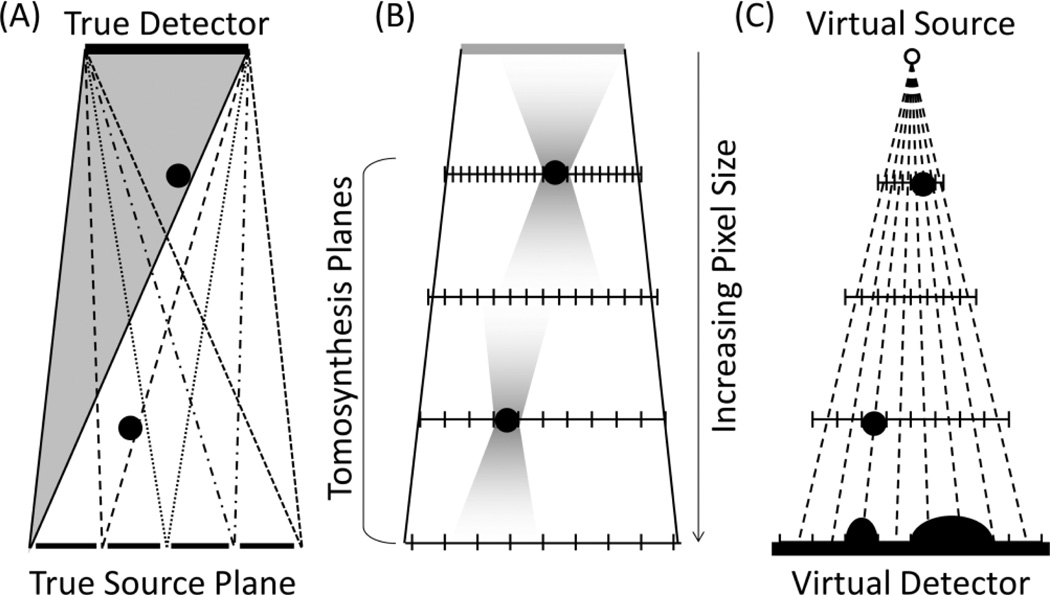
Existing methods for stereoscopic imaging using conventional XRF geometries have several drawbacks. Using the two gantries of a conventional biplane XRF system does not allow the x-ray sources to be positioned close enough to each other to create the stereoscopic effect; the parallax is too great for the operator to fuse the two images into a single 3D scene.⁶ In addition, there is a limited area of overlap between the two views where an object can be imaged stereoscopically (Figure 1B). Special XRF tubes with two anodes produce image pairs suitable for stereoscopic visualization,^{3, 4} however they use a common detector and must make alternating x-ray exposures (Figure 1C). It is possible for a device in the heart to move between the two exposures, which may be distracting to the user or possibly misrepresent an object’s depth.

Figure 1.

Stereoscopic XRF methods can be adapted from conventional XRF geometries (A) by using two complete gantries (B) or a special dual-anode x-ray tube with a common detector (C), but both methods have drawbacks.

We present a novel stereoscopic imaging technique using Scanning Beam Digital X-ray (SBDX) technology that provides simultaneous stereo projection images at fluoroscopic frame rates using a single gantry. SBDX is a cardiac x-ray fluoroscopy system designed to reduce x-ray dose by up to 84% through scatter rejection, detector efficiency, and inverse geometry beam scanning.^{7, 8} In inverse geometry beam scanning, a scanning x-ray source with an electromagnetically deflected focal spot and large area target is used to generate thousands of narrow overlapping x-ray projections of the patient in every frame period. These projections are directed at a small high-speed photon-counting detector. Full field-of-view images are produced for each frame by first reconstructing a stack of tomosynthetic image planes and then forming a multiplane composite image similar to a conventional 2D projection.

We show that by dividing the raw SBDX detector data into two datasets corresponding to different regions of the detector and modifying the reconstruction procedure, it is possible to produce a stereoscopic pair of SBDX images for each image frame. A major enabler of this technique is a recently redesigned SBDX detector in which the width was approximately doubled to 10.6 cm×5.3 cm to increase image SNR. This width increase makes it possible to reconstruct a stereoscopic pair of composite images originating from different points. This paper describes the method of stereoscopic reconstruction, reports its performance through stereoscopic 3D localization of objects, and demonstrates stereoscopic imaging of a cardiac interventional device.

2. THEORY

2.1 SBDX imaging

SBDX has an array of collimated focal spots that are sequentially illuminated to generate a scanning x-ray beam (Figure 2). The system used in this study had a source to detector distance of 150 cm with the gantry isocenter 45 cm above the source. The detector array featured 160×80 detector elements with 0.66 mm pitch. The multihole collimator on the source supports up to 100×100 focal spot positions with a focal spot pitch of 2.3 mm. Typical operation uses the central 71×71 focal spots.

Figure 2.

SBDX produces a sequence of overlapping narrow beams (beamlets) using a raster scanned focal spot and multihole collimator. The full field-of-view is imaged at up to 30 frame/sec. Up to 100x100 positions are used in a frame period.

Shift-and-add digital tomosynthesis is performed at multiple planes for each scan frame. Details of the procedure may be found in Ref 8. Here we describe aspects of the reconstructed pixel grid and multiplane compositing which are relevant to our stereoscopic method. By convention, i) the pixel grid array for each tomosynthetic image is centered on the line connecting the center of the detector and the center of the source scan pattern, ii) the pixel size is zero at the detector and increases linearly toward the source plane where the pixel size is 0.23 mm, and iii) the image planes are cropped to the same number of rows and columns. It follows that the pixels in each plane at a fixed column and row position (u,v) will fall along a ray diverging from the center of the detector (see Figure 3C).

Figure 3.

(A) During SBDX image formation, each beamlet emerging from the collimator illuminates part of the field of view. The grayed region represents a single beamlet. Black dots represent two objects at different distances from the source. (B) Shift-and-add reconstruction is performed at planes using pixel dimensions that increase linearly toward the source plane. The objects appear blurred at planes above and below the object. (C) The composite image uses pixel values that fall along rays based on local contrast and sharpness. Geometry is exaggerated for clarity.

The individual tomosynthetic images portray in-plane objects in focus and out-of-plane objects as blurred. The multiplane composite is generated to provide a 2D display with all objects in focus simultaneously. This is accomplished with a pixel-by-pixel plane selection algorithm which, for each pixel position (u,v), extracts the pixel values along the corresponding ray and selects the value from the plane with highest local contrast and sharpness. Taken together the rays for all pixel positions form a cone diverging from a point centered on detector. Thus, the multiplane composite may be modeled as a “virtual projection”, with the “virtual source” located at the center of the detector and the “virtual detector” located at the source plane (Figure 3C).

2.2 Stereoscopic image reconstruction

The location of the virtual source is normally centered on the true detector. However, a virtual projection arising from any point on the detector can be generated by adjusting the definition of the pixel grid positioning vs. plane position during tomosynthetic image reconstruction. The primary requirements are that the center of the tomosynthetic images in the image stack should fall along the central ray between the new virtual source point and virtual detector, and the actual raw detector images used in image reconstruction should be cropped symmetrically about the new virtual source point so that tomographic blurring from a point object remains symmetric about the lines arising from the virtual source. This last constraint helps to reduce artifacts in the multiplane compositing process. The pixel-by-pixel plane selection algorithm itself does not require modification.

Extending the idea of a virtual projection, two virtual projections can be created from the detector data acquired in a single frame period to create a stereoscopic image pair (Figure 4). The depth at which the parallax is zero (where the central rays of the two projections “cross”) is determined by the pixel grid layout and the positioning of the virtual source points. Both can be adjusted by reconstruction parameters, allowing the user to adjust depth perception. Figure 4 shows three possible stereoscopic geometries using the proposed method. Figure 4A creates a stereoscopic image with zero parallax at the virtual detector plane such that when viewed all objects will appear to be in front of the 3D display. Figure 4B will appear similar to 4A, but with less parallax which may be preferable for presentation on a large display or one that is close to the viewer’s eyes. Figure 4C places the plane of zero parallax at the patient center such that objects will appear in front of or behind the 3D display. This geometry maximizes parallax versus depth while limiting the overall maximum parallax in the field of view, which ensures that the viewer will not lose the 3D effect due to excessive parallax.

Figure 4.

The SBDX stereoscopic projection pairs can be directed anywhere in the full field of view. (A) Stereoscopic projection pair with zero parallax at the virtual detector plane. (B) is the same as (A), but with the virtual sources closer together which decreases the amount of parallax versus distance from the source. (C) Offsetting the two virtual detectors creates zero parallax near isocenter, which is useful for visualization.

When viewed in a 3D format, the viewer will have the perspective equivalent to having their left and right eyes located and the left and right virtual source points, respectively, and looking toward the virtual detector. In terms of real gantry components, the viewer will have the perspective of looking from the true detector toward the true source. Therefore, objects that are oriented toward the true detector will appear to be oriented toward the viewer, and objects oriented toward the true source will appear to be oriented away from the viewer.

3. METHODS

3.1 Quantitative phantom validation

To evaluate the accuracy of the virtual projection model and stereoscopic image pairs, an existing 3D localization technique for stereoscopic imaging⁹ was applied to SBDX stereoscopic images of a geometric phantom. A poly(methyl methacrylate) (PMMA) cylinder was constructed with steel spheres embedded along the surface in a helical pattern (85 mm nominal cylinder diameter, 22.5° angular increment between spheres, 61 mm helical pitch, 1.6 mm sphere diameter, central sphere 2.4 mm diameter). The phantom was positioned at mechanical isocenter of the gantry, about 45 cm above the source plane. An additional 11.7 cm of PMMA was placed in the beam below the phantom for added filtration. The phantom was imaged at 80kV tube potential, 150 mA peak tube current, 71 × 71 focal spots, 15 frames/sec, and 15 frames were integrated to reduce image noise.

Three virtual projection geometries were examined. The first configuration separated the detector into left and right halves, with virtual sources centered on each half, resulting in a separation distance of 5.3 cm (Figure 4A). This represented a reasonable upper limit of separation distance, producing the most stereo parallax while using all of the data collected by the detector. The second configuration used a smaller separation distance (2.6 cm) that produces less parallax across the imaging volume (Figure 4B). The third configuration (Figure 4C) used the same virtual source spacing as Figure 4A, but with the plane of zero parallax at the gantry isocenter instead of the virtual detector plane.

For each configuration, a tomosynthetic image plane stack was reconstructed for the left and right virtual projections. Each plane stack had 32 image planes centered about mechanical isocenter (45 cm above the source plane) with 5 mm between planes. From each plane stack, a multiplane composite was formed to create a virtual projection. Reconstructions and multiplane compositing were performed using a software simulation of the SBDX reconstructor.

In preparation for 3D stereo localization, the left and right virtual projection images were automatically segmented to find the centroid of each of the spheres in the phantom. The segmentation algorithm identified the spheres by first applying a morphological bottom-hat filter with a disk structuring element slightly larger than the spheres in the image. This removed the background intensity variation due to the varying thickness of the PMMA cylinder. The filtered image was converted to a binary image by applying a threshold at 20% below the background intensity. Individual spheres were identified with connected component labeling, and the centroid of each connected group was calculated and used as the center for the sphere. The coordinates of the sphere centers were converted to physical units (mm) by scaling them by the pixel size at the virtual detector plane.

Three dimensional localization of the spheres was performed using a method designed for stereo projection pairs from different sources projecting onto the same detector plane⁹, which matches our stereo reconstruction geometry. Following the same notation as the method described by Ref. 9, the 3D position of an object can be determined by its 2D position in the left and right virtual projections, respectively (u₁,v₁) and (u₂,v₂), the position of the perpendicular ray of left virtual projection (u₀,v₀), the distance between the two virtual sources, b, and the source to image distance, SID. Figure 5 shows a schematic of the relevant values. Assuming that (v₁ = v₂), the 3D position can be calculated using Eq. 1.

$$\left[\begin{array}{c}\hfill x\prime \hfill \\ \hfill y\prime \hfill \\ \hfill z\prime \hfill \end{array}\right]=\frac{b}{(u_1-u_2)+b}\left[\begin{array}{c}\hfill [(u_1-u_0)+(u_2-u_0)-b)]/2\hfill \\ \hfill [(v_1-v_0)+(v_2-v_0)]/2\hfill \\ \hfill SID\hfill \end{array}\right]$$ (1)

Figure 5.

The 3D localization method computes the position of a point (x,y,z) using its image coordinates in the two projections, (u₁,v₁) and (u₂,v₂), the image coordinates of the perpendicular ray of one of the projections, (u₀,v₀), the separation between the two virtual sources, b, and the source to image (i.e. detector) distance, SID.

When Eq. 1 is applied to the SBDX stereo geometry, the z’ coordinate originates at the true detector. This is opposite the SBDX convention in which Z coordinates originate at the true x-ray source and increase towards the detector. To restore the usual coordinate system, a simple transform is applied to the z’ coordinates:

$$\left[\begin{array}{c}\hfill x\hfill \\ \hfill y\hfill \\ \hfill z\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \\ \hfill SID\hfill \end{array}\right]+\left[\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill -1\hfill \end{array}\right]\left[\begin{array}{c}\hfill x\prime \hfill \\ \hfill y\prime \hfill \\ \hfill z\prime \hfill \end{array}\right]$$ (2)

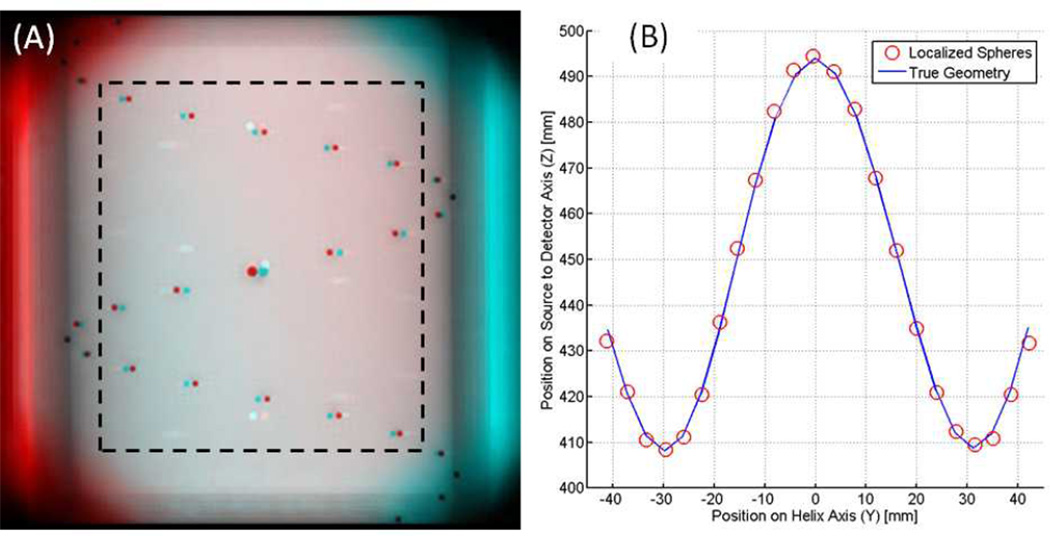
Of the 29 spheres visible in the image field of view, three at the top and three at the bottom of the FOV were excluded because they fell in a region where x-ray intensity rolls off. The remaining 23 spheres were segmented and localized using the proposed method. Error analysis was based on the central 15 spheres. The spheres at the periphery of the cylindrical phantom were excluded from analysis to avoid errors in automatic segmentation that can arise from the strong background gradient and relatively low SNR. The central spheres occupied 56% of the total image width and 63% of the total image height (See Figure 6). Their Z coordinates between source and detector spanned 85 mm.

Figure 6.

(A) Red/cyan stereoscopic anaglyph of the helical phantom. There is zero parallax at the center of the helix. The 15 spheres within the dashed line box were used for error calculation. (B) Localized sphere positions (circles) are plotted against the true phantom geometry (line) after registration.

In order to calculate localization error, the coordinate frame of the SBDX gantry was registered to that of the helix phantom using a closed form, point based rigid registration.¹⁰ After determining the correspondence between the localized spheres and those in the actual phantom, the rigid body transform was applied. The residual error was calculated as the root-mean-square (RMS) difference between the post-registration sphere coordinate and the true coordinate. The residual error served as a quantitative measure of our ability to reconstruct the phantom geometry using the localization method, which is directly dependent on accurate modeling of virtual projection geometry. For the three stereo geometries tested, the residual RMS error was calculated for each directional component (X,Y,Z) and by overall error magnitude across all of the localized spheres.

3.2 Qualitative catheter visualization

Although stereoscopic reconstruction enables 3D localization, the primary goal is to perform 3D stereo visualization during real-time fluoroscopic imaging. One application is anatomically-targeted interventions within the cardiac chambers, where knowledge of catheter position and orientation relative to the chamber walls is critical. To demonstrate how SBDX stereoscopic image pairs can resolve device orientation, an RF ablation catheter (2.7 mm diameter, 8 mm tip length, three electrode rings, each 1.3 mm long) was imaged at mechanical isocenter with the tip oriented toward the true detector. Standard composite images and stereoscopic image pairs were reconstructed from the same scan data. Parameters of the stereo reconstruction were set to create strong parallax versus depth with zero parallax at mechanical isocenter (Figure 4C). Stereo images can be prepared and viewed using a variety of 3D technologies. For this work, the stereo images were prepared as red/cyan anaglyphs and viewed with red/cyan glasses^*. For quantitative evaluation, 3D stereoscopic localization was performed on the tip, most proximal ring, and a portion of the proximal catheter shaft using the same method as the helical phantom to provide an objective measure of orientation.

4. RESULTS

Figure 6A shows a stereoscopic image of the geometric phantom using the high parallax source separation (presented in red/cyan anaglyph format), and Figure 6B shows typical sphere localization results compared to the true phantom geometry. The Y-axis runs from bottom to top in the image field of view, and the Z-axis runs from the true SBDX source towards the detector. Table 1 shows the 3D localization accuracy results for the central 15 spheres. The 3D residual RMS error was 0.81 mm for the geometries shown in Figures 4A and 4C, and 1.93 mm for the geometry shown in Figure 4B.

Table 1.

Quantitative results from 3D localization of the central 15 spheres in the helix phantom. Errors were greatest along the Z direction. Decreasing the separation between the virtual source points increased the error. Changing the plane of zero parallax had no effect on localization errors.

			Residual RMS Error [mm]
Virtual Source Separation [cm]	Zero Parallax Plane	Figure 4 Reference	X	Y	Z	Magnitude
5.3	Virtual Detector	A	0.09	0.15	0.79	0.81
2.6	Virtual Detector	B	0.33	0.07	1.90	1.93
5.3	Gantry Isocenter	C	0.09	0.15	0.79	0.81

In all three of the geometries tested, errors along the Z-axis contributed most to the overall error. For geometries shown in Figure 4A and 4C, which have the same virtual source separation, the RMS errors along the X and Y directions were 0.09 mm and 0.15 mm, respectively, and the error along the Z direction was 0.79 mm. Changing the plane of zero parallax while maintaining the virtual source separation had no effect on the error. This was expected because changing the plane of zero parallax does not affect the physical location of the virtual detector coordinates used in Eq. 1. Decreasing the virtual source separation to the geometry shown in Figure 4B increased the errors, with RMS X and Y errors of 0.33 mm and 0.07 mm, respectively. RMS error along the Z direction increased to 1.93 mm. This increase in error was expected for this geometry because it increased the magnitude of the 2D segmentation errors relative to the distance between the point projections in the two views, and 2D localization errors in the projection images propagate to large 3D errors along the Z direction.

Overall, the sphere localization results in Table 1 demonstrate that the 3D information contained in the SBDX stereoscopic images was in good agreement with the true 3D geometry of the phantom. The 3D information can be confirmed qualitatively by viewing the image of the phantom (Figure 6A) with red/cyan glasses. Without glasses, the Z-coordinate (depth) of a sphere can be inferred from the relative position of the red and cyan images. When the Z-coordinate is low the red image appears to the right, and when z-coordinate is high the red image appears to the left.

Stereoscopic visualization of the RF ablation catheter’s orientation was successful using a red/cyan anaglyph format (Figure 7). Standard reconstruction of the catheter produced images in which the true orientation of the catheter was ambiguous (see Figure 7A and 7B). On the other hand, visualization through stereo reconstructions (Figure 7C and 7D) was able to resolve the catheter orientation, towards the true detector and towards the viewer.

Figure 7.

An RF ablation catheter was oriented toward the true x-ray detector, imaged with SBDX, and reconstructed using standard and stereo methods. In the standard reconstructions (A,B), the orientation is ambiguous. The true orientation of the catheter can be resolved in the stereo reconstructions (C,D) using red/cyan glasses. Without glasses, the change in parallax (i.e. difference in depth) between the shaft and the tip of the catheter is still prominent. Z coordinates are in millimeters above the true x-ray source. Note figure colors are optimized for viewing in electronic formats.

Additional confirmation of catheter orientation was obtained by applying the 3D localization algorithm to the catheter tip and the catheter body. In Figure 7C, the catheter tip has the highest position along the Z axis (z = 487 mm), followed by the ring (z = 475 mm), with the shaft having the lowest Z value (z = 454 mm). In Figure 7D, the tip and the ring are at similar depths (z = 482 and 484 mm, respectively) with the shaft at a lower position (z = 453 mm). For the stereo geometry used, the Z axis increases toward the viewer, so these localization results agree with the perceived orientation when viewed stereoscopically.

5. DISCUSSION AND CONCLUSIONS

In this work, we present a stereoscopic imaging method using SBDX, an inverse geometry cardiac fluoroscopy system. Virtual projections are generated from tomosynthetic image sets. The geometry of the projections is adjustable to anywhere within the full imaging field of view, enabling reconstruction of two, slightly offset projections to form a stereoscopic imaging pair. To validate the geometry of the virtual projection model, the projections were used to localize objects in 3D with magnitude RMS errors ranging between 0.81 and 1.93 mm, depending on geometry. In addition, the stereoscopic imaging method was used to determine the orientation of an interventional device along the source-detector axis, which would be impossible from a conventional monoplane x-ray projection.

The proposed method offers more flexibility than stereoscopic methods using conventional XRF. Stereo imaging is achieved using a single gantry. Generating the SBDX stereoscopic image simply requires two reconstruction engines and a 3D stereoscopic display. The two stereoscopic views are reconstructed from raw data acquired in the same frame period. Consequently, there is no temporal disparity between the stereoscopic views. The spacing between the two virtual sources is an adjustable parameter, whereas a conventional, dual-anode x-ray tube has a fixed distance between the two focal spots. This allows for the parallax to be adjusted by the user to ensure comfortable viewing. Finally, since the stereoscopic image formation is preceded by tomosynthesis reconstruction, there exists the novel possibility of producing stereo images with a prescribed depth-of-field excluding unwanted background. Future studies may elucidate the value of stereoscopic visualization during interventional procedures.