Closed loop adaptive optics for microscopy without a wavefront sensor

Abstract

A three-dimensional wide-field image of a small fluorescent bead contains more than enough information to accurately calculate the wavefront in the microscope objective back pupil plane using the phase retrieval technique. The phase-retrieved wavefront can then be used to set a deformable mirror to correct the point-spread function (PSF) of the microscope without the use of a wavefront sensor. This technique will be useful for aligning the deformable mirror in a widefield microscope with adaptive optics and could potentially be used to correct aberrations in samples where small fluorescent beads or other point sources are used as reference beacons. Another advantage is the high resolution of the retrieved wavefont as compared with current Shack-Hartmann wavefront sensors. Here we demonstrate effective correction of the PSF in 3 iterations. Starting from a severely aberrated system, we achieve a Strehl ratio of 0.78 and a greater than 10-fold increase in maximum intensity.

1. INTRODUCTION

Currently there is a lot of interest in using adaptive optics in three-dimensional fluorescence microscopy. Adaptive optics promises to increase the sensitivity and accuracy of fluorescence microscopy by correcting the optical aberrations that occur when imaging below the surface of the sample [1-5]. The sources of aberrations are the refractive index difference between the sample and coverslip and the refractive index variations of the sample itself. The correction of these aberrations is especially important in live imaging where the sample refractive index cannot be modified with fixation and clearing techniques.

In astronomy, adaptive optics systems typically comprise a Shack-Hartmann Wavefront Sensor (SHWFS) for measuring the wavefront and a deformable mirror (DM) for correcting the wavefront [6]. The system is run in a closed feedback loop, maintaining a flat corrected wavefront for the image that is sent to the science camera. A bright star is frequently used as a point source for measuring the wavefront with the SHWFS. In ophthalmological uses of adaptive optics, a SHWFS and DM are run in a closed loop as well. Here the reflected light from a confocal spot is used as the source for the SHWFS.

In biological microscopy using a SHWFS is problematic. In microscopy light is received from throughout the sample so that wavefronts from throughout the sample in different focal planes and with different aberrations would be received by the sensor simultaneously [1]. Using reflected or scattered light (from the excitation source in a confocal microscope, for example) to determine the wavefront can eliminate the problem of wide-field imaging, but leads to ambiguities in the wavefront determination and problems with speckle from coherent sources. Therefore, in microscopy, many systems have been developed that use a deformable mirror for wavefront correction, but do not rely on a wavefront sensor. Wavefront sensor-less techniques typically use a search algorithm that adjusts the DM to maximize an image quality metric such as the image sharpness or intensity [2, 7, 8]. Nonetheless wavefront sensing has been achieved in fluorescence microscopy. Booth et al. developed an AO system for confocal microscopy that uses a novel modal wavefront sensor [9]. Denk developed a multiphoton system that uses backscattered excitation light to measure the wavefront using coherence-gated wavefront sensing [3]. Recently a SHWFS has been demonstrated on a wide-field microscope using fluorescent beads as guide stars [10].

Here we demonstrate the use of phase retrieval as the wavefront sensing technique in three-dimensional wide-field fluorescence microscopy. In phase retrieval, the phase of the electric field of the light is calculated from multiple measurements of the intensity at different planes along the optic axis. The multiple intensity measurements provide the extra information required to calculate the missing phase information. In the original phase retrieval algorithm, the phase was calculated from intensity measurements in the focal and pupil planes of a low NA system [11] yielding the phase in the pupil plane. Phase retrieval has been demonstrated for high numerical aperture microscopes [12, 13]. In this case the phase in the back pupil plane of the microscope objective is determined from multiple images around the focal plane. In references [12, 13], a fluorescent bead with diameter smaller than the microscope resolution served as an effectively coherent point source. Taking images through the focus in this case yields the three-dimensional point spread function (PSF) [14]. Using phase retrieval to determine the wavefront has the advantage that no special wavefront sensing hardware is required.

An important application of the technique we describe here is system calibration in fluorescence microscopy. As mentioned above, many adaptive optics microscopy systems do not have wavefront sensors. Some systems use search algorithms to optimize the wavefront. Others use open-loop methods to correct the wavefront depending on field position or focal position [4, 15]. For systems like these, it is important to set the baseline DM shape that corrects for the aberrations of the optical path because these aberrations are not corrected by predictive wavefront correction. System calibration using an image sharpness metric has been implemented for the case of predictive correction of off-axis aberration [15, 16]. Phase retrieval also provides very high resolution wavefront reconstructions. Thus it can be an important sensing technique for applications with high resolution wavefront correctors with the goal of achieving very high Strehl ratios.

2. METHODS

2.1 Microscope Design

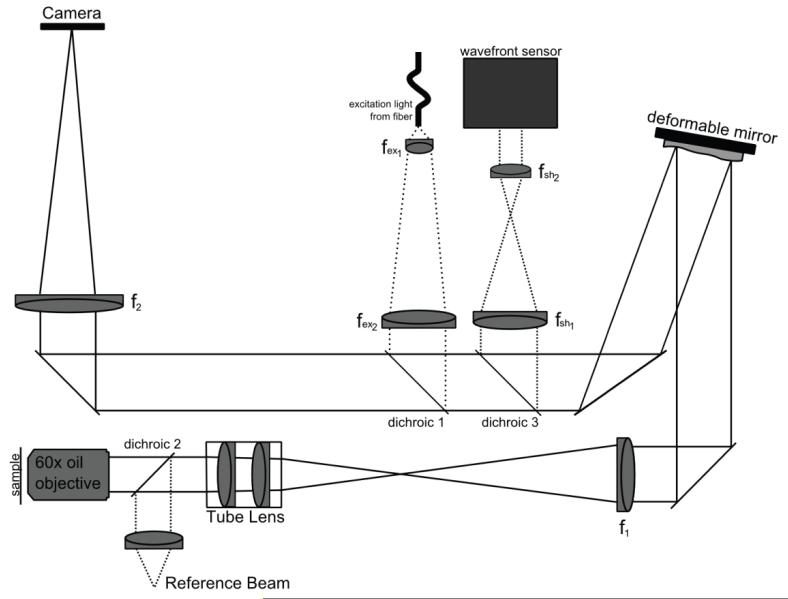
Figure 1 shows the layout of the microscope which has been previously described in [4]. The objective (Olympus, 60×, 1.42 PlanApo N) collimates the light from the object. The tube lens (Olympus, 180mm) and lens f₁ (350mm achromat, OptoSigma) create an image of the objective back pupil plane on the deformable mirror. The magnification is chosen so that the desired NA of the system fills the deformable mirror. We have chosen the NA of the system to be 1.285. Lens f₂ (800mm doublet, OptoSigma) then creates an image on the CCD camera. The total magnification of the system, M_obj(f₂/f₁) is chosen so that the object is sampled at the Nyquist frequency on the CCD camera. Here, d_pixel = 94.8nm in sample coordinates. The CCD camera is from Astronomical Research Cameras, Inc. and uses a cooled CCD57-10 chip with a 13um pixel size from e2v technologies.

Figure 1.

Microscope Layout. See text for details.

The excitation light enters the system through a multimode fiber with a 600um core (Ocean Optics). The end of the fiber is imaged onto the deformable mirror with lenses f_ex1 and f_ex2 and inserted into the main optical path with dichroic 1 (Semrock FF495-Di02). Thus, the excitation is also corrected for the depth aberrations. While this is not critical for wide-field illumination, correction of the excitation is equally as important as correction of the emission in techniques such as structured illumination microscopy [17, 18].

The final optical path in the system injects a red laser into the system for monitoring and controlling the shape of the deformable mirror. The beam from a HeNe laser is cleaned and expanded with a pinhole and then collimated. The light is inserted into the optical path with dichroic 2 (Semrock FF579/644-Di01). It then follows the optical path until it is taken out of the main optical path with dichroic 3 (Semrock FF579/644-Di01) and sent to a Shack-Hartmann wavefront sensor (Imagine Optic Haso 32). Lenses f_sh1 and f_sh2 demagnify the beam to image the deformable mirror onto the lenslet array.

The microscope slide is mounted above the objective on a custom-designed mount that uses a Newport 462 xyz stage. The focal plane is moved through the sample with a piezo stack attached to the z-axis micrometer (Physik Instrumente P-810 piezo and E661.CP controller), and the stage position is measured with a capacitive sensor (Queensgate NS2000-L). An image stack is collected by sequentially moving the fluorescent bead through focus by moving the sample stage with the piezo actuator and collecting two-dimensional images.

This microscope was designed to correct depth aberrations with an open loop system. Thus the system was not built with a wavefront sensor for measuring the wavefront from the sample, and the method described here was developed to optimize the DM shape for imaging at the coverslip.

2.2 Adaptive Optics

For the deformable mirror, we chose the Mirao52D from Imagine-Optic (www.imagine-optic.com) because it is capable of large displacements and thus permits the correction of aberrations deep into a sample. The 15mm diameter mirror has 52 actuators on a square grid with 2.5mm spacing. The mirror is capable of a maximum displacement of +/−75 microns for the focus mode ($Z_2^0$) and +/−8 microns for the first order spherical aberration ($Z_4^0$). The mirror can take the shape of any Zernike mode through order 4 with an rms wavefront error of less than 20nm.

We control the mirror by measuring the wavefront of the HeNe laser with the wavefront sensor (reference path in figure 1). We reference the wavefront to a measurement with all actuators set to zero, and then measure the wavefront on the 32×32 lenslet array for each of the 52 actuators activated individually, yielding a 1024×52 matrix. To set a desired mirror shape, we use the standard singular value decomposition technique [19] to determine the matrix S which will yield the actuator values for a desired wavefront. Typically, we only retain the first 45 singular values.

2.3 Phase Retrieval

Phase retrieval was performed using an iterative algorithm described in [20] to minimize the relative entropy (MRE) between the measured PSF and the PSF calculated from the field in the back pupil plane. This algorithm is similar to the modified Gerchberg-Saxton (GS) algorithm described in [12]. In the GS algorithm the phase is chosen is selected to minimize the difference in amplitude between the simulated and measure data. In the MRE algorithm, the phase is chosen to minimize the intensity difference. For the experiments described in this paper, we performed 64 iterations of the phase retrieval algorithm on image stacks with 256×256 pixel slices and different numbers of slices through focus. The pixel size (in sample coordinates) was 94.8nm. Image stacks were taken with 21 slices at a 0.2 micron step, 9 slices at a 0.5 micron step and 5 slices at a 1.0 micron step.

2.4 Sample Preparation

To measure the PSF, we imaged 200nm diameter Yellow-Green fluorescent beads (Molecular Probes F-8811). Because this bead is smaller than the diffraction spot, its image represents the point-spread function (PSF) of the microscope. The beads are dispersed in water at a concentration of 2% by weight and were diluted by an additional factor of 10⁶ in water to a concentration of 3.9×10⁶ beads/ml (Molecular Probes Application Note “FluoSpheres Fluorescent Microspheres”). To image beads at 0 depth (on the coverslip), 15 microliters of bead solution were dried on a coverslip and mounted on a slide with 5 microliters of glycerol.

2.5 Mirror Optimization

To optimize the deformable mirror, a slide with a dilute layer of fluorescent beads is placed on the microscope, and a single bead is placed in focus in the center of the field of view. The DM is placed in its starting configuration which is typically either the last known flat calibration or 0V on all the actuators. An image stack is collected, and the phase retrieval algorithm is applied to the image stack to determine the amplitude and phase in the back pupil plane. The phase in the back pupil plane is decomposed onto the Zernike basis. And the negative of the Zernike values are used to set the shape of the deformable mirror. Describing the back pupil plane in terms of Zernike coefficients is a convenient way to convert from the size of the phase retrieved back pupil plane to the size of the array used to set the deformable mirror. Phase retrieval was performed on an image stack with 256×256 pixel lateral dimensions and the deformable mirror is set with the wavefront measured by the SHWFS which is 32×32 pixels and not perfectly centered. A left-right inversion of the phase retrieved pupil is performed to account for the imaging of the back pupil plane on the wavefront sensor.

The Zernike decomposition was performed using a set of orthonormal vector polynomials derived from the Zernike functions [21, 22]. This allows us to determine the Zernike coefficients from the derivatives of the back pupil plane phase, and thus avoids problems with phase wrapping.

After setting the mirror, a new image stack is measured, and the process is repeated. Typically we ran the measurement for a set number of cycles, but the measurement could easily be terminated once the Strehl ratio reached an acceptable value. The tip, tilt and focus Zernike modes are retained so that the final PSF is centered in the image stack. The Strehl ratio is calculated as

$$S=\frac{{\mid \int A(x,y)dxdy\mid }^2}{(\int {\mid A(x,y)\mid }^{2}dxdy)(\int dxdy)}$$

where the integral is over the pupil size for the nominal NA of 1.285, and A(x, y) is the field amplitude in the back pupil plane.

3. RESULTS

3.1 Phase retrieval measurements

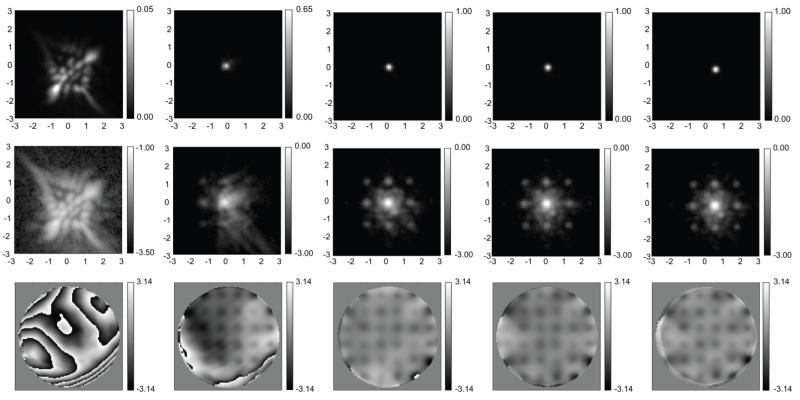
Figure 2 shows slices from a representative image stack, and the results of a phase retrieval measurement on that stack for a well corrected PSF. The image stack was 256×256 pixels with 21 slices at a 0.2 micron spacing. We let the phase retrieval run for 64 iterations which took 46 seconds on a Core 2 Duo Intel processor. The retrieved phase is very close to the final retrieved phase after only 16 iterations so the process could be sped up by a factor of 4.

Figure 2.

Example of phase retrieval. (a), (b) and (c) are slices from the image of a 200nm fluorescent bead. (a) is 2 microns below focus. (b) is the in focus image, and (c) is 2 microns above focus. The units are microns. (d) and (e) are the amplitude and phase of the field amplitude in the back pupil plane.

The out-of-focus PSF does not have the axial symmetry typical of a microscope because the actuators on the deformable mirror are on a rectangular grid which distorts the PSF. The manufacturing process results in a small distortion of the mirror surface at each actuator, and this array of bumps (“print through”) diffracts the light causing a small distortion of the image. In the out-of-focus slices this manifests itself as a square shape in the PSF. In focus, the PSF has an array of weak satellite spots around the central peak of the PSF. The magnitude of these satellites is ~1% of the main peak so they are not visible on a linear scale in figure 2, but are visible on a log scale in figure 4. Because the DM is conjugate to the back pupil plane the print through is visible in the phase of the back pupil plane image (fig. 2e). The magnitude of the print through varies from actuator to actuator but is approximately 0.8 radians (λ/8). The RMS phase over the back pupil plane is 0.58 radians.

Figure 4.

Iterative correction of the microscope point spread function. Top row: In focus image of the PSF, linear scale. Second row: same as first row but on a log scale. Third row: phase in the back pupil plane calculated from phase retrieval with the tip, tilt and focus terms removed. First column: before correction; DM actuators all set to zero volts. Each successive column is after a round of iteration.

3.2 Accuracy and linearity of phase retrieval

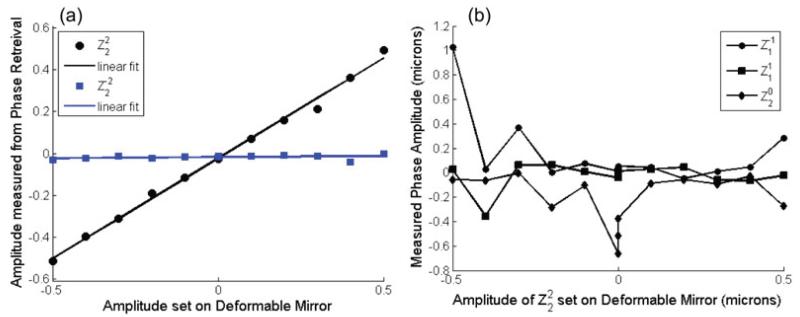
To test the linearity and open loop control of the system, we set the deformable mirror shape to $Z_2^2$ (0° astigmatism) with amplitudes between −0.5 and 0.5 microns and measured the phase in the back pupil plane using phase retrieval. The phase was then decomposed into the Zernike polynomials to test the linearity and cross-talk of the system. Figure 3a shows plots of the retrieved amplitude of $Z_2^2$ and $Z_2^{-2}$ (45° astigmatism) vs. the amplitude of $Z_2^2$ set by the deformable mirror. For $Z_2^2$, the slope is 0.96 and the root mean square error (RMSE) is 20.9nm. For $Z_2^{-2}$, the slope is 0.0097 and the RMSE is 9.9nm. Here the slope is 1% of the value for $Z_2^2$ indicating only weak crosstalk between the Zernike modes.

Figure 3.

(a) Plot of the amplitude of $Z_2^2$ (circles) and $Z_2^{-2}$ (squares) determined by phase retrieval vs. the amplitude of $Z_2^2$ set on the deformable mirror. The solid lines are linear fits to the data. The slope of the fit to $Z_2^2$ is 0.96 and the RMSE is 20.9nm. The slope of the fit to $Z_2^{-2}$ is 0.0097 and the RMSE is 9.9nm. (b) Plot of the amplitude of $Z_1^{-1}$, $Z_1^1$, and $Z_2^0$ determined by phase retrieval vs. the amplitude of $Z_2^2$ set on the deformable mirror. There is substantial drift from measurement to measurement.

We tested the linearity for setting other Zernike modes on the deformable mirror with similar results. The exception was in setting tip, tilt and focus ($Z_1^{-1}$, $Z_1^1$, and $Z_2^0$). With these modes, stage drift could cause substantial variations from measurement to measurement. Figure 3b shows the retrieved amplitudes of $Z_1^{-1}$, $Z_1^1$, and $Z_2^0$ vs. setting $Z_2^2$.

3.3 Correction of PSF

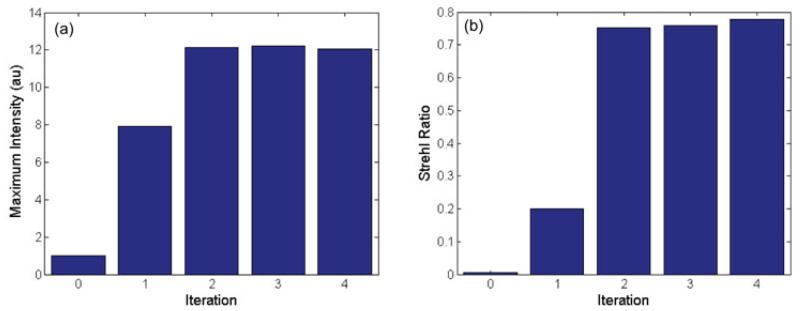
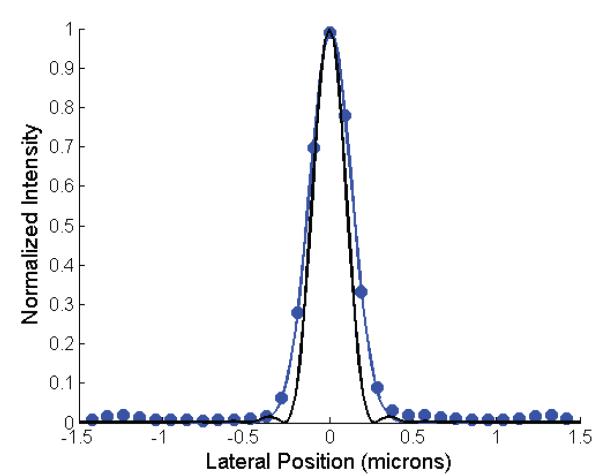
Figure 4 shows the results of using the retrieved phase to set the deformable mirror. Column 1 shows the PSF with all the actuators on the DM set to 0V. The PSF is strongly distorted with a calculated Strehl ratio of 0.005. (Although for such a strongly distorted PSF, the Strehl ratio is not that meaningful since the peak intensity is not at the center of the PSF.) Column 2 shows the results after correcting the DM with the retrieved phase. The PSF is dramatically improved. The Strehl ratio is 0.2, an improvement of 40 fold. Another round of correction improves the strehl ratio to 0.75. We let the loop run through two more cycles, but the Strehl ratio did not substantially improve, ultimately reaching 0.78. For figure 4, each image stack was 21 slices from 2.0 microns below focus to 2.0 microns above focus in 0.2 micron steps. Figure 5 shows the improvement in peak intensity and Strehl ratio for the data of figure 4. Figure 6 compares the width of the corrected PSF to the ideal image of a 200nm bead. The measured PSF has a FWHM of 290nm, about 20% greater than the ideal case.

Figure 5.

(a) Maximum Intensity of the measured PSF for each iteration of the wavefront optimization. (b) Corresponding Strehl ratio.

Figure 6.

Lateral in-focus cross section of the final PSF from figure 4 (circles). Gaussian fit to the data (blue line). Theoretically calculated image of a 200nm bead from an ideal pupil of NA 1.285 (black line).

We performed the same measurement but taking only 5 slices per image stack with a step of 1.0 microns. Taking fewer steps speeds up the phase retrieval and also reduces the light exposure of the sample, but results in a less robust phase retrieval. In this case the Strehl ratio increased from 0.0004 to 0.30 and the intensity increased by a factor of 8.2 in 4 cycles.

4. DISCUSSION AND CONCLUSION

We have demonstrated closed loop wavefront control without a wavefront sensor using phase retrieval as the wavefront sensing algorithm. We believe that this technique could prove very useful for system calibration in fluorescence microscopes with a DM, and we hope to apply the technique to wavefront control in imaging biological samples.

The most significant disadvantage of this technique is speed. Each phase retrieval step took many seconds so the entire process of optimizing the wavefront took a few minutes. This is far too slow for many applications, and we are investigating faster algorithms for phase retrieval. For example, parameterizing the phase using Zernike polynomials and performing a conjugate gradient search to minimize the error metric [23] could be significantly faster for setting a small number of Zernike coefficients. Another problem with this technique is the need to image out-of-focus light. Because the intensity falls off rapidly away from focus, high signal to noise ratio is required to accurately retrieve the wavefront. For system calibration these problems are not significant. A system would be calibrated by imaging a fluorescent bead on the coverslip as described here. In this case the signal to noise ratio is very high and there is no need for fast correction.

We are also interested in using this technique to measure the phase from a fluorescent bead embedded in a biological sample. Here an important problem will be retrieving the phase from a source sitting on top of a nonuniform background signal. Phase retrieval has been shown to be robust in the presence of distortions not related to the PSF such as dirt on an optical element [13]. This is because the phase retrieval process optimizes the wavefront for the features in the image which match a three-dimensional PSF. Features which don’t change with focus are suppressed by the phase retrieval process. Here the strength of the out-of-focus PSF compared to the background fluorescence will be an issue. But because bead fluorescence increases with the diameter to the third power, measuring a strong PSF signal from a bead should be possible in many situations by appropriately choosing the bead diameter and fluorescence wavelength.

A significant advantage of this technique is that it provides significantly better resolution in the back pupil plane than a Shack-Hartmann Wavefront Sensor. A SHWFS that samples the wavefront on a 32×32 grid provides only 803 data points within the circular pupil. Phase retrieval can provide many more by imaging a larger field of view and the resolution can be determined at the time of the measurement. Our measurements were performed on 256×256 pixels with a 94.8nm pixel size, yielding over 10,000 data points within the pupil. Because of its high resolution, phase retrieval should be well suited to applications where the wavefront is being set by high resolution devices such as spatial light modulators. Using a spatial light modulator as the “tweeter” in an adaptive optics system could help eliminate the print through effect seen in the wavefront from the Mirao deformable mirror. It will also be interesting to study if the use of phase retrieval and an SLM could correct for optical imperfections in the microscope objective. It has been observed that the phase of the pupil of a microscope objective can become severely aberrated near the edge of the aperture [24].

In conclusion, we have demonstrated the closed loop optimization of the wavefront in three-dimensional wide-field fluorescence microscopy using phase retrieval as the wavefront sensing mechanism.