Insight into the Interaction between DNA Bases and Defective Graphenes: Covalent or Non-covalent

Abstract

Although some metal clusters and molecules were found to more significantly bind to defective graphenes than to pristine graphenes, exhibiting chemisorptions on defective graphenes, the present investigation shows that the adsorption of DNA bases on mono- and di-vacant defective graphenes does not show much difference from that on pristine graphene, and is still dominantly driven by noncovalent interactions. In the present study the adsorptions of the nucleobases, adenine (A), cytosine (C), guanine, (G), and thymine (T) on pristine and defective graphenes, are fully optimized using a hybrid-meta GGA density functional theory (DFT), M06-2X/6-31G*, and the adsorption energies are then refined with both M06-2X and B97-D/6-311++G**. Graphene is modeled as nano-clusters of C₇₂H_24, C₇₁H₂₄, and C₇₀H₂₄ for pristine, mono- and divacant defective graphenes, respectively, supplemented by a few larger ones. The result shows that guanine has the maximum adsorption energy in all of the three adsorption systems; and the sequence of the adsorption strength is G>A>T>C on the pristine and di-vacant graphene and G>T>A>C on the mono-vacant graphene. In addition, the binding energies of the DNA bases with the pristine graphene are less than the corresponding ones with di-vacant defective graphene; however, they are greater than those of mono-vacant graphene with guanine and adenine, while it is dramatic that the binding energies of mono-vacant graphene with thymine and cytosine appear larger than those of pristine graphene.

1. Introduction

As one of the most recent interesting material due to its unique chemical and electronic properties,[1] graphene has attracted wide attention to its promising applications in bio-medicine and microelectronic devices. For example, nano-graphene has been proposed to make sensors for small molecules such as H₂, H₂O, NO, and NH₃ [2–3] and for biomolecules like carbohydrates, proteins, nucleic acids,[4–5] and to convey drug and gene for cancer treatment.[6] Like carbon nanotubes,[7–8] a major barrier for biomedical applications of nano-graphene is its low solubility in aqueous solutions. Strategic approaches toward solubilization of nanographene have been developed through non-covalent functionalization, which can not only enhance solubility of nanographene but also maintain its attractive geometric, electronic and mechanical properties. It is apparent that carbohydrates, proteins, and nucleic acids are very important species for functionalizing graphene in living systems.

With different models for pristine graphene, a variety of the first-principles based methods have been widely employed to investigate the binding of the nucleobases to pristine graphene, including local density approximation (LDA) type of density functional theory(DFT), GGA, meta-hybrid GGA, plane-wave GGA type of DFT, dispersion-corrected DFT (DFT-D) as well as second-ordor Mφller-Plesset perturbation theory (MP2).[9–16] Using B97-D, B2PLYP-D and SCS-MP2 methods, Antony et al. extensively investigated the adsorption of the DNA nucleobases on a variety of graphene clusters from 24 to 150 carbon atoms.[10] The interaction sequence after basis set superposition error correction (BSSE) at B2PLYP-D/TVZ(2df,2pd)//B97-D/TZV(d,p) level for DNA bases on C₅₄H₁₈ is, G (23.9 kcal/mol)>A (19.7 )>T(18.5)>C(18.2 ), and they suggested the proper size of nano graphene with at least about 50 carbon atoms. MP2/6-311+G(d,p) results in the binding order of G(24.6 kcal/mol)>A(21.7 kcal/mol)≈T(21.4 kcal/mol)>C(18.4 kcal/mol),[9] parallel to the polarizability of the DNA bases. The plane-wave LDA method usually considerably underestimates the binding strength, like only 9.0 and 11.03 kcal/mol for cytosine.[9, 12] Both the B3LYP-D/6-31G(d) with 55 C₆ rings for graphene,[14] and vdw-HF/6-31G(d,p) with twenty C₆ rings[11 ] reproduce the binding sequence, G>A>T>C, (17.5>15.0>14.3>13.3kcal/mol;[14] 19.1>17.8>16.6>14.5kcal/mol[11]); however, the absolute binding energies for the given base are a few kcal/mol lower than those predicted by the above B2PLYP-D method.[10] Van der Waals density functional (vdW-DF)[17–19] for adenine on graphene also yields a too low binding (16.4 kcal/mol), ¹[13] as compared to the result of Antony and Grimme (19.7kcal/mol[10]). The binding energies from the wB97XD/6-31G(d,p) with 8×8-ring graphene sheet[16] agree very well within 0.1–1.4 kcal/mol with those of Antony et al.,[10] yet the relative strength for T and C are switched (G>A>C>T, 22.5>20.3>18.9 and 18.4 kcal/mol). Varghese et al. carried out an experimental investigation into the binding of DNA nucleobases with graphene using isothermal titration calorimetry (ITC).[11] They indicated that the relative interaction energies of the nucleobases decrease in the order G>A>C>T, although the C and T seems to be interchangeable. Even before BSSE, the M06-2X/6-31G(d) in the scheme of ONIOM (M06-2X/6-31G*:AM1) results in a rather weak binding and different sequence (14.8, 14.1, 16.0 and 13.8 kcal/mol for G, A, T and C.)[14] Although B3LYP-D/6-31G(d)//M06-2X/6-31G(d) done by Umadevi et al also brings about the sequence G>A>T>C,[14] the BSSE correction (9.6 kcal/mol) for cytosine-graphene complex was predicted dramatically high, while others were regular in 3.1–6.2 kcal/mol. In spite of extensive theoretical investigations into the binding between DNA bases to pristine graphene, the above discussion indicates that there is still a controversial with respect to binding strength and binding sequence. In this present study, in order to assess its performance as well as to provide consistent result for a comparison with adsorptions on defective graphene the M06-2X will be further used to optimize the adsorptions of DNA on pristine graphene and then improve the binding energy with B97-D.

During production of graphene from the thermal expansion of graphite oxide (GO), some carbon atoms are missing to form defective graphene.[20] The most common defects of graphene include mono-vacancies, multivacancies, pentagon heptagon pairs, and adatoms.[21–23] Divacant defective graphene is energetically favored over the mono-vacant one because of its reconstruction without dangling bond.[24] Because of carbon vacancies the defective graphene may demonstrate significant influences on the chemical and physical characteristics of graphene, for example, chemisorptions on the defect sites.[25–27] Very recently, the adsorptions of metal clusters on the mono-vacant and di-vacant defective (5–8-5 defect) graphenes were investigated.[28–32] The structural and electronic properties of the nanoparticles adsorbed on the defective graphene usually show peculiarities. The defective sites sever as anchoring points for the nanoparticles, and undercoordinated neighboring carbons further strengthen the binding of the nanoparticles to graphene layer. Catalytic reactivity of the adsorbed nanoparticles may be also enhanced. Lim found that the most stable conformation of Pt₁₃ on mono-vacant defective graphene has D_4h symmetry, rather than the isolated I_h symmetry, and the Pt₁₃ donates electron to the defective graphene and the adsorbed O₂.[29] The binding of Pt₄ to mono-vacant graphene was 3–4 times higher than to pristine graphene.[32] A variety of gas molecules (O₂, CO, N₂, B₂, H₂O) can be chemically adsorbed on the di-vacancy defective graphene, with a magnitude of 3–13eV binding energy.[3] The DFT predicted chemisorption of H₂S on the mono-vacancy defective graphene by forming weak covalent bond (1.55eV).[24] However, in spite of many publications for the adsorptions of DNA nucleobases on pristine graphene as described above, to the best of our knowledge the adsorption of the defective graphene with DNA nucleobases has not been reported. Obviously, it is important to reveal the binding behavior (covalent or noncovalent) of the defective graphene with DNA nucleobases in biomedical science because the defect site of graphene could give rise to a local electronic structure change around it.[33] In the present work M06-2X and B97-D were employed to study the interaction of DNA nucleobases with mono- and di-vacant defective graphene.

2. Computational Methods

Accurate description for noncovalent weak interaction systems like the π-stacked systems is still a challenge for density functional theory (DFT), a promising quantum mechanics method for large systems, although considerable improvements have been achieved over LDA and such conventional hybrid DFT as B3LYP in the recent years. [34–35] Recently, the novel hybrid meta-GGA functional, M06-2X, developed by Truhlar et al.,[33] provides relatively reasonable results for π⋯π stacking systems.[36] Therefore, in this paper the geometric parameters of all nucleobase-graphene adsorption complexes are fully optimized in gas phase at M06-2X/6-31G(d) level. To obtain accurate binding energy, the bigger basis set of 6-311++G(d,p) was employed to refine the stationary point energy at both M06-2X and B97-D levels of theory with BSSE correction. Based on the suggestion of Antony and Grimme,[10] the pristine graphene is modeled with C₇₂H₂₄, which is also compared with C₇₈H₂₄, C₈₆H₂₆, and C₁₀₆H₂₈. The defective graphenes are modeled with C₇₁H₂₄ for mono-vacancy and C₇₀H₂₄ for di-vacancy. All calculations were done using the Gaussian09 version B01.[37]

3. Results and Discussion

3.1 Adsorptions of DNA nucleobases on pristine graphene

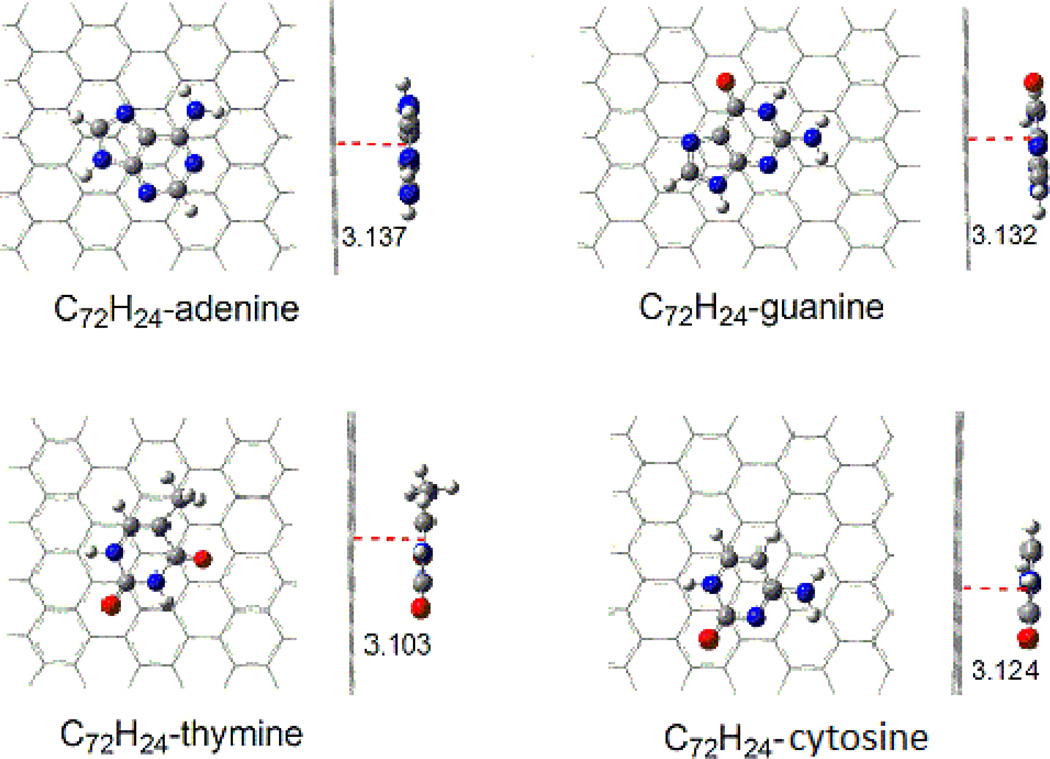
The structures of the adsorption complexes of DNA nucleobases on pristine graphene are shown in Figure 1. The graphene sheet is modeled by C₇₂H₂₄, larger than the suggested minimum carbon cluster of C₅₄ for graphene. [10] C₇₂H₂₄ keeps planar and basically parallel to the rings of nucleobases. Table 1 lists the distances between graphene and the nucleobase plane for the adsorption complexes optimized at the M06-2x/6-31G(d) level. For all of the four nucleobases, the distances from the graphene to the hexagon rings are in the range of 3.103–3.137Å, and those to the pentagon rings of adenine and guanine are 3.156 and 3.163 Å, respectively. However, the electronegative O atom is closer to the graphene with vertical distances of 2.964, 2.943, and 2.968 Å for C₇₂H₂₄-guanine, C₇₂H₂₄-thymine, and C₇₂H₂₄-cytosine, respectively. There may be a stronger interaction of nucleobase oxygen with the graphene plane (C=O⋯π) than the rings of nucleobases (π⋯π). Although the distances of the N atoms of NH₂ group from graphene are nearly identical to those of hexagon rings of nucleobases, the H atoms of the NH₂ group have shorter distances of 2.864, 2.606, and 2.900 Å for C₇₂H₂₄-adenine, C₇₂H₂₄-guanine, and C₇₂H₂₄-cytosine, respectively. For the methyl group of connected in thymine there are the distances of 3.253 and 2.580Å from the C atom and one of the H atoms, respectively, to graphene. Because of the short distances of both amine and methyl groups with graphene, there is also weak interaction of the H atom of amino (N-H⋯π ) or methyl group (C-H⋯π ) with graphene.

Figure 1.

Top and side views for the configurations of C₇₂H₂₄-nucleobase complexes (distances/Ǻ).

Table 1.

Distances (Å) between pristine graphene and nucleobases in the binding complexes optimized at the M06-2X/6-31G(d) level

Distance	hexagon	pentagon	O	NH2		CH3
				N	H	C	H
C72H24-Adenine	3.137	3.156		3.126	2.864
C72H24-Guanine	3.132	3.163	2.964	3.129	2.606
C72H24-Thymine	3.103		2.943			3.253	2.580
C72H24-Cytosine	3.124		2.968	3.124	2.900

Table 2 lists the binding energies of nucleobases with graphene together with reference data. With the C₇₂H₂₄ model of graphene, the binding energies at the M06-2X/6-31G(d) level are 20.2, 16.6, 15.8, and 15.6 kcal/mol for G, A, T, and C, respectively. The predicted binding is much stronger than that with ONIOM(M06-2X/6-31G*:AM1) (14.8, 14.1, 16.0, and 13.8 kcal/mol for G, A, T, and C),[14] and also shows a different sequence. The basis set 6-311++G(d,p) including diffuse and polarization of H increases the binding energies by 3.0–4.0 kcal/mol; yet the BSSE decreases the binding energies by 4.5–6.0 kcal/mol. As a result, the binding energies of G, A, T and C with C₇₂H₂₄ at M06-2X/6-311++G(d,p)//M06-2X/6-31G(d) level are 18.2, 14.7, 14.2, and 14.1 kcal/mol, respectively, which agree very well with the results from vdW-HF/6-31G**[11] and B3LYP-D/6-31G*//(M06-2X/6-31G*:AM1),[14] yet they are still less than the theoretical values of MP2, B2PLYP-D and wB97XD.[9–10, 16] Similar to the adsorption of DNA bases on C₆₀ derivatives and single-walled carbon nanotubes,[38–40]^,44 the M06-2X again is insufficient for the noncovalent interaction systems. It is known that the dispersion energy plays an important role in physisorption. For the long distance interaction between nucleobase and graphene we thus refined the binding energies with the dispersion corrected DFT, B97-D/6-311++G(d,p) for the geometries optimized with the M06-2X/6-31G(d). Table 2 shows that the binding energies at B97-D/6-311++G(d,p)//M06-2X/6-31G(d) for G, A, T and C are 27.0, 23.3, 20.8, and 19.9kcal/mol, while they lessen to 21.6, 18.4, 16.3, and 15.8 kcal/mol, respectively with the BSSE correction. As compared with those of M06-2X/6-311++G(d,p), the binding energy increases by 3.4, 3.7, 2.1 and 1.7 kcal/mol for G, A, T and C, respectively, indicating that the dispersion energies of the adenine and guanine are larger than the thymine and cytosine because of the larger molecular sizes of G and A than those of T and C. Obviously, these binding energies are 2–5 kcal/mol higher than the results from B3LYP-D/6-31G*//ONIOM(M06-2X/6-31G*:AM1),[14] and only 1–2 kclal/mol less than the ones of B2PLYP-D/TVZ(2df,2pd).[10] It is essential that the present binding order (G>A>T>C) at the three levels agrees with that from the high levels such as MP2/6-311++G**,⁹ and B2PLYP-D/TVZ(2df,2pd),¹⁰ yet for T and C opposite to the most recent result from wB97XD/6-31G**.¹⁶ In order to assess the validity of the graphene size, we extended the adsorption of adenine on other three larger graphene models, C₇₈H₂₄, C₈₆H₂₆, and C₁₀₆H₂₈ as shown in Table 2. Compared with the binding energy for C₇₂H₂₄, the maximum deviations are only 0.4 and 0.6 kcal/mol at the M06-2X/6-31G* and B97-D/6-311++G** levels, respectively; they are excellently consistent at the M06-2X/6-311++G** level. This shows that C₇₂H₂₄ can well represent graphene adsorbing nucleobases in this study.

Table 2.

Binding energies (kcal/mol) of DNA nucleobases on nano graphene (C₇₂H₂₄, C₇₈H₂₄, C₈₆H₂₆, C₁₀₆H₂₈) at the M06-2x and B97-D levels. The data in Basis sets, A:6-31G(d); B: 6-311++G(d,p); C:6-31G(d,p)

	M06-2X /A	M06-2X/B// M06-2X/A	B97-D/B//M06-2X/A	MP2/Ba	B97D/TZ V(2d,2p)b	vdW-HF/Cc	LDAd	vdW-DFe	B3LYP-D/A// (M06-2X/A:AM1)f	wB97XD/Cg
C72H24-Adenine	(16.6)	14.7 (20.1)	18.4 (23.3)	21.7	20.2	14.8	14.1	16.4	15.0	20.3
C78H24-Adenine	(16.4)	14.7 (20.2)	18.9 (23.9)
C86H26-Adenine	(16.4)	14.5 (20.0)	18.4 (23.4)
C106H28-Adenine	(16.2)	14.6 (20.0)	19.0 (23.9)
C72H24-Guanine	(20.2)	18.2 (24.2)	21.6 (27.0)	24.6	24.2	15.1	11.3		17.5	22.5
C72H24-Thymine	(15.8)	14.2 (19.1)	16.3 (20.8)	21.4	19.0	14.8	11.3		14.3	18.4
C72H24-Cytosine	(15.6)	14.1 (18.6)	15.8 (19.9)	18.4	18.5	7.9	11.3a 9.0d		13.3	18.9

^aRef. [9]

^bRef.[10]

^cRef.[11]

^dRef.[12]

^eRef.[13]

^fRef. [14]

^gRef.[16]

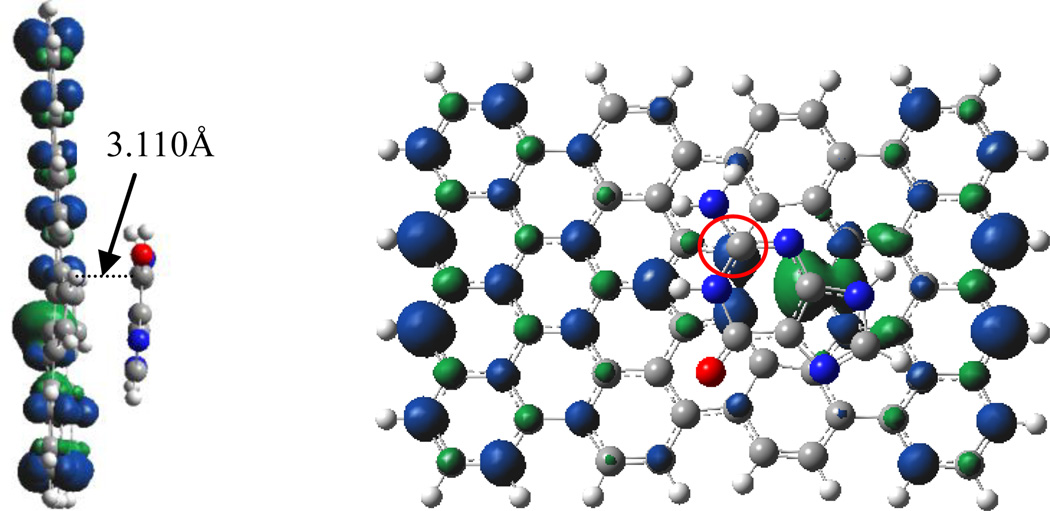
Figure 2 displays the highest occupied frontier molecular orbitals of the C₇₂H₂₄-guanine complex, as an example to illustrate the interaction between nucleobases and graphene. There is almost no orbital component from guanine in HOMO, rather small contribution to HOMO-1 and HOMO-5. It is apparent that there is not much contribution of these molecular orbitals to the combination of guanine and graphene. In contrast, HOMO-2, −3 and −4 exhibit the orbital interaction between guanine and graphene. The orbital overlap of HOMO-2, −3 and −4 mainly takes place through π-π type in the hexagon and pentagon of guanine with graphene, while the p(O)-π and p(N)-π overlaps appear in HOMO-2 and HOMO-4. However, these π-π, po-π and pnh-π interactions are quite weak because of the long distance of ~ 3 Å. In fact, the adsorption energy primarily comes from dispersion interaction aside from the orbital interaction, as mentioned in the above section.

Figure 2.

Top and side views of orbital iso-surfaces (0.002au) of graphene-guanine complex from HOMO to HOMO-5. Orbital energies are in parantheses. Orbital interaction occurs only in HOMO-2, HOMO-3 and HOMO-4.

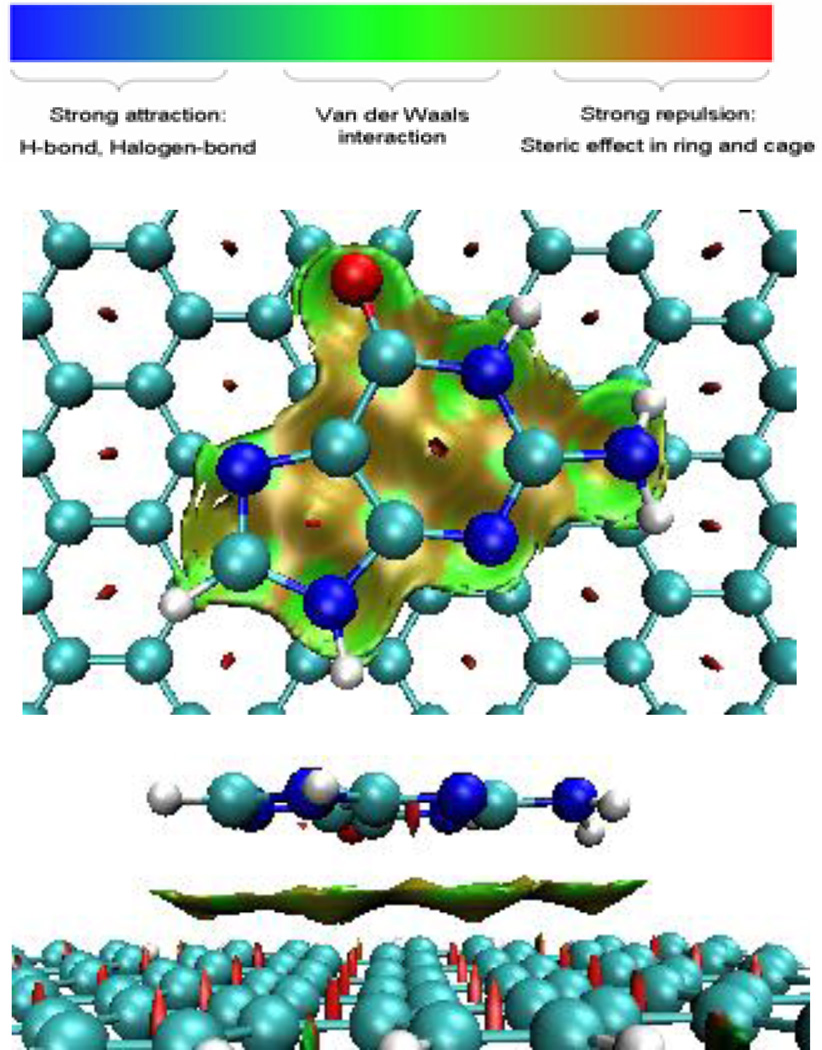
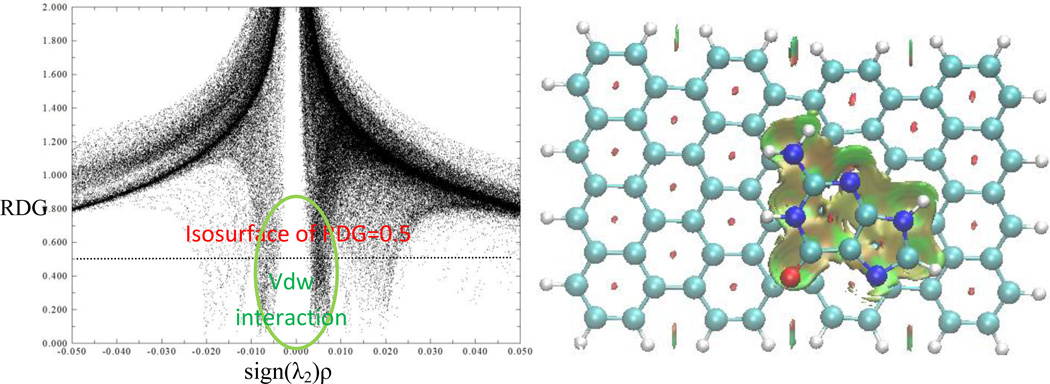
In order to analyze and visualize the noncovalent interactions in these systems, an approach developed by Yang et al. was adopted.[41] In this approach, the reduced density gradient, defined as RDG=1/(2(3π²)^1/3)| ∇ρ|/ρ^4/3, together with electron density (ρ), were used to distinguish the covalent bonding and noncovalent interactions. In order to identify the noncovalent interaction, the sign of the second largest eigenvalue (λ₂) of the electron-density Hessian was utilized as a tool to distinguish bonded (λ₂<0) from nonbonded (λ₂>0).[41] The gradient isosurfaces are colored according to the corresponding values of sign(λ₂)ρ. Large negative values of sign(λ₂)ρ are indicative of attractive interactions (such as dipole-dipole or hydrogen bonding); while if sign(λ₂)ρ is large and positive, the interaction is nonbonding.[41] Values near zero indicate very weak, van der Waals interactions. The gradient isosurfaces provide a visualization of noncovalent interaction as broad regions of real space, rather than simple pairwise contacts between atoms. The functions such as RDG and sign(λ₂)ρ were calculated with Multiwfn software.[42] The gradient isosurface was plotted with VMD.[43] Figure 3 shows the plot of reduced density gradient (RDG) isosurface of guanine-graphene complex. The isosurface in green color represents the van de Waals interaction corresponding to the all atoms of guanine molecule with graphene. Especially, the groups of NH₂ and O have slightly stronger vdW interaction through respective N-H⋯ π and C=O⋯π. The binding energy of guanine with graphene thus originates from both orbital interaction and vdW interaction.

Figure 3.

Top (top) and side (bottom) views of sign(λ₂)ρ isosurface of graphene-guanine complex. Green and yellow denotes vdW interaction between guanine and graphene through π⋯ π, C=O⋯ π, and N/C-H⋯ π.

3.2 Adsorptions of DNA nucleobases on mono-vacant graphene

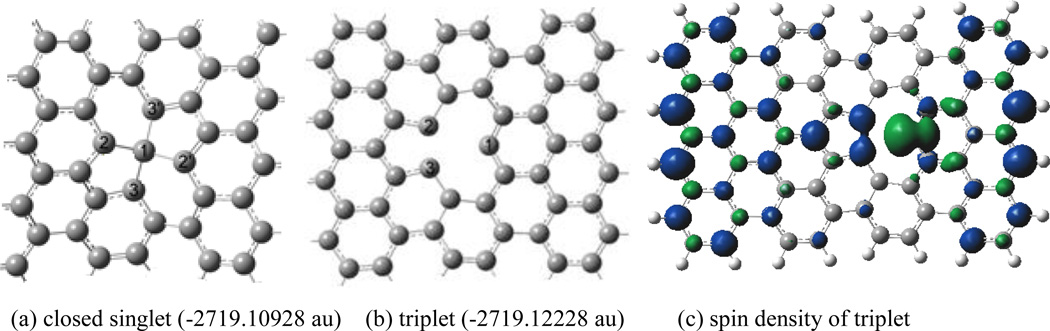
The mono-vacant defective graphene model, C₇₁H₂₄, is derived from the pristine graphene model, C₇₂H₂₄, by removing a carbon atom, as shown in Figure 4. The geometries of C₇₁H₂₄ were optimized for four electronic states. For the closed shell singlet state (a) the configuration has two pentagon rings and the C1 atom is of near tetrahedral structure, a significant distortion of the graphene plane. The open shell singlet configuration (not shown) has one pentagon ring and a carbene-like atom, C1, and much less stable than the closed shell by 32.0 kcal/mol. The C2-C3 bond length of the triplet configuration in Figure 4b is 1.715 Å and the atomic distances of C1-C2 and C1-C3 are 2.650 Å, and the triplet is more stable than the closed and open shell singlet states by 8.1 and 40.1 kcal/mol, respectively. In addition, the quintet configuration of C₇₁H₂₄ has similar structure to triplet, in which the bond length of C2-C3 is 1.748 Å and the atomic distances of C1-C2 and C1-C3 are 2.635 Å; however, it is less stable than the triplet one by 1.5 kcal/mol. Thus, the ground state of C₇₁H₂₄ exhibits biradical character and the triplet state was thus used to investigate the adsorption of DNA nucleobases on graphene.

Figure 4.

Structures of C₇₁H₂₄ at singlet and triplet at M06-2x/6-31G*, and spin density for the triplet. (a) C₁-C₂=1.5946 Å, C₁-C₃=1.6141 Å, ∠C₂C₁C₂,=138.3°, ∠C₃C₁C₃,=138.1° (b) triplet state: C₁-C₂=2.6502 Å, C₁-C₃=2.6502 Å , C₂-C₃=1.7153 Å. (quintet: C₁-C₂=2.6344 Å, C₁-C₃=2.6345 Å , C₂-C₃=1.7484 Å) (c) Spin density (isosurface=0.004au)

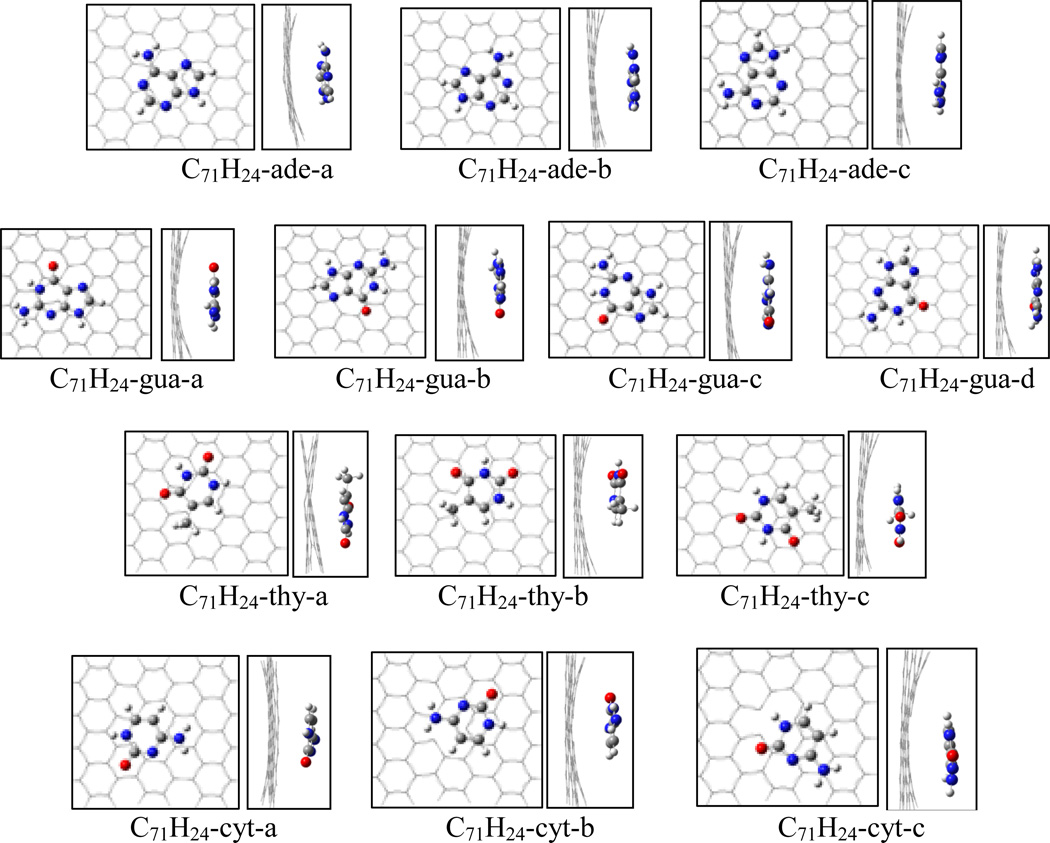
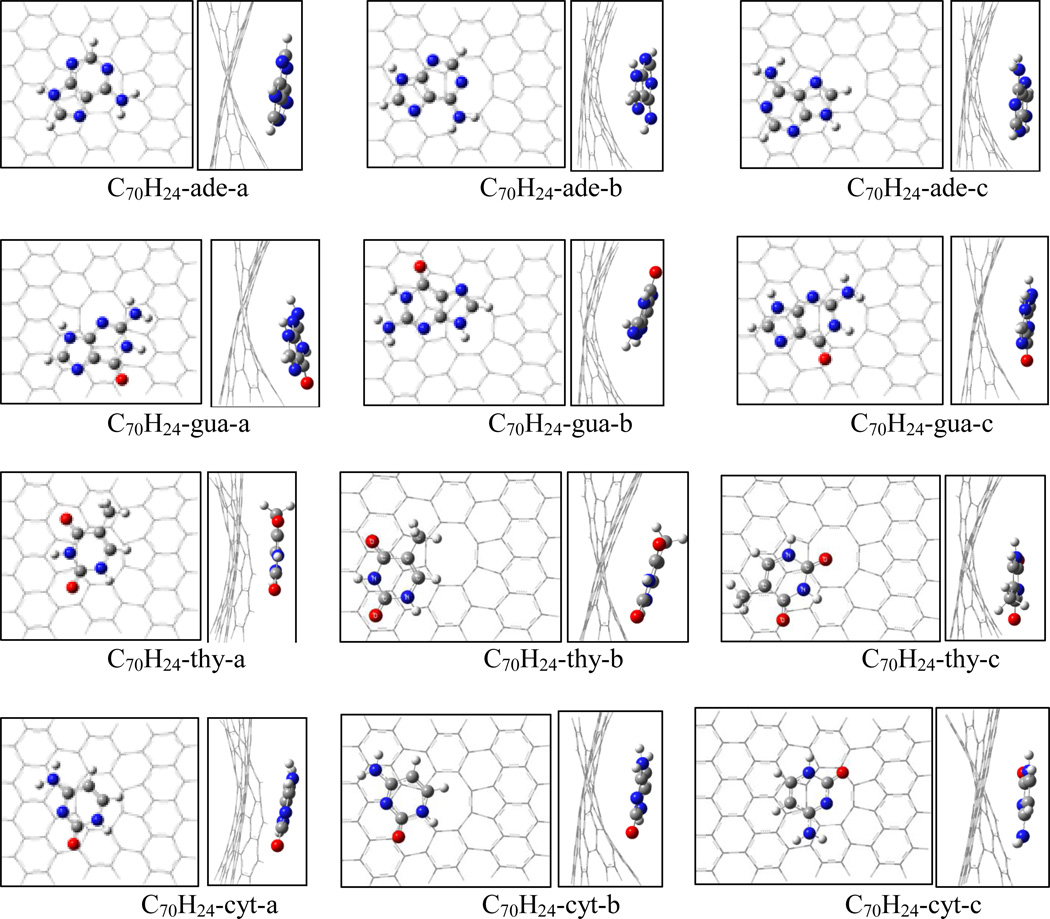
Figure 5 shows the structures of the adsorption complexes of nucleobases on mono-vacant defective graphene of the triplet C₇₁H₂₄. Because of the missing carbon atom in the graphene plane, the interaction between graphene and nucleobase causes the graphene plane a slightly bending. The different position of the hexagonal ring of nucleobase over the defective graphene leads to a number of adsorption complexes. For C₇₁H₂₄-adenine complex three configurations are located at the M062x/6-31G* level of theory. The adsorption energies are summarized in Table 3. Among the three complexes C₇₁H₂₄-ade-a has the highest adsorption energy of 16.2 kcal/mol at the M062x/6-31G*, and is more stable than C₇₁H₂₄-ade-b and C₇₁H₂₄- ade-c by 0.8 and 0.9 kcal/mol, respectively. The distances of C₁-C₂ and C₁-C₃ of C₇₁H₂₄ in C₇₁H₂₄-ade-a only slightly stretch to 2.661Å from 2.650Å of the free C₇₁H₂₄, while the C₂-C₃ compresses a little to 1.709Å from 1.715Å. The shortest atomic distance in C₇₁H₂₄-ade-a is ~3.180Å. With BSSE correction the adsorption energies for C₇₁H₂₄-ade-a, -b and -c are 14.2, 13.4, and 13.5 kcal/mol, respectively, at the M062x/6-311++G(d, p) level; while they respectively increase to 17.5, 16.3, and 16.4 kcal/mol at the B97D/6-311++G(d, p) level. In addition, the complex of the bigger graphene model with adenine, C₁₀₅H₂₈-ade-a, was reoptimized to compare with C₇₁H₂₄-ade-a, and the adsorption energy is just slightly higher by 0.1 and 0.5 kcal/mol at the M062x and B97D levels, respectively.

Figure 5.

Top and side views for the adsorption complexes of nucleobases on monovacancy defective graphene (C₇₁H₂₄).

Table 3.

Binding energies (kcal/mol) of DNA nucleobases on mono-vacant defective graphene (C₇₁H₂₄) at the M06-2X and B97-D levels. The data in the parenthesis refer to those without BSSE. Basis sets, A:6-31G(d); B:6-311++G(d,p)

	M06-2X/A	M06-2X/B//M06-2X/A	B97-D/B//M06-2X/A
Adenine
C71H24-ade-a	16.2	14.2 (19.2)	17.5 (22.2)
C105H28-ade-a	16.5	14.3 (19.5)	18.0 (22.8)
C71H24-ade-b	15.4	13.4 (18.4)	16.3 (21.0)
C71H24-ade-c	15.3	13.5 (18.2)	16.4 (20.8)
Guanine
C71H24-gua-a	18.7	16.6 (22.3)	18.9 (24.2)
C71H24-gua-b	18.4	16.4 (22.0)	17.1 (22.3)
C71H24-gua-c	19.2	17.0 (22.5)	19.5 (24.6)
C71H24-gua-d	17.8	15.7 (21.0)	18.8 (23.7)
Thymine
C71H24- thy-a	15.2	13.7 (18.3)	14.4 (18.6)
C71H24-thy-b	16.7	15.3 (19.8)	17.3 (21.5)
C71H24-thy-c	17.3	15.8 (20.2)	18.3 (22.3)
Cytosine
C71H24-cyt-a	14.2	12.4 (16.9)	13.2 (17.3)
C71H24-cyt-b	16.0	14.5 (18.9)	16.1 (20.2)
C71H24-cyt-c	15.3	13.8 (18.0)	15.8 (19.6)

For the C₇₁H₂₄-guanine system, four adsorption complexes were located at the M06-2X/6-31G* level, as shown in Figure 5. Among the four adsorption complexes the most stable complex is C₇₁H₂₄-gua-c, with the adsorption energies of 17.0 and 19.5 kcal/mol at the M06-2X/6-311++G(d, p) and B97D/6-311++G(d, p) levels, respectively. Similar to the adsorptions on pristine graphene, guanine more strongly binds to the defective graphene than adenine does.

For the C₇₁H₂₄-thymine system, C₇₁H₂₄-thy-c has the highest adsorption energy among three adsorption configurations. With BSSE correction at 6-311++G(d,p), the adsorption energy of C₇₁H₂₄-thy-c is 15.8 kcal/mol at M06-2X level, 2.1 and 0.5 kcal/mol greater than C₇₁H₂₄-thy-a and C₇₁H₂₄-thy-b, respectively; while at the B97D level the adsorption energy of C₇₁H₂₄-thy-c is 18.3 kcal/mol, greater than C₇₁H₂₄-thy-a and C₇₁H₂₄-thy-b by 3.9 and 1.0 kcal/mol, respectively. Although cytosine has the same hexagon ring as thymine, the different substitutes may lead to the adsorption energy of C₇₁H₂₄-cytosine less than that of C₇₁H₂₄-thymine. The most stable complex among three C₇₁H₂₄-cytosine configurations is C₇₁H₂₄-cyt-b with the binding energies of 14.5 and 16.1 kcal/mol at the M06-2X and B97D/6-311++G(d,p) levels, respectively. The adsorption energy of C₇₁H₂₄-cyt-b is 2.1 and 2.9 kcal/mol higher than those of C₇₁H₂₄-cyt-a at M06-2X and B97D levels, respectively; while it is only 0.7 and 0.3 kcal/mol respectively greater than the ones of C₇₁H₂₄-cyt-c.

Although the mono-vacant defective graphene was shown to chemically bind to various molecules and metal cluster through the defective sites, dramatically stronger than to pristine graphene,[3, 24, 28–29, 32] the above discussions reveal that the DNA bases adsorbs on the mono-vacant graphene through noncovalent interaction with the shortest atomic distances of approximately 3.1–3.2Å. The spin density in Figure 6 for C₇₁H₂₄-gau-c dominantly locates over the mono-vacant graphene, also indicating the noncovalent interaction between the DNA base with the defective graphene. On the contrary, the spin density of the complex of Pt₄ and monovacant graphene considerably delocalizes over the Pt (65%) and graphene (35%) clusters, which can be to attributed to the similar SOMOs of Pt₄ and C₁₀₃H₂₈ clusters (−0.185 vs −0.162au) and thus significant orbital overlap leads to strong binding.[32] The difference between the HOMO of guanine and the SOMO of C₇₁H₂₄ (0.258 vs 0.193au) is relatively high, and the minor orbital overlap excludes the covalent interaction and van der Waals interaction is still the dominant interaction between DNA bases and the defective graphene.

Figure 6.

the side (left) and top (right) views for the spin density of C₇₁H₂₄-gua-c (0.004 au).

The noncovalent van der Waals interaction was illustrated in Figure 7 through the color filled sign(λ2)ρ at the isosurface of RDG=0.5, where the green and yellow areas show the vdW interaction between guanine and the mono-vacant graphene through π⋯ π, C=O⋯ π, and N/C-H⋯ π. A comparison among the most stable complexes for DNA bases indicates that the adsorption energies decrease by the sequence of G (19.5kcal/mol)>T (18.3) >A (17.5~18.0)>C (16.1), which is different from the adsorptions on pristine graphene C₇₂H₂₄ (G>A>T>C: 21.6, 18.4~19.0, 16.3, 15.8 kcal/mol) by switching the sequence of adenine and thymine. In addition, the adsorption energies of adenine and guanine on the defective graphene C₇₁H₂₄ are approximately 1–2 kcal/mol less than on the pristine graphene C₇₂H₂₄, while C₇₁H₂₄-thymine and C₇₁H₂₄-cytosine are 2.0 and 0.3 kcal/mol greater than those of C₇₂H₂₄-thymine and C₇₂H₂₄-cytosine, respectively. This difference may be related to the orbital overlaps and electrostatic interactions between the graphene and nucleobases. The frontier orbitals of nucleobases with C₇₁H₂₄ and C₇₂H₂₄ are displayed in Supplementary Information document. For both C₇₂H₂₄-ade and C₇₂H₂₄-gua, their HOMO-2, −3 and HOMO-4 have significant orbital overlaps, but the HOMOs of both C₇₁H₂₄-ade and C₇₁H₂₄-gua have much smaller orbital overlaps because of the missing carbon atom. The electrostatic attractive energies between graphene and nucleobase in C₇₂H₂₄-ade and C₇₂H₂₄-gua are also about 0.5 kcal/mol higher than those in C₇₁H₂₄-ade and C₇₁H₂₄-gua, as in Table 4. This implies that the combining strength of the defective graphene with adenine and guanine lessens slightly relative to that of the pristine graphene with adenine and guanine. On the contrary, there is no much orbital overlap between C₇₂H₂₄ and thymine in the investigated HOMOs of C₇₂H₂₄-thy, but the HOMO-5 and HOMO-7 of C₇₁H₂₄-thy show small orbital interaction. For both C₇₂H₂₄-cyt and C₇₁H₂₄-cyt, the HOMO-4 orbitals have small overlap between graphene and cytosine, while the other HOMOs do not present orbital interaction. Also, the electrostatic energies of both parts of C₇₂H₂₄-thy and C₇₂H₂₄-cyt are slightly less than those of C₇₁H₂₄-thy and C₇₁H₂₄-cyt, respectively, the former by 0.13 kcal/mol and the latter by 0.03 kcal/mol. This may account for the adsorption energies of C₇₂H₂₄-thy and C₇₂H₂₄-cyt smaller than those of C₇₁H₂₄-thy and C₇₁H₂₄-cyt, respectively.

Figure 7.

The scatter plot of RDG vs sign(λ2)ρ (left), and color filled sign(λ2)ρ at the isosurface of RDG=0.5. It has the same color code as in Figure 3. Green and yellow areas show the vdW interaction between guanine and the mono-vacant graphene through π⋯ π, C=O⋯ π, and N/C-H⋯ π.

Table 4.

Electrostatic energy estimated with CHelpG charges (kcal/mol)

	C72H24	C71H24	C70H24-base
Adenine	−0.940	−0.330	−1.681
Guanine	−2.603	−2.113	−3.048
Thymine	−1.043	−1.171	−1.060
Cytosine	−1.784	−1.813	−1.564

3.3 Adsorptions of DNA Nucleobases on Divacancy Defective Graphene

In addition, the divacant graphene (C₇₀H₂₈) with two missing carbon atoms has also been studied. The triplet C₇₀H₂₈ again is the ground state with 5–8-5-ring structure, 8.9 and 10.8 kcal/mol more stable than the singlet and quintet states, respectively. Figure 8 shows the structures of the adsorption complex of C₇₀H₂₈ with nucleobases at the M06-2x/6-31G* level and Table 5 lists the adsorption energies at the M06-2x and B97-D levels. The adsorption between di-vacant graphene and nucleobase seems not favorable on the twisted graphene surface and at the octagonal vacant position because of bigger vacant hole of the octagonal ring. Among the three adsorption complexes of C₇₀H₂₄-adenine, the least stable complex is C₇₀H₂₄-ade-a, in which the hexagonal ring of adenine mostly sits above the octagonal ring of C₇₀H₂₄ and the graphene surface is twisted, while C₇₀H₂₄-ade-b and C₇₀H₂₄-ade-c have stronger adsorption because the fragment of adenine is located on the octagonal boundary of C₇₀H₂₄. With BSSE correction for C₇₀H₂₄-ade-a, -b, and -c, the respective adsorption energies are 12.7, 14.7, and 15.9 kcal/mol at M06-2X/6-311++G**; and they increase to 16.6, 19.0, and 19.9 kcal/mol at B97-D/6-311++G**. For the case of C₇₀H₂₄-gua at the M06-2X/6-31G* level the adsorption energy of C₇₀H₂₄-gua-a is the highest among three adsorption structures, while with 6-311++G** basis set the adsorption energies of C₇₀H₂₄-gua-a and -b are almost identical. However, at the B97-D/6-311++G** level C₇₀H₂₄-gua-b has the highest adsorption energy. Table 5 shows that the adsorption energies of C₇₀H₂₄-gua-a, -b, and -c are 19.1, 19.0, and 18.0 kcal/mol, respectively, at M06-2X/6-311++G** level, and 21.4, 23.3, and 21.5 kcal/mol at B97-D/6-311++G**, which are obviously greater than those of C₇₀H₂₄-ade. As for both C₇₀H₂₄-thy and C₇₀H₂₄-cyt, the most stable structures are C₇₀H₂₄-thy-c and C₇₀H₂₄-cyt-b, respectively. At the B97D+BSSE level the adsorption energy of the former is 18.9 kcal/mol and the latter is 16.9 kcal/mol. The adsorption energy of C₇₀H₂₄-thy is about 2.0 kcal/mol more than that of C₇₀H₂₄-cyt, and ~1.0 and 4.4 kcal/mol less than those of C₇₀H₂₄-ade-c and C₇₀H₂₄-gua-b, respectively. The adsorption energies of DNA bases on the divacant graphene descend by the sequence of G>A>T>C, which is consistent with the sequence of C₇₂H₂₄-nucleobases and slightly different from that of C₇₁H₂₄-nucleobases.

Figure 8.

Top and side views of the adsorption complexes of nucleobases on di-vacant defective graphene (C₇₀H₂₄).

Table 5.

Binding energies (kcal/mol) of DNA nucleobases on divacancy defective graphene (C₇₀H₂₄) at the M06-2x and B97-D levels. Basis sets: A, 6-31G(d); B, 6-311++G(d,p). Numbers in parentheses refer to the binding energies without BSSE.

	M062x/A	M062-2X/B//M06-2X/A	B97D/B//M06-2X/A
Adenine
C70H24-ade-a	(15.1)	12.7 (17.6)	16.6 (21.2)
C70H24-ade-b	(16.6)	14.7 (19.7)	19.0 (23.6)
C70H24-ade-c	(17.9)	15.9 (21.0)	19.9 (24.6)
Guanine
C70H24-gua-a	(21.8)	19.1 (24.3)	21.4 (26.1)
C70H24-gua-b	(21.0)	19.0 (24.6)	23.3 (28.4)
C70H24-gua-c	(20.6)	18.0 (23.7)	21.5 (26.8)
Thymine
C70H24-thy-a	(15.8)	14.1 (18.6)	16.4 (20.5)
C70H24-thy-b	(16.4)	14.5 (19.2)	17.4 (21.7)
C70H24-thy-c	(17.6)	16.0 (20.5)	18.9 (23.1)
C86H26-thy-a	(15.9)
C86H26-thy-b	(15.8)
C86H26-thy-c	(18.2)
Cytosine
C70H24-Cytosine-a	(14.7)	13.2 (17.6)	15.3 (19.3)
C70H24-Cytosine-b	(15.6)	14.2 (18.6)	16.9 (21.0)
C70H24-Cytosine-c	(13.8)	11.6 (16.1)	14.8 (18.8)

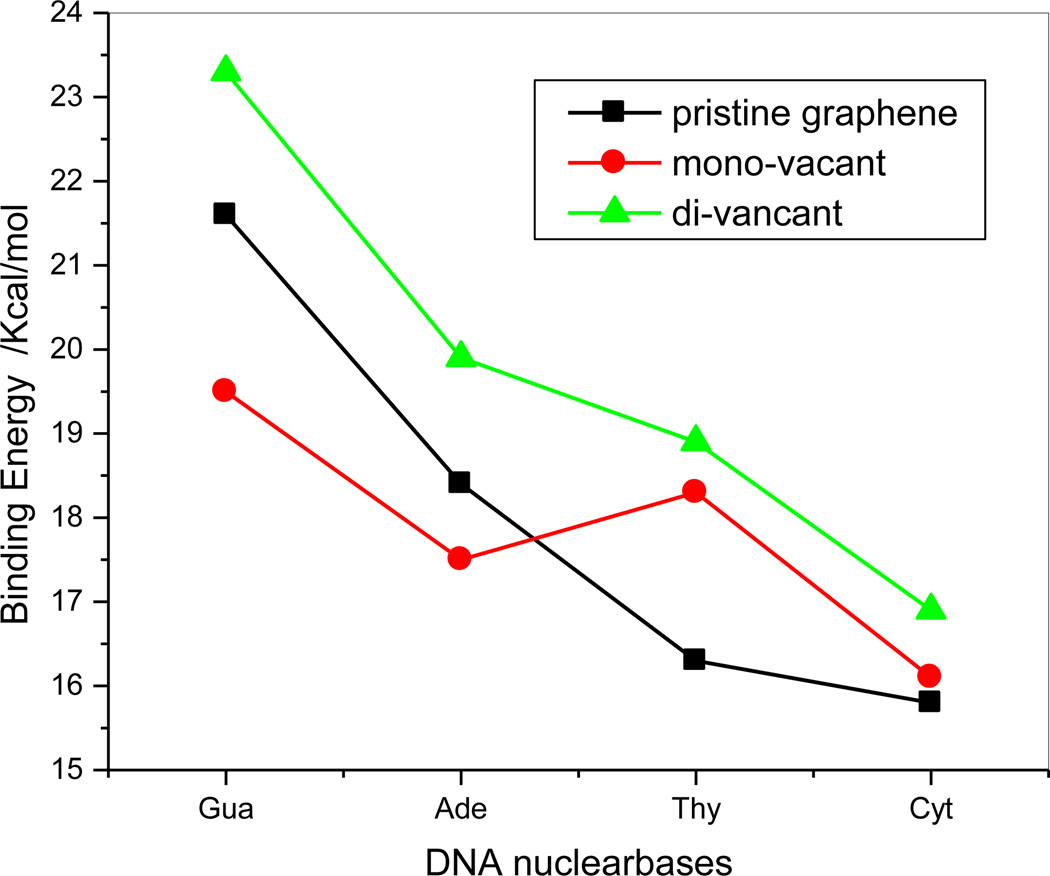
From the above discussion, although the binding for the three adsorption systems is different with respect to strength and sequence, but van der Waals interactions are dominant for the adsorptions of DNA bases on pristine and the defective graphenes. A comparison of the adsorption energies on the pristine, mono- and di-vacant graphenes at the B97-D/6-311++G(d,p) level with BSSE correction is shown in Figure 9. The adsorption energies of DNA bases on the di-vacant graphene are larger than that of pristine graphene by 1.1–2.6 kcal/mol; however, for the mono-vacant defective grapheme the adsorption energies of both C₇₁H₂₄-gua and C₇₁H₂₄-ade are less than those of C₇₂H₂₄-gua and C₇₂H₂₄-ade by 2.1 and 0.9 kcal/mol, respectively, while the adsorption energy of C₇₁H₂₄-thy is 2.0 kcal/mol significantly larger than that of C₇₂H₂₄-thy and the adsorption energy of C₇₁H₂₄-cyt is almost equal to that of C₇₂H₂₄-cyt. This implies that, from pristine graphene to mono-vacancy, the binding strength decreases for guanine and adenine and increases only for thymine.

Figure 9.

Comparison of the binding energies of three kinds of adsorption systems. (■: pristine graphene; ; )

Conclusion

The adsorptions of the nucleobases G, A, C, and T on pristine, mono-vacant, and di-vacant graphenes are fully optimized at M062x/6-31G(d) level, and the adsorption energies are refined with a larger basis set of 6-311++G(d,p) at the M062x and B97D levels. Although some metal clusters and molecules tend to chemically bind to defective graphenes, it is interesting that the present investigation shows that the adsorption of DNA bases on mono- and di-vacant defective graphenes does not show much difference from that on pristine graphene, and is still dominantly driven by non-covalent interactions. At the B97D/6-311++G(d,p)//M06-2X/6-31G(d) level, the respective adsorption energies of G, A, T, and C on the pristine graphene are predicted to be 21.6, 18.4, 16.3, and 15.8 kcal/mol, and on the mono-vacant graphene they change to 19.5, 17.5, 18.3, and 16.1 kcal/mol; yet on the di-vacant graphene their binding were enhanced to 23.3, 19.9, 18.9, and 16.9 kcal/mol, respectively. This result shows that the binding strength increases from pristine graphene to di-vacant graphene for all of the four nucleobases, and to mono-vacant graphene always increase for thymine and cytosine and yet decreases for guanine and adenine. In three adsorption systems, the sequence of the adsorption strength is G>A>T>C for the pristine and di-vacant graphenes and G>T>A>C for the mono-vacant graphene.

Highlights.

• ➢For the first time reveal the non-covalent interaction between DNA bases and defective graphene;
• ➢Provide the binding sequence of DNA bases with the mono- and di-vacant defective graphene;
• ➢Demonstrate the non-covalent interaction between DNA bases and defective graphene through binding energy as well as sign(λ₂)ρ visualization.