Quantifying bursting neuron activity from calcium signals using blind deconvolution

Abstract

Advances in calcium imaging have enabled studies of the dynamic activity of both individual neurons and neuronal assemblies. However, challenges, such as unknown nonlinearities in the spike–calcium relationship, noise, and the often relatively low temporal resolution of the calcium signal compared to the time-scale of spike generation, restrict the accurate estimation of action potentials from the calcium signal. Complex neuronal discharge, such as the activity demonstrated by bursting and rhythmically active neurons, represents an even greater challenge for reconstructing spike trains based on calcium signals. We propose a method using blind calcium signal deconvolution based on an information-theoretic approach. This model is meant to maximise the output entropy of a nonlinear filter where the nonlinearity is defined by the cumulative distribution function of the spike signal. We tested our maximum entropy (ME) algorithm using bursting olfactory receptor neurons (bORNs) of the lobster olfactory organ. The advantage of the ME algorithm is that the filter can be trained online based only on the statistics of the spike signal, without any assumptions regarding the unknown transfer function characterizing the relation between the spike and calcium signal. We show that the ME method is able to more accurately reconstruct the timing of the first and last spikes of a burst compared to other methods and that it improves the temporal precision fivefold compared to direct timing resolution of calcium signal.

1. Introduction

The development of fluorescent indicators and imaging technology has enabled the monitoring of the activity of both individual neurons and large populations of neurons via calcium imaging (Grinvald et al., 1988; Zochowski et al., 2000). However, reconstructing spike trains from a calcium signal remains a challenging issue due to hidden nonlinearities in the spike–calcium relationship, contamination by noise, and the often relatively low temporal resolution of the calcium signal compared to the action potential generation time-scale (Neher and Augustine, 1992; Sasaki et al., 2008; Sjulson and Miesenböck, 2007; Vogelstein et al., 2009). A variety of methods have been introduced to reconstruct spike timing from calcium transients in tonically active neurons. For instance, template-matching algorithms (Kerr et al., 2005) and multiscale filtering combined with template convolution (MSF TC) (Quan et al., 2010) exploit the shape of the calcium transient associated with a single spike (typically a fast rise and exponential decay). These methods, however, require extraction of the template from the calcium signal; thus, they may fail to capture the characteristic shape of a transient when temporal resolution is low. Temporal deconvolution of the calcium transient (Yaksi and Friedrich, 2006) is another method that is based on reconstructing changes in the firing rate of a population of neurons by deconvolving the low-pass filtered calcium transient; however, this method may be vulnerable to noisy data. Other techniques, such as the sequential Monte Carlo method (Vogelstein et al., 2009) or the principal component analysis-support vector machine (PCA-SVM) algorithm (Sasaki et al., 2008), require either hypotheses to establish the model or considerable training data to define parameters.

Many neurons are rhythmically active and form a variety of oscillating neural assemblies that operate in numerous physiological and pathophysiological processes of the peripheral and central nervous systems (e.g., Marder and Calabrese, 1996; Lisman, 1997; Izhikevich et al., 2003; Buzsaki and Draguhn, 2004; Krahe and Gabbiani, 2004). These neurons intrinsically generate bursts of action potentials, which is distinctive; however, variables such as the ionic basis of rhythm generation and the frequency and temporal pattern of action potentials within bursts can vary significantly. While rhythmically active neurons play an important role in various aspects of neural system function, methods used to analyse their activity that are based on calcium imaging are considerably immature compared to methods used for tonic cells.

Here, we propose a blind deconvolution method based on an information-theoretic approach to analyse burst spike timing. Our study is applied to the activity of bursting olfactory receptor neurons (bORNs) of the lobster olfactory organ (Bobkov and Ache, 2007; Bobkov et al., 2012). bORNs are inherently rhythmic neurons in which rhythms can be entrained by intermittent stimuli. We use calcium imaging to elucidate which aspects of stimulus-related information are encoded and conveyed by bORNs acting in an ensemble and the mechanisms underlying these processes. Neuronal discharge characterised by complex patterns, such as that demonstrated by rhythmically active neurons, presents a significant challenge for reconstructing spike trains based on the neuronal calcium signal. Among these challenges are the variability of intra-burst spike patterning, relatively high instantaneous frequencies, and typically relatively low temporal resolution of the calcium signal (~4.2 Hz in the given case). We circumvent some of these challenges by limiting our analysis to quantifying only the inter-burst interval (IBI) and burst duration rather than the individual spikes in a burst. This was achieved by reconstructing the first and last spikes in a burst. We model the calcium signal as the response of an unknown linear channel when the input comprises a burst of spikes. Assuming that electrophysiological recordings are not available and that the relationship between spikes and the calcium signal is unknown, we approached the problem using a blind deconvolution method using an information-theoretic approach based on the maximum entropy (ME) algorithm (Bell and Sejnowski, 1995; Haykin, 2000; Erdogmus et al., 2003, 2004; Principe, 2010).

We show that the proposed ME method is able to reliably reconstruct the timing of the first and last spikes in a burst with greater accuracy compared to other methods. The advantage of the ME algorithm is that the filter can be learned online based only on the statistics of the spike signal without assumptions regarding the spike–calcium relationship. The test results further prove that the ME method is quite robust and that reliable performance may be obtained even when the filter parameters are optimised for one neuron and applied to other neurons.

2. Materials and methods

2.1. Preparation

The in situ preparation of the lobster (Panulirus argus) ORNs was conducted as previously described (Bobkov and Ache, 2007; Ukhanov et al., 2011). Briefly, a single annulus was excised from the lateral antennular filament. After treatment with trypsin (1 mg/ml) for approximately 20–40 min, the cuticle found on the side opposite from the olfactory (aesthetasc) sensilla was clipped and the ensheathing tissue covering the clusters of ORNs was removed to allow access to neuronal somata. Specimens were mounted on a plastic or glass-bottom 35 mm Petri dish and placed on the stage of an inverted microscope (Axiovert 100, Zeiss, Germany or IX-71, Olympus, Japan). The cell bodies and the olfactory sensilla of the ORNs were continuously superfused with 7.9 pH Panulirus saline (PS) containing (mM): 486 NaCl, 5 KCl, 13.6 CaCl₂, 9.8 MgCl₂ and 10 HEPES. Superfusion contours were gravity-fed at constant flow rates.

2.2. Data recording

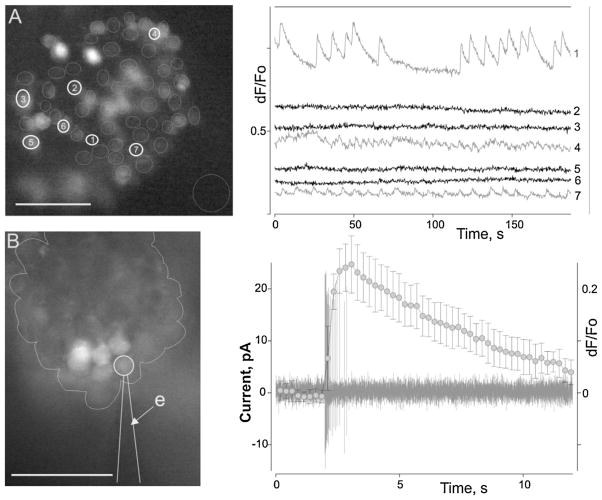
Action potentials (spikes) were exrtacellularly recorded from bORNs using loose-patch recording. Patch electrodes were pulled from borosilicate capillary glass (BF150-86-10, Sutter Instrument, Novato, CA, USA) using a Flaming-Brown micropipette puller (P-87, Sutter Instrument) and filled with PS. Electrode resistance was 1–5 mΩ as measured in PS. Voltages/currents were measured with an Axopatch 200B patch-clamp amplifier (Molecular devices, Sunnyvale, CA, USA) using an AD–DA converter (Digidata 1320A, Molecular devices), low-pass filtered at 5 kHz, sampled at 5–20 kHz. Data were collected and analysed with pCLAMP software (Molecular Devices) in combination with SigmaPlot (Systat Software, Inc. San Jose, CA, USA). The time of spike occurrence was taken as the time of peak current deflection, i.e., the peak of the spike. For calcium imaging, the olfactory antennular segments were placed in an Eppendorf tube in PS containing a 10 μM fluorescent calcium indicator (Fluo-4AM) prepared with 10% Pluronic F-127 (Invitrogen, Grand Island, NY, USA). The tube was shaken for approximately 30–60 min using an orbital shaker (~70 rpm). The tissue was transferred into fresh PS and mounted for imaging. Fluorescence imaging was performed on an inverted microscope (Olympus IX-71) equipped with a cooled CCD camera (ORCA R2, Hamamatsu, NJ, USA) that was controlled by Imaging Workbench 6 software (INDEC Systems, Santa Clara, CA, USA). This software allows synchronisation of both the optical and electrical signal acquisition. A standard FITC filter set (excitation at 510 nm, emission at 530 nm) was used. Images were collected at the rate of ~4.23 Hz. Recorded data were stored as image stacks and analysed off-line using Imaging Workbench 6 (INDEC Systems) or ImageJ 1.42 (Rasband WS. ImageJ, U.S. National Institutes of Health, Bethesda, Maryland, USA, imagej.nih.gov/ij/, 1997–2012) and pCLAMP. Fig. 1 shows the population activity of lobster ORNs and individual ORN activity monitored in situ both electrophysiologically and with calcium imaging.

Fig. 1.

Activity of lobster ORNs monitored in situ using calcium signal recording (A) or both calcium signal and electrophysiological recording (B). (A) ORN population activity recorded from a single neuronal cluster (A, left). Cells were loaded with a calcium sensitive dye (Fluo4-AM). Circles mark individual ORN somata (analysis regions). Seven raw calcium signal traces are shown (A, right panel). Note that some cells exhibit profound spontaneous calcium oscillations of differing patterns and frequencies. (B) ORN calcium oscillation is a typical characteristic of bursting ORNs (bORNs). Simultaneous extracellular spike and calcium signal recording from an oscillating ORN (B, left) demonstrates the relationship between calcium oscillatory events and burst generation. (B) Right – a typical burst of the ORN (black trace) overlapping the average calcium event (grey line and symbols, bars – SD, n = 15). Bursting parameters for the cell (mean inter-burst interval (IBI) ± SD, s; number of spikes in burst; burst duration, s; n): 16.8 ± 0.9, 17.7 ± 0.7, 0.63 ± 0.05, 30. (B) Left – the line outlines an individual ORN cluster. Micrographs in (A) and (B) were taken under different magnifications. e indicates the recording electrode. Scale bar = 50 μm.

2.3. Data pre-processing

As mentioned above, electrophysiological and optical signal recordings were acquired at different frequencies: 5 kHz and ~4.23 Hz, respectively. To appropriately implement the proposed methodology, the electrophysiological data were downsampled to 200 Hz, and the calcium signal data were upsampled by spline interpolation to the same frequency; this yielded a 5 ms temporal resolution. A first-order high-pass Butterworth filter with a normalised cutoff frequency of 0.1 Hz was used to remove slow occurring variations in the calcium signal. The calcium signal was scaled from −1 to 1 after mean removal and the spike trains were expressed as 1 or 0 (Spiking: 1 and Non-spiking: 0).

3. Results

3.1. Spike timing reconstruction from maximum entropy deconvolution

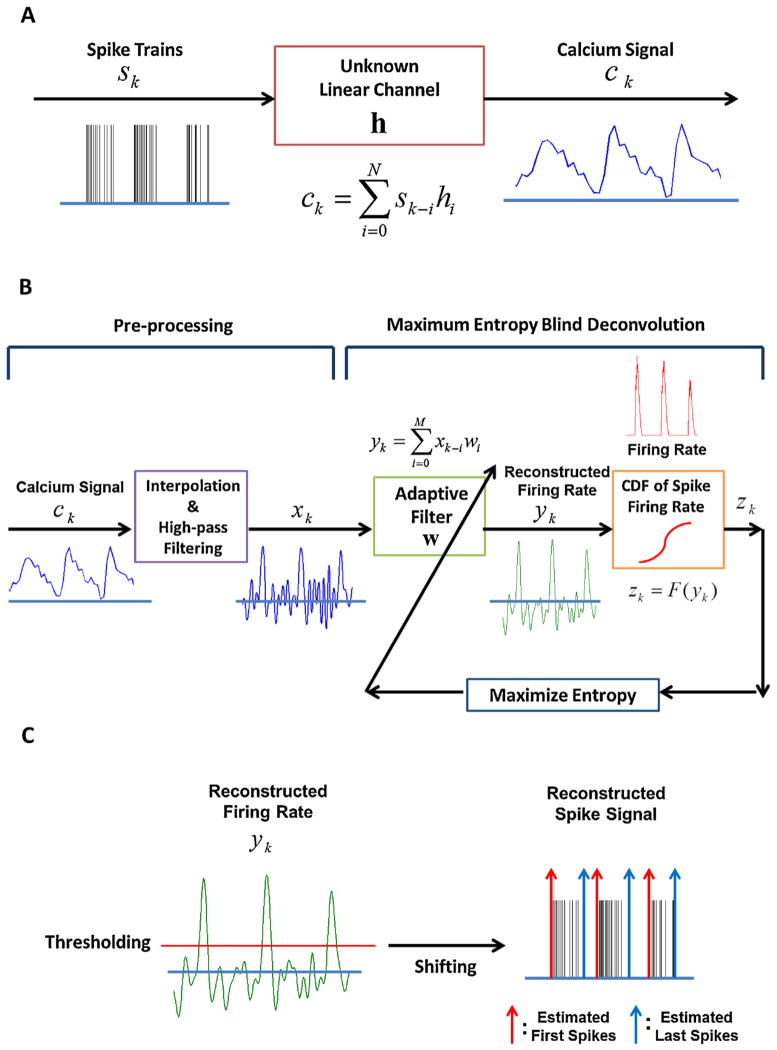
We modelled the calcium signal (Fig. 2A), which is characterised by a smooth and slow response, as the output of an unknown linear channel h when the input is the spike burst (Helmchen et al., 1996; Yaksi and Friedrich, 2006; Holekamp et al., 2008; Quan et al., 2010). In this context, we can reconstruct the spike signals from the calcium signal using deconvolution (Yaksi and Friedrich, 2006; Holekamp et al., 2008). However, Yaksi and Friedrich (2006) assume that the unknown channel is an exponential function defined as exp(−t/τ_decay), truncated at t = 2τ_decay, where τ_decay is a decay time constant. Deconvolution is performed by convolving the calcium signal with the inverse of the discrete Fourier transform (DFT) of the exponential function. Holekamp et al. (2008) also assume that the unknown channel has an exponential impulse response and apply a Wiener filter to deconvolve the calcium signal. Here we will attempt a blind deconvolution approach, which does not require a model for the channel distortion and has been successfully applied in communication systems to reverse the effect of distortion in digital information transmission (Benveniste et al., 1980; Shalvi and Weinstein, 1990; Inouye and Sato, 1999; Chi and Chen, 2001). The information-theoretic approach is a possible solution to the blind deconvolution problem (Bell and Sejnowski, 1995; Haykin, 2000; Erdogmus et al., 2004; Principe, 2010). As applied here (Fig. 2B), blind deconvolution is intended to maximise the output entropy of a nonlinear filter built as the cascade of a linear finite impulse response (FIR) filter described by its parameters w, followed by a static nonlinearity. The static nonlinearity is shaped by the cumulative distribution function (CDF) of the input data as suggested by Bell and Sejnowski (1995). Entropy is one of the descriptors of the probability density function (PDF), and the shape of the PDF at the output of an FIR filter can be controlled by changing its parameters to yield maximum or minimum entropy (Principe, 2010). For instance, in our case, maximising the output entropy after the nonlinearity forces uniformity of its PDF. When the nonlinearity is matched to the input data CDF, the adaptive filter w approaches the inverse of h (Benveniste et al., 1980). In our application, this means that the spike signal can be approximately reconstructed from the calcium signal using an adaptive filter followed by a nonlinearity defined by the input CDF. Because the spike signal has only two discrete values (0 or 1), we estimate the CDF from the firing rate of the spike signal. Therefore, the adaptive filter attempts to reconstruct the firing rate of the spike signal. The blind deconvolution described in Fig. 2B details processing of the calcium signal at each step. As explained in Section 2.3, the calcium signal is pre-processed by interpolation and high-pass filtering. The high-pass filtered calcium signal is similar to the spike firing rate, but it retains undesirable fluctuations. However, through blind deconvolution, these fluctuations are suppressed to approximately zero and the desired signal is enhanced. This means that the distribution (PDF) of the reconstructed signal approximates the distribution of the firing rate. Unlike the communication problem, here the calcium signal is severely undersampled compared to the spike signal; a reduction of temporal resolution in the deconvolution process is thus expected. The advantage of this method versus straight deconvolution (Yaksi and Friedrich, 2006; Holekamp et al., 2008) is that just one signal source (the calcium signal) is necessary to implement the method once the CDF is estimated from the spike data and no model of the distortion is required.

Fig. 2.

Reconstruction of a spike signal using ME blind deconvolution (A) unknown linear model for spike and calcium signal (B) schematic diagram of ME blind deconvolution (C) Estimation of the first and last spike timings by thresholding and shifting the reconstructed firing rate.

The ME deconvolution is described by four parameters (filter length M, step size η, kernel size σ, and Parzen window size L). These parameters are determined by simulations of the training set. To reconstruct the first and last spike timings, we first quantify two variables: filter output peak timing and burst duration. A threshold is applied to the filter output y to detect peaks and estimate the burst duration (Fig. 2C). If the estimated burst duration is less than 0.15 s, we do not consider it a burst. This procedure helps remove falsely detected bursts, especially when the calcium signal is noisy. Because the time delay between the first spike and the filter output peak is almost invariant, we shifted the filter output by the mean of its values calculated from the events in the training set. Therefore, we consider the shifted peak timing as the first spike timing (first spike timing = filter output peak timing − time delay) and compute the last spike timing by adding the estimated burst duration to the first spike timing (last spike timing = first spike timing + burst duration). The mathematical description of the whole process is summarised in Appendix, and the method is programmed and simulated using MATLAB.

3.2. Testing the maximum entropy deconvolution approach using experimental data

The proposed method was applied to one experimental data set for parameter optimisation and tested using four other data sets composed of simultaneous recordings of spikes and calcium signals from five bORNs of different signal to noise ratios. Each set is composed of 53, 53, 17, 38, 37 responses, respectively. Each bORN is characterised by its own bursting frequency and structure, i.e., the number of spikes in the burst and the instantaneous frequency of spikes in the burst. Their features are specified in Table 1. We quantified the performance measurement in terms of the event detection rate (EDR), false discovery rate (FDR), and root-mean square error (RMSE) for the first and the last spike times in a burst computed from the patch clamp data and estimated data. EDR and FDR are defined as the ratio of the detected true events to the total true events and the ratio of the false events to the sum of the true events and false events, respectively. These ratios basically measure the accuracy of the rates for the first spike. Tested results from the ME method were compared to those obtained by peak detection and temporal deconvolution (Yaksi and Friedrich, 2006).

Table 1.

Data specification for five bursting olfactory receptor neurons (bORNs). Each bORN has its own spontaneous rhythm.

	# of spikes in a burst	Burst duration (s) (Mean ± SD)	Frequency of spikes in burst (Hz)		IBI (s) (Mean ± SD)
			Maximum	Average (Mean ± SD)
Data 1	9–21	0.3000 ± 0.0474	166.67	50.90 ± 10.04	2.93 ± 0.87
Data 2	4–8	0.2887 ± 0.0567	61.73	23.16 ± 5.34	4.95 ± 2.01
Data 3	11–22	0.4515 ± 0.1417	128.21	41.87 ± 11.32	17.92 ± 5.80
Data 4	5–11	0.1848 ± 0.0639	100.00	47.82 ± 9.28	22.36 ± 16.52
Data 5	9–29	0.4155 ± 0.1498	142.86	50.50 ± 17.22	4.18 ± 5.73

3.2.1. Learning parameters for the maximum entropy method

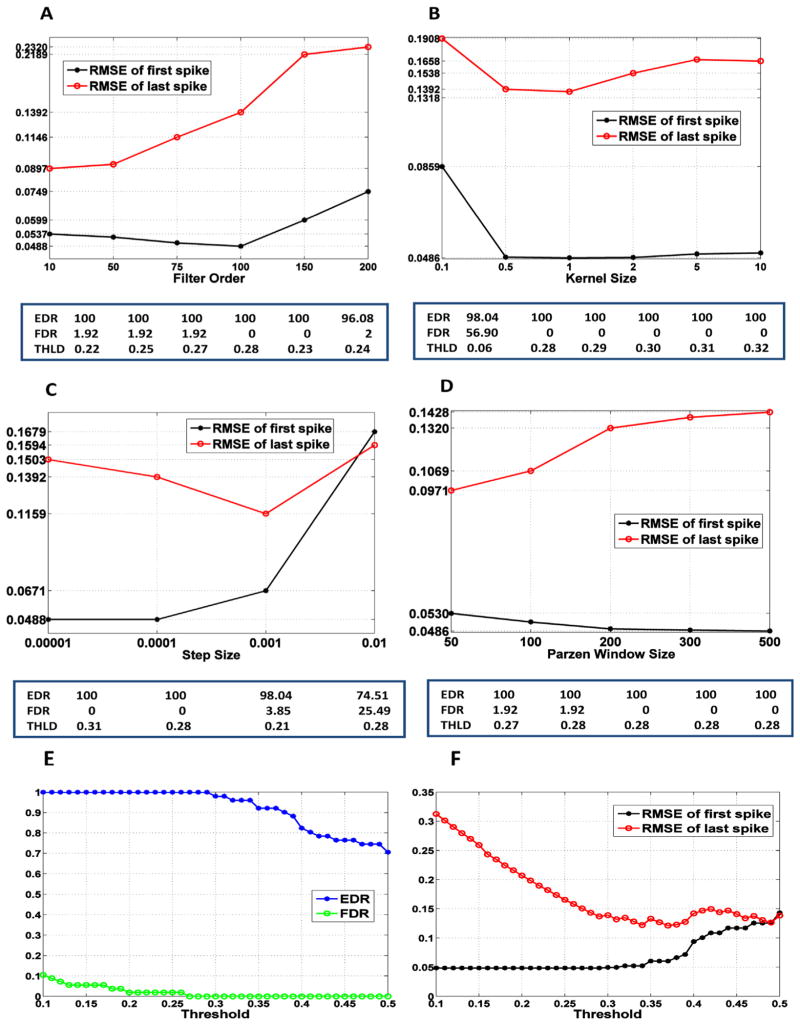
The finite impulse response (FIR) filter was adapted by applying the ME cost function to data set 1 for parameter optimisation. The nonlinearity was set to the CDF of the spike firing rate, which was estimated from 53 events in data set 1 via kernel density estimation (Appendix). We then examined the effect of a threshold on the performance of spike timing reconstruction to determine its appropriate value. To define the optimal parameters, we varied the parameters specifying the filter (filter length M, step size η, kernel size σ, and Parzen window size L) in certain ranges and selected the values exhibiting the best performance, i.e., EDR = 100%, FDR = 0%, and the smallest RMSE for first and last spike timings. Note that these are the rates of the first spike in the burst. Fig. 3A–D displays performance as a function of a single parameter when the other parameters are fixed. The optimal threshold specified in the table below each figure was used to quantify the performance for each value of the filter parameters. From the results, the best performance was 100%, 0%, 0.0468 s, and 0.1370 s for EDR, FDR, RMSE (first spike timing) and RMSE (last spike timing), respectively. This performance was achieved using the parameters of filter length M = 100, step size η = 0.0001 (convergence: 1000 samples), kernel size σ = 1, Parzen window size L = 300, and the threshold of 0.29. We also explored the threshold effect on performance when the filter parameters were fixed at the optimal values (Fig. 3E and F). The results demonstrate that the time accuracy for the first spike is highly consistent because the distribution of the time delay between the first spike and the filter output peaks was highly concentrated around the mean of 0.4788 s. However, the last spike estimation is quite dependent on the threshold; the burst duration varies with the threshold value. We selected the optimal threshold as the value that maximises the EDR and minimises the FDR, but if several thresholds yielded the same EDR and FDR, then the RMSE for the last spike timing was considered to select the best value.

Fig. 3.

Performance of the ME method using the training dataset (dataset 1) as a function of a filter parameter (unit: s) (A–D) and a threshold (E and F). (A) Filter order M (η = 0.0001, σ = 0.5, L = 300), (B) kernel size σ (M = 100, η = 0.0001, L = 300), (C) step size η (M = 100, σ = 0.5, L = 300), (D) Parzen window size L (M = 100, η = 0.0001, σ = 0.5). (E) The event detection rate (EDR) and false discovery rate (FDR) of the peaks as a function of a threshold. These are the rates of the first spike in the burst. (F) The root-mean square error (RMSE) for first and last spike timings in a burst as a function of a threshold. In (E) and (F), the filter parameters are fixed at the optimal values (M = 100, η = 0.0001, σ = 1, L = 300).

3.2.2. Comparison of methods for reconstructing spike timings

The performance of the ME algorithm for reconstructing the first and last spike in a burst is compared with two methods: peak detection and temporal deconvolution (Yaksi and Friedrich, 2006). One simple approach (peak detection method) to infer inter-burst intervals is to detect calcium peaks and subtract sequential peak timings because every time a burst occurs, the calcium signal peaks, as shown in Fig. 1B. Note that estimation of the burst spike timings is impossible using this approach; the time difference between the calcium peak and the first or last spike in a burst is variable across events. For the peak detection method, we first removed the slow occurring variation in the calcium signal using a first order high-pass Butterworth filter with a normalised 0.05 Hz cutoff frequency and then sequentially smoothed the calcium signal to remove small fluctuations using a first order low-pass Butterworth filter with normalised 0.005 Hz cutoff frequency. We assumed that every peak was detected accurately. From the detected peaks, the inter-burst interval (IBI) was computed and used as a reference to compare performance between methods. In the temporal deconvolution method, we applied the same filters (high-pass and low-pass Butterworth filters) used in the peak detection method to pre-process the calcium signal. The optimal decay time constant f the exponential kernel, τ_decay, was estimated from dataset 1. Values ranging from 1 s to 10 s were applied to obtain an optimal value for τ_decay. The best performance (EDR = 100%, FDR = 0%, RMSE for first spike timing = 0.0793, RMSE for last spike timing = 0.2524) was obtained when τ_decay was 5 s and the threshold was 0.19. The parameters were fixed and applied to test sets. Fig. 4 shows the burst detection and estimated IBI distributions from the ME and two other methods applied to the test datasets. On the left side of the figure, the filter outputs (black) and detected peaks (blue) are illustrated with the actual bursts (red). We concluded that the ME method is more robust than the temporal deconvolution method with respect to noise; noisy calcium traces caused undesirable peaks in deconvolution. Increased robustness of the ME method is also supported by the results reported in Table 2, which lists the error performance of the three methods in terms of the EDR, FDR, and RMSE. In most datasets, the ME algorithm yields no or fewer falsely detected peaks than temporal deconvolution. The IBI distribution computed from the estimated first spikes are shown on the right side of Fig. 4. The distribution of the estimated IBI obtained by the ME algorithm is most similar to the actual distribution than those obtained using the two other methods. Overall, the performance of the ME algorithm is better than the peak detection and temporal deconvolution methods. The ME method can reconstruct the first spike timing more reliably and reduce the error by 25–55% compared to the temporal deconvolution method. Estimation of the last spike time in a burst was more challenging in both methods because the timing of the last spike is dependent on the threshold. The error for the last spike timing tends to increase as the ratio between the IBI and burst duration increases (data 4). Nevertheless, the error for the last spike timing in a burst of the proposed ME method was reduced by 40–60%, when compared to the temporal deconvolution method. The IBI was also more reliably estimated and the errors are reduced by 45–60% and 70–85% in the proposed ME method, compared to the temporal deconvolution and the peak detection method, respectively.

Fig. 4.

Comparison of three methods (ME, temporal deconvolution, and peak detection) tested using the four datasets (dataset 2–dataset 5). (A–D) left column: filter outputs (black), bursts (red) and detected peaks (blue dots) by thresholding; peaks with an estimated burst duration less than 0.15 s are removed. (A–D) right column: the actual IBI distribution and estimated IBI distributions obtained using the three methods. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of the article.)

Table 2.

Comparison of the methods: peak detection, temporal deconvolution, ME in terms of the RMSE, EDR, and FDR tested on four data sets (dataset 2–dataset 5).

Cell	Peak detection	Temporal deconvolution					ME blind deconvolution
	RMSE (ms)	RMSE (ms)			%		RMSE (ms)			%
	IBI	First Spike	Last Spike	IBI	EDR	FDR	First Spike	Last Spike	IBI	EDR	FDR
Data 2	312.1	80.4	339.0	111.2	100	12.1	41.5	190.2	50.3	100	8.93
Data 3	240.0	114.1	398.3	119.2	100	11.8	62.7	178.9	57.9	100	0
Data 4	235.0	84.4	445.6	95.2	94.4	24.4	63.4	261.0	51.8	89.0	5.88
Data 5	223.7	144.5	320.6	165.3	97.14	15.0	66.2	129.3	66.9	97.14	8.11

The normalised reconstructed firing rate from the two methods (ME and temporal deconvolution) and the reconstruction efficiency are displayed in Fig. 5. The reconstruction efficiency (represented by the correlation coefficient between the actual firing rate and the reconstructed firing rate) is computed based on work by Yaksi and Friedrich (2006). To represent the firing rate, the spike trains are convolved with the Gaussian kernel. The kernel size is set to 0.1 s, which is one-third of the average burst duration of the training data, and the kernel is truncated at three times the kernel size. We defined the reconstructed firing rate as the filter output processed with thresholding and shifting. This process improves the accuracy of the firing rate estimation because thresholding removes fluctuations in silent (no spike) regions and shifting aligns firing regions. The threshold is set to the same value as used previously (ME: 0.29; TD: 0.19) and the shift is determined using the training data (ME: 0.36 s; TD: 0.28 s). The results demonstrate that the reconstruction efficiency of both methods is comparable.

Fig. 5.

Normalised reconstructed firing rates and reconstruction efficiency of the ME and temporal deconvolution (TD) methods. Reconstruction efficiency is the correlation coefficient between the actual and estimated firing rates. Firing rate is the filter output processed with thresholding and shifting (threshold – ME: 0.29, TD: 0.19, shift – ME: 0.36, TD: 0.28).

Fig. 6 displays histograms of the absolute error for first and last spike timings and the IBI obtained using ME and the temporal deconvolution methods for all responses in the test datasets. The error from the temporal deconvolution method exhibits larger mean values and variance than the one obtained using the ME method. The first spike timing error and the IBI error are mostly <80 ms and <60 ms, respectively, when the ME method is used. On the other hand, the error for the last spike timing has higher dispersion but is mostly <300 ms. This time precision of the ME method is acceptable; the minimum IBI observed in the data was 886 ms.

Fig. 6.

Histograms of the absolute error for first spike timing (A), last spike timing (B), and IBI (C) obtained using the ME and temporal deconvolution methods (unit: s). These plots were obtained from all errors in the test datasets (dataset 2–dataset 5).

4. Discussion and conclusions

In the present study, we applied the blind deconvolution method to reconstruct the first and last spike timings in a burst by modelling the calcium signal as the response of an unknown linear channel when the input is a spike burst. We did not make any assumptions regarding the relationship between spikes and the calcium signal. Blind deconvolution was performed using an information-theoretic approach to maximise the output entropy of a nonlinear filter where the nonlinearity is set to the CDF of the spike firing rate.

Our study focused on quantifying the recently discovered intrinsically bursting olfactory receptor neurons, i.e., bORNs. Each bORN has its own spontaneous rhythm of activity. A bORN ensemble presumably has the capacity to encoding odour stimulus-related temporal information. Our preliminary modelling of bORNs indicates that this information is conveyed in the inter-burst interval rather than in individual spike timings. Therefore, the first spike timings in each burst are sufficient to model the role of bORNs. Our test results demonstrated that the ME method yields better performance in estimating the first and last spike timings in a burst and the IBI when compared to the temporal deconvolution (Yaksi and Friedrich, 2006) and peak detection methods. There are multiple plausible reasons for this. For the temporal deconvolution method, parameters such as the time decay constant vary across the cells. The time decay constant parameter estimated from the training data may be too small for some cells that have a long decay time constant, e.g., those found in datasets 3 and 4. In addition, high sensitivity to noise prevents the accurate detection of the events (dataset 4). For the peak detection method, the number of spikes in a burst may cause large variation in delay, but this is not considered when the intervals calcium between peaks are computed. The ME method was able to reconstruct the inter-burst interval with a mean error of approximately 45 ms from a 4.23 Hz sampled calcium image sequence. This means that the final ME timing resolution was improved fivefold when compared to the direct timing resolution given by the sampling period (236 ms). Furthermore, we can reduce the inter-burst interval error by more than 45% using the ME method when compared to the other two methods. The disadvantage of our method is that a threshold was used to detect the peaks and estimate burst duration. However, we showed that the threshold does not need to be adjusted for each new data set generated by the same type of neurons to reliably detect peaks. We did not investigate potential improvements by tuning this threshold to each new recording, but this procedure would be more time consuming.

Note that in our studies, we were not interested in the number of spikes and their relative timing within a burst; therefore, we used a 4.23 Hz sampling frequency for calcium imaging, which is rather low. With such a large gap in timing resolutions between spike sampling frequency and calcium imaging (a factor of 1000), we have not attempted to count or estimate spike timing. However, it should be noted that the accuracy of time estimates can be improved by higher temporal resolution images, and we expect that the fivefold improvement will be maintained with respect to the base sampling frequencies within a large range of frequencies (up to approximately 100 Hz). Therefore, if an application requires the number of spikes to be quantified, the experimenter can use ME accurately if the sampling rate of the calcium imaging is increased appropriately. Overall, the ME method can be a useful tool for inferring parameters of bursting neurons in general and, in particular, olfactory bursting neurons with great time efficiency and may increase understanding of the mechanisms and functions of bursting-based neuronal sensory coding.

HIGHLIGHTS.

• We propose a method for quantifying bursting neuron activity using calcium imaging.

• The method is based on blind deconvolution using the maximum entropy algorithm.

• We demonstrate that the proposed method is more robust than other conventional methods.

Appendix

To perform the ME blind deconvolution, the cumulative distribution function (CDF) of the spike firing rate must be determined. To estimate the CDF of the firing rate, spikes (0 or 1) are convolved with the exponential function truncated at t = 2τ defined as

$$r(t)=\frac{1}{\tau }exp\left(-\frac{t}{\tau }\right)$$ (1)

where τ is equal to the average burst duration and the kernel density estimation (Rosenblatt, 1956; Parzen, 1962) is used to estimate the CDF. The kernel density estimator is given by

$${\widehat{f}}_h(x)=\frac{1}{nh}\sum _{i=1}^n\kappa \left(\frac{x-x_i}{h}\right)$$ (2)

where κ(·) is the kernel function. Here, we use the Gaussian or normal density function for the kernel defined as

$$\kappa (x)=\phi (x)=\frac{1}{\sqrt{2\pi }}exp\left(\frac{-x^2}{2}\right)$$ (3)

The kernel size h is chosen based on Silverman’s rule of thumb given by

$$h=1.06\widehat{\sigma }{n}^{-0.2}$$ (4)

where σ̂ denotes the standard deviation of input samples and n is total number of samples.

Our methodology uses Renyi’s entropy instead of Shannon entropy because of the simplicity in estimating entropy from the data (Principe, 2010). Renyi’s entropy of order α for the output Z (Erdogmus et al., 2004; Principe, 2010) is given by

$$H_{\alpha }(Z)=\frac{1}{1-\alpha }log\int f_Z^{\alpha }(z)dz$$ (5)

where the limit when α → 1 yields Shannon entropy.

For α = 2, the entropy of the output Z is defined using quadratic Renyi’s entropy as

$$H_2(Z)=-log\int f_Z^2(z)dz.$$ (6)

When Renyi’s entropy is used as a cost function for adaptation as in this work, we can remove the logarithm because it is a monotonic function and will not affect the location of the extrema of the filter parameter space (Principe, 2010). In fact, maximising Eq. (6) is equivalent to minimising

$$V(Z)=\int f_Z^2(z)dz$$ (7)

where V(Z) is called the information potential. The information potential can be easily estimated non-parametrically using the Parzen density estimator, yielding (Principe, 2010)

$$\widehat{V}(Z)=\frac{1}{N^2}\sum _{k=1}^N\sum _{i=1}^N{\kappa }_{\sigma }(z_k-z_i)$$ (8)

where the kernel is chosen as the Gaussian function given by

$${\kappa }_{\sigma }(x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp\left(\frac{-x^2}{2{\sigma }^2}\right)$$ (9)

where σ is the kernel size. This methodology greatly simplifies our algorithm because it does not require a model for the PDF. Eq. (8) requires a batch approach and is quadratic on the number of samples. One can simplify this cost even further by working with the stochastic approximation of V(Z) (Erdogmus et al., 2003; Principe, 2010), which works with a window of L samples right aligned with the current sample, given by

$${\widehat{V}}_k=\widehat{V}(z_k)=\frac{1}{L}\sum _{i=k-L}^{k-1}{\kappa }_{\sigma }(z_k-z_i)$$ (10)

From Eq. (10), the stochastic gradient of entropy with respect to the weight vector W is computed as

$$\begin{array}{l}\frac{\partial {\widehat{V}}_k}{\partial \mathbf{w}}=\frac{1}{L}\sum _{i=k-L}^{k-1}{\kappa }_{\sigma }^{\prime }(z_k-z_i)\left(\frac{\partial z_k}{\partial \mathbf{w}}-\frac{\partial z_i}{\partial \mathbf{w}}\right)\\ =\frac{1}{L}\sum _{i=k-L}^{k-1}{\kappa }_{\sigma }^{\prime }(z_k-z_i)\left({\mathbf{x}}_K\frac{\partial z_k}{\partial y_k}-{\mathbf{x}}_i\frac{\partial z_i}{\partial y_i}\right)\end{array}$$ (11)

where z_k = F(y_k), y_k = w^Tx_k; W and X_k are M × 1 vectors and ${\kappa }_{\sigma }^{\prime }(x)$ is the derivative of the kernel function. By applying the online stochastic gradient descent learning rule, the weights are updated by

$${\mathbf{w}}_{k+1}={\mathbf{w}}_k-\eta \frac{\partial {\widehat{V}}_k}{\partial \mathbf{w}}$$ (12)

where η is the step size.