Abstract
The three-dimensional spatial arrangement of the cortical microcirculatory system is critical for understanding oxygen exchange between blood vessels and brain cells. A three-dimensional computer model of a 3 × 3 × 3 mm3 subsection of the human secondary cortex was constructed to quantify oxygen advection in the microcirculation, tissue oxygen perfusion, and consumption in the human cortex. This computer model accounts for all arterial, capillary and venous blood vessels of the cerebral microvascular bed as well as brain tissue occupying the extravascular space. Microvessels were assembled with optimization algorithms emulating angiogenic growth; a realistic capillary bed was built with space filling procedures. The extravascular tissue was modeled as a porous medium supplied with oxygen by advection–diffusion to match normal metabolic oxygen demand. The resulting synthetic computer generated network matches prior measured morphometrics and fractal patterns of the cortical microvasculature. This morphologically accurate, physiologically consistent, multi-scale computer network of the cerebral microcirculation predicts the oxygen exchange of cortical blood vessels with the surrounding gray matter. Oxygen tension subject to blood pressure and flow conditions were computed and validated for the blood as well as brain tissue. Oxygen gradients along arterioles, capillaries and veins agreed with in vivo trends observed recently in imaging studies within experimental tolerances and uncertainty.
Keywords: Hemodynamics, Oxygen perfusion, Capillary morphometrics, Microvasculature, Cerebral vasculature
INTRODUCTION
Oxygen transport is critical for the brain to meet the rapidly changing metabolic demands during neuronal firing. Neurovascular coupling is a mechanism for matching the rise in the mitochondrial oxidative metabolism of neurons with a local increase in cerebral blood flow.45 Recent studies have begun to uncover the significance of the spatial arrangement of the cortical microvasculature for oxygen supply.22,24,54 The morphology of cerebral microcirculation appears to play a significant role in ensuring adequate oxygen transport from the blood to brain cells.
A series of anatomical and physiological studies by Duvernoy, Cassot, and Lauwers delineated the morphometrics of blood vessels in the cerebral cortex.6,7,12,38 Their studies uncovered the particular arrangement of cortical blood vessels centering around pial draining veins which are irrigated by three to six penetrating arterioles.12 Recent topology studies confirmed the spatial allocation of the cortical microvasculature.3,22 Fresh arterial blood enters each territory through the leptomeningeal vessels depicted in Fig. 1a, which discharge into descending arterioles shown in Fig. 1b. From the cortical surface, descending—often also referred to as penetrating—arterioles dive into the gray matter carrying blood and oxygen deeper into the cerebral cortex. Figure 1c shows descending arterioles traversing the six cortical layers where they bifurcate into gradually narrowing binary trees, whose terminal leaves discharge into the capillary bed. The capillary bed does not conform to a binary tree, because it contains anastomoses which create loops. The multi-scale morphometrics of binary arterial and venous trees as opposed to the mesh-like capillary bed was studied in detail.42
FIGURE 1.
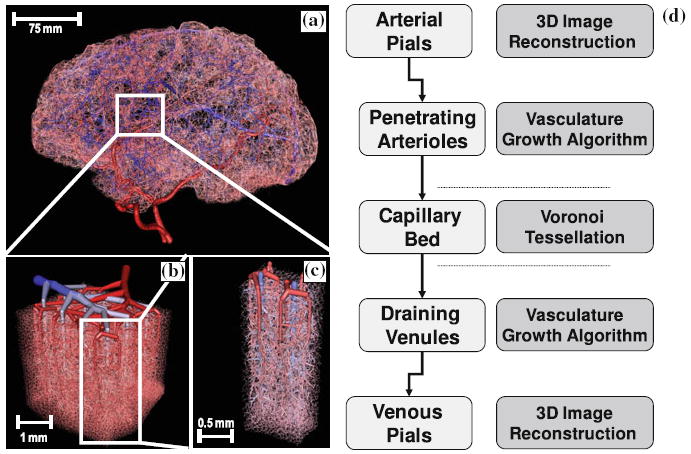
Overall multi-scale hierarchy of the human cerebral circulation. (a) Sagittal view of the full brain vasculature model generated in silico by combing image data with constrained constructive optimization. (b) Magnified section of the secondary cortex next to the collateral sulcus in the right temporal lobe, showing the arrangement of the network of pial arteries and veins at the cortical surface. (c) Isolated view of the territories of two draining pial veins supplied by six penetrating arterioles. (d) The construction principles for the computer aided construction and analysis of cerebral blood flow networks. This article is limited to structures ranging from the pial arterioles to the pial veins are discussed.
A single endothelial cell layer lines the capillary wall thus creating a large mass exchange surface between oxygen-rich blood and the extravascular space. Mass transfer also occurs between arterioles and venules.14,75 Red blood cells traveling with the blood stream carry oxyhemoglobin which can release free oxygen into the plasma. Oxyhemoglobin dissociation is facilitated by a basicity-mediated conformational change in hemoglobin. Blood pH is reduced by carbonic acid which is a byproduct of cellular respiration.30 Free plasma oxygen permeates the vessel endothelial layer and diffuses to brain cells driven by concentration gradients. Due to the mitochondrial oxidative metabolism, oxygen tension in the extravascular tissue is lower than in the blood stream.
However, oxygen exchange between the microvessels and the brain cells, especially with respect to the spatial arrangement of vessels, have not been fully quantified. Goldman proved that random and tortuous blood vessel networks greatly enhance mixing and oxygen distribution compared to evenly spaced, ordered vessel configurations.18 Boas developed in vivo optical measurements of tissue oxygenation in relation to cerebral blood flow. Their experiments are beginning to unravel the spatiotemporal characteristics of the blood flow and oxygen responses after neuronal activation.4,27 Their computational models also explored the evolution of tissue oxygen tension around a single cylindrical blood vessel, as well as for a more realistic anatomical microvessel network of the rat.14 Plouraboue reconstructed microvascular networks from synchrotron CT images to investigate coupling and robustness of intra-cortical vascular territories.20,22 Weber emphasizes the need for topologically accurate models to investigate the effect of local vascular dilation and occlusion on the flow in the surrounding network.24,54,61 Lorthois, Cassot and Lauwers demonstrated the quantitative relationship between the diameter of a pial draining vein and the size of the surrounding neuronal activated area.38,43,44
Anatomically and physiologically accurate computer models are an important tool for analyzing tissue metabolism coupled to micro-hemodynamics. Table 1 summarizes the characteristics of several recent microvasculature models. These computational methods can address the need for (i) better interpreting optical measurements acquired in open cranial windows in rodents,3,60 (ii) for exploring intracellular transport phenomena on length scales currently not accessible to imaging methods,34,35 and (iii) for making inferences for humans38,44 for whom invasive experimentation is not an option.
TABLE 1.
Overview of microvascular simulation models and their features.
| References | Species | Model characteristics | Number of vessels | Extracell. space | Venous tree | Capillary bed | Oxygen tension |
|---|---|---|---|---|---|---|---|
| This work | Human | Geometric construction, 3D | 256,000 | 600,000 | ● | ● | ● |
| Lorthois et al. 44 | Human | Image Segmentation. 3D | 10,318 | – | ● | ||
| Safaeian et al.59 | Human | Geometric Construction, 2D | 112 | – | ● | ● | |
| Lauwers et al.38 | Human | Morphometric Study, 3Da | 359,242 | – | ● | ● | |
| Zagzoule and Marc-Vergnes 78 | Human | Geometric Construction, 2D | 316,858 | – | ● | ● | |
| Guibert et al.20 | Marmoset | Image Segmentation, 3D | 16,000 | – | ● | ||
| Weber et al. 76 | Macaque | Morphometric Study, 2Da | NS | – | ● | ● | |
| Niimi et al. 47 | Cat | Image Segmentation, 2D | 45 | – | |||
| Goldman and Popel18 | Hamster | Geometric Construction, 3D | 11 | – | ● | ● | |
| Fang 14 | Rodent | Image Segmentation, 3D | NS | 600,000 | ● | ● | |
| Blinder et al.3 | Rat | Morphometric Study, 2Da | 200 | – | |||
| Reichold et al.54 | Rat | Image Segmentation, 3D | NS | – | ● | ● | |
| Boas et al. 4 | Rat | Geometric Construction, 2D | 254 | – | ● | ● | ● |
| Huppert et al. 27 | Rat | Geometric Construction, 2D | NS | – | ● | ● | ● |
| Kasischke et al. 34 | Mouse | Biophysical Study, 2D | NS | – | ● | ● | |
| Tsai et al. 70 | Mouse | Morphometric Study, 3Da | ~6,300 | – | ● |
NS Not stated in referenced work.
No Computations, morphometric studies only.
This work introduces a detailed three-dimensional computer model for cerebral microcirculation inside a subsection of the human secondary cerebral cortex. A network model was used to perform hemodynamic simulations of the microcirculation. The microvessel network was embedded inside the extravascular space to compute the oxygen exchange between blood and cortical brain tissue. Hemodynamic characteristics of blood flow, convective transport, and oxygen perfusion to the cortical tissue were predicted. In addition to computing blood oxygen tension, oxygen gradients around arteries and capillaries were predicted at different cortical depths. We validated critical morphometric and hemodynamic predictions against prior experimental studies in the open literature. Oxygen gradients predicted for a relatively large cortical domain (27 mm3 subsection of the secondary cortex in humans) matches trends observed in in vivo imaging studies.
MATERIALS AND METHODS
A three-dimensional model of the microcirculatory system inside a 3 × 3 × 3 mm3 subsection of the human secondary cortex was generated with principles illustrated in Fig. 1. The morphometrics of our artificial microcirculation matched human experimental data acquired with confocal microscopy by Lauwers,38 the comparison of the model with prior experiments are summarized in Fig. 2. The vascular network was embedded inside the porous brain tissue. For modeling the extravascular domain, we lumped the intracellular space, neurons and glial cells of the gray matter and meshed this space as a single continuum. Oxygen exchange between the blood and the porous tissue were computed by solving for advection, diffusion and metabolism simultaneously with custom-coded computer programs.
FIGURE 2.
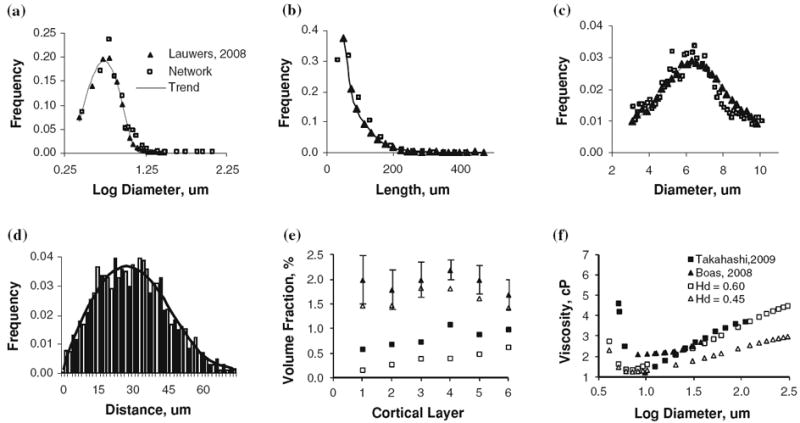
Summary and validation of morphometric properties and blood rheology of the microvessels of the secondary cortex next to the collateral sulcus in the right temporal lobe. Closed symbols show measured morphological properties with best fit solid line, open symbols show morphometrics of our artificially constructed microvessel structure. Panels a–d compare this work against morphological analysis of confocal microscopy work of the human secondary cortex.12,38 (a) Diameter distribution of all vessels in the microvascular network. (b) Length distribution of all vessels in the network. (c) Normal distribution of capillary vessels diameter with a mean diameter of 6 μm. (d) Histogram of distance to nearest capillary vessel in the cortical tissue, solid line shows polynomial best-fit. (e) Laminar distribution of volume fraction for vessels in cortical subsection, Triangles (Δ) indicate the total vessel pattern, squares (□) represent only the capillary spectra, compared with laminar network morphometrics obtained by scanning electron microscopy of corrosion casts of the macaque visual cortex.76 The volume density for the synthetic human microvasculature is lower than the macaque, as reflected in the values reported in Table 2. (f) Diameter dependent viscosity as determined by the Fahraeus–Lindqvist equation (Eq. 4) in comparison to values reported by Boas 4 and Takahashi.68 In the simulations, we used Hd = 0.45.
Microvasculature Construction
Because the spatial arrangement and hierarchal connectivity of all cerebral microvessels inside large domains such as the proposed cortical subsection of 27 mm3 are not easy to acquire experimentally,81 we generated an anatomically consistent computer model of cortical oxygen exchange. Customized vessel construction algorithms ensured proper topology of the microvessels and blood flow rheology. Different construction principles accounted for structural differences between arterial and venous trees, in contrast to the mesh-like capillary bed. The resulting computer model of the detailed microvascular network is a cyclic graph of logically connected cylindrical segments. Figure 1d gives an overview of the microvasculature construction principles used to generate the microcirculatory system.
Arterioles and Veins
A backbone of visible larger vessels was generated by geometric reconstruction from high resolution cortical images,12 which matches the morphology of the pial arteries. The conversion of image data into computational meshes is executed with image analysis techniques described elsewhere.40 Laminar microvessel density, diameter spectra, and capillary arrangement were used as the geometric basis for our model. In the model, the blood supply to the cortical subsection was provided by a single larger pial artery (inner diameter, di = 150 μm) and drained by only one pial surface vein (di = 180 μm), which compares well to the topological observations of the human brain.12 The pial network bifurcated into 36 penetrating arterioles (di = 40 μm ± 1 μm). The location of arteriole penetrations centered in circular patterns around 12 draining veins (di = 115 μm ± 5 μm), a spatial pattern originally discovered by Duvernoy. Penetrating arterioles descended from the cortical surface about 2.5 mm deep into cortex reaching down to the gray-white matter intersection.12
The backbone of penetrating arterioles was extended by sprouting additional arterial bifurcations into the six cortical layers. The smaller artificially generated segments were added using constrained constructive optimization (CCO) invented by Schreiner31-33,63 with desired segments-per-volume and fractal order.32,33 The location of the bifurcation coordinates as well as the hydraulic diameters of the two branching segment were determined, so that each terminal leaf of the emerging vascular tree discharged equal flow, yet whose blood lumen was minimal.31 During sequential segment addition, geometric constraints prohibit segment overlap, as well as enforce morphologically consistent bifurcation angles and smooth vessel diameter transitions.19,71 Optimal segment position was determined by solving the non-linear constrained optimization problem given in Eq. (1). Figure 3 illustrates the geometric optimization, where is the optimal position of the bifurcation fork leading to the minimum tree volume, di and li are the segment diameters and lengths, ΔP is the pressure drop, and Fi is the volumetric flow rate across segment i. Equality constraints enforce that overall tree dimensions and morphology satisfy the simplified flow equations. Note that this simple flow model is only used for constructing vascular trees, the actual hemodynamic simulations are described later in Eqs. (2)-(4). Microvascular tree growth involves random segment addition and the repeated solution of global minimization problems, until the diameters of terminal leafs in the gradually thinning binary tree narrowed to about 12 μm, the physiologic diameter of the pre-capillaries. Segment addition requires repeated solutions of Eq. (1) which we implemented with non-linear constrained optimization algorithms developed by our group.69,79,80 The resulting network is an acyclic binary graph composed of cylindrical elements, where N is the number of segments belonging to the tree.
FIGURE 3.
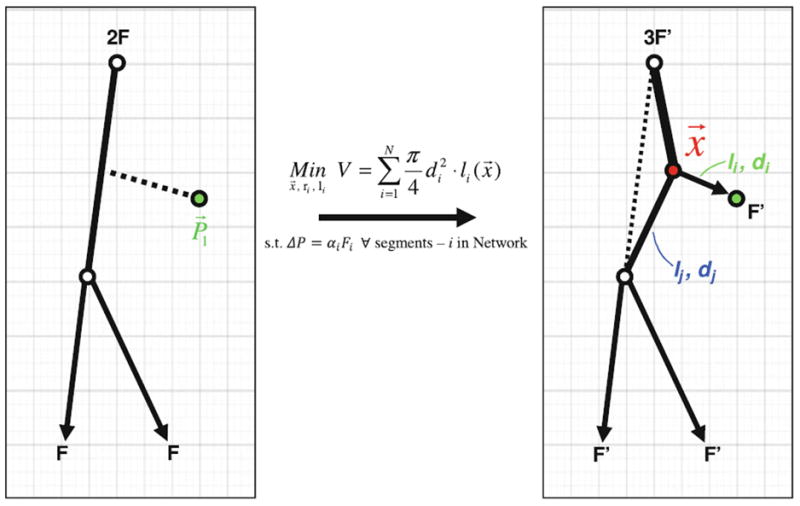
Schematic of a single vessel segment addition using the modified Constrained Constructive Growth (CCO) algorithm.63 Segment addition begins with the selection and connection of a point in the domain to the existing tree. The position of this connection point, highlighted in red, is optimized to create a tree with the smallest luminal volume. During the optimization, the diameters di and dj, as well as the lengths li and lj of the two daughter branches, are selected so that all terminal leaves discharge equal blood flow F. N is the number of segments belonging to the tree. The application of these optimization principles leads to networks with topological features similar to vascular structures.
Minimum tree volume optimization
| (1) |
For the venous drainage, tree generation was executed in reverse order until all tributary branches connected to the trunk of the single draining vein, which in turn discharged into the network of pial veins.
Capillaries
The capillary bed is not a tree, but a cyclic graph whose bifurcations and anastomoses form loops.39 Existing algorithms like CCO,31,63 angiogenic61,62,67 or fractal growth54 do not generate mesh-like capillary structures. We created anatomically realistic capillary beds by a novel triangulate-prune-smooth procedure. To build a capillary artifact with desired topology, the domain was meshed by tetrahedral Delaunay triangulation. The dual of the Delaunay mesh, known as a Voronoi mesh, was generated using TetGen.65 The edges of the each cell of the Voronoi dual mesh constitute the preliminary capillary network, and overall mesh structure was adjusted so that average Voronoi cell edge length was approximately equal to the desired mean capillary segment length. The implementation details of the novel computational method to synthesize realistic mesh-like capillary networks are given in Appendix 1.
Unfortunately, three-dimensional Voronoi meshes have trifurcations which occur rarely in vivo. To correct this, we removed one arc of each Voronoi cell, while avoiding the creation of dangling segments. This automatic pruning process ensured bifurcations in most junctions as observed in nature. In our final capillary bed, 86% of the 136,037 junctions were bifurcations. The perivascular space close to penetrating arteries exhibits a capillary-depleted zone as observed by Duvernoy12 and Kasischke.34 We accounted for a capillary-depleted zone in a radial distance of 50 μm around the larger penetrating arteries. Capillary vessels surrounding the vicinity of penetrating arterioles were removed only in the molecular layer.
The diameters of the preliminary Voronoi edges were smoothed for implementing a hemodynamically and anatomically sound normally distributed diameter spectrum found in real capillary beds,38 as shown in Figs. 2a–2e. Segments with pressures associated with the watershed between arterial and venous sides were assigned the smallest vessel diameters. An iterative averaging scheme was executed, resulting in smooth diameter spectra in the capillary bed according to the probability density function in Fig. 2b. To further procure realistic pressure drops, the degree of tortuosity of the Voronoi tessellation can be altered by deploying Bezier interpolation of the connecting arcs. Structural parameters of the tessellation, such as vessel density and edge length were controlled to ensure accurate morphometrics and realistic hemodynamic resistance. Additional information on Bezier arcs can be found in Appendix 2.
Furthermore, one study found that the density of microvessels does not match the strong variations in neuronal density,34 other studies did report variations in vascular densities in different cortical layers in both animal models76 and humans.38 Microvasculature density is an easily adjustable model construction parameter, and was tuned to the laminar volume fraction patterns observed by Weber76 as shown in Fig. 2e.
Using the tree and mesh construction principles described above, a closed network connecting penetrating arterioles through the capillary bed to the draining vein emerged. A partial view showing only two venous territories is shown in Fig. 4. Arteriole trees accounted for 8,388 segments, venous trees were composed of about 6,804 vessels, and the capillary bed is comprised of 241,697 segments. The entire microvasculature of the cortical subsection, shown in Fig. 5, had 36 descending arterioles, 12 draining venules, and a dense capillary bed which altogether totaled more than 256,000 segments.
FIGURE 4.
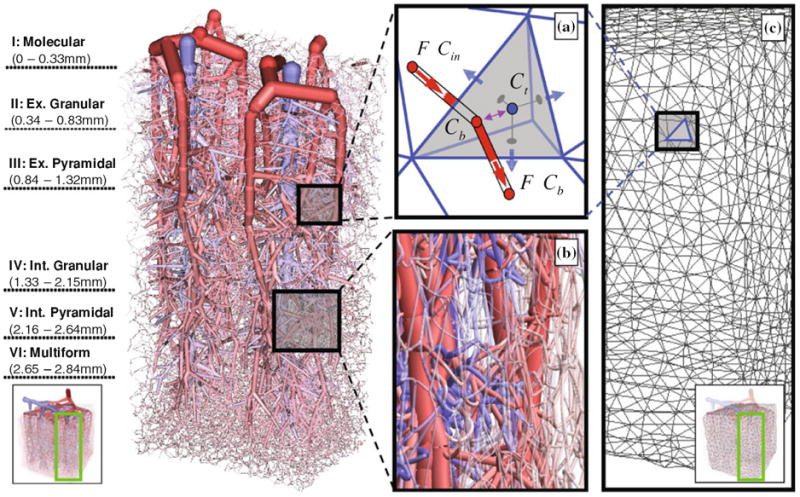
Partial view of the territories drained by two penetrating venules with their six descending arterioles as well as the capillary bed, cut out from the 27 mm3 subsection of the secondary cortex for better visibility. The six cortical layers of the extravascular space are occupied by brain tissue. The extravascular space is modeled as a porous medium into which oxygen is transported from the blood and metabolized by brain cells. (a) The nodal balance envelope encompasses the sum of half of the cylindrical volumes connected to it (red semi-cylinders). Blood convects oxygen with concentration Cin into a nodal volume and out with concentration Cb (red arrows). Oxygen exchange (purple arrow) occurs between the blood volume (node volume at Cb) and the extravascular tissue cell (tetrahedral cell at Ct). Oxygen can also diffuse freely inside the extravascular space (blue arrows). Oxygen diffusion and metabolism is solved by a finite volume method using an unstructured tetrahedral mesh. (b) Close up of microcirculatory pre-capillaries arterioles feeding the capillary bed, the site of oxygen mass exchange. (c). Detail of the continuous extravascular space composed of an unstructured tetrahedral mesh.
FIGURE 5.
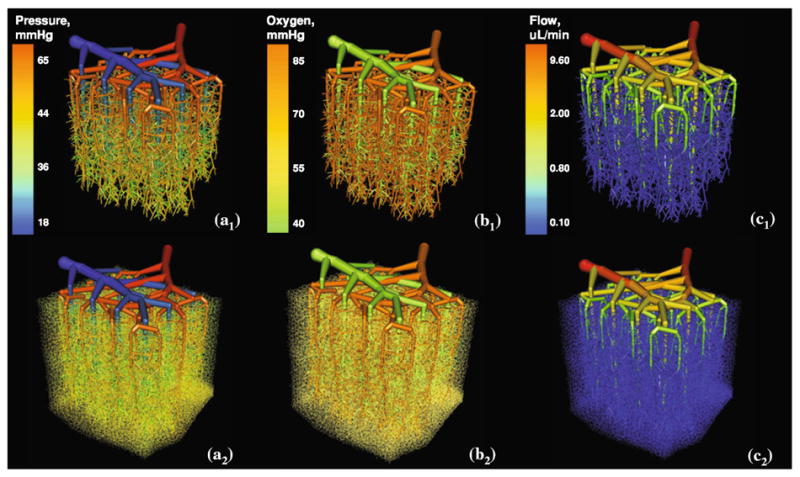
Visualization of a relatively large 27 mm3 subsection of the secondary cortex with computed steady state blood pressure, volumetric flow rate, and oxygen profiles projected onto the vessel architecture. Top row—larger vessels (capillary bed without showing small vessels, d <10 μm). Bottom row—all vessels, including capillary bed, are shown. (a) Blood pressure, (b). Oxygen tension, and (c). Volumetric blood flow value profiles.
Hemodynamics
Blood flow was described using established hemodynamic network models.52 Flow resistance of each cylindrical segment was approximated by the Poiseuille law as given in Eq. (3), where ΔP is pressure drop across a single segment, l is its length, d is the diameter, and α is the apparent blood flow resistance. The continuity equation was applied for each node shown in Eq. (2), where ū is the steady state flow per area entering or leaving a network node. Due to low Womersley numbers (Wo < 0.1), the pulsatile nature of cortical blood micro-flow can be ignored, and a quasisteady flow assumption is reasonable.1 Because of the low Reynolds numbers in microcirculation (Re < 1), inertia is also neglected in our simplified fluid flow model.16 The effect of biphasic blood rheology was approximated by the Fahraeus–Lindqvist equation in Eq. (4), which predict the apparent viscosity, ηvitro, as a function of diameter, d, and hematocrit,52 Hd, as shown in Fig 2f. Hematocrit distribution was assigned a constant value (Hd = 0.45). Viscosity is weakly dependent on hematocrit, as predicted by the Fahraeus-Lindqvist effect, at the diameter range investigated in this paper.51 For this reason, Pries’ in vitro model for diameter dependent viscosity was implemented instead of in vivo models which are very sensitive to hematocrit levels.51 Phase separation and plasma skimming are known to lead to lower hematocrit in microvessels (d0 < 100 μm) compared to the systemic hematocrit. We chose for this study to maintain the constant hematocrit, although methods of Plouaboue21 can be used to compute hematocrit variations in the blood flow network.
The pressure drop was set to 47 mmHg across the microcirculation from the pial arteriole (Parterial = 65 mmHg)13 to the draining venule (Pvenous = 18 mmHg).82 Capillaries at the boundary of our large cortical subsection were connected to similar size vessels at another boundary in the same cortical layer, thus implementing periodic boundary conditions. Due to the size of the computational domain, penetrating arteries and draining veins did not leave the subsection, thus not requiring special boundary closures necessary in thin computational models. The simultaneous solution of the discretized set of linear algebraic equations with Duff’s MA48 algorithm 10 gave the pressure distribution in the nodes; the blood flow velocities were determined with Eq. (2) for all segments. In this first paper, we chose not to incorporate the phase separation effect in order to keep the blood flow model simple. Models for the inclusion of phase separation effects are established,21 but still await experimental validation in the human cortex.
Blood Flow
| (2) |
| (3) |
| (4) |
Oxygen Transport
| (5) |
| (6) |
Oxygen Perfusion from the Cerebral Microvasculature to the Cortical Tissue
For simulating oxygen exchange between blood and surrounding brain cells with tractable problem size, we developed a novel dual mesh technique using two computational domains: (i) a vasculature network of cylindrical segments to account for arterioles, capillaries and venules described in the previous section and (ii) a volumetric brain mesh surrounding the vascular network to represent the cell matrix.
The vascular network contained about 256,000 segments. Blood oxygen tension was assigned to the node of each vascular segment; this choice produced a favorable staggering of the oxygen field in relation to the flow field which is computed on the edges. Each vascular network node is located in exactly one tetrahedral cell. However, a tetrahedral cell may contain multiple vascular nodes. The spatial relation between a vascular network node with oxygen tension, Cb, connecting two cylindrical vascular segments with their associated tetrahedral tissue cell with oxygen concentration, Ct, is depicted in Fig. 4a. The species conservation for each network node was balanced with Eq. (5), where Cb is the nodal oxygen concentration. Vb is the blood volume associated with each node, which is equal to half of the sum of the cylindrical segment volumes connected to the node, Cb. Sb is the surface area of the semi-cylindrical segments connected to node, Cb. The overall mass transfer coefficient, U, in Eq. (5) is a function of wall thickness, w, and the oxygen permeability of epithelial tissue Kw with values given in Table 2. Oxygen mass exchange is driven by the concentration difference between free oxygen in blood and oxygen concentration in the brain tissue, ΔCb−t. All molar oxygen concentrations were reported as partial pressures, assuming a temperature of 37 °C, pH = 7.4, and the empirically derived gas solubility constant of 0.003 mL O2/100 mL/mmHg2.
TABLE 2.
Morphometrics of the computer network compared to prior work.
| Parameter | This work | Literature | Animal | References |
|---|---|---|---|---|
| Vessel Density | 9,487/mm3 | 7,473–14,069/mm3 | Human | Lauwers et al. 38 |
| 4,991–9,140/mm3 | Primate | Risser et al. 56 | ||
| Surface Area/Volume | 13.60 mm2/mm3 | 10.19–12.85 mm2/mm3 | Human | Lauwers et al. 38 |
| 4.04–5.84 mm2/mm3 | Marmoset | Risser et al. 57 | ||
| 13.3 ± 3.2 mm2/mm3 | Cat | Pawlik et al. 50 | ||
| 5.19–7.24 mm2/mm3 | Rat | Risser et al.57 | ||
| Capillary Diameters | 6.46 ± 2.7 μm | 6.66 ± 1.70 μm | Human | Lauwers et al. 38 |
| 7–9 μm | Human | Duvernoy et al.12 | ||
| 5.91 ± 1.30 | Human | Cassot et al.5 | ||
| 5.0 μm | Cat | Zweifach and Lipowsky 82 | ||
| Mean Capillary Length | 56.16 μm | 52.95 ± 49.75 μm | Human | Lauwers et al. 38 |
| 57.37 ± 50.98 μm | Human | Lorthois et al. 44 | ||
| Vascular Fraction | 2.49% | 2.43–3.02% | Human | Lauwers et al. 38 |
| 3.19% | Marmoset | Risser et al. 56 | ||
| 2.52% | Rat | Reichold et al. 54 | ||
| Cortical Perfusion | 64 mL/100 g/min | 51–65 mL/100 g/min | Human | Rostrup et al. 58 |
| 60 mL/min/100 mL | Rat | Reichold et al. 54 | ||
| Pial Arteriole Blood Velocity | 14 mm/s | ~14 mm/s | Cat | Lipowsky 41 |
| 9.2 ± 4.8 mm/s | Rat | Nishimura et al. 48 | ||
| Arterial Oxygen Tension | 85 mmHg | 82.4 ± 3.5 mmHg | Rat | Vovenko and Chuikin 74 |
| 94 ± 18 mmHg | Mouse | Kasischke, 34 | ||
| Capillary Oxygen Tension | 50 mmHg | 50–60 mmHg | Rat | Vovenko and Chuikin 74 |
| 28 ± 11 mmHg | Mouse | Kasischke, 34 | ||
| Microvasculature Pressure Drop | 47 mmHg | 52–78 mmHg | Human | Espagno et al. 13 |
| 50 mmHg | Cat | Guibert et al. 20 | ||
| 70–35 mmHg | Cat | Zweifach and Lipowsky 82 | ||
| Transit Time | 0.41 s | 0.61 s | Human | Sorenson 66 |
| 0.51–0.75 s | Human | Yang et al. 77 | ||
| 1.1 ± 0.4 s | Human | Gjedde et al. 17 | ||
| CMRO | 8.2 × 10−4cm3O2/cm3/s | 8.2 × 10−4cm3O2/cm3/s | Human | Mintun et al. 45 |
| Tissue Diffusivity (D) | 1.8 × 10−5cm2/s | 1.8 × 10−5cm2/s | Human | Mintun et al. 45 |
| Epithelial Permeability (Kw) | 5 × 10−8uL/mm/s/mmHg | 5 × 10−8uL/mm/s/mmHg | Rat | Vovenko 73 |
| Capillary Wall Thickness (w) | 1 μm | 1 μm | Human | Nolte and Sundsten 49 |
| Arterial Wall Thickness (w) | 2–10 μm | 2–10 μm | Rat | Rakusan and Wicker 53 |
| Venous Wall Thickness (w) | 0.5–1.5 μm | 0.5–1.5 μm | Rabbit | Rhodin 55 |
| Arterial Inlet Pressure | 65 | 60 | Cat | Lipowsky 41 |
| Venous Outlet Pressure | 18 | 25 | Cat | Lipowsky 41 |
The vascular network was co-registered in the same spatial domain with an unstructured tetrahedral brain mesh as seen in Fig. 4. The volumetric mesh representing the extravascular space was modeled as a single continuum with extracellular and intracellular space lumped together. The brain mesh was grouped into six cortical layers with the following depths scaled from imaging data38 to the depth of 2.5 mm: 0–0.33 mm (I: molecular), 0.33–0.83 mm (II: external granular), 0.83–1.32 mm (III: external pyramidal), 1.32–1.68 mm (IV: internal granular), 1.68–2.02 mm (V: internal pyramidal), and 2.02-2.50 mm (VI, multiform). The finest mesh with 600,000 tetrahedral elements had an average edge length of 34 μm. We computed the oxygen concentration for each tissue cell, Ct, by solving the oxygen conservation balance in Eq. (6). Here Vt is the volume of extravascular space, which is equal to the tetrahedral volume reduced by the outer lumen of all blood network nodes contained in the cell. Oxygen transfers from the blood into the tissue as a function of the concentration, ΔCb−t. Since each tetrahedral tissue cell may contain multiple vascular network nodes, Eq. (6) sums the mass transfer into the tissue cell from M vascular nodes. Oxygen is also consumed at a cellular metabolic rate. The metabolic oxygen demand for normal brain activity45 expressed as the cerebral metabolic rate of oxygen consumption, was set to CMRO = 8.2 × 10−4cm3O2/cm3/s. Oxygen is further free to diffuse in the extravascular space, ∇D ∇C with diffusion coefficient,45 D = 1.8 × 10−5 cm2/s. All parameters and constants are listed in Table 2.
The boundary conditions for the oxygen exchange simulations include a constant pial oxygen partial pressure of, Cin = 85 mmHg. For the gray-white matter interface we assumed zero oxygen exchange. All boundaries of the large cortical subsection were assigned symmetric boundary conditions as shown in Eq. (6). Table 3 summarizes all types of boundary conditions and values for the vascular network and tissue domains.
TABLE 3.
Boundary conditions.
| Physiological description | Boundary type | Value |
|---|---|---|
| Pial artery inlet (Parterial), di = 38 μm | Dirichlet | 65 mmHg |
| Pial vein outlet (Pvenule), di = 100 μm | Dirichlet | 18 mmHg |
| Oxygen tension at pial inlet | Neumann | 80 mmHg/s |
| Capillary bed domain edge (A) | Periodic | – |
| Capillary bed domain edge (B) | Neumann | Symmetry (No Flux) |
| Cortical tissue domain edge | Neumann | Symmetry (No Flux) |
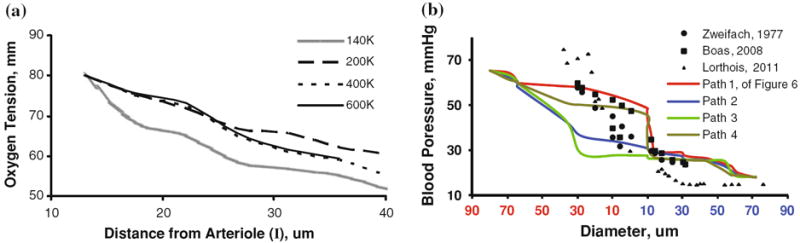
Oxygen exchange between blood and tissue was solved simultaneously after full discretization of Eqs. (5)-(6) over the two domain meshes using finite volume techniques developed by our group.39 Repeated simulations with increasingly fine meshes, ranging from 140,000 to 600,000 volumetric elements, established mesh-independence at 400,000 elements as shown in Fig. 6a. The steady state spatial distribution of oxygen in the tissue (400,000 equations) and the vascular network (256,000 equations) was solved simultaneously (656,000 equations) with an iterative SOR29 method. The simulation solved on a 2.8 GHz Intel Core 2 Duo processor in less than eight CPU minutes.
FIGURE 6.
Mesh independence study and blood pressure validation. (a) Model prediction of extravascular oxygen gradient in the capillary-depleted cylinder surrounding a descending arteriole (I)—discussed in detail in Fig. 6—as a function of mesh density. Predicted oxygen tension stabilized after increasing the number of tetrahedral elements from 400,000 to 600,000. All results are reported for the 400,000 element mesh. (b) Microvasculature pressure gradients of multiple paths (paths 1–4 introduced in Fig. 6) from a penetrating arteriole to its corresponding draining venule of our subsection of the secondary cortex, compared to point measurements made to animal and computational models. The chosen pressure boundary conditions or pial arterioles (Parterial = 65 mmHg) to the draining venule (Pvenous = 18 mmHg) govern the pressure drop of the model. Trends compares well against empirical results82 and models4 with similar boundary conditions.
RESULTS
Morphometrics
The statistics of Figs. 2a–2e summarize the morphological validation of the cortical microvasculature in terms of vessel density, diameter, and length.38 The mean capillary diameter of 6.46 ± 2.7 μm agrees well with reported values38 of 6.47 μm, as shown in Fig. 2c. The mean distance between capillaries reported in Fig. 2d is 16–46 μm compared to 24–42 μm reported in previous work.26,34 73% of the tissue elements are no further than 40 μm away from the nearest blood vessel. Laminar volume fractions in Fig. 2e for the cortical subsection microvasculature match vascular topology studies by Weber, however the human trends are somewhat below those found in the macaque cortex.76 Table 2 lists a vascular density of 9,487 vessels/mm3, compared to 7,473–14,069 vessels/mm3 in prior human ex vivo measurements.38 Segment length per unit volume was 601 mm/mm3, which lies within two standard deviations above an empirical ex vivo measurement in the human cortex.38 The volume ratio of vessel lumen to surrounding extravascular space was 2.49%, comparing well to the range of 2.4–3.2% reported in other microvasculature studies shown in Table 2. The capillary volume density is 1.43%; which compared well to the 1.0–1.5% capillary volume fraction reported in the literature.38,76 The lumen ratios between the arteriole, venous and capillary compartments were 29.4, 10.8 and 59.7%, which matches measurements in microvascular4 and whole brain studies.11,28
Flow and Oxygen Exchange in the Entire Subsection
The simulation results for blood flow and oxygen tension in a large cortical section are summarized in Fig. 5. For clarity, the top row shows only the arterial and venous tree without capillary bed, the lower depicts the same results including the capillary bed. The blood flow simulations, the pial arterial inlet pressure was set to 65 mmHg, the pial venous drain had 18 mmHg.
Currently the experimental evidence for pial arterial pressure in humans in scarce. Espagno13 performed blood pressure measurement on cortical arteries of several dozen patients prior to removing cortical tumors. Averaged pressure measurements in “sub-millimeter” pial arteries, without precisely specifying the diameters vary over a range. The blood pressure throughout the entire microvasculature subsection of the cortex are shown in Fig. 5a. A comparison of pressure drops to three models by other researchers is shown in Fig. 6b. The scarcity in the experimental evidence about pial blood pressures is reflected by the wide variations among different models. However, the overall trends seem to be similar, except for choices in boundary conditions. The differences between predictions for microcirculatory models are expected to align better as soon as reliable pressure measurements become available. The volumetric blood flow rate is depicted in Fig. 5c. The oxygen tension in the microvasculature of the entire domain gradually drops from 85 mmHg in the pial artery down to 40 mmHg in pial vein as depicted in Fig. 5b. The redirected oxygen extraction compares well to cortical measurements.73 To better analyze the flow and oxygen tension in detail, we turn next to the territory of a single draining vein in the interior of the subsection and its tributary arterioles.
Microvascular Blood Pressure
Hemodynamic simulations for a pressure drop between penetrating arterioles and draining vein of 40 mmHg are depicted in Fig. 7a. Pressure drops in the territory were computed as 8.2 ± 2.1 mmHg across the arteriole tree, 20 ± 1.3 mmHg across the capillary bed, and 9.3 ± 1.6 mmHg across the venous side. Accordingly, the capillaries offer the largest flow resistance.
FIGURE 7.
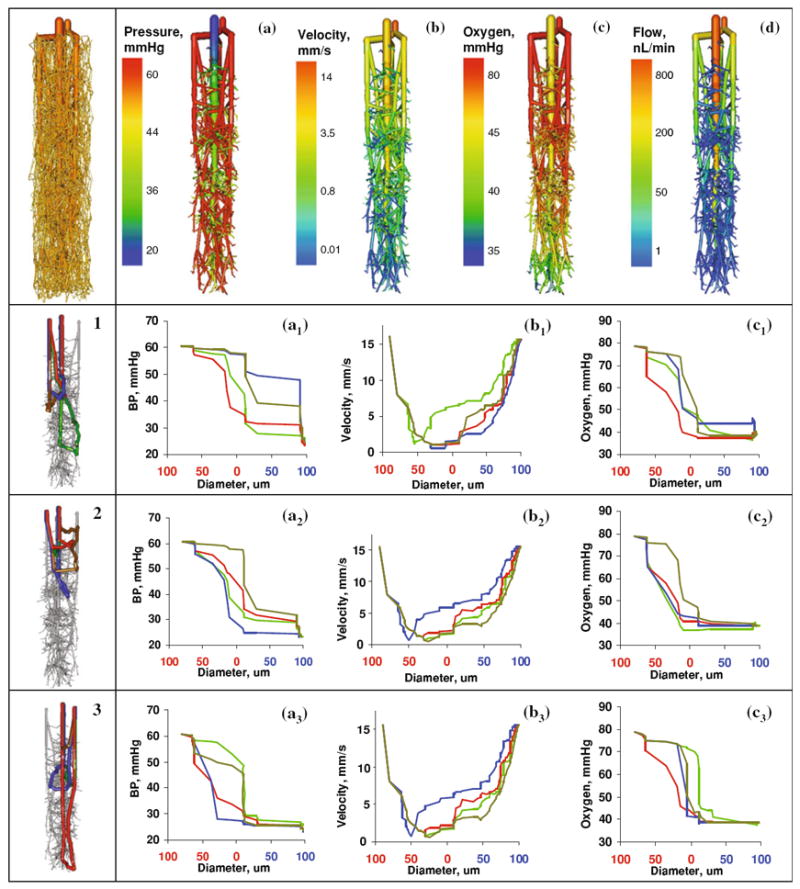
Detailed study of hemodynamics of a typical vascular territory of a single draining vein with its associated arterioles and capillaries. (a) Blood pressure distribution. (b) Blood flow velocity. (c) Blood oxygen tension. (d) Volumetric blood flow rate. Analysis of twelve distinct paths a single red blood cell may take when traveling from a feeding descending arteriole to a nearby draining venule. Panels 1–3 each depict four typical sample paths chosen randomly, colored blue, green, yellow, and red. In total there are >236,000 number of paths for a single territory.
Blood Flow and Velocity Predictions
Blood flow through a single draining venule was predicted as 800 nL/min as shown in Fig. 7d; this number equals a perfusion of 68 mL/100 g/min. This simulation blood perfusion result agrees with experimental values of 50–70 mL/100 g/min found in the open literature.58 Blood velocity can be established as 15 mm/s at the arteriole inlets, 0.1 mm/s in capillary vessels and 14 mm/s at the venous outlet as shown Fig. 7b. These predictions compare well to prior velocimetry studies which measured arteriole blood velocity at 14 mm/s.41
Hemodynamic State Changes Along Multiple Erythrocyte Paths
We further investigated hemodynamic state properties along multiple paths of red blood cells traveling from the penetrating arterioles to the draining vein. Alternate pathways commenced at pial surfaces then descend into the penetrating arterioles, traversed the capillary labyrinth, and finally terminated at the draining vein. At each junction, a random choice among alternative downstream paths was made, and the hemodynamic states—blood pressure, velocity, and oxygen content—along the itinerary were recorded with results visualized in Fig. 7. A total of more than 236,000 different paths were identified connecting a penetrating arteriole to the draining vein. Twelve typical samples were selected as illustrated in panels 1–3 of Fig. 7. Path lengths varied from 1.78 to 6.81 mm. Figure 7a demonstrates that the blood pressure decreases monotonically in all paths; yet the profiles are not identical. Figure 7b depicts that the blood flow velocity is highest in the penetrating arterioles, va = 15 mm/s, at a minimum in the capillaries, vc ~ 100 μm/s, and again rises in the draining vein, vv = 14 mm/s, which has been qualitatively observed in previous studies.78 Blood pressure dropped about 40 mmHg from the penetrating arteriole to the corresponding vein.
Simulated Transit Times
We determined dynamic trajectories of contrast agent infused into the cortical microcirculation to quantitatively analyze transit time behavior similar to a clinical angiography exam (figures not shown) with Eq. (7). The mean transit time between the inlet penetrating arteriole (di = 39 μm) and the draining vein (di = 120 μm) was found to be, τ = 0.4 s. This value reported in Table 2 falls within the range of human microvasculature transit times.17,66,77
Dynamic Contrast Agent Dilution
| (7) |
Axial Oxygen Gradients
Axial gradients across microcirculatory paths inside the territory of a single draining vein are depicted in Fig. 7c. The computations show the gradual drop in arteriole oxygen tension from the penetrating arteriole of 80 mmHg to 40 mmHg in the draining vein. These numbers are similar to trends in oxygen tension found for the rodent cortex.73 There is a wide spectrum of path lengths through the microcirculation. We also found that longer paths tend to leave the capillary bed with lower oxygen tension than shorter paths. The venous mixing effect resulting from capillary inflow with varying oxygen tension was predicted by the network model and has been well established experimentally.74 In our model the arterioles contributed 20% of the total oxygen extraction, while the bulk occurred in the capillary bed. These fractions of oxygen extraction match the 20% reported by Vovenko and Popel.64,73
Radial Oxygen Perfusion Profiles
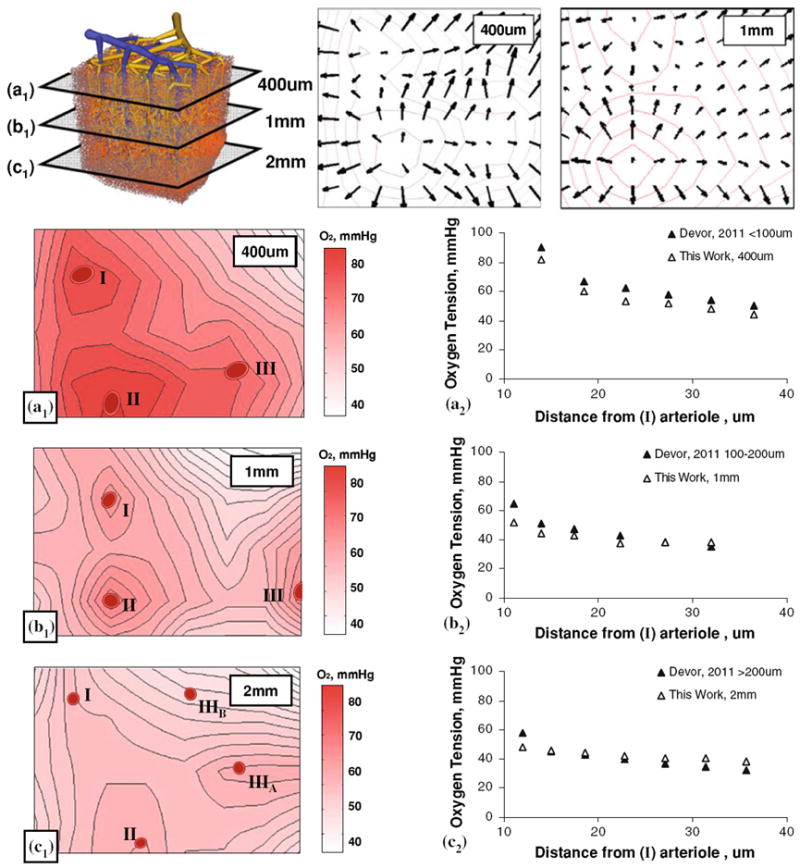
Radial oxygen perfusion profiles in the tissue were assessed as a function of radial distance to the nearest blood vessel. As shown in Fig. 8, a single penetrating arteriole marked as (I) was selected as a vessel of interest. Its perivascular oxygen tension field was traced as it descended through the cortical layers. Radial oxygen gradients were captured for this penetrating arteriole in the molecular, external pyramidal and internal pyramidal layers. To better assess the evolution of oxygen tension profiles, laminar tissue slices of the microvascular subsection were created and contour maps of the oxygen tension field were generated. We also produced a display of the tissue oxygen gradient fields (vector field depicted by arrows) for the 400 μm and 1 mm laminae of the cortical tissue shown in the top row of Fig. 8. The radial oxygen gradients around the penetrating arteriole were higher near the cortical surface than in deeper regions. Radial oxygen tension in the molecular layer ranged from 80 mmHg at a distance of 10 μm, to 45 mmHg at 50 μm distance. The oxygen tensions in the external and internal pyramidal layers were ~50 mmHg at 10 μm, to 40 mmHg at 50 μm of distance as shown in panels A, B, and C of Fig. 8. The computed profiles agreed with the trends of laminar oxygen gradients obtained in the rodent cortex.9,14 These oxygen gradients seem to be a result of the capillary-depleted regions adjacent to larger arterioles. The high oxygen tension in the perivascular space make it plausible why there is no need for capillaries close to arterioles.
FIGURE 8.
Radial oxygen gradient as a function of cortical depth 400 μm (a), 1 mm (b), and 2 mm (c) below the cortical surface. Top row also shows the oxygen tension gradient in the molecular layer (a) as a vector field at 400 μm and 1 mm. In-plane radial oxygen gradients of three arterials (I–III) are displayed in the left hand column (Panels A1, B1, C1). The right hand column shows in-plane oxygen tension as a function of distance to arterioles (I). The simulated oxygen gradient agrees with trends observed in vivo in the rat cortex9 in panels A2 to C2.
We also simulated oxygen tension in regions embedded in the dense capillary mesh, but situated further away from larger blood vessels. Our simulations for regions without larger vessels show shallow oxygen profiles, completely flattening about 30 μm away from the nearest capillary. We also investigated whether intracapillary gradients became steeper with higher oxygen demand. To emulate this effect, we adjusted the parameters CMRO within physiologic ranges. The parameter sensitivity studies as a function of CMRO revealed that the level of oxygen tension dropped with increasing metabolic demand (Results not shown).
DISCUSSION
We presented a computer model to predict oxygen exchange between the microvasculature and brain cells in a relatively large cortical subsection. We developed a novel dual mesh technique to overcome problem size limitations that would be required in simulations with a single computational mesh smoothly connecting microvessels and brain cells at the length scale of individual capillaries. The use of two distinct coarse overlapping meshes avoided the need for a contiguous mesh sharply separating both compartments. The numerical quality of the method was established with mesh independence studies and validation against the analytical approaches. Our novel method applied to a relatively large cortical subsection captured every single blood vessel including all capillaries, yet kept the problem size for steady blood flow as well as oxygen exchange between blood and tissue tractable.
We also introduced a novel method to build pial and cortical arterial as well as venous trees by combining real image data with a modified CCO technique to synthesize blood vessels below the image resolution. We further presented a new method to create an anastomosed capillary bed based on Voronoi tessellation. We described the step-by-step construction mechanism as well as the mathematical operations to attain desirable properties such as segment length, degree of tortuosity and smooth diameter transitions from pre-capillaries to post-capillary venules. The capillary bed algorithm offers consistent closure to microcirculation models with a physiological basis significantly advancing prior models limited to arterial trees, or merely using mathematical arguments to “close” the system equations without anatomically consistent representation of the capillary bed.
Our morphologically accurate, physiologically consistent, multi-scale computer network model of the cortical microcirculation encompasses the spatial arrangement of all cerebral vessels ranging from the pial arterioles and venules down to the level of individual capillaries as well as the surrounding extravascular space. Distribution of vessel blood pressure, flow, velocity and oxygen tension in both vessels and cerebral tissue were predicted in three dimensional spatial coordinates. A detailed comparison with prior experiments as well as the extensive compilation of earlier models demonstrates that our large models matched known literature values for blood flow, blood flow velocities, cerebral blood flow per volume and trends of pressure distribution. The large portion of blood flow resistance predicted for the microvascular bed implicate capillaries as an effective location for blood flow control, and in effect also an ideal actuator site to regulate oxygen supply. Small changes in capillary lumen or boundary layer resistance41 would very sensitively impact flow distribution and indirectly control oxygen exchange.
Perivascular oxygen gradients were found to be flatter in deeper pyramidal layers compared to the molecular layer closer to the cortical surface. Our model also quantified the gradual oxygen extraction along penetrating arterioles; a trend observed previously in the cortex of animals. The predicted three-dimensional oxygen distribution also showed larger oxygen gradients around arterioles, whereas areas distant of larger blood vessels exhibited flatter oxygen gradients. Also, the oxygen tension around capillaries appears to be almost uniform. It seems plausible that the random arrangement of the cortical microvasculature is capable of ensuring adequate oxygen levels for neurons irrespective of their location in the cortex.
The flatter profiles in deeper cortical layers should not be mistaken for lacking oxygen gradients between the extra- and intracellular compartments. The current tissue model does not distinguish between the extra- and intracellular spaces. Consequently, the mass transfer from the extracellular compartment through the cell membrane to the site of mitochondrial metabolism of oxygen are currently not resolved in our computations. Instead, a simplified first order cellular metabolism rate has been assigned to the lumped extravascular compartment. Intracellular oxygen gradients and oxygen tension in the mitochondria have not been addressed in this study.
Our simulations are carried on such a large computational domain without cutting large vessels so that the resolution of the boundary interface for the capillary vessels and the tissue elements does not impact the results in the interior. Our large scale approach also addresses the call for a new methodological framework to reduce the number of boundary nodes. Our in silico subsection of the brain has a very small number of boundary nodes, roughly 3.0% for the vascular network and only 2.2% for the tissue mesh. A large model with only a small fraction of boundary nodes frees the analysis from the burden of engineering specific boundary conditions for each vessel group; a process which runs the risk of importing undue boundary effects into the computational domain.
Future work should include more complete cellular metabolic mechanisms involving ATP production, glucose, CO2 transport, and pH calculation. A two phase model for the bound and free oxygen could be incorporated by considering the relationship between oxygen concentration and oxygen tension as described by the Hill equation.23 Moreover, the formation and dissociation of carboxylic acid is a major factor in controlling pH levels, which affects the oxygen binding kinetics of hemoglobin. Future models should also easily incorporate variable hematocrit. Pulsatile blood flow through compliant blood vessels would allow for open and closed loop control of cerebral blood flow, and more interestingly oxygen dynamics to better elucidate BOLD signals in functional MRI. Detailed dynamics of vasodilation and vasoconstriction in cerebral autoregulation have also not yet been addressed in this work. Regional activation of specific cortical layers requires closed loop dynamics of autoregulatory control, possibly through oxygen-chemo-receptive neurons which release biochemical signaling agents such as nitric oxide or catecholamine.46
Our model elucidates the role of the three-dimensional spatial arrangement of the microcirculation on cortical oxygen supply. Extensive literature validation confirmed the model’s ability to match hemodynamic and oxygen tension trends within experimental tolerances and uncertainty. Using the proposed dual mesh techniques, it is conceivable that a biological simulation encompassing each brain cell will become tractable in the near future.
Acknowledgments
The authors would like to gratefully acknowledge NIH for their financial support of this project, NIH-5R21EB004956. The project was also partially supported by NSF grants CBET-0756154 and CBET-1301198.
APPENDIX 1: GENERATION OF MESH-LIKE CAPILLARY BED
We invented a novel computational method to synthesize mesh-like capillary networks. A mesh-like capillary bed connected to the arterial and venous trees is essential for the anatomically consistent closure of hemodynamic simulations with the following key properties: (i) even random spacing of desired average segment length (ii) connection to arteriole and venule terminals (iii) adjustable degree of tortuosity, and (iv) smooth diameter transitions from the pre-capillaries to post-capillary venules. To the best of our knowledge, this algorithm for capillary synthesis has never been proposed in the literature.
The methodology encompasses a six step procedure illustrated Fig. 9 frames a–e. In the first step, the computational domain between the terminal nodes of the arterial (a1, a2) and venous (v1) trees is evenly divided by Delaunay triangulation.8 The Delaunay mesh creates an even partition of the intravascular space. This partition is shown in Fig. 9a by triangles for clarity. The new Delaunay nodes are more densely spaced than the arterial and venous terminals (a1, a2, v1). The number of Delaunay nodes controls the desired average capillary segment length in the emerging capillary bed. It is tempting to use the Delaunay edges directly as capillary segments. However, the branching factor of three-dimensional Delaunay meshes is not physiological, easily exceeding 50 edges per node in complex brain geometries, while real capillary meshes have only bifurcations (branching factor of two).
FIGURE 9.
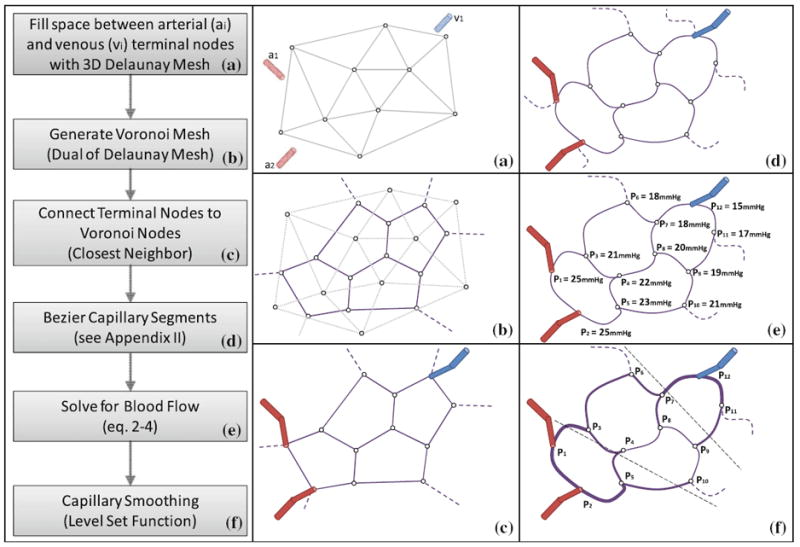
Stepwise construction of capillary beds. (a) Delaunay triangulation of the space between the terminal nodes of the arteriole tree (a1, and a2) and the venous tree (v1). Mesh density (shown as triangles for clarity) controls the segment length of the desired capillary bed. (b) Construction of Voronoi tessellation, which is the dual of the Delaunay mesh. (c) Connection of arterial and venous terminal to the closest neighbor capillary node. (d) Bezier curve approximation of capillary segments to adjust desired degree of tortuosity. (e) Network flow simulation yields a pressure field to determine the mean capillary pressure, P. Segments within a desired pressure range, P ± 2σF, are assigned the smallest capillary diameter, Dmin = 3 μm. (f) Diameters of capillary segments are according to an iterative averaging scheme, producing smooth transitions form the pre-capillary arterioles to the post–capillary venules. Steps E to F can be repeated to eliminate sharp diameter transitions at the inlets and outlets of the capillary bed.
Therefore, we construct the dual mesh, know as a Voronoi tessellation,72 as depicted in Fig. 9b. The Voronoi cells have branching factors of two in two dimensions, and three in for three dimensions. To provide closure, each arterial terminal is connected to the closest capillary node. Similarly, each terminal node of the venous tree is linked to the Voronoi mesh without allowing a venous and an arterial terminal to connect to the same capillary node. In effect, the arterial and the venous trees are linked through the capillary bed creating a closed network structure without dangling segments. The crude Voronoi capillary mesh depicted in Fig. 9c requires three more refinement steps for better physiological match with real capillary beds.
In every capillary node with more than three segment connections, one superfluous segment can be deleted. This process we term pruning is required only three dimensional Voronoi meshes (not shown). We choose to eliminate the shortest edge, whose removal does not leave another node connected to the deleted edge dangling. We refrained from pruning Voronoi trifurcations in which no edge can be removed without causing dangling capillary nodes.
Several researchers have pointed out the significance of the tortuosity in hemodynamic simulations.18 Optionally, we can control tortuosity of capillary segments by Bezier curve interpolation, as depicted in Fig. 9D with detailed mathematical description given in Appendix 2.
The pruned, tortuous capillary bed still requires the reasonable diameters for each segment. A simple choice is constant diameters for all segments, but has the disadvantage of sharp transitions from the arteriole tree to the capillary bed, and from the capillary bed to the venous tree. We propose to enforce smooth diameter transitions with slight tapering coming from the arteriole side and slow diameter increases towards the venous side as follows: We perform blood flow simulations as in Eq. (2)-(3) through the network as a function of segment length and diameter. The mean pressure, P, is defined as the arithmetic mean of all capillary node pressures; σF is its standard deviation. All segments within the pressure range, P ± 2σF were assigned the minimum diameter, Dmin = 3 μm. Pre- and post capillary segments connecting to arteriole and venule terminals were assigned a diameter commensurate with their parent terminal. For all segments between the terminals and the minimum diameter group, we computed their diameters by iteratively executing the averaging scheme given in Eq. (8). This method for ensuring smooth diameter transitions is similar to physiological regularization techniques. Our level-set type approach gives rise to smooth diameter transitions, which monotonically decreases from inlet pre-capillary vessels to the smallest capillaries, then increase to the post-capillary veins.
Capillary diameter smoothing
| (8) |
where di,j is the diameter of segment j connected to segment i
If needed to further reduce sharp diameter transitions, the flow computations can be repeated with the adjusted diameters. Additional passes of diameter averaging can be performed until a sufficiently smooth diameter transition and spectrum is achieved.
APPENDIX 2: CUBIC BEZIER CURVES
A cubic Bezier curve is a vector function in terms of the scalar parameter t as defined in Eq. (9). It is defined by two end points, and and two control points, and as shown in Panel a of Fig. 10. The endpoints delineate the curve; the control points dictate the shape of the curve.
| (9) |
FIGURE 10.
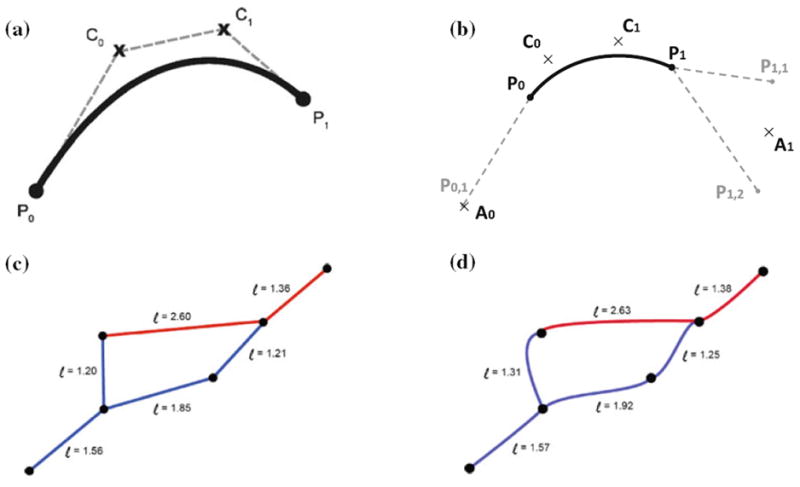
Bezier Curve adjustment of capillary tortuosity. (a) Depiction of a Bezier curve between endpoints, , and control points, , . (b) Automatic generation of control points based on segments connected to the current Bezier segment. (c) Straight line segments. (d) Tortuous capillary segment with Bezier curve parameter, α = 0.25.
For each capillary segment between points and , a 3D Bezier curve with desired degree of tortuosity can be constructed. To ensure reasonable transitions between different segments, we derive the control points for a given segment as a function of its neighboring segments. The first step is to find the auxiliary point , defined as the average of the set of points, connected to exclusive of as given in Eq. (10). Similarly, auxiliary point , is found from the set of points, connected to . except for .
connect to , except for
| (10) |
Finally, the desired control and are calculated with Eq. (11), where the scalar α controls the degree of tortuosity: α = 0 produces a straight line, α = 1.0 gives in the most tortuous curve. We recommend a value of α = 0.25 for natural capillary mesh appearance. Sample meshes with and without Bezier vessels are depicted in panels C and D of Fig. 10. Note that arc lengths of Bezier curves given in Eq. (12) in are always greater than the straight line counterpart.
| (11) |
Analytically arc length:
where Bi(t) are the components of B(t)
Numerically
| (12) |
where are the numerical derivatives of the components of B(t) along the arc t
APPENDIX 3: KROGH CYLINDER: DISCRETE AND ANALYTICAL SOLUTION
At the request of one reviewer, we also included a comparison of our dual mesh technique with an analytical Krogh model. Even though the Krogh cylinder offers an analytical solution to the oxygen diffusion with 0th order reaction, it has several limitations including the lack of axial dispersion which makes it imperfect for numerical validation studies.36 Several extension of the Krogh model have been proposed by Secomb,25 but approaches like Green’s function are beyond the intended scope of numerical validation of our network.
We plotted the results for a cylindrical domain with a single blood vessel in its center as described in Krogh’s original work.37 The analytical radial concentration profiles, C(r,z) at different levels of the axial coordinate are given Eq. (13) and Eq. (14) as a function of the product of the inlet concentration, C0, and the bulk velocity, V, the radius of the vessel, rC, the thickness of the wall tm, the radius of the tissue cylinder, rT, and the zero order rate of solute destruction in the tissue, R0, and the diffusion of the solute in tissue, D. The concentration of solute in the tissue at the wall boundary, C̄rc+tm equal to the flux of transport through the vessel governed by the mass transport coefficient, K0, as shown in Eq. (14). Finally, Eq. (14) includes the axial concentration profile inside the blood vessel, C(z), at the axial coordinate, z. The radial and axial solute gradients were computed for the analytic solution as shown in Fig. 11.
| (13) |
| (14) |
FIGURE 11.
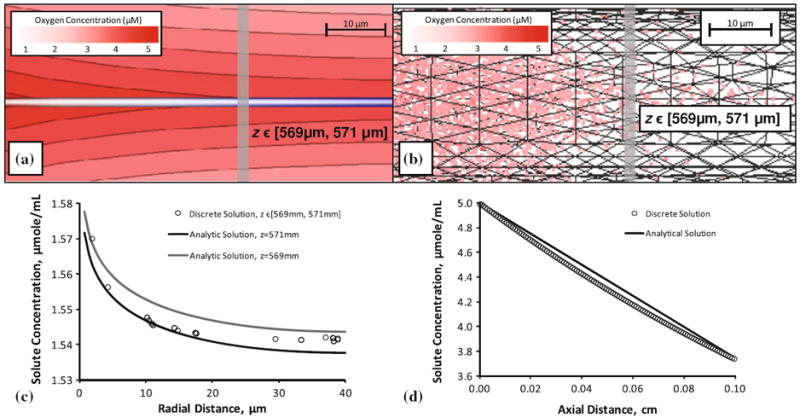
Krogh cylinder solution of tissue oxygen perfusion from a single vessel, comparison of analytical and discrete methods. (a) Analytical solution of a Krogh cylinder with capillary radius (rC = 5 μm) and capillary length (L = 1000 μm) and surrounding tissue radius (rT = 40 μm) and a constant injection of solute (C0 = 5 μM/mL). This radial distribution was determined at z = 570 μm. (b) Solution of the same system using the discrete approach described in this paper. (c) Discrete radial concentration of solute compared to realizations of the analytical solution for z = 569 mm and z = 571 mm (d) axial distribution of oxygen between the analytical and the discrete solution.
We compare oxygen extraction numerically computer with our model to the analytical Krogh model.15 The central blood vessel was discretized with cylindrical segments of Δz = 8 μm in length. A relatively coarse tetrahedral mesh to represent the extravascular space was constructed with the same dimensions, a mesh edge length of 34 μm, which is the same resolution as used the main paper. Flow, oxygen inlet concentration, mass transfer and 0th order oxygen consumption were implemented with the same parameters as in the Krogh model listed compactly in Table 4. Figure 11 summarize the results for the analytical and the numerical methods described in this work. Radial oxygen profiles of all tetrahedral cells falling with at an axial range of z = 570 ± 1 mm were plotted as dots in Fig. 11. For the analytical solution, two profiles were drawn for z = 569 mm and z = 571 mm, corresponding to the extreme axial positions of the tetrahedral elements in that zone. The analytical and our numerical results are in excellent agreement as expected.
TABLE 4.
Parameters of distribution using the Krogh model.
| C0 | V | rC | L | tm | rT | D | R0 | K0 |
|---|---|---|---|---|---|---|---|---|
| 5 μmole/cm3 | 500 μm/s | 5 μm | 1000 μm | 0.5 μm | 40 μm | 800 μm2/s | 0.01 μmole/cm3/s | 0.575 μm/s |
For completeness, we also checked total oxygen exchange and plotted the radial oxygen profiles. Although the total oxygen exchange matches exactly within numerical tolerances, the extraction profile along the axis cannot be identical as expected. This result is valid, as the Krogh model neglects axial dispersion, while our model does not. Therefore the slight mismatch is actually a confirmation of the quality of the proposed technique.
Additionally, a molar balance was constructed to determine the soundness of the discrete method and enforcement of mass conservation. The rate of 5 μmole/cm3 entering the cylinder at a velocity of 500 μm/s with a cross sectional area of 78.5 μm2 gives an inlet flux of 19.63 × 10−8 μmole/s. The outlet concentration from cylinder was determined as 3.74 μmole/cm3 in the analytical, and 3.72 μmole/cm3 in the discrete model. These outlet concentrations give rise to an outlet flux of 14.69 × 10−8 μmole/s in the analytical solution and 14.61 × 10−8 μmole/s in the discrete model. The volume of the tissue cylinder (total tissue cylinder volume minus the vessel volume) is 4.93 × 106 μm3 in the analytical domain and 4.98 × 106 μm3 in the discrete domain, giving a volumetric 0th order reaction rate of 4.93 × 10−8 μmole/s and 4.98 × 10−8 μmole/s, respectively. This compares to the 0th destruction rate computed by the analytical and discrete methods with a reported numeric error <0.002. This error scales accordingly for the large microvessel subsection model presented in this paper.
Footnotes
No conflicts of interest were posed in the conduct of this research.
References
- 1.Aroesty J, Gross JF. The mathematics of pulsatile flow in small vessels. I. Casson theory. Microvasc Res. 1972;4:1–12. doi: 10.1016/0026-2862(72)90012-x. [DOI] [PubMed] [Google Scholar]
- 2.Behera D. Textbook of Pulmonary Medicine. Jaypee Brothers Medical Pub; 2010. [Google Scholar]
- 3.Blinder P, Shih AY, Rafie C, Kleinfeld D. Topological basis for the robust distribution of blood to rodent neocortex. Proc Natl Acad Sci USA. 2010;107:12670–12675. doi: 10.1073/pnas.1007239107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Boas DA, Jones SR, Devor A, Huppert TJ, Dale AM. A vascular anatomical network model of the spatio-temporal response to brain activation. NeuroImage. 2008;40:1116–1129. doi: 10.1016/j.neuroimage.2007.12.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cassot F, Lauwers F, Fouard C, Prohaska S, Lauwers-Cances V. A novel three-dimensional computer-assisted method for a quantitative study of microvascular networks of the human cerebral cortex. Microcirculation. 2006;13:1–18. doi: 10.1080/10739680500383407. [DOI] [PubMed] [Google Scholar]
- 6.Cassot F, Lauwers F, Lorthois S, Puwanarajah P, Cances-Lauwers V, Duvernoy H. Branching patterns for arterioles and venules of the human cerebral cortex. Brain Res. 2010;1313:62–78. doi: 10.1016/j.brainres.2009.12.007. [DOI] [PubMed] [Google Scholar]
- 7.Cassot F, Lauwers F, Lorthois S, Puwanarajah P, Duvernoy H. Scaling laws for branching vessels of human cerebral cortex. Microcirculation. 2009 May;16:331–344. doi: 10.1080/10739680802662607. 2 p following 344. [DOI] [PubMed] [Google Scholar]
- 8.Delaunay B. Sur la sphere vide. Bull Acad Science USSR VII: Class Sci Mat. 1934:793–800. [Google Scholar]
- 9.Devor A, Sakadzic S, Saisan PA, Yaseen MA, Roussakis E, Srinivasan VJ, Vinogradov SA, Rosen BR, Buxton RB, Dale AM, Boas DA. “Overshoot” of O(2) is required to maintain baseline tissue oxygenation at locations distal to blood vessels. J Neurosci. 2011;31:13676–13681. doi: 10.1523/JNEUROSCI.1968-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Duff IS, Reid JK. The design of MA48: A code for the direct solution of sparse unsymmetric linear systems of equations. ACM Trans Math Softw. 1996;22:187–226. [Google Scholar]
- 11.Duong TQ, Kim SG. In vivo MR measurements of regional arterial and venous blood volume fractions in intact rat brain. Magnetic Resonance in Medicine. 2000;43:393–402. doi: 10.1002/(sici)1522-2594(200003)43:3<393::aid-mrm11>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- 12.Duvernoy HM, Delon S, Vannson JL. Cortical blood vessels of the human brain. Brain Research Bulletin. 1981;7:519–579. doi: 10.1016/0361-9230(81)90007-1. [DOI] [PubMed] [Google Scholar]
- 13.Espagno J, Arbus L, Bes A, Billet R, Gouaze A, Frerebeau Ph, Lazorthes Y, Salamon G, Seylaz J, Vlahovitch B. La circulation cerebrale. Neuro-Chirurgie. 1969;15 [Google Scholar]
- 14.Fang Q, Sakadzic S, Ruvinskaya L, Devor A, Dale AM, Boas DA. Oxygen advection and diffusion in a three- dimensional vascular anatomical network. Optics Express. 2008;16:17530–17541. doi: 10.1364/oe.16.17530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fletcher J. Mathematical modeling of the microcirculation. Mathematical Biosciences. 1978;38:159–202. [Google Scholar]
- 16.Fung YC, Zweifach BW. Microcirculation—mechanics of blood flow in capillaries. Annu Rev Fluid Mech. 1971;3:189. [Google Scholar]
- 17.Gjedde A, Kuwabara H, Hakim AM. Reduction of functional capillary density in human brain after stroke. Journal of Cerebral Blood Flow and Metabolism. 1990;10:317–326. doi: 10.1038/jcbfm.1990.60. [DOI] [PubMed] [Google Scholar]
- 18.Goldman D, Popel AS. A computational study of the effect of capillary network anastomoses and tortuosity on oxygen transport. Journal of Theoretical Biology. 2000;206:181–194. doi: 10.1006/jtbi.2000.2113. [DOI] [PubMed] [Google Scholar]
- 19.Gould IG, Marinnan T, Maurice C, Qader M, Henry B, Pervais M, Vaicaitis N, Zhu Y, Rogers A, Linninger AA. Hemodynamics of cerebral vasculature. Presented at the Proceedings of the 11th International Symposium on Process Systems Engineering; Singapore. 2012. [Google Scholar]
- 20.Guibert R, Fonta C, Plouraboue F. Cerebral blood flow modeling in primate cortex. Journal of Cerebral Blood Flow and Metabolism. 2010;30:1860–1873. doi: 10.1038/jcbfm.2010.105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Guibert R, Fonta C, Plouraboue F. A new approach to model confined suspensions flows in complex networks: application to blood flow. Transport in Porous Media. 2010;83:171–194. [Google Scholar]
- 22.Guibert R, Fonta C, Risser L, Plouraboue F. Coupling and robustness of intra-cortical vascular territories. NeuroImage. 2012;62:408–417. doi: 10.1016/j.neuroimage.2012.04.030. [DOI] [PubMed] [Google Scholar]
- 23.Hill AV. The combinations of haemoglobin with oxygen and with carbon monoxide. I. Biochem J. 1913;7:471–480. doi: 10.1042/bj0070471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hirsch S, Reichold J, Schneider M, Szekely G, Weber B. Topology and hemodynamics of the cortical cerebrovascular system. Journal of Cerebral Blood Flow and Metabolism. 2012;32:952–967. doi: 10.1038/jcbfm.2012.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hsu R, Secomb TW. A Green’s function method for analysis of oxygen delivery to tissue by microvascular networks. Mathematical Biosciences. 1989;96:61–78. doi: 10.1016/0025-5564(89)90083-7. [DOI] [PubMed] [Google Scholar]
- 26.Hunziker O, Frey H, Schulz U. Morphometric investigations of capillaries in the brain cortex of the cat. Brain Research. 1974;65:1–11. doi: 10.1016/0006-8993(74)90332-1. [DOI] [PubMed] [Google Scholar]
- 27.Huppert TJ, Allen MS, Benav H, Jones PB, Boas DA. A multicompartment vascular model for inferring baseline and functional changes in cerebral oxygen metabolism and arterial dilation. Journal of Cerebral Blood Flow and Metabolism. 2007;27:1262–1279. doi: 10.1038/sj.jcbfm.9600435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ito H, Kanno I, Iida H, Hatazawa J, Shimosegawa E, Tamura H, Okudera T. Arterial fraction of cerebral blood volume in humans measured by positron emission tomography. Annals of Nuclear Medicine. 2001;15:111–116. doi: 10.1007/BF02988600. [DOI] [PubMed] [Google Scholar]
- 29.James KR, Riha W. Convergence criteria for successive overrelaxation. Siam Journal on Numerical Analysis. 1975;12:137–143. [Google Scholar]
- 30.Jensen FB. Red blood cell pH, the Bohr effect, and other oxygenation-linked phenomena in blood O2 and CO2 transport. Acta Physiologica Scandinavica. 2004;182:215–227. doi: 10.1111/j.1365-201X.2004.01361.x. [DOI] [PubMed] [Google Scholar]
- 31.Karch R, Neumann F, Neumann M, Schreiner W. A three-dimensional model for arterial tree representation, generated by constrained constructive optimization. Computers in Biology and Medicine. 1999;29:19–38. doi: 10.1016/s0010-4825(98)00045-6. [DOI] [PubMed] [Google Scholar]
- 32.Karch R, Neumann F, Neumann M, Schreiner W. Staged growth of optimized arterial model trees. Annals of Biomedical Engineering. 2000;28:495–511. doi: 10.1114/1.290. [DOI] [PubMed] [Google Scholar]
- 33.Karch R, Neumann F, Podesser BK, Neumann M, Szawlowski P, Schreiner W. Fractal properties of perfusion heterogeneity in optimized arterial trees: a model study. Journal of General Physiology. 2003;122:307–321. doi: 10.1085/jgp.200208747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kasischke KA, Lambert EM, Panepento B, Sun A, Gelbard HA, Burgess RW, Foster TH, Nedergaard M. Two-photon NADH imaging exposes boundaries of oxygen diffusion in cortical vascular supply regions. Journal of Cerebral Blood Flow and Metabolism. 2011;31:68–81. doi: 10.1038/jcbfm.2010.158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Keller AL, Schuz A, Logothetis NK, Weber B. Vascularization of cytochrome oxidase-rich blobs in the primary visual cortex of squirrel and macaque monkeys. Journal of Neuroscience. 2011;31:1246–1253. doi: 10.1523/JNEUROSCI.2765-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kreuzer F. Oxygen supply to tissues: the Krogh model and its assumptions. Experientia. 1982;38:1415–1426. doi: 10.1007/BF01955753. [DOI] [PubMed] [Google Scholar]
- 37.Krogh A. The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. Journal of Physiology. 1919;52:409–415. doi: 10.1113/jphysiol.1919.sp001839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lauwers F, Cassot F, Lauwers-Cances V, Puwanarajah P, Duvernoy H. Morphometry of the human cerebral cortex microcirculation: general characteristics and space-related profiles. NeuroImage. 2008;39:936–948. doi: 10.1016/j.neuroimage.2007.09.024. [DOI] [PubMed] [Google Scholar]
- 39.Linninger AA. Biomedical systems research—New perspectives opened by quantitative medical imaging. Computers & Chemical Engineering. 2012;36:1–9. [Google Scholar]
- 40.Linninger AA, Somayaji MR, Erickson T, Guo X, Penn RD. Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue. Journal of Biomechanics. 2008;41:2176–2187. doi: 10.1016/j.jbiomech.2008.04.025. [DOI] [PubMed] [Google Scholar]
- 41.Lipowsky HH. Microvascular rheology and hemodynamics. Microcirculation. 2005;12:5–15. doi: 10.1080/10739680590894966. [DOI] [PubMed] [Google Scholar]
- 42.Lorthois S, Cassot F. Fractal analysis of vascular networks: insights from morphogenesis. Journal of Theoretical Biology. 2010;262:614–633. doi: 10.1016/j.jtbi.2009.10.037. [DOI] [PubMed] [Google Scholar]
- 43.Lorthois S, Cassot F, Lauwers F. Simulation study of brain blood flow regulation by intra-cortical arterioles in an anatomically accurate large human vascular network. Part II: flow variations induced by global or localized modifications of arteriolar diameters. NeuroImage. 2011;54:2840–2853. doi: 10.1016/j.neuroimage.2010.10.040. [DOI] [PubMed] [Google Scholar]
- 44.Lorthois S, Cassot F, Lauwers F. Simulation study of brain blood flow regulation by intra-cortical arterioles in an anatomically accurate large human vascular network: part I: methodology and baseline flow. NeuroImage. 2011;54:1031–1042. doi: 10.1016/j.neuroimage.2010.09.032. [DOI] [PubMed] [Google Scholar]
- 45.Mintun MA, Lundstrom BN, Snyder AZ, Vlassenko AG, Shulman GL, Raichle ME. Blood flow and oxygen delivery to human brain during functional activity: theoretical modeling and experimental data. Proc Natl Acad Sci U S A. 2001;98:6859–6864. doi: 10.1073/pnas.111164398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Neubauer JA, Sunderram J. Oxygen-sensing neurons in the central nervous system. Journal of Applied Physiology. 2004;96:367–374. doi: 10.1152/japplphysiol.00831.2003. [DOI] [PubMed] [Google Scholar]
- 47.Niimi H, Komai Y, Yamaguchi S, Seki J. Microembolic flow disturbances in the cerebral microvasculature with an arcadal network: a numerical simulation. Clin Hemorheol Microcirc. 2006;34:247–255. [PubMed] [Google Scholar]
- 48.Nishimura N, Schaffer CB, Friedman B, Lyden PD, Kleinfeld D. Penetrating arterioles are a bottleneck in the perfusion of neocortex. Proc Natl Acad Sci U S A. 2007;104:365–370. doi: 10.1073/pnas.0609551104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Nolte J, Sundsten JW. The human brain: an introduction to its functional anatomy. 5. St. Louis: Mosby; 2002. [Google Scholar]
- 50.Pawlik G, Rackl A, Bing RJ. Quantitative capillary topography and blood flow in the cerebral cortex of cats: an in vivo microscopic study. Brain Research. 1981;208:35–58. doi: 10.1016/0006-8993(81)90619-3. [DOI] [PubMed] [Google Scholar]
- 51.Pries A. Biophysical aspects of blood flow in the microvasculature. Cardiovascular Research. 1995;32:657–667. [PubMed] [Google Scholar]
- 52.Pries AR, Secomb TW, Gaehtgens P, Gross JF. Blood flow in microvascular networks. Experiments and simulation. Circulation Research. 1990;67:826–834. doi: 10.1161/01.res.67.4.826. [DOI] [PubMed] [Google Scholar]
- 53.Rakusan K, Wicker P. Morphometry of the small arteries and arterioles in the rat heart: effects of chronic hypertension and exercise. Cardiovascular Research. 1990;24:278–284. doi: 10.1093/cvr/24.4.278. [DOI] [PubMed] [Google Scholar]
- 54.Reichold J, Stampanoni M, Lena Keller A, Buck A, Jenny P, Weber B. Vascular graph model to simulate the cerebral blood flow in realistic vascular networks. J Cereb Blood Flow Metab. 2009;29:1429–1443. doi: 10.1038/jcbfm.2009.58. [DOI] [PubMed] [Google Scholar]
- 55.Rhodin JA. Ultrastructure of mammalian venous capillaries, venules, and small collecting veins. Journal of Ultrastructure Research. 1968;25:452–500. doi: 10.1016/s0022-5320(68)80098-x. [DOI] [PubMed] [Google Scholar]
- 56.Risser L, Plouraboue F, Cloetens P, Fonta C. A 3D-investigation shows that angiogenesis in primate cerebral cortex mainly occurs at capillary level. International Journal of Developmental Neuroscience. 2009;27:185–196. doi: 10.1016/j.ijdevneu.2008.10.006. [DOI] [PubMed] [Google Scholar]
- 57.Risser L, Plouraboue F, Steyer A, Cloetens P, Le Duc G, Fonta C. From homogeneous to fractal normal and tumorous microvascular networks in the brain. Journal of Cerebral Blood Flow and Metabolism. 2007;27:293–303. doi: 10.1038/sj.jcbfm.9600332. [DOI] [PubMed] [Google Scholar]
- 58.Rostrup E, Law I, Blinkenberg M, Larsson HBW, Born AP, Holm S, Paulson OB. Regional differences in the CBF and BOLD responses to hypercapnia: a combined PET and fMRI study. NeuroImage. 2000;11:87–97. doi: 10.1006/nimg.1999.0526. [DOI] [PubMed] [Google Scholar]
- 59.Safaeian N, Sellier M, David T. A computational model of hemodynamic parameters in cortical capillary networks. J Theor Biol. 2010 Dec 2; doi: 10.1016/j.jtbi.2010.11.038. [DOI] [PubMed] [Google Scholar]
- 60.Sakadzic S, Roussakis E, Yaseen MA, Mandeville ET, Srinivasan VJ, Arai K, Ruvinskaya S, Devor A, Lo EH, Vinogradov SA, Boas DA. Two-photon high-resolution measurement of partial pressure of oxygen in cerebral vasculature and tissue. Nature Methods. 2010;7:755–759. doi: 10.1038/nmeth.1490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Schneider M, Hirsch S, Weber B, Szekely G. Physiologically based construction of optimized 3-D arterial tree models. Med Image Comput Comput Assist Interv. 2011;14:404–411. doi: 10.1007/978-3-642-23623-5_51. [DOI] [PubMed] [Google Scholar]
- 62.Schneider M, Reichold J, Weber B, Szekely G, Hirsch S. Tissue metabolism driven arterial tree generation. Medical Image Analysis. 2012;16:1397–1414. doi: 10.1016/j.media.2012.04.009. [DOI] [PubMed] [Google Scholar]
- 63.Schreiner W, Karch R, Neumann M, Neumann F, Szawlowski P, Roedler S. Optimized arterial trees supplying hollow organs. Medical Engineering & Physics. 2006;28:416–429. doi: 10.1016/j.medengphy.2005.07.019. [DOI] [PubMed] [Google Scholar]
- 64.Sharan M, Vovenko EP, Vadapalli A, Popel AS, Pittman RN. Experimental and theoretical studies of oxygen gradients in rat pial microvessels. Journal of Cerebral Blood Flow and Metabolism. 2008;28:1597–1604. doi: 10.1038/jcbfm.2008.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Si H. TetGen, A Quality Tetrahedral Mesh Generator and Three-Dimensional Delaunay Triangulator. 1.4. Berlin: 2006. [Google Scholar]
- 66.Sorenson AG, Copen WA, Ostergaard L, Buonanno FS, Gonsalez RG, Rordorf G, Rosen BR, Schwamm LH, Weisskoff RM, Koroshetz WJ. Hyperacute stroke: simultaneous measurement of relative cerebral blood volume, relative cerebral blood flow, and mean tissue transit time. Neuroradiology. 1999;210:519–527. doi: 10.1148/radiology.210.2.r99fe06519. [DOI] [PubMed] [Google Scholar]
- 67.Su SW, Catherall M, Payne S. The influence of network structure on the transport of blood in the human cerebral microvasculature. Microcirculation. 2012;19:175–187. doi: 10.1111/j.1549-8719.2011.00148.x. [DOI] [PubMed] [Google Scholar]
- 68.Takahashi T, Nagaoka T, Yanagida H, Saitoh T, Kamiya A, Hein T, Kuo L, Yoshida A. A mathematical model for the distribution of hemodynamic parameters in the human retinal microvasculature network. J Biorheol. 2009;23:77–86. [Google Scholar]
- 69.Tang W, Zhang L, Linninger A, Tranter RS, Brezinsky K. Solving kinetic inversion problems via a physical trust region gauss-newton method. Industrial and Engineering Chemistry Research. 2005;44:3626–3637. [Google Scholar]
- 70.Tsai PS, Kaufhold JP, Blinder P, Friedman B, Drew PJ, Karten HJ, Lyden PD, Kleinfeld D. Correlations of neuronal and microvascular densities in murine cortex revealed by direct counting and colocalization of nuclei and vessels. Journal of Neuroscience. 2009;29:14553–14570. doi: 10.1523/JNEUROSCI.3287-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Vaičaitis NM, Sweetman BJ, Linninger AA. A computational model of cerebral vasculature, brain tissue, and cerebrospinal fluid. Presented at the 21st European Symposium on Computer-Aided Process Engineering; Greece. 2011. [Google Scholar]
- 72.Voronoi G. Nouvelles applications des parametres continus a la theorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. Journal für die reine und angewandte Mathematik. 1908;134:198–287. [Google Scholar]
- 73.Vovenko E. Distribution of oxygen tension on the surface of arterioles, capillaries and venules of brain cortex and in tissue in normoxia: an experimental study on rats. Pflugers Archiv European Journal of Physiology. 1999;437:617–623. doi: 10.1007/s004240050825. [DOI] [PubMed] [Google Scholar]
- 74.Vovenko EP, Chuikin AE. Oxygen tension in rat cerebral cortex microvessels in acute anemia. Neuroscience and Behavioral Physiology. 2008;38:493–500. doi: 10.1007/s11055-008-9007-4. [DOI] [PubMed] [Google Scholar]
- 75.Vovenko EP, Chuikin AE. Tissue oxygen tension profiles close to brain arterioles and venules in the rat cerebral cortex during the development of acute anemia. Neuroscience and Behavioral Physiology. 2010;40:723–731. doi: 10.1007/s11055-010-9318-0. [DOI] [PubMed] [Google Scholar]
- 76.Weber B, Keller AL, Reichold J, Logothetis NK. The microvascular system of the striate and extrastriate visual cortex of the macaque. Cerebral Cortex. 2008;18:2318–2330. doi: 10.1093/cercor/bhm259. [DOI] [PubMed] [Google Scholar]
- 77.Yang Y, Engelien W, Xu S, Gu H, Silbersweig DA, Stern E. Transit time, trailing time, and cerebral blood flow during brain activation: measurement using multislice, pulsed spin-labeling perfusion imaging. Magnetic Resonance in Medicine. 2000;44:680–685. doi: 10.1002/1522-2594(200011)44:5<680::aid-mrm4>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- 78.Zagzoule M, Marc-Vergnes JP. A global mathematical model of the cerebral circulation in man. Journal of Biomechanics. 1986;19:1015–1022. doi: 10.1016/0021-9290(86)90118-1. [DOI] [PubMed] [Google Scholar]
- 79.Zhang LB, Kulkarni K, Somayaji MR, Xenos M, Linninger AA. Discovery of transport and reaction properties in distributed systems. AIChE Journal. 2007;53:381–396. [Google Scholar]
- 80.Zhang LB, Xue C, Malcolm A, Kulkarni K, Linninger AA. Distributed system design under uncertainty. Industrial and Engineering Chemistry Research. 2006;45:8352–8360. [Google Scholar]
- 81.Zweifach BW. Quantitative studies of microcirculatory structure and function. I. Analysis of pressure distribution in the terminal vascular bed in cat mesentery. Circulation Research. 1974;34:843–857. [PubMed] [Google Scholar]
- 82.Zweifach BW, Lipowsky HH. Quantitative studies of microcirculatory structure and function. III. Microvascular hemodynamics of cat mesentery and rabbit omentum. Circulation Research. 1977;41:380–390. doi: 10.1161/01.res.41.3.380. [DOI] [PubMed] [Google Scholar]


