Characterization of Monomeric Mn^II/III/IV–Hydroxo Complexes from X- and Q-Band Dual Mode Electron Paramagnetic Resonance (EPR) Spectroscopy

Abstract

Manganese–hydroxo species have been implicated in C–H bond activation performed by metalloenzymes, but the electronic properties of many of these intermediates are not well characterized. The present work presents a detailed characterization of three Mnⁿ–OH complexes (where n = II, III, and IV) of the tris[(N′-tert-butylureaylato)-N-ethylene]aminato ([H₃buea]³⁻) ligand using X- and Q-band dual mode electron paramagnetic resonance (EPR). Quantitative simulations for the [Mn^IIH₃buea(OH)]²⁻ complex demonstrated the ability to characterize similar Mn^II species commonly present in the resting states of manganese-containing enzymes. The spin states of the Mn^III and Mn^IV complexes determined from EPR spectroscopy are S = 2 and 3/2, respectively, as expected for the C₃ symmetry imposed by the [H₃buea]³⁻ ligand. Simulations of the spectra indicated the constant presence of two Mn^IV species in solutions of [Mn^IVH₃buea(OH)] complex. The simulations of perpendicular- and parallel-mode EPR spectra allow determination of zero-field splitting and hyperfine parameters for all complexes. For the Mn^III and Mn^IV complexes, density functional theory calculations are used to determine the isotropic Mn hyperfine values, to compare the excited electronic state energies, and to give theoretical estimates of the zero-field energy.

INTRODUCTION

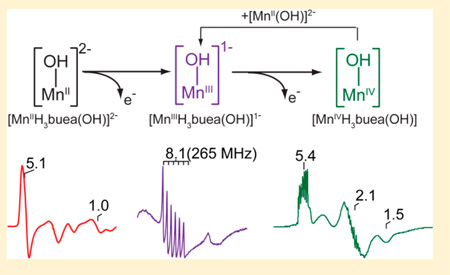
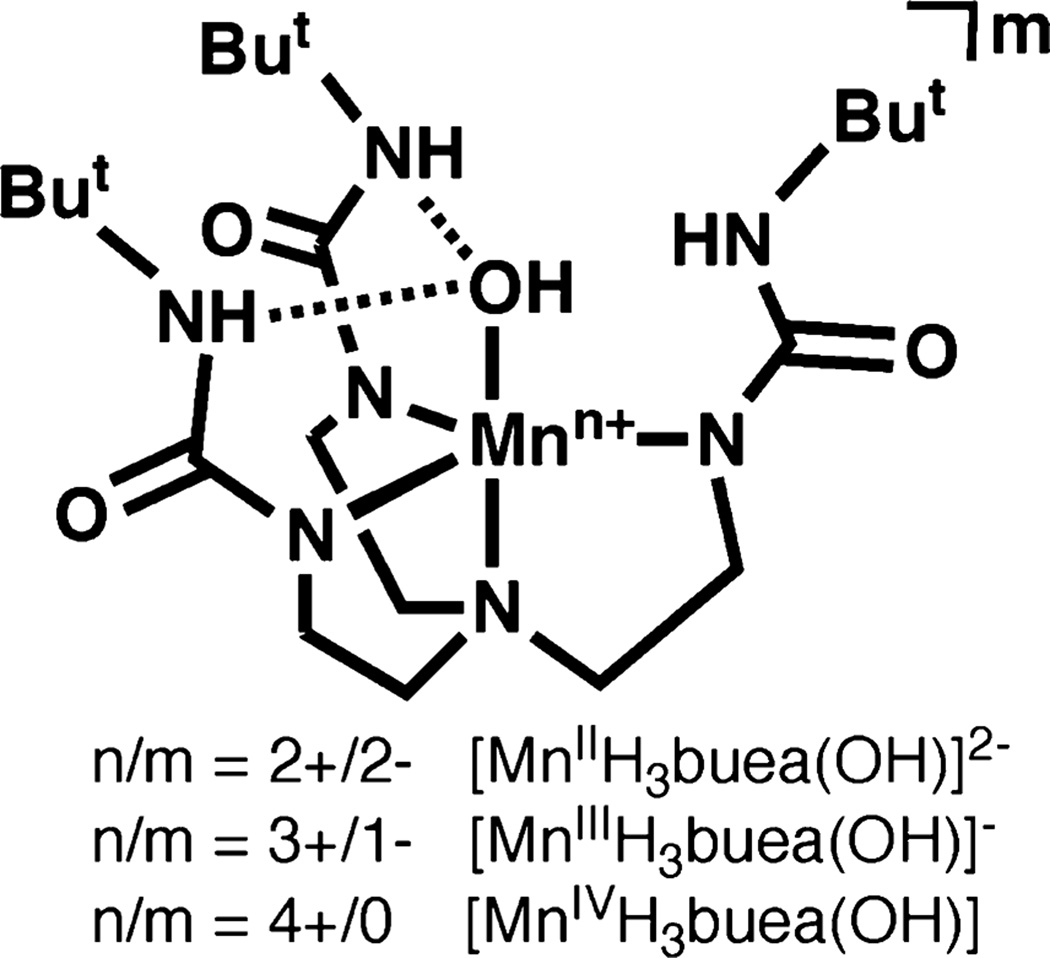
Non-heme manganese and iron complexes with terminal hydroxo and oxo ligands are proposed intermediates in the catalytic cycles of a variety of metalloproteins.^1–4 The protonation state of the terminal oxygen ligand is a key factor in the reactivity of these intermediates.⁵ For example, the stepwise conversion of a Mn–OH₂ species to a Mn–oxo species has been proposed to be essential for water oxidation in Photosystem II complex.^6,7 Similarly, a high-valent Fe–oxo species is believed to convert to an Fe–OH complex via a rebound mechanism during the hydroxylation of C–H bonds in cytochrome P450.^8–13 Biomimetic complexes have provided insight into the effects of protonation of the metal–oxo species without the added complexity introduced by the surrounding protein structure. For instance, the ligand tris[(N′-tert-butylureaylato)-N-ethylene]aminato ([H₃buea]³⁻) forms both monomeric M–OH and M–oxo (M = Fe, Mn) complexes in various oxidation states at the metal center. This ligand has butylureaylato arms that form a H-bonding cavity around the M–O(H) unit.¹⁴ In addition, anionic ureato N-donors are used to enforce local trigonal symmetry at the metal center, thereby stabilizing high-spin electronic states for these complexes (Figure 1).

Figure 1.

Structure of the [MnⁿH₃buea(OH)]^m complexes characterized in this report.

We have characterized previously the electronic properties of the Feⁿ–O(H) (n = II, III, or IV).¹⁵ In this report, the electronic properties of the corresponding Mnⁿ–OH complexes (n = II, III, or IV) are determined from electron paramagnetic resonance (EPR) spectroscopy. EPR spectroscopy has long been important for the characterization of Mn complexes; however, the interpretation of spectra is often more complicated than the corresponding Fe complexes. The spin-orbit interactions of S = 5/2 Mn^II complexes result in lower zero-field energies (~D) that are comparable to the microwave energy (hv) for common X-band spectrometers. This causes mixing of spin states and multiple overlapping transitions, and consequently, the interpretation of spectra has been qualitative. High-field EPR studies on monomeric Mn^II and Mn^II have been reported in literature, which can give more accurate determinations of g- and D-values ^16–20. We have developed a methodology for quantitative interpretation based on computer simulation of spectra, and here we demonstrate its use in the interpretation of X- and Q-band spectra for both parallel (B₁ ‖ B) and perpendicular (B₁ ⊥ B) orientations of the oscillating microwave field (B₁) relative to the static field (B)²¹. The simulations allow unambiguous determination of the electronic parameters and the Mn^II concentrations directly from spectra. The analysis described for [Mn^II H₃buea(OH)]²⁻ is presented as a case study for interpretation of EPR signals from S = 5/2 Mn^II complexes, which can also be applied to manganese enzymes.

Oxidation of [Mn^II H₃buea(OH)]²⁻ yields the integer-spin (S = 2) Mn^III–OH analog, which is best observed with B1 ‖ B, and our methodologies were applied to determine the electronic parameters and species concentrations for this species. Further oxidation produced the S = 3/2 Mn^IV–OH complex [Mn^IVH₃buea(OH)], a new addition to this series. Half integer-spin Mn^IV complexes typically give simpler spectra due to the larger D-values relative to Mn^II , but simulations of the spectra showed that two S = 3/2 species were always present in a constant ratio. Density functional theory (DFT) calculations were performed to determine ground-state structures and electronic parameters, and comparisons of these results were made to the experimental values where possible. The ability to chemically prepare monomeric Mn– OH complexes in three oxidation states provided an opportunity to experimentally determine and compare the electronic properties of Mnⁿ–OH complexes having the same primary and secondary coordination spheres.

EXPERIMENTAL METHODS

Preparation of Mnⁿ⁺–OH Complexes

All reagents were purchased from commercial sources and used as received, unless otherwise noted. Solvents were sparged with argon and dried over columns containing Q-5 and molecular sieves. DMF was stored over activated 4 Å molecular sieves for 2 days in a Vacuum Atmospheres, Co. drybox under an Ar atmosphere and then decanted onto a second portion of 4 Å molecular sieves for 2 days before use. The syntheses of metal complexes were conducted in an Ar atmosphere. The preparation of K₂[Mn^IIH₃buea(OH)], K[Mn^IIIH₃buea(OH)], and [Cp₂Fe]BF₄ followed the literature procedure.^14,22,23

Sample Preparation for EPR Measurements

A solution of [Mn^IIH₃buea(OH)]²⁻ (5.0 µmol, 180 µL of a 28 mM solution in 1/1 THF/DMF) containing 2 equiv of 18-crown-6 ether (2.6 mg, 10 µmol) in an EPR tube was cooled to −78 °C in an acetone/dry ice bath for 15 min. The ether tightly bound to K⁺ ions to form an (18-crown-6 ether)(K⁺) pair, which provided better solubility of the Mn^II starting material. The same EPR signals were observed in the absence of ether. For generating [Mn^IVH₃buea(OH)], 2 equiv of [Cp₂Fe]BF₄ (10 µmol, 40 µL of 250 mM solution in DMF) was injected with a gas tight syringe. The solution was allowed to sit for an additional 15 min and then frozen in liquid N₂. A similar procedure was used for generating [Mn^IIIH₃buea(OH)]⁻ in situ from [Mn^IIH₃buea(OH)]²⁻ using 1 equiv of [Cp₂Fe]BF₄ (5.0 µmol, 20 µL of 250 mM solution in DMF). The same procedures were used when the samples with different concentrations were prepared.

EPR Spectroscopy

X-band EPR spectra were recorded on a Bruker 300 spectrometer equipped with an Oxford ESR-910 liquid helium cryostat. Q-band (34.0 GHz) EPR spectra were recorded on a Bruker 200 spectrometer with a home-built microwave probe and cryostat.²⁴ The quantification of all signals is relative to a CuEDTA spin standard, the concentration of which is derived from an atomic absorption standard (Aldrich). For both instruments, the microwave frequency was calibrated with a frequency counter and the magnetic field with a NMR gaussmeter. A modulation frequency of 100 kHz was used for all EPR spectra. The EPR simulation software (SpinCount) was written by one of the authors.²¹ The software diagonalizes the electronic spin Hamiltonian H = β_eB·g·S + S·D·S, where S is the total spin of the complex unless explicitly stated and the parameters have the usual definitions. The hyperfine term (S·A·I) is treated as a perturbation in second order for the energies of the spin states. The line width of the spectra is dominated by a distribution in the rhombicity E/D, where one standard deviation in the distribution is σ_E/D. The quantitative simulations are least-squares fits of the experimental spectra generated with consideration of all intensity factors, which allows computation of simulated spectra for a specified sample concentration.

DFT Calculations

The DFT calculations were performed using the hybrid functional B3LYP and the basis set 6–311G provided by Gaussian 03 (Revision E.01) software package.²⁵ Geometry optimizations were terminated upon reaching the default convergence criteria and were performed for Mn^II–OH (S = 5/2), Mn^III–OH (S = 2), and Mn^IV–OH (S = 3/2) complexes without imposing any symmetry on the complexes. The optimizations of the molecular structures for the Mn^II–OH and Mn^III–OH were initiated using coordinates obtained from their structures determined via X-ray diffraction methods²³ and Mn^IV–OH calculation was initiated using the X-ray diffraction structure of the Mn^III–OH complex. Time-dependent (TD) DFT calculations were performed for the S = 2 and S = 1 states of the Mn^III–OH complex and S = 3/2 states of the Mn^IV– OH complex. The TD-DFT calculations gave positive excitation energies suggesting that the self-consistent field (SCF) solutions represent the ground states.

RESULTS AND DISCUSSION

Oxidation of Mn^II–OH to Mn^IV–OH

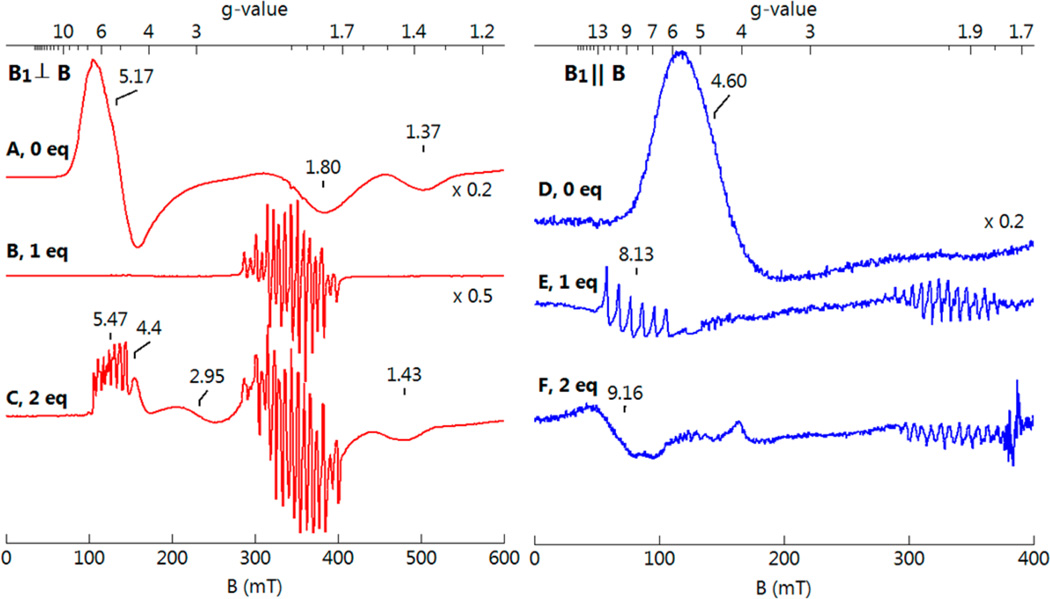
A series of EPR samples were prepared by treating [Mn^IIH₃buea(OH)]²⁻ with increasing amounts of the oxidant [Cp₂Fe]BF₄. The spectral changes are first summarized, and then further detail of each complex is given. EPR spectra of a typical oxidation experiment for the microwave magnetic field (B₁) perpendicular (left side, red) or parallel (right side, blue) to the static magnetic field (B) are shown in Figure 2. The EPR data of the starting Mn^II–OH complex (Figure 2A,D) showed strong signals at g = 5.17, 1.80, and 1.37 in perpendicular mode and g = 4.60 in parallel mode from the S = 5/2 spin center. The addition of 1 equiv [Cp₂Fe]BF₄ resulted in the loss of the Mn^II–OH signals and the appearance of a six-line hyperfine signal centered at g = 8.14 (A = 270 MHz, a = 9.6 mT) in parallel mode (Figure 2B,E). This signal originates from an S = 2 spin center and is assigned to the Mn^III–OH complex. The multiple-line hyperfine signal centered at g = 2 in perpendicular mode was from a minority binuclear mixed-valence species generated during the oxidation of the Mn^II–OH complex. The binuclear species was preparation dependent and accounted for less than 10% of the total Mn in the sample. The signal was also present in parallel mode due to imperfect alignment of B₁ and B. The addition of another equivalent of [Cp₂Fe]BF₄ resulted in the loss of the six-line signal from the Mn^III–OH complex in parallel mode and the appearance of signals in perpendicular mode (Figure 2C,F) at g = 5.47, 2.95, and 1.43. The positions of these resonances are indicative of an S = 3/2 spin state, and this signal is assigned to the Mn^IV–OH complex. The signal at g = 4.4 was from slight excess of [Cp₂Fe]BF₄ still present in the reaction mixture. The residual broad signal at g = 9.16 was from an impurity of unknown origin, and its amount was preparation dependent. As discussed below, the stepwise addition of [Cp₂Fe]BF₄ resulted in the near quantitative oxidation of the Mn^II–OH complex to the Mn^III–OH complex, and then to the Mn^IV–OH complex. The signals from the Mn^III–OH and Mn^IV–OH complexes are distinctly different than the signals of the corresponding Mn–oxo complexes.²⁶

Figure 2.

Perpendicular mode (red) and parallel mode (blue) EPR spectra of (A, D) 10 mM Mn^II–OH in in DMF/THF; (B, E) +1 equiv [Cp₂Fe]BF₄; (C, F) +2 equiv [Cp₂Fe]BF₄. Experimental conditions: temperature, 10 K; power, 0.2 mW; frequency, 9.63 (red), 9.29 (blue) GHz.

Mn^II–OH Complex

The EPR spectra are complicated by resonances from multiple overlapping transitions, which is often true for Mn^II complexes, but advances in simulation capabilities can now provide a detailed interpretation with specific resonance assignments. The present work is a relatively rare presentation of data from perpendicular and parallel modes at both X-band and Q-band microwave frequencies. Half-integer spin systems for which the Kramers doublets (±m_s) are well separated in energy (D ≫ hv) normally have no intensity in parallel mode. For Mn^II complexes, however, the magnitude of zero-field splitting (D) is often comparable to the energy of the microwave quantum (hv) for X-band spectrometers. For this regime, the magnetic m_s levels are significantly mixed and m_s is not a strictly good quantum number. In such instances, parallel mode signals can be observed. Figure 3 shows X-band EPR spectra of [Mn^IIH₃buea(OH)]²⁻ on a wider magnetic scale than that of Figure 2 with simulations using the parameters of Table 1. The simulation intensity quantitatively predicted the sample concentration determined from the weight of the complex dissolved in the solvent. The simulations indicated a small rhombicity (E/D = 0.03), and as discussed later, this complex is nearly axial in comparison to the corresponding Fe^III–OH complex with [H₃buea]³⁻ (E/D = 0.17).

Figure 3.

X-band EPR spectra (colored) and simulations (black) of the Mn^II –OH complex, 5 mM in DMF/THF, (A) B₁ ⊥ B, (B) B₁ ‖ B. The complex is the same state as that of Figure 2A, D but shown for a wider field range. Experimental conditions: temperature, 10 K; power, 0.2 mW; frequency, 9.634 (A), 9.299 (B) GHz. The simulation parameters are in Table 1.

Table 1.

EPR Parameters of the Mnⁿ⁺–OH Complexes

complex	S	D, cm−1	E/D, σE/D	g	A, MHz	Aiso, MHz
MnII–OH	5/2	−0.28(1)	0.031(3), 0.006	1.95(5), 1.99(5), 1.99(5)		250(25)
MnIII–OH	2	+1.7(5)	0.05, 0.02	−, −, 2.040a	−, −, 270(5)a	212
MnIV–OH (S1)	3/2	+0.88(5)	0.31(1), 0.015	2.00(5), 2.01(5), 2.00(5)	257, 190(2), 210(2)	219
MnIV–OH (S2)	3/2	+0.67(5)	0.17(1), 0.015	2.00(5), 2.05(5), 2.00(5)	252, 210(2), 210(2)	224

^aValues with “−” are not determined.

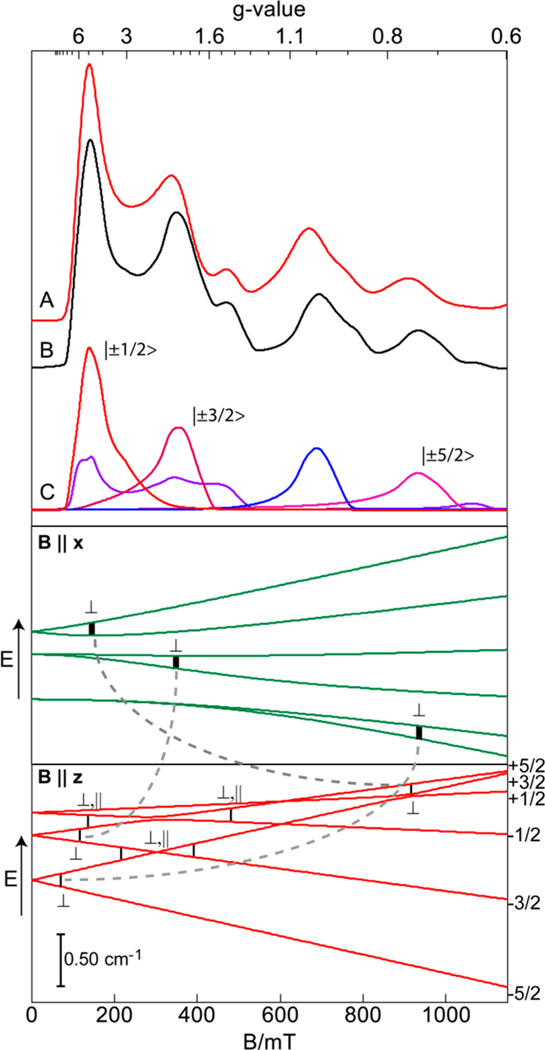
The Mn^II–OH spectra were complicated by the overlap of resonances from many different transitions within the S = 5/2 manifold. Figure 4C shows the simulated contribution of the signal from each transition for B₁ ⊥ B, which are plotted as absorption spectra to simplify the presentation. Figure 4B shows the resulting sum of all the individual signals of Figure 4C, which matched the experimental absorption spectrum of Figure 4A. The lower region in Figure 4 shows the energy levels for B parallel to the x and z directions of the molecular frame determined by the D-tensor. The corresponding transitions are indicated with the polarization of incident field that induced the transitions. For B ‖ x, there are three signals with large contributions (reddish simulations) from the approximate |±m_s〉 transitions indicated on the figure. In the limit of large D-value, the |1/2〉 transition would display (in the absence of hyperfine) the common g = 6.0 resonance that dominates EPR spectra of iron complexes (e.g., ferric porphyrins). As the field rotates toward the z-axis, the resonances move as indicated by the dashed line. The two bluish simulations are interdoublet (looping) transitions that have no contribution for B ‖ x but have contributions for field angles of θ < 60° with B₁ ⊥ B. These interdoublet transitions are also the dominate contributions to the B₁ ‖ B spectra of Figure 3B, the most intense is at g = 4.4 and corresponds to the transition |+3/2 〉↔|−1/2〉. Several of the levels are separated by an energy spacing close to the D-value, allowing an accurate determination from simulation, D = −0.28(1) cm⁻¹. The sign and magnitude of the D-value are determined from fitting 2 and 10 K spectra (Figure S1, Supporting Information). The A-tensor for Mn^II ions is typically isotropic with a magnitude of approximately 250 MHz (89 G).²⁹ The hyperfine splitting for the Mn^II–OH complex was unresolved because of broadening by intermo-lecular interactions; however, the line widths are a strong function of the unresolved hyperfine broadening. The hyperfine term of the spin Hamiltonian has a different magnetic field dependence than the other terms that typically dominate the line width, specifically distributions in D and E/D. Consequently, an approximate A-value of 250 ± 25 MHz was determined from simulations of the experimental spectra, which have different microwave frequencies and multiple transitions.

Figure 4.

Top panel: Absorption X-band EPR spectrum (A) and simulation (B) of the Mn^II–OH complex. The simulation parameters are in Table 1. (C) The contributions from approximate |±m_s〉 transitions (reddish lines) and interdoublet transitions (bluish lines). Bottom two panels: The energies of the S = 5/2 spin manifold versus magnetic field B are shown for applied field along the x-axis (green) and z-axis (red) of the D-tensor. The vertical bars correspond to 9.6 GHz and indicate the important transitions for microwaves oscillating B₁ ⊥ B and B₁ ‖ B.

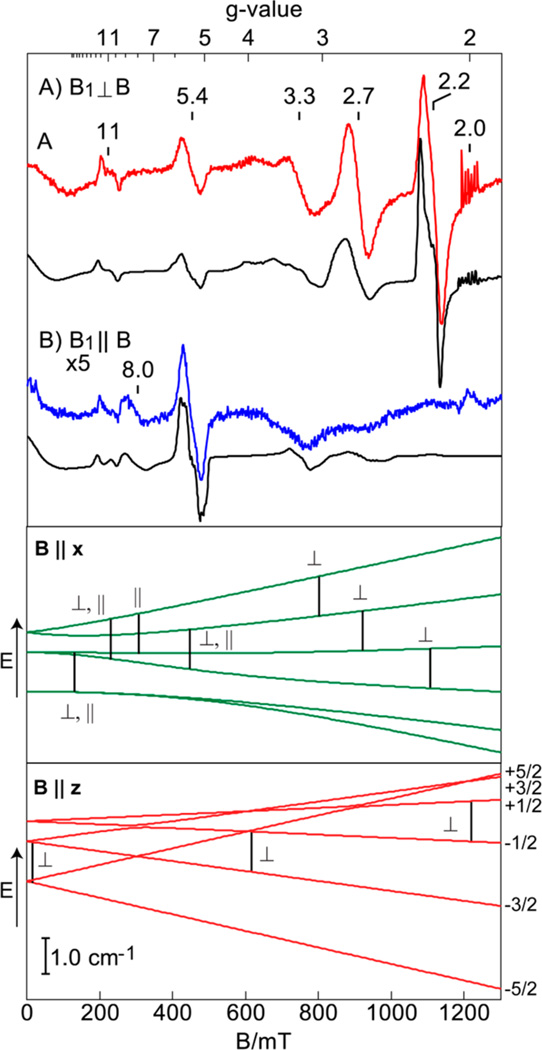
Figure 5 shows perpendicular and parallel mode Q-band EPR spectra and simulations for the electronic parameters of Table 1. As in Figure 4, the energy level diagrams in Figure 5 indicate the transitions with higher intensity and the direction of the incident oscillating microwave field for the transition. Similar to the X-band features, the higher intensity signals in perpendicular mode for Q-band (Figure 5A) originate from transitions with B ‖ x. The marked transitions for B ‖ z are allowed, but the corresponding signals are generally weak due to the polycrystalline average of the nearly axial complex, which results in relatively few molecules with B ‖ z. The most intense signals are at g = 3.3, 2.7, and 2.2 and are transitions obeying the standard selection rule Δm_s = ±1. In parallel mode (Figure 5B), the g = 8 and 5.4 signals are from Δm_s = ±2 transitions. The signal at g = 2.0 is from an unknown minority Mn^II impurity (<0.1% of total Mn).

Figure 5.

Q-band EPR spectra (colored lines) and simulations (black lines) of 5 mM Mn^II –OH in DMF/THF, (A) B₁ ⊥ B; (B) B₁ ‖ B. Experimental conditions: temperature, 11 K; frequency, 33.90 GHz; power, 5 µW (A), 50 µW (B). The energy diagrams are for the same spin system as Figure 4. The vertical bars correspond to 33.9 GHz and indicate the important transitions for microwaves oscillating B₁ ⊥ B and B₁ ‖ B.

The simulations of Figures 3–5 used the same parameters (Table 1) to fit the parallel and perpendicular mode spectra at both X- and Q-band frequencies. A simultaneous fit of all these spectra gave a unique result that quantitatively predicted the amount of the Mn^II –OH complex However, the simulation of the parallel mode X-band spectrum (Figure 3B) predicted resonances that are overall sharper than the experimental spectrum. Simply increasing various parameters that control line widths resulted in overly broad resonances for the other three spectra (both modes of Q-band, and perpendicular mode of X-band). Currently, we are unable to explain the overly broad parallel mode X-band spectra. We have observed a similar problem in parallel mode spectra of MnEDTA and for Mn^II bound protein systems. Intermolecular interactions can be ruled out as the source of broadening for the latter. The magnitude of the broadening is too large to be associated with ligand hyperfine (¹H, ¹⁴N). As well, g-strain for Mn^II complexes is insufficient because the intrinsic g-values are close to 2.00. The lineshapes are a strong function of D-strain (mainly E/D) and the unresolved ⁵⁵Mn hyperfine splitting, but the proper values of these distributions are well determined by the simulations of the other three spectra. The hyperfine term is treated as a perturbation to second order for the energies of the spin states, but we have not fully considered the corrections to the wave functions. We remain open to this possibility even though the broadening appears to be most problematic at higher magnetic fields, where second order corrections should be less important.

Electronic Excited State Energies

The d-orbitals of [Mn^IIH₃buea(OH)]²⁻ are singly occupied giving a ground orbital singlet with S = 5/2. The excited electronic state corresponding to the S = 3/2 configuration contributes via spin-orbit coupling to the zero-field energies of the ground S = 5/2 state. The experimental D-value of the isoelectronic Fe – OH complex (−2.4 cm⁻¹ ) is an order of magnitude greater than the Mn^II complex (−0.28 cm⁻¹ ). From DFT calculations, the SCF energy for a vertical excitation to the S = 3/2 state for the Mn^II –OH and Fe^III –OH complexes were 1.76 and 0.8 eV, respectively. TD-DFT calculations to determine the other higher lying excited S = 3/2 and S = 1/2 states were not performed. The magnitude of the D-value is in part dependent on the energies of the excited electronic states, and the smaller vertical SCF energy for the Fe^III –OH complex is consistent with the larger magnitude of D-value as compared to the Mn^II complex. However, a delicate balance of other contributions is present for d⁵ systems that can raise or lower the D-value, making accurate theoretical calculations difficult. ^30,31

Mn–OH Complex

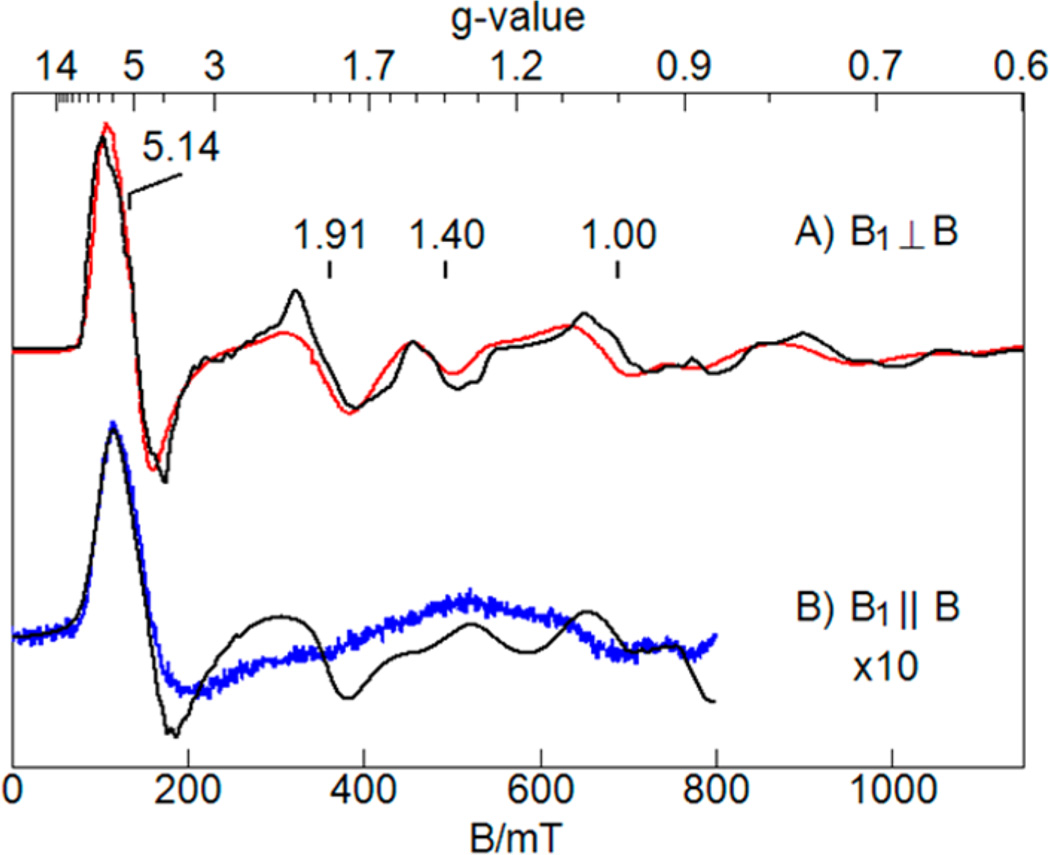
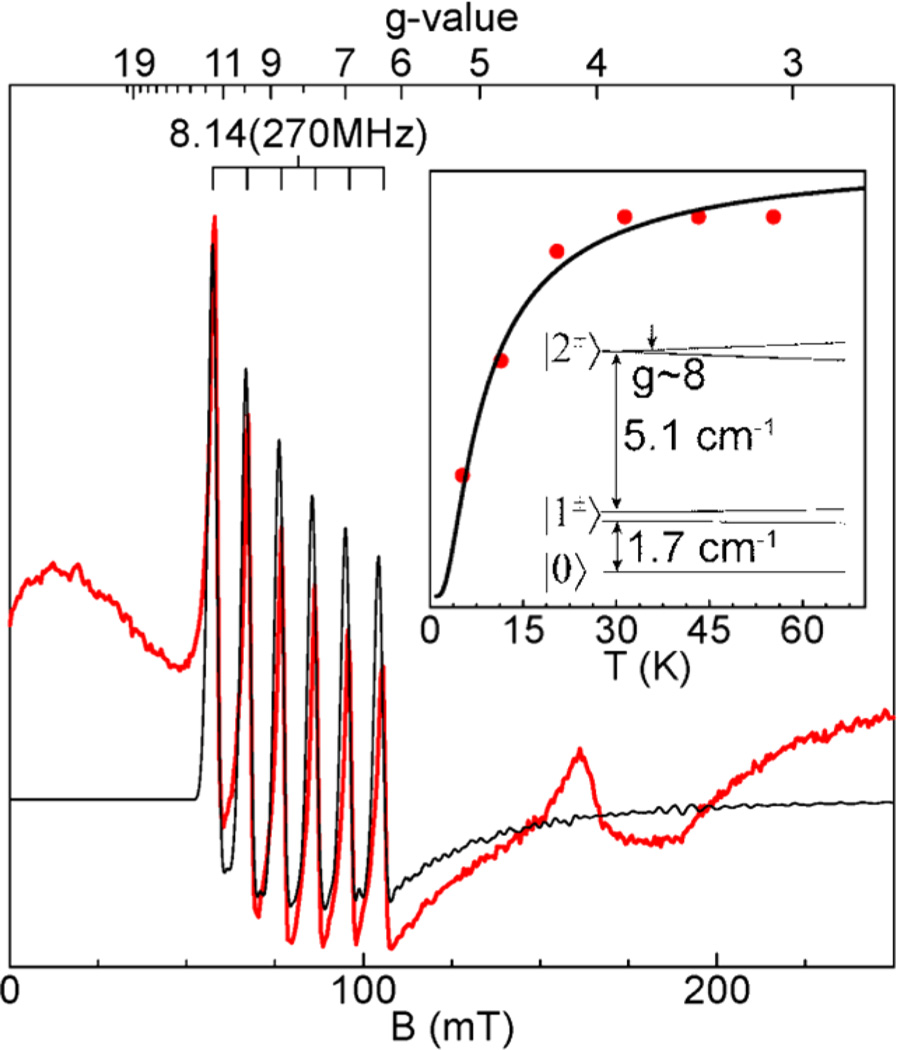
Figure 6 shows a higher resolution EPR spectrum of [Mn^IIIH₃buea(OH)]⁻ and a simulation using the parameters given in Table 1. The complex showed a six-line hyperfine pattern at g = 8.14 in parallel mode that originated from a transition within the |2^±〉 levels of an S = 2 spin manifold, where |2^±〉 = (|+2〉 ± |−2〉)/√2 for an integer-spin system with axial symmetry. The temperature dependence (Figure 6, inset) of this signal indicated D = +1.7(5) cm⁻¹. The resonance condition for this doublet is (hv)² = Δ₂² + [4g_ZβB cos θ]², where θ is the angle between the molecular z-axis defined by the D-tensor and B, and the zero-field splitting of the doublet is Δ₂ = 3(E/D)²D³². The concentration of a species determined from the spectrum depends on the value of Δ₂ and the g-value. To accurately determine both Δ₂ and the g-value, data from at least two microwave frequencies is required. This was applied successively to the Fe^IV–oxo complex of the same ligand where both X- and Q-band spectra were observed.¹⁵ We could not detect a signal in the Q-band EPR spectrum of the Mn^III–OH complex, because the small value of Δ₂ corresponds to a signal intensity below the sensitivity of our spectrometer. However, this limits the range of the g-value value to within the literature range of g-values of Mn^III ions (1.95 < g < 2.04).^19,33–37 For this range, the species concentration determined from the EPR spectrum was in agreement with the concentration of the Mn^II complex (10 mM) prior to oxidation. The broad underlying negative feature in the experimental spectrum near g ~ 8 was from a preparation dependent impurity of unknown origin. The signal at g = 4 was from small amount of O₂ in the sample.

Figure 6.

Parallel mode EPR spectrum of Mn^III–OH in DMF/THF. (Inset) signal intensity times temperature versus temperature of g = 8.14 signal (dots) and a theoretical curve (line) for the |2^±〉 transition of an S = 2 spin manifold with D = +1.7(5) cm⁻¹. Experimental condition: temperature, 10 K; power, 20 mW; frequency, 9.298 GHz.

Excited State Energies and D-Value

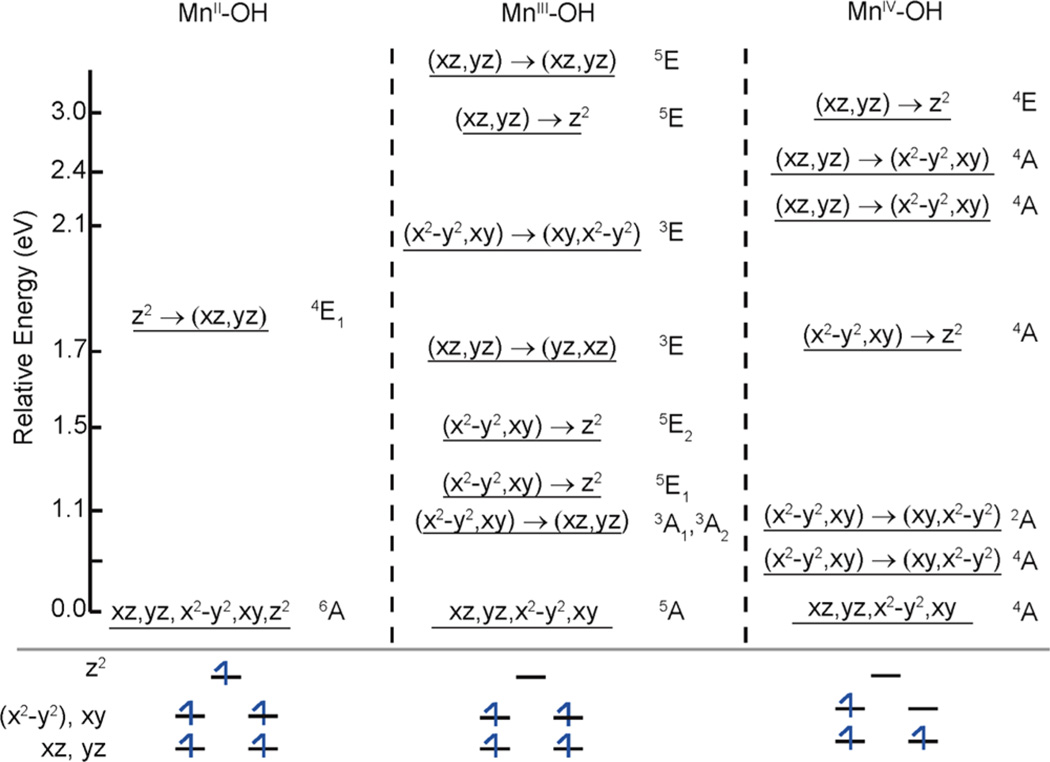
TD-DFT calculations were performed to give a theoretical estimate of the zero-field splitting of the Mn^III–OH complex. As shown in Figure 7, the lowest eight excited electronic configurations having S = 2 are a set of two degenerate pairs near 1.3 eV and another set of two degenerate pairs near 3 eV above the ground S = 2 state. These excited configurations correspond to the promotion of an electron from the d_x²_−y², _xy (1.3 eV) and d_{xz, yz} (3 eV) orbitals to the unoccupied d_z² orbital. The ⁵E configurations near 1.3 eV do not contribute to the D-tensor because the matrix elements of the angular momentum operator (L) between d_z² and d_x²−_y², _xy vanish. For the ⁵E configurations near 3 eV, the matrix elements of L for d_z² and d_{xz, yz} are nonzero and these configurations contributed to the D-tensor. The UV–vis spectra of the complex will be published elsewhere. Two prominent bands are observed with peaks at 1.7 and 2.9 eV, which are reasonably close to the TD-DFT calculated energies for the transitions d_x²−_y², _xy → d_z² and d_{xy, xz} → d_z², respectively.

Figure 7.

Relative energies of the excited states from TD-DFT calculations for the Mn^II, Mn^III, and Mn^IV trigonal complexes reported here. The orbitals connected by horizontal arrows indicate the d–d electronic transition with respect to the ground state configuration. The bottom panel shows the electronic configuration of the ground state.

The triplet-spin excited states may also contribute to the D-tensor. The lowest triplet configuration, calculated by computing the SCF energy for a vertical excitation from the ground state, is approximately 1.1 eV higher in energy than the quintet state. TD-DFT calculations revealed three more triplet states near this energy. The spin-orbit contributions to the D-value of a quintet state from the S = 1 (D₁) and the S = 2 (D₂) excited configurations using second-order perturbation theory are¹⁵

$$D_2={\xi }^2\frac{3{\gamma }_{z^2}{\gamma }_{xz}}{16{\mathrm{\Delta }}_{xz,yz\to z^2}}{D}_1={\xi }^2[\frac{2{\gamma }_{x^2-y^2}{\gamma }_{xy}}{3{\mathrm{\Delta }}_{xy\leftrightarrow x^2-y^2}}+\frac{{\gamma }_{yz}{\gamma }_{xz}}{6{\mathrm{\Delta }}_{xz\leftrightarrow yz}}-\frac{{\gamma }_{xz}{\gamma }_{xy,x^2-y^2}}{6{\mathrm{\Delta }}_{xz,yz\to xy,x^2-y^2}}-\frac{{\gamma }_{xz}{\gamma }_{x^2-y^2,xy}}{6{\mathrm{\Delta }}_{x^2-y^2,xy\to xz}}]$$ (2)

where ζ is the single electron spin–orbit coupling constant and has a value of ≈350 cm⁻¹,³⁸ γ are covalency factors, and Δ_i is the energy gap corresponding to the electronic transition denoted by the subscript. The covalent interactions in the metal–ligand bonds can give values of γ_i less than 1. A simplistic analysis allowed an estimate of the covalency due to delocalization of a d-electron onto a single ligand p-orbital.³⁹ The covalency factors from the Mulliken populations are given in Table S1 (Supporting Information). Using the excitation energies calculated from TD-DFT and the covalency factors in eq 2 gave D-value contributions: D₂ = +0.5 cm⁻¹ and D₁ = +3.5 cm⁻¹ and a total value of D = D₁ + D₂ = +4.0 cm⁻¹.

Compared to the isoelectronic Fe^IV–O complex, [Fe^IVH₃buea(O)]⁻, in which the calculated and the experimentally determined D-values were in excellent agreement,¹⁵ the theoretical value (+4.0 cm⁻¹) for the Mn^III complex was significantly greater than the experimentally determined D-value (+1.7 cm⁻¹). A plausible explanation comes from the Mulliken spin density of the d-orbitals for the Mn^III ion. Covalency of the metal–ligand bonds would delocalize the ligand spin density onto the metal orbitals to give Mulliken spin populations that are greater than 1 for the formally singly occupied metal orbitals. However, the Mulliken populations of the d_x²−_y² and d_yz orbitals determined from DFT are less than 1 (Table S1, Supporting Information), suggesting that these orbitals are mixed with the empty d_z² orbital and thus invalidating the simplistic analysis of the covalency factors.

The isoelectronic Fe^IV–O and Mn^III–O complexes of the same ligand exhibit positive D values.^15,26 For d⁴ metal ions in approximate axial C₃ symmetry, the molecular orbital configuration causes the magnitude of the negative components of the D-tensor to be smaller than the positive component, implying such symmetry will exhibit D > 0.

Mn^IV–OH Complex

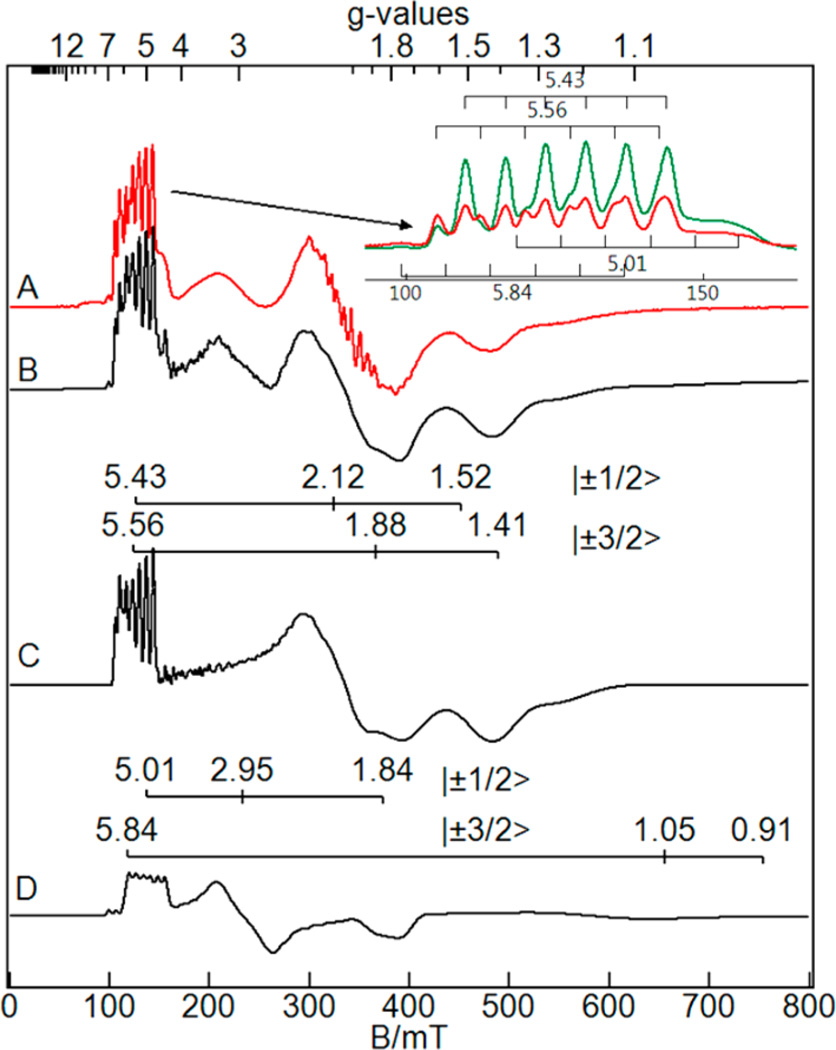
The perpendicular mode EPR spectrum of [Mn^IVH₃buea(OH)] is shown in Figure 8A for a sample with less of the binuclear mixed-valence Mn impurity than the series of Figure 2. The complex showed signals near g = 5, 2, and 1.5, which were in the range expected for an S = 3/2 spin manifold. The spectra recorded at 2 and 10 K show signals from the ground |±1/2〉 and excited |±3/2〉 doublets. The spectra at these two temperatures indicate the presence of two S = 3/2 species, as it is impossible to simulate all the features with a single S = 3/2 species. The spectra consistently showed a ratio of species concentrations S1:S2 equal to 70:30 for multiple synthetic preparations and multiple solvents in DMF, DMF/THF (1:1), DMF/THF (1:2), and possibly for DMA/ THF, but the spectra are much broader. Figure 8B shows simulation of the spectrum of the Mn^IV–OH complex with two distinct species, using the parameters given in Table 1. The two species have similar D-values and A-tensors, but species S2 was significantly more axial (E/D = 0.17) in comparison to species S1 (E/D = 0.31). Figure 8C,D shows the individual simulations and g-values for each species. As shown in the inset of Figure 8, both species showed hyperfine splitting in the low field region from the ground and excited doublets. The six-line patterns centered at g = 5.43 (A = 190 MHz〉 and 5.56 (A = 210 MHz) are from the |±1/2〉 and |±3/2〉 doublets of species S1, respectively, with hyperfine constants in parentheses. The signals at g = 5.01 (A = 210 MHz) and 5.84 (A = 210 MHz) are from the |±1/2〉 and |±3/2〉 doublets of species S2, respectively. The relative intensities of signals allowed an accurate determination of the D-values for both complexes. The observed speciation is solvent independent suggesting an equilibrium of two conformations of the complex. The large change is symmetry for the two conformations suggests a change in the primary coordination sphere of the metal, such as the orientation of the hydroxide bond relative to the equatorial Mn–N bonds.

Figure 8.

(A) 5 mM Mn^IV–OH in DMF/THF, (B) simulation sum of the contributions of species S1 (C) and species S2 (D). The g-values of the corresponding |±m_s〉 transitions of the S = 3/2 manifold are shown for the two species. Inset: The low field region at 2 K (green) and 10 K (red). Experimental condition: temperature 10 K, power 0.2 mW, frequency 9.630 GHz.

TD-DFT calculations were performed on the Mn^IV–OH complex to determine the energies of the excited electronic states. The SCF energy for the vertical transition to the S = 1/2 state was 0.7 eV. The positive vertical SCF energy was consistent with the S = 3/2 ground state configuration for the optimized geometry. There are six electron excited states with S = 3/2 configuration within 3 eV of the ground state (Figure 7). The first excited state is 0.5 eV higher than the ground state, corresponding to promotion of an electron in the occupied equatorial orbital (d_x²−_y², _xy) to the unoccupied equatorial orbital (d_x²−_y², _xy). This transition represents the stabilization in the energy induced by Jahn–Teller distortion between the otherwise degenerate equatorial orbitals. The distortion results in significant mixing between the axial and the equatorial orbitals. The orbital mixing causes off-diagonal terms in the D-tensor, consequently, no simple derivation of the D-value from perturbation theory is available. The UV–vis spectra of the complex will be published elsewhere. A broad absorbance is observed between 1.6 and 3.2 eV with a peak at 2.7 eV. The energy of this broad absorbance agrees with the TD-DFT energies of transitions from the ground configuration to the multiple S = 3/2 configurations above 1.7 eV shown in Figure 7.

Symmetry of the Mnⁿ–OH complexes

Relative to the Mⁿ-oxo complexes of [H₃buea]³⁻, the Mⁿ–OH complexes are significantly more rhombic (less axial).¹⁵ Two possible interactions that can lower symmetry are (1) the differential interaction of the lone pairs on the hydroxo ligand with the metal d-orbitals and (2) the distortion of the urea arms caused by steric interaction from the hydroxo ligand. The distortion of a urea arm is observed in all DFT calculated structures and crystal structures of the Mⁿ–OH complexes, whereas the Mⁿ– oxo complexes show no distortion of the urea arms, and the EPR spectroscopy of these complexes also indicate near axial symmetry.^14,23 Mn^III–OH and Fe^III–OH complexes of the amide-based ligand tris(N-isopropylcarbamoylmethyl)aminato have also been characterized.^40,41 These complexes lack the urea arms, and consequently, no steric interactions with the hydroxo ligand. Nevertheless, both the Fe and Mn complexes of this ligand do not display axial electronic symmetry: Fe^III– OH (E/D = 0.1),⁴⁰ Mn^III–OH (E/D ≥ 0.1). These comparisons indicate that the differential interaction of the hydroxo lone pairs with the metal d-orbitals is the dominate cause for the loss of axial symmetry.

The Mn^II–OH complex are significantly more axial relative to the isoelectronic Fe^III–OH complex (E/D = 0.03 and 0.17, respectively).¹⁵ Consistent with the charge and ionic size, the bonds of the Mn^II complex are 0.16 Å longer on average as compared to the Fe^III–OH complex (Table S2, Supporting Information). Consequently, the Mn^II–OH complex more easily accommodates the hydroxide with less interaction of the lone pair of electrons on hydroxide and the metal d-orbitals. Notably, the urea arms are also bent for the Mn^II–OH complex but the electronic symmetry is near axial, which corroborates the lone pair interaction of the hydroxo ligand as a determinant of symmetry.

⁵⁵Mn Isotropic Hyperfine Interaction

Table 1 gives the isotropic ⁵⁵Mn hyperfine constant (A_iso) for various Mn complexes characterized in this report. For the S = 2 Mn^III complex, only the component of the A-tensor along the z-coordinate of the molecular frame can be determined experimentally. DFT calculations have been shown to accurately predict the dipolar component but underestimate the Fermi contact term of the A-tensor.⁴² Therefore, the A_iso value for this complex is calculated using the expression A_iso = A_z – A^dip._z, where A_z (±270 MHz) is the experimentally observed hyperfine splitting, and A^dip._z (−58 MHz) is the theoretical dipolar contribution to the A-tensor from DFT calculation. The sign of A-tensor cannot be determined from EPR spectroscopy, giving possible values of A_iso = −212 or +328 MHz. The value of Fermi contact term for ⁵⁵Mn nucleus is negative,^20,43 ruling out the positive value. The A_iso value for the series of Mn^II,III,IV–hydroxo complexes are 250, 212, 219 (S1), or 224 (S2) MHz, respectively. In comparison with literature values for each respective oxidation state, the present values are within the observed ranges of isotropic hyperfine constants for Mn.^{20,34,35,44–46}

CONCLUSION

Three 5-coordinate Mn–OH complexes, [Mn^IIH₃buea-(OH)]²⁻, [Mn^IIIH₃buea(OH)]⁻, and [Mn^IVH₃buea(OH)] were characterized with EPR spectroscopy to give spin, g-values, zero-field, and hyperfine parameters for all complexes. These complexes with localized C₃ symmetry are high-spin, giving detectable EPR signals in perpendicular and parallel mode at X-band and/or Q-band microwave frequencies. These complexes demonstrate the ability to quantitatively interpret relatively complicated EPR spectra from multiple different oxidation states of the same ligand. Sequential oxidation of [Mn^IIH₃buea(OH)]²⁻ showed nearly quantitative conversion to [Mn^IIIH₃buea(OH)]⁻ and to [Mn^IVH₃buea(OH)]. DFT calculations provided an explanation for the relatively high symmetry of the Mn^II and Mn^III complexes. The large rhombicity found for the Mn^IV complex is caused by Jahn– Teller distortions expected for an S = 3/2 spin system in trigonal symmetry.