1 Introduction
In longitudinal studies individuals are followed over time and their time-varying information on treatment, outcomes, and covariates is collected at certain intervals. Ideally, one would want these intervals as short as possible to consider data collection continuous for all practical purposes. Unfortunately, continuous recording, though sometimes approximately possible for certain outcomes (e.g., death status), is infeasible for most study variables. Rather, the time-varying information is typically collected only during the times when subjects are observed. These times of observation are usually pre-specified in randomized experiments and in certain observational studies in which the subjects' data are recorded at regular intervals. For example, participants in the Multicenter AIDS Cohort Study (MACS) are scheduled to show up at the research center every 6 months,1 and participants in the Nurses' Health Study are asked to return a self-reported questionnaire every two years.2
On the other hand, in many observational studies the observation regime or plan varies across individuals. For example, some observational studies are based on information that is collected for clinical purposes (e.g., databases from health care organizations) and thus the recording of information occurs at irregular and possibly subject-specific intervals. Because the intervals may depend of an individual's clinical history (treatment, symptoms, etc.), we refer to these as dynamic observation plans. Some studies combine the features of dynamic and pre-specified (static) observation plans. For example, the French Hospital Database on HIV (FHDH) collects information whenever an individual comes to an outpatient or inpatient hospital visit for clinical reasons (dynamic observation plan) but also attempts to collect information at least every six months (static observation plan) by reviewing medical records.3 Even studies with a static observation plan like the MACS may have a dynamic component if individuals who do not show up for a scheduled visit do so because of reasons related to their clinical history.
In epidemiology, cohort studies with a predominantly static observation plan are often referred to as interval cohorts because they have regular intervals between visits, whereas cohort studies with a dynamic observation plan are often referred to as clinical cohorts because the interval between visits depends on the clinical evolution of the patient. In this paper we discuss the biases that may arise in interval cohorts with static observation plans, and in clinical cohorts when the dynamic observation plans are not explicitly incorporated in the analysis. We also discuss some analytic approaches that, under certain conditions, allow to adjust for the bias caused by dynamic observation plans. We highlight issues that are implicit in previous work by Robins and colleagues on marginal structural models4,5 and missing data.6
This paper is structured as follows. Section 2 describes inverse probability weighting (IPW) techniques to estimate treatment effects in longitudinal studies with a single static plan (e.g., an interval cohort study). To fix ideas, we summarize the methods previously used to estimate the effect of anti-retroviral treatment on mean CD4 cell count in the MACS/Women's Interagency HIV Study (WIHS) cohorts.7,8 We describe the key assumption of coincidence between observation times and times of potential treatment change. Section 3 extends the discussion to studies in which subjects follow one of several static regimes. Section 4 considers studies with dynamic observation plans (e.g., clinical cohorts), describes two potential biases that may arise in these studies, and proposes IPW-based approaches to adjust for them. Section 5 presents an application of IPW to estimate the effect of antiretroviral treatment on the evolution of the mean CD4 cell count in the FHDH, and Section 6 presents some brief conclusions. Throughout the paper we use causal diagrams to describe the causal structure and some of the key assumptions underlying the IPW approach.
2 A single static observation plan
Consider an observational cohort study to estimate the effect of antiretroviral treatment on the evolution of the mean CD4 cell count. All participants are required to show up for a study visit at baseline and then every 6 months. We refer to this observation plan, similar to the one used in the MACS/WIHS, as single because it is the only one followed by all subjects, and as static because it is pre-specified before the study starts. This section recapitulates the notation and methodology used in our previous analyses of the MACS/WIHS.8
Time is denoted by t and is measured in months since the beginning of a subject's follow-up. The times of observation are, under the study's static observation plan, t = 0, 6, 12, 18, 24, … We make the approximation that observations occur the first day of the month. We use capital letters to represent random variables and lower-case letters to represent possible realizations (values) of random variables. Yi,t is a time-varying variable denoting subject i's CD4 cell count value (in cells/μL) at time t, Li,t denote subject's i vector of time-varying covariates that predict future CD4 count Yi,m for m > t, such as CD4 count and viral load measured at t (Yi,t is included in Li,t). The variables in Li,t are measured at the times of observation. Ai,t is a time-varying dichotomous variable indicating whether subject i is on antiretroviral treatment during the interval (t, t +6]. We assume that the value of treatment Ai,t can only change right after the measurement of Li,t, that is, the observation times are the only times of potential treatment change. We discuss this assumption in section 2.4 below. For any time-dependent variable, we use overbars to denote the history of that variable up to and including t; for example, L̅i,t= (Li,0, Li,1, …, Li,t) is the covariate process through t. We often suppress the i subscript denoting individual, because we assume that the random vector for each subject is drawn independently from a distribution common to all subjects. For the time being, we will assume that there is no censoring due to loss to follow-up or competing risks, that is, the time of end of follow-up K + 1 (last time the outcome Y is observed) is constant for all subjects. We use the symbol ∐ to indicate statistical independence; for example, A II B|C means that A is conditionally independent of B given C.
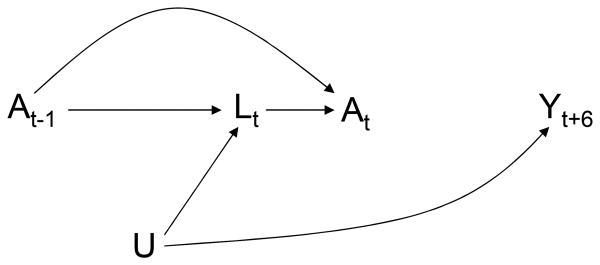
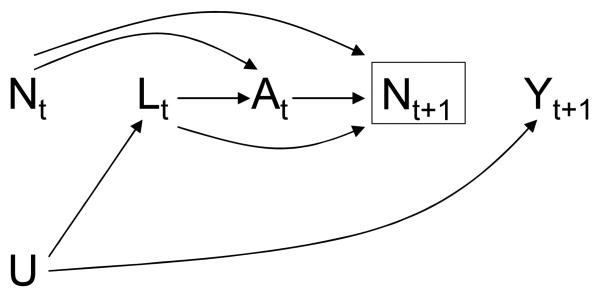
A simplified version of the causal structure of these variables is depicted in the causal directed acyclic graph (DAG) of Figure 1. To avoid clutter, Figure 1 represents only two arbitrary observation times and omits the arrows from treatment A and covariates L to future outcomes Y, i.e., the DAG represents the causal null hypothesis of no treatment effect. The variable U is a vector of unmeasured, and possibly unknown, causes of the covariate process Lt (we are agnostic as to whether U is fixed or time-varying; for simplicity, the DAG represents U as fixed). At each observation time t, physicians and patients decide treatment At based on the information recorded in prior treatment A̅t−1 and covariate L̅t history, which is represented in the DAG by the arrows from At−1 and Lt to At. That is, in the observed data, a subject's treatment plan is dynamic because the value of treatment At at time t is not pre-specified but rather depends on the evolving values of prior covariate history L̅t−1.
Figure 1. A longitudinal study with a single static observation plan.
Dynamic treatment regimes are generally expected in observational longitudinal studies. Typically the observed dynamic treatment regimes depend on some time-varying variables that are risk factors for the outcome (i.e., cause, or share common causes with the outcome). We then say that there is confounding over time, or time-dependent confounding, and refer to the variables Lt that can be used to remove the time-dependent confounding as time-dependent confounders.9 When, as in Figure 1, the time-dependent confounders are affected by prior treatment, conventional methods for confounding adjustment such as stratification and regression may introduce selection bias in the estimation of the causal effect of treatment.10,11 Hence other methods, such as inverse probability weighting (IPW) of marginal structural models or g-estimation of nested structural models, are needed. We now describe IPW of a marginal structural model similar to the one we have used in previous analyses to estimate the effect of antiretroviral treatment.8
2.1 Marginal structural mean model
So far we have vaguely referred to “the causal effect of treatment.” We now provide a formal definition of causal contrasts and propose a structural model to parameterize them.
To describe causal contrasts, we first need to introduce notation for treatment regimes. For simplicity, we restrict our description to static treatment regimes. We consider treatment regimes a̅ = {a0, a 1, …,aK} where at = 1, for t = 0, 1…K, if the regime specifies the subject is to be on treatment at time t and a̅t represents treatment history under regime a̅ through time t. Note a̅K = a̅.
Associated with each of the 2K treatment regimes a̅ are the potential or counterfactual outcomes , which denote subject i's outcome Y at time t had, possibly contrary to the fact, subject i followed treatment regime a̅. The subject's observed outcome Yi,t is the counterfactual outcome , for the treatment regime a̅ that the subject did indeed take. That is, , where a̅ = A̅ is the subject's observed treatment history. The random variables are counterfactual because they represent a subject's outcome had, possibly contrary to fact, the subject received the static treatment regime a̅ rather than his observed dynamic treatment regime A̅. For each regime a̅ we are assuming a subject's responses are well defined, although generally unobserved, and that if the regimes a̅ and a̅′ agree before t. To fix ideas, and without loss of generality, we will focus on the causal contrast where a̅ = 1̅ = {1, 1, …, 1} is the regime “always treat through time t,” and a̅′ = 0̅ = {0, 0, …, 0} is the regime “never treat before time t.”
Suppose we model the mean of the counterfactual outcomes, which are measured at observation times 6, 12, 18, …, as functions of the treatment regime received through the previous time. That is, we assume
| (1a) |
where g (·) is a known function and β is a parameter to be estimated. Let us further assume that
| (1b) |
is correctly specified, with β0 +β2t+β3t2 acting as a time-varying intercept β0,t (i.e., a fixed intercept β0 plus parameters β2, β3 for a deterministic function of time). Then . The assumption that model (1) is correctly specified allows us to use a simple parameterization of the contrast . We refer to model (1) as a marginal structural mean model. Other examples of marginal structural models, perhaps more plausible from a subject-matter standpoint, would lead to alternative parameterizations.8 For example, model (1) states that the mean of Y at time t depends on the duration of treatment from times 0 to t – 1, and that each additional month of treatment within that period has the same impact on (i.e., adds β1 to) the mean of Y. Alternative models could state that the mean of Y at time t depends on the duration of treatment from times 0 to t – 3, or from times t – 9 to t – 3, or that the impact of recent treatment (say, at time t – 1) is greater than that of past treatment (say, at time t – 9). Although we selected model (1) for simplicity, readers may choose any other model that they consider more realistic. Since the choice of structural model does not affect the conceptual issues discussed throughout this paper, we will not reiterate the need for a correctly specified structural model.
2.2 Inverse probability weighting
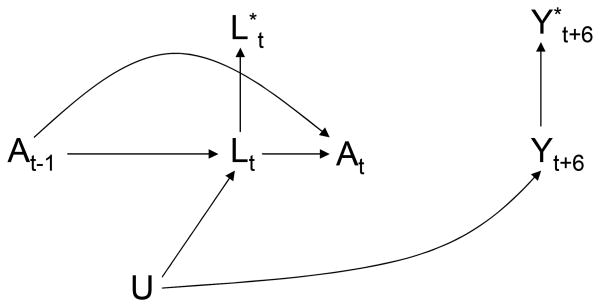
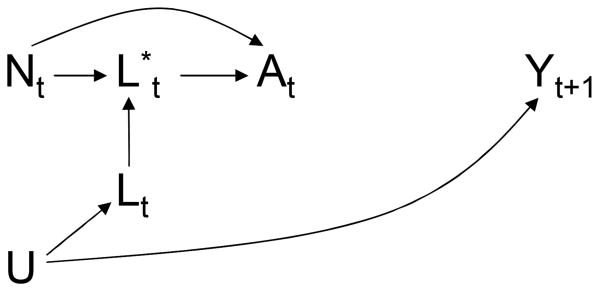
We now describe how to estimate β1 by IPW. One way of thinking about IPW is the following: IPW simulates a pseudo-population in which treatment At does not depend on prior covariate history L̅t–1, i.e., a pseudo-population in which the arrow from Lt to At in Figure 1 does not exist and thus the treatment regime is no longer dynamic.9 The causal DAG in Figure 2 represents the static treatment regime in the pseudo-population in which there is no confounding for the effect of the treatment process At on the outcome process Yt.
Figure 2. A longitudinal study with a single static plan and a carried forward covariate L*.
We can simulate the pseudo-population associated with the DAG in Figure 2 by assigning, to each
subject in the original population, the subject-specific and time-varying stabilized weights
where f (Ak|A̅k–1, L̅k) is, informally, the probability that a subject received the treatment Ak that she actually received at observation time k, conditional on her past covariate and treatment history; and f (Ak|A̅k–1) is defined analogously but conditional on past treatment history only. The factors f (Ak|A̅k–1, L̅k) and f (Ak|A̅k–1) need to be estimated from the data, typically by using parametric models,8 but only for the times k at which the value of treatment A may change (i.e., the observation times 0, 6, 12… under our assumptions). At all other times, the ratio because both numerator and denominator equal 1 (i.e., treatment cannot change). In our study, the analyst can use a logistic regression model to predict the probability of being treated at each time of potential treatment change k, Pr [Ak= 1|A̅k–1, L̅k], conditional on covariates that summarize treatment and covariate history through k. (In many applications the weights are further stabilized by adding a subset V of the baseline variables L0to the conditioning event in the numerator, and as covariates in the structural model.) As a result, the effect estimates will be biased if the models used to estimate the inverse probability weights are misspecified.
We then fit the mean model
| (2a) |
where
| (2b) |
to the weighted data (i.e., the pseudo-population). A 95% confidence interval around γ̂ can be constructed by computing the variance through bootstrapping or by using the sandwich estimator12,13 of the variance (which results in a conservative confidence interval14).
Under the assumptions described below, the parameter vector γ in the pseudo-population equals β in the original population, and therefore a weighted least squares estimate γ̂ is consistent for β. If those assumptions hold, one can consistently estimate the contrast by γ̂1 (t–1).
2.3 Identifiability assumptions
The parameter β1 of marginal structural mean model (1) is consistently estimated by γ̂1 under the following three assumptions:
| (CA) |
| (EA) |
and
| (PA) |
We refer to assumption (CA) as consistency, to assumption (EA) as exchangeability, and to assumption (PA) as positivity. An important clarification: the times denoted by k in assumptions (EA) and (PA) refer to the times in which the value of the treatment process Ak may change. Under our assumption that the times of potential treatment change coincide with the times of observation, exchangeability (EA) and positivity (PA) automatically hold at all other time points.
Assumption (CA) means that a subject's counterfactual outcome under the same treatment regime that he actually followed is, precisely, his observed outcome. Although the consistency of counterfactuals cannot always be taken for granted in observational studies,15,16 assumption (CA) seems reasonable in many pharmacoepidemiologic applications like ours.
Assumption (EA) means that, at every observation time k and conditional on prior treatment and covariate history, the treated and the untreated are exchangeable. This conditional exchangeability, also known as the no unmeasured confounding or sequential randomization assumption, holds in the study represented in Figure 1 because there are no direct arrows from unmeasured variables U to the treatment process At. In real observational studies, however, the lack of arrows from unmeasured variables to treatment cannot be checked and thus assumption (EA) is not empirically verifiable. Investigators need to use their subject-matter knowledge to propose time-dependent confounders Lt, obtain repeated measures of the variables in Lt, and then hope that the assumption holds approximately conditional on all variables recorded. A technical clarification: assumption (EA) is too strong for our purposes in this example. To estimate a contrast of two mean counterfactual outcomes such as , assumption (EA) can be replaced by the weaker mean independence assumption
which is implied by assumption (EA). Below we refer to assumption (EA) as necessary, but bear in mind that only its consequence, mean independence, is necessary for our current purposes.
Assumption (PA), also known as the assumption of experimental treatment assignment, requires that, at every observation time k, the probability of finding all treatment levels conditional on past treatment and covariate history is positive. The assumption is satisfied if the population contains both treated and untreated individuals in all strata defined by prior treatment and covariate history.
2.4 Times of treatment change not restricted to observation times
So far we have assumed that the value of treatment At can only change at the observation times Formally, the assumption of no treatment change at non observation times can be represented as
| (O) |
where Ni,t is a time-varying observation indicator: Ni,t = 0 when subject i is not observed at time t, and Ni,t = 1 when subject i is observed at time t. This assumption would hold true if subjects had no access to treatment except at study visits and if subjects could not discontinue treatment on their own. However, in many epidemiologic studies the assumption of full coincidence between times of observation and times of potential treatment change is not tenable. For example, in the MACS/WIHS subjects are seen every 6 months at times 0, 6, 12… but they can initiate or stop treatment at any time between visits. Further, in many epidemiologic studies with static observation plans, the changes in the value of treatment At that occur at times other than observation times can be ascertained while the value of the confounders Lt at those times remains unmeasured. For example, in the MACS/WIHS, changes in treatment status during the months between two study visits (say, at month t = 9) are learned by investigators at the next visit (month t = 12) assuming the subject did not die or was lost to follow-up, but the value of CD4 cell count in the non-observation month (t = 9) remains unknown.
The result of the discordance between observation times and times of potential treatment change is bias. To see why, consider the following example. In the MACS/WIHS, a patient with CD4 cell count of 400 measured at consecutive observations times 6 and 12 may have started treatment in non-observation month 9 because her CD4 cell count had dropped to 250 in month 8. The CD4 cell count of 250 was observed by the patient's treating physician, which triggered the change in treatment status. However, the 250 value was not recorded in the study data, and thus cannot be used to adjust for confounding by indication. In other words, if time point t represented in the causal DAG of Figure 1 corresponds to a non-observation time, then Lt is unmeasured and there is intractable confounding for the effect of At or of any function of treatment that involves At (e.g., “always treated” or “never treated”). Equivalently, the exchangeability assumption (EA) is violated because the decision to initiate or stop treatment is partly determined by Lt, a variable that is not available at all times t of potential treatment change.
A simplistic approach to deal with the lack of data on the confounders Lt at all times t of potential treatment change is to carry forward the the confounder values. Let be the most recently recorded value of L at time t. For example, in the MACS/WIHS analyses, for t = 9 because L6 is the most recently measured CD4 cell count at time 9, and for t = 12 because the CD4 cell count is measured at time 12. When Lt is unavailable, one could replace Lt by in the estimation of the weights . This carry-forward approach allows to estimate the parameter γ1 from the weighted regression model (2), even if data on Lt is unavailable at all times t of potential treatment change. However, the associational parameter γ1 will not generally equal the causal parameter β1 of the structural model (1). This is so because the redefined weights that use rather than Lt do not generally create a pseudo-population in which the arrow from Lt to At in Figure 1 does not exist for all times t. The causal DAG in Figure 3 is similar to that in Figure 1 except that it includes the carried-forward value The arrows into from Lt (shown in the DAG) and from L measured at the most recent observation time before t (not shown in the DAG) are deterministic because the carried-forward covariate value is then .
Figure 3. Explicit representation of a single static observation plan.
The uncoupling of the times of observation and of potential treatment change is often a limitation in longitudinal studies with a static observation plan (i.e., interval cohorts). The coarser the observation plan, the larger the unmeasured confounding is expected to be. Previous analyses of interval cohorts recognized this potential for residual confounding: Cole et al17 explained that their estimates “may be sensitive to the relative infrequency of data collection (i.e., 6-month intervals). Misclassification due to this coarse measurement (with respect to time) could have reintroduced some confounding, which could have biased the estimated difference in either direction.”
Lack of exchangeability (EA), or residual confounding, when assumption (O) does not hold may arise in the presence of both static and dynamic observation plans. Therefore this problem applies throughout all settings discussed in this paper even if, to keep a smooth flow of arguments related to other issues, we sometimes ignore it.
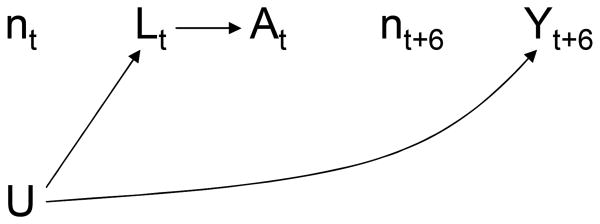
2.5 No bias if times of observation times and of treatment change coincide
We define a static observation plan as n̅ = {n0, n1, …, nK}. For example, if a subject is to be observed at months 0, 6, 12, …, as in the MACS/WIHS, we say that his static observation plan is {1, 0, 0, 0, 0, 0, 1, 0, 0, …}. The causal DAG in Figure 4 depicts two time points of a cohort study in which all subjects follow the same static observation plan n̅ (e.g., all subjects are observed every 6 months). The node for At–1 is omitted for simplicity. The nodes for the observation variable Nt are represented by lowercase letters because their value (1 or 0) does not change across subjects. In other words Nt is not really a random variable because Ni,t= Nj,t for any two subjects i and j, and thus needs not be considered in the analysis. This is the justification for omitting the observation plan from the analysis of interval cohorts (e.g., the MACS/WIHS) in which all subjects follow a static observation plan: the IPW analysis described above is mathematically equivalent to one that explic- itly incorporates the single static observation plan. There is no need to make the function g (a̅t; β) explicitly dependent on n̅t because n̅t is constant across subjects. Hence the entire analysis, including the inverse probability weights , is implicitly conditional on the observational plan n̅.
Figure 4. Multiple static observation plans.
Thus, under assumption (O), no bias results from failing to explicitly consider a static observation plan in the analysis. But an explicit consideration of the observation plan, even if static, is necessary to characterize the causal effect that is being estimated. This is so because the causal effect of a time-varying treatment generally depends on the observation plan. For example, consider a therapy that is beneficial for HIV-infected subjects but only if they start taking the therapy within a month of having a CD4 cell count less than 200. Now consider two longitudinal studies to estimate the effect of the therapy among HIV-infected subjects. No subject is on the therapy at baseline in either study. In the first study subjects are observed every month n̅ = {1, 1, 1, …}; in the second study subjects are only observed at months 0, 6, 12, … In the first study, all subjects with a CD4 cell count below 200 will be put on therapy within one month and thus the beneficial effects of treatment will be realized. In the second study, some subjects' CD4 cell count will drop below 200 during no-observation months so that, by the time the subject is observed, it will be too late for the therapy to exert its beneficial effect. Thus the estimated beneficial effect of therapy will be stronger in study 1 than in study 2. This simple example illustrates an important point: the effect of a treatment regime a̅ cannot be defined in isolation. Rather, we always estimate the effect of the joint regime with two components, observation plan and treatment regime, even if we often do not explicitly mention the observation plan.
3 Multiple static observation plans
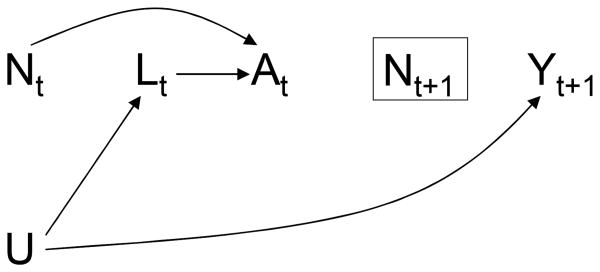
Let us now consider a hypothetical follow-up study in which each subject is randomly assigned to one of several static observation plans. For example, some subjects will be observed every month n̅ = {1, 1, 1, …}, others will be observed every other month n̅′ = {1, 0, 1, …}, etc. The causal DAG in Figure 5 depicts two consecutive time points of such study. The nodes for the observation indicators N are now uppercase because Nt is a random variable: in general Ni,t≠ Nj,t for subjects i and j.
Figure 5. Selection bias due to a dynamic observation plan.
A rectangle around a variable signifies that the analysis is conditional on (restricted to) some levels of the variable. Thus the rectangle around Nt+1 means that only person-times with Nt+1 = 1 will contribute to the fit of weighted model (2) at time t because those are the only ones with a known value of the outcome Yt+1. Similarly, model (1) is redefined as E [Yt+1|A̅t, Nt+1 = 1] = g (A̅t; γ). We did not draw a rectangle around Nt because under assumption (O) the value of treatment process At is known for person-times with both Nt = 1 (because treatment changes occur and are recorded at those times) and Nt = 0 (because treatment cannot change at those times and therefore its value equals the most recently recorded one), and thus whether those person-times contribute to model fitting depends only on whether Nt+1 = 1. There is also an arrow from Nt to At as treatment can only change when Nt = 1. In contrast, there are no arrows pointing to Nt because whether an observation Nt takes place at time t is predetermined and hence does not depend on the subject's prior history.
The causal DAG in Figure 5 lacks a direct arrow from the observation indicator Nt to the measured covariates Lt, which represents the assumption that the observation plan can only affect the measured values through its effects on the treatment of interest. Under this assumption of no direct effect of observation on measured values, frequent observations may lead to better outcome (e.g., a higher CD4 cell count) than rare observations, but only because, as discussed in the example of the previous section, they allow for more timely treatment. A corollary of the assumption of no direct effect of observation on the measured covariates is no direct effect of Nt on the outcome Yt. The assumption of no direct effect of observation on measured values would not hold if effective medical interventions are administered, but unrecorded, during observation times, or if the observation itself affects the outcome. Suppose, for example, that a pharmacological treatment for high blood pressure requires frequent clinic visits (say, to monitor blood levels of the drug), which increase the blood pressure in some subjects who find medical encounters stressful.
Because we always estimate the effect of a joint regime (n̅, a̅), we need to define as the counterfactual outcome under observation plan n̅ and treatment regime a̅, and re-express our causal contrast of interest to clarify that the contrast depends on the observation plan. In fact, marginal structural model (1) is really the model , which incorporates the assumption of no direct effect of observation Nt on the outcome Yt, because the function g (a̅t; β) does not depend on n̅t: the mean counterfactual outcome is assumed to be the same for all observation plans in the study. Under this assumption of no direct effect of the observation plan, the parameter β1 quantifies the effect in any population with the same mixture of observation plans as the study population. For example, consider again two longitudinal studies to estimate the effect of an antiretroviral therapy that is beneficial only if started within a month of having a CD4 cell count less than 200. In the first study, subjects are randomly assigned to several static observation plans with 75% of the patients assigned to the plan “observe at every month”; in the second study, subjects are randomly assigned to several static observation plans with 5% of the patients assigned to the plan “observe at every month”. More subjects with a CD4 cell count below 200 will be put on therapy within a month in the first study than in the second study. Thus the absolute value of β1 will be greater in the first study than in the second study.
This dependence of the interpretation of the causal parameter on the mixture of observation plans in the study population may compromise the generalizability or “transportability” of the estimated treatment effect to other populations. For example, an effect estimated under a health care system that schedules frequent medical encounters for all HIV-infected subjects in the population may be less relevant for a second population with more barriers to access to the health care system. Two possible solutions to this problem are 1) censoring subjects when they deviate from the observational plans of interest, and 2) expanding the structural model to relax the assumption of no direct effect of the observation plan. We now describe both approaches.
3.1 Artificial censoring
Suppose we want to estimate the effect of treatment if all subjects had been observed every month, even though in our study population some subjects were unobserved at some months. That is, we are only interested in the effect of treatment in the population under observation plan n̅ = {1, 1, 1, …} “observe at every month”. We can estimate this effect by censoring subjects as soon as they deviate from the observation plan of interest (i.e., the first month they are not observed), and then estimate the parameters of model (1) by restricting the fitting of model (2) to the uncensored person-time. This artificial censoring does not result in selection bias because the static observation plans were randomly assigned at baseline, and therefore the observation times are independent of both the time-varying treatment and the outcome.
The artificial censoring approach can be extended to any set of static or dynamic observation plans. For example, suppose that we want to estimate the effect of treatment if all subjects had been observed at least once every 3 months, even though in our study population some subjects went unobserved for periods longer than 3 months. That is, we are only interested in the effect of treatment in a population in which subjects follow observations plans such as {1, 0, 1, …} and {1, 0, 0, 1, …}, but never observation plans such as {1, 0, 0, 0, 1…}. We would then censor subjects as soon as they deviate from the observation plans of interest, i.e., 3 months after their last observation. Again this artificial censoring introduces no bias because the observation plans were randomized at baseline.
The effect estimated in the artificially censored data can be interpreted as the effect in a population in which all subjects follow the set of observation plans of interest (e.g., be observed at least once every 3 months), and in which the distribution of these observation plans is the same as in the study population.
3.2 Modeling the effect of the observation plan
The assumption of no direct effect of the observation plan can be relaxed by making the structural model explicitly dependent on the observation plan. For example, model (1) can be expanded to
| (3a) |
| (3b) |
where, for simplicity of presentation, we chose to summarize the observation plan through time t + 1 by a linear term for the proportion of times that the subject was observed through t + 1 and a product term between the indicator for being observed at t and the term for treatment regime. Alternative summaries of the observation plan may be more appropriate in many settings, but the choice of summary does not alter the reasoning below. Section 3.3 describes how to estimate the model parameters by IPW.
Estimating the parameters of model (3) in the entire data set has several advantages compared with estimating the parameters of model (1) in the artificially censored data. First, a test of (β4, β5) = (0, 0) from model (3) is a test of the hypothesis of no direct effect of the observation plan. Second, in the presence of a direct effect, the model allows one to estimate under any static observation plan n̅ and thus the model helps “transport” the effect estimated in one population with certain mixture of static plans to another population a particular observation plan. Third, if few subjects followed the observation plans of interest, artificial censoring may result in effect estimates with wide confidence intervals. On the other hand, estimating model (3) in the entire data set has several disadvantages compared with estimating model (1) in the artificially censored data. First, the artificial censoring approach is agnostic about the relative effects of different observation plans and thus requires fewer parametric assumptions than model (3). Second, a blind use of model (3) may lead to extrapolation beyond the data. For example, model (3) would allow to compare two treatment regimes under the observation plan n̅ = {1, 1, 1, …} “observe at every month” even if nobody in the population had been actually observed every month, whereas the artificial censoring approach decreases the risk of extrapolating beyond the available data.
Note that artificial censoring can be combined with modeling the effect of the observation plan. For example, one could first use artificial censoring to restrict the inference to a set of observation plans, and then estimate the parameters of model (3) in the artificially censored data to make inferences under a particular observation plan within the set of observation plans of interest.
3.3 Inverse probability weighting
IPW estimation of the parameters of model (3) is identical for studies with a single static observation plan and for studies with multiple static observation plans randomly assigned at baseline. To see this, first note that, when the observation plan is explicitly considered in the analysis, we can redefine the inverse probability of treatment weights as
where, under assumption (O), the ratio if Nk = 0. Effectively, this means that we only need to estimate the factors in the numerator and denominator of the weights for the observation times Nk = 1 when the value of treatment may change. The inverse probability weights create a pseudo-population in which the treatment regime A̅t only depends on prior observation history.
Second, since we are estimating the joint effect of treatment regime and observation plan, one could think that we also need to estimate inverse probability weights
to create a pseudo-population in which the regime N̅t+1 would only depend on prior treatment history, and then compute the product to create a pseudo-population in which the joint regime (a̅t, n̅t+1) is static. However, in our setting with multiple static observation plans, for all k because numerator and the denominator are equal. (The equality of numerator and denominator holds for any process randomized at baseline.18) As a result, the subject-specific weights equal , and static observation plans do not need to be explicitly considered in the analysis. When observation plans are static, the parameters of the model weighted by only can be causally interpreted as the direct effect of treatment A̅t on Yt+1 that is not mediated through Nt+1 (because the analysis is conditioned on Nt+1 = 1).
Similarly, assumptions (CA), (EA), and (PA) can be more generally re-expressed as
| (C) |
| (E) |
and
| (P) |
respectively. It is trivial to check that, when all observation plans are static and randomly assigned, assumptions (C)-(E)-(P) will hold true whenever assumptions (CA)-(EA)-(PA) hold true.
Under assumptions (C)-(E)-(P)-(O) and no weight model misspecification, the parameters of model (3) can be consistently estimated by fitting the mean model
| (4a) |
where
| (4b) |
to the weighted data (i.e., the pseudo-population). Also, under the same assumptions, the parameters of model (1) in a population in which everybody follows one of the observation plans of interest can be consistently estimated by fitting model (2) to the artificially censored, and weighted, data.
So far we have considered a setting in which the static observation plans are randomly assigned at baseline. Consider now a setting in which the static observation plans are still randomly assigned at baseline but the randomization probabilities vary across levels of some baseline variables V (a subset of the variables in L0). The generalization of the analysis to a setting in which the static observation plans are assigned conditional on baseline variables is straightforward. The only difference is that the ratio will not equal 1 in that setting and thus the weights for observation need to be estimated. Alternatively, one could add the baseline variables V as covariates to model (3) and also to the conditioning event of the numerator of the weights so that the ratio , where V is included in L̅k–1, equals 1 and thus a explicit consideration of the observation plan becomes unnecessary again.
We can still push it a bit more. Consider a setting in which the observation times depend on the time-varying treatment At but not on the time-varying covariates Lt, i.e., an arrow is added from At to Nt+1 in Figure 5. Because the observation times are not prespecified at baseline but rather depend on the dynamic treatment A, the observation plans are now dynamic. However, the ratio is still equal to 1 and thus the analysis does not need to explicitly consider this particular type of dynamic observation plan that does not depend on the time-varying covariates. We now turn our attention to the most general case: dynamic observation plans that depend both on the time-varying treatment A and the time-varying covariates L.
4 Dynamic observation plans
The previous section shows that there is no need to explicitly consider the observation plan in the analysis when all subjects follow static observation plans. We now consider a follow-up study in which the recording of information (treatment, outcomes, and covariates) occurs at irregular, and subject-specific, intervals. The times of observation depend on the subject's past treatment and covariate history and thus we say that the observation plan is dynamic. For example, in the FHDH the observation plan is dynamic because, in any given month, subjects who are receiving treatment or have a recently measured low CD4 cell count are more likely to be observed. Unlike static observation plans, dynamic observation plans need to be explicitly accounted for in the analysis. Otherwise, the effect estimates will be biased. The time-dependent biases induced by dynamic observation plans can be classified into two types, which we refer to as selection bias and confounding. In this section we describe each of these two biases and the assumptions under which IPW can be used to eliminate them.
4.1 Selection bias
The causal DAG in Figure 6 represents the causal structure of a study with a dynamic observation plan—again under the null hypothesis of no treatment effect and limited to two arbitrary time points. As explained above, the box around Nt+1 denotes that the analysis is restricted to person-months with Nt+1 = 1, the only ones with a known value of the outcome Yt+1 and thus the only ones that can contribute to the fit of the weighted model.
Figure 6. Confounding due to a dynamic observation plan.
The key difference between Figures 5 and 6 is that Figure 6 includes arrows into the N nodes from prior observations N, covariates L, and treatment A. That is, whether a person is observed at a given time t may be affected by her prior history. These additional arrows into N will generally introduce bias because the analysis is conditioned on a common effect (Nt+1) of treatment (At) and a cause (U) of the outcome. We refer to this bias as selection bias because it is due to the selection of person-months with Nt+1 = 1 into the analysis.11 Section 4.3 describes how to adjust for this bias via IPW.
The structure of the selection bias induced by a dynamic observation plan is identical to the structure of informative censoring due to loss to follow-up.11 In fact, censoring is an extreme case of observation plan in which a subject censored at t is never observed again. Censoring is a monotonic observation process in which the observation process Nt can only change its value once (from uncen-sored 1 to censored 0). Censoring by administrative end of follow-up is a monotonic static observation plan because the administrative end of follow-up is prespecified at baseline, whereas censoring by loss to follow-up is a monotonic dynamic observation plan because the time of loss to follow-up varies across subjects. Many studies have used IPW to adjust for the bias induced by dynamic monotonic observation plans (i.e., censoring). The IPW method described in Section 4.3 is simply a generalization to non monotonic observation plans.
Finally, note that a dynamic observation plan will not induce selection bias if the outcome can be independently ascertained. For example, in mortality studies in the U.S., death status can be learned from the National Death Registry even if subjects are not observed by the investigators and thus there is no need to condition on Nt+1 = 1. This lack of selection bias may have no practical consequences as one may still want to use IPW to adjust for confounding (see below) or to increase transportability of the effect estimate, or both.
4.2 Confounding
To explain the second bias due to dynamic observation plans, we need to modify the causal DAG in Figure 6. In fact, Figure 6 is an incorrect, though useful, oversimplification of the actual data structure. The causal DAG in Figure 7 is a better representation of a study with a dynamic observation plan. We have omitted Nt+1 and the arrows into it because those components of the diagram, which were appropriately represented in Figure 6, play no role in the generation of this second bias.
The key difference between Figures 6 and 7 is the introduction of , the most recently recorded value of the confounders L by time t. Because in many studies the value of is used by physicians and patients to decide whether to initiate or discontinue therapy At at time t, the DAG in Figure 7 includes an arrow from to At. The value of equals that of Lt only when both Nt = 1 and the confounders L were actually measured at time t, otherwise the value of equals that of the most recent L measurement (e.g., Lt–3 if the last measurement of L took place during an observation at time t – 3). Because of the partial dependence of on Lt, the DAG in Figure 7 includes an arrow from Lt to . (Again the DAG is restricted to two arbitrary time points to avoid clutter; otherwise it would also include arrows from Lm to , for m < t.) There is no direct arrow from the generally unknown variable Lt to At because treatment decisions are entirely mediated through the measured value . Under the assumption of no direct effect of observation on the covariates, there is no direct arrow from Nt to Lt. There is, however, an arrow from Nt to the measured covariates because the value of is a function of whether the subject is observed at time t. For example, in our study a subject will have certain value of CD4 cell count, say 200, at time t whether or not the subject sees the doctor at time t, but this value will only be revealed if the subject is observed at t.
In Figure 7, treatment At and outcome Yt+1 share the common cause U and one needs to simultaneously adjust for and Nt in order to estimate the effect of treatment on the outcome. In graph-theoretic terms, one would say that conditioning on both and Nt is required to block the open back-door paths between At and Yt+1. Because epidemiologists often refer to the bias that arises from the existence of common causes of treatment and outcome as confounding,20 we say that ignoring the components Nt of the dynamic observation plan in the analysis creates confounding. Section 4.3 describes how to adjust for this bias via IPW.
4.3 Inverse probability weighting
We have described marginal structural models that either assume no direct effect of the observation times on the outcome [model (1)] or allow for a direct effect of the observation times on the outcome [model (3)]. We now describe how to use IPW for estimating the parameters of marginal structural models like (1) and (3) in the presence of selection bias or confounding due to a dynamic observation plan.
For the remainder of this paper, let us redefine the weights and the assumptions assumptions (C)-(E)-(P) with Lk is replaced by . The redefined weights create a pseudo-population in which the joint regime (a̅t,n̅t+1) is static, i.e., the arrows from into Nt for m < t and from into At for m ≤ t are erased. Hence the selection bias is eliminated by assigning to each subject her weight and then fitting a weighted model like (2) or (4). In contrast with the multiple static regimes setting of Section 3, the observation weights are not equal to 1 in the presence of dynamic observation regimes. Hence one needs to use parametric (e.g., logistic) models to estimate the factors in the numerator and denominator of the weight. In our example, these are models for the probability of being observed at each time, , conditional on covariates that summarize observation, treatment, and covariate history through that time. Under (C)-(E)-(P)-(O) and no weight model misspecification, IPW removes the selection bias and provides consistent estimators of the parameter of the structural model.
Let us suppose for a moment that the selection bias does not exist and that we only need to adjust for confounding bias. Under our assumptions, one could naively argue that this confounding bias is eliminated by assigning to each subject an estimate of the weight
at each time t, and then fitting a weighted regression model such as E [Yt+1|A̅t, N̅t, Nt+1 = 1] = g (A̅t, N̅t; γ). This appears to be a logical approach since the confounders are now expanded to . However, under assumption (O), this approach violates positivity (P) because, at times k with no observation, Nk = 0, treatment is a deterministic function of prior treatment. As a result, the probability is not positive, and the effect estimates will be biased. Of course, in the absence of condition (O), exchangeability (E) is generally violated because the reasons for treatment change at times Nk = 0 remain unmeasured, i.e., there are some direct arrows from Lm to At for m ≤ t as shown in Figure 3. But even if (E) were not violated, one would be estimating the treatment effect in a population with the same mixture of dynamic observation plan as in the study population, which may affect the transportability of the effect estimate to other populations.
For the reasons stated in the previous paragraph, a preferable approach to deal with confounding would be assigning to each subject her estimated weights and then fitting a weighted regression model like (2) or (4). Under the modified assumptions (C)-(E)-(P)-(O) and no weight model misspecification, this IPW approach simultaneously adjusts for selection bias and confounding, and allows data analysts to estimate the treatment effect estimate under different observation plans.
Let us now discuss the plausibility of the exchangeability assumption (E) for the observation plan N. Exchangeability requires that, at every time k, the mean counterfactual outcomes of subjects who are observed equal those of subjects who are not observed, conditional on the measured observation, treatment and covariate histories (N̅k–1, A̅k–1, L̅k–1). The practical implication of the exchangeability condition is that all joint predictors of observation Nk at time k and of future outcome values need to be correctly measured and appropriately included in the model for . One could naively think that assumption (E) holds if, as in Figure 6, there is no direct arrow from unmeasured causes U of the outcome Yt+1 to Nt+1. However, because of the nature of dynamic observation plans, (E) is in fact a stronger condition than ‘no arrows from the unmeasured variables U into the observation indicators N’. To see this, suppose that developing symptoms of HIV disease at time k – 1 is a strong predictor of both seeing the doctor at time k (Nk = 1) and of later outcome. Then the variable ‘symptoms at k – 1’ should be included in the model. However, the value of the variable ‘symptoms at k – 1’ will only be measured among those patients who were observed at time k – 1 (Nk = 1) and thus will not be generally available for all patients. Thus the variable cannot be added to the model and exchangeability (E) is violated. Hence assumption (E) holds for dynamic observation plans only when, at every time t, one can achieve conditional exchangeability between observed and unobserved subjects by using the A, L values measured at the most recent time each subject was observed, whenever that time was for each subject. For example, (E) holds in settings in which, at each observation time, doctors decide the time of the next observation based on the current treatment and covariate values (e.g., CD4 cell count), but (E) will not hold if patients decide when to be observed based on their covariate values (e.g., symptoms) in between visits, which are by definition unmeasured variables in clinical cohorts.
An alternative approach to estimate the effect of interest under a continuous observation plan n̅ = {1, 1, 1…1} is, as discussed above, artificially censoring those subjects who deviate from the plan. For example, previous applications of artificial censoring in interval cohorts8,19 estimated the treatment effect under the observation plan n̅ = {1, 1, 1…1} “observe at every visit” by censoring subjects the first time they missed a scheduled visit. In the presence of dynamic observation plans, this artificial censoring may be informative and thus needs to be adjusted for. To adjust for the potential selection bias induced by informative censoring, these investigators estimated weights , where
and Dk is an indicator (1: yes, 0: no) for being censored at time k. (Note that, in this case, Dk–1 = 0 implies Nk = 1 for all k and thus adding N̅t – 1 to the conditioning event is redundant.) Artificial censoring simplifies the analysis by transforming the non monotonic observation plans into monotonic observation plans. Under modified assumptions (C)-(E)-(P)-(O) with Nk replaced by Dk and N̅t –1 replaced by Dk–1 = 0, and no weight model misspecification, this approach allows one to consistently estimate the parameters of the marginal structural mean model
| (5a) |
| (5b) |
by fitting the weighted mean model
| (6a) |
| (6b) |
When the goal is to estimate the treatment effect under the observation plan n̅ = {1, 1, 1…1}, artificial censoring may be a more robust strategy than modeling the full observation plan: it can be argued that exchangeability for the observation process becomes more plausible when one does not need to predict the probability of observation for subjects who have not been recently observed, and that therefore lack recent data on covariates. On the other hand, artificial censoring may be statistically inefficient because it ignores the information that becomes available when subjects return to the study after having missed a scheduled observation time.
Artificial censoring may be used to help estimate the treatment effect under observation plans other than n̅ = {1, 1, 1…1}. For example, suppose that we want to estimate the treatment effect in our clinical cohort if everybody were seen by a doctor at least once every, say, 3 months. More generally, we may want to restrict our inference to observation plans of the form “observe at least once every q months,” for a fixed period q, and artificially censor subjects who deviate from these plans. The observation plan n̅ = {1, 1, 1…1} is a particular case with q = 1. Following our reasoning above, one could argue that the shorter the period q, the more plausible exchangeability becomes. Formally, we define the censoring variable Dt as follows
If k < q, then Dk = 0
If k ≥ q then Dk = 1 if either otherwise
Again, under our assumptions, one can consistently estimate the parameters of marginal structural model (5) by fitting model (6) to the data weighted by . Note that, by definition, all subjects observed at time k, Nk = 1, remain uncensored with probability 1 in the interval [k + 1, k+q−1]. Thus the probability of censoring at k needs only be estimated among those subjects who had their last visit at exactly time k–q. That is, by definition, and needs to be estimated from the subset of the data with Dk–1 = 0 and .
However, when the goal is to estimate the treatment effect under observation plans other than n̅ = {1, 1, 1…1}, the observation plan may still be dynamic in the artificially censored data. Thus adjusting for selection bias or confounding may require the estimation of inverse probability weights for a weighted analysis of the artificially censored data. The weights can be further stabilized by adding N̅k–1 to the conditioning event in the numerator of the weight, but then the effect estimate would need to be interpreted as the effect of treatment if everybody had been observed at least once every q months and the pattern of observations in the time interval [0, k – q – 1] would not jointly predict future treatment and outcome at time k or later.
5 Data analysis
We estimated the effect of initiating highly active antiretroviral therapy At on mean CD4 cell count Yt among HIV-infected subjects included in the FHDH.3 The FHDH was created in 1992 to collect prospective clinical information on HIV-infected patients managed in 29 of the 30 French HIV/AIDS centers. The data include basic demographic characteristics, HIV transmission group, usual HIV biological markers (CD4 lymphocyte count and HIV RNA level), clinical manifestations, use of anti-retroviral therapy and other treatments, and death status. As of June 2006, the database included data on over 59, 000 patients infected with HIV-1 and with no history of use of antiretroviral therapy before January 1997. For each subject, we defined baseline as the earliest month with concurrent (within 6 months) measurements of both CD4 cell count and HIV RNA (i.e., viral load) after December 1996. We then restricted the analysis to subjects who had never received antiretroviral therapy before baseline. As in previous analyses,7,8 we assumed that once individuals started highly active antiretroviral therapy, they remained on it thereafter. We make this assumption to weaken the exchangeability condition (EA) as we now do not need to ensure exchangeability for the times subsequent to initiation, i.e., we do not need to measure and adjust for the joint determinants of therapy discontinuation and the outcome. The price that we pay for the assumption of “once on therapy, always on therapy” is that our effect estimates have an intention-to-treat flavor8 because they are estimates of the contrast “assigned to treatment at baseline” versus “never treated”, rather than of the contrast “always treated” versus “never treated.” The magnitude of the difference between these two contrasts depends on the proportion of initiators who later discontinue therapy. Because HIV patients are supposed to stay on antiretroviral therapy for their entire life, we suppose the difference is small.
Time of follow-up t was measured in months from baseline (t = 0) to June 2006, death, pregnancy, or 12 months without a visit, whichever occurred earlier. That is, we restricted our inferences to the effect estimate under observation plans included in the set “observe at least once every 12 months.” As a result, our models for the outcome Yt+1 are conditional on being observed at time t +1 (Nt+1 = 1), not being artificially censored due to 12 months without a visit by time t (Dt = 0), and not being censored due to pregnancy or death by time t + 1 (Ct+1 = 0). Our analysis included 23, 076 subjects with an average follow-up of 34.5 months. Of these subjects, 9, 823 initiated highly active antiretroviral therapy during the follow-up. The average interval between visits was 3.2 (median 2.0) months in our analysis, but patients with a more severe disease or in the first few years of treatment are seen more frequently than the others. Thus the observation plan is dynamic and ignoring it in the analysis may result in bias, as explained in the previous section. Note that assumption (O) is essentially guaranteed to hold in the FHDH because all hospital visits are recorded and treatment can only be modified during visit hospitals.
As a preliminary analysis, we fit the mean model
by ordinary least squares, where At is an indicator for therapy initiation by time t (1: yes, 0: no), Nt is an indicator for being observed at time t (1: yes, 0: no), Dt is an indicator for censoring due to deviation from the observation plans of interest by time t (1: yes, 0: no), Ct is an indicator for censoring due to death or pregnancy by time t (1: yes, 0: no), and γ0(t) is a time-varying intercept estimated by adding parameters for a deterministic function of time (we used cubic splines with 5 knots but other flexible functions could be used). The parameter estimate γ̂1 was 0.22 (robust standard error [SE]: 0.15). That is, those who initiated therapy at baseline had, on average, 0.22 more CD4 lymphocytes per μL and per month of follow-up than those who did not initiate therapy. This essentially null association between therapy initiation and mean CD4 cell count is most likely the result of uncontrolled confounding by indication as the model does not attempt to adjust for any confounders.
To partly adjust for confounding by indication, we fit the model
where V is a vector of potential baseline confounders including CD4 cell count (6 categories), HIV RNA (3 categories), use of prophylaxis for PCP, geographic origin, transmission risk group, and time since HIV infection (<1 yr., other), age, and sex. The parameter estimate γ̂1 was 5.13 (SE: 0.15), that is, therapy initiation was associated with an average monthly increase of 5.13 CD4 lymphocytes per μL. The positive association between therapy initiation and the outcome suggests that the therapy is beneficial but the model still does not adjust for confounding by indication due to time-varying factors. Because those who develop more severe HIV disease (i.e., low CD4 cell count and high viral load) during the follow-up are more likely to initiate therapy, one would expect that further adjustment for time-varying CD4 cell count would result in a larger effect estimate. Two approaches to adjust for time-varying confounders are 1) adding them to the model, and 2) using them to estimate inverse probability weights. The first method may result in biased effect estimates when the time-varying confounders are themselves affected by prior treatment,10,11 as we expect to be the case for time-varying confounders such as CD4 cell count and HIV RNA. Nonetheless, we used this approach here for comparison purposes.
Hence, in a naive attempt to adjust for time-varying confounding, we first fit the model
where is a vector including the most recently available measurement of CD4 lymphocyte count (6 categories) and viral load (3 categories) at t, and history of an AIDS-defining illness at t. The parameter estimate γ̂1 was 0.89 (SE: 0.04). The decrease in the effect estimate after further adjustment for time-varying covariates is an empirical proof of the bias caused by adding the time-varying confounders to the outcome model. One could argue that much of the bias occurs because includes the most updated value of the time-varying confounders at time t, a time which is for many subjects subsequent to the time of treatment initiation. Thus a better strategy might be to update the values of the time-varying covariates until either the time of treatment initiation or time t, whichever occurs first. After this redefinition of , the parameter estimate γ̂1 was 4.31 (SE: 0.12). This strategy could be refined by ensuring that the covariates of the non initiators of therapy are also partially updated, with a distribution of updating times similar to that of the initiators of therapy. However, partial updating of the time-varying covariates is a feasible approach only when the treatment process is monotonic (e.g., once treated, always treated). In more general settings in which treatment use goes on and off or treatment dosing changes in response to the evolving (time-varying) covariates, one cannot choose a single time point at which the updating of time-varying covariates should stop. In fact, the structure of the bias induced by choosing one such time (e.g., the time of treatment initiation when treatment may be discontinued later on) is similar to the structure of the confounding bias due to the uncoupling of the times of observation and of potential treatment change (Figure 3). In contrast, IPW can be used to adjust for time-varying confounders in more general settings, and to obtain effect estimates that are not conditional on the time-varying covariates.
We then fit the mean model with each person-month weighted by an estimate of the stabilized inverse probability weight . A strategy to estimate the stabilized weights for treatment, for observation time, and for artificial censoring has been described above. Specifically, we fit separate logistic models for , , and to estimate, respectively, the denominator of . We fit three similar logistic models, except that they did not include the covariates , to estimate the corresponding numerators. We summarized N̅t, the observation history through t, by the time-varying covariate ‘months since last visit’ (5 categories). The stabilized censoring weights were estimated analogously, as described in previous publications.8 Although not discussed in this paper, censoring Ct may introduce time-dependent selection bias11 and thus needs to be adjusted for. For simplicity, we pooled both causes of censoring in a single model and did not pursue more sophisticated strategies to deal with censoring by death.21 Because the probability of observation, artificial censoring, and censoring by pregnancy or death may change after a subject starts antiretroviral therapy, we added product terms between treatment initiation and all the other covariates in the models. The estimated weights had mean 1.04 (percentile 1: 0.12, percentile 99: 3.2).
The parameter estimate γ̂1 from the weighted model was 6.11 (SE: 0.22). Under expanded assumptions (C)-(E)-(P), including exchangeability and positivity for artificial censoring D and censoring C, and the assumption of no model misspecification, this is a consistent estimate of the average monthly increase in CD4 cell count caused by therapy initiation under under an observation plan that guarantees at least one visit every 12 months, and in which the frequency of visits is equal to that in the FHDH. That is, γ̂1 consistently estimates the parameter β1 from the marginal structural model that assumes no direct effect of the observation plan. The estimate γ̂1 was 6.00 (SE: 0.22) when we relaxed the assumption of no direct effect of the observation plan by adding the covariate ‘months since last visit’ to the weighted model.
To explore the magnitude of the bias possibly introduced by the dynamic observation plan, we also fit a weighted model using estimated weights . To estimate the weights for treatment, we did not assume that treatment changes may only happen at observation times N = 1. That is, we fit a logistic model for . The estimate γ̂1 was 6.46 (SE: 0.25), which suggests that disregarding the dynamic observation plan leads to little bias in the FHDH.
6 Conclusion
The analysis of longitudinal studies often needs to be restricted to the times at which information was collected. In this paper we have described a bias that can occur under any observation plan when the times of observation and of potential treatment do not coincide, and two biases that can be induced by dynamic observation plans—confounding and selection bias. The selection bias component is a missing data problem: static observation plans result in data missing completely at random, and dynamic observation plans result, at best, in data missing at random (conditional on the measured covariates). Other authors have proposed methods that observation plans in continuous time,22 and that relax the assumption of exchangeability (or of ‘data missing at random’) for the observation plan.23 The confounding component is, in pharmacoepidemiologic studies, a form of confounding by indication. We described some assumptions under which these biases can be eliminated by IPW.
As a motivating example, we focused on studies that attempt to estimate the effect of antiretroviral therapy on the evolution of CD4 cell count and in which the only available CD4 cell count measurements are those obtained at the times when subjects happen to be observed. Because the times of observation are not generally chosen at random—rather the probability of observing an individual at any given time may be partly determined by prior treatment and covariate history—, an analysis that does not adjust for the dynamic observation plan may be biased. Our analysis of the FHDH data, a prospective study of HIV-infected individuals, adjusted for the dynamic observation plan in two stages. First, we artificially censored individuals that had a period longer than 12 months without an observation, and estimated inverse probability weights to adjust for the potential bias introduced by the artificial censoring. That is, we restricted the inference to observation plans that did not include periods longer than 12 months without an observation. Second, we estimated inverse probability weights to adjust for the potentially non random times of observation within the set of observation plans that did not include periods longer than 12 months without an observation. Interestingly, our IPW adjustment for observation plan had little impact on the effect estimates from the FHDH. This finding may be partly explained by the relatively frequent observation times that are guaranteed by design for most FHDH subjects. In general, it is advisable to design prospective studies with frequent observations, regardless of the subject's clinical history.
Acknowledgments
We thank Dr. James Robins for crucial comments on the structure of confounding bias due to dynamic observation plans, and Dr. Roger Logan for technical assistance with data analysis. This study was partly supported by NIH R01 grant AI073127.
References
- 1.Kaslow RA, Ostrow DG, Detels R, Phair JP, Polk BF, Rinaldo CR. The Multicenter AIDS Cohort Study: Rationale, organization, and selected characteristics of the participants. American Journal of Epidemiology. 1987;126:310–8. doi: 10.1093/aje/126.2.310. [DOI] [PubMed] [Google Scholar]
- 2.Grodstein F, Manson JE, Colditz GA, Willett WC, Speizer FE, Stampfer MJ. A prospective, observational study of postmenopausal hormone therapy and primary prevention of cardiovascular disease. Annals of Internal Medicine. 2000;133:933–941. doi: 10.7326/0003-4819-133-12-200012190-00008. [DOI] [PubMed] [Google Scholar]
- 3.Grabar SV, Le Moing V, Goujard C, Leport C, Kazatchkine MD, Costagliola D, Weiss L. Clinical outcome of patients with HIV-1 infection according to immunologic and virologic response after 6 months of highly active antiretroviral therapy. Annals of Internal Medicine. 2000;133:401–410. doi: 10.7326/0003-4819-133-6-200009190-00007. [DOI] [PubMed] [Google Scholar]
- 4.Robins JM. 1997 Proceedings of the Section on Bayesian Statistical Science. Alexandria, VA: American Statistical Association; 1998. Marginal structural models; pp. 1–10. [Google Scholar]
- 5.Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Halloran E, Berry D, editors. Statistical Models in Epidemiology: The Environment and Clinical Trials. New York: Springer-Verlag; 1999. pp. 95–134. [Google Scholar]
- 6.Robins JM, Rotnitzky A, Zhao LP. Analysis of semiparametric regression models for repeated outcomes in the presence of missing data. Journal of the American Statsitical Association. 1995;90:106–121. [Google Scholar]
- 7.Hernán MA, Brumback B, Robins JM. Estimating the causal effect of zidovudine on CD4 count with a marginal structural model for repeated measures. Statistics in Medicine. 2002;21:1689–1709. doi: 10.1002/sim.1144. [DOI] [PubMed] [Google Scholar]
- 8.Cole SR, Hernán MA, Margolick JB, Cohen MH, Robins JM. Marginal structural models to estimate the effect of highly active antiretroviral therapy initiation on CD4 cell count. American Journal of Epidemiology. 2005;162:471–478. doi: 10.1093/aje/kwi216. [DOI] [PubMed] [Google Scholar]
- 9.Robins JM, Hernán MA. Estimation of the causal effects of time-varying exposures. In: Fitzmaurice G, Davidian M, Verbeke G, Molenberghs G, editors. Advances in Longitudinal Data Analysis. New York: Chapman and Hall/CRC Press; 2008. in press. [Google Scholar]
- 10.Robins JM. A new approach to causal inference in mortality studies with a sustained exposure period Application to the healthy worker survivor effect [published errata appear in Mathl Modelling, 14, 917-21 (1987)] Mathematical Modelling. 1986;7:1393–512. [Google Scholar]
- 11.Hernán MA, Hernández-Díaz S, Robins JM. A structural approach to selection bias. Epidemiology. 2004;15:615–625. doi: 10.1097/01.ede.0000135174.63482.43. [DOI] [PubMed] [Google Scholar]
- 12.Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22. [Google Scholar]
- 13.Zeger SL, Liang KY. Longitudinal data analysis for discrete and continuous outcomes. Biometrics. 1982;42:121–130. [PubMed] [Google Scholar]
- 14.Pierce DA. The asymptotic effect of substituting estimators for parameters in certain types of statistics. The Annals of Statistics. 1982;10:475–478. [Google Scholar]
- 15.Robins JM, Greenland S. Comment on “Causal inference without counterfactuals”. Journal of the American Statistical Association. 2000;95:477–82. [Google Scholar]
- 16.Hernán MA, Taubman SL. Does obesity shorten life? The importance of well defined interventions to answer causal questions. International Journal of Obesity. 2008 doi: 10.1038/ijo.2008.82. in press. [DOI] [PubMed] [Google Scholar]
- 17.Cole SR, Hernán MA, Robins JM, Anastos K, Chmiel J, Detels R, Ervin C, Feldman J, Green-blatt R, Kingsley L, Lai S, Young M, Cohen M, Muñoz A. Effect of highly active antiretroviral therapy on time to acquired immunodeficiency syndrome or death using marginal structural models. American Journal of Epidemiology. 2003;158:687–694. doi: 10.1093/aje/kwg206. [DOI] [PubMed] [Google Scholar]
- 18.Hernán MA, Brumback B, Robins JM. Marginal structural models to estimate the joint effect of non randomized treatments. Journal of the American Statistical Association. 2001;96:440–448. [Google Scholar]
- 19.Patel K, Hernán MA, Williams PL, Seeger JD, McIntosh K, Seage GR for the Pediatric AIDS Clinical Trials Group 219/219C Study Team. Long-term effectiveness of highly active anti-retroviral therapy on the survival of children and adolescents infected with HIV-1: a ten year follow-up study. Clinical Infectious Diseases. 2008;46:507–515. doi: 10.1086/526524. [DOI] [PubMed] [Google Scholar]
- 20.Hernán MA. Confounding. In: Everitt B, Melnick E, editors. Encyclopedia of Quantitative Risk Assessment. New York: John Wiley; 2008. in press. [Google Scholar]
- 21.Shepherd BE, Gilbert PB, Jemiai Y, Rotnitzky A. Sensitivity analyses comparing outcomes only existing in a subset selected post-randomization, conditional on covariates, with application to HIV vaccine trials. Biometrics. 2006;62:332–42. doi: 10.1111/j.1541-0420.2005.00495.x. [DOI] [PubMed] [Google Scholar]
- 22.Lin H, Scharfstein DO, Rosenheck RA. Analysis of longitudinal data with irregular, outcome-dependent follow-up. Journal of the Royal Statistical Association. 2004;66:791–813. [Google Scholar]
- 23.Orellana L, Rotnitzky A. Estimation of the effect of dynamic treatment regimes under flexible dynamic visit regimes. Technical Report, Department of Biostatistics, Harvard School of Public Health; 2007. [Google Scholar]