Abstract
Pooling based strategies that combine samples from multiple participants for laboratory assays have been proposed for epidemiologic investigations of biomarkers to address issues including cost, efficiency, detection, and when minimal sample volume is available. A modification of the standard logistic regression model has been previously described to allow use with pooled data; however, this model makes assumptions regarding exposure distribution and logit-linearity of risk (i.e., constant odds ratio) that can be violated in practice. We were motivated by a nested case-control study of miscarriage and inflammatory factors with highly skewed distributions to develop a more flexible model for analysis of pooled data. Using characteristics of the gamma distribution and the relation between models of binary outcome conditional on exposure and of exposure conditional on outcome, we use a modified logistic regression to accommodate non-linearity due to unequal shape parameters in gamma distributed exposure for cases and controls. Using simulations, we compare our approach with existing methods for logistic regression for pooled data considering: 1. Constant and dose-dependent effects; 2. Gamma and log-normal distributed exposure; 3. Effect size, and; 4. The proportions of biospecimens pooled. We show that our approach allows estimation of odds ratios that vary with exposure level, yet has minimal loss of efficiency compared to existing approaches when exposure effects are dose-invariant. Our model performed similarly to a maximum likelihood estimation approach in terms of bias and efficiency, and provides an easily implemented approach for estimation with pooled biomarker data when effects may not be constant across exposure.
Keywords: pooling, biomarkers, case-control studies, logistic regression, gamma distribution
1. Introduction
Biomarkers are commonly used in epidemiological investigations to provide quantitative information regarding exposure. However, use of biomarkers for epidemiologic investigation entails significant expense related both to collection of biospecimens from study participants and performance of laboratory tests to measure the biomarker of interest. Additionally, practical limitations including those with instrumentation (such as detection limits) and the availability of adequate sample volume may hinder epidemiologic biomarker studies. In order to address these issues, pooling based approaches, as well as random sampling, have been described [1-8].
Given a population of biospecimens of size N, pooling typically involves physically combining biospecimens in pools of group size p and performing assays on the N/p resulting pools. Laboratory assays commonly have the goal of measuring the concentration of the biomarker of interest as units per volume. In such a setting, when equal volumes of two individual biospecimens are combined, it is commonly assumed that the concentration in the resultant pool represents the average of biospecimens in the pool, given that any error introduced through the pooling process (e.g., due to incomplete mixing) is minor [3-7]. Thus, pooling designs are efficient for estimation of the mean [2]. A comparable random sampling approach might entail random selection of N/p unpooled samples for assaying, which while less efficient for mean estimation, retains individual level information and provides more efficient estimation of variance than pooling [2]. A natural extension of pooling is a hybrid design that exploits the benefits of pooling with those of random sampling for estimation of both means and variance, respectively. This approach entails performing assays on a sample that includes some pooled specimens and some specimens unpooled according to optimality criteria that have been described [4].
Use of pooled exposure assessment for studies of binary disease has been previously described [4,7]. Weinberg and Umbach (1999) introduced the ‘set-based logistic model’ to evaluate the relation between a binary outcome variable and exposure measured in pools grouped by outcome status [7]. The set-based logistic regression approach entails use of the measured value for a pool, the pool size, and the assumption that measurements in pools represent the arithmetic means of individual measurements to reconstruct the sum of individual concentrations (equal to the set’s measurement multiplied by pool size). Weinberg and Umbach have shown that use of this sum in a logistic model that includes pool size as a predictor and the log ratio of case sets to control sets as an offset can be used to estimate exposure effects. In the case-control setting, set-based logistic regression has been shown to yield valid risk estimates with minimal loss of efficiency compared to individual assays of exposures distributed as normal, lognormal or gamma under the assumption of linear dose-response when a single estimate adequately describes the relation between exposure levels and risk [7].
In this paper, we consider applications of a logistic regression model in a hybrid design setting for assessment of risk related to biomarkers of exposure when the association depends on the exposure level. In section 2, we introduce a case-control study of miscarriage and biomarkers of inflammation as a motivating example and discuss potential limitations of the set-based logistic regression model as previously described [7] that may apply in scenarios observed with studies using biomarkers. In section 3, we propose an alternative method based on a gamma model and describe modeling approaches to estimate the parameters of interest. In section 4, we present results of a simulation study evaluating the approach under a range of scenarios. In section 5, we revisit the motivating example and apply the proposed approaches to a dataset from a case-control study of miscarriage and circulating levels of chemokines. We conclude in section 6 with a discussion of our results.
2. Motivating example – chemokines and miscarriage
2.1 Study design and population
Estimates of the proportion of recognized pregnancies that end in miscarriage range from 15 to 31% [9]. Inflammation and immune related factors have been considered as possible mediators of pregnancy loss. Chemokines are small cell signaling proteins involved in immunomodulatory and other biological processes. After binding to cell surface receptors, chemokines trigger intracellular signaling that can stimulate feedback regulation through up- or down-regulation of transcription, promote inflammation/immune responses, stem-cell survival, chemotaxis of leukocytes, and angiogenesis and have suspected involvement in pregnancy failures [10-13].
To evaluate the role of circulating chemokine levels as early indicators of miscarriage, we conducted a case-control study nested in the Collaborative Perinatal Project (CPP), utilizing the design of recently conducted studies of cytokines and pregnancy outcomes in the CPP [13, 14, 15]. The CPP is a multi-site study of pregnancy and pediatric outcomes that prospectively collected biospecimens and was conducted from 1959 to 1974 [16]. Because of the large sample size and prospective sample collection of the CPP, it has great utility to address questions of early gestation biomarker levels and uncommon pregnancy outcomes, such as late miscarriage. Details of the sampling for this study have been previously described [13]. Biospecimens from a total of 370 miscarriage cases and 388 controls were available for assay in the current study. Assays were performed using a 10-plex assay from BioSource (Invitrogen, Carlsbad, CA, USA) and the Luminex 100IS platform (Luminex Corp, Austin, TX) as described elsewhere [13]. As specimens had been previously collected with all identifying information removed, the Office of Human Subjects Research from the National Institutes of Health and the University of Florida IRB determined this study to be exempt from the requirement for further IRB approval.
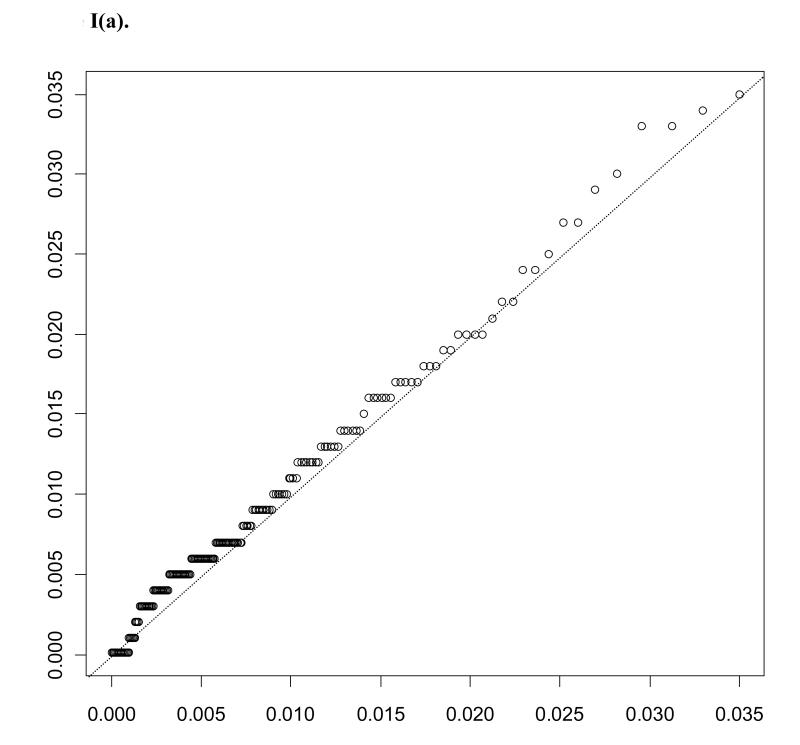
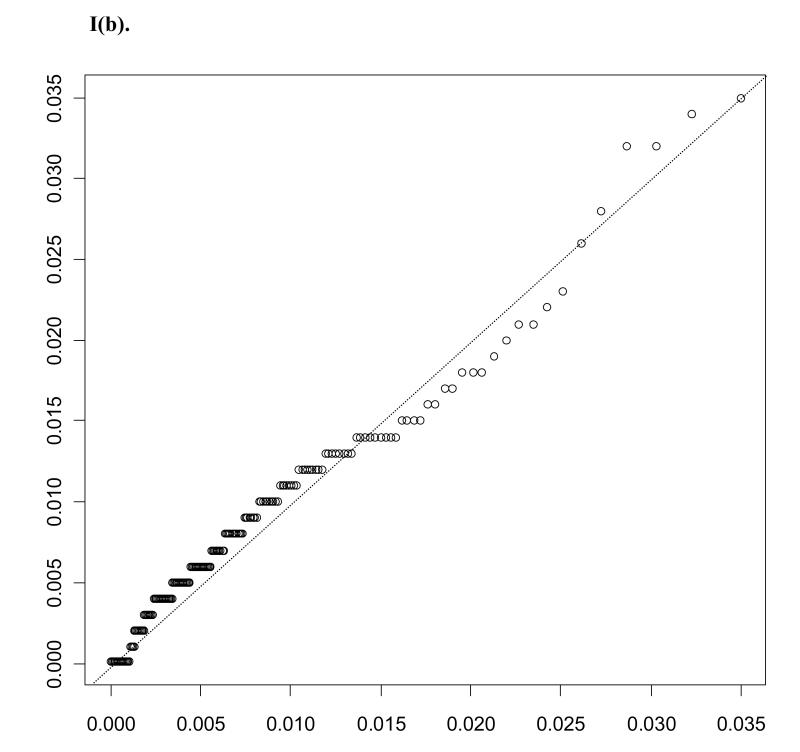
In considering results of these assays, chemokine distributions were observed to be highly right skewed. Q-Q plots for eotaxin, one of the chemokines evaluated, among miscarriage cases and controls are shown in Figure 1, illustrating the gamma distributions’ fit to the data. Lognormal distributions were considered as well, and distributions were compared using the Akaike Information Criterion (AIC). Gamma (AICcases = −3097.9; AICcontrols = −3380.2) was observed to provide a better fit compared to lognormal (AICcases = −3047.8; AICcontrols = −3353.0). The distribution of eotaxin is representative of the other chemokines evaluated.
Figure I.
Displays Q-Q plots for miscarriage cases (a) and controls (b). Levels of eotaxin are plotted on the x axis against gamma distribution quantiles based on maximum likelihood estimates for gamma distribution parameters (αY, βY), Y in {0, 1}.
Assays such as enzyme-linked immunosorbent assays and multiplexed immunoassays may be costly, and while sample volume requirements for these assays are low, ranging from 100-200μl, there is often limited available volume for subjects of particular interest in repositories such as that for the CPP. For these reasons, we were motivated to explore pooling based approaches using these case-control data. In addition to assessments on individual samples, chemokines were measured in case-status specific pools (i.e., cases with cases, etc.) for those with sufficient available sample volume.
2.2 Implications of the set-based logistic regression model
Existing methodology for analysis of pooled case-control data has considered normal as well as skewed exposures in models to assess dose-invariant relations with disease risk, i.e., a single odds ratio that does not vary by exposure level [7]. Such models have implications for the exposure distribution in cases and controls. For example, in the case of an exposure distributed gamma in the population, a constant risk model implies equal shape parameters for the case and control distributions.
Non-linear response models have been suggested in toxicology and risk assessment literature to model several physiological response mechanisms [17]. Dose-varying effects may be observed for factors that: are subject to feedback regulatory mechanisms such as receptor up- or down-regulation; promote secondary cell-signaling effects; or follow a threshold model [17,18]. Dose-varying effects have been suggested for toxicants including heavy metals [19,20] and endocrine disrupting compounds [21] as well as for endogenous factors involved in immune response [22].
In the context of biomarker research a more flexible model may be desirable, particularly for skewed exposures. While quantiles and variable transformations are commonly used to allow for departures from linearity or log(it)-linearity in the unpooled setting, they are not accommodated by the set-based logistic regression model for pooled exposure assessment [7], and an extension of this approach is needed.
3. A flexible logistic regression model for pooling with gamma distributed exposure
Let X denote a biomarker measured continuously in individuals with disease status Y (1 if present; 0 if not). Suppose X follows a skewed distribution for each disease status, for which a gamma model may be more appropriate than a normal model. Specifically, we assume that given Y = y, X follows a gamma distribution with parameters (αy, βy). The corresponding density function is given by
| (1) |
To understand the association between X and Y, we can use Bayes’ law to deduce from (1) that
| (2) |
where
Thus, the log-odds ratio corresponding to a unit increase in X (from x to x + 1) is not constant in x, but rather given by
which can be plotted as a function of x upon substituting estimates of (αy, βy), y = 0, 1.
Estimation of the relevant parameters is straightforward if X is measured on each individual subject. Suppose, however, that X is measured for pooled specimens from subjects in a case-control study. We assume pooling is homogeneous (cases with cases, controls with controls) but otherwise random. Let the subscripts ij denote the jth subject in the ith pool, and Xi = (Xi1,…, Ximi′ and Yi = (Yi1, …, Yimi′, j = 1, … , mi, i = 1, … , n. The pooling mechanism implies that Yi is a constant vector (0 or 1). Unless mi = 1, we do not observe the Xij; rather, the measured value in the ith pool represents the average of the j specimens in that pool. From these measured values, the sum of individual specimens can be calculated as by multiplying measurements by mi. It is important to observe that given Yi = y1, Xi+ also follows a gamma distribution with parameters (miαy, βy). Thus the parameters (αy, βy) can be estimated by maximizing the likelihood
| (3) |
where I(·) is the indicator function. Maximization of the above likelihood and close approximation of the corresponding observed information matrix can be accomplished directly using optimization routines available in standard statistical software (e.g., [23]); however, variance estimation and performance of hypothesis tests are not straightforward. Alternately, parameter estimation can be carried out using available routines for gamma regression. In particular, well known properties of gamma distributions imply that
In other words, Xi+ in a case pool follows a gamma regression model with a log link, an intercept log(α1)−log(β1), an offset log(mi), and a dispersion parameter . Replacing the subscript 1 with 0 yields the parallel model for control pools. These models can be fitted to case pools and control pools separately, and the resulting parameter estimates can be converted into estimates for (αy, βy), y = 0, 1, which can be further converted into estimates for (θ1,θ2). These approaches are theoretically sound but may not be easy to implement by practitioners.
A more direct approach to estimate the risk associated with a given biomarker is based on the more traditional binary regression model for Yi but given Xi+ in lieu of individual Xi. This was the approach of Weinberg and Umbach (1999) who demonstrated that a set-based model could be used to assess risk consistently in a variety of scenarios. Their method does however, have the limitation of assuming logit-linearity in exposure, imposing difficulty with non-linear transformations, and their result may not be directly applicable to the present situation. Extending previous work, we can deduce a logistic regression model for Yi given Xi+ directly from the gamma distribution of Xi+ given Yi. Invoking Bayes’ law once again, we obtain
| (4) |
where
r(mi) is the number of case pools of size mi divided by the number of control pools of the same size, andθ1 andθ2 are the same as in (2). Hereθ1 andθ2 are the parameters of interest, while is essentially a nuisance parameter that depends on unknown parameters in a fairly complex way.
Just as with Weinberg and Umbach, standard software can be used to approximate the fit of model (4) to allow for non-constant risk related to exposure. One may use logistic regression after replacing with mi(as a categorical variable), thereby accounting for the dependence of on mi, as well as log r(mi) as an offset, though the term drops out of the model in designs with equal numbers of case and control pairs. This way of handling is convenient and the associated loss of information should be small when the number of different pool sizes is relatively small, as is often the case. The logistic approach can be performed in virtually any statistical software with standard error estimates and tests on regression parameters available in standard output. The log-odds ratio ψ (defined earlier) can be estimated by
where denotes the estimates from logistic regression. Let denote the estimated variance matrix for . Then the corresponding variance estimate for is given by
which can be used to make inference about ψ.
4. Simulation Study
4.1 Constant versus dose-dependent effect estimation with varying pooling proportions
We conducted a simulation study to compare the proposed approach with the Weinberg-Umbach set-based logistic regression with respect to bias and mean squared error. We initially considered: 1. Constant and dose-dependent effects of varying sizes for the effect of exposure on disease risk, and; 2. Varying proportions of samples pooled.
For the simulations, 1000 datasets were generated. In order to assess the impact of the size and type (i.e., constant or dose-dependent) on estimates, a gamma distributed exposure was generated with case status specific parameters α0 = 1, β0 = 1, α1 = {1.0, 1.5}, β1 = 1/{1.0, 1.25,2}. The number of assays performed (i.e., total of pools and individuals assayed) was fixed at 2000. Pools of size mi= 2 were considered to mirror the data example, and as this pool size affords the largest cost savings while minimizing loss of individual level information. The proportion of samples pooled was varied to evaluate the method in the context of the hybrid pooled-unpooled study design, and was set equal to 0 (all unpooled); 0.25 (250 pools of 2 and 750 unpooled observations per disease status), 0.50, 0.75, or 1.
Table I displays results of the simulations evaluating effect size and dose-dependency; results are shown under 50% pooling, and are representative of those for other pooling proportions. Relative bias and root mean squared error for estimates from the Weinberg-Umbach model and from our proposed flexible approach are shown. The top half of the table displays simulation results where exposure has a constant, dose-independent, effect and the Weinberg-Umbach model is correctly specified, whereas our proposed flexible approach includes an unnecessary non-linear term in the model (i.e., θ2milog(Xi+) from (4)) . Our proposed flexible approach yielded approximately identical estimates to those of the Weinberg-Umbach approach, and both methods resulted in very low relative biases ranging from −0.4% to 1.1%. There was a small loss of precision with use of the flexible approach reflected by slightly larger RMSEs due to the additional term to allow for non-linearity, θ2.
Table I.
Relative bias and root mean squared error of odds ratio estimates from the Weinberg-Umbach set-based logistic regression and the flexible approach under various scenarios
| Simulated parameter values | Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| True OR | Relative bias | RMSE | |||||||
| α 1 | β 1 | (Q1):(Q2):(Q3) | Model | Q1 | Q2 | Q3 | Q1 | Q2 | Q3 |
| 1.0 | (1.000): (1.000): (1.000) |
Flexible
W-U |
0.003
0.002 |
0.002
0.002 |
0.002
0.002 |
0.042
0.038 |
0.037
0.038 |
0.043
0.038 |
|
| 1 | 0.8 | (1.221): (1.221): (1.221) |
Flexible
W-U |
0.005
0.003 |
−0.001
0.003 |
−0.004
0.003 |
0.057
0.047 |
0.051
0.047 |
0.061
0.047 |
| 0.5 | (1.649): (1.649): (1.649) |
Flexible
W-U |
0.011
0.004 |
−0.001
0.004 |
−0.007
0.004 |
0.082
0.072 |
0.075
0.072 |
0.090
0.072 |
|
| 1.0 | (2.116): (1.563): (1.312) |
Flexible
W-U |
−0.020
−0.202 |
−0.035
0.080 |
−0.041
0.286 |
0.141
0.437 |
0.134
0.151 |
0.157
0.385 |
|
| 1.5 | 0.8 | (2.584): (1.909): (1.602) |
Flexible
W-U |
−0.012
−0.181 |
0.008
0.108 |
0.022
0.320 |
0.179
0.484 |
0.133
0.239 |
0.176
0.527 |
| 0.5 | (3.488): (2.577): (2.163) |
Flexible
W-U |
−0.019
−0.170 |
0.031
0.124 |
0.063
0.339 |
0.257
0.618 |
0.180
0.366 |
0.238
0.754 |
|
Notes: Results shown for hybrid pooled-unpooled design with 50% pooling. W-U corresponds to the Weinberg-Umbach set-based logistic regression approach [7]
The bottom half of Table I compares the two approaches when the shape parameters are unequal for cases and controls, θ2 ≠ 0 and effect estimates are dose-dependent. As shown in the table, in this setting, the constant effect model is misspecified and the effect of this misspecification varies with the difference in the shape parameters. Whereas relative bias was similar across quartiles and under all scenarios evaluated for the correctly specified flexible approach, the same was not true for the Weinberg-Umbach approach; at the median, relative bias ranged from −3% to 12%, but was larger at the 25th (from −20% to −17%) and 75th percentiles (from 29% to 34%).
The importance of the additional term for model specification is further illustrated in Table II, which considers statistical inference under each approach. The table displays the proportion of simulations where parameter estimates from each of the models had P-values less than 0.05 for the 50% pooled and fully pooled circumstances. Under scenarios where cases and controls were distributed gamma with equal shape parameters (α0 = α1 = 1), the Weinberg-Umbach model was correctly specified and significant exposure effects were consistently observed; the flexible approach yielded similar results, with the log-linear exposure term significant in 91% of simulations. The flexible model appropriately determines the risk to be truly linear with the estimate of θ2 significant 11% of the time. While this is greater than the 5% that would be expected, the magnitude of θ2 in these instances was small, and the estimated departure from constant risk negligible; this is further shown in Table III. Under scenarios where cases and controls were distributed gamma with unequal shape parameters (α0 ≠ α1) and our flexible approach model was correctly specified, the model captured differences in shape and scale parameters, whereas the Weinberg-Umbach model conflates differences of scale with those of shape. The Weinberg-Umbach model correctly identified the increased risk due to exposure, but mistakenly characterized it with a single OR estimate because it is restricted to linear risk where our flexible approach was unrestricted.
Table II.
Statistical testing results: proportion of simulations with statistically significant parameter estimates from the Weinberg-Umbach set-based logistic regression and the flexible approach under various scenarios of risk
| SIMULATED VALUES | % of simulations with P<0.05 | ||||
|---|---|---|---|---|---|
|
pooling
proportion |
α 1 | β 1 | W-U 1 | Flexible 2 | |
| Coeff. | Coeff. 1 | Coeff. 2 | |||
| 1.00 | 0.062 | 0.034 | 0.032 | ||
| 1.0 | 0.80 | 1 | 0.916 | 0.121 | |
| 0.50 | 1 | 1 | 0.113 | ||
| 0.5 | |||||
| 1.00 | 1 | 0.788 | 1 | ||
| 1.5 | 0.80 | 1 | 0.905 | 1 | |
| 0.50 | 1 | 0.997 | 1 | ||
|
| |||||
| 1.00 | 0.055 | 0.033 | 0.038 | ||
| 1.0 | 0.80 | 1 | 0.816 | 0.037 | |
| 0.50 | 1 | 1 | 0.042 | ||
| 1.0 | |||||
| 1.00 | 1 | 0.047 | 1 | ||
| 1.5 | 0.80 | 1 | 0.509 | 0.999 | |
| 0.50 | 1 | 0.982 | 0.993 | ||
Notes: α0 = 1, β0 = 1.
W-U corresponds to the Weinberg-Umbach [7] set-based logistic regression approach; coefficient is β from: logit P(Yi =1) = μ(mi) + β Xi+ + log(rmi)
Coefficient 1 is θ1, and coefficient 2 is θ2 from:
logit P(Yi = 1) = θ0 (mi) + θ1Xi + θ2mi log(Xi +) + log(rmi)
Table III.
Simulation results comparing different pooling proportions with regard to risk estimates and standard errors with dose-invariant exposure effects a with the number of assays (i.e., total measurements) fixed at 2000 (i.e., 1000 cases and 1000 controls)
| Pooling proportion |
Number of assays by pooling status |
Total N assayed |
Exposure effect estimates | ||||||
|---|---|---|---|---|---|---|---|---|---|
| pools | individual samples |
SE b | |||||||
| W-Uc | Flexible d | W-U | Flexible d | ||||||
| 0.00 | 0 | 2000 | 2000 | 1.228 | 1.228 | 0.059 | 0.059 | ||
| 0.25 | 500 | 1500 | 2500 | 1.227 | 1.221 | 0.053 | 0.055 | ||
| 0.50 | 1000 | 1000 | 3000 | 1.225 | 1.220 | 0.047 | 0.051 | ||
| 0.75 | 1500 | 500 | 3500 | 1.225 | 1.222 | 0.045 | 0.048 | ||
| 1.00 | 2000 | 0 | 4000 | 1.223 | 1.224 | 0.042 | 0.043 | ||
Exposure was distributed gamma with parameter values: α1 = 1.0, β1=0.8; α0=1.0, β0=1.0 (yields true OR = 1.221)
Standard errors are empirical
W-U corresponds to the Weinberg-Umbach set-based logistic regression approach [7]
Estimates are shown for the median exposure value
Table III illustrates the performance of the flexible approach compared with the W-U model when risk is truly constant across exposure levels, and considered different pooling proportions. Point estimates from the two models were similar to each other, reflecting the new more flexible approach’s ability to estimate constant as well as varied risk, and also yielded nearly identical estimates of the odds ratio as the proportion pooled increases. As seen in the standard error columns, efficiency increases as the proportion of pooled increases, which has been shown for other estimators and is often the motivation for analyzing pooled samples. This was observed to a similar extent for both methods, with only a negligible decrease in efficiency for including the additional flexibility. These results show that in the setting where the W-U model is correctly specified (i.e., constant odds ratio), our flexible approach is not impacted by the additional parameter allowing for dose-variability nor by the pooling proportion; the flexible approach yields similar point estimates and efficiency for estimation of odds ratios to a dose-invariant estimation approach.
4.2 Comparison of flexible logistic approach with maximum likelihood estimation
Under the assumption that exposure in cases and controls follows a gamma distribution, we considered a maximum likelihood approach based on the gamma model. Additional simulations were conducted in order to compare the proposed flexible logistic with a maximum likelihood approach based on maximization of equation (3). For these simulations 1000 datasets were generated with exposure following a gamma distributed with case status specific parameters α0 = 1, β0 = 1, α1 = 1.5, β1 = 0.8. These correspond to a true odds ratio of 1.91. Datasets included a total of 1000 cases and 1000 controls with exposure measured individually and in pools of size mi= 2.
Results of these simulations are shown in Table IV. In both the unpooled and pooled cases, the maximum likelihood approach leads to noticeably more precise estimates of the regression parameters θ1 and θ2 than use of a logistic regression model; however, there is little difference between the approaches for estimates of the odds ratio. Similar results were observed with pooling. The maximum likelihood approach lead to better efficiency than our proposed flexible logistic regression for pooled data, but this difference was negligible for odds ratio estimates. Additionally, as expected, pooling was an effective approach to improve efficiency. Estimates based on 1000 assays using pools of two (i.e., 1000 cases and 1000 controls in pools) were markedly more efficient for odds ratio estimates than those based on 1000 assays of individual samples (i.e., 500 cases and 500 controls).
Table IV.
Simulation results comparing standard logistic regression, flexible logistic regression for pooling, and maximum likelihood approaches with regard to parameter and odds ratio estimates under different pooling conditions and sample sizes.
| Pooling approach | Estimates | ||||||
|---|---|---|---|---|---|---|---|
| Model |
m
pool size |
N
sample size |
N/m
assays |
Mean 1(SD) | Mean 1 (SD) | Mean ln(SD) | Mean (SD) |
| Logistic regression | 1 | 1000 | 1000 | 0.208 (0.097) | 0.502 (0.107) | 0.656 (0.071) | 1.932 (0.138) |
| Maximum likelihood | 1 | 1000 | 1000 | 0.207 (0.087) | 0.503 (0.096) | 0.655 (0.071) | 1.930 (0.137) |
|
| |||||||
| Logistic regression | 1 | 2000 | 2000 | 0.198 (0.075) | 0.503 (0.085) | 0.647 (0.043) | 1.912 (0.082) |
| Flexible logistic regression | 2 | 2000 | 1000 | 0.199 (0.112) | 0.505 (0.140) | 0.649 (0.051) | 1.916 (0.098) |
| Maximum likelihood | 2 | 2000 | 1000 | 0.201 (0.084) | 0.501 (0.107) | 0.647 (0.050) | 1.912 (0.096) |
Notes: 1,000 replications; true values: θ1, = 0.20, θ2 = 0.50, ln(OR) = 0.646, OR = 1.908
4.3 Evaluation of additional underlying dose-dependent risk models
In section 4.1, we considered an exposure distributed gamma in the population and exploited the relation between the true risk model and the case-status specific exposure distributions under the circumstance where case-status specific distributions are gamma, thereby extending previous work to remove restrictions on shape and rate parameters. Our next concern was for circumstances where exposure in the population and/or cases and controls may take distributions other than gamma. In this section, we consider these circumstances to evaluate the robustness of our flexible model when X|Y is not distributed gamma, and our approach misspecifies the risk model. For this assessment, we considered the circumstances where exposure is distributed log-normal, and the underlying risk model varies from that in (4). We simulated exposures with a log-normal distribution in the population and the following relation with disease risk,
where δ0 =0,δ1={−0.50, 0.50},δ2={−0.50, −0.25, 0.25, 0.50}. These parameters lead to ORs ranging from 0.44 to 2.22, with protective, harmful effects corresponding to δ1=−0.50, 0.50, respectively and positive or negative δ2resulting in decreasing or increasing ORs across biomarker levels. In this setting, we evaluated the proposed logistic regression approach. Additionally, we compared the flexible logistic regression approach with that of Weinberg-Umbach.
Bias and root mean squared error for each of the approaches are shown in Table V. Bias under the Weinberg-Umbach method was similar to that of the flexible approach with exposure at the median level but with bias increasing in magnitude moving towards exposures in the tails. Estimates from the proposed flexible approach were able to capture some of the dose variability of the ORs, though not as effectively as for the circumstance where the flexible model correctly specifies the underlying risk model. At the 25th and 75th percentiles, bias was of lower magnitude under the flexible approach than under Weinberg-Umbach method. In this setting, RMSE of the estimators was not substantially different between the two approaches; variance was slightly larger for the flexible approach but was offset by the reduction in bias.
Table V.
Evaluating the robustness of the proposed approach to misspecification of the underlying risk modela: simulation results for bias and RMSE of odds ratio estimates from the proposed flexible logistic approach.
| Simulated parameter values | Estimates | |||||||
|---|---|---|---|---|---|---|---|---|
| True OR | Bias | RMSE | ||||||
| δ 1 | δ 2 | (Q1):(Q2):(Q3) | Q1 | Q2 | Q3 | Q1 | Q2 | Q3 |
| 0.50 | 0.50 | (2.224): (2.084): (1.981) | −0.075 | 0.027 | 0.111 | 0.268 | 0.255 | 0.293 |
| 0.25 | (1.915): (1.854): (1.807) | −0.017 | 0.027 | 0.065 | 0.228 | 0.212 | 0.230 | |
| −0.25 | (1.420): (1.466): (1.504) | 0.060 | 0.035 | 0.012 | 0.159 | 0.139 | 0.145 | |
| −0.50 | (1.222): (1.304): (1.372) | 0.087 | 0.039 | −0.008 | 0.152 | 0.113 | 0.113 | |
|
| ||||||||
| −0.50 | 0.50 | (0.818): (0.767): (0.729) | −0.050 | −0.023 | 0.002 | 0.088 | 0.064 | 0.061 |
| 0.25 | (0.704): (0.682): (0.665) | −0.021 | −0.009 | 0.002 | 0.073 | 0.063 | 0.065 | |
| −0.25 | (0.522): (0.539): (0.553) | 0.012 | −0.001 | −0.012 | 0.060 | 0.058 | 0.064 | |
| −0.50 | (0.450): (0.480): (0.505) | 0.020 | −0.001 | −0.021 | 0.060 | 0.056 | 0.064 | |
Risk model used to determine case status: logit P(Y = 1) = δ0 + δ1X + δ2 X0.5
5. Motivating example revisited
We compared use of the Weinberg-Umbach set-based model with our flexible set-based model using the cytokines and miscarriage nested case-control dataset. Serum chemokine levels were measured for all samples individually as well as in pools of two where pooling was performed by case status. For this analysis, we therefore have individual measurements for 370 cases and 388 controls, as well as measurements for 185 samples of two pooled cases and 194 samples of two pooled controls. We considered five pooling scenarios: 1. One with no pooling; 2-4. Hybrid approaches with 25, 50 and 75% pooled, and; 5. Fully pooled.
Results of this comparison are shown in Table VI. In the unpooled data, the Weinberg-Umbach set-based approach yielded an OR estimate of 0.997 (P=0.96). In the analyses using pooling (i.e., the hybrid pooled-unpooled and fully pooled), non-significant estimates were observed, with odds ratio point estimates that ranged from 1.00 to 1.08. We used the flexible approach to evaluate the possibility of a dose-varying association that the Weinberg-Umbach method would not detect. Under the flexible approach, odds ratio estimates were not statistically significant at the evaluated quartiles, and significant dose-variability was not observed. Consistent with our simulations, estimates at the median were close to the Weinberg-Umbach estimate. The quartile specific estimates from our flexible approach varied only slightly and non-significantly. Pooling further reduced differences across quartiles of the exposure. Estimates varied minimally as the pooling proportion increased from 25% to fully pooled. Given the P-value on θ2 of the flexible approach, a single OR may be reported, in this case indicating no significant log-linear relation between serum eotaxin levels and miscarriage risk.
Table VI.
Results from models of miscarriage risk and levels of eotaxin in the nested case-control study – odds ratio estimatesa and 95% confidence intervals from Weinberg-Umbach set-based logistic regression and the proposed flexible logistic regression
| W-Ub | Flexible logistic model | |||||||
|---|---|---|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | ||||||
| Pooling | [95% CI] | [95% CI] | [95% CI] | [95% CI] | ||||
| none | 1.013 | [0.865, 1.187] | 1.034 | [0.867, 1.232] | 0.978 | [0.797, 1.201] | 0.970 | [0.774, 1.216] |
| 0.25 | 1.072 | [0.936, 1.228] | 1.083 | [0.941, 1.246] | 1.039 | [0.865, 1.247] | 1.032 | [0.845, 1.261] |
| 0.50 | 1.096 | [0.972, 1.235] | 1.102 | [0.975, 1.245] | 1.068 | [0.904, 1.261] | 1.063 | [0.886, 1.274] |
| 0.75 | 1.058 | [0.959, 1.168] | 1.069 | [0.965, 1.183] | 1.022 | [0.893, 1.170] | 1.015 | [0.875, 1.178] |
| all | 1.065 | [0.968, 1.172] | 1.066 | [0.968, 1.174] | 1.058 | [0.926, 1.210] | 1.057 | [0.913, 1.224] |
Estimates for the flexible logistic model are shown at the 25th(Q1), 50th (Q2), and 75th (Q3) percentiles of the eotaxin distribution
W-U corresponds to the Weinberg-Umbach [7] set-based logistic regression approach
6. Discussion
Biomarker assessment using pooled study designs has been described for assessment of binary variables, as with group testing for presence of an antibody [1] or for detection of rare genotypes [24]. When exposures are continuous, previous work has required assumptions of multiplicative risk and logit-linearity in exposure [7]. In this paper we have described a more flexible method for analysis of case-control data. We considered a gamma distributed exposure that allows for unequal shape parameters between cases and controls. This increased flexibility is appropriate when investigators suspect a dose-dependent effect. This relaxation of assumptions entails little cost in terms of efficiency; in simulations where exposure effects were set to be constant across dose, mean squared error for the flexible approach compared favorably with that of a constant, dose-invariant exposure effect model. Notably, in case-control biomarker studies, investigators may use available data to assess distributions of exposure conditional on outcome status, and the risk models that are implied.
In comparisons of our flexible model with the Weinberg-Umbach model, statistical differences between models were seen in our simulations using a sample size of 2000 (1000 cases and 1000 controls); however, estimation of dose-varying effects is impacted by sample size and the nature of the exposure effect. In simulations with minimal departures from log-linearity of risk, the additional dose-varying risk term in the flexible model was not significant, and flexible model estimates were approximately equal to those of the Weinberg-Umbach model. Similarly, pooling was observed to impact the flexible model and the requirement for the dose-varying term. As the pooling proportion increased, differences between the models were less pronounced. This reflects the impact of pooling on the tails of skewed distributions; the reduction in skewness that occurs with pooling led to reduced differences in shape between cases and controls in our data.
The relation between risk models that describe a binary outcome distribution conditional on exposure, and models of exposure distribution conditional on binary outcome status is closely related to classical discriminant function analysis [25]. In the discriminant function analysis setting, prior work considering normally distributed exposures has shown that efficiency of log odds ratio estimation can be improved relative to use of the corresponding logistic regression model [26]. Similarly, in comparison with the logistic regression approach in the current setting, use of a maximum likelihood estimation approach [expression (3)] resulted in improved efficiency for estimates of model parameters (θ1 and θ2), but only minimal difference in empirical standard errors for odds ratio estimates, which are the quantities of greatest interest. Although the efficiency for this logistic approach may be slightly lower than for a true maximum likelihood analysis of model (4), the convenience advantage is substantial as it may be employed in virtually any statistical software, allows for straightforward inference, and is less directly reliant upon the gamma distributional assumptions.
In our analysis, we considered exposures with right skewed distributions; the gamma distribution was a good fit to the data from our nested case-control study of cytokines and miscarriage. Highly skewed distributions are often appropriate to describe biomarkers. In epidemiological studies of biomarkers, exposure is frequently modeled to allow for non-linearity. Categorization of a continuous exposure into biologically significant ranges or into quantiles is a common practice; however, this approach results in decreased statistical power and a loss of information if parametric assumptions can be made. We considered a gamma for the X|Y distributions in cases and controls; however, estimates from our method capture dose-variance effects that result from underlying risk models other than the gamma case upon which it is based. In scenarios that considered exposure distributed log-normal at the population level with alternative underlying risk models that give rise to the X|Y distributions, the proposed flexible approach had lower bias than existing approaches for analysis of pooled data when exposure effects vary and a single effect estimate is not valid. We did not evaluate other risk models such as a threshold effect. As previously noted, investigators should consider available information regarding the X|Y distributions, whether under pooling or otherwise, to empirically assess the validity of assumptions required by modeling approaches.
Previous work has described inclusion of covariates to the set-based model by inclusion of sums across individuals in each set [7]. While we did not explicitly demonstrate this here, covariates could be included in a similar manner here given that our model is merely an expansion of that previous work. We plan in future work to explore alternative means of accommodating such covariate adjustment in the case of right-skewed exposure. An alternative for incorporating covariates when important covariates are known to investigators prior to creating pools is a “smart pooling” approach. Specifically, pool groups may be formed such that the sample is stratified to address covariates.
Pooled biomarker assessment strategies in case-control studies hold potential to address cost constraints as well as situations when biospecimen volumes are limited; however, analysis of such data has previously been limited to dose-invariant effects, which correspond to an equal variance assumption for normally distributed biomarkers, or to an equal shape parameter assumption for gamma distributed biomarkers. Our proposed flexible logistic regression approach for pooled case-control data allows for estimation of exposure effects with minimal loss of efficiency and without limiting to constant, dose-invariant effects.
Acknowledgements
This research was partially supported by the Long-Range Research Initiative of the American Chemistry Council and the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, National Institutes of Health.
Appendix
The following R code is provided for implementation of maximum likelihood estimation of gamma distribution parameters (αy ,βy) by maximizing the likelihood in equation (3) of section 3.
OR.f.g.mle=function(data0,data1,poolsize0,poolsize1){
mmu.0=mean(data0)
vvar.0=var(data0)
op=optim(c(mmu.02/vvar.0,mmu.0/vvar.0),likelihood,control=list(m
axit=10000),data=data0,poolsize=poolsize0)$par
a.0.hat=abs(op[1])
b.0.hat=abs(op[2])
mmu.0=mean(data1)
vvar.0=var(data1)
op=optim(c(mmu.02/vvar.0,mmu.0/vvar.0),likelihood,control=list(m
axit=100000),data=data1,poolsize=poolsize1)$par
a.1.hat=abs(op[1])
b.1.hat=abs(op[2])
logit.g.abx(a0=a.0.hat,b0=b.0.hat,a1=a.1.hat,b1=b.1.hat,x=1,offs
et=1,thetas=T)[2:4]
}
likelihood=function(para,data,poolsize) {
a=abs(para[1])
b=abs(para[2])
logl=0
for(i in 1:length(data)) {
temp=dgamma(data[i],shape=a*poolsize[i],rate=b)
logl=logl+log(temp)
}
return(-logl)
}
logit.g.abx=function(a0,b0,a1,b1,x,offset=1,thetas=F){
t0=log(offset)+a1*log(b1)-
a0*log(b0)+log(gamma(a0)/gamma(a1))
t1=b0-b1
t2=a1-a0
output=t0+t1*x+t2*log(x)
if(thetas){output=c(output,t0,t1,t2)}
output
}
Contributor Information
Brian W. Whitcomb, Division of Biostatistics and Epidemiology, School of Public Health and Health Sciences, University of Massachusetts Amherst.
Neil J. Perkins, Division of Epidemiology, Statistics, and Prevention Research, Eunice Kennedy Shriver National Institute of Child Health and Human Development, NIH/DHHS
Zhiwei Zhang, Division of Epidemiology, Statistics, and Prevention Research, Eunice Kennedy Schriver National Institute of Child Health and Human Development, NIH/DHHS
Aijun Ye, Division of Epidemiology, Statistics, and Prevention Research, Eunice Kennedy Schriver National Institute of Child Health and Human Development, NIH/DHHS
Robert H. Lyles, Department of Biostatistics and Bioinformatics, The Rollins School of Public Health of Emory University
References
- 1.Dorfman R. The detection of defective members of large populations. Annals of Mathematical Statistics. 1943;14:436–40. [Google Scholar]
- 2.Faraggi D, Reiser B, Schisterman EF. ROC curve analysis for biomarkers based on pooled assessments. Statistics in Medicine. 2003;22:2515–27. doi: 10.1002/sim.1418. [DOI] [PubMed] [Google Scholar]
- 3.Mumford SL, Schisterman EF, Vexler A, Liu A. Pooling biospecimens and limits of detection: Effects on ROC curve analysis. Biostatistics. 2006;7:585–98. doi: 10.1093/biostatistics/kxj027. [DOI] [PubMed] [Google Scholar]
- 4.Schisterman EF, Vexler A, Mumford SL, Perkins NJ. Hybrid pooled-unpooled design for cost-efficient measurement of biomarkers. Statistics in Medicine. 2010;29:597–613. doi: 10.1002/sim.3823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schisterman EF, Vexler A. To pool or not to pool, from whether to when: Applications of pooling to biospecimens subject to a limit of detection. Paediatric and Perinatal Epidemiology. 2008;22:486–96. doi: 10.1111/j.1365-3016.2008.00956.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vexler A, Liu A, Schisterman EF. Efficient design and analysis of biospecimens with measurements subject to detection limit. Biometrical Journal. 2006;48:780–91. doi: 10.1002/bimj.200610266. [DOI] [PubMed] [Google Scholar]
- 7.Weinberg CR, Umbach DM. Using pooled exposure assessment to improve efficiency in case-control studies. Biometrics. 1999;55:718–26. doi: 10.1111/j.0006-341x.1999.00718.x. [DOI] [PubMed] [Google Scholar]
- 8.Zhang SD, Gant TW. Effect of pooling samples on the efficiency of comparative studies using microarrays. Bioinformatics. 2005;21:4378–83. doi: 10.1093/bioinformatics/bti717. [DOI] [PubMed] [Google Scholar]
- 9.Wilcox AJ, Weinberg CR, O'Connor JF, Baird DD, Schlatterer JP, Canfield RE, Armstrong EG, Nisula BC. Incidence of early loss of pregnancy. New England Journal of Medicine. 1988;4:189–94. doi: 10.1056/NEJM198807283190401. [DOI] [PubMed] [Google Scholar]
- 10.Chaiworapongsa T, Romero R, Tolosa JE, Yoshimatsu J, Espinoza J, Kim YM, Kim JC, Bujold E, Kalache1 K, Edwin S. Elevated monocyte chemotactic protein-1 in amniotic fluid is a risk factor for pregnancy loss. Journal of Maternal, Fetal and Neonatal Medicine. 2002;12:159–64. doi: 10.1080/jmf.12.3.159.164. [DOI] [PubMed] [Google Scholar]
- 11.Jones RL, Hannan NJ, Kaitu'u TJ, Zhang J, Salamonsen LA. Identification of chemokines important for leukocyte recruitment to the human endometrium at the times of embryo implantation and menstruation. Journal of Clinical Endocrinology and Metabolism. 2004;12:6155–67. doi: 10.1210/jc.2004-0507. [DOI] [PubMed] [Google Scholar]
- 12.Madhappan B, Kempuraj D, Christodoulou S, Tsapikidis S, Boucher W, Karagiannis V, Athanassiou A, Theoharides TC. High levels of intrauterine corticotropin-releasing hormone, urocortin, tryptase, and interleukin-8 in spontaneous abortions. Endocrinology. 2003;6:2285–90. doi: 10.1210/en.2003-0063. [DOI] [PubMed] [Google Scholar]
- 13.Whitcomb BW, Schisterman EF, Klebanoff MA, Baumgarten M, Rhoton-Vlasak A, Luo X, Chegini N. Circulating chemokine levels and miscarriage. American Journal of Epidemiology. 2007;166:323–31. doi: 10.1093/aje/kwm084. [DOI] [PubMed] [Google Scholar]
- 14.Whitcomb BW, Schisterman EF, Klebanoff MA, Baumgarten M, Luo X, Chegini N. Circulating levels of cytokines during pregnancy: thrombopoietin is elevated in miscarriage. Fertility and Sterility. 2008;89:1795–802. doi: 10.1016/j.fertnstert.2007.05.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Whitcomb BW, Schisterman EF, Luo X, Chegini N. Maternal serum granulocyte colony-stimulating factor levels and spontaneous preterm birth. Journal of Women’s Health (Larchmt) 2009;18:73–8. doi: 10.1089/jwh.2008.0883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hardy JB. The collaborative perinatal project: Lessons and legacy. Annals of Epidemiology. 2003;5:303–11. doi: 10.1016/s1047-2797(02)00479-9. [DOI] [PubMed] [Google Scholar]
- 17.Andersen ME, Yang RSH, French T, Chubb LS, Dennison JE. Molecular circuits, biological switches, and nonlinear dose-response relationships. Environmental Health Perspectives. 2002;110:971–978. doi: 10.1289/ehp.02110s6971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.May S, Bigelow C. Modeling nonlinear dose-response relationships in epidemiological studies: statistical approaches and practical challenges. Dose-Response1. 2005;3:474–490. doi: 10.2203/dose-response.003.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Canfield RL, Henderson CR, Cory-Slechta DA, Cox C, Jusko TA, Lanphear BP. Intellectual impairment in children with blood lead concentrations below 10 μg per deciliter. New England Journal of Medicine. 2003;348:1517–26. doi: 10.1056/NEJMoa022848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jusko TA, Lockhart DW, Sampson PD, Henderson CR, Canfield RL. Response to: “What is the meaning of non-linear dose-response relationships between blood lead concentrations and IQ?”. Neurotoxicology. 2006;27:1123. doi: 10.1016/j.neuro.2006.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Andersen ME, Garton HA. Biological regulation of receptor-hormone complex concentrations in relation to dose response assessments for endocrine-active compounds. Toxicological Sciences. 1999;48:38–50. doi: 10.1093/toxsci/48.1.38. [DOI] [PubMed] [Google Scholar]
- 22.Liu S-Z. Nonlinear Dose-Response Relationship in the Immune System Following Exposure to Ionizing Radiation: Mechanisms and Implications. Nonlinearity in Biology, Toxicology, Medicine. 2003;1:71–92. doi: 10.1080/15401420390844483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.SAS Institute, Inc. SAS IML 9.1User’s Guide. SAS Institute; Cary, NC: 2004. [Google Scholar]
- 24.Otto EA, Ramaswami G, Janssen S, Chaki M, Allen SJ, Zhou W, Airik R, Hurd TW, Ghosh AK, Wolf MT, Hoppe B, Neuhaus TJ, Bockenhauer D, Milford DV, Soliman NA, Antignac C, Saunier S, Johnson CA. Hildebrandt F; the GPN Study Group. Mutation analysis of 18 nephronophthisis associated ciliopathy disease genes using a DNA pooling and next generation sequencing strategy. Journal of Medical Genetics. 2011;48:105–116. doi: 10.1136/jmg.2010.082552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cornfield J. Joint dependence of risk of coronary heart disease on serum cholesterol and systolic blood pressure: A discriminant function analysis. Fed Proc. 1962;21:58–61. [PubMed] [Google Scholar]
- 26.Lyles RH, Guo Y, Hill AH. A fresh look at the discriminant function approach for estimating crude or adjusted odds ratios. American Statistician. 2009;63:320–7. doi: 10.1198/tast.2009.08246. [DOI] [PMC free article] [PubMed] [Google Scholar]