AFFINE-CORRECTED PARADISE: FREE-BREATHING PATIENT-ADAPTIVE CARDIAC MRI WITH SENSITIVITY ENCODING

Abstract

We propose a real-time cardiac imaging method with parallel MRI that allows for free breathing during imaging and does not require cardiac or respiratory gating. The method is based on the recently proposed PARADISE (Patient-Adaptive Reconstruction and Acquisition Dynamic Imaging with Sensitivity Encoding) scheme. The new acquisition method adapts the PARADISE k-t space sampling pattern according to an affine model of the respiratory motion. The reconstruction scheme involves multi-channel time-sequential imaging with time-varying channels. All model parameters are adapted to the imaged patient as part of the experiment and drive both data acquisition and cine reconstruction. Simulated cardiac MRI experiments using the realistic NCAT phantom show high quality cine reconstructions and robustness to modeling inaccuracies.

1. INTRODUCTION

The challenge in cardiac magnetic resonance (MR) imaging is to create a high resolution image of the heart in the presence of two physiological motions: cardiac and respiratory. Owing to the limited speed of MR acquisition, it is usually not possible to sample the entire k-space (spatial Fourier transform) at the required Nyquist temporal sampling rate. A typical approach to bypassing this problem is to attempt to effectively freeze cardiac and respiratory motion through ECG-gating and breath-holding, respectively. However these methods can only provide a static view of the dynamic process (and not a real-time motion movie) time-averaged over several heart cycles. Besides, gated techniques are incapable of imaging transient cardiac phenomena present in certain pathologies and are ineffective in arrhythmic patients.

In general, ignoring the effect of respiratory motion results in image quality degradation in form of blurring and ghosting artifacts. Two commonly used approaches to handle respiratory motion are respiratory gating and breath-holding. In the former approach, data is acquired only during a small window in the respiratory cycle. This greatly increases the total scan time, and the resultant reconstruction represents the dynamic object time-averaged over several breathing cycles. Breath-holding, on the other hand, limits the total available data acquisition time and is inconvenient for the subject being imaged. Also, the reconstructed images may be degraded due to unsteady breath-holds and respiratory drifts.

In this work, we present a parallel MRI scheme that is adapted to both cardiac and respiratory models and does not require cardiac or respiratory gating or breath-holds. The proposed method builds upon the PARADISE imaging scheme [1] by explicitly accounting for the respiratory motion through affine motion modeling. As in the case of breath-hold PARADISE cardiac MRI, our free-breathing (FB-PARADISE) method overcomes the limitations of conventional parallel imaging techniques [2] by incorporating elaborate patient-adapted modeling [3] for minimally-redundant acquisition.

2. MODELS OF THE HEART AND RESPIRATION

The time-varying object (TVO) in the absence of respiratory motion is denoted by I(r, t), r ∈ ℝ^d. Fourier transforms (FT) of signals are indicated by the variables used, e.g., I(k, f) is the Fourier transform of I(r, t) with respect to r and t; k and f refer to the spatial and temporal frequencies respectively.

Heart Model: The banded spectral model [3], characterizes the cardiac object, I(r, t), by its support ℬ = supp {I(r, f)} in the dual k-t (DKT) space, i.e., the x-y-f space, as shown in Fig. 1. It captures the approximate periodicity of cardiac motion reflected in the quasi-harmonic banded temporal spectrum with frequency spacing determined by the heart-rate. It also incorporates the fact that the highly dynamic portion of the field-of-view (FOV) is localized in the central heart region. The specific parameters for the model differ among patients depending on their heart rate, heart-rate variability and heart position, and are robustly estimated using a pilot scan [3].

Fig. 1.

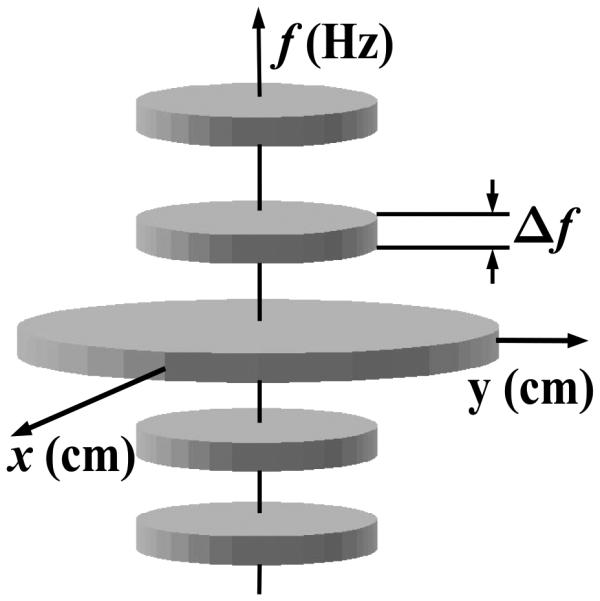
The banded spectral DKT model for the heart.

The banded spectral model accounts for the cardiac dynamics, but does not explicitly model respiratory motion. However, as long as the respiratory motion is relatively slow and the spatial displacements are small, the effect can be modeled as widening of the harmonic bands in the DKT support. This increase in the overall DKT support area will, in general, require higher temporal sampling rates. In case of mild respiratory drifts during imaging, the required sampling rate increase is insignificant. Free-breathing imaging, however, significantly spreads the DKT support resulting in either an infeasible sampling-rate requirement or unacceptable imaging artifacts [4]. With this motivation, in this work, we introduce an object model together with an adaptive parallel imaging scheme that explicitly accounts for respiratory motion.

Respiratory Model: The respiratory motion (identified throughout the paper by a tilde over the various variables) is modeled by a time-varying affine transform of the spatial coordinates, i.e., the TVO is:

$$\tilde{I}(\mathbf{r},t)=I(\mathbf{P}\left(t\right)\mathbf{r}+\mathbf{q}\left(t\right),t)$$ (1)

where P(t) ∈ ℝ^d×d and q(t) ∈ ℝ^d define the affine motion at time t; and I(r, t) is the respiration-free cardiac TVO. Affine motion has been shown to be the dominant component of the motion of the heart walls and coronary arteries induced by respiration [5]. The affine model includes all forms of translation models such as the superior-inferior translation as well as 3-D contraction and rotation models. Affine motion models have been previously used in prospective correction of respiratory motion in ECG-gated coronary MR angiography [6].

3. FREE-BREATHING PARADISE ACQUISITION

PARADISE Acquisition: For any dynamic parallel imaging scheme, the sampling strategy, which defines the acquisition procedure, is subject to an inherent time-sequential (TS) sampling constraint: for each receiver channel, only limited data in k-space can be acquired at any one time [7]. Given the banded spectral model, the goal in PARADISE sampling design is to find a multi-channel TS sampling pattern in k-t space such that alias-free reconstruction of the underlying TVO would be possible, the requirements on sampling speed are met, and optimal SNR performance is achieved [1]. To accomplish this, we search over all reconstructible TS lattices [1] that achieve or exceed a predetermined sampling-rate requirement while optimizing the resulting SNR over the dynamic FOV. The optimal sampling scheme acquires the data in the k-t space in a scrambled order defined by a multi-channel TS sampling schedule Ψ = {k^TS(n), nT_R}_n where k^TS (n) is the k-space location sampled by all channels at time nT_R. The TS sampling schedule is optimally adapted to the coil sensitivities and the DKT support ℬ which is previously estimated from the MR data as will be described in Section 5.

Affine-Corrected PARADISE Acquisition: Each of the L parallel receiver channels (coils) is characterized by its complex spatial sensitivity s_ℓ(r) which is assumed to be known. From (1), the object sensed by the ℓ-th channel is:

$${\tilde{D}}_{\ell }(\mathbf{r},t)\triangleq s_{\ell }\left(\mathbf{r}\right)\tilde{I}(\mathbf{r},t)=s_{\ell }\left(\mathbf{r}\right)I(\mathbf{P}\left(t\right)\mathbf{r}+\mathbf{q}\left(t\right),t)$$ (2)

For each receiver channel with sensitivity profile s_ℓ(r) define its time-varying counterpart ${\tilde{s}}_{\ell }(\mathbf{r},t)$ as:

$${\tilde{s}}_{\ell }(\mathbf{r},t)\triangleq s_{\ell }({\mathbf{P}}^{-1}\left(t\right)\mathbf{r}-{\mathbf{P}}^{-1}\left(t\right)\mathbf{q}\left(t\right))$$ (3)

Hence, $s_{\ell }\left(\mathbf{r}\right)={\tilde{s}}_{\ell }(\mathbf{P}\left(t\right)\mathbf{r}+\mathbf{q}\left(t\right),t)$ and from (2) it follows that:

$${\tilde{D}}_{\ell }(\mathbf{r},t)={\tilde{s}}_{\ell }(\mathbf{P}\left(t\right)\mathbf{r}+\mathbf{q}\left(t\right),t)I(\mathbf{P}\left(t\right)\mathbf{r}+\mathbf{q}\left(t\right),t)$$ (4)

Note that

$$D_{\ell }(\mathbf{r},t)\triangleq {\tilde{s}}_{\ell }(\mathbf{r},t)I(\mathbf{r},t)$$ (5)

would be the object sensed by the ℓ-th coil if the respiration-free TVO, I(r, t), were to be imaged. According to this definition and (4), we have that:

$${\tilde{D}}_{\ell }(\mathbf{r},t)=D_{\ell }(\mathbf{P}\left(t\right)\mathbf{r}+\mathbf{q}\left(t\right),t)$$ (6)

From (6), we derive the relation between the spatial Fourier transforms of D_ℓ and ${\tilde{D}}_{\ell }$ to be:

$$D_{\ell }(\mathbf{k},t)=\mid \mathbf{P}\left(t\right)\mid e^{-j2\pi {\mathbf{k}}^T\mathbf{q}\left(t\right)}{\tilde{D}}_{\ell }[{\mathbf{P}}^T\left(t\right)\mathbf{k},t]$$ (7)

where | · | denotes the determinant. If P(t) and q(t) are known, we can calculate D_ℓ(k₀, t) using (7) for any desired k₀ by acquiring ${\tilde{D}}_{\ell }({\mathbf{P}}^T\left(t\right){\mathbf{k}}_0,t)$ instead. This suggests the following acquisition scheme:

• (i)Design a PARADISE sampling schedule Ψ = {k^TS(n), nT_R}_n for sampling D_ℓ(k, t) that will enable recovery of I(r, t).
• (ii)Because D_ℓ(k, t) is not directly observable, instead acquire samples of ${\tilde{D}}_{\ell }(\mathbf{k},t)$ on the affine-corrected sampling schedule Γ = {P^T (t)k^TS(n), nT_R}_n.
• (iii)Using (7), compute the samples of D_ℓ(k, t) on Ψ.
• (iv)Reconstruct the respiration-free TVO I(r, t) from {D_ℓ (Ψ), ℓ = 1, …, L}.
• (v)If desired, use (1) to reconstruct the actual TVO, $\tilde{I}$.

Now, owing to the relationship (5), Steps (i) and (iv) correspond to a modified version of PARADISE, in which I(r, t) has the usual DKT model with known fixed support ℬ, but the known coil sensitivities $\left\{{\tilde{s}}_{\ell }(\mathbf{r},t)\right\}$ are time-varying. We describe this modified PARADISE method in the next section.

4. PARADISE WITH TIME-VARYING CHANNELS

In order to reconstruct I(r, t), we need to solve a multi-channel TS imaging problem with time-varying channels. In this section, we derive the corresponding inverse problem that needs to be solved and propose an efficient numerical algorithm for solving it.

Taking the Fourier transform of (5), the MR data obtained in Step (iii) above from the ℓ-th coil is given by

$$D_{\ell }(\mathbf{k},t)={\int }_{FOV}{\tilde{s}}_{\ell }(\mathbf{r},t)I(\mathbf{r},t)e^{-i2\pi k.r}d\mathbf{r}$$ (8)

where r = [x y]^T for 2-D imaging. Acquisition along the readout (k_x) direction is sufficiently fast to be assumed instantaneous relative to the temporal dynamics of the object. Therefore, the effect of sampling along k_x is ignored in our analysis. Consequently, we have a 2-D TS sampling problem in the (k_y, t) domain, where each point corresponds to a horizontal line in (k_x, k_y).

Consider a temporally-uniform TS sampling lattice Λ with basis matrix A. According to multi-dimensional sampling theory, sampling on Λ in (k_y, t) will result in replications of the spectrum in the DKT domain, i.e., (y, f). This is equivalent to convolution of the spectrum in (y, f) domain with the following point spread function:

$$h(y,f)=\frac{1}{\mid \mathbf{A}\mid }\sum _{\mathbf{n}\in {\mathbb{\mathbb{Z}}}^2}\delta \left(\left[\begin{array}{c}\hfill y\hfill \\ \hfill f\hfill \end{array}\right]-A^{\ast }n\right)$$ (9)

where A* = A^−T is basis matrix for the polar lattice Λ*. For any n ∈ ℤ² define $\left[\begin{array}{c}\hfill \Delta y_{\mathbf{n}}\hfill \\ \hfill \Delta f_{\mathbf{n}}\hfill \end{array}\right]\triangleq A^{\ast }n$. Sampling on Λ in (k_y, t) and taking the inverse FT in k_y and forward FT in t of the ℓ-th coil measurement, we arrive at:

$$D_{\ell }(y,f)=\frac{1}{\mid \mathbf{A}\mid }\sum _{\mathbf{n}\in {\mathbb{\mathbb{Z}}}^2}\left({\tilde{s}}_{\ell }{⊛}_{\mathrm{f}}I\right)(y-\Delta y_{\mathbf{n}},f-\Delta f_{\mathbf{n}})$$ (10)

where ⊛_f denotes convolution along temporal frequency.

FB-PARADISE Reconstruction Problem: Given the transformed coil data D_ℓ(y, f) for ℓ = 1, ⋯ , L for all y and f, the coil sensitivity profiles ${\tilde{s}}_{\ell }(y,f)$, and the basis A of the TS sampling lattice, solve the linear inverse problem in (10) for I(y, f).

With time-invariant channels ${\tilde{s}}_{\ell }(y,f)=\delta \left(f\right){\tilde{s}}_{\ell }\left(y\right)$, and (10) would reduce to a SENSE-type linear matrix equation as stated and discussed in [1]. Here we present an numerical algorithm for solving the reconstruction problem in (10). As the first step, we write:

$$\begin{array}{cc}\hfill \left({\tilde{s}}_{\ell }{⊛}_{\mathbf{f}}I\right)(y,f)& ={\int }_{\phi =-\infty }^{\infty }{\tilde{s}}_{\ell }(y,\phi )I(y,f-\phi )d\phi \hfill \\ \hfill & \approx \Delta \omega \sum _{p=-\infty }^{\infty }{\tilde{s}}_{\ell }(y,p\Delta \omega )I(y,f-p\Delta \omega )\hfill \end{array}$$

where a truncated Riemann sum expansion is used to discretize the convolution integral (the mesh size Δω is sufficiently small). In practice, the coil sensitivities are smooth and the affine-motion applied to them is expected to be relatively slow. Therefore, we can assume that ${\tilde{s}}_{\ell }(y,p\Delta \omega )$ is negligible for |p| > 𝒫, where 𝒫 is some appropriate integer. Combining this approximation with (10) for a fixed (y₀, f₀) ∈ ℬ gives:

$$D_{\ell }(y_0,f_0)\approx \frac{\Delta \omega }{\mid \mathbf{A}\mid }\sum _{\mathbf{n}\in {\mathbb{\mathbb{Z}}}^2}\sum _{p=-\mathcal{𝒫}}^{\mathcal{𝒫}}{\tilde{S}}_{\ell }(y_0-\Delta y_{\mathbf{n}},p\Delta \omega )I(y_0-\Delta y_{\mathbf{n}},f_0-\Delta f_{\mathbf{n}}-p\Delta \omega )$$ (11)

Equation (11) can be written in matrix form as follows: (12)

$$\overrightarrow{D}(y_0,f_0)\approx \tilde{S}(y_0,f_0)\overrightarrow{I}(y_0,f_0)$$ (12)

where $\overrightarrow{D}(y_0,f_0)$ contains the transformed coil outputs, $\overrightarrow{I}(y_0,f_0)$ contains the set of unknowns, and $\tilde{\mathbf{S}}(y_0,f_0)$ is the forward matrix consisting of coil sensitivities.

Denote by $\overrightarrow{\mathcal{𝒬}}(y_0,f_0)$, the set of (y, f) locations of all the elements in $\overrightarrow{I}(y_0,f_0)$. Given the transformed MRI data, $\overrightarrow{D}(y_0,f_0)$ is known for all (y₀, f₀) ∈ ℬ and solving the inverse problem in (12) will recover the main replica of the spectrum for all members of $\overrightarrow{\mathcal{𝒬}}(y_0,f_0)$. It can be shown that the collection of all $\overrightarrow{\mathcal{𝒬}}(y,f)$ provides a partitioning of the DKT support ℬ. Hence, inverting (12) for all such sets recovers the object in the (y, f) domain. Since the coil measurements are corrupted by additive noise, a regularized linear minimum variance estimator is used to solve (12) where the noise covariance matrix is estimated from the MR data. Subsequently, the object is reconstructed by an inverse FT along f. This procedure can be repeated for all k_x to recover the whole 2-D object. Extension to 3-D imaging is achievable in a similar fashion. Finally, note that I(r, t) represents the way the cardiac TVO would appear in the absence of respiratory motion. If desired, $\tilde{I}(\mathbf{r},t)$, which represents the true physical object with both respiratory and cardiac motion present, can also be computed using (1) and eknowledge of the affine motion parameters.

5. OVERVIEW OF FB-PARADISE IMAGING SCHEME

In order to account for respiratory motion, we adapt the k-space sample locations as described in Section 3. In particular, instead of acquiring data on the straight line $k_y=k_y^{\mathrm{TS}}\left(n\right)$ at time nT_R as specified by the multi-channel sampling schedule Ψ, we follow the affine-corrected sampling schedule Γ, and acquire data for the oblique k-space trajectory:

$$\mathbf{k}{\left(n\right)}^{\mathrm{AC}-\mathrm{TS}}={\mathbf{P}}^T\left(n{T}_R\right)\left[\begin{array}{c}\hfill k_x\hfill \\ \hfill k_y^{\mathrm{TS}}\left(n\right)\hfill \end{array}\right],\mid k_x\mid <k_x^{\max }$$ (13)

The gradients in the pulse sequence will be modified accordingly, to acquire the oblique line segment, with the readout direction coinciding with the direction of the line. The proposed affine-corrected MR data acquisition scheme has two stages as described below.

Pre-Imaging: The goal in this stage is to determine the DKT support ℬ and to calibrate the motion model, i.e., to find the patient-adaptive relationship between [P(t), q(t)] and the respiratory phase η(t) (relative time within the breathing cycle). This information is required to adapt the FB-PARADISE sampling pattern during the imaging stage.

A scheme to calibrate the motion model in MRI has recently been proposed [6]. The respiratory phase, η(t), can be measured by a respiratory bellow or navigator echoes positioned on the diaphragm. Using the calibrated motion model, we can then estimate the instantaneous affine motion parameters [P(t), q(t)] = [P(η(t)), q(η(t))] using the measured phase.

Estimating the DKT support from the MR data, as described in [3], involves sampling $\tilde{I}$ along k-space lines parallel to k_x = 0, i.e., with k_x as the phase encode direction and k_y as the readout direction. Similarly to (13), to account for breathing motion, we modify the k-space sampling locations by pre-multiplying the desired k-space trajectory by P^T (t) as described above. This is then used to adapt the pulse sequence gradients. From the acquired data, the DKT support ℬ is estimated. Using the estimated ℬ and coil sensitivity estimates, the PARADISE sampling schedule Ψ (Section 3) is computed, which would achieve the required acceleration and yield the optimal SNR performance for the nominal (static) coil sensitivity profiles and respiration-free object [1].

Imaging: The aim of the image acquisition stage is to acquire samples of $\tilde{I}$ on the FB-PARADISE sampling schedule Γ, i.e., along the k-space trajectory in (13). In order to determine Γ, we estimate [P(nT_R), q(nT_R)] by monitoring the breathing phase, η(t), and using the previously calibrated motion model. Reconstruction of the TVO is performed as described in Section 4.

6. SIMULATION RESULTS AND DISCUSSIONS

A 4-D cardiac cine corresponding to a supine male patient was generated using a modified version of the NCAT phantom [8] with MR-adjusted contrast (bright blood imaging). Two versions of the simulated cine were generated: one with only cardiac motion and one with both respiratory and cardiac motions. For both phantoms, the doubly-oblique short-axis slices were extracted and resized to a 128 × 128 image matrix size. The average heart rate was taken to be 60 beats per minute. The DKT support of the respiration-free phantom was computed and 94% of the energy (in the ℓ₂ sense) was captured by the first 12 harmonic bands of width Δf = 0.1 Hz each. The dynamic region was assumed to occupy 45% of the FOV along the y direction. The MR scanner was assumed to have 8 receiver channels and the coil profiles were obtained using numerical simulation of Bio-Savart’s law for a spherical water phantom. In order to isolate the motion artifacts from SNR performance, the experiments were run with no additive noise.

As discussed earlier, affine motion is a reasonable model for motion of the heart and adjoining structures in the FOV due to breathing. In the first experiment, an exact affine motion model was used for the respiratory motion. The parameters for the affine motion were chosen based on experimentally observed values [6], with tidal breathing period of 4 seconds. The affine respiration-induced motion was applied to the respiration-free phantom, and MR data, as prescribed by each of the PARADISE and FB-PARADISE schemes, was generated for a total scan time of 25 seconds. As expected, the resulting reconstructions showed severe ghosting and blurring artifacts for the PARADISE scheme and visually artifact-free reconstructions for the FB-PARADISE method. These results are not shown for reasons of space.

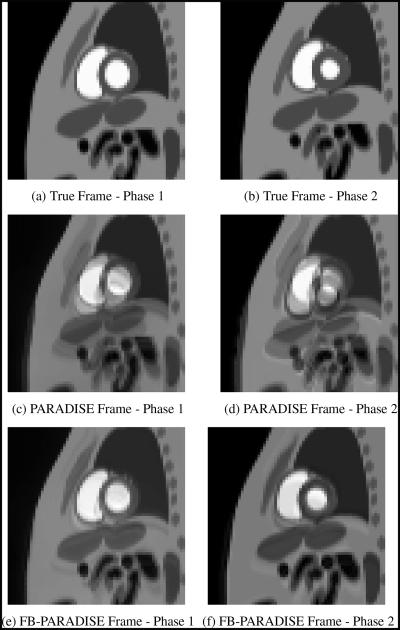
Note, however, that the assumption that the entire imaged slice undergoes the same respiratory affine motion as the heart does not hold in practice. For example, the spine is relatively stationary during the breathing cycle. The respiratory motion simulated by the free-breathing NCAT phantom is based on in-vivo CT data and is not affine [8]. The second set of numerical experiments aimed at testing the robustness of the FB-PARADISE method to modeling inaccuracies in the respiratory motion model. In order to achieve that, the NCAT phantom was utilized to simulate typical tidal respiratory motion with maximum diaphragm displacement of 2 cm and anterior-posterior chest expansion of of 1.2 cm. The extent of the heart’s lateral motion during breathing was set to 0.2 cm. Figures 2(a) and 2(b) show two snapshots of the free-breathing phantom. The two frames have different cardiac and respiratory phases.

Fig. 2.

Two reconstructed short-axis frames of the free-breathing cine along with the ground truth.

For this second set of experiments, the simulation setup was similar to the first experiment, i.e., the same DKT model parameters were assumed for the respiration-free cardiac object and same resolution goals were desired. First, the PARADISE-sampled data was generated and the cine was reconstructed. Figures 2(c) and 2(d) show two frames of the reconstructed cine corresponding to the same time points of the true frames shown in panels (a) and (b). Significant blurring and ghosting artifacts are seen in the images. These are the effects of the respiratory motion, which is not accounted for in PARADISE.

The NCAT phantom is capable of separately generating the displacement vectors due to respiration for all frames. This data was used to fit an affine-motion model to the NCAT respiratory motion. The resulting affine model was used to acquire and reconstruct the FB-PARADISE cine. Figures 2(e) and 2(f) show the corresponding reconstructed frames. Though both imaging methods show image degradation due to incorrect modeling of the respiratory motion, the reconstructions are clearly superior to those of PARADISE, as seen in the figures. Therefore, although we model the effect of breathing by an affine motion, our simulations indicate that even for more complicated motions in the imaged slice, fair reconstructions can be achieved. In practice, in addition to the form of respiratory motion, the results will also depend upon the accuracy with which the calibration model is estimated and its approximate time-invariance between the pre-imaging and imaging acquisition stages.