Abstract
There is growing interest in models of regulatory sequence evolution. However, existing models specifically designed for regulatory sequences consider the independent evolution of individual transcription factor (TF)–binding sites, ignoring that the function and evolution of a binding site depends on its context, typically the cis-regulatory module (CRM) in which the site is located. Moreover, existing models do not account for the gene-specific roles of TF-binding sites, primarily because their roles often are not well understood. We introduce two models of regulatory sequence evolution that address some of the shortcomings of existing models and implement simulation frameworks based on them. One model simulates the evolution of an individual binding site in the context of a CRM, while the other evolves an entire CRM. Both models use a state-of-the art sequence-to-expression model to predict the effects of mutations on the regulatory output of the CRM and determine the strength of selection. We use the new framework to simulate the evolution of TF-binding sites in 37 well-studied CRMs belonging to the anterior–posterior patterning system in Drosophila embryos. We show that these simulations provide accurate fits to evolutionary data from 12 Drosophila genomes, which includes statistics of binding site conservation on relatively short evolutionary scales and site loss across larger divergence times. The new framework allows us, for the first time, to test hypotheses regarding the underlying cis-regulatory code by directly comparing the evolutionary implications of the hypothesis with the observed evolutionary dynamics of binding sites. Using this capability, we find that explicitly modeling self-cooperative DNA binding by the TF Caudal (CAD) provides significantly better fits than an otherwise identical evolutionary simulation that lacks this mechanistic aspect. This hypothesis is further supported by a statistical analysis of the distribution of intersite spacing between adjacent CAD sites. Experimental tests confirm direct homodimeric interaction between CAD molecules as well as self-cooperative DNA binding by CAD. We note that computational modeling of the D. melanogaster CRMs alone did not yield significant evidence to support CAD self-cooperativity. We thus demonstrate how specific mechanistic details encoded in CRMs can be revealed by modeling their evolution and fitting such models to multispecies data.
Keywords: enhancer, evolution, cis-regulatory module, cooperativity, simulation
Introduction
The evolution of a nucleotide sequence can be modeled by various broadly applicable evolutionary models (Felsenstein 1981; Hasegawa et al. 1985; Halpern and Bruno 1998) as well as evolutionary models designed for a specific type of sequence (e.g., protein-coding sequences [Halpern and Bruno 1998] and structured RNA [Jow et al. 2002; Bradley and Holmes 2009]). In recent years, there has been a growing interest in evolutionary models for regulatory sequences such as transcription factor (TF)–binding sites, especially in light of reports of frequent binding site turnover despite functional constraints (Moses et al. 2006; Doniger and Fay 2007; Spivakov et al. 2012) and reports of ultraconserved genomic segments being associated with regulatory function (Visel et al. 2008). Models of binding site evolution have a prominent role in annotating the regulatory genome: Computational approaches for motif discovery and enhancer prediction rely on such models to compare orthologous noncoding sequences and assess their regulatory potential (Moses et al. 2004; Sinha et al. 2006; He et al. 2009).
The first generation of site-evolution models included applications of the Halpern–Bruno model (Halpern and Bruno 1998) and the F81 model (Felsenstein 1981), parameterized by the position weight matrix (or motif) that represents the binding specificity of the TF (Moses et al. 2004; Siddharthan et al. 2005; Sinha et al. 2006). Both of these models assume that each nucleotide in the binding site evolves independently, an assumption that is commonly made for modeling neutral DNA sequences but is questionable for TF-binding sites. Lässig and coworkers (Berg et al. 2004; Mustonen and Lässig 2005) proposed a more advanced model where selection was modeled as acting on the entire binding site rather than each position independently, and used this model to estimate selection strength on cAMP receptor protein-binding sites in bacteria (Mustonen and Lässig 2005) and to demonstrate the possibility of rapid adaptive evolution of binding sites (Berg et al. 2004), a question that had been previously addressed by Stone and Wray (2001). A simplified version of the same idea was used by Kim et al. (2009) to model TF-binding site evolution in Drosophila. In their model, called the site-level selection (SS) model, the functional effect of a mutation is dependent on the binding energy of the site before and after the mutation. All sites with energy above a threshold (henceforth called the strong sites) are assumed to be functionally equivalent, as are all sites with energy below the threshold (henceforth called the weak sites). A mutation that changes a strong site to a weak site is considered functionally harmful and is selected against based on a TF-specific selection coefficient that is estimated from data. In the SS model, evolution at all nucleotides in the binding site is linked together by this common functional constraint. Kim et al. (2009) showed that the SS model more accurately fits the observed patterns of binding site conservation between D. melanogaster and D. yakuba than does the Halpern–Bruno model.
Although these studies demonstrated the benefit of an evolutionary model where selection acts at a binding site level, they are unable to accurately explain observed levels of regulatory sequence conservation. When applied to evolutionary data from two closely related Drosophila genomes, the SS model predicts higher evolutionary conservation than the Halpern–Bruno model, and this prediction is closer to the actual level of conservation (Kim et al. 2009). However, the evolutionary data displays even greater conservation than predicted by the SS model. We speculate that the underprediction of site conservation may be due to at least three factors that the SS model neglects:
The continuous nature of the functional effect of mutations. As mentioned earlier, the SS model assumes that the functional effect of a site is determined by whether the site is strong or weak. In other words, the SS model defines a binary fitness for binding sites. However, it is reasonable to expect that the functional contribution of a binding site can be at multiple levels based on the binding energy of the site (Stormo and Fields 1998), which is typically estimated by the agreement between the sequence and the TF motif.
The context within which a binding site evolves. The SS model assumes that each site in a cis-regulatory module (CRM) evolves independently of all other sites in that CRM, and in a manner that is independent of the expression driven by the CRM, that is, independent of CRM function. In reality, however, one may expect that some binding sites can tolerate somewhat deleterious changes (Spivakov et al. 2012) while other sites stay immutable across large evolutionary distances (Visel et al. 2008), even if the sites are bound by the same TF and with similar strengths. This is because the fitness consequence of an in-site mutation, and hence its evolutionary fate, depends on the contribution of that site to the CRM’s regulatory function, and the precise effect of the mutation on function. The SS model tries to mitigate this issue to an extent by learning a different selection coefficient for each TF. This approach only captures the fact that sites from different factors evolve differently, while forcing sites from the same factor to evolve under the same constraints, regardless of context. Here, context may refer to the entire CRM or to the immediate neighborhood of a site. For instance, a given CRM may have a functional excess of sites for a specific TF, thereby reducing the selective pressure for individual sites. On the other hand, it is possible that a nearby site increases the selective pressure by mediating cooperative or competitive binding.
The evolutionary changes in the context of the binding site. Because the SS model (like all other models mentioned above) ignores the context of a site, it also ignores evolutionary changes in the context. In reality, the context of a site evolves with the site and may lead to interesting evolutionary dynamics, such as compensatory mutations in two different sites of the same CRM (Ludwig and Kreitman 1995; Durrett and Schmidt 2008). For example, the strong pressure for conservation of a site could be relaxed if a nearby site from the same TF is made stronger or if a new site for the same TF is created. Conversely, a site under relatively weak pressure for conservation could be forced into a situation where no mutations are tolerated, by the weakening of a nearby site of the same TF or by the strengthening of a site with an opposing regulatory effect.
We propose that these factors contribute to the disagreement between SS model predictions and data, and develop two models of binding site evolution to address these shortcomings. The first model, called “Predicted Expression-Based Site Evolution Simulator” or “PEBSES,” simulates the evolution of a binding site in the context of its CRM. The evolutionary simulations include mutations within the binding site only and not in the rest of the CRM, but selection is modeled based on the predicted function of the entire CRM. In particular, a thermodynamic model that relates CRM sequence to its function is used to determine the selection pressure on the site, which then guides the evolutionary fate of in-site mutations. The second model that we present, called “Predicted Expression-Based CRM Evolution Simulator” or “PEBCRES,” generalizes this to allow mutations anywhere in the CRM, and not just within the site being modeled. In other words, PEBCRES is a simulation model of CRM evolution, based on a realistic model of CRM function.
First, we examine whether the new models provide better fits to evolutionary data from Drosophila genomes, compared with existing models. For this, we examine over 800 predicted TF-binding sites located across dozens of experimentally characterized CRMs in D. melanogaster as well as their orthologous sequences from 11 other Drosophila genomes. Following Kim et al. (2009), we summarize this evolutionary data in two different statistical representations, with one summary focusing on site conservation on relatively short evolutionary scales and the other capturing site loss across larger divergence times. We then compare each statistical summary with that predicted from evolutionary simulations initialized with the D. melanogaster CRM, and identify the model that agrees most with the data. We find that both expression-based models perform better than the SS model, which is based only on the predicted strength of the site under study.
The new simulation frameworks developed here allow us to incorporate mechanistic changes to the underlying sequence-to-expression (i.e., genotype-to-phenotype) model and repeat the simulations using the resulting fitness function. Taking advantage of this feature, we fit different variants of the PEBCRES model to data on site loss across the 12 Drosophila genomes. We find that a sequence-to-expression model that incorporates self-cooperative DNA binding by the TF Caudal (CAD) provides significantly better fits than an otherwise identical model that lacks this mechanistic aspect. Cooperative DNA binding by CAD has not been directly demonstrated in the literature. Therefore, we pursue this hypothesis further by statistically examining the distribution of intersite spacing between adjacent CAD sites and find a significant preference for a specific range of spacing values. Finally, we perform experimental tests that confirm 1) direct homodimeric interaction between CAD molecules and 2) self-cooperative DNA binding by CAD that favors a particular spacing between binding sites. We note that the hypothesis about CAD self-cooperativity was also tested previously through computational modeling of D. melanogaster CRMs by He et al. (2010) and not found to have statistically significant support; yet, we found clear support for this hypothesis when the same model of CRM function was utilized in modeling evolutionary data. This exercise demonstrates, for the first time (to our knowledge), how specific mechanistic details encoded in cis-regulatory sequences can be revealed by modeling their evolution and fitting such models to multispecies sequence data. The source code of the simulation programs presented here is available at http://veda.cs.uiuc.edu/evolsimul (last accessed October 11, 2013).
Results
A Framework for Context-Aware Simulation of Binding Site Evolution
We developed a framework for simulating binding site evolution where the fitness effect of a mutation in the binding site is 1) continuous rather than binary, 2) depends on the context, that is, on other binding sites present in the CRM within which the binding site is located, and 3) depends on the predicted effect of that mutation on the expression driven by the CRM. In this new evolutionary simulation program, called PEBSES, the evolving genotype is a CRM and the fitness is determined by the entire CRM sequence; however, mutations are allowed only within a predesignated TF-binding site in the CRM.
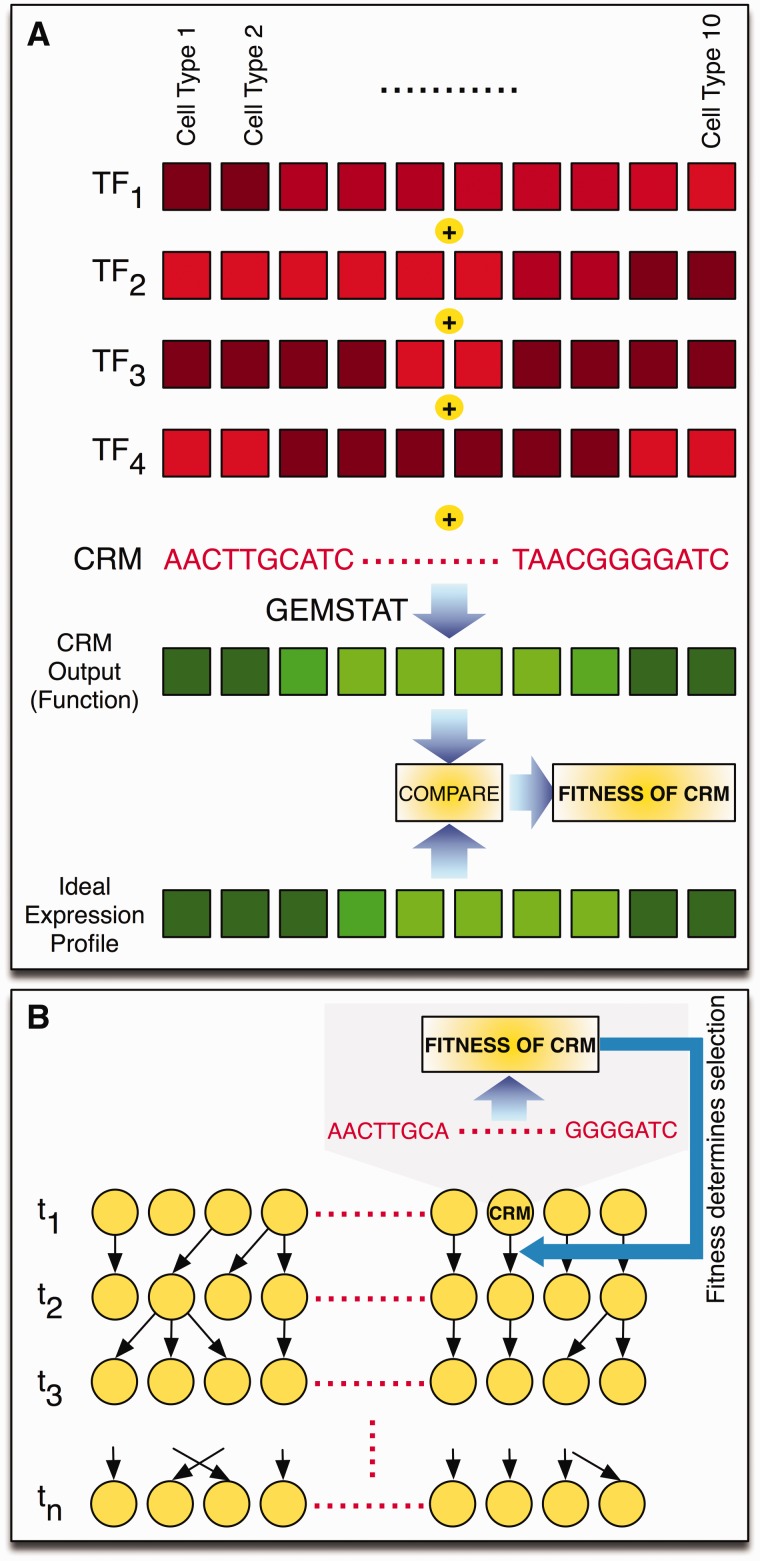
PEBSES uses a thermodynamics-based model called GEMSTAT (He et al. 2010) to predict CRM expression from its sequence (see Materials and Methods) and uses changes in this predicted expression to assess the fitness of a genotype. We represent the regulatory function of a CRM by an “expression profile” (a vector of gene expression levels in well-defined cell types; fig. 1A). There is a fixed expression profile, called the “ideal expression profile,” that serves as the phenotype under purifying selection. The fitness of a CRM sequence is determined by 1) predicting the expression profile of that CRM using the GEMSTAT model and 2) comparing this predicted expression profile to the ideal expression profile (fig. 1A).
Fig. 1.
Methodology. (A) The regulatory function of a CRM is represented by an expression profile, that is, gene expression levels in well-defined cell types. An ideal expression profile (shown in green, with brighter shades representing higher expression) is designated and the fitness of a CRM sequence is computed by comparing this ideal expression profile to that predicted as being the CRM’s output (a more similar CRM output profile has greater fitness). The CRM’s output is computed based on its sequence and the concentration values of relevant TFs (shown in red) in the same set of cell types. This computation is done using the thermodynamics-based GEMSTAT model (He et al. 2010), which additionally uses the binding motifs of those TFs to predict CRM function from sequence. (B) Cartoon illustration of Wright–Fisher simulations underlying the PEBCRES model. A fixed-sized population of individuals (CRMs) is evolved for n generations (t1, t2, … tn). Random mutations are introduced in each generation using a predetermined mutation rate parameter. Each individual is sampled independently at random from the population in the previous generation, and this sampling probability is dependent on the fitness of the individual, which in turn is determined by the CRM’s output as shown in (A).
Our new evolutionary model, PEBSES, simulates a continuous time Markov process describing substitutions within a binding site (see Materials and Methods). It is exactly analogous to the SS model of Kim et al. (2009) except for the fitness function used; instead of a fitness function based on the predicted affinity of a binding site, we use the fitness function from He et al. (2012), which compares the GEMSTAT-predicted expression pattern of a sequence with an ideal expression pattern. This addresses the main shortcomings of the SS model, because the functional effect of a mutation is dependent not only on the mutation and the binding site but also on the expression profile and on the CRM in which the site is located. Moreover, as GEMSTAT predicts expression from sequence based on site strengths, not based on a threshold on site strengths, the fitness function defines a continuous rather than binary landscape on all mutations.
We emphasize that while the fitness function used in PEBSES is based on the expression pattern driven by the entire CRM, the evolutionary process is limited to a single binding site, with mutations being restricted to the boundaries of the binding site. We designed PEBSES as binding site-level simulation for two main reasons: 1) it is computationally efficient, and 2) it provides a fair comparison with the binding site-evolution models examined in Kim et al. (2012), especially the SS model.
The Context Plays an Important Role in a Site’s Evolutionary Dynamics
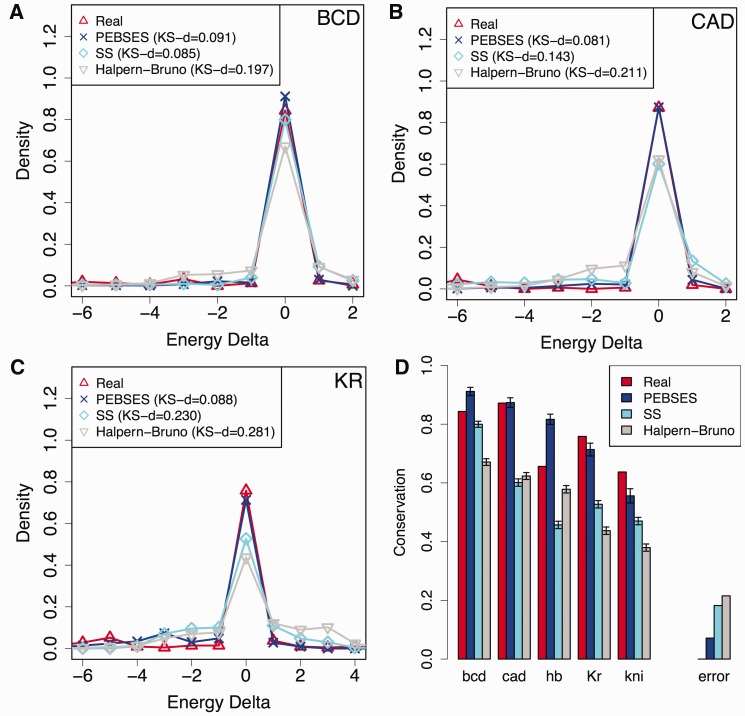
We adopted the methodology of Kim et al. (2009) to generate summary statistics of binding site conservation for each of five different TFs—Bicoid (BCD), CAD, Hunchback (HB), Kruppel (KR), and Knirps (KNI)—in 37 different CRMs from D. melanogaster. These CRMs were selected because each of them is associated with an experimentally characterized expression profile and because these experimental profiles can be predicted with moderate accuracy from respective sequences by the GEMSTAT model (supplementary fig. S1, Supplementary Material online). To generate descriptive statistics of binding site conservation, 1) D. melanogaster CRM sequences were aligned to orthologous D. yakuba sequences, 2) for every predicted binding site in a D. melanogaster sequence, the binding energy of the site and its orthologous site was predicted using the TF’s motif (represented by a position-specific weight matrix [PWM]), 3) the difference in computed binding energies was noted as the “energy difference,” and 4) a histogram of energy differences of orthologous sites was created by examining sites across all CRMs (see supplementary methods [Supplementary Material online] for a brief overview). This histogram serves as the evolutionary data to be modeled. An analogous histogram was computed based on the simulations of evolutionary models such as the Halpern–Bruno model, the SS model, or PEBSES model, and compared with the evolutionary data. The results (fig. 2) show that PEBSES models the evolutionary data more accurately than either the SS or the Halpern–Bruno model. For instance, when focusing on sites of the TF KR (fig. 2C), the energy difference histogram from PEBSES predictions is in strong agreement with that from real data, as measured by the Kolmogorov–Smirnoff (KS) d statistic. The fits are significantly worse for the SS and Halpern–Bruno models. The same is true for sites of the TF CAD (fig. 2B). For BCD sites, the PEBSES and SS models have comparable values of the KS d statistic (fig. 2A). Results for HB and KNI sites are shown in supplementary figure S2 (Supplementary Material online), and, in both cases, the PEBSES model has the lowest KS d statistic value, implying better fits. An alternative, more compact way to compare the different models is to plot the fraction of sites for which energy difference is 0 (indicating perfectly conserved sites), in the real data as well as in simulations under each model. Following this criterion, figure 2D shows that the PEBSES model makes the most accurate predictions of the observed evolutionary characteristics of binding sites. Its overall error is the lowest of the three models compared, and it makes the most accurate predictions for CAD, KR, and KNI sites (for BCD and HB sites, the best fits belong to the SS and Halpern–Bruno models, respectively).
Fig. 2.
(A–C) Energy difference histograms from real data and from three evolutionary models—Halpern–Bruno (Halpern and Bruno 1998), SS (Kim et al. 2009), and PEBSES (this work)—for binding sites of TFs BCD (A), CAD (B), and KR (C). A binding site in a Drosophila melanogaster CRM was compared with its aligned site in D. yakuba (for real data histogram) or in a simulated descendent (for model-based histograms), and the difference in predicted binding energies (LLR scores) of the two sites was noted. This was repeated for each of 159, 171, and 239 binding sites of BCD, CAD, and KR. For model-based histograms, each site’s evolution was simulated on an average of 28 times. (D) The fraction of sites for which energy difference between D. melanogaster and D. yakuba orthologs is 0 (Conservation; y axis) is shown for real data and for the Halpern–Bruno, SS and PEBSES models, and for five different TFs. The difference between real data and a model’s prediction of this fraction is deemed the TF-specific error of that model, and the absolute value of error is averaged over the five TFs and shown as the error of each model.
We note that PEBSES uses only one free parameter (see Materials and Methods), whereas the SS model uses one free parameter per TF (Kim et al. 2009). In addition to being a more constrained model, PEBSES is arguably a more realistic model of binding site evolution. It uses a state-of-the-art sequence-to-expression model to assign fitness to sequences, and this underlying model is in turn trained on sequence and expression data for a large number of CRMs. Moreover, it is easy to change the underlying model used in PEBSES and simulate the evolution of a site under different mechanistic assumptions, for example, cooperativity between TFs, short range repression, synergy activation. We explore this feature in a later section. The sequence-to-expression model used in these simulations incorporates self-cooperative DNA binding by BCD and KNI (as suggested in He et al. [2010]), but no other TF.
The earlier mentioned results suggest that the context of a site, represented by the sequence surrounding it and the expression driven by the sequence, plays an important role in the evolutionary dynamics of that site. Capturing this role in simulating binding site evolution leads to better fits to evolutionary data. It has been speculated that phenomena, such as homotypic clustering, may buffer a CRM against mutation in the sites (Spivakov et al. 2012), thereby increasing the frequency of in-site mutations. Our earlier findings reveal a complementary phenomenon, that is, that the context of a site can also increase the selection pressure for conservation at the site.
A Framework for Evolution of Entire CRMs
In the previous section, we showed that the context of a site plays an important role in the evolution of that site. However, PEBSES does not account for the possibility of additional changes in the context of a site. It simulates the evolution of a single site in the context of a CRM sequence, while that context itself remains unchanged. However, as explained in the Introduction, changes in the context of a site can interact with mutations within the site itself, therefore shaping the evolutionary fate of the site. To model this phenomenon, it is necessary to simulate the evolution of the entire CRM. The continuous time Markov chain simulation implemented in PEBSES is not appropriate for this purpose. It assumes that a mutation is expected to fix (or be eliminated) before another mutation arises. This assumption is reasonable for short sequences, for example, a single binding site, but may not be true of approximately 500-bp-long CRMs.
In this section, we describe a framework that we call PEBCRES, which we use to simulate the evolutionary fate of an entire CRM (see Materials and Methods). PEBCRES is the discrete-time population-based evolutionary simulation framework that was presented in our earlier work (He et al. 2012), as the means to a theoretical exploration of the evolutionary origins of homotypic-binding site clustering. Here, we show for the first time how that framework can be used to study the evolution of real CRMs and to model the evolutionary dynamics of binding sites within those CRMs. We also name the framework here. PEBCRES utilizes a sequence-to-expression model (GEMSTAT, fig. 1A) to evaluate the fitness of a genotype, but unlike PEBSES, it allows mutations to appear anywhere in the CRM sequence (and not just within a specified site). Also unlike PEBSES, it simulates a population of evolving individuals (CRMs) rather than one evolving genotype (fig. 1B). This allows a user of this program to examine the interplay between selection and random drift (Hedrick 2011) as it relates to CRM evolution. Given a CRM from D. melanogaster, it initializes all individuals of a population to have that sequence as the genotype, and then performs discrete-time Wright–Fisher simulations of a fixed-sized population for an appropriate number of generations (see Materials and Methods). The evolutionary fate of a specific binding site in the original CRM is determined by averaging over all individuals in the final generation.
As mentioned earlier, PEBCRES is an application of the framework from He et al. (2012) to model real evolutionary data. It differs from the application in He et al. (2012) in the following aspects: 1) In PEBCRES simulations, the population is initialized with the sequence from a real CRM from D. melanogaster, instead of a random sequence. 2) The “ideal” expression pattern is the pattern predicted by GEMSTAT for the D. melanogaster CRM and, consequently, PEBCRES simulates evolution under negative selection instead of positive selection. 3) The evolutionary time of the simulation is determined to match real evolutionary distances between two species, as opposed to an arbitrarily fixed number of generations.
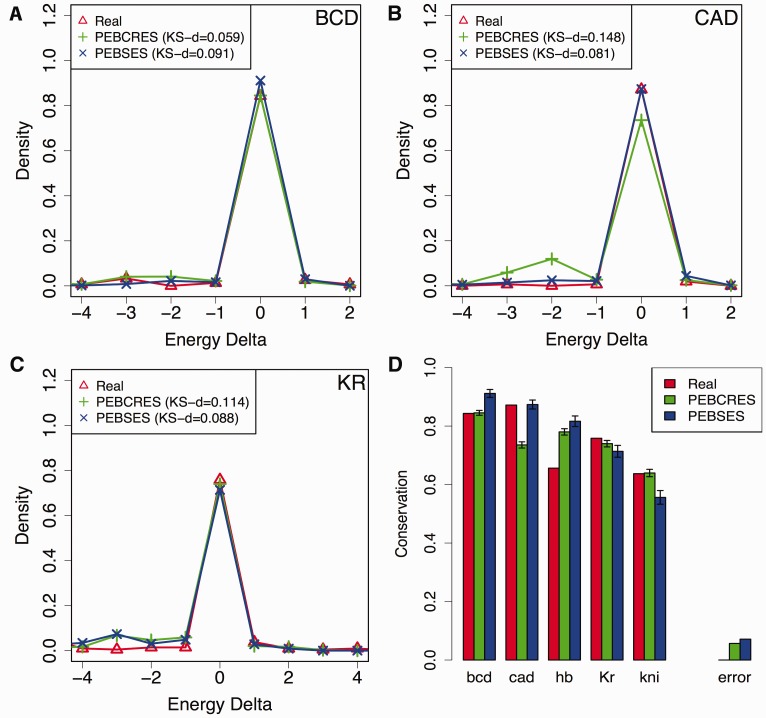
Figure 3 compares the histogram of binding site energy differences from PEBCRES and PEBSES simulations to evolutionary data. We find that PEBCRES simulations provide significantly better fits to data on BCD and KNI sites, and significantly worse fits for CAD sites, while both models exhibit similar levels of agreement with data on HB and KR sites. We also performed a set of PEBCRES simulations that included insertions and deletions (indels) as evolutionary events using indel rates and length distributions suggested in the literature (He et al. 2012). These simulations agreed with evolutionary data better than the SS model, although the agreement is slightly worse than in the simulations without indels (supplementary fig. S3, Supplementary Material online). We note that while indels are important sources of variation for Drosophila noncoding sequence (Sinha and Siggia 2005; Nourmohammad and Lässig 2011), the statistical summaries of evolution that we used here focus only on aligned sites, therefore the goodness of fit is not expected to be sensitive to such sources of variation.
Fig. 3.
(A–C) Energy difference histograms from real data and from the two evolutionary models—PEBSES and PEBCRES—presented in this work, for TFs BCD (A), CAD (B), and KR (C). (D) The fraction of sites for which energy difference between D. melanogaster and D. yakuba orthologs is 0 (Conservation; y axis), shown for real data and for the PEBSES and PEBCRES models. The error of either model, as defined in legend of figure 2, is also shown.
A curious, possibly coincidental, observation about the earlier mentioned results is that the two TFs—BCD and KNI—for which PEBCRES simulations yield significantly more accurate predictions than PEBSES are also the two TFs that are modeled as binding DNA with self-cooperativity (in the underlying sequence-to-expression model). Self-cooperative DNA binding introduces stronger dependencies between mutations in different sites of the same TF, and evolution of individual sites in the presence of such dependencies is expected to be modeled better with a CRM-level simulation (PEBCRES) than a site-level simulation (PEBSES). By the same reasoning, the relatively inaccurate predictions of CAD site conservation, made by the PEBCRES simulations, could reflect self-cooperative binding by CAD, which is not incorporated in the underlying thermodynamic model of regulatory function. We return to this point in a later section.
Modeling Binding Site Loss Rates
In the previous sections, we attempted to explain evolutionary data summarized in the form of energy difference histograms for orthologous pairs of sites in two closely related species (D. melanogaster and D. yakuba), where most strong sites in one species are retained as strong sites in the other species. Kim et al. (2009) proposed a complementary method to describe binding site evolution, which is geared toward larger evolutionary spans. Using D. melanogaster as a reference species, they counted what percentage of predicted sites of a given TF is lost in a second Drosophila species (see supplementary methods [Supplementary Material online] for a brief overview). Here, a site loss was called if the D. melanogaster site was partly or entirely deleted in the second species or had accumulated mutations that reduce its predicted binding affinity below the defining threshold. The site loss percentage thus computed was plotted for different choices of the second species, revealing that this percentage varies linearly with divergence time. Our next tests of evolutionary models deal with this alternative summarization of evolutionary data.
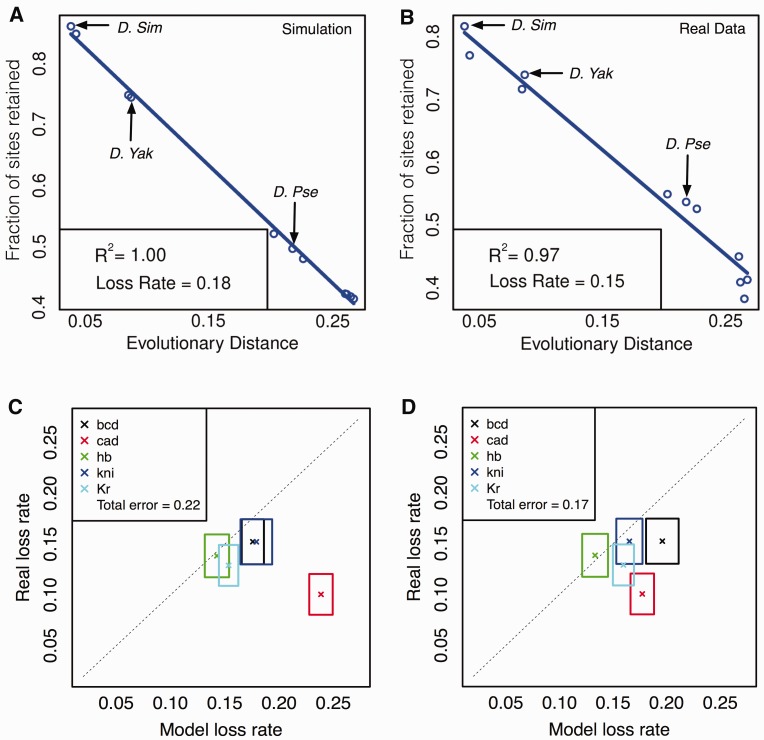
We performed PEBCRES simulations of CRM evolution for a fixed number of generations that matches the evolutionary distance between D. melanogaster and D. willistoni (see Materials and Methods) and recorded the site loss percentage between D. melanogaster and each of 11 other Drosophila species—D. simulans, D. sechellia, D. erecta, D. yakuba, D. ananassae, D. pseudoobscura, D. persimilis, D. virilis, D. grimshawi, D. mojavensis, and D. willistoni, with D. willistoni representing the greatest divergence and D. simulans representing the least divergence. This site loss profile was computed for each of five different TFs, examining sites over the same 37 D. melanogaster CRMs analyzed in previous sections. Each TF’s site loss profile was compared with the analogous profile obtained from alignments of the 37 D. melanogaster CRMs with orthologous CRMs in the 11 other species, as in Kim et al. (2009). Figure 4A and B show the site loss profile for the TF BCD, from PEBCRES simulations and real data, respectively. The first thing to note in both profiles is that the percentage of D. melanogaster sites lost in a second species increases linearly (R2 of 1.00 and 0.97, respectively) with the evolutionary divergence between D. melanogaster and that species. Observing such a “molecular clock” in evolutionary data is often taken as evidence against species (or branch) specific adaptive evolution, and indicates that the collection of sites analyzed evolved predominantly under purifying selection. Indeed, this was the interpretation offered by Kim et al. (2009). In our simulations, the observation of a molecular clock is trivial as the model imposes no branch-specific selection. However, the slope of the linear relationship, which we call the “loss rate,” may be treated as a summary statistic to be compared between model and data. Thus, in figure 4A and B, the loss rate of 0.15 from real data is well matched to the value of 0.18 observed in PEBCRES simulations. To our knowledge, this is the first attempt to quantitatively explain the rate of binding site loss or gain with models of sequence function and evolution. Note that we only examine site loss rates here (and not gains), for the same technical reasons encountered by Kim et al. (2009): A recorded site loss is a more reliable observation, whereas site gains are more likely to be conflated with spurious site predictions.
Fig. 4.
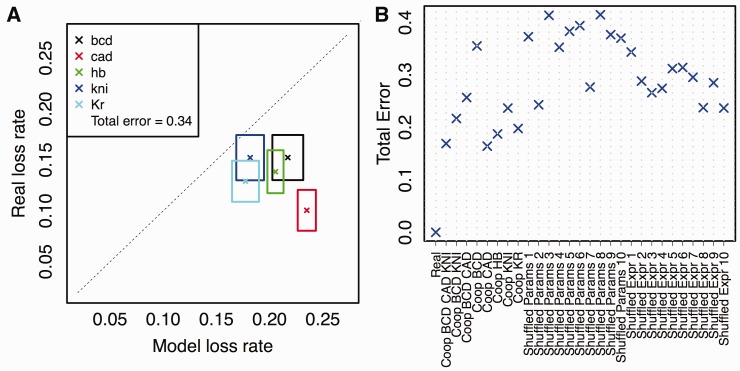
(A, B) Site conservation for BCD (y axis) as a function of evolutionary distance between Drosophila melanogaster and a second Drosophila species (x axis), based on PEBCRES simulations (A) and real data (B). Evolutionary distance is measured as the average number of substitutions in aligned positions in the pairwise alignment (see Materials and Methods). The inset shows the R2 value and the (negative of) the slope of the best fit straight line, called the loss rate. (C, D) Site loss rate from real data (y axis) and from PEBCRES simulations (x axis), shown by cross marks for each TF. Sides of the each rectangle indicate the standard deviation of loss rates observed from bootstrap samples. The two panels show this information with two different models of regulatory function—one with self-cooperative DNA binding by BCD and KNI (C) and one with self-cooperativity for BCD, KNI, and CAD (D). The total error of a model was calculated as the horizontal distance between each cross and the diagonal, summed over all TFs, and is shown in the inset.
To better illustrate the agreement between loss rates from model and data, we devised the representation scheme shown in figure 4C, where each TF is represented by a rectangle. The x and y axes of the plot represent the loss rate inferred from model simulations and real data, respectively. The center of the rectangle (marked by a cross) represents the respective loss rates from the procedure outlined earlier, that is, from an examination of sites in all 37 CRMs included in our analysis. The sides of the rectangle represent an error estimate as calculated by a resampling procedure using 50 samples of 18 CRMs each (out of the full set of 37) for real data and 50 samples of 500 CRMs each (∼10–15 simulations per CRM) for model predictions. The diagonal line represents perfect agreement between data and model. All five TFs whose sites were examined are represented on this plot. We find the model-based loss rates to agree with real loss rates for four out of five TFs, with the model overpredicting by approximately 0.02 (14%) on average. However, for sites of the TF CAD the real loss rate of 0.10 is grossly overestimated by the model, at 0.24. We examine this anomaly in depth in the next subsection, and find it to point to self-cooperative DNA binding by this TF.
Evidence for CAD Self-Cooperativity
Figure 4C reveals that the PEBCRES model shows reasonable agreement with observed site loss rates for all TFs except CAD. A similar disagreement was observed earlier (fig. 3) when comparing energy difference histograms of CAD sites from real data and simulations. As mentioned there, we hypothesized that this discrepancy may be due to self-cooperative DNA binding by CAD. Such cooperativity has not been reported in the literature and is not incorporated into the GEMSTAT model that was used in predicting genotype fitness values in our simulations. However, some evidence for such a mechanism was offered in the original analysis of Kim et al. (2009), where the distance between CAD sites was found to strongly correlate with loss rates, a potential signature of cooperative binding. A similar observation was made by Papatsenko et al. (2009). In the context of our analysis, such cooperativity may explain the apparent anomalies pertaining to CAD site evolution that are revealed by figures 3 and 4. If a pair of CAD sites act cooperatively, a model that ignores this effect will underpredict the fitness effect of a mutation in either site, and simulations based on such a model will lead to overprediction of site loss.
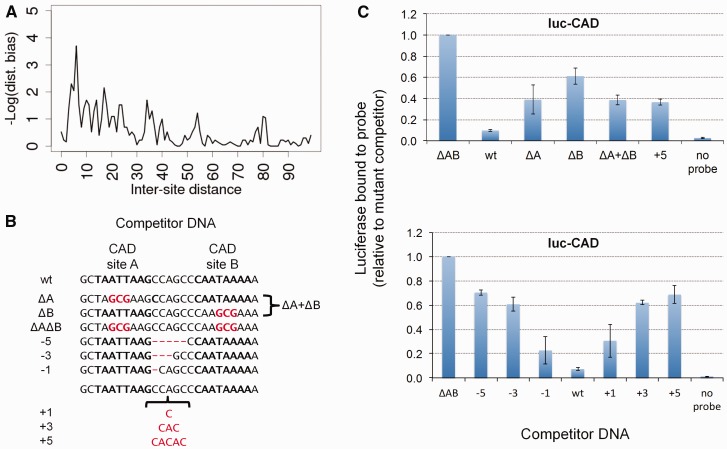
Pursuing the earlier mentioned hypothesis, we modified the GEMSTAT model of CRM function to include CAD self-cooperativity, and retrained all model parameters on the 37 CRMs from D. melanogaster. We performed PEBCRES simulations again to predict the site loss rates for all TFs. Figure 4D shows the results of this exercise, in the same format as figure 4C. The new simulations predicted a loss rate of 0.17 for CAD sites, significantly closer to the real value of 0.10 than had been predicted above (0.24). The change in model affected predictions for other TFs but the overall agreement (see legend) for the model with CAD self-cooperativity was better than the model without it. We also repeated the experiments in figure 3, now with the new model, and observed improved agreement with real data on CAD site conservation between D. melanogaster and D. yakuba (supplementary fig. S4, Supplementary Material online). We note that the GEMSTAT model in its default configuration (figs. 2, 3, and 4C) incorporates self-cooperative DNA binding by BCD and KNI because He et al. (2010) found evidence for these mechanistic features by a statistical analysis of the same 37 D. melanogaster CRMs that were studied by us. However, in that work, the evidence for CAD self-cooperativity was not statistically significant. In contrast, our analysis, which “fits” the GEMSTAT model to evolutionary data on those 37 CRMs via evolutionary simulations, suggests the presence of CAD self-cooperativity. Additionally, we repeated the earlier mentioned exercise with several alternative formulations of the GEMSTAT model, where we modeled self-cooperativity for the single TFs (BCD, CAD, HB, KNI, and KR) and combinations of TFs (BCD and CAD; BCD and KNI; BCD, KNI, and CAD) at a time. We found (fig. 5B) that the evolutionary data on site loss rates are best explained by models that include self-cooperativity for CAD (e.g., a model that includes self-cooperativity for BCD, CAD, and KNI, reported in fig. 4D). These results can be viewed as evolutionary evidence for cooperative interaction between CAD binding sites. We also found that the spacing between neighboring CAD sites in D. melanogaster has a statistically significant bias for a range of 0–10 bp (base pairs), especially at 6 bp (fig. 6A; see Materials and Methods), providing additional evidence for our hypothesis. (The sequence-to-expression model allows cooperative interactions between two homotypic-bound sites that are within 50 bp of each other, and thus does not by itself suggest the preferred spacing between cooperatively bound sites.)
Fig. 5.
(A) Real and simulation-based site loss rates (crosses) and their sampling variations (sides of rectangles), where simulations were performed with TF expression patterns randomly shuffled. (B) Total error, as defined above, for simulations performed with different configurations of the GEMSTAT model—self-cooperative DNA binding by each of BCD, CAD, and KNI (Coop BCD CAD KNI; the model of fig. 4D), by BCD and CAD only (Coop BCD CAD), by BCD and KNI only (Coop BCD KNI; the model of fig. 4D), by BCD only (Coop BCD), CAD only (Coop CAD), by HB only (Coop HB), by KNI only (Coop KNI), and by KR only (Coop KR)—and for different types of negative controls—with randomly reassigned TF parameters (Shuffled Params 1–10) and with randomly reassigned TF expression profiles (Shuffled Expr 1–10).
Fig. 6.
(A) Logarithm (base 10) of P value of CAD intersite spacing bias at different values of the spacing (x axis). (B) A schematic representation of competitor DNA used to experimentally assess cooperative DNA binding by CAD in vitro. The competitor DNA might include mutations that disrupt one (ΔA, ΔB) or both (ΔAB) of the CAD-binding sites as well as deletions (−1, −3, −5) or insertions (+1, +3, +5) that change the spacing between the two sites. ΔA + ΔB indicates the inclusion of both DNA with mutations to the first site (ΔA) and DNA with mutations to the second site (ΔB). (C) DNA-binding site measurements for CAD homotypic interaction. In experiments, the biotinylated DNA sequence is either wild type or not included (no probe). The competitor DNA used is indicated on the x axis. The luciferase activity recovered using a competitor in which both CAD binding sites are mutated is set to a value of one and used as a nonspecific DNA-binding control to normalize the remaining samples. Addition of a wild-type DNA sequences effectively competes for binding to the probe and reduces the recovery of Luc-CAD. Changes in either the individual CAD-binding sites or in the spacing between the binding sites results in reduced binding to the competitor DNA compared with wild type and an increased recovery of Luc-TF with the biotin-labeled DNA. Error bars indicate the standard deviation (see supplementary table S2 [Supplementary Material online] for individual measurements and more detailed sequence information).
Experimental Validation
We tested for direct physical interaction between CAD protein molecules using a variation of the LUMIER method (Barrios-Rodiles et al. 2005; Vizoso Pinto et al. 2009), modified to analyze direct binding in vitro (Cheng et al. 2013). A full length CAD coding region was fused to either luciferase (Luc) or maltose-binding protein (MBP), and physical interaction was tested by measuring recovery of Luc-CAD following incubation with and purification of MBP-CAD. A 7-fold increase in recovered luciferase activity was observed with Luc-CAD compared with an unfused Luc control. This ratio is referred to as the luminescence intensity ratio (LIR). In contrast, previously published negative control TF pairs all showed an LIR below 7 (Cheng et al. 2013; Kazemian et al. 2013). To further control for nonspecific interactions, negative controls using unfused MBP, MBP fused to the Circadian Locomotor Output Cycles Kaput (CLK) TF or Luc fused to CLK (Cheng et al. 2013; Kazemian et al. 2013) were also shown to result in lower recovery of luciferase. These results confirm the homodimerization of CAD molecules in vitro (supplementary table S1, Supplementary Material online).
We next determined whether properly spaced pairs of CAD binding sites exhibited higher binding affinity than individual sites or the same sites with altered spacing. We identified two adjacent CAD binding sites with an optimal intersite spacing of 6 bp (see Materials and Methods) and used a modification of a previously described oligobinding assay (Hallikas and Taipale 2006; Cheng et al. 2013; Kazemian et al. 2013) by mixing luc-tagged TFs with biotin-labeled DNA sites with an excess of unlabeled competitor DNAs. These competitors either match the wild type sequence or have mutations that alter the CAD binding sites or the spacing between them (fig. 6B). Differences in affinity are reflected in the ability of different competitor DNA molecules to prevent TF binding to the biotin-labeled DNA probe and thus reduce recovery of the associated luciferase activity with streptavidin beads. The wild type sequence containing both binding sites at the optimal spacing was the most effective competitor, reducing luciferase recovery to near background levels (fig. 6C; supplementary table S2, Supplementary Material online). On the other hand, when each site was provided on separate DNA molecules, or when both sites are on the same molecule but the spacing between the sites was increased by 5 bp, the competition was much less than with the wild type sequence, similar to the level seen with a single site. More detailed analysis revealed that an increase or decrease of 1 bp between the sites partly reduced binding while a change of 3 bp decreased binding to levels similar to that seen with a 5 bp change or a single site. From this result, we concluded that the CAD sites must be properly spaced for cooperative binding.
Negative Controls
We claim above that the GEMSTAT model of CRM function, with self-cooperativity for BCD, KNI, and CAD, provides the best fitness function to use with PEBCRES simulations to explain site loss profiles in the 12 Drosophila species. The total error (see legend of fig. 4) of loss rate predictions from this model is 0.17. We next performed two different types of negative control experiments where we did not expect the simulation-based loss rates to agree with data. These controls were intended to provide us a characterization of the total error values expected by chance. The effect of a TF on the expression of a CRM depends, among other things, on the thermodynamic parameters in the GEMSTAT model and the TF’s concentration profile. In each set of controls, we randomized one of these factors while keeping the other factor unaltered. These are strong controls because most of the information contained in the original model is also present in the negative control.
In the first set of controls, we reassigned the thermodynamic parameters representing activation/repression strengths of TFs in the GEMSTAT model, in a random manner. For instance, if BCD (an activator) and KR (a repressor) have parameter values of +4 and −3 in the original model (positive and negative values signifying activation and repression, respectively), the reassignment may assign a parameter value of −3 (repressive role) to BCD and a value of +4 (activating role) to KR. The reassignment is not necessary a simple swap between two TFs. For example, BCD might be assigned the parameters from KR, which receives KNI’s parameters, whereas KNI is assigned the parameters from BCD. We performed 10 independent negative controls of this type, each with its own random reassignment of parameter values among TFs, ran PEBCRES simulations of CRM evolution with the randomized GEMSTAT model, and recorded the total error of loss rate predictions. We found the best total error in these control experiments to be 0.24, with an average of 0.35 (fig. 5B; Shuffled Params 1–10).
In the second set of negative controls, we randomly shuffled the mapping between TFs and their expression profiles. For example, in the original model of anterior–posterior patterning in the embryo, BCD expression peaks in the anterior end and decays toward the middle of the embryo, whereas CAD expression peaks at the posterior end of the embryo and is weakest in the anterior end. A shuffled control might reassign these profiles so that BCD is active in the posterior end while CAD becomes active in the anterior. We repeated PEBCRES simulations ten times with this type of a randomized GEMSTAT model. Results from one such control are shown in detail in figure 5A, with a total error of 0.34. The best total error in these experiments is 0.24 and the average is 0.29 (fig. 5B; Shuffled Expr 1–10). In summary, our negative control experiments confirm that the GEMSTAT model with self-cooperativity for BCD, KNI, and CAD (total error = 0.17) provides an accurate explanation of site loss rates in 12 Drosophila species.
Discussion and Conclusion
We described here a principled approach to understand binding site evolution at a higher resolution than previous studies. A seemingly surprising finding of comparative genomics is the unexpected degree of evolutionary flux in regulatory sequences (Dermitzakis and Clark 2002; Balhoff and Wray 2005; Moses et al. 2006). For instance, Emberly et al. (2003) noted that known binding sites in functional CRMs are not much more conserved (between two Drosophila species) than in sequences randomly sampled from the genome. A similar exercise of recording the extent to which TF-binding sites are conserved at varying evolutionary distances was conducted more comprehensively by Kim et al. (2009). The conclusion from that study was that sites are lost at a roughly constant rate, that is, the number of site losses is proportional to evolutionary divergence, as might be expected in the absence of lineage-specific selection. (“Site loss” was defined relative to one reference species rather than the common ancestor and, for technical reasons, the study examined losses only.) However, cataloging of site-level evolutionary changes does not address the more fundamental questions: Is the observed rate of site loss lower or greater than expected? What is the expected rate? Is there a better way to define this expectation than to base it on random genomic segments (one extreme) or to presume that a functional binding site must remain a binding site, that is, match the TF motif (other extreme)? Why is the site-loss rate for one TF different from another TF? These are the questions that we hope to begin answering with our work. We link the expected evolutionary flux on a TF’s binding site to our understanding of that site’s function. For this purpose, we take recourse to the regulatory system where current understanding of cis-regulatory logic, that is, the roles of various binding sites, is among the most advanced—the A/P patterning system in the fruitfly embryo (Segal et al. 2008; He et al. 2010). A state-of-the-art computational model of a CRM’s regulatory function is coupled with evolutionary simulations under mutation and selection, and the evolutionary histories of a binding site under repeated simulations are used to define the expected rates of site loss and conservation. These expectations agree by and large with the observed rates. Moreover, to a first approximation this approach also explains why sites of one TF evolve at a different rate from those of another TF, although there is room for improvement in this regard. An important aspect of our approach is to assert, in the evolutionary simulations, that the fitness effect of an in-site mutation is context dependent; put simply, what a mutation does to a site depends on what other sites are nearby. We demonstrate that explicitly modeling this reasonable assertion leads to a better quantitative explanation of binding site evolution.
Simulation frameworks for CRM evolution have recently been proposed in at least two different studies—Lusk and Eisen (2010) and He et al. (2012). In both of these studies, the goal was to explain features of CRM architecture (e.g., proximity constraints on pairs of sites [Lusk and Eisen 2010] or homotypic clustering of sites [He et al. 2012]) by using a model of CRM function with evolutionary simulations. Our methodology is similar in spirit to Lusk and Eisen (2010), though our goal is to explain features of CRM evolution under purifying selection, a fundamentally different goal.
Other frameworks to model the evolution of the regulatory machinery using simulations include (Francois et al. 2007; Cooper et al. 2009; Pujato et al. 2013), all of which study evolution at the gene-regulatory network level. Also noteworthy is the study in Stewart et al. (2012), where a population genetics framework is used to explain the emergence of cooperative binding in regulatory systems, and in Josephides and Moses (2011), where a maximum parsimony approach is used to enumerate all maximally parsimonious evolutionary paths from an inferred ancestral to the current known sequence in Saccharomyces cerevisiae. However, our model is fundamentally different from those models in its resolution: We model evolution at the sequence level, whereas the aforementioned studies model evolution at a higher level, with the exception of Stewart et al. (2012), where a sequence simulation was used mainly to validate the population genetics model. At the same time, our model may be used in conjunction with some of the above approaches in future studies.
We attempted to model patterns of binding site conservation and turnover under purifying selection on the CRM’s expression readout. This is in contrast to studies that considered a collection of binding sites as evolving under an energy-dependent fitness model (Mustonen and Lässig 2005; Doniger and Fay 2007; Kim et al. 2009) and were concerned primarily with quantifying the average strength of purifying selection on the collection of sites. A similar approach to testing for purifying selection was utilized by Moses (2009). He et al. (2011) recently noted that these approaches are not ideal for detecting positive selection on binding sites, and they examined patterns of polymorphism and divergence in two closely related species (D. melanogaster and D. simulans) to test for signatures of selection. They found functional site evolution to be primarily under purifying selection. Our study is consistent with this—we found patterns of site conservation (figs. 2 and 3) in closely related species to be well explained by our simulations, which only implement purifying selection. They also presented evidence for positive selection for both gains and losses of binding sites. We find patterns of site loss (fig. 4) across larger evolutionary spans to be roughly consistent with predictions from a model that ignores positive selection, but there is much room for improvement in the goodness of fit. As such, we do not claim that site loss is adequately explained by purifying selection alone; in fact, some of the missing accuracy may be due to ignoring positive selection. PEBCRES simulations are not meant to be a test for positive selection, especially because the signal is mixed with the dominant signals of purifying selection acting on each CRM’s output.
In trying to explain evolutionary data using our understanding of regulatory function, we also realized that the exact same framework may be used to test and improve our understanding of regulatory function using evolutionary data. We observed that the default configuration of the GEMSTAT model of regulatory function (used in the fitness function) led to evolutionary simulations that by and large agreed with real data on site evolution, but revealed one glaring disagreement—that is for CAD sites. We took this as a cue that the GEMSTAT model of cis-regulatory logic may be flawed in some respect, and altered the model to include self-cooperative DNA binding by CAD. This led to much improved fits to evolutionary data, and subsequently the hypothesis of CAD self-cooperativity was experimentally confirmed both through PPI assays and DNA competition assays. Interestingly, two essential pairs of CAD-binding sites have been previously described in the fushi tarazu (FTZ) promoter (Dearolf et al. 1989), and a recent study (Bakkali 2011) of population variation in this promoter reported evidence of purifying selection, but the role of cooperative CAD binding and binding site spacing was not examined. Furthermore, one of the mammalian proteins related to CAD has been demonstrated to bind DNA as a dimer (Suh et al. 1994), indicating that dimer formation by members of this homeodomain family is conserved across species.
It is worth noting that a recent study by Kaplan et al. (2011) reported that protein interactions, including cooperative DNA binding, play an insignificant role in determining TF occupancy at accessible regions of chromatin. We do not interpret their results as contradictory to our finding of self-cooperative DNA binding by CAD. The data type examined and modeled by Kaplan et al. are ChIP data on genomewide TF-DNA binding levels, whereas we identified CAD self-cooperativity by modeling evolutionary data on CRMs and CAD binding sites within them. Moreover, our finding is not meant to be a broader statement on the prevalence of protein interactions in regulatory systems; it is only a demonstration of the possibility of hypothesizing such interactions through evolutionary analysis. The significance of this strategy for mechanistic investigation becomes clearer upon noting that the hypothesis of self-cooperative binding by CAD was also tested by He et al. (2010), in exactly the same expression-modeling framework (GEMSTAT) but on D. melanogaster CRMs alone, and not found to have significant support. It was only when we tried to explain CAD site evolution that an expression-model with CAD self-cooperativity appeared a much better alternative to a model without such cooperativity. We anticipate that there may be many more mechanistic insights about cis-regulatory logic that are not captured when we simply try to model expression from sequence, as in GEMSTAT and will emerge only when we attempt to explain evolutionary data from such models. In this sense, our work may be a proof-of-concept of an entirely new strategy for modeling gene expression.
There are various technical issues involved in studying binding site evolutionary patterns that were addressed carefully by Kim et al. (2009), and we adopt their methodology throughout this work. One such issue is that of alignment errors. We performed all alignments using the PECAN program (Paten et al. 2009), which was shown by Kim et al. (2009) to lead to the same conclusions as those based on alignments from another program used there, called ProbConsMorph. A separate benchmarking study of alignment programs also found PECAN to be superior for aligning noncoding sequences (Kim and Sinha 2010). A second technical issue is that of binding site predictions, which, being based on motif matches alone, are prone to false positives. Again, this issue was addressed by Kim et al. (2009), who assessed the false positive rate for each of the TFs studied there. We excluded the TF Giant (GT) from our analysis as the estimated false positive prediction rate of its sites was high. In light of the same technical problem, we limited our study of site evolution on longer time scales to site loss events only, as gain events are more prone to being confounded with spuriously predicted sites.
We presented two closely related evolutionary simulators, called PEBSES and PEBCRES, with the only difference being that PEBSES allows mutations only within a predesignated-binding site in the CRM and PEBCRES allows mutations anywhere in the CRM. Although PEBCRES is a more realistic simulator, we do not dismiss the utility of PEBSES because of the following: 1) It was designed to match the SS and Halpern–Bruno models closely and therefore represents a fair comparison with these models; 2) it is computationally efficient for typical TFBS lengths (up to 20 bp long); and 3) it isolates the evolution of a site from the evolution of the nearby sites, allowing for the testing of different hypotheses.
The main caveats to note in this work are that both GEMSTAT and PEBCRES are imperfect models. There are aspects of gene expression, some known and perhaps several unknown, that are not encoded in the GEMSTAT model. The parameter learning procedure will, to a certain degree, compensate for mechanisms missing in the model by attributing their effects to other mechanisms. For instance, chromatin remodeling effects of pioneer factors (Harrison et al. 2011; Nien et al. 2011) that potentially make the local chromatin more accessible to other TFs may be inaccurately modeled as being distance-dependent cooperative binding between two TFs. Likewise, there are many deficiencies in the evolutionary simulation framework adopted here, some of which are well known (e.g., not modeling several phenomena such as recombination, varying population size, and potential errors in evolutionary parameters used) but were not addressed by us for simplicity and efficiency. Additionally, our simulation framework relies on the assumption that the expression patterns do not change in any of the 12 Drosophila species. This is one of the reasons why we conducted this study on the segmentation network in the early Drosophila embryo, for which there is evidence of deep conservation at the gene expression level (Hare et al. 2008; Weirauch and Hughes 2010; Swanson et al. 2011). However, the assumption may not be valid for other systems of interest. Therefore, if evolutionary data does not agree with simulation results or agrees more with one model of regulatory function than another, one should treat this as merely suggestive of mechanistic hypotheses and as a starting point for further exploration.
In conclusion, we have presented here a new quantitative framework for exploring binding site evolution and cis-regulatory logic in an integrated manner. We show that this framework can offer a reasonable quantitative explanation of conservation and loss of individual TF-binding sites, and can also provide useful insights into biochemical mechanisms of gene regulation. This approach also has the potential to provide a theoretical framework for examining the outstanding issues of the day related to CRM architecture and evolution, such as homotypic clustering of binding sites (He et al. 2012), enhancer synergy (Yao et al. 2008), and shadow enhancers (Perry et al. 2010; Barolo 2012). Our future work will attempt to explain such phenomena using the general strategy presented here.
Materials and Methods
Overview of Models
The PEBSES and PEBCRES models of CRM evolution have three main components: 1) a sequence-to-expression model; 2) a fitness function based on the CRM’s predicted expression readout; and 3) an evolutionary simulation model. The evolutionary model is responsible for generating mutations and simulating the evolutionary fate of those mutations. The fitness function influences the evolutionary fate of a mutation and is based on a comparison between the predicted expression pattern for a CRM and an ideal expression pattern. The sequence-to-expression model is used to predict the expression pattern driven by a CRM. The evolutionary model is the difference between PEBSES and PEBCRES (both described in later sections), whereas the sequence-to-expression model and the fitness function are identical between them.
Sequence-to-Expression Model
PEBSES and PEBCRES rely on a sequence-to-expression model to compute the fitness of a CRM. We used the GEMSTAT model of He et al. (2010) to predict the expression profile driven by any CRM sequence. Here, expression profile refers to the gene expression levels, due to the regulatory effect of the sequence, in a series of cell types (fig. 1A). A set of TFs relevant to the CRM is defined as input and each cell type is described by the concentration of each TF in that cell type. For instance, in the case of the CRMs studied here, the cell types correspond to different positions along the anterior–posterior (A/P) axis in the Drosophila embryo at the blastoderm stage (discussed in detail later). Additionally, the GEMSTAT model requires for each TF the binding specificity (modeled as a PWM) of the TF, as well as a pair of parameters related to the Kd of TF-DNA binding and the TF’s activating or repressive potency. The model offers the option of modeling self-cooperative DNA binding by any of the relevant TFs, in which case an additional parameter reflecting the strength of homodimeric interaction is required.
CRMs studied in this work were previously shown to drive patterned expression along the A/P axis in the blastoderm stage D. melanogaster embryo. The expression pattern of each of these CRMs, as determined experimentally, is represented as a 60-dimensional vector of values in the range [0,1], with the dimensions of the vector corresponding to uniformly spaced positions along the A/P axis from 20% egg length to 80% egg length. CRM sequences and their experimental expression profiles were as collected by He et al. (2010). The relevant TFs used to model CRM function were BCD, CAD, KR, KNI, GT, and HB. TF motifs were taken from the Fly Factor Survey database. Values of TF-specific free parameters were learned by simultaneous fits of the model to the 37 D. melanogaster CRMs. We used the same 37 D. melanogaster CRMs for our evolutionary simulations; however, the model fitting and evolutionary simulation steps were run independently, and therefore the parameter values were unaffected by the evolutionary simulations. By default, we configured the GEMSTAT model to use self-cooperativity for BCD and KNI, as this model had been found to be the optimal model by He et al. (2010). When performing simulations with different configurations of GEMSTAT, for example, self-cooperativity for a different subset of TFs, the free parameters of the model were retrained on the same data set.
Fitness Function
An important component of PEBSES and PEBCRES is the fitness function that compares the predicted expression pattern for a CRM sequence with the ideal expression pattern. A desirable fitness function has three properties: 1) the value of the fitness function is maximum when the predicted expression pattern is a perfect match to the ideal expression pattern; 2) any deviation from the ideal expression pattern is penalized by decreasing the fitness function; and 3) the penalty value is monotonically increasing with the amount of deviation.
With these considerations in mind, we used the weighted pattern generating potential (wPGP) score of Samee and Sinha (2013) to compare the ideal expression with a predicted expression. Let 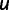 be the predetermined ideal expression profile for the CRM. Let
be the predetermined ideal expression profile for the CRM. Let 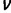 represent the expression profile predicted by GEMSTAT for a given genotype
represent the expression profile predicted by GEMSTAT for a given genotype 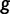 , and let
, and let 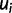 and
and 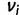 represent the ideal expression and predicted expression, respectively, in cell type
represent the ideal expression and predicted expression, respectively, in cell type  . The fitness of genotype
. The fitness of genotype  is defined from the wPGP score between
is defined from the wPGP score between 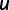 and
and  , as follows:
, as follows:
| 1. Compute “reward” as | 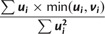 |
| 2. Compute “penalty” as | 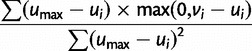 |
| 3. Compute “wPGP” as | wPGP(u) = reward − penalty |
| 4. Compute “fitness functional” as | f(g)=[max(0, wPGP(u))]2 |
| 5. Compute “fitness” as | F(g)=1+Kf(g) |
where 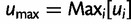 and
and 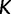 is a free parameter representing a scaling constant. The fitness function
is a free parameter representing a scaling constant. The fitness function 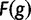 was used in He et al. (2012). Note that wPGP, and therefore
was used in He et al. (2012). Note that wPGP, and therefore 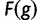 , is maximized when the reward is maximum and the penalty is minimum. The reward is maximized when
, is maximized when the reward is maximum and the penalty is minimum. The reward is maximized when 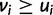 for every cell type
for every cell type 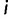 ; in other words, a sequence is rewarded for driving higher expression in cell type
; in other words, a sequence is rewarded for driving higher expression in cell type  . On the other hand, penalty is minimized when
. On the other hand, penalty is minimized when 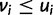 , or, in other words, overexpression in any cell type
, or, in other words, overexpression in any cell type 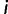 is penalized. Putting reward and penalty together, we have that fitness
is penalized. Putting reward and penalty together, we have that fitness 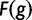 is maximized when
is maximized when 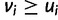 and
and 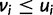 , which only happens when
, which only happens when 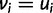 . Having
. Having 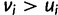 for any cell type
for any cell type  increases penalty while reward remains the same and having
increases penalty while reward remains the same and having 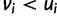 decreases reward with penalty remaining the same. The wPGP score, and thus also the fitness function has all the aforementioned properties. Additionally, overexpression and underexpression are penalized differently, and overexpression is penalized only up to a saturation point. The advantages of the wPGP score over either the sum of squared errors or a correlation coefficient are discussed in Samee and Sinha (2013). The fitness functional
decreases reward with penalty remaining the same. The wPGP score, and thus also the fitness function has all the aforementioned properties. Additionally, overexpression and underexpression are penalized differently, and overexpression is penalized only up to a saturation point. The advantages of the wPGP score over either the sum of squared errors or a correlation coefficient are discussed in Samee and Sinha (2013). The fitness functional 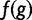 is a number between 0 and 1, with a value of 1 representing perfect match between
is a number between 0 and 1, with a value of 1 representing perfect match between 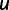 and
and 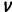 . The parameter K can be interpreted as the selection coefficient when the two competing genotypes have
. The parameter K can be interpreted as the selection coefficient when the two competing genotypes have 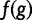 equal 0 and 1, respectively.
equal 0 and 1, respectively.
PEBSES
PEBSES is a continuous-time Markov chain simulator that follows the theory of Kimura and Ohta (Kimura and Ohta 1969; Mustonen and Lässig 2005; Kim et al. 2009). It simulates the evolution of a single binding site located within a CRM, using the function 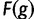 described earlier to estimate the fitness effect of any mutation. The inputs to PEBSES include 1) a complete GEMSTAT model, 2) a CRM sequence, and 3) the coordinates of a binding site within the CRM. The simulation proceeds as a continuous-time Markov process of evolutionary changes in the binding site. The rate of substitution from a site
described earlier to estimate the fitness effect of any mutation. The inputs to PEBSES include 1) a complete GEMSTAT model, 2) a CRM sequence, and 3) the coordinates of a binding site within the CRM. The simulation proceeds as a continuous-time Markov process of evolutionary changes in the binding site. The rate of substitution from a site  to a site
to a site  , denoted by
, denoted by 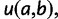 is calculated as per the following formula:
is calculated as per the following formula:
where 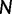 represents the effective population size,
represents the effective population size, 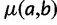 is the background rate of mutation from site
is the background rate of mutation from site 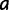 to site
to site 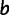 and
and 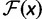 is the fitness of a site
is the fitness of a site 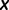 relative to the current site. We set
relative to the current site. We set 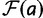 in this formula to be 1, and
in this formula to be 1, and 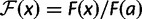 . This leads to
. This leads to 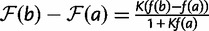 , which we approximate as
, which we approximate as 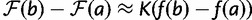 , because
, because 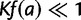 as explained below.
as explained below.
In each step of the simulation, PEBSES enumerates every site 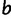 that differs from the current site (
that differs from the current site (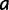 ) by exactly one nucleotide and calculates
) by exactly one nucleotide and calculates 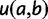 . One of the enumerated sites will be randomly selected with probability proportional to
. One of the enumerated sites will be randomly selected with probability proportional to 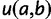 . After each step, the simulation time is incremented by sampling from an exponential distribution with rate
. After each step, the simulation time is incremented by sampling from an exponential distribution with rate 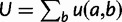 , where the sum is over every site
, where the sum is over every site 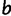 that differs from
that differs from 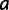 by at most one nucleotide. The simulation stops when the simulation time is larger than or equal to a predetermined value. In our experiments, this predetermined value was the evolutionary distance between D. melanogaster and D. yakuba. We note that this simulation procedure is an extension of the SS model of Kim et al. (2009) to a nonbinary fitness function for binding sites.
by at most one nucleotide. The simulation stops when the simulation time is larger than or equal to a predetermined value. In our experiments, this predetermined value was the evolutionary distance between D. melanogaster and D. yakuba. We note that this simulation procedure is an extension of the SS model of Kim et al. (2009) to a nonbinary fitness function for binding sites.
Parameter Fitting
PEBSES has one free parameter, 4NK (see supplementary text, Supplementary Material online), which can be used to adjust the predicted binding site conservation level. In general, increasing the value of 4NK will increase the predicted conservation for each of the TFs. To find the value of 4NK that best matches the observed data, we ran PEBSES with different values of 4NK to simulate the evolution of binding sites from D. melanogaster. For each value of 4NK, we run 5,000 simulations per TF, with binding sites chosen randomly among high affinity binding sites in D. melanogaster that are well conserved in the other 11 species. The value of 4NK that results in the best fit to data for all TFs is chosen for reporting. We avoid overfitting by using a single 4NK for all TFs.
Limit on Site Length
PEBSES makes an implicit assumption that at any point during the evolutionary simulation a maximum of two versions of a site are competing. This assumption is only valid if the expected time for a mutation to arise in a site is larger than the expected time for a mutation to fix in the population (or to be eliminated from the population). Because the rate of mutations in a site grows with the site length, this assumption is only valid for short (e.g., binding site length) sequences. Therefore, PEBSES is not appropriate to simulate the evolution of an entire CRM.
Computational Complexity
At every generation, PEBSES enumerates every possible single nucleotide mutation to a binding site sequence and uses GEMSTAT to predict the expression of the mutated sequence. This requires a linear number of GEMSTAT calls and is efficient for typical binding site lengths (up to 20 bp).
Comparison with the SS Model
One of our goals was to compare the results of PEBSES simulations with those of the SS model of Kim et al. (2009). We therefore implemented the SS model within the PEBSES framework by redefining 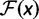 as
as
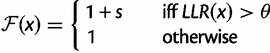 |
where 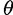 is a threshold on site strength as used by the SS model and
is a threshold on site strength as used by the SS model and 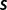 > 0. Thus, the PEBSES and SS models use an identical evolutionary framework and differ only in the fitness function.
> 0. Thus, the PEBSES and SS models use an identical evolutionary framework and differ only in the fitness function.
PEBCRES
PEBCRES is the simulation framework from He et al. (2012), used here to study and explain real evolutionary data. In the original application, the framework was used to simulate the evolution of an artificial expression pattern under positive selection for a fixed number of generations and the number of binding sites was counted in the final population. Our application, on the other hand, simulates the evolution of 37 real expression patterns from the A/P patterning system in Drosophila, under negative selection. We stop our simulations at a time determined by the evolutionary distance between two Drosophila species (in our experiments either D. melanogaster and D. yakuba or D. melanogaster and D. willistoni). To evaluate how well our simulations match real data, we use two summary statistics from Kim et al. (2009) that reflect evolutionary changes in binding sites between the initial and final population.
PEBCRES simulates the evolution of an entire CRM using discrete-time Wright–Fisher simulation with a fixed-sized population size. Similarly to PEBSES, it uses the wPGP score of Samee and Sinha (2013) to assign a realistic fitness value 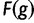 to genotypes. The inputs to PEBCRES are 1) a complete GEMSTAT model and 2) a CRM sequence. A population of 2N = 100 copies of the original CRM sequence is created at the start of the simulation and in each generation, random mutations are introduced in the population with a fixed rate (
to genotypes. The inputs to PEBCRES are 1) a complete GEMSTAT model and 2) a CRM sequence. A population of 2N = 100 copies of the original CRM sequence is created at the start of the simulation and in each generation, random mutations are introduced in the population with a fixed rate (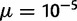 ) per generation, per individual, per base pair. After each generation, 2N new individuals are sampled, with replacement, from the previous generation. The probability of sampling individual
) per generation, per individual, per base pair. After each generation, 2N new individuals are sampled, with replacement, from the previous generation. The probability of sampling individual  is proportional to its fitness
is proportional to its fitness  , as defined earlier, where
, as defined earlier, where 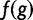 is calculated from the wPGP score and K is a free parameter.
is calculated from the wPGP score and K is a free parameter.
Parameter Fitting
The only free parameter (K) is determined by fitting evolutionary data, in a procedure similar to the one used in PEBSES: We run several experiments with different values of K, each experiment consisting of 1,000 simulations of randomly selected CRMs, and choose the K that most closely matches the evolutionary data. As with PEBSES, we use a single parameter for all TFs to minimize overfitting. Other parameters of PEBCRES, such as population size and mutation rate, were set as in our previous work (He et al. 2012), on which PEBCRES is based.
Time Rescaling
The parameters used in PEBCRES, especially population size (N) and mutation rate µ, are set using time rescaling (Hoggart et al. 2007) to speed up simulation time following He et al. (2012). We note that standard values in the literature are in the range of 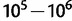 for population size (2N) (Thornton and Andolfatto 2006) and
for population size (2N) (Thornton and Andolfatto 2006) and  for mutation rate (
for mutation rate (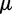 ) (Drake et al. 1998), resulting in 2N
) (Drake et al. 1998), resulting in 2N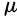 in the range of
in the range of  , with our value of 2N
, with our value of 2N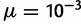 within that range.
within that range.
Estimating Evolutionary Distances
PEBCRES simulation proceeds generation by generation until the average number of substitutions in individuals in the current population is greater than the evolutionary distance between D. melanogaster and the target species. We used the average number of substitutions per aligned base pair as a measure of evolutionary distance, We estimated this distance between D. melanogaster and each of the 11 other species by 1) generating a pairwise alignment of CRM sequences from the two species using the Pecan tool Paten et al. (2009) with default parameters and 2) counting the number of substitutions in aligned positions. The resulting evolutionary distances are consistent with those reported by Sinha and Siggia (2005) and our model can tolerate small deviations in the distance estimation due to the free parameter K. When calculating the loss rates across multiple species, we run the evolutionary simulation for the distance of farthest species and record intermediary populations at time points representing each of the other species.
Reporting Results in Population-Based Simulation
PEBCRES is a population-level simulation program and each simulation yields 2N sequences in the final population. We treat each of these sequences as an independent result when plotting the histograms for figure 3 and calculating the conservation reported in figure 4.
Spacing Bias Analysis
We extracted the top 500 segments of size 500 bp each that are predicted to bind by CAD using STUBB program and are within the top 10% accessible region of the genome revealed by DNase I hypersensitivity data (Li et al. 2011). We then searched these segments for biases in the intersite spacing between adjacent pairs of CAD binding sites using the iTFs program (http://veda.cs.uiuc.edu/iTFs, last accessed October 11, 2013; [Kazemian et al. 2013]). The adjacent CAD-binding sites at optimal intersite distance of 6 bp were selected from a putative A/P transcriptional enhancer, gt_-10_construct.
Experimental Validation
Details of the experimental procedure are as described in Cheng et al. (2013). In brief, a full length coding region for CAD was transferred from pDNR clone BS01123 (from the Berkeley Drosophila Genome Project) to vectors for in vitro expression of the protein as a fusion to MBP or luciferase (Luc). Protein–protein interactions were measured by examining the percentage of Luc-tagged CAD recovered following pull down of MBP compared with a luciferase only control. Additional controls were performed using Luc-CAD with MBP only or substituting MBP-CLK or Luc-CLK proteins that were previously shown to form heterodimers with the protein CYC (Cheng et al. 2013). Protein–DNA interactions were measured by examining the percentage of Luc-tagged CAD recovered following pull down of a biotin-labeled double stranded DNA fragment in the presence of a 60-fold molar excess of unlabeled competitor DNA. In the sample labeled ΔA+ΔB, two DNA fragments, each at a 60-fold molar excess, were added, resulting in a 60-fold excess of specific binding sites and a 120-fold total excess of unlabeled competitor DNAs. The oligonucleotide sequences used and their alignment to the wild type sequence is shown in supplementary table S2 (Supplementary Material online), which also includes all raw and processed luciferase data.
Supplementary Material
Supplementary methods, text, tables S1 and S2, and figures S1–S4 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
This work was supported by the National Institutes of Health grant GM085233 and the National Science Foundation grants DBI-0746303 and EFRI-1136913 to S.S. and the National Human Genome Research Institute grant HG004744 to M.H.B.
References
- Bakkali M. Microevolution of cis-regulatory elements: an example from the pair-rule segmentation gene fushi tarazu in the Drosophila melanogaster subgroup. PLoS One. 2011;6:e27376. doi: 10.1371/journal.pone.0027376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balhoff JP, Wray GA. Evolutionary analysis of the well characterized endo16 promoter reveals substantial variation within functional sites. Proc Natl Acad Sci U S A. 2005;102:8591–8596. doi: 10.1073/pnas.0409638102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barolo S. Shadow enhancers: frequently asked questions about distributed cis-regulatory information and enhancer redundancy. Bioessays. 2012;34:135–141. doi: 10.1002/bies.201100121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrios-Rodiles M, Brown KR, Ozdamar B, et al. (17 co-authors) High-throughput mapping of a dynamic signaling network in mammalian cells. Science. 2005;307:1621–1625. doi: 10.1126/science.1105776. [DOI] [PubMed] [Google Scholar]
- Berg J, Willmann S, Lässig M. Adaptive evolution of transcription factor binding sites. BMC Evol Biol. 2004;4:42. doi: 10.1186/1471-2148-4-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley RK, Holmes I. Evolutionary triplet models of structured RNA. PLoS Comput Biol. 2009;5:e1000483. doi: 10.1371/journal.pcbi.1000483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Q, Kazemian M, Pham H, Blatti C, Celniker SE, Wolfe SA, Brodsky MH, Sinha S. Computational identification of diverse mechanisms underlying transcription factor-DNA occupancy. PLoS Genet. 2013;9:e1003571. doi: 10.1371/journal.pgen.1003571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper MB, Loose M, Brookfield JF. The evolutionary influence of binding site organisation on gene regulatory networks. Biosystems. 2009;96:185–193. doi: 10.1016/j.biosystems.2009.02.001. [DOI] [PubMed] [Google Scholar]
- Dearolf CR, Topol J, Parker CS. The caudal gene product is a direct activator of fushi tarazu transcription during Drosophila embryogenesis. Nature. 1989;341:340–343. doi: 10.1038/341340a0. [DOI] [PubMed] [Google Scholar]
- Dermitzakis ET, Clark AG. Evolution of transcription factor binding sites in mammalian gene regulatory regions: conservation and turnover. Mol Biol Evol. 2002;19:1114–1121. doi: 10.1093/oxfordjournals.molbev.a004169. [DOI] [PubMed] [Google Scholar]
- Doniger SW, Fay JC. Frequent gain and loss of functional transcription factor binding sites. PLoS Comput Biol. 2007;3:e99. doi: 10.1371/journal.pcbi.0030099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW, Charlesworth B, Charlesworth D, Crow JF. Rates of spontaneous mutation. Genetics. 1998;148:1667–1686. doi: 10.1093/genetics/148.4.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R, Schmidt D. Waiting for two mutations: with applications to regulatory sequence evolution and the limits of Darwinian evolution. Genetics. 2008;180:1501–1509. doi: 10.1534/genetics.107.082610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emberly E, Rajewsky N, Siggia ED. Conservation of regulatory elements between two species of Drosophila. BMC Bioinformatics. 2003;4:57. doi: 10.1186/1471-2105-4-57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Evolutionary trees from DNA sequences: a maximum likelihood approach. J Mol Evol. 1981;17:368–376. doi: 10.1007/BF01734359. [DOI] [PubMed] [Google Scholar]
- Francois P, Hakim V, Siggia ED. Deriving structure from evolution: metazoan segmentation. Mol Syst Biol. 2007;3:154. doi: 10.1038/msb4100192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallikas O, Taipale J. High-throughput assay for determining specificity and affinity of protein-DNA binding interactions. Nat Protoc. 2006;1:215–222. doi: 10.1038/nprot.2006.33. [DOI] [PubMed] [Google Scholar]
- Halpern AL, Bruno WJ. Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol Biol Evol. 1998;15:910–917. doi: 10.1093/oxfordjournals.molbev.a025995. [DOI] [PubMed] [Google Scholar]
- Hare EE, Peterson BK, Iyer VN, Meier R, Eisen MB. Sepsid even-skipped enhancers are functionally conserved in Drosophila despite lack of sequence conservation. PLoS Genet. 2008;4:e1000106. doi: 10.1371/journal.pgen.1000106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harrison MM, Li XY, Kaplan T, Botchan MR, Eisen MB. Zelda binding in the early Drosophila melanogaster embryo marks regions subsequently activated at the maternal-to-zygotic transition. PLoS Genet. 2011;7:e1002266. doi: 10.1371/journal.pgen.1002266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa M, Kishino H, Yano T. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J Mol Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- He BZ, Holloway AK, Maerkl SJ, Kreitman M. Does positive selection drive transcription factor binding site turnover? A test with Drosophila cis-regulatory modules. PLoS Genet. 2011;7:e1002053. doi: 10.1371/journal.pgen.1002053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Duque TS, Sinha S. Evolutionary origins of transcription factor binding site clusters. Mol Biol Evol. 2012;29:1059–1070. doi: 10.1093/molbev/msr277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Ling X, Sinha S. Alignment and prediction of cis-regulatory modules based on a probabilistic model of evolution. PLoS Comput Biol. 2009;5:e1000299. doi: 10.1371/journal.pcbi.1000299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X, Samee MA, Blatti C, Sinha S. Thermodynamics-based models of transcriptional regulation by enhancers: the roles of synergistic activation, cooperative binding and short-range repression. PLoS Comput Biol. 2010;6:e1000935. doi: 10.1371/journal.pcbi.1000935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick PW. Genetics of populations. Sudbury (MA): Jones and Bartlett Publishers; 2011. [Google Scholar]
- Hoggart CJ, Chadeau-Hyam M, Clark TG, Lampariello R, Whittaker JC, De Iorio M, Balding DJ. Sequence-level population simulations over large genomic regions. Genetics. 2007;177:1725–1731. doi: 10.1534/genetics.106.069088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Josephides C, Moses AM. Modeling the evolution of a classic genetic switch. BMC Syst Biol. 2011;5:24. doi: 10.1186/1752-0509-5-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jow H, Hudelot C, Rattray M, Higgs PG. Bayesian phylogenetics using an RNA substitution model applied to early mammalian evolution. Mol Biol Evol. 2002;19:1591–1601. doi: 10.1093/oxfordjournals.molbev.a004221. [DOI] [PubMed] [Google Scholar]
- Kaplan T, Li XY, Sabo PJ, Thomas S, Stamatoyannopoulos JA, Biggin MD, Eisen MB. Quantitative models of the mechanisms that control genome-wide patterns of transcription factor binding during early Drosophila development. PLoS Genet. 2011;7:e1001290. doi: 10.1371/journal.pgen.1001290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazemian M, Pham H, Wolfe SA, Brodsky MH, Sinha S. Widespread evidence of cooperative DNA binding by transcription factors in Drosophila development. Nucleic Acids Res. 2013;41:8237–8252. doi: 10.1093/nar/gkt598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, He X, Sinha S. Evolution of regulatory sequences in 12 Drosophila species. PLoS Genet. 2009;5:e1000330. doi: 10.1371/journal.pgen.1000330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Sinha S. Towards realistic benchmarks for multiple alignments of non-coding sequences. BMC Bioinformatics. 2010;11:54. doi: 10.1186/1471-2105-11-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Ohta T. The average number of generations until fixation of a mutant gene in a finite population. Genetics. 1969;61:763–771. doi: 10.1093/genetics/61.3.763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li XY, Thomas S, Sabo PJ, Eisen MB, Stamatoyannopoulos JA, Biggin MD. The role of chromatin accessibility in directing the widespread, overlapping patterns of Drosophila transcription factor binding. Genome Biol. 2011;12:R34. doi: 10.1186/gb-2011-12-4-r34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludwig MZ, Kreitman M. Evolutionary dynamics of the enhancer region of even-skipped in Drosophila. Mol Biol Evol. 1995;12:1002–1011. doi: 10.1093/oxfordjournals.molbev.a040277. [DOI] [PubMed] [Google Scholar]
- Lusk RW, Eisen MB. Evolutionary mirages: selection on binding site composition creates the illusion of conserved grammars in Drosophila enhancers. PLoS Genet. 2010;6:e1000829. doi: 10.1371/journal.pgen.1000829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moses AM. Statistical tests for natural selection on regulatory regions based on the strength of transcription factor binding sites. BMC Evol Biol. 2009;9:286. doi: 10.1186/1471-2148-9-286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moses AM, Chiang DY, Pollard DA, Iyer VN, Eisen MB. MONKEY: identifying conserved transcription-factor binding sites in multiple alignments using a binding site-specific evolutionary model. Genome Biol. 2004;5:R98. doi: 10.1186/gb-2004-5-12-r98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moses AM, Pollard DA, Nix DA, Iyer VN, Li XY, Biggin MD, Eisen MB. Large-scale turnover of functional transcription factor binding sites in Drosophila. PLoS Comput Biol. 2006;2:e130. doi: 10.1371/journal.pcbi.0020130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mustonen V, Lässig M. Evolutionary population genetics of promoters: predicting binding sites and functional phylogenies. Proc Natl Acad Sci U S A. 2005;102:15936–15941. doi: 10.1073/pnas.0505537102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nien CY, Liang HL, Butcher S, Sun Y, Fu S, Gocha T, Kirov N, Manak JR, Rushlow C. Temporal coordination of gene networks by Zelda in the early Drosophila embryo. PLoS Genet. 2011;7:e1002339. doi: 10.1371/journal.pgen.1002339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nourmohammad A, Lässig M. Formation of regulatory modules by local sequence duplication. PLoS Comput Biol. 2011;7:e1002167. doi: 10.1371/journal.pcbi.1002167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papatsenko D, Goltsev Y, Levine M. Organization of developmental enhancers in the Drosophila embryo. Nucleic Acids Res. 2009;37:5665–5677. doi: 10.1093/nar/gkp619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paten B, Herrero J, Beal K, Birney E. Sequence progressive alignment, a framework for practical large-scale probabilistic consistency alignment. Bioinformatics. 2009;25:295–301. doi: 10.1093/bioinformatics/btn630. [DOI] [PubMed] [Google Scholar]
- Perry MW, Boettiger AN, Bothma JP, Levine M. Shadow enhancers foster robustness of Drosophila gastrulation. Curr Biol. 2010;20:1562–1567. doi: 10.1016/j.cub.2010.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pujato M, MacCarthy T, Fiser A, Bergman A. The underlying molecular and network level mechanisms in the evolution of robustness in gene regulatory networks. PLoS Comput Biol. 2013;9:e1002865. doi: 10.1371/journal.pcbi.1002865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samee MA, Sinha S. Evaluating thermodynamic models of enhancer activity on cellular resolution gene expression data. Methods. 2013;62:79–90. doi: 10.1016/j.ymeth.2013.03.005. [DOI] [PubMed] [Google Scholar]
- Segal E, Raveh-Sadka T, Schroeder M, Unnerstall U, Gaul U. Predicting expression patterns from regulatory sequence in Drosophila segmentation. Nature. 2008;451:535–540. doi: 10.1038/nature06496. [DOI] [PubMed] [Google Scholar]
- Siddharthan R, Siggia ED, van Nimwegen E. PhyloGibbs: a Gibbs sampling motif finder that incorporates phylogeny. PLoS Comput Biol. 2005;1:e67. doi: 10.1371/journal.pcbi.0010067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha S, Liang Y, Siggia E. Stubb: a program for discovery and analysis of cis-regulatory modules. Nucleic Acids Res. 2006;34:W555–W559. doi: 10.1093/nar/gkl224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinha S, Siggia ED. Sequence turnover and tandem repeats in cis-regulatory modules in Drosophila. Mol Biol Evol. 2005;22:874–885. doi: 10.1093/molbev/msi090. [DOI] [PubMed] [Google Scholar]
- Spivakov M, Akhtar J, Kheradpour P, Beal K, Girardot C, Koscielny G, Herrero J, Kellis M, Furlong EE, Birney E. Analysis of variation at transcription factor binding sites in Drosophila and humans. Genome Biol. 2012;13:R49. doi: 10.1186/gb-2012-13-9-r49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart AJ, Seymour RM, Pomiankowski A, Plotkin JB. The population genetics of cooperative gene regulation. BMC Evol Biol. 2012;12:173. doi: 10.1186/1471-2148-12-173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone JR, Wray GA. Rapid evolution of cis-regulatory sequences via local point mutations. Mol Biol Evol. 2001;18:1764–1770. doi: 10.1093/oxfordjournals.molbev.a003964. [DOI] [PubMed] [Google Scholar]
- Stormo GD, Fields DS. Specificity, free energy and information content in protein-DNA interactions. Trends Biochem Sci. 1998;23:109–113. doi: 10.1016/s0968-0004(98)01187-6. [DOI] [PubMed] [Google Scholar]
- Suh E, Chen L, Taylor J, Traber PG. A homeodomain protein related to caudal regulates intestine-specific gene transcription. Mol Cell Biol. 1994;14:7340–7351. doi: 10.1128/mcb.14.11.7340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swanson CI, Schwimmer DB, Barolo S. Rapid evolutionary rewiring of a structurally constrained eye enhancer. Curr Biol. 2011;21:1186–1196. doi: 10.1016/j.cub.2011.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thornton K, Andolfatto P. Approximate Bayesian inference reveals evidence for a recent, severe bottleneck in a Netherlands population of Drosophila melanogaster. Genetics. 2006;172:1607–1619. doi: 10.1534/genetics.105.048223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visel A, Prabhakar S, Akiyama JA, Shoukry M, Lewis KD, Holt A, Plajzer-Frick I, Afzal V, Rubin EM, Pennacchio LA. Ultraconservation identifies a small subset of extremely constrained developmental enhancers. Nat Genet. 2008;40:158–160. doi: 10.1038/ng.2007.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vizoso Pinto MG, Villegas JM, Peter J, Haase R, Haas J, Lotz AS, Muntau AC, Baiker A. LuMPIS—a modified luminescence-based mammalian interactome mapping pull-down assay for the investigation of protein-protein interactions encoded by GC-low ORFs. Proteomics. 2009;9:5303–5308. doi: 10.1002/pmic.200900298. [DOI] [PubMed] [Google Scholar]
- Weirauch MT, Hughes TR. Conserved expression without conserved regulatory sequence: the more things change, the more they stay the same. Trends Genet. 2010;26:66–74. doi: 10.1016/j.tig.2009.12.002. [DOI] [PubMed] [Google Scholar]
- Yao LC, Phin S, Cho J, Rushlow C, Arora K, Warrior R. Multiple modular promoter elements drive graded brinker expression in response to the Dpp morphogen gradient. Development. 2008;135:2183–2192. doi: 10.1242/dev.015826. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.