Skip to main content
PMC home page
Molecular Biology and Evolution logoLink to Molecular Biology and Evolution
. 2013 Oct 10;31(1):201–211. doi: 10.1093/molbev/mst190

Modeling Gene Expression Evolution with an Extended Ornstein–Uhlenbeck Process Accounting for Within-Species Variation

Rori V Rohlfs 1,*, Patrick Harrigan 2, Rasmus Nielsen 1
PMCID: PMC3879452  PMID: 24113538

Abstract

Much of the phenotypic variation observed between even closely related species may be driven by differences in gene expression levels. The current availability of reliable techniques like RNA-Seq, which can quantify expression levels across species, has enabled comparative studies. Ornstein–Uhlenbeck (OU) processes have been proposed to model gene expression evolution as they model both random drift and stabilizing selection and can be extended to model changes in selection regimes. The OU models provide a statistical framework that allows comparisons of specific hypotheses of selective regimes, including random drift, constrained drift, and expression level shifts. In this way, inferences may be made about the mode of selection acting on the expression level of a gene. We augment this model to include within-species expression variance, allowing for modeling of nonevolutionary expression variance that could be caused by individual genetic, environmental, or technical variation. Through simulations, we explore the reliability of parameter estimates and the extent to which different selective regimes can be distinguished using phylogenies of varying size using both the typical OU model and our extended model. We find that if individual variation is not accounted for, nonevolutionary expression variation is often mistaken for strong stabilizing selection. The methods presented in this article are increasingly relevant as comparative expression data becomes more available and researchers turn to expression as a primary evolving phenotype.

Keywords: expression evolution, RNA-Seq, Ornstein–Uhlenbeck, evolutionary models, expression variation

Introduction

It has long been posited that gene expression differences explain the bulk of phenotypic diversity across species (King and Wilson 1975). Initial comparative expression analyses based on microarray technology across primates have produced interesting patterns of expression conservation and adaptation and a number of controversial results. For example, studies by Khaitovich et al. (2004a, 2004b) and Gilad et al. (2006) lead to quite different conclusions regarding the importance of natural selection in determining expression level differences and similarities among species. The degree to which selection is acting to modify expression levels is a standing question, especially on the human lineage.

With the advent of reliable technology to quantify gene transcription, the field is now better positioned to explore gene expression evolution and conservation (Gilad, Oshlack, Rifkin 2006; Khaitovich et al. 2006; Whitehead and Crawford 2006; Wang et al. 2009). Specifically, accurate comparative gene expression data is attainable with the developments of both RNA-Seq as a reliable method to quantify expression, and bioinformatical methods to appropriately normalize expression, accounting for species differences (Wang et al. 2009; Trapnell et al. 2010). Several statistical methods have been proposed to investigate the role of natural selection in expression evolution across divergent species by considering expression divergence between species and diversity within species (Hsieh et al. 2003; Rifkin et al. 2003; Nuzhdin et al. 2004; Gilad, Oshlack, Rifkin 2006; Khaitovich et al. 2006; Whitehead and Crawford 2006) or by modeling the expression evolution process (Butler and King 2004; Gu 2004; Oakley et al. 2005; Bedford and Hartl 2008; Blekhman et al. 2008; Chaix et al. 2008; Albert et al. 2012). However, a unified framework has yet to be established, which accounts for the complex variation of gene expression across species, individuals, tissues, environments, and technical replicates. Such sophisticated methods will enable rigorous investigation of the conservation of gene expression, the first step in exploring long-standing hypotheses about the contribution of expression to phenotype (Egger et al. 2004; Kleinjan and van Heyningen 2005; Esteller 2007; Johnstone and Baylin 2010).

A variety of approaches have been used to model gene expression evolution. A number of methods have been implemented considering the ratio of expression divergence to diversity to distinguish expression drift, stabilizing selection, and directional selection (Hsieh et al. 2003; Rifkin et al. 2003; Nuzhdin et al. 2004; Gilad, Oshlack, Rifkin 2006; Khaitovich et al. 2006; Whitehead and Crawford 2006). These nonparametric test statistic approaches are useful to quantify divergence and diversity empirically and may provide evidence of different modes of expression evolution but are limited by their inability to formulate complex evolutionary hypotheses or to compare specific models of evolution (Butler and King 2004). A variety of models have been implemented for regression and analysis of variance (ANOVA) analysis, including effect terms for gene, species, individual, microarray probe, interactions between those factors, residual error, and other factors, to explore cases of diverged and conserved expression levels (Rifkin et al. 2003; Gilad, Oshlack, Smyth, et al. 2006; Blekhman et al. 2008; Somel et al. 2009; Blekhman et al. 2010; Warnefors and Eyre-Walker 2012). However, these models typically implicitly assume independence between species and disregard phylogenetic relationships between species, inflating false-positive rates and making them less applicable to complex phylogenies (Felsenstein 1985). In multispecies phylogenies, differing shared evolutionary histories lead to a complex trait covariance structure that can add information and power to evolutionary analyses (Felsenstein 1985).

Phylogenetic structure is taken into account in models of expression evolution based on drift (Brownian motion) processes, allowing for both analysis considering dependencies induced by shared history and more specific formulation and comparison of selective hypotheses (Felsenstein 1985; Butler and King 2004; Gu 2004). Brownian motion processes can effectively model neutral drift (Khaitovich et al. 2005) but are less suitable to model stabilizing selection or conservation, which is expected in the case of gene expression, given simple cellular constraints on expression (Lynch and Hill 1986; Felsenstein 1988).

Ornstein–Uhlenbeck (OU) processes, which model random walks with some pull toward a particular state, have been proposed to model the evolution of quantitative traits subject to both drift and stabilizing selection (Hansen 1997; Butler and King 2004; Bedford and Hartl 2008; Hansen et al. 2008; Kalinka et al. 2010). OU processes include parameters for the degree of drift (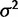Inline graphic), strength of pull (α), and the particular target value toward which the pull is aimed (θ). In a trait evolution framework, these parameters can be interpreted as phenotype change due to genetic drift, selective force, and optimally fit trait value, respectively, making OU processes a convenient framework in which to investigate selective hypotheses. OU processes have been shown to effectively model gene expression level evolution on divergent phylogenies elucidating the degrees of directional selection at play (Bedford and Hartl 2008; Kalinka et al. 2010; Perry et al. 2012). However, these methods may be limited by their assumption of phylogeny-based variation that does not allow for other sources of variation, for example, environmental, technical, or individual genetic variation (Oakley et al. 2005).

Here, we build upon this work to develop an appropriate statistical model to investigate evolutionary questions using comparative gene expression data with variation across individuals in each species. Gu (2004) alluded to a possible extension of his model that might accomplish this by accounting for “experimental errors” in trait evolution. Ives et al. (2007) proposed a model accounting for “measurement error” across quantitative observations of individuals in a phylogeny. Felsenstein (2008) outlined a model similar to ours based on the work of Lynch (1991), who considered sampling error in trait observations. More recently Hansen and Bartoszek (2012) have formulated an alternate model to account for trait observational and biological variation in evolutionary models. We present an OU model likelihood framework and outline specific hypothesis tests while accounting for phylogenetic relationships between species and variation over individuals within species. This model can be used for cases of nonevolutionary variation, neutral expression drift, stabilizing selection on expression, and lineage-specific shifts in expression level. Our framework builds directly upon that proposed by Bedford and Hartl (2008), which has been used effectively in the literature (Kalinka et al. 2010; Perry et al. 2012), but our model includes a new parameter for within-species variation (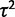Inline graphic). By modeling within-species variation, we allow the possibility of nonevolutionary expression variation, which is thought to be important in expression (Idaghdour et al. 2010; Pickrell et al. 2010; Price et al. 2011), and improve rigor of distinguishing different regimes of gene expression evolution.

Using the likelihood ratio test presented in this article, Brawand et al. (2011) considered selection on expression in a RNA-Seq data set of ten species, with two to six individuals per species, across six tissues. The analysis accounted for expression variation within species, and tests for shifts in expression levels in each species and branch were performed across the six tissues. This analysis showed that the testis had the largest number of expression shifts, while the brain showed few expression shifts. These results closely mimic those previously found at the DNA level, which suggest that testis-specific genes often are targeted by positive selection, while genes with primary expression in the brain tend to be highly conserved (Nielsen et al. 2005). An exception was the primate lineage, in which the largest number of expression optimum shifts was found in the brain. This could be caused by biological factors such as the evolution of more complex function, or perhaps, alternatively, reflect differences in sampling and treatment of tissues between primates and nonprimates.

Here, we expand upon the applied analysis, describing the method in detail and estimate power and false-positive rates of the tests performed under a variety of circumstances. Specifically, we compare the performance of the model proposed by Bedford and Hartl (2008) (species mean method) to our extended model accounting for variance within species (species variance method). Using simulations, we compare parameter estimation accuracy and ability to distinguish between various selective hypotheses between these two methods. Our results show that a nonevolutionary expression variance model may not be distinguishable from a model of severe stabilizing selection. When using the species mean method that does not allow for a nonevolutionary model, genes that are subject to nonevolutionary environmental variation will often be mistaken as being under intense stabilizing selection. However, we show that the addition of parameter describing within-species variation facilitates statistically valid investigation of nonevolutionary expression variance hypotheses and circumvents the problem of false inferences of strong stabilizing selection when within-species expression variation is large compared with between-species variation. We explore the power of these methods to detect expression shifts in phylogenies, finding the methods to have similar power. In addition to describing the extended species variance model and its power, our results further describe the behavior of the previously published and applied species mean model, which is necessary for rigorous interpretation of results from previous and current studies.

New Approaches

Expression Levels over Individuals within a Species

We implement two methods for modeling expression evolution: the species mean method (as described by Bedford and Hartl [2008]) and the species variance method. In the species mean method, the mean expression level is taken for each species and used as the value of the OU process at that node. In the species variance method, the gene expression levels are assumed to be normally distributed across individuals within a species, with mean given by the underlying OU process value for that species node and variance parameterized by 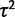Inline graphic. This additional parameter models biological and technical variance within species and allows formulation of an additional variance model, the nonevolutionary environmental variance model, as discussed further later.

Investigating Evolutionary Questions

This OU framework can model various specific hypotheses about the nature of gene expression evolution by placing constraint on what values parameters may take at different branches in the phylogeny. The likelihood function for the parameters of the process can be calculated using observed gene expression data for different models so that likelihood ratios can be used to test these models. We propose a series of models and likelihood ratios as a natural starting point to investigate basic questions in comparative analyses of gene expression evolution. We consider models for expression nonevolution, drift, stabilization, and lineage-specific shift. An overview of the nested hypothesis tests based on these models can be seen in table 1.

Table 1.

Nested Hypothesis Tests for Evolutionary Models.

Null Hypothesis Alternative Hypothesis
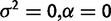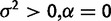Nonevolutionary versus drift Inline graphic Inline graphic
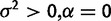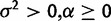Drift versus stabilization Inline graphic Inline graphic
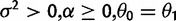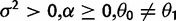Stabilization versus shift Inline graphic Inline graphic
Open in a new tab

Models

Four models were used to simulate data: 1) the nonevolutionary model where expression does not evolve over time but variation is due to technical, environmental, and individual genetic variation, 2) the neutral drift model where gene expression levels are subject to unconstrained neutral drift over the phylogeny, 3) the stabilizing selection model where gene expression levels drift randomly but are constrained by stabilizing selection, and 4) the selective shift model where expression level experiences stabilizing selection toward different optimally fit expression levels on different branches in the phylogeny, approximating directional (positive) selection in favor of change in expression levels on some lineages of a phylogeny.

If expression levels are not evolving, the observed variance in the data is explained by within-species variation (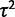Inline graphic) alone. That is, the comparative expression levels can be described by a star phylogeny with zero branch lengths. To construct this model, we eliminate evolutionary drift (set 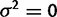Inline graphic) and stabilizing selection (set 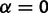Inline graphic) on every branch of the phylogeny. Under this model without phylogenetic signal, gene expression levels are normally distributed across species and individuals as 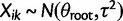Inline graphic. 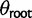Without stabilizing selection, the optimal gene expression value θ is undefined, and we instead estimate the ancestral gene expression value at the root, Inline graphic.

We modeled the case of neutral drift of expression levels by allowing evolutionary drift (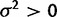Inline graphic) and disallowing stabilizing selection (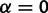Inline graphic), which enables covariance of gene expression values between species due to shared evolutionary history. Note that this OU process with 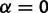Inline graphic is equivalent to a Brownian motion process of random unconstrained drift.

In the stabilizing selection model, expression levels are subject to drift with a pull toward an optimal (most fit) value. This is modeled by an OU process with 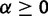Inline graphic, where expression evolution is driven toward an optimum expression level θ. Because under the stabilization model, θ is defined, we have some choice in how to model the expression value at the root. As an OU process has the stationary distribution 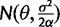Inline graphic, we can chose whether to proceed as in the nonevolving and drift models, including an additional parameter 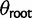Inline graphic, or to instead use the stationary distribution on this branch. Estimating 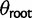Inline graphic is equivalent to requiring 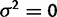Inline graphic on this branch. In this analysis, we use the stationary distribution to describe expression at the root node.

A shift in expression levels can be modeled by allowing θ to vary across the phylogeny. In the shifted expression model, each node i, the expression optimum 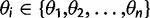Inline graphic where n specifies the number of optima hypothesized to act on the phylogeny. Expression at the root node is assumed to follow the OU process stationary distribution [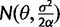Inline graphic] as in the stabilization model.

Simulating Expression Data

Using the models listed earlier, for a variety of parameter values, we determined the expression level distributions and simulated comparative expression data sets. For the phylogenetic structure, we used a ten-leaf phylogeny with two to six individuals per species, equivalent to that considered by Brawand et al. (2011), which we refer to here as “small tree.” To explore the effect of phylogeny size and sample size per species on power, we consider two additional phylogenetic structures: a “deep tree,” which is constructed with four copies of the small tree st as 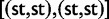Inline graphic with all connecting branches the length of st itself, and a “wide tree,” which is the same phylogenetic structure as the small tree, but with four times the individuals in each species (supplementary fig. S1, Supplementary Material online). For each method, power and false positive rate data points are shown based on 1,000 simulated replicates. The specific parameter values used for each simulation vary across models and are indicated on all figures.

Results

The Effect of Ignoring Individual Variation

The commonly used OU-based model for expression evolution does not directly account for measurement of expression levels in multiple individuals of the same species. Typically, when these models are used to calculate the probability of observed data, the sample means are used as species expression levels, a technique we refer to as the species mean method. As an alternative, we propose the species variance method, where within-species variation is taken into account with an additional parameter, 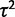Inline graphic. Note that the species mean method approximates the species variance method as the number of individuals per species increases. Using both the species mean and variance methods, where possible, we compute likelihood ratios to distinguish expression subject to nonevolutionary variance, drift, stabilization, and lineage-specific shifts (table 1).

Test 1: Testing for Phylogenetic Signal

Because the mean species method does not allow for within-species variation, in the absence of selection, any variation in mean expression levels between species must be explained by drift. In this way, under the species mean model, data simulated with any kind of variation between species is always more likely under the drift model (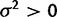Inline graphic) than the nonevolution model (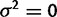Inline graphic). As an illustration, data were simulated with the species variance method under the nonevolutionary model and its likelihood computed for various values of 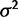Inline graphic. Figure 1 shows this likelihood surface with the species mean method to have a peak at 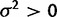Inline graphic, indicating that, even for data simulated without evolutionary information, the species mean method will assign some phylogenetic signal. Any attempt to perform the test for phylogenetic signal under the species mean model will result in rejection of the null hypothesis, meaning both power and false-positive rate are 1.0.

Fig. 1.

Fig. 1.

Open in a new tab

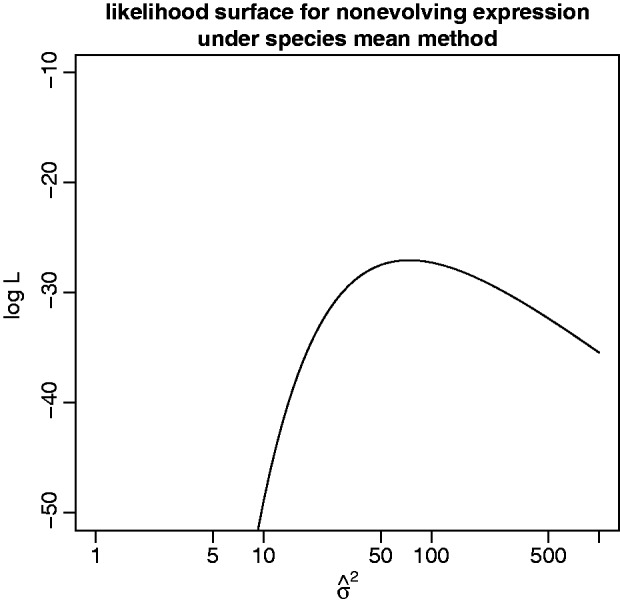
The species mean model log likelihood function for data simulated under the nonevolutionary species variance model with 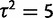Inline graphic (within-species variation) is computed with 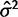Inline graphic (estimated drift) fixed and other parameters optimized (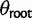Inline graphic [estimated expression at root] and 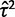Inline graphic [estimated within-species variation]).

Because the species variance method considers individual variation, it allows for species mean expression levels to vary even in the absence of evolutionary drift. In other words, the species variance method enables a nonevolutionary model for gene expression variance. So, with the species variance method, the probabilities of the observed individual expression levels can be compared under a model of nonevolutionary variation and a model of evolutionary drift (table 1). Distinguishing evolutionary and nonevolutionary variation is particularly relevant because the expression of many genes is thought to be subject to intense environmental variation (Idaghdour et al. 2010).

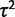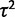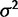Gene expression levels were simulated over the three phylogenetic structures under the nonevolutionary model with varying values of Inline graphic and under the drift model with varying values of both Inline graphic and Inline graphic. Using the species variance method, the likelihood ratio for nonevolution versus drift was computed for all these data, enabling simulation-based estimates of power and false-positive rates, as shown in figure 2. The critical value for hypothesis rejection was determined using the simulations under the null hypothesis to attain a nominal false-positive rate of 0.05. Because the nonevolution and drift models are simply nested and differ by one parameter, bounded at zero, the expected asymptotic distribution of the likelihood ratio test statistic is a 50:50 mixture of chi-square with one degree of freedom and a point mass at zero. As expected, power increases with drift (parameterized by 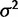Inline graphic), decreases with within-species variation (parameterized by 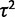Inline graphic), and is greater for larger phylogenies.

Fig. 2.

Fig. 2.

Open in a new tab

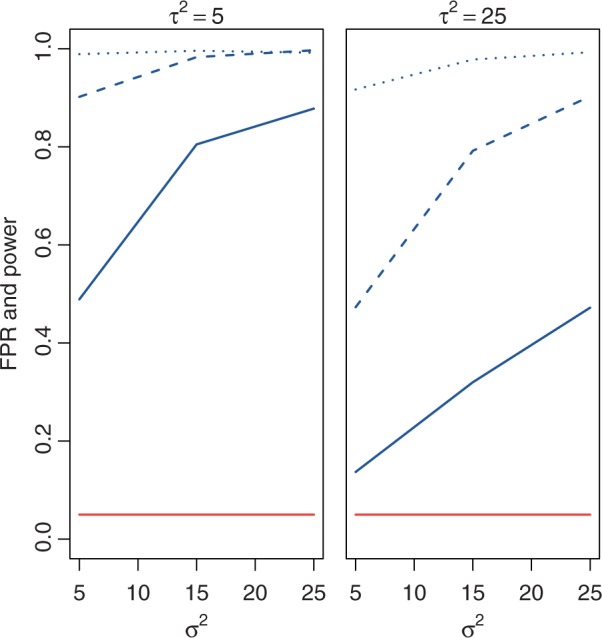
No evolution versus drift test (test 1) false-positive rate (lower curves) and power (upper curves) using the species variance model for various simulated values of 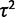Inline graphic (within-species variation) and 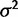Inline graphic (drift) using critical values for a nominal false-positive rate of 0.05, run with different phylogenetic structures (solid: small tree, dashed: wide tree, dotted: deep tree).

Test 2: Testing for Stabilizing Selection

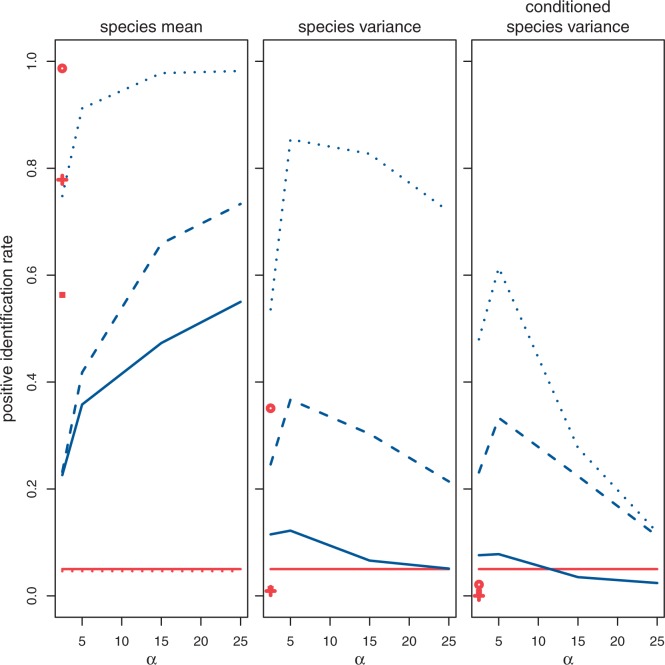
The likelihood function under both the drift and stabilizing selection models is fully computable using either the species mean or variance method. The resulting likelihood ratio can be used to distinguish data simulated under each model. This likelihood ratio was computed for data simulated under the nonevolutionary, drift, and stabilization models using a variety of parameter values. Figure 3 shows the positive identification rates of data simulated under drift (false-positive rate) and stabilization (power) using the species mean, species variance, and conditioned species variance methods. In the conditioned species variance method, rejection of the null hypothesis is conditioned on rejection of the nonevolutionary model as well. That is, a gene must be shown to be undergoing expression evolution according to the known phylogeny before further tests about the mode of expression evolution are performed. In this case, the nonevolutionary model must be rejected in favor of the drift model before the test for stabilizing selection is performed. So stabilizing selection is identified when both the nonevolutionary versus drift and the drift versus stabilization tests reject the null. Power is higher for larger phylogenies and using the species mean method, as opposed to the species variation models.

Fig. 3.

Fig. 3.

Open in a new tab

Drift versus stabilization test (test 2) false-positive rate (lower curves) and power (upper curves) using the species mean, species variance, and conditioned species variance models for various simulated values of α (strength of pull) using critical values for a nominal false-positive rate of 0.05, run with different phylogenetic structures (solid: small tree, dashed: wide tree, dotted: deep tree). Rates for data simulated under the nonevolutionary model and misidentified as under stabilizing selection are shown as points on the left of each plot (square: small tree, cross: wide tree, circle: deep tree).

However, data simulated under the nonevolutionary model is often misidentified as under stabilizing selection using the species mean method, as shown in table 2 and figure 3. This can be explained by a lack of identifiability when distinguishing between the nonevolutionary and stabilization models. In the limit of strong selection, all species expression levels will take the same (optimal) value. This is equivalent to the nonevolutionary model used here, where variation is not phylogenetic but individual. In the species mean method, within-species or sampling variation is not modeled, and similar expression mean values across species are better explained by intense stabilizing selection than by drift or nonevolution. As a result of using the species mean method, genes with no phylogenetic signal often appear to be under stabilizing selection, yielding high false-positive rates (table 2).

Table 2.

False-Positive Rate of Truly Nonevolutionary Data in Drift versus Stabilization Test.

Typical Tree Deep Tree Wide Tree
Species mean 0.56 0.99 0.78
Species variance 0.01 0.35 0.01
Conditioned species variance 0.01 0.02 0.00
Open in a new tab

Because the critical values for these tests are chosen to attain a null hypothesis false-positive rate of 0.05, critical values vary over phylogenetic structures and methods (supplementary table S1, Supplementary Material online). Specifically, because the deep tree contains more information that can be exploited with the species variance method, this configuration has more power to distinguish expression under drift and stabilization. In this case, data simulated under drift have very low likelihood ratio values, so the critical threshold is remarkably low to attain a false-positive rate as high as 0.05. When considering truly nonevolutionary expression in the drift versus stabilization test, this results in an elevated false-positive rate.

Using the species mean method, power increases with strength of stabilizing selection (α), while using the species variation method, power decreases with α. Again, consider the limit of expression under the intense stabilizing selection that erases information about ancestral expression levels in observations of extant species so that there is little to no variation in expression level between species. When using the species variation method, as α increases, the data may be better explained by parameter values resembling the nonevolutionary model than the stabilization model. So the test for stabilizing selection may actually lose power under intense stabilizing selection, because in our construction, it entertains a lack of phylogenetic signal as one of the possible alternatives.

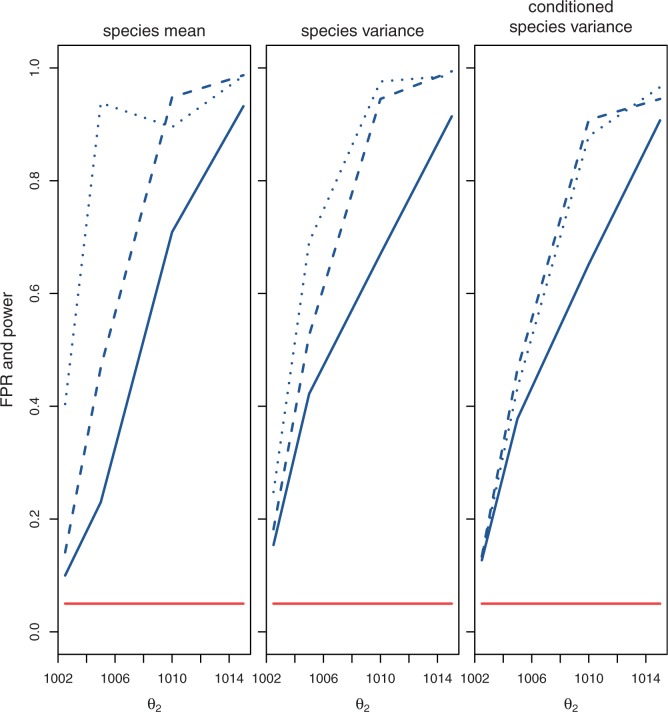
Test 3: Testing for Expression Level Shifts

Likelihood ratios comparing the stabilization and shift models were computed for data simulated under the stabilization and shift model with varying distances between the two optima (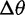Inline graphic). Again, critical values were chosen to achieve a nominal false-positive rate of 0.05. Figure 4 shows the power of this test for different phylogenies, values of 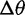Inline graphic, and methods. Power increases with phylogeny size and 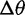Inline graphic. In these simulations, the species variance method has higher power than the species mean method, but the power is reduced with the conditioned species variance method. Because data simulated under selective shift depart from the phylogenetic structure, according to the magnitude of shift, the conditioned species variance method loses some power (supplementary table S2, Supplementary Material online).

Fig. 4.

Fig. 4.

Open in a new tab

Stabilization versus expression shift test (test 3) false-positive rate (lower curves) and power (upper curves) using the species mean, species variance, and conditioned species variation model for various simulated values of 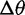Inline graphic (change in expression optimum) using critical values for a nominal false-positive rate of 0.05, run with different phylogenetic structures (solid: small tree, dashed: wide tree, dotted: deep tree).

The expression shift model produces patterns of expression levels that depart from those under the nonevolving, drift, and stabilizing models. Data simulated under both the nonevolving and drift models are rarely misidentified as a product of the expression shift model, as seen in tables 3 and 4.

Table 3.

False-Positive Rate of Truly Nonevolutionary Data in Stabilization versus Shift Test.

Typical Tree Deep Tree Wide Tree
Species mean 0.02 0.01 0.02
Species variance 0.01 0.00 0.00
Conditioned species variance 0.01 0.00 0.00
Open in a new tab

Table 4.

False-Positive Rate of Truly Drifting Data in Test of Stabilization versus Expression Shift.

Typical Tree Deep Tree Wide Tree
Species mean 0.07 0.03 0.05
Species variance 0.07 0.02 0.06
Conditioned species variance 0.07 0.02 0.06
Open in a new tab

Estimating Model Parameters

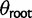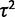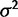For each of the four expression evolution models and the two individual variation methods the likelihood function is optimized to provide joint maximum likelihood estimates of all the parameters. The nonevolutionary model is parameterized in terms of the ancestral expression level (Inline graphic) and the within-species variance (Inline graphic); the drift model by Inline graphic, and strength of drift (Inline graphic); the stabilizing selection model by the optimal expression level (θ), 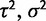Inline graphic, and the strength of stabilizing selection (α); and the selective shift model by the different optimal expression levels defined on specific branches (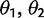Inline graphic for two optima) 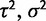Inline graphic, and α. Note that the within-species variation parameter 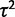Inline graphic is undefined in the species mean method.

In each case, we simulate data under the true model to assess best-case parameter estimation accuracy. The parameters for ancestral expression (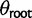Inline graphic) and within-species variance (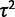Inline graphic) enter into the likelihood linearly as the mean and variance of expression under the nonevolutionary model, enabling accurate estimation with the species variance method (supplementary figs. S2 and S3, Supplementary Material online). Using the species mean model, likelihoods, and therefore parameter estimates, are not computable under a nonevolutionary model. 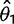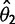Even in the more complex shift model, the expression level optima parameter estimates (Inline graphic and Inline graphic) are easily computed as the means of multivariate normal distributions (supplementary fig. S7, Supplementary Material online). In the case of expression shifts on shorter branches, the expression levels may not have had time to reach the optima, leading to reasonable underestimates of these values.

In the models where the parameters for drift (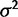Inline graphic) and stabilizing selection (α) are defined (drift, stabilization, shift), these parameters enter in a more complex way, making them more difficult to estimate with high accuracy (supplementary figs. S4–S6, Supplementary Material online). Nonetheless, it is interesting to consider how these estimates differ under the species variance and mean methods. Because the species mean method attributes all variation between species expression levels to drift, this method often overestimates 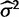Inline graphic when compared with estimates under the species variance method (supplementary figs. S4 and S5, Supplementary Material online). In part to compensate for this overestimation, under the stabilization model, the species mean method has a tendency to overestimate α as well, when compared with the species variation method which is more likely to underestimate α (supplementary fig. S6, Supplementary Material online).

Discussion

We have extended previous methods (Butler and King 2004; Bedford and Hartl 2008) to model gene expression evolution, including a term to account for within-species variation over individuals caused by biological, technical, and environmental inputs. Other studies have shown that RNA-Seq can accurately quantify gene expression levels, but that there can be substantial technical (Marioni et al. 2008; Mortazavi et al. 2008) and biological (Idaghdour et al. 2010; Pickrell et al. 2010; Price et al. 2011) variance. Through simulations, we have shown that this extended model can be used to more accurately infer underlying evolutionary mechanisms.

The parameters of this gene expression evolution model can be estimated using maximum likelihood procedures. In simulations, when considering the correct evolutionary model, some the species expression levels (θ) and within-species variation (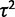Inline graphic) can be estimated with some accuracy (supplementary figs. S2, S3, and S7, Supplementary Material online). However, the parameter values for the strength of drift (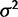Inline graphic) and stabilization (α) are dependent on each other, so their individual estimates are less reliable (supplementary figs. S4–S6, Supplementary Material online). Although we do not recommend interpreting the parameter estimates strongly in and of themselves, comparison of likelihood values between models can be used for model choice.

The first test for phylogenetic signal is only possible using the species variance method. In the species mean method, any difference between species expression levels is explained by drift, so the likelihood for realistic (nonpoint mass) data peaks at 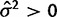Inline graphic (fig. 1) and the null hypothesis of nonevolutionary variation is always rejected, except if all individuals have the exact same expression level. The ability to perform this test is important because the expression of many genes appears to be subject to much environmental or individual variation, obscuring phylogenetic signal (Idaghdour et al. 2010; Pickrell et al. 2010; Price et al. 2011). Distinguishing these genes before investigating other hypotheses of selection provides a basic filter for nonevolutionary variation. Using the species variance method, power to detect phylogenetic signal increases with phylogeny size and strength of drift (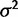Inline graphic) and decreases with within-species variation (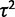Inline graphic) and can easily be controlled for a desired nominal false-positive rate (fig. 2).

The test for stabilizing selection versus neutral drift is possible using both the species mean and variation methods. The species mean method shows higher power than the species variance method (fig. 3) with critical values chosen to achieve false-positive rates of 0.05 under the null hypothesis of neutral drift. However, the species mean method also suffers from false-positive rates as high as 0.99 for expression levels that are truly nonevolving (table 2). This dramatically elevated false-positive rate renders the species mean method ineffective for distinguishing stabilizing selection. The species variance method has lower false-positive rates for truly nonevolving gene expression levels, though some false-positive rates are still uncontrolled. The false-positive rate can be controlled using the conditioned species variance method, but substantial power is lost as well. This problem of identifiability is explained by the fact that expression levels may not vary much among species under both extreme stabilizing selection and the nonevolving model. This presents an identifiability problem that results in lower power to identify stabilizing selection, even using the species variance method, especially for phylogenies the size of those currently available.

With this reduced power, the experimental results of the species variance method test for stabilizing selection, like those published by Brawand et al. (2011), are not easily interpretable. Robust analysis of stabilizing selection awaits larger data sets. Interestingly, the similarity of expression profiles of genes with nonevolutionary variance and genes under stabilizing selection may partially explain the results of a previous study where a nonevolutionary model was not rejected in favor of a drift model (Oakley et al. 2005).

A number of studies have been published claiming to show widespread conservation and stabilizing selection of gene expression levels. These studies generally either perform an ANOVA-style analysis where expression diversity within species is compared with divergence between species without regard to phylogeny (Lemos et al. 2005; Gilad, Oshlack, Smyth, et al. 2006; Staubach et al. 2010; Schroder et al. 2012; Warnefors and Eyre-Walker 2012) or the studies use an OU model like the species mean method without regard to within-species expression diversity (Bedford and Hartl 2008; Kalinka et al. 2010). Specifically, the species mean method that has been used to support claims of 80% of genes in a set of six Drosophila species across developmental time points are under stabilizing selection (Kalinka et al. 2010). For comparison, in our simulations for a ten-species phylogeny using the species mean method, we see 56% of genes with nonevolutionary expression variance are misidentified as being under stabilizing selection. Further, our power to identify stabilizing selection ranges from 22% to 55%. The specific false-positive rates and power depend on parameter values like within-species variance, strength of drift, and the strength of stabilization. We do not contest that stabilizing selection is crucial to functional expression level. However, because nonevolutionary variation is often mistaken as stabilizing selection and the power to identify stabilizing selection may be low, the precise degree to which stabilizing selection versus nonevolutionary variation cannot be distinguished using the species mean method. This results in a potential overstatement of the importance of stabilizing selection in expression evolution. As an increasing number of studies seem to reject neutral expression evolution in favor of stabilizing expression, it will be important to consider the possibility of nonevolutionary inputs to expression level.

The test for expression level shift, which was most prominently featured by Brawand et al. (2011), shows similar high power under both the species mean and species variance models, which is consistent with their strong interpretation of those results.

It is worth noting the interplay between statistical modeling and experimental design. Small organisms are commonly pooled before they are typed for expression level. Typing pooled samples effectively performs an “experimental mean” on expression level, which may reduce individual biological variance when compared with single individual samples. However, pooling samples may not reduce technical variance between typing runs, so modeling this variance is still important. Additionally, the implicit experimental mean may be more robust to biological variance, but it is subject to error and the true species mean is still unknown. As the species variance method allows for error in estimated species mean expression level and therefore allows for nonevolutionary expression differences, the species variance method is still preferable with pooled samples.

Although OU models provide a simple model of gene expression evolution with easily tested hypotheses about selective regimes, much remains to be explored about the mechanism and nature of gene expression evolution. The null hypothesis of nonevolution considered here allows expression levels for all individuals across species to be drawn from the same underlying normal distribution. Other possible models of nonevolution could allow species expression levels to vary in a nonphylogenetic manner, for example, according to different environmental conditions, which may more accurately represent the expression of genes highly influenced by environmental factors. In addition, the OU model implicitly assumes that the effect size of expression mutations follow a normal distribution (parameterized by 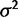Inline graphic). We have much to learn about the mechanisms of expression evolution. Mutation effect sizes may follow a Poisson distribution (Khaitovich et al. 2005) or some mixed model with common small effect sizes and rare large effect mutations (Chaix et al. 2008; Gruber et al. 2012).

As with other models of gene expression evolution, here we have considered a single gene’s expression level across species and individuals. The power we estimated is accurate for each marginal single gene’s expression levels. Of course, in typical data sets, expression levels are quantified for many genes simultaneously. Because expression levels across genes vary in response to each other over evolutionary time and environmental conditions, biological expression levels are not independent. When accounting for multiple testing across genes, assuming independence may lead to a loss in power. Complex correlations across genes must be considered simultaneously to rigorously understand the biological basis underpinned by full genetic architecture. A rigorous multigene expression evolution analysis awaits development of methods for correlated trait evolution based on previously described models (Lande and Arnold, 1983; Felsenstein, 1985, 1988; Lynch, 1991) that would increase information and power.

The simulations presented here indicate that these methods may be used to distinguish some regimes of gene expression evolution, particularly expression level shifts. However, some expression models, particularly nonevolutionary variance and stabilizing selection, result in similar patterns of expression levels, which are not distinguishable with currently available comparative expression data sets. As more extensive comparative expression data becomes available and the mechanisms of expression variation and evolution are better understood, increasingly appropriate models can be developed to explore hypotheses of gene expression evolution.

Materials and Methods

We model the evolution of a gene’s expression level over time as an OU process, which is defined by the stochastic differential equation

graphic file with name mst190m1.jpg (1)

where Xt is the process value at time 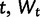Inline graphic is a normally distributed random variable with variance dt (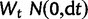Inline graphic), α parameterizes the strength of pull toward the optimal value θ, and σ parameterizes the strength of drift. The change in expression level (dXt) over interval dt is the sum of stochastic and deterministic components. The stochastic component (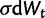Inline graphic) is a normally distributed random variate with variance 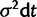Inline graphic, and the deterministic component (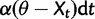Inline graphic) describes pull of the process toward θ. In modeling gene expression evolution, the stochastic component of change represents neutral drift in expression level and the deterministic component of change represents stabilizing selection.

The OU Process as a Model Gene Expression Evolution

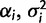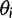For comparative analysis, we assume a phylogeny of known topology and branch lengths and assign an OU process to each branch. Formally, for every node i with expression level Xi, we assign the parameters Inline graphic, and Inline graphic to the branch leading to that node. Each node expression level Xi is distributed normally with

graphic file with name mst190m2.jpg (2)
graphic file with name mst190m3.jpg (3)

where Xp is the expression level at the parental node p and tip is the length of the branch separating i from its parent p. Each of these moments contains a contribution from the ancestral gene expression level that decays at a rate given by the strength of stabilizing selection α. For any two nodes i and j

graphic file with name mst190m4.jpg (4)

where Xa is the expression level at the most recent common ancestor of i and j and lij denotes the set of all nodes in the lineage of Xi not in the lineage of Xj. Similar to equations (2) and (3), the covariance of any two nodes is determined by the variance at the common ancestor and decays exponentially over the time the nodes have evolved independently since divergence, with a rate given by the strength of stabilizing selection.

The states of the OU processes at the terminal taxa (i.e., species expression levels) are distributed as a multivariate normal as described in equations (2)–(4). The likelihood function under such a specified OU model can be easily computed, enabling the use of maximum likelihood methods to estimate parameter values. Similarly, given a phylogeny and parameter values, the distribution of expression levels obtained according to the multivariate normal and data can be simulated.

Expression Levels in Individuals

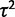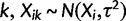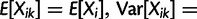
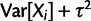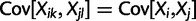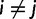In the species variance method, Inline graphic confounds all sources of individual variance (e.g., technical, environmental) into one parameter. Formally, at any species node i and individual Inline graphic, so that Inline graphic Inline graphic, and Inline graphic where Inline graphic.

Supplementary Material

Supplementary figures S1–S7 and tables S1 and S2 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).

Supplementary Data
supp_31_1_201__index.html (1.1KB, html)

Acknowledgments

The authors are immensely grateful to the individuals whose tissue samples were used in this study, without which none of this work would be possible. The authors also thank Mehmet Somel for his thoughtful discussions and anonymous reviewers for their helpful suggestions. This work was supported in part by National Institutes of Health grant 2R14003229-07 and National Science Foundation award 1103767. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  1. Albert F, Somel M, Carneiro M, et al. (14 co-authors) A comparison of brain gene expression levels in domesticated and wild animals. PLoS Genet. 2012;8:e1002962. doi: 10.1371/journal.pgen.1002962. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bedford T, Hartl D. Optimization of gene expression by natural selection. Proc Natl Acad Sci U S A. 2008;106:1133–1138. doi: 10.1073/pnas.0812009106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Blekhman R, Marioni J, Zumbo P, Stephens M, Gilad Y. Sex-specific and lineage-specific alternative splicing in primates. Genome Res. 2010;20:180–189. doi: 10.1101/gr.099226.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Blekhman R, Oshlack A, Chabot A, Smyth G, Gilad Y. Gene regulation in primates evolves under tissue-specific selection pressures. PLoS Genet. 2008;4:e1000271. doi: 10.1371/journal.pgen.1000271. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brawand D, Soumillon M, Necsulea A, et al. (18 co-authors) The evolution of gene expression levels in mammalian organs. Nature. 2011;478:343–348. doi: 10.1038/nature10532. [DOI] [PubMed] [Google Scholar]
  6. Butler M, King A. Phylogenetic comparative analysis: a modeling approach for adaptive evolution. Am Nat. 2004;164:683–695. doi: 10.1086/426002. [DOI] [PubMed] [Google Scholar]
  7. Chaix R, Somel M, Kreil D, Khaitovich P, Lunter G. Evolution of primate gene expression: drift and corrective sweeps? Genetics. 2008;180:1379–1389. doi: 10.1534/genetics.108.089623. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Egger G, Liang G, Aparicio A, Jones P. Epigenetics in human disease and prospects for epigenetic therapy. Nature. 2004;429:457–463. doi: 10.1038/nature02625. [DOI] [PubMed] [Google Scholar]
  9. Esteller M. Cancer epigenomics: DNA methylomes and histone-modification maps. Nat Rev Genet. 2007;8:286–298. doi: 10.1038/nrg2005. [DOI] [PubMed] [Google Scholar]
  10. Felsenstein J. Phylogenies and the comparative method. Am Nat. 1985;125:1–15. [Google Scholar]
  11. Felsenstein J. Phylogenies and quantitative characters. Annu Rev Ecol Syst. 1988;19:445–471. [Google Scholar]
  12. Felsenstein J. Comparative methods with sampling error and within-species variation: contrasts revisited and revised. Am Nat. 2008;171:713–725. doi: 10.1086/587525. [DOI] [PubMed] [Google Scholar]
  13. Gilad Y, Oshlack A, Rifkin S. Natural selection on gene expression. Trends Genet. 2006;22:456–461. doi: 10.1016/j.tig.2006.06.002. [DOI] [PubMed] [Google Scholar]
  14. Gilad Y, Oshlack A, Smyth GK, Speed TP, White KP. Expression profiling in primates reveals a rapid evolution of human transcription factors. Nature. 2006;440:242–245. doi: 10.1038/nature04559. [DOI] [PubMed] [Google Scholar]
  15. Gruber J, Vogel K, Kalay G, Wittkipp P. Contrasting properties of gene-specific regulatory, coding, and copy number mutations in Saccromyces cerevisiae: frequency, effects and dominance. PLOS Genet. 2012;8:e1002497. doi: 10.1371/journal.pgen.1002497. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Gu X. Statistical framework for phylogenomic analysis of gene family expression profiles. Genetics. 2004;167:531–542. doi: 10.1534/genetics.167.1.531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hansen T. Stabilizing selection and the comparative analysis of adaptation. Evolution. 1997;51:1341–1351. doi: 10.1111/j.1558-5646.1997.tb01457.x. [DOI] [PubMed] [Google Scholar]
  18. Hansen T, Bartoszek K. Interpreting the evolutionary regressions: the interplay between observational and biological errors in phylogenetic comparative studies. Syst Biol. 2012;61:413–425. doi: 10.1093/sysbio/syr122. [DOI] [PubMed] [Google Scholar]
  19. Hansen T, Pienaar J, Orzack S. A comparative method for studying adaptation to a randomly evolving environment. Evolution. 2008;62:1965–1977. doi: 10.1111/j.1558-5646.2008.00412.x. [DOI] [PubMed] [Google Scholar]
  20. Hsieh W, Chu T, Wolfinger R, Gibson G. Mixed-model reanalysis of primate data suggests tissue and species biases in oligonucleotide-based gene expression profiles. Genetics. 2003;165:747–757. doi: 10.1093/genetics/165.2.747. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Idaghdour Y, Czika W, Shianna K, et al. (11 co-authors) Geographical genomics of human leukocyte gene expression variation in southern Morocco. Nat Genet. 2010;42:62–67. doi: 10.1038/ng.495. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Ives A, Midford P, Garland T. Within-species variation and measurement error in phylogenetic comparative methods. Syst Biol. 2007;56:252–270. doi: 10.1080/10635150701313830. [DOI] [PubMed] [Google Scholar]
  23. Johnstone S, Baylin S. Stress and the epigenetic landscape: a link to the pathobiology of human diseases? Nat Rev Genet. 2010;11:806–812. doi: 10.1038/nrg2881. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kalinka A, Varga K, Gerrard D, Preibisch S, Corcoran D, Jarrells J, Ohler U, Bergman C, Tomancak P. Gene expression divergence recapitulates the developmental hourglass model. Nature. 2010;468:811–816. doi: 10.1038/nature09634. [DOI] [PubMed] [Google Scholar]
  25. Khaitovich P, Enard W, Lachmann M, Pääbo S. Evolution of primate gene expression. Nat Rev Genet. 2006;7:693–702. doi: 10.1038/nrg1940. [DOI] [PubMed] [Google Scholar]
  26. Khaitovich P, Pääbo S, Weiss G. Towards a neutral evolutionary model of gene expression. Genetics. 2005;170:929–939. doi: 10.1534/genetics.104.037135. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Khaitovich P, Weiss G, Lachmann M, Hellmann I, Enard W, Muetzel B, Wirkner U, Ansorge W, Pääbo S. A neutral model of transcriptome evolution. PLoS Biol. 2004a;2:e132. doi: 10.1371/journal.pbio.0020132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Khaitovich P, Muetzel B, She X, et al. (15 co-authors) Regional patterns of gene expression in human and chimpanzee brains. Genome Res. 2004b;14:1462–1473. doi: 10.1101/gr.2538704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. King M-C, Wilson A. Evolution at two levels in humans and chimpanzees. Science. 1975;188:107–116. doi: 10.1126/science.1090005. [DOI] [PubMed] [Google Scholar]
  30. Kleinjan D, van Heyningen V. Long-range control of gene expression: emerging mechanisms and disruption in disease. Am J Hum Genet. 2005;76:8–32. doi: 10.1086/426833. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lande R, Arnold SJ. Measurement of selection on correlated characters. Evolution. 1983;37:1210–1226. doi: 10.1111/j.1558-5646.1983.tb00236.x. [DOI] [PubMed] [Google Scholar]
  32. Lemos B, Meiklejohn CD, Cceres M, Hartl DL. Rates of divergence in gene expression profiles of primates, mice, and flies: stabilizing selection and variability among functional categories. Evolution. 2005;59:126–137. [PubMed] [Google Scholar]
  33. Lynch M. Methods for the analysis of comparative data in evolutionary biology. Evolution. 1991;45:1065–1080. doi: 10.1111/j.1558-5646.1991.tb04375.x. [DOI] [PubMed] [Google Scholar]
  34. Lynch M, Hill W. Phenotypic evolution by neutral mutation. Evolution. 1986;40:915–935. doi: 10.1111/j.1558-5646.1986.tb00561.x. [DOI] [PubMed] [Google Scholar]
  35. Marioni J, Mason C, Mane S, Stephens M, Gilad Y. RNA-seq: an assessment of technical reproducibility and comparison with gene expression arrays. Genome Res. 2008;18:1509–1517. doi: 10.1101/gr.079558.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mortazavi A, Williams B, McCue K, Schaeffer L, Wold B. Mapping and quantifying mammalian transcriptomes by RNA-seq. Nat Methods. 2008;5:621–628. doi: 10.1038/nmeth.1226. [DOI] [PubMed] [Google Scholar]
  37. Nielsen R, Bustamante C, Clark A, et al. (13 co-authors) Molecular signatures of natural selection. PLoS Biol. 2005;3:e170. [Google Scholar]
  38. Nuzhdin S, Wayne M, Harmon K, McIntyre L. Common pattern of evolution of gene expression level and protein sequence in Drosophila. Mol Biol Evol. 2004;21:1308–1317. doi: 10.1093/molbev/msh128. [DOI] [PubMed] [Google Scholar]
  39. Oakley T, Gu Z, Abouheif E, Patel N, Li W. Comparative methods for the analysis of gene-expression evolution: an example of using yeast functional genomic data. Mol Biol Evol. 2005;22:40–50. doi: 10.1093/molbev/msh257. [DOI] [PubMed] [Google Scholar]
  40. Perry G, Melsted P, Marioni J, et al. (12 co-authors) Comparative RNA sequencing reveals substantial genetic variation in endangered primates. Genome Res. 2012;22:602–610. doi: 10.1101/gr.130468.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pickrell J, Marioni J, Pai A, Degner J, Engelhardt B, Nkadori E, Veyrieras J-B, Stephens M, Gilad Y, Pritchard J. Understanding mechanisms underlying human gene expression variation with RNA sequencing. Nature. 2010;464:768–772. doi: 10.1038/nature08872. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Price A, Helgason A, Thorleifsson G, McCarroll S, Kong A, Stefansson K. Single-tissue and cross-tissue heritability of gene expression via identity-by-descent in related or unrelated individuals. PLoS Genet. 2011;7:e1001317. doi: 10.1371/journal.pgen.1001317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Rifkin S, Kim J, White K. Evolution of gene expression in the Drosophila melanogaster subgroup. Nat Genet. 2003;33:138–144. doi: 10.1038/ng1086. [DOI] [PubMed] [Google Scholar]
  44. Schroder K, Irvine KM, Taylor MS, et al. (25 co-authors) Conservation and divergence in toll-like receptor 4-regulated gene expression in primary human versus mouse macrophages. Proc Natl Acad Sci U S A. 2012;109:E944–E953. doi: 10.1073/pnas.1110156109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Somel M, Franz H, Yan Z, et al. (15 co-authors) Transcriptional neoteny in the human brain. Proc Natl Acad Sci U S A. 2009;106:5743–5748. doi: 10.1073/pnas.0900544106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Staubach F, Teschke M, Voolstra CR, Wolf JB, Tautz D. A test of the neutral model of expression change in natural populations of house mouse subspecies. Evolution. 2010;64:549–560. doi: 10.1111/j.1558-5646.2009.00818.x. [DOI] [PubMed] [Google Scholar]
  47. Trapnell C, Williams B, Pertea G, Mortazavi A, Kwan G, van Baren M, Salzberg S, Wold BJ, Pachter L. Transcript assembly and quantification by RNA-Seq reveals unannotated transcripts and isoform switching during cell differentiation. Nat Biotechnol. 2010;28:511–515. doi: 10.1038/nbt.1621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Wang Z, Gerstein M, Snyder M. RNA-Seq: a revolutionary tool for transcriptomics. Nat Rev Genet. 2009;10:57–63. doi: 10.1038/nrg2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Warnefors M, Eyre-Walker A. A selection index for gene expression evolution and its application to the divergence between humans and chimpanzees. PLoS One. 2012;7:e34935. doi: 10.1371/journal.pone.0034935. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Whitehead A, Crawford D. Variation within and among species in gene expression: raw material for evolution. Mol Ecol. 2006;15:1197–1211. doi: 10.1111/j.1365-294X.2006.02868.x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_31_1_201__index.html (1.1KB, html)
supp_mst190_sup.pdf (104.9KB, pdf)

Articles from Molecular Biology and Evolution are provided here courtesy of Oxford University Press

RESOURCES