Abstract
The ratio of divergence at nonsynonymous and synonymous sites, dN/dS, is a widely used measure in evolutionary genetic studies to investigate the extent to which selection modulates gene sequence evolution. Originally tailored to codon sequences of distantly related lineages, dN/dS represents the ratio of fixed nonsynonymous to synonymous differences. The impact of ancestral and lineage-specific polymorphisms on dN/dS, which we here show to be substantial for closely related lineages, is generally neglected in estimation techniques of dN/dS. To address this issue, we formulate a codon model that is firmly anchored in population genetic theory, derive analytical expressions for the dN/dS measure by Poisson random field approximation in a Markovian framework and validate the derivations by simulations. In good agreement, simulations and analytical derivations demonstrate that dN/dS is biased by polymorphisms at short time scales and that it can take substantial time for the expected value to settle at its time limit where only fixed differences are considered. We further show that in any attempt to estimate the dN/dS ratio from empirical data the effect of the intrinsic fluctuations of a ratio of stochastic variables, can even under neutrality yield extreme values of dN/dS at short time scales or in regions of low mutation rate. Taken together, our results have significant implications for the interpretation of dN/dS estimates, the McDonald–Kreitman test and other related statistics, in particular for closely related lineages.
Keywords: population genetics of dN/dS, codon evolution, genomic signatures of natural selection, Poisson random field approximation
Introduction
The extent to which selection promotes evolutionary change has long been a key question in the evolutionary sciences. Although at the phenotypic level the importance of selection is widely recognized, its role in modulating evolution at the molecular level remains debated (Nei et al. 2010). One popular indicator of selection acting on protein-coding DNA sequences is the dN/dS ratio. Because of its alleged simplicity and intuitive appeal, this measure has a strong tradition in evolutionary research, notably for the identification of genes with a history of positive selection (Nielsen 2005). In short, the dN/dS ratio quantifies the mode and strength of selection by comparing synonymous substitution rates (dS)—assumed to be neutral—with nonsynonymous substitution rates (dN), which are exposed to selection as they change the amino acid composition of a protein. Unity of the ratio is generally taken to indicate neutrality, values exceeding unity are interpreted as selection promoting change (positive selection), and values less than one are usually taken as an indication for selection suppressing protein change (purifying selection).
Originally the dN/dS ratio was developed in a phylogenetics context, and its estimation was based on codon sequences of distantly related lineages, where it is reasonable to assume that dN/dS represents the ratio of fixed nonsynonymous to synonymous differences between lineages (Miyata et al. 1980; Li et al. 1985; Nei and Gojobori 1986; Goldman and Yang 1994; Muse and Gaut 1994). The dN/dS ratio can then be approximated as a deterministic function of population size N and the selection coefficient s (Nielsen and Yang 2003; Kryazhimskiy and Plotkin 2008). However, recent empirical (Wolf et al. 2009) and theoretical work (Kryazhimskiy and Plotkin 2008; Peterson and Masel 2009) has challenged whether dN/dS appropriately reflects the outcome of selection across all relevant evolutionary time scales. As soon as we leave the realm of phylogenetics where single stereotypic genomes are compared and enter the realm of population genetics, the dN/dS ratio is no longer based on only fixed nonsynonymous versus synonymous differences. Segregating polymorphisms can substantially alter estimates of divergence and consequently estimates of dN/dS (Peterson and Masel 2009; Charlesworth 2010). As a consequence, both recently arisen lineage-specific variants as well as shared ancestral polymorphisms need to be taken into account. Kryazhimskiy and Plotkin (2008) theoretically investigated the two most extreme cases in timescale considering 1) the pure phylogenetics context, where the dN/dS ratio is based on fixed differences between distantly related lineages and 2) the pure population genetics context, where the dN/dS ratio is based on segregating polymorphisms within one panmictic population of conspecific individuals. In a phylogenetics context, codon evolution is modeled as a Markov process, which indirectly assumes that fixation of a mutation in the population occurs instantaneously (Goldman and Yang 1994; Muse and Gaut 1994). In a population genetics context, simulations of sequence evolution in the presence of selection are often based on Wright–Fisher sampling (Wright 1931). Under the assumptions that 1) codons evolve independently of each other under free recombination, and 2) polymorphic codon positions are not allowed to mutate further, allowing for a maximum biallelic state, the Markov model of codon evolution can be viewed as a time limit of a Wright–Fisher population process. That is, the jump rates of the Markov model of codon evolution can be interpreted in terms of the fixation probability of a Wright–Fisher population process with selection (Nielsen and Yang 2003). However, for closely related lineages the assumption that divergence time is large enough to view the Markov model of codon evolution as a time limit of a Wright–Fisher population process will be violated. This violation gives rise to a gap between pure population genetics and phylogenetic modeling approaches, neither of which can adequately capture the evolutionary relevant, temporal dynamics of the dN/dS ratio.
To fill this gap, we anchor the dN/dS ratio firmly in population genetics theory and develop a codon substitution model that allows us to describe the continuous dynamics of dN/dS across evolutionary time starting from a single panmictic population followed by a speciation event eventually resulting in deep phylogenetic divergence (fig. 1). We derive analytical expressions for the dN/dS measure in a Poisson Random Field framework integrating the relative contributions of ancestral polymorphisms, lineage-specific polymorphisms, and fixed differences through time. Our analysis shows under which evolutionary conditions, namely population size, selection coefficient, and mutation rate, polymorphisms influence the expectation for dN/dS at any given time point after speciation. The comprehensive mathematical description of dN/dS based on a ratio of stochastic variables further allows to estimate the associated variation and reveals that for recently diverged lineages stochastic forces acting on dN/dS are not negligible. In that, we provide a null model making apparent the inherent biases in the estimation of dN/dS generating false positive inference in the study of adaptive evolution. The results do not merely affect estimation of the dN/dS ratio itself, but are of likewise importance for related statistics such as the McDonald–Kreitman test (McDonald and Kreitman 1991) or the α-estimate (Smith and Eyre-Walker 2002). We finally advocate that a combination of divergence and polymorphism data be used to estimate true dN/dS ratios and associated confidence intervals for closely related lineages, something that appears to be feasible in light of the current progress in sequencing technology.
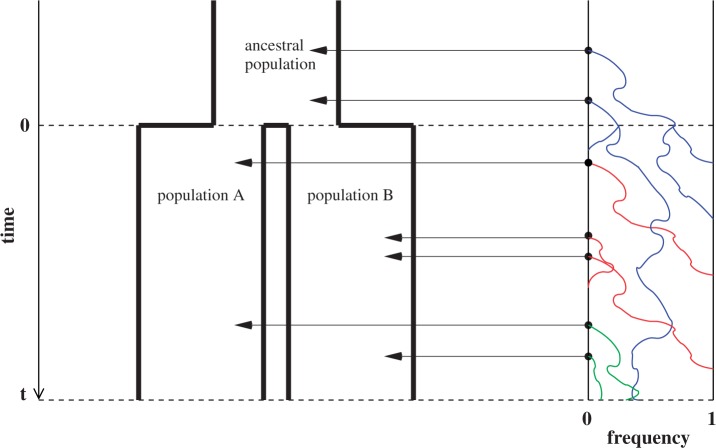
Fig. 1.
Scheme of the evolutionary model—Speciation occurs instantaneously at time 0 and the two populations evolve separately and do not interbreed until present time t. Mutations are depicted by black dots in the right part of the graph, where the arrows from right to left point to the population in which the mutation happened. The right part of the graph shows the path to absorption (fixation or extinction) of these mutations. The blue lines show paths of mutations that occurred before speciation, where paths evolve separately after speciation (ancestral polymorphism). At time 0, these mutations constitute shared polymorphisms. The red lines show paths to absorption of lineage-specific mutations that occurred and got absorbed in one of the two populations between 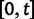 (fixed differences). The green lines show paths of lineage-specific mutations, which at present time t are still segregating in the respective population (lineage-specific polymorphism).
(fixed differences). The green lines show paths of lineage-specific mutations, which at present time t are still segregating in the respective population (lineage-specific polymorphism).
Results
Review of the Classical Definition of dN/dS
Over long time scales, selection is generally inferred from evolutionary change between divergent lineages that arose after a distant population split or speciation event. Each lineage is then represented by one stereotypic genome sequence, where sequence comparison allows quantifying evolutionary change at orthologous positions. Here, protein-coding sequences offer the great possibility that they allow to contrast nonsynonymous and synonymous changes, which yields intuitive insight into the mode and strength of selection. The problem of estimating the strength of selection then essentially becomes a problem of estimating substitution rates for two classes of changes. This has been addressed by two sets of methods, heuristic counting methods (Miyata et al. 1980; Nei and Gojobori 1986) and maximum likelihood based approaches (Goldman and Yang 1994; Muse and Gaut 1994), the latter modeling the substitution process as a continuous-time Markov process with 61 possible states corresponding to the 61 sense codons. Under an infinite sites model and under the assumptions of free recombination and instantaneous fixation of novel mutations, dN/dS can be recaptured based on Kimura’s expression for the probability of fixation of newly arising variants of frequency 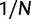 (Sawyer and Hartl 1992). To apply Kimura’s expression for the probability of fixation under a finite sites model, we have to make the additional assumption that polymorphic codon positions are not allowed to mutate further, such that there are never more than two alleles segregating at the same codon position (Nielsen and Yang 2003). It is then considered that synonymous mutations evolve in the population under neutral reproduction. Nonsynonymous mutations are influenced by selective forces in such a way that the fitness of the ancestral to the derived alleles are 1 to
(Sawyer and Hartl 1992). To apply Kimura’s expression for the probability of fixation under a finite sites model, we have to make the additional assumption that polymorphic codon positions are not allowed to mutate further, such that there are never more than two alleles segregating at the same codon position (Nielsen and Yang 2003). It is then considered that synonymous mutations evolve in the population under neutral reproduction. Nonsynonymous mutations are influenced by selective forces in such a way that the fitness of the ancestral to the derived alleles are 1 to 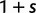 , where all nonsynonymous mutations have the same selection coefficient. Each time a derived allele becomes fixed fitness is reassigned such that the derived allele is considered as the new ancestral state and fitness is set to 1. The fitness of any potential new mutation (including back mutation) is set to
, where all nonsynonymous mutations have the same selection coefficient. Each time a derived allele becomes fixed fitness is reassigned such that the derived allele is considered as the new ancestral state and fitness is set to 1. The fitness of any potential new mutation (including back mutation) is set to 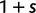 . Under this model, selection acts as a mechanism which promotes (
. Under this model, selection acts as a mechanism which promotes (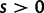 ) or prevents (
) or prevents (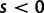 ) changes of codons involving amino acid replacements, and does not represent a preference for or against specific codon types (for discussion see Nielsen and Yang [2003]). If the chance of an immediate back mutation is small enough to be neglected, then for nonsynonymous mutations the fixation probability is given by (Kimura 1962),
) changes of codons involving amino acid replacements, and does not represent a preference for or against specific codon types (for discussion see Nielsen and Yang [2003]). If the chance of an immediate back mutation is small enough to be neglected, then for nonsynonymous mutations the fixation probability is given by (Kimura 1962),
| (1) |
where N is the (effective) population size, s is the selection coefficient, and 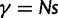 is the population-scaled selection coefficient. By taking
is the population-scaled selection coefficient. By taking 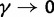 , we recover the neutral case of a synonymous mutation, for which the probability that a novel mutation gets fixed in the population is
, we recover the neutral case of a synonymous mutation, for which the probability that a novel mutation gets fixed in the population is 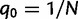 . Note that derivations of the probability of fixation are based on a haploid population of size N. Under the assumption of additive fitness effects in a diploid organism, these derivations are equivalent to a diploid population of size
. Note that derivations of the probability of fixation are based on a haploid population of size N. Under the assumption of additive fitness effects in a diploid organism, these derivations are equivalent to a diploid population of size 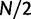 . The expected numbers of nonsynonymous and synonymous substitutions per generation scale with
. The expected numbers of nonsynonymous and synonymous substitutions per generation scale with 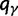 and q0, and hence dN/dS is interpreted as the ratio of these given by
and q0, and hence dN/dS is interpreted as the ratio of these given by
| (2) |
Here, 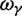 corresponds to the ω typically estimated from data using software packages such as PAML (Yang 2007). One objection to bear in mind is that fixation effects were assumed to be instantaneous, where sequence divergence is equal to the number of mutations that occurred and got fixed between two populations after population split. In practice, however, the sequence divergence of two populations is measured based on the number of differences observed at divergence time t between two sequences each sampled from one of the two distinct populations. Thus, in addition to mutations that occurred and got fixed after population split also shared ancestral and newly arisen lineage-specific polymorphisms will contribute to the total divergence (fig. 1).
corresponds to the ω typically estimated from data using software packages such as PAML (Yang 2007). One objection to bear in mind is that fixation effects were assumed to be instantaneous, where sequence divergence is equal to the number of mutations that occurred and got fixed between two populations after population split. In practice, however, the sequence divergence of two populations is measured based on the number of differences observed at divergence time t between two sequences each sampled from one of the two distinct populations. Thus, in addition to mutations that occurred and got fixed after population split also shared ancestral and newly arisen lineage-specific polymorphisms will contribute to the total divergence (fig. 1).
Definition of dN/dS in a Population Genetics-Phylogenetics Framework
We will now drop the assumption of instantaneous fixation and formulate an explicit codon substitution model that allows to describe the expectation of nonsynonymous and synonymous divergence at any point in time. Following the standard approach, dN/dS is derived from amino acid sequence divergence between two divergent lineages (or populations). We make the simplifying assumption that speciation follows an isolation-without-migration model as illustrated in figure 1. We thus consider two independent populations both of size N where each element is a sequence of L codons or 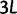 nucleotide sites. Let t denote the population-scaled evolutionary divergence time between the two populations at present time, where Nt generations have passed since population divergence time at t = 0. Mutation events occur at a rate
nucleotide sites. Let t denote the population-scaled evolutionary divergence time between the two populations at present time, where Nt generations have passed since population divergence time at t = 0. Mutation events occur at a rate 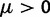 per individual (nucleotide) site and generation. Whenever a nucleotide is hit by mutation, a target nucleotide is chosen according to a
per individual (nucleotide) site and generation. Whenever a nucleotide is hit by mutation, a target nucleotide is chosen according to a 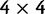 Markov chain transition probability matrix
Markov chain transition probability matrix 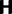 . Note that
. Note that 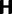 can be viewed as any commonly used nucleotide substitution model, such as the Jukes–Cantor model. The fate in the population of this newly introduced derived type nucleotide over subsequent generations is extinction or fixation, determined by a standard Wright–Fisher reproduction mechanism, which furthermore distinguishes between nonsynonymous and synonymous changes. We assume that codons evolve independently (free recombination) and that μ is sufficiently small to allow for a scenario where each new mutation will only affect monomorphic codon sites. Hence, in this model, codon sites will be at most biallelic.
can be viewed as any commonly used nucleotide substitution model, such as the Jukes–Cantor model. The fate in the population of this newly introduced derived type nucleotide over subsequent generations is extinction or fixation, determined by a standard Wright–Fisher reproduction mechanism, which furthermore distinguishes between nonsynonymous and synonymous changes. We assume that codons evolve independently (free recombination) and that μ is sufficiently small to allow for a scenario where each new mutation will only affect monomorphic codon sites. Hence, in this model, codon sites will be at most biallelic.
In each polymorphic site, the pair of ancestral and derived codon will be either synonymous or nonsynonymous. Mutations leading to synonymous changes evolve in the population under neutral reproduction, whereas mutations leading to nonsynonymous changes are influenced by selection such that the fitness of the ancestral to the derived alleles are 1 to 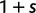 . Following practice in much of the population genetics literature including theoretical studies of dN/dS (Sawyer and Hartl 1992), we consider the diffusion approximation scaling regime of large N and small s, where the population-scaled selection coefficient
. Following practice in much of the population genetics literature including theoretical studies of dN/dS (Sawyer and Hartl 1992), we consider the diffusion approximation scaling regime of large N and small s, where the population-scaled selection coefficient 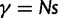 reflects the total (signed) selection pressure per site and generation. Similarly, the constant
reflects the total (signed) selection pressure per site and generation. Similarly, the constant 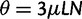 measures total mutation pressure per codon sequence and generation. In the Materials and Methods, we show that based on the fundamental parameters
measures total mutation pressure per codon sequence and generation. In the Materials and Methods, we show that based on the fundamental parameters 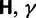 , and θ together with the knowledge of the genetic code, it is possible in the framework of our model to derive the proportions of mutation events leading to synonymous and nonsynonymous codon pairs. Hence, we can write
, and θ together with the knowledge of the genetic code, it is possible in the framework of our model to derive the proportions of mutation events leading to synonymous and nonsynonymous codon pairs. Hence, we can write
to distinguish synonymous and nonsynonymous changes, as well as sorting out an intensity 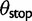 for events that lead to stop codons.
for events that lead to stop codons.
Now, to obtain dN/dS, we consider the sequence divergence between two sequences sampled from two distinct populations or lineages. Sequence divergence can be split into the two contributions of nonsynonymous and synonymous divergence and their ratio can be used to quantify the impact of selection acting on the entire coding sequence. To this end, we let  denote nonsynonymous divergence and
denote nonsynonymous divergence and  synonymous divergence at time t, and write
synonymous divergence at time t, and write 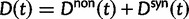 for the total divergence. Sequence divergence should naturally be proportional to sequence length and increase over time essentially with the same rate as that of substitutions occurring in either population from the time of population split and onward. This is indeed a property of our model, in which
for the total divergence. Sequence divergence should naturally be proportional to sequence length and increase over time essentially with the same rate as that of substitutions occurring in either population from the time of population split and onward. This is indeed a property of our model, in which  and
and 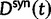 are independent and have approximate Poisson distributions with expected values
are independent and have approximate Poisson distributions with expected values
where 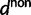 and
and 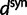 are functions of γ and t. The factor 2 arises from the fact that we consider divergence between two populations.
are functions of γ and t. The factor 2 arises from the fact that we consider divergence between two populations.
As a first measure of dN/dS we take the ratio of expected values
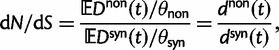 |
(3) |
where the normalization by  and
and 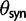 accounts for the difference in mutation pressure for nonsynonymous and synonymous changes, respectively. The ratio in equation (3) represents a measure of the average rates of nonsynonymous to synonymous divergence. Similar to previous work (Rocha et al. 2006; Kryazhimskiy and Plotkin 2008; Peterson and Masel 2009), our aim is to understand the relation between dN/dS and natural selection as a function of evolutionary time. Our contribution here is to provide more detailed expressions than reported earlier for
accounts for the difference in mutation pressure for nonsynonymous and synonymous changes, respectively. The ratio in equation (3) represents a measure of the average rates of nonsynonymous to synonymous divergence. Similar to previous work (Rocha et al. 2006; Kryazhimskiy and Plotkin 2008; Peterson and Masel 2009), our aim is to understand the relation between dN/dS and natural selection as a function of evolutionary time. Our contribution here is to provide more detailed expressions than reported earlier for 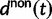 and
and 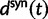 across all relevant evolutionary timescales with special attention to small t. At the same time, we are cautious about the use of equation (3) as a single dN/dS measure. After all, upon accepting the underlying model assumption that divergence is the result of random sampling from random populations of random sequences, it is restrictive in the end to only compare two expected values. To initiate a discussion of alternative measures of dN/dS, perhaps more suitable to reflect the various fluctuations involved, we will compare in the next subsection the ratio of the expected values
across all relevant evolutionary timescales with special attention to small t. At the same time, we are cautious about the use of equation (3) as a single dN/dS measure. After all, upon accepting the underlying model assumption that divergence is the result of random sampling from random populations of random sequences, it is restrictive in the end to only compare two expected values. To initiate a discussion of alternative measures of dN/dS, perhaps more suitable to reflect the various fluctuations involved, we will compare in the next subsection the ratio of the expected values 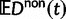 and
and 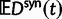 in equation (3) with the expected value of the ratio of the independent random variables
in equation (3) with the expected value of the ratio of the independent random variables  and
and 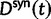 , see equation (7) later.
, see equation (7) later.
To incorporate the contribution of polymorphism and thus expand the classical definition of dN/dS we consider three levels of mathematical modeling which are described in detail in the Materials and Methods. In short, we begin with a full codon substitution model (the phylogenetics component) embedded in a population genetics framework represented by a discrete Markov chain. Because of the complexity of the model, analytical insight is limited. In a second step, we therefore resort to an analytically more tractable continuous time approximation. This allows us to find the codon equilibrium distribution and to extract the typical rates of synonymous and nonsynonymous mutations. For standard mutation models, the latter can be derived explicitly. Finally, in a third step, we argue that key properties including the rate of divergence over time are captured well by approximate Poisson distributions. This approach is reminiscent of the Poisson’s random fields model, which has been used for similar purposes earlier (Sawyer and Hartl 1992). The main assumptions for the model parameters are that N and L are both large while the ratio 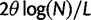 , which represents the fraction of polymorphic sites in the sequence, is kept sufficiently small. From this, we derive detailed results for the dN/dS ratio, in particular with regards to dependence on the selection parameter γ and divergence time t.
, which represents the fraction of polymorphic sites in the sequence, is kept sufficiently small. From this, we derive detailed results for the dN/dS ratio, in particular with regards to dependence on the selection parameter γ and divergence time t.
As a consequence of the Poisson approximation, we can treat nonsynonymous as well as synonymous divergence as the sum of three independent Poisson distributed components, arising from divergence due to fixation of new mutations since population divergence, lineage-specific polymorphisms, and shared ancestral polymorphisms. This basically corresponds to sampling two sequences, one sequence from each population, aligning them and counting the number of synonymous and nonsynonymous differences. We then distinguish three cases how these differences could have arrived. First, we distinguish mutations which occurred before or after population split. Second, for mutations that occurred after population split we make the further distinction whether the mutant is already fixed in its population or still segregating. The first case of mutations, which occurred before population split, are referred to as ancestral divergence (blue lines in fig. 1). Fixed differences due to mutations that occurred after population split are referred to as fixed divergence (red lines in fig. 1). Finally, mutations, which occurred after population split and are still segregating, are referred to as polymorphic divergence (green lines in fig. 1). Accordingly, the mean divergence splits into three types of contributions, and we can write
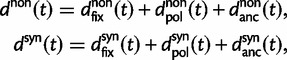 |
(4) |
where 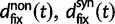 represent divergence due to fixation of new mutations since population divergence,
represent divergence due to fixation of new mutations since population divergence, 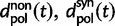 are contributions from sampling of lineage-specific polymorphic sites, and
are contributions from sampling of lineage-specific polymorphic sites, and 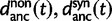 take into account the effect of ancestral polymorphisms which existed at t = 0. In the Materials and Methods, we present in detail approximation formulas for all of these, using three auxiliary functions which we denote by
take into account the effect of ancestral polymorphisms which existed at t = 0. In the Materials and Methods, we present in detail approximation formulas for all of these, using three auxiliary functions which we denote by 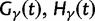 , and
, and 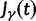 , Briefly,
, Briefly, 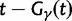 scales with the average number of fixations up to time t and
scales with the average number of fixations up to time t and 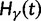 scales with the average number of lineage-specific polymorphisms that get sampled for its derived allele at time t, in both cases referring to mutations that occurred after population split. The function
scales with the average number of lineage-specific polymorphisms that get sampled for its derived allele at time t, in both cases referring to mutations that occurred after population split. The function 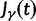 scales with the average number of sampled differences at t, which originate from mutations in the ancestral population.
scales with the average number of sampled differences at t, which originate from mutations in the ancestral population.
With time-explicit derivations of all terms in equation (4) established, we may sum up the expected divergence from each contribution, be it ancestral, polymorphic, or fixed, and compare nonsynonymous and synonymous terms, writing
| (5) |
The asymptotic limits are given by 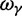 as
as 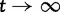 and by
and by 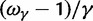 as
as  .
.
To help interpret the various contributions in equation (5), we proceed to look at the separate dN/dS ratios for each type, which we denote by 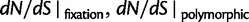 , and
, and 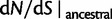 . The ratio
. The ratio 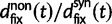 is insensitive to t and quickly converges to
is insensitive to t and quickly converges to 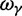 with increasing t. Hence, in agreement with equation (3), the contribution to dN/dS due to fixations of lineage-specific mutations is
with increasing t. Hence, in agreement with equation (3), the contribution to dN/dS due to fixations of lineage-specific mutations is
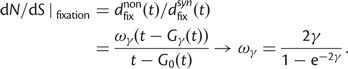 |
The slight deviation of 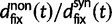 from
from 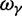 is essentially due to our definition of fixed differences, which are based on lineage-specific mutations only. In fact, fixed differences could arise due to lineage-specific mutations as well as due to shared ancestral polymorphisms. However, once the sum of the various distributions to divergence estimates is computed (as in
is essentially due to our definition of fixed differences, which are based on lineage-specific mutations only. In fact, fixed differences could arise due to lineage-specific mutations as well as due to shared ancestral polymorphisms. However, once the sum of the various distributions to divergence estimates is computed (as in 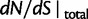 ), both kinds of fixed differences are considered. For divergence attributed to lineage-specific polymorphisms, we find that
), both kinds of fixed differences are considered. For divergence attributed to lineage-specific polymorphisms, we find that 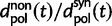 , which equals 1 at t = 0, quickly approaches a limiting value
, which equals 1 at t = 0, quickly approaches a limiting value 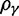 , such that
, such that
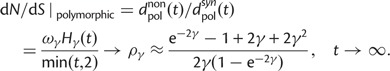 |
Finally, the ancestral contribution as time evolves has a limiting ratio 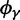 such that
such that
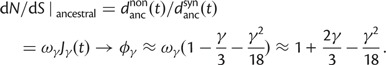 |
At t = 0, the ancestral ratio takes into account the effect of selection when we sample two individuals from the single population, which forms the common ancestry at population split. In equation (26) of the Materials and Methods, we show that 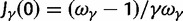 , so that we have the initial ratio
, so that we have the initial ratio
| (6) |
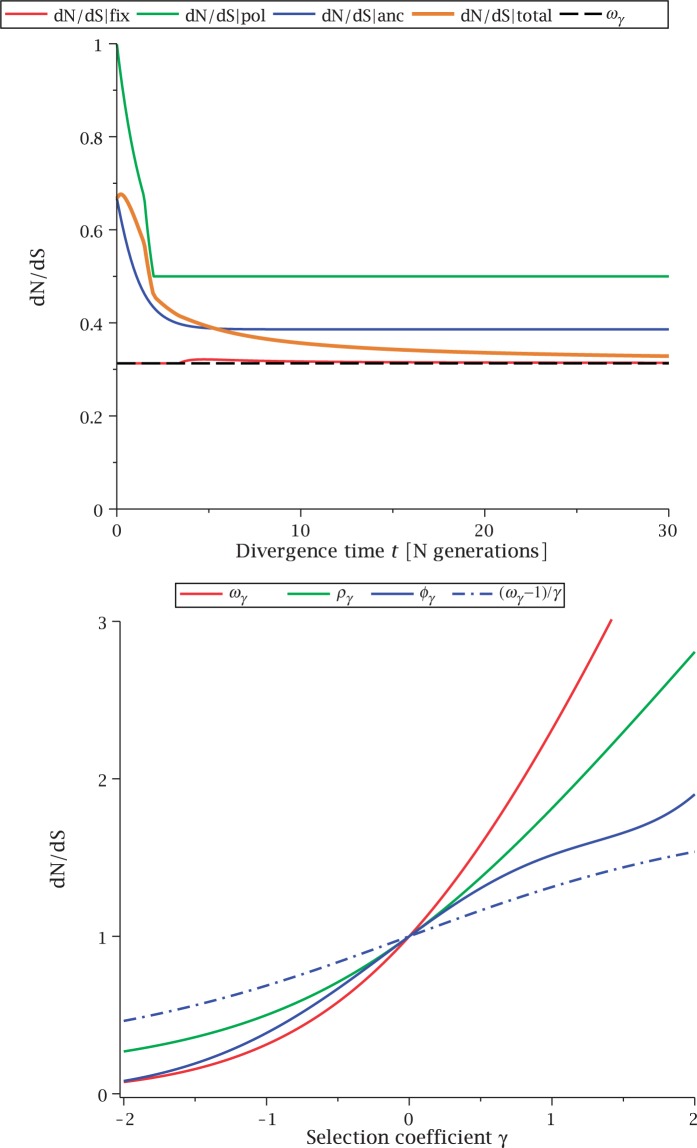
The time dependence of the various ratios is illustrated in the top panel of figure 2 for 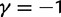 . The three separate ratios
. The three separate ratios  are plotted together with the ratio of total expectations
are plotted together with the ratio of total expectations 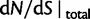 , as well as the limiting value
, as well as the limiting value 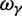 . In the bottom panel of figure 2, the limiting long time ratios
. In the bottom panel of figure 2, the limiting long time ratios 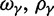 , and
, and 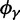 as well as the initial ancestral contribution
as well as the initial ancestral contribution 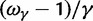 are plotted together as functions of γ.
are plotted together as functions of γ.
Fig. 2.
(Top) dN/dS ratios for fixation (red), polymorphic (green), ancestral (blue), and total (gold line) divergence for 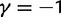 as a function of divergence time t; (bottom) the limiting values
as a function of divergence time t; (bottom) the limiting values 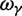 for
for 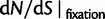 (red),
(red), 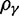 for
for 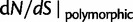 (green),
(green), 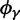 for
for 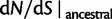 (solid blue), and the initial ancestral contribution
(solid blue), and the initial ancestral contribution 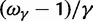 (dashed blue) as a function of γ.
(dashed blue) as a function of γ.
The interesting observation is that when combining the effects of all three contributions by forming 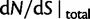 , the ancestral and polymorphic divergence influence the total divergence ratio over a substantial time period before settling down at
, the ancestral and polymorphic divergence influence the total divergence ratio over a substantial time period before settling down at 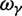 . With an increasing number of fixation events and hence actual lineage-specific nucleotide substitutions building up differences between the two populations over a considerable time span, it is of course the rate of linear increase in
. With an increasing number of fixation events and hence actual lineage-specific nucleotide substitutions building up differences between the two populations over a considerable time span, it is of course the rate of linear increase in 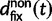 in comparison with that of
in comparison with that of 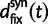 , which will ultimately decide the asymptotic dN/dS ratio. But as evident in figure 2, ancestral and lineage-specific polymorphisms which also generate differences between the observed sequences seek out their own preferred balance of nonsynonymous to synonymous change. As long as ancestral and polymorphic differences measure up on the scale of fixations, the limiting numbers
, which will ultimately decide the asymptotic dN/dS ratio. But as evident in figure 2, ancestral and lineage-specific polymorphisms which also generate differences between the observed sequences seek out their own preferred balance of nonsynonymous to synonymous change. As long as ancestral and polymorphic differences measure up on the scale of fixations, the limiting numbers 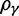 and
and 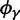 influence the total ratio. The ancestral initial value, which is manifestly different from
influence the total ratio. The ancestral initial value, which is manifestly different from  , ensures that the transition to fixation asymptotics is clearly visible on the evolutionary time scale. In summary, this clearly indicates that, indeed, dN/dS is naturally a function of time. For the case
, ensures that the transition to fixation asymptotics is clearly visible on the evolutionary time scale. In summary, this clearly indicates that, indeed, dN/dS is naturally a function of time. For the case 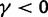 of negative selection, dN/dS decreases from its initial ratio
of negative selection, dN/dS decreases from its initial ratio 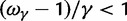 to
to 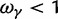 . If
. If 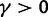 , then dN/dS increases from its initial ratio
, then dN/dS increases from its initial ratio 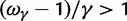 to
to 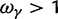 . Figure 3 illustrates the time dependence of
. Figure 3 illustrates the time dependence of 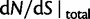 for five values of γ.
for five values of γ.
Fig. 3.
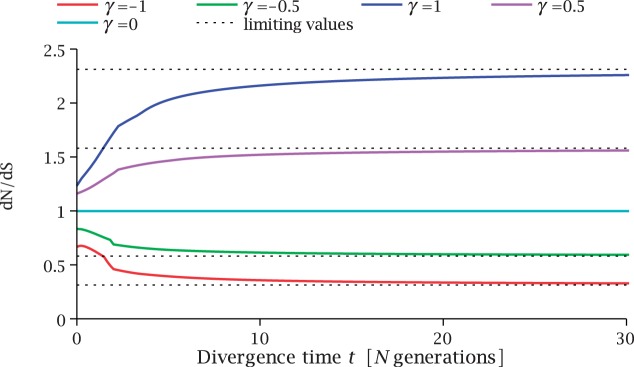
Total dN/dS-ratios for the five values 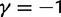 (red line),
(red line), 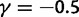 (green line),
(green line), 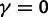 (turquoise line),
(turquoise line), 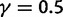 (purple line), and
(purple line), and 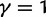 (blue line).
(blue line).
We conclude this section with additional remarks on the relation of our results to previous results in the literature. The work of Kryazhimskiy and Plotkin (2008) is concerned with the relationship between selection and dN/dS values measured from two sequences sampled from a single population. In this situation, differences between the sequences reflect segregating polymorphisms and not fixed differences. The authors offer a theoretical foundation of the dN/dS ratio for single population data and demonstrate that the frequent use of equation (2) in the context of intraspecific sequence data lacks proper justification and is inappropriate. The desired dN/dS ratio addressed in (Kryazhimskiy and Plotkin 2008) is closely related to 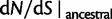 at t = 0 in our model, that is, the dN/dS ratio based on two sequences sampled from a single (ancestral) population existing prior to speciation. In fact, the initial ratio found to be
at t = 0 in our model, that is, the dN/dS ratio based on two sequences sampled from a single (ancestral) population existing prior to speciation. In fact, the initial ratio found to be 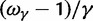 in equation (6) is a stationary dN/dS ratio for sequences sampled in a single population. However, the corresponding quantity
in equation (6) is a stationary dN/dS ratio for sequences sampled in a single population. However, the corresponding quantity 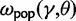 obtained in (Kryazhimskiy and Plotkin 2008), equation (5), depends not only on γ but also on θ. This fact can be traced back to the derivation of
obtained in (Kryazhimskiy and Plotkin 2008), equation (5), depends not only on γ but also on θ. This fact can be traced back to the derivation of 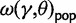 , which is based on a Wright–Fisher approximation that allows for back and forth mutations during the segregating phase, further assuming that θ is sufficiently small. It is then natural to interpret the
, which is based on a Wright–Fisher approximation that allows for back and forth mutations during the segregating phase, further assuming that θ is sufficiently small. It is then natural to interpret the 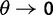 limit of
limit of 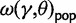 as a generic dN/dS ratio within populations, and straightforward to check that
as a generic dN/dS ratio within populations, and straightforward to check that 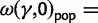
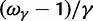 in complete agreement with equation (6).
in complete agreement with equation (6).
The work by Sawyer and Hartl (1992) form the theoretical basis for the McDonald–Kreitman test (McDonald and Kreitman 1991). These authors provide sampling formulas for fixed nonsynonymous and synonymous differences and for nonsynonymous and synonymous polymorphisms in a model setting, which is rather close to the model advocated in the present work. Regarding mutations, our rates 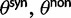 , which are derived from the codon substitution model, can be considered equivalent to the mutation rate parameters
, which are derived from the codon substitution model, can be considered equivalent to the mutation rate parameters 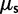 and
and 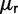 used by Sawyer and Hartl. Turning to the expected number of fixed differences Sawyer and Hartl assume linearity in time, whereas we get refined expressions for the number of fixed differences as we distinguish between fixed differences originated from shared ancestral polymorphisms and fixed differences originated from lineage-specific mutations. Our expressions are
used by Sawyer and Hartl. Turning to the expected number of fixed differences Sawyer and Hartl assume linearity in time, whereas we get refined expressions for the number of fixed differences as we distinguish between fixed differences originated from shared ancestral polymorphisms and fixed differences originated from lineage-specific mutations. Our expressions are 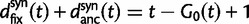 and
and 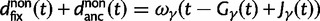 compared with t and
compared with t and 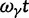 in (Sawyer and Hartl 1992), equation (13). However, the assumption of linearity in time is well justified for distantly related lineages and critical only for closely related lineages, where ancestral fixed differences measure up on the scale of lineage-specific fixed differences. Turning to the sampling formulas for nonsynonymous and synonymous polymorphisms Sawyer and Hartl consider arbitrary samples of size n and m from two species. In our settings,
in (Sawyer and Hartl 1992), equation (13). However, the assumption of linearity in time is well justified for distantly related lineages and critical only for closely related lineages, where ancestral fixed differences measure up on the scale of lineage-specific fixed differences. Turning to the sampling formulas for nonsynonymous and synonymous polymorphisms Sawyer and Hartl consider arbitrary samples of size n and m from two species. In our settings, 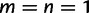 as typical in phylogenetic approaches. Their results (Sawyer and Hartl 1992), equations (17) and (18), with m = 1 correspond to
as typical in phylogenetic approaches. Their results (Sawyer and Hartl 1992), equations (17) and (18), with m = 1 correspond to
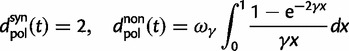 |
where we derive the time dependent functions 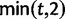 and
and  , see equations (21) and (22). The differences between our results and the results by Sawyer and Hartl arise from the fact that Sawyer and Hartl assume that the number of lineage-specific segregating sites has reached its equilibrium. Although this assumption is well justified for distantly related lineages, it is clearly violated for more closely related lineages. Our results better capture the reality of divergence between evolutionary young lineages, and converge to the results by Sawyer and Hartl for
, see equations (21) and (22). The differences between our results and the results by Sawyer and Hartl arise from the fact that Sawyer and Hartl assume that the number of lineage-specific segregating sites has reached its equilibrium. Although this assumption is well justified for distantly related lineages, it is clearly violated for more closely related lineages. Our results better capture the reality of divergence between evolutionary young lineages, and converge to the results by Sawyer and Hartl for  .
.
Statistical Properties of dN/dS
The previous section has treated the time dependence of the dN/dS ratio, measured as the ratio of expected values of two independent Poisson random variables. However, when the ratio of nonsynonymous to synonymous divergence is estimated from sequence data, we in fact do not know their expected values but rather carry out single observations of  and
and 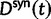 and consider the ratio of these. Regardless of the estimation procedure, for example, counting methods or maximum likelihood approaches, an estimation based on sequence data will always just reflect a single observation or measurement. This is important to notice, as the ratio of expected values is in general not equal to the expected value of a ratio. We are therefore interested in the statistical properties of the expected value of a ratio of two Poisson random variables rather than in a ratio of expected values. Proper statistical inference therefore must take into account the natural fluctuations of such a ratio of random variables. This leads us to studying the ratio of nonsynonymous to synonymous divergence in a population genetics framework as the scaled ratio of Poisson variables
and consider the ratio of these. Regardless of the estimation procedure, for example, counting methods or maximum likelihood approaches, an estimation based on sequence data will always just reflect a single observation or measurement. This is important to notice, as the ratio of expected values is in general not equal to the expected value of a ratio. We are therefore interested in the statistical properties of the expected value of a ratio of two Poisson random variables rather than in a ratio of expected values. Proper statistical inference therefore must take into account the natural fluctuations of such a ratio of random variables. This leads us to studying the ratio of nonsynonymous to synonymous divergence in a population genetics framework as the scaled ratio of Poisson variables
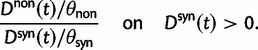 |
Thus, we define a new measure of dN/dS as the conditional expectation
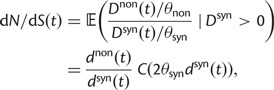 |
(7) |
which is based on a series approximation of the expected value of a ratio of two random variables. In the Materials and Methods, we introduce function C (eq. 28) and provide a detailed derivation of equation (7) and show that this function can be easily computed numerically. Note, however, that unlike the ratio  depends on the mutation pressure θ. In the limit
depends on the mutation pressure θ. In the limit 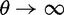 (which could be reached by an infinitely long codon sequence
(which could be reached by an infinitely long codon sequence 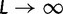 ), we recover the previous ratio of expected values, as
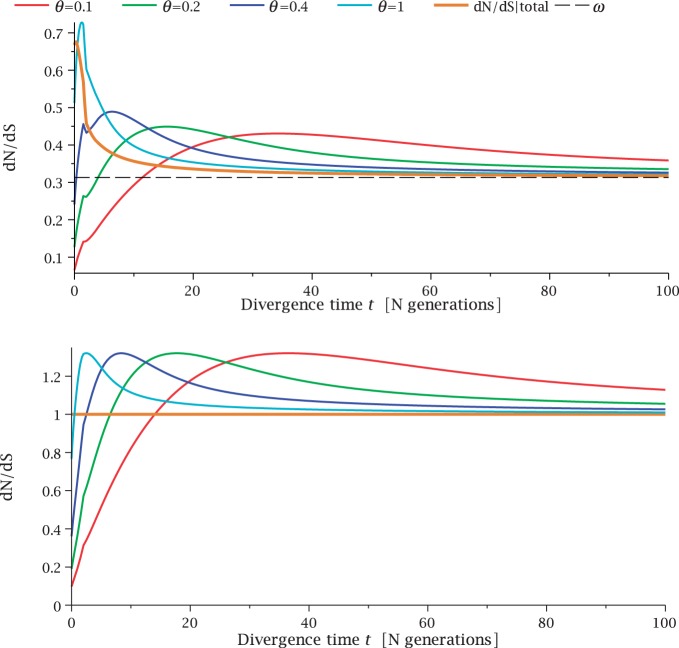
), we recover the previous ratio of expected values, as 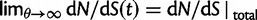 . To visualize the difference between the two measures, the upper panel of figure 4 illustrates the general shape of the curve
. To visualize the difference between the two measures, the upper panel of figure 4 illustrates the general shape of the curve 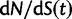 up to time t = 100 after population split for the case
up to time t = 100 after population split for the case 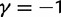 with the Jukes–Cantor mutation model and four different values of θ. Also shown in the same graph is
with the Jukes–Cantor mutation model and four different values of θ. Also shown in the same graph is 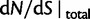 , that is, the ratio of expectations
, that is, the ratio of expectations 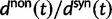 , and the limit
, and the limit 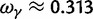 as
as 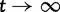 . The distinct change in appearance of the dN/dS curves with varying values of θ is somewhat similar to what the effect would be of changing the time scale from t to
. The distinct change in appearance of the dN/dS curves with varying values of θ is somewhat similar to what the effect would be of changing the time scale from t to 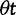 . Of course this comes natural since lowering the overall mutation pressure in the model would cause the system to run on a slower time scale. It is important to note that the striking deviation in figure 4 of the expected ratio
. Of course this comes natural since lowering the overall mutation pressure in the model would cause the system to run on a slower time scale. It is important to note that the striking deviation in figure 4 of the expected ratio 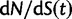 from the ratio of expectations
from the ratio of expectations 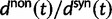 , is not directly an effect of the selection mechanism. On the contrary, the lower panel of figure 4 shows the corresponding set of curves for the neutral case
, is not directly an effect of the selection mechanism. On the contrary, the lower panel of figure 4 shows the corresponding set of curves for the neutral case 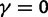 for which we have
for which we have 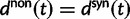 .
.
Fig. 4.
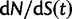 for θ equal to 0.1 (red), 0.2 (green), 0.4 (blue), 1 (cyan) compared with the ratio
for θ equal to 0.1 (red), 0.2 (green), 0.4 (blue), 1 (cyan) compared with the ratio 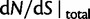 (gold). (Top)
(gold). (Top) 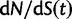 for
for 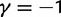 and (bottom)
and (bottom) 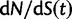 for
for 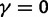 . The limiting value
. The limiting value 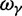 is indicated by the dashed black line, which in the lower panel is identical to unity and hidden by the golden line.
is indicated by the dashed black line, which in the lower panel is identical to unity and hidden by the golden line.
To provide insight into the shape of the dN/dS curves and their intrinsic random variations, we further estimate upper and lower confidence bands 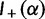 and
and 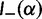 for dN/dS defined as a ratio of two Poisson random variables, such that
for dN/dS defined as a ratio of two Poisson random variables, such that
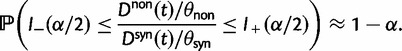 |
In the Materials and Methods, we obtain
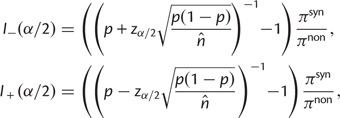 |
(8) |
where 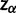 is the α-quantile of the standard normal distribution,
is the α-quantile of the standard normal distribution, 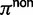 and
and 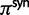 represent the proportion of nonsynonymous and synonymous changes, respectively, and
represent the proportion of nonsynonymous and synonymous changes, respectively, and
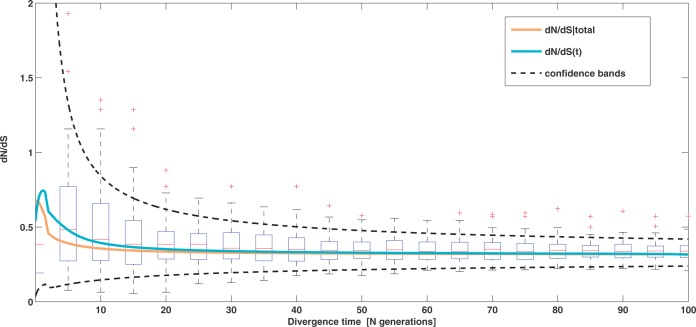
To cross-validate these derivations, we next explore the variation in dN/dS by 100 independent simulation runs with parameter settings 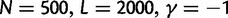 , and
, and 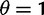 . We keep track of the precise numbers of nonsynonymous and synonymous differences between two populations from population split at t = 0 up to evolutionary time t = 100, and then plot the ratio of these differences at a resolution of every
. We keep track of the precise numbers of nonsynonymous and synonymous differences between two populations from population split at t = 0 up to evolutionary time t = 100, and then plot the ratio of these differences at a resolution of every 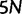 generations. The distribution and stochastic fluctuations in
generations. The distribution and stochastic fluctuations in 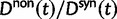 are visualized in figure 5. Also shown in figure 5 are
are visualized in figure 5. Also shown in figure 5 are 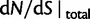 , the dN/dS-ratio in equation (7) as well as the shape of the confidence bands (eq. 8). The confidence bands represent a 5% chance of seeing larger fluctuations at a specific point in time and do not provide joint confidence for the entire function over time. For the present simulation of 100 runs, 14.3% of the data points fell outside of the region between upper and lower bands, where 9.7% fell above the upper band and 4.6% below the lower band. Moreover, note that during initial divergence extremely high dN/dS values that would be commonly taken as evidence for positive selection are frequently obtained even under negative selection pressure.
, the dN/dS-ratio in equation (7) as well as the shape of the confidence bands (eq. 8). The confidence bands represent a 5% chance of seeing larger fluctuations at a specific point in time and do not provide joint confidence for the entire function over time. For the present simulation of 100 runs, 14.3% of the data points fell outside of the region between upper and lower bands, where 9.7% fell above the upper band and 4.6% below the lower band. Moreover, note that during initial divergence extremely high dN/dS values that would be commonly taken as evidence for positive selection are frequently obtained even under negative selection pressure.
Fig. 5.
Joint simulated dN/dS for two populations with N = 500 and L = 2,000 shown from population split at t = 0 up to evolutionary time t = 100, with an accumulated ancestral population since 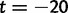 . Selection and mutation pressure are set to
. Selection and mutation pressure are set to 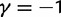 and
and 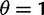 . Also shown in the graph are
. Also shown in the graph are 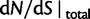 (golden), the dN/dS-ratio in (7) (cyan) and confidence bands given by (8) (black dashed lines).
(golden), the dN/dS-ratio in (7) (cyan) and confidence bands given by (8) (black dashed lines).
Discussion
Value and Limitations of the Model
The standard phylogenetic model of codon evolution and the estimation of dN/dS was introduced in a pure phylogenetics context in 1994 by two independent publications (Goldman and Yang 1994; Muse and Gaut 1994). The observations that dN/dS can be influenced by mutation rate (Wyckoff et al. 2005), branch length (Wolf et al. 2009), and polymorphisms motivated theoretical studies on the temporal dynamics of the measure. We here pick three previous studies of relevance and briefly discuss them in relation to our current approach. The first study by Rocha et al. (2006) describes the time dependence of dN/dS for closely related taxa, starting with a clonal population which over time becomes more diverse. As in our modeling approach their simulation study applies Wright–Fisher sampling in a population of fixed size where each generation is subject to mutation. However, instead of incorporating a full codon model each mutation is simply set to be synonymous with probability 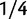 and nonsynonymous with probability
and nonsynonymous with probability 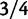 . The number of synonymous mutations is assumed to increase linearly in time, while nonsynonymous mutations are sampled with a selective weight. Importantly, the number of accumulated nonsynonymous mutations is assumed to reach a limiting value over time which means that possible fixations are not taken into account. Although this may not be critical for short time periods, for long timescales this leads to the inappropriate property that
. The number of synonymous mutations is assumed to increase linearly in time, while nonsynonymous mutations are sampled with a selective weight. Importantly, the number of accumulated nonsynonymous mutations is assumed to reach a limiting value over time which means that possible fixations are not taken into account. Although this may not be critical for short time periods, for long timescales this leads to the inappropriate property that 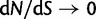 as
as 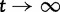 . Another model developed for similar purposes by Peterson and Masel (2009), is refined in several ways. As in our study, Peterson and Masel consider divergence between two populations after population split from a common ancestor and derive estimates of the expected divergence as function of divergence time. They include the effects of recent fixations and shared ancestral polymorphisms, but neglect the effect of lineage-specific polymorphisms. Their study was motivated by earlier studies on the effect of ancestral polymorphisms on estimates of mutation rate for closely related lineages, related to the apparent mutation rate acceleration (Ho and Larson 2006; Balbi and Feil 2007). A third study closely related to ours is the study by Kryazhimskiy and Plotkin (2008). Their emphasis is on the comparison of two extreme cases, where dN/dS is estimated from sequences of 1) conspecific individuals and 2) distantly related lineages. We expand on their approach as we study the continuous transition between these two cases. Ideally, our description of dN/dS would show the same initial value as the one described by Kryazhimskiy and Plotkin for conspecific individuals. At first glance, this is not the case. Kryazhimskiy and Plotkin use a mutation model that allows for back and forth mutation between the ancestral and the derived allele during the time of segregation, which in the setting of codon evolution seems to be inappropriate and yields different results. However, if we no longer allow for back and forth mutation by letting
. Another model developed for similar purposes by Peterson and Masel (2009), is refined in several ways. As in our study, Peterson and Masel consider divergence between two populations after population split from a common ancestor and derive estimates of the expected divergence as function of divergence time. They include the effects of recent fixations and shared ancestral polymorphisms, but neglect the effect of lineage-specific polymorphisms. Their study was motivated by earlier studies on the effect of ancestral polymorphisms on estimates of mutation rate for closely related lineages, related to the apparent mutation rate acceleration (Ho and Larson 2006; Balbi and Feil 2007). A third study closely related to ours is the study by Kryazhimskiy and Plotkin (2008). Their emphasis is on the comparison of two extreme cases, where dN/dS is estimated from sequences of 1) conspecific individuals and 2) distantly related lineages. We expand on their approach as we study the continuous transition between these two cases. Ideally, our description of dN/dS would show the same initial value as the one described by Kryazhimskiy and Plotkin for conspecific individuals. At first glance, this is not the case. Kryazhimskiy and Plotkin use a mutation model that allows for back and forth mutation between the ancestral and the derived allele during the time of segregation, which in the setting of codon evolution seems to be inappropriate and yields different results. However, if we no longer allow for back and forth mutation by letting 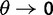 in Kryazhimskiy and Plotkin, their dN/dS measure converges to our measure based on a single population prior to speciation. Hence our analysis of dN/dS with regards to the single population prior to speciation is consistent with that of Kryazhimskiy and Plotkin for conspecific individuals not allowing for back and forth mutations. The second extreme case investigated by Kryazhimskiy and Plotkin also reflecting the classical definition of dN/dS as introduced in the pure phylogenetics context (Goldman and Yang 1994; Muse and Gaut 1994) is in full agreement with our description of the limiting value of dN/dS for
in Kryazhimskiy and Plotkin, their dN/dS measure converges to our measure based on a single population prior to speciation. Hence our analysis of dN/dS with regards to the single population prior to speciation is consistent with that of Kryazhimskiy and Plotkin for conspecific individuals not allowing for back and forth mutations. The second extreme case investigated by Kryazhimskiy and Plotkin also reflecting the classical definition of dN/dS as introduced in the pure phylogenetics context (Goldman and Yang 1994; Muse and Gaut 1994) is in full agreement with our description of the limiting value of dN/dS for 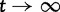 .
.
A further novelty of our work in comparison with Rocha et al. (2006), Peterson and Masel (2009), Kryazhimskiy and Plotkin (2008), or any other study investigating the temporal dynamics of dN/dS, is that we incorporate a full codon substitution matrix into our model, and consider selection for or against changes in the codon sequence. This is in contrast to the other works where estimates of dN/dS are based on a comparison of sites evolving under selective pressure versus neutrally evolving sites. The slightly more complicated, population genetic Markov model of codon sequence evolution seems a natural choice as it closely mimics biological reality. Moreover, our model allows to capture the dynamics of dN/dS at any point in time and expands its inferential value beyond mere phylogenetic considerations. In addition, the incorporation of a nucleotide substitution matrix and the resulting codon substitution matrix in a Markovian framework, should make it possible to specifically consider processes such as GC-biased gene conversion that are known to mimic the signature of selection (Berglund et al. 2009). Several other expansions of our model are conceivable. For its basic formulation, we restricted our model to instantaneous speciation not allowing for the occurrence of gene flow during the onset of divergence. We expect that under such an isolation-with-migration scenario the bias introduced by polymorphisms will extend for even longer times and would certainly be worth exploring. Besides, other less stringent model assumptions such as site-specific variation in selection strength or selection on synonymous changes via codon usage bias might be relevant to consider.
Implications for Empirical Evolutionary Genetics Studies
The dN/dS measure is commonly used to 1) disclose evolutionary processes across species (Wright and Andolfatto 2008; Ellegren 2009) or 2) to identify genes under positive selection for an evolutionary lineage of interest (Clark et al. 2003; Bustamante et al. 2005). We here demonstrated that dN/dS is biased for the comparison of evolutionary young lineages when using the standard (phylogenetic) model. Is this time dependence of dN/dS at all relevant for the paramater space empirical work is generally dealing with? Let us first consider the former case, where genome-wide mean dN/dS is used as a proxy for average selection pressure in specific lineages that are then related to life history traits of remnant species (Nikolaev et al. 2007; Wright and Andolfatto 2008). According to our model, we expect a clear upward bias of dN/dS estimates for short branches, as has been indicated by empirical evidence (Wolf et al. 2009). As branch length and life history traits such as body size or generation time are known to covary (Gillooly et al. 2005; Bromham 2009), this artifact may lead to erroneous conclusions. But how closely do lineages need to be related for this to be of concern? Let us consider the case of human–chimp divergence as an example. For a realistic value of 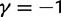 and considering a large enough sequence length L that dN/dS can be approximated by the ratio of expected values, our results suggest that dN/dS is on average upward biased by approximately 46% 2 Ne generations after speciation, and still by approximately 14% 10 Ne generations after the split. Assuming 5 million years for the split time between human and chimp from a common ancestor, an overall generation time of 20 years for the human lineage and a minimum effective population size of 14,000, we obtain an estimated time to the most common recent ancestor of approximately 18 Ne generations. At first sight, this suggests only a mild contribution of polymorphisms to dN/dS of the human lineage. Eighteen Ne generations, however, are an overestimate for two reasons. First, ancestral population sizes have been larger than current human effective population size. Assuming an average effective population size of
and considering a large enough sequence length L that dN/dS can be approximated by the ratio of expected values, our results suggest that dN/dS is on average upward biased by approximately 46% 2 Ne generations after speciation, and still by approximately 14% 10 Ne generations after the split. Assuming 5 million years for the split time between human and chimp from a common ancestor, an overall generation time of 20 years for the human lineage and a minimum effective population size of 14,000, we obtain an estimated time to the most common recent ancestor of approximately 18 Ne generations. At first sight, this suggests only a mild contribution of polymorphisms to dN/dS of the human lineage. Eighteen Ne generations, however, are an overestimate for two reasons. First, ancestral population sizes have been larger than current human effective population size. Assuming an average effective population size of 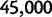 (Prüfer et al. 2012) split time would be 5 Ne rather than 18 Ne generations, which falls squarely within the critical range of an upward biased dN/dS. Second, our model does not allow for migration after speciation, which will extend the influence of polymorphisms over longer time frames. These considerations are qualitatively consistent with evidence from Prüfer et al. (2012) suggesting that approximately 3% of genetic variation in the human genome are cases of incomplete lineage sorting with respect to bonobo or chimp. We thus conclude that for human–chimp and lineages with similar or even shorter divergence histories, polymorphisms are an issue and need to be considered for correct inference of selection pressure. With some knowledge on divergence time and effective population sizes, our model can in principle be used to rescale dN/dS accordingly and correct for the bias.
(Prüfer et al. 2012) split time would be 5 Ne rather than 18 Ne generations, which falls squarely within the critical range of an upward biased dN/dS. Second, our model does not allow for migration after speciation, which will extend the influence of polymorphisms over longer time frames. These considerations are qualitatively consistent with evidence from Prüfer et al. (2012) suggesting that approximately 3% of genetic variation in the human genome are cases of incomplete lineage sorting with respect to bonobo or chimp. We thus conclude that for human–chimp and lineages with similar or even shorter divergence histories, polymorphisms are an issue and need to be considered for correct inference of selection pressure. With some knowledge on divergence time and effective population sizes, our model can in principle be used to rescale dN/dS accordingly and correct for the bias.
The second, more prominent application of dN/dS is the quest for genes under positive selection in specific lineages. Naturally, much effort has been devoted to isolate the genes (or gene classes) under adaptive selection in the human lineage (Clark et al. 2003; Bustamante et al. 2005). Within the context of our model, we can only discuss potential implications for approaches inferring selection for genes, and do not consider possible time dependencies of models inferring selection for single codon sites. Positive selection on genes or functional subsets of genes is generally inferred by comparing the likelihood of dN/dS being larger than in a neutral or nearly neutral scenario (Nielsen and Yang 1998) making use of software applications such as PAML that are based on the continuous Markov process with instantaneous fixation described earlier. These likelihood-based approaches used for inference on selection do not incorporate the contribution of ancestral or lineage-specific polymorphism and we may expect increased false positive detection for evolutionary young lineages, and, in particular, for genes where polymorphic sites substantially contribute to divergence. Judging from our results, we may predict which genes will be most severely affected. Looking at the per-gene level, we cannot any longer assume sequence length L to be large enough that dN/dS can be approximated by the ratio of expected values. Instead, we have to look at the statistical properties of the ratio of two Poisson random variables. Here, our results suggest that estimates of dN/dS will in particular be biased by polymorphisms if 1) the mutation pressure is low or 2) sequence length is short. Moreover, not only the expected value of dN/dS tends to be biased for such genes but also the random error or the intrinsic fluctuations in the estimate are particularly strong for the same set of genes, as indicated by wide confidence bands at shorter time scales. As a consequence the interpretation of dN/dS needs caution, and likelihood ratio tests are necessary to account for the random error. However, likelihood ratio tests can only account for the random error, but not for the systematic bias in the expected value caused by polymorphisms. This bias is expected to be strongest in genes with low divergence, which can either be due to recent divergence time, low mutation pressure, or short sequence length. Hence, the systematic bias caused by polymorphisms may at least partly explain the common observation that genes with low divergence are preferably found to be under positive selection, as has been indicated previously (Wolf et al. 2009).
Future Perspectives
We have here introduced an analytical model to illustrate the time dependence of dN/dS and aspects of the effects of estimating dN/dS as a ratio of two Poisson random variables. Our approach expands existing models on codon evolution and integrates the contribution of polymorphisms to amino acid sequence divergence. Although not explicitly formulated for this purpose, we hope that our model may provide the basis for a refinement of the underlying theory of the widely used McDonald–Kreitman test and might improve the inference on the mode and strength of selection for closely related lineages by jointly using polymorphism and divergence data. The 1000 human genome project (1000 Genomes Project Consortium 2012) and emerging population genomic studies in genetic nonmodel organisms (Ellegren et al. 2012) demonstrate that the necessary population genomic data sets will soon be readily available for a growing number of species.
Materials and Methods
A Stochastic Model of Codon Evolution
In this section, we introduce a detailed population genetics Markov model of codon sequence evolution and use it for two main purposes. First, we find natural equilibrium rates of synonymous and nonsynonymous mutations and show how to obtain them from standard assumptions of nucleotide mutation. These rates provide a reference for the volume fractions of the two types of mutations among the polymorphic sites and represent in the model an estimate of the number of synonymous and nonsynonymous sites found in data. Our second main purpose of introducing the model is to keep a sufficiently detailed record of all polymorphic sites over time to later help analyzing the rate of divergence between two populations over time. It is crucial to distinguish the contributions to sequence divergence attributed to ancestral, polymorphic, and fixed differences. This is what will enable us to count synonymous and nonsynonymous divergence taking into account all three of these mechanisms and in the end to estimate dN/dS.
A single population consists of N individuals. Each individual is represented by a sequence of nucleotide sites of length 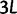 structured as L consecutive codon nucleotide triplets. Random mutation based on standard assumptions acts on each nucleotide in a triple and the genetic code allows us to distinguish synonymous and nonsynonymous mutations. The fate of a mutant allele is extinction or fixation determined by Wright–Fisher reproduction acting independently on the L sites with the 64 codon states at each site. Although new alleles which originate from synonymous codon transitions evolve under neutral conditions of population reproduction, the evolution of mutant codon alleles that are nonsynonymous with respect to the ancestral codon are affected by selective sampling. The chance to see two or more mutations at the same site overlap in time will be so small that for our purposes is justified to study the approximative biallelic model.
structured as L consecutive codon nucleotide triplets. Random mutation based on standard assumptions acts on each nucleotide in a triple and the genetic code allows us to distinguish synonymous and nonsynonymous mutations. The fate of a mutant allele is extinction or fixation determined by Wright–Fisher reproduction acting independently on the L sites with the 64 codon states at each site. Although new alleles which originate from synonymous codon transitions evolve under neutral conditions of population reproduction, the evolution of mutant codon alleles that are nonsynonymous with respect to the ancestral codon are affected by selective sampling. The chance to see two or more mutations at the same site overlap in time will be so small that for our purposes is justified to study the approximative biallelic model.
In the following, we will provide a detailed account of the assumptions for the codon mutation model and for reproduction with selection weights. This level of detail is necessary to introduce the appropriate notation and prepare for the analytical description of dN/dS through time.
A Markov Model for Codon Mutations
We begin by fixing the numbering of nucleotides 
 , T = 4 and an ordered list
, T = 4 and an ordered list 
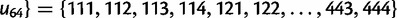 , which gives an enumeration of the 64 codon types. Here,
, which gives an enumeration of the 64 codon types. Here, 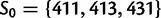 is the subset of stop codons. We write S for the remaining elements, the sense codons, so that
is the subset of stop codons. We write S for the remaining elements, the sense codons, so that 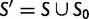 . By applying the biological code, we associate to each sense codon
. By applying the biological code, we associate to each sense codon 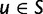 one of the 20 existing amino acids. The change of a nucleotide affects the first, second, or third position of the corresponding codon and causes a transition from the original codon to one of eight or nine possible target codons. If codon u changes to codon v in this manner the mutation is said to be synonymous if u and v are coding for the same amino acid and nonsynonymous if the amino acids are different. To record this information, we introduce for each pair of sense codons
one of the 20 existing amino acids. The change of a nucleotide affects the first, second, or third position of the corresponding codon and causes a transition from the original codon to one of eight or nine possible target codons. If codon u changes to codon v in this manner the mutation is said to be synonymous if u and v are coding for the same amino acid and nonsynonymous if the amino acids are different. To record this information, we introduce for each pair of sense codons 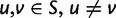 , the indicator variables
, the indicator variables
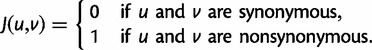 |
Mutations involving stop codons will happen with positive probability but will be regarded immediately extinct.
We assume that mutation occurs uniformly and independently over nucleotide sites with mutation rate 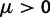 per site and per generation. Writing θ for the total mutation rate per generation, we have
per site and per generation. Writing θ for the total mutation rate per generation, we have 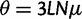 . A codon site is said to be clonal when all individuals share the same nucleotide triplet and is said to be polymorphic if not. For the type of model studied here, typically the number of polymorphic sites will be small in comparison with the length L and hence the number of polymorphic sites with more than two alleles will be even smaller. Applying the criteria that N is not too large in relation to L, see supplementary text equation (14) (Supplementary Material online), mutation is assumed to be suppressed in already polymorphic sites. Hence, all polymorphic sites are biallelic in the sense that one ancestral and one derived codon coexist with frequencies summing to one. Mutation is reactivated at extinction or fixation of the derived codon.
. A codon site is said to be clonal when all individuals share the same nucleotide triplet and is said to be polymorphic if not. For the type of model studied here, typically the number of polymorphic sites will be small in comparison with the length L and hence the number of polymorphic sites with more than two alleles will be even smaller. Applying the criteria that N is not too large in relation to L, see supplementary text equation (14) (Supplementary Material online), mutation is assumed to be suppressed in already polymorphic sites. Hence, all polymorphic sites are biallelic in the sense that one ancestral and one derived codon coexist with frequencies summing to one. Mutation is reactivated at extinction or fixation of the derived codon.
To find the rates of synonymous and nonsynonymous mutation events, we introduce a Markov chain of codon mutations. At the level of nucleotides, given that a mutation occurs at a site in one sequence of the population the nucleotide changes from i to j, 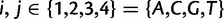 , according to a transition probability matrix
, according to a transition probability matrix 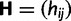 with zero diagonal elements, strictly positive nondiagonal elements and row sums equal to one. With probability one-third the affected site is the first, second, or third position of a codon. Thus, taking into account only one-site mutations, the nucleotide transitions in
with zero diagonal elements, strictly positive nondiagonal elements and row sums equal to one. With probability one-third the affected site is the first, second, or third position of a codon. Thus, taking into account only one-site mutations, the nucleotide transitions in  generate a corresponding Markov chain of codon mutations on the state space
generate a corresponding Markov chain of codon mutations on the state space  given by a
given by a 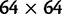 transition probability matrix
transition probability matrix 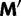 . Then to account for stop codons, we replace
. Then to account for stop codons, we replace 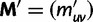 with the modified
with the modified  mutation probability matrix
mutation probability matrix 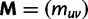 obtained by retaining all jumps to the states S0. More precisely, if
obtained by retaining all jumps to the states S0. More precisely, if 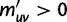 for some
for some 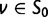 , we put
, we put 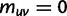 and
and 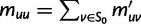 .
.
Now, we are in position to mark each mutation event synonymous, nonsynonymous, or stopped by decomposing the mutation matrix 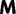 as
as
where 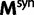 collects all nondiagonal elements muv for which the pair
collects all nondiagonal elements muv for which the pair 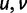 is synonymous (
is synonymous (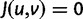 ), the elements of
), the elements of 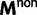 represent nonsynonymous changes (
represent nonsynonymous changes (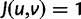 ) and
) and 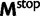 stores the diagonal elements
stores the diagonal elements 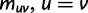 , of
, of 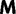 . Let
. Let  be a 64-column vector of only ones and let a and b denote the 64-column vectors
be a 64-column vector of only ones and let a and b denote the 64-column vectors
| (9) |
In these vectors, the kth elements ak and bk are the conditional probabilities to obtain synonymous and nonsynonymous derived codons, given that a mutation occurs in codon uk.
If we focus on a single codon site at a given generation, the chance to see a mutation is proportional to 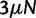 (which we may assume is much less than one). Hence, mutation events occur over time according to the transition probability matrix
(which we may assume is much less than one). Hence, mutation events occur over time according to the transition probability matrix 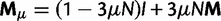 . Adding up the L sites of a sequence, it follows by independence of the mutation mechanism that the number of mutation events in a given generation is approximately Poisson distributed with mean θ. But only a small fraction of these events result in actual nucleotide substitutions, as we will see next by adding reproduction and selection to the model.
. Adding up the L sites of a sequence, it follows by independence of the mutation mechanism that the number of mutation events in a given generation is approximately Poisson distributed with mean θ. But only a small fraction of these events result in actual nucleotide substitutions, as we will see next by adding reproduction and selection to the model.
Discrete Time Wright–Fisher Model with Selection
For the reproductive dynamics of the model, we make the simplifying assumption that there is free recombination, that is, no linkage, between sites of a sequence. Each new generation is obtained from the previous generation by Wright–Fisher sampling acting on codons such that all codon sites develop independently of each other. Hence, a clonal site remains clonal until a newly mutated codon allele enters in one individual of the population. At this instance, the site becomes polymorphic and remains so over a period of time during which the frequency of the derived codon evolves according to a Wright–Fisher Markov chain until absorption. If the underlying mutation event is synonymous, then reproduction is neutral whereas if the mutation is nonsynonymous then the derived and ancestral codons are sampled with the selective weights 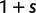 and 1, respectively. Typically, we consider selection to act deleteriously, prohibiting nonsynonymous changes by letting the selection parameter s be negative,
and 1, respectively. Typically, we consider selection to act deleteriously, prohibiting nonsynonymous changes by letting the selection parameter s be negative, 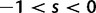 . This is, however, no restriction as the model covers positive selection,
. This is, however, no restriction as the model covers positive selection, 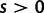 , as well. At the time of absorption, the site becomes clonal.
, as well. At the time of absorption, the site becomes clonal.
To summarize the dynamics of codon evolution in the population, we keep track of L triplets 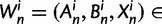
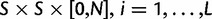 . In each generation
. In each generation 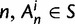 is the type of the ancestral codon at site
is the type of the ancestral codon at site 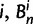 is the type of the derived codon if i is polymorphic and equal to
is the type of the derived codon if i is polymorphic and equal to 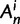 if i is clonal, and
if i is clonal, and 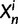 is the number of individuals with the derived codon allele at site i. By construction, the components
is the number of individuals with the derived codon allele at site i. By construction, the components 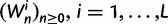 are independent and identically distributed discrete time Markov chains with state space
are independent and identically distributed discrete time Markov chains with state space 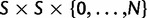 . The one-step transitions of the single codon site chain are as follows. For mutation, jumps
. The one-step transitions of the single codon site chain are as follows. For mutation, jumps 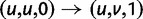 are governed by the transition matrix
are governed by the transition matrix 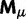 and occur with probability
and occur with probability 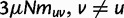 . For reproduction, we let Y denote a random variable with the binomial distribution Bin
. For reproduction, we let Y denote a random variable with the binomial distribution Bin 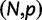 , where
, where 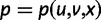 is the sampling probability
is the sampling probability
Then, the jumps and corresponding transition probabilities of Wright–Fisher sampling are given by
 |
Continuous Time Approximation of the Full Model
Next, we consider large population size N and apply to each discrete time single site Markov chain 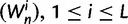 , the standard scheme of approximation
, the standard scheme of approximation 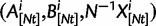 under the change of time and scale given by
under the change of time and scale given by
| (10) |
For the third component, it is well known that the derived allele frequency in the Wright–Fisher model with selection and no mutation converges as 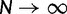 to a diffusion process with absorbing boundaries in 0 and 1 given by the solution of the stochastic differential equation
to a diffusion process with absorbing boundaries in 0 and 1 given by the solution of the stochastic differential equation
where 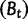 is Brownian motion. Here,
is Brownian motion. Here, 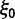 is the initial fraction of derived alleles. In our case
is the initial fraction of derived alleles. In our case  , which suggests that derived alleles would go extinct immediately. In our approach, however, the large population size scaling (eq. 10) is balanced against a total mutation intensity of order
, which suggests that derived alleles would go extinct immediately. In our approach, however, the large population size scaling (eq. 10) is balanced against a total mutation intensity of order 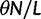 per codon site. Thus, we replace the frequency
per codon site. Thus, we replace the frequency 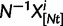 by a process
by a process 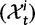 where each nonzero excursion follows a path of
where each nonzero excursion follows a path of  , with
, with 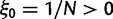 (the same approximation is used in Evans et al. [2007]). Then during the clonal periods, for which
(the same approximation is used in Evans et al. [2007]). Then during the clonal periods, for which  , the first two components in
, the first two components in  are continuous time Markov chains
are continuous time Markov chains 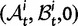 (forced to have
(forced to have 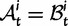 ) in holding until the next jump of
) in holding until the next jump of 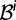 . As the jump probability per generation is
. As the jump probability per generation is 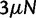 , it follows that the jump rate per N generations is
, it follows that the jump rate per N generations is 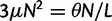 . Hence, the generator matrix of
. Hence, the generator matrix of 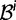 equals
equals 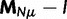 . Each jump of
. Each jump of 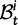 leaves
leaves 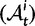 unaffected but initiates a diffusion path
unaffected but initiates a diffusion path 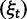 embedded in
embedded in 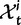 . If the faith of
. If the faith of 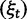 is extinction then
is extinction then 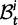 returns to its previous value stored in
returns to its previous value stored in 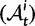 . If instead the path
. If instead the path 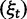 gets fixed then
gets fixed then 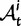 attains the current value of
attains the current value of 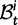 . More explicitly, we are approximating the discrete time Markov chain
. More explicitly, we are approximating the discrete time Markov chain 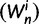 with a continuous time Markov process
with a continuous time Markov process 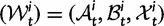 with state space
with state space 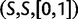 . The state space is a mixture of two jump coordinates and one continuous state coordinate and the process has the specific feature of holding and jumping from the boundary. We provide background information on diffusion processes with holding and jumping boundary in the supplementary text (Supplementary Material online). In our case, the boundary consists of all points
. The state space is a mixture of two jump coordinates and one continuous state coordinate and the process has the specific feature of holding and jumping from the boundary. We provide background information on diffusion processes with holding and jumping boundary in the supplementary text (Supplementary Material online). In our case, the boundary consists of all points 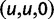 ,
, 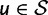 . If the current state of
. If the current state of  is
is  then after an exponential holding time of rate
then after an exponential holding time of rate 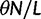 the process
the process 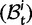 jumps to state v with probability muv. At the instance of such a jump
jumps to state v with probability muv. At the instance of such a jump 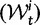 begins tracing a path of
begins tracing a path of 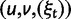 , with
, with
until time of absorption. If the absorption event is fixation, the process jumps to 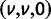 , if it is extinction, the jump is to
, if it is extinction, the jump is to 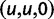 . Then again, the jump intensities apply until the next
. Then again, the jump intensities apply until the next 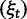 -excursion takes place, and so on. The summation measure process
-excursion takes place, and so on. The summation measure process
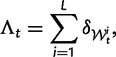 |
(11) |
now models the codon distribution in the entire sequence of length L across the population and over time, and provides a site frequency spectrum for the ensemble of clonal and polymorphic sites in the sequence. Each term features a record 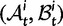 of ancestral and derived codon types plus a process
of ancestral and derived codon types plus a process 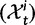 , which alternates between dormant periods and active sessions. In each cycle, the dormant period has exponential length with intensity
, which alternates between dormant periods and active sessions. In each cycle, the dormant period has exponential length with intensity 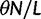 and the active session consists of a Wright–Fisher diffusion corresponding to the absorption time of a Wright–Fisher diffusion with initial value
and the active session consists of a Wright–Fisher diffusion corresponding to the absorption time of a Wright–Fisher diffusion with initial value 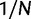 running until absorption in 0 or 1.
running until absorption in 0 or 1.
The Codon Equilibrium Distribution
The first component 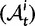 of each
of each 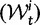 has its jumps restricted to times of actual nucleotide substitution events. Synonymous mutations get fixed with probability
has its jumps restricted to times of actual nucleotide substitution events. Synonymous mutations get fixed with probability  and nonsynonymous mutations fix with probability
and nonsynonymous mutations fix with probability 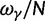 ,
, 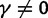 , with
, with 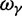 introduced in equation (2) (the formal background is given in eq. 2 of the supplementary text, Supplementary Material online). So, if we single out only substitution events then the Markov chain transition probabilities reduce to
introduced in equation (2) (the formal background is given in eq. 2 of the supplementary text, Supplementary Material online). So, if we single out only substitution events then the Markov chain transition probabilities reduce to 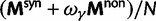 . Thus, we consider a continuous time Markov chain with infinitesimal generator
. Thus, we consider a continuous time Markov chain with infinitesimal generator
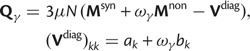 |
(12) |
where the total jump intensities stored in the diagonal matrix 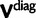 were introduced in equation (9). Here, the stop codons S0 are transient states. We conclude that the continuous time approximation
were introduced in equation (9). Here, the stop codons S0 are transient states. We conclude that the continuous time approximation 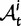 behaves as the Markov chain with generator
behaves as the Markov chain with generator 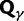 , except that each holding time is prolonged by the fixation time of the corresponding diffusion path in
, except that each holding time is prolonged by the fixation time of the corresponding diffusion path in 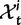 . To obtain a steady state codon distribution, however, one should restrict to the clonal population, which is given precisely by the Markov generator
. To obtain a steady state codon distribution, however, one should restrict to the clonal population, which is given precisely by the Markov generator 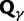 . Hence, we define η to be the unique stationary distribution which satisfies
. Hence, we define η to be the unique stationary distribution which satisfies 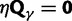 and which provides a steady state for the irreducible Markov chain restricted to S and with
and which provides a steady state for the irreducible Markov chain restricted to S and with  for
for 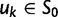 . Now for large N, we have the interpretation that substitutions occur according to
. Now for large N, we have the interpretation that substitutions occur according to 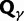 and the typical codon frequencies observed in a clonal site in equilibrium is given by η. Furthermore, in this equilibrium, we can measure the proportions of synonymous and nonsynonymous events among all mutations. For example, whenever a mutation event occurs according to
and the typical codon frequencies observed in a clonal site in equilibrium is given by η. Furthermore, in this equilibrium, we can measure the proportions of synonymous and nonsynonymous events among all mutations. For example, whenever a mutation event occurs according to 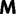 it is synonymous with probability given by the scalar product
it is synonymous with probability given by the scalar product 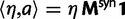 . Consequently, we introduce the probability distribution
. Consequently, we introduce the probability distribution 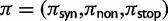 , by
, by
| (13) |
In conclusion, the typical rates at which mutation events are synonymous, nonsynonymous, or inert are obtained as the weighted mutation rates
and the conditional distribution of synonymous and nonsynonymous mutations given that a nonstop codon transition occurs is
As a consequence, the resulting synonymous and nonsynonymous mutation intensities for the population of sequences are given by
| (14) |
Mutation Rates for Standard Models
The probability distributions π and 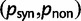 , and hence the rates
, and hence the rates 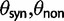 can be found explicitly for standard mutation matrices
can be found explicitly for standard mutation matrices 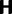 . The Kimura model with
. The Kimura model with 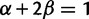 , takes into account a mutation ratio
, takes into account a mutation ratio 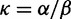 of transitions versus transversions. For this model, the uniform distribution on nonstop codons given by
of transitions versus transversions. For this model, the uniform distribution on nonstop codons given by 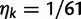 ,
, 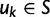 , is stationary for
, is stationary for  and hence
and hence 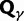 . This holds not only for the neutral case
. This holds not only for the neutral case 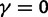 but also in general. Indeed,
but also in general. Indeed, 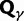 is doubly stochastic for any γ, and by equation (13),
is doubly stochastic for any γ, and by equation (13),
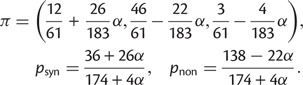 |
A special case of the Kimura model, which we have used for the simulation study in this work, is 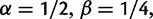
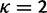 . Then
. Then
 |
Our model is flexible and allows for any other nucleotide substitution pattern, including asymmetric versions with nonzero diagonal elements hii. In general, if 
 is a steady state for
is a steady state for  , hence representing the typical fractions of nucleotides in the population, the corresponding steady state of codons will be
, hence representing the typical fractions of nucleotides in the population, the corresponding steady state of codons will be
and the vector π is again found from equation (13). Commonly used versions of the Goldman–Yang model (Goldman and Yang 1994), fall in this category.
Poisson Random Field Approximation
In equation (11), letting the initial times and paths of all active sessions form points of a Poisson random point measure leads to what has been called a Poisson random fields model (Sawyer and Hartl 1992). Although we do not pursue this line of argument formally, our approach is similar in spirit. The quantities of primary interest in this work, which measure divergence of sampled sequences between populations, are recognized as random functionals of 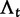 . These functionals count specific events that occur along the site processes with probabilities proportional to
. These functionals count specific events that occur along the site processes with probabilities proportional to 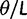 . With L independent sites, this leads to an approximate Poisson number of events over the total length of the sequence with mean proportional to θ. To find the expected values of the divergence functionals, we apply the site frequency spectrum, which arises by superposing Wright–Fisher diffusions starting in
. With L independent sites, this leads to an approximate Poisson number of events over the total length of the sequence with mean proportional to θ. To find the expected values of the divergence functionals, we apply the site frequency spectrum, which arises by superposing Wright–Fisher diffusions starting in 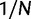 at Poisson times with rate
at Poisson times with rate 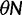 (Evans et al. 2007).
(Evans et al. 2007).
Recall from equation (12) that the typical codon frequencies are given by the steady state 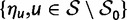 . Conditional on the first component of
. Conditional on the first component of 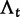 in site i being
in site i being 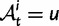 , then
, then 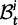 typically makes a large number of jumps from u to a sense codon neighbor v of u and then back to u, before one of these excursions eventually fixes and results in a change of state of
typically makes a large number of jumps from u to a sense codon neighbor v of u and then back to u, before one of these excursions eventually fixes and results in a change of state of 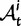 . Given such a
. Given such a 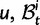 settles in a steady state with probabilities muv. Summing again over u with the stationary weight, we recover
settles in a steady state with probabilities muv. Summing again over u with the stationary weight, we recover 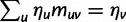 . Therefore, it is reasonable to assume that mutations occur along the time axis as an approximate Poisson process with intensity
. Therefore, it is reasonable to assume that mutations occur along the time axis as an approximate Poisson process with intensity 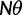 and each event sparks the excursion of a Wright–Fisher diffusion
and each event sparks the excursion of a Wright–Fisher diffusion 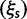 with
with 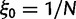 . The fractions of mutation events, which lead to synonymous and nonsynonymous codon pairs are obtained by the weighted summations
. The fractions of mutation events, which lead to synonymous and nonsynonymous codon pairs are obtained by the weighted summations
and the corresponding mutation intensities are given by 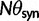 and
and 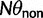 . A key feature here is that nonsynonymous and synonymous codon mutations evolve independently of each other.
. A key feature here is that nonsynonymous and synonymous codon mutations evolve independently of each other.
Rate of Divergence over Time
In this section, we consider a population split where a population of size N has been running indefinitely from the past and is replaced at time t = 0 instantaneously by two identical copies of the population. The new branches represent two emerging species both of population size N with initially the same number of clonal and polymorphic sites and with identical codon frequencies. From the splitting time and onwards each of the two populations evolve independently according to the same mechanisms of mutation and selection. To follow the onset of divergence between the species, we sample randomly one individual in each population. Let D(t) denote the number of nucleotide differences between these two sequences at time 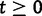 . We will analyze three types of differences which contribute to the total divergence D(t), by writing
. We will analyze three types of differences which contribute to the total divergence D(t), by writing
where
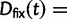 sequence divergence at t from mutations during [0, t] fixed uring [0, t],
sequence divergence at t from mutations during [0, t] fixed uring [0, t],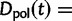 number of derived alleles sampled from lineage-specific polymorphic sites at t and
number of derived alleles sampled from lineage-specific polymorphic sites at t and 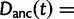 sequence divergence at t attributed to ancestral polymorphisms existing at t = 0.
sequence divergence at t attributed to ancestral polymorphisms existing at t = 0.
Here, 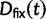 and
and 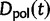 are sums of two independent contributions, one from each population, whereas
are sums of two independent contributions, one from each population, whereas  involves the joint initial state at t = 0. The dominant source of divergence between two sequences which is visible after a longer time span t, is the fixation of new alleles from recent mutations in each population during
involves the joint initial state at t = 0. The dominant source of divergence between two sequences which is visible after a longer time span t, is the fixation of new alleles from recent mutations in each population during 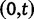 . The growth in the number of substitutions and the subsequent growth of
. The growth in the number of substitutions and the subsequent growth of 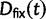 is essentially linear in t. This is the same mechanism, which is responsible for the mixing of codons and the appearance of a steady state of codon frequencies in the long run. The additional contributions to the total divergence D(t) are bounded as functions of t but are important to understand how the linear growth regime is attained after population split.
is essentially linear in t. This is the same mechanism, which is responsible for the mixing of codons and the appearance of a steady state of codon frequencies in the long run. The additional contributions to the total divergence D(t) are bounded as functions of t but are important to understand how the linear growth regime is attained after population split.
We will analyze the three types of divergence by relating the components of D(t) to suitable functionals of 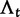 in equation (11), extended to cover a common ancestry for
in equation (11), extended to cover a common ancestry for  and two independent species populations for
and two independent species populations for  . At any given time, some of the L codons in the model are likely to be polymorphic and hence exempt from mutation events. But as the number of polymorphic sites is typically much smaller than L, we will apply the approximation that the total mutation intensity is
. At any given time, some of the L codons in the model are likely to be polymorphic and hence exempt from mutation events. But as the number of polymorphic sites is typically much smaller than L, we will apply the approximation that the total mutation intensity is 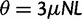 per sequence and generation, hence
per sequence and generation, hence 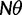 per sequence and time units t. It is the independent Poisson mutation processes in our model that drive the various contributions to D(t). In particular, nucleotide substitutions count into
per sequence and time units t. It is the independent Poisson mutation processes in our model that drive the various contributions to D(t). In particular, nucleotide substitutions count into 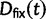 , which therefore has a Poisson distribution. Sampled differences, both ancestral and present polymorphic, arise at most one in each codon site. By equations (15) and (16) of the supplementary text (Supplementary Material online), the probability to see one of these differences at a given site after sampling sequences in two populations is proportional to the mutation intensity per codon and time unit, namely
, which therefore has a Poisson distribution. Sampled differences, both ancestral and present polymorphic, arise at most one in each codon site. By equations (15) and (16) of the supplementary text (Supplementary Material online), the probability to see one of these differences at a given site after sampling sequences in two populations is proportional to the mutation intensity per codon and time unit, namely 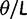 . Summing over L codons this gives a binomial, hence approximately Poisson, number of differences with mean proportional to θ. But then
. Summing over L codons this gives a binomial, hence approximately Poisson, number of differences with mean proportional to θ. But then 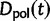 and
and  , and therefore D(t) itself have approximate Poisson distributions. Our next focus will be to find the corresponding expected values.
, and therefore D(t) itself have approximate Poisson distributions. Our next focus will be to find the corresponding expected values.
Expected Divergence after Population Split
We begin with divergence based on fixed differences. Our model associates with the Wright–Fisher diffusion  its fixation time
its fixation time  , extinction time
, extinction time  and absorption time
and absorption time  . The total number of mutation events in
. The total number of mutation events in  is Poisson with mean
is Poisson with mean 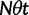 and conditional on this number the events are uniformly distributed on
and conditional on this number the events are uniformly distributed on 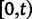 . One such mutation occurring at time s results in a fixation if
. One such mutation occurring at time s results in a fixation if 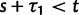 . Summing over both populations and taking into account the fractions of synonymous and nonsynonymous events, this gives
. Summing over both populations and taking into account the fractions of synonymous and nonsynonymous events, this gives
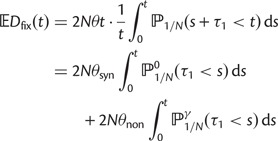 |
Rewrite as 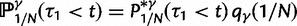 , where
, where 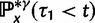 is the conditional probability given fixation (
is the conditional probability given fixation ( ) and
) and 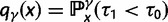 denotes the fixation probability of a mutated allele which emerges with frequency x in the population. By equation (2),
denotes the fixation probability of a mutated allele which emerges with frequency x in the population. By equation (2), 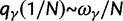 . Hence, in the large N limit,
. Hence, in the large N limit,
with
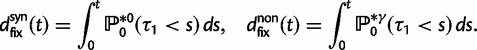 |
Equivalently,
which reveals the deviation from linear growth of 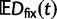 . For
. For 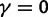 ,
,
with the function G0 defined in equation (12) of the supplementary text (Supplementary Material online). One option for the general selective case 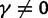 would be to apply a spectral representation for the transition density of the Wright–Fisher model with selection, and rely on numerical computations of the corresponding eigenvalue/eigenvector problem. To keep things simpler while retaining a reasonable degree of accuracy, instead we propose at this place the approximation
would be to apply a spectral representation for the transition density of the Wright–Fisher model with selection, and rely on numerical computations of the corresponding eigenvalue/eigenvector problem. To keep things simpler while retaining a reasonable degree of accuracy, instead we propose at this place the approximation
By applying a known integral expression for 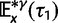 , see Karlin and Taylor (1981), Ch. 15, (9.9), and expanding the resulting integral in γ, we obtain
, see Karlin and Taylor (1981), Ch. 15, (9.9), and expanding the resulting integral in γ, we obtain
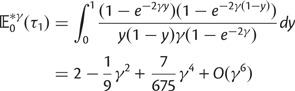 |
(15) |
and hence
In summary,
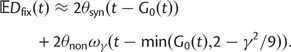 |
(16) |
Next, we turn to divergence based on lineage-specific polymorphisms. As discussed earlier, consider a mutation at a uniformly distributed time s in 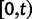 . The corresponding derived allele exists at time t if
. The corresponding derived allele exists at time t if 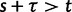 , in which case
, in which case 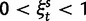 . In each population, we have sampled one particular individual. The probability that this individual carries the derived allele is approximately
. In each population, we have sampled one particular individual. The probability that this individual carries the derived allele is approximately 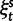 . Hence, the probability that this lineage-specific polymorphism contributes to estimates of divergence is
. Hence, the probability that this lineage-specific polymorphism contributes to estimates of divergence is
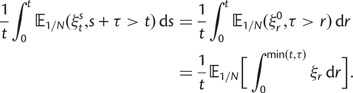 |
Now summing over all mutation events in  in both populations and splitting neutral synonymous ones from selective nonsynonymous mutations, we find
in both populations and splitting neutral synonymous ones from selective nonsynonymous mutations, we find
| (17) |
where
 |
To continue estimating  and
and 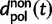 , it is a useful fact that the functional
, it is a useful fact that the functional 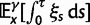 has an explicit representation as an integral over the corresponding Green’s function (for details see supplementary text, Supplementary Material online). Indeed, for
has an explicit representation as an integral over the corresponding Green’s function (for details see supplementary text, Supplementary Material online). Indeed, for 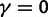 , we have
, we have 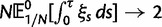 and for
and for 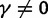 ,
,
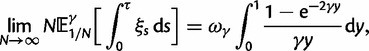 |
(18) |
as N tends to infinity. To accommodate the behavior for small t, we apply the approximation
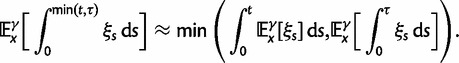 |
(19) |
Here 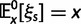 for
for 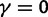 , so for large N
, so for large N
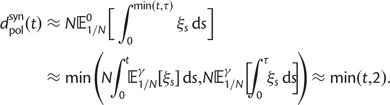 |
More generally, by conditioning,
The conditional expectations on the right hand side appear to be well approximated by those for the neutral case 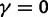 , which can be derived explicitly,
, which can be derived explicitly,
Thus,
| (20) |
and
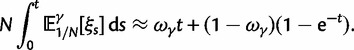 |
and if we plug this and equation (18) into equation (19) it follows
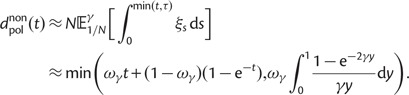 |
Thus, if we apply the integral approximation
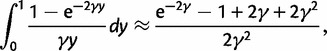 |
which should be sufficiently accurate at least in the range  , and put
, and put
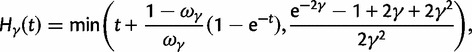 |
(21) |
then 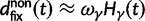 and we may sum up the contribution to divergence based on polymorphic sites as
and we may sum up the contribution to divergence based on polymorphic sites as
| (22) |
The ancestral contribution to divergence between the two populations has its origin in the common history of mutation events that has occurred at times 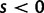 . Of all polymorphic sites which exist at the time of population split t = 0, those for which the sampled individuals at a later time are different in the two populations add to ancestral divergence. This includes polymorphic and fixed or extinct states as long as one is ancestral and the other derived. A derived allele starting at
. Of all polymorphic sites which exist at the time of population split t = 0, those for which the sampled individuals at a later time are different in the two populations add to ancestral divergence. This includes polymorphic and fixed or extinct states as long as one is ancestral and the other derived. A derived allele starting at 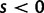 exists with frequency
exists with frequency 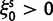 at time t = 0, if
at time t = 0, if 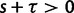 . Hence, conditionally given
. Hence, conditionally given 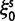 , the chance to see such a difference is
, the chance to see such a difference is
where each population is indicated with an additional upper index. By independence after time t = 0 this is
To average over all states at t = 0, we note that the number of mutation events over a finite interval 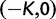 is Poisson with mean
is Poisson with mean 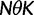 . Hence, conditional on the number of events the mutation times are uniformly distributed in
. Hence, conditional on the number of events the mutation times are uniformly distributed in 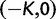 . The probability that one of these events contributes to ancestral divergence is
. The probability that one of these events contributes to ancestral divergence is
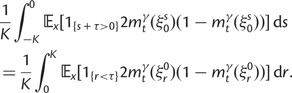 |
Letting  , and separating synonymous and nonsynonymous events,
, and separating synonymous and nonsynonymous events,
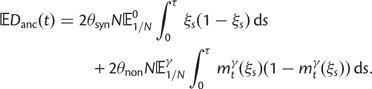 |
(23) |
Again, we rely on being able to evaluate functionals of the Wright–Fisher process of the type  for sufficiently nice functions g. First (eq. 5 of the supplementary text, Supplementary Material online),
for sufficiently nice functions g. First (eq. 5 of the supplementary text, Supplementary Material online),
For the second term in equation (23), we use again the approximation (20) of 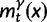 . Then
. Then
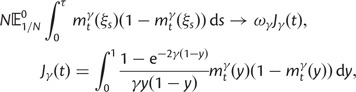 |
with
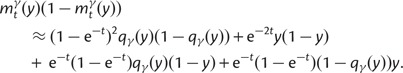 |
By expanding the resulting integrals in a series up to second order in γ,
| (24) |
Hence, we conclude from equation (23) that the expected divergence attributed to ancestral polymorphisms in this model is
| (25) |
At t = 0, as 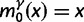 ,
,
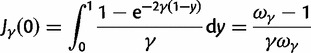 |
(26) |
so that
and we have the initial ratio
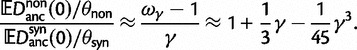 |
Now, we are in position to study synonymous and nonsynonymous divergence separately. By summing up the three parts of divergence in equations (16), (22), and (25), that is, fixed differences and divergence attributed to lineage-specific and ancestral polymorphisms, we find for any fixed t that  and
and  have approximate Poisson distributions with expected values
have approximate Poisson distributions with expected values
| (27) |
such that
and
with G0 defined in the supplementary text (Supplementary Material online),  in equation (21) and
in equation (21) and 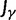 in equation (24).
in equation (24).
Statistical Properties of Divergence and Poisson Ratios
The codon evolution model introduced above allows us to study in detail the accumulation of fixed differences and the variation of sampled differences between sequences from two independent populations after the split from an ancestral population. We continue in this direction by studying the ratio of nonsynonymous to synonymous divergence dN/dS in a population genetics framework as a ratio of Poisson random variables.
Intrinsic Variation of Poisson Ratios
Considering the ratio of scaled Poisson variables
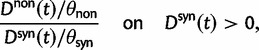 |
enables us to study dN/dS as a function of divergence time by defining
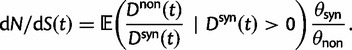 |
To compute this conditional expectation, we note that if Y is a Poisson random variable with mean m then
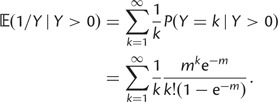 |
Hence, if we introduce the function
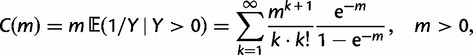 |
(28) |
it follows
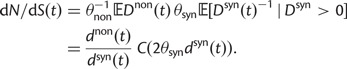 |
(29) |
Thus, we have two alternative methods to estimate dN/dS based on computing suitable expected values. The previous ratio of expected values  and the new expected value of a ratio. Our main motivation for introducing equation (29) is that current practice in empirical work on dN/dS does not per se seek to estimate the expected number of synonymous divergence or expected number of nonsynonymous divergence but rather aim at determining single observations of these quantities. Then forming the ratio of these observations leads to equation (29). It is noteworthy that the new estimate is simply a multiplicative perturbation of the previous ratio and that the prefactor
and the new expected value of a ratio. Our main motivation for introducing equation (29) is that current practice in empirical work on dN/dS does not per se seek to estimate the expected number of synonymous divergence or expected number of nonsynonymous divergence but rather aim at determining single observations of these quantities. Then forming the ratio of these observations leads to equation (29). It is noteworthy that the new estimate is simply a multiplicative perturbation of the previous ratio and that the prefactor  depends on both θ and t. However, the dependence is restricted to variations in the product
depends on both θ and t. However, the dependence is restricted to variations in the product 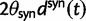 . If
. If 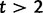 , this is
, this is 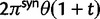 and if we take in addition the Jukes–Cantor mutation model, then the prefactor is approximately
and if we take in addition the Jukes–Cantor mutation model, then the prefactor is approximately 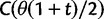 . For example, if
. For example, if 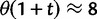 then
then 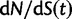 is more than 30% larger than
is more than 30% larger than 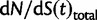 and if
and if 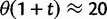 then
then 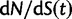 is more than 10% larger than the reference ratio. This said, one should also notice that for sufficiently large θ or t, the two estimates coincide. In fact,
is more than 10% larger than the reference ratio. This said, one should also notice that for sufficiently large θ or t, the two estimates coincide. In fact, 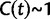 as
as 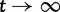 and hence
and hence 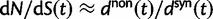 as
as 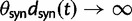 . For small t,
. For small t,
Confidence Intervals
Suppose we have fixed θ and H, and determined the vector π. Considering γ as an unknown parameter we suppose k and n – k are observations of the independent Poisson random variables 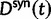 and
and  at some unknown time t. Then, given the sum
at some unknown time t. Then, given the sum 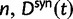 has a binomial distribution
has a binomial distribution 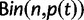 , where
, where
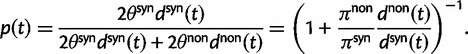 |
(30) |
Now apply a confidence interval 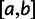 for p(t). It follows that
for p(t). It follows that 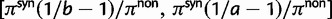 is a confidence interval for
is a confidence interval for 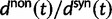 . If we apply specifically a 95% interval of the so-called Wilson type for p(t), based on normal approximation of the binomial distribution, then with
. If we apply specifically a 95% interval of the so-called Wilson type for p(t), based on normal approximation of the binomial distribution, then with 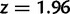 the limits a and b are given by
the limits a and b are given by
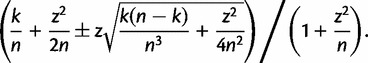 |
The lower und upper limits of the observed confidence interval for 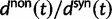 become
become
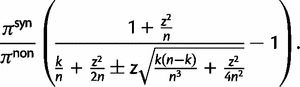 |
For example, if the upper limit would attain a value less than one we have evidence with a 5% degree of significance to reject a null hypothesis of neutral evolution in favor of negative selection.
Now we change the perspective and consider γ and hence 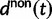 as known. We want to estimate the variation in
as known. We want to estimate the variation in 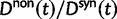 . Given that the total number of observed differences at time t is n, then with
. Given that the total number of observed differences at time t is n, then with 
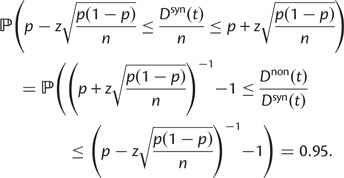 |
Hence, we may take p as in (30) and estimate n with 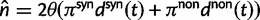 to get a 95% “confidence band” for
to get a 95% “confidence band” for 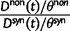 as
as
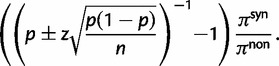 |
(31) |
Simulation of Codon Evolution
The accuracy of our analytical results of course depends on the degree to which the various approximations that we applied during their derivation have distorted the properties of the original model. In particular, our results were derived as large population size approximations based not only on the rescaling of time and mutation and selection parameters but also on Poisson approximations that ignored some of the subtler dependency structures in the model. Hence, one must ask if the dN/dS ratios derived here correctly capture the relation of nonsynonymous to synonymous changes over discrete generations as it evolves in the initial modeling setup. Furthermore, one would like to know whether the confidence bands in equation (31) derived with similar approximation methods reflect the true statistical variation in the original model, or not.
For the purpose of validating our analytical results, and hence providing evidence that our dN/dS ratios with reasonable accuracy indeed capture both the average behavior and the variation of nonsynonymous to synonymous divergence, we carried out a simulation study of the discrete time Wright–Fisher model with selection as introduced previously in the Materials and Methods. The code was written in Matlab (R2012b) and simulates the Markov chain 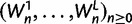 with the following choice of parameters:
with the following choice of parameters: 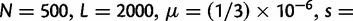
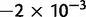 , and the mutation matrix
, and the mutation matrix 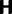 chosen to be the Kimura matrix with
chosen to be the Kimura matrix with 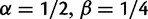 . As a consequence, we have the scaled parameters
. As a consequence, we have the scaled parameters 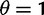 and
and 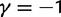 . The initial codon distribution was chosen to be clonal according to arbitrary codon usage. In other words, each independent component
. The initial codon distribution was chosen to be clonal according to arbitrary codon usage. In other words, each independent component 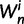 in the codon sequence is given the initial distribution
in the codon sequence is given the initial distribution 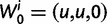 with u arbitrarily selected. Then, a single population was generated during a burn-in period of 10,000 generations (20 time units) to move toward equilibrium codon usage. The particular configuration of codons and its polymorphic states constitutes the distribution of shared ancestral polymorphisms. Then, two populations evolve in parallel but otherwise independent over 50,000 generations (100 time units). During the generation of these data, the code keeps track of the accumulated number of fixations as well as the resulting ancestral and polymorphic divergence if one sequence had been sampled from each population at that particular time. With the additional knowledge of the type of each fixed or sampled difference—nonsynonymous or synonymous—one obtains the simulated dN/dS ratio as a function over discrete time.
with u arbitrarily selected. Then, a single population was generated during a burn-in period of 10,000 generations (20 time units) to move toward equilibrium codon usage. The particular configuration of codons and its polymorphic states constitutes the distribution of shared ancestral polymorphisms. Then, two populations evolve in parallel but otherwise independent over 50,000 generations (100 time units). During the generation of these data, the code keeps track of the accumulated number of fixations as well as the resulting ancestral and polymorphic divergence if one sequence had been sampled from each population at that particular time. With the additional knowledge of the type of each fixed or sampled difference—nonsynonymous or synonymous—one obtains the simulated dN/dS ratio as a function over discrete time.
Supplementary Material
Supplementary text is available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).
Acknowledgments
This work was supported by a European Research Council grant ERC-2009-AdG-249976-NEXTGENMOLECOL to Hans Ellegren.
References
- 1000 Genomes Project Consortium. An integrated map of genetic variation from 1,092 human genomes. Nature. 2012;491:56–65. doi: 10.1038/nature11632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balbi KJ, Feil EJ. The rise and fall of deleterious mutation. Res Microbiol. 2007;158:779–786. doi: 10.1016/j.resmic.2007.09.005. [DOI] [PubMed] [Google Scholar]
- Berglund J, Pollard KS, Webster MT. Hotspots of biased nucleotide substitutions in human genes. PLoS Biol. 2009;7:e26. doi: 10.1371/journal.pbio.1000026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bromham L. Why do species vary in their rate of molecular evolution? Biol Lett. 2009;5:401–404. doi: 10.1098/rsbl.2009.0136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bustamante CD, Fledel-Alon A, Williamson S, et al. (14 co-authors) Natural selection on protein-coding genes in the human genome. Nature. 2005;437:1153–1157. doi: 10.1038/nature04240. [DOI] [PubMed] [Google Scholar]
- Charlesworth D. Don’t forget the ancestral polymorphisms. Heredity. 2010;105:509–510. doi: 10.1038/hdy.2010.14. [DOI] [PubMed] [Google Scholar]
- Clark AG, Glanowski S, Nielsen R, et al. (17 co-authors) Inferring nonneutral evolution from human-chimp-mouse orthologous gene trios. Science. 2003;302:1960–1963. doi: 10.1126/science.1088821. [DOI] [PubMed] [Google Scholar]
- Ellegren H. A selection model of molecular evolution incorporating the effective population size. Evolution. 2009;63:301–305. doi: 10.1111/j.1558-5646.2008.00560.x. [DOI] [PubMed] [Google Scholar]
- Ellegren H, Smeds L, Burri R, et al. (12 co-authors) The genomic landscape of species divergence in Ficedula flycatchers. Nature. 2012;491:756–760. doi: 10.1038/nature11584. [DOI] [PubMed] [Google Scholar]
- Evans SE, Shvets Y, Slatkin M. Non-equilibrium theory of the allele frequency spectrum. Theor Popul Biol. 2007;71:109–119. doi: 10.1016/j.tpb.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Gillooly JF, Allen AP, West GB, Brown JH. The rate of DNA evolution: effects of body size and temperature on the molecular clock. Proc Natl Acad Sci U S A. 2005;102:140–145. doi: 10.1073/pnas.0407735101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman N, Yang ZH. A codon-based model of nucleotide substitution for protein-coding DNA-sequences. Mol Biol Evol. 1994;11:725–736. doi: 10.1093/oxfordjournals.molbev.a040153. [DOI] [PubMed] [Google Scholar]
- Ho SYW, Larson G. Molecular clocks: when times are a-changin’. Trends Genet. 2006;22:79–83. doi: 10.1016/j.tig.2005.11.006. [DOI] [PubMed] [Google Scholar]
- Karlin S, Taylor HM. A second course in stochastic processes. New York: Academic Press, Inc.; 1981. [Google Scholar]
- Kimura M. On probability of fixation of mutant genes in a population. Genetics. 1962;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kryazhimskiy S, Plotkin JB. The population genetics of dN/dS. PLoS Genet. 2008;4:e1000304. doi: 10.1371/journal.pgen.1000304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li WH, Wu CI, Luo CC. A new method for estimating synonymous and nonsynonymous rates of nucleotide substitution considering the relative likelihood of nucleotide and codon changes. Mol Biol Evol. 1985;2:150–174. doi: 10.1093/oxfordjournals.molbev.a040343. [DOI] [PubMed] [Google Scholar]
- McDonald JH, Kreitman M. Adaptive protein evolution at the Adh locus in Drosophila. Nature. 1991;351:652–654. doi: 10.1038/351652a0. [DOI] [PubMed] [Google Scholar]
- Miyata T, Yasunaga T, Nishida T. Nucleotide sequence divergence and functional constraint in mRNA evolution. Proc Natl Acad Sci U S A. 1980;77:7328–7332. doi: 10.1073/pnas.77.12.7328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muse SV, Gaut BS. A likelihood approach for comparing synonymous and nonsynonymous nucleotide substitution rates, with application to the chloroplast genome. Mol Biol Evol. 1994;11:715–724. doi: 10.1093/oxfordjournals.molbev.a040152. [DOI] [PubMed] [Google Scholar]
- Nei M, Gojobori T. Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Mol Biol Evol. 1986;3:418–426. doi: 10.1093/oxfordjournals.molbev.a040410. [DOI] [PubMed] [Google Scholar]
- Nei M, Suzuki Y, Nozawa M. The neutral theory of molecular evolution in the genomic era. Annu Rev Genom Hum Genet. 2010;22:265–289. doi: 10.1146/annurev-genom-082908-150129. [DOI] [PubMed] [Google Scholar]
- Nielsen R. Molecular signatures of natural selection. Annu Rev Genet. 2005;39:197–218. doi: 10.1146/annurev.genet.39.073003.112420. [DOI] [PubMed] [Google Scholar]
- Nielsen R, Yang ZH. Likelihood models for detecting positively selected amino acid sites and applications to the HIV-1 envelope gene. Genetics. 1998;148:929–936. doi: 10.1093/genetics/148.3.929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R, Yang ZH. Estimating the distribution of selection coefficients from phylogenetic data with applications to mitochondrial and viral DNA. Mol Biol Evol. 2003;20:1231–1239. doi: 10.1093/molbev/msg147. [DOI] [PubMed] [Google Scholar]
- Nikolaev SI, Montoya-Burgos JI, Popadin K, Parand L, Margulies EH, National Institutes of Health Intramural Sequencing Center Comparative Sequencing Program. Antonarakis SE. Life-history traits drive the evolutionary rates of mammalian coding and noncoding genomic elements. Proc Natl Acad Sci U S A. 2007;104:20443–20448. doi: 10.1073/pnas.0705658104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson GI, Masel J. Quantitative prediction of molecular clock and K(a)/K(s) at short timescales. Mol Biol Evol. 2009;26:2595–2603. doi: 10.1093/molbev/msp175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prüfer K, Munch K, Hellmann I, et al. (41 co-authors) The bonobo genome compared with the chimpanzee and human genomes. Nature. 2012;486:527–531. doi: 10.1038/nature11128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocha EPC, Smith JM, Hurst LD, Holden MTG, Cooper JE, Smith NH, Feil EJ. Comparisons of dN/dS are time dependent for closely related bacterial genomes. J Theor Biol. 2006;239:226–235. doi: 10.1016/j.jtbi.2005.08.037. [DOI] [PubMed] [Google Scholar]
- Sawyer SA, Hartl DL. Population-genetics of polymorphism and divergence. Genetics. 1992;132:1161–1176. doi: 10.1093/genetics/132.4.1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith NG, Eyre-Walker A. Adaptive protein evolution in Drosophila. Nature. 2002;415:1022–1024. doi: 10.1038/4151022a. [DOI] [PubMed] [Google Scholar]
- Wolf JBW, Künstner A, Nam K, Jakobsson M, Ellegren H. Nonlinear dynamics of nonsynonymous (d(N)) and synonymous (d(S)) substitution rates affects inference of selection. Genome Biol Evol. 2009;1:308–319. doi: 10.1093/gbe/evp030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Evolution in mendelian populations. Genetics. 1931;16:97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright SI, Andolfatto P. The impact of natural selection on the genome: emerging patterns in Drosophila and Arabidopsis. Annu Rev Ecol Evol Syst. 2008;39:193–213. [Google Scholar]
- Wyckoff GJ, Malcolm CM, Vallender EJ, Lahn BT. A highly unexpected strong correlation between fixation probability of nonsynonymous mutations and mutation rate. Trends Genet. 2005;21:381–385. doi: 10.1016/j.tig.2005.05.005. [DOI] [PubMed] [Google Scholar]
- Yang ZH. PAML 4: phylogenetic analysis by maximum likelihood. Mol Biol Evol. 2007;24:1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.