Automated Label-free Quantification of Metabolites from Liquid Chromatography–Mass Spectrometry Data

Abstract

Liquid chromatography coupled to mass spectrometry (LC-MS) has become a standard technology in metabolomics. In particular, label-free quantification based on LC-MS is easily amenable to large-scale studies and thus well suited to clinical metabolomics. Large-scale studies, however, require automated processing of the large and complex LC-MS datasets.

We present a novel algorithm for the detection of mass traces and their aggregation into features (i.e. all signals caused by the same analyte species) that is computationally efficient and sensitive and that leads to reproducible quantification results. The algorithm is based on a sensitive detection of mass traces, which are then assembled into features based on mass-to-charge spacing, co-elution information, and a support vector machine–based classifier able to identify potential metabolite isotope patterns. The algorithm is not limited to metabolites but is applicable to a wide range of small molecules (e.g. lipidomics, peptidomics), as well as to other separation technologies.

We assessed the algorithm's robustness with regard to varying noise levels on synthetic data and then validated the approach on experimental data investigating human plasma samples. We obtained excellent results in a fully automated data-processing pipeline with respect to both accuracy and reproducibility. Relative to state-of-the art algorithms, ours demonstrated increased precision and recall of the method. The algorithm is available as part of the open-source software package OpenMS and runs on all major operating systems.

The identification and quantification of compounds in biological samples play a crucial role in biological and biomedical research, as concentration changes of specific metabolites may be descriptive of a system's response to disease or environmental influences. Liquid chromatography coupled to mass spectrometry (LC-MS) has become the primary analytic platform for metabolic profiling experiments (1). Such experiments usually follow one of two main strategies. Targeted metabolomics allows for the simultaneous, absolute quantification of hundreds of known metabolites by comparison to internal standards. In contrast, the aim of the nontargeted strategy is to detect as many metabolites in a biological system as possible. This raises two important issues: the identification of the metabolites in question, and their accurate quantification. Quantification based on the intensity ratio of isotope-labeled compound pairs has potential limitations, such as increased time and complexity of sample preparation, a requirement for increased sample concentrations, high costs of the reagents, and incomplete labeling. Thus, there has been increased interest in label-free techniques to achieve faster and simpler quantification results. In label-free quantitative metabolomics, control and case samples are analyzed via LC-MS individually, and quantification is achieved through the comparison of a metabolite's corresponding chromatographic peak intensities (2). An LC-MS profile from a complex biological sample usually yields several hundreds to tens of thousands of signals (3). This complexity of the data often creates a bottleneck in data analysis for experimental studies (4). Consequently, automated label-free quantification of metabolites from LC-MS data is an essential procedure for meeting today's experimental requirements.

A typical data-processing pipeline includes centroiding, signal processing, feature detection, and retention time alignment (see supplemental Fig. S1). Starting from a set of profile data files, spectra are usually first centroided and then refined with signal processing methods such as noise/baseline reduction and mass recalibration. Feature detection is employed to extract ion signals from the raw or centroided data against the background of measurement noise and to condense this information into a table of compound-specific peak intensities (5). Alignment methods adjust measurements across different samples to correct for random and systematic variations in the observed elution time and group coinciding signals (4). A key feature of such processing pipelines is data reduction, whereby the data complexity of a single measurement is reduced from step to step to facilitate the simultaneous computational analysis of hundreds or thousands of samples (6). Whereas in other approaches to LC-MS data processing the filtering, retention time alignment, and feature detection are strongly intertwined and thus consider all samples at the same time (7), the presented pipeline processes each sample individually and then computes the otherwise computationally expensive alignment on the condensed datasets afterward.

Feature detection (or feature finding) reduces the data volume to improve the running time of further analysis steps. We use the term “feature” to denote the LC-MS signal that arises from some compound (e.g. a metabolite). In a feature, a compound is represented by its mass-to-charge ratio, retention time, and signal intensity. The extraction of LC-MS signals of true metabolites is hampered by the nonspecific nature of the electrospray ionization process, resulting in more than 90% background signals in the spectra (8). Therefore, the challenge for a feature-finding algorithm is to identify all signals caused by true metabolites while avoiding the detection of false positives (9). Detector noise; poor signal-to-noise ratios for low-abundance metabolites; and the presence of numerous peaks from isotopes, contaminants, and in-source degradation products make this task difficult (5). Moreover, metabolites can occur in different charge states and form different adducts in electrospray ionization, giving rise to multiple features per analyte.

Software tools for the aforementioned data-processing tasks are available but are often difficult to combine with one another or not flexible enough to allow for rapid prototyping of a new analysis workflow. Particularly, the feature-detection procedures therein pursue different strategies to overcome the mentioned difficulties.

These strategies can be grouped into those that merely extract chromatographic peaks from the given raw data and others that additionally perform deisotoping (i.e. assembling subsets of chromatographic peaks into isotope patterns that most likely originate from the same compound).

A widely used tool for metabolomics data is the XCMS package implemented within the R statistical framework (7). XCMS implements a binning strategy in the m/z dimension and thereby avoids the problem of searching for peaks in the m/z direction. Simultaneous feature detection and noise removal are then achieved in a bin-wise manner by a second derivative Gaussian matched filter. Other R packages are also available, such as apLCMS for LC-MS profiles with high mass accuracy (3). Neither of these provides built-in functionality for isotope pattern assembly, which has to be provided by additional packages such as CAMERA (10, 11).

Though it has been argued that it is impossible to define optimal bins for all circumstances (12), binning in the m/z dimension is also performed by other tools such as MZmine (13) and MAVEN (5).

Software tools such as MEND, MapQuant, and MZmine identify chromatographic peaks by matching them with a particular model profile such as a Gaussian or an exponentially modified Gaussian (13–16). However, detection based on such a predefined model may have low sensitivity, as the shapes of elution profiles vary greatly from one compound to another and peaks that do not conform to the predefined shape will be discarded.

Aberg et al. compared a two-dimensional representation of LC-MS data with the behavior of signals and noise on a radar screen. They implemented a Kalman filter for intrasample tracking and alignment of mass spectra into pure ion chromatograms (12).

In addition to the detection of chromatographic peaks, several tools such as MEND (14), MapQuant (15), and msInspect (17) pursue different deisotoping strategies. In msInspect (17), chromatographic peaks that co-elute over time and show similar profile shapes are pooled together and are considered as isotopes of the same compound. Another strategy is fitting a three-dimensional model of a generic isotope pattern against the raw data and subtracting the fit from the signal (18). In MapQuant (15), peaks are deisotoped by fitting isotope patterns to the observed two-dimensional data.

In proteomics, a popular choice for many feature-detection algorithms is to match the shape of peptide isotope patterns against an “averagine” model (19, 20). However, for nonpeptide compounds such as metabolites, the observed isotope patterns will not match, as they differ considerably in their chemical composition as assumed by the “averagine” model. Many available software solutions depend on numerous parameters that are difficult to interpret. These need to be optimized in order to obtain high-quality results, which often proves challenging, as their influence on the tools' behavior is hard to predict for the user (3, 21).

In this work, we present the novel software tool FeatureFinderMetabo for the label-free quantification of metabolites from LC-MS data. The algorithm detects chromatographic peaks in a robust and efficient manner without the need to bin the data in the m/z dimension. Because there are no assumptions regarding the chromatographic peak shape, low-intensity peaks are detected with high sensitivity. Furthermore, the algorithm constitutes a new method for model-based deisotoping of metabolite LC-MS data that is based on support vector machine classification. This novel classifier is designed to capture isotopic abundances of organic molecules in general and thus is also applicable to the wide array of small organic molecules. We designed the algorithm to be configurable mainly by three intuitive parameters that reflect the characteristics of typical LC-MS data. The straightforward and intuitive configuration of our software tool allows researchers to achieve fast and high-quality results and to focus more on downstream analysis. To assess the performance of our algorithm, we examined the influence of the adjustable parameters on a simulated benchmark dataset and the algorithm's quantification capability on a real-world dataset from human plasma samples. These samples were spiked with a set of standard compounds in a wide range of concentrations to reveal the relationship between the detected feature intensities and the actual quantities. We compared our algorithm's performance to that of XCMS in combination with the CAMERA package on both the simulated and the spiked human plasma data.

Although designed with metabolomics applications in mind, the algorithm is applicable to all small-molecule data and thus has applications beyond metabolomics (e.g. drug substance analytics, lipidomics, peptidomics, environmental analysis). Initial experiments also indicated that the algorithm deals well with data from separation technologies other than HPLC—for example, capillary electrophoresis mass spectrometry.

The presented algorithm is implemented as part of the OpenMS framework. OpenMS, together with TOPP (The OpenMS Proteomics Pipeline), was designed as a versatile and functional framework for developing mass spectrometry data analysis tools, providing rich functionality ranging from basic data structures to sophisticated algorithms for data analysis and visualization (4, 22, 23). It is open source software and incorporates all steps needed for building powerful computational metabolomics workflows.

MATERIALS AND METHODS

Algorithm

Overview

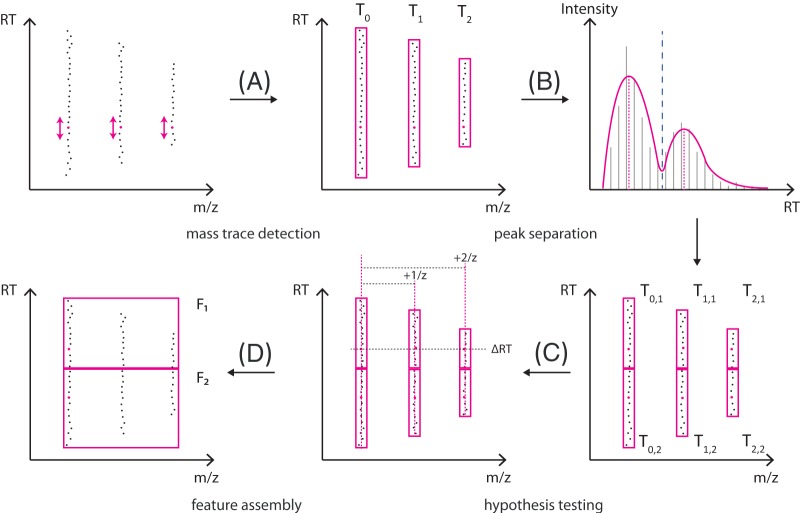
The feature-finder algorithm comprises two main stages, namely, the mass trace detection and feature assembly. In the first stage, signals in centroid LC-MS data that occur repeatedly over the retention time within a machine-dependent margin of mass error are gathered in a mass trace. Initially, a mass trace may contain signals from two different analytes (e.g. isobaric compounds overlapping in their elution profiles). To resolve this, the algorithm performs a filtering step to split these mass traces into individual chromatographic peaks. In the second stage, mass traces corresponding to the same metabolite are assembled into features. Hypotheses sharing mass traces between distinct analytes are resolved via a scoring procedure. An overview of the algorithm is shown in Fig. 1.

Fig. 1.

General procedure of feature finding. A, starting with the most intense peaks (magenta dots), potential mass traces are extended with peaks compatible in m/z back and forth in retention time. B, each mass trace is smoothed to facilitate the determination of chromatographic maxima. Multimodal elution profiles are split into smaller mass traces with respect to the number of maxima. C, based on this set of mass traces, potential feature hypotheses are generated and scored according to their compatibility with theoretical isotope patterns. D, finally, the best-scoring hypotheses are assembled to features.

Mass Trace Detection

For mass trace detection, we assume that the LC-MS data have already been centroided (by either the instrument software or some other peak-picking algorithm). The data then consist of a large number of spectrometric peaks P = {p_k}, where an individual peak p_k is defined by its retention time t_k, mass-to-charge ratio m_k, and intensity i_k.

To prepare the input for the mass trace detection stage, we sort the set P by decreasing intensity and remove peaks that do not exceed a user-defined intensity threshold. Based on the resulting list P′, the algorithm iterates first over the most intense peaks and considers each as a potential seeding point for the construction of mass traces. We define a mass trace T as a list of n mass spectrometric peaks p_k ∈ P′ that exhibit a similar m/z and occur in adjacent survey scans of an LC-MS run.

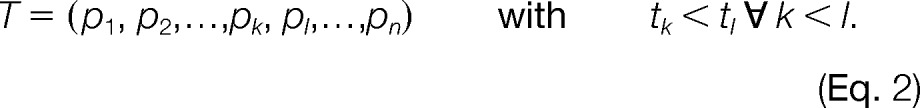For each peak p_k ∈ P′, we initialize an empty candidate mass trace T with p_k as a seeding point. Starting from this seeding point, the algorithm attempts to extend T along the retention time axis in both directions. This is accomplished by recruiting new peaks from P′ that are close in m/z to all peaks gathered so far in T and thus most likely originate from the same ion mass. Depending on the accuracy of the underlying MS technology, mass spectrometric peaks will exhibit scan-to-scan deviations from the true mass of the measured ion. These m/z errors follow a heteroscedastic noise model; that is, low-intensity peaks are expected to have a less reliable mass than higher-intensity peaks (24). We describe this error model by an intensity-weighted Gaussian distribution N with parameters μ (mean) and σ² (variance). The recruitment of suitable peaks to T depends on the accurate estimation of these parameters. To this end, we employ an online m/z density estimator (25) that refines the mean and variance estimates for each newly recruited peak p_n+1 by the recursive expressions

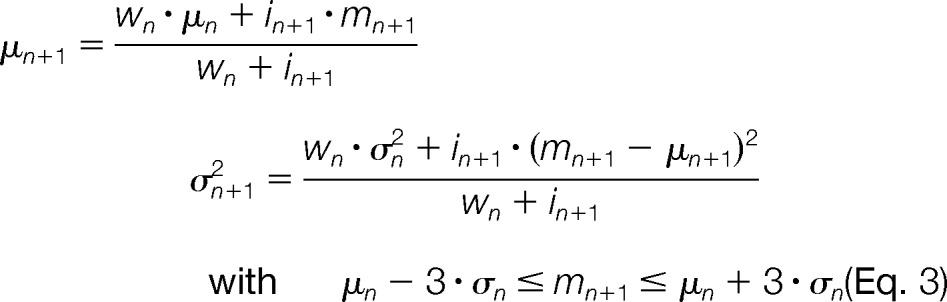where $w_n={\displaystyle {\sum }_k^n{i}_k}$ represents the accumulated weights of the preceding trace peaks and i₀ = 1. Furthermore, we restrict the recruitment to those peaks that are most likely under the previously estimated m/z distribution N(μ_n, σ_n²). The recursion is initialized with a variance of σ₀² that is chosen in proportion to the expected mass error of the mass spectrometer. In most cases, this mass error turns out to be a rough estimate, because the online density estimator yields a more accurate estimate of σ² after only a few recursion steps and thus avoids erroneously recruiting potential outliers to the mass trace. The algorithm is thus quite robust against an incorrect choice of this user-defined mass accuracy parameter.

The extension of mass trace T aborts as soon as a specified number of scans has been observed without finding an adequate peak. Such missing trace peaks occur more often in the fronting and tailing regions of a chromatographic peak as the mass trace starts to fade into the noise. We define a centroid m/z value for mass trace T by m̄ = μ_n, where μ_n corresponds to the last mean estimate before the trace extension was aborted. Trace peaks that were recruited by T are removed from the list P′. They can neither be used as a seeding point nor be part of other mass traces created in the subsequent iterations.

Analytes with mass-to-charge ratios sufficiently similar to be indistinguishable at the instrument resolution and sufficiently close retention times can form overlapping elution peaks within a mass trace (see Fig. 1, upper right). Based on the elution profiles, these mass traces need to be split. The algorithm detects the chromatographic maxima of the respective elution profiles and minima between them. This is complicated by the fact that peak intensities along an elution profile tend to be noisy, in particular at low intensities. We use local regression (LOWESS) with a polynomial of degree two as a smoothing technique, which offers the advantage of not needing a specific chromatographic peak shape to be defined in advance (26). An important parameter that influences the degree of smoothing is the window size s, which describes the number of peaks the local polynomial fit is applied to. An optimal choice of s should roughly cover the extent of a chromatographic peak. We found that good estimates for the window size are the number of trace peaks that are covered within the full-width-at-half-maximum Δt_0.5 of a typical chromatographic peak. LOWESS smoothing is not very sensitive to changes in the window size. As long as the window size is reasonably close to Δt_0.5 of most chromatographic peaks—a parameter that is generally well known for the chromatographic separation system—the smoothing will yield the desired result. Thus, we set the window size according to

where t_scan designates the time between two consecutive MS scans.

The mass trace detection algorithm offers the option to automatically infer a good estimate of Δt_0.5 based on the data. To this end, we consider the distribution of peak widths that are gathered throughout the mass trace extraction phase. From this distribution, we can estimate an average peak width that is used for smoothing with good accuracy.

On the smoothed elution profiles, chromatographic peaks are detected. A mass trace peak is regarded as a local chromatographic maximum if it has a higher intensity than at least 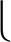s/2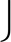 trace peaks in each direction (increasing and decreasing in retention time). This condition guarantees that in order to be regarded as separable, the chromatographic maxima of two consecutive overlapping elution profiles must be at least Δt_0.5 apart. If there is more than one chromatographic maximum within the same mass trace, the position with the minimum intensity between each pair of maxima is determined. These minima are used as splitting points between two separable chromatographic peaks (see supplemental Fig. S2). The splitting of mass trace T with c chromatographic maxima results in c shorter mass traces T₁, T₂,…,T_c. After the splitting step, we can define the retention time for each mass trace T_j by the position of the chromatographic peak maximum. Additionally, we approximate the chromatographic peak area under the elution profile of a mass trace T_j by the Riemann sum

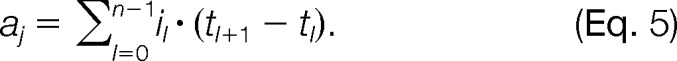Finally, each individual mass trace T_j is added to a global list M that holds all detected mass traces for the following feature assembly.

Feature Assembly

The goal of the feature-assembly stage is to find sets of mass traces that most likely originate from the same analyte. A set is regarded as a valid isotope pattern if its mass traces do co-elute, have correct m/z distances with respect to charge z, and exhibit correct isotopic abundance ratios (see supplemental Fig. S3). The feature-assembly algorithm reconstructs the isotopic patterns of multiple adduct ions of one analyte as individual features rather than aggregating them into one single feature. Following the modular approach of the OpenMS framework, such adduct features can be clustered subsequently or considered for improving the results of accurate mass queries against databases.

We define a set of k + 1 mass traces as a feature hypothesis

where the mass trace T₀ corresponds to the monoisotopic and T₁, T₂,…,T_k to the higher isotopic mass traces of an analyte. To enumerate all potential feature hypotheses in a list C, the algorithm traverses all mass traces in M in order of ascending m/z. Each mass trace therein is iteratively assumed to be the monoisotopic trace T₀ of a candidate feature hypothesis H. After initializing H with T₀, the algorithm searches the list M for mass traces that are compatible with T₀ in terms of their retention times, m/z distances, and intensity ratios. Instead of processing the complete list, we restrict the search for candidates to a subset of mass traces that lie in the vicinity of T₀ in both m/z and retention time dimension. The criteria for m/z and retention time compatibility are regarded as independent and are therefore modeled separately. Traces that fulfill these criteria are added to the feature hypothesis H.

In contrast to proteomics, there is no averagine model available to assess the correct m/z spacings and isotope abundance ratios within a putative metabolite isotope pattern. Thus, we built a comprehensive set of isotope patterns characteristic of metabolites and studied novel models to validate our feature hypothesis H. Although isotope patterns of typical metabolites could be obtained from metabolite databases, we chose a different approach in order to prevent bias due to the limited size and potential biases of these databases. To generate a set of valid isotope patterns, we first employed the HiRes software, a chemical formula generator that has been further developed by integrating heuristics to filter out unlikely sum formulas (28). We generated all sum formulas based on the elements C, H, O, N, P, and S in a mass range between 1 and 1,000 Da. This yielded about 24 million distinct sum formulas. We randomly sampled a subset of 115,000 compositions spread evenly over the mass range of interest. We then computed the theoretical isotope patterns of these compositions with the program emass (29). For each isotope pattern, we extracted the mass differences and abundance ratios between the monoisotopic and each of the higher isotope masses. The underlying distributions of these theoretical mass differences and abundance ratios provided the basis for novel isotope pattern models geared toward metabolites.

For each distribution of mass differences, we computed the mean and standard deviation. Based on the shifting elemental ratios toward higher masses and the distinct differences in mass between isotopes of different elements, we observed that the mass differences between isotope mass distributions are not constant. Instead, they change slightly, but systematically. We observed that the mass differences increased linearly from lower to higher isotopes. Instead of using fixed Gaussian models 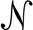(μ, σ²) for approximating each isotope mass spacing, we generalized the model generation by the linear equations

where j = 1, 2, …, 5 corresponds to the higher isotope peaks considered. This generalization simplifies the validation of feature hypotheses based on the mass differences Δm between the monoisotopic mass trace T₀ and an arbitrary number of higher isotopic mass traces T_j (j = 1, 2, …, k). The m/z distance m(j) = |m₀ − m_j| corresponds to the difference in their m/z estimates computed during the mass trace detection stage.

To assess the similarity between the observed and theoretical m/z distances, we formulated the following error model: For each pair of traces T₀, T_j with m/z variances σ₀² and σ_j² and a hypothetical charge z, the Gaussian models N_Δmz(μ(j), σ²(j)) are evaluated, where

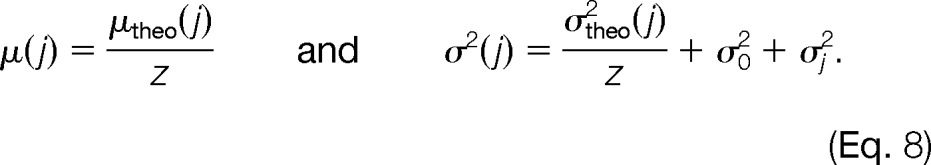This leads to the following scoring function for pairwise m/z distances:

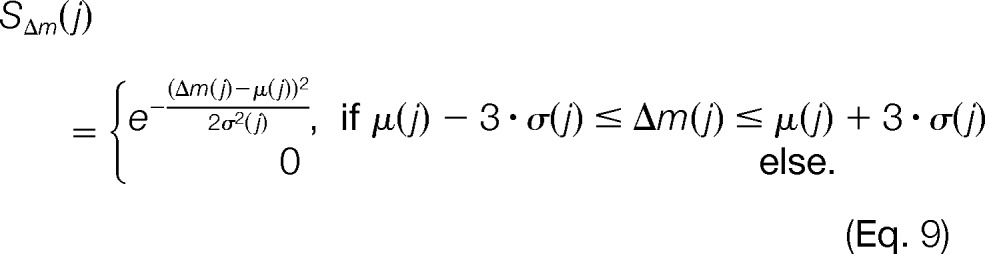In a nutshell, this scoring function assesses how likely it is that a set of mass traces were caused by the same metabolite based on a comparison to the precomputed mass difference distributions of potential metabolite compositions. It yields scores close to 1 for small mass differences, and scores decrease with increasing deviation from μ(j). For values that lie outside the interval defined by three times the standard deviation σ(j), the score becomes 0.

To ensure that mass traces compatible in m/z also exhibit similar elution profiles, we implemented a correlation similarity score as an orthogonal criterion. For each pair of mass traces T₀ and T_j, our algorithm first detects all peaks that are overlapping in both mass traces' full width at half-maximum regions. If this overlapping stretch comprises most of both full width at half-maximum regions (at least 70%), we compute the similarity score; otherwise, we set the score to 0. Given the mass traces' T₀ and T_j matched peak intensities (x_l, y_l), we compute their similarity with

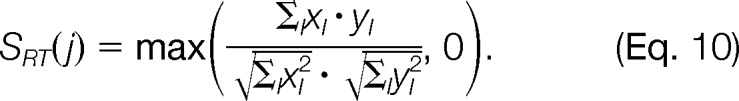If the algorithm finds a suitable candidate mass trace T_j for j = 1, the scoring procedure is repeated to find the subsequent higher isotope traces for j = 2, …, 5. We restrict the size of a feature hypothesis to up to six isotopic traces (monoisotopic trace plus up to five satellite traces). As soon as the list of potential candidates is exhausted, we select the mass trace next in M as a reference and construct all hypotheses supported by it. A candidate list C keeps track of all hypotheses that have been generated throughout this iterative process.

For each hypothesis H ∈ C, we compute a combined score S_combined as

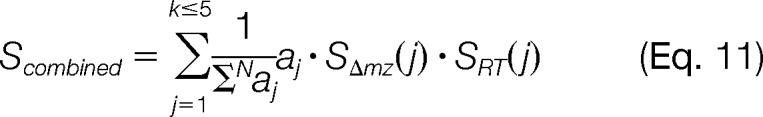In order to give preference to high-intensity signals over low-intensity ones, we weigh each score with the peak area a_j of mass trace T_j normalized by the total sum of the N detected mass traces in M.

We sort the candidate list C by decreasing score. Because C contains hypotheses built merely of mass traces compatible in retention time and m/z dimensions, it is very likely that co-eluting or partly overlapping isotope patterns are merged into one single hypothesis instead of distinct ones. Furthermore, a trace that is actually a higher isotopic trace of another pattern might erroneously be chosen as the monoisotopic trace of a hypothesis. To filter out such invalid hypotheses, we first consider each hypothesis by decreasing score, giving precedence to high-scoring hypotheses. Subsequently, we apply an isotope abundance filter to reject unlikely metabolite hypotheses.

Based on the theoretical isotope abundances extracted before, we train a support vector machine to distinguish typical metabolite patterns from unlikely intensity ratios. For each of the roughly 115,000 isotope patterns, we extract the first three isotope abundance ratios together with the monoisotopic mass. These constitute the four features of a training instance for the support vector machine classifier. Because the classifier must cope with isotope ratios from real-world measurements that are generally prone to errors, it might misclassify measured ratios when it is trained merely on theoretical isotope abundances. Consequently, we added Gaussian noise to each of the theoretical abundance ratios in order to model a root-mean-square error of 5%.

With the support vector machine classifier, the algorithm assesses each feature hypothesis H ∈ C. Hypotheses classified as invalid are discarded from C. In the final step, we traverse C sorted by descending hypothesis scores S_total and subsequently transfer feature hypotheses to a list of accepted features. In order to guarantee that no mass trace occurs in more than one feature, all remaining hypotheses containing already accepted mass traces are removed from C.

The final list of features is stored in an XML-based file format (featureXML) that contains both key properties (retention time, m/z, intensity, full width at half-maximum, and charge) and potential meta-information (e.g. unique identifier). The algorithm offers the option to report the feature intensity as either the chromatographic peak area of the monoisotopic trace alone or the sum of all isotopic peak areas.

Datasets

Assessing quantification algorithms is a difficult task, and one may be severely hampered by the complexity of the data and the lack of an exact ground truth if experimental datasets are used (for example, the presence of unknown/unexpected contaminants). At the same time, there is not a single performance measure for a quantification algorithm. It needs to be sensitive, accurate, fast, and robust. In order to assess the different aspects of our algorithms, we devised two complementary benchmarking strategies. For the first benchmarking setup, we conducted MS measurements with a concentration series of standard compounds that were spiked in human plasma. The resulting dataset allowed us to assess the algorithm's quantitation capabilities when used with a complex real-world sample. However, the exact number of true metabolite features in our experimental data is not known, and thus classical assessment by sensitivity and specificity is not feasible. Because there exist only a few freely available and fully annotated metabolomics datasets that could be used as ground truths, we computationally generated a synthetic dataset based on a published list of 500 well-characterized plant metabolites. This ground truth provided the basis for our second benchmarking setup, in which we aimed to quantify the algorithm's performance in terms of recall and precision rates.

Quantification Dataset

For the spike-in experiments with human plasma, we selected a set of seven standard compounds that provided both a reasonable distribution within the experimental gradient and good mass coverage. The standard compounds, together with their mass-to-charge ratios and retention times under the given experimental conditions, are shown in Table I.

Table I. Standard compounds of the spike-in experiments.

Standard	CAS-RN	m/z (u)	Retention time (min)
Propionyl-l-carnitine-d3	1182037-75-7	221.15751	1.4
Nialamide	51-12-7	299.15025	5.7
Sulfadimethoxine-d6	73068-02-7	317.11851	8.4
Reserpine	50-55-5	609.28065	10.6
Terfenadine	50679-08-8	472.32099	12.4
Hexadecanoyl-l-carnitine-d3	1334532-26-1	403.36096	16.6
Octadecanoyl-l-carnitine-d3	N.A.	431.39227	18.6

Sample Preparation

All aqueous solutions were prepared using LC-MS-grade water from Chromosolv®, Fluka Analytical (Sigma-Aldrich, Munich, Germany). LC-MS-grade acetonitrile and methanol were purchased from Chromosolv®, Fluka Analytical (Sigma-Aldrich, Munich, Germany). Formic acid (ultra-high-performance LC-MS grade) was procured from Biosolve (Valkenswaard, The Netherlands), and sodium hydroxide (≥98%) was obtained from Roth (Karlsruhe, Germany). Leucine enkephaline (≥95% HPLC grade), nialamide (95%), reserpine (≥99% HPLC grade), sulfadimethoxine-d6 (Vetranal^TM), and terfenadine were purchased from Sigma-Aldrich (Munich, Germany). [3,3,3-d3]-propionyl-l-carnitine hydrochloride, [16,16,16-d3]-hexadecanoyl-l-carnitine hydrochloride, and [18,18,18-d3]-octadecanoyl-l-carnitine hydrochloride were purchased from Dr. H.J. ten Brink Laboratory (Amsterdam, The Netherlands).

A stock solution for each standard was prepared at a concentration of 1 g/l. Each standard was mixed at the same concentration in 20% acetonitrile solution. An experimental standard serial dilution at 10 mg/l, 5 mg/l, 2 mg/l, 1 mg/l, 0.5 mg/l, 0.2 mg/l, 0.1 mg/l, 0.05 mg/l, 0.02 mg/l, and 0.01 mg/l was set. In addition, a non-spiked sample was included in the experiment.

Fresh EDTA blood was collected from healthy male donors. Blood plasma was prepared via centrifugation at 2,000g at 4 °C for 7 min. The resulting plasma was pooled, mixed, and aliquoted for storage at −80 °C until analysis.

Frozen EDTA plasma was thawed on ice and vortex-mixed for 30 s prior to treatment. The protein precipitation extraction was performed by adding cold acetonitrile (1 ml) to a plasma volume (250 μl). After the organic solvent had been added, the samples were vortex-mixed for 30 s at room temperature and centrifuged at 15,294g for 10 min at 4 °C. The dried samples were reconstituted in 50 μl of the different experimental standard solutions.

Ultra-high-performance LC-MS Analysis

Sample analysis was performed using a Waters Aquity ultra-high-performance LC system coupled to a Synapt HDMS oa-Q-TOF mass spectrometer (Waters, Milford, MA) equipped with an electrospray ion source operating in positive mode. The gradient chromatographic separation was performed with a C18 Vision HT-HL ultra-high-performance LC column (2 × 150 mm, 1.5 μm, Alltech Grom GmbH, Rottenburg-Hailfingen, Germany). Elution buffer A was water containing 0.1% formic acid, and elution buffer B was acetonitrile. The flow rate was set at 0.300 ml/min. The linear-gradient method consisted of 5% B over 0–1.12 min, 5% to 100% B over 1.12–22.27 min, and 100% B until 29.49 min, after which the gradient was returned to 5% B at 29.56 min. In order to equilibrate the column with the initial mobile phase, 5% B was maintained until minute 35. The column oven was set to 40 °C, and the sample manager temperature to 4 °C. A solution of leucine enkephalin (556.2771 u, 400 pg/μl) in MeOH/H₂O:1/1 containing 0.1% formic acid was infused as lockmass compound at a flow rate of 5 μl/min. The spectra were acquired in centroid mode within a range of 50–1000 u. The detection parameters are described in the supplemental material (see supplemental Table S6).

The samples were measured in randomized triplicate and alternated with blank samples consisting of 20% acetonitrile. All data files were converted into mzML format (31) using the command line tool msconvert of the ProteoWizard suite (32).

For each measurement, we extracted metabolite features with our algorithm and stored the resulting feature map in the featureXML data format (6). For the following processing steps, we used existing software solutions from the OpenMS framework (version 1.10). Features coinciding on at least two measurements were aggregated to consensus features and stored in the consensusXML format using the FeatureLinkerUnlabeledQT software. The consensusXML file was exported to a tabular text format with the TextExporter tool. All further analyses were conducted with the MATLAB R2012b (33) and R 2.15.2 (34) software packages.

Simulated Plant Metabolite Dataset

For the generation of synthetic LC-MS datasets, we employed the software package MSSimulator (35). The simulator creates profile data based on the experimentally determined retention time and the composition of a set of compounds. It can simulate different instrument resolutions, noise levels, and chromatographic performances. The datasets created here were based on experimentally identified metabolites and thus captured the complexity of a real-world sample. At the same time, the simulator provides complete control over signal-to-noise ratio, accuracy, and similar parameters that would be very difficult to vary independently of each other experimentally.

The dataset was based on a list of identified plant metabolites from a rather comprehensive study by Giavalisco et al. (36). The authors reported the elemental composition, intensity, and retention time of hundreds of metabolites in the supplementary information for their study. This information is all that was needed in order to create synthetic datasets with characteristics typical of a complex metabolomics study. MSSimulator performed a raw signal simulation of 500 metabolites within the range of 100–1,000 m/z and with a simulated gradient runtime of 25 min. The machine-dependent settings of MSSimulator were chosen to be close to those of our experimental MS setup: The simulated MS resolution R was set to 20,000, and the scan time was set at 0.25 s. The output of MSSimulator consists of a centroided LC-MS measurement and a feature map summarizing all simulated metabolites with theoretical retention times, m/z ratios, and intensities. This feature map facilitates comparison between the ground truth (the simulator's input) and the features detected by our algorithm applied to the same simulated data.

To assess the influence of different sources of noise on the feature-finding performance, we conducted three series of MS simulations, each affected by detector noise, m/z variation, or elution profile distortion. In the first series, we simulated increasing levels of detector noise that were controlled by the Gaussian standard deviation σ_det. The second series comprised two datasets simulated with moderate and strong mass errors (Gaussian standard deviation σ_m/z set to 10 ppm and 40 ppm, respectively). For the third series, we simulated elution profiles with ideal peak shapes and heavily distorted shapes. In MSSimulator, the degree of distortion is controlled by the number of iterations n_dist; that is, the greater the number of iterations performed, the more the elution profiles deviate from their smooth Gaussian shape. The configuration for each simulation is summarized in the supplemental material (see supplemental Table S5).

For performance evaluation, we computed both the recall r and the precision p based on the number of ground truth features and the number of features found or missed by our algorithm. These measures can be combined into the F-score (37), defined as

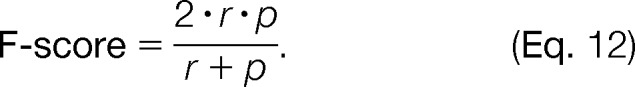For each of the simulated datasets, we employed our algorithm to detect a feature map and compute its F-score. The resulting scores were plotted with respect to either varying MSSimulator parameters (e.g. σ_det) or parameters of our feature-finding algorithm.

Comparison to Related Methods

We repeated the performance assessments done with our algorithm with the XCMS and CAMERA packages (Bioconductor versions 1.34 and 1.14, respectively) (7, 10), which are currently considered to be among the leading feature-detection algorithms. For each experiment, we adjusted the corresponding parameter settings of the XCMS software to the best of our knowledge. Because the feature set found by XCMS was not deisotoped and thus would not allow for a fair comparison, we additionally employed the CAMERA package to detect higher isotope masses in the XCMS output.

To allow for a direct comparison to our method, we first converted the XCMS/CAMERA output to a compatible feature map. For each set of annotated isotope traces in the XCMS/CAMERA output, we kept the retention time, m/z value, and intensity of the first isotope in a tabular format and discarded the higher ones. CAMERA clustered multiple adducts belonging to the same compound together; we resolved these clusters and stored each contained feature individually. Non-annotated features were regarded as singleton mass traces and were added to the same table. This extraction procedure resulted in condensed feature lists that were converted to the featureXML file format with the FileConverter software (6). We employed the FeatureLinkerUnlabeledQT software to link features that were detected by both our algorithm and XCMS/CAMERA.

RESULTS

In this section, we assess the performance of our algorithm from different perspectives. First, we present the results obtained from the quantification dataset as introduced in the section “Quantification Dataset”. We examine the linearity of the response observed in spike-in experiments as a measure of the quality of absolute and relative quantification. Then, we assess the reproducibility of the feature-finding process by determining the number of features detected over technical replicates. In order to dissect some effects of the data quality on the behavior of the algorithm in more detail, we show results obtained with a simulated dataset. With the general quality of the methods already demonstrated on real-world data, simulated data permit the independent variation of certain characteristics and the determination of an independent ground truth. Finally, we repeated the benchmarking studies with the state-of-the-art software packages XCMS and CAMERA, and we compare the results to the performance of our algorithm.

Quantification Linearity and Reproducibility

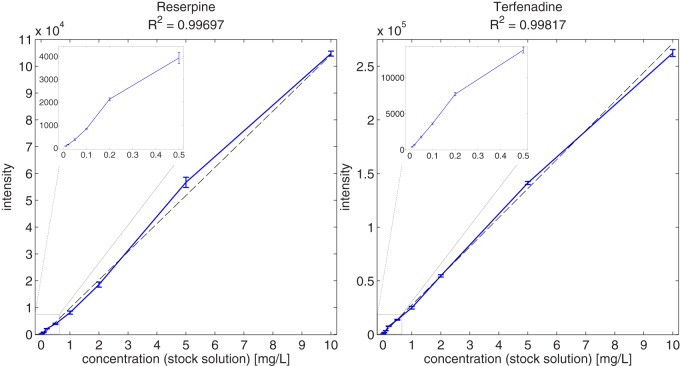
Based on the spike-in series in a complex plasma background, we can assess both the linearity (11 different concentrations spanning 3 orders of magnitude) and the reproducibility of the quantification (based on triplicate measurements). With the detection of the standard compound features for each of the human plasma spike-in experiments and their subsequent linking, we obtained intensities for each analyte and dataset. Supplemental Table S10 lists the corresponding mean feature intensities and standard deviations across the triplicate measurements performed for each concentration of the analytes. We show the relationship between the analytical concentrations and their corresponding feature intensities for two selected standard compounds (reserpine and terfenadine) in Fig. 2; the reader may refer to the supplemental material for the remaining standard compounds (see supplemental Figs. S11 and S12). For each concentration, we found rather little variation between the triplicate feature intensities (in general, 2 orders of magnitude smaller than the mean intensity) and thus good reproducibility of both the LC-MS measurements and the feature-detection algorithm. The Pearson correlation coefficient between each compound's concentrations and corresponding feature intensities revealed an excellent linear relationship (R≥ 0.98 for all standard compounds). This result suggests that the relative quantification of analytes with our algorithm is reliable for a wide range of concentrations (in the presented example, about 3 orders of magnitude). In the case of the propionyl-l-carnitine-d3 standard, we could not detect any signals for the first six concentrations, either with our algorithm or by visual inspection of the raw data.

Fig. 2.

Relationship between stock solution concentrations and feature intensities for reserpine and terfenadine. For each concentration, an error bar depicts the standard deviation of the triplicate intensities. The solid line connects the mean intensities obtained from each of the 11 triplicates. For each compound, a line was fit via linear regression to the 33 concentration-intensity data points with the goodness-of-fit R² (dashed line). The inlaid plots show a close-up of the low-concentration range between 0 and 0.5 ppm.

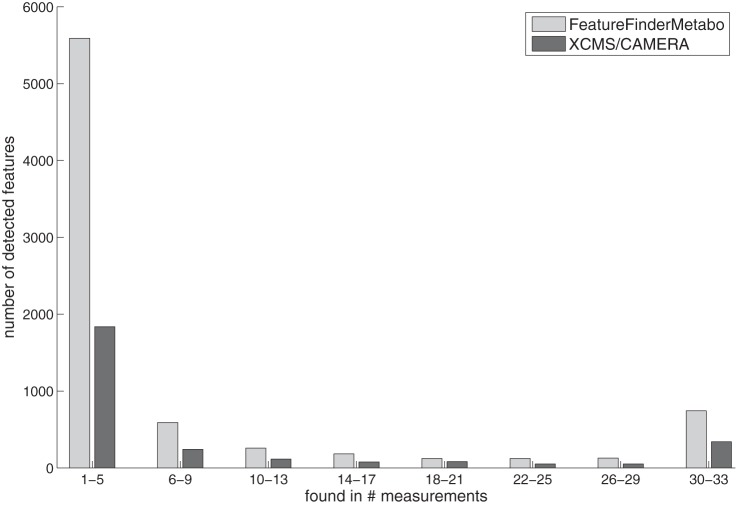
Apart from the standard compounds, the algorithm detected on average 2,020 ± 236 features per measurement, of which about 351 were singly, 12 doubly, and 6 triply charged. The remaining features were singleton mass traces that exhibited no isotope pattern (e.g. low signal intensity) and thus did not allow a determination of the charge state. Because the ground-truth set of real metabolites was unknown for the plasma samples, a distinction between real metabolite features and random features (e.g. noise, contaminants) was not possible. To address this issue, we determined the percentage of measurements in which each feature was detected. This detection rate is a measure of reproducibility and may serve as a rough guide to distinguish randomly occurring features from potential metabolite features. A bar plot shows the distribution of these detection rates (see Fig. 3). We found a set of 1,168 features to be reproducible in at least 50% of all measurements. We then compared this feature set to the features detected in each individual measurement and determined the size of the intersection. On average, we found 1,066 ± 36 reproducible features in each of the 33 measurements—that is, about 53% with respect to the average feature number of 2,020. When we queried this feature list against the Human Metabolome Database (38), 768 of the accurate masses yielded a hit (i.e. about 74% could be assigned to at least one potential metabolite ID).

Fig. 3.

Numbers of reproducible features yielded by our algorithm and XCMS/CAMERA in the spike-in human plasma dataset. Each bin of the histogram plot represents a number of measurements a feature was reproducibly detected in. The bars show the absolute numbers of features that were detected with the respective reproducibility.

Finally, we considered the variation in the intensity of coinciding features among all measurements (features corresponding to the spiked-in standard compounds were excluded). We grouped these features into three intensity bins (i.e. magnitudes of order) to determine the dependence of feature quantification as a function of feature intensity (see Fig. 4). In the first intensity bin (intensities between 10² and 10³), we observed a median variation of about 16.0%. The second intensity bin (intensities between 10³ and 10⁴) showed a median variation of 14.9%; this value finally reached 14.7% in the highest intensity bin (intensities between 10⁴ and 10⁵). These findings confirm good reproducibility in terms of feature intensity when feature sets are compared between technical replicates even for low-intensity features.

Fig. 4.

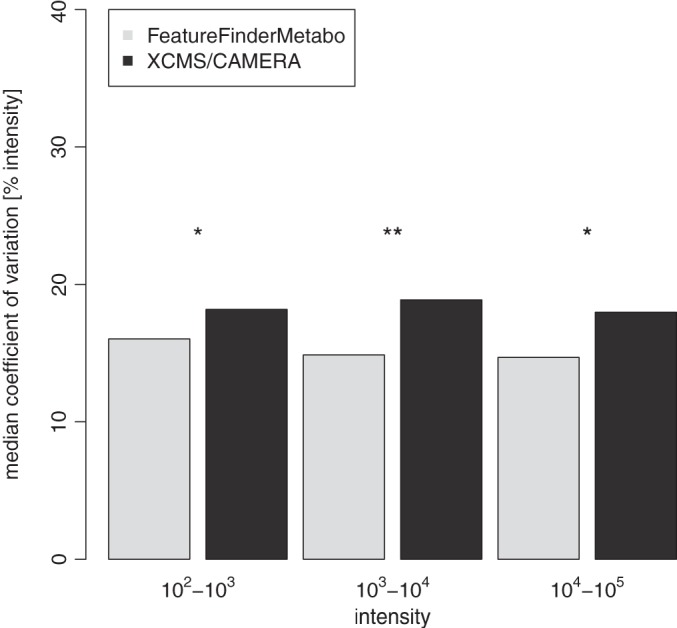
Intensity variation between features that were matched in at least half of the 33 spike-in human plasma measurements. For each matched feature, we computed the intensities' coefficients of variation over the respective measurements. All matched features were distributed to three bins with respect to the intensity's magnitude of order. Based on the intensity bin's underlying distributions, median coefficient of variation values were determined and are depicted in the bar plot. We conducted one-sided Wilcoxon tests to investigate whether the observed difference in the median coefficients of variation among the methods was significant. The results from the pairwise comparisons are marked according to significance level (asterisks). To enable a direct comparison of FeatureFinderMetabo and XCMS/CAMERA feature intensities, we normalized all measurements by quantile normalization.

Recall, Precision, and Robustness of the Algorithm

In order to determine the precision and recall of the methods, as well as the dependence of the algorithm's performance on noise and instrument accuracy, we chose to employ simulated datasets. For the human plasma dataset, the computation of these metrics was not possible because the ground truth was unknown. Thus, we created a dataset with a known ground truth that was based on a metabolomics investigation of plant metabolites (36); however, elution profiles and isotope patterns were created synthetically so that we could control these parameters independently, which is not easily done in an arbitrary fashion experimentally. Even if it were varied experimentally—for example, by repeated measurements modifying instrument resolution—we would not be able to remove intersample variance. The simulation also did not contain unknown contaminants so we could determine true recall and precision rates based on the known (simulated) ground truth.

When we simulated the dataset with parameters set to simulate experimental results most closely, we observed excellent precision and recall of the features of 97% and 96%, respectively (see Table II).

Table II. Performance scores computed for the simulated plant metabolite dataset (the algorithmic parameters were set appropriately to the simulated characteristics of the data).

Method	Recall	Precision	F-score
FeatureFinderMetabo	0.96	0.97	0.97
XCMS/CAMERA	0.88	0.37	0.52

Unsurprisingly, increasing noise levels in the simulated data decreased both the precision and the recall of the method. In extreme noise settings, F-scores can drop to significantly lower values. The decline in performance primarily resulted from the loss in feature recall rate—detecting features reliably becomes more difficult as the signal-to-noise ratio decreases. Details of this experiment are shown as part of the supplemental material (see supplemental Fig. S7). The method was more robust against increases in the mass error and chromatographic distortion. In such cases, it yielded maximum F-scores between 0.97 and 0.9. Because mass accuracy and chromatographic peak width are parameters of the algorithms, it is interesting to observe how performance is affected by an incorrect choice of these parameters. For both parameters, we found that the performance decreased marginally with a moderate underestimation and remained stable with a moderate overestimation. These results suggest that our algorithm is robust against significant deviations of these parameters from the characteristics of the dataset (see supplemental Figs. S8 and S9).

Comparison to Related Methods

By repeating the benchmarks described above with XCMS/CAMERA, we were able to compare the performance of our method to that of the current leading algorithms in the field. Results of that comparison are summarized in Table II. For each of the human plasma measurements, XCMS/CAMERA yielded 691 ± 72 features. We linked the feature sets of all 33 experiments and computed their detection rates (see Fig. 3). Features with a detection rate above 50% were extracted, yielding a set of 544 reproducible features. For the comparison of XCMS/CAMERA with our algorithm in terms of performance, we considered the overlap between the reproducible feature sets. Both methods detected a set of 361 common features, whereas XCMS/CAMERA and our algorithm found 183 and 807 exclusive features, respectively. Thus, our algorithm detected a substantial proportion (66%) of the XCMS/CAMERA feature set. At the same time, XCMS/CAMERA found only about 31% of our algorithm's feature set. The high number of exclusive features indicates that our algorithm exhibited greater sensitivity than XCMS/CAMERA. To verify the soundness of our exclusively detected feature set, we examined its intensity distribution and found the majority of feature intensities to be between 10² and 10³. This suggests that the exclusive features stemmed mainly from high sensitivity in the low-intensity range. As we restricted this comparison to highly reproducible features, we assumed that our algorithm's exclusive features originated from weakly concentrated analytes rather than spuriously detected artifacts, an assumption that was confirmed by visual inspection of the datasets. With regard to intensity variation between replicate features, the comparison revealed that our algorithm exhibited slightly less variation (14.7% to 16.0%) than XCMS/CAMERA (18.0% to 18.9%) across all intensity ranges (see Fig. 4). We observed that these differences in intensity variation were statistically significant between XCMS/CAMERA and our method, but not between different intensity ranges (based on a Wilcoxon test with p < 0.05).

We compared the benchmarking results of XCMS/CAMERA and our algorithm in terms of simulated mass error and chromatographic peak distortion. In both mass error simulations, our algorithm gave higher F-scores for the complete range of tested parameter settings than XCMS/CAMERA (see supplemental Fig. S8). When we set the algorithm's mass error parameters according to the simulated error of 10 ppm (40 ppm), XCMS/CAMERA achieved an F-score of 0.52 (0.75) and our algorithm achieved an F-score of 0.97 (0.95). Furthermore, the performance plots revealed differences in the robustness of the mass error parameter. Whereas the parameter was insensitive to moderate under- and overestimation in our algorithm, in XCMS/CAMERA it was more susceptible to minor changes (see supplemental Fig. S8, right-hand plot).

Availability

The feature-detection algorithm presented in this work was implemented and integrated in the open-source framework OpenMS (version 1.10) as the software tool FeatureFinderMetabo. The FeatureFinderMetabo tool can be evoked on the command-line or out of TOPPView, the OpenMS graphical user interface for processing and analyzing mass spectrometry data. Parameter settings are stored in XML-based configuration files (*.ini) that can be modified using the INIFileEditor tool (see supplemental Fig. S13). As an input file format, FeatureFinderMetabo accepts the mzML standard (31) and stores the results in the featureXML file format. FeatureXML files can be read and further processed by other OpenMS tools, such as MapAlignmentPoseClustering for retention time correction or FeatureLinkerUnlabeledQT for linking coinciding features from multiple experiments.

OpenMS offers the functionality to build custom processing and analysis pipelines through the graphical workflow editor TOPPAS (22). We employed TOPPAS to construct an example workflow for label-free metabolite quantification. This tool chain comprises feature detection, retention time correction, feature linking, and the ability to export to a tabular text file for subsequent statistical analyses. In order to allow for easy integration of downstream analysis methods such as statistical learning, we implemented this workflow in KNIME, a powerful platform for information mining (39). Both OpenMS 1.10 and workflows based on FeatureFinderMetabo are available online at the OpenMS website (6).

DISCUSSION

The feature-finding method introduced in this work, the OpenMS FeatureFinderMetabo, is a sensitive and reliable method for identifying metabolite features in LC-MS data. It is based on sensitive mass trace detection and hypothesis-driven feature assembly. Model scoring with a hybrid mass deviation and isotope profile scoring results in accurately assembled features. An important component of the scoring function is the detection of likely metabolite profiles by means of statistical learning methods.

The algorithm can determine feature intensities of metabolites with high sensitivity and specificity (above 95% on typical data). Even in complex backgrounds (human plasma), we found excellent linearity of the quantification based on repeated spike-in experiments. In a direct comparison, FeatureFinderMetabo was able to outperform established methods for LC-MS feature detection. Primarily in the low-intensity range, we were able to pick up signals with poor signal-to-noise ratios, and thus analyzing LC-MS data with FeatureFinderMetabo might reveal interesting new metabolites, or at least expand the dynamic range of metabolomics analyses. Implementation of FeatureFinderMetabo as an OpenMS/TOPP tool could ensure platform independence of the tool and convenient availability.

We designed the feature assembly algorithm to reconstruct isotope patterns only. Although it is a common strategy to also detect different adducts and charge states belonging to the same analyte and integrate these into a unique feature, we believe that this problem should be tackled in a separate processing step. Adducts of the same compound may show great variation in their ionization behavior and thus are difficult to detect accurately.

Future improvements of the algorithms will include a more advanced noise estimation model in order to increase the specificity of the algorithm. We are also exploring methods making use of multiple (replicate) measurements that collate information across multiple LC-MS runs in order to increase both the precision and the recall of the method.