Finite Element Modeling of Impulsive Excitation and Shear Wave Propagation in an Incompressible, Transversely Isotropic Medium

Abstract

Elastic properties of materials can be measured by observing shear wave propagation following localized, impulsive excitations and relating the propagation velocity to a model of the material. However, characterization of anisotropic materials is difficult because of the number of elasticity constants in the material model and the complex dependence of propagation velocity relative to the excitation axis, material symmetries, and propagation directions. In this study, we develop a model of wave propagation following impulsive excitation in an incompressible, transversely isotropic (TI) material such as muscle. Wave motion is described in terms of three propagation modes identified by their polarization relative to the material symmetry axis and propagation direction. Phase velocities for these propagation modes are expressed in terms of five elasticity constants needed to describe a general TI material, and also in terms of three constants after the application of two constraints that hold in the limit of an incompressible material. Group propagation velocities are derived from the phase velocities to describe the propagation of wave packets away from the excitation region following localized excitation. The theoretical model is compared to the results of finite element (FE) simulations performed using a nearly incompressible material model with the five elasticity constants chosen to preserve the essential properties of the material in the incompressible limit. Propagation velocities calculated from the FE displacement data show complex structure that agrees quantitatively with the theoretical model and demonstrates the possibility of measuring all three elasticity constants needed to characterize an incompressible, TI material.

1. Introduction

Physicians use manual palpation as part of the diagnostic process because diseased tissue is often stiffer than surrounding healthy tissue. Recently, a number of imaging methods have been developed for characterizing tissue stiffness in vivo by exciting shear waves in the tissue and measuring the shear wave propagation speed (Sarvazyan, et al., 1998; Sandrin, et al., 2003). These systems generate shear waves in tissue using either external mechanical excitation coupled to the body wall (Yin, et al., 2007; Huwart, et al., 2006) or acoustic radiation force impulse (ARFI) excitations to remotely palpate tissue at the focal region of an acoustic beam (Bercoff, et al., 2004; Chen, et al., 2004; Nightingale, et al., 2003). Wave propagation is monitored in space and time by a real-time imaging modality such as magnetic resonance imaging or ultrasound tracking, and the tissue stiffness is determined quantitatively by measuring the shear wave propagation speed.

Two elasticity constants are required to characterize a linear, elastic, isotropic material (Lai, et al., 1999). For example, the Lamé constants λ and μ could be specified and used to calculate related constants such as the Young’s modulus, bulk modulus, and Poisson’s ratio. For nearly incompressible materials such as many biological tissues, λ and μ often differ by a factor on the order of 10⁶, with a corresponding difference in longitudinal and shear wave speeds of 10³. Finite element (FE) models of these materials use a Poisson ratio nearly equal to the limiting value of 0.5 which characterizes an incompressible material (Palmeri, et al., 2005). Typically, ultrasonic or magnetic resonance imaging methods used to track wave propagation in these material only attempt to measure the shear modulus.

The characterization of anisotropic materials requires more elasticity constants in the material model. For example, in a linear, elastic, transversely isotropic (TI) material, a symmetry axis exists and the material can be characterized by five elasticity constants (Lai, et al., 1999). Muscle is an example of a TI material with the symmetry axis defined by the orientation of the muscle fibers. Measurements of shear wave speed for propagation along and across the muscle fibers has been reported (Gennisson, et al., 2003; Papazoglou, et al., 2006; Gennisson, et al., 2010; Royer, et al., 2011). Recently,Wang, et al. (2013a) have measured the angular dependence of phase and group velocities for shear wave propagation in muscle using 3D volumetric measurements performed using a 2D matrix array (Wang, et al., 2013b).

Wave propagation in anisotropic materials has been studied in several diverse areas. One example of wave propagation in TI materials occurs in layered media in seismology where the symmetry axis is perpendicular to the layers (Carcione, 2001; Tsvankin, 2001). Another example occurs in crystallography (Auld, 1990; Musgrave, 1970), where the hexagonal crystal structure has TI symmetry.

In this study, we consider FE modeling of impulsive excitation and wave propagation in an incompressible, TI medium. The focus of the study centers around three primary components as follows. First, the elasticity constants needed to describe an incompressible, TI material are identified, and FE models are constructed using a nearly incompressible material model which preserves the essential properties of the incompressible model. Second, the geometrical configuration for the excitation, material symmetry axis, and wave propagation are chosen to simulate the experimental setup commonly used in ARFI excitation and ultrasonic tracking experiments. Finally, the angular dependence of measured wave velocities are compared with theoretical predictions to demonstrate how the elasticity constants can be determined from experimental measurements. The results of the study demonstrate that with an appropriate experimental configuration, it is possible to measure all of the elasticity constants required to characterize an incompressible, TI material such as muscle.

2. Wave Propagation in an Incompressible, TI Medium

2.1. TI Materials

In the limit of small displacements, such as those produced in ARFI excitations, the stress-strain relationship in an anisotropic material is linear and can be described by a generalized Hooke’s law as

$${\sigma }_{ij}=c_{ijkl}{\epsilon }_{kl}$$ (1)

where c_ijkl are components of a fourth-order stiffness tensor and summation over repeated indices is implied. Symmetries of the stress and strain tensors and the existence of a strain energy allow the stiffness tensor to be expressed in terms of 21 independent elements (Lai, et al., 1999). Then the stress-strain relations (1) can be written as a matrix product,

$$\left(\begin{array}{c}\hfill {\sigma }_{11}\hfill \\ \hfill {\sigma }_{22}\hfill \\ \hfill {\sigma }_{33}\hfill \\ \hfill {\sigma }_{23}\hfill \\ \hfill {\sigma }_{31}\hfill \\ \hfill {\sigma }_{12}\hfill \end{array}\right)=C\left(\begin{array}{c}\hfill {\epsilon }_{11}\hfill \\ \hfill {\epsilon }_{22}\hfill \\ \hfill {\epsilon }_{33}\hfill \\ \hfill 2{\epsilon }_{23}\hfill \\ \hfill 2{\epsilon }_{31}\hfill \\ \hfill 2{\epsilon }_{12}\hfill \end{array}\right)$$ (2)

where C is a 6 × 6 symmetric stiffness matrix (Lai, et al., 1999).

Transversely isotropic (TI) materials possess an axis of symmetry  such that reflection symmetry exists across every plane parallel to  and rotation symmetry exists about Â. Muscle is an example of a TI material with the axis  given by the direction of the muscle fibers. These symmetries imply that five independent elastic constants are required to specify the stiffness matrix C (Lai, et al., 1999). Relative to an x₁, x₂, x₃ coordinate system oriented so that x̂₃ = Â, C is given by (Lai, et al., 1999)

$$C=\left(\begin{array}{cccccc}\hfill C_{11}\hfill & \hfill C_{12}\hfill & \hfill C_{13}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill C_{12}\hfill & \hfill C_{11}\hfill & \hfill C_{13}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill C_{13}\hfill & \hfill C_{13}\hfill & \hfill C_{33}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{55}\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{55}\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill C_{66}\hfill \end{array}\right)$$ (3)

where missing elements are zero and

$$C_{66}=\frac{C_{11}-C_{12}}{2}.$$ (4)

For TI materials, the elements of the stiffness matrix can be expressed in terms of Young’s moduli E_T and E_L, Poisson’s ratios ν_LT and ν_TT, and shear moduli μ_T and μ_L where the longitudinal (L) and transverse (T) directions are defined relative to the material symmetry axis. In terms of the compliance matrix S = C⁻¹ (Lai, et al., 1999),

$$S=C^{-1}=\left(\begin{array}{cccccc}\hfill 1/E_T\hfill & \hfill -{\nu }_{TT}/E_T\hfill & \hfill -{\nu }_{LT}/E_L\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -{\nu }_{TT}/E_T\hfill & \hfill 1/E_T\hfill & \hfill -{\nu }_{LT}/E_L\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -{\nu }_{LT}/E_L\hfill & \hfill -{\nu }_{LT}/E_L\hfill & \hfill 1/E_L\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1/{\mu }_L\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1/{\mu }_L\hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 1/{\mu }_T\hfill \end{array}\right)$$ (5)

where

$${\mu }_T=\frac{E_T}{2(1+{\nu }_{TT})}.$$ (6)

2.2. Incompressible TI Materials

For an incompressible material, the fractional volume change, or dilatation e, of an infinitesimal volume subjected to stresses must be zero. The dilatation is given by the trace of the strain tensor (Lai, et al., 1999) and can be expressed in terms of the elastic constants using (2) and (5) as

$$e=\frac{1}{E_T}(1-{\nu }_{TT}-{\nu }_{LT}\frac{E_T}{E_L})({\sigma }_{11}+{\sigma }_{22})+\frac{1}{E_L}(1-2{\nu }_{LT}){\sigma }_{33}.$$ (7)

For an incompressible material, both of the terms on the right hand side of (7) must be zero, and the Poisson ratios satisfy two conditions,

$${\nu }_{TT}=1-\frac{E_T}{2E_L}$$ (8)

and

$${\nu }_{LT}=\frac{1}{2}.$$ (9)

These results agree with those of Papazoglou, et al. (2006). Thus, three independent elastic constants are needed to describe an incompressible TI material compared to five constants in the general TI case. In the following, results are expressed in terms of the constants μ_T, μ_L, and E_T/E_L.

2.3. Wave Dynamics

Assuming no external body forces, the acceleration of an infinitesimal volume of material with density ρ can be expressed using Newton’s second law in terms of the displacement u⃗ and the stress gradient across the volume as (Tsvankin, 2001)

$$\frac{\partial {\sigma }_{ij}}{\partial x_j}=\rho \frac{{\partial }^2{u}_i}{\partial t^2}.$$ (10)

Expressing elements of the strain tensor in terms of the gradient of displacement and using (1) gives the wave equation,

$$c_{ijkl}\frac{{\partial }^2{u}_k}{\partial x_j\partial x_l}=\rho \frac{{\partial }^2{u}_i}{\partial t^2}.$$ (11)

Plane wave solutions of (11) with phase velocity ν = ω/k, propagation direction n̂, and polarization P⃗ = (P₁, P₂, P₃)^T (i.e., the direction of the particle displacement) are given by

$$\overrightarrow{u}=\left(\begin{array}{c}\hfill P_1\hfill \\ \hfill P_2\hfill \\ \hfill P_3\hfill \end{array}\right)e^{i(k\mathrm{n̂}·\overrightarrow{r}-\omega t)}.$$ (12)

Inserting (12) into (11) gives an eigenequation for the phase velocities and polarization vectors,

$$\left(\begin{array}{ccc}\hfill {\mathrm{\Gamma }}_{11}\hfill & \hfill {\mathrm{\Gamma }}_{12}\hfill & \hfill {\mathrm{\Gamma }}_{13}\hfill \\ \hfill {\mathrm{\Gamma }}_{21}\hfill & \hfill {\mathrm{\Gamma }}_{22}\hfill & \hfill {\mathrm{\Gamma }}_{23}\hfill \\ \hfill {\mathrm{\Gamma }}_{31}\hfill & \hfill {\mathrm{\Gamma }}_{32}\hfill & \hfill {\mathrm{\Gamma }}_{33}\hfill \end{array}\right)\left(\begin{array}{c}\hfill P_1\hfill \\ \hfill P_2\hfill \\ \hfill P_3\hfill \end{array}\right)=\rho {\nu }^2\left(\begin{array}{c}\hfill P_1\hfill \\ \hfill P_2\hfill \\ \hfill P_3\hfill \end{array}\right)$$ (13)

where elements of the matrix Γ are given by Γ_ij = c_ijkln_kn_l.

2.4. PT, QT, and QL Propagation Modes in a TI Medium

The three solutions of (13) give the polarizations and phase velocities for three plane wave propagation modes. Explicit solutions for these modes can be obtained by choosing a coordinate system oriented with x̂₃ = Â and n̂ in the x₁ − x₃ plane at an angle θ relative to the x₃ axis so that n̂ = (sinθ, 0, cosθ)^T. For a TI medium with stiffness matrix (3), Γ is given by

$$\mathrm{\Gamma }=\left(\begin{array}{ccc}\hfill C_{11}{\text{sin}}^2\theta +C_{55}{\text{cos}}^2\theta \hfill & \hfill 0\hfill & \hfill (C_{13}+C_{55})\times \text{sin}\theta \text{cos}\theta \hfill \\ \hfill 0\hfill & \hfill C_{66}{\text{sin}}^2\theta +C_{55}{\text{cos}}^2\theta \hfill & \hfill 0\hfill \\ \hfill (C_{13}+C_{55})\times \text{sin}\theta \text{cos}\theta \hfill & \hfill 0\hfill & \hfill C_{55}{\text{sin}}^2\theta +C_{33}{\text{cos}}^2\theta \hfill \end{array}\right).$$ (14)

Using (14), one solution of (13) consists of particle displacements perpendicular to the x₁ − x₃ plane. We refer to this solution as the pure transverse (PT) mode,

$${\mathrm{P̂}}_{PT}=\left(\begin{array}{c}\hfill 0\hfill \\ \hfill 1\hfill \\ \hfill 0\hfill \end{array}\right),$$ (15)

and

$$\rho {\nu }_{PT}^2={\mu }_T{\text{sin}}^2\theta +{\mu }_L{\text{cos}}^2\theta$$ (16)

where C₆₆ = μ_T and C₅₅ = μ_L from (3) and (5).

The polarization vectors of the second and third eigensolutions of (13) lie in the x₁ − x₃ plane, but are not, in general, longitudinal and transverse to the propagation direction (Carcione, 2001). We refer to these solutions as the quasi-longitudinal (QL) and quasi-transverse (QT) propagation modes,

$${\mathrm{P̂}}_{QL,QT}=\left(\begin{array}{c}\hfill \sqrt{\frac{C_{33}{\text{cos}}^2\theta +C_{55}{\text{sin}}^2\theta -\rho {\nu }_{QL,QT}^2}{C_{11}{\text{sin}}^2\theta +C_{33}{\text{cos}}^2\theta +C_{55}-2\rho {\nu }_{QL,QT}^2}}\hfill \\ \hfill 0\hfill \\ \hfill \sqrt{\frac{C_{11}{\text{sin}}^2\theta +C_{55}{\text{cos}}^2\theta -\rho {\nu }_{QL,QT}^2}{C_{11}{\text{sin}}^2\theta +C_{33}{\text{cos}}^2\theta +C_{55}-2\rho {\nu }_{QL,QT}^2}}\hfill \end{array}\right),$$ (17)

and

$$\rho {\nu }_{QL,QT}^2=\frac{1}{2}(C_{11}{\text{sin}}^2\theta +C_{33}{\text{cos}}^2\theta +C_{55}\pm \sqrt{\mathrm{\Delta }})$$ (18)

where the QL and QT labels correspond to the upper and lower signs in (18), respectively, and

$$\mathrm{\Delta }={[(C_{11}-C_{55}){\text{sin}}^2\theta +(C_{55}-C_{33}){\text{cos}}^2\theta ]}^2+4{(C_{13}+C_{55})}^2{\text{sin}}^2\theta {\text{cos}}^2\theta .$$ (19)

2.5. Propagation Modes in an Incompressible TI Medium

The phase velocities and polarization vectors in an incompressible medium can be found by expressing the elements of the stiffness matrix in terms of the elasticity constants using (5), and evaluating (15), (16), (17), and (18) in the limit with the Poisson ratios given by (8) and (9). For the PT propagation mode, (15) and (16) are independent of the Poisson ratios and these relations hold for both compressible and incompressible media. For the QL and QT propagation modes, it can be shown that ν_QL diverges and that ν_QT is given by

$$\rho {\nu }_{QT}^2={\mu }_L+4(\frac{E_L}{E_T}{\mu }_T-{\mu }_L){\text{sin}}^2\theta {\text{cos}}^2\theta .$$ (20)

This result agrees with those given by Chadwick (1993) and Papazoglou, et al. (2006). Also in the incompressible limit, it can be shown that the QL and QT polarizations in (17) are purely longitudinal and purely transverse, respectively.

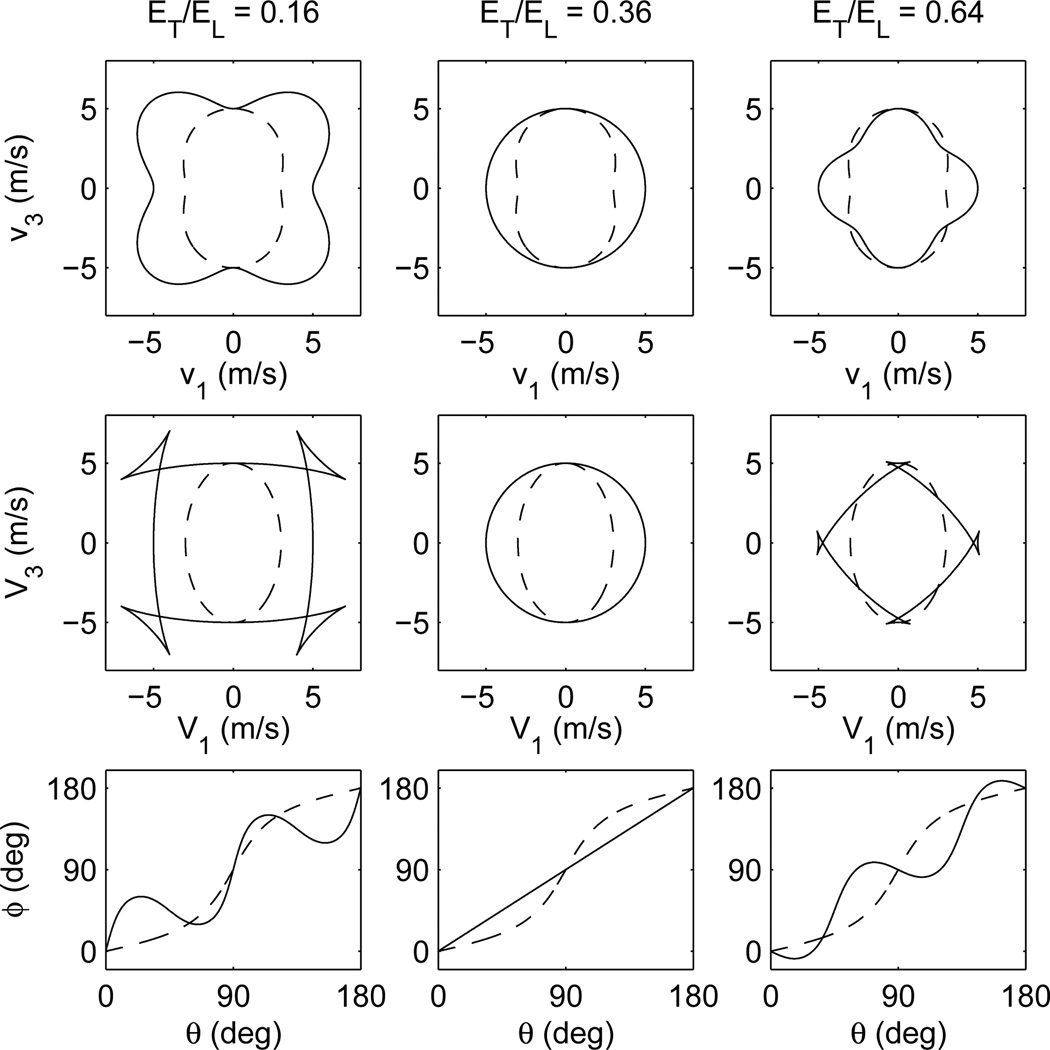
The top row of Fig. 1 shows parametric plots of the PT and QT phase velocities calculated using (16) and (20) with μ_T = 9 kPa, μ_L = 25 kPa, and E_T/E_L = 0.16, 0.36, and 0.64.

Figure 1.

Parametric plots of phase (top row) and group (middle row) velocities for the PT (dashed) and QT (solid) propagation modes calculated using (16), (20), (22), and (24) with μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16 (left), 0.36 (center), and 0.64 (right). The bottom row shows plots of group propagation angle ϕ calculated using (25) as a function of phase propagation angle θ.

2.6. Group Velocity

Impulsive excitations generate localized displacement fields that can be described by a superposition of plane waves with a range of frequencies, amplitudes, phases, polarizations, and propagation directions. After the excitation, these waves evolve in time and continue to interfere, forming wave packets that propagate radially away from the excitation region with a group velocity V⃗. This velocity can be measured experimentally by ultrasonic tracking of the wave packets. In terms of the phase velocity ν and propagation wave vector k⃗ = kn̂, the group velocity is given by (Born and Wolf, 1980; Berryman, 1979; Tsvankin, 2001)

$$\overrightarrow{V}=\frac{\partial (k\nu )}{\partial k_1}{\mathrm{x̂}}_1+\frac{\partial (k\nu )}{\partial k_2}{\mathrm{x̂}}_2+\frac{\partial (k\nu )}{\partial k_3}{\mathrm{x̂}}_3.$$ (21)

For TI materials with plane wave propagation in the x₁ − x₃ plane, the components of group velocity are given in terms of the phase velocity and angle as (Tsvankin, 2001)

$$V_1=\nu \text{sin}\theta +\frac{\partial \nu }{\partial \theta }\text{cos}\theta ,$$ (22)

$$V_2=0,$$ (23)

and

$$V_3=\nu \text{cos}\theta -\frac{\partial \nu }{\partial \theta }\text{sin}\theta .$$ (24)

Thus, the group propagation vector N̂ also lies in the x₁ − x₃ plane and can be written as N̂ = (sinϕ, 0, cosϕ)^T where the group propagation angle ϕ is given by

$$\varphi ={\text{tan}}^{-1}\left(\frac{V_1}{V_3}\right)=\theta +{\text{tan}}^{-1}\left(\frac{1}{\nu }\frac{\partial \nu }{\partial \theta }\right).$$ (25)

The second row of Fig. 1 shows parametric plots of PT and QT group velocities for the same sets of constants used to calculate the phase velocities in the top row. For the PT propagation mode, the components of group velocity form an ellipse,

$$\frac{\rho V_{PT,1}^2}{{\mu }_T}+\frac{\rho V_{PT,3}^2}{{\mu }_L}=1.$$ (26)

The bottom row of plots in Fig. 1 shows the group propagation angle ϕ as a function of phase propagation angle θ. In some cases, the inverse relation θ(ϕ) and resulting group velocities are triple valued, leading to the cusp structure seen in the plots.

3. Methods

3.1. Excitation and Wave Propagation Geometry

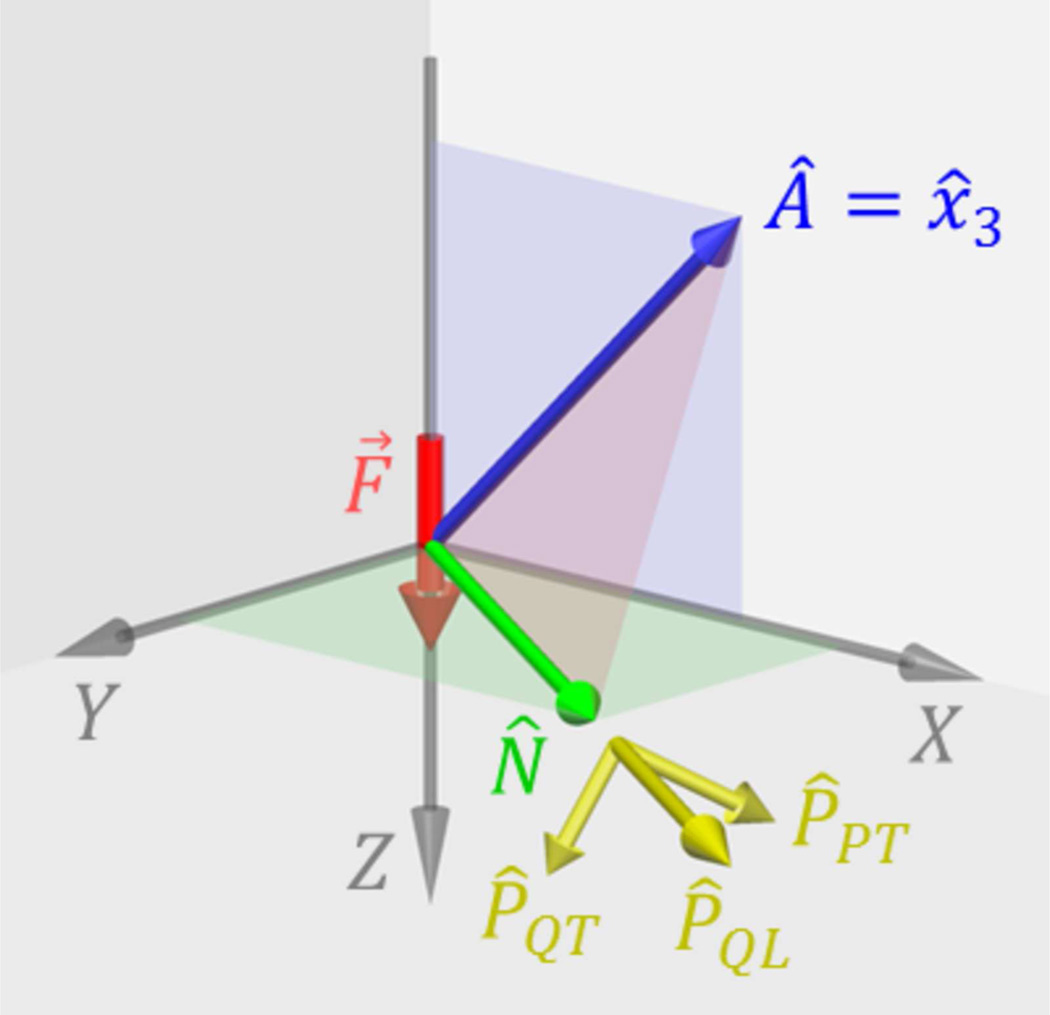
For experimental measurements in a TI medium, the ARFI excitation axis can be positioned in any orientation relative to the material symmetry axis, and this flexibility can be used to increase the sensitivity of experimental measurements to a particular elasticity constant. To specify this orientation, we introduce a second, experimental coordinate system with axes labeled by X, Y, Z that is distinct from the x₁, x₂, x₃ coordinate system in Sec. 2. Figure 2 shows the experimental setup used for the FE models in this study. The excitation force F⃗ was directed along the Z axis at the center of the modeled volume. As indicated in the figure, only propagation directions N̂ in the X − Y plane are considered here to simulate the experimental configuration typically used in ARFI excitations with ultrasonic tracking of wave propagation perpendicular to the excitation axis. The FE simulations in this study were performed with the material symmetry axis  tilted at an angle of 45° in the X − Z plane of the experimental coordinate system. As discussed in Sec. 5, this tilted configuration allows the propagation velocities measured in the X − Y plane to be sensitive to all three elasticity constants required to characterize an incompressible, TI material. While the exact angle is not critical, the value of 45° simplifies the analysis and gives the greatest sensitivity to the E_T/E_L elasticity constant.

Figure 2.

Experimental coordinate system used for the FE simulations. The ARFI excitation force F⃗ is directed along the Z axis and wave propagation is observed for propagation directions N̂ perpendicular to the excitation axis in the X − Y plane. As discussed in Sec. 3.1 the material symmetry axis  is tilted at an angle of 45° relative to the excitation axis. The x₁, x₂, x₃ coordinate system used to calculate the theoretical propagation velocities in Sec. 2 is oriented with x̂₃ =  and wave propagation in the x₁ − x₃ plane, i.e., the  − N̂ plane shown in red in the figure. Thus, the orientation of the x₁, x₂, x₃ coordinate system relative to X, Y, Z varies for different propagation directions N̂ in the X − Y plane. The P̂_PT, P̂_QL, and P̂_QT polarization vectors are defined relative to the x₁ − x₃ plane with P̂_PT perpendicular to the plane, and P̂_QL, and P̂_QT in the plane.

The propagation velocities predicted by the theoretical analysis in Sec. 2 were determined relative to the experimental X, Y, Z coordinate system as follows. For each propagation direction N̂, the x₁, x₂, x₃ coordinate system used in Sec. 2 is oriented so that x̂₃ =  and wave propagation occurs in the x₁−x₃ plane, i.e., the  − N̂ plane shown in red in Fig. 2. The group propagation angle ϕ relative to the material symmetry axis  was found using

$$\varphi ={\text{cos}}^{-1}(·\mathrm{N̂}).$$ (27)

Corresponding values of phase propagation angles θ were determined by inverting the ϕ − θ relation shown in Fig.1. These values were used to calculate the theoretical propagation velocities using (16) and (20). For the E_T/E_L = 0.16 and E_T/E_L = 0.64 cases, some ranges of ϕ gave three values for θ and the corresponding propagation velocities.

In addition, the orientation of the polarization vectors for the PT and QT propagation modes are determined relative to the x₁ − x₃ plane, i.e., the  − N̂ plane. Thus, the orientation of the polarization vectors relative to the X, Y, Z axes varies depending on the propagation direction N̂. As shown in Fig. 2, P̂_PT is oriented perpendicular to the  − N̂ plane, and P̂_QL and P̂_QT lie in the  − N̂ plane. However, P̂_QL and P̂_QT are parallel and perpendicular, respectively, to the phase propagation direction n̂, and are parallel and perpendicular to the group propagation direction N̂ only if ϕ = θ and n̂ = N̂.

3.2. Finite Element Modeling

Previously validated FE models were used to simulate the dynamic response of an elastic, TI solid to impulsive, acoustic radiation force excitations (Palmeri, et al., 2005). The excitation force was modeled as a three-dimensional Gaussian distribution to approximate a typical ARFI interrogation,

$$\overrightarrow{F}=F_0(t)e^{-(x^2+y^2+z^2)/2{\sigma }^2}Ẑ$$ (28)

where F₀(t) is a time dependent force amplitude and σ = 2 mm. The force was applied only during the excitation interval 0 < t < 200 µs during which time the amplitude was set to a constant value chosen empirically to achieve a maximum, on-axis displacement of roughly 20 µm which is consistent with experimental ARFI methods.

The three-dimensional, dynamic response of the elastic, TI solid was solved through the balance of linear momentum using LS-DYNA3D (Livermore Software Technology Corp., Livermore, CA) with an explicit, time-domain method (Palmeri, et al., 2005). The FE mesh had dimensions of 40 × 40 × 40 mm³ with element dimensions of 0.25 × 0.25 × 0.25 mm³. The model used non-reflecting boundaries to simulate an infinite volume without reflection artifacts. Simulations were performed for a total time of 6 ms with intermediate results saved at intervals of 25 µs. Calculations were performed on a Linux cluster with an average CPU speed of 2.6 GHz. In addition to LS-DYNA3D, calculations were performed using Matlab (The MathWorks, Natick, MA).

3.3. Material Models

Materials were modeled as linear, elastic solids with a density of ρ = 1 g/cm³. To simulate incompressibility, materials were described using Poisson ratios chosen to retain the essential properties of an incompressible model (Palmeri, et al., 2005). Specifically, ν_TT was set equal to the value given by (8) so that the dilatation (7) is given by

$$e=\frac{1}{E_L}(\frac{{\sigma }_{11}+{\sigma }_{22}}{2}+{\sigma }_{33})(1-2{\nu }_{LT}).$$ (29)

With this approach, the dilatation (29) remains sensitive to each normal stress, and the compressibility is controlled by the value of one Poisson ratio, ν_LT. In this study, ν_LT was set equal to the value of 0.499 (Palmeri, et al., 2005).

FE simulations were performed using the three sets of elasticity constants listed in Table 1. The values of μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16, 0.36, and 0.64 are the same as used for the results shown in Fig. 1. Relations (8) and (6) were used to calculate ν_TT and E_T, respectively.

Table 1.

Values of elasticity constants used for the three FE simulations.

Constant	ET/EL = 0.16	ET/EL = 0.36	ET/EL = 0.64
μL (kPa)	25.0	25.0	25.0
μT (kPa)	9.0	9.0	9.0
ET/EL	0.16	0.36	0.64
νLT	0.499	0.499	0.499
νTT	0.92	0.82	0.68
ET (kPa)	34.56	32.76	30.24
EL (kPa)	216.0	91.0	47.25

3.4. Determination of Shear Wave Velocity

The results of the FE simulations were compared with theoretical predictions by measuring the propagation speeds from displacement vs. time data along radial trajectories directed away from the excitation region. The propagation velocities were determined using the Radon sum approach described by Rouze, et al. (2010). This method identifies the spatio-temporal trajectory which maximizes the sum of the displacement data along the trajectory. For the displacement data shown in Fig. 3, the PT and QT propagation modes can give two propagation velocities for the same trajectory. In this case, only the speed corresponding to the trajectory with the largest Radon sum was identified.

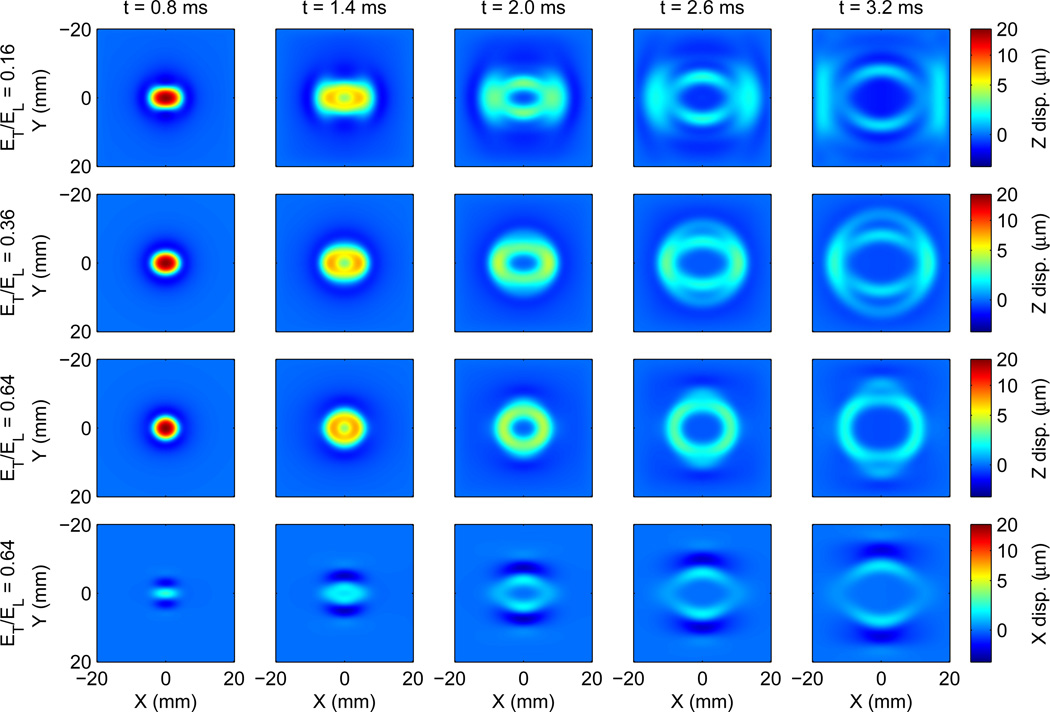
Figure 3.

Results of the FE models showing displacement data in the X−Y plane at time steps of 0.8, 1.4, 2.0, 2.6, and 3.2 ms. The top three rows show the Z component of displacements (which is the only component of displacement that is tracked during ARFI imaging) calculated using the elasticity constants in Table 1 with E_T/E_L = 0.16 (top row), E_T/E_L = 0.36 (second row), and E_T/E_L = 0.64 (third row). The fourth row shows the X component of displacements for the E_T/E_L = 0.64 case. Note the nonlinear color scale.

4. Results

4.1. Nearly Incompressible Material Model

The effect of setting ν_LT = 0.499 in the FE models can be evaluated by comparing the exact velocities of the QT and QL propagation modes evaluated using (18) with the velocities obtained in the incompressible limit with ν_LT = 0.5. For the QT mode, there is less than a 0.05% difference between the velocities calculated using (18) and (20) for each of the cases in Table 1. For the QL propagation mode, the theoretical velocity diverges in the incompressible limit, and the appropriate comparison is between the relative sizes of ν_QL and the characteristic shear wave speeds of 3 m/s and 5 m/s that correspond to the shear moduli μ_T and μ_L. Using (18) gives results with less than 0.04% angular dependence and mean values of ν_QL = 232.5, 150.9, and 108.8 m/s, which are significantly greater than the shear wave speeds, but of course, still an order of magnitude lower than observed for the velocity of longitudinal waves in tissue.

4.2. Displacement Images

Images of displacements in the X − Y plane are shown in Fig. 3 at time steps of 0.8, 1.4, 2.0, 2.6, and 3.2 ms. The first three rows in Fig. 3 shows the Z component of displacements obtained from the three FE models using the material constants in Table 1. The fourth row shows the X component of displacements for the E_T/E_L = 0.64 case. The color map used in these plots is nonlinear to increase the dynamic range for smaller displacements at later times.

We observe that the Z displacement results shown in the first three rows of Fig. 3 are large at early times soon after the excitation, and the displacement magnitude decreases as the wave propagates away from the excitation region. Structure in the wave shape develops at later times after sufficient time elapses for the variations in the angular dependence of the velocities to become apparent.

For the X components of displacements shown in the fourth row of Fig. 3, the displacements are approximately zero at early times because the ARFI excitation force is directed in the Z direction. Structure in the wave shape develops at later times with a negative X displacement preceeding the positive X displacement for propagation along the Y axis. The corresponding images in the third row of Fig. 3 show two waves with positive Z displacements that separate in time. This behavior is an example of shear splitting (Shearer, 2009) in which the PT and QT modes propagate with different velocities causing their displacement fields to separate spatially. The propagation modes can be identified by the orientation of their polarization vectors. Referring to Figs. 1 and 2, for propagation along the Y axis, the  − N̂ plane is oriented at an angle of 45° to the X − Y plane and ϕ = θ = 90°. Relative to the X, Y, Z coordinate system, the PT and QT polarization vectors are ${\mathrm{P̂}}_{PT}=\frac{1}{\sqrt{2}}{(1,0,1)}^T$ and ${\mathrm{P̂}}_{QT}=\frac{1}{\sqrt{2}}{(-1,0,1)}^T$, respectively. Thus, we interpret the X and Z displacement data in the third and fourth rows of Fig. 3 as the propagation of PT and QT modes along the Y axis with V_QT > V_PT.

4.3. Group Propagation Velocities

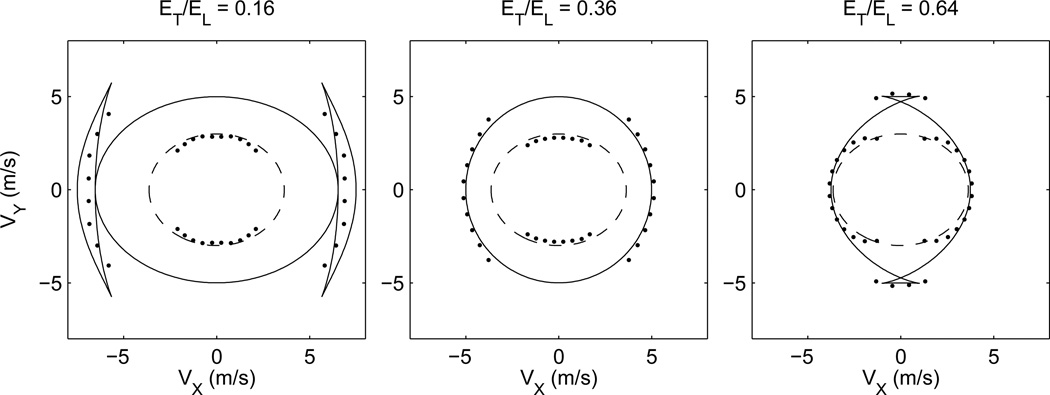
Figure 4 shows parametric plots of the theoretical group propagation velocities in the X − Y plane for the PT and QT propagation modes calculated using the procedure described in Sec. 3.1. Results are shown for each of the three sets of elasticity constants listed in Table 1. We observe that the theoretical velocities shown in Fig. 4 have the same magnitudes as the group velocities shown in Fig. 1. However, the angular dependence of the results shown in Fig. 4 is more complicated than in Fig. 1 because, for any given propagation direction N̂, the group propagation angle ϕ must be determined relative to the material symmetry axis  using (27) before calculating the velocity.

Figure 4.

Parametric plots of theoretical group propagation velocities in the X − Y plane calculated using the procedure described in Sec. 3.1. Results are shown for the PT (dashed) and QT (solid) propagation modes calculated using μ_L = 25 kPa, μ_T = 9 kPa, and E_T/E_L = 0.16 (left), 0.36 (center), and 0.64 (right). The data points show velocities calculated from the displacement results of the FE models for wave propagation along trajectories directed radially away from the excitation region, see Sec. 3.4.

The plots in Fig. 4 also show the velocities calculated from the results of the FE models using the Z component of displacement data and the procedure described in Sec. 3.4. Velocities were calculated for propagation directions directed radially away from the excitation region. Only one velocity is determined for each propagation direction even though the displacement data contains contributions from all three propagation modes. We observe that the calculated velocities are in good agreement with one of the theoretically predicted propagation velocities. However, the agreement switches between the PT and QT modes as a function of propagation direction depending on the relative displacement amplitude for the two modes.

5. Discussion

The FE simulations described in this paper have been designed to model ARFI excitations and shear wave propagation in an incompressible, TI medium. To be compatible with FE simulation, the material model used here is constructed to be nearly incompressible with the compressibility controlled by the value of a single Poisson ratio. At the same time, the elasticity constants μ_T, μ_L, and E_T/E_L are identical to the values used in an incompressible model. The excitation and propagation configuration is chosen so that the plane in which wave propagation is monitored is perpendicular to the excitation axis, and the modeled volume and tracking time are similar to those used in experimental measurements. Results are presented in Figs. 3 and 4 using the Z component of displacement, i.e., the displacement component parallel to the excitation force as would be measured using ultrasonic tracking.

The development of the structures seen the Figs. 3 and 4 can be understood as follows. Material displacements resulting from the excitation process can be expressed as a superposition of plane waves with a range of frequencies, amplitudes, phases, polarizations, and propagation directions. After the excitation, these waves evolve in time and continue to interfere, forming wave packets that propagate radially away from the excitation region with the group propagation velocity. Multiple wave packets can travel in the same direction with different propagation velocities. In addition, the PT, QT, and QL propagation modes are defined relative to the  − N̂ plane so that the decomposition of displacement data into the three propagation modes depends on the propagation direction. As a consequence, the results shown in Figs. 3 and 4 are surprisingly complex even though the material and excitation models are relatively simple.

It is interesting to compare the displacement images shown in Fig. 3 with the velocity plots shown in Fig. 4. These results show surprisingly similar structures even though the figures display different quantities. These similarities are a result of the relatively short duration of the excitation compared to the propagation time so that the position r⃗ of a wave packet traveling away from the excitation region is given approximately as r⃗ = V⃗t. Thus, the position and velocity have roughly the same angular dependence, and the structures appearing in Figs. 3 and 4 are similar.

Figure 4 shows relatively good, but not perfect, agreement between the theoretically predicted velocities and the velocities measured from the FE displacement data. These differences arise because the displacement data used to calculate the propagation velocities is the sum of displacements from both PT and QT propagation modes, and it is not possible to isolate displacements from a single mode. Similarly, near the cusps in the QT mode, three wave packets propagate with nearly the same velocity, and displacements cannot be separated to identify a single propagation velocity. Extending the spatial and temporal ranges would allow for increased separation of the wave packets from different modes, but at the expense of decreased displacement amplitude. It is encouraging to see the good agreement shown in Fig. 4 using temporal and spatial ranges similar to those used experimentally.

Finally, we consider the ARFI and ultrasonic tracking experimental measurements needed to characterize a TI material. For an incompressible material, it is necessary to measure three elasticity constants, for example, μ_T, μ_L, and E_T/E_L. To date, experiments in muscle have measured μ_T and μ_L by measuring the shear wave speed for wave propagation parallel and perpendicular to the muscle fibers. In addition, Wang, et al. (2013a) have measured the angular dependence of both the phase and group velocities for the PT propagation mode.

Measurement of the third elasticity constant E_T/E_L is more difficult because this constant only contributes to the QT propagation mode, for example, in (20). However, excitation of the QT mode can be difficult because the polarization vector for this mode lies in the  − N̂ plane, and the propagation direction must be chosen carefully relative to the excitation and material symmetry axes. Furthermore, for typical ARFI displacement amplitudes on the order of a few microns, only the Z components of displacements can be detected using ultrasonic tracking. Thus, when using ultrasonic imaging to monitor motion, it is not possible to identify the PT and QT propagation modes from measurements of the X component of displacements as in the images shown in the fourth row of Fig. 3.

For the FE models in this study, orienting the material symmetry axis at an angle of 45° as shown in Fig. 2 allows the QT mode to be observed. For wave propagation along the X axis, the Z component of displacements will consist of only the QT propagation mode, and, as shown in Fig. 3, the amplitude of these displacements will be relatively large. Furthermore, with propagation along the X axis, ϕ = θ = 45° and (20) gives

$${\nu }_{QT}(\varphi =\theta =45°)=\frac{1}{\rho }\sqrt{\frac{E_L}{E_T}{\mu }_T}$$ (30)

so that E_T/E_L can be determined if μ_T is known. Thus, an experimental configuration similar to that shown in Fig. 2 should allow measurement of μ_T, μ_L, and E_T/E_L and a complete characterization of an incompressible, TI material.

Experimental demonstration of the methodology described in this study is the subject of future work. These measurements are complicated by several factors that have not been considered in the idealized simulations presented here. One complicating factor is that the orientation of the muscle fibers must be known before the ARFI excitation axis can be positioned. However, the muscle fiber orientation is not typically known with high precision, especially for in vivo measurements. One method that could be used experimentally would be to determine the fiber orientation using either a high frequency ultrasound probe or an initial measurement using a 3-D probe as described by Wang, et al. (2013a), and then to position the excitation probe so that the axis is near the ideal 45° angle. Alternatively, a probe capable of generating a steerable excitation axis could be used to determine the fiber orientation, and then to position the axis for the measurement. Of course, the exact angle of 45° is not required since the ratio E_T/E_L and its uncertainty can be determined from measured values of μ_T, μ_L and θ using (20). In addition, the structure of muscle is complicated by inhomogeneities in fiber orientation and interfaces between of fiber bundles. Effects of these complications have been neglected in the current study and also in previous measurements of propagation velocities along and across the muscle fiber orientation. The impact of these non-idealized structures on experimental measurements of elasticity parameters is complicated and remains to be addressed.