Shared Genomic Segment Analysis: The Power to Find Rare Disease Variants

Summary

Shared genomic segment (SGS) analysis is a method that uses dense SNP genotyping in high-risk pedigrees to identify regions of sharing between cases. Here, we illustrate the power of SGS to identify dominant rare risk variants. Using simulated pedigrees, we consider 12 disease models based on disease prevalence, minor allele frequency, and penetrance to represent disease loci that explain 0.2% to 99.8% of total disease risk. Pedigrees were required to contain ≥15 meioses between all cases and to be high-risk based on significant excess of disease (p<0.001 or p<0.00001). Across these scenarios the power for a single pedigree ranged widely. Nonetheless, fewer than 10 pedigrees was sufficient for excellent power in the majority of the models. Power increased with the risk attributable to the disease locus, penetrance, and the excess of disease in the pedigree. Sharing allowing for one sporadic case was uniformly more powerful than sharing using all cases. Further, we do a SGS analysis using a large Attenuated Familial Adenomatous Polyposis pedigree and identified a 1.96 Mb region containing the known causal APC gene with genome-wide significance (p<5×10⁻⁷). SGS is a powerful method for detecting rare variants and offers a valuable complement to GWAS and linkage analysis.

Introduction

Recently the availability and decreased cost of high-density genome-wide single nucleotide polymorphism (SNP) arrays has led to the development of new analytical techniques that can take advantage of this wealth of information. One avenue of new development is the use of these data in large pedigrees. Conventionally, linkage analysis has been used for pedigree analyses; however, such an approach is computationally intensive in extended pedigrees and problematic when high-density data are used. Linkage disequilibrium (LD) must be accounted for and subtle undetected genotyping errors can disrupt inheritance estimation. Computationally tractable gene-mapping methods for high-density SNP data have recently been developed that attempt to identify genomic regions of sharing between affected individuals (cases) in pedigrees. These new methods focus on assessing the number of consecutive markers (“runs”) with alleles that are identical-by-state (IBS) across the cases (Leibon et al., 2008, Thomas et al., 2008) to infer regions that they share identical-by-descent (IBD); that is, chromosomal segments inherited from the same ancestral founder. Computationally, IBS sharing is simple to calculate. Excessively long runs of IBS that are not expected by chance are likely to be IBD. High-risk pedigrees containing multiple related cases are ideal for these new methods because genomic sharing across multiple meioses happens seldom by chance and is short in length. The identification of long runs of IBS sharing by distant relatives with a disease can therefore indicate regions harboring predisposition alleles.

Growing evidence suggests that rare variants contribute to several different diseases (Manolio et al., 2009, Owen et al., 2009, Sabatelli et al., 2009, Schork et al., 2009), and that these variants may account for some of the missing heritability not captured by risk variants identified by genome-wide association studies (GWAS). Genome-wide association studies use common SNPs and lack the power to find rare risk variants (Iles, 2008). This is because power decreases as the disease minor allele frequency (MAF) decreases due to low correlation (r²) between SNPs on the GWAS arrays and the disease SNP. It has been shown that the overall sample size needs to increase by a factor of 1/r² to maintain power (Pritchard & Przeworski, 2001). For example, the maximum correlation between a tagging SNP (tSNP) with a MAF of 0.05 and a disease SNP with a MAF of 0.0005 is r²=0.0095 (VanLiere & Rosenberg, 2008), and hence the sample size would need to be increased by about 100-fold to maintain power. If the disease had prevalence 1% and a penetrance of 0.2, and the true disease SNP (MAF 0.0005) was tested, only 100 cases and 100 controls would be required for 80% power based on an trend test with alpha=0.05 (Slager & Schaid, 2001). However, when using tSNPs (MAF≥0.05) at a minimum the sample size would need to increase to 10,000 cases and 10,000 controls to maintain the 80% power. In contrast, use of SGS with large pedigrees has been suggested as a powerful method to identify rare disease variants (Manolio et al., 2009). Thus far, SGS has identified novel shared regions containing possible rare variants for prostate cancer (Thomas et al., 2008) and a rare form of inherited kidney disease (Leibon et al., 2008). The SGS technique indicates potential in these applied examples, but the power of the method has not been explored in depth. Here, we examine the power of an SGS method (n sharing and n-1 sharing) across several different underlying disease models and selection procedures for pedigrees. For a subset of these scenarios, we also compare power to classical multipoint linkage analysis.

Lastly, we also provide a proof-of-principle example by applying SGS analysis to a large Attenuated Familial Adenomatous Polyposis (AFAP) pedigree with a known disease locus. AFAP is a colon cancer predisposition syndrome that is characterized by less than 100 adenomatous polyps in the colon and an increased risk of developing colon cancer. Mutations in the APC gene on chromosome 5 have been shown to cause AFAP (Burt et al., 2004, Neklason et al., 2004, Pilarski et al., 1999, Knudsen et al., 2010) and, in particular, a dominant founder mutation (c.426_427delAT) has been identified in the pedigree presented (Neklason et al., 2008).

These power estimates and illustrative proof-of-principle example provide important insight into how this new technique can be used for gene-finding studies.

Methods

Simulated data are used to estimate power and type 1 error. For our proof-of-principle example, the study was approved by the University of Utah Institutional Review Board and by the University of Utah Resource for Genetic and Epidemiologic Research which oversees the appropriate use of the Utah Population Database. Informed consent was obtained from all research participants.

Shared Genomic Segment method

An SGS analysis uses dense SNP data in extended pedigrees to identify significantly long runs of IBS sharing by multiple related cases.

It has already been shown that the genome-wide probability that there is an allele at a locus that is shared IBD by a set of individuals separated by ‘M’ meioses is:

$$\frac{35M+22}{2^{M-2}}$$ (1)

for a single pedigree with two ancestral founders, assuming an autosomal genome measuring 35 Morgans (Thomas et al., 2008), where M indicates the number of meiotic events the locus must survive to segregate to all individuals in the set.

Based on equation (1), the genome-wide probability of chance IBD sharing at a locus is approximately 0.05 for individuals separated by 15 meioses. Hence, high-risk pedigrees with M≥15 are good candidates for an SGS analysis and are the focus of our investigations here.

We assume each SNP is biallelic with alleles 1 and 2. Let n be the number of cases in a pedigree and denote n_i11, n_i12 and n_i22 as the number of cases with genotypes 11, 12 and 22 at the i^th SNP (n_i11,+ n_i12 + n_i22= n). The number of cases sharing at least one allele IBS at the i^th SNP can then be simply written as:

$$S_i=n-min(n_{i11},n_{i22})$$ (2)

We define R_i(t) to be the number of consecutive SNPs (which includes the i^th SNP) for which at least one allele is shared IBS by at least t of the n cases, that is,

$${\mathrm{R}}_i(t)=\text{length of IBS sharing containing the}{i}^{\text{th}}\text{SNP where}{\mathrm{S}}_i\ge t\text{for all}i\text{in the run}.$$ (3)

This partitions the genome into segments of potential sharing (runs of IBS) separated by regions that are not shared by at least t of the n cases. In Thomas et al (2008) a single test was suggested, comparing the maximum R_i(t) in the genome (maxR_i(t)) to the maxima from a set of simulated null genomes –these were not matched on genomic position. This single test addresses one hypothesis based on maxR_i(t) and leaves all other runs unexplored. Furthermore, because it ignores the location of the observed maximum it will have reduced power to identify true disease loci that occur in areas with low LD. Here, we present a point-by-point procedure. We assess R_i(t) for every SNP, compared to an empirical null distribution for the same SNP position (R_i(t|null)). In the empirical assessment, sharing under the null is calculated for precisely the same set of individuals. Null genotype configurations for those individuals are generated conditional on an LD and recombination model and their precise pedigree structure. The LD model is estimated across entire chromosomes using a graphical modeling approach (Thomas, 2009). This LD model is used to assign haplotypes to pedigree founders. A gene-drop of these haplotypes is then performed based on the precise pedigree structure with recombination events based on a genetic model for the SNPs. The p-value for each SNP is the proportion of R_i(t|null) that are at least as large as the observed R_i(t). The number of null simulations used to estimate these p-values is user-defined (for example, for the proof-of-concept case-study we used 2 million). The significance for a run is then defined as the mean p-value across all SNPs contained in the run. The mean p-value achieves the correct type 1 error rate (see Results), compared to the minimum p-value in the run which has marginally better power, but also marginally inflated type 1 errors (data not shown). The programs used for this analysis are freely available at http://medicine.utah.edu/internalmedicine/geneticepidemiology/analysis.php.

Simulated data: Power

For our investigation of power, we generated extended pedigrees with affection status based on various disease models. We focused on models with rare disease allele frequencies (0.005, 0.0005 and 0.00005), as these are scenarios where current GWAS approaches are underpowered (Iles, 2008, Pritchard & Przeworski, 2001). Prevalence of the disease (1% or 0.5%) and penetrance of the risk allele (0.2 or 0.5, assuming a dominant model) were also considered. A sporadic rate was calculated for each model based on the prevalence of disease, penetrance, and disease allele frequency. These models correspond to disease loci that explain a wide range of the total attributable risk (0.2% to 99.8%).

We used a large, fixed pedigree structure as a backbone to generate simulated extended high-risk pedigrees. Genotypes and phenotypes were generated based on the disease model under consideration and hence varied for each simulation. For each generated pedigree, only the structure required to connect the cases was maintained. The backbone structure was a five-generation pedigree with two ancestral founders and 168 descendants (including 104 lateral founders that marry-in at the 2^nd-4^th generations for a total of 274 individuals). The pedigrees generated were the type of extended pedigree structures often seen in pedigree studies in the literature, including from the San Antonio Family Heart Study (e.g., Santamaria et al., 2007), Canadian and American Hutterites (e.g., Prasad et al., 2001), the Genetics of Coronary Artery Disease in Alaska Natives (GOCADAN) Study (e.g., Howard et al., 2005), the Carolinas Region Interaction of Aging, Genes and Environment Family (e.g., Chen et al., 2010), isolate population studies (e.g., Vitart et al., 2010, Wijsman et al., 2003, Williams-Blangero et al., 2002, Choh et al., 2001), in addition to studies from the Utah Population Database (e.g., Camp et al., 2006). The upper generations were considered missing, as is the situation in reality. Thus only the bottom two generations of descendants (n=128) were considered. A high-risk pedigree was defined to be one where the number of cases was significantly higher than expected based on a Poisson distribution conditional on the disease prevalence in the model. The use of a statistical high-risk definition is advantageous for pedigree-based studies, because it leads to pedigrees that are enriched for genetic disease, rather than simply a chance clustering of sporadic disease. We considered two criteria for defining high-risk pedigree status (p<0.001 and p<0.00001). For our backbone pedigree structure, these definitions of high-risk correspond to requiring a pedigree to contain ≥6 and ≥8 cases, respectively, for models with a 1% disease prevalence and ≥4 and ≥6 cases for models with a 0.5% disease prevalence.

We assumed an Illumina 610Q array for SNP positions with MAFs and LD structure estimated from the CEU Utah trio parents (n=60) available in HapMap (The International HapMap Consortium, 2003). The disease locus (dSNP) was placed in the middle of the q arm of Chromosome 21. There are 7785 SNPs on Chromosome 21 on the 610Q array. A chromosome-wide LD model was estimated using a graphical modeling method (Thomas, 2009). This LD model was used to assign haplotypes to the founders in the pedigrees. We know that, due to the frequency difference between a rare disease allele and common alleles of SNPs on a high-density array, the correlation (r²) between the dSNP and the array SNPs will be negligible. Hence, to place our dSNP, we identified a SNP uncorrelated with any other and assigned that to be the dSNP position. We then removed the HapMap genotypes at that position and replaced them with dSNP genotypes based on the disease MAF. To assign haplotypes to descendants, a gene-drop was performed assuming Mendelian inheritance and including recombination according to the genetic map for the 610Q SNPs. Affection status was assigned based on a disease model. The dSNP genotypes were then removed. Generated pedigrees that satisfied high-risk status and contained at least 15 meioses between cases were the focus of our study. Figure 1 illustrates some examples of the high-risk pedigrees generated.

Figure 1.

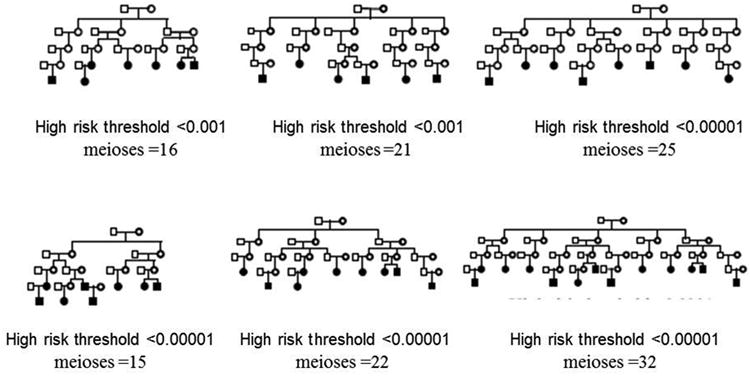
Examples of simulated high-risk pedigrees (penetrance=0.5, prevalence=1% and disease MAF=0.0005).

The power of sharing methods, such as SGS, depends largely on the dSNP genotypes assigned to the founders. For example, a founder genotype set (F_j) that includes a single ancestral founder being heterozygote for the dSNP (and all other founders wildtype) will have the potential to generate pedigree configurations with good sharing across cases at the dSNP and hence the potential for good power in an SGS analysis. In contrast, a founder set that is wildtype at the dSNP in all founders will have little potential for power and will likely resemble simply the type 1 error rate. It is therefore convenient to estimate power by considering the different founder genotype sets separately and appropriately summing across the results. Further, because we consider only pedigrees that are high-risk (HR) and that contain at least 15 meioses (15M) between the cases, this must be taken into account also. Hence, power for the SGS method was estimated as follows:

$$\mathrm{P}(\text{reject}{\mathrm{H}}_0|\text{alternative is true})=\sum _j\mathrm{P}(\text{reject}{\mathrm{H}}_0|{\mathrm{F}}_j|\text{HR}\cap 15\mathrm{M})\mathrm{P}({\mathrm{F}}_j|\text{HR}\cap 15\mathrm{M})=\sum _j\mathrm{P}(\text{reject}{\mathrm{H}}_0|{\mathrm{F}}_j|\text{HR}\cap 15\mathrm{M})\frac{\mathrm{P}(\text{HR}\cap 15\mathrm{M}|{\mathrm{F}}_j)\mathrm{P}({\mathrm{F}}_j)}{\mathrm{P}(\text{HR}\cap 15\mathrm{M})}$$ (4)

where F_j is the j^th set of founder genotypes at the dSNP locus under the alternative hypothesis.

To determine power, each of the four components was estimated separately and combined as indicated in equation (4). Details of the simulation procedures are found in the appendix.

Simulated data: Type 1 error

For accurate type 1 error estimation it is important that the phenotypic configurations of the pedigrees match those from the alternate hypothesis (i.e. HR and 15M); but, the dSNP genotypes should lack correspondence between genotype and phenotype. To achieve this, we selected pedigrees generated under the alternative hypothesis (as described above), removed the dSNP genotypes and replaced these with genotypes under the null using a Mendelian gene-drop. A total of 1000 such null simulations were generated to determine the type 1 error rate for SGS with n and n-1 cases sharing.

Proof-of-Principle Real Data Example: AFAP and APC

The large AFAP pedigree analyzed is shown in Figure 2. It has 34 meioses between five AFAP cases genotyped using Affymetrix Genome-Wide Human SNP Array 6.0. Data on the same platform for the 60 CEU HapMap founders were used to estimate an appropriate LD model. SNPs out of Hardy-Weinberg equilibrium in the 60 HapMap founders (p<0.001) and SNPs that were monomorphic in both the five cases and 60 HapMap founders were excluded, leaving 47,674 SNPs on Chromosome 5 where the known causal APC gene resides (829,558 genome-wide). Significance of observed SGS runs were determined empirically, conditional on the CEU HapMap LD model and the AFAP pedigree structure.

Figure 2.

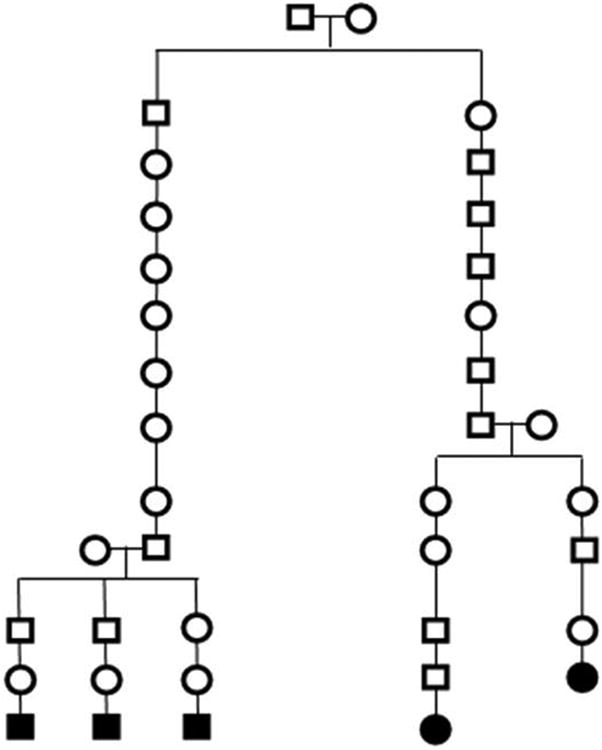
AFAP pedigree.

We determined the genome-wide significant threshold for the AFAP real data example by performing a Bonferroni correction based on the number of SGS runs expected across the genome under the null hypothesis. We determined the number of SGS runs for 1000 null genomes based on the AFAP pedigree structure and the LD model. The number of runs was very stable, with an average of 100,341 runs (95% CI 99,186-101,496; range 98,318-102,138). Hence, we considered 5.0 × 10⁻⁷ to be the genome-wide significant threshold for the AFAP pedigree.

Results

As expected, the results from the type 1 error simulations indicated that the empirical assessment of significance for SGS for n and n-1 sharing were both valid. For SGS across n cases, the estimated type 1 error rate was 0.053 and for n-1 it was 0.042; neither is significantly different than the usual nominal benchmark of 0.05.

The results of power for a single pedigree are shown in Table 1. Single-pedigree power varied substantially across the disease models considered (5.4% to 86.2%). In general, the power increased with increased stringency in the high-risk pedigree definition and penetrance. For a given prevalence and MAF, the power increased with an increase in the disease attributable risk. For the models considered, power was consistently higher for sharing across n-1 cases (i.e., allowing for one sporadic case) which is perhaps unsurprising given the disease models all included the possibility for sporadic disease.

Table 1. Power of correctly identifying the disease SNP location using one pedigree.

				All n cases sharing		n-1 cases sharing
				Significant threshold for designation of high-risk		Significant threshold for designation of high-risk
Prevalence	MAF	Penetrance	Attr. risk (%)	<0.00001	<0.001	<0.00001	<0.001
0.50%	0.005	0.5	100	53.6%	52.8%	56.6%	55.9%
		0.2	40	30.3%	25.5%	38.9%	33.5%
	0.0005	0.5	10	71.0%*	42.3%	86.2%*	51.2%
		0.2	4	48.5%	17.5%	65.9%	23.3%
	0.00005	0.5	1	30.8%	10.2%	37.3%	11.5%
		0.2	0.4	32.4%*	6.2%	42.5%*	6.7%
1%	0.005	0.5	50	68.9%	54.2%*	85.2%	68.0%*
		0.2	20	24.2%	19.7%	33.2%	25.7%
	0.0005	0.5	5	32.3%	18.2%	42.6%	24.1%
		0.2	2	39.8%	9.2%	62.5%	11.8%
	0.00005	0.5	0.5	35.2%	7.8%	47.2%	9.1%
		0.2	0.2	12.6%	5.4%	17.6%	5.6%

Note: MAF, minor allele frequency. The number of cases (n) in a pedigree varied based on the genetic model and the high-risk threshold. For models with a prevalence of 1% the average number of cases was 8.2 and 9.7 for the high-risk thresholds of p<0.001, and p<0.00001, respectively. For models with a prevalence of 0.5% the average number of cases was 4.0 and 6.2 for the high-risk thresholds of p<0.001, and p<0.00001, respectively.

^*indicates a scenario also investigated by classical multipoint linkage analysis for comparison.

While SGS is designed to analyze a single pedigree, in practice multiple high-risk pedigrees may be ascertained and each analyzed separately. Based on the single-pedigree power estimates, Table 2 shows the number of pedigrees required to attain at least 80% power overall (i.e., the probability that at least one pedigree will identify a disease locus). Note that the multiple pedigrees are not required to share the same disease susceptibility loci. As seen in Table 2, for the vast majority of the scenarios considered (18/24 for n, and 19/24 for n -1), fewer than 10 pedigrees would be sufficient for ≥ 80% power overall. Furthermore, five or fewer pedigrees would provide good power for at least half of the scenarios investigated.

Table 2. Number of pedigrees needed to have greater than 80% power of detecting disease SNP after adjusting for multiple testing.

				All n cases sharing		n-1 cases sharing
				Significant threshold for designation of high-risk		Significant threshold for designation of high-risk
Prevalence	MAF	Penetrance	Attr. risk (%)	<0.00001	<0.001	<0.00001	<0.001
0.50%	0.005	0.5	100	3	3	2	2
		0.2	40	5	6	4	4
	0.0005	0.5	10	2	3	1	3
		0.2	4	3	9	2	7
	0.00005	0.5	1	5	16	4	14
		0.2	0.4	5	26	3	24
1%	0.005	0.5	50	2	3	1	2
		0.2	20	6	8	4	6
	0.0005	0.5	5	5	8	3	6
		0.2	2	4	17	2	13
	0.00005	0.5	0.5	4	20	3	17
		0.2	0.2	12	30	9	28

Note: MAF, minor allele frequency.

Table 3 shows the average length of the shared segment for the significant results in single pedigrees. The shared segments were short for the analysis with n cases (average 3.17 Mb, range 1.6-7.2 Mb), and shortest for the 1% disease prevalence and the 0.2 penetrance (average 2.53 Mb, 1.6-3.7 Mb). For n-1 cases sharing, the shared lengths were longer (average 7.98 Mb, 5.0-14.1 Mb).

Table 3. Average length of sharing (in Mb) for significant SGS runs.

				All n cases sharing		n-1 cases sharing
				Significant threshold for designation of high-risk		Significant threshold for designation of high-risk
Prevalence	MAF	Penetrance	Attr. risk (%)	<0.00001	<0.001	<0.00001	<0.001
0.50%	0.005	0.5	100	7.2	7.2	11.9	12.2
		0.2	40	5.8	6.0	11.7	13.0
	0.0005	0.5	10	5.0	5.2	9.9	12.6
		0.2	4	4.4	5.2	10.5	13.3
	0.00005	0.5	1	4.5	5.2	9.4	14.1
		0.2	0.4	4.5	4.9	10.4	14.0
1%	0.005	0.5	50	4.3	4.9	8.6	10.0
		0.2	20	2.1	3.7	5.9	8.8
	0.0005	0.5	5	3.1	3.8	7.1	9.3
		0.2	2	1.8	3.2	5.2	9.5
	0.00005	0.5	0.5	2.7	4.0	6.7	10.8
		0.2	0.2	1.6	2.8	5.0	8.9

Note: MAF, minor allele frequency.

The results of the real data AFAP proof-of-principle example are illustrated in Figure 3. The longest shared segment in the genome for all five cases was found on Chromosome 5 and this shared segment achieved genome-wide significance (p< 5×10⁻⁷; none of 2,000,000 simulations were as extreme as the observed sharing). This SGS shared region stretched from 111,641,797 to 113,606,106 bp (1.96 Mb) and contained the known disease-causing APC gene.

Figure 3.

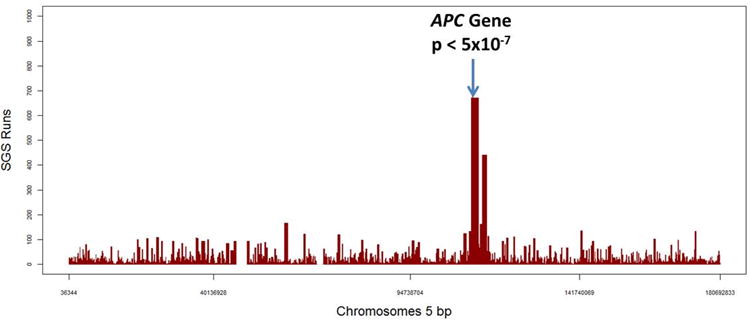
AFAP SGS runs for chromosome 5.

Discussion

We found that SGS can be a powerful method for detecting rare disease variants. In general very few pedigrees (<10) were required to generate a well-powered study. Useful for study design, we observed patterns in the power based on the underlying disease model, the criterion for high-risk pedigree status, and the consideration of n or n -1 sharing. As intuitively expected, power generally increased with the attributable risk for the disease locus. Also, the extreme high-risk pedigree definition (significant excess disease, p<0.00001) also uniformly produced better power. For the stricter high-risk pedigree definition, the power advantage was most pronounced at the lowest disease MAF (0.0005) and lower attributable risks (<10%). A perhaps counter-intuitive pattern seen within scenarios with the extreme high-risk pedigree definition was that of decreased power with increasing disease MAF for a prevalence of 0.5% (specifically, MAF 0.005 compared to MAF 0.0005). We identified this to be because the strict high-risk definition led to pedigrees segregating multiple disease alleles (for the higher MAF of 0.005) which generated a lack of sharing of the exact same disease allele across the n or n -1 cases. While these particular examples all had good power (single pedigree power >50%), the pattern highlights that the strength of the SGS method lies in identification of rare disease alleles, especially in relation to the disease prevalence, and that the method will have reduced power for common disease alleles. Finally, the power was consistently higher for n-1 sharers, compared to n. This is consistent with the disease models generated, which all included the possibility for sporadic disease. This also likely better reflects reality.

While not the focus of this investigation, because classical linkage analysis is the historical mainstay for pedigree-based analyses for identifying rare risk variants, we also investigated the power of multipoint linkage analysis for a few scenarios. We selected three scenarios to represent SGS n sharing performed at the high, moderate and low end for power performance (these are indicated with an asterisk in Table 1). We note that due to the structure of the pedigrees, multipoint linkage could not be performed in software such as Genehunter (Kruglyak et al., 1996) or Merlin (Abecasis et al., 2002),and instead a Monte Carlo Markov chain method was employed (Mclink; (Thomas et al., 2000). Single pedigree linkage analyses assuming a general dominant model (disease allele frequency=0.003; penetrances: 0.0005 0.5, 0.5) and based on a trimmed set of “LD-free” SNP genotypes were performed. As a single test for linkage at the known true disease locus, power was assessed at alpha=0.05. Under the first scenario (high-risk pedigree criterion p<0.00001, disease prevalence 0.5%, disease MAF=0.0005 and a penetrance of 0.5) multipoint linkage in 1000 simulated pedigrees yielded 68.8% power, compared to 71.0% and 86.2% for SGS n and n -1 sharing, respectively. For the second scenario (high risk p<0.001, prevalence 1%, disease MAF 0.005 and penetrance 0.5) linkage yielded 57.2% power compared to 54.2% and 68.0% for SGS n and n -1 sharing. For the final scenario (high-risk p<0.00001, prevalence 0.5%, disease MAF 0.00005, penetrance 0.2) linkage produced 34.8% power compared to 32.4% and 42.5% for SGS n and n -1 sharing. Hence, multipoint linkage and SGS n sharing appear near-equivalent for power; however, both are outperformed by SGS n -1 sharing due to its increased robustness to intra-familial heterogeneity. For localization, we identified the size of the region identified by the 1-LOD support interval in the pedigrees that successfully identified the true locus with multipoint linkage analysis. For the three scenarios outlined above, these localized linkage regions were found to be 8.5 Mb, 7.6 Mb and 8.0 Mb on average, respectively.

Another widespread study design is the GWAS, although it is well-acknowledged not to be a study design of choice for rare risk variant detection. Here, we have shown that: there are scenarios where a single pedigree has >80% power; five or fewer pedigrees are sufficient to attain >80% power for over half of the scenarios considered; and in the vast majority of scenarios less than ten pedigrees are required to be well-powered in an SGS analysis. Pedigrees in our simulation study contained 4.0-9.7 cases on average; hence, with an SGS approach and between one to ten pedigrees, fewer than 100 (and may be as few as four) very well selected cases can produce a well-powered study. This is quite remarkable when compared to the 10,000 cases and 10,000 controls required to achieve 80% power in a traditional case-control GWAS study design.

A further advantage of the SGS method is that it clearly localizes the region for follow-up sequencing efforts, and these regions are generally quite small (average for n sharing 3.17 Mb, range 1.6-7.2 Mb, and average for n -1 sharing 7.98 Mb, 5.0-14.1 Mb). SGS not only provides focused regions for sequencing but also identifies the sharers to sequence. Hence, it is an efficient and extremely cost-effective strategy for focused regional next generation sequencing technology. The regional approach also radically reduces the amount of sequence data generated allowing it to be explored more thoroughly, and it is plausible to search for risk variants in non-coding regions. Furthermore, variant filtering based on sharing between multiple relatives provides a distinct advantage in prioritizing sequence variants potentially underlying disease susceptibility. Lastly, we note that although the power for multipoint linkage and SGS n sharing appear to be very similar, the shared segments identified for SGS were substantially shorter than the 1-LOD support intervals suggested by the linkage analysis.

Finally, our analysis of the extended AFAP pedigree with a known causal gene provided a positive proof-of-principle example. We illustrated that SGS was able to produce genome-wide significant results in the region containing the known mutation. In line with our finding outlined above, this shared genomic segment was small (1.96 Mb) which was substantially smaller than the previously identified 7.17 Mb using linkage analysis on the reduced density 10K SNP array (Neklason et al., 2008).

In conclusion, both our power study and the proof-of-principle example suggest that the SGS method (particularly n-1 sharing) will be an extremely valuable new analysis tool, and will help to fill a much needed gap for localizing rare disease variants. From our results, it is apparent that the SGS approach will not attain excellent power for all possible disease models involving rare variants; however, it is also evident that there are many scenarios where using this technique on a small number of extended high-risk pedigrees will have more power to identify rare disease variants than multipoint linkage analysis or extremely large GWAS studies. Our results suggest that SGS analyses have the potential to play an important role in identifying rare risk variants by localizing small genomic regions that are practical for intense sequencing, and by thorough sequence variant analyses facilitating the identification of novel disease variants

Appendix.

Here we describe the details of the estimation of power based on equation (4) which is repeated here for convenience:

$$\mathrm{P}(\text{reject}{\mathrm{H}}_0|\text{alternative is true})=\sum _j\mathrm{P}(\text{reject}{\mathrm{H}}_0|{\mathrm{F}}_j|\text{HR}\cap 15\mathrm{M})\frac{\mathrm{P}(\text{HR}\cap 15\mathrm{M}|{\mathrm{F}}_j)\mathrm{P}({\mathrm{F}}_j)}{\mathrm{P}(\text{HR}\cap 15\mathrm{M})}$$

The four components of this are: (A) The probability that a pedigree is high-risk and contains at least 15 meioses between cases, denoted P(HR ∩15M). This probability depends on the definition for high-risk pedigree status (significant excess disease p<0.001 or p<0.00001) and the disease model (12 considered, see Table 1); (B) The probability of a set of founder genotypes for the dSNP, denoted P(Fj). This probability depends on the disease model allele frequency; (C) The probability that a pedigree will be high-risk and have ≥15 meioses separating cases conditional on a specific set of founder genotypes, denoted P(HR ∩15M| Fj). This probability depends on the definition for high-risk status and the disease model; and (D) The probability of rejecting the null hypothesis (p<0.05) under a disease model (12 considered) conditional on a high-risk pedigree with ≥15 meioses separating cases with a specific set of founder genotypes, denoted P(reject H₀ | Fj | HR ∩15M). This can be thought of as the power specific to a certain founder genotype set. This probability depends on the high-risk pedigree definition and the disease model.

A. P(HR ∩ 15M)

For each disease model and high-risk definition, we estimated P(HR ∩ 15M) using simulation. Based on our backbone pedigree, we simulated 25,000 pedigrees for each disease model. We identified the pedigrees from each 25,000 that satisfied both high-risk status (based on the two definitions; p<0.001 and p<0.00001) and at least 15 meioses between cases. For each disease model and high-risk definition, the proportion of pedigrees from the 25,000 that satisfied these conditions was used as the estimate for the probability.

B. P(Fj)

The probability for each founder genotype set was calculated explicitly. Because there is substantial redundancy in many of the sets, some sets were grouped together. For example, the genotype set created by the female ancestral founder being heterozygous for the dSNP plus all other founders wildtype is equivalent to the genotype set created by the male ancestral founder being heterozygous for the dSNP and all other founders wildtype. Such equivalent sets are considered together as a single F_j. For each F_j, the probability is simply the product of genotype frequencies multiplied by the number of equivalent sets. In our backbone pedigree there are 106 founders. For example, the probability that a single ancestral founder is in heterozygous and all other founders are wildtype is:

$$\left(\begin{array}{c}2\\ 1\end{array}\right){\left[{(1-p)}^2\right]}^{105}[2p(1-p)]$$ (5)

where p is the disease allele MAF.

C. P(HR ∩15M/F_j)

We estimated P(HR ∩15M| F_j) using simulation. For each disease model we simulated between 15,000-150,000 pedigrees (more to estimate low probability values). We conditioned on each dSNP founder genotype set F_j, performed a gene-drop, and assigned disease status according to the model. Pedigrees were assessed for high-risk status and ≥15 meioses between cases. The proportion that satisfied both conditions provided the estimate for the probability.

D. P(reject H₀ | F_j | HR ∩15M)

Genomic sharing between multiple distant relatives is highly unlikely by chance. The SGS method is based on identifying this sharing between related cases and will therefore have most power for a rare, dominant risk allele that has entered the pedigree in heterozygous form via an ancestral founder and segregated to the related cases. Given this assumption, and for efficiency of simulations, we conservatively consider only two founder genotypes sets at the dSNP (Fj) for the above conditional power. All other F_j were assumed to produce only 5% power (i.e. the chance probability of rejecting the null at the disease position when testing at the 0.05 level). The two founder genotype sets considered were: (1) dSNP heterozygous in a single ancestral founder and all other founders wildtype; and (2) dSNP heterozygous in one ancestral founder and in one 4^th generation lateral founder and all other founders wildtype.

The conditional power (P(reject H₀ | F_j| HR ∩15M)) was estimated via simulation for each disease model and high-risk definition. From the 15,000-150,000 simulations generated for each model in (C) above, we selected 1000 pedigrees for the F_j of interest that satisfied both high-risk status and ≥15 meioses between cases. For each of these 1000 pedigree sets and 24 scenarios (12 models, two high-risk definitions), we determined the run length R_i(t) that spanned the true disease locus for both t=n and t=n-1 sharing. The significance of this run was determined empirically as the mean of the p-values of each SNP contained in the run. The null hypothesis was rejected for this single test if the significance of the run was p≤0.05 (i.e. alpha=0.05). The conditional power was considered to be the proportion of the 1000 pedigrees where the null hypothesis was rejected.