Modeling Alternative Splicing Variants from RNA-Seq Data with Isoform Graphs

Abstract

Next-generation sequencing (NGS) technologies need new methodologies for alternative splicing (AS) analysis. Current computational methods for AS analysis from NGS data are mainly based on aligning short reads against a reference genome, while methods that do not need a reference genome are mostly underdeveloped. In this context, the main developed tools for NGS data focus on de novo transcriptome assembly (Grabherr et al., 2011; Schulz et al., 2012). While these tools are extensively applied for biological investigations and often show intrinsic shortcomings from the obtained results, a theoretical investigation of the inherent computational limits of transcriptome analysis from NGS data, when a reference genome is unknown or highly unreliable, is still missing. On the other hand, we still lack methods for computing the gene structures due to AS events under the above assumptions—a problem that we start to tackle with this article. More precisely, based on the notion of isoform graph (Lacroix et al., 2008), we define a compact representation of gene structures—called splicing graph—and investigate the computational problem of building a splicing graph that is (i) compatible with NGS data and (ii) isomorphic to the isoform graph. We characterize when there is only one representative splicing graph compatible with input data, and we propose an efficient algorithmic approach to compute this graph.

1. Introduction

Next-generation sequencing (NGS) technologies allow massive and parallel sequencing of biological molecules (DNA and RNA) and have a huge impact on molecular biology and bioinformatics (Metzker, 2010). In particular, RNA-Seq is a recent technique to sequence expressed transcripts, characterizing both the type and the quantity of transcripts expressed in a cell (its transcriptome). Challenging tasks of transcriptome analysis via RNA-Seq data (Trapnell et al., 2010; Nicolae et al., 2011; Feng et al., 2011) are reconstructing full-length transcripts (or isoforms) of genes and estimating their expression levels.

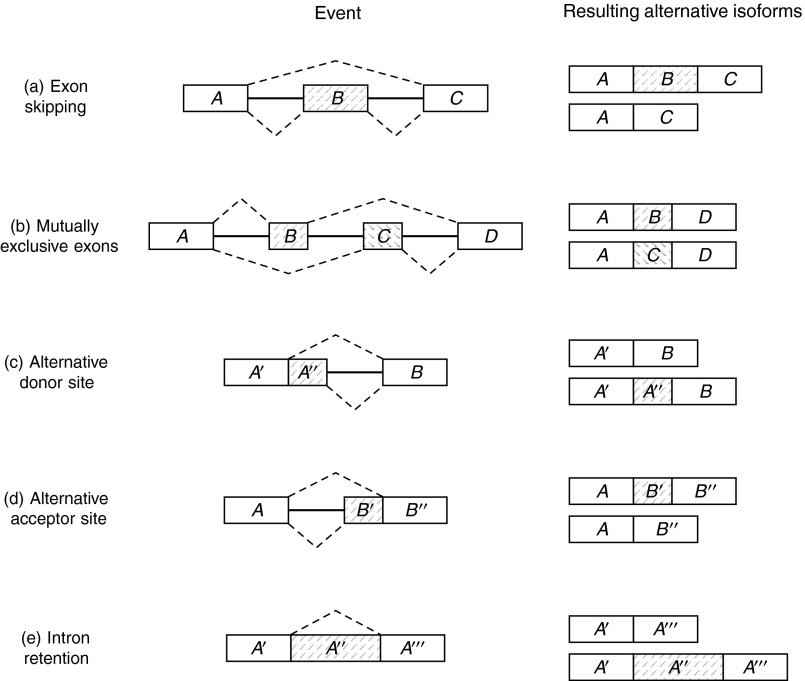
A gene is a DNA region coding for a protein, and in eukaryotic organisms it is composed of exons (coding regions or exon-coding regions) alternated with introns (noncoding regions). DNA and RNA molecules are sequences of the nucleotides {a, c, g, t} and {a, c, g, u}, respectively. During transcription, the DNA sequence of the gene is replicated into a pre-mRNA molecule, substituting each occurrence of the nucleotide t (in DNA) with the nucleotide u (in pre-mRNA). Then, the splicing phase removes gene introns from the pre-mRNA molecule, which is transformed into a mature mRNA (messenger RNA), also called a transcript (Fig. 1). Finally, mRNA is translated into a protein. Notice that only exons are concatenated in an mRNA. The most recent studies indicate that alternative splicing (AS) is a major mechanism, generating functional diversity in humans and vertebrates, as at least 90% of human genes exhibit splicing variants. This process allows production of different mRNAs (or gene isoforms) starting from a single pre-mRNA molecule by including or excluding different exon-coding regions of the gene. The annotation of alternative splicing variants and AS events, in order to differentiate and compare organisms, is one of the central goals in transcriptomics. Alternative splicing is involved in the onset of several diseases (Caceres and Kornblihtt, 2002). AS can be summarized in the following five events as reported in Figure 2: (a) exon skipping (one exon may be removed or retained); (b) mutually exclusive exons (only one of two exons can be retained); (c) alternative donor site (only one prefix of an exon is retained by changing the right exon boundary); (d) alternative acceptor site (only one suffix of an exon is retained by changing the left exon boundary); and (e) intron retention (an exon substring is spliced out) (Sammeth et al., 2008).

FIG. 1.

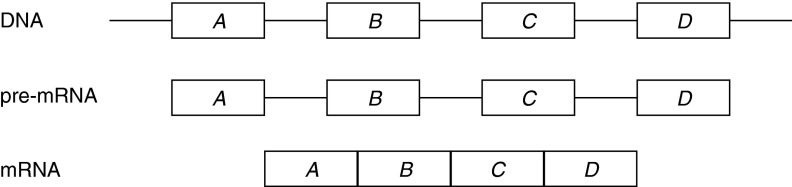
Mechanism of gene expression. Rectangles A, B, C, and D represent exons while the thin lines represent introns.

FIG. 2.

Basic alternative splicing events. The exon-coding regions involved in each event are highlighted in gray. The isoforms are represented by dashed paths.

The most widely used pipeline in transcriptomics (Trapnell et al., 2012) starts by aligning all input reads against a reference genome, just as other available pipelines do. We point out that in some cases, such as highly fragmented or altered data (usually extracted from tumor tissues), reads cannot be reliably aligned against the reference genome, which is obtained from healthy individuals. At the same time, the use of NGS data without a reference genome is simply not as advanced, hence justifying our interest.

The most studied problem when a reference genome is unknown is de novo transcript assembly [attacked with methods such as Trinity (Grabherr et al., 2011), TransAbyss (Robertson et al., 2010), and Oases (Schulz et al., 2012)]. All those methods are built on the concept of de Bruijn graphs; this construction results in tools that are computationally expensive and can find only most of the annotated isoforms, while providing a large amount of nonannotated full-length transcripts that need to be experimentally validated. In fact, these tools have to employ sophisticated steps to process the de Bruijn graph before computing the transcripts or the assembly.

Moreover, there is an additional problem. When the reference is unknown, it is impossible to align a transcript against the genome. Since such an alignment is the standard procedure for determining the gene structure from the full-length transcripts, that procedure cannot be applied in our setting. In fact, the computed transcripts should be split into putative exons by identifying common portions, a procedure that can easily become time consuming for genes that exhibit a complex structure (for instance, the TTN gene has over 300 exons with an exon-coding region longer than 80,000 bases and more than 40 transcripts).

Another limitation of the current approaches is that they are not well suited to the analysis of the whole genome, since transcripts should be clustered together according to the originating gene—a task that is made harder by repeated regions in the genome. From the computational and algorithmic perspective a theoretical study of the inherent limits of current methods built only on RNA-Seq data is missing. In fact in this article, we are interested in a theoretical study of a compact representation of AS events in genes that may be built from RNA-Seq data and of the main computational problems that may arise. Moreover, we are aiming to make genome-wide analysis a task that is manageable on a standard workstation, providing a concise result, such as a graph or an easy-to-understand listing of AS events for each gene, even if for the originating gene the input RNA-Seq data is unknown.

For this purpose, we study and adapt the notion of isoform graphs (Lacroix et al., 2008), which has been introduced as a tool for studying isoform quantification. Since the original setting is orthogonal to ours, where abundance is not considered, we need to introduce a different definition in which only unweighted isoform graphs are considered. We also acknowledge the influence that a graph representation of splice variants—the splicing graph (Heber et al., 2002)—has on our approach.

The focus of our article is to reconstruct the isoform graph from NGS data (i.e., RNA-Seq single reads) without a known reference genome. More precisely, a fundamental question we are going to investigate in this article is: Under which conditions can the reconstruction of a gene structure be efficiently accomplished using only information provided by RNA-Seq data? In order to partially answer this question, we introduce the formal definition of the computational problem of reconstructing the gene structure from RNA-Seq data when the solution is represented by an isoform graph, and we study when the problem can be uniquely or efficiently solved. Moreover, we give some necessary or sufficient conditions to infer the isoform graph, and finally we describe an efficient heuristic for our problem, even on data violating the conditions necessary to exactly infer the isoform graph. The proposed algorithm explores a hashing technique for short reads, and it works in time that is linear in the total size of the input data.

We believe that our article introduces some fundamental problems and definitions that deserve a more thorough exploration toward the understanding of the possibilities and limitations of computing the distinct gene structures from which genome-wide RNA-Seq or short reads data have been extracted, without any knowledge of the reference genome.

2. The Isoform Graph And The Sgr Problem

Briefly, a splicing graph is the graph representation of a gene structure, inferred from a set of RNA-Seq data, where isoforms correspond to paths of the splicing graph, while splicing events correspond to specific subgraphs. In this section, first we give a formal (computational) definition of gene. Then we formalize the problem of reconstructing the splicing graph that represents the gene whose input is the RNA-Seq data derived from the transcripts of .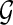

Let 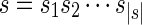be a sequence of characters, which is a string. Then s[i : j] denotes the substring 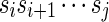of s, while s[: i] and s[j :] denote respectively the prefix of s ending with the i-th symbol and the suffix of s starting with the j-th symbol of s. We denote with pref(s, i) and suff(s, i), respectively, the prefix and suffix of length i of s. Among all prefixes and suffixes, we are especially interested in LH(s) = pref(s, |s|/2) and RH(s) = suff(s, |s|/2), which are called the left half and the right half of s¹. Given two strings s₁ and s₂, their overlap ov(s₁, s₂) is the length of the longest suffix of s₁ that is also a prefix of s₂. The fusion of s₁ and s₂, denoted by φ(s₁, s₂), is the string s₁[: |s₁| – ov(s₁, s₂)]s₂ obtained by concatenating s₁ and s₂ after removing from s₁ its longest suffix that is also a prefix of s₂. We extend the notion of fusion to a sequence of string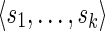s as 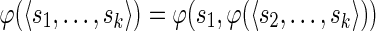if k > 2, and .

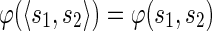In this article we consider discrete genomic regions (i.e., a gene or a set of genes) and their full-length isoforms or transcript products of the genes along these regions. A gene isoform is a concatenation of some of the exon-coding regions of the gene respecting their order in the genomic region. Alternative splicing regulates how different exon-coding regions are included to produce different full-length isoforms or transcripts, which are modeled here as sequences of blocks. Formally, a block b is an abstract object containing a string, denoted by s(b), typically taken over the alphabet Σ = {a, c, g, t}. Notice that two blocks can contain equal strings.

In our framework, a gene exon-coding region is a sequence (that is, an ordered set) 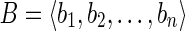of blocks, and the string exon-coding region for B is the string 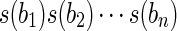obtained by orderly concatenating the strings of the blocks in B. Intuitively a gene exon-coding region is the sequence of all the exon-coding regions on the whole genomic sequence for the studied gene. We define a block isoform f compatible with B, as a subsequence of B, that is 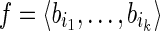where i_j < i_j+1 for 1 ≤ j < k. A sequence of blocks that are consecutive in some isoforms is called a strip (of blocks). The string of a strip is the concatenation of the strings of the blocks that compose the strip. We distinguish between classical isoforms (defined on exons or genomic regions) and block isoforms (defined on blocks). Nonetheless, we will use interchangeably the terms isoforms and block isoforms whenever no ambiguity arises. By a slight abuse of language, we define the string of f, denoted by s(f), as the concatenation of the strings of the blocks of f.

Definition 1

An expressed gene is a pair 〈B, F〉, where B is a gene exon-coding region, F is a set of block isoforms compatible with B, where (i) each block of B appears in some isoform of F; (ii) for each pair (b_i, b_j) of blocks of B, appearing consecutively in some isoform of F, there exists an isoform 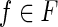such that exactly one of b_i or b_j appears in f.

We point out that Definition 1 is mostly compatible with that of Lacroix et al. (2008), where a block is defined as a maximal sequence of adjacent exons, or exon fragments, that always appear together in a set of isoforms or variants. One of the main differences between those definitions is that ours explicitly allows blocks with identical strings.

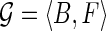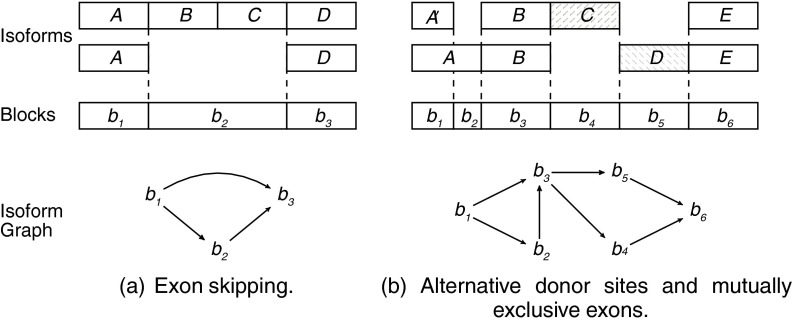
Given an expressed gene , the isoform graph of 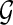is a directed graph G_I = (B, E), where an ordered pair (b_i, b_j) is an arc of E iff b_i and b_j are consecutive in some isoforms of F. Figure 3 represents two examples of expressed genes and their isoform graphs. Notice that G_I is a directed acyclic graph, since the sequence B is a topological order of G_I. Moreover, isoforms correspond to paths in G_I, while the converse is not always true. For example, in Figure 3b the path 〈b₁, b₂, b₃, b₄, b₆〉 is not an isoform.

FIG. 3.

Two examples of expressed genes and their isoform graphs. Capital letters correspond to exons (of “classical” isoforms). In (a) we have a skipping of the two consecutive exons B and C of the second isoform with respect to the first one. Since there does not exist an isoform with exactly one of exons B or C, block b₂ corresponds to the concatenation of the two exons B and C. In (b) we can find an alternative donor site between exons A and A′, which is a prefix of A, and two mutually exclusive exons C and D.

The first aim of the article is to characterize when the isoform graph of an expressed gene can be reconstructed from a set of substrings (i.e., RNA-Seq data) of the isoforms of the gene.

Notice that the isoform graph is the real gene structure that we would like to infer from data but, at the same time, we must understand that the transcript data might not be sufficient to determine the isoform graph, as we have no information on the genomic sequence and on the blocks in particular. Therefore we aim to compute a slightly less informative kind of graph: the splicing graph G_S, which is a directed graph where each vertex v is labeled by a string s(v). Notice that the splicing graph gives no assurance that a vertex is a block, nor does it contain any indication regarding whether (and where) the string labeling a vertex appears in the genomic region.

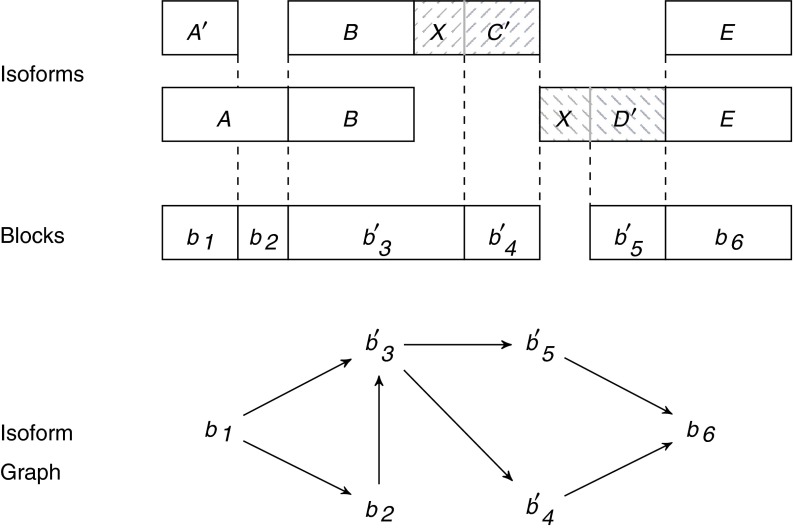
For instance, let us consider the isoform graph of Figure 3b. Assume that s(b₄) and s(b₅) share a common prefix, that is, the exons C and D can be respectively written as XC′ and XD′ (as shown in Fig. 4). Then if we only know the strings of the isoforms, the splicing graph of Figure 4 could be as plausible as the isoform graph of Figure 3b. However, observe that the isoform graph and the “alternative” splicing graph are structurally identical (they are isomorphic) and only the labels change.

FIG. 4.

An example of a different subdivision in blocks of the expressed gene of Figure 3b if exons C and D share a common prefix X (i.e., C := XC′ and D := XD′). Notice that the isoform graph is isomorphic to that of Figure 3b but it is different since the strings of the blocks do not coincide.

Since the case presented in the example is quite common, we formalize it with the notion of ambiguous block's borders and ambiguous expressed gene. Let 〈B, F〉 be an expressed gene. We say that a block 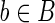is right-ambiguous if all the blocks succeeding b in the isoforms of F share a (not-empty) prefix. Conversely, b is left-ambiguous if all the blocks preceding b in the isoforms of F share a (not-empty) suffix. An expressed gene is ambiguous if some block in B is left-ambiguous or right-ambiguous.

Clearly both isoform and splicing graphs are directed labeled graphs (isoform graphs are also acyclic). Even though we distinguish those two kinds of graphs since they semantically represent two different views of a gene structure, for ease of exposition, whenever no confusion arises, we will treat an isoform graph as a special class of splicing graph.

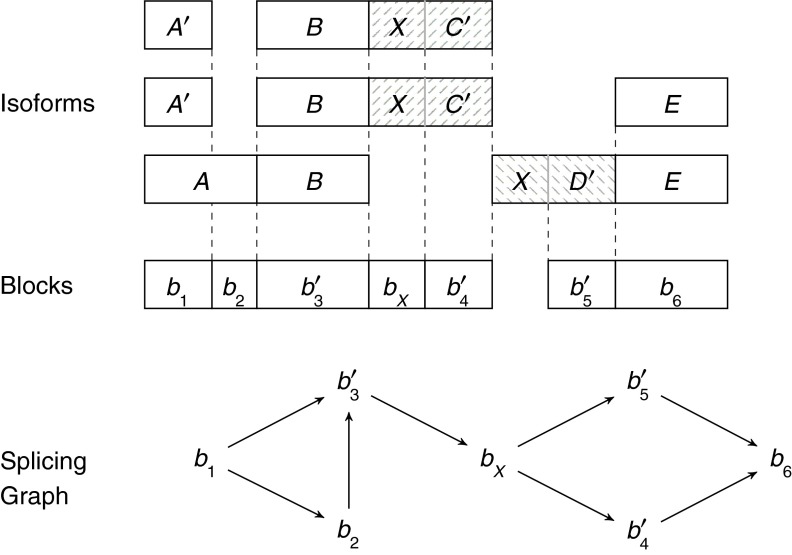
In Figure 5 we give a different splicing graph for the same isoforms of Figure 4. Since both graphs are correct explanations of the input isoforms, the figure points out the need to clearly differentiate between the notion of the “true” isoform graph and of a “possible” splicing graph. Moreover, Figure 5 allows us to make another observation. If the first (and topmost) isoform is removed, the splicing graph is still a correct explanation of the remaining isoforms; therefore, there are some situations that we might not be able to distinguish. These observations that multiple solutions are possible and multiple instances might have the same solution are fundamental in our article.

FIG. 5.

A different splicing graph for Figure 4. Notice that each block also contains the nucleotide sequence of the corresponding genomic region.

We need a few more definitions related to the fact that we investigate the problem of reconstructing a splicing graph, which explains a set of isoforms only from RNA-Seqs obtained from the gene transcripts. Let 〈B, F〉 be an unknown expressed gene. Then, an RNA-Seq read (or simply read) extracted from 〈B, F〉 is a substring of the string s(f) of some isoform. 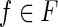Notice that we know only the nucleotide sequence of each read and not its position in s(f). From this observation we can define the notion of splicing graph compatible with a set of reads.

Definition 2

Let R be the set of all the possible l-long reads extracted from an expressed gene 〈B, F〉, and let G_S be a splicing graph. Moreover, let R_S be the set of all the possible l-long reads extracted from the set Π_S of all the possible paths of G_S. Then G_S is compatible with R if R = R_S.

Problem 1. Splicing graph reconstruction (SGR) problem

Input: a set R of all the possible l-long reads extracted from an (unknown) expressed gene 〈B, F〉.

Output: a splicing graph compatible with R.

Clearly SGR can only be a preliminary version of the problem, as we are actually interested in finding a splicing graph that is most similar to the isoform graph of 〈B, F〉. Therefore, we need to introduce some criteria to rank all splicing graphs compatible with R. The parsimonious principle leads us to a natural objective function (albeit we do not claim it is the only possibility): to minimize the weight of the graph, where the weight is defined as the sum of the lengths of strings associated with the vertices (mimicking the search for the shortest possible string exon-coding region). We call this graph a minimum-weight splicing graph. In the rest of the article the SGR problem will ask for a minimum-weight splicing graph.

The definition of the SGR problem is quite strict, as it requires that the set R contains all the reads extracted from the expressed gene. We point out that this fact has no real practical consequences, as our algorithm can be applied also to instances in which the set of reads is only a part of all possible l-long reads extracted from an expressed gene. We also notice that a weaker definition of compatibility is not appropriate to our purposes. In fact, if, for example, we only require that the set R is contained in the set R_S (and not equal as we did), then a “degenerate” minimum-weight splicing graph (such as the complete directed graph with |Σ| vertices labeled with the symbols of the alphabet) would be a universal solution to the SGR problem.

Albeit not appearing of practical interest, such a strict problem definition is instead useful to highlight the intrinsic limits of the reconstruction of a splicing graph starting from the reads, even in ideal conditions. This is, in particular, the aim of Section 3. Moreover, this formulation of the SGR problem is also useful for devising an efficient algorithm (presented in Section 4) for the reconstruction of a minimum-weight splicing graph in an “ideal” scenario. Such an algorithm is then extended in Section 5 in order to effectively deal with the cases in which the ideal conditions do not hold, without sacrificing much of its efficiency. Clearly, in this case, we implicitly solve a sort of “relaxed” version of the SGR problem, where the compatibility to the set of reads and the minimality of the splicing graph weight is not strictly required. The soundness of our model and of our approach is also empirically supported by an experimentation (Section 6) on synthetic datasets generated from real annotated genes.

3. When The Sgr Problem Cannot Be Solved

In this section, we show that if some conditions do not hold, then the isoform graph of the given expressed gene is not isomorphic to a solution of the SGR problem. Even though such conditions seem to highlight the limits of our model, our definition of compatibility and our formulation of the SGR problem are intuitive and ensure ideal conditions, hence what is highlighted are actually the intrinsic limits of any formulation of the reconstruction problem starting only from the information provided by a set of short reads. Clearly, our study is intended as a first step toward the theoretical understanding of the limits, as well as the advantages, of using short reads as a way to investigate the contributions of alternative splicing on the expansion of the complexity of transcriptome. Additional kinds of information—such as paired end, existing annotations, and digital expression levels—can and should be exploited to further improve the accuracy of the predictions. Nonetheless, we still believe that such theoretical results support and advocate the use of graph structures (like the one we propose) to describe and summarize the AS events occurring in a set of related full-length isoforms. In fact, those theoretical limits show that de novo reconstruction of full-length transcripts possibly produces unreliable long-range predictions and, if this uncertainty is not properly taken into account in the downstream analyses, it could introduce biases in the final findings. Instead, graph structures summarizing AS events (especially according to our notion of compatibility with a set of reads) only represent local predictions that are potentially more accurate than long-range predictions, thus the risk of introducing biases in downstream analyses is reduced. Obviously, depending on the data and on the final needs, a trade-off between local predictions only and long-range predictions must and should be reached. However, how this trade-off can be reached is, to the best of our knowledge, an interesting open question.

The main notion we introduce in this section is that of solvable expressed gene, where we say that an expressed gene 〈B, F〉 is solvable if its isoform graph is isomorphic to a minimum-weight splicing graph compatible with the set R of all the l-long reads extracted from 〈B, F〉.

The basic, yet important, limits on the possibility to correctly reconstruct a splicing graph, representing the true (and unknown) isoform graph, are formally presented in the following lemma, which states some conditions that must be verified in order to have a solvable expressed gene 〈B, F〉.

Lemma 3

An expressed gene 〈B, F〉 is not solvable if some of the following conditions hold:

• 1. 〈B, F〉 is ambiguous;

• 2. there exists a string α of length l – 1 that occurs in the label of two distinct blocks b_i and b_j;

• 3. there exists a string α of length l – 1 that occurs twice in the label of a block b.

Proof. We show that if any condition holds, then 〈B, F〉 is not solvable because there exists a splicing graph G_S that (i) is distinct from the isoform graph G_I, (ii) is compatible with the set R of all the l-long reads extracted from G_I, and (iii) whose weight is strictly smaller than that of the isoform graph.

Case 1. Let us suppose that B = {b, b₁, b₂} and 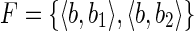. Moreover, let s(b₁) = xs₁ and s(b₂) = xs₂, that is, the strings of both blocks b₁ and b₂ begin with the symbol x, followed by the strings s₁ and s₂, respectively. Consider now the splicing graph G_S = (V, E) where 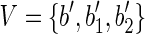and 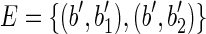, and which 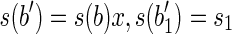, and 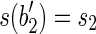. (Informally, we moved the symbol x from the beginning of b₁ and b₂ to the end of b.) The splicing graph is compatible with the set R of all the reads extracted from 〈B, F〉 and, in addition, we have 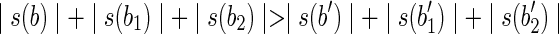. However, the splicing graph is distinct from the isoform graph of 〈B, F〉, thus 〈B, F〉 is not solvable. A similar example shows that an expressed gene 〈B, F〉 having a left-ambiguous block is not solvable.

Case 2. In this case, an (l – 1)-long string α occurs in the labels of two distinct blocks b_i and b_j. Hence the two strings can be expressed as: s(b_i) = p_iαs_i and s(b_j) = p_jαs_j. Then, construct a splicing graph G_S starting from G_I as follows. First replace the nodes (i.e., the blocks) b_i and b_j with the nodes 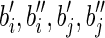, and a, where 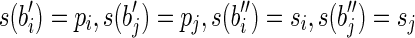, and s(a) = α. Then add the arcs 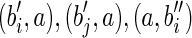, and 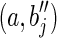. Let R_S be the set of all possible reads extracted from the splicing graph G_S. To verify that G_S is compatible with R, we have to show that R = R_S. Since G_S is built starting from the isoform graph and replacing some nodes, the only reads that could be different are the ones extracted from such nodes. More precisely, by splitting s(b_i) and s(b_j) over three nodes each (of which one is in common), all the reads in R are clearly also in R_S, and the only reads in R_S that could not belong to R would be the ones extracted from the paths 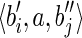and 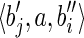. In any case, since α has length l – 1, there cannot exist a read containing both a suffix of 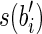and a prefix of 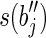or both a suffix of 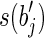and a prefix of 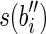. It follows that R_S = R. Moreover, the sum of lengths of the labels of the splicing graph is smaller than that of the isoform graph. Hence, G_I is not a minimum-weight graph compatible with R and, thus, 〈B, F〉 is not solvable. Notice that, if the repeated substring α has length less than l – 1, then it would be possible to extract some reads combining a suffix of 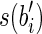with a prefix of 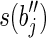(or a suffix of 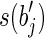and a prefix of 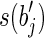) that are not in R.

Case 3. In this case, an (l – 1)-long string α occurs twice in the string s(b) of a block 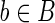. We must distinguish two subcases: the two occurrences do not overlap (i.e. s(b) = s₁αs₂αs₃) or the occurrences overlap. In the first subcase, as previously done, we derive a splicing graph G_S, compatible with R, from G_I by replacing the node b with the nodes {b₁, b₂, b₃, a}, and setting s(b₁) = s₁, s(b₂) = s₂, s(b₃) = s₃, and s(a) = α. The arcs incident to b are replaced with arcs incident to b₁, the arcs starting from b are replaced with arcs starting from b₃, and the new arcs {(b₁, a), (a, b₂), (b₂, a), (a, b₃)} are added. As in the previous case, since G_S is built starting from the isoform graph and replacing some nodes, the only reads that could be different are the ones extracted from such nodes. More precisely, the only reads that could violate the compatibility would be the ones extracted from the path 〈b₁, a, b₃〉. In any case, since α has length l – 1, there cannot exist a read containing both a suffix of s₁ and a prefix of s₃. It follows that R is equal to the set of all the reads extracted from G_S and, since the weight of the splicing graph is smaller than that of the isoform graph, the isoform graph of 〈B, F〉 is not a minimum-weight splicing graph compatible with R, hence 〈B, F〉 is not solvable. The subcase where the two occurrences of α overlap is similar to the other subcase but without the node b₂ and with a new arc (a, a). In fact, since any l-long read extracted from the path 〈a, a〉 is also in R, we have that G_S is compatible with R and that its weight is less than that of G_I, thus 〈B, F〉 is not solvable.      ■

Notice that the three cases have different impacts on the differences between the (unknown) isoform graph and a minimum-weight splicing graph (which is the one computed by any procedure solving the SGR problem). In fact, if 〈B, F〉 is ambiguous, then the isoform graph and the minimum-weight splicing graph are isomorphic, and the only differences are on the vertices' labels. This is clearly a minor difference, and the splicing graph can be considered as (almost) correctly reconstructed. In the other two cases, a long string that occurs in multiple positions induces quite a substantial difference between the isoform graph and the splicing graph. This fact clearly shows the intrinsic limits of any approach that only considers the information provided by a set of reads. However, the constant advances on the sequencing technologies will soon lessen the strength of these limits, as the reads are quickly becoming both longer and sequenced with greater accuracy.

4. Methods

In this section, we propose a fast method for solving the SGR problem based on the efficient use of hash tables indexing a compact representation of the reads given as input. The basic idea of our method is that we can find two disjoint subsets U and S of the input set R of reads, where the reads of U, called unspliced, can be assembled to form the nodes of the splicing graph G_S, while the reads of S, called spliced, are an evidence of a junction between two blocks (hence they form the arcs of G_S). Computationally expensive pairwise comparisons among the reads are avoided by using the hash tables. Moreover, a compact binary encoding of the reads allows to reduce the memory usage and to exploit the fast bit-level operations offered by modern hardware architectures. In particular, our method is composed of three steps: first, reads are preprocessed and classified in three distinct categories, then “chains” of overlapping reads corresponding to the putative blocks of the expressed gene are computed, and, finally, arcs among the putative blocks are added on the basis of the evidence provided by reads not used to form the putative blocks.

We will show that our algorithm reconstructs the isoform graph of well-expressed genes in polynomial time, and that such a graph is also a minimum-weight good splicing graph compatible with the set R of all the possible reads extracted from the expressed gene, where expressed genes that are well-expressed and good splicing graphs are defined below. In the next section, instead, we discuss how our method can be extended in order to effectively deal with instances in which the correctness conditions do not hold, and in Section 6 we give experimental evidence that our algorithm can be successfully applied even on expressed genes that are not well-expressed, as in most cases it is able to compute a splicing graph highly similar to the isoform graph.

Definition 4

An expressed gene 〈B, F〉 is well-expressed if and only if:

• a) 〈B, F〉 is not ambiguous;

• b) for each edge (b_i, b_j) of the isoform graph of 〈B, F〉, either outdegree(b_i) ≠ 1 or indegree(b_j) ≠ 1;

• c) the length of each block is at least l;

• d) there does not exist an (l/2)-long substring that occurs twice in the set of strings composed by (a) the strings of the blocks and (b) the strings obtained by concatenating suff(s(b_i), l/2 – 1) pref(s(b_j), l/2 – 1) for each arc (b_i, b_j) of the isoform graph of 〈B, F〉.

Similarly, a splicing graph is good if the string of each vertex has length at least l and if no (l/2)-long string occurs twice in the set of strings composed of the strings of its vertices and the strings suff(s(v_i), l/2 – 1) pref(s(v_j), l/2 – 1) for each of its arcs (v_i, v_j). Clearly, the isoform graph of a well-expressed gene is a good splicing graph. We claim that if we require that feasible solutions of the SGR problem are good graphs, then each instance extracted from an expressed gene that is well-expressed has a unique feasible solution, which is therefore optimal. In fact, let us call borders all (l/2)-long prefixes and suffixes of each block. Notice that an (l/2)-long string s is a border iff there exist two reads r₁ and r₂ such that (i) LH(r₁) = LH(r₂) = s and r₁[l/2 + 1] ≠ r₂[l/2 + 1] or (ii) RH(r₁) = RH(r₂) = s and r₁[l/2] ≠ r₂[l/2]. Since the set of borders depends only on the set of input reads, all feasible solutions (including the isoform graph) share the same set of borders. A similar argument shows that all feasible solutions share the same set of arcs. Now, let b be any block of a feasible solution. Let R_b be the sequence of l-long substrings of s(b) and let s₁, s₂ be two consecutive substrings in R_b. Notice that s₁ and s₂ have overlap l – 1. Clearly such common (l – 1)-long substring appears only in one block of each feasible solution, therefore s₁ and s₂ appear consecutively in the same block of each feasible solution. This fact immediately implies that all feasible solutions have the same set of blocks. As we said, the algorithm is based on a preliminary classification of reads. Formally, reads are classified as follows.

Definition 5

Let r be a read of R. Then r is spliced if there exists a read 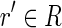, with 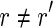, such that pref(r, k) = pref(r′, k) or suff(r, k) = suff(r′, k), for some k ≥ l/2. Moreover, a read r is perfectly spliced if there exists a read 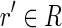, with 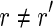, such that the longest common prefix (or suffix) of r and r′ is exactly of length l/2. A read that is not spliced is called unspliced.

Intuitively, for expressed genes that are well-expressed, it should be clear that spliced reads are those crossing the borders of (the strings of) two consecutive blocks in some isoform, while unspliced reads are those that occur within (the string of) a single block. (A single small exception to this rule is discussed while proving the algorithm's correctness.) In fact, let us suppose, for example, that two isoforms f′ and f″ of an expressed gene that is well-expressed share a common block b that is then followed by a block b′ in f′ and by a different block b″ in f″. Then, there exists two reads r′ and r″ such that LH(r′) = LH(r″) = suff (s(b), l/2) and RH(r′) = pref (s(b′), l/2) and RH(r″) = pref (s(b″), l/2). The two reads r′ and r′′ are spliced (perfectly spliced) and indicate that the vertex of the splicing graph whose string ends with LH(r) should be connected to the vertices whose strings start with RH(r′) and RH(r″). Conversely, in an expressed gene that is well-expressed, the reads extracted from the string of a single block are unspliced, since there exists a single occurrence of each of their (l/2)-long prefixes, and it is clearly followed by an occurrence of the corresponding (l/2)-long suffix. As such, we can first distinguish between the reads that will form the putative blocks (hence the vertices of the splicing graph), and the reads that will form the arcs between the vertices of the splicing graph. Our three-step procedure, presented and discussed in the remainder of this section, formalizes this intuitive idea.

In the following, for convenience, we assume that the reads have length l = 64. This choice, as we will see, allows us to compactly represent each half of a read with a 64-bit number, which can be then efficiently managed and processed by modern computer architectures. Nonetheless, our method can be easily extended to process longer reads in at least two ways. The first way is to extract some (or all) of the 64-long substrings of each read longer than 64 and to process the resulting set. This strategy possibly discards some information, but preserves the practical efficiency of operating on 64-bit integer numbers. The second way, instead, is to use the real length of the reads. In this way, the method does not actually change and, clearly, becomes less sensitive to the presence of repeated sequences. However, it would become harder to find short blocks, and the implementation would also suffer some penalty in terms of efficiency. A strategy that mixes the previous ones is also possible, and different trade-offs can thus be reached depending on the needs and the characteristics of the dataset to be analyzed.

4.1. Step 1: read preprocessing and classification

Each 64-long read can be unambiguously encoded by a 128-bit binary number, exploiting the fact that we can encode each symbol of the nucleotide alphabet Σ = {a, c, g, t} with 2 bits as follows: enc(a) = 0 = 00₂, enc(c) = 1 = 01₂, enc(g) = 2 = 10₂, enc(t) = 3 = 11₂. Since such encoding is a one-to-one mapping between reads and numbers between 0 and 2¹²⁸ – 1, we will use interchangeably a string and its binary encoding. Moreover, given a read r, we define left fingerprint and right fingerprint respectively as the leftmost and the rightmost 64 bits of the encoding of r.

The main purpose of this step is to partition the reads of an input set R into three classes: U, composed of the unspliced reads, PS, composed of the perfectly spliced reads, and S, composed of the (nonperfectly) spliced reads. To avoid pairwise comparison, we first construct two hash tables 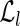and 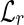, both of which are indexed by 64-bit fingerprints. More precisely, 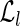has an entry indexed by each left fingerprint, while 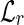has an entry indexed by each right fingerprint. The entry of 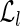, associated with the left fingerprint f_l, consists of a list of all the right fingerprints f_r such that the concatenation f_lf_r is a read in the input set R. The role of 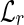is symmetrical.

The classification of each read is then performed querying the two hash tables. In fact, a read r is unspliced iff both the entry of 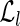indexed by its left fingerprint and the entry of 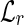indexed by its right fingerprint are lists with only one element. Moreover, let f_l be the left fingerprint of some reads, let 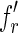and 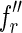be two fingerprints in the list of 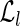indexed by f_l, such that the first character of 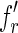is different from that of 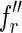. Then the two reads 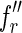and 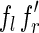are perfectly spliced. The remaining reads, instead, are nonperfectly spliced.

The time required by this step, including the creation of the two hash tables and the classification of the reads, is proportional to the number of input reads.

4.2. Step 2: block creation

The procedure BuildBlocks described in Algorithm 1 takes as input the sets U and PS coming from the partition (computed in the previous step) of the set R of RNA-Seq reads and produces a set B_S of (labeled) putative blocks (corresponding to the vertices of the sought splicing graph) that can be obtained from R. The putative blocks are built by first looking for a set of maximal chains [part (A) of Alg. 1], and then merging those which “significantly” overlap [part (B)]. Finally, block labels are refined in order to correctly manage a special case [part (C)]. We define a chain as a sequence 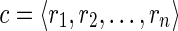of unspliced reads such that RH(r_i) = LH(r_i+1) for 1 ≤ i < n. Moreover, we say that a chain c is maximal if no super-sequence of c is also a chain. The first part of the procedure composes the unspliced reads in order to form maximal chains. The algorithm selects (and extracts) a read r of U and tries to find a right extension of r, that is, another unspliced read 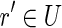such that RH(r) = LH(r′). Afterward the algorithm recursively looks for a right extension of r′, until such a right extension no longer exists. Then the algorithm recursively looks for a left extension of r, while it is possible. Finally, the new chain c is labeled with the fusion of its reads and is added to the set B_S.

The time required by part (A) is O(|U|l), hence, is linear in the input size. In fact, each unspliced read is considered only once, and finding the left or right extension of a read r can be performed in amortized constant time using the left/right fingerprints and the hash tables 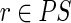and 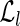. The fusion of the reads is clearly linear in the total length of the reads, giving the total bound O(|U|l).

Moreover, notice that |B_S| ≤ |U| ≤ |R|.

In the second part, we merge all pairs of chains that, under the conditions of Definition 4, correspond to the same block of the expressed gene. This step is necessary because by assembling unspliced reads that have a l/2 overlap, it may happen that there exists more than one chain representing the same block. In particular, assuming that the expressed gene is well-expressed, such chains are all the possible l/2 – 1 shifts of the reads in the block. In this part, for each chain c we extract the substring f = s(c)[i : i + l/2] for increasing values of i ranging from 2 to l/2, and we determine if there exists a chain c′ whose string starts with f, exploiting the 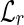table. If such a chain c′ is found, then c′ is removed from B_S and the string of c is updated with the fusion of the two strings s(c) and s(c′). The time required by this part is O(|B_S|l), since for each chain we perform O(l) queries to the hash tables.

At the end of the part (B), under the hypothesis that the expressed gene 〈B, F〉 from which the reads are extracted is well-expressed, it is possible to prove that there exists a one-to-one mapping between the set B_S and the set of blocks B. However, the strings associated to the chains (now putative blocks) do not always correspond to those associated with the (real) blocks. In fact, if a vertex of the isoform graph has indegree or outdegree equal to 1, then the chain composed in part (A) for that block “overflows” on the left side (if indegree is 1), on the right side (if outdegree is 1), or on both (if indegree and outdegree are 1). Suppose, for example, that there exists a vertex b_i of the isoform graph such that outdegree(b_i) = 1, and that b_j is the only other vertex such that (b_i, b_j) is an edge. Then, the reads suff(s(b_i), k) pref(s(b_j), l−k) with k > l/2 are all unspliced, even if they cross the blocks' borders. Intuitively, in that direction, there is no alternative splicing, as b_i is always followed by b_j, and the splicing event is only recognized in the opposite direction, as b_j is preceded by b_i and (at least) another block b_h [recall that in an isoform graph of a well-expressed gene, for each edge (u, v), we have outdegree(u) ≠ 1 or indegree(v) ≠ 1]. In a well-expressed gene, evidence of alternative splicing is provided by the reads suff(s(b_i), l/2) pref(s(b_j), l/2) and suff(s(b_h), l/2) pref(s(b_j), l/2), which are perfectly spliced. As a consequence, the chains corresponding to block b_i include some unspliced reads crossing the real block's borders and, after we merged them to form a putative block, we needed to trim their string of (exactly) l/2 – 1 characters. This is the aim of part (C) of our procedure, where the putative blocks are analyzed and, if the right fingerprint (or left fingerprint, respectively) of a perfectly spliced read matches with an internal part of the associated string, then an (l/2 – 1)-long prefix (suffix, resp.) is trimmed from the string. In particular, since we know that putative blocks may overflow by exactly l/2 – 1 characters, each iteration of part (C) requires two queries to the hash tables, hence the running time is O(|B_S|).

We claim that if the gene 〈B, F〉, from which the set R of reads is extracted, is well expressed, then procedure BuildBlocks (Alg. 1) computes a set B_S of blocks equal to set B.

Lemma 6

Let 〈B, F〉 be a well-expressed gene. Then Algorithm 1 with input the (preprocessed) set R of all the reads extracted from 〈B, F〉 computes a set B_S equal to set B.

Proof. Since R contains all the reads extracted from 〈B, F〉, conditions 4 (d) and 4 (c) imply that, for each block 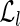, there exists at least one read 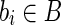such that r_i is a substring of s(b_i) and that uniquely identifies the block itself. By construction, each read r_i, which uniquely identifies a block of 〈B, F〉, will also uniquely identify a block b_s of B_S. As a consequence, it is easy to see that such unspliced reads induce a one-to-one mapping between B and B_S (in fact, by construction, blocks of B_S are composed by “chaining” reads that overlap with l/2 characters, and substrings of length l/2 uniquely identify a single block of B).

We now have to show that the strings of each block in B_s are equal to those of the corresponding blocks in B. First, notice that, for each 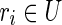such that the outdegree of b′ in the isoform graph is greater than 1, the reads whose prefix is equal to suff(s(b′), k) for some k > l/2 are not unspliced. (By condition 4 (a), and since outdegree(b′) > 1, there exists at least two reads with the same left fingerprint and different right fingerprints.) The same holds for the symmetrical case where indegree(b′) > 1 and, obviously, if the indegree or the outdegree is equal to 0. As a consequence, the fusion of reads belonging to chains computed in part (A) of the algorithm, and corresponding to blocks whose indegree and outdegree is different from 1, is entirely contained in the string of the block. Moreover, since part (A) computes all the maximal chains contained in b′, after these chains are merged in part (B), the string of the putative block and that of the corresponding “real” block coincide. The only remaining case is that of blocks 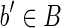where indegree(b′) = 1 or outdegree(b′) = 1. Let us consider the case outdegree(b′) = 1 and let b′′ be the only other block of B such that (b′, b′′) is an edge of the isoform graph. All the reads r_k = suff(s(b′), k) pref(s(b′′), l – k), with l/2 < k ≤ l are unspliced, since there does not exist other reads with the same left fingerprint [by condition 4 (d)]. As such, the string of these putative blocks after part (B) “overflows” the real block's border by (exactly) l/2 – 1 characters (in fact, k > l/2, thus the longest prefix of s(b′′), which is included in an unspliced read has length l/2 – 1). Since R contains all the reads extracted from 〈B, F〉, and since b′b′′ is a strip, there exists the read r = suff(s(b′), l/2) pref(s(b′′), l/2), and such a read is perfectly spliced (by definition of block, there must exist, in fact, a block 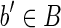such that bb′′ is a strip, hence the read 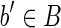). Since the left fingerprint of r occurs in the string of a putative block 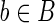at position 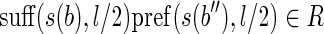, we know that a suffix of (of length l/2 – 1) must be discarded in order to have that 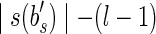coincides with the string s(b′) of the corresponding block. The case where indegree(b′) = 1 is symmetrical.      ■

4.3. Step 3: edge creation

Algorithm 2 computes the arcs of the output graph using the set PS of perfectly spliced reads and the set B_S of putative blocks computed in the previous step. As intuitively explained above, perfectly spliced reads provide evidence that two putative blocks are linked together in some isoform of the expressed gene. As such, a perfectly spliced read r is called a link for the pair of putative blocks (b_i, b_j), if LH(r) = suff(s(b_i), l/2) and RH(r) = pref(s(b_j), l/2). In this case, we also say that b_i and b_j are respectively left-linked and right-linked by r.

Given a perfectly spliced read r, we assign to LeftEnd(r) and RightEnd(r) the putative blocks that are, respectively, left-linked and right-linked by r. In other words, r is a link for the pair of chains (LeftEnd(r), RightEnd(r)). Moreover, each such pair will be an arc of the graph. Both LeftEnd(r) and RightEnd(r) are computed in the main cycle. At the end, for each perfectly spliced read r in PS, the arcs of G_S are computed by adding the pair (LeftEnd(r), RightEnd(r)) to the set of arcs E_S.

Finally, Algorithm 2 has the ability to handle reads that can link multiple putative blocks by transforming LeftEnd(r) and RightEnd(r) into sets (due to the fact that the gene might not be well expressed).

We claim that if the gene 〈B, F〉, from which the set R of reads is extracted, is well expressed, then procedure LinkBlocks (Alg. 2) computes the isoform graph of 〈B, F〉.

Lemma 7

Let 〈B, F〉 be a well-expressed gene. Then, Algorithm 2, with input the set B_S of blocks computed by BuildBlocks and the set PS of perfectly spliced reads, computes the isoform graph of 〈B, F〉.

Proof. By Lemma 6, the blocks of B_S and their strings coincide with the blocks of the expressed gene (and their strings). Since R contains all the reads extracted from 〈B, F〉, and since the string of each block has length at least l, for each arc (b′, b′′) of the isoform graph there exists at least a perfectly spliced read r (in particular, one of them is composed of the concatenation of suff(s(b′), l/2) and pref(s(b′′), l/2)) linking the two blocks. Moreover, by condition 4 (d), such a read is also unique. Since the preprocessing step correctly identifies all the perfectly spliced reads, and since the procedure iterates on all the putative blocks, the procedure LinkBlocks computes all (and only) the edges of the isoform graph.   ■

5. Low Coverage, Errors, And Single-Nucleotide Polymorphism Detection

In this section, we discuss what happens when the characteristics of the set of reads or of the expressed genes do not comply with the theoretical requirements discussed in the previous sections. More precisely, the most critical situation that we have to tackle is suboptimal coverage (i.e., the set of reads does not contain all the reads that can be extracted from the expressed gene). Other possible issues are errors, single-nucleotide polymorphisms (SNPs), and repeated sequences. We present some practical solutions to those problems.

5.1. Low coverage

The initial assumption of our model was the presence, in the input set R, of all the possible l-mers of the gene isoforms (full coverage). Still, we usually have suboptimal coverage, which affects the construction of both chains and links. In other words, we now face the problem of having a set R, where some reads are missing (low coverage). Notice that the typical effect of suboptimal coverage is that a chain is shortened or split. Anyway, it is possible to overcome this problem with a simple variant of the chain-merging step of Algorithm 1 that considers all the possible shifts of a chain (and not only the first l/2 – 1 shifts). The chain-merging step needs only to find two reads, one for each chain, with overlap at least l/2.

The situation is a bit more complex when there are not enough perfectly spliced reads (which are used to create arcs). We infer a set of additional reads to be added to the input set, obtaining an enriched set, so that the actual junction can be determined. To this aim we have designed a procedure to reconstruct from R the nucleotide sequences around block junctions, from which we extract the additional reads. Basically, the algorithm clusters the reads spanning a block junction in order to compose sequences that describe the junction.

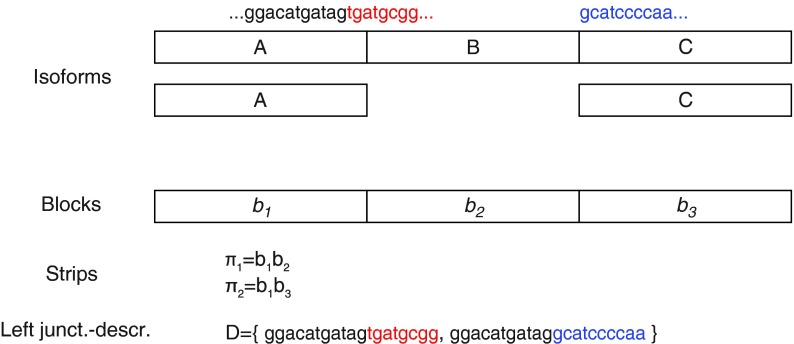
Let us consider a set 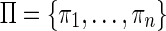of n strips of the isoform graph, sharing the first m blocks 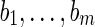, such that 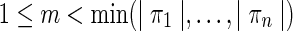. That is, the sequences s(π_i) have a common (proper) prefix 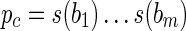. By denoting 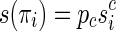, then we call left junction-description a set 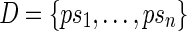of n sequences, where p is some suffix of p_c, and s_i is some prefix of (Fig. 6). The definition of a right junction-description is symmetrical and describes a set of n strips sharing the last m blocks. More precisely, a right junction-description is a set 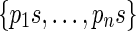of sequences having a proper common suffix s. In the following, we will denote description prefix (resp. description suffix) as p (resp. s).

FIG. 6.

Example of left junction-description D composed of two sequences; π₁ and π₂ are two strips sharing the block b₁. The description prefix is represented by letters in black.

We want to reconstruct putative left and right junction-descriptions from the set R of the input RNA-Seq reads. We will use the term junction-description to denote any set of sequences sharing a common prefix (or suffix).

Given two reads r and r′, we say that r′ is a left half-overlap (or simply lh-overlap) of r, if LH(r′) occurs in r at some position k. Let us consider a set 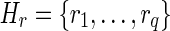of lh-overlaps of r occurring at positions 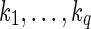(not necessarily distinct). Let p be the longest prefix of r such that pref(r_i, |p| – k_i + 1) is equal to suff(p, |p| – k_i + 1), for 1 ≤ i ≤ q. In other words, p is the longest prefix of r overlapping to each r_i in H_r. If |p| < l, then we say that position |p| + 1 is a putative junction on r, and we call H_r a left junction-set related to r (Fig. 7). Hence |p| ≥ l/2. It is also easy to derive, starting from H_r, a junction-description referred to as D_r. Let us consider the set 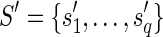of the suffixes 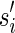such that 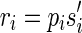(p_i is the prefix of r_i overlapping with p), and let 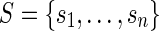be the largest subset of S′ such that s_i is not a prefix of s_j for i ≠ j. Then, the set 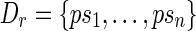is obtained by concatenating p to each one of the sequences in S. It is easy to extend the notion of junction set, related to a read, to any set of sequences (of at least l nucleotides) that are lh-overlaps of that read. The definitions of rh-overlap, right junction-set and right junction-description are symmetrical. In our framework, junction-sets and junction-descriptions represent putative block junctions.

FIG. 7.

Example of left junction-set H_r = {r₁, r₂, r₃} and junction-description D_r related to read r. The longest prefix p and the putative junction on r are underlined and in bold, respectively.

For simplicity, we will deal only with the left side, since the right side is symmetrical. Notice also that searching a read in R, by its left or right half, can be performed in constant time, as described in Section 4.

Initially, each input read r is labeled as free and is associated with an empty junction-description D_r. The first step consists of iterating over R. For each free read r, let 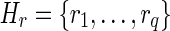be the subset of R composed of the lh-overlaps of r. The time for computing H_r is linear in l plus the size of H_r. In fact, we scan r from left to right and, for each position k, retrieve all the reads having the left half occurring at k. Each lh-overlap r_i is then replaced in H_r by its set 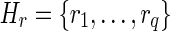, if this set is not empty (i.e., r_i has been previously processed, and a putative junction has already been detected on it). In fact, it is easy to show that the sequences in 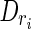are lh-overlaps of r. Finally, if H_r is a junction-set for r, a left junction-description D_r is derived. In this case, each r_i is tagged as included into a junction-set, and r is tagged as the origin of a junction-set.

At the end of the first step, every D_r of an origin read gives a left junction-description. By construction, the sequences in D_r have a length of at most (3l/2 – 1) and share a common prefix p, such that l/2 ≤ |p| ≤ (l – 1). Since the procedure iterates on R and, for each read, the set H_r is retrieved in linear time l, the computational time of this step (in the worst case scenario) is proportional to the size of R and the overall size of the sets H_r. Anyway, since in normal datasets the number of origin reads r, for which the set H_r is not empty, is very small with respect to the entire set R, the overall time required by this step is mainly dependent on the size of R.

Afterward, since not all the reads describing a putative junction are included in the junction-description (in fact, for example the rightmost ones are not lh-overlapping the origin read), the procedure tries to extend the junction-descriptions by looking for free reads that overlap with the description prefix and including all of them. Moreover, in order to guarantee that there are no junction-descriptions that represent the same putative junction, we merge all the junction-sets having an overlapping description prefix.

Finally, the produced nonmergeable junction-descriptions 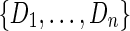must be validated. Without entering into detail, the procedure tries to discard all the fake description sequences originated by situations violating the conditions of well-expressed genes (see Definition 4) in order to enrich the input set R without introducing new artifacts in the reconstructed splicing graph. As anticipated before, all the l-long substrings of the computed description sequences are added to the input set R.

5.2. Errors and SNPs

Another issue that could cause some problems in the computation of the splicing graph is the presence of errors and SNPs in the input reads. As for the lack of reads analyzed in the previous section, errors affect the sets of unspliced and spliced reads, since reads may be misclassified, thus inducing our method to shorten or split gene blocks.

Luckily, the same variant of chain-merging step of Algorithm 1 mentioned in Section 5.1, which considers all the possible shifts of a chain, is only partially affected by errors. In fact, as long as there are only a few errors, there exist some overlapping error-free unspliced reads that span the same block as the erroneous read. Those unspliced reads allow for the correct reconstruction of the chain spanning the block, while the ones containing the errors will lead to chains that will remain isolated (and can be discarded).

Moreover, the fact that the definition of perfectly spliced reads asks for two reads with the same left (or right) fingerprint makes our approach more resistant to errors. In fact, a single error is not sufficient to generate a new perfectly spliced read and so a new arc in the splicing graph. On the other hand, if an error occurs in a perfectly spliced read, this one (and possibly the perfectly spliced read sharing a half sequence with it) can be misclassified, and the corresponding arc(s) will be missing. In any case, this problem can be solved by using the same procedure that was used for the low coverage case (see Section 5.1).

Finally, we point out that our approach could help in SNP detection. The main problem is being able to distinguish between errors and SNPs. Let us consider an example that illustrates a strategy for overcoming this problem. Let e be a block containing an SNP; that is, s(e) can be yaz or ybz, where y and z are two strings and a, b are two characters. Moreover, since this situation is an SNP, roughly the same number of reads support yaz as ybz, most of which are classified as spliced (although they are not supporting an AS event). Therefore, there are two reads r₁ and r₂ such that r₁ supports yaz while r₂ supports ybz, and LH(r₁) = LH(r₂) or RH(r₁) = RH(r₂). As anticipated, r₁ and r₂ are two spliced reads supporting the SNP. This case can be easily and quickly detected by examining the list of reads sharing the left (or right) fingerprints and then looking for a set of reads supporting the SNP (again exploiting the fact that the fingerprint of half of the reads in the set is known).

Moreover, as for the error scenario, the presence of SNPs in a node of the isoform graph may produce the splitting of the corresponding node of the splicing graph into several (sub)nodes. These latter nodes are usually isolated except for the first (which corresponds to a prefix of the isoform block) and the last (which corresponds to a suffix of the isoform block) ones. To overcome this issue we have designed a post-processing method that tries to link these nodes of the splicing graph into a single one.

This procedure starts by looking for pairs of perfectly spliced reads, having a Hamming distance (denoted as d_H) of 1 (caused by the presence of an SNP). Then, it tries to fuse both the elements of a pair with the elements of another one having an overlap of l – 1 each in order to create two strings of length l + 1 each (with Hamming distance of 1). More precisely, given two pairs of perfectly spliced reads 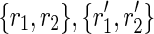having a Hamming distance of 1 (i.e., 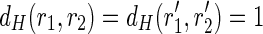), the post-processing checks whether 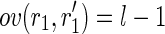and 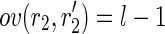or vice versa (i.e., 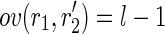and 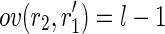) and, if so, it fuses those pairs of reads. The result is a pair of strings of length l + 1 each, having a Hamming distance of 1, in which the differing characters are exactly at the middle of the strings. This also means that these two strings have the same (l/2)-long prefix and the same (l/2)-long suffix. In fact, the method verifies if there are two nodes of the splicing graph that can be linked by those prefixes and suffixes, and if so, it creates the corresponding arc (keeping track of the SNP). Finally, the newly created linear paths are contracted to a single node, in which the sequence label contains both of the different characters. In this way, the nodes of the splicing graph that are split into more (sub)nodes due to the presence of SNPs can have a correct correspondence to nodes of the isoform graph.

5.3. Repeated sequences

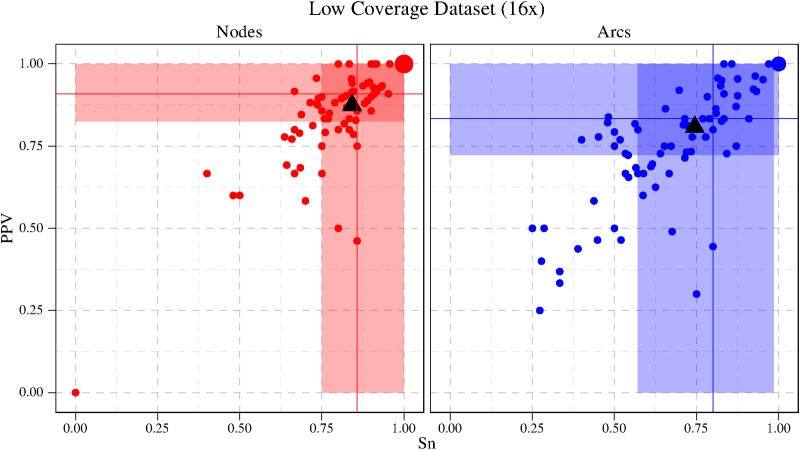
It is well known that repeated sequences present challenging computational issues in the analysis of both the genome and the transcriptome using NGS technologies, which are still characterized by short read lengths (Treangen and Salzberg, 2011). We previously showed that our method is not sensitive to repetitions shorter than l/2, as the chain construction step is based on finding (l/2)-long identical substrings in the input reads. If there is a repeated sequence longer than l/2, this step could produce a putative block that merges (parts of) two “real” blocks. However, if the coverage is not full (i.e., the input set does not contain all the reads that could be extracted from the expressed gene), maybe no pair of reads that cover the two occurrences of the repetition also share the same fingerprint, hence, the two blocks containing a common substring are not merged into a new (wrong) vertex of the splicing graph. This fact is highly dependent on the distribution of reads along the sequenced transcript and, as such at this point, provide strong theoretical guarantees about the behavior of our method when the gene is not well expressed and the read coverage is low. Nonetheless, the following experimental section will provide some empirical evidence that our method is not heavily affected by the presence of repetitions longer than l/2 (which are present in a dataset of real genes). In particular, the absence of some repeated fingerprints in the low coverage scenario explains (at least partially) the slightly better overall accuracy that we obtain in the low-coverage scenario as compared with the full coverage one. Moreover, notice that the increasing read length of newer (and future) sequencing technologies will lessen the impact of repetitions on the accuracy of our reconstruction since the greater the read length, the longer the fingerprints, and, thus, the number of repetitions that we are not able to disambiguate decreases.

We remark that de novo transcript assembly methods based on de Bruijn graphs are highly sensitive to repetitions longer than the chosen k-mer length, as they must merge k-long repetitions into a single vertex. Moreover, memory constraints often limit the largest k-mer length that can be processed and, thus, the ability to disambiguate longer repetitions. Procedures aimed at “resolving” cycles of the de Bruijn graphs due to repeated sequences are able to correctly handle some cases, but they also increase the computational burden. Finally, we note that default k-mer lengths are usually much smaller than l/2, hence, these methods are sensitive to repetitions that our method correctly processes. For example, Trinity (Grabherr et al., 2011), one of the most used (and highly regarded) de novo transcriptome assembly tools, fixes the k-mer length to 25 and cannot be changed by the user.

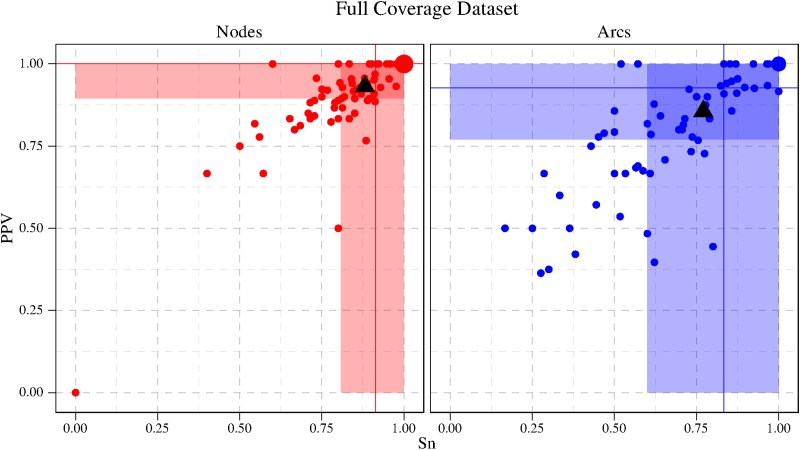
6. Experimental Results

The implementation of our method “RNA-seq-Graph” is available on the authors' website under the AGPLv3. A primary goal of the method and of the implementation was to use only a limited amount of memory, thus the program can be executed on standard workstations, even for quite large input sets.

The experimental validation of our method has been performed on simulated RNA-Seq data obtained from a set of 112 genes extracted from the 13 ENCODE regions used as a training set in the EGASP competition. [We refer the interested reader to (Guigó et al., 2006) for the complete list of regions and genes.] Two arguments support our decision to adopt EGASP data for our experimental validation. First, as the EGASP project was aimed at assessing the accuracy of computational methods to predict protein-coding genes, the genomic regions they chose should represent the characteristics of the whole human genome. Hence the results we obtain in this experimental evaluation should be representative of a large portion of the human genes. Second, these regions contain both highly similar genes and long-repeated sequences shared by different genes, making it difficult to analyze by computational methods that rely only on short reads. Hence, this set of genes should be able to highlight both the strengths and the limits of our approach. Furthermore, our decision of focusing on a relatively small number of (representative and hard to analyze) genes allows us to manually inspect the results in order to determine the causes of incorrect predictions.

These genes have high-quality manual annotations produced by the GENCODE project (including full-length transcripts). We used the most up-to-date version (v3.1), downloaded from online. Isoform graphs have been derived from such annotations. The associated genomic sequences have been retrieved from online corresponding to the NCBI human genome build 35. Our definition of similarity between a reconstructed splicing graph (denoted as G_S) and an isoform graph (denoted as G_I) should consider the topology of the graphs and the labels of their vertices, but should not penalize small differences in the labels (such as some missing nucleotides at the block borders) as they do not compromise the correct detection of AS events. Therefore, we designed a new procedure for the comparison of graphs G_S and G_I, which works as follows. For clarity's sake, we identify each vertex (block) with its label (string). Let s, t be two strings. Then s and t are said to be p-trim equivalent if it is possible to obtain the same string by removing from s and t a prefix and/or a suffix no longer than p. Notice that the removed prefixes and suffixes might be empty and can differ, in length and symbols, between s and t. Let v and w be respectively a vertex of G_S and of G_I. Then v maps to w, if v and w are five-trim equivalent. Moreover, we say that v predicts w if v maps to w and no other vertex of G_S maps to w. We can generalize these notions to arcs and graphs, where an arc (v₁, v₂) of G_S maps to (predicts, resp.) an arc (w₁, w₂) of G_I if v₁ maps to (predicts, resp.) w₁ and v₂ maps to (predicts, resp.) w₂. Finally, G_S perfectly predicts G_I, if those two graphs have the same number of vertices and the same number of arcs, and each vertex/arc of G_S predicts a vertex/arc of G_I.

Prediction accuracy is evaluated with two standard measures, sensitivity (Sn) and positive predictive value (PPV), considered at vertex and arc level. Sensitivity is defined as the proportion of vertices (or arcs) of the isoform graph G_I that have been correctly predicted by a vertex (or arc) of the computed splicing graph G_S, while PPV is the proportion of the vertices (or arcs) of the splicing graph that correctly predicts a vertex (or an arc) of the isoform graph.

The experimental evaluation is structured in five parts. The aim of the first experimental part (Section 6.1) is the evaluation of the prediction accuracy in the best possible (ideal) scenario. Thus, we simulated a dataset composed of all the error-free RNA-Seq reads of length 64 that can be extracted from the sequences of all the full-length transcripts annotated for the chosen genes. The coverage of this dataset (i.e., the number of reads overlapping each position of the transcript sequences) is 64x, and it is the maximum that can be achieved without the presence of duplicated reads. We refer to this dataset as the full coverage dataset. Moreover, in this experiment the prediction has been performed separately on each gene using only the reads extracted from that gene. The aim of the second experimental part (Section 6.2) is the evaluation of the prediction accuracy when the RNA-Seq data has a coverage considerably lower than the one simulated before (namely, 16x). As in the previous part, the prediction has been performed separately on each gene. This low coverage dataset has been simulated by randomly sampling reads from the full coverage dataset. In the third experimental part (Section 6.3), we aim to evaluate how much accuracy is affected if the prediction is performed on the whole set of genes. The dataset used in this part is the full coverage dataset, but only a single (global) prediction is performed using all the reads composing the dataset. The aim of the fourth part (Section 6.4) is to evaluate prediction accuracy if SNPs are present. To this aim, the dataset contains reads sequenced from the transcripts of a diploid genome with SNPs simulated according to dbSNP data. Similarly to the first part, all the possible 64-long reads are extracted from these transcripts, and the prediction is performed separately on each gene. Finally, the fifth part (Section 6.5) is aimed at comparing the accuracy of our approach to that of another widely used state-of-the-art approach, called Trinity (Grabherr et al., 2011). Since the output of Trinity is not a splicing graph but a set of predicted full-length transcripts, we devised a procedure to infer a splicing graph from Trinity's output. This procedure is based on the alignment of the transcripts to the genomic sequence. As we wanted to evaluate the accuracy of Trinity in the best scenario, we performed the prediction with Trinity separately on each gene using the full coverage dataset. The rest of the section describes each experimental part in details.

6.1. Full coverage dataset

In the first experimental part we analyzed the behavior on the full coverage dataset where data originating from each gene have been elaborated separately and independently. The goal of this experiment is to show the soundness of our approach, since obtaining satisfying results under full coverage is a requisite even for a prototype. Notice that these genes are usually not well expressed (as defined in Def. 4), mostly due to the presence of short blocks or relatively long repeated regions. Therefore, there are no theoretical guarantees of being able to reconstruct the isoform graph. Nonetheless, accuracy of the method (at both vertex and arc level) is generally high. More precisely, our method has perfectly reconstructed the isoform graph of 45 genes (out of 112), that is, Sn and PPV are both 1 at vertex and arc level. Moreover, we have obtained average Sn and PPV values that are 0.88 and 0.93 at vertex level, respectively, and 0.77 and 0.86 at arc level, respectively. Also, the median values of Sn and PPV are 0.91 and 1 at vertex level and 0.83 and 0.93 at arc level, respectively.

The plots in Figure 8 give a detailed overview of the quality of the predictions in the first experiment, in which each point corresponds to a gene. More specifically, for each gene in the considered dataset, the Sn versus PPV values are plotted (Sn on the x-axis and PPV on the y-axis) for both nodes (left plot) and arcs (right plot). The plots demonstrate that the predictions are good. In fact, the points at node level are concentrated in the upper-right corner, which corresponds to values of Sn and PPV close to 1. On the other hand, points at arc level are more scattered than those at node level, which reflects lower accuracy at arc level. This fact is due to our definitions of Sn and PPV, as if a node is mispredicted then all the arcs incident to it are considered as mispredicted (decreasing both the Sn and the PPV values of the gene).

FIG. 8.

Sensitivity (Sn) and Positive Predictive Value (PPV) at vertex and arc level in the first experiment. Each point represents a gene while the triangles represent the mean values. Point sizes are proportional to the number of genes that overlap at those coordinates. The colored rectangles (on both axes) represent the areas from the first to the third quartile. Solid-colored lines represent the median values of Sn and PPV. Notice that the third quartile in both the plots is equal to 1, hence at least 25% of genes have Sn and/or PPV equal to 1.

6.2. Low coverage dataset

The second experimental part is similar to the first, but it was performed on a low coverage dataset. The dataset has been generated by randomly sampling, for every full-length transcript of every gene, one quarter of the reads of the full coverage dataset, which corresponds to an average 16x coverage. The aim of this experimental part, which has been performed separately on each gene, is the assessment of the accuracy under a more realistic coverage. Notice that, in this experimental part, reads have been preprocessed (and “enriched”) according to the procedure described in Section 5.1.

In this experimental part, we have perfectly reconstructed the isoform graph of 34 genes (out of 112), and we have obtained average Sn and PPV values that are respectively 0.84 and 0.87 at vertex level, while 0.74 and 0.81 at arc level. The median values of Sn and PPV are 0.86 and 0.91 at vertex level, while 0.80 and 0.83 at arc level, respectively.

The plots in Figure 9 give a detailed overview of the quality of the predictions in the second experimental part. It is possible to notice that points at both node level (left plot) and arc level (right plot) follow the same distribution of the first experimental part. Also in this experimental part accuracy at arc level is lower than that at node level, for the same reason as in the previous experimental part.

FIG. 9.

Sn and PPV values at vertex and arc level in the second experiment. Each point represents a gene, while the triangles represent the mean values. Point sizes are proportional to the number of genes that overlap at those coordinates. The colored rectangles (on both the axes) represent the areas from the first to third quartile. Solid-colored lines represent the median values of Sn and PPV.

Finally, in order to have a better statistical evaluation of the results, we have performed a one-tailed test of hypothesis on Sn and PPV at both node and arc levels. More precisely, the goal of these binomial tests is to assess if the prediction accuracy obtained in the full coverage experiment is (less or) equal to the one obtained in this experiment (null hypothesis), or if the prediction accuracy in the former experiment is greater than that of this experiment (alternative hypothesis). Results show that the null hypothesis on Sn and PPV is rejected in favor of the alternative hypothesis with p-values less than 10⁻⁵ at both node and arc levels.

Although the statistical analysis we performed shows that there has been a statistically significant reduction of the prediction accuracy of this experiment (with respect to the one of the full coverage experiment), we want to point out that the accuracy values obtained in the low coverage experiment are still good (and so are the predicted splicing graphs). This means that a reduction in the coverage does not have a big impact on the predicted splicing graphs and that our method, thanks to the preprocessing procedure of Section 5.1, is able to overcome the lack of reads.

6.3. Mixed genes dataset

The main goal of the third experimental part is to study the scalability of our approach, determining how much repetitions occurring in different genes negatively affect the accuracy of the predictions. Moreover, a secondary goal is to check if the method is robust to the negative influence of analyzing data that originated from several different genes. In other words, we want to check if the computed splicing graph is similar to the union of the splicing graphs obtained in the first experimental part. The dataset used in this part is the full coverage dataset, but a single prediction has been performed on the reads that originated from all the genes.

The expected output of this part is a large isoform graph G_I with 1521 vertices and 1966 arcs (obtained by the union of the 112 isoform graphs retrieved from the annotation) whose connected components are, in most cases, in a 1–1 mapping with the input genes. The isoform graph of some genes is disconnected, hence, those genes are represented by more than one connected component of the complete isoform graph. We used a strategy based on BLAST (Altschul et al., 1990) to map each connected component of the predicted splicing graph to an input gene (thus, to its connected components of the complete isoform graph). Precisely, we aligned the predicted node labels to the annotated full-length transcripts, keeping only the best matches reported by BLAST. A connected component of the predicted splicing graph has been mapped to the gene to which the majority of the node labels aligned. At this point, the predicted splicing graph G_S is partitioned into the subgraphs , where is the corresponding gene, and the comparison between each 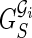and the corresponding isoforms graph 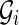is performed as described before.

The predicted splicing graph was composed of 140 connected components that have been assigned to 109 genes. According to our mapping procedure, three genes have no correspondence in the predicted splicing graph (namely, CTAG1B, RBM12, and RFPL2). In general, these three genes are highly similar to other genes of the set; while one of them, CTAG1B, is perfectly identical to CTAG1A (as they are located in a duplicated region of human chromosome X). It is unlikely that this case, in particular, can be correctly handled by a computational method acting without a reference genome, as the presence of such a long duplicated region cannot be reliably detected.

Overall results are similar to those of the first experimental part. In fact, the number of correctly identified vertices goes from 1306 (first experimental part) to 1271 (the current part). Similarly, the number of correctly identified arcs goes from 1425 to 1391. At node level, the overall sensitivity is 0.836 and the PPV is 0.883 (0.859 and 0.926, respectively, in the first experimental part), while at arc level the sensitivity is 0.708 and the PPV is 0.780 (0.725 and 0.824, respectively, in the first experimental part). Thus, we can conclude that the accuracy of the predictions is only barely influenced by the fact that the program is run on the data coming from 112 different genes. Figure 10 shows the isoform graph and the predicted graph for the gene POGZ.

FIG. 10.

The gene POGZ: The isoform graph is shown on the left, and the splicing graph predicted in the third experiment is on the right. The number inside each node represents the length of the the related block. The only difference between the two graphs is the gray vertex that is missing in the predicted splicing graph.

Finally, since one of the goals of our method is that of being efficient in terms of both running time and memory usage, we evaluated the computational requirements of the prediction of this experimental part. We chose only this scenario because it is the most computationally demanding (as all the reads have been analyzed at the same time) and, moreover, because it is one of the most realistic scenarios, as reads coming from different genes are processed all together. In fact, in the other datasets, each gene is processed separately, thus the time and space requirements are very low. Construction of the splicing graph on the whole dataset (composed of about 1.4 million reads of length 64) took about 25 seconds and less than 130MB of memory on a standard workstation with a single Intel^™ Xeon 2.8GHz processor and 12GB of RAM running Ubuntu Linux 10.04 (64bit). This result supports the efficiency of our method, which should be able to process up to 50M reads on a workstation with 4GB of RAM (the actual amount of memory also depends on the amount of redundancy in the dataset).

6.4. Full coverage SNP dataset

The goal of this experiment is to analyze the behavior of our method in the presence of SNPs. To this aim, all the 64-long RNA-Seq reads have been extracted from two copies of each transcript, where each copy is transcribed from one haploid sequence of a simulated diploid genome. One haploid sequence corresponds to the original genomic sequence (NCBI build 35), while the other sequence has been obtained by simulating SNPs according to dbSNP data (retrieved from table snp125 of the UCSC database hg17). 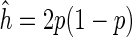We randomly replaced the nucleotide in each SNP locus with probability p according to average heterozygosity (assuming that ) when available in dbSNP, or 0.5 otherwise. Predictions were then performed on the reads extracted from the transcripts of each gene separately.

In this experiment, each output splicing graph (denoted as G_S) has been post-processed, by using the method explained in Section 5.2, before comparing it to the related isoform graph (denoted as G_I). In fact, as explained before, SNPs may produce in G_S several nodes that map to different substrings of the same block of G_I. More precisely, it may happen that a block of G_I is covered by different isolated nodes of G_S; usually there are at most two isolated blocks for each gene. To overcome this issue we have performed the post-processing of G_S, trying to link these nodes into a single node mapping to a unique node of the isoform graph.

After the post-processing, we have obtained average Sn and PPV values that are 0.79 and 0.78 at vertex level, respectively, and 0.63 and 0.67 at arc level, respectively. Also, the median values of Sn and PPV are 0.83 and 0.87 at vertex level and 0.64 and 0.71 at arc level, respectively. These results show that the predictions are significantly less accurate than the ones obtained in the full coverage experiment (without SNPs).

This difference is also confirmed by a one-tailed test of hypothesis on Sn and PPV, at both node and arc levels, between the full coverage experiment and this one. More precisely, in the performed binomial tests, the null hypothesis is that the prediction accuracy in the first experiment (full coverage) is (less or) equal to that of this experiment (with SNPs), while the alternative hypothesis is that the accuracy of the former experiment is greater than that of this one. Results on Sn and PPV show that the null hypothesis is rejected in favor of the alternative hypothesis, with p-values less than 10⁻¹² at both node and arc level.

One of the main causes of the reduction of accuracy is that SNPs may induce the splitting of nodes into “nonlinear” paths (that are not resolved by the developed post-processing step). For example, in gene BPIL2, a node X of the isoform graph is split into nodes A, B (of 12 bp), and C. Moreover, there is a node B′ that is an “alternative” version of B (caused by two very close—10 bp—SNPs), which differs from B by the first and last nucleotide (i.e., the SNPs' positions). Node A is connected to both B and B′, and these two latter nodes are connected to C. This fact creates two paths from A to C that cannot be collapsed into a single node in the post-processing step. This graph structure is very similar to the bubbles that SNPs may generate in a De Bruijn graph constructed from RNA-Seq reads (Sacomoto et al., 2012). Therefore, a similar technique for identifying bubbles in a De Bruijn graph may be used also in our framework for detecting SNPs.

In addition to the previous problem, and like the other experiments, the mapping of arcs is also highly influenced by mapping the corresponding nodes. As a consequence, an arc connecting two nodes of the splicing graph is mapped only if the two nodes are mapped and the nodes they are mapped to are also connected by an arc. This means that if one of these conditions is not satisfied, the arc is not considered as mapped.

Finally, there are some other situations in the resulting splicing graphs, caused by the presence of SNPs, that (adversely) affect the prediction results. In fact, if an isoform block containing an SNP is sufficiently short, all the simulated reads covering this block might be spliced. Thus, the corresponding chain cannot be reconstructed, also causing false negative arcs. This fact can produce isolated nodes or split the splicing graph into connected components.

In any case, we would like to underline that the overall quality of the results obtained is not highly affected by the presence of SNPs. The plots in Figure 11 give a detailed overview of the quality of the predictions in this experiment.

FIG. 11.

Sn and PPV values at vertex and arc level in the experiment with single nucleotide polymorphisms (SNPs). Each point represents a gene, while the triangles represent the mean values. Point sizes are proportional to the number of genes that overlap at those coordinates. The colored rectangles (on both axes) represent the areas from the first to third quartile. Solid-colored lines represent the median values of Sn and PPV.

6.5. Comparison with Trinity

In this experiment, we have compared the accuracy of our approach with that of another state-of-the-art tool. To the best of our knowledge, no other tools are specifically aimed at reconstructing splicing events without a reference genome. The most common aim (and the one most similar to our's) of tools operating on RNA-Seq data without a reference genome is the reconstruction of the putative full-length transcripts (i.e., de novo transcript assembly). Among them, we have decided to use Trinity (Grabherr et al., 2011) since it has been reported that it performs well across various conditions (Zhao et al., 2011).

In order to lessen the impact of possible confounding factors, the comparison has been performed under the ideal (perfect) conditions, that is, using the same full-coverage, error-free dataset of Section 6.1 separately on each gene. Trinity (version r2013-02-25) has been executed using all the default suggested parameters and specifying that the input RNA-Seq reads are strand-specific (in forward orientation). We remark that such scenario is the most favorable for Trinity.

In order to compare the accuracy of our method to that of Trinity, which only reconstructs the full-length transcripts and does not directly provide a graph representation of the alternative splicing events, we have devised a method to build the splicing graph from the transcripts assembled by Trinity. This method first aligns the assembled transcripts to the genomic sequence, then it determines the blocks and the arcs connecting them according to the given alignments. Transcript prefixes or suffixes that do not correctly align back to the genomic sequence are considered as new blocks (connected with the blocks of the parts which successfully align).

Accuracy of the reconstructed splicing graphs has been evaluated according to the metrics introduced in the previous sections. Different aligners could introduce systematic errors that, eventually, induce errors in the derived splicing graphs, hence underestimating Trinity's accuracy. As a consequence, we have decided to perform the alignments with three different state-of-the-art spliced alignment tools: GMap (Wu and Watanabe, 2005), PIntron (Pirola et al., 2012), and Spidey (Wheelan et al., 2001). The first one, in particular, is the tool suggested by the official Trinity documentation for aligning the assembled transcripts to the genomic sequence. All these tools have been able to align the reconstructed transcripts (at least partially) to the genomic sequence of the ENCODE region to which the gene belongs. For each gene, we have selected the alignments that allowed us to reconstruct the splicing graph achieving highest Sn and PPV in the comparison with the isoform graph. This strategy should reduce the potential bias of employing a single alignment tool and should provide a fair ground for the comparison among our approach and Trinity.

As for the other experiments, we have assessed the accuracy of the predictions of Trinity by measuring sensitivity and positive predictive value of the reconstructed splicing graphs. In particular, average Sn and PPV values of Trinity are 0.84 and 0.89 at vertex level, respectively, and 0.77 and 0.84 at arc level, respectively. Also, the median values of Sn and PPV are 0.92 and 0.95 at vertex level and 0.86 and 0.91 at arc level, respectively. Plots in Figure 12 give a detailed overview of the prediction accuracy on the genes.

FIG. 12.

Sn and PPV values at vertex and arc level in the Trinity experiment. Each point represents a gene while the triangles represent the mean values. Point sizes are proportional to the number of genes that overlap at those coordinates. The colored rectangles (on both axes) represent the areas from the first to third quartile. Solid-colored lines represent the median values of Sn and PPV.

These results are very close to the ones obtained by our method in the full coverage experimental part (Section 6.1), with our approach being slightly more accurate. In fact, in terms of average values, our approach has better Sn and PPV at node level (0.88 vs. 0.84 and 0.93 vs. 0.89, respectively) and better PPV at arc level (0.86 vs. 0.84), while Sn at arc level is essentially the same for the two tools (0.770 vs. 0.774). In terms of median values, our approach has better PPV than Trinity at both node level (1 vs. 0.95) and arc level (0.93 vs. 0.91), and it has essentially the same Sn as Trinity at node level (0.914 vs. 0.917), while Trinity has better Sn than our approach at arc level (0.83 vs. 0.86). We tested the statistical significance of such differences with a series of binomial (one-sided) hypothesis tests on Sn and PPV, at both node and arc levels, on the accuracy obtained by our approach and Trinity. The null hypothesis is that the prediction accuracy of the first tool is (less or) equal to that of the second one, while the alternative hypothesis is that the accuracy of our approach is greater than that of Trinity. Table 1 reports the resulting p-values. As it is possible to observe, although the accuracy of our method is often better than that of Trinity, the only statistically significant difference (p-value ≤ 0.05) regards the PPV at node level (in favor of our approach).

Table 1.

P-values of the One-Sided Binomial Hypothesis Tests on Sn and PPV, at Both Node and Arc Levels, Achieved by our Approach and by Trinity

	Node p-values		Arc p-values
Alternative hypothesis	Sn	PPV	Sn	PPV
Our approach > Trinity	0.228	0.020	0.452	0.191
Trinity > our approach	0.839	0.990	0.640	0.870

The null hypothesis is that the prediction accuracy of the first approach is (less or) equal to that of the second one, while the alternative hypothesis is that the accuracy of one of the approaches is better than that of the other. Values below the significance level (α = 0.05), and for which the null hypothesis is rejected in favor of the alternative one, are highlighted in bold.

Finally, we would like to remark that, although the prediction results obtained by Trinity have good accuracy overall, the process for constructing the splicing graphs (hence the putative splicing events and/or the gene structures) from the assembled transcripts is not straightforward and requires the alignment of the transcripts to the genomic sequence, whereas our approach completely works in absence of the reference genome.

7. Conclusions

In this article we started to study the problem of reconstructing and representing alternative splicing events occurring in a gene starting from a set of RNA-Seq reads extracted from that gene and without relying on a reference genome. We have formalized the problem as the Splicing Graph Reconstruction (SGR) problem. The outcome of the SGR problem is a graph representation of AS variants, that is, local predictions that are likely to be more accurate than the long-range predictions that can be deduced from full-length transcript computed by available tools.

We first show the intrinsic limits of any approach based only on the evidence provided by a set of reads (which are typically short). We also present a novel efficient algorithm that is able, under some assumptions, to correctly reconstruct the graph structure of the gene. Moreover, we discuss some strategies to deal with instances in which the assumptions do not hold. In addition to the theoretical investigation, we provide empirical evidence of the good accuracy, obtained by the proposed method, on a set of representative genes. This experimental evaluation further confirms the soundness of our theoretical model and algorithmic approach.

This work is intended as the first step of a theoretical investigation aimed at understanding the potential and the limits of reference-free transcriptome analysis using RNA-Seq data. Additional sources of information, such as paired-end reads or expression levels, can be used to overcome some of the problems we highlighted in this work. For example, paired-end reads can help solve some issues related to the presence of repetitions. Future work will be devoted to the integration of these kinds of information into our formal model. Moreover, future work will also be devoted to combining our novel algorithm with traditional tools such as PIntron (Pirola et al., 2012) and ESTGenes (Eyras et al., 2004), which predict alternative splicing events and full-length isoforms from ESTs and transcript data. In fact, combining predictions of AS events from expressed sequences obtained with traditional sequencing technologies with ones from NGS data would greatly improve our knowledge of the alternative splicing phenomena on several evolved species.

Finally, we would like to note the importance of having a compact and accurate representation of all the alternative splicing variants of a gene. This graph structure, provided by the splicing graph, avoids all the problems related to the reconstruction of full-length isoforms and can be incorporated into a pipeline of transcript analysis to support and confirm some steps from a different point of view. In fact, de novo transcriptome assembly tools only compute a set of putative full-length isoforms without providing a concise representation of the relationships among the predicted sequences. In order to reliably obtain such a representation, which helps to highlight the potential alternative splicing events that have occurred, it is necessary to resort to the alignment of the predicted sequences to the genomic sequence, while our tool operates in absence of such information.

Acknowledgments

S.B., P.B., Y.P., and R.R. are supported by the Fondo di Ateneo 2011 grant “Metodi algoritmici per l'analisi di strutture combinatorie in bioinformatica.” G.D.V. is supported by the Fondo di Ateneo 2011 grant “Tecniche algoritmiche avanzate in Biologia Computazionale.” P.B. and G.D.V. are supported by the MIUR PRIN 2010-2011 grant “Automi e Linguaggi Formali: Aspetti Matematici e Applicativi,” code H41J12000190001. This is an extended version of the article “Reconstructing isoform graphs from RNA-Seq data” by Beretta et al. (2012).

Author Disclosure Statement

No competing financial interests exist.