Streaming fragment assignment for real-time analysis of sequencing experiments

Abstract

We present eXpress, a software package for highly efficient probabilistic assignment of ambiguously mapping sequenced fragments. eXpress uses a streaming algorithm with linear run time and constant memory use. It can determine abundances of sequenced molecules in real time, and can be applied to ChIP-seq, metagenomics and other large-scale sequencing data. We demonstrate its use on RNA-seq data, showing greater efficiency than other quantification methods.

The proliferation of high-throughput sequencing experiments has produced a high volume of data that is increasingly expensive to archive and unwieldy to process¹. Challenges brought by the rapidly increasing depths of modern sequencing experiments include the feasibility of long-term archiving as well as the increased memory requirements of informatics tools and analysis pipelines. For example, uncompressed alignments to the transcriptome for a typical human RNA-Seq experiment require approximately 1 GB of space for every million fragments sequenced.

One of the key computational bottlenecks in large sequencing-based² experiments is the problem of fragment assignment³, or how to infer the origin of ambiguously mapping sequenced fragments. This problem is currently best addressed using the batch expectation-maximization (EM) algorithm with restrictions on the extent of ambiguity allowed for multi-mapping reads^4,5. The algorithm alternates between assigning fragments to targets with a probability according to abundance parameters (expectation step), and updating abundances to the maximum likelihood solution based on the expectation step assignments (maximization step). Limits are necessary because, unlike algorithms used for read mapping, the batch EM algorithm is not trivially parallelizable. For example, when restrictions on multi-mapping are relaxed, large numbers of targets must be considered simultaneously for fragment assignment (Supplementary Fig. 1). Even with restrictions, current methods scale poorly with sequencing depth.

Fragment assignment is a crucial step in many experiments based on high-throughput sequencing, including RNA-seq, ChIP-seq⁶, and metagenomic analysis⁷. In such applications, sequenced reads may map to many transcriptomic or genomic locations, and resolving the ambiguity is frequently the focus of the biological question being investigated. Ad hoc heuristics in fragment assignment algorithms can produce biased results⁸. Furthermore, as sequencing depth increases, the data can overwhelm hardware resources and confound algorithms relying on heuristics that may not scale.

In order to address these difficulties, we have developed an online algorithm for fragment assignment that processes data one fragment at a time. We specialized the online EM algorithm⁹ to the fragment assignment problem and adapted it to work directly with estimated counts rather than relative abundances¹⁰(Online Methods). In the algorithm, each incoming fragment may map to an arbitrary number of target sequences and is apportioned to the targets it maps to according to previously estimated counts (Fig. 1). Parameter estimates for the fragment length distribution, sequence bias¹¹, and a sequencing error model for reads (including mismatches and indels) are simultaneously updated. As fragments are processed, they are assigned increasing “mass” to allow the algorithm to adapt to improving parameter estimates (Online Methods and Supplementary Fig. 2).

Figure 1.

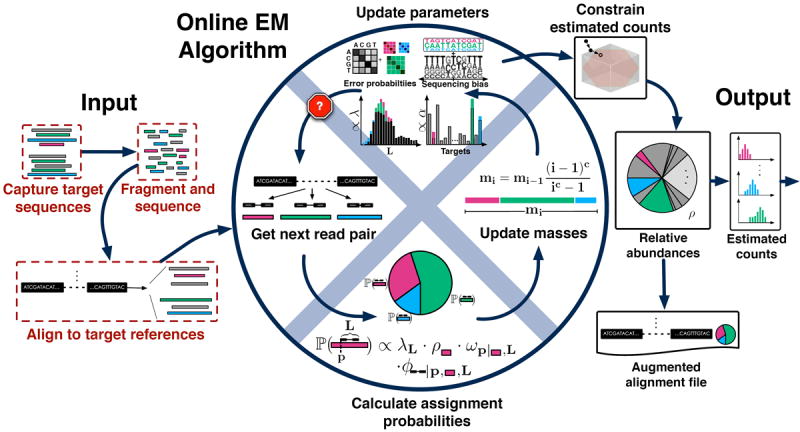
Overview of eXpress. The input consists of either single or paired-end reads aligned to a set of target sequences and provided in a file or streamed to eXpress. For single fragments that map to multiple sites, assignment probabilities are calculated for each site given previous estimates of target sequence abundances (initially a uniform prior is used). Next, a “forgetting mass” is calculated and partial counts are distributed to the target sequences according to the assignment probability. Parameters for fragment length distribution, sequence bias, and sequence read errors are updated in a similar fashion and used in the next round of alignment. Once the input data has been processed, relative abundances are calculated from the count distributions, along with distributions of estimated and effective counts. An alignment file that includes mapping probabilities can be generated. eXpress can determine whether further sequencing is needed by monitoring relative abundances, making it applicable to real-time sequencing and analysis.

This dynamic scheme has favorable convergence properties that are crucial for the performance of the online algorithm (Supplementary Fig. 3). Moreover, the convexity of the likelihood function guarantees that the online algorithm converges to the global maximum. While updating relative abundance and count estimates, uncertainties in assignment are propagated so that posterior count distributions can be estimated. The methods are implemented in open-source software called eXpress, which is suitable for many applications requiring probabilistic fragment assignment. eXpress not only reduces the memory needed for processing, but also achieves a dramatic breakthrough in speed over previous approaches.

To quantify the tradeoffs in speed, efficiency and accuracy between (restricted) batch methods and the online EM algorithm, we simulated 75 bp paired-end reads from the sequencing of one billion RNA-seq fragments (Online Methods) and compared the performance of RSEM⁴ and Cufflinks⁵ to eXpress (Fig. 2 and Supplementary Fig. 4). RSEM uses a model and input similar to that used in eXpress but uses the batch EM algorithm for optimization, allows limited multi-mapping, and lacks a sequence bias model¹². Cufflinks is a widely used tool for RNA-seq which employs an EM algorithm similar to RSEM, but is based on genomic rather than transcriptomic mapping to limit multi-mapping and improve efficiency.

Figure 2.

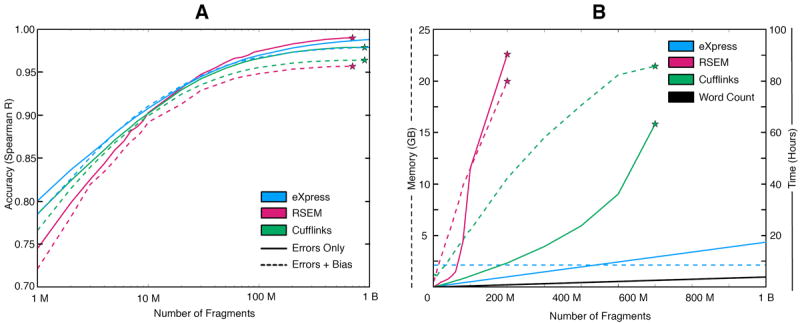
(a) Accuracy of eXpress, RSEM, and Cufflinks at multiple sequencing depths in a simulation of one billion read pair fragments generated with (dashed lines) and without (solid lines) sequencing bias. Accuracy for different abundance levels can be found in Supplementary Figure 4. (b) Comparison of time and memory requirements. Since eXpress only stores counts for each of the targets and auxiliary parameters, its memory use is constant in the number of fragments processed. The running time scales linearly with the number of fragments. Stars represent an imposed memory constraint of 24 GB or a software crash

Since RSEM does not model bias in sequencing experiments, we first compared it to eXpress in a simulation with no sequence bias (Fig. 2a). As expected, RSEM slightly outperforms eXpress when more than 20 million fragments are provided, although eXpress is initially more accurate due to its use of a prior. Performance is similar on individual genes (Fig. 3), for which eXpress abundance estimates are more stable at low coverage. The high accuracy of the online EM algorithm in comparison to the batch algorithm, despite the fact that data is processed in a piecemeal fashion, can be attributed to the appropriate choice of forgetting factors (Supplementary Fig. 3) and the convergence properties of stochastic gradient ascent that it approximates⁸ (Online Methods). The fast convergence is corroborated by a direct comparison of likelihoods. Remarkably, the accuracy achieved by the online EM algorithm in one pass through the data is equivalent to 38 rounds of the batch EM algorithm (Supplementary Fig. 5). Furthermore, when data order is randomized—as is the case in current high-throughput sequencing experiments—it has an insignificant effect on abundance estimates (Supplementary Fig. 6).

Figure 3.

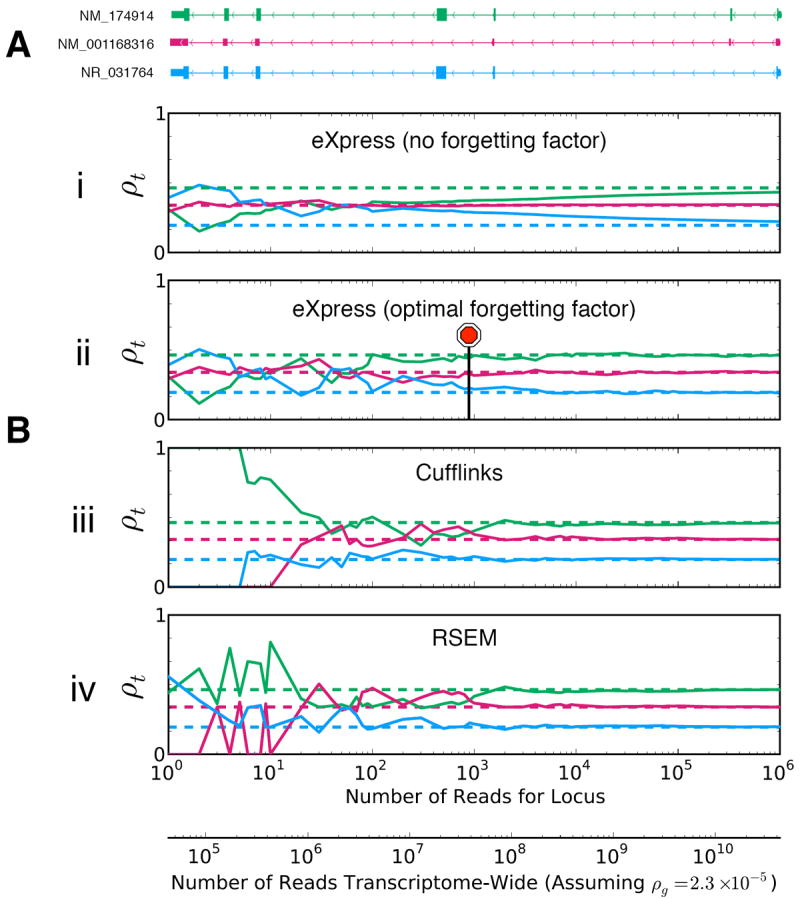
Example of abundance estimation by eXpress, RSEM, and Cufflinks at different depths of simulated data for the three-isoform human gene UGT3A2. The RefSeq annotation is shown at top. Dashed lines indicate the ground-truth relative abundances used for the simulation. eXpress only processes each fragment once whereas RSEM and Cufflinks perform many iterations before converging to the maximum likelihood solution. Nevertheless, as more fragments are observed, all three algorithms converge toward the correct answer at approximately the same depth. In fact, eXpress is more robust than the batch algorithms at low depth due to its use of a prior. The stop sign shows where eXpress using an optimal forgetting factor would automatically stop if a convergence threshold was set to 10^-6 in terms of the Kullback-Leibler divergence between the abundance estimates at intervals of 100 fragments. The lower x-axis shows the estimated depth required to observe the corresponding number of reads mapping to this gene (upper x-axis) at a fixed gene-level abundance. Abundance was calculated using a human embryonic stem cell RNA-seq dataset (Online Methods).

Cufflinks slightly underperforms both RSEM and eXpress due to the limited number of EM rounds for genomic multi-read disambiguation (Supplementary Fig. 7) and the absence of a sequencing error model. On the other hand, the tradeoff allows for easy parallelization and Cufflinks is faster and more memory efficient than RSEM (Fig. 2b). Most striking is the performance of eXpress, which displays a run time linear in the number of fragments and memory requirement proportional only to transcriptome size. This is similar to the UNIX word count ‘wc’ program that simply counts the number of characters in a file (Fig. 2b). However, simply counting the number of fragments mapping to target sequences (without fragment assignment) cannot be used as a proxy for abundance. We compared eXpress to a modified version of NEUMA¹³ (Online Methods) that avoids explicit read assignment by incorporating a “mappability” index and length correction for each transcript. Even with this improvement over raw fragment counting, the accuracy of NEUMA does not match that of eXpress, RSEM, or Cufflinks (Supplementary Fig. 8). The combined speed and accuracy of eXpress means that it can be used in the analyses of much deeper sequencing experiments than previously possible.

The eXpress model includes parameters for the fragment length distribution, sequencing errors (including indels), and sequence-specific biases thought to result from the fragmentation and priming steps during library preparation¹¹. All of these are estimated jointly with abundances, enabling eXpress to be used for a wide range of experiments. It is interesting to note that estimates of the auxiliary parameters converge rapidly, typically after less than 5 million fragments (Supplementary Fig. 9). To assess the impact of bias modeling in RNA-Seq, we simulated another billion fragments using a bias profile learned from a human embryonic stem cell RNA-Seq dataset (Online Methods). With bias affecting the prevalence of fragments in specific positions, eXpress and Cufflinks outperform RSEM, highlighting the importance of modeling this effect (Fig. 2a). The overall improvement of eXpress with respect to Cufflinks is due to the improvement in assignment of genomic multi-reads and the inclusion of an error model in eXpress (Online Methods), although Cufflinks outperforms eXpress on very high abundance transcripts (Supplementary Fig. 4). To establish the effectiveness of eXpress’ bias correction on experimental data, we re-examined previous comparisons of RNA-Seq to quantitative PCR from the “gold standard” MAQC¹⁴ dataset and confirmed that the bias correction in eXpress improves the accuracy of abundance estimates (Supplementary Table 1).

To enable the use of relative abundance and count estimates in downstream applications, eXpress quantifies uncertainties in the estimates. Specifically, for every transcript, the posterior fragment count distribution is approximated by a shifted beta binomial distribution (Online Methods). The accuracy of the approximation was confirmed by simulation study (Supplementary Fig. 10). We noted that on average, counts could be estimated within 5.4% of the true value, implying that for many transcripts, estimated counts obtained by eXpress can be used directly in differential expression packages such as DEseq¹⁵ that model count variability in biological replicates. When there is uncertainty in the count estimate, the count distribution can be incorporated in differential analysis¹⁶.

The ability of eXpress to accurately assign fragments using a streaming algorithm means that it is compatible with novel single-molecule sequencing technologies that produce reads incrementally¹⁷. In a dynamic sequencing pipeline, eXpress could be coupled directly to a sequencer and be used to estimate abundances of target sequences in real time as individual fragments are sequenced. We examined the use of stopping criteria based on the relative increments of the global likelihood or the local likelihood for a group of target sequences and found that eXpress can automatically determine when sufficiently many reads have been processed to guarantee convergence (Fig. 3), thus avoiding the complicated issue of choosing a sequencing depth. We note that such an approach to high-throughput sequencing also eliminates the need for storing read sequences, providing an alternative to cloud-based bioinformatics¹⁸.

The eXpress software is freely available on the Nature Methods website and at http://bio.math.berkeley.edu/eXpress.

Online Methods

Probabilistic model

Our approach to fragment assignment is based on a probabilistic graphical model for sequencing experiments (Supplementary Fig. 11). In this framework, experiments produce multiple random fragments (according to the random variable F) that consist of pairs of sequences (reads) from a set of target sequences. F depends on hidden random variables describing fragment length (L), target sequences of origin (T), and starting positions within target sequences (P). The probability distributions for the random variables are based on parameters for target abundances, fragment length probabilities, sequence biases affecting the start and end locations of the fragment, and probabilities for sequencing errors in reads. The generative model stipulates that the joint probability of obtaining a fragment f of length l sequenced from position p in target t is given by

$$\mathbb{P}(F=f,P=p,T=t,L=l)={\lambda }_l{\tau }_{l\mid t}{\pi }_{p\mid t,l}{\varphi }_{f\mid p,t,l}$$ (1)

where the parameters of the model are the conditional probabilities ϕ_f∣p,t,l: = ℙ(F = f∣P = p, T = t, L = l), π_p∣t,l: = ℙ(P = p∣T = t, L = l), τ_t∣1: = ℙ(T = t∣L = l) and λ_l: = ℙ(L = l).

From this we obtain the likelihood function

$$L(\lambda ,\tau ,\pi ,\varphi \mid F)={\prod }_{f\in F}{\sum }_{l=1}^{M_L}{\sum }_{t\in J}{\sum }_{p=1}^{l(t)-l+1}{\lambda }_1{\tau }_{t\mid l}{\pi }_{p\mid t,l}{\varphi }_{f\mid p,t,l}$$ (2)

where F is the set of sequenced fragments,J is the set of target sequences, M_L is the maximum length of a fragment and l(t) is the length of target sequence t. The likelihood function is derived from the generative model, but there is a more convenient form that is useful computationally and which corresponds more directly to the main quantities of interest: the relative abundances of target sequences. If ρ_t denotes the relative abundance of target t, and the probability of generating a fragment of arbitrary length from a target t is ${\tau }_t={\sum }_l{\tau }_{t\mid 1}$, then rewriting the likelihood function in terms of the τ_t yields

$$L(\lambda ,\tau ,\pi ,\varphi \mid F)\propto {\prod }_{f\in F}{\sum }_{l=1}^{M_L}{\sum }_{t\in T}{\sum }_{p=1}^{l(t)-l+1}{\lambda }_l{\tau }_t\frac{w_{p\mid t,l}}{\stackrel{\sim }{l}(t)}{\varphi }_{f\mid p,t,l}$$ (3)

where the remaining auxiliary parameters consist of λ, ϕ, normalized weights¹⁰ w_{p∣t, l} satisfying

$${\pi }_{p\mid t,l}=\frac{w_{p\mid t,1}}{{\sum }_{q=1}^{l(t)-l+1}{w}_{q\mid t,l}}$$ (4)

and an effective length¹⁰

$$\stackrel{\sim }{l}(t)={\sum }_{l=1}^{M_L}{\sum }_{p=1}^{l(t)-l+1}{\lambda }_1{w}_{p\mid t,l}.$$ (5)

The weights w_{p∣t, l} reflect sequence bias resulting in preferential selection of certain fragments¹⁰ so that

$${\tau }_{t\mid l}=\frac{{\rho }_t{\sum }_{p=1}^{l(t)-l+1}{w}_{p\mid t,l}}{{\sum }_r{\rho }_r{\sum }_{q=1}^{l(r)-l+1}{w}_{q\mid r,l}}.$$ (6)

The derivation that (3) is equivalent to (2) is based on the cancellation of the numerator of (6) with the reciprocal of (5) after summing over lengths, followed by the application of (4). The ϕ parameterize an error model that provides probabilities for fragment sequences to originate from different reference sequences. This is specified in the form of a first order Markov chain of substitution probabilities that depend on read position and, in the case of paired-end reads, their respective sequencing order. Each position also has a probability of insertion (of 0-10 sites) or deletion (0-10 sites) initialized with a truncated geometrically distributed prior (p=0.73) on the insertion/deletion (indel) length. The model described here is similar to the Cufflinks model^5,12, but incorporates a different order for fragment length selection in the generative model and includes the modeling of errors and indels.

Lemma 14 in the Supplementary Material of the Cufflinks paper⁵ explains how to recover the abundances ρ_t from the parameters τ_t. Abundances are reported in FPKM⁴ units in eXpress.

The online EM algorithm for maximum likelihood estimation

The online EM algorithm is an iterative algorithm that consists of computing vectors ${\tau }^i{\{{\tau }_t^i\}}_{t\in J}$ where n = 1,2, …, |F| If the fragments are ordered as f₁, …, f_|F| then each ${\tau }_t^i$ represents an estimate of the parameter τ_t after processing the fragments, f₁, …, f_i. The update procedure is given by

$${\tau }^{i+1}=(1-{\gamma }_{i+1}){\tau }^i+{\gamma }_{i+1}{\stackrel{\sim }{\tau }}^i$$ (7)

where ${\gamma }_i=\frac{1}{i^c}$ for some constant $\frac{1}{2}<c\le 1$ and

$${\stackrel{\sim }{\tau }}_t^i=\mathbb{P}(T=t\mid F=f_i).$$ (8)

The probabilities in (8) can be calculated using Bayes rule from the conditional probabilities described in the section above.

Theorem 1^9,10

The online EM algorithm is asymptotically equivalent to stochastic gradient ascent in the space of sufficient statistics. Moreover, assuming that $\frac{1}{2}<{\gamma }_n\le 1$ together with mild regularity assumptions⁹, it converges to a local maximum of the likelihood function.

For fixed auxiliary parameters the model (2) is convex⁵ and it follows that the online algorithm (also called the stepwise EM algorithm) converges to the (unique) global maximum.

Updating (7) requires O(|J|) operations at every step making the algorithm intractable for large numbers of target sequences. There are two reasons for this. First, computing (8) requires, in principle, calculation of a normalization constant that is based on a sum taken over all positions in all targets. Second, the update in (7) requires changing ${\tau }_t^i$ for all t ∈ T.

The first difficulty can be overcome by limiting the calculation to locations where fragments map using one of many heuristic alignment programs, such as Bowtie¹⁹. This is reasonable because the probabilities ℙ(T = t∣F = f_i) are approximately zero when a fragment does not align to a target, due to the relatively low probability of sequencing errors. Nevertheless, Bowtie, and many other fast read mappers might lead to biased quantification results because they restrict mappings in ad-hoc ways. For example, in Bowtie an exact matching seed is required and at most 3 mismatches can be allowed only at the end of reads. To confirm that such heuristics do not affect performance in practice, we performed a detailed analysis with the mapper Hobbes²⁰, which finds all mappings within a specified Hamming distance, and compared the results to Bowtie (Supplementary Table 2). It is important to note that different mappers may be suitable for other types of sequencing reads (e.g. SOLiD), but the model for assignment is independent of the technology used. The second difficulty can be addressed by a change of coordinates that greatly simplifies the calculation:

We replace the ${\tau }_t^i$ with variables ${\alpha }_t^i$ where i ∈ {1,2, …, |F|} and instead of iterating (7) we compute

$${\alpha }^{i+1}={\alpha }^i+m_i{\stackrel{\sim }{\tau }}^i$$ (9)

where

$$m_{i+1}=m_i\left(\frac{{\gamma }_i+1}{1-{\gamma }_i}\right)\frac{1}{{\gamma }_i}$$ (10)

is called the forgetting mass and depends on the forgetting factors γ_i. It is convenient to use the form ${\gamma }_i=\frac{1}{i^c}$ where $\frac{1}{2}<c\le 1$. In that case the recursion (10) reduces to the formula in Fig. 1. Note that ${\stackrel{\sim }{\tau }}_t^i=0$ implies ${\alpha }_t^{i+1}={\alpha }_t^i$ enabling efficient updating of (9). Thus, the online EM algorithm scales linearly with the number of fragments analyzed, with a (small) constant number of operations per iteration.

Each vector ${\alpha }_t^i$ represents an estimate of the number of fragments originating from t from among the fragments f₁, …, f_|F| and the τ are related to the α via ${\tau }_t^i=\frac{{\alpha }_t^i}{{\sum }_{r\in J}{\alpha }_r^i}$. The α estimates can also be interpreted as parameters of Dirichlet distributions, providing a Bayesian interpretation of the online EM algorithm⁸. In eXpress, the online EM algorithm is used to estimate the auxiliary parameters alongside the abundances.

Counts

We distinguish between two forms of useful output in an RNA-Seq experiment. The relative abundances of targets (encoded in the parameters ρ discussed above) are of primary interest. However, also of interest are the posterior distributions of counts. The latter describe, for each target, the number of fragments estimated to originate from each target given the read mappings. For example, if a target sequence t has k fragments mapping to it and all the k fragments map uniquely to the set of target sequences, then the posterior count distribution for t is the discrete distribution with all its mass at k. However, ambiguous fragments are assigned probabilistically and result in posterior count distributions with wider support. Count estimates can be further refined to account for sequence bias and bias introduced by fragmentation. The effective count distribution for a transcript is defined to be the posterior count distribution assuming the experiment had no sequence bias and all fragments had length one. Effective counts are useful because they can be directly compared across experiments after normalizing for sequencing depth. They can be calculated from estimated counts and the effective lengths (5), by rescaling the counts for a transcript t by l(t)/l̃(t).

In eXpress, fragment count distributions are modeled by shifted beta binomial distributions as follows: For each target sequence t, the number of unique (Uniq_t) and total (Tot_t) fragments mapping to the target sequence are computed. Then a beta binomial distribution with n = Tot_t - Uniq_t is used to approximate the posterior distribution by fitting moments. Specifically, for each target, the mean of the beta binomial distribution is estimated as the mean of the posterior assignment probabilities for all fragments that ambiguously aligned to it. This is computed online (together with other parameters, as in the previous section). The variance of the posterior distribution is also computed online by compounding the variances associated with the ambiguous fragment assignments.

To address instability of assignment in targets with few mapped reads, a flag (referred to as the solvability flag) is assigned to each target sequence. Initially all target sequences are unsolvable. After target sequences become solvable they can never revert back to their previous state. There are two ways by which a target sequence can become solvable: if a fragment maps uniquely to a target sequence then that target sequence becomes solvable, or if a fragment maps ambiguously to a set of target sequences and all but one is solvable, then the remaining one becomes solvable. Unsolvable targets are assigned the uniform distribution whereas solvable targets are assigned a beta binomial with support n by fitting moments.

For the above procedure to work it is necessary that the estimated counts always lie between Uniq_t and Tot_t. Moreover, the structure of (2) can be used to provide bounds on the scaled maximum likelihood solution for the abundances:

Theorem 2

For each target t, let Uniq_t and Tot_t denote the unique number and total number of reads mapping to t respectively. The maximum likelihood solution ρ̂_t satisfies Uniq_t ≤ Nρ̂_t ≤ Tot_t where N is the total number of reads sequences in an experiment. Equivalently, the maximum likelihood solution ρ̂ must lie inside the count polytope defined by the inequalities above, together with the constraint Σ_t ρ̂_t = 1.

The theorem follows from the fact that the likelihood increases at every step of the EM algorithm. However, because the online EM algorithm incorporates forgetting factors at each step, it may be that the reported result for the estimated number of counts does not lie in the count polytope. In order to report estimates that are meaningful, we project the solution into the count polytope using von Neumann’s alternating projection method, which in our case consists of alternate projection to the cube and the hyperplane which intersect to form the count polytope. The algorithm converges in a finite number of steps.

Implementation of eXpress

eXpress takes as input alignments in SAM or BAM format and makes use only of required fields. It can therefore be applied to alignments made with any tool that outputs SAM format. The output of eXpress consists of three files containing the estimated abundances and fragment counts for each target sequence, parameter estimates, and the variance-covariance matrix for the posterior count distributions. A modified SAM file containing the posterior probability of each alignment or a single alignment for each read, sampled from the posterior distribution, can also be optionally output.

Fragments are processed in a multi-threaded pipeline. One thread parses the file (or input stream) into individual alignment objects. A second thread takes a set of fragment read alignments, computes the likelihood of each, and updates the model parameters based on the posterior probabilities of fragment origin. A third thread asynchronously updates the auxiliary parameters for the target objects (sequence bias and effective length), while simultaneously recalculating the expected fragment length distribution The algorithm is seeded by assigning one pseudo-count per 100 sites per target. This equivalent to setting a uniform prior on target abundances via the Bayesian interpretation of the online EM algorithm mentioned above. Once convergence of auxiliary parameters is reached, one final pass through the targets is made, and the thread is terminated. Currently, convergence is assumed to occur by the time five million fragments have been processed, but a dynamic stopping criterion based on the KL divergence could be used instead.

In current applications in which alignments are stored on disk before analysis, eXpress accuracy can be improved with multiple passes through the data, either by repeating the online EM algorithm or coupling the batch EM algorithm to the online EM algorithm¹⁰. We explored different strategies for improving performance by re-examining fragments and found that the coupled method using a single pass of the online EM algorithm followed by additional rounds of the batch algorithm provides more improvement than the repeated online EM after 21 rounds (Supplementary Fig. 5). Neither method requires additional memory, but both require a substantial, yet practical increase in running time that is linear in the number of iterations. The coupled iteration method can be accessed with the -B option followed by an integer specifying the number of rounds. The repeated online EM feature can be executed using the -O option, again followed by an integer specifying rounds.

Two approximations were used in the implementation of bias correction in order to improve performance. First, instead of calculating the effective length as described above, the average fragment bias weight for each target was calculated by taking the product of the average 5’ and 3’ bias weights. The average bias was then multiplied by the effective length with bias parameters omitted (w_p∣t,l = 1 in (5)) to get an approximate bias-corrected effective length. Second, when learning the expected sequence bias distributions, only the weights at the center position in each window were calculated, and these parameters were used to approximate all window positions.

eXpress is an open-source C++ program and is freely available in both source and binary at http://bio.math.berkeley.edu/eXpress/. eXpress is distributed under the Artistic 2.0 License and runs on Mac OS X, Linux, and Windows.

Simulation RNA-Seq study

Two sets (one with sequence bias, one without) of a billion reads from an RNA-Seq experiment were simulated using the generative model (above and Supplementary Fig. 11) with parameters for the model determined by running eXpress on RNA-Seq data from the ENCODE project human embryonic stem cells (cell line H1-hESC) consisting of 50,170,737 75bp paired-end reads (Accession SRX026669). Bowtie was used for the mapping with the same settings as below, providing proper alignments for 33,189,908 of the pairs. The 73,660 transcripts in the UCSC Genes hg19 annotation (http://genome.ucsc.edu) were used as the target set. The simulated reads together with the parameters used are available at http://bio.math.berkeley.edu/eXpress/simdata/.

Software comparisons

To generate the alignments used by eXpress, RSEM, and NEUMA, we used Bowtie¹⁹ v0.12.7 (http://bowtie-bio.sourceforge.net/index.shtml) with the options -a to report all mappings, -X 800 to allow fragments up to length 800, and -v 3 to allow up to three mismatches in each read. With these parameters 97.7% of the simulated read pairs mapped to the reference genome.

Additional alignments were generated by Hobbes²⁰ v1.4 (http://hobbes.ics.uci.edu/) with the options -a to report all mappings, −max 800 to allow fragments up to length 800, and -g 7 –hamming -v 9 to allow for up to nine mismatches in each read. Results for the Hobbes mappings can be found in Supplementary Table 2.

eXpress v1.2.0 was used for all experiments with default parameters. The FPKM values, which are proportional to the abundances, were used for performance comparisons.

The RSEM⁴ software requires the same type of input as eXpress (reads mapped to transcripts) and therefore the identical read mappings were used for both programs. RSEM v1.1.11 downloaded from http://deweylab.biostat.wisc.edu/rsem/ was used in all experiments. The rho value reported by RSEM was used as the abundance measure.

NEUMA¹³ uses Bowtie internally to map the raw reads. However, we found that the Bowtie options used by NEUMA in default mode reduce its accuracy by not accommodating errors in the reads. We modified the internal mapping to allow for up to 3 mismatches in each read, thus greatly increasing the accuracy of NEUMA in our tests (Supplementary Fig. 8). Other then this improvement, default options were used. Because NEUMA only outputs abundances for a subset of the transcripts that it deems measurable (56,658 out of the 73,660 UCSC hg19 transcripts), we limited our analysis of other methods to this same subset when NEUMA was also compared. NEUMA v1.1.2 (http://neuma.kobic.re.kr/) was used in all experiments where it was tested. The reported iFVKM¹¹ values were used as the abundance measures.

Since Cufflinks⁵ requires (spliced) alignments to the genome, we mapped reads using TopHat v2.0.0 (http://tophat.cbcb.umd.edu/) with the Map2GTF feature enabled. This feature aligns reads to transcript sequences using Bowtie and then projects the mappings onto the genome. The options used were -T to enable Map2GTF, -n 3 to allow up to 3 mismatches in each read, and -G to provide the genome annotation used to generate the transcript sequences (hg19, UCSC Genes). Cufflinks was also provided the hg19 UCSC Genes annotation as the reference transcriptome. To improve read assignment with Cufflinks in cases where reads map to different genomic locations, we modified the program to include an optional extra single round of batch EM after initial deconvolution of read assignments within genes (Supplementary Fig. 7, the modification has been distributed in versions following 1.0.0). All experiments in this paper were run with Cufflinks v1.4.0. (http://bio.math.berkeley.edu/cufflinks/) utilizing this option (-u) as well as bias correction¹² (-b), and with −max-bundle-frags set sufficiently high so that no bundles were skipped. The FPKM value was used as the abundance measure.

The wc program is a Unix utility that originally appeared in AT&T Unix. It counts the words, lines and characters in an input file. For the purposes of Fig. 2 we ran wc on the SAM alignment files.

In order to compare accuracy, we presented each algorithm with the same, multi-sized subsets of 1 billion simulated fragments and calculated the Spearman ranked correlation coefficient between the resulting estimates and ground-truth abundance values used in the simulation. The software was run on a server with 512 GB of RAM to allow RSEM and Cufflinks to process a large number of reads. These results are presented in Fig. 2a and Supplementary Fig. 7–8.

In order to assess and compare performance on typical hardware, each algorithm was tested individually on an 8-core Intel Xeon 2.27 GHz Mac Pro with 24 GB of RAM and 16 hyper threads. Cufflinks and RSEM were allowed eight threads for processing, and both were run with the same options as above. As before, each algorithm was presented with the same multi-sized subsets of one billion simulated reads. For each input size, the total run time and peak memory use were measured. Cufflinks and RSEM were halted once they crashed or began to report memory errors. These results are presented in Fig. 2b.