High-throughput genome scaffolding from in-vivo DNA interaction frequency

Abstract

Despite advances in DNA-sequencing technology, assembly of complex genomes remains a major challenge, particularly for genomes sequenced using short reads, which yield highly fragmented assemblies. Here we show that genome-wide in vivo chromatin interaction frequency data, which are measurable with chromosome conformation capture–based experiments, can be used as genomic distance proxies to accurately position individual contigs without requiring any sequence overlap. We also use these data to construct approximate genome scaffolds de novo. Applying our approach to incomplete regions of the human genome, we predict the positions of 65 previously unplaced contigs, in agreement with alternative methods in 26/31 cases attempted in common. Our approach can theoretically bridge any gap size and should be applicable to any species for which global chromatin interaction data can be generated.

Massive amounts of short DNA sequencing reads can be assembled into sets of small contigs but joining these contigs into scaffolds, a process known as scaffolding, is often difficult owing to the presence of repetitive sequences^4,5. Improving the degree of completion of genome sequences typically relies on low-throughput methods such as FISH^6–9 or BAC-based sequencing¹⁰. Although the advancement of sequencing technology is producing longer reads and thus increasing the size of contigs, recent assessments of genome assemblers^11,12 show that complex genome assemblies which rely only on sequencing data, are still highly ambiguous and fragmented, owing to gap sizes beyond that of long-insert molecules. In fact, even in the human genome, despite the massive effort invested in its completion, approximately 30 Mb of euchromatic DNA remains unassembled⁹. Thus, high throughput sequencing and genome assembly technology have reached a point in which an increase in the number of short reads does not substantially improve assembly quality.

Hi-C is an experimental technique that measures the in vivo spatial interaction frequency between chromatin segments over the whole genome, by cross-linking loci that are in close physical proximity and quantifying them with high-throughput paired-end sequencing¹³. Every uniquely mapped paired-end read indicates an interaction between two genomic loci, so that the number of read pairs that map to distant DNA fragments can be treated as a measure of the frequency that the fragments interact. Notably, all Hi-C experiments in eukaryotes to date have shown, in addition to species-specific and cell-type specific chromatin interactions, two canonical interaction patterns. One pattern, distance-dependent decay (DDD), is a general trend of approximately exponential decay in interaction frequency as a function of genomic distance. The second pattern, cis-trans ratio (CTR), is a significantly higher interaction frequency between loci located on the same chromosome, even when separated by tens of megabases of sequence, versus loci on different chromosomes^13–18. These patterns may reflect general polymer dynamics, where proximal loci have a higher probability of randomly interacting¹⁹, as well as specific nuclear organization features such as the formation of chromosome territories, the phenomenon of interphase chromosomes tending to occupy distinct volumes in the nucleus with limited interchromosomal mixing²⁰. Although the exact details of these two patterns may vary between species, cell-types and cellular conditions, they are ubiquitous and prominent. In fact, these patterns are so strong and consistent that they are used to assess experiment quality and are usually normalized out of the data in order to reveal detailed interactions^14,15,21.

Here we propose that genome assembly technology can take advantage of the three-dimensional structure of genomes. We show that the features which make the canonical Hi-C interaction patterns a hindrance for the analysis of specific looping interactions, namely their ubiquity, strength and consistency, make them a powerful tool for estimating the genomic position of contigs or short scaffolds, similar to those obtained by standard massively parallel sequencing and assembly methods.

We first use the CTR pattern to tackle the problem of scaffold augmentation, in which most of the genome is assumed to be correctly assembled and the challenge is to predict both the chromosome and locus of an unplaced contig, based on its pattern of interaction with the placed contigs. This is the situation for the majority of published ‘finished’ complex genomes, including human and mouse. Because most of the genome is assembled, it is possible to observe, quantify and computationally model the DDD and CTR interaction patterns, even if they are genome-specific or condition-specific. This model can then be used to estimate the positions of new contigs. Prior knowledge of the canonical patterns for a particular species is not needed.

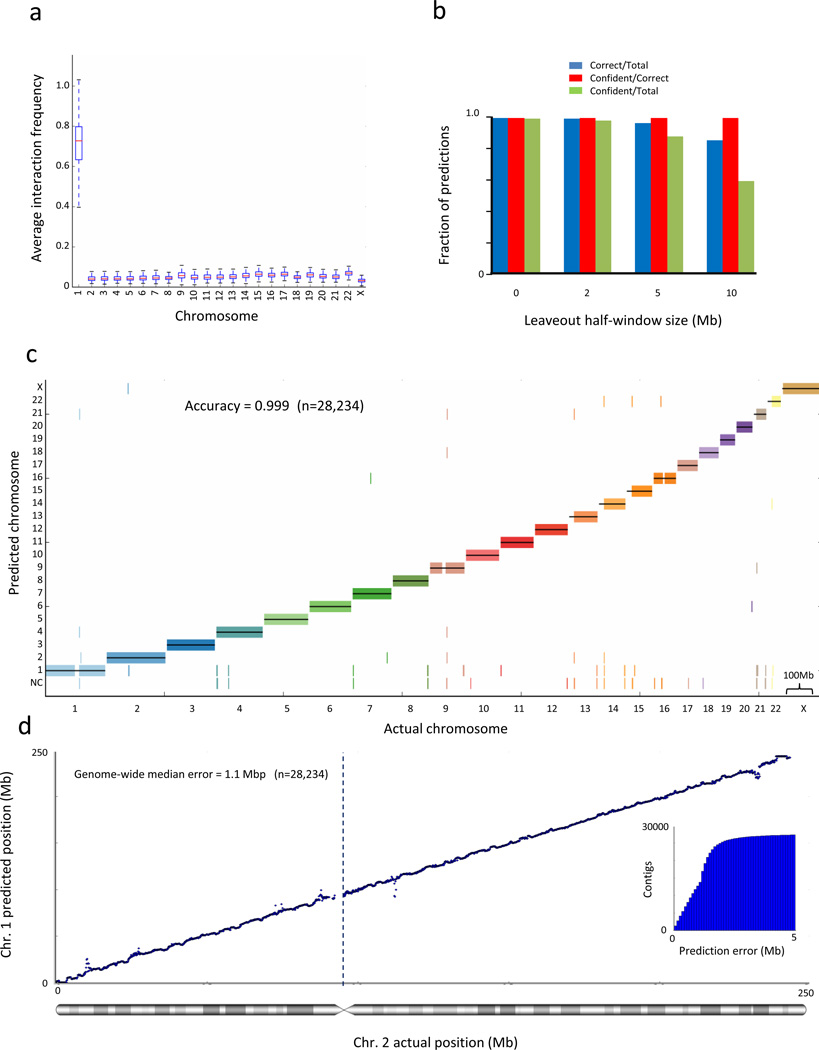
As an initial test, we performed simulations on human genome hg19 assembly²² and a previously published Hi-C dataset²³ obtained from H1 ES cells. To demonstrate the robustness of our approaches when using a relatively low number of reads, we chose to use only a third of the Hi-C reads available for this cell-type in the dataset. We first quantified the CTR pattern by partitioning the human genome into 100kb bins, each representing a large virtual contig, and calculated for each placed contig its average interaction frequency with each chromosome. To simulate a more difficult scenario and evaluate localization over long ranges, we omitted from this statistic the interaction data of the contig with its flanking 1mb on each side, where the strongest Hi-C interaction signals are present. Then, we asked how well this statistic separates interchromosomal interactions from intrachromosomal interactions (Fig. 1a). We find that the average interaction frequency strongly separates inter- from intra- chromosomal interactions, with an average AUC of 0.9998, suggesting this statistic is highly predictive of which chromosome a contig belongs to.

Figure 1.

Interaction frequency accurately predicts chromosome and locus for scaffold augmentation. (a) Average interaction frequency strongly separates interchromosomal from intrachromosomal interactions. For each 100kb contig in chromosome 1, we calculate its average interaction frequency with each chromosome. We exclude interaction data from the contig’s 1 Mb regions on each side, where the strongest interaction frequencies are typically found. The box plot shows the distribution of average interaction frequencies of all contigs over all chromosomes and demonstrates that the distribution of interchromosomal interaction frequencies is separated from intrachromsomal interaction frequencies. Whiskers represent minimal and maximal points within 1.5 of the interquartile range. (b) Naïve Bayes predictive performance at various gap sizes. We trained a Naïve Bayes classifier and predicted the chromosome of each contig, leaving out a 1/2/5/10 Mb flanking region on each side of the contig. The accuracy of all cross-validated predictions and of the confident predictions is shown by the left y-axis and the blue and red lines, respectively. The fraction of total predictions that are confident is shown by the right y-axis and the black line. (c) Genome-wide view of Naïve Bayes predictive performance. The prediction for each contig is marked by a short vertical line, colored according to its true chromosome. Predictions showed were performed leaving out a 1 Mb flanking region on each side of the contig. Predictions that did not pass the confidence threshold are marked as “NC”. (d) Interaction frequencies accurately predict chromosomal locus. For every contig, we exclude interaction data from the contig’s 1Mb flanking regions on each side and then predict its location in cross-validation. The inset shows the cumulative distribution of the absolute prediction error. All statistics are genome-wide.

Because we know the positions and interaction frequencies of all placed contigs, it is possible to use supervised machine learning algorithms to fit functions that predict a contig’s chromosome and locus, given its interaction frequencies with other contigs and their known locations. We trained a simple multiclass model, a Naïve Bayes classifier, to predict the chromosome of each contig (Online Methods). To test the classifier, for each contig in the genome, we removed the interaction data for the contig and a flanking region of 0, 0.5, 1, 2, 5 or 10 Mb on each side, and used the classifier to predict the position of the contig solely from Hi-C data (Fig. 1b,c), achieving an accuracy of 0.998 when leaving out 1 Mb on each side. By thresholding the probabilities for each prediction output by the classifier to identify high-confidence predictions, we find that at a threshold of the classifier can achieve a near-constant error rate of less than 0.005 even when leaving 10 Mb gaps on each side of the contig (100 times the size of the contig). We conclude that the CTR interaction pattern can be used to accurately predict to which chromosome an unplaced contig belongs, even if it is flanked by large gaps.

Next we sought to predict the genomic locus along a chromosome of an unplaced contig, given its chromosome and interaction pattern with placed contigs on the chromosome. We use the assembled portion of the genome to fit a probabilistic single-parameter exponential decay model describing the relationship between Hi-C interaction frequency and genomic distance (the DDD pattern). Next, we removed in turn each contig from the chromosome, along with a flanking region of 1 Mb on each side, for the reasons mentioned above, and estimated its position by finding the location in which the interaction profile best fits the decay model (Fig. 1d). We quantified the prediction error as the absolute value of the distance between the predicted position and the actual position. Our results show a cross-validated genome-wide median error of 1.1 Mb. Additionally, 89.5% of the contigs are placed within 2 Mb of their actual position and 24.0% are within 0.5 Mb of their actual position (Fig. 1d, inset). We conclude that the DDD interaction pattern can be used to accurately predict the position of an unlocalized contig.

To show the utility of our approach for improving finished genomes, we collected two sets of contigs from hg19²² and HuRef⁷, totaling 65 contigs (13.6 mb in total) that had sufficient Hi-C interaction data for further analysis and predicted their locations (Fig. 2a,b and Supplementary Table 1). As validation, we compared our predictions to a recent study⁹ that used a more compliacated strategy to predict the location of some of these contigs using extensive population SNP data to perform admixture mapping. Our predictions agree with the previous results for 26/31 (84%) of the contigs placed by both methods (Online Methods and Supplementary Table 1). In addition, 24/30 (80%) of our predictions were consistent with FISH localization measurements compiled in the same study. We conclude that our method can be used to increase the level of completion of complex genome assemblies by placing contigs that have proven difficult to assemble despite years of efforts, as in the case of the human genome.

Figure 2.

Scaffold augmentation of the human genome. (a) Interaction frequency data of an unplaced contig with its predicted chromosome. Green bar marks the predicted contig position. (b) Predicted positions of unplaced contigs. Vertical lines indicate contigs. Green and red colors indicate agreement and disagreement with previous predictions⁹. Black: newly placed contigs with no previous predictions.

We also explored whether Hi-C data could be used for de novo genome scaffolding. The challenge is to determine the karyotype (i.e. the number of chromosomes and the chromosomal assignment) and position of all contigs simultaneously based on their mutual interaction frequencies. De novo scaffolding is markedly more difficult than scaffold augmentation for two main reasons. First, as we have no knowledge of any contig positions, we cannot observe or fit the CTR and DDD functions. Instead, we must make assumptions regarding how interaction frequencies relate to genomic distance and hope that these crude approximations produce useful results. Second, instead of resolving only the distances of a single unplaced contig from an array of placed contigs, all distances between all contigs must be resolved jointly. Under most problem formulations, calculation of a global optimal solution cannot be guaranteed.

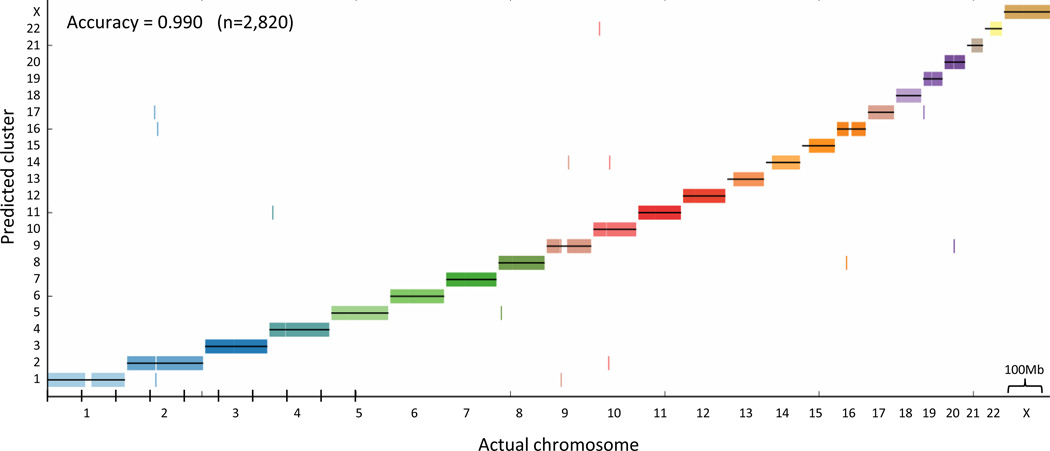
To examine scaffolding over long genomic ranges, we simulated a large gap scenario where we retained every 10^th contig in the human genome so that we were left with an array of 100kb virtual contigs separated by 900kb gaps, thus omitting the bulk of the Hi-C signal. First, we asked whether it is possible to group all the contigs into their respective chromosomes de novo (de novo karyotyping). Assuming the DDD is approximately exponential, we transformed the matrix of interaction frequencies into approximate unscaled genomic distances (Online Methods). These distances are very crude approximations, because at far distances the Hi-C interaction frequency, given as a discrete read number, will approach zero and thus will not be able to distinguish between vastly different far distances. We applied standard average-linkage hierarchical clustering to the approximate distance matrix, There was a high correspondence between the clusters and chromosomes; 99.5% of all contigs were placed on the correct chromosome (Fig. 3b).

Figure 3.

De novo karyotyping (chromosome assignment). We retained every tenth 100 kb contig in the genome, leaving 0.9 Mb gaps between contigs. We then transformed the interaction frequencies into approximate distances and applied standard average linkage hierarchical clustering to the approximate distance matrix, without using any prior knowledge regarding the positions of the contigs. The cluster assignment for each contig is marked by a short vertical line, colored according to its true chromosome.

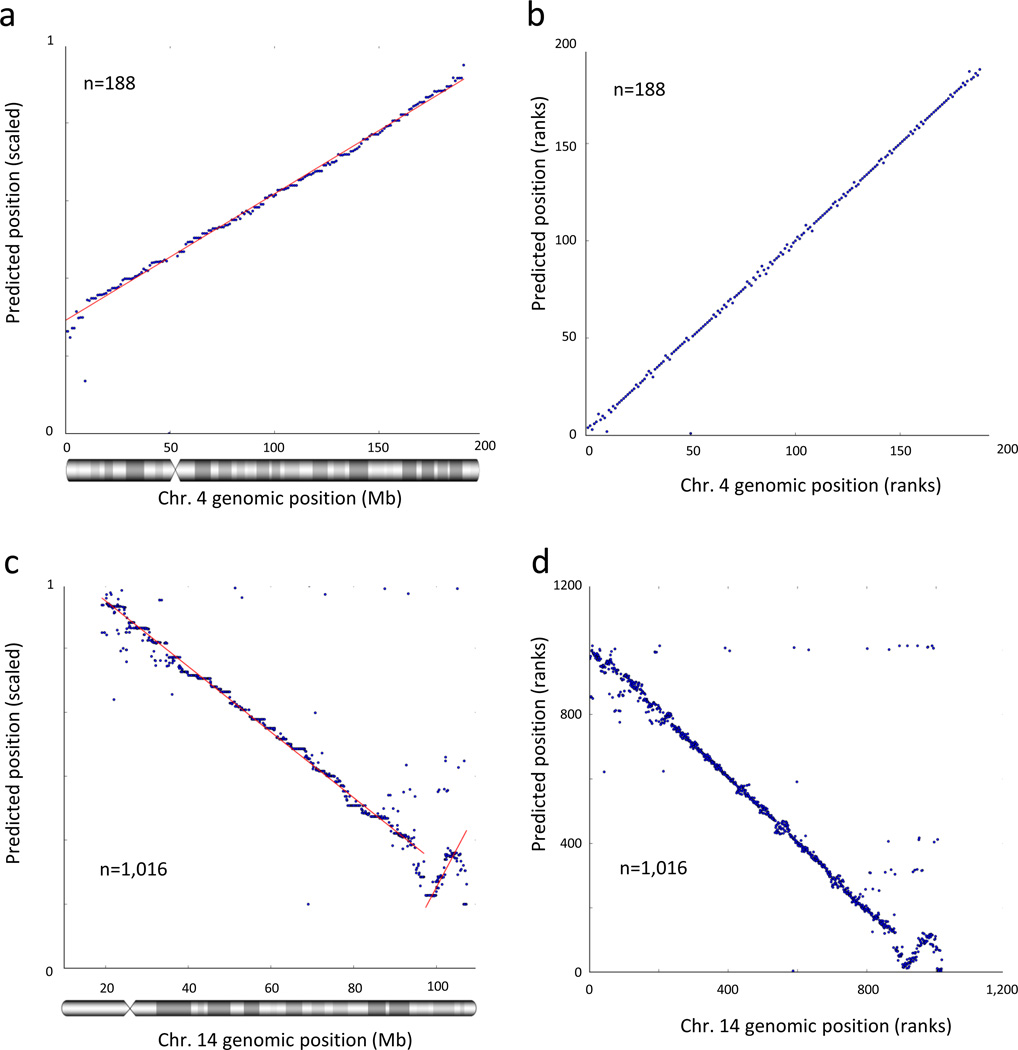
Finally, we asked whether we could use interaction frequencies between unlocalized contigs to estimate their positions along a chromosome. This task can be addressed by multidimensional scaling and manifold learning techniques. We used a probabilistic model that assumes the DDD is approximately exponential, and attempted to find a set of likely contig positions for our simulated 100 kb virtual contigs (Online Methods). We arbitrarily scaled the predicted contig positions to range from 0 to 1. We then compared our predicted positions with the actual positions. The predicted positions were highly consistent with their actual positions along most of the chromosomes (Fig. 4a and Supplementary Fig. 2a,c). We estimate a median error rate of ~2 Mb and an error less than 10 Mb in ~93% of the predictions (Supplementary Table 2). As an alternative measure of evaluation, we compared the ranks of the (contig order) predicted and actual positions (Fig. 4b). The ranked predictions seem slightly more accurate than the predicted positions, with an estimated median rank error of 1 (Supplementary Table 2), possibly suggesting that the distances between neighboring contigs may be distorted because of local variations in the DDD function. This is expected owing to the presence of locus-specific structures such as chromatin loops and structural domains^16,19,24. Notably, our approach is able to lay out an entire contiguous scaffold for each chromosome, rather than the highly fragmented scaffolds resulting from long-insert scaffolding. Most chromosomes contain no significant translocation or inversion errors, with a minority of chromosomes containing 1–2 major inversion errors.

Figure 4.

Accurate de novo chromosome scaffolding with interaction frequencies. (a, b) We retained every 10^th 100 kb contig in the genome, leaving 0.9 Mb gaps between contigs. We then estimated the positions of all contigs, without using any prior knowledge regarding their positions. We arbitrarily scaled the predicted positions to the interval [0,1]. Note that the slope, which reflects scaling and orientation, is arbitrary. (a) Scaled predicted contig positions versus actual contig positions on chromosome 4. (b) Ranks of predicted contig positions versus rank of actual contig positions. (c, d) De novo scaffolding applied to a real set of contigs from chromosome 14 (see Methods). (c) Shown are the scaled predicted contig positions versus actual contig positions. (d) Ranks of predicted contig positions versus rank of actual contig positions.

We next applied de-novo scaffolding to a previously published set of contigs for human chromosome 14 produced by the ALLPATHS-LG assembler²⁵ from actual sequencing libraries as part of the GAGE assembly¹² evaluation. We mapped Hi-C data to the assembled set of contigs, and estimated their chromosomal positions using our approach for de novo chromosome scaffolding (Online Methods). We then compared the predicted positions to the actual positions of the contigs when aligned to hg19 (Fig. 4c,d). The contigs were assembled into one large segment, containing one major inversion. Within each segment, the predicted positions were consistent with the actual positions. We estimate a median error of 976 kb with less than 10 Mb error in 3.6% of the predictions, and a median rank error of 6 (Supplementary Table 3). We conclude that the DDD pattern can be used to achieve accurate de novo chromosome scaffolding in various assembly scenarios. Again, precise knowledge of the decay function may not be mandatory for this task.

In conclusion, we show how each of the computational problems that we present can be mapped to a well-studied problem in the field of machine learning. Scaffold augmentation generally fits problems in the supervised learning framework, and de novo scaffolding generally fits problems in the unsupervised learning framework. Each of these known problems is supported by an extensive theoretical background, several algorithms for solution, and strategies for evaluating results, providing opportunities for further improvement. However, these are by no means the only possible strategies (Supplementary Discussion). The power of our method may be attributed not to the sophistication of the computational tools, which are purposefully simple, but rather to two canonical interaction patterns. The fact that these patterns are strong, consistent across the genome, and ubiquitous in all species, cell types and conditions observed to date, suggests that this method is widely applicable. Finally, we have addressed only two out of several possible applications of Hi-C data, which include targeted assembly (e.g. by using 4C^27,28 or 5C²⁹), detection of assembly errors, resolution of non-unique genomic sequences and detection of chromosomal aberrations.