Nonparametric Inference for Median Costs with Censored Data

Summary

Increasingly, estimations of health care costs are used to evaluate competing treatments or to assess the expected expenditures associated with certain diseases. In health policy and economics, the primary focus of these estimations has been on the mean cost, because the total cost can be derived directly from the mean cost, and because information about total resources utilized is highly relevant for policymakers. Yet, the median cost also could be important, both as an intuitive measure of central tendency in cost distribution and as a subject of interest to payers and consumers. In many prospective studies, cost data collection is sometimes incomplete for some subjects due to right censoring, which typically is caused by loss to follow-up or by limited study duration. Censoring poses a unique challenge for cost data analysis because of so-called induced informative censoring, in that traditional methods suited for survival data generally are invalid in censored cost estimation. In this article, we propose methods for estimating the median cost and its confidence interval (CI) when data are subject to right censoring. We also consider the estimation of the ratio and difference of two median costs and their CIs. These methods can be extended to the estimation of other quantiles and other informatively censored data. We conduct simulation and real data analysis in order to examine the performance of the proposed methods.

1. Introduction

Estimations of medical costs have become a widely used tool for evaluating the economic implications of competing treatments. Because resources are limited in a society, it is important that new treatments are developed with the proper cost considerations. The mean (average) cost has been the predominant summary measure of cost data in the health policy and economics fields, since it relates directly to the total cost, which then reflects the economic burden on society. However, it is well known that the cost distribution is highly skewed in general and that the mean could be influenced greatly by outliers or erroneous data. Therefore, in some situations the mean alone may offer incomplete information. The median cost could better represent typical costs paid or expected for a majority of individuals, and could provide additional information unrevealed by the mean. While median costs have not yet been adopted into health policy decision making, the estimation of median costs and the comparison of these among different groups (e.g., use of nonparametric tests such as the Wilcoxon test) have been topics of interest to health researchers (Kapur et al., 1999; Thomson et al., 2002; Taira et al., 2003). The median, along with other quantiles, has long been used for characterizing monetary data such as housing price, mortgage, income, and quantile-based methods have been studied extensively in the econometrics literature, see Koenker (2005). A quantile-based analysis can provide more specific and comprehensive information than one based on the mean. For example, it is not uncommon to see the highest 10 percentiles show a significantly increasing trend over time, while the lowest 10 percentiles show constant or decreasing trends. In such cases, use of a single summary measure such as the mean alone could be limiting or even misleading (DeNavas-Walt, Proctor, and Mills, 2004).

Today, cost data are collected increasingly through clinical trials and observational studies (Ramsey et al., 2005; Faries et al., 2010). Similar to survival data, the cost data collected from these studies can be censored due to incomplete follow-up before the clinical event of interest (e.g., death) is reached. Although it is often reasonable to assume that the time of event and the time of censoring are independent or conditionally independent, the assumption of independence generally does not hold for the associated costs. That is, cost at event and cost at censoring are no longer independent. This censoring mechanism is called “induced informative censoring,” as noted by Lin et al. (1997). Since a person who accumulates cost slowly would have smaller costs at both censoring time and event time, the censored total cost and the uncensored total cost tend to be positively correlated. Therefore, the analysis of censored cost data faces a special challenge, one that invalidates most of the standard statistical methods developed for censored survival data (e.g., the Kaplan–Meier estimator, the Cox model, the log-rank test). Over the past decade, we have seen various methods developed to address this challenge in different statistical settings. In particular, the task of estimating the mean cost with censored data has been studied by Lin et al. (1997), Bang and Tsiatis (2000), Zhao and Tian (2001), O'Hagan and Stevens (2004), Raikou and McGuire (2004), Young (2005), Zhao et al. (2007), Pan and Zeng (2011), among others. As for quantile-based methods for censored cost, the median regression model was developed by Bang and Tsiatis (2002). To our knowledge, however, to date there has been no method proposed for the estimation and inference of the median or other quantiles of costs with censored data.

In this article, we propose estimation and inference procedures for the median and other quantiles of medical costs subject to right censoring, by extending the techniques developed for the median survival time (Brookmeyer and Crowley, 1982; Gardiner, Susarla, and Ryzin, 1986). In addition, we develop inference procedures for the ratio and difference of two median costs. We consider the ratio measure as a natural and intuitive extension of the difference measure, similar to the risk difference and the risk ratio which are commonly considered together in clinical and epidemiologic research. In fact, the ratio could be a more meaningful measure when comparing different quantiles between the groups, or when comparing results from studies conducted at different time periods since it is scale invariant. Because of censoring, it is virtually impossible to consider the costs accumulated over a person's lifetime without introducing some assumptions that are unverifiable. Hence, we consider costs accumulated over a limited time L (e.g., 3 or 5 years), where L is often chosen to be the time so that a reasonable amount of data are still available at L. In general, the same time restriction is also required for the estimation of the mean cost, without making further assumptions about the distribution for the survival time and the cost (Huang, 2009).

This article is organized as follows. In Section 2, we explain how to estimate the median and its confidence interval (CI) (one sample problem) and then extend the methods to the ratio and difference of the medians (two sample problems). We propose inefficient and efficient estimators. Section 3 presents simulation studies, where we examine sample properties of the proposed methods numerically. We apply our methods to a cardiovascular clinical trial and summarize our results in Section 4. Finally, we conclude with discussions in Section 5.

2. Methods

2.1 Notation

We adopt a set of standard notations for survival analysis, denoting the time to event by T_i and the time of right censoring by C_i, for the ith subject (i = 1, . . . , n). We also assume that the subject is accumulating cost over time, and cumulative cost at time u is denoted by M_i(u). The variable C is independent of both the event time T and the cost accumulation process M(·). This assumption could be reasonable in well-conducted clinical trials where most censoring occurs due to staggered entry and study termination. It is adopted in most survival data analyses (Kalbfleisch and Prentice, 2002). We denote the associated survivor function for T by S^T (u) = Pr(T > u) and the survival function for C by K(u) = Pr(C > u).

As we noted in the Introduction, due to the presence of censoring, it is generally impossible to estimate costs over the entire health history without making some distributional assumptions. Therefore, we concentrate on the costs accumulated up to a prespecified time limit, denoted by L, where one has a reasonable amount of complete data available over the time period [0, L]. As a result, the survival time T_i will be replaced by $T_i^L=\min (T_i,L)$, but for notational convenience, we will use T_i instead of $T_i^L$ throughout the manuscript.

Typically, observed data are the random vectors of

$$\{X_i,{\Delta }_i,M_i\left(u\right):0\le u\le X_i,i=1,\dots ,n\},$$

where X_i = min(T_i, C_i), Δ_i = I(T_i ≤ C_i), and the cost history data M_i(u) are ascertained in discrete fashion (e.g., monthly or daily). We further define the observed total medical costs for the ith subject by M_i = M_i(X_i).

In the following subsections, we propose methods for the estimation and inference of the median cost as in the one sample problem, and of the ratio (or difference) of two median costs as in the two sample problem. Define the survival distribution of total medical costs as S(x) = Pr{M_i(T_i) > x}, the median cost can be written as

$$\tau =\inf \{x:S\left(x\right)\le 0.5\}.$$

In addition, if we define the median costs from groups 1 and 2 as τ₁ and τ₂, the ratio and the difference of the two medians are denoted, respectively, as

$$\gamma =\frac{{\tau }_2}{{\tau }_1};d={\tau }_2-{\tau }_1.$$

We will consider the inference problem for τ, γ, and d, when only final cost data are available for each subject (i.e., M_i(X_i), one observation per subject), and when longitudinal cost history data are also available (i.e., M_i(u) : 0 ≤ u ≤ X_i, multiple observations per subject).

2.2 Estimating the Survival Function of Costs with Censored Data

In order to estimate the median cost and its CI, we first need to estimate the survival distribution of the cost, denoted by Ŝ(x), and to establish its asymptotic properties. Although the survival function for the failure time T under random censoring mechanism has been proposed by Kaplan and Meier (1958), the same technique cannot be used validly for the survival function of medical costs due to the induced informative censoring mechanism as we explained earlier. We will use, instead, a method based on the inverse probability weighting scheme which was originally proposed by Horvitz and Thompson (1952) for analyzing survey data, and later employed extensively for handling various statistical problems in biostatistics, including censored data, missing data, and causal inference.

A simple weighted estimator for S(x) can be obtained by

$${\widehat{S}}_{SW}\left(x\right)=n^{-1}\sum _{i=1}^n\frac{{\Delta }_i}{\widehat{K}\left(T_i\right)}I(M_i>x),$$ (1)

where K̂(T_i) is the Kaplan–Meier estimator for the survival function of the censoring time variable C, K(u) = Pr(C > u), evaluated at T_i. The underlying idea of this weighting scheme is that one uncensored/complete observation T_i represents 1/K(T_i) observations that might have been observed if censoring had not occurred.

Following similar arguments used in Zhao and Tsiatis (1997), and based on the theory of counting processes and the general theory for missing data problems (Fleming and Harrington, 1991; Robins and Rotnitzky, 1992; Robins, Rotnitzky, and Zhao, 1994; Tsiatis, 2006), we can show that this simple weighted estimator is consistent and asymptotically normal:

$$\frac{{\widehat{S}}_{SW}\left(x\right)-S\left(x\right)}{{\sigma }_{SW}\left(x\right)}\stackrel{\mathcal{D}}{\to }N(0,1)$$ (2)

with the asymptotic variance ${\sigma }_{SW}^2\left(x\right)=\mathrm{Var}\left\{{\widehat{S}}_{SW}\left(x\right)\right\}$ that can be estimated by

$${\widehat{\sigma }}_{SW}^2\left(x\right)=n^{-1}{\widehat{S}}_{SW}\left(x\right)\{1-{\widehat{S}}_{SW}\left(x\right)\}+n^{-2}\sum _{i=1}^n\frac{1-{\Delta }_i}{{\left\{\widehat{K}\left(C_i\right)\right\}}^2}\left[\widehat{G}(B,C_i)\{1-\widehat{G}(B,C_i)\}\right],$$ (3)

where

$$\widehat{G}(B,C_i)=\frac{1}{n{\widehat{S}}^T\left(C_i\right)}\sum _{j=1}^n\frac{{\Delta }_j{B}_{j}I(T_j\ge C_i)}{\widehat{K}\left(T_j\right)},$$

with B_j = I(M_j > x) and Ŝ^T (C_i) being the Kaplan–Meier estimator for S^T (u) = Pr(T > u) evaluated at time C_i.

This simple weighted estimator is easy to use and well suited for the case where only the final cost is available from each patient. However, it is destined to be inefficient, because censored cost data and cost history are not utilized in estimation. If data on the cost history are available for each subject, additional information contained in the history can be used and may lead us to more efficient estimators.

One effective way to improve efficiency is to redefine the endpoint for each person, adapting the approach used in the estimation of quality-adjusted lifetime (Zhao and Tsiatis, 1997) as follows: For a fixed x, if M_i exceeds x, then this would be known at any time s such that s ≥ s_i(x), where s_i(x) = inf{s : M_i(s) ≥ x}. Then redefine $T_i^{\ast }\left(x\right)=\min (T_i,s_i\left(x\right)\}$, $X_i^{\ast }\left(x\right)=\min \{T_i^{\ast }\left(x\right),C_i\}$, and ${\Delta }_i^{\ast }\left(x\right)=I\{T_i^{\ast }\left(x\right)\le C_i\}$ so that a more efficient estimator can be formulated as

$${\widehat{S}}_{EF}\left(x\right)=n^{-1}\sum _{i=1}^n\frac{{\Delta }_i^{\ast }\left(x\right)}{{\widehat{K}}^{\ast }\left\{T_i^{\ast }\left(x\right)\right\}}I(M_i>x),$$ (4)

where ${\widehat{K}}^{\ast }\left\{T_i^{\ast }\left(x\right)\right\}$ is the Kaplan–Meier estimator for the survival function of the censoring time variable C, evaluated at $T_i^{\ast }\left(x\right)$, based on data $\{X_i^{\ast }\left(x\right),{\Delta }_i^{\ast }\left(x\right),i=1,\dots ,n\}$.

Using similar techniques as Zhao and Tsiatis (1997), we can show that this efficient estimator is consistent and asymptotically normal,

$$\frac{{\widehat{S}}_{EF}\left(x\right)-S\left(x\right)}{{\sigma }_{EF}\left(x\right)}\stackrel{\mathcal{D}}{\to }N(0,1),$$ (5)

where the variance for this estimator can be obtained in a similar fashion as in (3), but using redefined $T_i^{\ast }\left(x\right)$ and ${\Delta }_i^{\ast }\left(x\right)$ for each x and corresponding Ŝ^T*(·) and K̂*(·) in places of T_i and Δ_i, Ŝ^T (·), and K̂(·), i.e.,

$${\widehat{\sigma }}_{EF}^2\left(x\right)=n^{-1}{\widehat{S}}_{EF}\left(x\right)\{1-{\widehat{S}}_{EF}\left(x\right)\}+n^{-2}\sum _{i=1}^n\frac{1-{\Delta }_i^{\ast }\left(x\right)}{{\left\{{\widehat{K}}^{\ast }\left(C_i\right)\right\}}^2}\left[{\widehat{G}}^{\ast }(B,C_i)\{1-{\widehat{G}}^{\ast }(B,C_i)\}\right],$$ (6)

where

$${\widehat{G}}^{\ast }(B,C_i)=\frac{1}{n{{\widehat{S}}^T}^{\ast }\left(C_i\right)}\sum _{j=1}^n\frac{{\Delta }_j^{\ast }\left(x\right)B_{j}I\{T_j^{\ast }\left(x\right)\ge C_i\}}{{\widehat{K}}^{\ast }\left\{T_j^{\ast }\left(x\right)\right\}},$$

with B_j = I(M_j > x).

Note that for a fixed x, this efficient estimator uses cost information not only from those complete observations, but also from the censored observations whose accumulated costs are larger than x. Therefore, in many practical situations where censoring rate is high, this estimator would be more efficient than the simple weighted estimator. This effect is demonstrated in our simulation studies and the cardiovascular example considered later on.

2.3 Estimating the Median Costs and CIs: One Sample Problem

After we have an estimator for the survival distribution of the medical cost M_i, Ŝ(x), using either the simple weighted Ŝ_{S W} (x), or the more efficient estimator Ŝ_{E F} (x), the median cost estimator, $\widehat{\tau }$, can be obtained from solving the following equation:

$$\widehat{\tau }=\inf \{x:\widehat{S}\left(x\right)\le 0.5\}.$$ (7)

For obtaining the CI of the median cost, we avoid a direct (e.g., Wald-type) method based on the large sample distribution of the median estimator $\widehat{\tau }$, since this usually involves estimating the density function of the cost distribution, which can be difficult or unstable. Instead, we consider an alternative approach, similar to the idea of Brookmeyer and Crowley (1982) who considered the problem of obtaining a CI for the median survival time.

Denoting the true median cost by τ₀, from (2) and (5), we have, asymptotically,

$$\frac{{\{\widehat{S}\left({\tau }_0\right)-0.5\}}^2}{{\widehat{\sigma }}^2\left({\tau }_0\right)}\stackrel{\mathcal{D}}{\to }{\chi }_1^2,$$ (8)

so that an approximate α-level test for testing the null hypothesis, H₀ : τ = τ₀, is not to reject the null hypothesis whenever

$$\frac{{\{\widehat{S}\left(x\right)-0.5\}}^2}{{\widehat{\sigma }}^2\left(x\right)}\le c_{\alpha },$$

where c_α satisfies $\mathrm{Pr}\{{\chi }_1^2>c_{\alpha }\}=\alpha$. Hence, an asymptotic 1 – α confidence region R_α for the median can be obtained as the set of all parameter values meeting the condition of

$$R_{\alpha }=\left[x:\frac{{\{\widehat{S}\left(x\right)-0.5\}}^2}{{\widehat{\sigma }}^2\left(x\right)}\le c_{\alpha }\right],$$ (9)

where Ŝ(x) can be obtained by either the simple weighted estimator (1) or the efficient estimator (4), and ${\widehat{\sigma }}^2\left(x\right)$ can be obtained by corresponding variance estimators (3) or (6). Since Ŝ(x) is a step function, the identification of the lower and upper bound of the CI can be achieved by searching for the lowest and highest values of x at those places of jumps where the chi-square statistics are smaller than the critical value c_α.

2.4 Estimating the Ratio (or Difference) of the Median Costs and Their CIs: Two Sample Problem

Here, we suppose that we have cost data from two groups and we want to compare their medians via the ratio or difference. We consider the ratio first. After obtaining the estimators of the median costs for each group, ${\widehat{\tau }}_1$ and ${\widehat{\tau }}_2$, where the subscript denotes the group indicator, using the methods outlined in Section 2.3 (either the simple weighted or efficient estimator), the ratio of the two medians can be estimated by

$$\widehat{\gamma }=\frac{{\widehat{\tau }}_2}{{\widehat{\tau }}_1}.$$

Then our goal is to obtain the CI for γ.

Let S_k (x) be the survival function for medical costs for each group k (k = 1, 2) and Ŝ_k (x) be its estimator, which can be obtained using the methods from Section 2.2 (equations (1) and (4)), and let ${\widehat{\sigma }}_k^2\left(x\right)$ be an estimator of ${\sigma }_k^2\left(x\right)=\mathrm{Var}\left\{{\widehat{S}}_k\left(x\right)\right\}$ (equations (3) and (6)). Since it is generally difficult to study asymptotic properties of a ratio statistic directly, we consider an approach similar to the one used in Su and Wei (1993) concerning the ratio of two median survival times, which is based on the distribution of the minimum dispersion test statistic (Basawa and Koul, 1988). Define

$$W({\gamma }_0,{\tau }_1)=\frac{{\{{\widehat{S}}_1\left({\tau }_1\right)-0.5\}}^2}{{\widehat{\sigma }}_1^2\left({\widehat{\tau }}_1\right)}+\frac{{\{{\widehat{S}}_2\left({\gamma }_0{\tau }_1\right)-0.5\}}^2}{{\widehat{\sigma }}_2^2\left({\widehat{\tau }}_2\right)},$$ (10)

where γ₀ is the true ratio. Since τ₁ is a nuisance parameter here, we minimize W(γ₀, τ₁) with respect to τ₁ so that we have

$$G\left({\gamma }_0\right)=\underset{{\tau }_1}{\min }W({\gamma }_0,{\tau }_1).$$

In the Web Appendices A and B, we first establish that our median cost estimator $\widehat{\tau }$ is a consistent estimator of the true median τ, and then we show that G(γ₀) has a chi-square distribution with 1 degree of freedom asymptotically, under the null hypothesis that the true ratio is γ₀. Therefore, an asymptotic 1 – α confidence region R_α for γ can be formulated from

$$R_{\alpha }=\{\gamma :G\left(\gamma \right)\le c_{\alpha }\},$$

where c_α is a value such that $\mathrm{Pr}\{{\chi }_1^2>c_{\alpha }\}=\alpha$. Since both Ŝ₁(x) and Ŝ₂(x) are step functions, the Wstatistic is also a step function. The lower and upper bounds of the CI for γ can be identified by the smallest and largest ratios among all the pairs formed by all the jump places from each of the two groups, while keeping the W statistic below the critical value c_α.

Using similar strategies, the difference of the two medians, d = τ₂ – τ₁, can be estimated by

$$\widehat{d}={\widehat{\tau }}_2-{\widehat{\tau }}_1.$$

An asymptotic (1 – α) confidence region R_α for d can be formulated from

$$R_{\alpha }=\{d:G\left(d\right)\le c_{\alpha }\},$$

where

$$G\left(d\right)=\underset{{\tau }_1}{\min }W(d,{\tau }_1),$$

and

$$W(d,{\tau }_1)=\frac{{\{{\widehat{S}}_1\left({\tau }_1\right)-0.5\}}^2}{{\widehat{\sigma }}_1^2\left({\widehat{\tau }}_1\right)}+\frac{{\{{\widehat{S}}_2(d+{\tau }_1)-0.5\}}^2}{{\widehat{\sigma }}_2^2\left({\widehat{\tau }}_2\right)}.$$ (11)

2.5 Extension to Other Quantiles

It is straightforward to extend the methods above to other quantiles of cost data, such as the lower (25%) and upper (75%) quartiles. If we denote the pth percentile as τ_p such that

$$S\left({\tau }_p\right)=1-p∕100,$$

then the general formula for estimating τ_p would be

$${\widehat{\tau }}_p=\inf \{x:\widehat{S}\left(x\right)\le 1-p∕100\}.$$

The CI for τ_p can be obtained by replacing 0.5 with 1 – p/100 in (9). Similarly, the CI for the ratio or difference of the pth percentiles (γ_p = τ_2p/τ_1p, or d_p = τ_2p – τ_1p) can be obtained by substituting 0.5 for 1 – p/100 in (10) or (11), respectively.

3. Simulation Studies

Here, we conduct simulation experiments to evaluate the finite sample properties for our proposed methods. We assume the event of interest is death so that T is survival time. The cost data are generated as follows: The total cost for each individual consists of the diagnostic cost incurred at the beginning of the study, the fixed annual cost, the random annual cost that varies from year to year, and the terminal death cost incurred during the final year of life. In group 1, the diagnostic cost, fixed annual cost, random annual cost, and final year cost are log normally distributed with parameters (9, 0.245²), (6.5, 0.245²), (4, 0.245²), and (9, 0.632²), respectively. In group 2, the cost is generated similarly except the initial cost is log normal (10, 0.245²), and the fixed cost is log normal (6, 0.245²). Compared to group 1, group 2 has higher initial costs, but smaller fixed annual costs. We consider two types of distributions for survival times: (1) a uniform distribution on [0, 11.5] years for group 1 and a uniform distribution on [0, 12] for group 2; and (2) an exponential distribution with mean of 8 years for group 1 and an exponential distribution with mean of 10 years for group 2. Simulations based on a log normal distribution for the survival time have been conducted and conclusions are similar to those based on uniform or exponential distribution. The true median costs are 19,912 and 32,393 for groups 1 and 2 for uniform distributions, and 17,679 and 30,241 for groups 1 and 2 for exponential distributions.

We also consider two scenarios for the distribution of the censoring variable C: (1) C_i is uniform on [0, 22] years and (2) C_i is uniform on [0, 15] years, independent of all other variables. The first setting is referred to as light censoring, resulting in 25–29% censoring, and the latter is referred to as heavy censoring, corresponding to 37–44% censoring for two different survival time distributions. The sample size varies from 100 to 300 for each group, and the number of simulations is 1000. Our interest is to estimate the median, 25% and 75% quantiles, for costs accumulated over 10 years, and their CIs for each group, as well as the ratios of the quantiles from the two groups and their CIs. We also examine the median lengths of the CIs. We consider the following methods based on different estimators for survival functions of cost: (1) the Kaplan–Meier estimator (KM) that treats cost data as survival data; (2) the empirical survival estimator that uses only complete/uncensored data (CP); (3) the empirical survival estimator that uses both censored and uncensored costs ignoring censoring status (AL); (4) the simple weighted estimator (SW); and (5) the efficient estimator (EF). Approaches (1) to (3) can be regarded as naive estimators, whereas (4) and (5) would provide consistent estimators. Here an empirical survival estimator simply calculates the percentage of subjects that have costs greater than a given number.

Table 1 shows the empirical coverage probabilities of the 95% CIs for the median, 25% and 75% quantiles along with the median lengths of the estimated 95% CIs, for different sample sizes, levels of censoring and distributions of the survival times for group 2.

Table 1.

Empirical coverage probabilities (median lengths) of the 95% confidence intervals for different quantiles of cost for group 2

			Light censoring		Heavy censoring
Quantile	Sample size	Method	Uniform survival	Exponential survival	Uniform survival	Exponential survival
25%	100	KM	0.923 (4065)	0.795 (3901)	0.868 (4404)	0.568 (4306)
		CP	0.937 (4201)	0.948 (4025)	0.932 (4772)	0.952 (4660)
		AL	0.188 (3807)	0.495 (3407)	0.020 (3725)	0.149 (3319)
		SW	0.950 (4226)	0.936 (4052)	0.935 (4889)	0.951 (4952)
		EF	0.946 (4172)	0.939 (3887)	0.944 (4693)	0.962 (4339)
	300	KM	0.817 (2367)	0.429 (2259)	0.448 (2515)	0.088 (2550)
		CP	0.944 (2414)	0.944 (2328)	0.945 (2690)	0.932 (2674)
		AL	0.006 (2174)	0.080 (1924)	0.000 (2066)	0.001 (1886)
		SW	0.950 (2459)	0.960 (2348)	0.950 (2806)	0.958 (2786)
		EF	0.946 (2395)	0.964 (2201)	0.943 (2650)	0.958 (2443)
50%	100	KM	0.905 (4628)	0.729 (4601)	0.775 (5046)	0.490 (5090)
		CP	0.944 (4571)	0.939 (4540)	0.947 (5121)	0.940 (5180)
		AL	0.373 (4047)	0.572 (3716)	0.140 (3994)	0.271 (3660)
		SW	0.965 (4724)	0.941 (4583)	0.942 (5375)	0.952 (5325)
		EF	0.957 (4588)	0.940 (4361)	0.948 (5006)	0.958 (4750)
	300	KM	0.820 (2633)	0.372 (2607)	0.381 (2897)	0.058 (2989)
		CP	0.921 (2653)	0.949 (2642)	0.946 (2943)	0.931 (2966)
		AL	0.022 (2353)	0.148 (2176)	0.000 (2286)	0.007 (2142)
		SW	0.944 (2733)	0.957 (2651)	0.944 (3105)	0.947 (3116)
		EF	0.948 (2638)	0.957 (2500)	0.945 (2943)	0.952 (2740)
75%	100	KM	0.883 (6685)	0.755(6659)	0.803 (7594)	0.591 (7969)
		CP	0.956 (6286)	0.936 (6279)	0.949 (7044)	0.930 (7501)
		AL	0.756 (5500)	0.810 (5280)	0.467 (5503)	0.623 (5286)
		SW	0.944 (6434)	0.964 (6309)	0.952 (7312)	0.953 (7245)
		EF	0.942 (6320)	0.961 (5984)	0.948 (7027)	0.962 (6597)
	300	KM	0.795 (3638)	0.466 (3728)	0.663 (4113)	0.131 (4361)
		CP	0.950 (3594)	0.936 (3592)	0.931 (3930)	0.916 (3983)
		AL	0.285 (3062)	0.457 (2933)	0.027 (3061)	0.121 (2898)
		SW	0.949 (3626)	0.951 (3490)	0.943 (4185)	0.951 (4150)
		EF	0.953 (3567)	0.947 (3360)	0.940 (4035)	0.960 (3797)

It is clear that the naive approaches using the Kaplan–Meier estimator (KM) or all data (AL) yield incorrect coverage probabilities for the 95% CIs for the median or other quartiles of costs. The coverage probabilities do not improve with increased sample sizes. The complete data only (CP) method seems to produce reasonable coverage probabilities for many scenarios in these simulations. However, one drawback we notice is that the coverage probability deteriorates when the sample size increases from 100 to 300 for the exponential survival distribution, heavy censoring case. Since this estimator uses only the complete observations, which tend to consist of those with short survival times, these costs can be biased downward (or upward) when people with shorter survival times have smaller (or larger) costs. Additional simulations we performed indicate that if we simply decrease the initial costs and terminal costs for the uniform survival distribution scenario considered here, the coverage probability can become as low as 0.515. Since, in general, the failure time and the total costs are correlated, we should avoid using this estimator, as advised in the case of estimating the mean cost (Lin et al., 1997; Bang and Tsiatis, 2000).

The proposed approaches using the simple weighted (SW) estimator and the more efficient estimator (EF) produce coverage probabilities that are close to the nominal value. This is true for the median, upper, and lower quartiles, for different survival distributions, and for both light and heavy censoring cases. The coverage probability improves, and the median length of the CI becomes shorter as the sample size increases from 100 to 300. We also note that the median lengths of the CIs for the efficient estimator generally are shorter than those for the simple weight estimator, and the difference becomes more pronounced when the censoring is heavier. Hence it would be advantageous to use the efficient estimator when the censoring is heavy and cost history data are available.

Table 2 shows the results for the ratios and the differences of the medians, lower and upper quartiles of costs between group 2 and group 1, for the two valid methods—the simple weighted estimator and the efficient estimator.

Table 2.

Empirical coverage probabilities (median lengths) of the 95% confidence intervals for the ratio (Part A) and the difference (Part B) of different quantiles of cost between two groups

Part A: Ratios of quantiles
			Light censoring		Heavy censoring
Quantile	Sample size	Method	Uniform survival	Exponential survival	Uniform survival	Exponential survival
25%	100	SW	0.975 (0.490)	0.976 (0.492)	0.980 (0.554)	0.980 (0.592)
		EF	0.973 (0.489)	0.978 (0.474)	0.986 (0.554)	0.988 (0.546)
	300	SW	0.967 (0.266)	0.960 (0.267)	0.975 (0.305)	0.977 (0.320)
		EF	0.967 (0.263)	0.972 (0.257)	0.979 (0.297)	0.976 (0.292)
50%	100	SW	0.974 (0.418)	0.976 (0.454)	0.971 (0.486)	0.976 (0.538)
		EF	0.973 (0.415)	0.983 (0.437)	0.976 (0.477)	0.982 (0.498)
	300	SW	0.967 (0.240)	0.970 (0.252)	0.969 (0.273)	0.971 (0.297)
		EF	0.971 (0.236)	0.975 (0.242)	0.974 (0.265)	0.973 (0.276)
75%	100	SW	0.978 (0.489)	0.975 (0.531)	0.978 (0.567)	0.977 (0.624)
		EF	0.981 (0.480)	0.973 (0.518)	0.977 (0.554)	0.979 (0.591)
	300	SW	0.966 (0.266)	0.968 (0.297)	0.967 (0.310)	0.971 (0.339)
		EF	0.964 (0.261)	0.968 (0.291)	0.967 (0.303)	0.974 (0.326)

Part B: Differences of quantiles
			Light censoring		Heavy censoring
Quantile	Sample size	Method	Uniform survival	Exponential survival	Uniform survival	Exponential survival
25%	100	SW	0.974 (6013)	0.970 (5518)	0.973 (6857)	0.976 (6641)
		EF	0.977 (5984)	0.972 (5266)	0.979 (6756)	0.985 (6111)
	300	SW	0.963 (3366)	0.969 (3069)	0.970 (3880)	0.960 (3653)
		EF	0.965 (3286)	0.971 (2903)	0.967 (3736)	0.967 (3327)
50%	100	SW	0.973 (6769)	0.986 (6304)	0.967 (7695)	0.977 (7416)
		EF	0.973 (6620)	0.980 (5999)	0.977 (7424)	0.977 (6794)
	300	SW	0.955 (3754)	0.967 (3472)	0.958 (4286)	0.968 (4124)
		EF	0.957 (3664)	0.961 (3333)	0.958 (4084)	0.974 (3780)
75%	100	SW	0.979 (9797)	0.977 (9381)	0.976 (11375)	0.976 (11115)
		EF	0.979 (9539)	0.977 (9148)	0.980 (11014)	0.976 (10463)
	300	SW	0.965 (5280)	0.974 (5167)	0.977 (6045)	0.977 (5907)
		EF	0.964 (5197)	0.975 (5021)	0.977 (5859)	0.980 (5574)

We observe that the coverage probabilities stay above 95% under all scenarios, indicating that the CIs tend to be conservative. Similar results are reported for the median estimation of survival time as well (Su and Wei, 1993). The coverage probabilities are closer to the nominal level when the sample size increases from 100 to 300. This is observed consistently for estimating different quantiles, using different survival distribution, and with both light and heavy censoring. As predicted by theory, the median length of the CIs decreases as the sample size increases, and the efficient method produces shorter CIs, compared to the simple weighted estimator.

4. Example

The Multicenter Automatic Defibrillator Implantation Trial II (MADIT-II) was a multicenter clinical trial designed to evaluate the potential survival benefit of a prophylactically implanted defibrillator in patients with a prior myocardial infarction and other selection criteria (Moss et al., 2002). Patients were recruited into the study over time and were randomized into either the implantable cardiac defibrillator (ICD) arm or the conventional therapy arm (CONV), with a allocation ratio of 2:1. After the trial was completed, it was shown (Moss et al., 2002) that the ICD arm has a survival advantage with an estimated hazard ratio of 0.69 (95% CI: 0.51–0.93; p = 0.016).

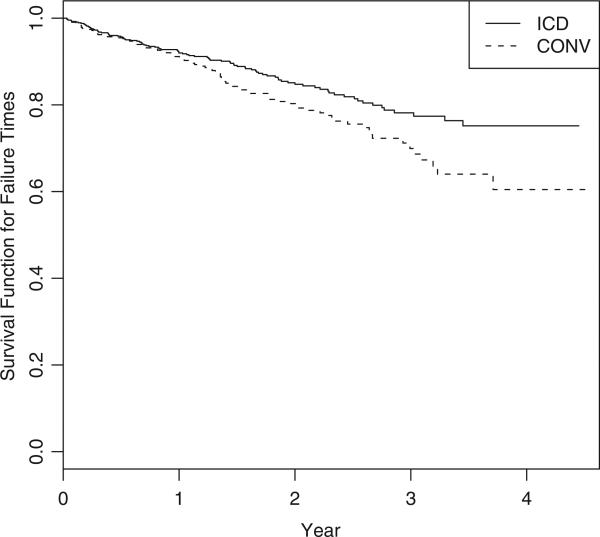
Due to the high cost associated with the defibrillator and the implantation process, a subsequent economic evaluation was done to elucidate the cost implications of the new treatment (Zwanziger et al., 2006). The cost-effectiveness analysis was based on patients from the US centers, with 664 patients in the ICD arm and 431 in the CONV arm. The average follow-up time for this subpopulation was 22 months. We will examine costs accumulated over L = 3.5 years, or equivalently 1278 days, as in the original paper (Zwanziger et al., 2006). As a result, 77.3% of subjects from the ICD group and 74.2% subjects from the CONV arm were censored. The probability of survival for each treatment arm is presented in Figure 1.

Figure 1.

Kaplan–Meier survival curves for the MADIT-II study.

Detailed information about the cost structure and components was provided in table 2 of Zwanziger et al. (2006), e.g., the average initial cost for the ICD group is $32,578, which includes the device costs and implantation costs; the average monthly cost is $1,357 for the CONV arm and $1,489 for the ICD arm; the cost associated with death is estimated to be $6,706 for the CONV arm and $8,477 for the ICD arm.

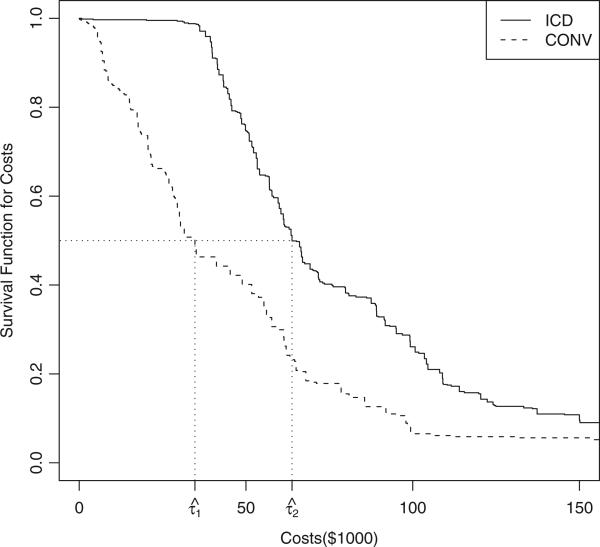
Figure 2 displays the estimated survival functions for costs, for both the ICD and the CONV groups, using the simple weighted estimator, where the median cost estimates for each group are marked on the plot. It is clear that the ICD group is associated with much higher costs, compared to the CONV arm. Due to the high initial cost in the ICD group, the survival line is flat near the baseline. This is also what we assumed in our simulation setting.

Figure 2.

Estimated survival function for medical costs for the MADIT-II study.

The estimated median, upper, and lower quartiles of costs for each group, and their 95% CIs, using the proposed estimators, are shown in Table 3. Also shown are the ratios of these quantiles, and their 95% CIs.

Table 3.

Quantile estimation (and 95% confidence intervals) in $1000 for the MADIT-II study

		Group
Quantile	Method	CONV	ICD	Ratio
25%	SW	17.7 (9.0,26.1)	49.8 (44.5,53.4)	2.8 (1.8,5.6)
	EF	15.1 (11.4,20.6)	48.7 (44.5,51.0)	3.2 (2.2,4.3)
50%	SW	34.7 (26.9,53.8)	63.8 (58.2,75.8)	1.8 (1.2,2.5)
	EF	28.0 (22.4,34.7)	63.5 (60.0,66.6)	2.3 (1.8,2.9)
75%	SW	62.0 (55.6,80.9)	100.7 (89.2,114.0)	1.6 (1.2,1.9)
	EF	56.1 (41.5,65.0)	100.7 (89.2,109.0)	1.8 (1.5,2.6)

On the whole, the efficient estimator produces tighter CIs than does the simple weighted one. In contrast to the mean costs of $44,900 and $84,100 for the CONV and ICD groups (Zwanziger et al., 2006), the corresponding median estimates using the efficient estimator are much smaller, $28,000 and $63,500, respectively. The estimates for the lower 25% percentile are $15,100 and $48,700 respectively, which means that 25% of the patients have medical costs less than or equal to $15,100 in the CONV group, and $48,700 in the ICD group. The estimates for the upper 25% percentile are $56,100 and $100,700 respectively. The ratio of the mean costs for the ICD versus CONV arm is 1.9, while the ratio of the median costs for the two groups is 2.3. The ratio of the lower quartiles is larger than the ratio of the medians, whereas the ratio of the upper quartiles is smaller than the median ratio. The quantile measures and the mean together would provide a more complete picture for the costs incurred during the MADIT-II study.

5. Discussion

This article considers a problem of nonparametric inferences for medical costs when data are subject to right censoring. Looking at the entire distribution by estimating various quantiles is customary in the analysis of national income data and some other economic data. A similar approach could be useful in medical cost analysis as well. We propose methods for estimating medians and other quantiles and for obtaining their CIs. We also propose methods for estimating the ratios and differences of these quantile measures and for obtaining their CIs. These methods could provide valuable tools for economic evaluations of treatments, especially when the data are subject to censoring, as is common in prospective studies.

In our simulation, we demonstrate that the naive methods that either ignore censoring or fail to account for it properly (by using either uncensored data only, treating censored data as if they were not censored, or using the Kaplan–Meier estimator on cost estimation assuming censoring is random) produce biased results. Use of these methods should be avoided in the analysis of censored cost data. For valid estimation and inference, we produce two estimators—simple weighted and efficient estimators. The simple weighted estimator can be useful and convenient when we have only the total costs for each subject. In contrast, when cost history data are available, we recommend the efficient estimator, especially when the censoring rate is high.

In this article, we propose one efficient estimator. However, additional approaches to improve efficiency could be devised, for example, based on the ideas employed in Zhao and Tian (2001), Robins (1996), and Tsiatis (2006). The methods proposed here can be applied to other informatively censored data (Huang and Louis, 1998). Future research can be directed to investigate these problems further.