DCE-MRI defined subvolumes of a brain metastatic lesion by principle component analysis and fuzzy-c-means clustering for response assessment of radiation therapy

Abstract

Purpose: To develop a pharmacokinetic modelfree framework to analyze the dynamic contrast enhanced magnetic resonance imaging (DCE-MRI) data for assessment of response of brain metastases to radiation therapy.

Methods: Twenty patients with 45 analyzable brain metastases had MRI scans prior to whole brain radiation therapy (WBRT) and at the end of the 2-week therapy. The volumetric DCE images covering the whole brain were acquired on a 3T scanner with approximately 5 s temporal resolution and a total scan time of about 3 min. DCE curves from all voxels of the 45 brain metastases were normalized and then temporally aligned. A DCE matrix that is constructed from the aligned DCE curves of all voxels of the 45 lesions obtained prior to WBRT is processed by principal component analysis to generate the principal components (PCs). Then, the projection coefficient maps prior to and at the end of WBRT are created for each lesion. Next, a pattern recognition technique, based upon fuzzy-c-means clustering, is used to delineate the tumor subvolumes relating to the value of the significant projection coefficients. The relationship between changes in different tumor subvolumes and treatment response was evaluated to differentiate responsive from stable and progressive tumors. Performance of the PC-defined tumor subvolume was also evaluated by receiver operating characteristic (ROC) analysis in prediction of nonresponsive lesions and compared with physiological-defined tumor subvolumes.

Results: The projection coefficient maps of the first three PCs contain almost all response-related information in DCE curves of brain metastases. The first projection coefficient, related to the area under DCE curves, is the major component to determine response while the third one has a complimentary role. In ROC analysis, the area under curve of 0.88 ± 0.05 and 0.86 ± 0.06 were achieved for the PC-defined and physiological-defined tumor subvolume in response assessment.

Conclusions: The PC-defined subvolume of a brain metastasis could predict tumor response to therapy similar to the physiological-defined one, while the former is determined more rapidly for clinical decision-making support.

INTRODUCTION

Dynamic contrast enhanced magnetic resonance imaging (DCE-MRI, see Table 1) is a noninvasive imaging tool extensively used in oncology for diagnosis and therapy assessment,¹ and also as an imaging biomarker for development of antiangiogenic drugs.² The DCE-MRI technique is based upon rapid acquisition of a series of T1-weighted images from a tissue of interest before, during, and after intravenous bolus injection of a gadolinium-based contrast agent (CA).³ As the CA perfuses into the tissue under investigation, T1 values of the tissue water decrease to an extent which depends upon the CA concentration. Hence, the characteristic signal intensity time course, relating to the CA concentration, in a region of interest or a voxel of the tissue can be subsequently analyzed by a pharmacokinetic (PK) model. By fitting the DCE-MRI data to a PK model, a set of volumetric maps of physiological parameters can be obtained, for example, tissue perfusion, microvascular permeability, and extravascular extracellular volume.⁴ Longitudinal changes in maps of the physiological parameters of a tissue of interest from pre- to post-treatment could aid in for assessment and prediction of treatment response and outcome as well as for drug development.^{5, 6}

Table 1.

Frequently used abbreviation.

Abbreviation	Description
2W	Week 2
AIF	Arterial Input Function
AUC	Area Under Curve
cPC	Projection Coefficient
cPDF	Pooled Histogram
DCE-MRI	Dynamic Contrast Enhanced Magnetic Resonance Imaging
FCM	Fuzzy-C-Means Clustering
GTV	Gross Tumor Volume
H	Histogram: Interchangeably used with Probability Density Function
P	Progressive
PCA	Principle Component Analysis
PDF	Probability Density Function: interchangeably used with Histogram
PK	Pharmacokinetic
Pre-RT	Prior to Radiation Therapy
R	Responsive lesions
rCBV	Regional Cerebral Blood Volume
ROC	Receiver Operating Characteristic
ROI	Region of Interest
S	Stable lesions
SV	Sub-volume
WBRT	Whole Brain Radiation Therapy

The physiological parameter maps derived from the PK models, although useful and meaningful for diagnosis and therapy assessment, involve in a series of uncertainties.⁷ Foremost, the DCE-MRI data often cannot be fitted to a selected PK model perfectly, and hence may be a source of errors affecting the accuracy of the physiological parameters. In addition, the “physiological parameters” derived from the PK models may not accurately reflect the underlying physiology, due to oversimplification in the models and lack of physiological validation of the models. For example, interpretation of K^trans derived from the Toft model depends upon flow limited, permeability limited, or mixed. Also, computing the physiological parameters by fitting the DCE-MRI data into the PK models is a time consuming process, which is inadequate for real-time decision making support in adaptive radiation therapy, especially to handle the number of patients and the clinical workload. Hence, a modelfree approach to analyze the DCE-MRI data, e.g., the methods based on factor analysis,^{8, 9} independent component analysis (ICA),¹⁰ and principal component analysis (PCA),^{11, 12, 13, 14} could potentially facilitate the development of the real-time decision-making supportive tools in diagnosis and therapy assessment. PCA has shown the potential to be a very robust and fast technique in analyzing the DCE-MRI data,^{11, 12, 13, 14, 15, 16} and especially in prostate^{12, 13, 14} and breast^{15, 16} cancer. Eyal et al.¹² applied PCA to dynamic intensity-scaled (IS) and enhancement-scaled (ES) datasets to develop and evaluate a method for image processing of the dynamic contrast enhanced MRI of the prostate cancer. They found that the first IS-eigenvector captured the major part of the signal variance, and the next two IS-eigenvectors captured the signal changes due to the tissue contrast-enhancement; whereas the remaining eigenvectors captured noise fluctuations. When they were applying the approach to distinguish benign lesions from malignant prostate cancers, the high values of 2nd and 3rd eigenvectors were able to differentiate the two.¹³ Although the model-based approach achieved the similar results, the PCA-based methods were fast and robust for analyzing the DCE data. Furthermore, the PCA-based approach has been applied to the DCE images of breast cancer, in which the 2nd and 3rd eigenvectors were found to be indicators of the wash-in and wash-out of the contrast agent.¹⁵ However, although these works have shown promising results for diagnostic purposes, to the best of our knowledge, no standard approach has been proposed so far to incorporate PCA into an automatic supportive tool for decision-making in therapy assessment.

A previous study¹⁷ has shown that an early change in the subvolume of a brain metastatic tumor with high-rCBV and high-K^trans is a better predictor for postradiation therapy response than a tumor volumetric change and a change in the mean tumor rCBV observed in the same time interval. In this previous work, the physiological imaging-defined tumor subvolume, as a response-predictor, is determined through a two-step process: (1) deriving the physiological parameters by fitting the DCE MRI data to a PK model and (2) delineating the subvolume by analysis of the physiological parameters in the tumor using a fuzzy-c-means (FCM)-based technique. Hence, in this work our main goal is to develop a general framework to derive a response-predictor from DCE-MRI data without using the PK modeling and to have a semiautomated or fully automated tool for response assessment and therapy guidance in radiation therapy of brain metastases, the most common form of intracranial tumors exceeding the number of primary brain tumors by at least ten times and occurring in approximately 25% of all patients with cancers.¹⁸ In our proposed approach, we transfer the DCE curves into an N-dimensional feature space using principal component analysis, then, identify the most response-related features using a FCM-based technique similar to what is proposed in Ref. 17, and finally combine the features to define the tumor subvolumes. We evaluate whether our modelfree approach could provide a similar or even better metric, in defining the subvolume of a tumor compared to the subvolume defined by the physiological parameters obtained from the PK model.

MATERIALS AND METHOD

Patients

Twenty patients (11 women and 9 men, ages 41–76 yr), diagnosed with brain metastases and enrolled in an institutional review board (IRB)-approved prospective MRI study and previously described in Ref. 17, were also included in this study (Table 2). The histology consisted of melanoma (11), nonsmall cell lung cancer (6), renal cell carcinoma (1), breast cancer (1), and head & neck squamous cell carcinoma (1). All patients received standard WBRT with a total dose of 30 Gy in 10 fractions (13 patients) or 37.5 Gy in 15 fractions (7 patients). If a patient had less than three brain metastatic lesions, all lesions were included. If a patient had more than three lesions, only the three largest lesions were included. If a patient had more than three lesions larger than 1 cm³, up to three lesions greater than 1 cm³ were also included. As a total, 45 lesions with a median volume of 1.65 cm³ and a range of 0.1–17.6 cm³ were analyzed.

Table 2.

Patient characteristics information.

			Total accumulated	Concurrent drug	No. of	Volume
Pt. #.	G/Age (Y)	Histology	dose/Fx (Gy)	treatment	lesions	range (cm3)
1	Female/54	Breast Cancer	37.5/2.5	None	3	4.23–11.78
2	Male/63	Renal Cell Carcinoma	30/3	Bortezomib	2	13.23–14.67
3	Male/41	Melanoma	37.5/2.5	Bortezomib	3	0.15–1.24
4	Female/60	NSC Lung Cancer	37.5/2.5	None	1	0.52
5	Female/52	Melanoma	37.5/2.5	Bortezomib	1	2.74
6	Female/45	Melanoma	30/3	Bortezomib	1	2.07
7	Male/49	Melanoma	30/3	Bortezomib	2	0.17–4.09
8	Female/51	NSC Lung Cancer	30/3	Bortezomib	3	0.50–4.55
9	Male/61	Melanoma	37.5/2.5	Bortezomib	4	6.64–17.67
10	Male/52	NSC Lung Cancer	30/3	None	1	0.479
11	Female/55	Melanoma	30/3	Bortezomib	2	0.42–0.54
12	Male/76	Melanoma	30/3	Bortezomib	1	0.68
13	Female/46	Melanoma	30/3	Bortezomib	6	1.25–1.95
14	Female/57	Melanoma	30/3	Bortezomib	2	0.94–1.58
15	Female/64	NSC Lung Cancer	37.5/2.5	None	1	0.108
16	Male/60	Melanoma	30/3	Bortezomib	3	0.18–1.31
17	Female/74	Melanoma	30/3	Bortezomib	4	0.69–5.81
18	Male/43	Head & Neck SCC	30/3	None	1	0.60
19	Male/58	NSC Lung Cancer	30/3	None	3	2.38–10.69
20	Female/66	NSC Lung Cancer	37.5/2.5	None	1	0.95

¹Abbreviation: Pt. #. = patient number; G = Gender; Y = year; NSC Lung Cancer = non-small cell Lung Cancer; and Head & Neck SCC = Head and Neck squamous cell carcinoma.

Imaging acquisition

All patients had MRI scans on a Philips 3T scanner prior to radiation therapy (Pre-RT), 2 weeks after the start of RT (2W), and 1 month after the completion of treatment (1M Post-RT). MRI scans included pre and post-Gd-DTPA volumetric T1 weighted images, multislice 2D T2 weighted images, and volumetric DCE T1 weighted images. The 3D volumetric DCE-images were acquired during bolus injection of a standard dose (0.1 mmol/kg) of Gd-DTPA with an injection rate of 2 cc/s. The DCE-images were acquired in the sagittal plane with an image matrix of 128 × 128 × 80, a field-of-view of 240 × 240 × 160 (mm), a voxel size of 2 × 2 × 2 (mm³), a flip angle(α) of 20⁰, and TE/TR of 1.04/5.14 ms and a temporal resolution of 4-6 s. Using an in-house software package, both anatomical and DCE-MR images were coregistered and resampled to have a voxel size of 0.9375 × 0.9375 × 3 (mm³). Each lesion of interest was manually contoured by a physician on the post-Gd T1 weighed images obtained preRT, 2W and 1M post-RT.

Pharmacokinetic modelfree framework

Our proposed PK modelfree framework consists of two phases: development phase and usage phase. In the development phase, a sample of the DCE data from brain metastases is processed and analyzed to develop the model and the predictive metric. In the usage phase, we determine if the predictive metric could be extracted rapidly from the DCE data of a new patient scan.

Development phase

A flowchart of the development phase, shown in Fig. 1, includes preprocessing, modeling of DCE curves of a sample of brain metastases (including PCA and feature classification) to obtain a single metric, and evaluating the metric for response assessment. Each step is described in Subsections 2D1, 2F in detail.

Figure 1.

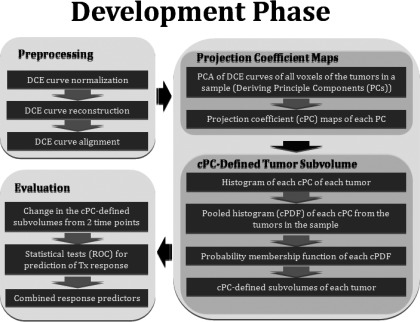
The flowchart of our proposed PK model free approach based upon tumor DCE data for supporting decision-making of assessment of therapy response. cPC: Projection coefficient map; cPDF: Pooled histogram corresponding to a cPC.

Preprocessing

DCE curves normalization

The dynamic curve at each voxel represents the temporal changes in signal intensity after the contrast injection. We calculate the signal intensity change ΔS from pre (baseline) to postcontrast as following:¹⁹

$$\Delta S\left(t\right)\equiv \frac{S\left(t\right)-S_0}{S_0},$$ (1)

where S(t) and S₀ represent signal intensities of a DCE curve at times t and 0 (the time of contrast injection), respectively. Note that ΔS(t)/S₀ is proportional to ΔR1·T₁₀, the change in relaxation rate caused by the contrast agent weighted by the initial spin-lattice relaxation time, as long as TR · R₁ is much smaller than one. To account for the individual hemodynamic response to contrast, we normalize ΔS at each voxel using the peak of the arterial input function, AIF_max, obtained during the same scan as

$$\Delta S_N\left(t\right)=\Delta S\left(t\right).\frac{1}{AI{F}_{\max }}.$$ (2)

An arterial input function can be determined from a region of interest (ROI) in a large artery (e.g., carotid artery for our application) manually, semiautomatically, or automatically. In the current work, a region of interest containing brain and neck is initially contoured. Then, DCE curves within the contour are averaged to determine the peak enhancement, T_max, in the tissue. Assuming that the arterial input function reaches the enhancement peak prior to tissue, the first 20 voxels with the maximum enhancement in ΔS(T_max − Δt), one time frame before T_max, within the contour are thresholded, and then the corresponding DCE curves are averaged to be considered as an arterial input function.

DCE curve reconstruction

The DCE curves in each scan may not be acquired with the exactly same temporal resolutions and time durations. Hence, we standardize the DCE curves in such a way that all curves have the same temporal resolution and length. We use the spline curve-fitting method²⁰ to reconstruct each DCE curve, and then resample them to have a temporal resolution of 4 s and a total length of 120 s, respectively.

DCE curve alignment

The DCE curves from voxels within the tumor volumes of all patients need to be temporally aligned for further processing. We use the arterial input function (AIF) obtained from each patient scan to align the DCE curves of voxels in the tumor volumes. First, we fit the Gamma variate function²¹ to each AIF as follows:

$$\begin{array}{ccc}& & g=\left\{\begin{array}{cc}{\left(t-t_0\right)}^{\alpha }ex{p}^{-\beta \left(t-t_0\right)}\hfill & t\ge t_0\hfill \\ 0\hfill & t<0\hfill \end{array}\right.\hfill \\ & & \mathrm{AIF}=g\left(t\right)+\lambda \underset{0}{\overset{t}{\int }}g\left(t-t^{\prime }\right)d{t}^{\prime }.\hfill \end{array}$$ (3)

All AIFs are then aligned at t₀ that is resigned to be time 0. Using the resultant time shifts, the DCE curves from each scan are adjusted accordingly. This makes all DCE curves aligned based on the start of enhancement in the arterial input function.

Projection coefficient map from Karhumen-Loeve expansion of DCE curves

Our primary goal is to extract response-predictive features rapidly and directly from the DCE curves. Hence, we expand the DCE curves using a set of basis functions, by which the coefficients of the projection vectors for each DCE curve are a unique representation in a new space. First, in the development stage, using DCE data from a sample of brain metastases (e.g., pretherapy DCE data), we construct matrix C (N × T) in which each row represents a DCE curve from one voxel in the tumors. N is the total number of voxels in all tumors and T is the number of time points in each curve. Next, we apply PCA to C to obtain a complete set of a total of T orthonormal principal components (PC_i). Then, we perform the Karhumen-Loeve transformation of each DCE curve, ΔS_N, in each voxel of the tumor to

$$\Delta S_N={\sum }_{i=1}^T{a}_{i}P{C}_i\to \Delta S_N\equiv (a_1,a_2...,a_T),$$ (4)

where a_i is the projection coefficient (cPC) corresponding to the ith principal component. Hence, each DCE curve in a tumor volume is represented uniquely by {α_i} in a T-dimensional coefficient space. However, Eq. 4 can be truncated at the first M principal components which contain 99% of energy of the original DCE curves. We will show that M is noticeably smaller than T. Decomposing DCE curves of a new tumor to the first M PCs is much faster than fitting them to a PK model.

Projection coefficient defined tumor subvolumes

Probability density function of a projection coefficient in a tumor

Each PC depicts a feature of the tumor DCE curve. Each voxel in a tumor has a unique projection coefficient on each PC. For each PC, the projection coefficients of the voxels in a tumor, which can be presented as a volumetric map of a lesion, have a distinct role in predicting the treatment response and outcome. The distribution of the projection coefficients in a large tumor is heterogeneous, similar to the physiological parameters. Hence, similar to what has been done previously for the physiological parameters,¹⁷ we analyze the distribution patterns of a projection coefficient, a_i, in the lesions, and subsequent changes during treatment. A probability density function (PDF) or histogram of a_i of a lesion is generated using a nonparametric PDF estimator. The PDF consists of 150 evenly spaced points to cover the range of a_i for all the lesions of interest. A value of the PDF at a point x, H(a_i = x), of a lesion is calculated as

$$H\left(a_i=x\right)\equiv n_i:x-\varepsilon \le a_i<x+\varepsilon ,$$ (5)

where n_i is the number of voxels within |a_i-x| < ɛ, and ɛ is a smooth factor of H and set as $\varepsilon =\frac{\sigma }{4}$, where σ denotes a standard deviation of the a_i distribution in the tumor. For each lesion, PDFs are calculated for scans at baseline [e.g., pretherapy as H_Pre(x)] and after starting therapy [e.g., at week-2 during therapy as H_2W(x)]. After H_Pre(x) is normalized to have an area under the PDF curve equal to one ($\int H\left(x\right)dx=1$), the H_Pre(x)s of all the lesions are summed to generate a pooled PDF (cPDF), in which each lesion has an equal contribution regardless of its size. Figure 2 shows an example of a typical a₁ PDF for a lesion with a volume of 17.6 cm³ at pretherapy and the pretherapy a₁ pooled PDF, respectively.

Figure 2.

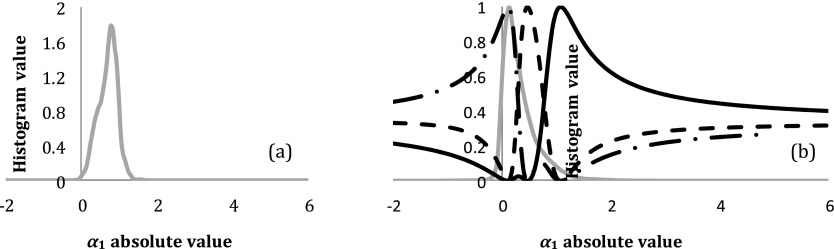
(a) An example of the pre-RT a₁ histogram of a brain metastasis with a tumor volume of 17.6 cm³. (b) The pooled PDF (light gray) of the pre-RT a₁ (cPDF₁) from all the lesions and the three probability membership functions determined by FCM clustering. The cPDF₁ is partitioned into three classes: representing low (dotted-dashed black), intermediate (dashed black), and high (solid black) a₁ classes. a₁: coefficient projection of the DCE curves on the 1st principal component.

Probabilistic membership functions of projection coefficients

Previous studies have suggested that the rCBV (or K^trans) distribution in a brain tumor is abnormal compared to normal cerebral tissue, as elevated rCBV in a subvolume of the tumor and low rCBV in another one.^{22, 23, 24} A renormalization of tumor vasculature, such as decreasing the elevated rCBV and increasing the low one, could be an indicator of a tumor response to treatment.²⁵ The DCE-derived physiological parameters (e.g., rCBV and K^trans) and projection coefficients, (a₁, a₂…, a_T), are two representations of the DCE curves. Therefore, it is reasonable to assume that a_i in the brain metastases could also distribute abnormally in contrast to normal tissue, and changes during treatment could predict tumor response to therapy. Hence, similar to what has been done for rCBV previously,¹⁷ we classify the pooled distribution of H_pre(a_i) to three classes as high, intermediate, and low a_i classes using FCM clustering analysis by minimizing the objective function J_m:

$$J_m={\sum }_{i=1}^N{\sum }_{j=1}^C{P}_j{\left(a_i\right)}^m\parallel a_i-c_j^2\parallel ,1\le m<\infty ,$$ (6)

where c_j is a prototype vector of the jth class, P_j(a_i) is a probabilistic membership of a a_i value belonging to the jth class, and m is a fuzzy exponent and chosen as 2. The probabilistic membership function, P_j(a_i), describes that a voxel having a projection coefficient a_i has a probability P belonging to a class j, which is a new representation of a a_i value of a tumor voxel (mathematically transfers the data from the a_i space into a new space).

Projection coefficient defined tumor subvolume

Our primary interest is to test if a change in a subvolume of the tumor defined by high, intermediate, or low a_i values is related to tumor treatment response. We define a subvolume (SV) of a tumor with low, intermediate, or high a_i using the probabilistic membership function P_j(a_i), and calculate a percentage change in the SV from pretherapy to after starting treatment (e.g., 2 weeks) as follows:

$$\begin{array}{ccc}& & \widehat{\Delta }S{V}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{j}}\left(a_i\right)=\frac{{\mathrm{GTV}}_{2\mathrm{W}}·\int P_j\left(a_i\right).H_{2\mathrm{W}}\left(a_i\right)d{a}_i-{\mathrm{GTV}}_{\mathrm{Pre}}·\int P_j\left(a_i\right).H_{\mathrm{Pre}}\left(a_i\right)d{a}_i}{{\mathrm{GTV}}_{\mathrm{Pre}}·\int P_j\left(a_i\right).H_{\mathrm{Pre}}\left(a_i\right)d{a}_i}·100\hfill \\ & & j\in \left\{\mathrm{low},\mathrm{intermediate},\mathrm{or}\mathrm{high}\right\},\hfill \end{array}$$ (7)

where GTV denotes the gross tumor volume. We will test whether a change in each of the first M cPC defined tumor subvolumes during RT is associated with post-RT tumor response in a group of patients, which will be described in Sec. 2F.

Tumor subvolume defined by combined projection coefficients

The overall aim of developing a prediction model for a clinical decision support system is to find a combination of factors that accurately anticipate an individual patient's outcome.²⁶ Hence, we would like to test if combining different cPCs could improve prediction for tumor response compared to using one cPC. To do so, first a joint histogram of (a₁, a₂…, a_M) of a lesion is computed, e.g., H(a₁ = x₁, a₂ = x₂, …, a_M = x_M). Then, a joint probability function, P({a_i}, {β_i}), is defined as follows:

$$\begin{array}{c}\hfill P\left(\left\{a_i\right\},\left\{{\beta }_i\right\}\right)=\frac{P_j\left(a_1\right)+{\sum }_{i=2}^M{\beta }_i{P}_j\left(a_i\right)}{1+{\sum }_{i=2}^M{\beta }_i},{\beta }_1=1,\\ \hfill \end{array}$$ (8)

where β_i is the weighting factor of each coefficient and j ∈ {low, intermediate, or high}. Applying the joint probability function to Eq. 7, a percentage change in a subvolume of a tumor defined by {a_i} classes from pretherapy to after starting treatment [e.g., 2 weeks (2W)] is given by

$$\begin{array}{ccc}& & \widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W}}\left(\left\{a_i\right\},\left\{{\beta }_i\right\}\right)\hfill \\ & & =\frac{{\mathrm{GTV}}_{2\mathrm{W}}·\int \int ...\int P\left(\left\{a_i\right\},\left\{{\beta }_i\right\}\right)H_{2\mathrm{W}}\left(a_1{a}_2...a_M\right)d{a}_1...d{a}_M-{\mathrm{GTV}}_{\mathrm{Pre}}·\int \int ...\int P\left(\left\{a_i\right\},\left\{{\beta }_i\right\}\right)H_{\mathrm{Pre}}\left(a_1{a}_2...a_M\right)d{a}_1...d{a}_M}{{\mathrm{GTV}}_{\mathrm{Pre}}·\int \int ...\int P\left(\left\{a_i\right\},\left\{{\beta }_i\right\}\right)H_{\mathrm{Pre}}\left(a_1{a}_2...a_M\right)d{a}_{1}d{a}_2...d{a}_M}·100.\hfill \end{array}$$ (9)

The weighting factor {β_i} is selected based upon the best prediction of response from a developmental dataset and is evaluated by an independent dataset. We will demonstrate the principal in Sec. 3C.

Usage phase

For a new patient scan, first, we perform preprocessing of the DCE curves and then compute the projection coefficient maps of the first M or selected principal components. Next, we compute the histograms or a joint histogram of the selected coefficients within the tumor. Then, using the probability membership function obtained in the development step, we calculate the cPC-defined tumor subvolumes by Eqs. 8 or 9. Finally, a change of the subvolume from pretherapy to during or post-therapy is determined (Fig. 3).

Figure 3.

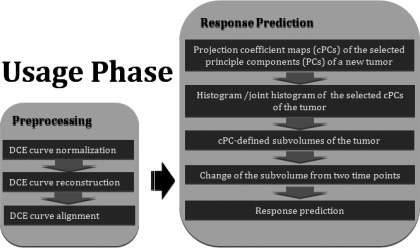
A flowchart of the procedure required for a new patient scan.

Evaluation

Endpoint

A percentage change in the gross tumor volume (GTV) from pre to post-RT was used as an endpoint for response assessment. Several patients did not have 3 or 6 months post-treatment imaging followups. For the patients in whom 3 and 6 months post-RT images were available, there were good correlations in the GTV changes between 1 and 3 months post-RT and between 3 and 6 months post-RT. Also, previous studies indicate that brain metastases exhibit little pseudoresponse and pseudoprogression one month after RT.²⁷ Therefore, we used a percentage change in the GTV from pre-RT to 1 month post-RT, $\widehat{\Delta }{\mathrm{GTV}}_{\mathrm{Pre}\to 1\mathrm{MPost}-\mathrm{RT}}$, as a measure of tumor response to therapy. From pre-RT to 1M post-RT, 16 tumors had a decrease in the GTV at least 25%, defined as responsive, 11 tumors had an increase at least 25%, defined as progressive, and the remaining 18 were defined as stable. We noticed that there were heterogeneous responses of multiple lesions from a single patient. Thus, each lesion was considered independently.

Parameter selection and evaluation

First, we ranked the priority of the candidate parameters and subvolumes by testing if the changes in $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}-\mathrm{RT}\to 2\mathrm{W},i}\left(a_i\right)$ significantly differentiated responsive tumors from combined stable and progressive ones using Mann-Whitney U Test. Considering M principal components and two independent subvolumes (only two of the three are independent) for each component, a p-value < (0.05/2M) with Bonferroni correction was considered as a significant cutoff to select the parameters. The conventional metrics, such as a percentage change in the GTV from pre-RT to 2W ($\widehat{\Delta }{\mathrm{GTV}}_{\mathrm{Pre}\to 2\mathrm{W}}$) and a change in the mean rCBV values of a tumor from pre-RT to 2W ($\widehat{\Delta }{\mu }_{\mathrm{Pre}\to 2\mathrm{W}}\left(\mathrm{rCBV}\right)$), were not considered as the candidate parameters in our model, and thus not used for multiple comparison justification. Next, we performed univariate analysis to evaluate sensitivity and specificity of the selected significant metrics identified in the previous test for predicting responsive tumors using Receiver Operating Characteristic analysis (software package ROCKIT).²⁸ Also, we compared these newly developed metrics with the conventional metrics including a percentage change in the GTV from pre-RT to 2W, $\widehat{\Delta }{\mathrm{GTV}}_{\mathrm{Pre}\to 2\mathrm{W}}$, and a change in the mean rCBV values of a tumor from pre-RT to 2W, $\widehat{\Delta }{\mu }_{\mathrm{Pre}\to 2\mathrm{W}}\left(\mathrm{rCBV}\right)$, for predicting post-treatment response. The significant difference of the area under ROC curves (AUC) between the metrics was compared by t-test, for which the standard error and the difference between the two AUCs were calculated by the method proposed by DeLong et al.²⁹ To create the tumor subvolume defined by combining more than one cPC, we used the maximum AUC to determine the {β_i}.

RESULTS

Principal components

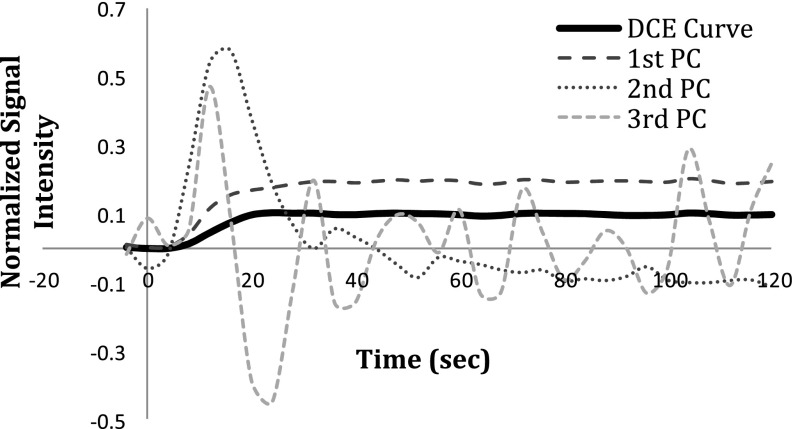
PCA revealed that the first three PCs comprised more than 99.99% of the energy of the DCE curves of brain metastases, of which the first component contributed approximately 99.8%, while the second and third components had 0.08% and 0.02% contributions, respectively (see Fig. 4). The first component (the predominant component) is highly related to the area under each DCE curve with the cross correlation coefficient of 0.99. Figure 5 shows the heterogeneous distributions of the first three cPC maps of a brain metastasis, indicating that an average cPC in the tumor would not be sensitive to a heterogeneous change. Therefore, the analysis described in Sec. 2 was applied to the histograms of the first three cPCs in a tumor to determine the subvolume of the tumor with a given class.

Figure 4.

An example of a typical AIF_max-normalized DCE curve of a voxel in a brain metastatic lesion and the first three principle components (PCs) resulted after applying PCA to the DCE-matrix. The coefficient map achieved by projecting the DCE curve onto the first component (the predominant component) is related to the area under the DCE curve (see the text for more details).

Figure 5.

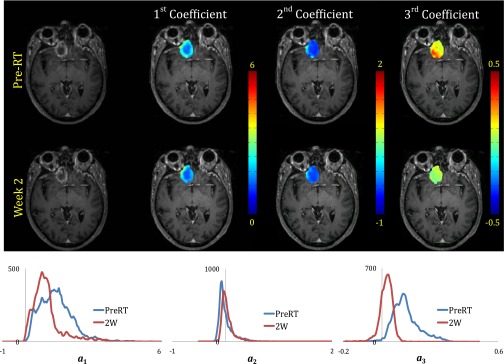
Distribution patterns and histograms of the first three projection coefficient maps for a responsive brain metastasis (from patient #19) overlaid on T1-weighted images at pre-RT and week 2 after start of whole brain radiation therapy.

Association of the cPC-defined tumor subvolumes with response

Associations of the changes in the first three cPC-defined brain metastases subvolumes with high, intermediate, or low coefficients from pre-RT to 2W with the tumor response to treatment are given in Table 3. Since we only compare the first three components, a p-value < 0.01 was considered as significance to select the candidate parameters. Median changes of −63.7 (range:-95.5 to 123), −13 (range: −98 to 198.4), and 44 (range: −42 to 444.3) were observed in the subvolume of the tumor with high-a₁ (the most dominant component) from pre-RT to 2W for the responsive, stable, and progressive lesions, respectively. We found that for the responsive group, a percentage decrease in the high-a₁ subvolumes of the tumors from pre-RT to 2W differed significantly from the group combining progressive and stable tumors (p < 0.0017), Table 3. We observed a similar but weaker trend for the high-a₂ subvolume (p < 0.07). Furthermore, a percentage decrease in the low-a₃ subvolume of the tumor was associated with tumor response (p < 0.01). A percentage decrease in the subvolumes defined by combining the high-a₁ and low-a₃ classes from pre-RT to 2W revealed that adding a₃ improved the statistical significance for differentiating the responsive tumor from the group of stable and progressive lesions compared to either coefficient alone but a₂ did not add discriminatory information. As a postanalysis, the comparisons between other lesion groups are also given in Table 3.

Table 3.

Differences between responsive, stable and progressive brain metastases using cPC defined tumor subvolume, physiological defined tumor subvolume and conventional metrics

			Group of lesions
			Analysis	Post Analysis
			R vs. {S & P}	R vs. S	S vs. P	R vs. P
	Metric				p-value
Projection Coefficient Defined Tumor Subvolumes	$\widehat{\Delta }S{V}_{Pre\to 2W,j}\left(a_1\right)$	j = low	0.5937	0.8766	0.7024	0.3878
		j = intermediate	0.0773	0.2477	0.3339	0.0457
		j= high	0.0017**	0.0199*	0.1321	0.0015**
	$\widehat{\Delta }S{V}_{Pre\to 2W,j}\left(a_2\right)$	j = low	0.4843	0.7431	0.7702	0.3359
		j = intermediate	0.5774	0.8766	0.2002	0.1596
		j= high	0.0661	0.3979	0.0561	0.0096**
	$\widehat{\Delta }S{V}_{Pre\to 2W,j}\left(a_3\right)$	j= low	0.0094**	0.0068**	0.2002	0.1323
		j = intermediate	0.4133	0.7693	0.2909	0.2083
		j = high	0.8403	0.1522	0.0143	0.1088
	$\widehat{\Delta }S{V}_{Pre\to 2W,high,low}\left(a_1,a_3,0.3\right)$^		0.0005	0.0018	0.3568	0.0053
Physiological Defined Tumor Subvolumes	$\widehat{\Delta }S{V}_{Pre\to 2W,high}\left(rCBV\right)$		0.0057**	0.0338*	0.3568	0.0072**
	$\widehat{\Delta }S{V}_{Pre\to 2W,high}\left(k^{trans}\right)$		0.4992	0.6663	0.0162*	0.0406*
	$\widehat{\Delta }S{V}_{Pre\to 2W,high,high}\left(rCBV,k^{trans},0.6\right)$		0.0015**	0.0199*	0.0687	0.0012**
Conventional Metrics	$\widehat{\Delta }{\mu }_{Pre\to 2W}\left(rCBV\right)$		0.0066**	0.0049**	0.2336	0.1088
	$\widehat{\Delta }{\mu }_{Pre\to 2W}\left(k^{trans}\right)$		0.8775	0.5233	0.1704	0.5704
	$\widehat{\Delta }GT{V}_{Pre\to 2W}$		0.0124*	0.1086	0.0653	0.0039**

¹Abbreviations: GTV = gross tumor volume; R = responders; S = stables; P = Progressive; cPC = projection Coefficient; ^ The optimum value of β₃ is 0.3, see the results of the ROC analysis.*: P<0.05;**: P<0.01. The candidate subvolume for each principle component is highlighted.

For comparison, the results of the rCBV-K^trans analysis that were reported previously¹⁷ and other conventional metrics are included in Table 3. In summary, we found that the percentage decrease in the high-rCBV subvolumes of the brain metastases from pre-RT to 2W of the responsive group differed significantly from the progressive group (p < 0.0072) and from a group combining progressive and stable tumors (p < 0.0057), but not from the stable group (p = 0.033) (Table 3). The percentage decrease in the brain metastases subvolumes defined by both the high rCBV and high K^trans classes from pre-RT to 2W differentiated the three groups with improved statistical significances, compared to using either variable alone. Specifically, the responsive group significantly differed from the progressive group (p = 0.0012) and from the group combining the progressive and stable tumors (p = 0.0015). In this case, median changes of −47.8 (range: −88.5 to 213.84), −2 (range: −90 to 959.42), and 46 (range: −22 to 254.5) were observed in the subvolume of the tumor with high-rCBV and K^trans from pre-RT to 2W for the responsive, stable, and progressive lesions, respectively. The statistical analysis regarding the conventional metrics, such as changes in the mean of the tumor rCBV and K^trans and the GTV from pre-RT to 2W are also given in Table 3. These data show that both physiological-defined and cPC-defined subvolumes of a brain metastasis achieve a similar level of statistical significance in differentiation of responsive, stable, and progressive brain metastatic lesions.

Predictive values of the cPC-defined tumor subvolumes

We explored the predictive value of the decrease in the subvolumes of the brain metastases defined by the cPCs from pre-RT to 2W for predicting responsive tumors post-RT, and compared their performance with the decrease in subvolumes of the tumors defined by the high rCBV and high K^trans and two conventional metrics. The ROC analysis showed that the AUCs were 0.83 ± 0.06(±SEM), 0.77 ± 0.07, 0.80 ± 0.07, 0.70 ± 0.08, 0.67 ± 0.08, and 0.56 ± 0.09 for $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{high}}\left(a_1\right)$, $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{low}}\left(a_3\right)$, $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{high}}\left(\mathrm{rCBV}\right)$, $\widehat{\Delta }{\mu }_{\mathrm{Pre}\to 2\mathrm{W}}\left(\mathrm{rCBV}\right)$, $\widehat{\Delta }{\mathrm{GTV}}_{\mathrm{Pre}\to 2\mathrm{W}}$, and $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{high}}\left(K^{\mathrm{trans}}\right)$, respectively (Fig. 6), indicating the high-a₁ defined subvolume of the tumor had the best performance among the tested variables for predicting responsive tumor. The subvolumes defined by the high-a₁ and low-a₃ classes with the weighting factor = 0.3, determined by empirical evaluation of the AUCs (right panel of Fig. 6), resulted in the largest AUC, 0.88 ± 0.05. The subvolumes defined by the high-rCBV and high-K^trans classes with the weighting factor = 0.6 resulted in the AUC of 0.86 ± 0.06.

Figure 6.

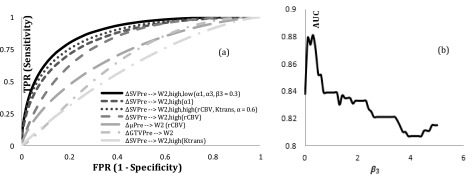
(a) ROC curves of the metrics listed in Table 3 for predicting responsive tumors; (b) AUC vs β₃ in Eq. 9. FPR: False Positive Rate TPR: True Positive Rate; AUC: Area Under Curve.

The statistical analysis of the pairwise ROC curves revealed that $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{high},\mathrm{high}}\left({\alpha }_1,{\alpha }_3,0.3\right)$ was a predictor slightly but not significantly better than $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{high}}\left(a_1\right)$, and $\widehat{\Delta }{\mathrm{SV}}_{\mathrm{Pre}\to 2\mathrm{W},\mathrm{high},\mathrm{high}}\left(\mathrm{rCBV},k^{\mathrm{trans}},0.6\right)$ (p = 0.1 and p = 0.4, respectively). However, it was a predictor significantly better than $\widehat{\Delta }{\mu }_{\mathrm{Pre}\to 2\mathrm{W}}\left(\mathrm{rCBV}\right)$ and $\widehat{\Delta }{\mathrm{GTV}}_{\mathrm{Pre}\to 2\mathrm{W}}$ (p = 0.0463 and p = 0.02), respectively. Finally, the predictive value of $\widehat{\Delta }{\mu }_{\mathrm{Pre}\to 2\mathrm{W}}\left(\mathrm{rCBV}\right)$ was slightly but not significantly better than $\widehat{\Delta }{\mathrm{GTV}}_{\mathrm{Pre}\to 2\mathrm{W}}$ (p < 0.4).

Probability membership function maps

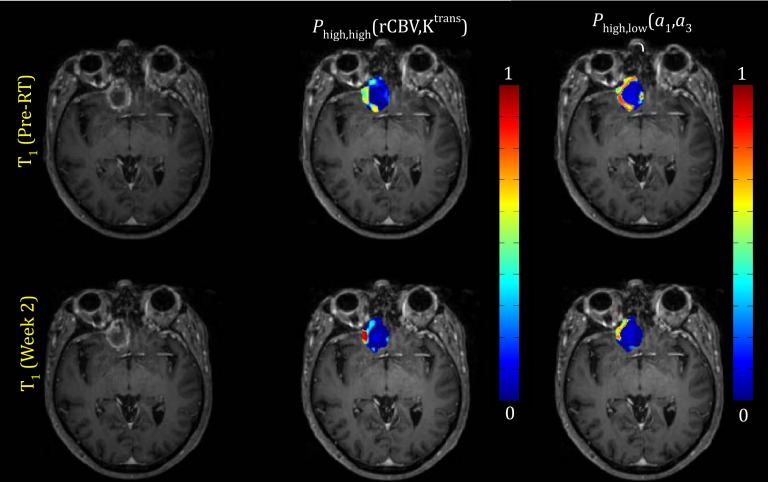
Examples of maps of the first coefficient maps and the corresponding histograms, and the probability functions belonging to the classes of high-rCBV and high-K^trans and the classes of high-a₁ and low-a₃, of a responsive lesion pre-RT and at 2W are shown in Figs. 57, respectively. For this lesion, the voxel probability functions belonging to the high rCBV-K^trans class decreased about 47% from pre-RT to 2W. A similar pattern was also observed for the probability functions belonging to the class of high-a₁ and low-a₃.

Figure 7.

Top row: Pre-RT T₁ weighted image (left), probability function map of the class with the high-rCBV and high K^trans pre-RT (middle) and probability function map of the class with the high-a₁ and low-a₃ pre-RT (right). Bottom row: the similar images at 2W. This lesion is responsive. The images are from patient #19 in Table 3.

DISCUSSION AND CONCLUSION

In this paper, we proposed a general framework based on PCA and a pattern recognition technique for directly delineating the response-driven subvolume of brain metastases from the DCE-MRI data. We compared the predictive values of the PC-defined tumor subvolume with the physiological-parameter-defined one [based upon regional cerebral volume (rCBV) and K^trans] in the patients treated with whole brain radiation therapy. We found that the two approaches could predict the tumor response to therapy similarly while the PC-defined subvolume can be delineated more rapidly, which is required for supporting clinic decision making. In overall, our findings indicate that the projection coefficient maps from the first three PCs may contain almost all response-related information of the DCE curves. Our further investigation revealed that the first coefficient that is related to the area under the DCE curve is the main factor to determine the response (AUC = 0.83), while the third component could have complimentary information (AUC = 0.88). Our approach had the potential to be an effective tool for supporting real-time decision making.

Our proposed approach to analyze the DCE-MRI data has several advantages compared with the other model-free techniques which are based on factor analysis,^{8, 9} ICA,¹⁰ or extracting characteristic features, such as time to peak or maximum enhancement, from the DCE curves.³⁰ Foremost, for each tumor type or body site, a set of PCs used in calculation of the coefficient maps can be achieved offline and are available before a new patient is scanned. Also, we address the heterogeneous distributions of the principal component coefficients within a tumor by using fuzzy clustering analysis to determine the probability membership functions of classes that the principal component coefficients belong to. Again, this relationship is established offline. Hence, for a new patient scan, computations for the DCE curves only involve in preprocessing the DCE curves, projecting them onto a couple of predetermined principal components, calculating the histograms of the two projection coefficients in the tumor, and computing the metric given in Eq. 9. Computing a couple of principal component coefficients is a much faster process than fitting PK modeling. Our model can be updated when the new patients’ data are accumulated, including PCs, the probability membership functions, and the predictive statistics given in Fig. 6a. Also, realigning and reconstructing all DCE curves from all tumors in the DCE-matrix to determine the PCs has the potential to overcome the interscan variation in the DCE time series. In addition, the set of projection coefficients obtained for each curve is a complete representation of the curve in an N-dimensional feature space wherein the data reduction is performed with the best approximation and without noticeable concerns regarding the information loss. As shown, almost all response-related information is derived from the first three components. However, for the approaches based on feature extraction, there is no guarantee that the computed features incorporate all relevant information for therapy assessment.

One very important note regarding the proposed methodology is that it is critical to use the arterial input function to normalize the DCE curves. Our investigations showed the enhancement peak of AIF is not linearly correlated with the enhancement peaks of the DCE curves of other tissues, such as normal white matter, gray matter, and even veins, indicating intrapatient variation on the peak enhancement. Also, the enhancement peak of AIF manifests great interpatient variation. It is worthwhile to point out that the projection coefficients (e.g., also first three components) and subsequent delineated subvolume determined by our approach have great tolerances on the temporal resolution and total acquisition time of the DCE curves, while the image acquisition parameters may affect the accuracy of the physiological parameters derived from the PK models.³¹ Hence, we may be able to estimate the projection coefficient maps of a tumor accurately using a lower temporal resolution, by which a high spatial resolution can be achieved to delineate the tumor heterogeneity. However, it is worthwhile to mention that due to the temporal resolution variation in the data, we had to use a spline-fitting to standardize the DCE curves in the DCE matrix. But, any manipulation of the original datasets may introduce errors and bias, and may affect the final results. Hence, an optimized and standardized protocol in terms of spatial and temporal resolution could decrease the errors in the dataset and improve the statistical power of the evaluation of response. Also, using a standard acquisition protocol could avoid the additional preprocessing of the data in the PK model-free approach, which is important using response assessment during the course of radiation therapy for adaptation treatment guidance. In the adaptation treatment setting, it requires to develop fully automated, fast, and robust algorithms to compute the quantitative response metric. Further development of such an algorithm and comparing its performance with the PK-model based metric are ongoing. In addition, in our calculation, we neglected T₁₀ in normalization of the DCE data. We recognize that T₁₀ can vary within the tumor volume. However, the influence of T₁₀ on identifying a robust biomarker for therapy assessment needs to be further verified.

In summary, in this paper, we proposed a general framework for directly analyzing the DCE-MRI data to delineate the response-driven subvolume of a brain metastatic tumor. However, this approach needs to be further validated using an independent and larger dataset. Also, it could be extended and recalibrated to other tumor types, e.g., glioblastoma, for early assessment of tumor response to therapy.