Design of Implementation Studies for Quality Improvement Programs: An Effectiveness–Cost-Effectiveness Framework

Abstract

Translational research applies basic science discoveries in clinical and community settings. Implementation research is often limited by tremendous variability among settings; therefore, generalization of findings may be limited. Adoption of a novel procedure in a community practice is usually a local decision guided by setting-specific knowledge. The conventional statistical framework that aims to produce generalizable knowledge is inappropriate for local quality improvement investigations. We propose an analytic framework based on cost-effectiveness of the implementation study design, taking into account prior knowledge from local experts. When prior knowledge does not indicate a clear preference between the new and standard procedures, local investigation should guide the choice. The proposed approach requires substantially smaller sample sizes than the conventional approach. Sample size formulae and general guidance are provided.

It is common in implementation studies to adapt existing procedures, or to improvise new procedures, to accommodate local conditions in a specific community care setting. From an evidence-based principle, these decisions can often be informed by conducting a local investigation or quality improvement study to evaluate the pros and cons for viable options under consideration. For example, within the primary care setting and emerging medical home practices, primary care clinics may implement focused procedures to engage high-risk, high-complexity patients with emotional and medical conditions such as depression and diabetes. Such procedures might include focused physical and emotional health screening and multidisciplinary health care delivery procedures. Before replacing the existing intake and care delivery procedures, the clinic may benefit from pilot testing the new procedure to examine its potential utility and impact on patient care. The results of this pilot investigation can then be used to inform the decision (which intake procedure to use) for future patients including a broader “roll-out” of the successful procedures.

The primary purpose of these local investigations is to produce local knowledge (such as which intake procedure is more effective for the specific clinic) to inform local implementation decisions. The pilot testing of these procedures is not intended to produce generalizable knowledge that can be applied universally to other care settings. This underlines the difference between implementation science that aims to produce generalizable knowledge¹ and quality improvement projects that aim to produce local knowledge with a focus on an organization’s own delivery system and process.² As such, quality improvement projects for local knowledge do not meet the criterion for human participants research as defined by the Office for Human Research Protections, the federal agency with oversight over human participants protection and institutional review boards. Research means a systematic investigation, including research development, testing, and evaluation, designed to develop or contribute to generalizable knowledge.³

To avoid the confusion with human participants research that aims to produce generalizable knowledge, we use the term local investigation to highlight the distinction, and also to suggest that those investigations might qualify for exemptions from certain human participants regulations. Local investigations often deal with components (“nuts and bolts,” such as a specific intake procedure) of an overall implementation program. Making appropriate nuts-and-bolts decisions is important for the successful assemblage of the overall implementation “engine.” A specific implementation engine might consist of numerous nuts and bolts. Therefore, it is conceivable that multiple local investigations might be conducted in an implementation program for a specific care setting, each addressing the needs for a specific component of the engine.

A variety of designs can be used for local investigations, including randomized designs and nonrandomized quasiexperimental designs.⁴ To illustrate the difference between local investigations that aim primarily to produce local knowledge, and the usual research studies that aim primarily to produce generalizable knowledge, we focused on randomized designs for this type of quality improvement project.

CONVENTIONAL DESIGN FRAMEWORK

Research studies are usually designed to achieve a prespecified statistical accuracy, such as a 5% type I error rate and an 80% power. For example, when one is comparing the health outcomes of a new treatment against the standard by using a 2-sided t test, the required sample size to detect a standardized effect size of 0.25 is 500, with 250 randomized to each arm. This conventional approach is inappropriate for quality improvement projects for various reasons.

First, research studies are usually designed under the assumption of a very large patient horizon (the total number of patients eligible for the treatment decision being studied—i.e., the population size).^5,6 Usually, if a new pharmaceutical product is found to be efficacious and safe, and receives approval from the Food and Drug Administration, there are millions of patients eligible for the new treatment. Therefore, the stake is enormous and calls for a high level of accuracy in the research studies to protect the welfare for future patients. Because the number of future patients usually dominates the number of patients participating in a research study, even for a large phase 3 trial, the emphasis is usually placed on the welfare for future patients. The ethical cost to the trial participants (such as the chance to be assigned to the inferior treatment option) is usually small compared with the improved outcomes for future patients.

The statistical framework is very different for quality improvement investigations that aim primarily to produce local knowledge for local consumption. For a primary care clinic with a total of 500 patients comorbid with depression and diabetes, a conventional design with 5% type I error and 80% power will need to enroll the entire patient population into the trial, leaving no patients to “consume” the findings from the trial. For a quality improvement program that aims to optimize the welfare for the 500 patients in the local clinic, this conventional design is obviously inappropriate. The finite nature of the patient horizon needs to be taken into account in the design of these local investigations to achieve the optimal welfare for the entire patient population at the local clinic. In particular, unlike in the usual research studies, the ethical cost to the trial participants is no longer small compared with the welfare for future patients from the same clinic, and needs to be taken into consideration explicitly, along with improved outcomes for future patients from the same clinic. This aspect is in line with the patient-centered approach in quality improvement.⁷

Second, local experts in the specific setting may have prior knowledge about the specific procedures under consideration. To reach appropriate decisions, it is important to take this prior knowledge into consideration. It is conceivable that sometimes the prior knowledge is strong enough to indicate that an empirical investigation is not necessary—say, if the local experts have compelling reasons to believe that the new intake procedure is far superior to the standard intake procedure. At the same time, it is also important to identify the situations with ambivalent prior knowledge, so that an appropriately designed local investigation will lead to better patient welfare than relying on the prior knowledge alone.

Third, the novel procedure under investigation is expected to lead to improved health outcome, but the cost of the procedure is not usually taken into account in the design of the usual research studies. For example, a slightly less effective but much cheaper procedure may allow the community to compensate through the cost saved. Conversely, a more expensive or labor-intensive procedure may prove to be cost-effective if the outcome is far superior and worth the extra cost.

Finally, new procedures may emerge on a regular basis, either from local sources such as new innovations, or from external sources such as state and federal agencies. Therefore, it is important to take into account the “shelf life” for a new procedure. It is imperative that local investigations be conducted over a short period of time to stay relevant, before the shelf life for the procedures under investigation runs out.⁸ A timely process, along with a patient-oriented approach, is in fact one of the aims for quality improvement projects in accordance with the Institute of Medicine.⁷

In light of these considerations, the purpose of this article is to revisit the fundamental issues of sample size considerations for local investigations with a finite patient horizon (i.e., a population with a finite number of patients available for treatments in the local clinical setting).^5,6,9 Our specific goal is to introduce a cost-effectiveness framework for quality improvement. The consideration of cost-effectiveness in sample size determination is not new^10—12; however, the recent works are motivated by designing studies that assume a large, or essentially infinite, patient horizon. Meanwhile, few consider statistical methods for comparative studies in a finite patient horizon,^13,14 but none considers cost-effectiveness analysis in the context of finite horizon studies.

AN EFFECTIVENESS–COST-EFFECTIVENESS FRAMEWORK

We describe an effectiveness–cost-effectiveness framework for the design for quality improvement studies. We begin with a cost-effectiveness framework, of which the effectiveness framework is a special case.

The cost-effectiveness consideration provides a useful framework to formulate the statistical issues involved in designing local investigations for implementation studies. Decision-making based on a cost-effectiveness analysis depends on 3 parameters. The first parameter, defining the effectiveness component, is the effect size (denoted by δ) of the new procedure (relative to the standard procedure) on patient health outcome, such as the mean difference of depression symptoms (e.g., Patient Health Questionnaire-9) between cognitive–behavioral therapy supplemented with enhanced care management and cognitive–behavioral therapy with standard delivery.¹⁵

Two other parameters define the cost components—specifically, the additional cost (denoted by c) of the new procedure relative to the standard and the value (denoted by b) per unit increase in the health outcome. With these 3 parameters, the incremental net benefit (INB) of the novel procedure is defined as INB = bδ − c, where the term bδ represents the value attributable to the effectiveness δ; therefore, the difference, bδ – c, represents the net benefit that adjusts the value of the effectiveness, bδ, by the cost, c, needed to produce the effectiveness. The new procedure is defined to be more cost-effective than the standard procedure if the INB is positive.

The value parameter b can often be approximated by the cost reduction because of reductions in the subsequent hospitalization and other expensive medical procedures, by using secondary data sources in a decision analysis model.¹⁶ The procedure cost parameter c can often be assessed prospectively with existing information about the level of efforts required for the novel procedure.

We assume that the value parameter b is known to be positive (i.e., b > 0) on the basis of the interpretation that the improved health outcome has a positive value. We do not impose any restrictions on the procedure cost parameter c, allowing all possible scenarios: c > 0; c < 0; and c = 0.

In the first scenario, the novel procedure enhances the standard procedure for an extra cost. Under this scenario, the value of the improved health outcome, bδ, needs to offset the positive procedure cost, c, for the new procedure to be cost-effective compared with the standard procedure. Under the second scenario, the procedure cost is negative (i.e., the novel procedure might be a way to streamline the standard procedure to simplify its delivery and save cost). This scenario may occur in the context of noninferiority studies where the goal is to show a new, less expensive approach is not much inferior than the existing approach (e.g., group therapy vs individual therapy). Under this scenario, the effectiveness parameter δ can be slightly negative (i.e., the new procedure can be slightly less effective than the standard procedure) and the new procedure still remains cost-effective compared with the standard procedure if the negative health benefit, bδ, is smaller in magnitude than the cost savings, c.

This cost-effectiveness framework simplifies to an effectiveness framework when the procedure cost parameter c is zero. This scenario can be interpreted in 2 ways. First, in the cost-effectiveness framework, this scenario assumes that the procedure cost is neutral between the new and standard procedures: the 2 procedures are equivalent in cost; therefore, the cost-effectiveness is determined by the value of the improved health outcome, bδ. Alternatively, this scenario can be interpreted as an effectiveness framework, in which we only consider effectiveness, and ignore any difference in procedure costs.

For most purposes, the design of the local investigation depends on the cost parameters b and c only through the cost-to-benefit ratio, λ : = c/b, which measures the procedure cost parameter c relative to the value parameter b. In other words, the design remains invariant if both b and c are multiplied or divided by the same constant, say, when the unit of cost and value is changed from US dollar to British pound.

The primary objective of the local investigation is to assess the effect size δ of the new procedure compared with that of the standard procedure. We assume in the next section that the cost parameters b and c are known a priori. It is of course possible to address the uncertainty about the cost parameters with sensitivity analysis.

EVIDENCE-BASED ADOPTION OF NOVEL PROCEDURES

In practice, the adoption of new procedures within individual clinics often depends on subjective judgment and varies from community to community. Some clinics always stay with the standard approach (often described as late adopters), whereas some always adopt the novel procedure (early adopters). As an alternative, we propose an evidence-based adoption (EBA) strategy specified as follows. Suppose in a community with a patient horizon N, we conduct a local investigation and randomize n patients to the new procedure and n patients to the standard procedure, and perform a statistical test for the null hypothesis, H₀ : INB ≤ 0, versus the alternative hypothesis, H_A : INB > 0, by using a 1-sided t test. More specifically, let D_n denote the mean health outcome in the n patients in the experimental arm minus that of the standard arm. Then the null hypothesis is rejected if

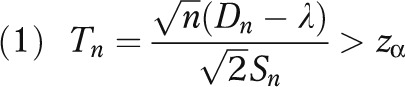where z_α is the upper α-critical value from the standard normal distribution (e.g., z_α = 1.96 when α = 0.025) and S_n is the pooled sample standard deviation of the observed health outcomes. If H₀ is rejected, the new procedure will be adopted for the remaining N – 2n patients.

Conversely, if H₀ is accepted, the remaining N – 2n patients will receive the standard procedure.

This EBA strategy can be viewed as a 2-stage procedure, with the 2n study patients being the trial stage and the remaining N – 2n patients being the “consumption” stage where the local knowledge obtained from the trial stage is consumed. We assume that the 2n study patients are sampled randomly from the pool of N eligible patients in the specific clinic. For some procedures, it is possible to select study patients randomly from the roster of patients eligible for the procedure by using electronic health records. For some procedures, patient selection might be made by selecting consecutive patients who present at the clinic. In this situation, we need to make an additional assumption of stationarity (i.e., the order in which patients present at the clinic is random); therefore, patients who present early (and are thus enrolled into the local investigation) are representative of patients who present late (and are thus reserved for the “consumption” phase).

To assess the relative merits of various strategies, we take the late-adopter as the reference, and compare other decision strategies to this benchmark. The total net gain for the late-adopter is thus defined to be G₀ = 0, as there is no difference in the total net gain when one compares the late adopter to itself as the reference. For the early adopter, the total net gain relative to late adopter is G₁ = N(bδ − c).

Although the effect size δ is unknown, some prior knowledge about δ is usually available, based on the intimate knowledge of local experts about the community. We assume that the prior knowledge about δ, and the uncertainty in the prior knowledge, are represented in the form of a normal distribution with mean δ₀ and variance τ². The elicitation of personal belief has received much attention in the Bayesian literature since the seminal work of Savage¹⁷ with accelerating research in clinical trials.^18—20 In the current setting, the hyperparameters δ₀ and τ² can be interpreted as the mean and variance of the prior belief about δ among local experts. After the values of δ₀ and τ² are elicited, the expected net gain of the early adopter will be evaluated as E(G₁) = N(bδ₀ − c).

If the only options are to choose between the early adopter and the late adopter, the early adopter is justified if E(G₁) > 0; and conversely for the late-adopter if E(G₁) < 0. As such, we define the cost-effectiveness equipoise to hold if bδ₀ − c = 0 (i.e., δ₀ =  λ).

Under cost-effectiveness equipoise, there is no preference among the local experts between early adoption and late adoption, because E(G₁) = E(G₀) = 0. The incremental benefit of the new procedure (bδ₀) is offset by the incremental cost (c). The cost-effectiveness equipoise defined here simplifies to the usual equipoise based only on the consideration of effectiveness, 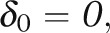when the cost parameter c is zero.

The 2-stage EBA strategy can outperform both the early adopter and late adopter, indicating that the local investigation is informative and leads to better decisions than relying entirely on the local experts’ prior knowledge. To be more precise, if the effect size δ were known, the total net gain for the evidence-based adopter (relative to the late-adopt strategy) would be equal to

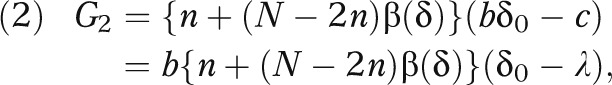where β(δ) is the power function of the t test given in equation 1 under the effect size δ and is an increasing function of δ. With a normal prior distribution for δ, the expected net gain of the EBA strategy is given by

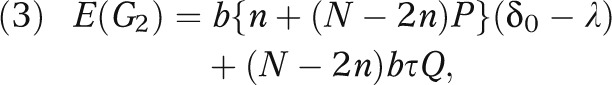where

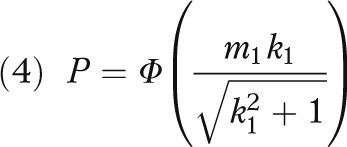and

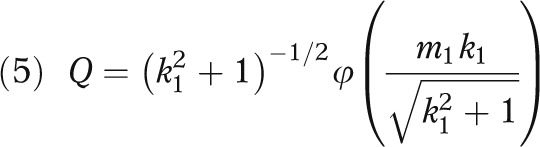with

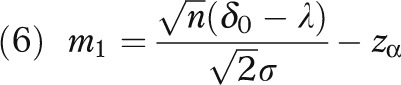and

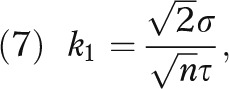σ is the standard deviation of the health outcome, and Φ and φ respectively denote the distribution function and density function of the standard normal distribution. (The derivation for equation 3 is given in the technical appendix, available as a supplement to the online version of this article at http://www.ajph.org.)

Note that the expected net gain (equation 3) depends on the prior mean δ₀ via its relative location to λ, i.e., δ₀ - λ. It is also important to note that Q > 0. Therefore, under cost-effectiveness equipoise (i.e., δ₀ =  λ), the evidence-based adopter outperforms both the early adopter and the late adopter in terms of expected net gain:

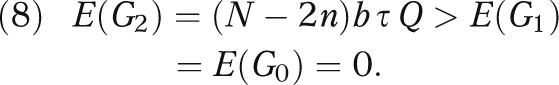In other words, under equipoise, some local investigation (regardless of the sample size n) is always better than no local investigation, in terms of the cost-effectiveness of the overall strategy. This finding is consistent with the intuition that, under equipoise, the prior knowledge does not provide an obvious way to choose between the new procedure and the standard procedure, therefore suggesting that a local investigation should be conducted to guide the choice.

GENERAL DESIGN GUIDELINES

The 2-stage EBA strategy is specified by 2 design parameters, the sample size n and the critical value z_α. The conventional statistical approach usually determines these 2 parameters with respect to a type I error rate of 2.5% or 5%, and a power of 80%. However, as illustrated earlier, this design may lead to an inappropriate sample size for local investigations. We propose a design approach to determine n and z_α jointly so as to maximize the expected net gain E(G₂) defined in equation 3 for the EBA strategy, in comparison with the expected net gain E(G₀) and E(G₁) for the late and early adopter. Our main results follow.

Result 1

For any given n, the critical value that maximizes E(G₂) is given by

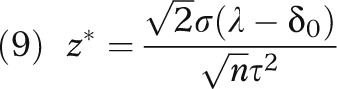(The derivation for result 1 is given in the technical appendix, available as a supplement to the online version of this article at http://www.ajph.org.)

It is noteworthy that, under equipoise, the optimal critical value z* equals 0 and corresponds to a 50% 1-sided type I error rate. This stands in stark contrast with the conventionally conservative hypothesis testing approach.

Alternatively, if the local experts have a slight optimism about the cost-effectiveness of the new procedure in that the previous INB is positive, δ₀ – λ > 0, then, the optimal z* is negative, corresponding to a 1-sided type I error rate larger than 50%. Intuitively, because the local experts are already in favor of the new procedure, they need only to confirm their prior knowledge in the local investigation.

On the other hand, if the local experts have a slight pessimism about the new procedure (i.e., δ₀ – λ < 0), then the optimal z* is positive, corresponding to a 1-sided type I error rate smaller than 50%. This is reasonable as the previous pessimism indicates that the study needs to show stronger evidence against the null hypothesis than the evidence required under equipoise to overcome the initial pessimistic assumption. The usual design with a 5% type I error rate corresponds to a rather strong pessimism, which might not be consistent with the prior knowledge for the local experts.

Result 2

Under cost-effectiveness equipoise (i.e., bδ₀ – c = 0), the sample size that maximizes E(G₂) can be evaluated as

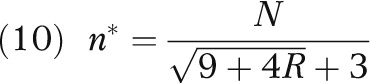where R = N τ² /(2 σ²). (The derivation for result 2 is given in the technical appendix, available as a supplement to the online version of this article at http://www.ajph.org.)

As a simple consequence to the fact that R > 0, the optimal sample size n* is less than N/6. In other words, a general design guideline is not to randomize more than one third of the patients during the trial phase.

Furthermore, it is an easy consequence to result 2 that the optimal expected net gain is equal to

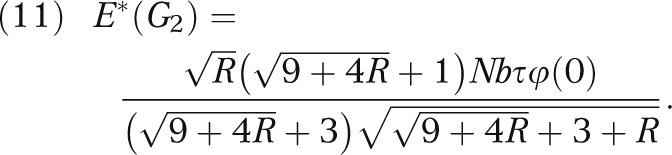Note that E*(G₂) approaches zero when R approaches zero. In other words, if there is a strong prior knowledge (small τ) or if the empirical observations are uninformative (large σ), the potential gain of the local investigation is small, albeit positive. Conversely, if there is a weak prior knowledge (large τ) or if the empirical observations are highly informative (small σ), the potential net gain can be substantial.

Colton¹³ derived the same expression as equation 10 under effectiveness-only equipoise with c = 0. Result 2 thus extends Colton’s result to the general cost-effectiveness framework. As there is no closed-form expression for the optimal sample size when the prior knowledge deviates from cost-effectiveness equipoise, we provide numerical illustrations in the next section to demonstrate that the optimal sample size n* decreases as the prior knowledge deviates from equipoise.

NUMERICAL ILLUSTRATIONS

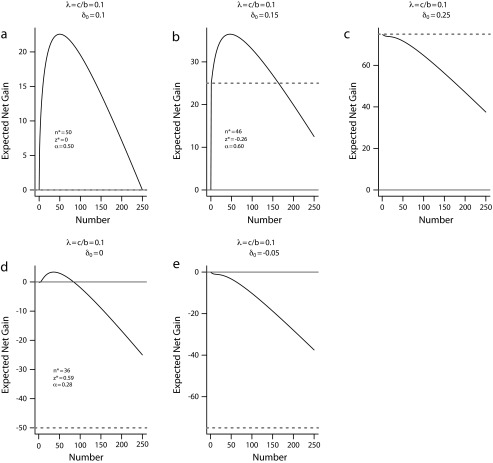
Consider a community with N = 500 patients. The sample size per arm of the local investigation can range from n = 0 (indicating no local investigation) to n = 250 (placing all eligible patients into the trial without a consumption stage). We assume that b = 1 and c = 0.1, so that the cost-to-benefit ratio λ = 0.1, and that τ = 0.2 and σ = 1. Figure 1 plots the expected net gain for the EBA strategy, E(G₂) in equation 3, for each possible sample size n and the corresponding optimal critical value z* defined in equation 9 under a variety of prior mean δ₀. For comparison, we also show the expected net gain for the late-adopter, E(G₀) = 0, and that for the early adopter E(G₁).

FIGURE 1—

Expected net gain for the evidence-based adoption strategy E(G₂) versus sample size at optimal z* under a variety of prior mean δ₀.

Note. The gray solid horizontal line indicates the expected net gain for late adopter E(G₀); the gray dotted line for early adopter E(G₁).

Figure 1a plots the expected net gain of the EBA plan against sample size under cost-effectiveness equipoise, δ₀ = 0.1 = λ. This figure shows that the EBA strategy has a positive expected net gain for all n, and is thus superior to both the late-adopt strategy and the early- adopt strategy (shown as the gray solid line and the gray dotted line, which coincide on the bottom of this plot). The figure also shows that the expected gain attains its maximum of 22.6 when n* = 50, with z* = 0 and α* = 50% according to the formula in equation 9. It thus provides a concrete recommendation of sample size for the local investigation, placing 100 patients into the trial, with 50 in each arm, and leaves 400 patients to consume the local knowledge gained from the trial.

Figure 1b presents results for a slightly optimistic scenario with δ₀ = 0.15 > λ, under which the early adopter (gray dotted line) is preferable to late-adopter (gray solid line) with an expected net gain of 25. The EBA strategy provides further gain if designed properly, namely, it achieves a net gain of 36.5 when n* = 46, with z* = −0.26 and α* = 60%. However, the 2- stage EBA strategy with a large trial stage (precisely, n > 164) is less cost-effective than the early adopter. This example illustrates that some local investigation is preferred to no investigation when the local experts have a belief slightly more favorable than the equipoise. In contrast, Figure 1c depicts a scenario in which the local experts have a strong opinion for the new procedure with δ₀ = 0.25 > >λ. Under this scenario, E(G₁) > E(G₂) for all n, indicating that the new procedure should be adopted outright without a local investigation.

Figure 1d presents results for a pessimistic scenario with δ₀ = 0 < λ; that is, the new procedure is not expected to improve the health outcome over the standard procedure. With this pessimistic prior assumption, the figure suggests that some investigation may still be better than no investigation, although the magnitude of the net gain is small (at 3.4 when n* = 36, with z* = 0.59 and α* = 28%). In situations where there is a fixed cost for conducting the local investigation, such a small expected net gain may not warrant the local investigation. Figure 1e presents a scenario where the prior knowledge is strongly pessimistic (with δ₀ = −0.05 < < λ); under this scenario, the EBA strategy is uniformly inferior to the late-adopt strategy and, therefore, the standard procedure should be adopted outright without a local investigation.

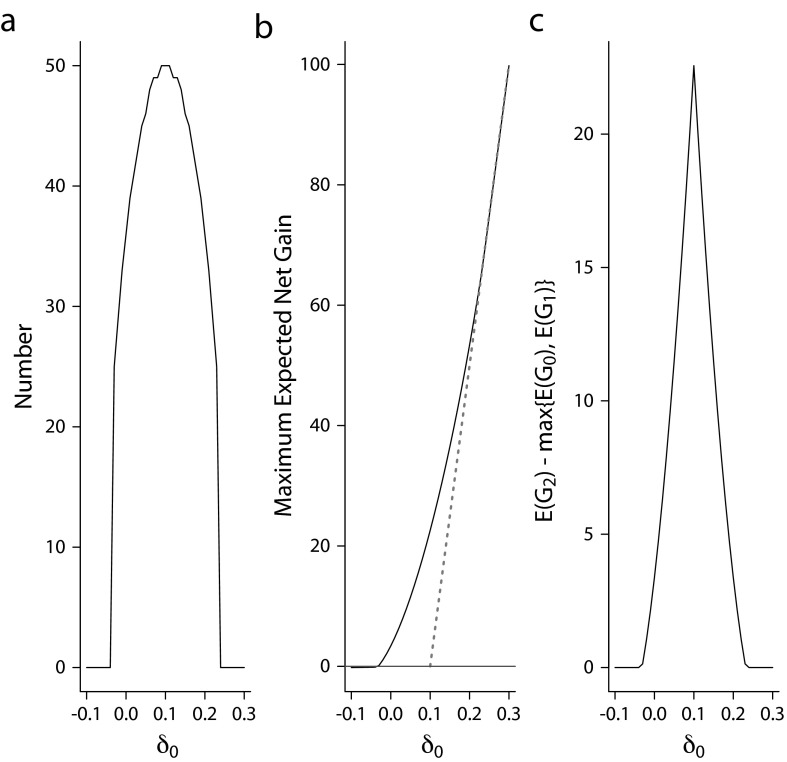
These scenarios illustrate that the use of the expected net gain (equation 3) provides a concise quantitative criterion as to whether a local investigation should be carried out, as well as the optimal sample size n* and the critical value z* for the local investigation if indicated. Figure 2a plots the optimal sample size versus δ₀ and shows that the maximum sample size is indicated under equipoise (with n = 50; Figure 1a). This illustrates that the formula in equation 10 serves as an upper bound for sample size required in a local investigation regardless of the previous mean, δ₀. As δ₀ moves away from the equipoise value λ = 0.1, the optimal sample size decreases and reaches 0 when δ ₀ ≤ −0.04 or ≥ 0.24. An optimal n = 0 implies that the optimal decision is not to conduct a local investigation, but rather to act in accordance with the prior knowledge. In Figures 2b and 2c, we show that the gain of the EBA strategy relative to the better of the late adopter and early adopter strategies ranges from 0 to 22.6. This set of illustrations considers a fairly informative prior knowledge with τ/σ = 0.2. As suggested by equation 11, the magnitude of net gain will increase with larger τ to σ ratios (less informative prior knowledge).

FIGURE 2—

Design properties under a variety of prior mean δ₀ for (a) optimal sample size, (b) expected net gain of the 3 strategies, and (c) expected net gain of evidence-based adoption relative to the better of the early and late adopters.

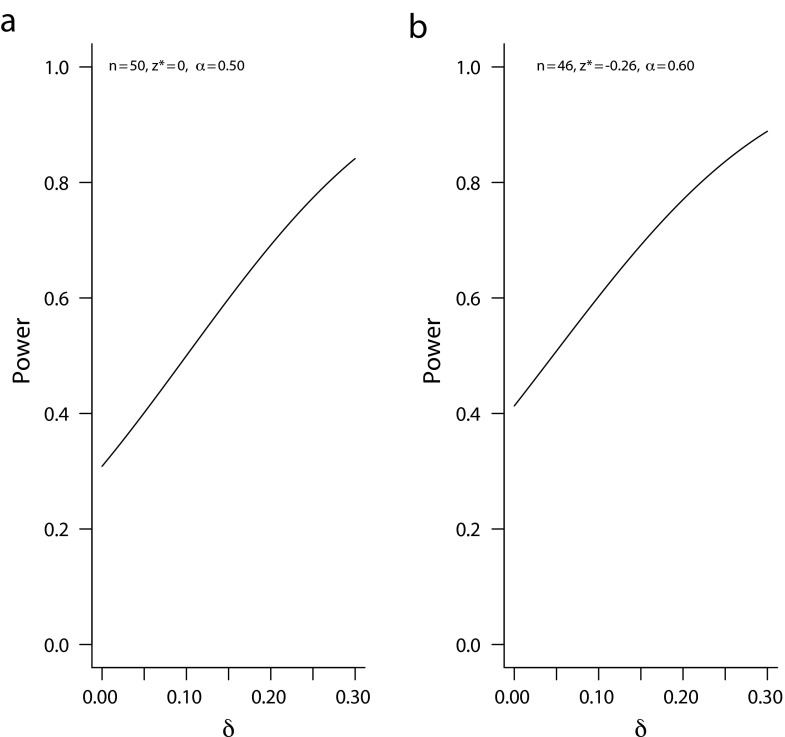
It is also instructive to evaluate the operating characteristics of the proposed sample size n* and significance threshold z* by using the conventional criteria. Figure 3a plots the power function of a local investigation with n = 50 and z_α = 0 (1-sided α = 0.50) over the range of nonnegative δs. This design will achieve an 80% power only when the true effect size δ is substantially larger than δ₀ (greater than 0.26 to be precise). Figure 3b depicts similar performance: high false-positive under small δ and relatively modest power at large effect size. With 1-sided α ≥ 0.50 and power often under 80%, these designs are very different from the conventional designs used in the usual research studies based on the assumption of very large patient horizons. These examples illustrate the needs to rethink how we design local investigations when the patient horizon is limited.

FIGURE 3—

Conventional power plots for the proposed sample sizes under various true δ.

CONCLUSIONS

The statistical formulation for medical trials in a finite patient horizon can be traced back to 1960s.^5,9,13 There was little follow-up work in the literature since, perhaps because of the fact that clinical trials in the past half century focused on drug and device development for the broad general patient population. However, the recent interest in conducting implementation studies calls for further research in this area.

We propose using a cost-effectiveness framework to assess the merits of local investigations, and provide guidelines on sample size determination for such investigations. In general, if the local experts do not have strong prior knowledge regarding the procedures under consideration, an appropriately designed local investigation should be conducted to guide the choice. On the other hand, if the local experts have strong prior knowledge that deviates substantially from equipoise, a local investigation is not warranted and the decision can be made according to the local experts’ prior knowledge.

The proposed sample size formula appears to yield subpar accuracy than the conventional approach (Figure 3). However, as discussed previously, accuracy bears practical relevance only when there is a large number of patients (an essentially infinite patient horizon) to benefit from the knowledge learned. For local investigations conducted to inform local decisions, the conventional design approach is not appropriate. This, of course, presumes the philosophy that we do not reward learning for the sake of learning if the knowledge obtained does not benefit patients. In this sense, a local investigation is not a research study, but rather an attempt to improve the quality of care. Conversely, it is also important not to overinterpret the results in a local investigation and make a generalizable statement based on the study finding.

It is of course possible that some local investigations might yield generalizable knowledge that can be applied to other care settings. However, we assume that the primary objective for the local investigation is quality improvement for the local patients; the knowledge produced is meant to be applied locally first and foremost. Any incidental application of this local knowledge to other care settings is a byproduct, not the primary objective to be relied upon for the design of the local investigation.

A potential difficulty in local investigation is the determination of the population size N, which may not be known accurately or may be drifting over a period of time. Although result 2 indicates that the optimal sample size n* in the trial stage is a function of N, it also suggests that it may be adequate to randomize about one third of an underestimate of N during the trial stage. A promising approach is the use of adaptive designs that accrue patients sequentially and adjust the sample size calculation throughout; adaptive designs in clinical trials for infinite patient horizon (e.g., stroke) have been increasingly used²¹ and regulated.²² For finite patient horizon, some simulation results in the literature¹⁴ suggest that adaptive randomization can mitigate the lack of precise knowledge about N, although theoretical behaviors of these methodologies warrant further investigation.