Modularity-based graph partitioning using conditional expected models

Abstract

Modularity-based partitioning methods divide networks into modules by comparing their structure against random networks conditioned to have the same number of nodes, edges, and degree distribution. We propose a novel way to measure modularity and divide graphs, based on conditional probabilities of the edge strength of random networks. We provide closed-form solutions for the expected strength of an edge when it is conditioned on the degrees of the two neighboring nodes, or alternatively on the degrees of all nodes comprising the network. We analytically compute the expected network under the assumptions of Gaussian and Bernoulli distributions. When the Gaussian distribution assumption is violated, we prove that our expression is the best linear unbiased estimator. Finally, we investigate the performance of our conditional expected model in partitioning simulated and real-world networks.

I. INTRODUCTION

Graph theory methods have been applied to study the structure and properties of a wide range of systems, including the World Wide Web [1,2], social networks [3,4], biological networks [5,6], and many others. Often network analysis focuses on identifying natural divisions of networks into groups, and two broad classes of algorithms have been used for this goal: divisive and agglomerative techniques. Divisive techniques partition the network into multiple subnetworks by removing edges between them, whereas agglomerative techniques start with individual nodes and progressively join them into clusters using similarity criteria.

Both approaches are popular and successful in analyzing networks [7–9]; however, they also suffer from shortcomings. For example, the minimum-cut method [10], a divisive algorithm that minimizes the sum of weights of the removed edges, has the disadvantage of often dividing the network very unevenly [11]. To deal with this problem, researchers have proposed methods with modified cost functions that normalize the cost of the removed edges. This is achieved using either the cardinality of the resulting clusters, as with average cuts and ratio cuts [12], or the ratio of the within cluster connections to the total cluster connections, as with normalized cuts [13]. However, while minimizing the cost of removed connections, these methods are not specifically designed to preserve another important feature of the network: its community structure.

Real-life networks divide into modules (communities, groups) within which the network connections are strong, but between which the connections are weak. Modules are groups of nodes that share the same properties or play similar roles in the whole network. Networks can have different properties at the modular level than in the scale of the entire network, and without information about the modular structure of the network, these properties may be difficult to detect [14,15]. More essential than the node-level analysis of the graph, topologically detecting community structure can be of great value in identifying the substructures of the network that have distinguishable and important functions. For example, Web pages dealing with the same topic form a Web community [16], while in biology modules can be defined as groups of proteins or mRNA associated with specific cellular functions [17]. In brain imaging, modules may consist of brain regions that are densely connected or are functionally highly correlated [18]. There are multiple formal definitions of a community structure [19], ranging from local definitions, such as n-clique [20], k-plex, and weak-community [21], to those using global measures on the graph [22,23].

Newman et al. introduced a measure of the quality of a particular division of a network, called modularity [22], and later presented a spectral graph partition algorithm that maximizes modularity [23]. Along with many ongoing theoretical explorations [24–28], modularity-based partitioning has become popular recently in a broad range of applications [24,29–38]. Unlike traditional clustering methods that seek to minimize weighted combinations of the number of edges running between the modules, such as minimum cuts or normalized cuts [13], modularity-driven clustering methods compare each edge against its expected value when clustering nodes into corresponding modules. If a natural division of a network exists, we should expect connections within a module to be stronger than their expected values, and the opposite should hold true for connections between modules. Central to this idea is the expected network, or the “null model,” which is defined as a random network conditioned to have the same number of nodes, edges, and degree distribution as in the original graph but in which the links are randomly placed [39]. In graph theory, the set of random networks that has predetermined node degrees is called the configuration model and has been extensively studied [40–42].

In this paper, we propose a new null graph model that can be used for modularity-based graph partitioning and provide analytic solutions for specific parametric distributions. We extend the results originally presented in our conference publication [43]. We first provide closed-form solutions for the expected strength of an edge when it is conditioned only on the degrees of its two neighboring nodes. We then provide an improved estimate of the expected network, where we condition the strength of an edge on the nodes making up the whole network. We analytically compute the expected network under the assumption of Gaussian and Bernoulli distribution. When the Gaussian assumption is violated, we prove that our expression is the best linear unbiased estimator. Finally, we use our conditional expected network to partition graphs and demonstrate its performance in simulated and real-world networks.

II. MODULARITY AND EXPECTED GRAPH MODELS

In this section we first describe modularity and the null model used in Ref. [23] for the estimation of modularity. We then introduce our null models, which are analytically computed for specific probability distributions for the edges of the network.

We assume an undirected network with N nodes and L edges, and the weight of the edge connecting nodes i and j denoted as the A_ij element of a weighted adjacency matrix A. If the network is unweighted, then A is a binary adjacency matrix with every edge of unit strength. We extend the definition of the degree of node i as k_i = Σ_j A_ij, i.e., the sum of the weights of edges associated with node i. This definition is consistent with the definition of degree for binary graphs and allows us to apply our method to both binary and weighted networks, similarly to Ref. [44]. We also denote the total sum of the weights of all edges in the network as $m=\frac{1}{2}{\sum }_{i,j}{A}_{ij}=\frac{1}{2}{\sum }_i{k}_i$.

A. Modularity

Optimal partitioning of a network requires specification of an appropriate cost function. Among the most popular is “modularity” [22], which uses the idea that if a natural division of a network exists, connections within a module should be stronger than their expected values, and the opposite should hold true for connections between modules. If an edge is stronger than its expected value, it contributes positively to modularity, provided that the two nodes connected by the edge belong to the same module. Divisions that increase modularity are preferred, because they lead to modules with high community structure.

Evaluation of modularity requires the computation of an expected network, or “null model,” which has the same configuration as the original network but contains no community structure because of a random placement of its edges. Newman [23] considered a random network where the probability of having a connection between two nodes i and j is proportional to the product of their degrees:

$$R_{ij}=\frac{k_i{k}_j}{2m},\forall i,j\le N.$$ (1)

Under this random graph model, modularity is expressed as [23]

$$Q=\frac{1}{2m}\sum _{i,j}(A_{ij}-R_{ij})\delta (C_i,C_j),$$ (2)

where C_i indicates group membership of node i. The Kronecker delta function equals one when nodes i and j belong to the same group and is zero otherwise. Therefore, modularity increases when A_ij − R_ij (edge strength minus expected edge strength) is positive for within-module edges (third column of Fig. 1).

FIG. 1.

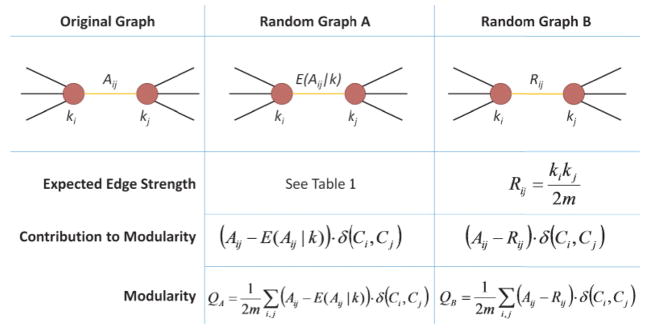
Random graph models and modularity. First column: Nodes i and j of the original graph are connected with an edge A_ij. Second column: Random graph A has the same node degrees k_i and k_j as the original graph, but the edge strength is replaced by its conditional expected value E(A_ij|k), with analytic expressions given in Table I. The contribution of this edge to modularity is A_ij − E(A_ij |k) when the two nodes are assigned to the same group, and the total modularity involves a sum over all edges of the graph. Third column: Similarly for random graph B, with the exception that R_ij in Eq. (1) is used instead of the conditional expected edge strength.

B. Random network partially conditioned on node degrees

We denote by E(A_ij) the expected value of edge strength between nodes i and j. Instead of using R_ij, we propose the null graph model whose expected edge strength E(A_ij|k_i,k_j) is conditioned on the degrees k_i and k_j of the neighboring nodes. The idea of conditioning on the degrees of neighboring nodes is based on the observation that the significance of an edge is directly related to the total connections of its nodes. If two nodes have high degrees, there is a high chance they are connected even on a random network without a community structure. The opposite holds true for nodes with low degrees, where even weak connections could be important. Even though R_ij also has a dependency on node degrees [Eq. (1)], it is not in the explicit form of a conditional expected value.

The conditional expected value of edge A_ij can be calculated using the Bayesian formulation:

$$\begin{array}{l}E(A_{ij}\mid k_i,k_j)=\int t·P(A_{ij}=t\mid k_i,k_j)dt\\ =\int t·\frac{P(k_i,k_j\mid A_{ij}=t)P(A_{ij}=t)}{\int P(k_i,k_j\mid A_{ij}=u)P(A_{ij}=u)du}dt.\end{array}$$ (3)

To solve Eq. (3), we need to specify the joint distribution of the network edges. Appendix A provides detailed derivation for the cases of Gaussian and Bernoulli distributions. For the case of Gaussian random networks with independent and identically distributed (i.i.d.) edges with mean μ and variance σ², we obtain the following analytic expression:

$$E(A_{ij}\mid k_i,k_j)=\{\begin{array}{ll}\frac{k_i+k_j-(N-2)\mu }{N},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}.$$ (4)

For binary networks, we can solve Eq. (3) for edges following an i.i.d. Bernoulli distribution with parameter p, where p is the probability of having a nonzero edge:

$$E(A_{ij}\mid k_i,k_j)=\{\begin{array}{ll}\frac{k_i{k}_j}{k_i{k}_j+(N-1-k_i)(N-1-k_j)·(p/(1-p))},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}.$$ (5)

C. Random network fully conditioned on node degrees

In the previous section, we conditioned an edge only on the neighboring node degrees k_i and k_j. A better representation of the null model structure is to condition an edge on the degrees of all nodes making up the network:

$$E(A_{ij}\mid k_1,k_2,k_3,\dots ,k_N)=E(A_{ij}\mid \mathbf{k}).$$ (6)

To find the above expectation, we first concatenate the elements of the adjacency matrix A into a column vector x. When graph topology does not allow self-loop connections, we use the transformation A_ij = x_l, where $l=\frac{(2N-j)(j-1)}{2}+(i-j)$, ∀(0 < j < i ≤ N). This transformation simply takes into account the symmetric nature of the adjacency matrix and concatenates only the elements of the lower triangle, excluding the main diagonal. To allow self-loop connections, we use a similar transformation but also include the diagonal elements.

We now consider the linear mapping Hx = k, where H is the N × L incidence matrix of the graph [45,46], a uniquely defined matrix that connects the edge strengths x to the node degrees k. Figure 2(a) shows an example graph consisting of four nodes. The corresponding matrix H, edge vector x, and degree vector k are

FIG. 2.

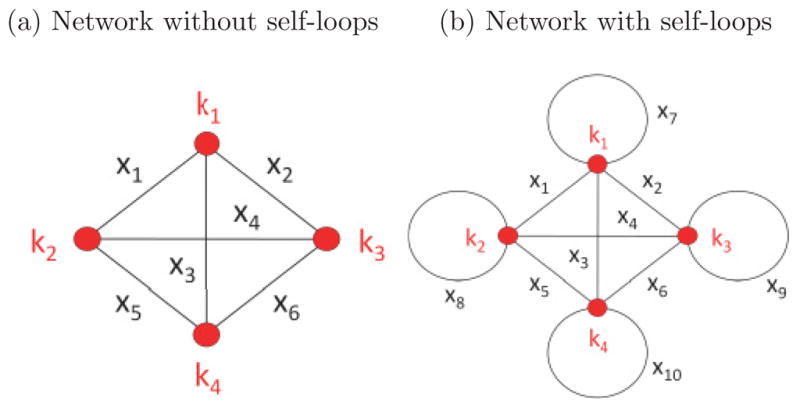
Two simple four-node complete networks with different topological configurations.

$$\begin{array}{l}\mathbf{H}=\left(\begin{array}{cccccc}1& 1& 1& 0& 0& 0\\ 1& 0& 0& 1& 1& 0\\ 0& 1& 0& 1& 0& 1\\ 0& 0& 1& 0& 1& 1\end{array}\right),\\ \mathbf{x}={(x_1{x}_2{x}_3{x}_4{x}_5{x}_6)}^T,\mathbf{k}={(k_1{k}_2{k}_3{k}_4)}^T.\end{array}$$ (7)

The incidence matrix H represents the permissible structure of a null graph model and, for example, can be a fully connected network with or without self-loops or even have missing edges. Figure 2(b) gives an example of a network with self-loops; it is straightforward to update the incidence matrix H and edge vector x for this case.

With the above notation, the conditional expectation of edge strengths now becomes

$$E(\mathbf{x}\mid \mathbf{k})=E(\mathbf{x}\mid \mathbf{Hx}=\mathbf{k})=\int \mathbf{x}·P(\mathbf{x}\mid \mathbf{Hx}=\mathbf{k})d\mathbf{x}.$$ (8)

D. Gaussian random network

While there is no general analytical solution to the conditional probability P(x|Hx = k) of the above equation, a closed form exists for the multivariate Gaussian distribution. We refer to the random network whose edges are Gaussian distributed with mean vector μ_x and covariance Σ_x as a Gaussian random network.

Given that k is a linear transformation of x, k is also Gaussian distributed with mean μ_k = Hμ_x and covariance Σ_k = HΣ_xH^T. The conditional probability P(x|Hx = k) is also a multivariate Gaussian distribution with the conditional expected value and covariance [47]:

$$E(\mathbf{x}\mid \mathbf{Hx}=\mathbf{k})={\mathit{\mu }}_{\mathbf{x}\mid \mathbf{k}}={\mathit{\mu }}_{\mathbf{x}}+{\mathbf{\sum }}_{\mathbf{xk}}{\mathbf{\sum }}_{\mathbf{k}}^{-1}(\mathbf{k}-{\mathit{\mu }}_{\mathbf{k}}),$$ (9)

$${\mathbf{\sum }}_{\mathbf{x}\mid \mathbf{k}}={\mathbf{\sum }}_{\mathbf{x}}-{\mathbf{\sum }}_{\mathbf{xk}}{\mathbf{\sum }}_{\mathbf{k}}^{-1}{\mathbf{\sum }}_{\mathbf{kx}},$$ (10)

where the cross-covariance matrix is Σ_xk = Σ_xH^T.

The above expression relaxes the non-negative edge weight assumption for the R null model in [23]. Furthermore, the definition of mean and covariance of the edge vector x allows us to provide prior information to the null network model. For example, network edges may be correlated with each other or have different mean and variance because of measurement considerations and noise rather than a true underlying network structure; adjusting the mean μ_x and variance matrix Σ_x can account for such effects.

E. Gaussian random network with independent identically distributed edges

For the special case of a Gaussian random network with independent identically distributed edges with μ_x = μ1 and Σ_x = σ²I, we can simplify Eq. (9). As derived in Appendix B, the conditional expectation of the lth component of the edge vector x (or equivalently the A_ij element of the adjacency matrix) becomes

$$E(A_{ij}\mid \mathbf{k})=E(x_l\mid \mathbf{k})=\{\begin{array}{ll}\frac{k_i+k_j}{N-2}-\frac{2m}{(N-1)(N-2)},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}.$$ (11)

The first term on the right-hand side of the above equation (when i ≠ j) shows that the expected value of a specific edge is positively correlated with the summation of the degrees of the two associated nodes, whereas the second term shows that the expected edge strength decreases when the total weight of the network increases while the associated degrees are kept the same. In a real network this fact translates to the following. When two specific nodes are more densely connected to the network, we expect the link between them to be stronger. At the same time, if the degrees of the two nodes are kept the same, we expect the connection between them to be weaker when the entire network becomes more densely or heavily connected.

F. Non-Gaussian random networks and BLUE

Searching for a network null model can be seen as an estimation problem. Given the degree vector k, we need to estimate the unknown edge vector x̂_|k. We can consider the best estimate in the minimum mean-squared error sense (MMSE). An important property of the MMSE estimator is that it is unbiased, which is highly desirable for graph clustering because the criterion we use to partition a graph is the measured edge strength versus its expected value. The MMSE estimator is defined as

$${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{MMSE}}=arg\underset{{\widehat{\mathbf{x}}}_{\mid \mathbf{k}}}{min}\mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})=arg\underset{{\widehat{\mathbf{x}}}_{\mid \mathbf{k}}}{min}E\{{\mid {\widehat{\mathbf{x}}}_{\mid \mathbf{k}}-\mathbf{x}\mid }^2\}$$ (12)

and is solved by setting the derivative to zero, which gives

$${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{MMSE}}=E(\mathbf{x}\mid \mathbf{k})={\mathit{\mu }}_{\mathbf{x}\mid \mathbf{k}}.$$ (13)

Therefore, the MMSE estimator of the unknown random edges x given observation k is also the conditional expectation, as in Eq. (8). As we have shown, in the Gaussian case this is found analytically using Eq. (9).

In practice the MMSE estimator, even if it exists, often cannot be found [47]. In this case it is reasonable to resort to a suboptimal estimator, and a common approach is to restrict the estimator to be linear in the data. We then find the linear estimator that is unbiased and has minimum variance, which is termed the Best Linear Unbiased Estimator (BLUE) [47]. In our case the best linear (with respect to the degree observation k) estimator x̂ that minimizes the mean square error is

$${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}=arg\underset{{\widehat{\mathbf{x}}}_{\mid \mathbf{k}}}{min}\mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})\text{such}\text{that}{\widehat{\mathbf{x}}}_{\mid \mathbf{k}}=\mathbf{Lk}+\mathbf{b}$$ (14)

for some matrix L and vector b. The solution ${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}$ of the above minimization problem is the same as Eq. (9):

$${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}=\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}={\mathit{\mu }}_{\mathbf{x}}+{\mathbf{\sum }}_{\mathbf{xk}}{\mathbf{\sum }}_{\mathbf{k}}^{-1}(\mathbf{k}-{\mathit{\mu }}_{\mathbf{k}})$$ (15)

with the derivation given in Appendix C. This equivalence indicates that our null model under the Gaussian assumption is also the BLUE estimator of the null model under any probability distribution.

Notice that, in general, ${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}$ is not the expected network μ_x|k. However, ${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}$ best explains the observed degree vector k among all linear estimations, while at the same time remaining unbiased.

III. PARTITION IMPLEMENTATION

There are multiple methods to maximize modularity through graph partitioning: greedy agglomerative hierarchical clustering [48–52], spectral partitioning [14,23], external optimization [53], simulated annealing [54], and many others. Comparison of these methods is beyond the scope of this paper; rather we are interested in investigating the effectiveness of our novel null models. To achieve this goal, we chose the sequential spectral partitioning method [23] to perform clustering, and a brief description follows below.

We use two expressions for modularity: Q_A based on our null models (Table I), which we now jointly call ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$, and Q_B based on the null model R [Eq. (1)]. Modularity is maximized over an indicator vector s_A (or s_B) denoting group membership:

$${\widehat{\mathbf{s}}}_{\mathbf{A}}=arg\underset{{\mathbf{s}}_{\mathbf{A}}}{max}{Q}_A=arg\underset{{\mathbf{s}}_{\mathbf{A}}}{max}\left\{\frac{{{\mathbf{s}}_{\mathbf{A}}}^T\left(\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}\right){\mathbf{s}}_{\mathbf{A}}}{4m}\right\},$$ (16)

$${\widehat{\mathbf{s}}}_{\mathbf{B}}=arg\underset{{\mathbf{s}}_{\mathbf{B}}}{max}{Q}_B=arg\underset{{\mathbf{s}}_{\mathbf{B}}}{max}\left\{\frac{{{\mathbf{s}}_{\mathbf{B}}}^T(\mathbf{A}-\mathbf{R}){\mathbf{s}}_{\mathbf{B}}}{4m}\right\}.$$ (17)

TABLE I.

Expected edge strength for several different types of random networks.

Null model	Expected edge strength
Expected Bernoulli random network conditioned on degrees of associated nodes.	$E(A_{ij}\mid k_i,k_j)=\{\begin{array}{ll}\frac{k_i{k}_j}{k_i{k}_j+(N-1-k_i)(N-1-k_j)·(p/(1-p))},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}$
Expected Gaussian random network conditioned on degrees of associated nodes.	$E(A_{ij}\mid k_i,k_j)=\{\begin{array}{ll}\frac{k_i+k_j-(N-2)\mu }{N},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}$
Expected Gaussian random network conditioned on whole degree sequence. Also, BLUE null model in the non-Gaussian case.	$E(\mathbf{x}\mid \mathbf{Hx}=\mathbf{k})={\mathit{\mu }}_{\mathbf{x}}+{\mathrm{\sum }}_{\mathbf{xk}}{\mathrm{\sum }}_{\mathbf{k}}^{-1}(\mathbf{k}-{\mathit{\mu }}_{\mathbf{k}})$
Expected i.i.d. Gaussian random network conditioned on whole degree sequence.	$E(A_{ij}\mid \mathbf{k})=\{\begin{array}{ll}\frac{k_i+k_j}{N-2}-\frac{2m}{(N-1)(N-2)},\hfill & i\ne j\hfill \\ 0,\hfill & i=j\hfill \end{array}$

Specifically, the ith element of s_A (s_B) is 1 or −1, depending on which of the two groups the ith node belongs to after one partition. Partitioning proceeds by selecting vectors s_A and s_B that maximize modularity. Based on spectral graph theory, when s_A and s_B are allowed to have continuous values, maximization of Q_A and Q_B is achieved by selecting the maximum eigenvalues and eigenvectors of matrices $\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ and A − R, respectively. The elements of vectors s_A and s_B are then discretized to {−1, 1} by setting a zero threshold. Because of discretization, s_A and s_B do not align with the eigenvector with largest eigenvalue, and further fine tuning is necessary to approach the global maximum, which can be done using the Kernighan-Lin algorithm [55]. We have further optimized this algorithm by randomizing the sequence of nodes and allowing them to change group membership more than once. This still does not guarantee a global optimum, but represents a tradeoff between computational cost and accuracy.

To partition the network into more than two groups, we recursively dichotomize the resulting subnetworks by maximizing Eqs. (16) and (17) for each subnetwork separately. After sufficient partitioning steps, Q_A and Q_B will stop increasing, at which point we have reached maximum modularity for the entire network, and therefore no more sequential partitioning should be performed. This corresponds to a formal partition stopping criterion, which is an attractive property of modularity not shared by other clustering methods as we discuss in Sec. VII.

IV. PARTITION PROPERTIES

A. Node degrees

An important property of the null graph models ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ and R is that they have the same node degrees as the original graph. For the model ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ this is enforced by construction, because it is conditioned on the node degrees k of the original graph. For the model R we can show this property as follows. Since the degree of a node is defined as the sum of edges that connect to this node, multiplication of the adjacency matrix A with a unit vector results in the degrees of all the nodes of the network: A · 1 = k. Similarly, for the expected network R, the degree of node i is the ith column of R · 1:

$${(\mathbf{R}·\mathbf{1})}_i=\sum _{j=1}^N{R}_{ij}=\sum _{j=1}^N\frac{k_i{k}_j}{2m}=k_i·\sum _{j=1}^N\frac{k_j}{2m}=k_i.$$ (18)

Considering all nodes, we have R · 1 = k, which implies that the degrees of all nodes of the expected network R are the same as those of the original network A. It can also be shown that ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}·\mathbf{1}=\mathbf{k}$. For example, consider the Gaussian random network in Eq. (11):

$$\begin{array}{l}{\left({\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}·\mathbf{1}\right)}_i=\sum _{j=1}^N{\left({\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}\right)}_{ij}\\ =\sum _{j=1,j\ne i}^N\left\{\frac{k_i+k_j}{N-2}-\frac{2m}{(N-1)(N-2)}\right\}\\ =k_i.\end{array}$$ (19)

As a consequence of preserving the node degrees, the two networks satisfy

$$\left(\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}\right)·\mathbf{1}=\mathbf{0},$$ (20)

$$(\mathbf{A}-\mathbf{R})·\mathbf{1}=\mathbf{0}.$$ (21)

As described in the previous section, maximization of modularity is performed by selecting the maximum eigenvalues and eigenvectors of matrices $\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ and A − R. Based on the above equations, vector 1 is always an eigenvector of these matrices with zero contribution to modularity (its eigenvalue). This is reminiscent of the matrix known as the graph Laplacian [46] and is important in the spectral graph cut algorithm for the following reason. The unit vector indicates trivial partitioning, because it leads to grouping of all nodes into one cluster while at the same time the other cluster is left empty. This property gives a clear stopping criterion for dividing a graph: When the largest eigenvalue of $\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ or A − R is zero, there is no way to further divide the nodes into two clusters to increase modularity.

B. Network topology

Even though both null models maintain the node degrees of the original network, network R does not maintain the same topology. In particular, even though a real network often involves nodes where self-loops are not allowed or are not meaningful, network R always includes self-loops:

$$R_{ii}=\frac{k_i^2}{2m}\ne 0.$$

The positive values assigned to self-loops lead to a bias in the R random model such that the diagonal values of the adjacency matrix are overestimated, whereas the rest of the connections are generally underestimated. This does not happen with the ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ model because the allowed network topology is already included in matrix H by construction. For example, Eq. (11) was derived for an expected network where self-loops are not allowed and therefore

$${\left({\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}\right)}_{ii}=0.$$

C. Isolated nodes

A network node i is isolated if it does not connect to other nodes in the graph, which implies A_ij = 0, ∀ j ≠ i. Random network models ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ and R treat isolated nodes differently. Null model R leaves these nodes isolated, and it does not matter where they will eventually be assigned. In contrast, model ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ assigns nonzero expected connections between the isolated nodes and the rest of the network, based on the underlying probability distribution. As a result, isolated nodes are eventually assigned to clusters rather than treated as “don’t-cares.”

Connecting isolated nodes to specific clusters may seem counterintuitive at first glance, but there is an argument that supports such behavior. An isolated node is a part of the network, so the fact that it did not connect to any node can be considered an unexpected and noteworthy event. Consider two examples: (1) a network with two clusters of unequal size, N₁ ≫ N₂, but with equal within-cluster edge strength; (2) a network with two clusters of equal size, N₁ = N₂, but with larger within-cluster edge strength for the first cluster. In the former case, it is more surprising that the isolated node did not connect to the larger cluster rather than the smaller cluster, because many potential connections exist in the larger cluster. In the latter case, it is more surprising that the isolated node did not connect to nodes which have overall strong connections. Our partition algorithm favors the least surprising of the above events, so it tends to assign isolated nodes to small clusters consisting of nodes with overall small degrees. Furthermore, the assignment of isolated nodes to clusters is nontrivial for networks with both positive and negative edges: for instance, correlations versus anticorrelations in functional brain networks [56], friends versus foes in social networks [57], ferromagnetic versus antiferromagnetic couplings in ising or spin-glass models [58], etc. In such cases, a zero edge is stronger than a negative edge.

D. Resolution limit

Modularity has a resolution limit that may prevent it from detecting relatively small clusters with respect to the entire graph, even though such small clusters can be defined as communities using local properties, for example, cliques [24,59,60]. Originally derived using a Potts model approach, one solution to this problem is to introduce a resolution parameter that weights the null model when computing modularity [61,62]:

$$Q_B(\lambda )=\frac{1}{2m}\sum _{i,j}{(\mathbf{A}-\lambda \mathbf{R})}_{ij}\delta (C_i,C_j)$$ (22)

and then solve for the partitioning results C_i that maximize the above equation. The same approach can be applied with our null models, in which case we maximize

$$Q_A(\lambda )=\frac{1}{2m}\sum _{i,j}{\left(\mathbf{A}-\lambda {\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}\right)}_{ij}\delta (C_i,C_j)$$ (23)

and similarly tune the resolution parameter λ to focus on either local structures (λ > 1) or global structures (λ < 1).

V. PARTITION EVALUATION

To evaluate the accuracy of partition algorithms, rather than requiring perfectly accurate partition results, we assess the overall similarity between the resulting and correct partition using the normalized mutual information (NMI) measure [63–66]. Denoting the number of true communities as C_T and the number of communities, resulting from either Eq. (16) or (17) as C_R, NMI is defined as

$$\text{NMI}(C_T,C_R)=\frac{-2{\sum }_{i\in C_T}{\sum }_{j\in C_R}\frac{N_{ij}}{N}log\left(\frac{N_{ij}N}{N_{i·}{N}_{·j}}\right)}{{\sum }_{i\in C_T}\frac{N_{i·}}{N}log\left(\frac{N_{i·}}{N}\right)+{\sum }_{j\in C_R}\frac{N_{·j}}{N}log\left(\frac{N_{·j}}{N}\right)},$$ (24)

where N_ij is the number of nodes in the true community (cluster) i that appear in the resulting community j. For the case where an algorithm is unable to perform a partition and incorrectly finds the whole graph to be a single cluster (inseparable graph), we define NMI = 0.

VI. RESULTS

We assessed the performance of Q_A and Q_B modularity-based algorithms in partitioning simulated graphs as well as real-world networks. Modularity Q_A assumes several null models, depending on the underlying edge strength distribution (Table I), whereas Q_B is based on the null model in Eq. (1). We simulated graphs that follow a Gaussian or Bernoulli distribution of edge strength, as assumed by the null models in Table I. Moreover, to test whether the BLUE estimator performs well on non-Gaussian cases, we measured its performance on Bernoulli networks. Real-world networks include the karate club network in Ref. [67], a structural brain network in Ref. [18], and a resting-state functional brain network from the 1000 Functional Connectomes Project (http://www.nitrc.org/projects/fcon1000/).

A. Gaussian random networks

We simulated Gaussian graphs by drawing from an i.i.d. Gaussian distribution with fixed mean μ = 8 and several levels of variance σ². For each level of variance, we simulated two clusters with variable size N₁ ≥ N₂, such that N₁ + N₂ = N, where N = 20 is the total number of nodes. This community structure was enforced by randomly allocating the stronger values of the Gaussian distribution as intracluster edges and the weaker values as intercluster edges. To test robustness against noisy measurements, we added i.i.d. Gaussian noise with mean zero and variance ${\sigma }_N^2$. Our goal is to evaluate the performance of partition algorithms for several levels of edge variance σ², noise variance ${\sigma }_N^2$, and cluster size ratio N₁/N. For each configuration of the above parameters, we simulated 1000 random network realizations and then used Eqs. (16) and (17), which maximize modularity Q_A and Q_B respectively, in order to partition graphs. For Q_A modularity, we used the null model in Eq. (11), which is optimal for i.i.d. Gaussian networks. Partition quality is measured with NMI and averaged across the 1000 realizations.

Figure 3(a) displays the NMI similarity metric, averaged over the 1000 random networks, across several levels of edge variance σ², for the case of no noise ( ${\sigma }_N^2=0$) and cluster size ratio N₁/N = 0.6 (top row: 12 vs 8 cluster size) and N₁/N = 0.5 (bottom row: 10 vs 10 cluster size). Figure 3(b), 3(c), and 3(d) displays sample realizations of the network adjacency matrix A, and its difference with the null models used for Q_A and Q_B, $\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ and A − R, respectively.

FIG. 3.

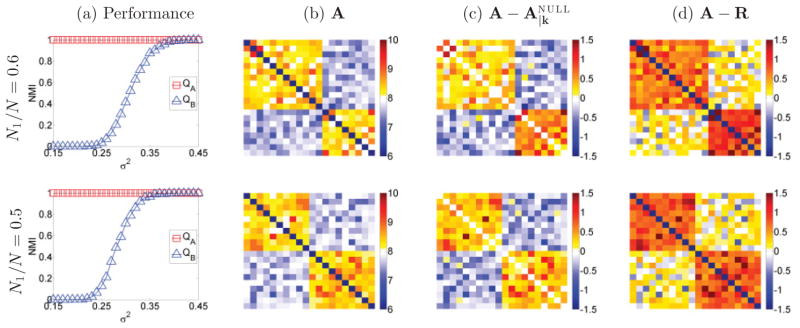
Partition results for Gaussian graphs. (a) Performance against different values of variance (σ²) of the Gaussian distribution and zero additive noise ( ${\sigma }_N^2=0$); (b) adjacency matrix; (c) difference between adjacency matrix of original graph versus null model ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$; (d) same for R null model. Top row: 12 vs 8 cluster size; bottom row: 10 vs 10 cluster size. Method Q_A accurately partitions the graph for all values of σ², whereas method Q_B fails for low values of σ².

Partition results based on Q_A are practically identical with the underlying structure of the simulated network, as indicated by NMI = 1, for all values of σ². Conversely, for the configuration parameters in Figure 3, method Q_B has a considerable performance drop with decreased values of variance σ², eventually reaching NMI = 0. In fact, for low values of variance it was unable to divide the network, considering it inseparable most of the times.

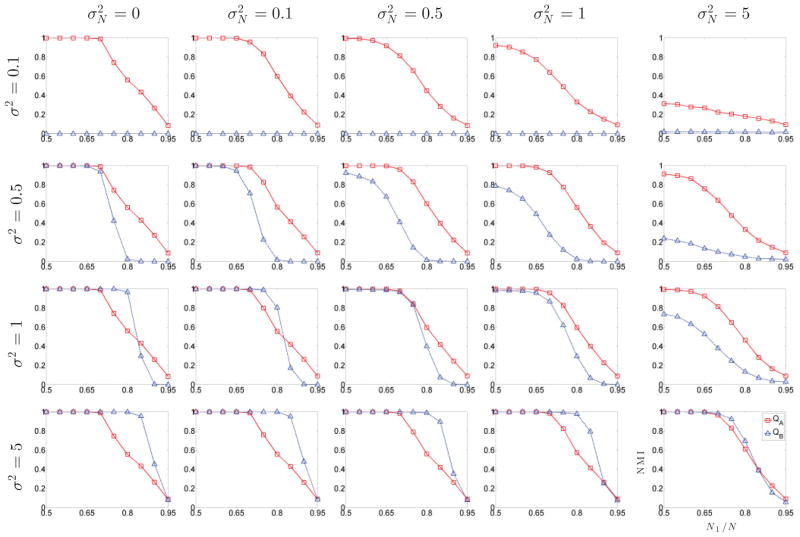
Figure 4 shows the performance of the two partition methods for several levels of edge variance σ², noise variance ${\sigma }_N^2$, and cluster size ratio N₁/N. As expected, the additive Gaussian noise deteriorates the partition performance, as indicated by the drop of NMI when ${\sigma }_N^2$ increases. However, the Q_A method is much more robust to noise interference than Q_B.

FIG. 4.

Partition results of Gaussian graphs for several levels of edge variance σ², noise variance ${\sigma }_N^2$, and cluster size ratio N₁/N. Method Q_A is more robust to noise, and method Q_B fails for small values of σ² but performs better for large values of σ².

Changing the edge variance σ² has little effect on method Q_A performance. This is not the case with method Q_B, which fails completely for small values of σ²; however, it performs better than Q_A for large values of σ². Both methods deteriorate when cluster sizes are very asymmetric, with very low NMI values when N₁/N is close to one.

The null model R in modularity Q_B requires positive edge strength to ensure that the product of degrees of two nodes is a meaningful measure of their expected connection. There is no such constraint for the null models in Q_A. Figure 5 displays a network with negative connections. It consists of two equal size clusters of 10 nodes each. Connections follow a Gaussian distribution with mean ±0.4 (positive for intercluster and negative for intracluster connections) and variance 0.04. When subtracting the null model from the adjacency matrix A, network structure is still visible in the $\mathbf{A}-{\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$ case, but not in the A − R case. We further address the issue of networks with negative connections in the Discussion.

FIG. 5.

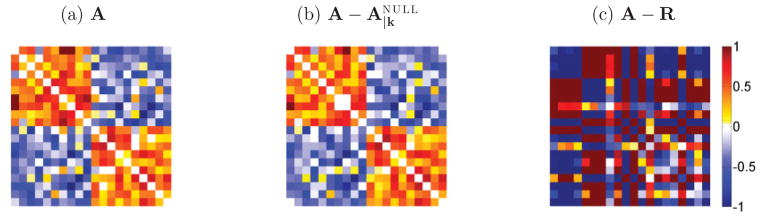
Partitioning graphs with both positive and negative connections. (a) Adjacency matrix; (b) difference between adjacency matrix of original graph versus null model ${\mathbf{A}}_{\mid \mathbf{k}}^{\text{NULL}}$; (c) same for R null model. In the presence of negative connections, null model R fails to partition the graph, as indicated by the lack of structure of matrix A − R.

B. Binary random networks

Random rewiring schemes, involving permutation of existing edges of a network, have been proposed to construct binary random networks [68]. Here we explore the similarity of our null graph models to these networks.

We consider the random rewiring scheme proposed in Ref. [68], which keeps the degrees of all network nodes constant. A numerical algorithm first selects a pair of edges, e_AB and e_CD, connecting nodes A-B and C-D, respectively. The two edges are then rewired to connect nodes A-C and B-D, effectively eliminating the original two edges and replacing them with e_AC and e_BD. To avoid multiple edges connecting the same nodes, the rewiring step is aborted if at least one of the edges, e_AD or e_BC, already exists. Following a modification in Ref. [69], the constraint of no self-loops is added to the rewiring algorithm by requiring nodes A, B, C, and D to be different. To produce a sufficiently random binary graph, the rewiring step is repeated multiple times.

Our Monte Carlo simulation includes generating 200 different binary undirected networks of size N without self-loops. For each network, we create 1000 random rewired graphs, each produced by multiple rewiring steps, and then average them to produce a mean adjacency matrix W. The number of rewiring steps was set to be equal to N_r times the total number of edges in the graph for values of N_r from 25 to 400.

We compute the distance d(W,A_|k^NULL) between W and our null model A_|k^NULL using the root-mean-square difference between the elements of the two corresponding adjacency matrices:

$$d(\mathbf{W},{{\mathbf{A}}_{\mid \mathbf{k}}}^{\text{NULL}})=\sqrt{\frac{{\sum }_{i,j}{\left({{\mathbf{A}}_{\mid \mathbf{k}}}^{\text{NULL}}-\mathbf{W}\right)}_{ij}^2}{N^2}}.$$ (25)

The above procedure results in 200 estimates of the distance metric for each null model tested. We evaluated the null models in Eqs. (1) and (5), as well as the BLUE null model in Eq. (15). In the later case, we assumed i.i.d. edges with diagonal covariance matrix, so the BLUE model is the same as Eq. (11).

For a fixed network size N = 10, we repeated the above analysis for various values of N_r. As shown in Fig. 6(a), N_r does not affect the distance between the rewiring networks and the null models. Furthermore, the Bernoulli null model is the most similar to the rewiring procedure, followed by the BLUE model and then the R model, which either includes (Q_B) or does not include ( $Q_B^{\ast }$) the diagonal terms in the calculation of Eq. (25). We consider both $Q_B^{\ast }$ and Q_B to test whether the deviation of the R model from the random rewiring graphs is only attributed to the diagonal terms (cf. Sec. IV B, which indicates that the topology of network R always requires self-loops, even though they are not necessarily present in the original network). Although a considerable amount of dissimilarity is explained by the diagonal terms, $Q_B^{\ast }$ is still more distant from a rewiring graph than our null models.

FIG. 6.

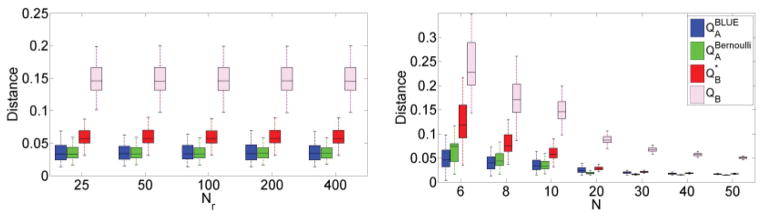
(Comparison of null graph models against a random rewiring scheme. Distance is expressed as root-mean-square difference between the elements of the adjacency matrices of the graphs [Eq. (25)]. For each box plot, the central mark is the median, the edges of the box are the 25th and 75th percentiles, and the whiskers extend to the most extreme data points not considered outliers. Left: Distance does not depend on the number of rewiring steps N_r. Right: As the size of graph N increases, distance becomes smaller. Overall, Q_A null models are closer to an actual rewiring scheme than Q_B models.

We also evaluated networks with various sizes N, as shown in Fig. 6(b), while fixing N_r = 50. Overall, Bernoulli and BLUE null models were closer to the rewiring scheme than the R model for all values of N. However, the difference dissipates with increased N. The BLUE estimator is best for network sizes N < 8, whereas the Bernoulli estimator is best for larger networks.

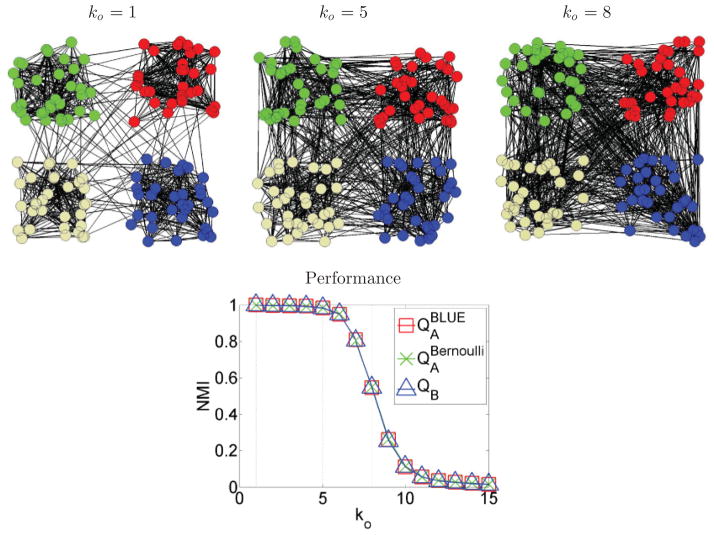
To test the performance of the partition methods Q_A and Q_B in binary networks, we simulated a graph introduced in Ref. [54]. The graph consists of 128 nodes, arranged in four cluster of 32 nodes each. Edges follow Bernoulli distribution with probability p_i for within-cluster connections and p_o for between-cluster connections. The average degree k of each node has two components: k_i = 31p_i from connections within the same cluster, and k_o = 96p_o from connections to nodes in other clusters. Probabilities p_i and p_o are selected such that the average degree of each node is k = k_i + k_o = 16. We created 100 realizations of this network, each for different values of k_o, ranging from 1 to 15. High values of k_o lead to less community structure, as displayed in the top row of Fig. 7.

FIG. 7.

Partition results for the binary network described in Ref. [4]. Top row: Higher values of k_o lead to less community structure of the network. Bottom row: Partition results for different values of k_o. Performance of all methods is practically equal.

We quantified the performance of method Q_B, as well as method Q_A using the Bernoulli null model, with probability value p = 16/127, and the BLUE model. The probability value was selected because each node on average connects to 16 out of 127 potential nodes to the rest of the graph. All three methods had roughly the same performance, as shown in the bottom row of Fig. 7. Partition accuracy drops as k_o increases, given that community structure is less detectable when nodes from different clusters become more and more densely connected.

We further tested all methods with another benchmark introduced in Ref. [70], and online code is available at http://sites.google.com/site/andrealancichinetti/files. This benchmark generates random binary graphs with a fixed number of nodes and a desired average degree. Node degrees, as well as the size of communities, were sampled from power-law distributions. Each node had a fraction 1 − μ of its links with its community, where μ is a mixing parameter with values between zero and one. We used a network size of N = 500 and averaged results of 100 realizations of networks. Methods $Q_A^{\text{BLUE}},Q_A^{\text{Bernoulli}}$, and Q_B have almost identical performance, as shown in Fig. 8.

FIG. 8.

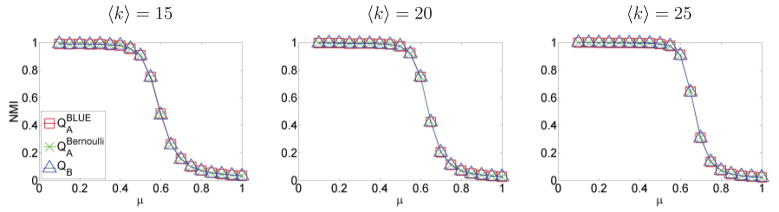
Results of benchmark in Ref. [70] for Q_A and Q_B methods. The performance of all methods is almost identical for all values of mixing parameter μ and average degree 〈k〉.

We also explored the performance of partitioning binary networks with variable cluster size ratio. Similar to the Gaussian case described earlier, we simulated N = 20 node graphs and varied the cluster size ratio N₁/N, but now edge strength followed a Bernoulli distribution with parameters p = 0.8, and 0.1 for within and between-cluster connections, respectively. Parameters were selected so that the graph has community structure in the weak sense [21], which requires that for every cluster the sum of within connections is larger than the number of between connections divided by two. This was true for the cluster size ratio simulated, which included clusters of size ≤17.

For each cluster size ratio, we simulated 1000 random graph realizations and then applied Q_A and Q_B methods to segment the graph. For Q_A, we used both the BLUE model, and the Bernoulli model with p value estimated from the data. Figure 9 shows that all methods have practically the same performance for all tested cluster size ratios.

FIG. 9.

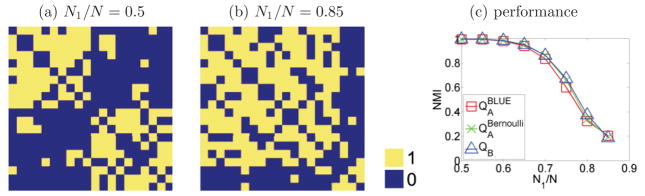
Partition results for a binary network for different values of cluster size ratio. (a) Adjacency matrix for 10 vs 10 cluster size; (b) adjacency matrix for 17 vs 3 cluster size. (c) Performance is very similar for all methods, across all cluster size ratio values.

C. Real-world networks

We tested Q_A and Q_B modularity partition methods on the karate club network given in Ref. [67]. In this binary network, individual members are represented by nodes on the graph, and edges connect nodes if a relationship exists between the corresponding individuals. After a conflict between the club officers and the instructor, the club was divided into two organizations. We tested whether Q_A and Q_B partition methods predict the actual division of the group. $Q_A^{\text{Bernoulli}}$ is the Q_A method based on the Bernoulli random network model in Eq. (5), and $Q_A^{\text{BLUE}}$ is the Q_A method based on the BLUE null model in Eq. (15).

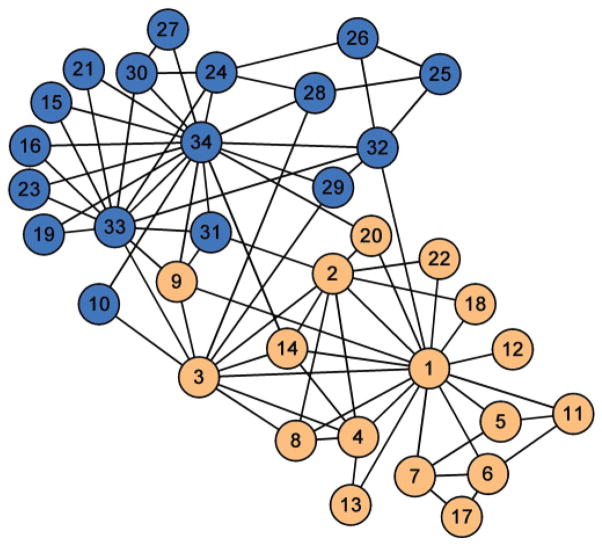
The original paper that presented the karate club network [67] describes two possible partitions, one based on the factions of its members and the other on the actual split of the network. The two partitions are almost identical, with the exclusion of person 9, who was friendly to both groups, with two friends in the instructor’s group (relationship strength 2 and 5) and three friends in the officer’s group (relationship strength 3, 4, and 3). The faction partition weakly assigns person 9 to the officer’s group; however, after split he actually joined the instructor’s group, for reasons explained as personal interest to obtain his black belt. In this paper, we use the actual split of the network as a reference partition, because it is the most objective measure describing the network; as described in Ref. [67], “The factions were merely ideological groupings, however, and were never organizationally crystallized. There was an overt sentiment in the club that there was no political division, and the factions were not named or even recognized to exist by club members.”

Figure 10 shows the karate club network, with color indicating the actual subsequent club split due to conflicts. Table II shows the modularity achieved by three methods, Q_B, $Q_A^{\text{Bernoulli}}$, and $Q_A^{\text{BLUE}}$, for three different ways of bipartitioning the network: the club split, club split with the exception of node 9 classified into the other group, and club split with the exception of node 9 and 10 classified into the other group. Bold fonts indicate maximum modularity for each method, which also represents the final partition results achieved with our implementation of each method. Modularity values are shown based on the binary values of indicator vectors s_A and s_B. Only $Q_A^{\text{Bernoulli}}$ precisely predicted the true split of the club. However, all methods produced very similar results, and inspection of Fig. 10 shows that nodes 9 and 10 are actually very close to both groups.

FIG. 10.

Karate club network. Nodes indicate 34 club members, and color indicates the actual split of the group after a conflict between its members.

TABLE II.

Results of karate club binary network partitioning using three methods: Q_B, $Q_A^{\text{Bernoulli}}$, and $Q_A^{\text{BLUE}}$. Values represent modularity achieved for the three partition results on the columns of the table. Bold font indicates maximum modularity, which also represents the final partition results achieved by each method.

	Club split	Club split except node 9	Club split except nodes 9 and 10
QB	0.3582	0.3715	0.3718
$Q_A^{\text{Bernoulli}}$	0.4671	0.4667	0.4662
$$Q_A^{\text{BLUE}}$$	0.3741	0.3872	0.3869

We additionally applied the above methods to the weighted version of the karate club network (Fig. 3 in Ref. [67]). All methods achieved maximum modularity for the actual club split with the exclusion of node 9, which effectively corresponds to the faction partition of the network. We also point out that modularity can increase further, for both the unweighted and weighted versions of the karate club network, with subsequent partition into four communities.

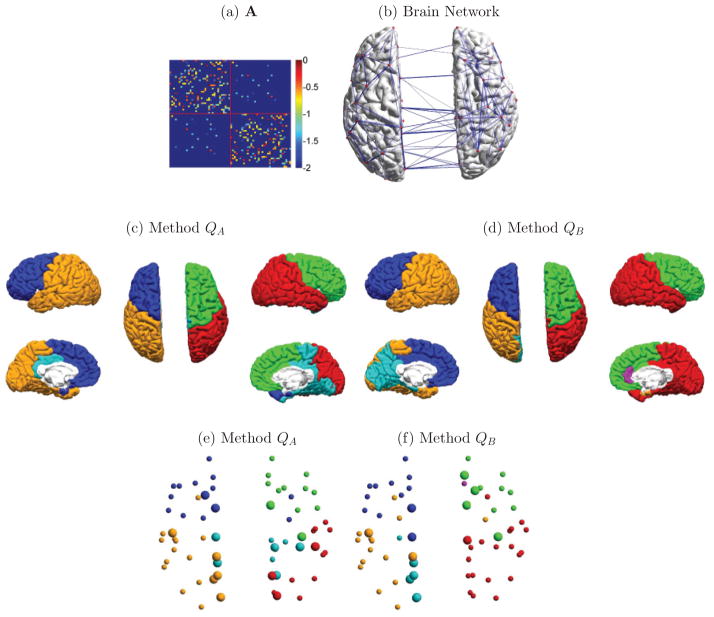
We further applied the Q_A and Q_B clustering methods to structural brain network data described in Ref. [18]. In this undirected weighted network, each node represents one of the 66 FreeSurfer-parcellated regions of the cerebral cortex, and edges represent the connection of regions in terms of axonal fiber density. Axonal fibers were extracted from diffusion spectrum imaging data, and then averaged across five subjects as described in Ref. [18]. Figure 11(a) and 11(b) displays the complete network, and Fig. 11(c) and 11(d) shows our clustering results with methods Q_A and Q_B. For method Q_A we used the BLUE null model in Eq. (15). Nodes for different groups are plotted using different colors. We also label hub nodes with larger spheres. Hub nodes denote regions that are highly connected to the network and were identified as those with a participation coefficient greater than 0.5 [18].

FIG. 11.

Graph analysis of a structural network based on diffusion brain imaging. (a) Adjacency matrix with the upper-left and lower-right quadrants corresponding to regions of interest on the right and left hemispheres, respectively; (b) structural brain network with edges greater than 0.1; (c) partition results for method Q_A. Color indicates cluster membership; (d) same as before for method Q_B; (e) partition results for method Q_A, but now spheres indicate ROIs and larger spheres indicate network hubs; (f) same as before for method Q_B.

Although the ground truth for this network is unknown, we observe that method Q_A produced a more symmetric between-hemisphere subnetwork structure than method Q_B [Fig. 11(c) and 11(d)]. Furthermore, several resting state studies [56] have identified the central role of precuneus and posterior cingulate in regulating brain activity in the default network. Method Q_A identified several hub nodes in this area, with a more symmetric organization than method Q_B [Fig. 11(e) and 11(f)].

To test Q_A and Q_B methods on a network with both positive and negative connections, we used the Beijing data set from the 1000 Functional Connectomes Project in NITRC (http://fcon1000.projects.nitrc.org/). The data set consists of 191 subjects of age 18–26, each having 7.5 minutes resting state fMRI recordings. The available data were already motion corrected, registered into the Harvard-Oxford probabilistic atlas, segmented, spatial smoothed, bandpass filtered, and subjected to nuisance analysis [71]. We constructed a functional network using a total of 96 available cortical ROIs as nodes and computed the correlation coefficient between the fMRI recordings in every pair of ROIs. The correlation coefficients were then transformed to z values using the Fisher transform z = arctanh(r) [72], which produces a weighted adjacency matrix A.

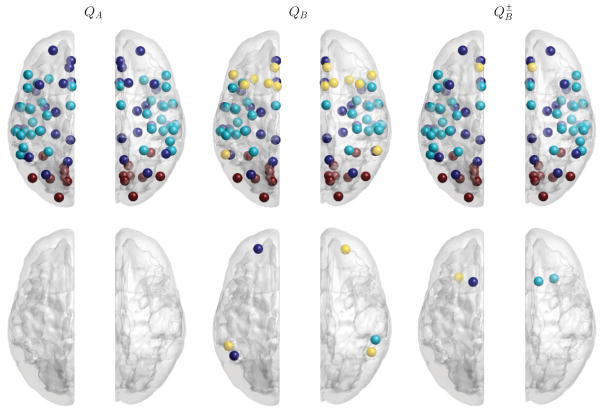
This real-world network contains both positive and negative connections, the former representing correlated spontaneous fluctuations within a network, and the latter anticorrelations between networks [56,74]. We applied Q_A and Q_B methods to partition the network, as well as a generalization of Q_B, denoted as $Q_B^{\pm }$, that can deal with negative connections [73]. Figure 12 shows that Q_A is the only method that achieves perfect across-hemisphere symmetry. The dark blue spheres represent the task-negative network, which includes a set of regions often termed the “default network,” namely, the posterior cingulate, precuneus, medial prefrontal areas, and others [56]; the cyan spheres represent the task-positive network, which includes the insula, sensory and motor cortices, and others; the red spheres represent the visual cortex, which has no intrinsic preference for either network.

FIG. 12.

Partitioning results with Q_A, Q_B, and $Q_B^{\pm }$ [73] methods of a real functional brain network. Different modules detected by the algorithm are labeled by color. First row indicates the symmetric across-hemisphere results while the second row highlights the asymmetric ROIs.

Method Q_B has unpredictable behavior with the presence of negative connections, and does not accurately cluster the task-negative network. Method $Q_B^{\pm }$ produces very similar results to Q_A; however, there are four asymmetric nodes and an additional cluster of yellow spheres that encompasses the left-right middle medial frontal cortex and the right Broca’s area.

VII. DISCUSSION

We have proposed several null models for modularity-based graph partitioning. Apart from being optimal for specific parametric distributions of edge strength, these models are also not limited by two constraints of the R null model, namely non-negative edge strength and the assumption of self-loops.

Model R uses the product of degrees of two nodes to evaluate their expected connection strength. This measure becomes meaningless when negative edges are allowed, because it can arbitrarily change sign. As a result, A − R has a random structure and is not useful to partition graphs, as indicated in Fig. 5(c). This is a well-known constrain and there are multiple studies generalizing the modularity definition to accommodate the negative values [73,75,76]. The basic idea behind these methods is to calculate modularity based on a weighted summation of two terms, each based on separate null models derived from either positive or negative edges. Although they overcome the problem of negative edges, these methods represent heuristic solutions with a required selection of weighted coefficients that affects clustering results [76]. In contrast, the Gaussian and BLUE null models require no model modifications or selection of mixing parameters. Nodes with negative connections are treated not only as disjoint, but also as repelling each other. The functional brain network in Fig. 12 illustrates such an example, with negative edges representing anticorrelations. Unlike the conventional method (Q_B) and its extension for negative edges ( $Q_B^{\pm }$), the BLUE null model achieves perfectly symmetric partition results.

As discussed in Sec. IV, model R always assumes self-loops, because the diagonal elements of the adjacency matrix are nonzero. However, real-world networks often do not allow self-loops, for example, traffic networks, brain networks, etc. As a result, model R often overestimates self-loop connections. This by itself may not seem important for partitioning graphs. But, given that model R has the same node degrees as the original graph (total sum of edges is constant), this also means that it underestimates all between-node connections. Figure 3(d) displays A − R, which has a negative bias in diagonal elements and a positive bias in off-diagonal elements. In particular, diagonal elements are strongly negative, while off-diagonal elements are mostly positive, even in the terms corresponding to intercluster connections (top right and bottom left quadrants). The latter causes the graph to often become inseparable with method Q_B, leading to NMI = 0 as indicated in our results. Method Q_A does not suffer from similar bias, and network topology can be properly modeled using matrix H.

Figures 3 and 4 show that method Q_B greatly benefits from increased values of σ². This is because increased σ² amplifies the difference between inter- and intracluster connections, which is a consequence of our graph simulation approach: We randomly draw from the Gaussian distribution and assign stronger values as intracluster edges and weaker values as intercluster edges. After some threshold, the difference between inter and intracluster connections is so large that the aforementioned bias in the Q_B approach no longer makes the graph inseparable [Fig. 3(a)]. On the other hand, method Q_A does not benefit as much from increased σ², because the null model (11) does not depend on the variance of the Gaussian distribution.

Both Q_A and Q_B methods have decreased performance when cluster sizes become very asymmetric (N₁/N very large). This is because the community structure becomes less prominent, eventually not even satisfying the weak sense community structure property [21].

Rewiring results in Fig. 6 show that method Q_B is not as close as Q_A to an actual rewiring scheme. This is true regardless of whether we include (Q_B) or exclude ( $Q_B^{\ast }$) diagonal terms and is explained by the aforementioned bias of the conventional null model toward increased self-loop connections and decreased intercluster connections. The $Q_A^{\text{Bernoulli}}$ model outperforms the $Q_A^{\text{BLUE}}$ model for all cases other than N < 8, where the small size of the network severely limits possible rewiring selections using the algorithm in Ref. [68].

Our partition results on binary networks show that all methods perform similarly. This includes the BLUE model, which is statistically optimal for Gaussian distributions of edge strength, but still performs well for the Bernoulli distribution. This may be indicative of a more general robustness of the BLUE model in cases that deviate from the multivariate Gaussian assumption.

Our karate network partition results with Q_B method are different from the ones reported in Ref. [22], even though both use the same null model R. This is because Ref. [22] used a different implementation of the Kernighan-Lin algorithm (discretization of elements of vector S_B), which may have resulted in a local maximum that produces different results for node 10. However, method Q_B achieves higher modularity for the partition result in the third column of Table II. Given that nodes 9 and 10 are about equally connected to both clusters and modularity is very close for all partitions, these results seem rather coincidental. For the karate club network, even higher modularity can be achieved by subsequent partitioning of the network into four subnetworks. However, by tuning the resolution parameter lambda in Eq. (23), results can be restricted to two clusters by selecting a value λ < 0.59 for the BLUE null models (a value smaller than one biases toward a more global structure).

To perform clustering, we selected the spectral partitioning method proposed in Ref. [23]. This method performs sequential bipartitions of the graph until maximum modularity is achieved. A variant of this method would be to use multiple eigenvectors to directly estimate multiple clusters [14,27,46,77]. While such method can potentially achieve better clustering results, this requires a priori knowledge of the number of clusters, a general problem dealt with by many methods with different levels of success [78–82].

Selecting which null model to use for clustering depends on the network at hand. In general, we recommend using the BLUE model in Eq. (16). Our results indicate that it performs reliably in a variety of networks regardless of the probability distribution of the network edges. It is also the optimal estimator (in the MMSE sense) when edges follow a Gaussian distribution. In the most common case of no prior information, the covariance matrix Σ_x is identity and the BLUE model is estimated by Eq. (11). Furthermore, if network topology allows for self-loops, the BLUE model can be estimated using Eq. (9) with an appropriate incidence matrix H. For the specific case of binary networks, the Bernoulli expected network in Eq. (5) and the BLUE model in Eq. (11) perform nearly equivalently.

Regarding the estimation of parameters for the null models, the mean in Eq. (4) can be estimated as $\mu =\frac{2m}{N(N-1)}$, while the probability parameter p in Eq. (5) can be estimated as $p=\frac{2m}{N(N-1)}$. The mean μ_x and covariance Σ_x in Eq. (16) depend on the prior information about the network. The commonly used null model in Eq. (11) does not require any parameter estimation.

VIII. CONCLUSION

Graph partition algorithms based on modularity have become increasingly popular in identifying network community structure. In this paper we introduced null models that are consistent for their assumed underlying distributions and in some cases lead to improved graph partitioning. The BLUE model performed well in all cases and therefore can be considered as a general method for graph partitioning and not restricted in its use to only Gaussian edge distributions.

Our models do not have some of the limitations of the R model, namely, they do not assume self-loops and can deal with negative connections. In addition, they accommodate possible network topology changes and can be more robust to noise. They performed well in our simulations and also appeared to successfully detect the community structure of real-world networks.

APPENDIX A: RANDOM NETWORK PARTIALLY CONDITIONED ON NODE DEGREES

Here we derive Eqs. (4) and (5), namely, the conditional expected network for the cases of Gaussian and binary networks, respectively. First, consider the conditional expected network in Eq. (3) for a Gaussian random network with independent identically distributed edge strengths with mean μ and variance σ². We assume a complete graph, i.e., a graph where every pair of distinct nodes is connected by a unique edge. We exclude self-loops; therefore the degree of a node in the graph is the sum of N − 1 Gaussian variables. For two nodes i and j with degrees k_i and k_j and connected with edge strength A_ij = t, we define two new random variables: $k_i^{\prime }=k_i-t$ and $k_j^{\prime }=k_j-t$. These variables represent the sum of all edges connected to nodes i and j, respectively, excluding the common connection A_ij. Therefore, their distribution is the sum of N − 2 Gaussian independent random variables with mean μ and variance σ². The conditional expectation in the right-hand side of Eq. (3) becomes

$$\begin{array}{l}P(k_i,k_j\mid A_{ij}=t)=P(k_i^{\prime }=k_i-t,k_j^{\prime }=k_j-t)\\ =P(k_i^{\prime }=k_i-t)·P(k_j^{\prime }=k_j-t),\end{array}$$ (A1)

where the first equality uses the newly defined random variables and the second equality results from the independence of $k_i^{\prime }$ and $k_j^{\prime }$, since they do not share any common edges.

We can now substitute in the right-hand side of Eq. (3) the known distributions:

$$P(A_{ij}=t)=\frac{1}{\sqrt{2\pi {\sigma }^2}}exp\left\{\frac{-{(t-\mu )}^2}{2{\sigma }^2}\right\},$$ (A2)

$$P(k_i^{\prime }=k_i-t)=\frac{1}{\sqrt{2\pi (N-2){\sigma }^2}}\times exp\left\{\frac{-{[k_i-t-(N-2)\mu ]}^2}{2(N-2){\sigma }^2}\right\},$$ (A3)

which produces the expression in Eq. (4).

For the binary network, the Bayesian formula (3) can be written as

$$\begin{array}{l}E(A_{ij}\mid k_i,k_j)=\sum _{t=0}^{1}t·P(A_{ij}=t\mid k_i,k_j)\\ =\sum _{t=0}^{1}t\frac{P(k_i,k_j\mid A_{ij}=t)P(A_{ij}=t)}{{\sum }_{u=0}^{1}P(k_i,k_j\mid A_{ij}=u)P(A_{ij}=u)}.\end{array}$$ (A4)

Following the same analysis as above for the Gaussian case, if we assume all edges in the binary network follow i.i.d. Bernoulli distribution with parameter p, we have

$$P(k_i,k_j\mid A_{ij}=t)P(A_{ij}=t)=\{\begin{array}{ll}P(k_i^{\prime }=k_i-1)·P(k_j^{\prime }=k_j-1)·p,\hfill & t=1,\hfill \\ P(k_i^{\prime }=k_i)·P(k_j^{\prime }=k_j)·(1-p),\hfill & t=0.\hfill \end{array}$$ (A5)

In this case, the corresponding node degrees $k_i^{\prime }$ follow a binomial distribution, as the sum of N − 2 i.i.d. Bernoulli random variables. For example,

$$P(k_i^{\prime }=k_i-1)=\left(\begin{array}{c}N-2\\ k_i-1\end{array}\right)p^{k_i-1}{(1-p)}^{N-1-k_i}.$$ (A6)

To obtain Eq. (5) for a binary network whose edges follow i.i.d. Bernoulli distribution, we apply Eqs. (A5) and (A6) to Eq. (A4).

APPENDIX B: GAUSSIAN RANDOM NETWORK WITH INDEPENDENT IDENTICALLY DISTRIBUTED EDGES

For the case of Gaussian random networks with independent identically distributed edge strengths, we have μ_x = μ1 and Σ_x = σ²I, which simplify the covariance matrices:

$${\mathrm{\sum }}_{\mathbf{k}}=\mathbf{H}{\mathrm{\sum }}_{\mathbf{x}}{\mathbf{H}}^T={\sigma }^2{\mathbf{HH}}^T,{\mathrm{\sum }}_{\mathbf{xk}}={\mathrm{\sum }}_{\mathbf{x}}{\mathbf{H}}^T={\sigma }^2{\mathbf{H}}^T.$$

Therefore, Eq. (9) now becomes

$$E(\mathbf{x}\mid \mathbf{Hx}=k)=\mu \mathbf{1}+{\mathbf{H}}^T{({\mathbf{HH}}^T)}^{-1}{\mathbf{k}}^{\ast },$$ (B1)

where k^* ≡ k − μ_k. The product HH^T has the structure

$${({\mathbf{HH}}^T)}_{ij}=\{\begin{array}{ll}N-1,\hfill & i=j\hfill \\ 1,\hfill & i\ne j\hfill \end{array},$$ (B2)

and we can write HH^T in the following format:

$${\mathbf{HH}}^T=(N-2){\mathbf{I}}_2+{\mathbf{1}}_N{\mathbf{1}}_N^T.$$ (B3)

The physical meaning of (HH^T)_ij is the number of common edges that nodes i and j share. In a complete graph without self-loops there is only one edge that links two distinct nodes while there are N − 1 edges associated with one node (on the diagonal of HH^T).

To calculate the inverse of HH^T, we apply the matrix inversion lemma [83] to Eq. (B3):

$${(\mathbf{A}+\mathbf{UCV})}^{-1}={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}\mathbf{U}({\mathbf{C}}^{-1}+{\mathbf{VA}}^{-1}\mathbf{U}){\mathbf{VA}}^{-1}$$ (B4)

with A = (N − 2)I_N, U = 1_N, $\mathbf{V}={\mathbf{1}}_N^T$, and C = 1. We denote I_N the identity matrix with dimension N and 1_N a unit column vector with dimension N. The inverse becomes

$${({\mathbf{HH}}^T)}_{ij}^{-1}=\{\begin{array}{ll}\frac{1}{N-2}-\frac{1}{2(N-1)(N-2)},\hfill & i=j\hfill \\ -\frac{1}{2(N-1)(N-2)},\hfill & i\ne j\hfill \end{array}.$$ (B5)

For the lth element of x, the conditional expectation in Eq. (B1) is

$$\begin{array}{l}E(x_l\mid \mathbf{Hx}=\mathbf{k})={(\mu \mathbf{1}+{\mathrm{\sum }}_{\mathbf{xk}}{{\mathrm{\sum }}_{\mathbf{k}}}^{-1}{\mathbf{k}}^{\ast })}_l\\ =\mu +{({\mathbf{H}}^T)}_l{({\mathbf{HH}}^T)}^{-1}·{\mathbf{k}}^{\ast }\\ =\mu +\frac{k_i^{\ast }+k_j^{\ast }}{N-1}-\sum _{s=1,s\ne i,s\ne j}^N\frac{k_s^{\ast }}{(N-1)(N-2)}\\ =\frac{k_i+k_j}{N-2}-\frac{2m}{(N-1)(N-2)},\end{array}$$ (B6)

where ${\mathbf{H}}_l^T$ denotes the lth row of H^T. In the above we used the fact that the ith and j th are the only nonzero elements of row ${\mathbf{H}}_l^T$. They are equal to one, indicating which nodes are associated with edge x_l. Therefore, a left multiplication with ${\mathbf{H}}_l^T$ results in the addition of ith and j th rows of matrix (HH^T)⁻¹.

APPENDIX C: DERIVATION OF BEST LINEAR UNBIASED ESTIMATOR (BLUE)

To solve for the BLUE estimator ${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}=\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}$ in Eq. (14), we set the corresponding derivatives with respect to L̂ and b̂ to zero:

$${\frac{\partial \mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})}{\partial \widehat{\mathbf{b}}}|}_{{\widehat{\mathbf{x}}}_{\mid \mathbf{k}}={\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}=\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}}=0,$$ (C1)

$${\frac{\partial \mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})}{\partial \widehat{\mathbf{L}}}|}_{{\widehat{\mathbf{x}}}_{\mid \mathbf{k}}={\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}=\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}}=0.$$ (C2)

The objective function 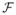(x̂_|k) can be written as

$$\mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})=E\{{({\widehat{\mathbf{x}}}_{\mid \mathbf{k}}-\mathbf{x})}^T({\widehat{\mathbf{x}}}_{\mid \mathbf{k}}-\mathbf{x})\}=E\{tr({\widehat{\mathbf{x}}}_{\mid \mathbf{k}}-\mathbf{x}){({\widehat{\mathbf{x}}}_{\mid \mathbf{k}}-\mathbf{x})}^T\}.$$ (C3)

To compute (C1) and (C2), we need to estimate derivatives of the trace of several matrix products. We will therefore use the following formulas, which are true for any matrices A, B, C, and X, that result in an n × n argument for trace tr():

$$\frac{\partial tr(\mathbf{AXB})}{\partial \mathbf{X}}=\frac{\partial tr({\mathbf{B}}^T{\mathbf{X}}^T{\mathbf{A}}^T)}{\partial \mathbf{X}}={\mathbf{A}}^T{\mathbf{B}}^T,$$ (C4)

$$\frac{\partial tr({\mathbf{AXBX}}^T\mathbf{C})}{\partial \mathbf{X}}={\mathbf{A}}^T{\mathbf{C}}^T{\mathbf{XB}}^T+\mathbf{CAXB}.$$ (C5)

A proof of these formulas is given later in this section.

The derivatives are now estimated as follows:

$$\begin{array}{l}\frac{\partial \mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})}{\partial \widehat{\mathbf{b}}}=\frac{\partial }{\partial \widehat{\mathbf{b}}}\{E[tr((\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x}){(\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x})}^T)]\}\\ =E\left[\frac{\partial }{\partial \widehat{\mathbf{b}}}\{tr((\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x}){(\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x})}^T)\}\right]\\ =E[2\widehat{\mathbf{L}}\mathbf{k}+2\widehat{\mathbf{b}}-2\mathbf{x}]\\ =2\widehat{\mathbf{L}}{\mathit{\mu }}_{\mathbf{k}}+2\widehat{\mathbf{b}}-2{\mathit{\mu }}_{\mathbf{x}},\end{array}$$ (C6)

$$\begin{array}{l}\frac{\partial \mathcal{F}({\widehat{\mathbf{x}}}_{\mid \mathbf{k}})}{\partial \widehat{\mathbf{L}}}=\frac{\partial }{\partial \widehat{\mathbf{L}}}\{E[tr((\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x}){(\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x})}^T)]\}\\ =E\left[\frac{\partial }{\partial \widehat{\mathbf{L}}}\{tr((\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x}){(\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}-\mathbf{x})}^T)\}\right]\\ =E[2\widehat{\mathbf{L}}{\mathbf{kk}}^T+2\widehat{\mathbf{b}}{\mathbf{k}}^T-2{\mathbf{xk}}^T]\\ =2\widehat{\mathbf{L}}E[{\mathbf{kk}}^T]+2\widehat{\mathbf{b}}E[{\mathbf{k}}^T]-2E[{\mathbf{xk}}^T]\\ =2\widehat{\mathbf{L}}({\mathbf{\sum }}_{\mathbf{k}}+{\mathit{\mu }}_{\mathbf{k}}{\mathit{\mu }}_{\mathbf{k}}^T)+2\widehat{\mathbf{b}}{\mathit{\mu }}_{\mathbf{k}}^T-2({\mathbf{\sum }}_{\mathbf{xk}}+{\mathit{\mu }}_{\mathbf{x}}{\mathit{\mu }}_{\mathbf{k}}^T).\end{array}$$ (C7)

By setting both derivatives to zero and solving the resulting system of equations with respect to L̂ and b̂, we get

$$\Rightarrow \{\begin{array}{l}\widehat{\mathbf{b}}={\mathit{\mu }}_{\mathbf{x}}-{\mathbf{\sum }}_{\mathbf{xk}}{\mathbf{\sum }}_{\mathbf{k}}^{-\mathbf{1}}{\mathit{\mu }}_{\mathbf{k}}\hfill \\ \widehat{\mathbf{L}}={\mathbf{\sum }}_{\mathbf{xk}}{\mathbf{\sum }}_{\mathbf{k}}^{-\mathbf{1}}.\hfill \end{array}$$ (C8)

Therefore, the BLUE estimator becomes the same as Eq. (9), also given here for convenience:

$${\widehat{\mathbf{x}}}_{\mid \mathbf{k}}^{\text{BLUE}}=\widehat{\mathbf{L}}\mathbf{k}+\widehat{\mathbf{b}}={\mathit{\mu }}_{\mathbf{x}}+{\mathbf{\sum }}_{\mathbf{xk}}{\mathbf{\sum }}_{\mathbf{k}}^{-\mathbf{1}}(\mathbf{k}-{\mathit{\mu }}_{\mathbf{k}}).$$ (C9)

Equations (C4) and (C5) are given in the calculus section in Ref. [84], and a brief proof follows. Assume e_i a vector containing 1 in ith position and zeros elsewhere. Then $d\mathbf{X}/{dx}_{ij}={\mathbf{e}}_i{\mathbf{e}}_j^T$ [85]. Consequently,

$$\begin{array}{l}d/{dx}_{ij}(tr(\mathbf{AXB}))=tr\left({\mathbf{Ae}}_i{\mathbf{e}}_j^T\mathbf{B}\right)=tr\left({\mathbf{e}}_j^T{\mathbf{BAe}}_i\right)\\ ={\mathbf{e}}_j^T{\mathbf{BAe}}_i={(\mathbf{BA})}_{ji}={({\mathbf{A}}^T{\mathbf{B}}^T)}_{ij}.\end{array}$$ (C10)

Similarly,

$$\begin{array}{l}d/{dx}_{ij}(tr({\mathbf{AXBX}}^T\mathbf{C}))=tr\left({\mathbf{Ae}}_i{\mathbf{e}}_j^T{\mathbf{B}\mathbf{X}}^T\mathbf{C}+{\mathbf{AXBe}}_j{\mathbf{e}}_i^T\mathbf{C}\right)\\ =tr\left({\mathbf{Ae}}_i{\mathbf{e}}_j^T{\mathbf{B}\mathbf{X}}^T\mathbf{C}\right)+tr\left({\mathbf{AXBe}}_j{\mathbf{e}}_i^T\mathbf{C}\right)\\ =tr\left({\mathbf{e}}_j^T{\mathbf{B}\mathbf{X}}^T{\mathbf{CAe}}_i\right)+tr\left({\mathbf{e}}_i^T\mathbf{CAXB}{\mathbf{e}}_j\right)\\ ={({\mathbf{A}}^T{\mathbf{C}}^T{\mathbf{XB}}^T+\mathbf{CAXB})}_{ij}.\end{array}$$ (C11)