Rising inequalities in income and health in China: Who is left behind?

Abstract

In recent decades, China has experienced double-digit economic growth rates and rising inequality. This paper implements a new decomposition approach using the China Health and Nutrition Survey (1991–2006) to examine the extent to which changes in level and distribution of incomes and in income mobility are related to health disparities between rich and poor. We find that health disparities in China relate to rising income inequality and in particular to the adverse health and income experience of older (wo)men, but not to the growth rate of average incomes over the last decades. These findings suggest that replacement incomes and pensions at older ages may be one of the most important policy levers for reducing health disparities between rich and poor Chinese.

1. Introduction

The relationship between income and health, and the inequality in each of these, has been documented in many settings, but few countries have experienced changes in their income distribution as dramatic and as rapid as China has over the last few decades (Benjamin et al., 2008). China’s rapid transition since the early 1980s from a completely planned economy to a more market led economy has led to unprecedented economic growth: China’s real GDP in 2009 was more than twelvefold of its real GDP in 1980 (International Monetary Fund, 2010). Poverty reductions were similarly spectacular: between 1981 and 2005 the poverty headcount ratio ($1.25 poverty line) fell from 94% to 26% in rural areas and from 44% to 2% in urban areas (World Bank, 2005a). The income distribution has not only shifted upward, it has also substantially widened, leading to rising inequality in incomes (Benjamin et al., 2008) both within and between regions.

However, this rapid economic growth did not spark equally impressive health improvements. While, for instance, average life expectancy has continued to grow, China has lost its high achiever position. The Chinese average life expectancy is no longer higher than expected on the basis of average income, indicating that the pace of health gains has slowed down (World Bank, 2005b). Moreover, health disparities between urban and rural regions and between rich and poor have grown giving rise to increased public dissatisfaction (Tang et al., 2008). The Chinese government has recognized these challenges and has responded to them. Reform of health care has been ongoing for several years and in 2008 the Ministry of Health announced major new policy directions for achieving Healthy China by 2020 (Tang et al., 2008). These reforms have somewhat alleviated the health burdens faced by the (rural) poor, but concerns remain (Hougaard et al., 2011; Wagstaff et al., 2009a, b). At the same time, China has experienced several other demographic and economic transitions. The population is rapidly growing older, becoming more urbanized and economic activity has shifted from largely agricultural to industrial. A priori, it is not obvious how these dramatic changes in the Chinese society have influenced the relation between (changes in) income, health, their distributions and the health gaps between rich and poor.

One way of uncovering the mechanics underlying these relationships is to decompose the (changes in the) degree of income-related health inequality (IRHI). Contoyannis and Forster (1999) initiated the examination of conditions under which increases in income and income inequality will be associated with higher levels of IRHI as measured by a rank-based concentration index. Van Ourti et al. (2009) have generalized their argument using a cohort decomposition approach and have used it to examine inequalities in health by income in European countries in the 1990s. In this paper, we propose an extension and simplification of their decomposition framework to uncover these mechanics in China. The simplification derives from recognizing that health – unlike income – is a bounded variable at the upper end and using an adjusted rank-based measure of absolute inequality instead of the concentration index. The extension also considers the impact on IRHI of income mobility by summarizing differences in income re-ranking between groups defined by non-income characteristics. It proves to be crucial for an improved understanding of the evolution of IRHI. We then apply this framework to an analysis of inequalities in self-reported health by income in a cohort followed over 6 waves of the China Health and Nutrition Survey (CHNS) and spanning a period of 15 years (1991–2006).

We find that the degree to which health is associated to income – as measured by a rank-based measure of absolute inequality – more than tripled over those 15 years. This substantive rise turns out to be not related to the massive income growth and only weakly to the growth in income inequality. It is almost entirely explained by the very different income mobility by age and gender. Especially the much more adverse experience of older females in terms of their declining income position over time and lower than average health level seems to have been important. The lower than average income growth due to a lack of adequate retirement incomes and self-insurance mechanisms for sick and old women, especially in rural areas, is a likely candidate to explain this phenomenon.

In the next section we briefly review what is known on income and health developments in China since the start of the economic reforms. In Section 3 we discuss our new decomposition framework which is then applied to Chinese panel data in Section 4. We conclude with a discussion of potential implications.

2. Income, health and inequality in China

China is no different from any other country in exhibiting inequalities in income and health and a strong association between the two (Gustafsson et al., 2008; Liu et al., 2008; Chen and Meltzer, 2008; Tang et al., 2008). What makes China more unique is (i) the pace of changes in recent decades and (ii) the sheer size of the country reflecting such immense differences in levels of development.

The rapid growth in average incomes in China has been accompanied by an increased variability in incomes (Kanbur and Zhang, 2005; Gustafsson et al., 2008; Lin et al., 2008; Shen and Yao, 2008; Sutherland and Yao, 2011; Yang, 1999), wealth (Gustafsson et al., 2006) and consumption (Keidel, 2009). Developments in nationwide income inequality obviously mask important geographic differentials. Two geographic distinctions appear particularly relevant in this respect. A first important geographic division of China is that between eastern provinces near the coast and the western non-coast provinces. Historically the eastern coastal regions have had higher levels of GDP than the interior regions (Chen and Fleisher, 1996). More recently, the coastal provinces have coupled a stronger rise in mean per capita income with a more modest increase in income inequality compared to the interior regions (Benjamin et al., 2008). While the growth of the inter-regional inequality was anticipated by the government, which favored the coastal provinces in the early years of the reforms, the spillovers to other regions were insufficient to reduce the initial inter-regional income inequality (Brun et al., 2002).

A second geographic divide is that between rural and urban areas. Large urban-rural disparities in income have persisted for a long time due to, among others, the introduction of the labor-mobility restricting Hukou system (Wang and Piesse, 2010), and to welfare and financial policies that favored the urban areas (Yang, 1999). This inequality between rural and urban areas contributes substantially to total income inequality in China, and is rapidly growing (Yang, 1999) such that China’s urban-rural income gap is now one of the largest in the world (Chang, 2002; Sicular et al., 2007). Within-urban and within-rural income inequality are currently of similar magnitude (Sutherland and Yao, 2011).

Several studies have documented health variation by income and region in China. For example, Liu et al. (2008) report an income gradient in self-reported health in rural areas, while Chen and Meltzer (2008) report income gradients for hypertension and obesity. Other studies have documented substantial health variation by region, e.g. life expectancy between and within provinces (Tang et al., 2008), infant mortality between and within inland and coastal regions (Zhang and Kanbur, 2005) and between rural and urban areas (Shi et al., 2008), or self-reported health between rural and urban areas (Van de Poel et al., 2012).

Fewer studies have measured trends in IRHI. Chen et al. (2007) use the China Health and Nutrition Survey to find that child malnutrition was concentrated among the poor in 1989, and that this concentration decreased in the early nineties but rose again in 2000. Using the same data, Yip (2010) does not find these inequalities to have either widened or narrowed. Wagstaff et al. (2009a) use data from the maternal and child health (MCH) surveillance system of 2003 and report large inequalities in infant, under-five and maternal deaths across counties. Recently, Feng et al. (2010) examined the evolution of socio-economic disparities in maternal mortality by county (ranked by income) between 1996 and 2006 in the MCH and find no clear trend in the concentration index.

Overall, we conclude that (i) there is enormous variation in China in both the level and distribution of income and health, (ii) which are associated across place and time and (iii) no study has yet attempted to trace out how developments of income growth, income inequality and income mobility are related to income-related health inequality developments over the recent decades.

3. Decomposing income-related health inequalities into income growth, mean-preserving income changes and income mobility

We measure income-related health inequalities by the variation of health across the income dimension (Erreygers, 2009a; Wagstaff and van Doorslaer, 2000) and summarize its association with the income distribution using a decomposition methodology (Wagstaff et al., 2003). Since this paper explicitly focuses on the exceptional income growth rates that China experienced over the last three decades, we isolate the role of changes in average incomes from other changes in the income distribution. To this end, we extend the decomposition method proposed by Van Ourti et al. (2009) such that it accounts for the bounded nature of health (Erreygers and Van Ourti, 2011a). We also provide a new interpretation of this decomposition that – much like the work of Allanson et al. (2010) – stresses the role of income mobility or re-ranking.

3.1. Measurement of income-related health inequalities

IRHI is most commonly measured using the standard concentration index. It resembles a Gini index of health, but replaces the rank of health by the rank of income such that it measures the variation of health across the income dimension (Wagstaff et al., 1991). An important implicit value judgment is that equi-proportionate health changes leave the concentration index unchanged. This is a common assumption in the uni-dimensional income inequality literature (Lambert, 2001), but recent work shows that this condition is less innocuous in the case of bi-dimensional IRHI (Erreygers, 2009a,b; Erreygers and Van Ourti, 2011a,b; Lambert and Zheng, 2011; Wagstaff, 2009, 2011a, b). When health has a finite upper and lower bound (as in our empirical application) an impossibility result arises: starting from the same initial health distribution, the same equi-proportionate health change might rank inequalities in health and ill-health differently. Hence, when faced with a bounded health variable, one cannot satisfy at the same time the condition that inequalities in health and ill-health rank a set of health distributions similarly, and the condition that relative health changes leave the inequality ranking unchanged. We put more emphasis on the former condition. It follows that we can no longer resort to the concentration index, but instead use the Erreygers index (2009a) which indicates that IRHI remains unchanged under equal health additions¹:

$$C_E(h\mid y)=\frac{8}{n^2(h^{max}-h^{min})}\sum _{i=1}^n{z}_i{h}_i=\frac{8}{n^2}\sum _{i=1}^n{z}_i{h}_i$$ (1)

where h_i equals the level of health of individual i,² y_i equals income, and n stands for the number of observations. z_i equals the deviation of individual i’s income rank from the mean income rank³; and increases linearly between (1 − n)/2 and (n − 1)/2 and takes zero for the individual with the mean income rank. In other words, the z_i’s are negative for the poorest half of the population and positive for the richest half, and sum to zero across the entire population. Hence, the Erreygers index will be negative if the poor have overall better health than the rich (pro-poor IRHI), and positive values will imply the opposite (pro-rich IRHI).

3.2. Changes in the income distribution and IRHI: a decomposition approach

Our approach extends the approach of Van Ourti et al. (2009) in two ways. First, we simplify their decomposition by measuring IRHI with the Erreygers index. This simplification is the logical consequence of the change of focus from invariance to relative to invariance to absolute health changes, as it no longer requires to understand how changes in the income distribution are related to average health levels. Second, we show that the decomposition is richer than originally envisaged by the authors. Van Ourti et al. (2009) isolate the role of changes in average incomes from other changes in the income distribution, but we show that this implies that IRHI also depend on the association between income mobility and the evolution in other determinants of health.

Our extended decomposition is a cohort-decomposition, i.e. it unravels how IRHI evolves over time for a given cohort of individuals such that we can abstract from changes in IRHI that are driven by compositional changes of the underlying population. We show later in this section that our cohort-decomposition also isolates the aging-effect of our cohort such that we can study the change of IRHI over time in isolation from aging. We assume in this section that individuals remain in the cohort over the entire time period, but we allow for drop-out in the empirical part of the paper. In the remainder of this section, we discuss our extended decomposition in more detail.

We start by describing the association between health and income y_i conditional on a set of K other variables x_i (e.g. age, sex) and add a time subscript t = 1, …, T.

$$h_{it}=\alpha +\phi (y_{it})+x_{it}^{\prime }\beta$$ (2)

where φ(·) is a (non-linear) function of income, α is a parameter, and β is a parameter vector of dimension K. As the shape of the function φ(·) will largely determine the association between the evolution of IRHI and changes in the income distribution (see below), we allow for a very general functional form.

Three simplifying assumptions underlie Eq. (2). In the empirical part of the paper, we document that these assumptions are not inconsistent with our data. First, we rule out interactions between the non-linear function of income φ(·) and the set of other variables x_i. Second, we assume that the coefficients in Eq. (2) are fixed over time which has the advantage that changes in IRHI are associated to changes in the explanatory variables only (and not to changes in the coefficients). Finally, Eq. (2) ignores dynamics. We also neglect for now that one has to estimate the parameters α and β, and the function φ(·); and do not include an error term since we use an interval regression model to estimate these parameters in the empirical part of the paper (Van Doorslaer and Jones, 2003). We discuss this in more detail in Section 4.1.

We express the evolution of IRHI as the difference between the Erreygers index in period t and the first period, and substitute Eq. (2) in Eq. (1):

$$C_E(h_t\mid y_t)-C_E(h_1\mid y_1)=\frac{8}{n^2}\sum _{i=1}^n\left\{[z_{it}\phi (y_{it})-z_{i1}\phi (y_{i1})]+\sum _{k=1}^K{\beta }^k[z_{it}{x}_{it}^k-z_{il}{x}_{i1}^k]\right\}$$ (3)

Eq. (3) provides us with a decomposition of the evolution of IRHI into those related to changes in the income distribution (i.e. the first term between square brackets) and into those due to changes in other determinants, weighted by the respective z_i’s (i.e. the second term between square brackets); it does not, however, allow one to separate the effect of proportional income growth from other changes in the income distribution. Van Ourti et al. (2009) disentangle both effects by introducing two hypothetical health states in period t. The first is the situation of ‘proportional income growth’ (pg) in which total income growth benefits everyone proportionately such that individual incomes grow at the same rate as average income (Y_t), i.e. $h_{it}^{pg}=\alpha +\phi (y_{it}^{pg})+x_{it}^{\prime }\beta$ with $y_{it}^{pg}=y_{i1}(Y_t/Y_1)$. Second, we introduce a health state in which income ‘does not grow’ (ng), but the other variables evolve at their actual rate, i.e. $h_{it}^{ng}=\alpha +\phi (y_{i1})+x_{it}^{\prime }\beta$.⁴

We have now sufficient information to derive our extended decomposition:

$$\begin{array}{l}{C}_E(h_t\mid y_t)-C_E(h_1\mid y_1)=\underset{(2)\text{and}(3)}{\underbrace{[C_E(h_t\mid y_t)-C_E(h_t^{pg}\mid y_1)]}}+\underset{(1)}{\underbrace{[C_E(h_t^{pg}\mid y_1)-C_E(h_t^{ng}\mid y_1)]}}+\underset{(4)}{\underbrace{[C_E(h_t^{ng}\mid y_1)-C_E(h_1\mid y_1)]}}\\ =\frac{8}{n^2}\left\{\underset{(1)}{\underbrace{\sum _{i=1}^n{z}_{i1}[\phi (y_{it}^{pg})-\phi (y_{i1})]}}+\underset{(2)}{\underbrace{\sum _{i=1}^n[z_{it}\phi (y_{it})-z_{i1}\phi (y_{it}^{pg})]}}+\underset{(3)}{\underbrace{\sum _{i=1}^n(z_{it}-z_{i1})\left(\sum _{k=1}^K{\beta }^k{x}_{it}^k\right)}}+\underset{(4)}{\underbrace{\sum _{i=1}^n{z}_{i1}\left[\sum _{k=1}^K{\beta }^k(x_{it}^k-x_{i1}^k)\right]}}\right\}\end{array}$$ (4)

which exploits that $C_E(h_t^{pg}\mid y_t^{pg})\equiv C_E(h_t^{pg}\mid y_1)$ and $y_{it}^{ng}\equiv y_{i1}$. Eq. (4) shows that we can decompose the evolution of IRHI into four effects: (i) a term related to overall income growth; (ii) a term related to other mean-preserving changes in the income distribution; (iii) a term related to differences in income mobility across non-income variables; and (iv) a term related to the association between changes in the other variables and z_i in the first period.

Our proposed decomposition has similarities and dissimilarities with existing longitudinal decompositions. The Allanson et al. (2010) decomposition relies, unlike our decomposition, on the standard concentration index and is therefore more akin to Van Ourti et al. (2009). It disentangles the evolution of IRHI into two separate aspects, i.e. ‘income-related changes in health’ and ‘health-related changes in income rank’. The former measures the extent to which health improves more for the initially rich or poor, and the latter focuses on the extent to which those in good health were more successful in climbing the income ladder. Our decomposition coincides with Allanson et al. (2010) when the sole interest is the evolution of IRHI and not its association with changes in the income distribution. Formally, this would imply to removing Eq. (2) from our decomposition.⁵ With Eq. (2), terms 1 and 4 of our decomposition can be categorized as ‘income-related changes’, term 3 as ‘health-related’ while term 2 contains features of both aspects (see below for a more detailed discussion of term 2).

Income growth

Term 1 in Eq. (4) captures the association between the evolution of IRHI and average income growth. It describes the difference between IRHI in the hypothetical health state in which all individuals would have had their incomes changed proportionately and IRHI in the state in which incomes would have remained at the level of the first period. Recalling that the z_it’s sum to zero and increase linearly when moving from the poorest to the richest individual is sufficient to understand that a positive/negative value of term 1 will occur when $\phi (y_{it}^{pg})-\phi (y_{i1})$ is ‘on average’ increasing/decreasing with income. Intuitively this means that IRHI will rise/decrease when the same proportional income change has a larger/smaller health effect for individuals with a higher initial income.⁶ Whether and how this relationship between health and proportional income increases varies with income will depend on the shape of φ(·). This highlights the importance of choosing a flexible functional form for income in Eq. (2), rather than – as is usual in the literature – sticking to a functional form (like e.g. the natural logarithm) that predetermines how the health effect of proportional income changes varies with income.

Other mean-preserving changes in the income distribution

Term 2 in Eq. (4) measures the change in IRHI associated with changes in the distribution of income that are unrelated to proportional income growth. Each individual’s contribution can be re-written as $(z_{it}-z_{i1})\phi (y_{it})+[\phi (y_{it})-\phi (y_{it}^{pg})]z_{i1}$ which reveals that term 2 combines changes from z_i1 to z_it (which are a function of the income ranks) with mean-preserving changes in the income levels from $y_{it}^{pg}$ to y_it. These mean-preserving changes consist of income gains ( $y_{it}>y_{it}^{pg}$) and income losses ( $y_{it}<y_{it}^{pg}$) which will always cancel out on average. When the income ranks do not change over time (z_it = z_i1), the impact on IRHI will depend on the functional form of φ(·) and on the distribution of these mean preserving changes across initial income ranks. In practice, income ranks will most likely also change for some individuals (z_it ≠ z_i1), and the impact of this re-ranking on IRHI will depend on the interplay between re-ranking and the functional form of φ(·).

It thus seems that little can be said a priori about the effect of term 2 on IRHI,⁷ but when one considers more specific patterns for the mean-preserving income changes and the functional form of φ(·), this is no longer true. When initially richer individuals experience income gains and initially poorer individuals income losses (relative to $y_{it}^{pg}$) and when there are health returns to additional income (φ′(·)>0), IRHI will rise since $[\phi (y_{it})-\phi (y_{it}^{pg})]z_{i1}>0$ for all individuals; and this increase of IRHI will be further reinforced by income re-ranking since the value of re-ranking (z_it − z_i1) will be more heavily weighted for richer individuals since φ(·)>0. When alternative patterns for the mean-preserving income changes and/or the functional form of φ(·) are considered, one will in many cases still be able to predict the sign of term 2, but not always. In particular, when the sign of φ′(·) is not fixed – additional income may result in health returns or losses depending on the level of income – or when income gains and income losses (and hence also income re-ranking) do not on average cluster among the richer or poorer.

While the subdivision of term 2 in (z_it − z_i1)φ(y_it) and $[\phi (y_{it})-\phi (y_{it}^{pg})]z_{i1}$ helps to understand the mechanical relation between mean-preserving changes in the income distribution and the evolution of IRHI, we only calculate the total of term 2 in the empirical part of this paper. A further subdivision would contribute little to the goal (but increase the complexity) of understanding how changes in the income distribution – here subdivided in proportional income growth, mean-preserving income changes, and income re-ranking across non-income variables (term 3) – relate to the evolution of IRHI. This can be understood by comparing with our treatment of the non-income variables for which we do exploit the additional subdivision (i.e. terms 3 and 4). In these cases, the subdivision reveals whether changes in the non-income variables or income re-ranking matter most. In contrast, when further subdividing term 2, one learns whether changes in one dimension – expressed once as levels and once as ranks – matter most.

Income mobility across non-income variables

Term 3 in Eq. (4) illustrates that the evolution in IRHI is also driven by the association between the non-income variables in Eq. (2) and changes in the income ranks. Its interpretation depends on the sign of β^k, which measures the health effect of the non-income variables. When this effect is positive, all that is needed to increase IRHI is that those already experiencing better health because of the non-income variables, e.g. the young, move up in the income distribution, i.e. z_it > z_i1. When the health effect is negative, the opposite result holds. In other words, this term identifies the contribution of differences in income mobility across the non-income variables to IRHI (Allanson et al., 2010; Jones and Nicolás, 2004).

Similar to other decomposition methods (Fortin et al., 2011), the interpretation of term 3 is more complicated when x_it includes dummy variables representing categorical variables. First, ${\beta }^k{x}_{it}^k$ measures in that case the health effect of a change in the dummy from 0 to 1. Second, the choice of the reference category (e.g. whether we take males or females as the reference category) matters for the contribution of each dummy variable, but does not matter for the sum across all dummy variables.⁸ This means that the contribution of a separate dummy should be interpreted with respect to the reference group.

Changes in other variables and initial income ranks

Finally, term 4 shows that the evolution of IRHI is also determined by the way in which changes in other non-income variables are related to Z_i1 (which is a function of the income rank in the first period). For example, when age is included in X_it, term 4 will indicate whether the health effect of getting older ( ${\beta }^{\mathit{age}}(x_{it}^{\mathit{age}}-x_{i1}^{\mathit{age}})$) is related to the initial income rank. In other words, it will isolate the aging of our cohort from the evolution of IRHI over time.

Summing up, our approach decomposes the evolution of IRHI into four components and builds on a regression linking health to income and other non-income variables. The first two elements are related to the marginal income distribution only. First, equi-proportionate income growth is associated with rising IRHI when proportional income changes have larger health effects among those with higher incomes. Second, mean-preserving changes in the income distribution lead to rising IRHI when positive health returns to additional income are combined with mean-preserving income changes that are clustered as income gains among the richer individuals and as income losses among the poorer individuals. We re-emphasize the importance of allowing for a flexible functional form of income. The two remaining elements of the decomposition are related to the interdependence between changes in the income distribution and changes in the non-income variables. We find that income mobility (i.e. individuals moving up the income rank) will lead to increasing IRHI when it disproportionally favors those who are already healthy (e.g. the young). We also show that changes in non-income variables only matter insofar as these are related to the initial income rank.

4. Data and empirical implementation

We use the China Health and Nutrition Survey (CHNS) to analyze the evolution of IRHI in China, and the extent to which it is associated with changes in the Chinese income distribution. The CHNS is an ongoing panel data set that covers nine different provinces of China. For details of the CHNS we refer to the project website (Carolina Population Center, 2010).

4.1. Estimating the relation between health, income and non-income variables

Our measure of individual health is based on the four possible responses to a self-reported health (SAH) question. In all waves, individuals were asked “Right now, how would you describe your health compared to that of other people of your age?”: Excellent, Good, Fair or Poor?⁹ These ordered responses are not suitable for measuring inequality with a rank-dependent inequality index such as the Erreygers index since they impose that differences between subsequent SAH categories always represent the same health change (Erreygers and Van Ourti, 2011b). Instead, we use an interval regression estimation method proposed by Van Doorslaer and Jones (2003). It involves the estimation of an ordered probit model with thresholds not estimated but imposed from external data. This interval regression has the advantage of combining (i) the estimation of the relation between income and health in Eq. (2) with (ii) producing a predicted health score that we will use as the measure of health throughout our analyses and that has interval scale properties with a well-defined minimum and maximum value such that it is compatible with the Erreygers index:

$$h_{it}^{\ast }=a+f(y_{it})+x_{it}^{\prime }b+e_{it}$$ (5)

where $h_{it}^{\ast }$ equals latent health, e_it ~ N(0, σ²), and a, b, f( ) are the empirical counterparts of α, β and φ( ) in Eq. (2). We impose thresholds obtained from the cumulative distribution of the Chinese visual analog scale (VAS) in the World Health Organization’s Multi-Country Survey Study on Health and Responsiveness (Üstün et al., 2003). A visual analog scale allows respondents to rate their general health level along a continuous line. The VAS thresholds are obtained by calculating the cumulative frequency of VAS for each SAH category assuming a stable mapping of SAH into VAS (Van Doorslaer and Jones, 2003). The resulting thresholds are 0.91 (excellent/good), 0.80 (good/fair) and 0.50 (fair/poor); and the minimum and maximum VAS scores are 0 (minimum health) and 1 (maximum health). These thresholds allow us to interpret the predictions from the interval regression as VAS scores. They also show that the assumption of similar health differences between subsequent SAH categories – which would be imposed when using the ordered SAH responses – is unrealistic.

Household income is another crucial variable in this study. The CHNS collects detailed information on various income sources of the household, including income from wages, agriculture, own business and public/private transfers. Household income has been expressed in 2006 Yuan prices (¥100 = €9.83) using consumer price indices specific to each wave, province and county; an equivalence scale is used to allow for differences in household size by dividing household income by the square root of household size (Van de Poel et al., 2012). We use a flexible parameterization of the income effect since it is crucial for our decomposition approach to allow for heterogeneity in income effects across poor and rich individuals. We use a polynomial transformation of income as it is differentiable across the entire income range, and let the data determine the order of the polynomial by selecting the most parsimonious polynomial that does not statistically differ from a fifth order polynomial (at a 1% significance level).

The other variables x_it consist of a set of age–sex dummies, and a set of regional dummies. Sufficiently wide age ranges were adopted (10–29, 30–49, 50–69 and 70+) to ensure that all sex-age categories contain sufficient observations in each period over the 15 year study period. We also account for regional differences by including information on the region of residence. Following Bramall (2009) and Tafreschi (2011), we have divided the CHNS into four regions, defined by coastal/inland province and urban/rural areas reflecting that urban regions, and especially those in coastal provinces, have experienced the strongest economic development in China.

We only include demographic and regional non-income variables in Eq. (5) since we want to provide evidence on the total association between changes in the distribution of income and the evolution of IRHI. We have not included variables that are potentially endogenous and related to the mechanisms underlying this association (such as education, labor force behavior, lifestyles, health insurance) as it would affect the estimate of the magnitude of this association. Hence, we only include variables that are exogenous to the association between income and health. This obviously holds for the standardizing variables age and sex, but in our context also for region since the CHNS does not record migration. For the same reason, we have refrained from using time fixed effects since these could pick up part of the income trend over the 15 year study period.¹⁰ This leaves us with a version of Eq. (5) in which the non-linear income function features as the sole potentially endogenous variable. We have deliberately not addressed its potential endogeneity since we are interested in documenting the association between changes in the distribution of income and the evolution of IRHI in China. Turning to the underlying mechanisms is only sensible after the magnitude of this association has been established, and after the relative importance of “income growth”, “mean-preserving income changes”, and “income mobility” has been understood.

We estimate Eq. (5) on all CHNS waves using a pooled interval regression model, and allow for clustering at the community level (which is the primary sampling unit in the CHNS and therefore leads to conservative statistical inference). It is not feasible to implement an individual fixed effects specification and estimates obtained from a random effects model were very similar to those of the pooled model. Since the random effects model imposes stronger exogeneity assumptions, we prefer the pooled model.

Remember that we highlighted three simplifying assumptions underlying Eq. (2) – and thus also Eq. (5). Here, we provide some justifications. First, ruling out interactions between the non-linear income function, and age/sex/region is reasonable since alternative versions of the model in Eq. (5) show that most of the interactions are individually insignificant.¹¹ Our second assumption was to fix the coefficients in Eq. (5) over time. We have checked its validity by adding interactions between time and the non-linear income function, and found almost none of the individual interactions to be statistically significant.¹² Finally, we have ignored dynamics in the specification of Eq. (5) since the period between the various CHNS waves differs from wave to wave.¹³

4.2. Selection of our sample, attrition, descriptives and statistical inference

We use all waves of the CHNS that were available at the time of the analysis (1991, 1993, 1997, 2000, 2004, 2006), except for the first wave (1989) which does not include the SAH question.¹⁴ Table A2 in the appendix details our sample selection criteria. Since our decomposition follows a cohort, we consider only those individuals that were present in 1991 and follow these until 2006 (note that some individuals may drop out in one wave and reappear in a later one). We exclude the province of Heilongjiang since it did not participate in the first 1991 wave of our cohort (see row ‘Did not participate’ in Table A2). The province of Liaoning is included, but did not participate in the 1997 wave (see row ‘Did not participate’, column 1997 in Table A2). This will affect our decomposition of the evolution of IRHI between 1991 and 1997, but not for any of the other waves. All respondents under the age of 10 were deleted because they were not asked the SAH question in waves 1997, 2000 and 2004. We further drop all CHNS participants that did not report either the SAH, date of birth, or income questions. In addition, we remove the 2% highest incomes from each wave¹⁵ and observations with negative incomes in 1991¹⁶ (see rows ‘Household income…”).

During the 15 years of follow-up, 61.2% of the initial cohort drops out for a variety of reasons such as mortality, moving (out) of the household or refusal to participate in later waves (see Table A2). We correct for the impact of this dropout on the representativeness of the cohort we follow through time by applying inverse probability weights (IPW) to Eqs. (4) and (5) (Jones et al., 2006).¹⁷ We provide further details in Appendix 1.

We show descriptive statistics for our CHNS cohort in Table A3 in the appendix, with and without correction for sample attrition. We observe that health deteriorates with the aging of our cohort: in 1991, 75% of the cohort reported excellent or good health, and this declined to 56% in 2006. On the VAS scale, this corresponds to a drop of average predicted VAS from 0.812 in 1991 to 0.784 in 2006. Average equivalent income more than doubled (in real terms) and this increase was not equally distributed: the Gini index for our cohort grew from 0.330 in 1991 to 0.445 in 2006. Most of the respondents in our initial cohort live in the inland rural areas (45.7%), the cohort shares living in the inland urban and coastal rural areas are approximately equal, and the coastal urban areas had the smallest share of respondents (9.8%).

Finally, we allow in our statistical inference for clustering at the level of the primary sampling units (i.e. communities) and use robust standard errors. This is straightforward for Eq. (5), and for the wave-specific Erreygers indices (O’Donnell et al., 2008), but more difficult for the other elements of our decomposition in Eq. (4) since (i) two consecutive waves of a panel are not independent and (ii) the combined sampling variability in the estimates of the IPWs, Eq. (5), and proportional income growth (Y_t/Y₁) should be accounted for. To do this, we bootstrap the entire procedure, i.e. from IPWs to the 4 terms of our decomposition. We draw 2000 bootstrap samples of communities (Mills and Zandvakili, 1997) and address the dependence between panel waves by drawing bootstrap samples of the communities in the first wave only (and use these same communities for all later waves).

5. Results

We already showed that the 1991 cohort of the CHNS experienced a dramatic increase in average incomes and income inequality over the period 1991–2006. In this section, we link these changes to the evolution of IRHI.

5.1. Evolution of IRHI and changes in the income distribution in China

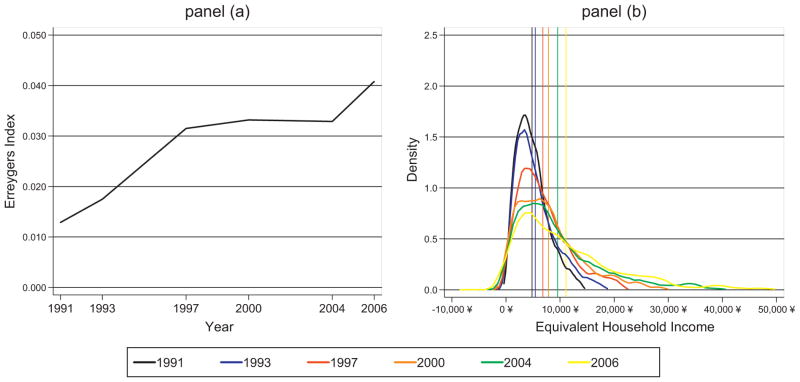
We illustrate trends in the income distribution in greater detail in panel b of Fig. 1 showing that, over and above the proportional income growth, the spread of incomes has increased between 1991 and 2006. Panel a of the same figure shows that IRHI more than doubled from 0.013 in 1991 to 0.041 in 2006, and this trend has favored the rich throughout as indicated by the positive values of the Erreygers indices. Our finding of a large increase in IRHI between 1991 and 2006 is a first and important finding of this paper, and the starting point for the subsequent analyses.

Fig. 1.

Evolution of IRHI and changes in the density function, of equivalent household income in China from 1991 to 2006.

Note: the vertical bars in panel (b) represent the average equivalent income levels per wave; results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).

5.2. The relation between health, income and non-income variables in China

An essential ingredient to understand these rising IRHI is the relationship between health and income conditional on the non-income variables. The interval regression estimates of Eq. (5) reported in column (1) of Table 1 show that demographics play a major role: (VAS-scaled) SAH deteriorates monotonically with age and is higher for males than females. We also find that those living in coastal and rural areas report better health, which is consistent with Van de Poel et al. (2012) who found urbanization in China to raise the probability of reporting poor health. Finally, the relationship between income and health is best described by a third degree income polynomial, giving rise to the income profile in Fig. 2 (the line for “income effect”): health increases with income at a decreasing rate, but for very high incomes (~ inflection point at 22,048 Yuan), the marginal effect of additional income starts rising again. The cumulative income distributions for 1991 and 2006 in Fig. 2 confirm that this only occurs for a minor share of our cohort: in 1991, no individuals had an income level above the point of inflection, whereas in 2006, this was about 13%.

Table 1.

Health equation estimates and drivers of differential income mobility.

Variable	Interval regression coefficienta,b	Share of individuals in age–sex/region category k					Difference between average weights zitc
		1993	1997	2000	2004	2006	1993	1997	2000	2004	2006
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
Females
10–29	Reference	0.194	0.147	0.069	0.031	0.021	32	619	1021	2028	2445
30–49	−0.041***	0.183	0.206	0.262	0.258	0.245	112	194	181	86	346
50–69	−0.105***	0.100	0.113	0.126	0.148	0.157	−287	−910	−608	−565	−544
70–89	−0.149***	0.030	0.045	0.054	0.077	0.087	−86	−356	−1168	−695	−1575
Males
10–29	0.005**	0.192	0.153	0.104	0.067	0.040	76	373	338	814	1547
30–49	−0.022***	0.177	0.185	0.211	0.200	0.213	64	135	109	−34	129
50–69	−0.084***	0.100	0.112	0.127	0.149	0.162	−215	−466	−173	−108	−165
70–89	−0.138***	0.022	0.038	0.048	0.069	0.076	−44	−1208	−1015	−292	−202
Region
Coastal – urban	0.010**	0.099	0.107	0.107	0.122	0.114	−38	−304	−121	634	5
Coastal – rural	0.023***	0.240	0.243	0.241	0.238	0.234	111	482	571	323	191
Inland – urban	−0.006***	0.205	0.203	0.210	0.214	0.225	−123	−915	−820	−1207	−880
Inland – rural	Reference	0.456	0.447	0.443	0.426	0.427	−1	172	24	28	150
Equivalent income/1000
Linear	3.442E–03***
Quadratic	−1.486E–04**
Cubic	2.247E–06**
Constant	0.832***

Note: Results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).

^aNumber of observations in pooled interval regions is 42,542; the division over the waves can be found in Table A3.

^bModel statistics: Wald chi(13) = 2.712 (P < 0.0001) LR cubic/quadratic income = 23.48 (P < 0.0001).

^c $(z_{it}/n_t^k)-(z_{i1}/n_1^k)$ equals the difference between the average weight z_it for age–sex/region category k in periods t and 1.

^**p < 0.05.

^***p < 0.01

Fig. 2.

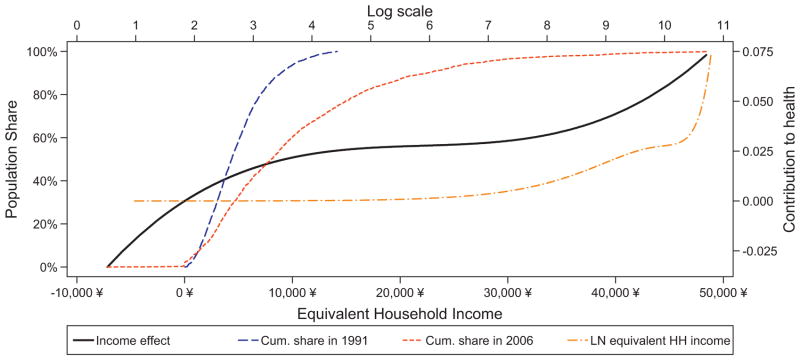
Effect of income on health and cumulative population shares, in first and final wave by income.

Note: results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5). The x-axis (equivalent income) applies to “income effect”, “cum. share 1991”, and “cum. Share in 2006”, while the x-axis (log scale) applies to “LN equivalent HH income”.

Fig. 2 also shows that proportional income changes have – for the majority of the population, except high incomes – similar health effects (see line LN(Equivalent HH income) in Fig. 2, and also Section 3.2). It follows that according to our decomposition framework, proportional income growth will on average – and ceteris paribus – only be marginally associated with IRHI. This is a second, and perhaps more surprising, finding of our paper: despite the enormous improvement of average incomes in China over the last few decades, these proportional income gains are not very important for understanding the rising IRHI in China.

5.3. Decomposition of evolution of IRHI in China

Fig. 3 and Table A4 in the appendix show estimates of the 4 terms of our decomposition: (i) income growth; (ii) other mean-preserving changes in the income distribution; (iii) differences in income mobility across non-income variables; and (iv) differences in the evolution of non-income variables across the initial income distribution. We discuss each of these terms, including statistical inference, in detail.

Fig. 3.

Decomposition of evolution in IRHI between year t and 1991.

Note: statistical inference of the decomposition is provided in Table A4; results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).

First, proportional income growth only shows a minor (and statistically insignificant) association with IRHI. This means that overall income growth in China is not related to rising IRHI, as was already anticipated by the earlier finding that proportional income changes have an overall uniform health effect across the income distribution.

Second, compared to proportional income growth, ‘other mean-preserving changes in the income distribution’ – which measure the effect of mean-preserving changes in the income levels with its associated income re-ranking – are more important for IRHI. Given that additional income leads to better health across the income spectrum (see Fig. 2), this must be due to ‘on average’ the rich gaining and the poor loosing, which is in line with Fig 1 (see also Section 3.2). Hence, our results confirm that the rise in Chinese income inequality is associated with increasing IRHI, but it also confirms that the other elements of our decomposition must be more important: in none of the waves the ‘mean-preserving changes’ account for more than 25% of the change in IRHI (and in several waves far less). It is also worth noting that the ‘direct’ effects of changes in the income distribution (i.e. term 1 and term 2) only account for around 30% of the rise in IRHI.

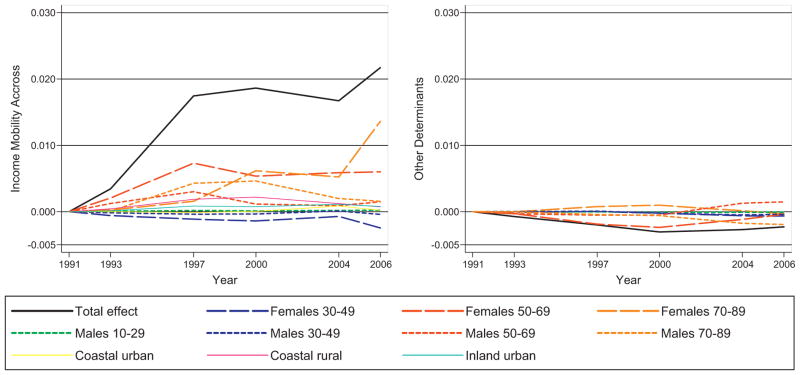
Third, differences in the evolution of the non-income variables (term 4) show a small, but statistically significant, negative effect on IRHI in Fig. 3. This effect is entirely driven by the evolution of age since sex and region are time-invariant in the CHNS. In other words, this term isolates the impact of aging on the change of IRHI over time. We find that aging contributes to IRHI (i.e. IRHI would have increased slightly more without aging) due to the initially rich experiencing larger health declines due to aging compared to the initially poor. This is confirmed by the right panel of Fig. 4 which shows the separate contributions of the different age–sex groups.¹⁸

Fig. 4.

Differences in income mobility across age, sex and region (panel a) and, differences in non-income variables across initial income (panel b).

Note: statistical inference is provided in Table A4; results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).

It is clear by now that most of the change in IRHI must be related to differential income mobility across the non-income variables (term 3 in Eq. (4)). Differential income mobility by age, sex and region accounts for around 70–90% of the total evolution in IRHI (see Fig. 3). This means that individuals that are sliding downward in the income distribution are less healthy compared to the reference group of young (and healthy) females living in inland-rural areas. The left panel of Fig. 4 and Table A4 illustrate that regional differences in income mobility have a small, and insignificant effect (reference category: inland-rural), and they are clearly dominated by the differential income mobility across sex-age categories (youngest females are the reference). There is no statistically significant difference between males younger than 50 and females younger than 30 (the reference category), and for females in the age group 30–50, we observe a negative insignificant effect. By far the strongest effects are observed for males and females above 50 years who were downwardly income mobile and less healthy than the younger age groups. The effects for 50+ females are in most cases also substantially larger and more significant than for 50+ males.

This begs the question why the effect for elderly females is that much larger than for elderly males. Closer inspection of term 3 in Eq. (4) reveals that the effect for a given age–sex category is driven by three components: (i) the health of this age–sex category (compared to the reference group), (ii) the share of people in this category, and/or (iii) whether this group has been upwardly or downwardly income mobile.¹⁹ In other words, elderly females can show a larger effect than elderly males for three reasons: because they report lower health, because there are more elderly women in our cohort in any given wave, or because elderly women are more downwardly mobile than elderly males. Table 1 presents some evidence on the relative importance of these three elements for all age–sex (and regional) categories. It shows that the diverging patterns between elderly women and men in Fig. 4 are mainly related to differences in income mobility (see columns 7–11), and less to the lower health level of females (column 1) or their relative group size (columns 2–6), although these clearly also matter.

We thus conclude that differential income mobility across age–sex groups is the single most essential element to understand the evolution of IRHI in China. Young (and healthier) individuals have been much more upwardly mobile compared to those above 50, and this age difference is more pronounced among females than males, in particular among those older than 70. While the inferior health of older women and the aging of the cohort have also contributed to this phenomenon, downward income mobility of elderly women (compared to young women) is much more important. We have also established that rising income inequalities account for less than a quarter of the change in IRHI and that aging in China even slightly reduces IRHI. Perhaps the most surprising result is the lack of any association between income growth and rising IRHI in China.

5.4. Further unraveling the downward income mobility of elderly (females): an exploration

Despite its importance for understanding the evolution of IRHI in China, Table 1 does not explain why the 50+ (and in particular women in the 70+ group) have experienced a greater downward shift in their income positions since 1991 compared to younger and healthier generations. In this section we explore a potential explanation.

A first useful observation is that our analysis has been based on equivalent incomes (see also Section 4.1). Hence, the downward shifts can be driven by changes in either the numerator (household income) or the denominator (household size), or both. It turns out that the diverging pattern for the elderly compared to younger age cohorts – and for elderly women compared to men – is not driven by changes in household size, but by changes in household incomes.²⁰ Therefore, explanations based on changes in household composition only cannot explain differential income mobility between the young/healthy and the old/unhealthy (and amongst the elderly) in China.

Instead, an explanation that focuses on changes in household incomes squares with evidence on replacement incomes and income support for the elderly in China. Elderly in rural areas –especially those above 70 – typically do not receive any pension benefits and still largely rely on family-based self-insurance mechanisms. These insurance mechanisms have become more uncertain due to a combination of China’s demographic transition leading to smaller family sizes, less co-residence and fewer extended families (Zhong, 2011)²¹ as well as to migration of (mainly young) adults from rural to urban areas (Giles et al., 2010). Similarly, urban dwellers – in spite of having more favorable pension arrangements than rural citizens – have been confronted with pension arrears, due to bankruptcies of state-owned enterprises and due to limited compliance with recent pay-as-you-go local pension initiatives. Traditional family-based insurance mechanisms have only partially protected elderly urban residents from these pension arrears (Cai et al., 2006). Nevertheless, urban residents have ‘on average’ continued to receive pension benefits that are largely unavailable to rural citizens (Feldstein, 1999; Yang, 1999; Song et al., 2012). Giles et al. (2010) show that less than 5% of elderly rural residents relied on pension incomes in 2005 whereas this share was 45% in urban areas. Moreover, and in line with our findings in Table 1, these authors report that pension incomes are more concentrated among elderly males in both rural and urban areas, while females rely more on family-based income support which, according to Meng et al. (2007), is explained by higher former labor market participation of males. Finally, Knight et al. (2004) show that rising income inequality in Chinese coastal cities was mainly related to changes in wage incomes whereas pension incomes accounted for the largest share of rising income inequalities in inland urban areas.

Two lessons emerge from this brief review for this paper. First, it confirms that our findings of differential income mobility between the young and old (and between elderly males and females) are in line with the evidence to date. Second, and more importantly, it points to a potentially crucial difference between rural and urban areas and between inland – urban and coastal – urban areas. All of these studies suggest that differential income mobility should play a more important role in rural and inland – urban areas than in coastal urban areas. Hence, we repeated our decomposition of IRHI in Section 5.3 (and the interval regression models in Section 5.2) separately for the four regions defined by inland/coastal and urban/rural. While this leaves us with more than 1000 observations for each of the rural regions, the number of observations in the urban regions becomes fairly small in the last wave of the CHNS, i.e. respectively 294 and 802 respondents in the urban – coastal and urban – inland areas.

Fig. 5 shows the evolution of IRHI for the four different regions. Inequalities were highest in the two inland and coastal-rural areas, and the magnitude of IRHI in these regions was comparable to that of the entire sample (in Fig. 1). The urban areas in the coastal provinces followed a different pattern and IRHI were smaller (and insignificant) in all periods. For each region, we present the decomposition of the evolution of IRHI between 1991 and 2006 in Fig. 6. These decompositions show a similar grouping for the two inland and coastal-rural areas versus the coastal urban area. The decomposition of the former three areas is very similar to that of the entire sample (but significance levels are lower) and is also here dominated by differences in income mobility across age groups. In contrast, income growth and other mean-preserving changes in the income distribution are more substantive in the coastal urban areas, while differential income mobility across age–sex categories is negligible. However, none of the terms of the decomposition for the urban-coastal region is still significant – probably as a result of small sample size – and we thus have to be careful in interpreting these as contributions to the evolution of IRHI.

Fig. 5.

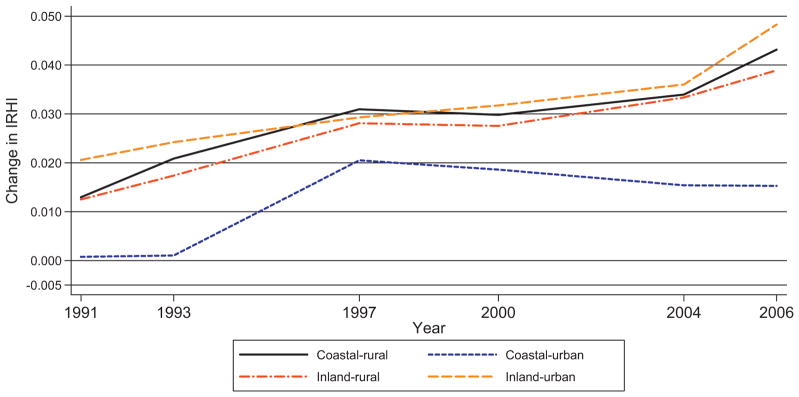
Evolution of IRHI in coastal/inland and urban/rural areas.

Note: results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).

Fig. 6.

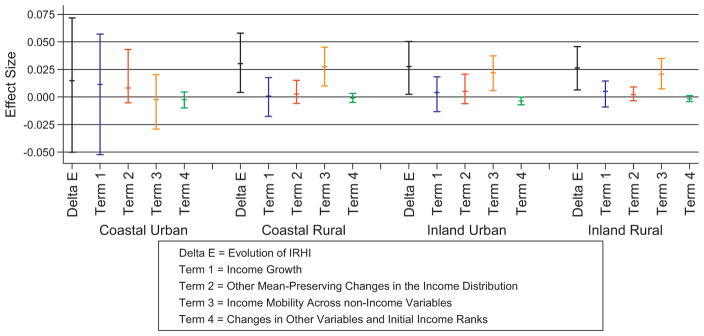
Decomposition of IRHI in coastal/inland and urban/rural areas in 2006 with 99% CI

Note: results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).

Our findings per region thus suggest that while overall in China IRHI are to a large extent driven by differences in income mobility between the young and the elderly, and between sexes amongst the elderly, regional differences in income protection (via family based insurance mechanisms or more formal pension systems) appear crucial to understand this phenomenon. It also means that the younger cohorts have gained most from the economic prosperity in recent decades in China, except for the coastal urban areas where all age groups seem to have benefited equally.

6. Conclusions

The rapid economic growth in China in recent decades has been accompanied by larger inequalities in society, not only with respect to income, but also with respect to health. This begs the question how the dramatic changes in both the level and distribution of Chinese household incomes over the last few decades have been related to the extent to which also health – as self-reported – is distributed unequally by income. We believe we make the following contributions. First, we propose a new cohort-decomposition of the changes in IRHI into four components: (i) the growth of mean income, (ii) mean-preserving changes in the distribution of incomes, (iii) the income mobility across other important variables like age and region, and (iv) the evolution of the other important variables – aging in our empirical analysis – across initial income rank. It differs from earlier approaches in two respects: (a) it extends and simplifies earlier decomposition approaches by replacing the standard concentration index by the Erreygers index which recognizes that health – unlike income – has a finite maximum; (b) it highlights the importance of income mobility when it varies across important determinants of health like age and region. Second, we empirically implement the approach using data from the CHNS, one of the longest running panel studies, by estimating health as a polynomial function of income, controlling for age, gender and region. While this does not allow for causal inference, the decomposition analysis does reveal which factors are important – and which are not – for understanding the evolution of health disparities by income in China.

Our findings are as follows. We find that IRHI rose quite substantially in this cohort: between 1991 and 2006 its degree has more than tripled. No other study had revealed this rise before, and in the absence of aging of our cohort the rise would have been larger. Also new is that this substantive rise turns out to be largely unrelated to the double digit average income growth rates and only weakly related to the overall growth in income inequality. Instead, what emerges is that most of the increase in IRHI relates to the very different income mobility by age and gender. Especially women over 50 in the cohort have experienced much more adverse trends than other groups in their income position (and their health) and this explains more than half of the growth in IRHI. This strongly suggests that elderly women were left behind in the rapid economic developments occurring in China and that low or absent replacement incomes for sick and old women are a key factor here. While we have not directly tested this hypothesis, it conforms to the literature on retirement incomes. This confirms that, especially in rural areas, pension entitlements are largely lacking for the majority of the population. Reliance on traditional, family-based self-insurance has also declined because of demographic transitions like smaller family sizes and migration. Urban and male residents have generally enjoyed more favorable pension arrangements because of their greater participation in the formal labor market. This explanation also squares with the regional differences in our findings: income mobility did not contribute as much to IRHI changes in the coastal urban areas as in the other regions. This suggests that income protection and pension arrangements, also for older women, in this region are better than in other parts of China.

Our study is thus a first step in understanding the evolution of IRHI in China and its relation with changes in the income distribution. Our findings strongly suggest that the following issues deserve attention in further research. First, how are age profiles of income related to age profiles of health in China, and in particular why are low replacement incomes associated with low health? Our results suggest that this is a structural relationship and Giles et al. (2010) emphasize that many elderly without any replacement income are still working. It is most likely that this has consequences for their health. Second, it appears relevant to investigate further the different experiences in urban coastal areas with other regions to find out which differences in institutions versus demographics matter. Finally, it would be of interest to examine whether differential income mobility among the elderly is related to changes in household composition due to mortality or migration of income earning members.

Appendix 1. Implementation of inverse probability weights

The IPW-methodology addresses non-random dropout from the cohort we follow over time – it is not a weighting scheme to make our data nationally representative – and consists of two distinct steps. First, for all respondents in the first wave, one estimates the probability of still being present in wave t, implicitly assuming that death is just another form of sample attrition. Second, the inverse of the resulting predicted probabilities are used as probability weights in wave t, i.e. as an IPW, in all analyses.

For each wave, we estimate a separate probit, and include the following wave 1 regressors: (a) a polynomial of equivalent income, (b) dummies for the separate SAH categories, and (c) sex-age dummies and regional dummies. The results in Table A1 show that the middle aged (30–70) are most likely to stay in the cohort, and that young females are most likely to leave the cohort (in later waves elderly males are least likely to stay probably due to mortality). We also observe that those living in rural areas²² and those in good health are most likely to stay in the cohort. The effect of income is non-linear in most waves and indicates that those with higher incomes (except for those with very low and very high incomes) are more likely to drop out of the cohort. Most importantly, we found that the interactions between the income polynomial and the set of SAH dummies were jointly insignificant and therefore removed these from the probit models. This indicates that selective health-income dropout is unlikely to be a serious problem in our data.

Table A1.

Probit models of the probability to be in wave t conditional on wave 1 characteristics.

Variable	1993		1997		2000		2004		2006
	Coef	p-Value	Coef	p-Value	Coef	p-Value	Coef	p-Value	Coef	p-Value
Females
10–29	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference
30–49	0.674	0.000	0.739	0.000	1.118	0.000	1.274	0.000	1.226	0.000
50–69	0.422	0.000	0.552	0.000	0.723	0.000	0.857	0.000	0.791	0.000
70–89	−0.030	0.730	−0.008	0.921	−0.055	0.520	−0.226	0.020	−0.439	0.000
Males
10–29	0.250	0.000	0.282	0.000	0.255	0.000	0.331	0.000	0.276	0.000
30–49	0.558	0.000	0.680	0.000	0.907	0.000	1.117	0.000	1.086	0.000
50–69	0.380	0.000	0.455	0.000	0.644	0.000	0.759	0.000	0.633	0.000
70–89	−0.110	0.261	−0.113	0.223	−0.218	0.036	−0.465	0.000	−1.100	0.000
Region
Coastal – urban	−0.268	0.000	−1.049	0.000	−0.277	0.000	−0.516	0.000	−0.500	0.000
Coastal – rural	0.129	0.001	−0.584	0.000	0.002	0.958	−0.073	0.021	−0.100	0.002
Inland – urban	−0.233	0.000	−0.217	0.000	−0.086	0.010	−0.179	0.000	−0.247	0.000
Inland – rural	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference
Income
Linear	4.852E–01	0.002	1.757E–01	0.017	−1.862E–02	0.000	8.328E–02	0.267	−9.428E–02	0.000
Quadratic	−2.174E–01	0.001	−7.389E–02	0.001			−5.136E–02	0.022	5.694E–03	0.000
Cubic	3.758E–02	0.003	8.920E–03	0.000			6.524E–03	0.010
Power four	−2.870E–03	0.005	−3.320E–04	0.000			−2.467E–04	9.739E–03
Power five	8.015E–05	0.008
SAH response
Excellent	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference	Reference
Good	0.019	0.673	0.034	0.358	0.003	0.939	0.052	0.172	0.028	0.466
Fair	−0.019	0.724	−0.003	0.946	−0.025	0.563	−0.008	0.852	−0.026	0.560
Poor	−0.418	0.000	−0.420	0.000	−0.420	0.000	−0.420	0.000	−0.383	0.000
Constant	0.618	0.000	0.124	0.156	−0.486	0.000	−0.656	0.000	−0.477	0.000

While the IPWs should in principle be used in all analyses, we only use them for the estimation of Eq. (5), for the weighted income Z_it’s²³ (Lerman and Yitzhaki, 1989), for calculating average income in each wave Y_t which is needed to calculate $y_{it}^{pg}$, and for the left-hand side Erreygers indices in Eq. (4).²⁴ The IPW’s are partially needed for terms 2 and 3 and not for terms 1 and 4 of Eq. (4). The latter two terms can be calculated without the IPWs since we know what would have been the age, sex, and region of individuals that have dropped out of the cohort. Similarly, we can calculate the incomes in the ‘proportional income growth’ scenario since equivalent income in the first period is known.

Our IPW approach assumes that death is just another form of sample attrition, conditional on initial SAH, gender, age, region and equivalent income. This assumption might be criticized since survivors are by construction in better health than the dead, but since only 8% of the initial CHNS cohort have died by 2006 (compared to an overall attrition rate of 61.2%), the resulting bias is most likely modest (see also footnote 17). Moreover, a probit model shows that survival in future waves is not related (in 1991, 1997 and 2004) or only modestly related (in 2000 and 2006) to income in 1991, conditional on the regressors used in the models in Table A1. Moreover, application of our decomposition approach to (i) the cohort excluding all individuals that died during the study period, but using IPWs for other forms of dropout; and (ii) the balanced cohorts, confirmed the decomposition results reported in this paper. We also calculated the evolution of the Erreygers indices under alternative imputation scenarios for the health and income levels of the deceased: only in the case where mortality is assumed to be strongly related to income, we underestimate the evolution of the Erreygers index. When more modest mortality selection is assumed, the evolution of the Erreygers index is similar to the evolution reported in the results section of this paper. More detailed results can be obtained upon request from the authors.

Appendix 2. Additional tables

See Tables A2–A4.

Table A2.

Reasons for dropout and exclusion from CHNS sample.

Exclusion criterion/reason for dropout	Wave
	1991	1993	1997	2000	2004	2006
Initial number of observationsa	27,812	11,577	11,577	11,577	11,577	11,577
Died before interview	0	102	366	569	789	898
Left household before interviewd	1113c	741	0	0	0	0
Did not participate in interview (reason unknown)e	11,914	632	3211	3423	4745	3432
Younger than 10 years	2540	–	–	–	–	–
Unknown date of birth	8	–	–	–	–	–
No household income	20	19	67	128	61	125
Household income smaller or equal to zerof	73	–	–	–	–	–
Household income among highest 2%	252	158	146	147	113	114
No self reported health	315	96	1042	2056	1217	2522
Total number of observations	11,577b	9829	6745	5254	4652	4486

^aBased on unique number of individuals participating in any wave of the CHNS.

^bThe 11,577 respondents form our cohort at baseline.

^cThese respondents participated in 1989, but not in 1991.

^dOnly recorded in 1991 and 1993.

^eIncludes households that did not participate at all.

^fOnly applicable in 1991.

Table A3.

Descriptives of CHNS 1991 cohort.

	Variable	1991	1993	1997	2000	2004	2006
	N	11,577	9829	6745	5254	4652	4486
Uncorrected	Percentage females	0.508	0.501	0.491	0.501	0.492	0.499
	Average age	35.7	37.7	42.2	47.2	51.6	53.4
	Region
	Coastal – urban	9.8%	9.1%	4.9%	8.0%	6.2%	6.6%
	Coastal – rural	24.0%	25.2%	19.9%	25.6%	25.5%	25.5%
	Inland – urban	20.5%	19.2%	21.3%	19.7%	18.7%	17.9%
	Inland – rural	45.7%	46.5%	54.0%	46.6%	49.6%	50.1%
	Average equivalent income (¥, 2006)	¥4823	¥5354	¥6508	¥7756	¥8833	¥10,270
	Income distribution (Gini)	0.330	0.370	0.371	0.403	0.432	0.443
	SAH response
	Excellent	13.6%	12.6%	11.3%	11.8%	10.5%	8.6%
	Good	61.7%	63.6%	60.9%	47.9%	42.6%	44.2%
	Fair	21.1%	20.1%	23.4%	33.2%	37.8%	38.0%
	Poor	3.7%	3.8%	4.5%	7.1%	9.1%	9.2%
	Average health	0.812	0.809	0.800	0.792	0.780	0.777
Corrected for dropout	Percentage females	0.508	0.508	0.512	0.51	0.514	0.51
	Average age	35.7	37.5	41.4	45.2	49.8	51.8
	Region
	Coastal – urban	9.8%	9.9%	10.7%	10.7%	12.2%	11.4%
	Coastal – rural	24.0%	24.0%	24.3%	24.1%	23.8%	23.4%
	Inland – urban	20.5%	20.5%	20.3%	21.0%	21.4%	22.5%
	Inland – rural	45.7%	45.6%	44.7%	44.3%	42.6%	42.7%
	Average equivalent income (¥, 2006)	¥4823	¥5424	¥6817	¥7861	¥9556	¥11,089
	Income distribution (Gini)	0.330	0.369	0.371	0.401	0.430	0.445
	SAH response
	Excellent	13.6%	12.7%	13.0%	13.0%	12.5%	9.9%
	Good	61.7%	63.3%	61.1%	48.4%	44.4%	46.2%
	Fair	21.1%	20.1%	22.6%	32.0%	37.0%	37.9%
	Poor	3.7%	3.9%	4.4%	7.0%	8.5%	8.2%
	Average health	0.812	0.809	0.803	0.796	0.787	0.784

Table A4.

Decomposition results.

Variable	1991	1993	1997	2000	2004	2006
N	11,577	9829	6745	5254	4652	4486
Average health	0.8119	0.809	0.8031	0.7957	0.7868	0.7837
Erreygers	0.013 (0.0049; 0.0222)	0.0175 (0.0082; 0.0260)	0.0315 (0.0211; 0.0402)	0.0332 (0.0237; 0.0415)	0.0329 (0.0169; 0.0459)	0.0408 (0.0222; 0.0556)
IRHI change w.r.t. 1991		0.0046 (−0.0011; 0.0086)	0.0185 (0.0105; 0.0252)	0.0203 (0.0114; 0.0277)	0.0199 (0.0053; 0.0331)	0.0278 (0.0100; 0.0432)
Main effects
Other mean preserving changes in the income distribution		0.0012 (0.0004; 0.0024)	0.0014 (0.0005; 0.0039)	0.0028 (0.0005; 0.0077)	0.0040 (−0.0018; 0.0159)	0.0068 (0.0005; 0.0158)
Income mobility across non-income variables		0.0034 (−0.0015; 0.0078)	0.0174 (0.0111; 0.0245)	0.0186 (0.0111; 0.0257)	0.0167 (0.0085; 0.0249)	0.0217 (0.0090; 0.0358)
Income growth		0.0007 (−0.0011; 0.0014)	0.0016 (−0.0036; 0.0041)	0.0019 (−0.0049; 0.0058)	0.0019 (−0.0077; 0.0091)	0.0017 (−0.0113; 0.0132)
Changes in other variables and initial income ranks		−0.0007 (−0.0015; 0.0000)	−0.0020 (−0.0032; −0.0007)	−0.0031 (−0.0047; −0.0016)	−0.0027 (−0.0045; −0.0009)	−0.0023 (−0.0039; −0.0007)
Contributions of individual variables to income mobility across non-income variables
Females
10–29		Reference	Reference	Reference	Reference	Reference
30–49		−0.0006 (−0.0014; 0.0002)	−0.0011 (−0.0025; 0.0002)	−0.0014 (−0.0033; 0.0003)	−0.0007 (−0.0030; 0.0016)	−0.0025 (−0.0052; 0.0006)
50–69		0.0021 (−0.0003; 0.0041)	0.0073 (0.0047; 0.0101)	0.0054 (0.0025; 0.0081)	0.0059 (0.0030; 0.0090)	0.0060 (0.0024; 0.0101)
70–89		0.0002 (−0.0014; 0.0019)	0.0016 (−0.0011; 0.0044)	0.0062 (0.0023; 0.0105)	0.0052 (0.0002; 0.0100)	0.0136 (0.0072; 0.0213)
Males
10–29		0.0000 (−0.0001; 0.0002)	0.0002 (0.0000; 0.0005)	0.0001 (0.0000; 0.0004)	0.0002 (0.0000; 0.0005)	0.0002 (0.0000; 0.0006)
30–49		−0.0002 (−0.0007; 0.0004)	−0.0004 (−0.0012; 0.0002)	−0.0004 (−0.0012; 0.0003)	0.0001 (−0.0008; 0.0010)	−0.0004 (−0.0018; 0.0010)
50–69		0.0012 (−0.0004; 0.0027)	0.0030 (0.0009; 0.0054)	0.0011 (−0.0009; 0.0035)	0.0009 (−0.0015; 0.0034)	0.0015 (−0.0016; 0.0051)
70–89		0.0001 (−0.0012; 0.0014)	0.0043 (0.0009; 0.0092)	0.0046 (0.0007; 0.0084)	0.0020 (−0.0071; 0.0087)	0.0016 (−0.0206; 0.0202)
Region
Inland – rural		Reference	Reference	Reference	Reference	Reference
Inland – urban		0.0001 (−0.0006; 0.0009)	0.0008 (−0.0007; 0.0030)	0.0007 (−0.0006; 0.0033)	0.0011 (−0.0009; 0.0037)	0.0008 (−0.0006; 0.0033)
Coastal – rural		0.0004 (−0.0020; 0.0030)	0.0019 (−0.0008; 0.0049)	0.0022 (−0.0002; 0.0054)	0.0012 (−0.0018; 0.0045)	0.0007 (−0.0027; 0.0038)
Coastal – urban		0.0000 (−0.0011; 0.0006)	−0.0001 (−0.0034; 0.0007)	0.0000 (−0.0022; 0.0010)	0.0008 (−0.0012; 0.0031)	0.0002 (−0.0020; 0.0032)
Contributions of individual variables to changes in other variables and initial income ranks
Females
10–29		Reference	Reference	Reference	Reference	Reference
30–49		−0.0001 (−0.0005; 0.0004)	0.0000 (−0.0008; 0.0009)	−0.0002 (−0.0013; 0.0008)	−0.0006 (−0.0021; 0.0007)	−0.0007 (−0.0021; 0.0006)
50–69		−0.0003 (−0.0011; 0.0004)	−0.0019 (−0.0034; −0.0004)	−0.0024 (−0.0046; −0.0003)	−0.0012 (−0.0040; 0.0016)	−0.0004 (−0.0036; 0.0026)
70–89		0.0000 (−0.0005; 0.0006)	0.0008 (−0.0005; 0.0021)	0.0010 (−0.0007; 0.0026)	0.0001 (−0.0022; 0.0024)	−0.0003 (−0.0030; 0.0022)
Males
10–29		0.0000 (−0.0001; 0.0000)	0.0000 (−0.0001; 0.0001)	−0.0001 (−0.0003; 0.0000)	−0.0001 (−0.0003; 0.0000)	−0.0001 (−0.0002; 0.0000)
30–49		0.0000 (−0.0002; 0.0003)	0.0001 (−0.0004; 0.0006)	−0.0002 (−0.0009; 0.0004)	−0.0005 (−0.0012; 0.0002)	−0.0004 (−0.0012; 0.0004)
50–69		−0.0003 (−0.0011; 0.0004)	−0.0005 (−0.0020; 0.0009)	−0.0005 (−0.0025; 0.0013)	0.0013 (−0.0011; 0.0036)	0.0015 (−0.0011; 0.0041)
70–89		0.0000 (−0.0006; 0.0004)	−0.0004 (−0.0017; 0.0010)	−0.0006 (−0.0024; 0.0012)	−0.0018 (−0.0040; 0.0004)	−0.0019 (−0.0046; 0.0006)

Note: 99% confidence intervals between brackets; results are obtained after applying inverse probability weights (IPW) to Eqs. (4) and (5).