Functional connectivity and graph theory in preclinical Alzheimer’s disease

Abstract

Alzheimer’s disease (AD) has a long preclinical phase in which amyloid and tau cerebral pathology accumulate without producing cognitive symptoms. Resting state functional connectivity MRI (rs-fcMRI) has demonstrated that brain networks degrade during symptomatic AD. It is unclear to what extent these degradations exist prior to symptomatic onset. In this study, we investigated graph theory metrics of functional integration (path length), functional segregation (clustering coefficient), and functional distinctness (modularity) as a function of disease severity. Further, we assessed whether these graph metrics were affected in cognitively normal participants with cerebrospinal fluid evidence of preclinical AD. Clustering coefficient and modularity, but not path length, were reduced in AD. Cognitively normal participants who harbored AD biomarker pathology also showed reduced values in these graph measures, demonstrating brain changes similar to, but smaller than, symptomatic AD. Only modularity was significantly affected by age. We also demonstrate that AD has a particular effect on hub-like regions in the brain. We conclude that AD causes large-scale disconnection that is present before onset of symptoms.

Introduction

Alzheimer’s disease (AD) is the most common form of dementia (Reitz et al. 2011) and has a long preclinical period wherein pathology accumulates in the absence of overt symptoms (Price and Morris 1999; Price et al. 2009; Braak et al. 2011). The pathological hallmarks of AD are the accumulation of amyloid beta (Aβ) plaques and tau neurofibrillary tangles (Blennow et al. 2006; Holtzman et al. 2011). The diagnostic specificity of these pathological changes has led to the elucidation of biomarkers with a proposed progression (Jack et al. 2011). Less is known, however, about how this pathology affects large-scale brain function at different stages of the disease.

The staging of AD can be quantified either clinically or pathologically. A well validated clinical method is the Clinical Dementia Rating (CDR) (Morris 1993). Because of the relatively long preclinical stage (Price and Morris 1999; Price et al. 2009) some individuals with normal cognition harbor AD pathology. Cerebrospinal fluid (CSF) levels of tau and Aβ may assist in staging of cognitively normal individuals with preclinical AD pathology (Sperling et al. 2011; Jack et al. 2012). It is hypothesized that by the time clinical symptoms are detected, at least some AD-related irreversible neurological damage has developed. The effect of this preclinical pathology is unclear and a greater understanding of these early brain changes would inform the pathophysiology as well as be relevant to treatment trials targeting the early stages of AD.

rs-fcMRI measures the temporal correlation of the blood oxygen level-dependent (BOLD) signal between different brain regions (Biswal et al. 1995). Regions that are functionally related, or co-activated during a cognitive task, tend to be temporally correlated at rest (Beckmann et al. 2005; Smith et al. 2009). Groups of temporally correlated regions are termed resting-state networks (RSNs). The first RSN implicated in AD pathophysiology was the default-mode network (DMN) (Greicius et al. 2004). By the time AD symptoms develop, widespread changes in functional connectivity are present throughout the brain (Wang et al. 2007). While debate exists as to the exact scope of changes that occur in early AD (Zhou et al. 2010), widespread loss of functional connectivity is present by mild AD (CDR 1) (Brier et al. 2012).

A potential shortcoming of the above studies is that they consider changes in the correlation structure without investigating these in the context of larger whole-brain networks. For example, some studies consider a large number of pair-wise correlations (Wang et al. 2007) and other studies average over sets of pair-wise correlations as a data reduction strategy (Brier et al. 2012). In both settings, the dynamics of the network as a whole are obscured either by exclusion (in the case of the former) or by averaging (in the case of the latter).

Graph theory is a mathematical technique that is capable of assessing the properties of systems that can be modeled as sets of vertices (i.e., brain regions) and edges (i.e., functional connections). Graph theory allows for a summary of entire networks properties with respect to segregation (termed “clustering coefficient”) and integration (termed “path length”). This method has been applied to rs-fcMRI. The first application demonstrated that the brain exhibits small-world character (Salvador et al. 2004). Small-world character occurs when there are many short range connections between related areas and relatively few long range connections between less related areas (Watts and Strogatz 1998). This results in an efficient organization that reduces the cost of maintaining many connections but also allows for efficient movement of information (Latora and Marchiori 2001). This efficient organization is lost with aging (Achard and Bullmore 2007) wherein the functional connectivity network structure becomes less modular (Meunier et al. 2009).

The application of graph theory to rs-fcMRI data in AD has provided conflicting results (Tijms et al. 2013). One rs-fcMRI study found that AD resulted in decreased clustering coefficient, but no change in average shortest path length (Supekar et al. 2008). However, another study showed that AD decreased average path length, but did not change clustering coefficient (Sanz-Arigita et al. 2010). A third study noted increased average path length in patients with amnestic mild cognitive impairment (MCI) (Wang, Zuo, et al. 2013). These studies can be interpreted as a disruption in small-world behavior (Supekar et al. 2008; Sanz-Arigita et al. 2010; Wang, Zuo, et al. 2013) albeit by different mechanisms. These disparate findings (with respect to mechanism of small-word disruption) could result from differences in methodology, relatively small sample sizes, and variability in the clinical definition of AD. Further, while these studies have investigated the effects of AD (Supekar et al. 2008; Sanz-Arigita et al. 2010; Ciftçi 2011) and amnestic MCI (Wang, Zuo, et al. 2013), none have investigated graph measures in cognitively normal individuals with biochemical evidence of AD.

The current study investigates the changes in graph theory measures on rs-fcMRI in a large, well-characterized sample using both CSF biomarkers and clinical examination. The effect of different levels of cognitive impairment on classic graph theory measures of functional connectivity and whether additional measures more fully capture brain dynamics in AD are examined. Finally, graph theoretical measures in cognitively normal individuals who have AD pathology (preclinical AD) as assessed by CSF biomarkers are investigated.

Methods

Subjects

Data were examined from participants enrolled in studies of memory and aging at the Charles and Joanne Knight Alzheimer’s Disease Research Center at Washington University in St. Louis. Participants were 43–89 years of age and in good general health, having no serious illnesses (e.g., end-stage renal disease requiring dialysis) that would preclude participation, nor medical contraindications to either CSF or MRI studies. Participants taking psychoactive medication or with severe psychiatric conditions were excluded. The Washington University in St. Louis Human Research Protection Office approved all procedures. Following informed consent, each participant had clinical examinations, neuropsychological testing, lumbar puncture (LP), and neuroimaging studies. Only participants who had neuroimaging performed within one year of LP and clinical assessment were included.

Clinical Assessment

Experienced clinicians conducted semi-structured interviews with the participant and a knowledgeable collateral source. The Clinical Dementia Rating (CDR) was used to determine the presence or absence of dementia and, when present, to stage the severity (Morris 1993). Participants were scored as either CDR 0, 0.5, or 1, corresponding to cognitive normality, MCI / very mild dementia, or mild dementia. All CDR > 0 participants in this study were considered to have symptomatic AD, a term that encompasses “MCI due to AD” (Sperling et al., 2011) and “AD dementia” (McKhann et al., 2011). The accuracy of that clinical diagnosis is supported by the presence of pathological AD in 93% of cases that come to autopsy (Berg et al., 1998), including those who meet criteria for MCI (Storandt et al., 2006). Findings from an independent neuropsychological assessment are provided in supplemental table 1 and further support the distinction of CDR0 from AD.

CSF Analysis

As previously described, CSF (20 – 30mL) was collected by LP using an atraumatic 22-gauge Sprotte spinal needle in the morning after overnight fasting (Fagan et al. 2006). CSF was collected in 50mL polypropylene tubes and was free of visible blood contamination. Following collection, the tube was immediately placed on ice and was gently inverted within one hour of collection to avoid possible gradient effects. The sample was briefly centrifuged at low speed (2000g, 15 min, 4°C) to remove cellular debris. The sample was aliquoted (500µL) into polypropylene tubes and frozen at −84°C. CSF was analyzed for tau and Aβ₄₂ by plate-based enzyme linked immunoabsorbent assay (INNOTEST; Innogenetics, Ghent, Belgium) according to the manufacturer’s specifications.

National Institute of Aging Classification of Preclinical AD

Recently proposed criteria by the National Institute of Aging proposes subdividing preclinical AD (i.e., CDR 0) into three categories based on cognitive and biomarker status (Sperling et al. 2011; Jack et al. 2012). Stage 0 is defined as no evidence of AD: normal cognition without amyloid pathology or neurodegeneration. Stage 1 is defined as normal cognition and the presence of amyloid pathology but without neurodegeneration. Stage 2 is defined by normal cognition with both amyloid and neurodegeneration pathology. Stage 3 is defined as both amyloid and neurodegeneration with subtle cognitive deficits. In this work we compared Stage 0 to Stage 1 and 2. The original criteria defined amyloid pathology as the presence of either fibrillar plaques using amyloid imaging studies or abnormal CSF Aβ₄₂ (Sperling et al. 2011; Jack et al. 2012). For this work, amyloid positivity was defined by a CSF concentration of Aβ₄₂ < 500 pg/mL. Presence of neurodegeneration in the original critera was defined by either reduced hippocampal volume or increased CSF tau. For this work we used CSF tau, with positivity defined as a concentration of tau > 440 pg/mL. These CSF cutoffs have previously been reported as sensitive and specific for discriminating CDR0 from CDR>0 (Tarawneh et al. 2011).

Image Acquisition

Imaging was performed as previously described (Brier et al. 2012) using a 3T Siemens scanner (Erlangen, Germany) equipped with a standard 12-channel head coil. A high-resolution structural scan was acquired using a 3-dimensional sagittal T1-weighted magnetization-prepared rapid gradient echo (MPRAGE, echo time [TE] = 16 msec, repetition time [TR] = 2,400 msec, inversion time [TI] = 1,000 msec, flip angle = 8°, 256 × 256 acquisition matrix, 1×1×1mm voxels). This scan was used for atlas registration. High-resolution 3-D oblique axial spin density/T2-weighted fast spin echo (FSE) structural images were also acquired using slice tilts and positions computed by slice preregistration (TE=455 msec, TR = 3,200 msec, 256 × 256 acquisition matrix, 1 acquisition, 1 × 1 × 1mm voxels). These T2-weighted FSE data were used for rs-fcMRI atlas registration. Rs-fcMRI scans were collected using a gradient spin-echo sequence (TE = 27 msec, TR = 2,200 msec, field of view = 256 mm, flip angle = 90°, 4mm isotropic voxels) sensitive to the BOLD contrast (T2* weighting). Complete brain coverage was obtained using 36 contiguous slices acquired parallel to the anterior commissure/posterior commissure plane. Two six minute rs-fcMRI runs (164 volumes per run) were acquired during which participants were asked to fixate on a visual cross-hair and not fall asleep.

Preprocessing of rs-fcMRI

Initial preprocessing followed conventional methods as previously described (Shulamn et al. 1997; Brier et al. 2012). Briefly, this included compensating for slice-dependent time shifts, elimination of systematic even-odd slice intensity differences due to interleaved acquisition and rigid body correction for head movement within and across runs. rs-fcMRI data were intensity scaled to obtain a mode value of 1000 (Ojemann et al. 1997). This scaling facilitated assessment of voxel-wise variance for the purposes of quality assurance but did not affect computed correlations, which are magnitude independent. Atlas transformation was performed using composition of affine transforms connecting the rs-fcMRI volumes with the T2-weighted and MPRAGE images. Head movement correction was included in a single resampling that generated a volumetric time-series in 3mm³ atlas space.

Additional processing was performed to allow for correlation mapping. This included spatial smoothing (6mm FWHM Gaussian blur in all directions), voxel-wise detrending across each run, temporal low-pass filtering of activity above 0.1 Hz, and reduction of spurious variance by regression of nuisance waveforms from white matter and CSF. This final step included removal of the time-series averaged over the whole brain which has been shown to improve detection of system specific activity and increase correspondence to anatomy (Fox et al. 2009).

Quality Assurance

Movement during scans can affect the quality rs-fcMRI data (Van Dijk et al. 2012). This persists after regression of the movement covariate (Power et al. 2012). For this dataset we employed a method that detected and removed volumes (without replacement) with excessively high whole brain root mean squared (rms) movement over time (Power et al. 2012). Only individuals with a fraction of frames excluded less than 20% were included. This analysis represents a subset of a larger previously published dataset (Brier et al. 2012). No significant differences existed in movement parameters between the groups.

Resting State Procedure

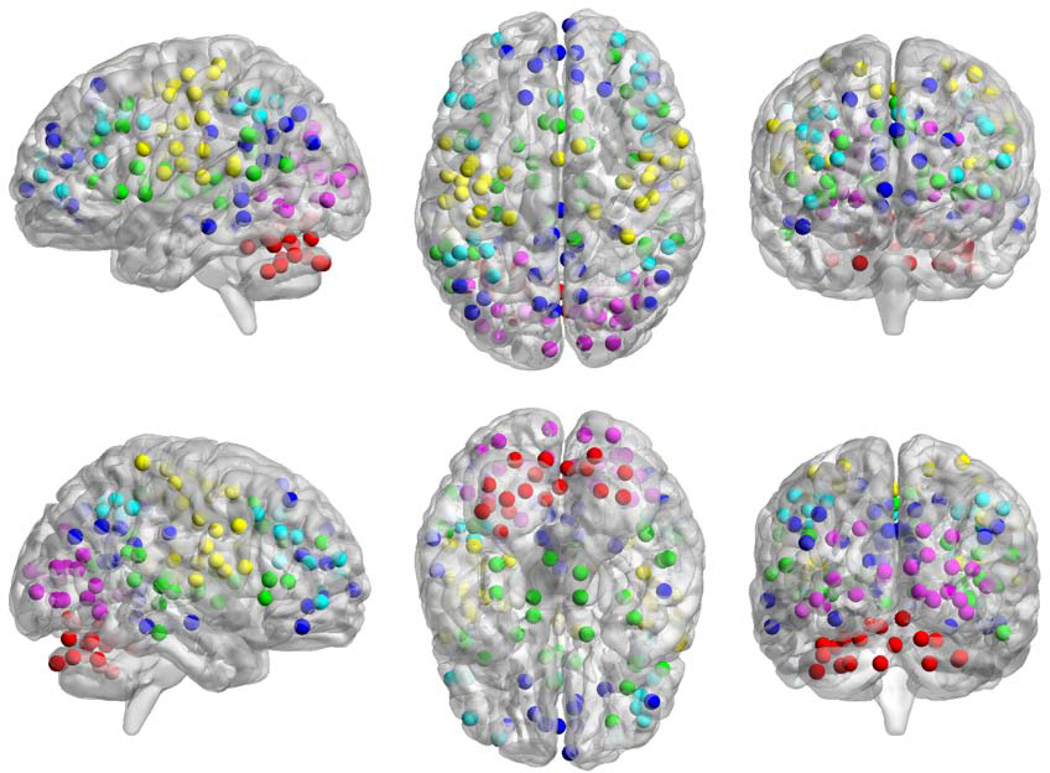
160 spherical (5mm radius) regions of interest (ROIs) were placed throughout the brain (Figure 1) based on previously published work (Dosenbach et al. 2010). These ROIs represent six a priori brain networks, but can be further divided into additional sub-networks (Power et al. 2011). These ROIs were selected because they have been previously validated as adequately sample various RSNs and sufficiently cover the entire brain. An assumption of graph theory is that the system is completely and independently sampled. These ROIs cover a majority of cortical and subcortical structures. Correlation maps were calculated by extracting the time course from each ROI. The Pearson correlation coefficient (r) was computed between the time course of one ROI and all other ROIs and then Fisher z(r) transformed.

Figure 1.

Map of ROI locations colored by network membership. Cerebellar network is red, cingulo-opercular network is green, default mode network is blue, fronto-parietal network is teal, occipital network is purple, and sensori-motor network is yellow.

Graph Calculations

Graph theory is an emerging mathematical construct for the analysis of complex systems. When applied to rs-fcMRI, different brain regions represent vertices (v) and functional connections represent edges (e). Graphs can be described through a number of fundamental quantities. The shortest average path length is defined as the shortest mean distance (in graph space) from a particular vertex to all other vertices (Watts and Strogatz 1998; Rubinov and Sporns 2010). A smaller path length represents greater integration. A second classic graph theory quantity is clustering coefficient. The clustering coefficient is defined as the fraction of a vertex’s neighbors which are themselves neighbors (Rubinov and Sporns 2010). A larger clustering coefficient represents greater segregation (Newman 2003). These two metrics, path length and clustering coefficient, form the basis of many graph theoretical investigations.

The first step of graph analysis is the construction of a graph from the correlation matrices. Several distinct types of graphs can be constructed (Rubinov and Sporns 2010). For this dataset, we used the z-transformed Pearson correlation to estimate connectivity. The strength of each connection (correlation between two ROIs) can be represented either as a weight (i.e., the magnitude of the z(r) value) or as a binary (present vs. not present above a certain threshold). Binary graph methods were used as they are computationally straightforward (Rubinov and Sporns 2010) and provide for simpler interpretation (Kaiser 2011).

Graphs were constructed from the single subject correlation matrix. For a single subject (s), the correlation between one ROI (i) and any other ROI (j) is contained in r_i,j where r_{i = j} = 0 because the identity matrix l has no meaning in this context. Values exceeding T were set to 1 (the connection exists) and values failing to exceed threshold T were set to 0 (the connection does not exist). This yielded an unweighted, undirected graph represented as an adjacency matrix (G). In graph theory terminology, a single ROI is a vertex (v = 160) and a connection is an edge ($e=\sum _{i,j,i\ne j}G$). The number of edges for a given vertex is the degree (k_i) and the average degree ($K=\frac{1}{v}\sum _i{k}_i$) is the average across vertices.

There is no single way to select the optimal T value, so for this analysis we varied T over a range of values. The value of T can be applied to the correlation coefficient or used to restrict the number of edges (e) (i.e., limit K). The value of T in this report was chosen such that each group in a particular analysis had identical K values. Instead of expressing graph quantities as a function of threshold values in terms of Pearson correlation coefficients, thresholds were chosen such that graph quantities were expressed as a function of K. This was done because graph quantities (as shown below) are sensitive to differences in both v and e (Sanz-Arigita et al. 2010). Furthermore, AD participants have previously been shown to have significantly reduced correlations throughout the brain (Greicius et al. 2004; Wang et al. 2007; Seeley et al. 2009; Brier et al. 2012) which would reduce e. This forces any observed differences to reflect differences in graph structure, rather than differences in overall connectedness. The range over which K was varied was constrained by the inequality v > K > ln(v) > 1 which forces the graph to be connected, but not fully connected (Watts and Strogatz 1998). In this work, the values of this inequality were 160 > K > 5.

Average Shortest Path Length (L)

Shortest path length is a measure of the shortest route (in terms of edges traversed) between two vertices (Rubinov and Sporns 2010; Wang et al. 2010). It is commonly referred to as a measure of functional integration (Rubinov and Sporns 2010). Average shortest path length (L) is the average shortest path between all pairs of vertices [also called the characteristic path length (Watts and Strogatz 1998)]. Vertices that are not connected have a shortest path length set to infinity. For this reason, L is only defined in connected graphs, but brains may have disconnected vertices, especially in disease. To handle this possibility, the harmonic mean of the shortest path lengths was used, and calculated as $L={\left[\frac{1}{V}\sum _{i,j,i\ne j}{(d_{i,j})}^{-1}\right]}^{-1}$ where d_i,j is the shortest path length between vertices i and j.

Clustering Coefficient (C)

Clustering coefficient is a measure of functional segregation. Clustering coefficient is defined as $C_i=\sum _i\frac{2t_i}{k_i(k_i-1)}$, where t is the number of triangles at the i-th vertex, $t_i=\frac{1}{2}\sum _{j,\mathit{h}}{G}_{ij}{G}_{i\mathit{h}}{G}_{\mathit{h}j}$. This value is normalized by either the degree k at each vertex, or collectively by average degree K. The latter is sometimes referred to as transitivity, $ℐ=\frac{{\Sigma }_{i}2t_i}{{\Sigma }_i{k}_i(k_i-1)}$ (Newman 2003). We use ℐ in this report, but use the abbreviation C in order to be consistent with previous literature. This measure can be averaged over the entire network or reported locally for a single vertex.

Small-Worldness (S)

The idea of small-world networks resulted from the notion that, in order to be efficient, networks should be segregated functional units with efficient connections between them (Watts and Strogatz 1998). In graph theoretical terms, a graph is small world if the path length is similar to that of a random graph, L ≥ L⁰, and has a clustering coefficient that is much greater than a random graph, C ≫ C⁰. It is customary to compare an empirically derived graph to randomly generated graphs to assess the properties of the empirical graph. Specifically, it is important to know the path length and clustering coefficient of a random graph (L⁰ and C⁰, respectively) with identical v and e. To do this, we generated 10,000 Erdos Renyi random graphs (Erdős and Rényi 1959) and calculated the distribution of calculated L⁰ and C⁰. It is often convenient to express these values in normalized terms, with criteria $\frac{L}{L^0}\approx 1$ and $\frac{C}{C^0}\gg 1$.

These criteria can be independently tested, however a single value expressing small-worldness is ideal. A single quantity, small-worldness, is defined as $S=\frac{\frac{C}{C^0}}{\frac{L}{L^0}}$, and has been shown to be sensitive and specific (Humphries and Gurney 2008), but its behavior at the limits of C and L have been questioned (Rubinov and Sporns 2010). Based on these criteria, a network is considered small world when S > 1.

Modularity (Q)

L and C are measures of integration and segregation, respectively, and provide good summaries of the behavior of graphs. However, they do not capture how graphs are integrated within modules (or sub-networks)(i.e. RSNs) and segregated between modules. Modularity captures this feature. Modularity is defined as the ability of a graph to be subdivided into modules that are maximally connected within a module and sparsely connected between modules (Newman and Girvan 2004). Computationally, it is expressed as $Q=\sum _{i\in M}[c_{ii}-{\left(\sum _{j\in M}{c}_{ij}\right)}^2]$, where i and j are individual modules in the set of all modules M, and c is the proportion of existing connections between two modules. In this study, we defined the modules as the 6 RSNs described previously (Dosenbach et al. 2010), as well as using a data driven technique (supplementary text).

Nodal Hub Measures

In addition to the metrics described above, an additionally interesting graph property is the tendency for a small number of brain regions to serve as “hubs.” A hub can be defined by two (not mutually exclusive) ways: a vertex that has many important connections running through it (i.e., is a member of the shortest path between many vertices) and a region that is associated (i.e., has edges between) many different RSNs or modules. Two quantities capture this behavior: betweenness (B) and participation coefficient (P), respectively. Betweenness is defined as $B_i=\frac{1}{(n-1)(\mathit{n}-2)}\sum _{j,h,h\ne j,h\ne i,j\ne i}\frac{{\rho }_{\mathit{h},j}(i)}{{\rho }_{\mathit{h},j}}$ where ρ_h,j is the number of shortest paths between h and j and ρ_h,j (i) is the number of those paths that pass through i. Large values of B_i indicate that a large number of shortest paths run through vertex i which identifies that as a hub. Participation coefficient is defined as $P_i=1-\sum _{m\in M}{\left(\frac{k_i(m)}{k_i}\right)}^2$ where k_i (m) is the number of edges between i and module m. Participation coefficient varies between 0 and 1. Values near 0 indicate that vertex i only has edges within its module and values near 1 indicate that it is homogeneously connected between all modules.

Statistical Tests

Each of these graph theory measures was calculated for a single participant. Statistical significance was assessed using one- or two-way ANOVAs. In addition to testing the effects of interest, the confounding effect of age was included in each of the models. Tests done on demographic data were one-way ANOVAs with CDR or NIA stage as factor. Tests on graph theory metrics were two-way ANOVAs with CDR or NIA stage and age as factors. Because these tests must be done over a range of T, we corrected p-values for multiple comparisons using the false discovery rate (FDR) correction.

Results

Participant Demographics

For all participants completing rs-fcMRI scans, clinical assessments, and CSF within 1 year of imaging, 326 had scans that passed quality assurance tests. The demographics of these participants are reported in Table 1. The groups did not differ significantly on age or gender composition. There was a significant effect of CDR on Mini Mental Status Exam (MMSE), wherein increasing CDR was associated with decreasing MMSE.

Table 1.

Demographic information by CDR status. Mean and (standard deviations) are shown. Mini Mental Status Exam (MMSE)(Folstein et al. 1975) ranges from 0(worst) to 30(best).

CDR	CDR 0	CDR 0.5	CDR 1
N	205	90	31
Age (years)	66.4 (9.8)	74.5 (7.5)	70.7 (11.4)
Sex (% Male)	32%	40%	42%
MMSE	29 (1.5)	27 (2.8)	20 (4.5)

CDR 0 participants exhibit small-worldness

Small-world character is exhibited by cognitively healthy individuals (Achard and Bullmore 2007). A graph is considered small world if L ≥ L⁰ and C ≫ C⁰, where “much greater” was defined as a significant difference, p < 0.001 (uncorrected for multiple comparisons). Supplementary Figure 1 shows the behavior of these two metrics as a function of varying threshold, K, in cognitively normal older adults. L calculated from the CDR 0 group was always larger than L calculated from the random graph. However, C was only significantly greater than C⁰ for K<43. To further quantify the small-world character of the CDR 0 group, we calculated the small-world coefficient (S) which defined a graph as small world (S > 1) or not (S ≤ 1)based on the ratio of normalized C to normalized L (Humphries and Gurney 2008). Based on these criteria, the CDR 0 group had small-worldness for K<34. Based on this observation, only thresholds satisfying S < K < 34 were used for subsequent analyses.

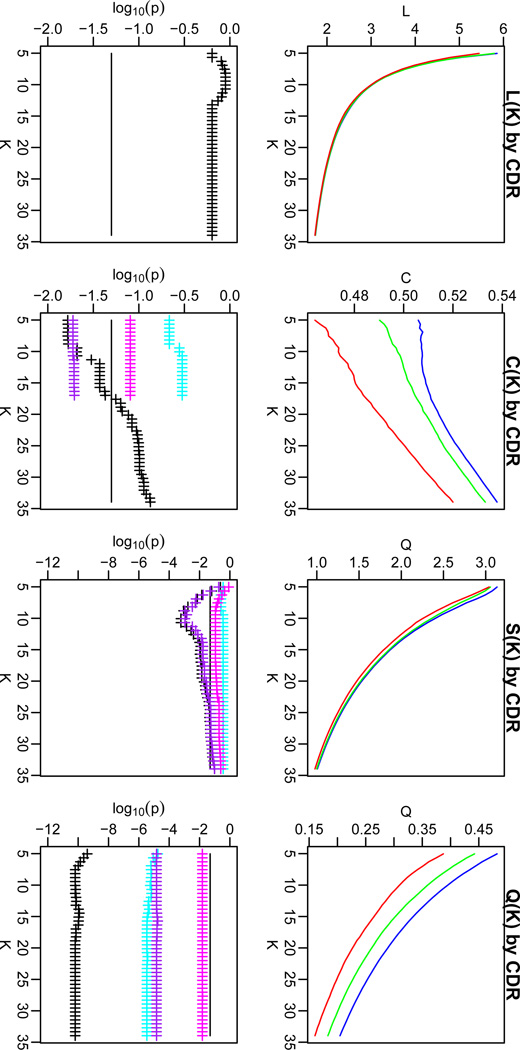
Decreases in C, but not L, were observed with increasing CDR

We next investigated the effect of advancing clinical status, as measured by the CDR, on graph theory metrics. Figure 2 shows L, C, and S measures across a range of K values for CDR 0 (blue), CDR 0.5 (green), and CDR 1 (red) groups. The lower portion of the panels shows the p-value (FDR corrected for multiple comparisons) for the main effect of CDR (black). There was no effect of CDR on L (all p > 0.05). However CDR led to a reduction in C. Over the range of K where the corrected p-value of the ANOVA was significant (p <0.05, FDR corrected), we examined pairwise contrasts for each CDR group. These values were also subjected to correction by the FDR. The CDR 0–CDR 0.5 (cyan) and CDR 0.5–CDR 1 (magenta) contrasts were not significant, but the CDR 0–CDR 1 (purple) contrast was significant. This shows that over the course of advancing clinical status, C declines from CDR 0 to CDR 1, with CDR 0.5 representing an intermediate, albeit not significantly different value. S followed a similar pattern to C. There were no significant effects of age or an interaction of age and CDR for any measure, at any of the thresholds (p > 0.1).

Figure 2.

Path length (L; left), clustering coefficient (C; middle left), small-worldness (S; middle right) and modularity (Q; right) for CDR 0 (blue), CDR 0.5 (green) and CDR 1 (red) groups as a function of K. The false discovery rate (FDR) corrected p-values (lower frames) for these effects are shown for the one-way ANOVA (black crosses), and for each of the contrasts [CDR 0 vs. CDR 0.5 (cyan), CDR 0.5 vs. CDR 1 (magenta), and CDR 0 vs. CDR 1 (purple)]. We investigated only the individual contrasts where the ANOVA showed a significant CDR effect. The black line indicates FDR corrected p = 0.05. The figure shows that there was a significant effect of CDR on C, S, and Q over certain ranges of K.

In order to localize these effects to known RSNs in the brain, we calculated the local clustering coefficient (i.e., the value that is averaged to create a global clustering coefficient) in each node and averaged nodal values within RSNs. These values were subjected to a two-way ANOVA with CDR status as factor. This was repeated for each RSN. We observed that the default-mode network and the occipital network demonstrated reduced clustering coefficient with advancing CDR stage (Table 2). These results suggest that these two RSNs primarily drive the global effect observed above. There were no significant effects of age or an interaction of age and CDR.

Table 2.

Analysis of clustering coefficient (C) values at individual vertices averaged across 6 resting state networks (RSNs) with CDR status as a factor. C was calculated for each vertex for each subject and averaged within RSNs and subjected to tests across CDR. For networks with significant effects, mean (sd) values are reported. Shading indicates significant pair-wise contrasts (p < 0.05).

Network	F	p	CDR 0	CDR 0.5	CDR 1
Cerebellar	1.25	0.29
Cingulo-opercular	0.59	0.55
Default	5.67	0.0038	0.46 (0.066)	0.44 (0.063)	0.41 (0.071)
Fronto-parietal	0.34	0.71
Occipital	9.94	0.000065	0.53 (0.10)	0.50 (0.10)	0.46 (0.10)
Sensori-motor	1.8	0.17

Modularity is reduced with increasing CDR

L and C are commonly investigated in graph theory analyses because of their relationship with small-worldness. In contrast to C, which measures the clustering around vertices, modularity (Q) is a measure both of clustering within networks, and separation between networks. We investigated the effect of increasing CDR on Q. Q was reduced with increasing CDR (Figure 2). This effect was significant (after correction for multiple comparisons) with differences in each of the pair-wise contrasts significant. This suggests that there is a step-wise decrease in Q from CDR 0 to CDR 0.5 and again from CDR 0.5 to CDR 1. The size of this effect (as indexed by the F-value) was larger for Q than C, suggesting that Q is more sensitive measure than C for assessing functional connectivity pathology. The localization analyses that was performed for C could not be used for Q because Q is explicitly based on the separation of individual resting state networks.

The calculation of modularity is dependent on the definitions of modules (RSNs). Different module definitions could result in opposing results. The module definitions used above were defined a priori based on a previous meta-analysis (Dosenbach et al. 2010), but may not be optimal for the elderly group studied here. To address the concern that different module definitions may produce inconsistent results we used a community detection algorithm to define the modules in an independent but demographically similar group and then performed the modularity analysis again. We produced a qualitatively similar result (See Supplementary Results, Supplementary Figures 2, 3 &4). Due to this consistency, the a priori modules were used in the remaining analyses.

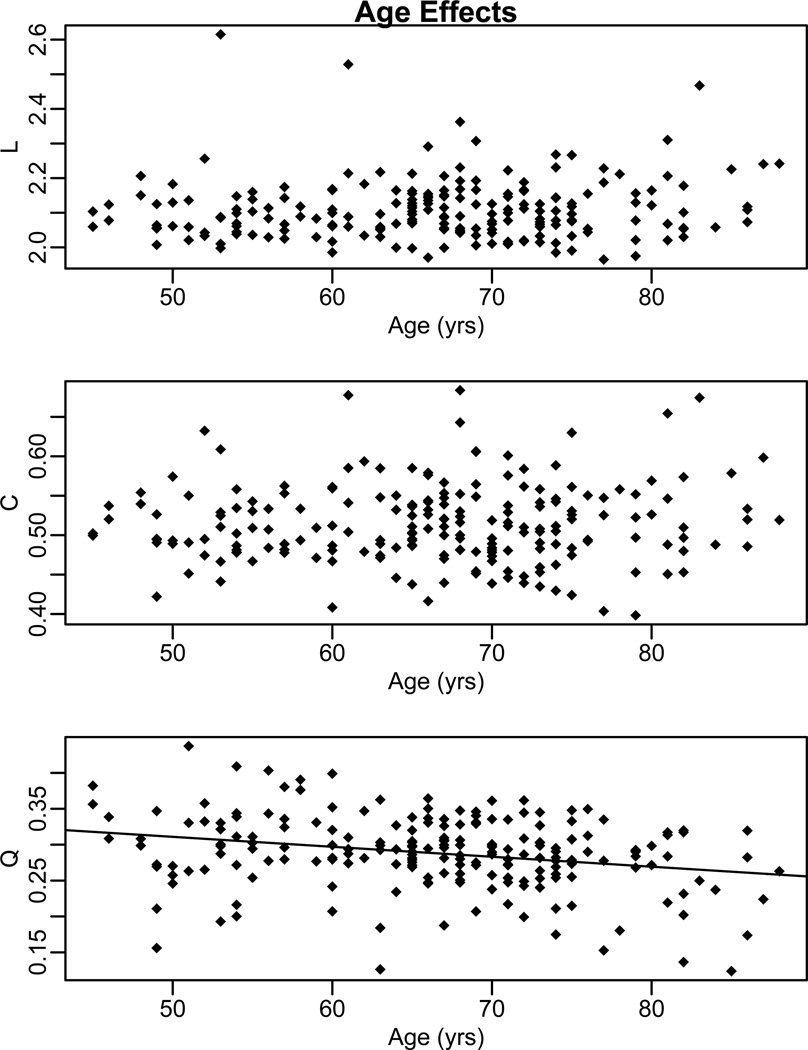
Age Reduces Q, but not L or C

In each of the statistical tests above, the effect of CDR, age, and the interaction of CDR and age were modeled. With respect to L and C, there was only a CDR effect. In contrast, there was a significant effect of age on Q (FDR corrected, p < 0.05). Because age is a continuous variable, main effects of age can be thought of as significant correlations between Q and age (after accounting for variance related to CDR). A significant negative relationship was observed between age and Q with differences greatest at a particular threshold (K = 30, Pearson r = −0.27, p = 0.0001) (Figure 3). This relationship was significant over all values of K (0.0001 ≤ p ≤ 0.015). The interaction between age and CDR on Q was not significant (p > 0.1).

Figure 3.

Scatter plots of path length (L), clustering coefficient (C), and modularity (Q) at a representative threshold (K= 30). No age effect was observed for path length or clustering coefficient. However, a significant age effect was seen for modularity.

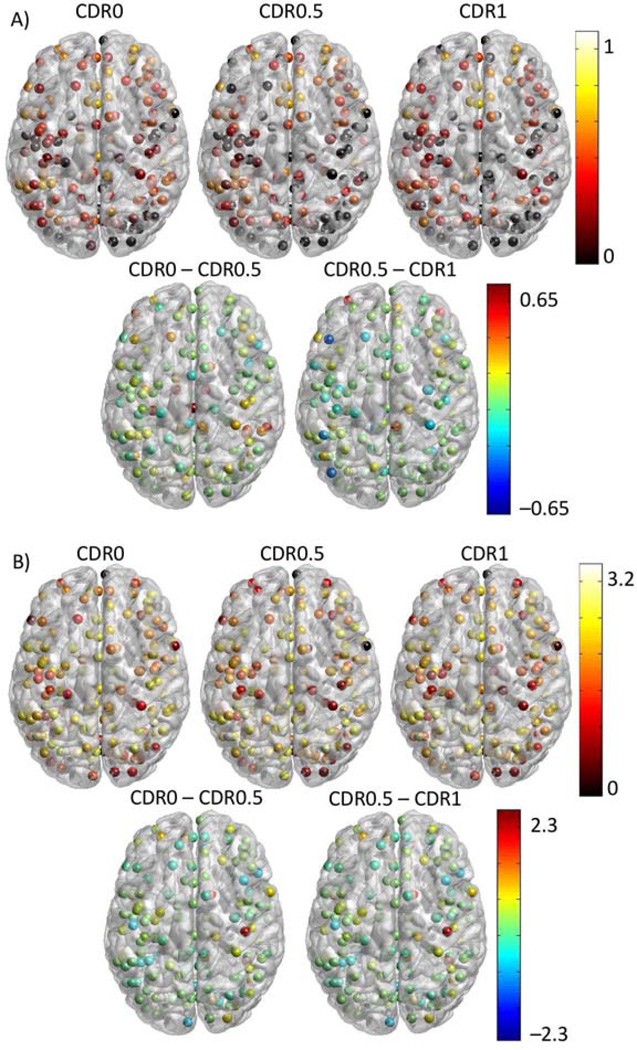
Changes in Nodal Hub-like Behavior

We examined the hub-like property of each ROI in each CDR group. Betweenness and participation coefficient were calculated (Figure 4) for each CDR group. The differences between the CDR stages demonstrated that while participation coefficient tended to decrease with increasing CDR, the betweenness measure showed both increases and decreases (Supplementary Figure 5).

Figure 4.

ROI maps of participation coefficient and betweenness. A: Participation coefficient at each vertex grouped by CDR status (first row). Areas with high participation coefficients are potential hubs. Difference images (second row) demonstrate where advancing CDR impacts participation coefficient. B: Betweenness maps for each of the CDR groups. Because the large range over which betweenness varies, the values displayed here are log₁₀ transformed for display purposes only. The difference maps show the difference in log values.

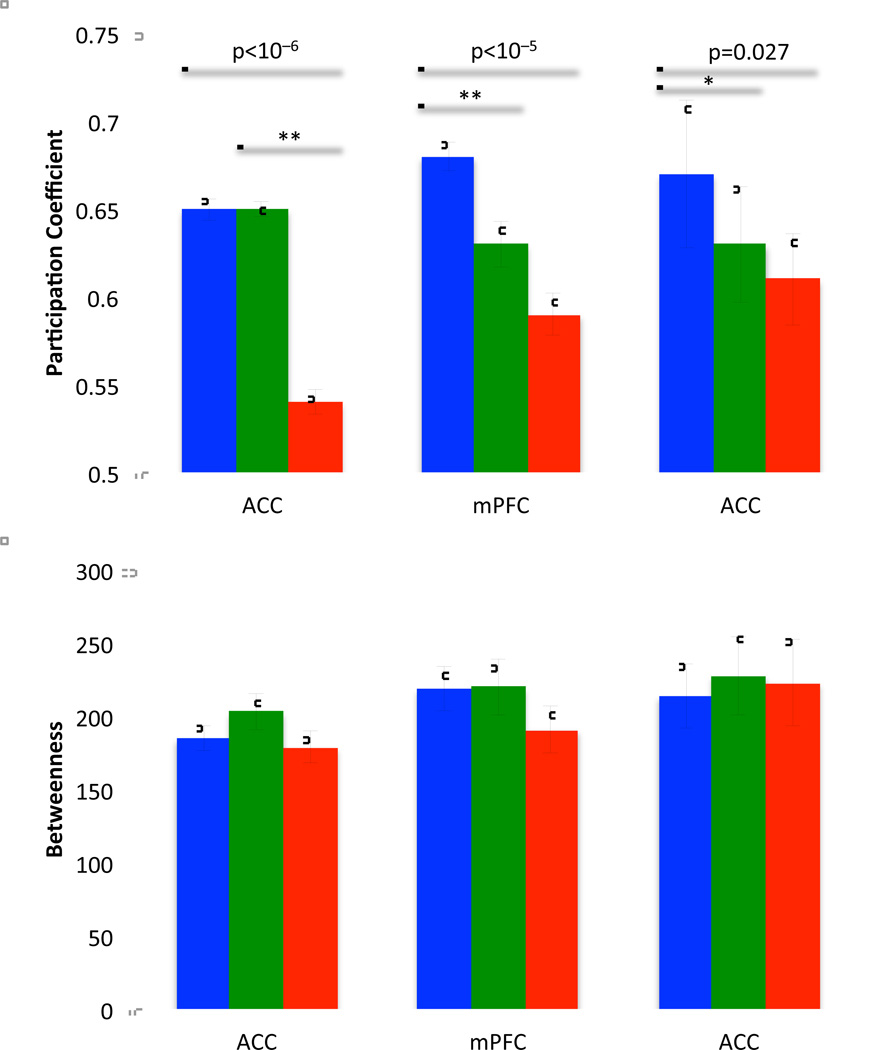
We hypothesized based on previous research (Buckner et al. 2009) that the regions identified as hubs may be particularly sensitive to the AD pathologic process. We identified hubs using the betweenness and participation coefficient. The criteria for hub identification was based on a betweenness score 1.5 standard deviations above the CDR0 mean and a participation coefficient greater than 0.6. These values identified outliers in the distribution. Only ROIs identified using both metrics were retained. 3 ROIs met criteria. Two were in the anterior cingulate cortex (−2,30,27; −1,28,40) and one was in the medial prefrontal cortex (0,15,45). We investigated the effect of increasing CDR on betweenness and participation coefficient in these three regions. We found significant effects on participation coefficient but not betweenness (Figure 5). This suggests that AD significantly impacts the regions of the brain that serve as hubs by reducing their interactions between networks but not by reducing the overall number of connections that involve a given region.

Figure 5.

Bar plots of participation coefficient and betweenness in the three hub regions identified as hubs. Overarching bars indicate significance of one-way ANOVA and pair-wise bars indicate significant contrasts. * indicates p<0.05, ** indicates p<0.01. There was no significant effect of CDR on betweenness (p > 0.10).

Presence of AD pathology is sufficient for network impairment in CDR0

We hypothesized that cognitively normal participants with preclinical AD would exhibit a milder AD network phenotype. Operationally, this may manifest in reductions in C and Q, but preservation of L. To investigate this effect, we compared the graph theory measures between participants exhibiting various stages of preclinical AD. Due to their relatively small number we combined all CDR0participants with NIA stage 1 and 2. Demographics for the three groups are shown in Table 3. Participants were well matched for age, but higher level NIA participants tended to be older. CSF values differed between groups, as this is the variable that defined group membership. L, C, and Q parameters were compared for CDR0 participants who either possessed (NIA stage ≥1) or did not possess (NIA stage 0) AD pathology compared with CDR 0.5 participants. We observed that AD pathology positive CDR 0 participants exhibited reduced C and Q compared to AD pathology negative CDR 0 participants, but not as reduced as CDR 0.5 participants (Figure 6). The differences isolated here are not as large as the effects of CDR but suggest that there may be some subtle resting state network change in the NIA ≥1 group, particularly in Q. Consistent with our previous analysis, there was no effect of pathology status on L. We investigated hub like behavior as in the above analyses but observed no effect of NIA stage on participation coefficient or betweenness.

Table 3.

Demographic information by proposed NIA stages for preclinical AD participants. Mean and (standard deviations) are shown.

NIA Stage	Stage 0	Stage 1	Stage 2
N	132	46	13
Age (years)	64 (9.5)	69 (8.9)	71 (6.8)
Sex (% Male)	33%	32%	31%
CSF AB42	749 (195)	283 (87)	355 (77)
CSF Tau	234 (80)	244(100)	585 (147)

Figure 6.

Path length (left), clustering coefficient (middle left), small-worldness (middle right) and modularity (right) for the NIA stage 0 (cyan), NIA stage 1&2 (purple) and CDR 0.5 (green) groups as a function of K. The FDR corrected p-values (lower frames) for these effects are shown for the one-way ANOVA (black crosses), and for each of the contrasts [NIA 0 vs. NIA 1&2 (red), NIA 1&2 vs. CDR 0.5 (green), and NIA 0 vs. CDR 0.5 (blue)]. We investigated only the individual contrasts where the ANOVA showed a significant CDR effect. The black line indicates FDR corrected p = 0.05.

Discussion

We demonstrate that graph theoretical measures applied to rs-fcMRI data can define changes due to AD, and that changes are present in cognitively normal participants with CSF measures indicative of preclinical AD. First, we observed that progressive clinical AD leads to a decrease in clustering coefficient but does not affect shortest path length. Second, we expand this result by showing that these reductions are parametric with respect to level of cognitive impairment. Third, we demonstrate that modularity is strongly decreased with advancing clinical status. Fourth, we identified changes in the hub-like character of specific important nodes with advancing AD stage. Finally, we show that the presence of abnormal CSF biomarkers consistent with AD pathology in cognitively normal individuals is associated with alterations in functional connectivity using graph theory metrics.

Three specific studies have used varying cohorts and different analytical methods (Supekar et al. 2008; Sanz-Arigita et al. 2010; Wang, Zuo, et al. 2013). A common finding among these studies is that cognitively normal participants display small-world character. We also observed small-worldness in our large cohort of cognitively normal participants. However, each existing study varies in regard to the effect of AD on path length and clustering coefficient. In the one study (Sanz-Arigita et al. 2010), 21 normal control and 18 symptomatic AD individuals were studied using synchronization likelihood as a measure of connectivity. This study observed that symptomatic AD decreased shortest path length, but did not affect clustering coefficient. In another study (Supekar et al. 2008), 18 normal control and 21 symptomatic AD individuals were studied using wavelets as a measure of connectivity. In that study, symptomatic AD decreased clustering coefficient, but did not affect shortest path length. Finally, a more recent study (Wang, Zuo, et al. 2013) assessed 47 normal control and 37 individuals with amnestic MCI. This study employed wavelet analysis and found that amnestic MCI increased shortest path length, but did not affect clustering coefficient. These studies have presented inconsistent primary findings. There are several potential explanations for the inconsistent results in those studies, and the data presented here. First, each study has used different measures of functional connectivity, from simple linear correlation to more complex non-linear methods. Further, the brain parcellation schemes differed with some using spherical ROIs and others using anatomically defined regions. Finally, the preprocessing applied to the data with respect to movement (Power et al., 2012), spatial smoothing (Sanz-Arigita et al., 2010) and nuisance signal regression (Fox et al., 2009) differs amongst studies. These methodological differences could explain some of the divergent results.

Our study differs from previous work in a number of ways. We studied a large cohort (N=326) of meticulously classified participants using the CDR and CSF. Further, all imaging data were subjected to rigorous pre-processing to minimize the effects of movement (Power et al. 2012; Van Dijk et al. 2012). We employed a simple measure of connectivity (i.e., Pearson correlation), which is commonly used in the non-graph theory rs-fcMRI literature. It was recently shown that simple linear correlation is sufficient to capture most of the dependence between BOLD time-series (Hlinka et al. 2011). We empirically derived the thresholds over which our graph theory measures were calculated, thus limiting our investigation to biologically plausible values (where cognitively normal individuals exhibit small-world character). We observed that increasing symptomatic AD severity causes progressive reductions in clustering coefficient, but not shortest path length. This effect was stable over a wide range of thresholds. It may be that disruptions in local connectivity reflect AD pathology. For example, it is known that amyloid pathology is related to decreased functional connectivity (Hedden et al. 2009; Sheline et al. 2010).

In addition to the observed decrement of clustering coefficient with AD, modularity is also strongly reduced in the presence and severity of clinical symptoms. Modularity is large when nodes are maximally connected within a module (i.e. RSN) but minimally connected between modules. This is in contrast to clustering coefficient, which focuses on the behavior within a cluster where a single node can belong to many clusters. Interestingly, modularity was the only measure that had a strong reduction with advancing age in our study. However, there was also a significant effect of CDR wherein participants with symptomatic AD demonstrated larger reductions in modularity than would be expected by age alone. This is consistent with the interpretation that AD is not an inevitable consequence of aging, but is rather a distinct pathological entity.

We also observed that three important brain hubs lost their hub-like character with advancing symptomatic AD stage. These regions in the anterior cingulate and medial prefrontal cortices were identified as being important hubs in the CDR 0 participants but lost their role as important members of network as AD advanced. This could indicate that these regions are no longer able to serve as hubs and may relate to the observed cognitive dysfunction. This expands previous results that found brain hub dysfunction in AD (Buckner et al. 2009) and expands those findings outside the default mode network to involve the same regions that predict performance on a Stroop task, suggesting that they are important for cognition (Duchek et al., 2013). In participants with AD pathology but no symptoms, these regions demonstrated normal hub-like characteristics, which suggest that the changes in clustering coefficient and modularity seen in preclinical AD may be driven by a different process than changes in the behavior of important hubs.

The changes observed in graph theory measures inform our understanding of how the brain changes in AD. First, the reduction in clustering coefficient indicates that regions of the brain that are typically well connected become less connected with disease progression. This has been shown previously using a variety of approaches, including pair-wise ROI correlations (Wang et al. 2007; Brier et al. 2012), measures of RSN integrity (Wang et al. 2010), and ICA (Greicius et al. 2004). However, clustering coefficient provides additional information because it not only considers the connection between a pair of regions, but also studies the connections between mutually connected regions. In this study we additionally localized this change in clustering to default mode and occipital regions. The default mode network involvement is consistent with previous work finding resting-state dysfunction there in AD (Greicius et al. 2004). This result extends those findings by characterizing the nature of the connectivity deficit as a decrease in clustering. This indicates that the functional pathology of AD is more profound than two areas simply becoming less connected. Instead, AD disintegrates the networks in a more global manner. The relationship between changes in neural function as measured by functional connectivity and structural changes associated with AD (e.g., cell death, amyloid deposition and atrophy) remain to be completely elucidated, though it is known that neural activity (Bero et al., 2011) and functional connectivity (Bero et al., 2012) are related to amyloid deposition. Large-scale neural dysfunction could lead to disruptions that cause or accelerate structural pathology.

The second graph measure that we found to be impaired was modularity. Modularity expands the interpretation based on clustering coefficient by concentrating not only to connections within clusters, but also those clusters that do exist become less discrete. That is to say, wherein a healthy brain demonstrates a dramatic distinction between correlated and not correlated brain regions (Fox et al. 2005), a diseased brain demonstrates a less dramatic distinction between present and absent connections. RSNs in a healthy brain tend to form distinct networks (Fox et al. 2005) and this is thought to reflect functional segregation that allows for effective cognition. Interestingly, modularity also showed steady declines with age, suggesting that these changes occur in normal aging. However, changes in modularity were greater for AD.

In this report, we also show that clustering coefficient and modularity begin to show the AD phenotype prior to the onset of cognitive symptoms. Here, for the first time in rs-fcMRI, we classify the presence of AD pathology based on NIA criteria (Sperling et al. 2011; Jack et al. 2012). The demonstration of pathological changes prior to cognitive symptoms is consistent with the observation that the accumulation of amyloid and tau pathology occurs over a prolonged period of time (Braak et al. 2011) and represents preclinical AD (Price and Morris 1999; Price et al. 2009). The presence of this pathology is known to affect RSNs (Hedden et al. 2009; Sheline et al. 2010; Wang, Brier, et al. 2013), and this report expands those localized findings to the whole brain network structure. This provides converging evidence that the presence of AD pathology is sufficient for network impairment in cognitively normal persons, and that this network impairment eventually leads to symptomatic AD.

Graph theory has been applied to other imaging modalities for the study of AD. Specifically, graph theory has been applied to structural connections derived from diffusion techniques. Those studies have found that AD is associated with increased path length and decreased whole brain efficiency (Lo et al. 2010; Bai et al. 2012). The identification of a path length effect contradicts the findings presented in this work, but it is reasonable to predict that structural and functional abnormalities may manifest differently in graph metrics. Future work directly comparing these results in the same participants would help to clarify this apparent discrepancy.

Taken together, these data confirm and expand previous results (Tijms et al. 2013) and show that AD impacts the clustering and modularity of RSNs. Further, these changes can be observed prior to the onset of symptoms, which suggests that, in addition to molecular pathology, there is preclinical functional pathology.