The culturally widespread verbal count list (“one, two, three…”), deployed in accord with what Gelman & Gallistel (1978) call the “counting principles,” represents the positive integers1. The counting principles provide an account of how the count list encodes the successor function; i.e. if a numeral “n” refers to cardinal value n and “p” immediately follows “n” in the count list then “p” refers to n + 1 (see Gelman & Gallistel, 1978, for the classic analysis of the successor function in terms of counting principles). Ever since the publication of Gelman & Gallistel’s (1978) seminal investigation of knowledge of counting in childhood, the question of the sources of the verbal counting principles has been a central concern to developmental psychologists. Following Spelke, Breilinger, Macomber, & Jacobsen (1992; see also Carey & Spelke, 1996) we take the view that evolutionarily ancient, innate “core knowledge” systems provide the cognitive primitives that support learning in childhood. Thus, on our view, determining what core systems support the acquisition of the counting principles is a key aspect of the investigation of their sources.
Gelman and Gallistel (1978, Gallistel & Gelman, 1992) suggested that the core representations underlying children’s successful mastery of verbal counting had the same structure as the verbal counting principles, except that they were formulated non-verbally. However, multiple lines of research have provided evidence against this contention. First, the core representations of number for which there is evidence in infancy differ from the count list both in their format (they do not represent number with an ordered list of discrete symbols) and their expressive power (none can represent exact numbers larger than 4; see Carey, 2004, and Feigenson, Dehaene, & Spelke, 2004, for reviews). Second, learning how the counting principles are implemented in the verbal count list (“one, two, three, four, five…”) is a challenging and protracted process in which children’s initial interpretation of the meaning of the numerals and of the count list itself dramatically deviates from the adult interpretation (e.g., Condry and Spelke, under review; Fuson, 1988; Le Corre, Van de Walle, Brannon, & Carey, 2006; Schaeffer, Eggleston, & Scott, 1974; Siegler, 1991; Wynn, 1990, 1992). Finally, some cultures still do not have any representational system remotely akin to the count list (Gordon, 2004; Pica, Lemer, & Izard, 2004), providing further evidence core knowledge does not comprise non-verbal counting principles.
Thus, the nature of the cognitive primitives out of which the verbal counting principles are learned remains unknown. The present paper explores proposals according to which these primitives are provided by core representations with numerical content for which there is evidence in infancy – namely, parallel individuation, set-based quantification, or analog magnitudes. Before laying out how these core systems could possibly support the acquisition process, we briefly review current characterizations of their structure.
Prelinguistic number representations: analog magnitudes, parallel individuation, and set-based quantification
Analog magnitude representations of number—what Dehaene (1997) calls “the number sense”— are found in human and non-human animals. Many models of this representational system have been proposed (Brannon, Wusthoff, Gallistel, & Gibbon, 2001; Dehaene, 2003; Dehaene & Changeux, 1993; Church & Broadbent, 1990; Church & Meck, 1984, Verguts & Fias, 2004), but all agree that it encodes cardinal values with analog symbols the magnitudes of which are proportional to the number of individuals in the represented sets. In short, analog magnitudes encode number as would a number line. In humans, this system is available at least by the sixth month of life (Brannon, 2002, Lipton & Spelke, 2003; McCrink & Wynn, 2004; Wood & Spelke, 2005b; Xu & Spelke, 2000). Its use is characterized by two related psychophysical signatures --Weber’s law and scalar variability. Weber’s law states that discriminability of two quantities is a function of their ratio (e.g. 5 and 10 are easier to discriminate than 45 and 50; see Dehaene, 1997 for a review). Scalar variability holds if the standard deviation of the estimate of some quantity is a linear function of its absolute value. For example, when prevented from counting, adults can estimate the numerical sizes of sets without counting by relying on mappings between symbols for number (Arabic digits or spoken numerals) and analog magnitudes. Under these conditions, both the average numeral produced and the variability of their estimates increase at the same rate as the sets grow larger (Cordes, Gallistel, and Gelman, 2001; Izard & Dehaene, under review; Whalen, Gallistel, & Gelman, 1999).
A second system of representation with numerical content deployed in non-human primates and young infants is “parallel individuation”2 (Carey & Xu, 2001; Feigenson & Carey, 2003, 2005; Feigenson, Carey, & Hauser, 2002; Hauser & Carey, 2003; Uller, Carey, Huntley-Fenner, & Klatt, 1999; Xu, 2003). This system represents sets of individuals by creating working memory models in which each individual in a set is represented by a unique mental symbol. The level of specification of the mental symbols in each set has not yet been well established. For example, whether a set of two dogs is represented as dogadogb or objectaobjectb or individuala individualb is still unknown. What is clear however is that this system has a hard capacity limit. In adults, it cannot hold any more than 4 individuals in parallel (e.g. Vogel, Woodman, & Luck, 2001). Many experiments suggest that the infant system cannot hold any more than 3 individuals in parallel (Feigenson & Carey, 2003, 2005; Feigenson et al., 2002), though one group of researcher has found that it too can hold up to 4 (Ross-Sheehy, Oakes, & Luck, 2003). Importantly, unlike the analog magnitude system, this system contains no symbols for number. However, it is clear that it has numerical content. Criteria for numerical identity (sameness in the sense of same one) determine whether a new symbol is created in a given model (Xu & Carey, 1996). Additionally, infants can create working memory models of at least two sets of 3 or fewer individuals, and can compare these models on the basis of 1-1 correspondence to determine numerical equivalence or numerical order (Feigenson & Carey, 2003, 2005; Feigenson & Halberda, 2004). Thus, number is represented implicitly in this system, through the criteria that maintain 1-1 correspondence between working memory symbols and individuals in the world, and through the computations that operate over mental models of small sets.
A third system available to non-linguistic primates and to preverbal infants is what we will call the “set based quantificational system.” This system is the root of the meanings of all natural language quantifiers (Chierchia, 1998; Link, 1983). To provide the basis for quantification, this system explicitly distinguishes the atoms, or individuals, in a domain of discourse from all the sets that can be comprised of them. For example, in English, this system connects atoms with the singular determiner “a” and sets with 2 or more individuals with the plural marker “-s” and with the quantifier “some.” In other languages, it supports the meanings of dual-markers (e.g. in Upper Sorbian, Corbett, 2000) or trialmarkers (e.g. in Larike, Corbett, 2000). Just as “a” picks out what atoms have in common, dual-markers pick out what sets consisting of just two atoms have in common, and trial-markers do so for sets of three atoms. Recent studies suggest that non-human primates and infants under the age of 2 command the resources of set-based quantification, at least at the level of the singular/plural distinction (Barner, Thalwitz, Wood, & Carey, in press, Barner, Wood, Hauser, & Carey, under review, Kouider, Harlberda, Wood, & Carey, 2006).
Pathways to the counting principles: possible mappings between core representations of number and the count list
Early in their third year, English-learning children learn to recite the count list in the standard order (i.e. “one, two, three, four, five,…”) at least up to “ten”. While it has the same form as the adult list, this early count list is numerically meaningless (Fuson, 1988; Le Corre et al., 2006; Wynn, 1990, 1992). Thus, the numerals in the list function as placeholders that can be mapped onto core representations of numbers to support the acquisition of the counting principles. Mappings between numerals in the placeholder count list and relevant core representations could plausibly be made via ostentation (e.g. map “three” onto a model of 3 individuals and/or onto an analog magnitude representation of 3 by hearing “three” used to refer to a set of 3 things). We now review three proposals for how such mappings might inform the acquisition of the counting principles.
The “analog magnitudes alone” hypothesis
Many have contended that mappings between the placeholder count list and analog magnitudes could support the acquisition of the counting principles on their own (Dehaene, 1997; Wynn, 1992, 1998)3. Mappings between numerals and magnitudes would endow the numerals with numerical meaning, but would not endow them with exact numerical meaning (where numerals have exact meaning if they only apply to a unique cardinality). Rather, they would endow them with approximate numerical meaning because analog magnitudes are a noisy representation of number. Given that the noise in analog magnitudes increases as a function of the represented number, this is particularly true for large numerals. Thus, while mapping “two” to analog magnitudes could create a close approximation of an exact numerical meaning, mapping “eight” wouldn’t. Rather, the latter mapping would support the application of this numeral to a range of sets centered around eight (e.g. 6, 7, 8, 9, and 10).
Despite their approximate character, analog magnitudes could play a key role in the acquisition of the counting principles. Indeed, since analog magnitudes can represent numerical ordering (e.g. 2 < 4 < 8) in prelinguistic infants (Brannon, 2002), mappings between numerals and analog magnitudes could allow children to make an “analogy between the magnitudinal relationships of their own representations of numerosities, and the positional relationships of the number words” (Wynn, 1992, p. 250). This would allow children could to learn a key property of the count list, namely that “later in the list means larger set,” where the content of “larger set” is given by analog magnitudes.
Evidence that numerals (and Arabic digits) are eventually mapped to magnitudes is plentiful (e.g. Cordes et al., 2001; Dehaene, 1997; Moyer & Landauer, 1967, Whalen, Gallistel, & Gelman, 1999). For example, when adults produce verbal estimates of the sizes of sets without counting, their estimates show the other signature of analog magnitudes, namely scalar variability (Izard & Dehaene, under review; Whalen et al., 1999; see also Cordes et al., 2001, for evidence of scalar variability in numeral comprehension). Much of this mapping is already in place in the preschool years (Duncan & McFarland, 1980; Huntley-Fenner, 2001; Lipton & Spelke, 2005; Sekuler & Mierkiewicz, 1977; Temple & Posner, 1998). For example, as long as they can count to “one hundred”, five-year olds can estimate the cardinal values of sets of up to one hundred objects without counting (Lipton & Spelke, 2005), suggesting that they have mapped most of the numerals in their count list to analog magnitudes. Therefore, the question isn’t whether children ever form mappings between their numerals and analog magnitudes but rather whether the formation of these mappings is a part of the acquisition of the counting principles.
The “enriched parallel individuation alone” hypothesis
Many have proposed that the counting principles could be entirely acquired out of mappings between “one”, “two”, “three”, and perhaps even “four” and representations of small sets provided by a capacity-limited system (Carey, 2004; Hurford, 1987; Khlar & Wallace, 1976). Though all proposals of this type have a similar structure, we focus on Carey’s (2004). On this view, children first acquire the verbal counting principles out of mappings between representations of small sets that are created out of enriched parallel individuation and set-based quantification. Hereafter, we will use the locution “enriched parallel individuation” to refer to the nuemrical representations created out of the combination of these two systems. Via its symbols for small sets of individuals (e.g. singular, dual, and trial markers or {ix}, {ix iy}, (ix iy iz}, respectively), set-based quantification provides the first meaning for children’s numerals. Each of these meanings is stored as a mapping between each numeral and a long-term memory model of a set. Thus, the meaning of “one” would be {ia} – a model containing a single individual file. The meaning for “one,” would at this point be the same as the meaning of the singular determiner “a.” Likewise, the meaning for “two” would be {ia, ib}, or the same as that of dual markers, and so on for all numerals up to “three” or “four”. The links between numerals and their corresponding models would be stored in long-term memory.
To use this system to apply the correct numeral to a given set (e.g. two dogs), children would have to (1) use parallel individuation to set up a working memory model the set in the world (e.g. doga, dogb), (2) compare this working memory model to the stored long-term memory models on the basis of one-to-one correspondence, and (3) select the numeral that has been mapped onto the long-term memory model that matches the working memory model (e.g. “two”). Mappings between the small numerals and models of individuals could support the acquisition of the counting principles for they could support the induction that “next in the count list” means “add 1 individual” (Carey, 2004; Klahr and Wallace, 1976; Hurford, 1987).
The “parallel individuation and analog magnitudes” hypothesis
A priori, there are no reasons why the counting principles should be acquired out of a single core system. Indeed, Spelke and her colleagues (Feigenson et al., 2004; Hauser & Spelke, 2004; Spelke & Tsivkin, 2001a) proposed that children acquire the counting principles by mapping the numerals in their placeholder count list onto representations from each of the core number systems. On this view, children would have to combine the insights provided by each system to acquire the counting principles. That is, they would only induce the counting principles once they have noticed that “next in the count list” means “add one individual” and that it means “larger cardinal value as encoded by analog magnitudes.”
Predictions
Two sources of data could adjudicate among these three hypotheses. First, they make different predictions concerning which numerals might acquire cardinal meanings prior to the acquisition of the counting principles. Enriched parallel individuation is, of course, capacity-limited. So, if enriched parallel individuation is the sole source of numerical content from which the counting principles are acquired, children should only be able to assign cardinal meanings to “one” through “three” or “four” prior to learning the counting principles. On the other hand, the analog magnitude system has no known upper limit4: it is the only core system that can represent the number of individuals in sets comprised of 5 or more, albeit approximately. Therefore, finding that there is no principled limit to the numerals that acquire numerical meaning as part of the acquisition process would provide strong evidence that analog magnitudes are recruited in this process, particularly if it involved acquiring numerical meanings for numerals beyond “four.”
A second source of data that would bear on deciding between these hypotheses is the pattern of variability in children’s use of mapped numerals. Cordes et al. (2001) showed that, in a task tapping the mapping between written numerical symbols and analog magnitudes in adults, scalar variability of numerical estimates can be found from 1 up. And one would certainly expect that young children’s numerical estimates would be noisier than those of adults. Therefore, the hypothesis that analog magnitudes are the sole basis of the mappings out of which the counting principles are acquired predicts that the variability of children’s use of mapped numerals should be scalar from “one” up: i.e., as soon as children have mapped numerals to analog magnitudes, they should be able to produce verbal estimates of the number of individuals in sets within the range of their mapping (e.g. children who have mapped numerals up to “ten” will be able to estimate the number of circles in sets of up to about 10 circles), and the standard deviation of their estimates should be proportional to the mean of their estimates, for all set sizes from 1 up.
The hypotheses that involve enriched parallel individuation make no clear predictions about the nature of noise in children’s use of the numerals “one” to “four” because the noise signature of this system has not been studied systematically. Nonetheless, we can identify two potential sources of noise in the process of numeral production envisioned in our enriched parallel individuation model: (1) the establishment and maintenance of the working memory model, and (2) the comparison of working memory models to long-term memory models on the basis of one-to-one correspondence.
Experimentation suggests that both of these processes are subject to greater error for larger set sizes. In infancy, using parallel individuation to compare two sets on the basis of one-to-one correspondence is harder for larger sets. For example, in Feigenson & Carey’s (2003) manual search task, 12-month-old infants saw balls hidden in an opaque box, were allowed to reach in the box to retrieve all but one ball, and were then given an opportunity to retrieve the remaining ball. To measure whether infants represented the exact number of balls in the box, Feigenson & Carey compared how long infants reached for the remaining ball to how long they reached in the box when it was completely empty. Infants successfully reached longer when the box still contained a ball as long as there were no more than three balls in the box. This suggests that they solved this task by holding a model of the balls hidden in the box in the capacity-limited parallel individuation system, and by ending their reaching when the set of retrieved balls matched the parallel individuation model on the basis of one-to-one correspondence. However, they succeeded more robustly when 2 balls were hidden (a comparison of 1 retrieved ball to an expected total of 2 balls) than when 3 balls were hidden (a 2 vs. 3 comparison), suggesting that matching sets in parallel individuation on the basis one-to-one correspondence is more difficult for larger sets.
Vogel, Woodman & Luck (2001) showed that, while the adult visual short-term memory can hold up to four objects in parallel, tasks that require maintaining three or four objects in visual working memory are more subject to error than tasks that only require maintaining one or two. Close scrutiny of their remarkably reliable results suggests that, for tasks involving one to four objects, the ratio of error rate to set size increases as a function of set size. This is unlike analog magnitudes where this ratio remains constant. Thus, the enriched parallel individuation hypothesis is consistent with error in children’s use of “one” to “four”, and may even predict that the ratio of the error in the use of each numeral over the mean set size to which each is applied should increase.
In sum, these hypotheses make distinct predictions concerning (1) the range of numerals that acquire numerical meaning (exact or approximate) as part of the acquisition process, and (2) the nature of the noise in the children’s use and comprehension of the numerals that are learned as part of the process. To truly test these predictions, it is necessary to evaluate both of these factors in children who have not yet acquired the counting principles, and in children who have just done so. Finding that children acquire numerical meanings for “one” to “four” prior to acquiring the counting principles, but only map numerals beyond “four” after having acquired the counting principles would provide strong evidence in favor of the enriched parallel individuation alone hypothesis. Evidence of a lack of scalar variability in children’s use of “one” to “four” both before and after the acquisition of the counting principles would add further support for this hypothesis. In contrast, if either of the hypotheses that involve analog magnitudes are correct, then, there should not be any principled limit to the numerals that have acquired numerical meaning by the time children have acquired the counting principles. Since the analog magnitude system is the only core numerical system that can represent the number of individuals in sets of 5 or more (albeit approximately), these hypotheses would receive particularly strong support in case of evidence that the acquisition process involves learning approximate numerical meanings for numerals beyond “four.” In case of such evidence, the nature of the noise in children’s use of numerals would determine whether the acquisition process involves analog magnitudes alone or whether it also involves representations of small sets provided by parallel individuation. If the former is correct, use of numerals should show scalar variability from “one” up. If the latter is correct, scalar variability should only obtain for “five” and beyond.
One of the posssibilities entertained above – namely, that children could map numerals beyond “four” onto analog magnitudes after acquiring the counting principles – may seem odd. Indeed, doesn’t knowledge of the counting principles implicate knowledge of the mappings between large numerals and analog magnitudes? Not necessarily. Many studies have shown that exact arithmetic facts (e.g. one-digit addition facts or multiplication tables) and analog magnitudes are independent representations of number (e.g. Dehaene & Cohen, 1992; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999; Lemer, Dehaene, Spelke & Cohen, 2003; Spelke & Tsivkin, 2001b). Insofar as exact arithmetic facts are represented in terms of symbols from the count list (i.e. numerals or Arabic digits), it may be possible to know the meaning of a numeral qua symbol in the count list without knowing its meaning qua symbol mapped onto an analog magnitude. Thus, there could be a period during which children who can determine what numeral to apply to a large set of objects (e.g. 10) by counting it, cannot do so if they are prevented from counting and are thereby forced to rely on the mapping between large numerals and analog magnitudes.
The nature of the mappings that support the acquisition of the counting principles: what is known and what remains to be determined
Many studies have investigated how children acquire meanings for the numerals in their count list prior to the acquisition of the counting principles. These studies have consistently found that, prior to mastering the counting principles, children laboriously learn exact numerical meanings (i.e. meanings whereby each numeral is applied to one and only number of individuals) for “one”, “two”, “three” and sometimes “four” in that order (Le Corre et al., 2006; Sarnecka & Gelman, 2004; Wynn, 1990, 1992). Condry & Spelke (under review) carried out the only previous study that investigated whether children also created approximate meanings for the large numerals via mappings to large analog magnitudes prior to acquiring the counting principles. Children who had not yet acquired the counting principles were presented with pairs of sets (e.g. 5 sheep and 10 sheep) and were asked to point to one of the sets (e.g. “Can you point to the ten sheep?” or “the five sheep?”). The pairs of sets were either comprised of a small set (1 to 4 objects) and a large set (more than 4) or of two large sets. The ratios of the pairs of sets always were very favorable; they never were greater than 0.5, a ratio sufficient for the 6-month-old analog magnitude system to discriminate numbers of objects (Xu & Spelke, 2000; Xu, Spelke, & Goddard, 2005). Therefore, if they had mapped large numerals onto analog magnitudes, children should have succeeded on all pairs. Yet, they only succeeded on pairs involving a small set; all of them failed on pairs exclusively comprised of large sets.
These results strongly suggest that children only map “one” through “four” onto core representations prior to acquiring the counting principles. However, the question of the nature of the ontogenetic sources of the counting principles is not yet resolved, for no study has investigated the nature of the mappings in children who have just acquired the counting principles. To be sure, some studies did investigate the mappings in children who knew the counting principles (Duncan & McFarland, 1980; Huntley-Fenner, 2001; Lipton & Spelke, 2005; Temple & Posner, 1988; Sekuler & Mierkiewicz, 1977) but only did so with children who were at least five years old – i.e. a full 12 to 18 months older than the age at which most children acquire the counting principles. Likewise, no study has investigated the nature of the noise in numerals that are mapped onto core representations as part of the acquisition process.
Thus, all three proposals are still consistent with available data. On the one hand, children may not map numerals beyond “four” until after they have acquired the counting principles, and their use of “one” to “four” may not show scalar variability. This would provide strong support for the enriched parallel individuation alone hypothesis. On the other hand, it could be that children do map numerals beyond “four” as part of the acquisition process but only do so late in this process. Therefore, it’s still possible that, whereas children who haven’t yet acquired the counting principles show little evidence of these mappings, all children who have acquired the counting principles would show such evidence. Depending on whether their use of mapped numerals showed scalar variability from “one” up or from “five” up these data would either support the analog magnitudes alone hypothesis or the hypothesis that implicated them along with parallel individuation.
The current studies
The completion of the investigation of the nature of the sources of the counting principles hinges on the answer to two questions: 1) whether children map numerals beyond “four” as part of the acquisition of the counting principles, and 2) whether children’s use of mapped numerals shows scalar variability. The current studies take on both of these questions. We will proceed in two steps. We will first categorize children into “knower-levels” on the basis of the numerals for which they have learned exact numerical meanings. Children who have learned an exact numerical meaning only for “one” will be referred to as “one”-knowers, those who have only learned exact meanings for “one” and “two” as “two”-knowers, and so on. Because they have only acquired exact meanings for a subset of their count list (e.g. many “one”-knowers can recite the count list up to “ten”), children who have not yet acquired the counting principles will be referred to as “subset-knowers”. Children who know the counting principles will be referred to as “CP-knowers”, where “CP” stands for “counting principles”.
We will then analyze children’s performance on a verbal numerical estimation task. In this task, children were simply shown sets of 1 to 10 individuals and were asked to provide estimates of the number of individuals in each set without counting. Each set size was presented to each child several times so that we obtained a mean estimate and a standard deviation for each set size for each child. These data will allow us to address the first critical question, namely whether the exact knower-levels exhaust the range of numerals mapped onto core representations in the acquisition of the counting principles (i.e. they only learn meanings for “one” to “three” or “four”) or whether the acquisition process also involves the creation of approximate meanings for large numerals via mappings to large analog magnitudes. Finding that, for some CP-knowers, the mean of estimates increases from 1 to 4 but remains constant for all larger set sizes would provide strong evidence that the acquisition process only involves mapping “one” to “four” onto core representations. On the other hand, finding that, by the time they are CP-knowers, all children provide larger estimates for larger set sizes for all set sizes tested would provide strong evidence that children map numerals beyond “four” onto analog magnitudes in the acquisition process. These data will also allow us to calculate the coefficient of variation – i.e. the ratio of the standard deviation over the mean – for children’s estimates of each set size. Analysis of this coefficient will allow us to address the second critical question, namely whether children’s use of mapped numerals shows the tell-tale signature of the analog magnitude system – i.e. scalar variability.
EXPERIMENT 1
In this Experiment, children’s knower-levels were assessed with Wynn’s (1990, 1992) Give-a- Number task. The verbal numerical estimation task, dubbed “Fast Cards,” required children to estimate the number of circles in arrays of 1 to 10 circles that were presented too quickly (1 second) to be counted. We also included a counting task to assess whether children’s count list was long enough in principle to allow them to at least provide rough verbal estimates of the sizes of large sets. All children were also presented with pairs of sets of circles (e.g. 6 vs. 10, and 8 vs. 10) and were asked to point to the set with more circles without counting. This allowed us to determine whether children’s performance on the verbal numerical estimation task was limited by the resolution of their non-verbal core representations of number.
Method
Participants
One hundred and sixteen 3-, 4-, and 5-year-olds participated in Experiment 1 (mean age = 3 years; 11 months, range = 3;0 to 5;7). All were fluent English speakers from the Boston area. The majority of the children were from middle-class backgrounds, and most were Caucasian although a small number of Asian, African American and Hispanic children participated. Participants were tested either at a university child development laboratory or at local day care centers or nursery schools. The families of participants tested in the laboratory were identified through commercially available lists and were initially recruited by letter. All children tested at the lab were accompanied by a caregiver. Children received a small gift for their participation and caregivers who brought them to the laboratory received reimbursement for their travel expenses. Testing in day care centers took place in rooms that were part of the center (e.g., staff rooms); day care centers were given children’s books in token appreciation of their participation. An additional ten children (mean age = 3;6, range = 3;0 to 3;9) participated in Experiment 1 but could not be included in the data analyses. One of them failed to provide data for each of the set sizes tested in the Fast Cards task (n = 1) and the others had count lists that were too short (n = 9; see results of count list elicitation task).
Materials
Count list elicitation task
The materials for this task consisted of ten small plastic animals (elephants or gorillas) presented in a single row.
Give a Number
The materials for this task consisted of three sets of ten to sixteen small plastic animals (fish, elephants, gorillas). The toys in each set were identical, or only differed in one feature (e.g. all fish had the same shape and size but some were brown and some were black). Each set was presented in a separate plastic container.
Fast Cards
The materials consisted of thirty-eight 11”×14” white cardboard cards with black circles on them. The circles were printed on white 8.5”×11” sheets, which were pasted on the cardboard cards, and were laminated with transparent plastic. Set sizes ranged from 1 to 15 for the modeling phase and from 1 to 10 for the test phase.
Non-Verbal Ordinal Judgments
The cards used for this task had the same properties as the cards used in Fast Cards, except that there were a total of twenty-four, and all cards were green.
Procedure
Children were tested in one of two orders: Fast Cards before the Non-Verbal Ordinal (NVO) task (n = 63 children) or NVO before Fast Cards (n = 54). To avoid framing the Fast Cards and NVO tasks as counting tasks, our two counting tasks – Give a Number and count list elicitation – were always done last, with Give a Number always administered before count list elicitation.
Count list elicitation
Children were presented with a single row of ten small toy animals and were asked to count them. If their counting was grossly wrong, the experimenter asked children to count the set one more time more slowly, and assisted their counting by pointing to each object as they counted. Objects were used to elicit children’s count list because simply asking them to count aloud may not have allowed us to determine if they could at least count to “ten”.
Give a Number
To begin, the experimenter placed a small bowl filled with plastic toys on a table in front of the child and asked, “Could you take one elephant out of the bowl and put it on the table?” After the initial demonstration, the experimenter proceeded to ask for larger numbers of toys. On trials where the E asked for 2 or more toys, children were always asked, “Can you count and make sure this is X?” (where X was the number requested) after they had given a set of objects, regardless of how many they had given. If children counted and the last number of their count did not match the number of objects requested, the experimenter then probed with “But I wanted X elephants — can you fix it so that there are X?”
The highest number on which children were tested was determined by a titration method modeled after Wynn, 1992). If children succeeded at giving X dinosaurs, the experimenter requested X + 1 on the next trial. If they then failed to give X + 1 dinosaurs, X was requested on the subsequent trial. Children were tested up to the smallest number that they could not give correctly at least two out of three times (thus, “one”-knowers were tested on 1 and 2, “two”-knowers on 1, 2, and 3, etc…) or up to 6. Following Wynn (1990, 1992), children were allowed a single counting error. Thus, they could be credited with having given the correct number even when they had actually given X ± 1, if they used counting to produce the set.
Fast Cards
To ensure that children understood that they were to estimate without counting, and to illustrate estimating the number of circles in large sets, the task was first modeled by the experimenter. Children sat facing the experimenter about 1m away from her. Before proceeding to model the task, the experimenter told children that they would see cards being flashed very quickly, and that she would guess how many circles were on the card as fast as she could. To encourage children to participate and to deter them from feeling like they had to count, the experimenter emphasized that guesses didn’t need to be perfect, and that all that really mattered in the game was “saying what number it looks like” or “saying what number you think of when you see the circles”. The experimenter then proceeded to simulate guessing the number of circles in arrays of 1 through 15 circles, presented in one of two pseudo-random orders. One order began with 2 and ended with 10, and the other began with 10 and ended with 2. The experimenter simulated guessing by saying things like “Hmm. I’m not sure what this is but it looks like seven circles”, but actually always said the correct answer. The cards in the modeling phase were not always flashed quickly but were sometimes presented for a longer time to make sure that children had clearly registered both the set of circles and the experimenter’s response.
The total surface area of the sets of circles (i.e. the sum of the individual areas of the circles comprising a set) presented in the modeling phase was negatively correlated with the number of circles in the set. The diameter of individual circles varied between 1.2 cm (for the set of 15) and 5.5 cm. (for the set of 1).
Four decks of cards were used for the test phase. Each deck contained sets of 1, 2, 3, 4, 6, 8 and 10 circles. At the beginning of each test trial, the experimenter held the card facing herself, attracted the child’s attention by saying “Ready?”, and then said “Go!” as she flipped the card over so that it would face the child for about 1 second. If children refused to produce an answer, the card was presented again for a longer period of time, and children were coaxed to make a guess while looking at the card. If children still did not answer, the experimenter told the child how many circles were on the card (e.g. “I think that was six circles”). Trials where cards were re-presented were only used in the hope of helping children feel more comfortable with the task, and were excluded from the final analyses.
In two of the decks of test cards, total surface area remained constant across set sizes, and in the other two, total surface area was negatively correlated with set size. For the sets with total area remaining constant, the diameter of individual circles varied between 2.0 cm (for the set of 10) and 6.3 cm (for the set of 1). For the sets with total area negatively correlated with number, the diameter of individual circles varied between 1.5 cm (for the set of 10) and 5.5 cm (for the set of 1). The configuration of sets in the test phase was such that all sets comprised of the same number of circles had different configurations (e.g. the configuration of each of the four sets of 6 circles was different from that of the other sets of 6), and such that sets comprised of large numbers of circles (i.e. 6, 8, or 10) could not be easily broken into smaller perceptual groups (e.g. none of the sets of 6 consisted of two parallel rows of 3 circles).
The sets were presented in one of two pseudo-random orders. In one, the first test card showed a showed a set within the range of parallel individuation (3 circles); in the other, the first test card was within the analog magnitude range (6 circles). In both orders, decks in which the total circle surface area remained constant and those in which it was negatively correlated with number were alternated, with the first deck being one in which total surface area remained constant. Repetitions of the same number were always separated by at least two trials. When the cards were presented to children, there was no noticeable pause between card decks. Thus, children experienced the task as one deck of 28 cards.
Non-verbal ordinal
This task began with the experimenter telling children that they would be shown cards with circles, and that they would have to find “the card with more circles”. Then, she placed two cards on a table between the child and herself and asked “Which card has more circles?”. After children had clearly indicated an answer, the experimenter moved on to the next trial and asked the same question. After several trials, the experimenter sometimes no longer asked the question as children sometimes pointed to the card with the larger number of circles before she had asked them to do it.
We wanted this task to be a non-verbal measure of the availability and accuracy of children’s analog magnitudes. Thus, if children tried to count, they were discouraged from doing so (e.g. the experimenter said “No counting!” or “Try to do it very quickly without counting. It’s more fun that way!”). Fortunately, very few children ever attempted to count, and those who did were easily discouraged from doing so. Trials on which children did count were discarded. Moreover, we wanted the task to tap children’s capacity to spontaneously represent set sizes with magnitudes. Thus, they were never given feedback. The experimenter simply praised children on almost every trial regardless of the accuracy of their choices.
The pairs tested were: 2 vs. 3, 2 vs. 6, 6 vs. 10, and 8 vs. 10. Each pair was presented three times, with the configuration of the circles in each set of the pair being as different as possible each time. For two of the exemplars of each number comparison, the more numerous set had a smaller cumulative surface area than did the less numerous set; for the third exemplar, all circles in both sets were the same size, so the more numerous set also had a larger cumulative surface area. For the trials where total surface area did not predict number, the diameter of the circles varied between 1.5 cm and 3.5. cm. For trials in which circles were the same size in both sets, all circles had a 4.5 cm. diameter.
The pairs were presented in two pseudo-random orders. In both orders, the same comparison pair never occurred on two consecutive trials, and the correct answer was never on the same side any more than two trials in a row.
Results
Knower levels (from Give-a-Number)
To be considered an N-knower, children had to:
Give N objects at least 67% of the time when asked for that number; and
Give N objects no more than half as often when asked for a different number.
For example, if a child always gave two objects when asked for “two” but gave two objects on more than half of the trials on which she was asked for other numbers, she would not be considered to know “two”. Children who succeeded with all numbers requested (i.e., children who could give at least up to “six”) were classified as CP-knowers. Other work (LeCorre et al., 2006; Wynn, 1990, 1992) demonstrates that this criterion for classifying children as CP-knowers captures all and only children who understand how counting represents the positive integers. Table 1 displays the mean age and the mean highest numeral in the count list of the children in each knower-level.
Table 1.
Age, count list length and knower-levels of participants in Experiment 1.
| Agea |
Count list lengthb |
||||
|---|---|---|---|---|---|
| Levels | N | Mean (SE) | Range | Mean (SE) | Range |
| “One”-knowers | 6 | 3;9(1.6) | 3;0 – 4;4 | 9.8 (0.3) | 8–12 |
| “Two”-knowers | 14 | 3;8(1.0) | 3;2 – 4;4 | 10.3 (0.4) | 9–11 |
| “Three”-knowers | 18 | 3;7(0.85) | 3;0 – 4;0 | 10.8 (0.3) | 10–12 |
| “Four”-knowers | 7 | 3;6(1.3) | 3;0 – 4;0 | 10.1 (0.2) | 10–11 |
| CP-knowers | 71 | 4;4(1.0) | 3;2 – 5;7 | 10.8 (0.3) | 10–16 |
Ages are in years and months (years; months).
Children’s count list length was determined by their longest count; e.g. the count list length for a child who once counted to “five” and once to “eight” would be 8.
Count list elicitation
To be sure that children’s performance on Fast Cards would not be limited by their counting range, we only wanted to include children who could at least count to “ten”. While most of the children in our sample (n = 104) could at least count to “ten”, some could not. Thus, in order to use as much of our sample as possible, we also included “one”-knowers who could only count to “eight” (n = 5), and “two”-knowers who could count only count to “nine” (n = 7).
Fast Cards
Although a few children attempted to count, all were easily prompted to guess without counting: more than 95% produced numerals without counting on at least 75% of trials, and all produced at least one numeral for every set size. To filter out uninterpretable noise, numerals greater than “thirty” were excluded from the analysis. Only 4 children (one “two”-knower and three “three”-knowers) ever produced numerals this large.
Assessment of the mapping between large numerals (“five” and beyond) and large analog magnitudes
To determine whether children had mapped large numerals onto large analog magnitudes, we calculated the average value of the numerals each child produced for each set size. For the sake of brevity, we will use the term “function” as a shorthand for “average numeral produced as a function of set size.” We then calculated the average function for each knower-level, where knower-level was determined by performance on Give-a-number. If children had mapped large numerals onto large magnitudes, they should have applied larger numerals to larger set sizes when they were presented with large set sizes (i.e. 6, 8, and 10). Therefore, the slope of their function in the large set size range (henceforth, their “6–10 slope”) should be greater than 0. The analyses below first test the 6–10 slope of subset-knowers’ functions against 0 and then examine whether all CP-knowers had functions with positive 6–10 slopes.
Subset-knowers
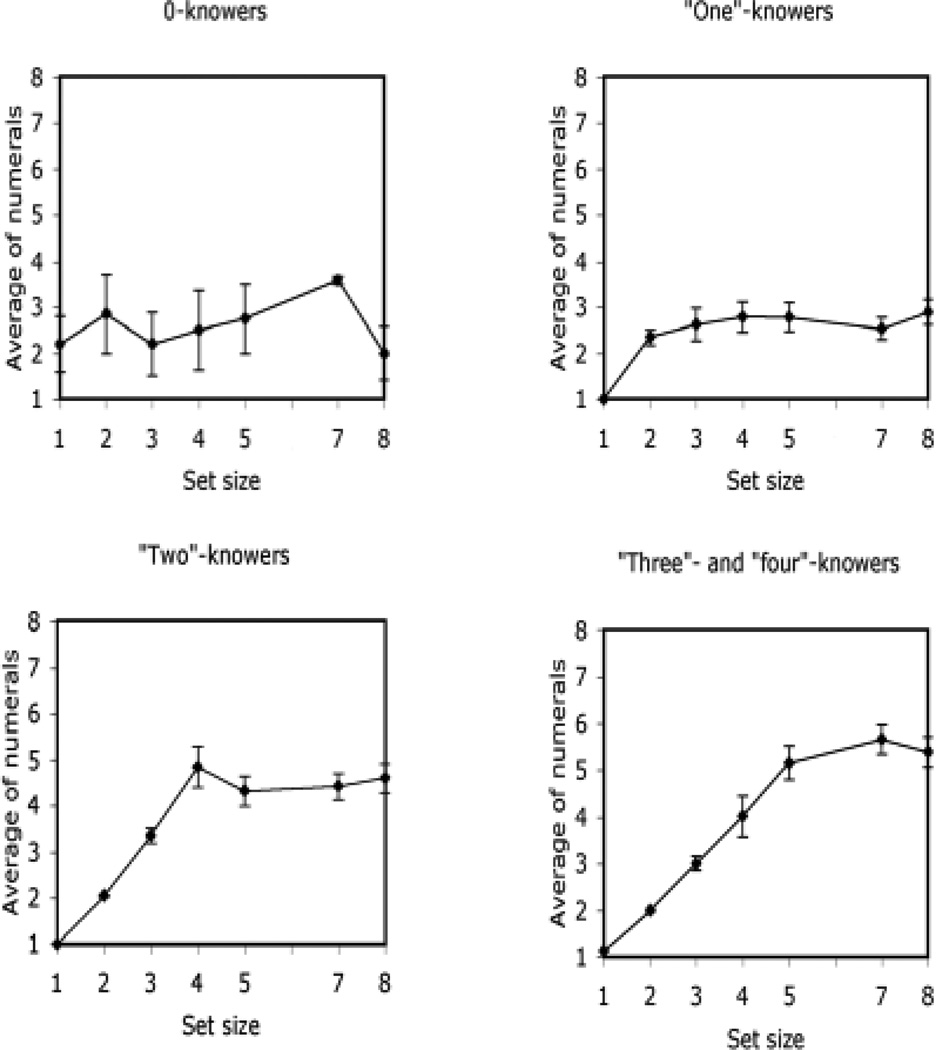
Because of the small size of the groups of “one”-knowers and “four”-knowers, we combined the function for “one”-knowers with that of “two”-knowers and we combined the function for “three”-knowers with that of “four”-knowers. These combinations were justified by analyses that showed that the functions of “one”-knowers did not differ from those of “two”-knowers, and that the functions of “three”-knowers did not differ from those of “four”-knowers. For “one”- and “two”- knowers, an ANOVA assessed the effects of knower-level (“one-” vs. “two-”) and set size (1, 2, 3, 4, 6, 8, or 10) on the average numeral produced. There was no effect of knower level, F(1, 18) = 1.2, ns, and no interaction between knower-level and set size, F(2, 39) = 2.2, ns. A comparable ANOVA examining the difference between “three-” and “four-” knowers also found no effect of knower level, F(1, 23) = 0.38, ns, and no interaction between knower-level and set size F(2, 59) = 0.87, ns). In each ANOVA, the only significant effect was that of set size (“one”-knowers vs. “two”-knowers: F(2,39) = 15.0, p < .001; “three”-knowers vs. “four”-knowers: F(2, 59) = 21.6, p < .001). The functions for the two composite groups are shown in Figure 1.
Figure 1.
Average numeral by set size functions for subset-knowers. “One”- and “two”-knowers were combined because their functions were not significantly different from each other; as were “three”- and “four”-knowers.
As can be seen in Figure 1, the 6–10 slope for “one”- and “two”-knowers’ function (M = 0.11, SE = 0.10) was not significantly different from 0, t(22) = 1.12, ns, In fact, the shape of “one”- and “two”-knowers’ function suggests that they had barely mapped any of the numerals beyond their Give a Number knower-level. They failed to apply larger numerals to larger set sizes when they were presented with sets of 3 or more circles – the 3–10 slope of their function (M = 0.04, SE = 0.04) did not differ from 0, t(22) = 0.95, ns. The 6–10 slope of “three”- and “four”-knowers’ function (M = 0.03, SE = 0.08) was not significantly different from 0 either, t(28) = 0.35, ns (see Figure 1). Thus, all subset-knowers failed to apply larger numerals to larger set sizes when they were presented with sets of 6 or more circles.
One aspect of “three”- and “four”-knowers’ function was not consistent with their Give a Number knower-level. Given their performance on Give a Number, “three”-knowers should have accurately estimated the size of sets of up to 3 circles and “four”-knowers should have accurately estimated the size of sets of up to 4 circles. Contrary to this prediction, “three”- and “four”-knowers’ average estimate of sets of 3 (M = 5.22, SE = 0.53) and 4 (M = 6.18, SE = 0.58) were quite off the mark. Insofar as it shows that their estimates of 3 and 4 were noisy, this may seem to suggest that these children used analog magnitudes to estimate these set sizes. However, evidence of noise isn’t sufficient to show that children used analog magnitudes. One must also show that this noise is scalar, a question we will address below (see “scalar variability” section).
“Three”- and “four”-knowers’ difficulties with estimating suggests that Fast Cards underestimated their knowledge of “three” and “four”. Thus, the group’s failure to estimate large set sizes may have been caused by non-numerical aspects of the task (e.g. the rate of presentation of the sets) rather than by their lack of knowledge of mappings between large numerals and magnitudes. However, some “three”-knowers could accurately estimate sets of up to 3 (i.e. their mean estimate for each of these set sizes was within ±?0.5 of the target; n = 7) and some “four”-knowers could accurately estimate sets of up to 4 (n = 2). The 6–10 slope for this group of 9 “three”- and “four”-knowers (M = - 0.23, SE = 0.14) was not positive either (indeed it was negative), and it was not significantly different from 0, t(8) = 1.69. This suggests that “three”- and “four”-knowers’ failure to estimate large set sizes was not exclusively due to task difficulty.
CP-knowers
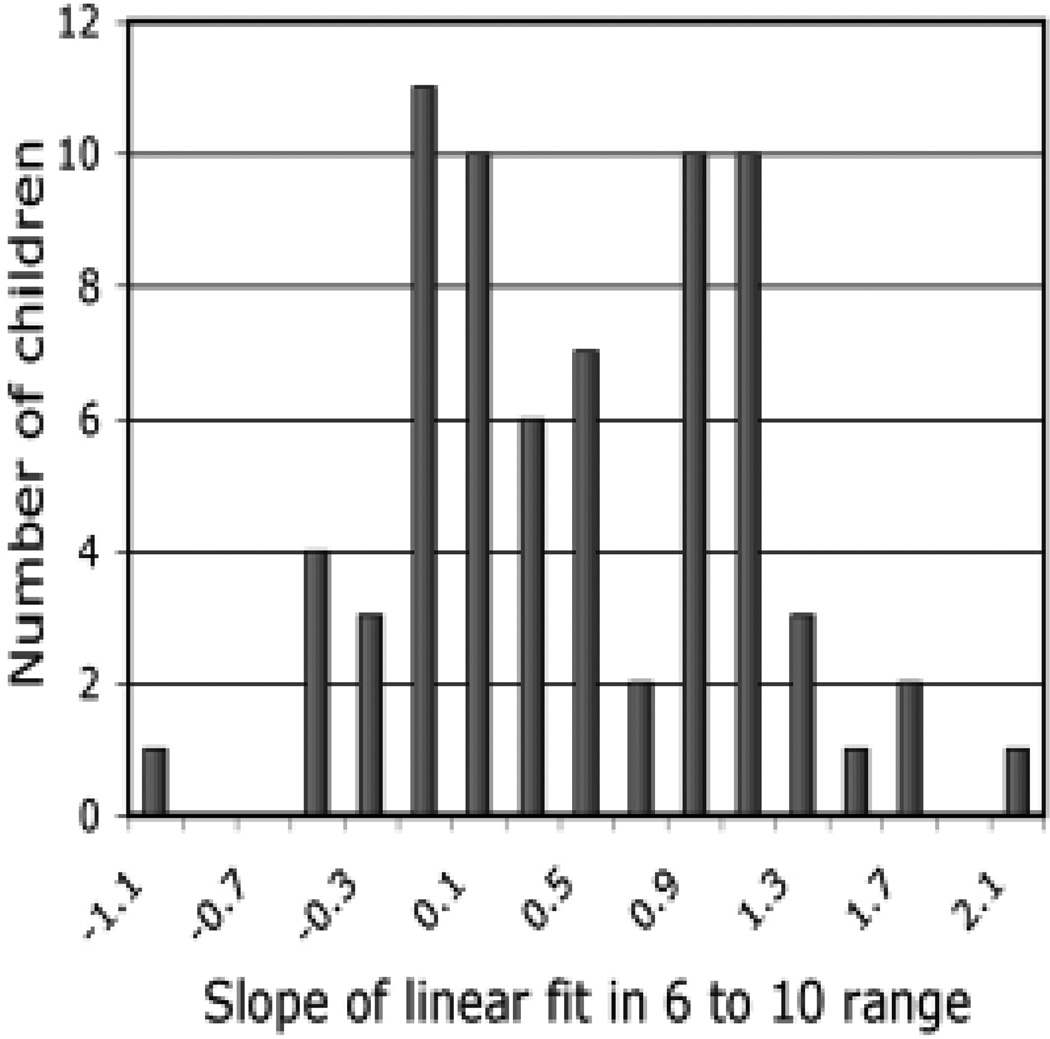
To determine whether all CP-knowers had mapped large numerals onto large magnitudes, we analyzed the distribution of individual 6–10 slopes for 71 CP-knowers (Figure 2). If children have mapped large numerals onto large magnitudes by the time they become CP-knowers, the distribution of their 6–10 slopes should have had a mean that was greater than 0 and it should have been a single normal distribution centered around this mean. While the mean of CP-knowers’ 6–10 slopes (M = 0.56, SE = 0.07) was significantly greater than 0, t(71) = 7.60, p < .001, it clearly wasn’t the center of the distribution of all 6–10 slopes. Indeed, rather than showing a single peak around 0.56, the distribution had two prominent peaks: one near 0, and one near 1.1. A Kolmogorov-Smirnov test of normality with Lilliefors correction confirmed that the shape of our distribution was significantly different from a single normal curve, D = 0.11, p < .05. These properties of the distribution of CP-knowers’ 6–10 slopes strongly suggest that the group of CP-knowers was actually composed of two groups: CP-knowers who hadn’t mapped numerals beyond “four” onto magnitudes (i.e. CP-knowers with 6–10 slopes distributed around 0) and CP-knowers who had mapped numerals beyond “four” onto magnitudes (i.e. CP-knowers with 6- 10 slopes distributed around 1). Hereafter, we will refer to the first group as “CP non-mappers” and to the latter as “CP mappers”.
Figure 2.
Distribution of the slopes of the linear fits of CP-knowers' average numeral by set size functions for set sizes between 6 and 10. Each bar represents the number of CP-knowers with 6–10 slopes of a given size.
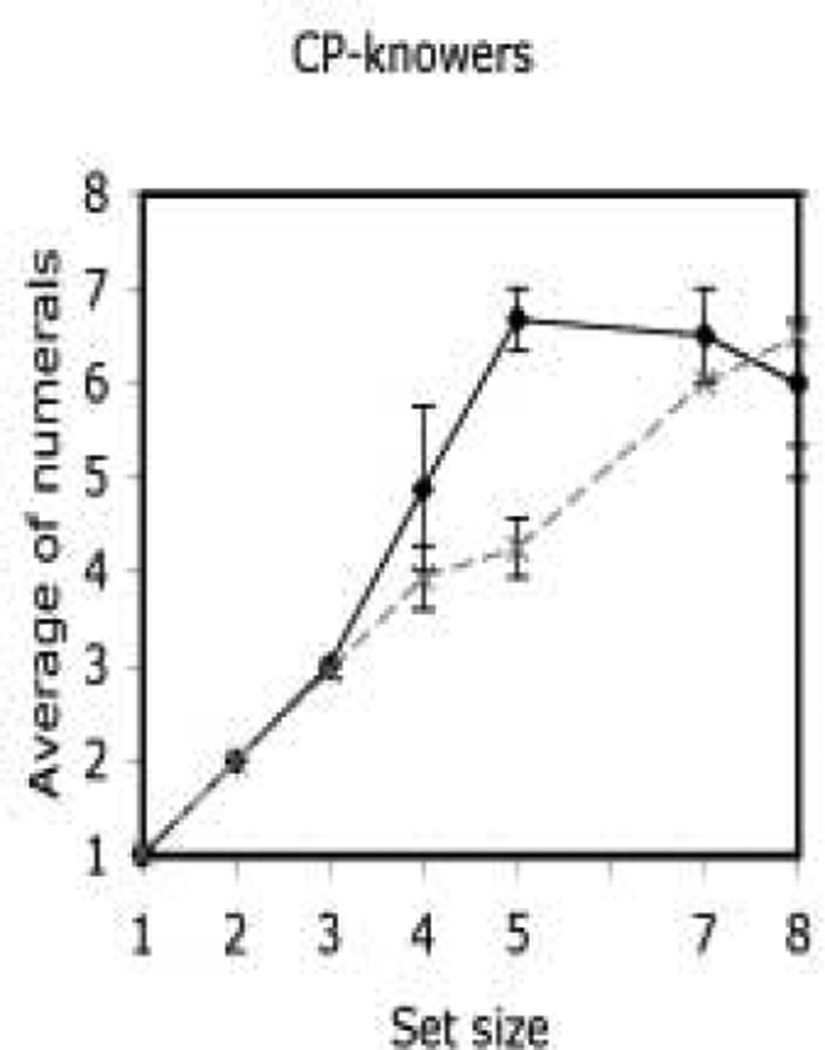
In light of these results, we plotted separate functions for CP mappers and non-mappers (see Figure 3). As this is the first report of the existence of CP non-mappers, we chose a relatively small 6–10 slope (0.3) as our cut-off between CP non-mappers and mappers. This ensured that the function for nonmappers would almost exclusively consist of data from children who hadn’t mapped their large numerals onto magnitudes. Given this criterion, there were 30 CP non-mappers and 41 mappers. If these two groups really reflect two stages of the acquisition of numeral meanings, the non-mappers should be younger than the mappers. As predicted, the non-mappers (mean age = 4;1; range: 3;2 to 5;6) were significantly younger than the mappers (mean age = 4;6; range: 3;5 to 5;7), t(70) = 2.65, p < .05. More generally, amongst CP-knowers, age and 6–10 slope were positively correlated with each other, r = 0.27, p < .05
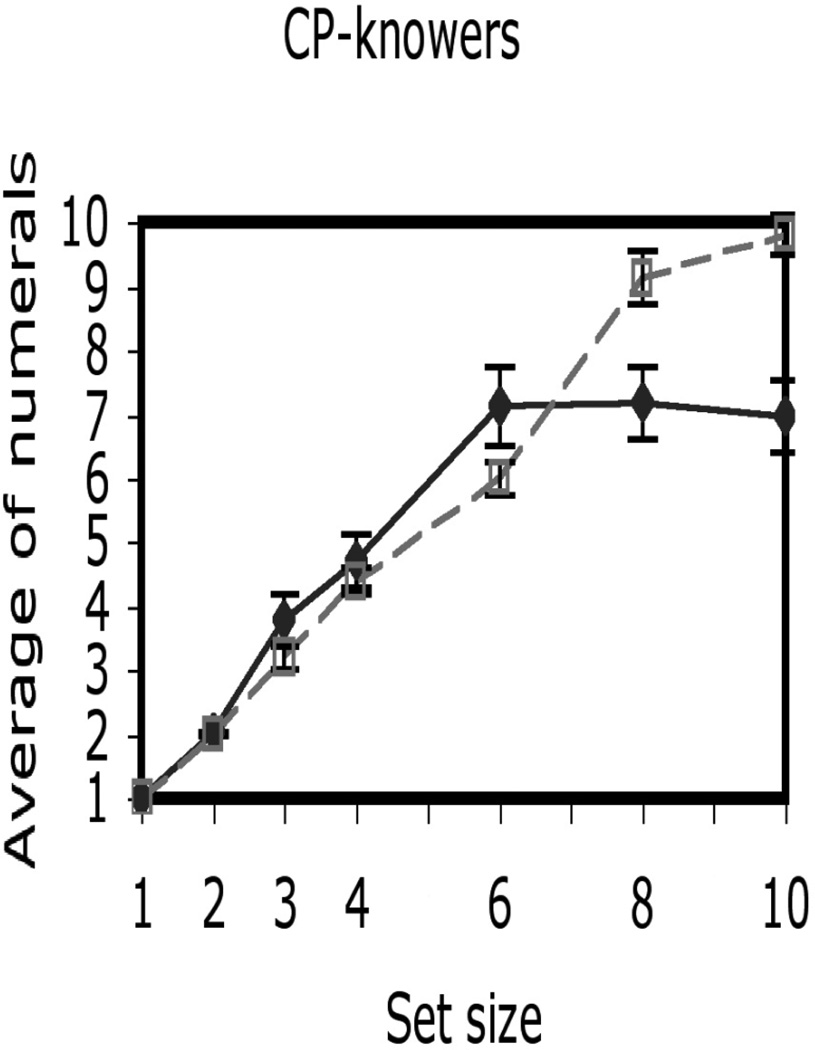
Figure 3.
Average numeral by set size functions for CP non-mappers (solid line) and CP mappers (dashed line). CP non-mappers were CP-knowers who had functions with slopes that were less than 0.3 in the unambiguous magnitude range (6–10); CP mappers had 6–10 slopes that were greater than 0.3.
As can be seen in Figure 3, the functions for CP non-mappers and CP mappers were qualitatively different in the 6–10 range. By definition, the average 6–10 slope of CP non-mappers was equal to 0 (M = −0.02, SE = 0.05). In sharp contrast, the average 6–10 slope of CP-mappers’ function was equal to 1 (M = 1.0, SE = 0.06). However, the 1–4 slopes of CP non-mappers’ (M = 1.27, SE = 0.15) and CP-mappers’ (M = 1.07, SE = 0.03) functions were not significantly different from each other, t(30) = 1.32, ns; both were nearly equal to 1. Indeed, Figure 3 shows that the two functions were identical in the small set size range (1–4). These properties of the two functions suggest that, while both groups had mapped “one” to “four” onto core representations of small sets, CP-mappers were the only ones who had mapped numerals beyond “four” onto analog magnitudes.
Analyses of individual numerals for CP non-mappers and CP mappers
Our data suggest that children only learn numerical meanings for “one” to “four” in the process of acquiring the counting principles. However, since children were not tested on sets of 5, it’s possible that children also learn a numerical meaning for “five” as part of the acquisition process, but that our analyses of the average numeral by set size functions missed this. To address this problem, we analyzed how CP non-mappers and CP mappers used each individual numeral as a function of set size. If children map “five” onto analog magnitudes as part of the acquisition process, we should see that both CP nonmappers and CP mappers were more likely to use this numeral when presented with sets of about 6 circles than when presented with sets of 8 or 10. On the other hand, finding that CP non-mappers applied “five” (and all other numerals beyond it) equally to all large set sizes would confirm that children do not learn numerical meanings for numerals beyond “four” as part of the acquisition process.
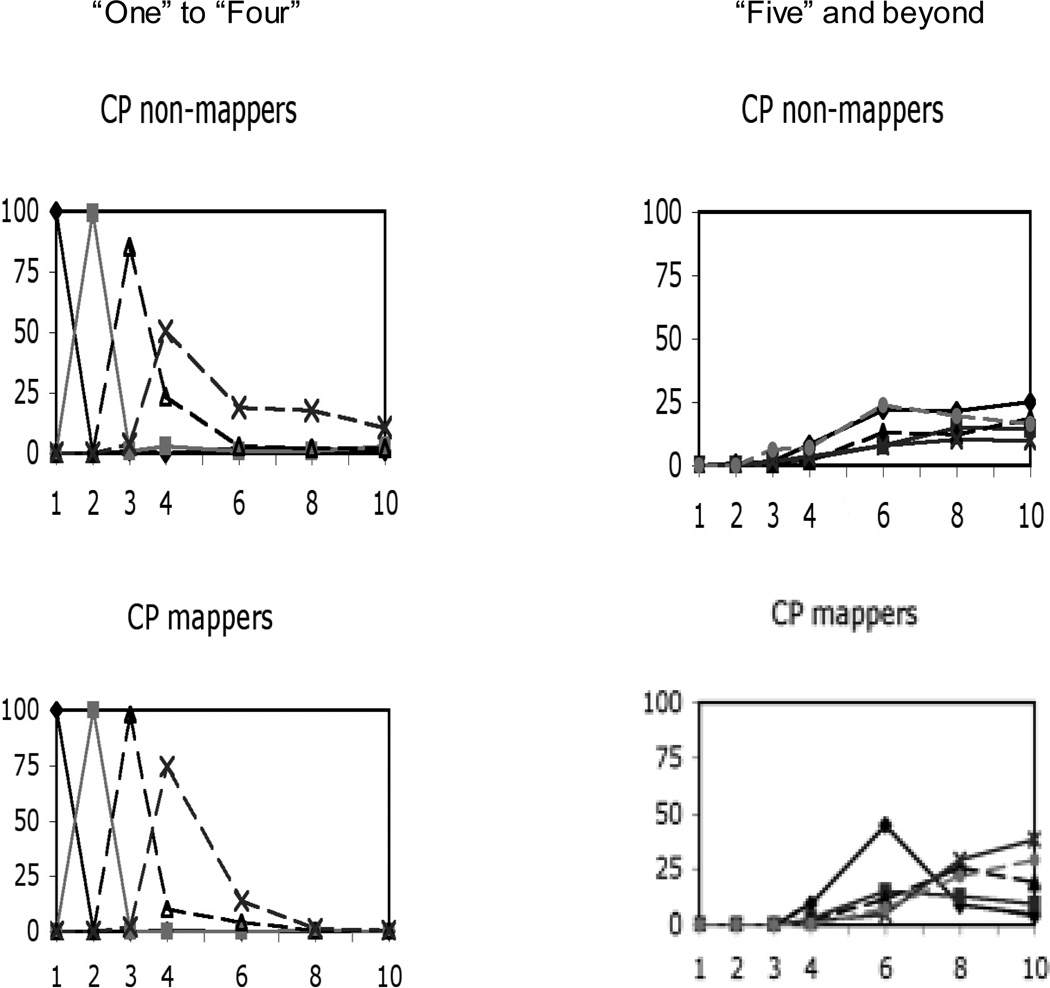
Distributions of application of each numeral as a function of set size were computed for CP non-mappers and CP-mappers5. Individual distributions were computed for each numeral between “one” and “six.” To simplify the exploration of these data, the distributions for “seven” and “eight” were added together into a single distribution, as were those for “nine” and “ten”, and for all numerals beyond “ten”. These distributions are reported in Figure 4. To obtain each distribution, we calculated the probability of application of each numeral to each set size as follows: we divided the total number of times each numeral was applied to a given set size by the total number of trials with this set size, and calculated this probability for each set size. For example, to compute the distribution of “one” for CP non-mappers, we added all the times CP non-mappers had applied “one” to sets of 1, divided this number by the total number of times they had been presented with 1 circle, and repeated this procedure for all other set sizes. Since all possible numerals (i.e. from “one” to “beyond ten”) were counted in this analysis, the probabilities of application added up to 1 for each set size.
Figure 4.
Numeral distributions for CP non-mappers and CP mappers. Each distribution represents the probability of using a given numeral as a function of set size. For example, for sets of 1 object, the distribution for “one” shows how often children applied “one” to this set size out of all trials with this set size. Figures in the left column show the distributions for “one” to “four” (“one”:  ; “two”:
; “two”:  ; “three”:
; “three”:  ; “four”:
; “four”:  ). Figures in the right column show the distributions for “five” (
). Figures in the right column show the distributions for “five” ( ), “six” (
), “six” ( ), “seven” and “eight” (
), “seven” and “eight” ( ); “nine” and “ten” (
); “nine” and “ten” ( ); and all numerals beyond “ten” (
); and all numerals beyond “ten” ( ). The distributions for “seven” and “eight” were added together to simplify the figures as were the distributions for “nine” and “ten” and the distributions for numerals greater than “ten”.
). The distributions for “seven” and “eight” were added together to simplify the figures as were the distributions for “nine” and “ten” and the distributions for numerals greater than “ten”.
The shape of the distributions in Figure 4 show that both CP mappers and non-mappers had mapped “one” to “four” onto core representations; i.e. for each group, the distributions for “one”, “two”, “three”, and “four” had clear peaks over set sizes of 1, 2, 3, and 4 respectively. Critically, they also suggest that CP mappers were the only ones who had mapped any numerals beyond “four” onto analog magnitudes; i.e. the distributions for numerals beyond “four” only showed peaks over large set sizes in CP mappers. To verify this impression, we analyzed how each group applied large numerals to large set sizes with one-way ANOVAs with large set size (6,8,10) as a repeated measure and probability of application as a dependent variable. Whereas CP mappers showed main effects of large set size for all numerals except “six” (ps for numerals other than “six” all < .005; for “six”, ns), CP non-mappers did not show any (all ps > .07). This strongly suggests that CP mappers were the only ones who had mapped any numerals beyond “four” onto analog magnitudes.
Scalar variability
One of the signs that numerals are mapped onto analog magnitudes is that their use in a verbal estimation task such as Fast Cards shows scalar variability (e.g. Whalen et al., 1999). Variability is scalar when the ratio of the standard deviation over the mean (the “coefficient of variation” or COV) is the same for each set size. Here we examine children’s COVs for two reasons. First, we establish that children who could produce rough numerical estimates of large set sizes – i.e. CP-mappers – did so by relying on analog magnitudes. CP mappers’ estimates of large set sizes did show scalar variability; a one-way repeated measures ANOVA of their COVs for large set sizes (6, 8, 10) showed no effect of large set size, F(2,78) = 1.55, ns (see Table 2)6. This strongly suggests that CP mappers used mappings between large numerals and large analog magnitudes to produce verbal estimates of the sizes of large sets.
Table 2.
Mean coefficients of variation (COVs) for “four” -knowers, CP non-mappers, and CP mappers.
| Knower-level | Set size |
||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 6 | 8 | 10 | |
| “Four”-knowers | 0 (0) | 0 (0) | 0.41 (.16) | 0.40 (.14) | --- | --- | --- |
| CP non-mappers | 0 (0) | 0.02 (.02) | 0.14 (.05) | 0.25 (.04) | --- | --- | --- |
| CP mappers | 0 (0) | 0 (0) | 0.01 (.01) | 0.12 (.03) | 0.22 (.03) | 0.24 (.03) | 0.18 (.02) |
Note: The coefficients of variation (COVs) in this table were computed as the ratio of the standard deviation of estimates over the mean of estimates for each given set size. The standard error for each COV is indicated in parentheses. “Four”-knowers’ and CP non-mappers’ COVs for large numerals were not computed because these children could not estimate the numerical size of large sets.
Second, we used COVs to examine what core representations support the numerical meanings of “one” to “four”. If the acquisition of the counting principles involves mapping “one” to “four” onto analog magnitudes alone, the COV for estimates of the sizes of sets of 1 to 4 should be constant by the time children have learned numerical meanings for these numerals; i.e. these COVs should be constant for “four”-knowers, CP non-mappers, and CP-mappers. Moreover, in children who have mapped large numerals onto analog magnitudes – i.e. CP mappers – the COV for small set sizes should be the same as that for large set sizes.
One-way ANOVAs with COV as the dependent measure and small set size (1–4) as a repeated measure showed that the COVs for small set sizes were not constant but rather increased significantly (see Table 2) in “four”-knowers, F(1,7) = 6.69, p < .05, CP non-mappers, F(3,87) = 15.65, p < .001, and CP mappers, F(1,41) = 15.62, p < .001. Moreover, for CP-mappers, the average COV for small sets (M = .03; SE =.01) was significantly smaller than that for large sets (M = .21; SE =.02), t(39)= 10.7, p < .001. This difference was not solely due to drastically smaller variance in CP-mappers’ estimates of 1 and 2; the COVs for 3 (M = .01, SE = .01) and 4 (M = .12, SE = .03) were both significantly smaller than the average COV for large sets (both t’s > 3.3, both p’s < .005).
These results strongly suggest that children do not map “one” to “four” onto analog magnitudes alone to acquire the counting principles. To be clear, the small size of the noise in children’s estimates of small set sizes is not what contradicts the “analog magnitudes alone” hypothesis. Indeed, since scalar variability predicts that noise should be smallest for small set sizes, the analog magnitudes alone hypothesis could potentially be consistent with little noise in estimates of small set sizes. The reason why these results are not consistent with this hypothesis is that they show that, for small set sizes, noise was not proportional to the mean of estimates. In other words, they show that, for small set sizes, variability (as measured by the standard deviation) was not scalar. Since scalar variability is the signature of absolute number estimation based on the analog magnitude system, this result poses serious problems for any view on which “one” to “four” are mapped onto analog magnitudes alone.
It is important to note that it would have been quite possible to observe scalar variability in the small set range. Cordes et al. (2001) have found that, in adults, the variability of numerical estimates produced without counting is scalar from 1 up. Therefore, despite the small size in the error of estimates of small sets, it is possible to find evidence of scalar variability from 1 up. Also, CP-mappers’ average COV for large set sizes (0.21) was almost identical to the average COV (0.23) reported by Huntler-Fenner (2001) for 5- to 7-year-olds’ estimates of large sets and to that reported by Cordes et al. (2001) for adults (about 0.2). This convergence across studies and ages suggests that the mean COV of CPmappers’ estimates of large set sizes is a valid index of what variability is like when analog magnitudes are used to estimate the numerical size of a set. Therefore, we can safely extrapolate that, if variability had been scalar, children’s COV for small set sizes should also have been equal to 0.2 at least by the time they had become CP-mappers. As reported above, this was not the case. CP-mappers’ COVs for sets of 1 to 4 were all smaller than 0.2, and CP-mappers’ and “four”-knowers’ COVs also departed from that value for most small set sizes (see Table 2). Thus, the analysis of the variability of children’s estimates strongly suggests that children relied on some representation system other than or in addition to analog magnitudes to estimate small set sizes. But what other representational system?
Only two other representational systems could have contributed to children’s estimates of the cardinal values of small set sizes: enriched parallel individuation and counting. Since sets were only presented for 1 second, our task was not conducive to counting. Yet, this presentation time may not have been short enough to prevent children from counting, particularly for small set sizes. Two aspects of our results suggest that counting was not the source of children’s estimates of small set sizes. First, since they had not yet acquired the counting principles, it is highly unlikely that “four”-knowers generated their estimates of small set sizes by counting. Second, Cordes et al. (2001) showed that the variability due to errors produced while counting is not scalar but binomial, even when counting small set sizes. When variability is binomial, the COV decreases as set sizes grow larger. The COVs for CP non-mappers’ and CP-mappers’ did not follow this trend. Rather, their COVs for small set sizes increased significantly as a function of set size (see Table 2). Therefore, these results suggest that small sets represented via parallel individuation must be part of the resources drawn upon to provide the meanings of “one” to “four.”
Non-Verbal Ordinal (NVO)
CP mappers were the only ones who could estimate the numerical size of large sets. This suggests that they were the only ones who had mapped large numerals onto analog magnitudes. Alternatively, it could be that other children (e.g. CP non-mappers) had also mapped large numerals onto large analog magnitudes, but that CP mappers were the only ones who could deploy these mappings in the Fast Cards task because their analog magnitude system was significantly more acute than that of children in all the other groups. To decide between these alternatives, we tested children on a non-verbal ordinal task in which they were presented with pairs of sets of circles (2 vs. 3, 2 vs. 6, 6 vs. 10, and 8 vs. 10) and were asked to point to the set with the largest set of circles. If children’s performance on verbal numerical estimation was controlled by non-verbal aspects of their numerical representations, then CPmappers’ non-verbal ordinal judgments should have been more accurate than all other groups, particularly on trials involving pairs of large sets (i.e. 6 vs. 10, and 8 vs. 10).
We examined the average accuracy of children’s non-verbal ordinal judgments as a function of their knower-level (see Figure 5)7. “Three”- and “four”-knowers’ results were plotted together because they were not significantly different from each other (see below) and because there were so few “four”- knowers. To be sure that children’s answers were not based on counting, we excluded all trials in which children showed any sign of attempting to count either by counting out loud, or by engaging in serial pointing. Very few attempted to count at all, and those who did only tried to count on the first one or two trials, and were easily discouraged from doing so on further trials.
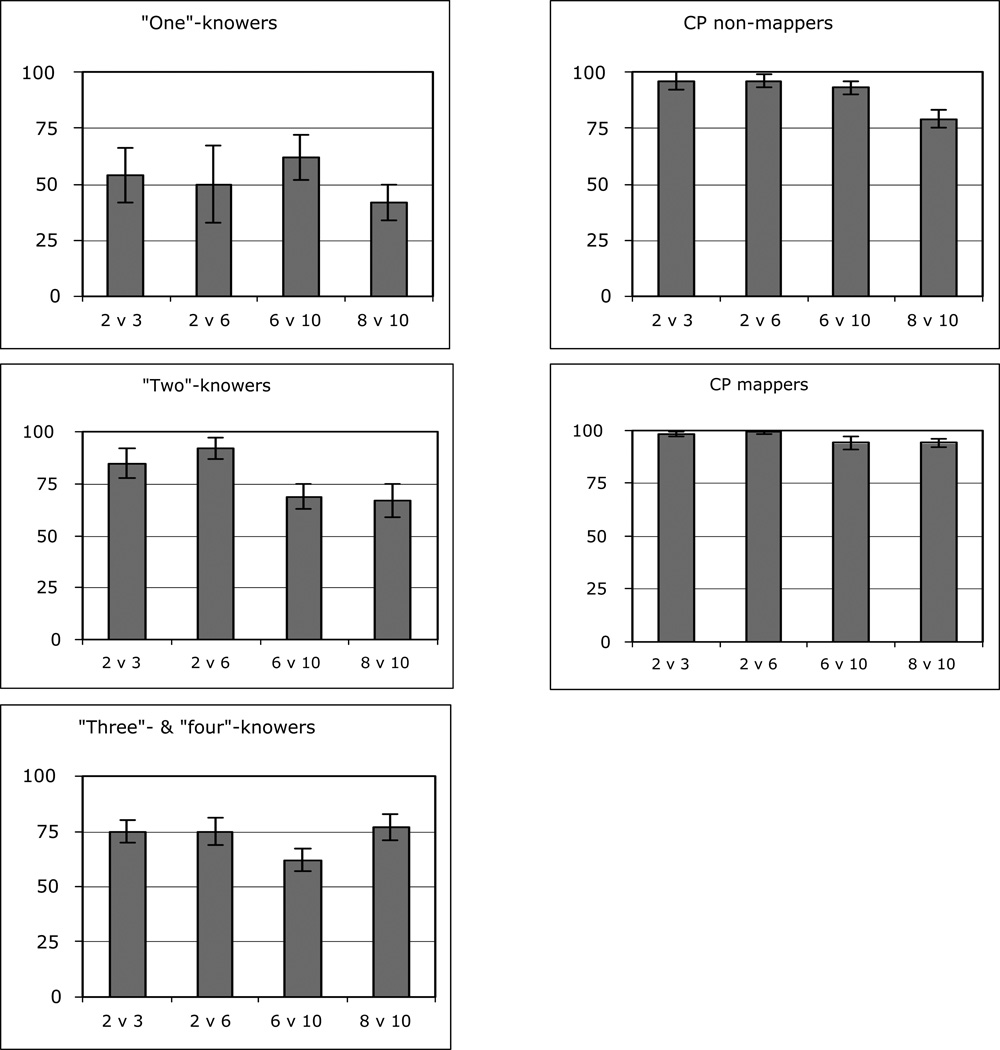
Figure 5.
Accuracy (in percent correct) of children’s non-verbal judgments as a function of comparison type (2 vs. 3, 2 vs. 6, 6 vs. 10, 8 vs. 10) and knower-level.
A 6×4×2×2 ANOVA with Pair and Area as repeated measures examined children’s performance (proportion correct) as a function of Knower-Level (“one”-knowers, “two”-knowers’, “three”-knowers, “four”-knowers, CP non-mappers, CP mappers), Pair (2 vs. 3, 2 vs. 6, 6 vs. 10, 8 vs. 10), Area (negatively correlated with set size, positively correlated with set size), and Order (order 1, order 2). The main effects of Knower-Level was the only significant effect, F(5, 103) = 11.4, p < .001. No other effects were significant. Post-hoc tests (Tukey’s HSD) of the effect of Knower-Level revealed that CP-mappers were significantly more accurate than all other groups (all p’s < .05), except CP nonmappers. Moreover, CP non-mappers were more accurate than “three”-knowers and “one”-knowers (both p’s < .05), and “two”-knowers were marginally more accurate than “one”-knowers (p = .05). Thus, to a first approximation, CP-mappers and non-mappers were not different from each other, and were both better than subset-knowers. Subset-knowers were not different from each other, except for “one”- knowers who were worse than “two”-knowers.
To determine whether the differences between knower-levels were qualitative (e.g. CP-mappers were the only ones who could discriminate the pairs) or quantitative (e.g. all groups could discriminate all pairs, but CP-mappers and CP non-mappers did better than the others), each knower-level’s performance was tested against chance for each pair. All groups except the “one”-knowers performed above chance on every comparison pair (all t’s > 1.98, all p’s < .05, 1-tailed); the “one”-knowers were at chance on all four comparison pairs (all t’s < 1.3, all p’s > .25).
Finally, we analyzed “three”-knowers’ and CP non-mappers’ reaction times in the non-verbal ordinal task to determine whether these children failed to estimate the sizes of large sets because the presentation times in Fast Cards were too short to allow them to form distinct representations of large set sizes. Reaction time data were collected for the 6 vs. 10 and 8 vs. 10 pairs for five randomly chosen “three”-knowers and five randomly chosen CP non-mappers. Reaction times were calculated from the moment the experimenter set the cards on the table to the moment the child pointed to one of the sets, and they were only calculated for trials with correct answers. On 6 vs. 10, “three”-knowers took an average of 1.8 s (SE = 0.11) to respond, and CP non-mappers took 2.0 s (SE = 0.19). On 8 vs. 10, “three”-knowers took an average of 2.0 s (SE = 0.18) to respond, and CP non-mappers took 2.8 s (SE = 0.60). A 2 X 2 ANOVA on reaction times with comparison type as a repeated measure and knower-level as a between-subjects factor showed no effect of comparison type, F(1,8) = 2.22, ns, no effect of knower-level, F(1,8) = 2.36, ns, and no interaction F(1,8) = 0.36, ns. Thus, on average, a total of 2.15 seconds per comparison was all that was required to encode the number of circles in each set, compare them, and plan and execute a response. This strongly suggests that the presentation time in Fast Cards (1 second) was long enough for children of this age to form distinct analog magnitude representations of each of the large set sizes presented in this task.
Summary: Experiment 1
Experiment 1 yielded four main results. First, all CP-knowers and some subset-knowers had could estimate the size of sets of 1 to 4 circles without counting. This suggests that mapping “one” to “four” to core systems is part of the process through which the counting principles are acquired. Second, all of our subset-knowers had only mapped “one” to “four” onto core systems; none of them showed evidence of having mapped numerals beyond “four” onto large analog magnitudes. Moreover, almost half of our CP-knowers also failed to show evidence of having numerals beyond “four” onto large analog magnitudes. This suggests that the creation of mappings between large numerals and analog magnitudes is not part of the acquisition process. Third, we established the age at which children map verbal numerals from “five” to “ten” onto analog magnitudes — namely, around 4;6, about 6 months to a year later than the average age at which children first acquire the counting principles (Le Corre et al., 2006; Wynn, 1990, 1992). Fourth, although the variability of CP-mappers’ estimates of sets of 6 or more was scalar, the variability of children’s estimates of sets of 1 to 4 was not scalar in any of the groups of children who had learned numerical meanings for “one” to “four”, namely “four”-knowers, CP nonmappers, and CP mappers. Rather, at all of these knower levels, variability grew faster than mean estimates in the small set range. This pattern of variability suggests that children did not rely on analog magnitudes alone to estimate small set sizes. Rather, they must have engaged representations in enriched parallel individuation, either alone or together with analog magnitudes.
The results of the non-verbal ordinal task strongly suggest that the children who failed to verbally estimate the numerical size of large sets in Fast Cards did so because they had not yet acquired the relevant mappings, not because of extraneous perceptual factors. CP mappers’ non-verbal ordinal judgments were more accurate than those of subset-knowers, but, critically, they were not more accurate than those of CP non-mappers. Therefore, CP non-mappers’ failure to estimate the numerical size of large sets without counting cannot have been due to limits on their capacity to perceive the numerical size of these sets without counting. Moreover, although they were less accurate than CP non-mappers and CP mappers, all subset-knowers (except “one”-knowers) performed above chance on all pairs of the nonverbal ordinal task. Thus, they should have at least been able to produce significantly larger numerals for sets of 10 than for sets 6, although the difference in their estimates of these sets may have been less pronounced than that in children who showed greater perceptual accuracy. Yet, they abjectly failed to apply larger numerals to sets of 10 than to sets of 6. Finally, “three”-knowers and CP non-mappers only needed about 2 seconds to correctly order 6 vs. 10 and 8 vs. 10 and report their choice. Thus, it seems unlikely that these children failed to estimate large set sizes because the 1-second presentation time in Fast Cards was not long enough to allow them to form distinct analog magnitude representations of the sizes of these sets.
What could have been cause for concern is “one”-knowers’ failure on all pairs of the non-verbal ordinal task. However, despite this failure, their performance on Fast Cards was not significantly different from that of “two”-knowers. This shows that the very pattern of verbal numerical estimation produced by “one”-knowers’ could obtain in children who had sufficiently accurate perceptual mechanisms to succeed on all pairs of the non-verbal ordinal task. Thus, “one”-knowers were left in our analyses of verbal numerical estimation.
The data from the NVO task make a few additional points which, while interesting, are only tangentially related to the question at hand. Thus, we only discuss them briefly. First, despite the large ratio difference between 2 vs.3 and 2 vs. 6, children performed equally well on these pairs. This suggests that children relied on representations other than or in addition to analog magnitudes to solve these problems. Quite possibly, these representations were provided by parallel individuation. Second, two details of our data confirm other reports that the acquisition of numerals affects performance on nonverbal numerical tasks. First, as Brannon & Van de Walle (2001) had found in their study of non-verbal ordinal judgments, “one”-knowers were the only ones who completely failed to order any of the pairs. Since pre-verbal infants can order both small (Feigenson & Carey, 2003, 2005; Feigenson & Halberda, 2004) and large (Brannon, 2002) sets, it seems unlikely that “one”-knowers’ failure was caused by representational limits on their core systems. Thus, we tentatively suggest that knowing at least two numerals (e.g. “one” and “two”) may make discrete number a more salient feature of experience, and may be instrumental for learning the discrete meaning of the verbal quantifier “more.” Second, CPknowers (mappers and non-mappers) outperformed subset-knowers on this non-verbal task. This result converges with Mix, Huttenlocher, & Levine's (1996) report that CP-knowers outperformed subsetknowers on cross-modal number comparisons. Again, we speculate that learning verbal numerals increases the salience of discrete number representations.
EXPERIMENT 2
Children’s reaction times on the non-verbal ordinal task provided evidence that the rapid rate of set presentation in Fast Cards did not mask mappings that children had in fact created. Data from a study conducted previously in our laboratory allowed us to directly test the effects of presentation time on children’s verbal numerical estimation. Part of this study used an adaptation of Gelman's (1993) “What’s on This Card?” task (WOC) to test the effects of performance demands on subset-knowers’ ability to solve numerical tasks using counting (Le Corre et al., 2006). In this task, children were presented with cards with sets of up to 8 stickers pasted on them. On the first trial of each set, the experimenter asked “What’s on this card?” and then modeled the use of numerals to elicit numeral production (e.g. “That’s right! It’s one apple!”). On further trials, the experimenter posed the same question to probe children to describe the number of stickers on the cards. Unlike Fast-Cards, WOC imposed no time pressure on numerical estimation and numeral production, for cards were left in children’s view for as long as they wished. This task thus allowed counting; in fact, in its initial design, it was meant to elicit counting. However, we discovered that subset-knowers often spontaneously produced numerals without counting. Rarely, CP-knowers also did so. Thus, the WOC task provided data that allowed us to test whether children’s verbal numerical estimation would improve in the absence of time pressure. As in Experiment 1, a count list elicitation task was included to make sure that children’s performance on the estimation task would not be limited by the number of numeral types in their count list.
Another difference between Experiments 1 and 2 was that, in Experiment 2, knower-levels were determined on the basis of children’s performance on the estimation task itself – i.e. What’s on This Card. This difference should be inconsequential, for Le Corre et al. (2006) have shown that knower-levels are essentially the same whether they are assessed with Give a Number or with What’s on this Card.
Method
Participants
Sixty-three 2- and 3-year-olds participated (mean age = 3 years; 1 month, range = 2;0 to 4;0) in Experiment 2 and produced estimates of both large and small set sizes without counting. All were fluent English speakers recruited in the New York City area and in the Greater Boston area. All were recruited and compensated in the same way as the participants in Experiment 1. The majority of the children were from middle-class backgrounds, and most were Caucasian although a small number of Asian, African American and Hispanic children participated. An additional 57 children participated in What’s on this Card but were not included in the study. 44 were excluded because they did not estimate large set sizes without counting (mean age = 3;2, range = 2;0 to 4;0) and 13 because they had too few numerals in their count list (mean age = 2;9, range = 2;3 to 3;6; see results below).
Materials
What’s on This Card? (WOC)
The materials for this task consisted of eight “decks” of cards with sets of 1–8 stickers placed on them in one or two rows. The cards in each deck had a distinct color and sticker type.
Count list elicitation task
The materials used for this task were small toy animals (e.g., frogs, puppies, whales) presented in a single row.
Procedure
What’s on This Card?
There were two versions of this study; they are presented together because there were no effects of version on the functions of estimates by set size (see section on “Effect of task version”). In both versions of the task, children were shown the first card in a deck (e.g. one apple) and were asked, “What’s on this card?” Regardless of the child’s response, the experimenter modeled the application of a single numeral to the set by saying, “That’s right, that’s N apple(s)”, where N was the number of stickers on the card. The experiment never counted to model; he or she always produced a single numeral. Modeling only occurred on the first trial of each deck; for the rest of the cards, the experimenter only asked “What’s on this Card?”. Because Experiment 2 (range 2;0 to 4;0) included younger children than Experiment 1(range 3;0 to 5;7), we expected that some of the children in Experiment 1 (e.g. the two year- olds) might not be able to count to “ten”. Thus, this estimation task only included sets of 1 to 8 elements rather than 1 to 10.
The versions differed in the model used. In the “1-model” version, directly modeled on Gelman’s task, the first card of every deck was a 1-card; thus, the use of number words was only modeled with “one”. This was followed by 2, and 3 (twice as 2, 3 and twice as 3, 2), then 4, 5 in either order, and then 6, 7, and 8, in random order. Following Gelman (1993) this version included some “probe” trials. If the child had given a cardinal response (e.g., “two cows”) the experimenter asked, “Can you show me?” to elicit a count response. If the child had spontaneously counted without providing a cardinal response, the experimenter asked, “So, what’s on this card?” to elicit a cardinal response. There were three probe trials per deck.
In the “multiple-models” version, children were presented with one block of two decks that started with 1-card models, and another block of decks that started with 7-card or 8-card models. Order of presentation of the blocks was counterbalanced. Thus, the experimenter modeled both the use of “one” and of large numerals--namely “seven” and “eight”. Sets used as models were not repeated within the same card deck. Cards in the 1-model decks were presented in four orders. Two started with 1, 2, 3 followed by 8, 4, 7 or 4, 8, 7, and two started with 1, 3, 2 followed by 7, 5, 8 or 5, 7, 8. Cards in the multiple-model decks were presented in the reverse order. No probes were used in this version of the task.
Count list elicitation task
Children’s count lists were elicited in one of two ways. Children tested in the 1-model version were prompted to count in the WOC task itself when the experimenter asked “Can you show me?” Children tested in the large models version were presented with a row of eight small toy animals after they had been tested on WOC. They were simply asked to count them. If their counting was grossly wrong, the experimenter asked them to count one more time more slowly, and assisted their counting by pointing to each object as they counted.
Results
Knower levels
To be granted knowledge of the exact meaning of a number word, children had to:
Say “N” at least 67% of the time when presented with N stickers8;
Say “N” no more than half as often when presented with different numbers; and
Satisfy conditions 1 and 2 for all numbers less than N.
To distinguish children who understood the cardinal principle (CP-knowers) from children who didn’t, we analyzed trials where children correctly counted the set (allowing for one error) and then produced a numeral (e.g. they said “1, 2, 3, 4, 5. That’s two bears!” or “1, 2, 3, 4, 5. Five!” on a trial with a set of 4, 5, or 6 stickers). If children understand counting, their numerals should match the last word of the preceding count. Thus, we obtained a “match score” for each child as follows: we calculated the number of trials for which children counted and then produced a numeral that matched the last numeral of their count and divided this number by the total number of trials for which children produced a count followed by any numeral, whether it matched the count or not. This allowed us to determine whether, given that they had counted a set, children knew that the last numeral of their count represented the size of the set. As we demonstrated elsewhere (Le Corre et al., 2006) children who don’t understand counting can have large match scores on small numbers (2 and 3) because of an accidental match between subitizing and numerically meaningless but procedurally correct counting. To avoid this confound, we only computed match scores for large numbers (4 to 8). To be considered CP-knowers, children had to meet criteria 1, 2, and 3 for “one”, “two” and “three” and had to have match scores greater or equal to 50% on cards with 4 or more stickers.
These criteria divided children into six knower-level groups: children who did not know the exact meaning of any numerals (hereafter referred to as “0-knowers), “one”-knowers9, “two”-knowers, “three”- knowers, “four”-knowers, and CP-knowers. The size, age and count list length of each of these knowerlevels are reported in Table 3. The “one”-knowers and the “two”-knowers in this experiment were younger than the ones in Experiment 1 (compare Tables 1 and 3). This difference was the product of the great variability in the age at which individual children achieve each knower-level; some two-and-a-half year olds are CP-knowers, but some three-year-olds are still “one”-knowers (see Le Corre et al., 2006; Wynn, 1992). The whole age range for “one”-knowers and “two”-knowers was included only in Experiment 2; Experiment 1 only included the oldest end of the range. Hence the difference in the average age of children in these knower-levels.
Table 3.
Age, count list length and knower-levels of children analyzed in Experiment 2.
| Agea |
Count list lengthb |
||||
|---|---|---|---|---|---|
| Levels | N | Mean (SE) | Range | Mean (SE) | Range |
| 0-knowers | 2 | 2;6 (4.6) | 2;6 – 3;4 | 9.0(1.0) | 8–11 |
| 1-knowers | 24 | 2;7(1.0) | 2;0 – 3;4 | 8.2 (0.4) | 6–10 |
| 2-knowers | 18 | 3;1 (1.3) | 2;0–3;11 | 9.0 (0.5) | 7–14 |
| 3-knowers | 9 | 3;5 (1.8) | 3;1–4;0 | 9.0 (0.4) | 8–11 |
| 4-knowers | 3 | 3;2 (4.6) | 2;5 – 3;7 | 11.3 (0.7) | 10–12 |
| CP-knowers | 7 | 3;8 (1.0) | 3;5–3;10 | 8.8 (0.3) | 8–10 |
Ages are in years and months (years; months).
Children’s count list length was determined by the children’s longest count; e.g. the count list length for a child who once counted to “five” and once to “eight” would be 8.
Count list elicitation
To be sure that children’s performance on What’s on this card? would not be limited by their counting range, we only wanted to include children who could at least count to “eight”. While threequarters of the children in our sample could recite the count list that far, the rest could not. Thus, in order to use as much of our sample as possible, we also included “one”-knowers who could only count to “six” (n = 6) or “seven” (n = 8), and “two”-knowers who could count only count to “seven” (n = 4). All others could at least recite the count list to “eight”, and all recited the count list in the standard adult order.
What’s On This Card?: Assessment of the mapping to core systems
The What’s on This Card? task provided children with enough time to count the sets, and children did sometimes count. Most of those who counted the sets to determine their cardinality were CP-knowers. Because numeral production based on counting (e.g. “One, two, three, four. That’s four bears!) does not necessarily tap mappings between numerals and core systems, we only included trials on which children produced numerals without having first counted the set.
As in Experiment 1, we calculated the average of each child’s verbal estimates as a function of set size, and averaged individual functions together for each knower-level. Functions were only computed for children who produced at least one numeral on 5, and one numeral on 7 or 8. Sixty-three children met this criterion; 25 were in the 1-model condition and 38 were in the multiple-models condition. “One”-knowers and “two”-knowers were analyzed separately because each group was large, but “four”-knowers were combined with “three”-knowers because there were so few of them. A 4 (knower-level: 0, “one,” “two”, “three/four”, CP) X 2 (task version: 1-model, multiple models) X 7 (set size) ANOVA with set size as a repeated measure assessed whether there were effects of task version on children’s average estimate. None of the effects involving task version were significant. The only significant effects were set size, F(6, 318) = 125.1, p < .001, knower-level, F(3, 53) = 11.57, p < .001, and the interaction between knower-level and set size, F(18, 318) = 10.1, p < .001. Thus, data from the different versions of the task were analyzed together. The resultant functions are shown in Figure 6. To determine whether children were able to estimate the numerical size of large sets (5, 7, and 8), we measured the slope of these functions in the large set size range (hereafter referred to as “5–8 slope”) for each knower-level, and determined whether these were significantly different from 0.
Figure 6.
Average numeral by set size functions for subset-knowers tested on What’s on this Card?. “Four”-knowers were grouped with “three”-knowers because there were only three of them.
Subset-knowers
Figure 6 shows that all of the groups of subset-knowers had functions with flat 5–8 slopes; i.e. none of the 5–8 slopes for subset-knowers were significantly different from 0 (see Table 4).
Table 4.
Subset-knowers’ 5–8 slopes for What’s on this Card.
| Knower-level | 5–8 slope | ta | df | p |
|---|---|---|---|---|
| “One”-knowers | 0.06 (0.09) | 0.64 | 23 | ns |
| “Two”-knowers | 0.04(0.10) | 0.44 | 17 | ns |
| “Three” and “four”-knowers | 0.16(0.21) | 0.76 | 12 | ns |
These are the results of 2-tailed one-sample t-tests of each 5–8 slope against 0. The 5–8 slope for 0-knowers was not tested against 0 because there were only two of them.
While all of the subset-knowers’ functions were flat in the 5–8 range, each of the groups had a distinct function. Although all of them could at least count to “seven”, 0-knowers used numerals randomly for all set sizes they were presented with; i.e. the average 1–8 slope for 0-knowers was equal to 0 (M = −0.02, SE = .04).
“One”-knowers, of course, accurately estimated the sizes of sets of 1, but, although all of them could at least count to “six”, most of them used numerals randomly when presented with sets of 2 or more stickers; i.e. the average 2–8 slope for “one”-knowers (M = 0.07, SE = .04) was not significantly different from 0, t(23) = 1.74, ns. In fact, many “one”-knowers applied the same numeral – usually “two” but sometimes “three” – to all sets greater than 1.
The shape of “two”-knowers’ function shows that they used numerals randomly when presented with sets of 4 or more stickers; i.e. the 4–8 slope for “two”-knowers (M = −0.07, SE = .11) was not significantly different from 0, t(16) = −0.64, ns. Thus, although all of them only met our knower-level criteria for being “two”-knowers, “two”-knowers’ function suggests that some of them were on their way to learning “three”. Indeed, seven “two”-knowers mostly said “three” for sets of 3, and rarely applied it to larger set sizes. This suggests that average numeral produced as a function of set size is a more sensitive measure of children’s knowledge of numerals than our knower-level categorization criteria. The other “two”-knowers really only knew “one” and “two”. Many of these children applied the same numeral – usually “three” – to all set sizes greater than 2. In sum, some “two”-knowers really only knew “one” and “two”, some were on their way to learning “three”, but none of them had mapped any numerals beyond “three” onto core systems.
Finally, “three”- and “four”-knowers produced accurate estimates of sets of 1, 2, 3, and 4, but used numerals randomly when presented with sets of 5 or more (see Table 4 for their 5–8 slope). The accuracy of this group’s estimates of the size of sets of 4 was mostly due to the “four”-knowers. However, two “three”-knowers were on their way to learning “four”; i.e. the average of the numerals they applied to 4 was between 4 and 4.5, and they rarely applied “four” to larger set sizes.
CP-knowers
The 5–8 slope (M = 0.51, SE = 0.22) for CP-knowers’ function was marginally greater than 0, t(6) = 2.35, p = 0.06. However, two of the seven CP-knowers had 5–8 slopes that were less than 0.3 (−0.55 and 0.14). The others all had 5–8 slopes that ranged between 0.5 and 1.1. As in Experiment 1, the CPknowers with 5–8 slopes less than 0.3 (M = 42.4 months, SE = 1.6) were younger than those with large 5- 8 slopes (M = 44.6 months, SE = 0.71). This suggests that, despite its small size, this sample of CP-knowers replicated Experiment 1; it included both mappers and non-mappers. Given these similarities with Experiment 1, the functions for CP-knowers with small 5–8 slopes (less than 0.3) and CP-knowers with large 5–8 slopes (more than 0.3) are graphed separately in Figure 7.
Figure 7.
Average numeral by set size functions for CP non-mappers (continuous line) and for CP mappers (dashed line). CP non-mappers were CP-knowers who had functions with 5–8 slopes that were less than 0.3; CP mappers had 5–8 slopes that were greater than 0.3.
Summary: Experiment 2
As in Experiment 1, all subset-knowers and some CP-knowers failed to estimate the numerical sizes of sets of five or more without counting. Unlike Experiment 1, Experiment 2 allowed children to take as much time as they wished to estimate the sizes of small and large sets. Therefore, their failure to estimate the sizes of large sets cannot be attributed to the rate of presentation of the sets. A potential problem with this interpretation is that the “one” and “two”-knowers in Experiment 2 were much younger than those in Experiment 1 (see Tables 1 and 3). However, the “three”- and “four”-knowers in both experiments were of comparable ages (about 3;6 on average). These children still failed to estimate the numerical size of large sets in Experiment 2. Thus, this strongly suggests that the age difference of the “one”- and “two”-knowers in Experiments 1 and 2 is not a cause for concern.
Moreover, subset-knowers’ and CP non-mappers’ failure to estimate large set sizes cannot be attributed to a lack of numerals, for all of them could count further than they could estimate. For example, all “one”-knowers could at least count to “six” but none of them could estimate the size of sets greater than 1. Finally, their failure to apply larger numerals to sets of 8 than to sets of 5 cannot be attributed to limits on the resolution of their analog magnitude system, for the non-verbal ordinal task in Experiment 1 showed that all children who were at least “two”-knowers could order pairs of sets the ratios of which were even less favorable than 5:8 (0.625) – i.e. 8 vs. 10 (0.8). The data from Experiment 2 thus confirm the conclusion of Experiment 1: the mapping of “one” to “four” onto core systems is part of the process whereby the counting principles are constructed, but the mapping of numerals beyond “four” onto analog magnitudes is not.
GENERAL DISCUSSION
These experiments yielded five important results. First, previous studies had found no “four”- knowers among subset-knowers (Wynn, 1990, 1992), or just a few (Le Corre et al., 2006; Sarnecka & Gelman, 2004). “Four”-knowers were also relatively rare in our sample. Nonetheless, Experiments 1 and 2 showed that CP-knowers (both mappers and non-mappers) could reliably estimate the number of individuals in sets of 1 to 4, distinguishing “four” from larger numerals in their estimates. Even some subset-knowers could do so. This result suggests that the numeral learning sequence leading to the acquisition of the counting principles not only involves learning numerical meanings for “one” to “three” one numeral at a time, but also involves learning a numerical meaning for “four”. The relative rarity of “four”-knowers, relative to other subset-knower levels or CP-knowers, that this knower-level phase is much shorter than the others.
Second, all subset-knowers could recite the count list beyond “four”; in fact, most could recite it up to “ten”. Yet, some could only estimate number for sets of 1, some could only do so for sets of 1 and 2, some could only do 1, 2, and 3, and others could only do 1, 2, 3, 4. None could estimate number for sets of more than 4 objects. That is, the 45 subset-knowers in Experiment 1 and the 54 in Experiment 2 all used numerals randomly when estimating the set sizes in the range of 5 to 10. Some even applied a single numeral to all sets beyond the largest set they could estimate. For example, many of those who could only estimate number for sets of 1 applied “two” to all sets larger than 1, and many of those who could only do so for sets of 1 and 2 applied “three” to all sets larger than 2. This suggests that subset-knowers had at most mapped “one” to “four” onto core representations of small sets – i.e. enriched parallel individuation, analog magnitudes, or both. These data converge with Condry & Spelke’s (under review) assessment of subset-knowers’ knowledge of the mappings between large numerals and analog magnitudes. Condry & Spelke tested subset-knowers’ knowledge of these mappings with a very different task. Indeed, theirs was a comprehension task. Thus, the results obtained here must not have been due to demands particular to our verbal estimation tasks.
Third, our experiments provide the first evidence that, for a period of about six months after mastering the counting principles, even CP-knowers fail to estimate the cardinality of sets of more than 4 objects; these children were dubbed “CP non-mappers”. This is a striking finding. Children who could use their count list to determine the number of objects in a set applied the same numerals to sets of 6, 8, and 10 circles when prevented from counting (e.g. some said “five” for all of these sets). Seeing their abject failure to estimate the size of large sets, one might wonder whether CP non-mappers actually understood the counting principles. Previous studies that attributed knowledge of the counting principles on the basis of the same tasks and criteria used here strongly suggest that they did (Le Corre et al, 2006; Wynn, 1990, 1992). These previous studies found that all and only children categorized as CP-knowers could use their count list to determine the number of objects in a set in a variety of sophisticated ways. For example, they could use counting to check whether a set contained some requested number of objects and to fix the number of objects if it was incorrect (Le Corre et al., 2006; Wynn, 1990, 1992), and could determine whether a third party had correctly counted out large numbers of objects (Le Corre et al., 2006). This suggests that all CP-knowers in our study – whether mappers or non-mappers – truly understood the counting principles. Therefore, the existence of CP non-mappers provides strong evidence that children need not map numerals beyond “four” onto large analog magnitudes to acquire the counting principles. Rather, the mappings between large numerals and analog magnitudes are formed many months after the acquisition of the counting principles.
Fourth, these results establish the age at which middle-class American children first create a mapping between numerals from 5 to 10 and analog magnitudes. Previous studies of knowledge of the mappings between large numerals and analog magnitudes in children either only included children who failed to show this knowledge (Condry and Spelke, under review) or children age 5 or older who succeeded (Duncan & McFarland, 1980; Huntley-Fenner, 2001a; Lipton & Spelke, 2005, Sekuler & Mierkiewicz, 1977; Temple & Posner, 1998). Thus, the average age of our CP-mappers provides the first estimate of the age at which children begin to map large numerals onto analog magnitudes – i.e. about four-and-a-half. Moreover, in Experiment 1, the shape of CP-mappers’ estimation function for large set sizes was nearly identical to the adult function both in its slope – which was nearly equal to 1 – and in its coefficient of variation – which was about 0.2 (see Cordes et al., 2001 & Whalen et al., 1999 for the adult values). This suggests that the mappings between “five” to “ten” and analog magnitudes reach their adult form soon after their creation
The last major finding is that children’s estimates of small sets (1 – 4) did not show the tell-tale signature of numerical estimation based on analog magnitudes, namely scalar variability. Variability is scalar when the ratio of the standard deviation of estimates over the mean estimate for a given set size (the coefficient of variation or COV) remains constant for all set sizes. Children’s estimates of the sizes of small sets failed to show scalar variability in two ways. First, “three”-knowers’, “four”-knowers’, CP non-mappers’ and CP-mappers’ COVs for small sets increased as a function of set size. Second, the average COV for CP-mappers’ estimates of small set sizes was significantly smaller than their average COV for large set sizes, those in the range where CP-mappers clearly used analog magnitudes. Taken together, these results strongly suggest that all children relied on some representation other than or in addition to analog magnitudes to estimate the sizes of small sets, presumably enriched parallel individuation.
The conceptual sources of the verbal counting principles
These five findings greatly constrain theories of the acquisition of the verbal counting principles. First, they clearly establish that, whereas mappings between “one” to “four” and core representations of small sets are part of the acquisition process, mappings between numerals larger than « four » and analog magnitudes play no role in it. Second, the existence of CP non-mappers militates against the Wynn (1992) and Spelke (Feigenson et al., 2004; Hauser & Spelke, 2004; Spelke & Tsivkin, 2001a) proposal that inferring that “further in the count list implies larger magnitude” is part of the process of acquiring the counting principles. Knowing the relation between the order of symbols in the count list and the size of analog magnitudes should have allowed children to rapidly learn the mappings between all numerals in their count lists and analog magnitudes. This expectation seems particularly reasonable for CPknowers, since these children actually know how to use the linear order of the numerals in their count list to determine the number of objects in a set. Therefore, it seems quite likely that CP non-mappers had not noticed the relation between the linear order of symbols in the count list and analog magnitude size. This, in turn, suggests that noticing this relation cannot be part of the acquisition of the counting principles.
Le Corre (under review) asked directly whether all CP-knowers can answer questions about numerical order on the basis of verbal information alone (e.g., “Which box has more fish inside; this one with ten fish or this one with six fish?”). He found that CP non-mappers can make ordinal inferences on the basis of expressions containing small numerals (e.g. “three fish” is more than “two fish”) but can’t make such inferences if the expressions contain only large numerals. For example, they do not know that the expression “ten fish” picks out more fish than the expression “six fish”. Children can only order expressions with large numerals once they become CP mappers. Le Corre’s results thus provide direct evidence that noticing the relation between linear order in the count list and the numerical value specified by analog magnitudes cannot be part of the process that leads to the acquisition of the counting principles.
Finally, Experiments 1 and 2 strongly suggest that “one” to “four” are mapped onto representations of small sets provided by enriched parallel individuation alone. Although analog magnitude representations are defined for small numbers, the lack of scalar variability in children’s estimates of sets of 1 to 4 objects shows that analog magnitudes alone do not support the first meanings of “one” through “four.” To repeat, finding variability in estimates does not by itself implicate analog magnitudes. Rather, all models of analog magnitudes not only predict variability in estimates, but predict scalar variability (Cordes et al., 2001; Izard & Dehaene, under review; Whalen et al., 1999). Nor does finding variability in estimates of small set sizes rule out that “one” to “four” are mapped onto representations provided by enriched parallel individuation. Indeed, as spelled out in the introduction, the pattern of error inherent to maintaining working memory models of individuals and to comparing the working memory models to the long-term models provided by set-based quantification may be exactly the one we obtained here, namely error increasing more rapidly than the mean (see Vogel, Woodman, & Luck, 2001).
Thus, the pattern of error in children’s estimates of small sets strongly suggests that representations provided by enriched parallel individuation are at least part of the mappings that support “one” to “four”. But we take our results support a stronger conclusion, namely that the counting principles are acquired from enriched parallel individuation alone. The reason is that this view predicts our main result, namely that children learn numerical meanings for “one”, “two”, “three” and “four” and nothing more as part of the acquisition process. In contrast, this result is an embarrassment for any view that implicates the analog magnitude system. In this system, the magnitude of the representations increases following a continuous function (either linear – e.g. Brannon, Wusthoff, Gallistel, & Gibbon, 2001 – or logarithmic – e.g. Dehaene, 2003; Izard & Dehaene, under review) in which there are no principled breaks between representations of large and small sets, as does the noise in the representations (i.e. it increases linearly in the linear model and it remains constant in the logarithmic model). Thus, the view that children map “one” to “four” onto analog magitudes representations to acquire the counting principles cannot provide any principled reason why the associative process that leads children to map these numerals onto small analog magnitudes would not also support mapping any numerals beyond “four” onto large analog magnitudes.
The acquisition of the counting principles involves the construction of a new representational resource
In a famous discussion with Noam Chomsky and several other cognitive scientists, Piaget argued that the history of mathematics involved the construction of new representations that were more powerful than those that preceded them (Piatelli-Palmarini, 1980). As briefly reviewed in the introduction, multiple lines of investigation converge to suggest that the acquisition of the verbal counting principles is not guided by innate, non-verbal counting principles. This same evidence warrants a stronger, albeit debated conclusion, namely that the counting principles may have been one of the earliest constructions in the history of human mathematics, and that it is the first new mathematical system constructed in the cognitive development of contemporary humans (see Cordes & Gelman, 2005; Gallistel & Gelman, 1992, 2000; Rips, Asmuth, & Bloomfield, in press; and Wynn, 1998 for dissenting views). Analysis of the structure of the core number systems for which there has been evidence in human infants suggests that all of them differ radically from counting principles both in their format and in their expressive power. Even when enriched with the symbolic devices of set-based quantification, parallel individuation cannot represent the cardinality of sets of more than 4 individuals. Analog magnitudes, on the other hand, are ratio-limited (e.g. 6 month-olds can only discriminate sets on the basis of number if their ratio is at least 2:1; Xu & Spelke, 2000; Xu, Spelke, & Goddard, 2005), and thus obscure the successor function (e.g. the 6-month-old’s system cannot discriminate 5 from 6). Moreover, while analog magnitudes could, in principle, have been generated by an iterative mechanism that implicitly defined the counting principles (see Gallistel & Gelman, 1992), there is now considerable evidence that this mechanism is not iterative, neither in adulthood (Barth, Kanwisher, & Spelke, 2003) nor in infancy (Wood & Spelke, 2005b). This suggests that analog magnitudes do not implement the counting principles. Thus, none of the core number systems could capture the verbal counting principles. This would explain why the acquisition of the verbal counting principles is so protracted and why it starts from an interpretation of the numerals and the list itself that markedly diverges from the adult interpretation. It would also explain why there are still small cultures whose language and cultural practices do not include anything that remotely looks like counting (Gordon, 2004; Pica et al., 2004).
The present data add further weight to the claim that the verbal counting principles are constructed. By suggesting that children do not map their numerals onto analog magnitudes to learn how counting represents number, they specifically undermine Gallistel and Gelman’s (1992) proposal that the acquisition of the verbal counting principles is guided by the mechanism that generates analog magnitudes. Also, by providing positive evidence that the verbal counting principles are learned from mappings between the small numerals in the count list and representations provided by enriched parallel individuation, they suggest that children construct the counting principles from a representational system that cannot express them.
Constructing the counting principles from enriched parallel individuation
Several authors have proposed that the counting principles could be constructed from enriched parallel individuation and the memorized verbal count list by a bootstrapping process (Carey, 2004; Hurford, 1987, Klahr and Wallace, 1976). The idea is that the child makes an analogy between two very different ordering relations: sequential order in the count list (e.g. “two” after “one” and “three” after “two”), and sets related by addition of a single individual ({ix}, {ix iy}, {ix iy iz}). This analogy then supports the induction that each numeral refers to a set that can be put into 1-1 correspondence with a set of a given cardinality, with cardinalities individuated by additional individuals. It also supports the induction that for each numeral on the list that refers to a set of cardinality n, the next numeral on the list refers to a set with cardinality n + 1. The present data are consistent with this proposal, but of course, they do not establish it. At the very least, we would want to compare subset-knowers with CP-knowers, finding that every CP-knower understands that sets labeled by successive integers are related by +1. Preliminary evidence suggests that subset-knowers do not realize this and that CP-knowers do (Sarnecka, Cerutti, & Carey, 2005).
A recent study comparing numeral learning in Japanese, Russian, and American English (Sarnecka, in press) provides evidence that children’s first hypothesis as to the meaning of the numerals in their count list is constrained by set-based quantification. This study showed that children learning Japanese, a classifier language with no singular-plural distinction, learn the cardinal meaning of “one” much later than do children learning Russian or English, in spite of learning the count routine as early as children learning the latter languages. Li, LeCorre, Shui, Jia, & Carey (2003) have replicated this finding in a comparison of Chinese and English learners. A reasonable interpretation of these results is that children learning English or Russian learn the numerals faster than children learning Japanese or Mandarin Chinese because their language marks the relationship between numerals and set-based quantification more explicitly and more richly, especially with respect to obligatory markings of the singular/plural distinction. Moreover, according to Hurford (1987), the historical construction of the counting principles similarly built upon parallel individuation enriched by the set-based quantification central to language. He argues that, until the counting principles became a widespread cultural construction, human languages only had distinct morphemes for sets of 1 to 3 or 4 individuals. His argument rests on multiple lines of evidence. First, he notes that cultures without count lists typically don’t have numerals for set sizes beyond “four” (see also Gordon, 2004, Pica et al., 2004)10. Second, he reviews evidence that the linguistic symbols for sets of 1 through 4 are the only ones that ever changed their form as a function of their syntactic environment (e.g. by agreeing in case and/or gender with the nouns they modified); symbols for set sizes greater than 4 have always been universally syntactically invariant. Hurford takes these two lines of evidence to show that the numerals for 1–4 were initially quantifiers the semantics of which were independent of counting principles, much like “a,” “many,” or “both”. Finally, he points out that in many languages the relation between cardinal and ordinal forms is irregular for small numerals but regular for large numerals. For example, in English, the rule “cardinal + th = ordinal” (with slight phonological alterations of the cardinal) only applies to numerals beyond “three”. Since the basic principle of the counting principles is to link ordinality with cardinality (e.g. the third numeral is the one that means three), Hurford takes this as further evidence to show that the small numerals existed prior to any list-based representation of number. While admittedly speculative, Hurford’s argument thus suggests that the ontogenetic construction of the counting principles mirrors its historical counterpart insofar as, in both cases, the acquisition of linguistic symbols for set sizes beyond 4 depends upon the creation of the counting principles. In fact, his specific model of the historical construction process is essentially the same as the developmental process proposed here.
Additional implications of the results
In addition to constraining theories of the process through which children acquire the count list representation of number, one of our major findings – the existence of CP non-mappers – also speaks to the nature of the relation between the count-based representation of the positive integers and analog magnitudes. When tested on Give a Number, CP non-mappers were able to use counting to create exact sets upon request, even if the experimenter had requested “five”, “six” or even “ten” objects. These are the very same children who, on average, applied the same numerals to sets of 6, 8, and 10 circles when prevented from counting. This interesting state of affairs provides very strong evidence that the system of numerical representations created via the verbal list of numerals is functionally independent from non- verbal analog magnitudes. In this sense, our discovery of CP non-mappers is entirely consistent with chronometric (Spelke & Tsivkin, 2001b), neuropsychological (Lemer et al., 2003) and brain imaging (Dehaene & Cohen, 1997; Dehaene et al., 1999) evidence that adult language-based representations of exact arithmetic are functionally and neurally dissociable from analog magnitudes.
Conclusions
Our investigation supports two conclusions concerning the nature of the conceptual sources of the verbal counting principles: 1) children acquire the counting principles by mapping “one” to “four” onto representations that must include representations of small sets in enriched parallel individuation; and 2) despite the availability of numerals beyond “four” in children’s placeholder count list, mappings between numerals beyond “four” and analog magnitudes are not part of the acquisition process. In fact, our data suggest that the role of analog magnitudes in the acquisition process is quite limited at best. First, our discovery of CP non-mappers suggests that the induction of the counting principles is not based on the generalization that “later in the count list means larger analog magnitude.” Second, evidence that acquisition only requires mapping numerals that pick out set sizes that fall within the representational capacity of the adult parallel individuation system, and that the COV increases as sets increase from 1 to 4, both for subset-knowers and CP-knowers, strongly suggests that parallel individuation may be the only core numerical system recruited in this process. Thus, our results surprisingly suggest that analog magnitudes may play no role in the acquisition process. Finally, they suggest that the counting principles are acquired from a conceptual resource – i.e. enriched parallel individuation – that cannot express the counting principles. Thus, our results contribute further evidence that the acquisition of the verbal counting principles involves the construction of a representational resource that is more powerful than those from which it is constructed.
Acknowledgements
The “1-model” version of “What’s on this card” was developed by Elizabeth Brannon and Gretchen Van de Walle. Much of the data from this condition were collected and analyzed in collaboration with them. Thanks to both for their invaluable input into the ideas developed in this paper. We also wish to thank Julie Goldman, Caryn Harris, Mindy Hsu, Yoon Lee, and Paul Muentener for their help with the collection and analysis of data for Experiment 1, and Rachel Beckhardt, Julie Burelle, Alice Dong, Geffen Goddard, Khurram Naik, Tom Noerper, and Shruti Ravikumar for their help with the collection and analysis of data for Experiment 2. Finally, we thank the many parents, children, and day care personnel who generously contributed to this project. This research was supported by FCAR Masters Research Scholarship 10378 to Mathieu Le Corre, and NIH grant # RO1-HD038338 and NSF ROLE grant #REC-0196471 to Susan Carey.
Footnotes
This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Strictly speaking, a finite count list deployed in accordance with the counting principles represents only a finite subset of the positive integers (see Rips, Asmuth, & Bloomfield, in press, for discussion of how the counting principles defined over a finite count list are generalized to represent natural number).
Parallel individuation should not be equated with Kahneman & Treisman’s “Object-File” system (e.g. Kahneman, Treisman, & Gibbs, 1992) nor with Pylyshyn’s “FINST” system (e.g. Pylyshyn, 2001). Rather, the structure of this system is much closer to what Vogel, Woodman, & Luck (2001) have in mind for visual short-term memory. The reason is that, in most cases, infants’ capacity to resolve problems involving small sets (e.g. removing up to 3 balls from a box; Feigenson & Carey, 2003, 2005; Feigenson & Halberda, 2004) implies that they can represent small sets of individuals, hold this representation in working memory, and compare it to a visible set on the basis of one-to-one correspondence. As far as we know, neither Object-Files nor FINSTs support the comparison of two sets on this basis; rather, they are meant to track unique individuals through space and time. The system Vogel et al.’s describe, on the other hand, is a working memory system that can hold representations of individuals (objects in their case) in parallel, and that can support comparisons between the working memory set and a visible set (in their case, comparisons based on color). Thus, Vogel et al’s system could possibly support comparisons of representations of sets on the basis of one-to-one correspondence.
Gallistel & Gelman (1992, 2000) have also proposed that analog magnitudes are the basis of the acquisition of the counting principles. However, they believe that the analog magnitude system instantiates the counting principles. Since our goal is to explore how the verbal counting principles could be acquired out of conceptual systems that do not function in terms of counting principles, Gelman & Gallistel’s proposal is not listed here.
In infancy, the conditions under which one system is deployed often seem to preclude the activation of the others. First, when using set-based quantification over small sets, infants fail to deploy either analog magnitudes or parallel individuation (Barner et al., in press). Second, when solving tasks using parallel individuation, infants fail to represent sets composed of more than three individuals (e.g. infants can represent three balls in a box but fail to represent four balls; Feigenson & Carey, 2003, 2005), and, when solving tasks using analog magnitudes, they fail to represent the cardinal value of sets containing fewer than four individuals (Lipton & Spelke, 2004; Wood & Spelke, 2005b; Xu, 2003). However, it’s not that analog magnitudes are not defined for small sets. For example, Brannon (2002) has shown that 11-month-old infants can order small set sizes relative to large sets sizes (e.g. 2 dots < 4 dots < 8 dots). Since the analog magnitude system is the only system that can in principle represent both small and large sets, this suggests that analog magnitudes are defined for small sets, from infancy on (see Cordes et al., and Dehaene, 1997 for evidence to the same effect in adults).
These distributions were also obtained for subset-knowers. While we do not report them here because they are not directly relevant to our central concerns, they can be consulted at http://www.wjh.harvard.edu/~lds/subsetdists.html. In short, these distributions confirm that subsetknowers had not mapped any numerals beyond “four” onto analog magnitudes. Moreover, they show that subset-knowers’ performance on Fast Cards was qualitatively consistent with their Give a Number knower-level; e.g. “one”-knowers had a peaked distribution for “one”, “two”-knowers had peaked distributions for “one”, and “two”, etc… This suggests that Fast Cards provided a sensible assessment of children’s knowledge of the numerical meaning of the numerals in their count list.
Table 2 does not display the COVs for large numerals for CP-non-mappers nor subset-knowers, because these children used numerals randomly for set sizes of 6 or larger. Because these children showed no evidence of having mapped large numerals onto any non-linguistic number representation system, it does not make sense to explore the source of noise in their estimates.
One “two”-knower had to be dropped because he showed a clear side-bias; he always picked the set on his right side.
If children incorrectly counted a set of n stickers and repeated the last word of the count, they were considered to have said “n” only if their count contained no more than one error. Trials in which the counts contained more than one error were excluded from this analysis.
Thirteen of our “one”-knowers actually did not produce any numerals on trials with 1 sticker because they always referred to sets of 1 with a singular noun (e.g. “a bear” or “bear”). However, they did produce numerals for set sizes beyond 1, but never used “one” to refer to these. Therefore, these children were classified as “one”-knowers. All of these children were in the 1-model condition. The fact that sets of 1 were the first card of each deck in this condition probably explains why these children preferred to refer to these cards with singular nouns.
To our knowledge,Pica et al. (2004) report the only exception to this rule. They show that, amongst the Munduruku, a small Amazonian tribe, most adults don’t have a count list but some sometimes use the word for hand to refer to sets of 5. However, the use of the word for hand as a symbol for 5 is much less widespread and much less productive than the use of numerals for sets of 1 to 4. Therefore, the Munduruku only provide a weak exception to this rule.
References
- Barner D, Thalwitz D, Wood J, Carey S. Children's ability to distinguish 'one' from 'more than one' and the acquisition of singular-plural morpho-syntax. Developmental Science. doi: 10.1111/j.1467-7687.2007.00591.x. (in press). [DOI] [PubMed] [Google Scholar]
- Barner D, Wood J, Hauser M, Carey S. Evidence for a non-linguistic distinction between singular and plural sets in wild rhesus monkeys. doi: 10.1016/j.cognition.2007.11.010. (under review). [DOI] [PubMed] [Google Scholar]
- Barth HC, Kanwisher N, Spelke E. The construction of large number representation in adults. Cognition. 2003;86:201–221. doi: 10.1016/s0010-0277(02)00178-6. [DOI] [PubMed] [Google Scholar]
- Brannon EM. The development of ordinal numerical knowledge in infancy. Cognition. 2002;83(3):223–240. doi: 10.1016/s0010-0277(02)00005-7. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Van de Walle GA. The development of ordinal numerical competence in young children. Cognitive Psychology. 2001;43:53–81. doi: 10.1006/cogp.2001.0756. [DOI] [PubMed] [Google Scholar]
- Brannon EM, Wusthoff CJ, Gallistel CR, Gibbon J. Numerical subtraction in the pigeon: Evidence for a linear subjective number scale. Psychological Science. 2001;12(3):238–243. doi: 10.1111/1467-9280.00342. [DOI] [PubMed] [Google Scholar]
- Carey S. Bootstrapping and the origin of concepts. Daedalus. 2004:59–68. [Google Scholar]
- Carey S, Spelke E. Science and Core Knowledge. Journal of Philosophy of Science. 1996;63:515–533. [Google Scholar]
- Carey S, Xu F. Beyond object-files and object tracking: infant representations of objects. Cognition. 2001;80:179–213. doi: 10.1016/s0010-0277(00)00154-2. [DOI] [PubMed] [Google Scholar]
- Chierchia G. Plurality of mass nouns and the notion of 'semantic parameter'. In: Rothstein S, editor. Events and Grammar. Great Britain: Kluwer Academic Publishers; 1998. pp. 53–103. [Google Scholar]
- Church RM, Broadbent HA. Alternative representations of time, number, and rate. Cognition. 1990;37:55–81. doi: 10.1016/0010-0277(90)90018-f. [DOI] [PubMed] [Google Scholar]
- Church RM, Meck WH. The numerical attribute of stimuli. In: Roitblatt HL, Bever TG, Terrace HS, editors. Animal Cognition. Hillsdale: Erlbaum; 1984. pp. 445–464. [Google Scholar]
- Condry KF, Spelke ES. Young children's understanding of number words and verbal counting. (under review). [Google Scholar]
- Corbett GG. Number. Cambridge, UK: Cambridge University Press; 2000. [Google Scholar]
- Cordes S, Gelman R. Campbell J, editor. The young numerical mind: When does it count? Handbook of mathematical cognition. 2005:127–142. [Google Scholar]
- Dehaene S. The number sense: How the mind creates mathematics. New York: Oxford University Press; 1997. [Google Scholar]
- Dehaene S. The neural basis of the Weber-Fechner law: a logarithmic mental number line. Trends in Cognitive Science. 2003;7:145–147. doi: 10.1016/s1364-6613(03)00055-x. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Changeux J-P. Development of elementary numerical abilities: A neuronal model. Journal of Cognitive Neuroscience. 1993;5(4):390–407. doi: 10.1162/jocn.1993.5.4.390. [DOI] [PubMed] [Google Scholar]
- Dehaene S, Cohen L. Neuropsychological dissociation between subitizing and counting. International Journal of Psychology. 1992;27(3–4):394–394. [Google Scholar]
- Dehaene S, Spelke E, Pinel P, Stanescu R, Tsivkin S. Sources of mathematical thinking: behavioral and brain-imaging evidence. Science. 1999;284:970–974. doi: 10.1126/science.284.5416.970. [DOI] [PubMed] [Google Scholar]
- Duncan EM, McFarland CE. Isolating the effects of symbolic distance and semantic congruity in comparative judgments: An additive-factors analysis. Memory & Cognition. 1980;8(6):612–622. doi: 10.3758/bf03213781. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S. Tracking individuals via object files: evidence from infants' manual search. Developmental Science. 2003;6(5):568–584. [Google Scholar]
- Feigenson L, Carey S. On the limits of infants' quantification of small object arrays. Cognition. 2005;97(1):B13–B23. doi: 10.1016/j.cognition.2004.09.010. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Carey S, Hauser M. The representations underlying infants' choice of more: Object files versus analog magnitudes. Psychological Science. 2002;13:150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Dehaene S, Spelke ES. Core systems of number. Trends in Cognitive Science. 2004;8(7):307–314. doi: 10.1016/j.tics.2004.05.002. [DOI] [PubMed] [Google Scholar]
- Feigenson L, Halberda J. Infants chunk object arrays into sets of individuals. Cognition. 2004;91(2):173–190. doi: 10.1016/j.cognition.2003.09.003. [DOI] [PubMed] [Google Scholar]
- Fuson KC. Children's counting and concepts of number. New York: Springer-Verlag; 1988. [Google Scholar]
- Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. Non-verbal numerical cognition: from reals to integers. Trends in Cognitive Sciences. 2000;4:59–65. doi: 10.1016/s1364-6613(99)01424-2. [DOI] [PubMed] [Google Scholar]
- Gelman R. Medin DL. A rational-constructivist account of early learning about numbers and objects. The psychology of learning and motivation. Advances in research theory. 1993;Vol. 30:61–96. [Google Scholar]
- Gelman R, Gallistel CR. The child's understanding of number. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Gordon P. Numerical cognition without words: Evidence from Amazonia. Science. 2004;306(5695):496–499. doi: 10.1126/science.1094492. [DOI] [PubMed] [Google Scholar]
- Hauser MD, Carey S. Spontaneous representations of small numbers of objects by rhesus macaques: Examinations of content and format. Cognitive Psychology. 2003;47(4):367–401. doi: 10.1016/s0010-0285(03)00050-1. [DOI] [PubMed] [Google Scholar]
- Hauser MD, Spelke ES. Evolutionary and developmental foundations of human knowledge: A case study of mathematics. In: Gazzaniga M, editor. The Cognitive Neurosciences. Vol. 3. Cambridge, MA: MIT Press; 2004. pp. 853–864. [Google Scholar]
- Huntley-Fenner G. Children's understanding of number is similar to adults' and rats': numerical estimation by 5-7-year-olds. Cognition. 2001;78:B27–B40. doi: 10.1016/s0010-0277(00)00122-0. [DOI] [PubMed] [Google Scholar]
- Hurford JR. Language and number : The emergence of a cognitive system. New York: B. Blackwell; 1987. [Google Scholar]
- Izard V, Dehaene S. Calibrating the mental number line. doi: 10.1016/j.cognition.2007.06.004. (under review). [DOI] [PubMed] [Google Scholar]
- Kahneman D, Treisman A, Gibbs B. The reviewing of object files: Object specific integration of information. Cognitive Psychology. 1992;24:175–219. doi: 10.1016/0010-0285(92)90007-o. [DOI] [PubMed] [Google Scholar]
- Kouider S, Harlberda J, Wood J, Carey S. The acquisition of English number marking: The singular/plural distinction. Language Learning and Development. 2006;2(1):1–25. [Google Scholar]
- Le Corre M. Disorder in the count list. under review). [Google Scholar]
- Le Corre M, Van de Walle GA, Brannon E, Carey S. Re-visiting the performance/competence debate in the acquisition of counting as a representation of the positive integers. Cognitive Psychology. 2006;52(2):130–169. doi: 10.1016/j.cogpsych.2005.07.002. [DOI] [PubMed] [Google Scholar]
- Klahr D, Wallace JG. Cognitive development: An information-processing view. Hillsdale, NJ: Erlbaum Associates; 1976. [Google Scholar]
- Lemer C, Dehaene S, Spelke E, Cohen L. Approximate quantities and exact number words: Dissociable systems. Neuropsychologia. 2003;41:1942–1958. doi: 10.1016/s0028-3932(03)00123-4. [DOI] [PubMed] [Google Scholar]
- Li P, LeCorre M, Shui R, Jia G, Carey S. Effects of plural syntax on number word learning: A cross-linguistic study; Paper presented at the 28th Boston University Conference on Language Development; Boston, MA. 2003. Oct, [Google Scholar]
- Link G. The logical analysis of plurals & mass terms: A lattice theoretical approach. In: Bauerle R, Schwartze C, Stechow Av, editors. Meaning, Use, and Interpretation of Language. Berlin: 1983. [Google Scholar]
- Lipton JS, Spelke ES. Origins of number sense: Large-number discrimination in human infants. Psychological Science. 2003;14(5):396–401. doi: 10.1111/1467-9280.01453. [DOI] [PubMed] [Google Scholar]
- Lipton JS, Spelke ES. Preschool children's mapping of number words to nonsymbolic numerosities. Child Development. 2005;76(5):978–988. doi: 10.1111/j.1467-8624.2005.00891.x. [DOI] [PubMed] [Google Scholar]
- McCrink K, Wynn K. Large-Number Addition and Subtraction by 9-month-old Infants. Psychological Science. 2004;15(11):776–781. doi: 10.1111/j.0956-7976.2004.00755.x. [DOI] [PubMed] [Google Scholar]
- Mix KS, Huttenlocher J, Levine SC. Do preschool children recognize auditory-visual numerical correspondences? Child Development. 1996;67:1592–1608. [PubMed] [Google Scholar]
- Moyer RS, Landauer TK. Time required for judgments of numerical inequality. Nature. 1967;215:1519–1520. doi: 10.1038/2151519a0. [DOI] [PubMed] [Google Scholar]
- Piatelli-Palmarini M. Language Learning: The Debate Between Jean Piaget and Noam Chomsky. Cambridge: Harvard University Press; 1980. [Google Scholar]
- Pica P, Lemer C, Izard V. Exact and approximate arithmetic in an Amazonian indigene group. Science. 2004;306(5695):499–503. doi: 10.1126/science.1102085. [DOI] [PubMed] [Google Scholar]
- Pylyshyn ZW. Visual indexes, preconceptual objects, and situated vision. Cognition. 2001;80(1–2):127–158. doi: 10.1016/s0010-0277(00)00156-6. [DOI] [PubMed] [Google Scholar]
- Rips LJ, Asmuth J, Bloomfield A. Giving the boot to the bootstrap: How not to learn the natural numbers. Cognition. doi: 10.1016/j.cognition.2005.12.001. (in press). [DOI] [PubMed] [Google Scholar]
- Ross-Sheehy S, Oakes L, Luck SJ. The development of visual short-term memory capacity in infants. Child Development. 2003;74(6):1807–1822. doi: 10.1046/j.1467-8624.2003.00639.x. [DOI] [PubMed] [Google Scholar]
- Sarnecka BW. From grammatical number to exact numbers: Early meanings of 'one,' 'two,' and 'three' in English, Russian, and Japanese. Cognitive Psychology. doi: 10.1016/j.cogpsych.2006.09.001. (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarnecka BW, Cerutti A, Carey S. Unpacking the cardinal principle of counting: A lastword rule + the successor function; Paper presented at the 4th Biennale Meeting of the Cognitive Development Society; San Diego, CA. 2005. [Google Scholar]
- Sarnecka BW, Gelman SA. Six does not just mean a lot: Preschoolers see number words as specific. Cognition. 2004;92:329–352. doi: 10.1016/j.cognition.2003.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaeffer B, Eggleston VH, Scott JL. Number development in young children. Cognitive Psychology. 1974;6:357–379. [Google Scholar]
- Sekuler R, Mierkiewicz D. Children's judgments of numerical inequalities. Child Development. 1977;48:630–633. [Google Scholar]
- Siegler RS. In young children's counting, procedures precede principles. Educational Psychology Review. 1991;3:127–135. [Google Scholar]
- Spelke ES, Breilinger K, Macomber J, Jacobsen K. Origins of knowledge. Psychological Review. 1992;99:605–632. doi: 10.1037/0033-295x.99.4.605. [DOI] [PubMed] [Google Scholar]
- Spelke E, Tsivkin S. Initial knowledge and conceptual change: space and number. In: Bowerman M, Levinson S, editors. Language Acquisition and Conceptual Development. Cambridge, UK: Cambridge University Press; 2001a. [Google Scholar]
- Spelke ES, Tsivkin S. Language and number: A bilingual training study. Cognition. 2001b;78:45–88. doi: 10.1016/s0010-0277(00)00108-6. [DOI] [PubMed] [Google Scholar]
- Temple E, Posner MI. Brain mechanisms of quantity are similar in 5-year-olds and adults. Proceedings of the National Academy of Sciences. 1998;95:7836–7841. doi: 10.1073/pnas.95.13.7836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uller C, Carey S, Huntley-Fenner G, Klatt L. What representations might underlie infant numerical knowledge? Cognitive Development. 1999;14(1):1–36. [Google Scholar]
- Verguts T, Fias W. Representation of number in animals and humans: A Neural model. Journal of Cognitive Neuroscience. 2004;16(9):1493–1504. doi: 10.1162/0898929042568497. [DOI] [PubMed] [Google Scholar]
- Vogel EK, Woodman GF, Luck SJ. Storage of features, conjunctions, and objects in visual working memory. Journal of Experimental Psychology: Human Perception and Performance. 2001;27:92–114. doi: 10.1037//0096-1523.27.1.92. [DOI] [PubMed] [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: The psychophysics of number representation. Psychological Science. 1999;10:130–137. [Google Scholar]
- Wood JN, Spelke E. Chronometric studies of numerical cognition in five-month-old infants. Cognition. 2005a;97(1):23–39. doi: 10.1016/j.cognition.2004.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood J, Spelke ES. Infants' enumeration of actions: Numerical discrimination and its signature limits. Developmental Science. 2005b;8(2):173–181. doi: 10.1111/j.1467-7687.2005.00404.x. [DOI] [PubMed] [Google Scholar]
- Wynn K. Children's understanding of counting. Cognition. 1990;36:155–193. doi: 10.1016/0010-0277(90)90003-3. [DOI] [PubMed] [Google Scholar]
- Wynn K. Children's acquisition of number words and the counting system. Cognitive Psychology. 1992;24:220–251. [Google Scholar]
- Wynn K. Psychological foundations of number: Numerical competence in human infants. Trends in Cognitive Sciences. 1998;2:296–303. doi: 10.1016/s1364-6613(98)01203-0. [DOI] [PubMed] [Google Scholar]
- Xu F. Numerosity discrimination in infants: evidence for two systems of representations. Cognition. 2003;89(1):B15–B25. doi: 10.1016/s0010-0277(03)00050-7. [DOI] [PubMed] [Google Scholar]
- Xu F, Carey S. Infants' metaphysics: The case of numerical identity. Cognitive Psychology. 1996;30:111–153. doi: 10.1006/cogp.1996.0005. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke E. Large number discrimination in 6-month-old infants. Cognition. 2000;74:B1–B11. doi: 10.1016/s0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
- Xu F, Spelke E, Goddard S. Number sense in human infants. Developmental Science. 2005;8(1):88–101. doi: 10.1111/j.1467-7687.2005.00395.x. [DOI] [PubMed] [Google Scholar]