Abstract
It is known that impact forces increase with running velocity as well as when stride length increases. Since stride length naturally changes with changes in submaximal running velocity, it was not clear which factor, running velocity or stride length, played a critical role in determining impact characteristics. The aim of the study was to investigate whether or not stride length influences the relationship between running velocity and impact characteristics. Eight volunteers (mass=72.4 ± 8.9 kg; height = 1.7 ± 0.1 m; age = 25 ± 3.4 years) completed two running conditions: preferred stride length (PSL) and stride length constrained at 2.5 m (SL2.5). During each condition, participants ran at a variety of speeds with the intent that the range of speeds would be similar between conditions. During PSL, participants were given no instructions regarding stride length. During SL2.5, participants were required to strike targets placed on the floor that resulted in a stride length of 2.5 m. Ground reaction forces were recorded (1080 Hz) as well as leg and head accelerations (uni-axial accelerometers). Impact force and impact attenuation (calculated as the ratio of head and leg impact accelerations) were recorded for each running trial. Scatter plots were generated plotting each parameter against running velocity. Lines of best fit were calculated with the slopes recorded for analysis. The slopes were compared between conditions using paired t-tests. Data from two subjects were dropped from analysis since the velocity ranges were not similar between conditions resulting in the analysis of six subjects. The slope of impact force vs. velocity relationship was different between conditions (PSL: 0.178 ± 0.16 BW/m·s-1; SL2.5: -0.003 ± 0.14 BW/m·s-1; p < 0.05). The slope of the impact attenuation vs. velocity relationship was different between conditions (PSL: 5.12 ± 2.88 %/m·s-1; SL2.5: 1.39 ± 1.51 %/m·s-1; p < 0.05). Stride length was an important factor that determined impact force magnitude. It is likely that lower extremity posture is a determining factor influencing impact characteristics.
Key Points.
As running velocity increased, the magnitude of the vertical ground reaction impact force increased as expected.
As running velocity increased, stride length increased as expected.
When stride length was constrained to be 2.5 m for all running velocities, the magnitude of the vertical ground reaction impact force did not increase as expected.
When running different velocities, the changes in the magnitude of the vertical ground reaction impact force was related to stride length changes.
Key words: Ground reaction force, impact attenuation, shock
Introduction
During distance running, a runner must perceive the salient features of the environment and modulate the movement pattern in order to successfully displace the body. A runner selects a movement pattern based upon many different factors. For example, surface characteristics, running shoes, body structure, physiological state and desired running velocity are factors that could influence a runner’s movement pattern. Ultimately, the movement pattern selected determines how economical a runner is from a physiological perspective - and running economy is an important aspect of distance running performance (Hogberg, 1952; Cavanagh and Williams, 1982; Cavanagh and Kram, 1985; Hamill et al. 1995).
During running, the ground reaction force, gravity and air resistance are the forces acting on the runner. While gravity is a constant force and air resistance force is of small magnitude, the ground reaction force is of high magnitude and varies based upon a variety of factors such as running velocity and running style. Therefore, it is understandable that there is a wealth of research on factors that influence ground reaction forces during running since this parameter ultimately provides some insight into running behavior.
The ground reaction force is typically analyzed by decomposing the resultant force vector into two shear components (i.e., anterior-posterior, medial-lateral) and a vertical component. The focus of this paper is on the vertical ground reaction force since it is the dominant force in terms of magnitude. There are many interesting characteristics of a vertical ground reaction force profile during running, but an important aspect of the force profile that is the impact force (i.e., F1, Figure 1a), which is the local maximum force generally observed within about 50 ms of ground contact (Nigg et al., 1995). A reason for the interest in the impact force is due to the hypothesis that running overuse injuries are related to the collision between the foot and ground with each foot-strike (Hreljac et al., 2000).
Figure 1.
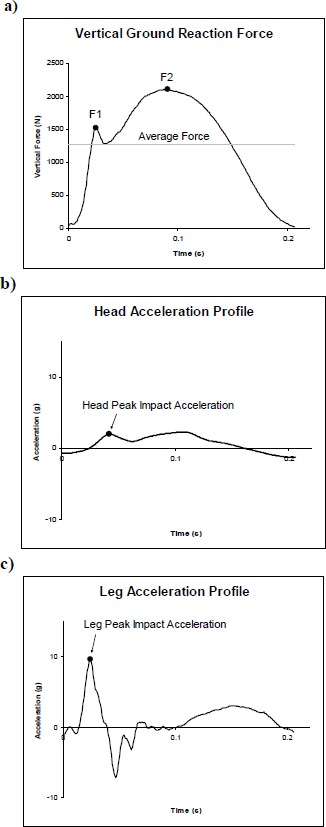
Typical trial data set consisting of force and acceleration data sets. For each running trial, the impact force (F1), active force peak (F2) and average force were recorded from the ground reaction force. From the acceleration profiles, the peak impact accelerations for the leg (aleg) and head (ahead) were also recorded for each trial.
Impact force magnitudes are influenced by running velocity such that force magnitudes increase with faster velocities (Hamill et al., 1983; Munro et al., 1987; Mercer and Vance, 2002). Impact force magnitudes are also influenced by changes in stride length (Derrick et al., 2000; Challis, 2001) such that force magnitudes increase with longer stride lengths. During running, this impact force is absorbed through joint actions as well as anatomical structures. The process of reducing the impact force is referred to as impact attenuation (Hamill et al., 1995; Derrick et al., 1998; Mercer et al., 2002a). Similar to impact force, impact attenuation increases with faster running velocities (Mercer et al. 2002b) and longer stride lengths for a given velocity (Hamill et al., 1995; Derrick et al., 1998).
In general, faster submaximal running velocities are accomplished primarily by changes stride length (Sinning and Forsyth, 1970; Luhtanen and Komi, 1978; Mercer et al., 2002b), which leads to the question: Are the changes in impact characteristics (i.e., impact force magnitude and impact attenuation) across velocities related to stride length changes?
Lower extremity geometry at impact has been related to impact force magnitude (Denoth, 1983; Gerritsen et al., 1995; Lafortune et al., 1996) as well as impact attenuation (Derrick et al., 1998; 2000). It seems reasonable to suspect that stride length imposes a constraint to lower extremity geometry at impact. Although there is a wealth of documentation regarding ground reaction forces during running, there is very little research on the effect of stride length changes on these forces. Therefore, the purpose of this study was to investigate whether or not stride length influences the relationship between running velocity and impact characteristics (i.e., impact magnitude and impact attenuation). The experiment that we designed to address this purpose consisted of having participants run at a variety of velocities with stride length either freely chosen or constrained by striking specific targets. The hypothesis that impact force is related to changes in stride length (regardless of velocity) would be rejected if impact force changed in a similar manner during both stride length conditions.
Methods
Participants
Volunteers (n = 8, mean standard deviation: mass = 72.4 ± 8.9 kg; height = 1.7 ± 0.1 m; age = 25 ± 3.4 years) gave written informed consent to participate in the study. All participants completed all running conditions and did not have any injury that interfered with running performance.
Instrumentation
Subjects were provided a laboratory running shoe (Asics American Corporation, Irvine, CA; model TN 415) to wear during testing. Ground reaction forces were measured using a force plate (Kistler Instrument Corporation USA, Amherst, NY; model 9281B) that was mounted flush with the floor in the middle of a 20 m runway. Impact attenuation was quantified by securing light weight uni-axial accelerometers (PCB Piezotronics, Depew, NY; model 353C67; mass = 2 grams; sensitivity = 100 mV·g-1; frequency range = 0.3 Hz - 12 kHz) on the right leg and head segments. The leg accelerometer was mounted on the distal anterior-medial aspect of the tibia using a custom wrap tightened to subject tolerance level. The head accelerometer was fixed to a rigid plastic head gear that was similar to a hat band and could be tightened around the head such that the accelerometer was aligned vertically in the middle of the forehead region. Running velocity was determined using two infrared photo sensors (Lafayette Instrument Corporation. USA, Lafayette, IN; model 63501IR) that triggered a signal when the participant ran past a sensor. Sensors were placed 1.5 m before and after the force plate in order to determine running velocity. All data were collected concurrently at 1080 Hz using Bioware (Kistler Instrument Corporation, Depew, NY; version: 3.21) data acquisition software.
Experiment
The goal of this experiment was to record ground reaction force and acceleration data during running at a variety of velocities when stride length was either self-selected or constrained. Therefore, participants completed multiple trials during each of two conditions: 1) preferred stride length (PSL), 2) stride length constrained to 2.5 m (SL2.5). Condition order was always PSL - SL2.5 since it was felt that constraining stride length may interfere with the natural self-selection of stride length. During PSL trials, no instructions regarding stride length were provided, while during SL2.5 participants were required to strike floor targets such that stride length would always be 2.5 m. The stride length of 2.5 m was chosen knowing that during slow speeds this stride length would be longer than a subject would normally choose and, likewise, would be shorter than a subject would normally choose while running faster speeds. Nevertheless, we chose this stride length based upon pilot work and we believed would allow subjects to achieve a wide range of running speeds.
During each condition, the goal was to collect 20 trials representing a variety of speeds such that the distribution of speeds was similar between conditions. For each condition, participants were instructed to run at a comfortable pace at first. A member of the research team then gave instructions to the participant to either increase or decrease velocity with the intent of recording a wide range of velocities that would be similar between conditions. During PSL, a successful trial required that the participant struck the force plate with the right foot and did not make any obvious changes to stride length in order to strike the force plate. During SL2.5, a successful trial required that the participant struck the force plate with the right foot and struck targets placed on the ground at specific intervals. A participant was allowed no more than 40 attempts per condition to achieve 20 successful trials. Data sets for two subjects were dropped from the study since the velocity distributions were not similar between conditions. This resulted in an analysis of data sets from 6 subjects (mass = 74 ± 9.5 kg; height = 1.7 ± 0.1 m; age = 26 ± 4.0 years). Of these six subjects, five completed 20 trials per condition while one completed 15 trials per condition.
The targets for SL2.5 were placed such that stride length would be 2.5 m. Markers were placed on the floor at 1.25 m intervals so that the participant could target left and right foot strikes. During the SL2.5 trials, different running velocities were achieved by manipulating stride frequency.
Data reduction
A typical trial data set consisting of force and acceleration data is illustrated in Figures 1a, 1b, and 1c. Running velocity was calculated by processing the square wave signals generated by each timing sensor triggered by the participant running through the test area. Leg and head acceleration data were smoothed using a 4th order, zero-lag Butterworth filter (cutoff frequency = 50 Hz). Stride length was determined by first identifying two consecutive leg peak impact accelerations (Figure 1c). The time between peaks was used to calculate stride frequency (strides·s-1) with stride length then calculated by dividing running velocity by stride frequency.
The impact force (F1, Figure 1a) from the vertical ground reaction force profile was recorded as well as the average vertical force during the stance phase. A force threshold of 20 N was used to identify contact and toe-off times of the force profile. We also calculated the resultant impact force (Fr) and direction (θ) of this force using the vertical and anterior-posterior forces. Finally, the head peak impact acceleration (ahead; Figure 1b) as well as the leg peak impact acceleration (aleg; Figure 1c) associated with contact of the force plate were recorded (Figure 1) and used to calculate impact attenuation using the formula: impact attenuation = (1- ahead/ aleg) 100.
Scatter plots of each parameter vs. running velocity were generated for each condition for each participant. A line of best fit was calculated for each parameter per condition per participant with the slope of this line recorded for analysis. For example, the impact force for each trial of PSL for participant 1 was plotted against running velocity. A line of best fit (i.e., y = mx + b; where m = slope and b = the y intercept) was calculated and the slope of this line was recorded for analysis. This procedure was repeated for all participants and all conditions for each parameter of interest.
Statistical analysis
The primary dependent variables were the slopes of impact force vs. running velocity (mF1) and impact attenuation (mIA) vs. running velocity relationships. Stride length condition (i.e., PSL, SL2.5) was the independent variable. In addition to these dependent variables, the slopes for average vertical force (mFavg), resultant impact force (mFr), direction of resultant force (mθ), stance time (mst), aleg (mleg), and ahead (mhead) were also compared between stride length conditions (i.e., PSL, SL2.5). Paired t-tests were used to compare each dependent variable between the two stride length conditions (α= 0.05).
Results
The velocities were distributed in a similar manner between conditions (PSL: 3.6 ± 0.1 m·s-1; SL2.5: 3.5 ± 0.1 m·s-1; p > 0.05). Stride length increased with running velocity during PSL but not during SL2.5 (Figure 2, Table 1, p < 0.05), indicating that we achieved our goal of similar running velocity distributions between conditions as well as achieving our stride length manipulation goal.
Figure 2.
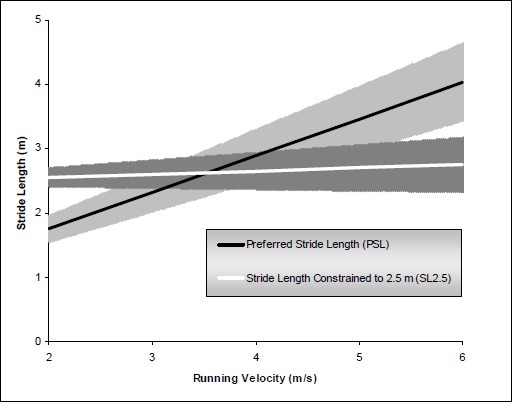
Illustration of the stride length and running velocity relationship during each running condition. The solid lines represent the group mean slope for impact force-velocity relationship while the shaded regions represent the between subject variability (i.e., slope standard deviation). The slopes were different between stride length conditions (p < 0.05).
Table 1.
Group mean parameters for the linear line of best fit (y = slope(x) + y-intercept) during running with preferred stride length (PSL) and constrained stride length (SL2.5). Units for slope are the parameter units per ms; units for y-intercept are the parameter units. Data are means (±SD).
| PSL | SL2.5 | ||||||
|---|---|---|---|---|---|---|---|
| Parameter | Slope (units/m·s-1) |
y-intercept (units) | Slope (units/m·s-1) |
y-intercept (units) |
|||
| Vertical Impact Force (BW) | .178 (.16) * | 1.11 (.48) | -.003 (.13) | 1.62 (.63) | |||
| Resultant Impact Force (BW) | .186 (.17) * | 1.09 (.51) | .001 (.13) | 1.62 (.63) | |||
| Resultant force direction (deg) | 1.00 (1.5) | 91.94 (5.33) | .41 (2.3) | 93.57 (7.58) | |||
| Active Force (BW) | .191 (.19) * | 1.92 (.21) | .049 (.9) | 2.22 (.58) | |||
| Average Force (BW) | .160 (.05) * | .91 (.22) | -.016 (.03) | 1.47 (.29) | |||
| Leg Impact Acceleration (g) | .89 (.61) | 1.95 (1.73) | .07 (.44) | 5.02 (2.55) | |||
| Head Impact Acceleration (g) | -.01 (.24) | 1.32 (.65) | -.09 (.11) | 1.54 (1.00) | |||
| Impact Attenuation (%) | 5.12 (2.88) * | 55.52 (11.91) | 1.39 (1.51) | 72.11 (9.14) | |||
| Stride Length (m) | .57 (.10) * | .61 (.38) | .05 (.07) | 2.46 (.21) | |||
| Stride Frequency (Hz) | .09 (.05) * | 1.04 (.26) | .36 (.04) | .08 (.11) | |||
| Stancetime (s) | -.048 (.01) * | .43 (.06) | -.077 (.02) | .54 (.08) | |||
* indicates the slopes were different between stride length conditions (p < 0.05).
The slope for each force parameter (mF1, mFavg, mFr) vs. running velocity relationship was different between conditions, with the slopes being greater during PSL vs. SL2.5 for each parameter (Table 1, p < 0.05). The slope of resultant force direction (mθ) was not different between stride length conditions (Table 1, p > 0.05). Figure 3 illustrates the relationship between vertical impact force and running velocity for each condition.
Figure 3.
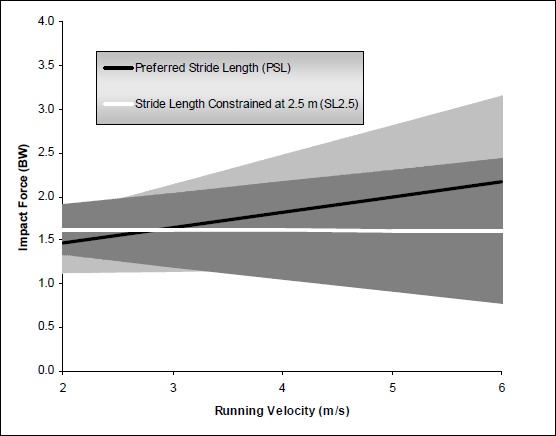
Illustration of the impact force and running velocity relationship during each running condition. The solid lines represent the group mean slope for impact force-velocity relationship while the shaded regions represent the between subject variability (i.e., slope standard deviation). The slopes were different between stride length conditions (p < 0.05).
The slope of the impact attenuation (mIA) vs. running velocity relationship was greater during PSL compared to the slope during SL2.5 (Figure 4, p < 0.05). Neither of the slopes for aleg (mleg) or ahead (mhead) were different between stride length conditions (Table 1, p < 0.05).
Figure 4.
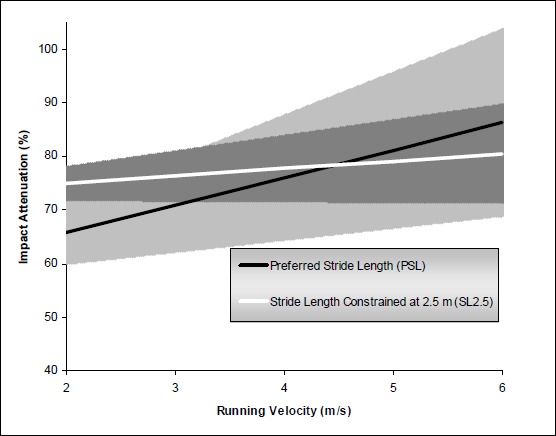
Illustration of the impact attenuation and running velocity relationship during each running condition. The solid lines represent the group mean slope for impact force-velocity relationship while the shaded regions represent the between subject variability (i.e., slope standard deviation). The slopes were different between stride length conditions (p < 0.05).
Discussion
Previous studies have determined that ground reaction forces change as running velocity changes (Hamill et al., 1983; Munro et al., 1987; Mercer and Vance, 2002). The basic kinematic descriptors of running behavior are stride length and stride frequency. In general, faster submaximal running velocities are achieved primarily by increases in stride length (Sinning and Forsyth, 1970; Luhtanen and Komi, 1978; Mercer et al., 2002b). Since stride length changes concurrently with changes in running velocity and changes in stride length influence impact force for a given running velocity (Derrick et al., 2000; Challis, 2001), it was not clear whether impact force changes due to velocity or stride length changes. By manipulating running velocity and either allowing stride length to naturally change or constraining stride length, we observed that stride length is critically related to impact force magnitude.
We observed that the impact force increased 0.178 BW/m·s-1 when stride length was freely chosen (i.e., PSL) across velocities ranging from about 2.5 m·s-1 to about 5.5 m·s-1. This relationship is similar to the impact force vs. running velocity relationship observed by Mercer and Vance (2002; 0.23 BW/m·s-1) but lower than other studies (0.41 BW/m·s-1; Hamill et al., 1983; 0.38 BW/m·s-1 Munro et al., 1987). Nevertheless, when stride length was constrained, the slope of the impact force-velocity relationship was dramatically different (-0.003 ± 0.14 BW/m·s-1) than during PSL (0.178 ± 0.16 BW m·s-1).
We considered that our study was limited by the analysis of data sets from six subjects. For example, one subject had no increase in impact force during PSL while impact force increased while stride length was constrained for a different subject. Previously, our laboratory had conducted a similar study (Mercer et al., 2001) where stride length was allowed to vary or was constrained at 2.5 m and 3.0 m. In that study (n = 10), it was also observed that the relationship between impact force and running velocity was influenced by constraints on stride length. Furthermore, combining the results from the current study with the 2.5 m data from the previous study yielded the same statistical outcome. However, we ultimately did not combine the two data sets for this study since acceleration data were not collected for those ten subjects.
In our study, impact attenuation increased with faster running velocities when stride length was allowed to vary. This was expected since it is well established that impact attenuation increases with faster running velocities (Shorten and Winslow, 1992; Mercer et al., 2002b). Mathematically, impact attenuation changed across velocities due to an increase in leg impact acceleration not head impact accelerations (Table 1). The leg impact accelerations tended to increase (p = 0.10) about 24% per m·s-1, which is lower than the 42% and 34% increase in leg impact acceleration per m·s-1 reported by Mercer et al. (2002b) and Clark et al. (1985), respectively. When stride length was constrained, there was no direct relationship between leg impact acceleration and running velocity. In contrast, the head impact acceleration relationship did not differ between stride length conditions. This was expected since head impact accelerations typically do not vary drastically between a variety of running conditions (e.g., Derrick et al., 1998; Derrick et al., 2002; Mercer et al., 2002a; Mercer et al., 2002b; Mercer et al., 2003) - which supports the hypothesis that anatomical structures and kinematic strategies result in attenuating impact frequencies (Hamill et al., 1995).
The importance of stride length changes on impact force and impact attenuation is that stride length is likely related to the lower extremity posture at impact. Simulated impact magnitudes have been related to lower extremity geometry at impact (Denoth, 1983; Gerritsen et al., 1995) and impact attenuation has been related to the distance between the direction of the line of action of the resultant ground reaction force and knee joint center (Derrick et al., 1998; 2004). Given that the slope of the direction of Fr (i.e., mθ) was not influenced by stride length condition, it is conjectured that impact characteristics (i.e., impact force magnitude and impact attenuation) were influenced by the lower extremity posture at impact. Specifically, it is conjectured that the lower extremity posture remained the same when stride length was constrained but changed when stride length was allowed to be freely chosen (i.e., PSL). Future research combining kinetic and kinematic information is needed to address this hypothesis.
Running is a complex movement pattern that is accomplished with very little conscious thought. As running velocity is increased it is expected that running behavior changes. We observed that stride length increased with faster running velocities during the PSL condition, which is similar to other studies (Sinning and Forsyth, 1970; Luhtanen and Komi, 1978; Mercer et al., 2002b). This leads to an interesting question: Why do runners choose to increase stride length to achieve faster submaximal running velocities? From our study, it does not seem that running behavior is based upon regulating impact force or impact attenuation since both parameters increased with faster running velocities when stride length was self-selected (i.e., PSL). Furthermore, as illustrated in Figure 3 (impact force vs. velocity), runners could select a stride length that results in a lower impact force than the freely chosen stride length. Hamill et al. (1995) also concluded that running behavior for a single velocity was not a function of impact attenuation. It may be, instead, that there is a target stride frequency that is being maintained across velocities.
We observed that stride frequency changed very little across a variety of submaximal running velocities during the PSL condition, which is a similar observation to other studies (Sinning and Forsyth, 1970; Luhtanen and Komi, 1978; Mercer et al., 2002b). It has been hypothesized that there is an optimal stride frequency that results in a minimal amount of oxygen consumption when running a given velocity (Hogberg, 1952; Cavanagh and Williams, 1982; Hamill et al., 1995). It may be that running behavior across velocities is based upon maintaining an optimal stride frequency, and changes to stride length are therefore a consequence to maintaining stride frequency. The importance of maintaining stride frequency may be related to the importance of selecting a movement pattern best suited for coordination of lower extremity movements that result in an economical movement pattern. In any case, a consequence of maintaining stride frequency across different velocities is increased impact force only because stride length is changing. Interestingly, despite increases in impact force, the runner seems to always absorb sufficient impact energy such that head impact accelerations are nearly constant despite a variety of impact force magnitudes. It may be that maintaining a stable visual field is a criteria driving running behavior.
Conclusions
There is a wealth of published research investigating factors that influence the ground reaction forces during running since these forces are likely related to overuse injuries commonly observed in runners and these are the forces that cause movement. We conducted an experiment in which ground reaction forces were analyzed across different velocities when subjects were allowed to either self-select stride length (PSL) or run with a specific stride length (i.e., SL2.5 m). We observed that stride length was an important factor that determined impact force magnitude. Future research is needed to determine which aspects of stride length are important determinants of impact characteristics.
Biographies
John A. MERCER
Employment
Biomechanics Laboratory Director, Assistant Professor
Degrees
PhD, BSc
Research interests
Biomechanics of locomotion.
E-mail: jmercer@unlv.nevada.edu
Neil E. BEZODIS
Employment
Student
Degrees
BSc(hons)
Research interests
3D analysis of rugby place kicking.
E-mail: sp1neb@bath.ac.uk
Mike RUSSELL
Employment
Student Physical Therapist at the University of Nevada Las Vegas
Degrees
BS, Kinesiology
Research interests
Athletic related injuries, biomechanics of running.
E-mail: bakasports@cox.net
Andy PURDY
Employment
Doctor of Physical Therapy Student (University of Southern California)
Degrees
BS
Research interests
Biomechanical Considerations on the restrictions of the talorcrural joint during jumping.
How motivation affects the rehabilitation process on post ACL injuries.
E-mail: purdy@usc.edu
David DeLION
Employment
Graduate Student
Degrees
B.S.
Research interests
Inertial tracking systems, prosthetic gait, overarm throwing.
References
- Cavanagh P.R., Kram R. (1985) The efficiency of human movement - a statement of the problem. Medicine and Science in Sports and Exercise 17, 304-308 [PubMed] [Google Scholar]
- Cavanagh P.R., Williams K.R. (1982) The effect of stride length variation on oxygen uptake during distance running. Medicine and Science in Sports and Exercise 14, 30-35 [DOI] [PubMed] [Google Scholar]
- Challis J. (2001) The variability in running gait caused by force plate targeting. Journal of Applied Biomechanics 17, 77-83 [Google Scholar]
- Clarke T.E., Cooper L., Clark D.E., Hamill C.L. (1985) The effects of increased running speed upon peak shank deceleration during ground contact. In: Biomechanics IX-B. Winter D.A., Norman R.W., Wells R.P., Hayes K.C., Patla A.E.Champaign, IL: Human Kinetics; 101-105 [Google Scholar]
- Denoth J. (1983) The dynamic behavior of a three link model of the human body during impact with the ground. In: Biomechanics IX-A. Winter D.A., Norman R.W., Wells R.P., Hayes K.C., Patla A.E.Champaign, IL: Human Kinetics; 102-106 [Google Scholar]
- Derrick T.R., Caldwell G.E., Hamill J. (2000) Modeling the stiffness characteristics of the human body while running with various stride lengths. Journal of Applied Biomechanics 16, 36-51 [Google Scholar]
- Derrick T.R., DeReu D.W., McLean S.P. (2002) Impacts and kinematic adjustments during an exhaustive run. Medicine and Science in Sports and Exercise 34, 998-1002 [DOI] [PubMed] [Google Scholar]
- Derrick T.R., Hamill J., Caldwell G.E. (1998) Energy absorption of impacts during running at various stride lengths. Medicine and Science in Sports and Exercise 30, 128-135 [DOI] [PubMed] [Google Scholar]
- Derrick T.R., Hamill J., Caldwell G.E. (2000) Modeling the stiffness characteristics of the human body while running with various stride lengths. Journal of Applied Biomechanics 16, 36-51 [Google Scholar]
- Derrick T.R. (2004) The effects of knee contact angle on impact forces and accelerations. Medicine and Science in Sports and Exercise 36, 832-837 [DOI] [PubMed] [Google Scholar]
- Gerritsen K.G.M., van den Bogert A.J., Nigg B.M. (1995) Direct dynamics simulation of the impact phase in heel-toe running. Journal of Biomechanics 28, 661-668 [DOI] [PubMed] [Google Scholar]
- Hamill J., Bates B.T., Knutzen K.M., Sawhill J.A. (1983) Variations in ground reaction force parameters at different running speeds. Human Movement Science 2, 47-56 [Google Scholar]
- Hamill J., Derrick T.R., Holt K.G. (1995) Shock attenuation and stride frequency during running. Human Movement Science 14, 45-60 [Google Scholar]
- Hogberg P. (1952) How do stride length and stride frequency influence the energy-output during running. Arbeitsphysiologie Bd, 14, 437-441 [PubMed] [Google Scholar]
- Hreljac A., Marshall R.N., Hume P.A. (2000) Evaluation of lower extremity overuse injury potential in runners. Medicine and Science in Sport and Exercise 32, 1635-1641 [DOI] [PubMed] [Google Scholar]
- Lafortune M.A., Lake M.J., Hennig E.M. (1996) Differential shock transmission response of the human body to impact severity and lower limb posture. Journal of Biomechanics 29, 1531-1537 [PubMed] [Google Scholar]
- Luhtanen P., Komi P.V. (1978) Mechanical factors influencing running speed. In Biomechanics VI Asmussen E., Jorgensen K.Baltimore: University Park Press; 23-29 [Google Scholar]
- Mercer J.A., Bates B.T., Dufek J.S., Hreljac A. (2003) Characteristics of shock attenuation during fatigued running. Journal of Sport Sciences 21, 911-919 [DOI] [PubMed] [Google Scholar]
- Mercer J.A., Black D., Branks D., Hreljac A. (2001) Stride length effects on ground reaction forces during running. Proceedings of the 25th Annual meeting of the American Society of Biomechanics. 205 [Google Scholar]
- Mercer J.A., DeVita P., Derrick T.R., Bates B.T. (2002a) The individual effects of stride length and stride frequency changes on shock attenuation during running. Medicine and Science in Sports and Exercise 35, 307-313 [DOI] [PubMed] [Google Scholar]
- Mercer J.A., Vance J, Hreljac A, Hamill J. (2002b) Characteristics of shock attenuation during high speed running. European Journal of Applied Physiology 87, 403-408 [DOI] [PubMed] [Google Scholar]
- Mercer J.A., Vance J. (2002) Put to the test: Spring-boots can reduce impact in runners. Biomechanics Magazine 9(5), 67-77 [Google Scholar]
- Munro C.F., Miller D.I., Fuglevand A.J. (1987) Ground reaction forces in running: A reexamination. Journal of Biomechanics 20, 147-155 [DOI] [PubMed] [Google Scholar]
- Nigg B.M., Cole G.K., Bruggemann G.P. (1995) Impact forces during heel-toe running. Journal of Applied Biomechanics 11, 407-432 [Google Scholar]
- Shorten M.R., Winslow D.S. (1992) Spectral analysis of impact shock during running. International Journal of Sports Medicine 8, 288-304 [Google Scholar]
- Sinning W.E., Forsyth H.L. (1970) Lower-limb actions while running at different velocities. Medicine and Science in Sports 2, 28-34 [PubMed] [Google Scholar]


