Random effects structure for confirmatory hypothesis testing: Keep it maximal

Abstract

Linear mixed-effects models (LMEMs) have become increasingly prominent in psycholinguistics and related areas. However, many researchers do not seem to appreciate how random effects structures affect the generalizability of an analysis. Here, we argue that researchers using LMEMs for confirmatory hypothesis testing should minimally adhere to the standards that have been in place for many decades. Through theoretical arguments and Monte Carlo simulation, we show that LMEMs generalize best when they include the maximal random effects structure justified by the design. The generalization performance of LMEMs including data-driven random effects structures strongly depends upon modeling criteria and sample size, yielding reasonable results on moderately-sized samples when conservative criteria are used, but with little or no power advantage over maximal models. Finally, random-intercepts-only LMEMs used on within-subjects and/or within-items data from populations where subjects and/or items vary in their sensitivity to experimental manipulations always generalize worse than separate F₁ and F₂ tests, and in many cases, even worse than F₁ alone. Maximal LMEMs should be the ‘gold standard’ for confirmatory hypothesis testing in psycholinguistics and beyond.

"I see no real alternative, in most confirmatory studies, to having a single main question—in which a question is specified by ALL of design, collection, monitoring, AND ANALYSIS."

Tukey (1980), “We Need Both Exploratory and Confirmatory” (p. 24, emphasis in original).

The notion of independent evidence plays no less important a role in the assessment of scientific hypotheses than it does in everyday reasoning. Consider a pet-food manufacturer determining which of two new gourmet cat-food recipes to bring to market. The manufacturer has every interest in choosing the recipe that the average cat will eat the most of. Thus every day for a month (twentyeight days) their expert, Dr. Nyan, feeds one recipe to a cat in the morning and the other recipe to a cat in the evening, counterbalancing which recipe is fed when and carefully measuring how much was eaten at each meal. At the end of the month Dr. Nyan calculates that recipes 1 and 2 were consumed to the tune of 92.9±5.6 and 107.2±6.1 (means ± S Ds) grams per meal respectively. How confident can we be that recipe 2 is the better choice to bring to market? Without further information you might hazard the guess “somewhat confident”, considering that one of the first statistical hypothesis tests typically taught, the unpaired t-test, gives p = 0.09 against the null hypothesis that choice of recipe does not matter. But now we tell you that only seven cats participated in this test, one for each day of the week. How does this change your confidence in the superiority of recipe 2?

Let us first take a moment to consider precisely what it is about this new information that might drive us to change our analysis. The unpaired t-test is based on the assumption that all observations are conditionally independent of one another given the true underlying means of the two populations—here, the average amount a cat would consume of each recipe in a single meal. Since no two cats are likely to have identical dietary proclivities, multiple measurements from the same cat would violate this assumption. The correct characterization becomes that all observations are conditionally independent of one another given (a) the true palatibility effect of recipe 1 versus recipe 2, together with (b) the dietary proclivities of each cat. This weaker conditional independence is a double-edged sword. On the one hand, it means that we have tested effectively fewer individuals than our 56 raw data points suggest, and this should weaken our confidence in generalizing the superiority of recipe 2 to the entire cat population. On the other hand, the fact that we have made multiple measurements for each cat holds out the prospect of factoring out each cat’s idiosyncratic dietary proclivities as part of the analysis, and thereby improving the signal-to-noise ratio for inferences regarding each recipe’s overall appeal. How we specify these idiosyncrasies can dramatically affect our conclusions. For example, we know that some cats have higher metabolisms and will tend to eat more at every meal than other cats. But we also know that each creature has its own palate, and even if the recipes were of similar overall quality, a given cat might happen to like one recipe more than the other. Indeed, accounting for idiosyncratic recipe preferences for each cat might lead to even weaker evidence for the superiority of recipe 2.

Situations such as these, where individual observations cluster together via association with a smaller set of entities, are ubiquitous in psycholinguistics and related fields—where the clusters are typically human participants and stimulus materials (i.e., items). Similar clustered-observation situations arise in other sciences, such as agriculture (plots in a field) and sociology (students in classrooms in schools in school-districts); hence accounting for the random effects of these entities has been an important part of the workhorse statistical analysis technique, the analysis of variance, under the name mixed-model ANOVA, since the first half of the twentieth century (Fisher, 1925; Scheffe, 1959). In experimental psychology, the prevailing standard for a long time has been to assume that individual participants may have idiosyncratic sensitivities to any experimental manipulation that may have an overall effect, so detecting a “fixed effect” of some manipulation must be done under the assumption of corresponding participant random effects for that manipulation as well. In our pet-food example, if there is a true effect of recipe—that is, if on average a new, previously unstudied cat will on average eat more of recipe 2 than of recipe 1—it should be detectable above and beyond the noise introduced by cat-specific recipe preferences, provided we have enough data. Technically speaking, the fixed effect is tested against an error term that captures the variability of the effect across individuals.

Standard practices for data-analysis in psycholinguistics and related areas fundamentally changed, however, after Clark (1973). In a nutshell, Clark (1973) argued that linguistic materials, just like experimental participants, have idiosyncrasies that need to be accounted for. Because in a typical psycholinguistic experiment, there are multiple observations for the same item (e.g., a given word or sentence), these idiosyncrasies break the conditional independence assumptions underlying mixed-model ANOVA, which treats experimental participant as the only random effect. Clark proposed the quasi-F (F′) and min-F′ statistics as approximations to an F-ratio whose distributional assumptions are satisfied even under what in contemporary parlance is called crossed random effects of participant and item (Baayen et al., 2008). Clark’s paper helped drive the field toward a standard demanding evidence that experimental results generalized beyond the specific linguistic materials used—in other words, the so-called by-subjects F₁ mixed-model ANOVA was not enough. There was even a time where reporting of the min-F′ statistic was made a standard for publication in the Journal of Memory and Language. However, acknowledging the widespread belief that min-F′ is unduly conservative (see, e.g., Forster & Dickinson, 1976), significance of min-F′ was never made a requirement for acceptance of a publication. Instead, the ‘normal’ convention continued to be that a result is considered likely to generalize if it passes p < 0.05 significance in both by-subjects (F₁) and by-items (F₂) ANOVAs. In the literature this criterion is called F₁ × F₂ (e.g., Forster & Dickinson, 1976), which in this paper we use to denote the larger (less significant) of the two p values derived from F₁ and F₂ analyses.

Linear Mixed-Effects Models (LMEMs)

Since Clark (1973), the biggest change in data analysis practices has been the introduction of methods for simultaneously modeling crossed participant and item effects in a single analysis, in what is variously called “hierarchical regression”, “multi-level regression”, or simply “mixed-effects models” (Baayen, 2008; Baayen et al., 2008; Gelman & Hill, 2007; Goldstein, 1995; Kliegl, 2007; Locker et al., 2007; Pinheiro & Bates, 2000; Quené & van den Bergh, 2008; Snijders & Bosker, 1999b).¹ In this paper we refer to models of this class as mixed-effects models; when fixed effects, random effects, and trial-level noise contribute linearly to the dependent variable, and random effects and trial-level error are both normally distributed and independent for differing clusters or trials, it is a linear mixed-effects model (LMEM).

The ability of LMEMs to simultaneously handle crossed random effects, in addition to a number of other advantages (such as better handling of categorical data; see Dixon, 2008; Jaeger, 2008), has given them considerable momentum as a candidate to replace ANOVA as the method of choice in psycholinguistics and related areas. But despite the widespread use of LMEMs, there seems to be insufficently widespread understanding of the role of random effects in such models, and very few standards to guide how random effect structures should be specified for the analysis of a given dataset. Of course, what standards are appropriate or inappropriate depends less upon the actual statistical technique being used, and more upon the goals of the analysis (cf. Tukey, 1980). Ultimately, the random effect structure one uses in an analysis encodes the assumptions that one makes about how sampling units (subjects and items) vary, and the structure of dependency that this variation creates in one’s data.

In this paper, our focus is mainly on what assumptions about sampling unit variation are most critical for the use of LMEMs in confirmatory hypothesis testing. By confirmatory hypothesis testing we mean the situation in which the researcher has identified a specific set of theory-critical hypotheses in advance and attempts to measure the evidence for or against them as accurately as possible (Tukey, 1980). Confirmatory analyses should be performed according to a principled plan guided by theoretical considerations, and, to the extent possible, should minimize the influence of the observed data on the decisions that one makes in the analysis (Wagenmakers et al., in press). To simplify our discussion, we will focus primarily on the confirmatory analysis of simple data sets involving only a few theoretically-relevant variables. We recognize that in practice, the complexity of one’s data may impose constraints on the extent to which one can perform analyses fully guided by theory and not by the data. Researchers who perform laboratory experiments have extensive control over the data collection process, and, as a result, their statistical analyses tend to include only a small set of theoretically relevant variables, because other extraneous factors have been rendered irrelevant through randomization and counterbalancing. This is in contrast to other more complex types of data sets, such as observational corpora or large-scale data sets collected in the laboratory for some other, possibly more general, purpose than the theoretical question at hand. Such datasets may be unbalanced and complex, and include a large number of measurements of many different kinds. Analyzing such datasets appropriately is likely to require more sophisticated statistical techniques than those we discuss in this paper. Furthermore, such analyses may involve data-driven techniques typically used in exploratory data analysis in order to reduce the set of variables to a manageable size. Discussion of such techniques for complex datasets and their proper application of is beyond the scope of this paper (but see, e.g., Baayen, 2008; Jaeger, 2010).

Our focus here is on the question: When the goal of a confirmatory analysis is to test hypotheses about one or more critical “fixed effects”, what random-effects structure should one use? Based on theoretical analysis and Monte Carlo simulation, we will argue the following:

1. Implicit choices regarding random-effect structures existed for traditional mixed-model ANOVAs just as they exist today for LMEMs;

2. With mixed-model ANOVAs, the standard has been to use what we term “maximal” random-effect structures;

3. Insofar as we as a field think this standard is appropriate for the purpose of confirmatory hypothesis testing, researchers using LMEMs for that purpose should also be using LMEMs with maximal random effects structure;

4. Failure to include maximal random-effect structures in LMEMs (when such random effects are present in the underlying populations) inflates Type I error rates;

5. For designs including within-subjects (or within-items) manipulations, random-intercepts-only LMEMs can have catastrophically high Type I error rates, regardless of how p-values are computed from them (see also Roland, 2009; Jaeger, 2011a; and Schielzeth & Forstmeier, 2009);

6. The performance of a data-driven approach to determining random effects (i.e., model selection) depends strongly on the specific algorithm, size of the sample, and criteria used; moreover, the power advantage of this approach over maximal models is typically negligible;

7. In terms of power, maximal models perform surprisingly well even in a “worst case” scenario where they assume random slope variation that is actually not present in the population;

8. Contrary to some warnings in the literature (Pinheiro & Bates, 2000), likelihood-ratio tests for fixed effects in LMEMs show minimal Type I error inflation for psycholinguistic datasets (see Baayen et al., 2008, Footnote 1, for a similar suggestion); also, deriving p-values from Monte Carlo Markov Chain (MCMC) sampling does not mitigate the high Type I error rates of random-intercepts-only LMEMs;

9. The F₁ × F₂ criterion leads to increased Type I error rates the more the effects vary across subjects and items in the underlying populations (see also Clark, 1973; Forster & Dickinson, 1976);

10. Min-F′ is conservative in between-items designs when the item variance is low, and is conservative overall for within-items designs, especially so when the treatment-by-subject and/or treatment-by-item variances are low (see also Forster & Dickinson, 1976); in contrast, maximal LMEMs show no such conservativity.

Further results and discussion are available in an online appendix (http://talklab.psy.gla.ac.uk/simgen).

Random effects in LMEMs and ANOVA: The same principles apply

The Journal of Feline Gastronomy has just received a submission reporting that the feline palate prefers tuna to liver, and as journal editor you must decide whether to send it out for review. The authors report a highly significant effect of recipe type (p < .0001), stating that they used “a mixed effects model with random effects for cats and recipes”. Are you in a position to evaluate the generality of the findings? Given that LMEMs can implement nearly any of the standard parametric tests—from a one-sample test to a multi-factor mixed-model ANOVA—the answer can only be no. Indeed, whether LMEMs produce valid inferences depends critically on how they are used. What you need to know in addition is the random effects structure of the model, because this is what the assessment of the treatment effects is based on. In other words, you need to know which treatment effects are assumed to vary across which sampled units, and how they are assumed to vary. As we will see, whether one is specifying a random effects structure for LMEMs or choosing an analysis from among the traditional options, the same considerations come into play. So, if you are scrupulous about choosing the “right” statistical technique, then you should be equally scrupulous about using the “right” random effects structure in LMEMs. In fact, knowing how to choose the right test already puts you in a position to specify the correct random effects structure for LMEMs.

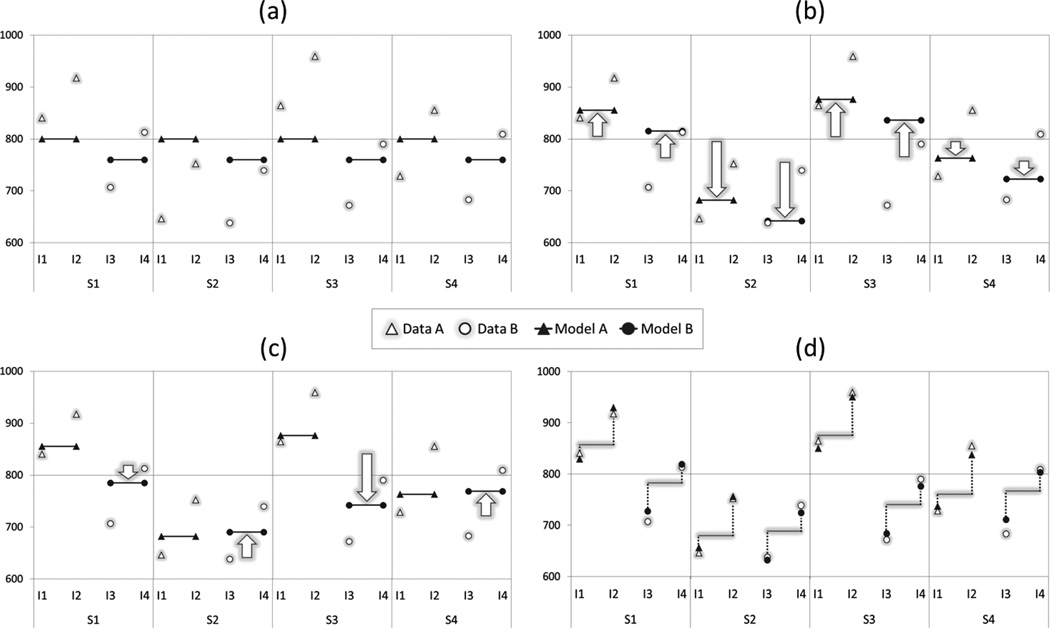
In this section, we attempt to distill the implicit standards already in place by walking through a hypothetical example and discussing the various models that could be applied, their underlying assumptions, and how these assumptions relate to more traditional analyses. In this hypothetical “lexical decision” experiment, subjects see strings of letters and have to decide whether or not each string forms an English word, while their response times are measured. Each subject is exposed to two types of words, forming condition A and condition B of the experiment. The words in one condition differ from those in the other condition on some intrinsic categorical dimension (e.g., syntactic class), comprising a word-type manipulation that is within-subjects and between-items. The question is whether reaction times are systematically different between condition A and condition B. For expository purposes, we use a “toy” dataset with hypothetical data from four subjects and four items, yielding two observations per treatment condition per participant. The observed data are plotted alongside predictions from the various models we will be considering in the panels of Figure 1. Because we are using simulated data, all of the parameters of the population are known, as well as the “true” subject-specific and item-specific effects for the sampled data. In practice, researchers do not know these values and can only estimate them from the data; however, using known values for hypothetical data can aid in understanding how clustering in the population maps onto clustering in the sample.

Figure 1.

Example RT data (open symbols) and model predictions (filled symbols) for a hypothetical lexical decision experiment with two within-subject/between-item conditions, A (triangles) and B (circles), including four subjects (S1–S4) and four items (I1–I4). Panel (a) illustrates a model with no random effects, considering only the baseline average RT (response to word type A) and treatment effect; panel (b) adds random subject intercepts to the model; panel (c) adds by-subject random slopes; and panel (d) illustrates the additional inclusion of by-item random intercepts. Panel (d) represents the maximal random-effects structure justified for this design; any remaining discrepancies between observed data and model estimates are due to trial-level measurement error (e_si).

The general pattern for the observed data points suggests that items of type B (I3 and I4) are responded to faster than items of type A (I1 and I2). This suggests a simple (but clearly inappropriate) model for these data that relates response Y_si for subject s and item i to a baseline level via fixed-effect β₀ (the intercept), a treatment effect via fixed-effect β₁ (the slope), and observation-level error e_si with variance σ²:

$$Y_{si}={\beta }_0+{\beta }_1{X}_i+e_{si},e_{si}~N(0,{\sigma }^2)$$ (1)

where X_i is a predictor variable² taking on the value of 0 or 1 depending on whether item i is of type A or B respectively, and e_si ~ N(0, σ²) indicates that the trial-level error is normally distributed with mean 0 and variance σ². In the population, participants respond to items of type B 40 ms faster than items of type A. Under this first model, we assume that each of the 16 observations provides the same evidence for or against the treatment effect regardless of whether or not any other observations have already been taken into account. Performing an unpaired t-test on these data would implicitly assume this (incorrect) generative model.

Model (1) is not a mixed-effects model because we have not defined any sources of clustering in our data; all observations are conditionally independent given a choice of intercept, treatment effect, and noise level. But experience tells us that different subjects are likely to have different overall response latencies, breaking conditional independence between trials for a given subject. We can expand our model to account for this by including a new offset term S_0s, the deviation from β₀ for subject s. The expanded model is now

$$Y_{si}={\beta }_0+S_{0s}+{\beta }_1{X}_i+e_{si},S_{0s}~N(0,{{\tau }_{00}}^2),e_{si}~N(0,{\sigma }^2).$$ (2)

These offsets increase the model’s expressivity by allowing predictions for each subject to shift upward or downward by a fixed amount (Figure 1b). Our use of Latin letters for this term is a reminder that S_0s is a special type of effect which is different from the βs—indeed, we now have a “mixed-effects” model: parameters β₀ and β₁ are fixed effects (effects that are assumed to be constant from one experiment to another), while the specific composition of subject levels for a given experiment is assumed to be a random subset of the levels in the underlying populations (another instantiation of the same experiment would have a different composition of subjects, and therefore different realizations of the S _0s effects). The S_0s effects are therefore random effects; specifically, they are random intercepts, as they allow the intercept term to vary across subjects. Our primary goal is to produce a model which will generalize to the population from which these subjects are randomly drawn, rather than describing the specific S _0s values for this sample. Therefore, instead of estimating the individual S _0s effects, the model-fitting algorithm estimates the population distribution from which the S _0s effects were drawn. This requires assumptions about this distribution; we follow the common assumption that it is normal, with a mean of 0 and a variance of τ₀₀²; here τ₀₀² is a random effect parameter, and is denoted by a Greek symbol because, like the βs, it refers to the population and not to the sample.

Note that the variation on the intercepts is not confounded with our effect of primary theoretical interest (β₁): for each subject, it moves the means for both conditions up or down by a fixed amount. Accounting for this variation will typically decrease the residual error and thus increase the sensitivity of the test of β₁. Fitting Model (2) is thus analogous to analyzing the raw, unaggregated response data using a repeated-measures ANOVA with S S _subjects subtracted from the residual S S_error term. One could see that this analysis is wrong by observing that the denominator degrees of freedom for the F statistic (i.e., corresponding to MS _error) would be greater than the number of subjects (see online appendix for further discussion and demonstration).

Although Model (2) is clearly preferable to Model (1), it does not capture all the possible by-subject dependencies in the sample; experience also tells us that subjects often vary not only in their overall response latencies but also in the nature of their response to word type. In the present hypothetical case, Subject 3 shows a total effect of 134 ms, which is 94 ms larger than the average effect in the population of 40 ms. We have multiple observations per combination of subject and word type, so this variability in the population will also create clustering in the sample. The S_0s do not capture this variability because they only allow subjects to vary around β₀. What we need in addition are random slopes to allow subjects to vary with respect to β₁, our treatment effect. To account for this variation, we introduce a random slope term S_1s with variance τ₁₁², yielding

$$Y_{si}={\beta }_0+S_{0s}+({\beta }_1+S_{1s})X_i+e_{si},(S_{0s},S_{1s})~N(0,[\begin{array}{cc}\hfill {{\tau }_{00}}^2\hfill & \hfill \rho {\tau }_{00}{\tau }_{11}\hfill \\ \hfill \rho {\tau }_{00}{\tau }_{11}\hfill & \hfill {{\tau }_{11}}^2\hfill \end{array}\left]\right),e_{si}~N(0,{\sigma }^2).$$ (3)

This is now a mixed-effects model with by-subject random intercepts and random slopes. Note that the inclusion of the by-subject random slope causes the predictions for condition B to shift by a fixed amount for each subject (Figure 1c), improving predictions for words of type B. The slope offset S_1s captures how much Subject s’s effect deviates from the population treatment effect β₁. Again, we do not want our analysis to commit to particular S_1s effects, and so, rather than estimating these values directly, we estimate τ₁₁², the by-subject variance in treatment effect. But note that now we have two random effects for each subject s, and these two effects can exhibit a correlation (expressed by ρ). For example, subjects who do not read carefully might not only respond faster than the typical subject (and have a negative S_0s), but might also show less sensitivity to the word type manipulation (and have a more positive S_1s). Indeed, such a negative correlation, where we would have ρ < 0, is suggested in our hypothetical data (Figure 1): S1 and S3 are slow responders who show clear treatment effects, whereas S2 and S4 are fast responders who are hardly susceptible to the word type manipulation. In the most general case, we should not treat these effects as coming from independent univariate distributions, but instead should treat S _0s and S _1s as being jointly drawn from a bivariate distribution. As seen in line 2 of Equation 3, we follow common assumptions in taking this distribution as bivariate normal with a mean of (0, 0) and three free parameters: τ₀₀² (random intercept variance), τ₁₁² (random slope variance), and ρτ₀₀τ₁₁ (the intercept/slope covariance). For further information about random effect variance-covariance structures, see Baayen (2004, 2008); Gelman & Hill (2007); Goldstein (1995); Raudenbush & Bryk (2002); Snijders & Bosker (1999a).

Both Models (2) and (3) are instances of what is traditionally analyzed using “mixed-model ANOVA” (e.g., Scheffe, 1959, chapter 8). By long-standing convention in our field, however, the classic “by-subjects ANOVA” (and analogously “by-items ANOVA” when items are treated as the random effect) is understood to mean Model (3), the relevant F-statistic for which is $F_1=\frac{M{S}_T}{M{S}_{TxS}}$, where MS_T is the treatment mean square and MS_TxS is the treatment-by-subject mean square. This convention presumably derives from the widespread recognition that subjects (and items) usually do vary idiosyncratically not only in their global mean responses but also in their sensitivity to the experimental treatment. Moreover, this variance, unlike random intercept variance, can drive differences between condition means. This can be seen by comparing the contributions of random intercepts versus random slopes across panels (b) and (c) in Figure 1. Therefore, it would seem to be important to control for such variation when testing for a treatment effect.³

Although Model (3) accounts for all by-subject random variation, it still has a critical defect. As Clark (1973) noted, the repetition of words across observations is a source of non-independence not accounted for, which would impair generalization of our results to new items. We need to incorporate item variability into the model with the random effects I_0i, yielding

$$Y_{si}={\beta }_0+S_{0s}+I_{0i}+({\beta }_1+S_{1s})X_i+e_{si},(S_{0s},S_{1s})~N(0,[\begin{array}{cc}\hfill {{\tau }_{00}}^2\hfill & \hfill \rho {\tau }_{00}{\tau }_{11}\hfill \\ \hfill \rho {\tau }_{00}{\tau }_{11}\hfill & \hfill {{\tau }_{11}}^2\hfill \end{array}\left]\right),I_{0i}~N(0,{{\omega }_{00}}^2),e_{si}~N(0,{\sigma }^2).$$ (4)

This is a mixed-effect model with by-subject random intercepts and slopes and by-item random intercepts. Rather than committing to specific I_0i values, we assume that the I_0i effects are drawn from a normal distribution with a mean of zero and variance ω₀₀². We also assume that ω₀₀² is independent from the τ parameters defining the by-subject variance components. Note that the inclusion of by-item random intercepts improves the predictions from the model, with predictions for a given item shifting by a consistent amount across all subjects (Figure 1d). It is also worth noting that the by-item variance is also confounded with our effect of interest, since we have different items in the different conditions, and thus will tend to contribute to any difference we observe between the two condition means.

This analysis has a direct analogue to min-F′, which tests MS_T against a denominator term consisting of the sum of MS_TxS and MS _I, the mean squares for the random treatment-by-subject interaction and the random main effect of items. It is, however, different from the practice of performing F1 × F2 and rejecting the null hypothesis if p < .05 for both Fs. The reason is that MS_T (the numerator for both F₁ and F₂) reflects not only the treatment effect, but also treatment-by-subject variability (τ₁₁²) as well as by-item variability (ω₀₀²). The denominator of F₁ controls for treatment-by-subject variability but not item variability; similarly, the denominator of F₂ controls for item variability but not treatment-by-subject variability. Thus, finding that F₁ is significant implies that β₁ ≠ 0 or ω₀₀²≠ 0, or both; likewise, finding that F₂ is significant implies that β₁ ≠ 0 or τ₁₁2 ≠ 0, or both. Since ω₀₀² and τ₁₁² can be nonzero while β₁ = 0, F₁ × F₂ tests will inflate the Type I error rate (Clark, 1973). Thus, in terms of controlling Type I error rate, the mixed-effects modeling approach and the min-F′ approach are, at least theoretically, superior to separate by-subject and by-item tests.

At this point, we might wish to go further and consider other models. For instance, we have considered a by-subject random slope; for consistency, why don’t we also consider a model with a by-item random slope, I_1i? A little reflection reveals that a by-item random slope does not make sense for this design. Words are nested within word types—no word can be both type A and type B— so it is not sensible to ask whether words vary in their sensitivity to word type. No sample from this experiment could possibly give us the information needed to estimate random slope variance and random slope/intercept covariance parameters for such a model. A model like this is unidentifiable for the data it is applied to: there are (infinitely) many different values we could choose for its parameters which would describe the data equally well.⁴ Experiments with a within-item manipulation, such as a priming experiment in which target words are held constant across conditions but the prime word is varied, would call for by-item random slopes, but not the current experiment.

The above point also extends to designs where one independent variable is manipulated within- and another variable between- subjects (respectively items). In case of between-subject manipulations, the levels of the subject variable are nested within the levels of the experimental treatment variable (i.e. each subject belongs to one and only one of the experimental treatment groups), meaning that subject and treatment cannot interact—a model with a by-subject random slope term would be unidentifiable. In general, within-unit treatments require both the by-unit intercepts and slopes in the random effects specification, whereas between-unit treatments require only the by-unit random intercepts.

It is important to note that identifiability is a property of the model given a certain dataset. The model with by-item random slopes is unidentifiable for any possible dataset because it tries to model a source of variation that could not logically exist in the population. However, there are also situations where a model is unidentifiable because there is insufficient data to estimate its parameters. For instance, we might decide it was important to try to estimate variability corresponding to the different ways that subjects might respond to a given word (a subject-by-item random intercept). But to form a cluster in the sample, it is necessary to have more than one observation for a given unit; otherwise, the clustering effect cannot be distinguished from residual error.⁵ If we only elicit one observation per subject/item combination, we are unable to estimate this source of variability, and the model containing this random effect becomes unidentifiable. Had we used a design with repeated exposures to the same items for a given subject, the same model would be identifiable, and in fact we would need to include that term to avoid violating the conditional independence of our observations given subject and item effects.

This discussion indicates that Model (4) has the maximal random effects structure justified by our experimental design, and we henceforth refer to such models as maximal models. A maximal model should optimize generalization of the findings to new subjects and new items. Models that lack random effects contained in the maximal model, such as Models (1)-(3), are likely to be misspecified—the model specification may not be expressive enough to include the true generative process underlying the data. This type of misspecification is problematic because conditional independence between observations within a given cluster is not achieved. Each source of random variation that is not accounted for will tend to work against us in one of two different ways. On the one hand, unaccounted-for variation that is orthogonal to our effect of interest (e.g., random intercept variation) will tend to reduce power for our tests of that effect; on the other, unaccounted-for variation that is confounded with our effect of interest (e.g., random slope variation), can drive differences between means, and thus will tend to increase the risk of Type I error.

A related model that we have not yet considered but that has become popular in recent practice includes only by-subject and by-item random intercepts.

$$Y_{si}={\beta }_0+S_{0s}+I_{0i}+{\beta }_1{X}_i+e_{si,}{S}_{0i}~N(0,{{\tau }_{00}}^2),I_{0i}~N(0,{{\omega }_{00}}^2),e_{si}~N(0,{\sigma }^2).$$ (5)

Unlike the other models we have considered up to this point, there is no clear ANOVA analog to a random-intercepts-only LMEM; it is perhaps akin to a modified min-F′ statistic with a denominator error term including MS _I but with MS_TxS replaced by the error term from Model 2 (i.e., with S S_error reduced by S S _subjects). But it would seem inappropriate to use this as a test statistic, given that the numerator MS_T increases as a function not only of the overall treatment effect, but also as a function of random slope variation (τ₁₁²), and the denominator does not control for this variation.

A common misconception is that crossing subjects and items in the intercept term of LMEMs is sufficient for meeting the assumption of conditional independence, and that including random slopes is strictly unnecessary unless it is of theoretical interest to estimate that variability (see e.g., Janssen, 2012; Locker et al., 2007). However, this is problematic given the the fact that, as already noted, random slope variation can drive differences between condition means, thus creating a spurious impression of a treatment effect where none might exist. Indeed, some researchers have already warned against using random-intercepts-only models when random slope variation is present (e.g., Baayen, 2008; Jaeger, 2011a; Roland, 2009; Schielzeth & Forstmeier, 2009). However, the performance of these models has not yet been evaluated in the context of simultaneous generalization over subjects and items. Our simulations will provide such an evaluation.

Although the maximal model best captures all the dependencies in the sample, sometimes it becomes necessary for practical reasons to simplify the random effects structure. Fitting LMEMs typically involves maximum likelihood estimation, where an iterative procedure is used to come up with the “best” estimates for the parameters given the data. As the name suggests, it attempts to maximize the likelihood of the data given the structure of the model. Sometimes, however, the estimation procedure will fail to “converge” (i.e., to find a solution) within a reasonable number of iterations. The likelihood of this convergence failure tends to increase with the complexity of the model, especially the random effects structure.

Ideally, simplification of the random effects structure should be done in a principled way Dropping a random slope is not the only solution, nor is it likely to be the best, given that random slopes tend to account for variance confounded with the fixed effects of theoretical interest. We thus consider two additional mixed-effects models with simplified random effects structure.⁶ The first of these is almost identical to the maximal model (Model 4) but without any correlation parameter:

$$Y_{si}={\beta }_0+S_{0s}+I_{0i}+({\beta }_1+S_{1s})X_i+e_{si,}(S_{0s},S_{1s})~N(0,[\begin{array}{cc}\hfill {{\tau }_{00}}^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {{\tau }_{11}}^2\hfill \end{array}\left]\right),I_{0i}~N(0,{{\omega }_{00}}^2),e_{si}~N(0,{\sigma }^2).$$ (6)

Note that the only difference from Model 4 is in the specification of the distribution of (S _0s, S _1s) pairs. Model 6 is more restrictive than Model 4 in not allowing correlation between the random slope and random intercept; if, for example, subjects with overall faster reaction times also tended to be less sensitive to experimental manipulation (as in our motivating example for random slopes), Model 6 could not capture that aspect of the data. But it does account for the critical random variances that are confounded with the effect of interest, τ₁₁² and ω₀₀².

The next and final model to consider is one that has received almost no discussion in the literature but is nonetheless logically possible: a maximal model that is simplified by removing random intercepts for any within-unit (subject or item) factor. For the current design, this means removing the by-subject random intercept:

$$Y_{si}={\beta }_0+I_{0i}+({\beta }_1+S_{1s})X_i+e_{si,}{S}_{1s}~N(0,{{\tau }_{11}}^2),I_{0i}~N(0,{{\omega }_{00}}^2),e_{si}~N(0,{\sigma }^2).$$ (7)

This model, like random-intercepts-only and no-correlation models, would almost certainly be misspecified for typical psycholinguistic data. However, like the previous model, and unlike the random-intercepts-only model, it captures all the sources of random variation that are confounded with the effect of main theoretical interest.

The mixed-effects models considered in this section are presented in Table 1. We give their expression in the syntax of lmer (Bates et al., 2011), a widely used mixed-effects fitting method for R (R Development Core Team, 2011). To summarize, when specifying random effects, one must be guided by (1) the sources of clustering that exist in the target subject and item populations, and (2) whether this clustering in the population will also exist in the sample. The general principle is that a by-subject (or by-item) random intercept is needed whenever there is more than one observation per subject (or item or subject-item combination), and a random slope is needed for any effect where there is more than one observation for each unique combination of subject and treatment level (or item and treatment level, or subject-item combination and treatment level). Models are unidentifiable when they include random effects that are logically impossible or that cannot be estimated from the data in principle. Models are misspecified when they fail to include random effects that create dependencies in the sample. Subject- or item- related variance that is not accounted for in the sample can work against generalizability in two ways, depending on whether on not it is independent of the hypothesis-critical fixed effect. In the typical case in which fixed-effect slopes are of interest, models without random intercepts will have reduced power, while models without random slopes will exhibit an increased Type I error rate. This suggests that LMEMs with maximal random effects structure have the best potential to produce generalizable results. Although this section has only dealt with a simple single-factor design, these principles extend in a straightforward manner to higher-order designs, which we consider further in the General Discussion.

Table 1.

Summary of models considered and associated 1mer syntax.

No.	Model	lmer model syntax
(1)	Ysi = β0 + β1Xi + esi	n/a (not a mixed-effects model)
(2)	Ysi = β0 + S0s + β1Xi + esi	Y~X+(1|Subject)
(3)	Ysi = β0 + S0s + (β1 + S1s)Xi + esi	Y~X+(1+X|Subject)
(4)	Ysi = β0 + S0s + I0i + (β1 + S1s)Xi + esi	Y~X+(1+X|Subject)+ (1 |Item)
(5)	Ysi = β0 + S0s + I0i + β1Xi + esi	Y~X+(1|Subject)+(1|Item)
(6)*	As (4), but S0s, S 1s independent	Y~X+(l|Subject)+(0+X|Subject)+(1| Item)*
(7)*	Ysi = β0 + I0i + (β1 + S1s)Xi + esi	Y~X+(0+X|Subject) + (1|Item)*

^*Performance is sensitive to the coding scheme for variable × (see Appendix)

Design-driven versus data-driven random effects specification

As the last section makes evident, in psycholinguistics and related areas, the specification of the structure of random variation is traditionally driven by the experimental design. In contrast to this traditional design-driven approach, a data-driven approach has gained prominence along with the recent introduction of LMEMs. The basic idea behind this approach is to let the data “speak for themselves” as to whether certain random effects should be included in the model or not. That is, on the same data set, one compares the fit of a model with and without certain random effect terms (e.g. Model 4 versus Model 5 in the previous section) using goodness of fit criteria that take into account both the accuracy of the model to the data and its complexity. Here, accuracy refers to how much variance is explained by the model and complexity to how many predictors (or parameters) are included in the model. The goal is to find a structure that strikes a compromise between accuracy and complexity, and to use this resulting structure for carrying out hypothesis tests on the fixed effects of interest.

Although LMEMs offer more flexibility in testing random effects, datadriven approaches to random effect structure have long been possible within mixed-model ANOVA (see the online Appendix). For example, Clark (1973) considers a suggestion by Winer (1971) that one could test the significance of the treatment-by-subjects interaction at some liberal α level (e.g., .25), and, if it is not found to be signficant, to use the F₂ statistic to test one’s hypothesis instead of a quasi-F statistic (Clark, 1973, p. 339). In LMEM terms, this is similar to using model comparison to test whether or not to include the by-subject random slope (albeit with LMEMs, this could be done while simultaneously controlling for item variance). But Clark rejected such an approach, finding it unnecessarily risky (see e.g., Clark, 1973, p. 339). Whether they shared Clark’s pessimism or not, researchers who have used ANOVA on experimental data have, with rare exception, followed a design-driven rather than a data-driven approach to specifying random effects.

We believe that researchers using ANOVA have been correct to follow a design-driven approach. Moreover, we believe that a design-driven approach is equally preferable to a data-driven approach for confirmatory analyses using LMEMs. In confirmatory analyses, random effect variance is generally considered a “nuisance” variable rather than a variable of interest; one does not eliminate these variables just because they do not “improve model fit.” As stated by Ben Bolker (one of the developers of lme4), “If random effects are part of the experimental design, and if the numerical estimation algorithms do not break down, then one can choose to retain all random effects when estimating and analyzing the fixed effects.” (Bolker et al., 2009, p. 134). The random effects are crucial for encoding measurement-dependencies in the design. Put bluntly, if an experimental treatment is manipulated within-subjects (with multiple observations per subject-by-condition cell), then there is no way for the analysis procedure to “know” about this unless the fixed effect of that treatment is accompanied with a by-subject random slope in the analysis model. Second, it is important to bear in mind that experimental designs are usually optimized for the detection of fixed effects, and not for the detection of random effects. Datadriven techniques will therefore not only (correctly) reject random effects that do not exist, but also (incorrectly) reject random effects for which there is just insufficient power. This problem is exacerbated for small datasets, since detecting random effects is harder the fewer clusters and observations-per-cluster are present.

A further consideration is that the there are no existing criteria to guide researchers in the data-driven determination of random effects structure. This is unsatisfactory because the approach requires many decisions: What α-level should be used? Should α be corrected for the number of random effects being tested? Should one test random effects following a forward or backward algorithm, and how should the tests be ordered? Should intercepts be tested as well as slopes, or left in the model by default? The number of possible random effects structures, and thus the number of decisions to be made, increases with the complexity of the design. As we will show, the particular decision criteria that are used will ultimately affect the generalizability of the test. The absence of any accepted criteria allows researchers to make unprincipled (and possibly self-serving) choices. To be sure, it may be possible to obtain reasonable results using a data-driven approach, if one adheres to conservative criteria. However, even when the modeling criteria are explicitly reported, it is a non-trivial problem to quantify potential increases in anti-conservativity that the procedure has introduced (see Harrell, 2001, chapter 4).

But even if one agrees that, in principle, a design-driven approach is more appropriate than a data-driven approach for confirmatory hypothesis testing, there might be concern that using LMEMs with maximal random effects structure is a recipe for low power, by analogy with min-F′, an earlier solution to the problem of simultaneous generalization. The min-F′ statistic has indeed been shown to be conservative under some circumstances (Forster & Dickinson, 1976), and it is perhaps for this reason that it has not been broadly adopted as a solution to the problem of simultaneous generalization. If maximal LMEMs also turn out to have low power, then perhaps this would justify the extra Type I error risk associated with data-driven approaches. However, the assumption that maximal models are overly conservative should not be taken as a forgone conclusion. Although maximal models are similar in spirit to min-F′, there are radical differences between the estimation procedures for min-F′ and maximal LMEMs. Min-F′ is composed of two separately calculated F statistics, and the by-subjects F does not control for the by-item noise, nor does the by-items F control for the by-subjects noise. In contrast, with maximal LMEMs by-subject and by-item variance is taken into account simultaneously, yielding greater prospects for being a more sensitive test.

Finally, we believe it is important to distinguish between model-selection for the purpose of data exploration on the one hand and model-selection for the purpose of determining random effects structures (in confirmatory contexts) on the other; we are skeptical about the latter, but do not intend to pass any judgement on former.

Modeling of random effects in the current psycholinguistic literature

The introduction of LMEMs and their early application to psycholinguistic data by Baayen et al. (2008) has had a major influence on analysis techniques used in peer-reviewed publications. At the time of writing (October 2012), Google scholar reports 1004 citations to Baayen, Davidson and Bates. In an informal survey of the 150 research articles published in the Journal of Memory and Language since Baayen et al. (from volume 59 issue 4 to volume 64 issue 3) we found that 20 (13%) reported analyses using an LMEM of some kind. However, these papers differ substantially in both the type of models used and the information reported about them. In particular, researchers differed in whether they included random slopes or only random intercepts in their models. Of the 20 JML articles identified, six gave no information about the random effects structure, and a further six specified that they used random intercepts only, without theoretical or empirical justification. A further five papers employed model selection, four forward and only one backward (testing for the inclusion of random effects, but not fixed effects). The final three papers employed a maximal random effects structure including intercept and slope terms where appropriate.

This survey highlights two important points. First, there appears to be no standard for reporting the modeling procedure, and authors vary dramatically in the amount of detail they provide. Second, at least 30% of the papers and perhaps as many as 60%, do not include random slopes, i.e. they tacitly assume that individual subjects and items are affected by the experimental manipulations in exactly the same way. This is in spite of the recommendations of various experts in peer-reviewed papers and books (Baayen, 2008; Baayen et al., 2008) as well as in the informal literature (Jaeger, 2009, 2011b). Furthermore, none of the LMEM articles in the JML special issue (Baayen et al., 2008; Barr, 2008; Dixon, 2008; Jaeger, 2008; Mirman et al., 2008; Quené & van den Bergh, 2008) set a bad example of using random-intercept-only models. As discussed earlier, the use of random-intercept-only models is a departure even from the standard use of ANOVA in psycholinguistics.

The present study

How do current uses of LMEMs compare to more traditional methods such as min-F′ and F₁ × F₂)? The next section of this paper tests a wide variety of commonly used analysis methods for datasets typically collected in psycholinguistic experiments, both in terms of whether resulting significance levels can be trusted—i.e., whether the Type I error rate for a given approach in a given situation is conservative (less than α), nominal (equal to α), or anticonservative (greater than α)—and the power of each method in detecting effects that are actually present in the populations.

Ideally, we would compare the different analysis techniques by applying them to a large selection of real data sets. Unfortunately, in real experiments the true generative process behind the data is unknown, meaning that we cannot tell whether effects in the population exist—or how big those effects are—without relying on one of the analysis techniques we actually want to evaluate. Moreover, even if we knew which effects were real, we would need far more datasets than are readily available to reliably estimate the nominality and power of a given method.

We therefore take an alternative approach of using Monte Carlo methods to generate data from simulated experiments. This allows us to specify the underlying sampling distributions per simulation, and thus to have veridical knowledge of the presence or absence of an effect of interest, as well as all other properties of the experiment (number of subjects, items and trials, and the amount of variability introduced at each level). Such a Monte Carlo procedure is standard for this type of problem (e.g., Baayen et al., 2008; Davenport & Webster, 1973; Forster & Dickinson, 1976; Quené & van den Bergh, 2004; Santa et al., 1979; Schielzeth & Forstmeier, 2009; Wickens & Keppel, 1983), and guarantees that as the number of samples increases, the obtained p-value distribution becomes arbitrarily close to the true p-value distribution for datasets generated by the sampling model.

The simulations assume an “ideal-world scenario” in which all the distributional assumptions of the model class (in particular normal distribution of random effects and trial-level error, and homoscedasticity of trial-level error and between-items random intercept variance) are satisfied. Although the approach leaves open for future research many difficult questions regarding departures of realistic psycholinguistic data from these assumptions, it allows us great flexibility in analyzing the behavior of each analytic method as the population and experimental design vary. We hence proceed to the systematic investigation of traditional ANOVA, min-F′, and several types of LMEMs as datasets vary in many crucial respects including between- versus within-items, different numbers of items, and different random-effect sizes and covariances.

Method

Generating simulated data

For simplicity, all datasets included a continuous response variable and had only a single two-level treatment factor, which was always within subjects, and either within or between items. When it was within, each “subject” was assigned to one of two counterbalancing “presentation” lists, with half of the subjects assigned to each list. We assumed no list effect; that is, the particular configuration of “items” within a list did not have any unique effect over and above the item effects for that list. We also assumed no order effects, nor any effects of practice or fatigue. All experiments had 24 subjects, but we ran simulations with both 12 or 24 items to explore the effect of number of random-effect clusters on fixed-effects inference.⁷

Within-item data sets were generated from the following sampling model:

$$Y_{si}={\beta }_0+S_{0s}+I_{0i}+({\beta }_1+S_{1s}+I_{1i})X_{si}+e_{si.}$$

with all variables defined as in the tutorial section above, except that we used deviation coding for X_si (−.5, .5) rather than treatment coding. Random effects S_0s and S_1s were drawn from a bivariate normal distribution with means µ_S = < 0,0 > and variance-covariance matrix $\mathrm{T}=\left(\begin{array}{cc}\hfill {{\tau }_{00}}^2\hfill & \hfill \rho s{\tau }_{00}{\tau }_{11}\hfill \\ \hfill \rho s{\tau }_{00}{\tau }_{11}\hfill & \hfill {{\tau }_{11}}^2\hfill \end{array}\right)$. Likewise, I_0i and I_1i were also drawn from a separate bivariate normal distribution with µ_I =< 0,0 > and variance-covariance matrix $\mathrm{\Omega }=\left(\begin{array}{cc}\hfill {{\omega }_{00}}^2\hfill & \hfill {\rho }_I{\omega }_{00}{\omega }_{11}\hfill \\ \hfill {\rho }_I{\omega }_{00}{\omega }_{11}\hfill & \hfill {{\omega }_{11}}^2\hfill \end{array}\right)$. The residual errors e_si were drawn from a normal distribution with a mean of 0 and variance σ². For between-item designs, the I_1i effects (by-item random slopes) were simply ignored and thus did not contribute to the response variable.

We investigated the performance of various analyses over a range of population parameter values (Table 2). To generate each simulated dataset, we first determined the population parametersy β₀, τ₀₀², τ₁₁², ρs, ω₀₀², ω₁₁², ρ_I, and σ² by sampling from uniform distributions with ranges given in Table 2. We then simulated 24 subjects and 12 or 24 items from the corresponding populations, and simulated one observation for each subject/item pair. We also assumed missing data, with up to 5% of observations in a given data set counted as missing (at random). This setting was assumed to reflect normal rates of data loss (due to experimenter error, technical issues, extreme responses, etc.). The online appendix presents results for scenarios in which data loss was more substantial and nonhomogeneous.

Table 2.

Ranges for the population parameters; ~ U(min, max) means the parameter was sampled from a uniform distribution with range [min, max].

Parameter	Description	Value
β0	grand-average intercept	~U(−3,3)
β1	grand-average slope	0 (H0 true) or .8 (H1 true)
τ002	by-subject variance of S0s	~ U(0,3)
τ112	by-subject variance of S1s	~U(0,3)
ρS	correlation between (S0s, S1s) pairs	~U(−.8,.8)
ω002	by-item variance of I0i	~ U(0,3)
ω112	by-item variance of I1i	~ U(0,3)
ρI	correlation between (I0i, I1i) pairs	~U(−.8,.8)
σ2	residual error	~ U(0,3)
pmissing	proportion of missing observations	~ U(.00, .05)

For tests of Type I error, β₁ (the fixed effect of interest) was set to zero. For tests of power, β₁ was set to .8, which we found yielded power around 0.5 for the most powerful methods with close-to-nominal Type I error.

We generated 100000 datasets for testing for each of the eight combinations (effect present/absent, between-/within-item manipulation, 12/24 items). The functions we used in running the simulations and processing the results are available in the R package simgen, which we have made available in the online appendix, along with a number of R scripts using the package. The online appendix also contains further information about the additional R packages and functions used for simulating the data and running the analyses.

Analyses

The analyses that we evaluated are summarized in Table 3. Three of these were based on ANOVA (F₁, min-F′, and F₁ × F₂), with individual F-values drawn from mixed-model ANOVA on the unaggregated data (e.g., using MS_treatment/MS_{treatment-by-subject}) rather than from performing repeated-measures ANOVAs on the (subject and item) means. The analyses also included LMEMs with a variety of random effects structures and test statistics. All LMEMs were fit using the lmer function of the R package lme4, version 0.999375-39 (Bates et al., 2011), using maximum likelihood estimation.

Table 3.

Analyses performed on simulated datasets.

Analysis	Test statistics
min-F′	min-F′
F1	F1
F1 ×F2	F1F2
Maximal LMEM	t, χ2LR
LMEM, Random Intercepts Only	t, χ2LR, MCMC
LMEM, No Within-Unit Intercepts (NWI)	t, χ2LR
Maximal LMEM, No Random Correlations (NRC)	t, χ2LR, MCMC
Model selection (multiple variants)	t, χ2LR

There were four kinds of models with predetermined random effects structures: models with random intercepts but no random slopes, models with withinunit random slopes but no within-unit random intercepts, models with no random correlations (i.e., independent slopes and intercepts), and maximal models.

Model selection analyses

We also considered a wide variety of LMEMs whose random effects structure—specifically, which slopes to include—was determined through model selection. We also varied the model-selection α level, i.e., the level at which slopes were tested for inclusion or exclusion, taking on the values .01 and .05 as well as values from .10 to .80 in steps of .10.

Our model selection techniques tested only random slopes for inclusion/exclusion, leaving in by default the by-subject and by-item random intercepts (since that seems to be the general practice in the literature). For between-items designs, there was only one slope to be tested (by-subjects) and thus only one possible model selection algorithm. In contrast, for within-items designs, where there are two slopes to be tested, a large variety of algorithms are possible. We explored the model selection algorithms given in Table 4, which were defined by the direction of model selection (forward or backward) and whether slopes were tested in an arbitrary or principled sequence. The forward algorithms began with a random-intercepts-only model and tested the two possible slopes for inclusion in an arbitrary, pre-defined sequence (either by-subjects slope first and by-items slope second, or vice versa; these models are henceforth denoted by “FS” and “FI”). If the p-value from the first test exceeded the model-selection α level for inclusion, the slope was left out of the model and the second slope was never tested; otherwise, the slope was included and the second slope was tested. The backward algorithm (“BS” and “BI” models) was similar, except that it began with a maximal model and tested for the exclusion of slopes rather than for their inclusion.

Table 4.

Model selection algorithms for within-items designs.

Model	Direction	Order
FS	Forward	by-subjects slope then by-items
FI	Forward	by-items slope then by-subjects
FB	Forward	“best path” algorithm
BS	Backward	by-subjects slope then by-items
BI	Backward	by-items slope then by-subjects
BB	Backward	“best path” algorithm

For these same within-items designs, we also considered forward and backward algorithms in which the sequence of slope testing was principled rather than arbitrary; we call these the “best-path” algorithms because they choose each step through the model space based on which addition or removal of a predictor leads to the best next model. For the forward version, both slopes were tested for inclusion independently against a random-intercepts-only model. If neither test fell below the model-selection α level, then the random-intercepts-only model was retained. Otherwise, the slope with the strongest evidence for inclusion (lowest p-value) was included in the model, and then the second slope was tested for inclusion against this model. The backward best-path algorithm was the same, except that it began with a maximal model and tested slopes for exclusion rather than for inclusion. (In principle, one can use best-path algorithms that allow both forwards and backwards moves, but the space of possible models considered here is so small that such an algorithm would be indistinguishable from the forwards- or backwards-only variants.)

Handling nonconvergence and deriving p-values

Nonconverging LMEMs were dealt with by progressively simplifying the random effects structure until convergence was reached. Data from these simpler models contributed to the performance metrics for the more complex models. For example, in testing maximal models, if a particular model did not converge and was simplified down to a random-intercepts-only model, the p values from that model would contribute to the performance metrics for maximal models. This reflects the assumption that researchers who encountered nonconvergence would not just give up but would consider simpler models. In other words, we are evaluating analysis strategies rather than particular model structures.

In cases of nonconvergence, simplification of the random effects structure proceeded as follows. For between-items designs, the by-subjects random slope was dropped. For within-items designs, statistics from the partially converged model were inspected, and the slope associated with smaller variance was dropped (see the appendix for justification of this method). In the rare (0.002%) of cases that the random-intercepts-only model did not converge, the analysis was discarded.

There are various ways to obtain p-values from LMEMs, and to our knowledge, there is little agreement on which method to use. Therefore, we considered three methods currently in practice: (1) treating the t-statistic as if it were a z statistic (i.e., using the standard normal distribution as a reference); (2) performing likelihood ratio tests, in which the deviance (−2LL) of a model containing the fixed effect is compared to another model without it but that is otherwise identical in random effects structure; and (3) by Markov Chain Monte Carlo (MCMC) sampling, using the mcmcsamp() function of lme4 with 10000 iterations. This is the default number of iterations used in Baayen’s pvals .fnc() of the languageR package (Baayen, 2011). This function wraps the function mcmcsamp(), and we used some of its code for processing the output of mcmcsamp (). Although MCMC sampling is the approach recommended by Baayen et al. (2008), it is not implemented in lme4 for models containing random correlation parameters. We therefore used (3) only for random-intercept-only and no-random-correlation LMEMs.

Performance metrics

The main performance metrics we considered were Type I error rate (the rate of rejection of H₀ when it is true) and power (the rate of failure to reject H₀ when it is false). For all analyses, the α level for testing the fixed-effect slope (β₁) was set to .05 (results were also obtained using α = .01 and α = .10, and were qualitatively similar; see the online appendix).

It can be misleading to directly compare the power of various approaches that differ in Type I error rate, because the power of anticonservative approaches will be inflated. Therefore, we also calculated Power′, a power rate corrected for anticonservativity. Power′ was derived from the empirical distribution for p-values from the simulation for a given method where the null hypothesis was true. If the p-value at the 5% quantile of this distribution was below the targeted α-level (e.g., .05), then this lower value was used as the cutoff for rejecting the null. To illustrate, note that a method that is nominal (neither anticonservative nor conservative) would yield an empirical distribution of p-values for which very nearly 5% of the simulations would obtain p-values less than .05. Now consider that a given method with a targeted α-level of .05, 5% of the simulation runs under the null hypothesis yielded p-values of .0217 or lower. This clearly indicates that this method is anticonservative, since more than 5% of the simulation runs had p-values less than the targeted α-level of .05. We could correct for this anticonservativity in the power analysis by requiring that a p-value from a given simulation run, to be deemed statistically significant, must be less than .0217 instead of .05. In contrast, if for a given method 5% of the runs under the null hypothesis yielded a value of .0813 or lower, this method would be conservative, and it would be undesirable to ‘correct’ this as it would artifically make the test seem more powerful than it actually is. Instead, for this case we would simply require that the p-value for a given simulation run be lower than .05.

Because we made minimal assumptions about the relative magnitudes of random variances, it is also of interest to examine the performance of the various approaches as a function the various parameters that define the space. Given the difficulty of visualizing a multidimensional parameter space, we chose to visually represent performance metrics in terms of two “critical variances”, which were those variances that can drive differences between treatment means. As noted above, for between-item designs, this includes the by-item random intercept variance (ω₀₀²) and the by-subject random slope variance (τ₁₁²); for withinitems designs, this includes the by-item and by subject-random slope variance (ω₁₁² and τ₁₁²). We modeled Type I error rate and power over these critical variances using local polynomial regression fitting (the loess function in R which is wrapped by the loessPred function in our simgen package). The span parameter for loess fitting was set to .9; this highlights general trends throughout the parameter space, at the expense of fine-grained detail.

Results and Discussion

An ideal statistical analysis method maximizes statistical power while keeping Type I error nominal (at the stated α level). Performance metrics in terms of Type I error, power, and corrected power are given in Table 5 for the betweenitem design and in Table 6 for the within-item design. The analyses in each table are (approximately) ranked in terms of Type I error, with analyses toward the top of the table showing the best performance, with priority given to better performance on the larger (24-item) dataset.

Table 5.

Performance metrics for between-items design. Power′ = corrected power. Note that corrected power for random-intercepts-only MCMC is not included because the low number of MCMC runs (10000) combined with the high Type I error rate did not provide sufficient resolution.

	Type I		Power		Power′
Nitems	12	24	12	24	12	24
	Type I Error at or near α = .05
min-F′	.044	.045	.210	.328	.210	.328
LMEM, Maximal, χ2LR	.070	.058	.267	.364	.223	.342
LMEM, No Random Correlations, χ2LR*	.069	.057	.267	.363	.223	.343
LMEM, No Within-Unit Intercepts, χ2LR*	.081	.065	.288	.380	.223	.342
LMEM, Maximal, t	.086	.065	.300	.382	.222	.343
LMEM, No Random Correlations, t*	.086	.064	.300	.382	.223	.343
LMEM, No Within-Unit Intercepts, t*	.100	.073	.323	.401	.222	.342
F1×F2	.063	.077	.252	.403	.224	.337
	Type I Error far exceeding α = .05
LMEM, Random Intercepts Only, χ2LR	.102	.111	.319	.449	.216	.314
LMEM, Random Intercepts Only, t	.128	.124	.360	.472	.217	.314
LMEM, No Random Correlations, MCMC*	.172	.192	.426	.582
LMEM, Random Intercepts Only, MCMC	.173	.211	.428	.601
F1	.421	.339	.671	.706	.134	.212

^*Performance is sensitive to coding of the predictor (see appendix); simulations use deviation coding

Table 6.

Performance metrics for within-items design. Note that corrected power for random-intercepts-only MCMC is not included because the low number of MCMC runs (10000) combined with the high Type I error rate did not provide sufficient resolution.

	Type I		Power		Power′
Nitems	12	24	12	24	12	24
	Type I Error at or near α = .05
min-F′	.027	.031	.327	.512	.327	.512
LMEM, Maximal, χ2LR	.059	.056	.460	.610	.433	.591
LMEM, No Random Correlations, χ2LR*	.059	.056	.461	.610	.432	.593
LMEM, No Within-Unit Intercepts, χ2LR*	.056	.055	.437	.596	.416	.579
LMEM, Maximal, t	.072	.063	.496	.629	.434	.592
LMEM, No Random Correlations, t*	.072	.062	.497	.629	.432	.593
LMEM, No Within-Unit Intercepts, t*	.070	.064	.477	.620	.416	.580
F1×F2	.057	.072	.440	.643	.416	.578
	Type I Error exceeding α = .05
F1	.176	.139	.640	.724	.345	.506
LMEM, No Random Correlations, MCMC*	.187	.198	.682	.812
LMEM, Random Intercepts Only, MCMC	.415	.483	.844	.933
LMEM, Random Intercepts Only, χ2LR	.440	.498	.853	.935	.379	.531
LMEM, Random Intercepts Only, t	.441	.499	.854	.935	.379	.531

^*Performance is sensitive to coding of the predictor (see appendix); simulations use deviation coding

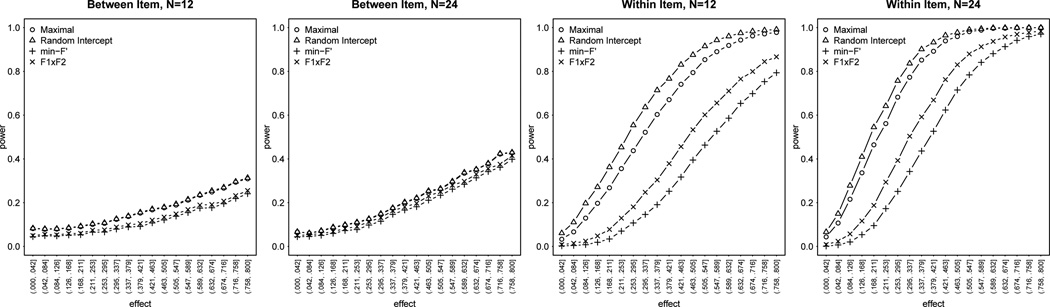
Only min-F′ was consistently at or below the stated α level. This is not entirely surprising, because the techniques that are available for deriving p-values from LMEMs are known to be somewhat anticonservative (Baayen et al., 2008). For maximal LMEMs, this anticonservativity was quite minor, within 1–2% of α.⁸ LMEMs with maximal random slopes, but missing either random correlations or within-unit random intercepts, performed nearly as well as “fully” maximal LMEMs, with the exception of the case where p-values were determined by MCMC sampling. In addition, there was slight additional anticonservativity relative to the maximal model for the models missing within-unit random intercepts. This suggests that when maximal LMEMs fail to converge, dropping within-unit random intercepts or random correlations are both viable options for simplifying the random effects structure. It is also worth noting that F₁ × F₂, which is known to be fundamentally biased (Clark, 1973; Forster & Dickinson, 1976), controlled overall Type I error rate fairly well, almost as well as maximal LMEMs. However, whereas anticonservativity for maximal (and near-maximal) LMEMs decreased as the data set got larger (from 12 to 24 items), for F₁ × F₂ it actually showed a slight increase.

F₁ alone was the worst performing method for between-items designs, and also had an unacceptably high error rate for within-items designs. Random-intercepts-only LMEMs were also unacceptably anticonservative for both types of designs, far worse than F₁ × F₂. In fact, for within-items designs, random-intercepts-only LMEMs were even worse than F₁ alone, showing false rejections 40–50% of the time at the .05 level, regardless of whether p-values were derived using the normal approximation to the t-statistic, the likelihood-ratio test, or MCMC sampling. In other words, for within-items designs, one can obtain better generalization by ignoring item variance altogether (F₁) than by using an LMEM with only random intercepts for subjects and items.

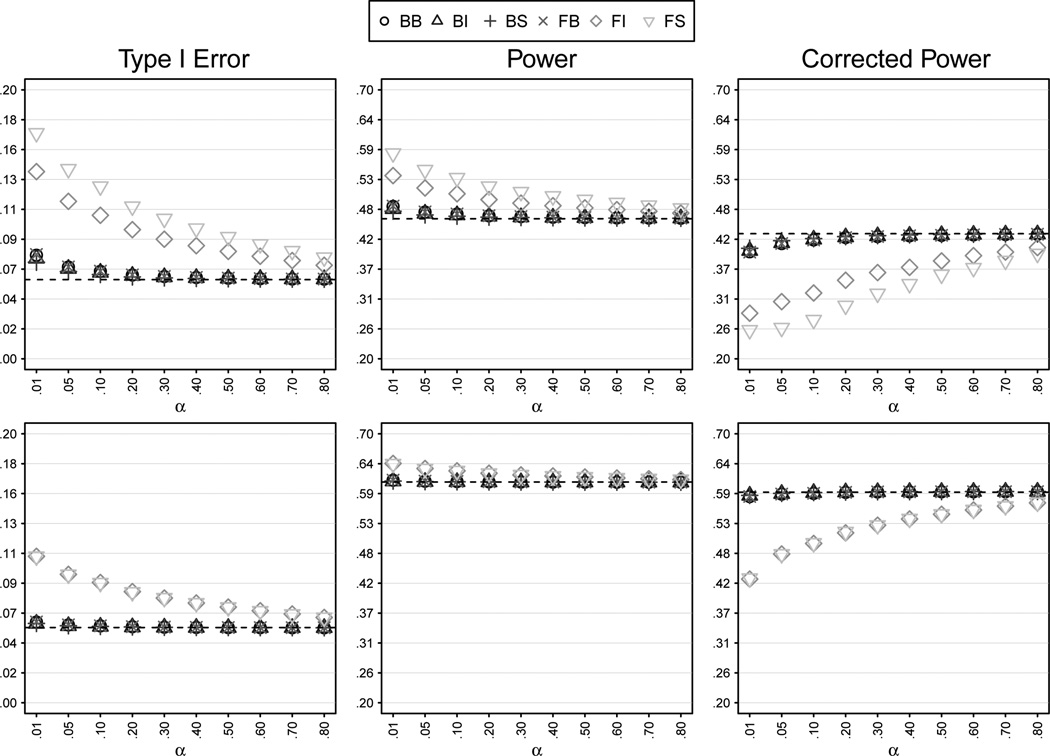
Figure 2 presents results from LMEMs where the inclusion of random slopes was determined by model selection. The figure presents the results for the within-items design, where a variety of algorithms were possible. Performance for the between-items design (where there was only a single slope to be tested) was very close to that of maximal LMEMs, and is presented in the online Appendix.

Figure 2.

Performance of model selection approaches for within-items designs, as a function of selection algorithm and α level for testing slopes. The p-values for all LMEMs in the figure are from likelihood-ratio tests. Top row: 12 items; bottom row: 24 items. BB = Backwards, “best path”; BI = Backwards, Item-Slope First; BS = Backwards, Subject-Slope First; FB = Forwards, “best path”; FI = Forwards, Item-Slope First; FS = Forwards, Subject-Slope First.

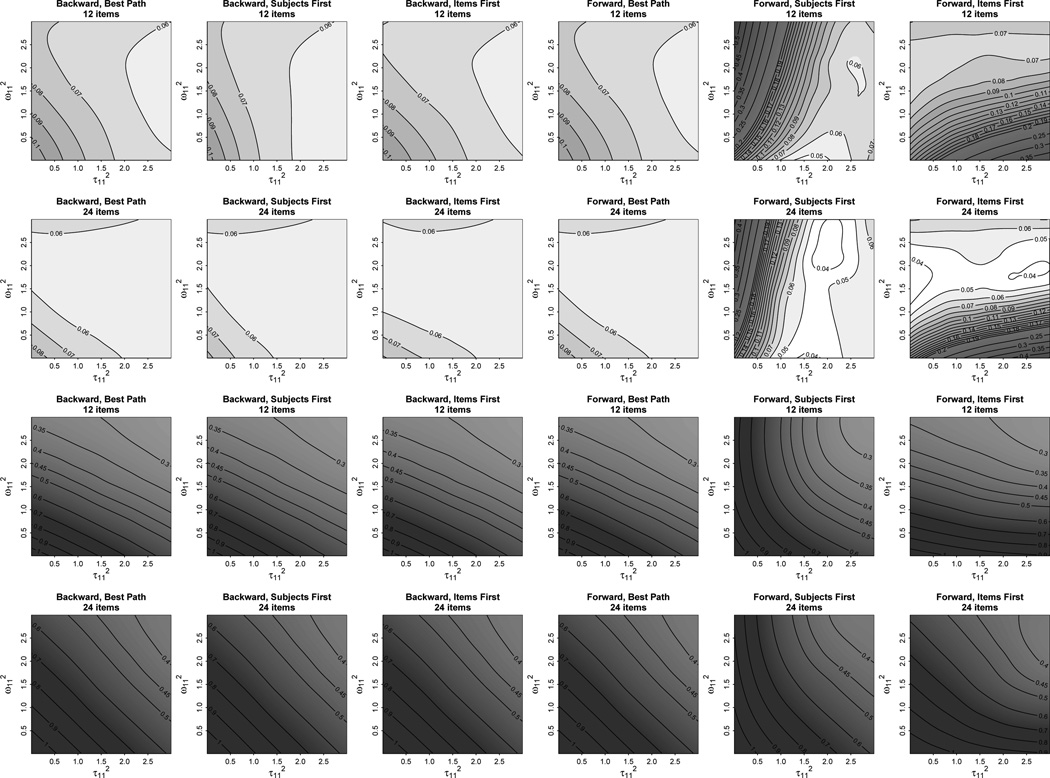
The figure suggests that the Type I error rate depends more upon the algorithm followed in testing slopes than the α-level used for the tests. Forward-stepping approaches that tested the two random slopes in an arbitrary sequence performed poorly in terms of Type I error even at relatively high α levels. This was especially the case for the smaller, 12-item sets, where there was less power to detect by-item random slope variance. In contrast, performance was relatively sound for backward models even at relatively low α levels, as well as for the “best path” models regardless of whether the direction was backward or forward. It is notable that these sounder data-driven approaches showed only small gains in power over maximal models (indicated by the dashed line in the background of the figure).

From the point of view of overall Type I error rate, we can rank the analyses for both within- and between-items designs in order of desirability:

1. min-F′, maximal LMEMs, “near-maximal” LMEMs missing within-unit random intercepts or random correlations, and model selection LMEMs using backward selection and/or testing slopes using the “best path” algorithm;

2. F₁ × F₂;

3. forward-stepping LMEMs that test slopes in an arbitrary sequence;

4. F₁ and random-intercepts-only LMEMs.

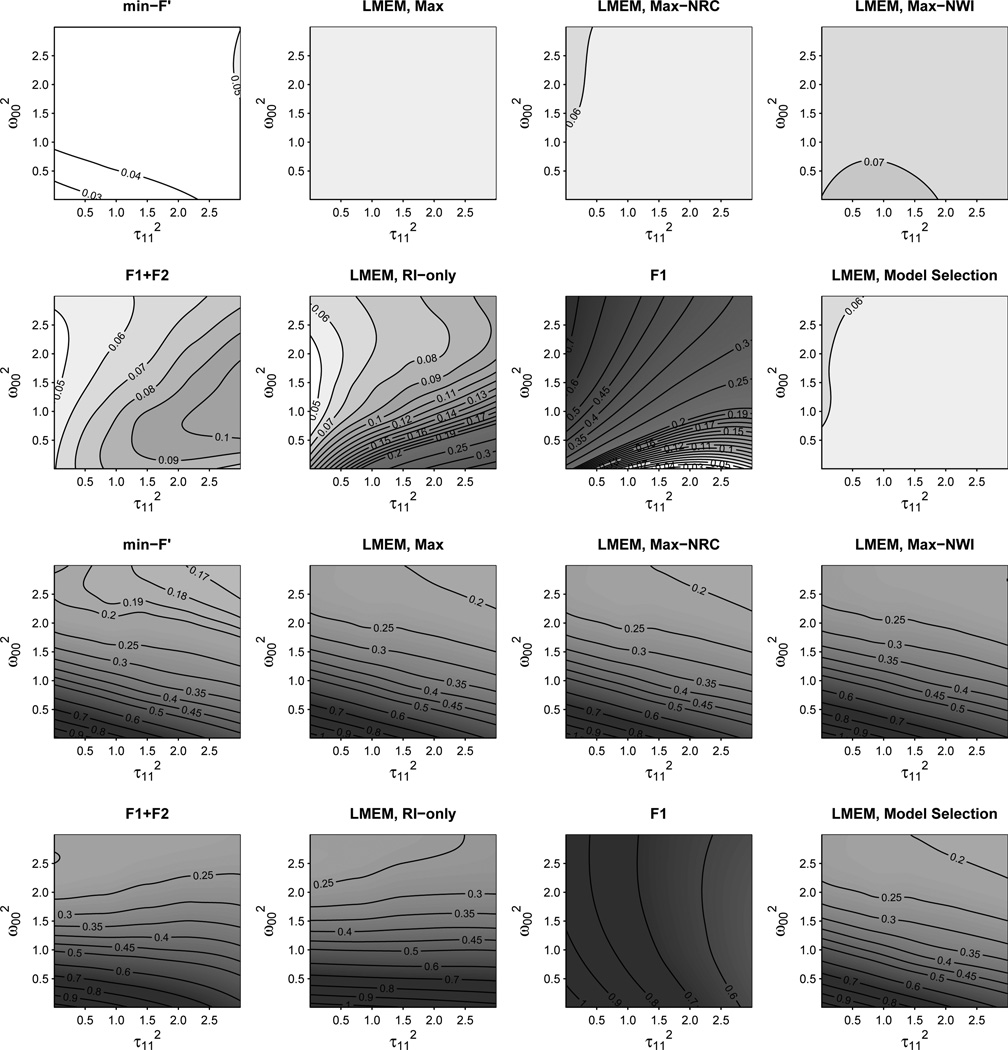
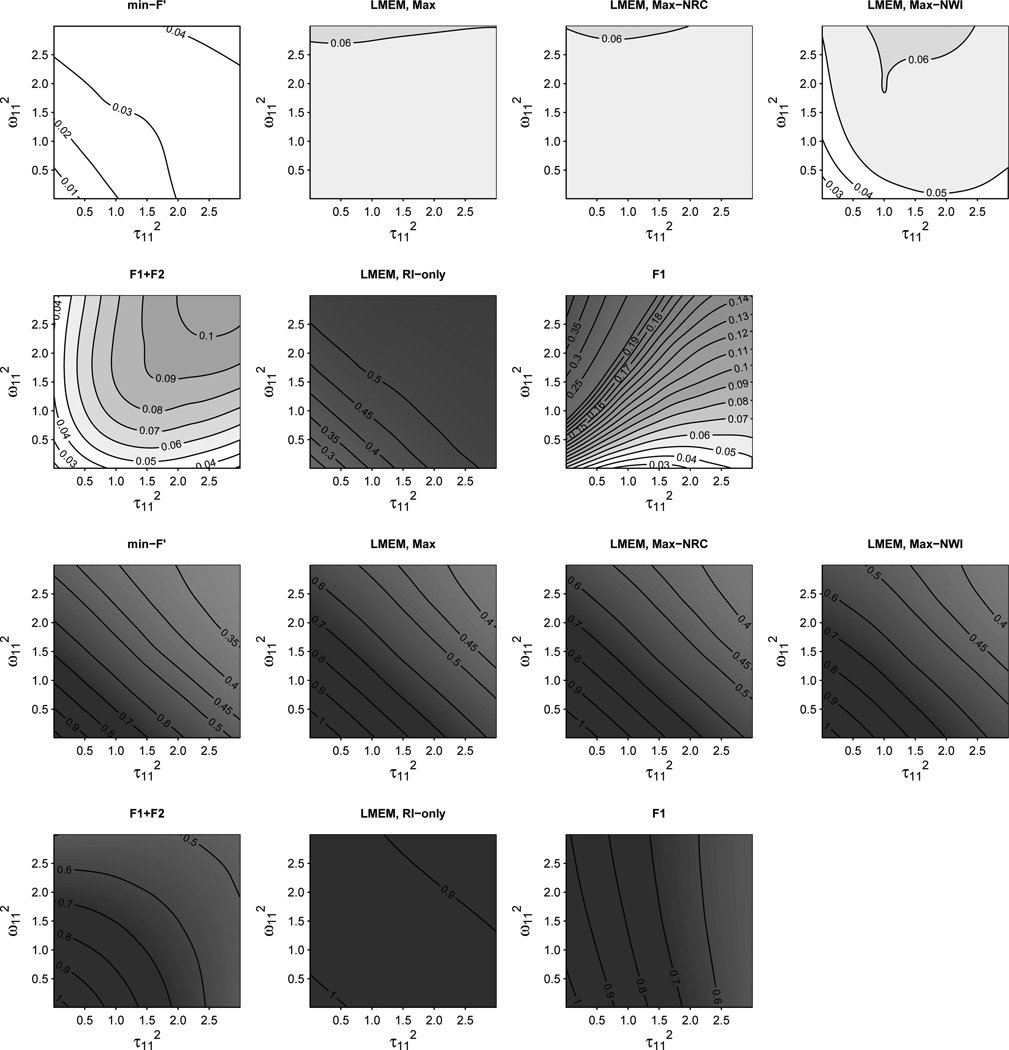
It would also seem natural to draw a line separating analyses that have an “acceptable” rate of false rejections (i.e., 1–2) from those with a rate that is intolerably high (i.e., 3–4). However, it is insufficient to consider only the overall Type I error rate, as there may be particular problem areas of the parameter space where even the best analyses perform poorly (such as when particular variance components are very small or large). If these areas are small, they will only moderately affect the overall error rate. This is a problem because we do not know where the actual populations that we study reside in this parameter space; it could be that they inhabit these problem areas. It is therefore also useful to examine the performance metrics as a function of the critical random variance parameters that are confounded with the treatment effect, i.e., τ ₁₁² and ω₀₀ ² for betweenitems designs and τ₁₁² and ω₁₁² for within-items designs. These are given in the “heatmap” displays of Figures 3–5.

Figure 3.

Type I error (top two rows) and Power (bottom two rows) for between-items design with 24 items, as a function of by-subject random slope variance τ₁₁² and by-item random intercept variance ω₀₀². The p-values for all LMEMs in the figure are from likelihood-ratio tests. All model selection approaches in the figure had α = .05 for slope inclusion. The heatmaps from the 12-item datasets show similar patterns, and are presented in the appendix.

Figure 5.

Type I error (top two rows) and power (bottom two rows) for design-driven approaches on within-items data, as a function of by-subject random slope variance τ₁₁² and by-item random slope variance ω₁₁² The p-values for all LMEMs in the figure are from likelihood-ratio tests. All approaches in the figure tested random slopes at α = .05.

Viewing Type I error rate as a function of the critical variances, it can be seen that of models with predetermined random effects structures, only min-F′ maintained the Type I error rate consistently below the α-level throughout the parameter space (Figure 3 and 4). Min-F′ became increasingly conservative as the relevant random effects got small, replicating Forster & Dickinson (1976). Maximal LMEMs showed no such increasing conservativity, performing well overall, especially for 24-item datasets. The near-maximal LMEMs also performed relatively well, though for within-item datasets, models missing withinunit intercepts became increasingly conservative as slope variances got small. Random-intercepts-only LMEMs degraded extremely rapidly as a function of random slope parameters; even at very low levels of random-slope variability, the Type I error rate was unacceptably high.

Figure 4.

Type I error (top three rows) and power (bottom three rows) for within-items design with 24 items, as a function of by-subject random slope variance τ₁₁² and by-item random slope variance ω₁₁² The p-values for all LMEMs in the figure are from likelihood-ratio tests. All model selection approaches in the figure had α = .05 for slope inclusion. The heatmaps from the 12-item datasets show similar patterns, and are presented in the online appendix.

In terms of Type I error, the average performance of the widely adopted F₁ × F₂ approach is comparable to that of maximal LMEMs (slightly less anticonservative for 12 items, slightly more anti-conservative for 24 items). But in spite of this apparent good performance, the heatmap visualization indicates that the approach is fundamentally unsound. Specifically, F₁ × F₂ shows both conservative and anticonservative tendencies: as slopes get small, it becomes increasingly conservative, similar to min-F′; as slopes get large, it becomes increasingly anticonservative, similar to random-intercepts-only LMEMs, though to a lesser degree. This increasing anticonservativity reflects the fact that (as noted in the introduction) subject random slopes are not accounted for in the F₂ analysis, nor are item random slopes accounted for in the F₁ analysis (Clark, 1973). The fact that both F₁ and F₂ analyses have to pass muster keeps this anti-conservativity relatively minimal as long as subject and/or item slope variances are not large, but the anti-conservativity is there nonetheless.

Figure 5 indicates that despite the overall good performance of some of the data-driven approaches, these models become anticonservative when critical variances are small and nonzero.⁹ This is because as slope variances become small, slopes are less likely to be kept in the model. This anticonservativity varies considerably with the size of the dataset and the algorithm used (and of course should also vary with the α-level, not depicted in the figure). The anticonservativity is present to a much stronger degree for the 12-item than for the 24-item datasets, reflecting the fact that the critical variances are harder to detect with smaller data sets. The forward stepping models that tested slopes in an arbitrary sequence were the most anticonservative by far. The model testing the by-subject slope first performed most poorly when that slope variance was small and the by-item slope variance was large, because in such cases the algorithm would be likely to stop at a random-intercepts-only model, and thus would never test for the inclusion of the by-item slope. By the same principles, the forward model that tested the by-item slope first showed worst performance when the by-item slope variance was small and the by-subject slope variance large.

In sum, insofar as one is concerned about drawing conclusions likely to generalize across subjects and items, only min-F′ and maximal LMEMs can be said to be fundamentally sound across the full parameter space that we surveyed. F₁-only and random-intercepts-only LMEMs are fundamentally flawed, as are forward stepping models that follow an arbitrary sequence, especially in cases with few observations. All other LMEMs with model selection showed small amounts of anticonservativity when slopes were small, even when the slopes were tested in a principled sequence; however, this level of anticonservativity is probably tolerable for reasonably-sized datasets (so long as there is not an extensive amount of missing data; see online appendix). The widely-used F₁ × F₂ approach is flawed as well, but may be acceptable in cases where maximal LMEMs are not applicable. The question now is which of these analyses best maximizes power (Tables 5 and 6; Figures 3 and 4).

Overall, maximal LMEMs showed greater power than min-F′. When corrected for their slight anticonservativity, maximal LMEMs exhibited power that was between 4% and 6% higher for the between-items design than the uncorrected values for min-F′. Although there does not seem to be a large overall power advantage to using maximal LMEMs for between-item designs, the visualization of power in terms of the critical variances (Figure 3) suggests that the power advantage increases slightly as the critical variances become small. In contrast, maximal LMEMs showed a considerable power advantage for withinitem designs, with corrected power levels for α=.05 (.433 and .592) that were 16% to 32% higher than the uncorrected power values for min-F′ (.327 and .512). This additional power of maximal LMEMs cannot be attributed to the inclusion of cases where slopes were removed due to nonconvergence, since in the worst case (the within-item dataset with 12 items) virtually all simulation runs (99.613%) converged with the maximal structure.

Note that the corrected power for random-intercepts-only LMEMs was actually below that of maximal LMEMs (between-items: .216 and .314 for 12 and 24 items respectively; within-items: .380 and .531). This means that most of the apparent additional power of maximal LMEMs over min-F′ is real, while most of the apparent power of random-intercepts-only LMEMs is, in fact, illusory.

Our results show that it is possible to use a data-driven approach to specifying random effects in a way that minimizes Type I error, especially with “best-path” model selection. However, the power advantage of this approach for continuous data, even when uncorrected for anticonservativity, is very small. In short, datadriven approaches can produce reasonable results, but their very small benefit to power may not be worth the additional uncertainty they introduce as compared to a design-driven approach.

The above analyses suggest that maximal LMEMs are in no way conservative, at least for the analysis of continuous data. To dispel this suspicion entirely it is illustrative to consider the performance of maximal LMEMs in an extreme case for which their power should be at its absolute worst: namely, when the random slope variance is negligible, such that the underlying process is best described by a random-intercepts-only LMEM. Comparing the performance of maximal LMEMs to random-intercepts-only LMEMs in this circumstance can illustrate the highest “cost” that one could possibly incur by using maximal LMEMs in the analysis of continuous data. Maximal LMEMs might perform badly in this situation because they overfit the underlying generative process, loosely akin to assuming too few degrees of freedom for the analysis rather than too many. But they might also perform tolerably well to the extent that the estimation procedure for LMEMs can detect that a random effect parameter is effectively zero. In this situation, it is additionally informative to compare the power of maximal LMEMs not only to random-intercepts-only LMEMs, but also to that of min-F′, since min-F′ is generally regarded as conservative, as well as to that of F₁ × F₂, since F₁ × F₂ is generally regarded as sufficiently powerful. If maximal LMEMs perform better than min-F′ and at least as well as F₁ × F₂, then that would strongly argue against the idea that maximal LMEMs are unduly conservative. To address this, we conducted an additional set of simulations, once again using the data-generating parameters in Table 2, except that we set all random-slope variances to 0, so that the model generating the data was a random-intercepts-only LMEM; also, we varied the true fixed effect size continuously from 0 to 0.8.

The results were unambiguous (Figure 6): even in this worst case scenario for their power, maximal LMEMs consistently showed higher power than min-F′ and even F₁ × F₂; indeed, for within-items designs, they far outstripped the performance of F₁ × F₂, an approach whose power is rarely questioned. For between-items designs, maximal LMEMs incurred a negligible cost relative to random-intercepts-only LMEMs, while for within-items designs, there was only a minor cost that diminished as the number of items increased. Overall, the cost/benefit analysis favors maximal LMEMs over other approaches. Note that over the four different sets of simulations in Figure 6, our maximal LMEM analysis procedure stepped down to a random-intercept model (due to convergence problems) on less than 3% of runs. Thus, these results indicate good performance of the estimation algorithm when random slope variances are zero.

Figure 6.

Statistical power for maximal LMEMs, random-intercepts-only LMEMs, min-F′, and F₁ × F₂ as a function of effect size, when the generative model underlying the data is a random-intercepts-only LMEM.

The case of within-item designs with few items showed the biggest difference in power between random-intercepts-only models and maximal LMEMs. The size of this difference indicates the maximum benefit that could be obtained, in principle, by using a data-driven approach. However, in practice, the ability of a data-driven approach to detect random slope variation diminishes as the dataset gets small. In other words, it is in just this situation that the power for detecting random slope variation is at its worst (see Figure 4 and the 12-item figures in the Appendix); thus, in this case, the payoff in terms of statistical power over the maximal approach does not outweigh the additional risk of anticonservativity.

In sum, our investigation suggests that for confirmatory hypothesis testing, maximal LMEMs yield nearly optimal performance: they were better than all other approaches except min-F′ at maintaining the Type I error rate near the nominal level. Furthermore, unlike F₁ × F₂ and certain model selection approaches, maximal LMEMs held the error rate relatively close to nominal across the entirety of the parameter space. And once corrected for anticonservativity, no other technique exceeded the power of maximal LMEMs. “best-path” model selection also kept Type I errors largely at bay, but it is not clear whether they lead to gains in statistical power.

The near-optimal performance of maximal models may be explained as follows. Including the random variances that could potentially be confounded with the effect of interest is critical to controlling the Type I error rate, by ensuring that the assumption of conditional independence is met. Including random variances that are not confounded with that effect (e.g., within-unit intercept variances) is not critical for reducing Type I error, but nonetheless reduces noise and thus increases the sensitivity of the test. Including only those random components that reduce noise but not those that are confounded with the effect of interest will lead to drastically anticonservative behavior, as seen by random-intercepts-only LMEMs, which had the worst Type I error rates overall.

General Discussion

Recent years have witnessed a surge in the popularity of LMEMs in psycholinguistics and related fields, and this growing excitement is well deserved, given the great flexibility of LMEMs and their ability to model the generative process underlying one’s data. However, there has been insufficient appreciation of how choices about random effect structure impact generalizability, and no accepted standards for the use of LMEMs in confirmatory hypothesis testing are currently in place. We have emphasized that specifying random effects in LMEMs involves essentially the same principles as selecting an analysis technique from the menu of traditional ANOVA-based options. The standard for ANOVA has been to assume that if an effect exists, subjects and/or items will vary in the extent to which they show that effect. This is evident in the fact that researchers using ANOVA have tended to assume the maximal (or near-maximal) random effects structure justified by the design.

Our survey of various analysis strategies for confirmatory hypothesis testing on data with crossed random effects clearly demonstrates that the strongest contenders in avoiding anti-conservativity are maximal LMEMs and min-F′ (see below for related discussion of data-driven approaches). These were the only approaches that consistently showed nominal or near-nominal Type I error rates throughout the parameter space. Although maximal LMEMs showed some minor anticonservativity, our analysis has uncovered a hidden advantage of maximal LMEMs over ANOVA-based approaches. This advantage was evident in the diverging performance of these approaches as a function of the critical variances (the variances confounded with the effect of interest). As these variances became small, maximal LMEMs showed better retention of their power relative to ANOVA-based approaches, which became increasingly conservative. In the limit, when the generative process did not include any random slope variation, the power of maximal LMEMs substantially outstripped that of ANOVA-based approaches, even F₁ × F₂. An apparent reason for this power advantage of maximal LMEMs is their simultaneous accommodation of by-subject and by-item random variation. ANOVA-based approaches are based on two separately calculated statistics, one for subjects and one for items, each of which does not control for the variance due to the other random factor. Specifically, the prominent decrease in power for ANOVA-based approaches when critical random variances are small could be due to the fact that separate F₁ × F₂ analyses cannot distinguish between random intercept variation on the one hand and residual noise on the other: by-item random intercept variation is conflated with trial-level noise in the F₁ analysis, and by-subject random intercept variation is conflated with trial-level noise in the F₂ analysis. Maximal LMEMs do not suffer from this problem.

The performance of LMEMs depended strongly on assumptions about random effects. This clearly implies that researchers who wish to use LMEMs need to be more attentive both to how they specify random effects in their models, and to the reporting of their modeling efforts. Throughout this article, we have argued that for confirmatory analyses, a design-driven approach is preferable to a datadriven approach for specifying random effects. By using a maximal model, one adheres to the longstanding (and eminently reasonable) assumption that if an effect exists, subjects and/or items will most likely vary in the extent to which they show that effect, whether or not that variation is actually detectable in the sample. That being said, it seems likely that effect variation across subjects and/or items differs among research areas. Perhaps there are even effects for which such variation is effectively negligible. In such cases, one might argue that a maximal LMEM is “overfitting” the data, which is detrimental to power. However, our simulations (Figure 6) show that maximal LMEMs would not be unreasonably conservative in such cases, at least for continuous data; indeed, they are far more powerful than even F₁ × F₂.

Many researchers have used a data-driven approach to determining the random effects structure associated with confirmatory analysis of a fixed effect of particular interest.¹⁰ Our simulations indicate that it is possible to obtain reasonable results with such an approach, if generous criteria for the inclusion of random effects are used. However, it is important to bear in mind that data-driven approaches always imply some sort of tradeoff between Type-I and Type-II error probability, and that it is difficult to precisely quantify the tradeoff that one has taken. It is partly for this reason that the use of data-driven approaches is controversial, even among statistical experts (Bolker et al., 2009; see also Harrell, 2001 for more general concerns regarding model selection). Our results show that data-driven approaches yield varying performance in terms of Type I error depending on the criteria and algorithm used, the size of the dataset, the extent of missing data, and the design of the study (which determines the number of random effect terms that need to be tested). It may be difficult for a reader lacking access to the original data to to quantify the resulting Type I/II error tradeoff, even when the inclusion criteria are known. Still, there are situations in which data-driven approaches may be justifiable, such as when the aims are not fully confirmatory, or when one experiences severe convergence problems (see below).

Overall, our analysis suggests that, when specifying random effects for hypothesis testing with LMEMs, researchers have been far too concerned about overfitting the data, and not concerned enough about underfitting the design. In fact, it turns out overfitting the data with a maximal model has only minimal consequences for Type I error and power—at least for the simple designs for typical psycholinguistic datasets considered here—whereas underfitting the design can incur levels of anticonservativity ranging anywhere from minor (best-path model selection) to extremely severe (random-intercepts-only LMEMs) with little real benefit to power. In the extreme, random-intercepts-only models have the worst generalization performance of any approach to date when applied to continuous data with within-subjects and within-item manipulations. This goes to show that, for such designs, crossing of random by-subject and by-item intercepts alone is clearly not enough to ensure proper generalization of experimental treatment effects (a misconception that is unfortunately rather common at present). In psycholinguistics, there are few circumstances in which we can know a priori that a random-intercepts-only model is truly justified (see further below). Of course, if one wishes to emphasize the absence of evidence for a given effect, there could be some value in demonstrating that the effect is statistically insignificant even when a random-intercepts-only model is applied.

Our general argument applies in principle to the analysis of non-normally distributed data (e.g., categorical or count data) because observational dependencies are mostly determined by the design of an experiment and not by the particular type of data being analyzed. However, practical experience with fitting LMEMs to datasets with categorical response variables, in particular with mixed logit models, suggests more difficulty in getting maximal models to converge. There are at least three reasons for this. First, the estimation algorithms for categorical responses differ from the more developed procedures in estimating continuous data. Second, observations on a categorical scale (e.g., whether a response is accurate or inaccurate) typically carry less information about parameters of interest than observations on a continuous scale (e.g., response time). Third, parameter estimation for any logistic model is challenging when the underlying probabilities are close to the boundaries (zero or one), since the inverse logit function is rather flat in this region. So although our arguments and recommendations (given below) still apply in principle, they might need to be modified for noncontinuous cases. For example, whereas we observed for continuous data that cases in which the random effect structure “overfit” the data had minimal impact on performance, this might not be the case for categorical data, and perhaps data-driven strategies would be more justifiable. In short, although we maintain that design-driven principles should govern confirmatory hypothesis testing on any kind of data, we acknowledge that there is a pressing need to evaluate how these principles can be best applied to categorical data.

In our investigation we have only looked at a very simple one-factor design with two levels. However, we see no reason why our results would not generalize to more complex designs. The principles are the same in higher-order designs as they are for simple one-factor designs: any main effect or interaction for which there are multiple observations per subject or item can vary across these units, and, if this dependency is not taken into account, the p-values will be biased against the null hypothesis.¹¹ The main difference is that models with maximal random effects structure would be less likely to converge as the number of within-unit manipulations increases. In the next section, we offer some guidelines for how to cope with nonconverging models.

Producing generalizable results with LMEMs: Best practices

Our theoretical analyses and simulations lead us to the following set of recommended “best practices” for the use of LMEMs in confirmatory hypothesis testing. It is important to be clear that our recommendations may not apply to situations where the overarching goal is not fully confirmatory. Furthermore, we offer these not as the best possible practices—as our understanding of these models is still evolving—but as the best given our current level of understanding.

Identifying the maximal random effects structure

Because the same principles apply for specifying subject and item random effects, to simplify the exposition in this section we will only talk about “by-unit” random effects, where “unit” stands in for the sampling unit under consideration (subjects or items). As we have emphasized throughout this paper, the same considerations come into play when specifying random effects as when choosing from the menu of traditional analyses. So the first question to ask oneself when trying to specify a maximal LMEM is: which factors are within-unit, and which are between? If a factor is between-unit, then a random intercept is usually sufficient. If a factor is within-unit and there are multiple observations per treatment level per unit, then you need a by-unit random slope for that factor. The only exception to this rule is when you only have a single observation for every treatment level of every unit; in this case, the random slope variance would be completely confounded with trial-level error. It follows that a model with a random slope would be unidentifiable, and so a random intercept would be sufficient to meet the conditional independence assumption. For datasets that are unbalanced across the levels of a within-unit factor, such that some units have very few observations or even none at all at certain levels of the factor, one should at least try to estimate a random slope (but see the caveats below about how such a situation may contribute to nonconvergence). Finally, in cases where there is only a single observation for every unit, of course, not even a random intercept is needed (one can just use ordinary regression as implemented in the R functions 1m() and g1m()).

The same principles apply to higher-order designs involving interactions. In most cases, one should also have by-unit random slopes for any interactions where all factors comprising the interaction are within-unit; if any one factor involved in the interaction is between-unit, then the random slope associated with that interaction cannot be estimated, and is not needed. The exception to this rule, again, is when you have only one observation for every subject in every cell (i.e., unique combination of factor levels). If some of the cells for some of your subjects have only one or zero observations, you should still try to fit a random slope.

Random effects for control predictors

One of the most compelling aspects of mixed-effects models is the ability to include almost any control predictor—by which we mean a property of an experimental trial which may affect the response variable but is not of theoretical interest in a given analysis—desired by the researcher. In principle, including control variables in an analysis can rule out potential confounds and increase statistical power by reducing residual noise. Given the investigations in the present paper, however, the question naturally arises: in order to guard against anti-conservative inference about a predictor X of theoretical interest, do we need by-subject and by-item random effects for all our control predictors C as well? Suppose, after all, if there is no underlying fixed effect of C but there is a random effect of C—could this create anti-conservative inference in the same way as omitting a random effect of X in the analysis could? To put this issue in perspective via an example, Kuperman et al. (2010) include a total of eight main effects in an LME analysis of fixation durations in Dutch reading; for the interpretation of each main effect, the other seven may be thought of as serving as controls. Fitting eight random effects, plus correlation terms, would require estimating 72 random effects parameters, 36 by-subject and 36 by item. One would likely need a huge dataset to be able to estimate all the effects reliably (and one must also not be in any hurry to publish, for even with huge amounts of data such models can take extremely long to converge).

To our knowledge, there is little guidance on this issue in the existing literature, and more thorough research is needed. Based on a limited amount of informal simulation, however (reported in the online Appendix), we propose the working assumption that it is not essential for one to specify random effects for control predictors to avoid anticonservative inference, as long as interactions between the control predictors and the the factors of interest are not present in the model (or justified by the data). Once again, we emphasize the need for future research on this important issue.

Coping with failures to converge

It is altogether possible and unfortunately common that the estimation procedure for LMEMs will not converge with the full random-effects specification. In our experience, the likelihood that a model will converge depends on two factors: (1) the extent to which random effects in the model are large, and (2) the extent to which there are sufficient observations to estimate the random effects. Generally, as the sizes of the subject and item samples grow, the likelihood of convergence will increase. Of course, one does not always have the luxury of using many subjects and items. And, although the issue seems not to have been studied systematically, it is our impression that fitting maximal LMEMs is less often successful for categorical data than for continuous data.

It is important, however, to resist the temptation to step back to randomintercepts-only models purely on the grounds that the maximal model does not converge. When the maximal LMEM does not converge, the first step should be to check for possible misspecifications or data problems that might account for the error. It may also help to use standard outlier removal methods and to center or sum-code the predictors. In addition, it may sometimes be effective to increase the maximum number of iterations in the estimation procedure.

Once data and model specification problems have been eliminated, the next step is to ask what simplification of one’s model’s random-effects structure is the most defensible given the goals of one’s analysis. In the common case where one is interested in a minimally anti-conservative evaluation of the strength of evidence for the presence of an effect, our results indicate that keeping the random slope for the predictor of theoretical interest is important: a maximal model with no random correlations or even missing within-unit random intercepts is preferable to one missing the critical random slopes. Our simulations suggest that removing random correlations might be a good strategy, as this model performed similarly to maximal LMEMs.¹²

However, when considering this simplification strategy, it is important to first check whether the nonconvergence might be attributable to the presence of a few subjects (or items) with small numbers of observations in particular cells. If this is the case, it might be preferable to remove (or replace) these few subjects (or items) rather than to remove an important random slope from the model. For example, Jaeger et al. (2011, section 3.3) discuss a case involving categorical data in which strong evidence for random slope variation was present when subjects with few observations were excluded, but not when they were kept in the data set.

For more complex designs, of course, the number of possible random-effects structures proliferate. Research is needed to evaluate the various possible strategies that one could follow when one cannot fit a maximal model. Both our theoretical analysis and simulations suggest a general rule of thumb: for whatever fixed effects are of critical interest, the corresponding random effects should be present in that analysis. For a study with multiple fixed effects of theoretical interest, and for which a model including random effects for all these key effects does not converge, separate analyses can be pursued. For example, in a study where confirmatory analysis of fixed effects for X₁ and X₂ is desired, two separate analyses may be in order—one with (at least) random slopes for X₁ to test the evidence for generalization of X₁, and another with (at least) random slopes for X₂ to test X₂. (One would typically still want to include the fixed effects for X₁ and X₂ in both models, of course, for the established reason that multiple regression reveals more information than two separate regressions with single predictors; and see also the previous section on random effects for control predictors.)

One fallback strategy for coping with severe convergence problems is to use a data-driven approach, building up in a principled way from a very simple model (e.g., a model with all fixed effects but only a single by-subjects random intercept, or even no random effects at all). Our simulations indicate that it is possible to use forward model selection in a way that guards against anticonservativity if, at each step, one tests for potential inclusion all random effects not currently in the model, and include any that pass at a relatively liberal α-level (e.g., .20; see Method section for further details about the “best path” algorithm). We warn the reader that, with more complex designs, the space of possible random-effects specifications is far richer than typically appreciated, and it is easy to design a model-selection procedure that fails to get to the best model. As just one example, in a “within” 2 × 2 design with factors A and B, it is possible to have a model with a random interaction term but no random main-effect slopes. If one is interested in the fixed-effect interaction but only tests for a random interaction if both main-effect random slopes are already in the model, then if the true generative process underlying the data has a large random interaction but negligible random main-effect slopes then forward model selection will be badly anti-conservative. Thus it is critical to report the modeling strategy in detail so that it can be properly evaluated.

A final recommendation is based on the fact that maximal LMEMs will be more likely to converge when the random effects are large, which is exactly the situation where F₁ × F₂ is anti-conservative. This points toward a possible practice of trying to fit a maximal LMEM wherever possible, and when it is not, to drop the concept of crossed random effects altogether and perform separate by-subject and by-item LMEMs, similar in logic to F₁ × F₂, each with appropriate maximal random effect structures. In closing, it remains unresolved which of these strategies for dealing with nonconvergence is ultimately most beneficial, and we hope that future studies will investigate their impact on generalizability more systematically.

Computing p-values

There are a number of ways to compute p-values from LMEMs, none of which is uncontroversially the best. Although Baayen et al. (2008) recommended using Monte Carlo Markov Chain (MCMC) simulation, this is not yet possible in lme4 for models with correlation parameters, and our simulations indicate that this method for obtaining p-values is more anticonservative than the other two methods we examined (at least using the current implementation and defaults for MCMC sampling in lme4 and languageR).¹³ Also, it is important to note that MCMC sampling does nothing to mitigate the anticonservativity of random-intercept-only LMEMs when random slope variation is present.

For obtaining p-values from analyses of typically-sized psycholinguistic datasets—where the number of observations usually far outnumbers the number of model parameters—our simulations suggest that the likelihood-ratio test is the best approach. To perform such a test, one compares a model containing the fixed effect of interest to a model that is identical in all respects except the fixed effect in question. One should not also remove any random effects associated with the fixed effect when making the comparison. In other words, likelihood-ratio tests of a fixed effect with k levels should have only k − 1 degrees of freedom (e.g., one degree of freedom for the dichotomous single-factor studies in our simulations). We have seen cases where removing the fixed effect causes the comparison model to fail to converge. Under these circumstances, one might alter the comparison model following the procedures described above to attempt to get it to converge, and once convergence is achieved, compare it to an identical model including the fixed effect. Note that our results indicate that the concern voiced by Pinheiro & Bates (2000) regarding the anti-conservativity of likelihood-ratio tests to assess fixed effects in LMEMs is probably not applicable to datasets of the typical size of a psycholinguistic study (see also Baayen et al., 2008, footnote 1).

Reporting results

It is not only important for researchers to understand the importance of using maximal LMEMs, but also for them to articulate their modeling efforts with sufficient detail so that other researchers can understand and replicate the analysis. In our informal survey of papers published in JML, we sometimes found nothing more than a mere statement that researchers used “a mixed effects model with random effects for subjects and items.” This could be anything from a randomintercepts-only to a maximal LMEM, and obviously, there is not enough information given to assess the generalizability of the results. One needs to provide sufficient information for the reader to be able to recreate the analyses. One way of satisfying this requirement is to report the variance-covariance matrix, which includes all the information about the random effects, including their estimates. This is useful not only as a check on the random effects structure, but also for future meta-analyses. A simpler option is to mention that one attempted to use a maximal LMEM and, as an added check, also state which factors had random slopes associated with them. If the random effects structure had to be simplified to obtain convergence, this should also be reported, and the simplifications that were made should be justified to the extent possible.

If it is seen as necessary or desireable in a confirmatory analysis to determine the random effects structure using a data-driven approach, certain minimal guidelines should be followed. First, it is critical to report the criteria that have been used, including the α-level for exclusion/inclusion of random slopes and the order in which random slopes were tested. Furthermore, authors should explicitly report the changed assumptions about the generative process underlying the data that result from excluding the random slope (rather than just stating that the slopes did not “improve model fit”), and should do so in non-technical language that non-experts can understand. Readers with only background in ANOVA will not understand that removing the random slope corresponds to pooling error across strata in a mixed-model ANOVA analysis. It is therefore preferable to clearly state the underlying assumption of a constant effect, e.g., “by excluding the random slope for the priming manipulation, we assume that the priming effect is invariant across subjects (or items) in the population.”

Concluding remarks

In this paper we have focused largely on confirmatory analyses. We hope this emphasis will not be construed as an endorsement of confirmatory over exploratory approaches. Exploratory analysis is an important part of the cycle of research, without which there would be few ideas to confirm in the first place. We do not wish to discourage people from exploiting all the many new and exciting opportunities for data analysis that LMEMs offer (see Baayen, 2008 for an excellent overview). Indeed, one of the situations in which the exploratory power of LMEMs can be especially valuable is in performing a “post-mortem” analysis on confirmatory studies that yield null or ambiguous results. In such circumstances, one should pay careful attention to the estimated random effects covariance matrices from the fitted model, as they provide a map of one’s ignorance. For instance, when a predicted fixed effect fails to reach significance, it is informative to check whether subjects or items have larger random slopes for that effect, and to then use whatever additional data one has on hand (e.g., demographic information) to try to reduce this variability. Such investigation can be extremely useful in planning further studies (or in deciding whether to cut one’s losses), though of course such findings should be interpreted with caution, and their post-hoc nature should be honestly reported (Wagenmakers et al., in press).

At a recent workshop on mixed-effects models, a prominent psycholinguist¹⁴ memorably quipped that encouraging psycholinguists to use linear mixed-effects models was like giving shotguns to toddlers. Might the field be better off without complicated mixed-effects modeling, and the potential for misuse it brings? Although we acknowledge this complexity and its attendant problems, we feel that one of the reasons why researchers have been using mixed-effects models inappropriately in confirmatory analyses is due to the misconception that they are something entirely new, a misconception that has prevented seeing the continued applicability of their previous knowledge about what a generalizable hypothesis test requires. As we hope to have shown, by and large, researchers already know most of what is needed to use LMEMs appropriately. So long as we can continue to adhere to the standards that are already implicit, we therefore should not deny ourselves access to this new addition to the statistical arsenal. After all, when our investigations involve stalking a complex and elusive beast (whether the human mind or the feline palate), we need the most powerful weapons at our disposal.