Abstract
Based on subjective survival probability questions in the Health and Retirement Study (HRS), we use an econometric model to estimate the determinants of individual-level uncertainty about personal longevity. This model is built around the modal response hypothesis (MRH), a mathematical expression of the idea that survey responses of 0%, 50%, or 100% to probability questions indicate a high level of uncertainty about the relevant probability. We show that subjective survival expectations in 2002 line up very well with realized mortality of the HRS respondents between 2002 and 2010. We show that the MRH model performs better than typically used models in the literature of subjective probabilities. Our model gives more accurate estimates of low probability events and it is able to predict the unusually high fraction of focal 0%, 50%, and 100% answers observed in many data sets on subjective probabilities. We show that subjects place too much weight on parents’ age at death when forming expectations about their own longevity, whereas other covariates such as demographics, cognition, personality, subjective health, and health behavior are under weighted. We also find that less educated people, smokers, and women have less certain beliefs, and recent health shocks increase uncertainty about survival, too.
Keywords: subjective expectations, survival, epistemic probability beliefs, ambiguity
1. Introduction
Textbook models of uncertainty usually treat probabilities as known or knowable objects. This is the case for outcomes of symmetric devices with known properties that are subject to random forces such as the toss of a coin or die, the shuffling of a deck of cards, or the shaking of an urn containing balls of different colors. In contrast, the probabilities that confront economic decision makers are usually less precisely known.1,2
In this paper, we investigate the probability beliefs held by a given individual about personal mortality risks elicited from survey questions on the Health and Retirement Study (HRS) that ask respondents about the numerical probability that he or she will survive to a given age that is 10–20 years in the future. In forming his belief about mortality risk, a person might consult a life table based on the experience of millions of individuals. The life table provides an estimate of the mean probability of survival for persons of a given age and sex with essentially no sampling error. However, the individual may be ambiguous about whether this probability represents the risk he himself faces. He may have personal information that makes him think that he has a higher or lower risk than the average person of his age and sex. Moreover, he may be unsure about the influence that personal information such as the ages at death of parents and relatives, health history and current symptoms, or exercise and dietary habits will have on his likely longevity. Finally, in answering the survey question, a person must construct a probability judgment “on the fly,” accessing whatever frequentist data or epistemic beliefs he may have stored in his brain and manipulating this information through reasoning or gut reaction to produce an answer to the specific question about, say, the probability he will survive to age 80, all within less than a minute.3
In this paper, we assume that probability beliefs about survival are ambiguous in the sense that an individual has in mind a range of possible values of the probability that can be described by a density function g(p) that can take on a variety of shapes depending on both its mean and the degree of ambiguity. The theory literature calls this density function second order probability beliefs (see, for example, Gilboa and Marinacci 2011).
We compare the predicted survival rates of our sample members to the actual survival of sample members eight years later, as reported in the 2010 wave of the HRS. The predictions from our models track actual mortality fairly closely for sample members who are younger than age 80, but begin to diverge substantially at the oldest ages, with older respondents being overly optimistic. The predicted survival rates covary with demographic characteristics, health status, parental mortality, smoking behavior, and cognitive status in largely the same way that they do in regressions that explain actual mortality. Thus, it appears that the subjective survival probability answers are good candidates for modeling individual-level heterogeneity in survival chances.4
The major contribution of this paper is to provide an estimate of ambiguity about survival probabilities that is embodied in the spread of g(p). We find that survival expectations are very uncertain in the HRS and that uncertainty varies in the population: more educated people have more certain beliefs, women have less certain beliefs, and deterioration of health, especially from previously excellent levels, leads to more uncertainty about survival chances.
Identifying second order probability beliefs is possible under the assumptions of our survey response model, the modal response hypothesis (MRH), which is a mapping from probability beliefs g(p) to survey responses. It assumes that people report the mode of g(p) whenever it exists, and they report 50% whenever g(p) is so ambiguous that it does not have a unique mode. The motivation for the MRH is twofold. First, imagine that people estimate the probabilities of certain events after observing some successes and failures of these events. Under some conditions a naïve estimator, which is the ratio of “good cases,” is exactly equal to the mode of the Bayesian updated posterior probability distribution. Moreover, this estimator is biased in finite samples. The MRH assumes that people report this simple, naïve estimator in surveys. The second motivation comes from the literature using numerical subjective probabilities on surveys. When people are asked to report a numerical probability using any digit between 0 and 100, an unusually large fraction of answers are heaped on 50. The excessive use of 50 has been interpreted as occurring because many people treat “50–50” as a synonym for “I don’t know” or even for “God only knows,” a sentiment that suggests that the true probability is unknowable (Bruine de Bruin and Carman 2012, Fischhoff and Bruine de Bruin 1999, Lillard and Willis 2001).5,6 Researchers have realized that these focal answers might introduce bias into estimates of subjective probabilities. As a remedy, Manski and Molinari (2010) think of focal responses as extreme versions of rounding, where some people always round to 0%, 50%, or 100%. Lumsdaine and Potter van Loon (2012) model the probability of providing a focal answer as a separate equation in their econometric model. These papers find that accounting for focal responses is important for valid inference. However, they are agnostic about the reasons so many people provide such answers. Our approach, instead, is to model focal responses with an economic model and relate it to the precision of beliefs of individuals. In our model, people answer with an epistemic 50% as a way of saying “I am very unsure” when their beliefs are too ambiguous. As far as we know, the MRH model is the first in the literature that makes use of the focal responses to learn something about the beliefs of individuals.
For comparison, we present an alternative model of survey response that assumes that the person reports the mean of g(p). We show that the MRH model can account quite well for heaping at 0, 50, and 100, whereas the mean response model cannot. The overuse of focal responses can be especially problematic when very low or very high probabilities are modeled since the high ratio of 50% responses can arbitrarily push the estimated mean probabilities away from their true, extreme values. We show in this paper that our modal response model, which explicitly models focal answers, works better than the simple mean model typically used in research on subjective probabilities. When the modal response model is used for extreme probabilities, both the estimated unconditional means and the average partial effects are closer to ones estimated from realized mortality data. Alternative models of focal responses, such as those of Manski and Molinari (2010) and Lumsdaine and Potter van Loon (2012), might work equally well to reduce this bias and to predict enough focal answers. The main advantage of the MRH is that it is based on an economic model of limited information and uncertain beliefs.7
Learning about the degree of uncertainty in individuals’ beliefs can be important for several reasons. First, the value of information about mortality risk, for example, should be a function of this uncertainty. Uncertain people might value information more, and certain people might rationally ignore any new information since they have already established a good understanding of the risks they face. Even in a fully Bayesian subjective expected utility (SEU) framework the degree of uncertainty might play an important role if the utility function is not linear in probabilities. This is the case, for example, if people can invest in learning about their own mortality risks.8 Second, learning about the degree of uncertainty in individuals’ beliefs is useful from a survey methodological point of view, too. People whose probability beliefs are more certain may answer probabilistic survey questions with greater precision. However, if beliefs are uncertain, as is the case with mortality expectations, we expect large measurement error in survey responses, which might even account for the discrepancy between subjective and objective survival probabilities at later ages. Future research should investigate the potential role of measurement error in subjective expectation data and its link to uncertainty in individuals’ beliefs. Third, learning about the degree of uncertainty in individuals’ beliefs might be very important in non-Bayesian/non-expected utility models. Although we do not work in these frameworks, empirical evidence on ambiguous beliefs may be useful to those who do.
This paper is organized as follows. In §2 we provide a quick overview of the literature on ambiguity and its role in economic decisions. Section 3 describes the subjective survival data in the HRS that we use in this paper. Section 4 introduces the MRH model that can be used to model any subjective expectation data that uses the HRS framework. Section 5 describes a simple and tractable model of individual survival curves. Section 6 discusses the estimation method and identification, §7 shows the results, and §8 concludes.
2. Ambiguity in Economics
Knightian uncertainty, epistemic uncertainty, and ambiguity are roughly synonymous terms that figure prominently in a longstanding and ongoing debate about the link between rationality and probability beliefs on the one hand, and the relationship between beliefs and decisions on the other hand. In an excellent and authoritative review of this debate since Pascal’s famous bet on the existence of God in 1670, Gilboa and Marinacci (2011) discuss the different models of expectation formation, including Bayesian and non-Bayesian models. They call the model we use in this paper the smooth model of ambiguity or second order probability beliefs. In typical models of ambiguity, agents have a set of possible probability distributions in mind, but they are not able to compound this information into a single probability distribution. The smooth model, however, makes compounding possible. The real question in the smooth model is whether agents have a preference for known probabilities (in other words, they are ambiguity averse) or not (in which case they are simple Bayesians). As Gilboa and Marinacci (2011, p. 45) write, “beyond the above mentioned separation [between beliefs and utilities], the smooth preferences model enjoys an additional advantage of tractability. Especially if one specifies a simple functional form for [preferences for known probabilities], one gets a simple model in which uncertainty/ambiguity attitudes can be analyzed in a way that parallels the treatment of risk attitudes in the classical literature.”
The major contribution of this paper is to provide an estimate of second order probability beliefs about survival probabilities that are embodied in the spread of g(p). It is important to clarify the role of this object in alternative views of uncertainty. Conventional economic theory of behavior under uncertainty, rooted in SEU theory (Savage 1954), is often interpreted as having erased the distinction between known and unknown probabilities because expected utility is a linear function of probabilities, that is, assume that the person’s ambiguous probability beliefs are described by g(p). His expected utility is
where p̄ is the mean of this ambiguous distribution. Clearly, expected utility is invariant to a mean preserving spread of g(p); hence, decisions based on expected utility are unaffected by ambiguity.
In the famous Ellsberg (1961) experiments, subjects were presented with choices of drawing balls from different urns whose compositions were either known or ambiguous. Most people revealed distaste for ambiguity that was at odds with the SEU theory. The survey by Gilboa and Marinacci (2011) provides a comprehensive and insightful discussion of this.
We separate the issues concerning ambiguity of probability beliefs from those concerning the effects of epistemic uncertainty and ambiguity aversion on decisions. We do so by utilizing survey data that ask directly about people’s probability beliefs. As Manski (2004) emphasizes, this approach differs from the practice in much of applied economics of assuming that individuals have exogenously given probabilities. It also differs from Savage’s (1954) theory, which infers probability beliefs from choice situations. This means that we can empirically explore how beliefs about risk and uncertainty vary in the population without being required to take a stand on how decisions are affected by probability beliefs.
3. Subjective Survival Probability Questions on the HRS
The Health and Retirement Study has asked probabilistic expectation questions on various topics since its beginning in 1992. The survival question that we use in this paper comes from the 2002 wave and it reads as follows: “What is the percent chance that you will live to be [target age] or more?” The target age exceeds the individual’s age by at least 10 years: it is 80 years for people younger than 70, and 85, 90, 95, and 100 for individuals in successive five-year age intervals.
Although the subjective probability responses in the HRS seem reasonable when averaged across respondents, individual responses appear to contain considerable noise and are often heaped on values of 0, 50, and 100 (for a discussion, see, for example, Manski 2004). Considering the whole group of probability questions in the HRS-1998, for example, whereas only 5% of respondents refused to answer the probability questions, 52% of questions were heaped on either 0 or 100, and an additional 15% were heaped on 50.
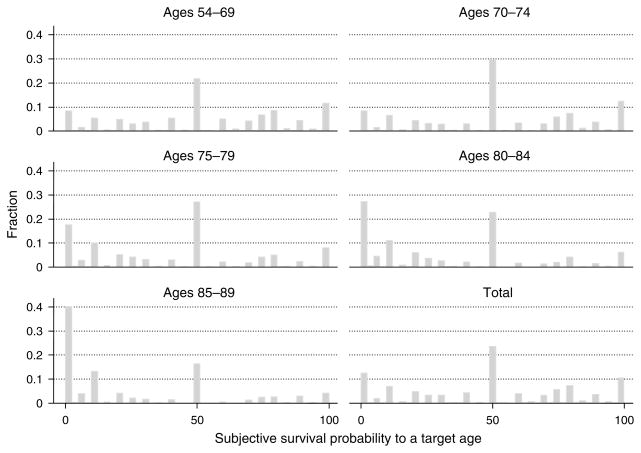
These patterns are illustrated in Figure 1 by histograms of responses to the HRS-2002 survival probability question. We have included separate histograms by the target age used in the survival question and a total histogram in the six panels of Figure 1. Each histogram shows a high frequency of focal answers, especially at 50. The ratio of 50 responses is somewhat smaller at old ages, where the actual survival probabilities are low, but it still accounts for 16% of the responses for people over 84.
Figure 1. Distribution of Survival Probabilities to Target Age, by Age of Respondent, HRS-2002.
Note. Target age is 80 years for people younger than 70, and it is 85, 90, 95, and 100 for individuals in successive five-year age intervals.
Some psychologists, especially Fischhoff, Bruine de Bruin, and their colleagues (Fischhoff and Bruine de Bruin 1999, Bruine de Bruin et al. 2000, Bruine de Bruin and Carman 2012) have argued that answers of 50 may reflect epistemic uncertainty, that is, a failure to have any probability belief at all about the event in question or, at least, to have no clear idea of what the probability could be. Alternatively, of course, an answer of 50 might reflect a very precise belief about the probability that a fair coin will come up heads or perhaps a somewhat less precise belief that a given event is about equally likely to occur or not occur. Indeed, although HRS probability questions offer participants a scale of integers from 0 to 100, the large majority of “non-focal” answers are integers ending in 5 or 0, suggesting that responses from most people involve rounding or approximation. See Manski and Molinari (2010) for a discussion of the different rounding practices of survey respondents in the HRS and of potential remedies.
There has been much less emphasis in the psychological literature on focal answers at 0 or 100. When a probability question concerns an event such as the chance of being alive 10 or 15 years from now, it does not seem credible to assume that a respondent who gives such an answer of 100 is completely certain he will be alive then, and, apart from a person diagnosed with a terminal illness, an answer of 0 should not be taken at face value either.9
Previous researchers have found that the tendency to give focal answers is associated with low education and lower cognitive ability, and it varies with other demographic variables, too (Hurd and McGarry 1995, Lillard and Willis 2001, Lumsdaine and Potter van Loon 2012). These covariates are known to correlate with mortality. Focal responses, thus, might bias estimated average survival probabilities if we take them at face value, and the bias might be stronger in situations where the underlying probability is far from 50%. To test whether this is the case, in the empirical part of this paper we will compare estimated individual survival curves to the actual survival of the respondents eight years later in 2010, which is the last available wave of the HRS.
4. Probability Beliefs and the Modal Response Hypothesis
In this section we describe a theoretical model that attempts to relate answers that an individual gives to a survey question about the subjective probability of a given event and his underlying probability beliefs. In our model, we distinguish between ambiguity and epistemic uncertainty, with the latter corresponding to cases when information is limited.
Let us assume that person i is faced with the problem of estimating the probability pi of an event A. Initially he has no information about the probability of this event; he has an uninformed prior , where U denotes the uniform distribution. The person observes event A happening αi − 1 times and not happening βi − 1 times. In the survival context, for example, this means that a person is aware of αi − 1 people similar to himself who survived to the given target age and βi − 1 similar people who died before reaching that age. It is well known that if this new information is used to Bayesian update one’s beliefs about pi, the posterior distribution has a Beta distribution with parameters α i and βi, pi ~ Beta(αi, βi).
When faced with a survey question about the probability of event A, the person might respond with the mean or the mode of this distribution. When αi and βi are larger than 1,10 the mean and the mode of the Beta distribution are
| (1) |
| (2) |
A Bayesian agent would report , which is the expected value of the Bayesian updated posterior distribution. Note that is exactly equal to the naïve estimator of the probability that can be computed by the number of “good cases,” which is αi − 1, over the number of all cases, which is αi + βi − 2. A frequentist agent, thus, would not report the mean, but rather the mode of the distribution gi(p). The modal response hypothesis assumes that people report rather than to probabilistic survey questions for at least two reasons. First, as Lillard and Willis (2001) argue, it is cognitively less burdensome for a respondent to answer a survey probability question quickly by reporting the most likely value of p, given by the mode of g(p), than it is to report the expected value given by . Second, is equal to a very simple rule-of-thumb estimator for the probability in question: the frequentist response. In a survey situation where people have to answer many questions in a very short time frame, it seems a reasonable assumption that they give frequentist approximations to probability questions instead of Bayesian updating their priors. Moreover, in this model, the mode is often a good approximation of the mean.
The formula in (2) does not give the mode of the distribution when either αi or βi is smaller than 1. Whenever αi < 1, β ≥ 1, the distribution is always decreasing and has a unique mode at 0. Whenever αi ≥ 1, β < 1, the distribution is always increasing, and its unique mode is at 1. Finally, if αi < 1, β < 1, the distribution has a U -shape, and it has two maxima at 0 and 1. In this case one finds it more probable that the probability of event A is 0 or 1 than that it is 50%.
We have motivated the use of the Beta distribution with a Bayesian framework where agents observe certain numbers of successes and failures. As we will show, however, the distributions that occur when either αi or βi is smaller than 1 cannot be derived from Bayesian updating based on evidence. Indeed, these distributions correspond to situations where, in effect, the agent has very little objective evidence on which to base his beliefs and, lacking evidence, tends to give conventional epistemic responses to survey questions about his probabilistic beliefs. In particular, we hypothesize that the person will respond with an extreme value of either 0 or 1 when g(p) is monotonically decreasing or increasing. When the distribution is U -shaped, we hypothesize that the person will answer “50” as a synonym for “God only knows” rather than necessarily as a belief that the outcome in question is equally likely to occur or not.11
To show how the shape of g(p) is related to the amount of evidence on which an individual bases his beliefs, we introduce two more parameters that are functions of α and β:
| (3) |
| (4) |
where μi is the expected value of the distribution of the probability in question, and ni is a measure of the precision of beliefs. Higher ni means more precise beliefs, that is, a tighter gi(p) density function. Earlier, we argued that an uninformed agent with a uniform prior over the unit interval would update his prior after observing α − 1 successes and β − 1 failures in a sample of N = α+β−2. Note that B(1, 1) is a uniform distribution so that ni = α + β = 2 for an uninformed agent. Equivalently, such an agent observes no data since N = 0. Thus, a necessary condition for Bayesian updating is that the agent observes a positive amount of data, which implies that α > 1, β > 1, and N > 2. As we have seen, any Beta function satisfying this condition is unimodal where the mode falls in the interval 0 < p < 1. Conversely, when α < 1 or β < 1, g(p) may be monotonically increasing, decreasing, or U -shaped, depending on the value of μ, and if α + β < 1, g(p) is always U -shaped. Obviously, Bayesian updating cannot be the source of such beliefs because one cannot observe a negative number of signals. That is why we label such beliefs as “epistemic” and distinguish them from “ambiguous” ones.
In our development of the Beta model, the precision parameter ni = αi + βi is assumed to be an integer equal to two less than the size of the sample that is observed by agent i. A broader and more useful interpretation of precision is that it measures the confidence that an individual has in his judgment of the risk of a given event. For instance, educated individuals can utilize, in addition to their personal experience, a broader knowledge of evidence about mortality and its causes from past coursework, wider reading, and better informed family and social networks. Thus, we may interpret precision as a measure of a person’s capacity to assess his survival risks based on his knowledge of mortality risks and his ability to translate personal information about his own health, health behavior, and family history into its implications for survival chances.
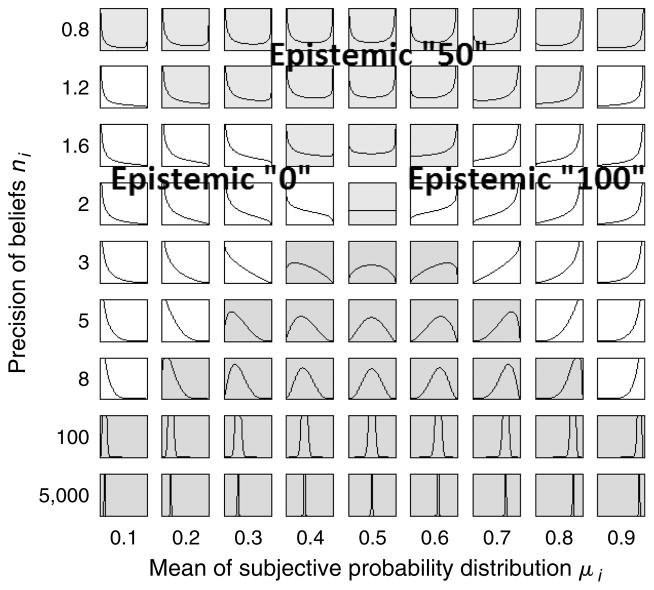
The relationship between ni, μi, and g(p) is depicted in Figure 2. The figure presents a matrix of 81 probability density functions—g(p | μi, ni)—corresponding to nine different values of the mean of g(p), given by μi on the horizontal axis, and nine different degrees of precision measured by ni on the vertical axis. The figure also illustrates the boundary between ambiguous beliefs that can be represented by a second order probability distribution based on Bayesian principles and epistemic uncertainty in which the individual has too little knowledge about the risk in question to be able to form an evidence-based probability judgment. Possible ambiguous densities appear in the darkly shaded, inverted U -shaped region in Figure 2 for which ni > 2. Note that throughout this region, reports of pmean and pmode tend to be very close to one another. The lightly shaded area at the top of the figure corresponds to epistemic 50% responses. As we can see, when uncertainty is high (ni is low) for any values of μi, the model predicts a 50% response, including cases when the mean probability is very low or very high. The MRH thus predicts that the large fraction of 50% answers, typical in subjective probabilistic expectation data, can in fact correspond to mean probabilities that are far from 50%. The two unshaded triangular regions in Figure 2 correspond to epistemic 0 and 100 responses. Such responses are typical in cases when the mean probability μi is also close to 0 or 100. However, when ni is close to 2, that is, beliefs are almost uniform; 0% and 100% answers can occur when μi is close to 50%. Thus, the MRH can predict a large fraction of focal 0, 50, and 100 answers, and the corresponding bias can be either positive or negative.
Figure 2.
Density of Probability Beliefs gi (p) for Different Mean μi and Precision ni Values
To summarize, the modal response hypothesis claims that survey respondents report a potentially rounded version of the mode of gi(p) whenever it exists, and they report 50% whenever gi(p) has a U shape,
| (5) |
The round function can be rounding to the closest 1%, 5%, 10%, or anything that seems appropriate in the context of the survey. Manski and Molinari (2010), for example, use a framework where there are individual differences in rounding practices. Their approach can also be modeled in our framework by letting the round function vary across individuals.
The hypothesis of this paper is that people answer subjective probabilistic expectation questions according to the MRH. It would be desirable, however, to test the MRH against other survey response models. A natural candidate for comparison is the mean model where people respond a potentially rounded version of the mean of gi(p),
| (6) |
In the mean model, the precision of beliefs ni is not identified; only the mean μi is. The mean and the mode models, however, converge to each other as ni goes to infinity; that is, the mean model is embedded in the MRH, and thus, a relatively small estimated belief precision n would be evidence in favor of the MRH.
5. Individual Subjective Survival Curves
In the previous section, we introduced two survey response models that transform second order probability distributions g(p | μi ni) into the survey response or . These models can be applied to any subjective probabilities in the HRS format and not just to survival data. To close the model, however, we need to specify the mean μi and the precision ni of beliefs. There is no unique way of modeling these two variables; it is the task of the researcher to find the appropriate model in the context of the particular project. In this section, we show how μi and ni can be modeled in the context of survival probabilities.
The so-called Gompertz model of longevity has been widely used in both demography and biology because its increasing mortality hazard assumption lines up very well with mortality data of humans and other species (Vaupel 1997). The Gompertz model assumes that the hazard of death is exponentially increasing with age:
| (7) |
where γ0 is a positive scale and γ1 is a positive shape parameter. By simple calculation, (7) leads to the following survival probability from age a to age t:
| (8) |
The main advantage of subjective survival data is that we can estimate individual heterogeneity in survival chances. With objective survival data, we can only identify group-specific survival probabilities by computing the ratio of survivors in a particular group. Unobserved heterogeneity within groups, however, is not identified. In contrast, subjective survival data enable us to estimate individual heterogeneity in survival chances as we collect probability data on the individual level. We follow Vaupel (1979) by allowing the scale parameter γ0 to have a gamma distribution with shape parameter k and scale parameter θ, and we assume that the shape parameter γ1 is fixed in the population:
| (9) |
The expected value of the gamma distribution is kθ, and thus both parameters increase mortality chances and decrease the probability of survival (see Equation (8)). The main advantage of using the gamma distribution, as we will argue, is analytic tractability. Note, however, that this is a flexible two-parameter distribution with both parameters being estimated, and hence this assumption is not very restrictive. The first advantage of the gamma distribution is that the average survival probabilities can be derived analytically. As we show in Appendix C, §C.2, in the e-companion (available as supplemental material at http://dx.doi.org/10.1287/deca.2013.0266), the average survival probabilities from age a to age t is
| (10) |
The second advantage of the gamma-Gompertz framework is that we can analytically derive the effect of individual heterogeneity on sample selection. Different survival chances are modeled by letting γ0 have a distribution in the population. In this paper, we refer to γ0 as “frailty” (Vaupel 1979), which includes genetic, environmental, and behavioral factors that affect the underlying mortality of individuals other than age. As long as survival chances are heterogeneous in a population, fit individuals will be overrepresented in the sample over time, as frail individuals are more likely to die and not participate in the HRS. By applying the formula from Vaupel (1979), we can analytically characterize this sample selection. See the Appendix C, §C.1, in the e-companion for details.
To sum up, we use the following structural equations for individual survival chances:
| (11) |
| (12) |
| (13) |
| (14) |
where θr represents the scale parameter of the gamma distribution in the reference cohort, which is the 50-year-old (r = 0.5). Equation (13) shows the effect of sample selection. The scale parameter θi is decreasing with age, as fit individuals are increasingly overrepresented in the sample. Equation (14) shows that we add covariates to the scale parameter of the 50-year-old cohort. Finally, Appendix C, §C.3, in the e-companion shows how average partial effects of the different covariates can be derived after fitting this model.
So far we have only talked about how to model the mean survival probability μi. For modeling the precision of beliefs ni, we use a very simple log-normal framework:
| (15) |
| (16) |
Equations (11)–(16) together with the survey response models of the previous section fully specify our model.
6. Estimation and Identification
Our structural model has two unobservables: λ0i, which is a function of the mean survival probability, and uni, which is the unobserved heterogeneity in the precision of beliefs. Based on the distributional assumptions from the previous section, the model is fully specified, and it can be estimated with maximum likelihood.
We only observe one survival probability answer in the HRS. In §3, we proposed two survey response models. The mean model assumed that people report a rounded version of their true survival chances, whereas the MRH model assumed that people report a rounded version of the mode of the distribution of probability beliefs g(p | μi, ni) or 50% when the mode does not exist.
The joint distribution of the two random variables λ0i and uni is complicated because one is gamma, the other is normal, and they enter the model in a nonlinear fashion. The estimation of the MRH can thus be carried out by maximum simulated likelihood. The estimation of the mean model is more straightforward because the precision of beliefs plays no role in the model. Appendix C, §§C.4 and C.5, in the e-companion show how the likelihood function of these two models can be constructed.
It is worth discussing how our main parameters are identified. We seek to estimate the following set of parameters: λ1, k, β θ,βn, σn. In the case of the mean model, parameters of the belief precision, βn and sigma;n, are not identified. Parameter λ1 is the shape parameter of the individual survival function, and it is identified from how fast the probability responses change with age ( ). Parameters k and βθ determine the scale parameter of the individual subjective survival curves λ0i, and they are identified from the location and dispersion of the individual responses and .
The identification of the belief precision parameters βn and σn primarily comes from the fraction of different focal answers in different demographic groups. If we have many focal answers, we expect ni to be small. If we have many different types of focal answers (0, 50, and 100), we expect a high sigma;n, indicating a high dispersion of belief precision in the population.
7. Empirical Analysis
Beliefs about subjective survival probabilities presumably depend on an individual’s knowledge of different risk factors and demographic differences in the society; his personal information about his own health, habits, and family members’ longevity; his ability to translate this information into a probability; and his level of optimism or pessimism. In the empirical model estimated in this section, we use the information available in the HRS to try to capture several of the major determinants of beliefs in a parsimonious fashion.
7.1. Sample and Measures Employed
The sample used in the empirical analysis consists of 13,038 age-eligible respondents to the 2002 Health and Retirement Study (over age 54 in 2002)12 who provided responses to the subjective survival probability question. Excluded from the sample are proxy respondents and nonrespondents in the 2000 wave of data collection. Also excluded are persons over 90 who were not asked the survival probability questions and people for whom we did not have realized survival information in 2010.13 Table A.1 in the appendix presents descriptive statistics for the variables used in our analyses. The average age of our sample members is just over 68 years (ranging from 54 to 89 years), and on average the target age was 16 years from their current age. The modal sample member is a white female with a high school education, although there is substantial variance in each of these dimensions.
Our theory suggests that people may utilize personal information in forming their subjective survival beliefs. Parents’ age at death and one’s own current health status and health behavior are such variables. As Table A.1 shows, 16% of our sample still has a living mother, but only 5% has a living father. The average age at death of the mothers is 76 years, whereas the corresponding number for the fathers is 72 years. We construct six variables about parental mortality. Three of them correspond to the mortality of the same-sex parent (father–son and mother–daughter pairs), and three correspond to the opposite-sex parent. Within each pair, we first take the age at death of the parent if he or she is dead. If he or she is alive, we impute the expected age at death of the parent based on his or her gender and age. In all models we include dummy variables about whether the parents are alive to control for potential imputation bias. Finally, we create a linear spline from the imputed parental mortality with a single cutoff point at the age of the interviewee. This approach is motivated by the idea that individuals might consider parental mortality less informative about their own survival chances if they have already lived longer than their parents.14 These four splines (two for each parent) together with the two dummies constitute our six parental mortality variables.
We also include in our analysis three sets of variables on health-related behavior. As Table A.1 shows, 43% of our sample reports regular exercise at least three times a week. Whereas only 14% of the sample smoked in 2002, almost 60% reported having smoked in the past. There is a big variation in the sample in drinking behavior. Roughly half of our sample (48%) reports that they drink alcohol sometimes, but the majority are not regular alcohol consumers. Among those who are, the average number of days when they drink is 3.4 days a week, and the average number of alcoholic beverages consumed is 1.9.
Self-rated health in the HRS is measured on a five-point scale: (1) excellent, (2) very good, (3) good, (4) fair, and (5) poor. We translate these into three categories: (1) excellent/very good, (2) good, and (3) fair/poor.15 We then construct dummy variables representing the combination of self-rated health in 2000 and 2002 for each respondent with excellent/very good in both years as the baseline case. In Table A.1, we show only the marginals of this joint distribution. As we can see, the fraction of people in “excellent/very good” health decreased from 47% in 2000 to 43% in 2002. The fraction of people in “good” health did not change much (31% and 32%), and the fraction in “fair/poor” health increased from 22% to 25%.
We also include two cognitive measures (Vocabulary and the 27-point cognitive capacity scale16), and the Center for Epidemiologic Studies Depression Scale (CESD) depression score, which measures depressive symptoms.17 Table A.1 shows that the average member of our sample has higher cognitive and lower depression scores than the average HRS respondent.
7.2. Maximum Likelihood Model Estimates
The objective of this section is to test the MRH through a series of performance tests. All of the results we present in this section are based on the 12 estimated models shown in Table A.2 in the appendix and Tables B1, B5, and B9 in Appendix B in the e-companion. Table A.2 reports models without covariates; Table B1 adds basic demographic information; Table B5 expands the model with cognition, personality, and parental mortality; and, finally, Table B9 contains all variables including subjective health. All tables present three models. The first columns show actual eight-year survival of the HRS respondents between 2002 and 2010, estimated with nonlinear least squares. The second columns shows results using subjective expectations based on the mean model, and the last two columns show results from the MRH “mode” model. All of the parameters of our model (γ0, θ50, n, γ1, k, sd(n)) are assumed to be positive, and thus their logarithms enter the likelihood function. Covariates potentially enter two equations. The first is the equation of θ50, which is the scale parameter of the gamma distribution of the mortality hazard at the age of 50. In the actual survival models, we model γ0 directly. Covariates with positive coefficients are estimated to increase the mortality hazard and decrease the survival chances. The magnitudes of these coefficients will be analyzed later when we derive average partial effects of them on various survival probabilities. The second equation where covariates appear is the equation of the precision of beliefs n. Positive coefficients mean tighter, more precise probability beliefs.
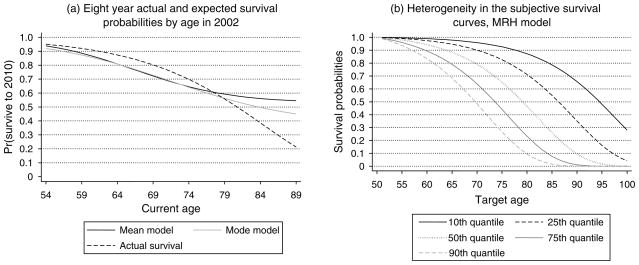
Figure 3(a) compares estimated actual eight-year survival probabilities of HRS respondents to subjective survival beliefs in 2002 computed from the models in Table A.2 with no covariates. The horizontal axis shows the current age of respondents in 2002, and the vertical axis shows the fitted average eight-year survival chances from the three models. As we discussed in §3, heterogeneity in survival chances leads to sample selection as people with better fitness are more likely to survive and become respondents of the HRS survey at older ages. In the case of realized survival, only the interpretation of the estimates changes, but we do not need to make any further adjustments of the parameters. The demography literature calls survival tables of this sort “survival probabilities of the survivors.” In the case of subjective survival chances, however, we do have to properly adjust for the unmeasured genetic and environmental differences of cohorts as discussed in §4. As we can see, both the mean and the MRH “mode” model track the actual survival chances very well up until about age 84, when the subjective probabilities become too optimistic. Whereas the eight-year actual survival chance of a 90-year-old is roughly 20%, the corresponding numbers in the MRH and mean models are ~ 45% and 55%, respectively. Thus, although the MRH model provides numbers that are closer to the true survival chances at older ages, these numbers are still too large on average. It is not obvious, however, whether these overly optimistic numbers are biases in people’s heads or biases because of measurement error in the survey. In this paper we do not try to separate these two types of bias, and we simply compare the mean, the mode, and the actual survival models using the raw data.
Figure 3.
Average Actual and Expected Survival Probabilities and Dispersion in Beliefs
Figure 3(b) shows the estimated heterogeneity of survival chances in our sample. The different curves correspond to different values of γ0 with lower values meaning better fitness. As we can see, there is notable variability in survival chances. For example, the difference in median survival (i.e., half-life) between those in the 10th and 90th percentiles of the estimated frailty distribution is about 25 years; that is, comparing two groups of 50-year-olds, half of those in the 90th percentile are expected to survive to age 70, whereas among those in the 10th percentile, half are expected to survive to age 95. Using only mortality data, one cannot identify the unobserved heterogeneity in survival chances.18
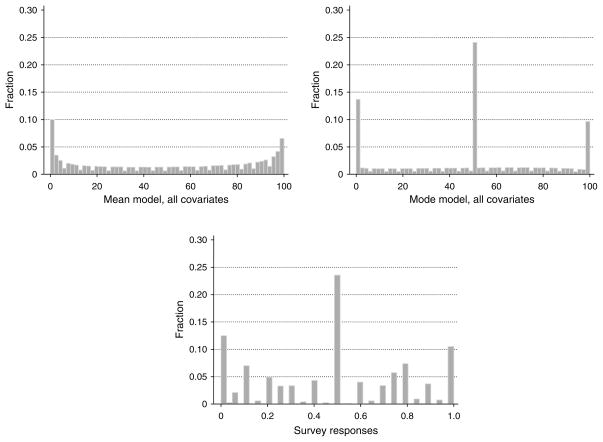
The reason the MRH model is somewhat better than the mean model in predicting low probability events is that the high fraction of 50% answers are allowed to be focal answers that do not arbitrarily push the mean survival chances up. To visualize this effect, we simulated survey responses based on the estimated models of subjective survival chances in the e-companion, Appendix B, Table B9. To get precise numbers, we used 651,900 observations for simulation, which is 50 times the size of our data set (651,900 = 50×13,038). As we can see in Figure 4, the MRH model is able to predict histograms of responses that are very similar to the histogram of actual responses in the bottom panel. The ratio of 50% answers is around 25%, whereas the ratio of 0% and 100% answers are both around 10%. More importantly the MRH model recognizes that the high fraction of focal answers should not be taken at face value because a large fraction of them reflect only imprecise knowledge. The mean model, however, takes all the focal answers at face value. Consequently, the mean model is not able to predict a histogram similar to actual responses, and it seriously biases the estimation of low or high probability events.
Figure 4.
Simulated Survey Responses Based on the Mean and the Mode Models with All Covariates and the Empirical Distribution of Survey Responses
Much of a person’s personal information about health is likely embodied in his assessment of the level and trajectory of self-rated health. To explore the effects of other covariates, we present estimates of models with and without subjective health in Tables 1 and 2, respectively. Both tables show estimated average partial effects of surviving from age 55 to 75 and from 75 to 95. Appendix B in the e-companion contains more detailed versions of these tables and further specifications, including models with only demographic variables and partial effects of surviving from 2002 to 2010.
Table 1.
Average Partial Effects of Surviving from Age 55 to 75 and from 75 to 95 in Three Models with Demographic, Personality, and Personal Information Variables: Actual Survival and the Mean and MRH Models of Subjective Survival Expectations
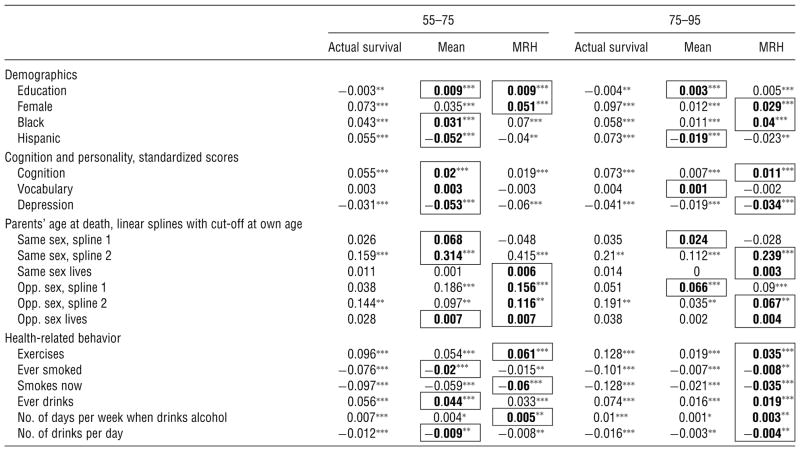
|
Note. Bold and bordered partial effects at the mean and the MRH models indicate that they are closer to the partial effects of actual survival.
Significant at the 10% level;
significant at the 5% level;
significant at the 1% level.
Table 2.
Average Partial Effects of Surviving from Age 55 to 75 and from 75 to 95 in Three Models with Demographic, Personality, Personal Information, and Subjective Health Variables: Actual Survival and the Mean and MRH Models of Subjective Survival Expectations
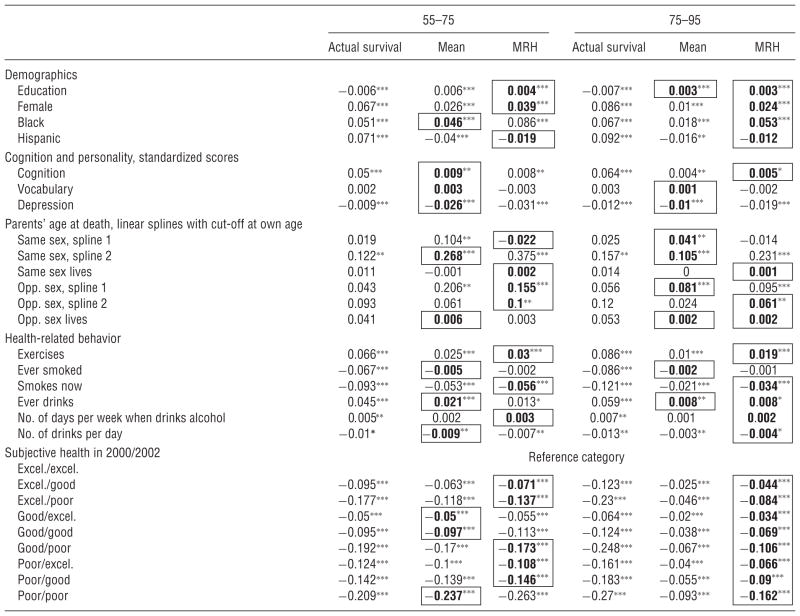
|
Note. Bold and bordered partial effects at the mean and the MRH models indicate that they are closer to the partial effects of actual survival.
Significant at the 10% level;
significant at the 5% level;
significant at the 1% level.
The tables show that the majority of the coefficients are smaller in absolute value when subjective as opposed to objective information is used, but the coefficients based on the MRH are closer to objective values. This pattern is more obvious for low probability events (surviving from age 75 to 95), because the coefficients are roughly two times as big in the MRH. Thus, not only the average survival probabilities (Figure 3), but also the average partial effects are closer to objective values compared to the mean model. We take it as evidence that the MRH model is more successful for modeling subjective probabilistic expectations, particularly for low probability events, because the bias from focal answers is modeled explicitly.
However, the majority of the coefficients are still smaller in absolute value in the MRH than in the actual survival models. There are two potential explanations for this. Either there is measurement error in the data or people are underestimating the effect of some variables when forming expectations about their longevity. Without further assumptions, measurement error, other than focal responses, is not identified in our model. Note, however, that not all coefficients are attenuated equally. In fact, two coefficients are systematically higher in absolute value in the subjective models: same-sex parents’ age at death and depression. This is consistent with a model in which agents base their expectations on easily observable determinants of mortality (parent’s survival) because they have limited information on demographic differences in the society and on the role of different behavioral factors, such as smoking and exercising, on survival. In this case, the partial effects of personal information are expected to be higher for subjective than for objective survival, and the pattern is expected to be the reverse for other variables. This is exactly what we see in the data.
Tables 1 and 2 also show that people are aware that regular exercise is beneficial, and smoking is harmful for them, although they underestimate the role of these factors. We can also see that regular but limited alcohol consumption is not damaging, although teetotalling and heavy drinking are. Even more interesting is the comparison of the models with and without controlling for subjective health. Not surprisingly, both the objective and subjective survival probabilities are less affected by behavior when subjective health is controlled. However, the subjective values shrink more strongly. For example, as Table 1 shows, those who quit smoking expect a two percentage point lower chance of surviving from age 55 to 75 compared to those who never smoked. However, this effect disappears when subjective health is taken into account (Table 2). It means that healthy quitters falsely believe that their survival chances are the same as those who never smoked, whereas quitters who had already acquired a disease understand its consequences.
It is also worth noting the demographic differences in subjective and objective survival. As expected, females are more likely to live longer, and this is reflected in their subjective expectations. Racial differences, however, are more complex. Conditional on education, personal information, health, and behavior, blacks and Hispanics have a higher chance of survival than whites in this age range. African Americans’ expectations reflect this difference, but Hispanics are more pessimistic than non-Hispanics. Tables B2–B4 in the e-companion show roughly similar patterns when only demographic variables enter the model. Finally, even though the educated are more likely to live longer (Tables B2–B4), when personality, personal information, and behavior are controlled for, the effect of education becomes negative. Further investigation, not shown in this paper, shows that this result is driven by the cognitive capacity variable. Education and cognition have a strong positive correlation, but cognition is a better predictor of survival than education. Moreover, the educated also have better subjective health, and thus the effect of education becomes even more negative when health is controlled for (Table 2). Moreover, the educated believe themselves to have better chances of surviving, independent of the control variables used.
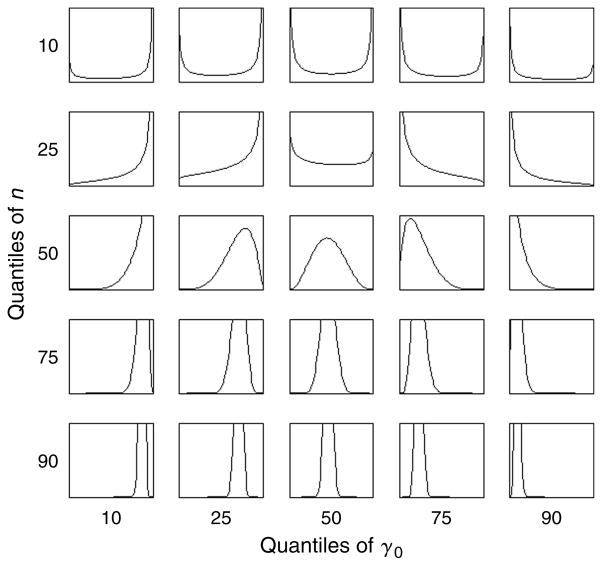
Finally, let us take a look at the estimated distribution of probability beliefs (second order probability distribution gi(p)) of HRS respondents. Based on the MRH model without covariates (Table A.2), we computed the 10th, 25th, 50th, 75th, and 90th quantiles of belief precision n and the scale parameter of the survival function γ0 for the cohort of age 50. These numbers can be found in Table A.3. Figure 5 shows the corresponding probability belief distributions of the probability of surviving from age 50 to age 80. As we can see, there is an enormous heterogeneity in probability beliefs. The median responder in the HRS (Figure 5, third row and third column) has a belief distribution that is single peaked but wide, having significant probability mass for any possible probability values between 0 and 1. It means that although the median responder’s best guess for the probability of surviving from age 50 to age 80 is roughly 50%, she is quite unsure about this probability. People with even less precise beliefs are very unsure. For example, already at the 25th percentile of belief precision (where n = 1.58), everyone provides a focal response of either 0, 50, or 100. At the 10th percentile (where n = 0.4), everyone has U -shaped beliefs and, thus, responds with an epistemic 50%.19 As we increase belief precision to the 75th percentile, the second order probability belief distribution becomes quite tight, having most of its mass in the neighborhood of the mean probability. It means that at least 25% of the respondents have very precise beliefs about their own survival chances.
Figure 5.
Estimated Distribution of Probability Beliefs gi (p) of Surviving from Age 50 to Age 80
Determinants of belief precision appear in Table 3 and the last columns of Tables B1, B5, and B9 in Appendix B in the e-companion. Positive coefficients mean tighter, more precise beliefs. As we can see, more educated people have more certain beliefs. This is consistent with our hypothesis, discussed in §3, that more educated people may have a broader knowledge of evidence about mortality and its causes. We can also see that the deterioration of health, especially from previously excellent levels, leads to more uncertainty about survival chances, perhaps because of uncertainty about the future course of a new disease. Those who were in poor health both in 2000 and in 2002, however, hold the most certain and pessimistic beliefs about their survival chances.
Table 3.
Predictors of Belief Precision n in Three Versions of the MRH Models of Subjective Survival Expectations
| ln(n)
|
|||
|---|---|---|---|
| Model 1 | Model 2 | Model 3 | |
| Demographics | |||
| Education | 0.056*** | 0.051*** | 0.053*** |
| Female | −0.139*** | −0.156*** | −0.157*** |
| Black | 0.053 | 0.041 | 0.02 |
| Hispanic | 0.188* | 0.155 | 0.132 |
| Cognition and personality, standardized scores | |||
| Cognition | 0.021 | 0.027 | |
| Vocabulary | 0.008 | 0.009 | |
| Depression | 0.067*** | 0.043* | |
| Parents’ age at death, linear splines with cutoff at own age | |||
| Same sex, spline 1 | −0.493* | −0.493* | |
| Same sex, spline 2 | 0.467 | 0.5 | |
| Same sex lives | −0.064 | −0.071 | |
| Opposite sex, spline 1 | −0.122 | −0.117 | |
| Opposite sex, spline 2 | 0.528 | 0.522 | |
| Opposite sex lives | 0.026 | 0.032 | |
| Health-related behavior | |||
| Exercises | 0.015 | 0.02 | |
| Ever smoked | −0.091* | −0.091* | |
| Smokes now | 0.007 | 0.006 | |
| Ever drinks | 0.174*** | 0.177*** | |
| No. of days per week when drinks alcohol | −0.014 | −0.015 | |
| No. of drinks per day | −0.035 | −0.033 | |
| Subjective health in 2000/2002 | |||
| Excellent/excellent | Reference category | ||
| Excellent/good | −0.172** | ||
| Excellent/poor | 0.122 | ||
| Good/excellent | −0.092 | ||
| Good/good | −0.05 | ||
| Good/poor | −0.059 | ||
| Poor/excellent | −0.106 | ||
| Poor/good | −0.042 | ||
| Poor/poor | 0.177** | ||
| Age and time horizon of the HRS question; variables divided by 100 | |||
| Age | −2.513* | −2.26 | −2.333 |
| Horizon | −7.503 | −9.823 | −10.037* |
| Age × Horizon | 25.438** | 27.698*** | 27.82*** |
| Constant | 1.572* | 1.845* | 1.882** |
Significant at the 10% level;
significant at the 5% level;
significant at the 1% level.
The effect of age and the time horizon of the survival question in the HRS have complicated relationships to uncertainty. For a fixed time horizon, the net effect of age on uncertainty is negative, because the interaction term dominates for any time horizon values used in the HRS (from 11 years to 26 years). Thus, older people seem to have more precise beliefs about their survival chances, which might reflect learning. For a fixed age, the net effect of the time horizon on uncertainty is also negative, because the interaction term dominates again. This means that people hold more precise views about their long-run than their short-run survival chances.
The two splines measuring same-sex parental mortality in Tables B5 and B9 show a “V” shape. This means that people are the most unsure about their survival chances when they are around the age when their same-sex parent died. We can also see that active smokers and those who have already quit have less precise survival expectations compared to those who never smoked, infrequent alcohol consumption leads to more precise beliefs, and women are less sure than men and depressed people are relatively more certain about their otherwise poor survival expectations.
8. Conclusion
The modal response hypothesis is used in this paper as the foundation for an econometric model that is intended to provide a mapping between survey responses to probability questions and the underlying subjective probability beliefs of individuals about their chances of surviving to a target age. In this paper, we have presented the MRH as a hypothesis designed to capture the kinds of “gut responses” to such questions that would be made after about 15 seconds of consideration by persons who vary in the amount of information they have about actuarial risks to health and about their own health-related circumstances, and in their capacity to process such information into subjective beliefs. We argued in §3 that reporting the mode is relatively easier from a cognitive point of view than the mean or the median, the mode is equal to a very simple rule-of-thumb estimator for the probability in question, and the mode often provides a good approximation to the expected probability that is called for in SEU theory.
Our empirical findings suggest that there is considerable heterogeneity in subjective survival risks, some of it associated with age, sex, race, education, health-related behavioral factors, parental mortality, and cognitive capacity. We have shown that subjective survival expectations line up with actual mortality very well when the objective probabilities are moderate. The subjective survival probabilities, however, become overly optimistic at old ages when the true survival probabilities are relatively low. We have shown that the MRH model does a better job compared to a standard mean model in reducing this bias as the MRH models focal answers in an explicit way. It remains for future research to learn whether the overly optimistic subjective expectations are biases in the heads of individuals, potentially having behavioral consequences, or are a result of survey measurement error, potentially related to uncertain beliefs.
In the empirical section of this paper, we also found substantial uncertainty about mortality risks, which is manifested by considerable spread in the estimated distribution of subjective survival probabilities for a typical respondent. In addition, we found significant variation in uncertainty, holding expected survival risk constant. It remains for future work to explore the explanation of these findings more deeply and to see whether survival risk and uncertainty about this risk play a role in decisions made by HRS respondents.
Acknowledgments
The authors thank the late Dan Hill and Mike Perry for their valuable insights. They also thank Gábor Kézdi and participants at a Duke University seminar for many useful comments on the current paper. The authors are grateful to the Behavioral and Social Research Program of the National Institute on Aging [Grant U01-AG09740] for supporting the collection of the HRS data used in this paper, and to NIA [Grant P01AG026571] for research support. The current paper builds on ideas presented in Hill et al. (2004).
Biographies
Péter Hudomiet is a Ph.D. candidate at the Economics Department of the University of Michigan, Ann Arbor. His primary interest is in occupational skill formation and occupational unemployment. He is currently conducting research on subjective stock market expectations and the response behavior of survey participants.
Robert J. Willis is a professor of economics at the University of Michigan, Ann Arbor. He received his Ph.D. in economics at the University of Washington, Seattle. He has made important contributions to research in labor economics and the economics of fertility and the family. He is currently conducting research on subjective stock market expectations, the effect of technological change on the labor supply, and the relationship between cognition and economic behavior. Dr. Willis is past director of the Health and Retirement Study and past president of the Society of Labor Economists and the Midwest Economic Association.
Appendix
Table A.1.
Descriptive Statistics, HRS-2002
| Mean | SD | |
|---|---|---|
| Alive in 2010 | 0.77 | 0.42 |
| Subjective survival probability to target age | 48.40 | 32.13 |
| Age | 68.15 | 8.69 |
| Target age less actual age | 15.97 | 4.17 |
| Female | 0.59 | 0.49 |
| Black | 0.12 | 0.33 |
| Hispanic | 0.06 | 0.24 |
| Years of education | 12.54 | 3.00 |
| Mother is alive | 0.16 | 0.37 |
| Mother’s age of death/100 or current age | 0.76 | 0.15 |
| Father is alive | 0.05 | 0.23 |
| Father’s age of death/100 or current age | 0.72 | 0.14 |
| Exercises at least 3 times a week | 0.43 | 0.49 |
| Ever smoked | 0.59 | 0.49 |
| Smokes now | 0.14 | 0.34 |
| Ever drinks alcohol | 0.48 | 0.50 |
| No. of days a week when drinks alcohol | 1.10 | 2.08 |
| No. of days a week when drinks alcohol if positive | 3.42 | 2.34 |
| No. of drinks when drinks alcohol | 0.61 | 1.18 |
| No. of drinks when drinks alcohol if positive | 1.92 | 1.36 |
| Health excellent/very good, 2002 | 0.43 | 0.49 |
| Health good, 2002 | 0.32 | 0.47 |
| Health fair/poor, 2002 | 0.25 | 0.43 |
| Health excellent/very good, 2000 | 0.47 | 0.50 |
| Health good, 2000 | 0.31 | 0.46 |
| Health fair/poor, 2000 | 0.22 | 0.42 |
| Cognition scorea | 0.08 | 1.01 |
| Vocabulary scorea | 0.11 | 0.97 |
| CESD depression scorea | −0.04 | 1.04 |
| N | 13,038 |
These variables were standardized to have mean 0 and standard deviation 1 in the total HRS sample.
Table A.2.
Actual Survival Until 2010 and the Mean and MRH Models of Subjective Survival Expectations, Models Without Covariates
| Actual survival | Mean model | MRH | |
|---|---|---|---|
| ln(γ0) | −8.404 [0.21]*** | ||
| ln(θ50) | −11.174 [0.150]*** | −8.827 [0.169]*** | |
| ln(n) | 1.978 [0.040]*** | ||
| ln(γ1) | 2.277 [0.024]*** | 2.73 [0.012]*** | 2.397 [0.020]*** |
| ln(k) | −0.656 [0.011]*** | 0.121 [0.025]*** | |
| ln(sd(n)) | 0.814 [0.025]*** | ||
| N | 13,038 | 13,038 | 13,038 |
| Log-likelihood | −57,961.459 | −47,058.606 |
Significant at the 1% level.
Table A.3.
Quantiles of Belief Precision n and Probabilities of Surviving from Age 50 to Age 80
| Quantiles | n | γ0 | S(50, 80) |
|---|---|---|---|
| 10 | 0.40 | 0.000022 | 0.87 |
| 25 | 1.58 | 0.000054 | 0.71 |
| 50 | 7.23 | 0.000120 | 0.47 |
| 75 | 33.12 | 0.000229 | 0.23 |
| 90 | 130.31 | 0.000370 | 0.10 |
Footnotes
Frank Knight, as early as in 1921, introduced the distinction between, as he called them, “risk” for known and “uncertainty” for unknown probabilities (Knight 1921).
Paté-Cornell (1996, pp. 96–97) observes that “uncertainties in decision and risk analyses can be divided into two categories: those that stem from variability in known (or observable) populations and, therefore, represent randomness in samples (aleatory uncertainties), and those that come from basic lack of knowledge about fundamental phenomena (epistemic uncertainties also known in the literature as ambiguity).”
The attempt to determine the probabilistic beliefs of lay people using direct questions on surveys has only become commonplace in the past two decades (Manski 2004). There is a related but somewhat separate tradition of eliciting probability beliefs of experts as part of risk assessments in engineering and operations research applications. See Paté-Cornell (1996) for a summary of this tradition.
Our findings about the external validity of the HRS subjective probability questions are consistent with those in earlier papers that studied these questions in the HRS (Hurd and McGarry 2002, Smith et al. 2001). The overly optimistic expectations of people over 75 in the HRS have also been noted by Hurd et al. (2005), who found the same pattern across 11 European countries in the SHARE (Survey of Health, Ageing and Retirement in Europe). There are also a few papers that use these questions in models of behavior under uncertainty such as, for example, Picone et al. (2004), who found that people who expect to live longer are more likely to choose medical screening tests.
In recent waves of the Health and Retirement Study, respondents have been asked a follow-up question if they answered 50 to the survival probability question: Do you think that it is about equally likely that you will die before 75 as it is that you will live to 75 or beyond, or are you just unsure about the chances? About two-thirds say that they are “just unsure.” In this paper, we use data from the 2002 wave of HRS, which did not have a follow-up question.
In addition, the answers to the survival questions also exhibit some heaping at 0 and 100. Taken literally, of course, these answers cannot represent rational probability beliefs, except perhaps in the case of 0 for persons who know themselves to be terminally ill or planning suicide.
Manski and Molinari (2010) discuss an alternative, more direct approach to learn about the imprecision of belief. They make use of a follow-up question in a different survey (the American Life Panel) asking about the range of probabilities responders had in mind when they provided their answers. Roughly half of the sample reported that their answers were “exact,” and the rest reported relatively wide ranges of probabilities, with the average width being 18%. We believe that this approach is very informative about general uncertainty in the population, but it is less obvious how to make use of the provided ranges. First, the meaning of an “exact” answer is ambiguous. Second, one would expect that 50% responders provide wider ranges of possible probabilities than people with other answers ending with 0 or 5 (like 10% or 15%). However, they did not find a strong pattern like that in their data.
Another example is the work of Bommier and Villeneuve (2012), who discuss a model of mortality risk aversion, where the utility function is not additively separable over time, and thus mortality probabilities enter the model in a nonlinear fashion as well.
It is possible to regard answers of 0 or 100 as approximations that are no different in kind than rounded answers of 5, 40, or 95. However, in a discussion of Gan et al. (2005), Willis (2005) provides evidence against this interpretation.
Other cases will be discussed later.
In the survival context, a U -shaped distribution could represent the beliefs of someone who is unsure whether he had inherited a genetically transmitted disease. In case he did, he might face a low survival probability to the target age, but if he did not, he has a high probability of surviving. The posterior distribution of the survival probability in this case can have a U -shape, where the extreme probabilities are more likely than any middle values. However, it is not plausible that such situations are common enough to account for the large number of “50” responses that we see in survey responses.
The 2002 HRS is a representative panel sample of the 54 and older population and their spouses.
Actual mortality of HRS respondents is very precisely measured from administrative data (the National Health Index), and it is even available for people who dropped out of the survey in a later wave.
Simple exploratory work suggested that parental mortality has a stronger effect on expectations when the parent died at an old age. The specification we use in this paper is not the only way to allow for such nonlinearity, and future work should explore alternative models.
These three categories represent relatively good, average, and relatively bad health. The reason for the aggregation is that we interact subjective health in 2000 and 2002, and adding 5 × 5 = 25 interactions would make the interpretation of these variables difficult.
The 27-point scale Langa–Weir method is discussed by Crimmins et al. (2011). HRS cognitive measures are described by Fisher et al. (2012).
There is a long history of discussion about the difficulty in separately identifying duration effects and unobserved heterogeneity. See, for example, Vaupel (1979) and Heckman and Singer (1984). Using subjective survival data, however, identifying unobserved heterogeneity in frailty is easier, because we observe probabilities of survival on the individual level. This contrasts with the use of mortality data, where it is hard to know which survivor is fit and which is simply luckier than other nonsurvivors. Even though we use a particular functional form for how unobserved heterogeneity enters the model (the gamma-Gompertz framework), it is important to note that these functional form assumptions are not needed for identifying unobserved heterogeneity in subjective frailty.
Note, however, that the particular shape of the distribution of beliefs is only identified from the lognormal functional form in the region where n is less than 1. Because there are many focal responses in the HRS data, the model estimates many uncertain responses where n < 1. It is hard to know, however, what the distribution of n looks like, conditional on being less than 1. The log-normality assumption might or might not describe this conditional distribution well. It is possible, for example, that no one has U -shaped beliefs, but all epistemic 50 responses come from a uniform distribution. If that is the case, then the log-normality assumption of n is inappropriate.
Supplemental Material
Supplemental material to this paper is available at http://dx.doi.org/10.1287/deca.2013.0266.
Contributor Information
Péter Hudomiet, Email: hudomiet@umich.edu.
Robert J. Willis, Email: rjwillis@umich.edu.
References
- Bommier A, Villeneuve B. Risk aversion and the value of risk to life. J Risk Insurance. 2012;79(1):77–104. [Google Scholar]
- Bruine de Bruin W, Carman KG. Measuring risk perceptions—What does the excessive use of 50% mean? Medical Decision Making. 2012;32(2):232–236. doi: 10.1177/0272989X11404077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruine de Bruin W, Fischhoff B, Halpern-Felsher BL, Millstein SG. Verbal and numerical expressions of probability: “It’s a fifty–fifty chance. Organ Behav Human Decision Processes. 2000;81(1):115–131. doi: 10.1006/obhd.1999.2868. [DOI] [PubMed] [Google Scholar]
- Crimmins EM, Kim JK, Langa KM, Weir DR. Assessment of cognition using surveys and neuropsychological assessment: The Health and Retirement Study and the Aging, Demographics, and Memory Study. J Gerontology: Ser B. 2011;66B(S1):i162–i171. doi: 10.1093/geronb/gbr048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellsberg D. Risk, ambiguity, and the savage axioms. Quart J Econom. 1961;75(4):643–669. [Google Scholar]
- Fischhoff B, Bruine de Bruin W. Fifty–fifty = 50%? J Behav Decision Making. 1999;12(2):149–163. [Google Scholar]
- Fisher GG, Hassan H, Rodgers WL, Weir DR. [Accessed April 1, 2012];Health and Retirement Study—Imputation of cognitive functioning measures: 1992–2010 early release. 2012 http://hrsonline.isr.umich.edu/modules/meta/xyear/cogimp/desc/COGIMPdd.pdf.
- Gan L, Hurd MD, McFadden D. Individual subjective survival curves. In: Wise D, editor. Analyses in the Economics of Aging. University of Chicago Press; Chicago: 2005. pp. 377–412. [Google Scholar]
- Gilboa I, Marinacci M. Working Papers 379, Innocenzo Gasparini Institute for Economic Research. Bocconi University; Milan, Italy: 2011. Ambiguity and the Bayesian paradigm. [Google Scholar]
- Heckman JJ, Singer B. A method for minimizing the impact of distributional assumptions in econometric models for duration data. Econometrica. 1984;52(2):271–320. [Google Scholar]
- Hill D, Perry M, Willis RJ. [Accessed April 1, 2012];Estimating Knightian uncertainty from survival probability questions on the HRS. 2004 http://cogecon.isr.umich.edu/publications/HPW2004.pdf.
- Hurd MD, McGarry K. Evaluation of the subjective probabilities of survival in the Health and Retirement Study. J Human Resources. 1995;30(5):268–292. [Google Scholar]
- Hurd MD, McGarry K. The predictive validity of subjective probabilities of survival. Econom J. 2002;112(482):966–985. [Google Scholar]
- Hurd MD, Rohwedder S, Winter J. Subjective probabilities of survival: An international comparison. RAND; Santa Monica, CA: 2005. Unpublished manuscript. [Google Scholar]
- Knight FH. In: Risk, Uncertainty, and Profit. Hart, Schaffner, Marx, editors. Houghton Mifflin Company; Boston: 1921. [Google Scholar]
- Lillard LA, Willis RJ. Working Paper, WP 2001–007. University of Michigan Retirement Research Center; Ann Arbor, MI: 2001. Cognition and wealth: The importance of probabilistic thinking. [Google Scholar]
- Lumsdaine RL, Potter van Loon RJD. [Accessed April 1, 2012, ];Wall street vs main street: A comparison of views. 2012 http://www.american.edu/cas/economics/news/upload/Lumsdaine-paper.pdf.
- Manski CF. Measuring expectations. Econometrica. 2004;72(5):1329–1376. [Google Scholar]
- Manski CF, Molinari F. Rounding probabilistic expectations in surveys. J Bus Econom Statist. 2010;28(2):219–231. doi: 10.1198/jbes.2009.08098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ofstedal MB, Fisher GG, Herzog AR. [Accessed April 1,2012];Documentation of cognitive functioning measures in the Health and Retirement Study. 2005 http://hrsonline.isr.umich.edu/sitedocs/userg/dr-006.pdf.
- Paté-Cornell ME. Uncertainties in risk analysis: Six levels of treatment. Reliability Engrg System Safety. 1996;54(2–3):95–111. [Google Scholar]
- Picone G, Sloan F, Taylor D. Effects of risk and time preference and expected longevity on demand for medical tests. J Risk Uncertainty. 2004;28(1):39–53. [Google Scholar]
- Savage LJ. The Foundations of Statistics. Wiley; New York: 1954. [Google Scholar]
- Smith VK, Taylor DH, Sloan FA. Longevity expectations and death: Can people predict their own demise? Amer Econom Rev. 2001;91(4):1126–1134. [Google Scholar]
- Vaupel JW. The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography. 1979;16(3):439–454. [PubMed] [Google Scholar]
- Vaupel JW. Trajectories of mortality at advanced ages. In: Wachter KW, Finch CE, editors. Between Zeus and the Salmon. National Academy Press; Washington, DC: 1997. pp. 17–37. [Google Scholar]
- Willis RJ. Discussion of “Individual subjective survival curves”. In: Gan L, Hurd MD, McFadden D, Wise D, editors. Analyses in the Economics of Aging. University of Chicago Press; Chicago: 2005. pp. 402–412. [Google Scholar]