Conformational Dynamics of the Partially Disordered Yeast Transcription Factor GCN4

Abstract

Molecular dynamics (MD) simulations have been employed to study the conformational dynamics of the partially disordered DNA binding basic leucine zipper domain of the yeast transcription factor GCN4. We demonstrate that back-calculated NMR chemical shifts and spin-relaxation data provide complementary probes of the structure and dynamics of disordered protein states and enable comparisons of the accuracy of multiple MD trajectories. In particular, back-calculated chemical shifts provide a sensitive probe of the populations of residual secondary structure elements and helix capping interactions, while spin-relaxation calculations are sensitive to a combination of dynamic and structural factors. Back calculated chemical shift and spin-relaxation data can be used to evaluate the populations of specific interactions in disordered states and identify regions of the phase space that are inconsistent with experimental measurements. The structural interactions that favor and disfavor helical conformations in the disordered basic region of the GCN4 bZip domain were analyzed in order to assess the implications of the structure and dynamics of the apo form for the DNA binding mechanism. The structural couplings observed in these experimentally validated simulations are consistent with a mechanism where the binding of a preformed helical interface would induce folding in the remainder of the protein, supporting a hybrid conformational selection / induced folding binding mechanism.

Introduction

Following initial discoveries that proteins can be fully functional in the absence of stable folded tertiary structures, intrinsically disordered proteins (IDPs) and the disordered regions of partially disordered proteins are increasingly recognized to play important functional roles in a significant fraction of eukaryotic and prokaryotic proteins ^1-3. Sequence based predictions of disorder estimate that ∼40% of the mammalian proteome is intrinsically disordered or contains disordered regions of > 50 amino acids. The function of intrinsically-disordered proteins are often associated with signaling and regulatory pathways in eukaryotes, as unstructured protein segments are capable of interactions with several partners, and are capable of obtaining highly specific interactions with low affinities ⁴. IDPs are also implicated in a variety of diseases, including neurodegenerative diseases such as Alzheimer's, Parkinson's and Huntington's disease ^4-6. Consequently, a structural understanding of IDP function is of great interest.

A central question in the study of IDPs is the mechanism by which IDPs bind their interaction partners^7-9. Two mechanistic extremes have been proposed for the coupling of IDP folding and binding. The conformational-selection model suggests that residual structure observed in the unbound state of an IDP ^10,11 reflects pre-formed native-like conformations that are selected by the interaction partner during binding ¹². Such elements of residual native structure should favor binding thermodynamically, by restricting conformational space and thus reducing the loss of entropy upon binding, as well as kinetically, by providing pre-nucleated interfaces for initial contacts and subsequent folding of the full binding interface. The induced-folding model, on the other hand, suggests that residual structure in IDPs is unrelated to the structure in the complex; folding is induced by association with the target through nonspecific electrostatic or hydrophobic initial contacts⁸. As with most dichotomies in biology, experimental and computational evidence has been presented in support of both models, indicating that any real IDP probably utilizes some combination of the two models. Reconciliatory models in which a balance between conformational selection and induced folding is used to fine-tune the thermodynamics and kinetics of binding have been proposed ^9,13. Recent studies have demonstrated that the alternate binding mechanisms of conformational selection and induced fit, of which induced folding is a special case, can be simultaneously accessible, while the relative flux through the two pathways is determined by the relative kinetics of preforming binding-competent states and converting non-specific encounter complexes into the bound state ^13-16.

Among biophysical and structural techniques, Nuclear Magnetic Resonance (NMR) spectroscopy is particularly well suited for the study of structurally heterogeneous IDPs, and can provide detailed sight specific information on local and global structural and dynamic features of disordered states¹⁷. Substantial progress has recently been made in computational methods that generate conformational ensembles of IDPs consistent with NMR measurements ^18-22. Among computational techniques, molecular dynamics (MD) simulations are unique in their ability to simultaneously probe both the structure and the dynamics of disordered proteins. Sufficiently accurate MD simulations could potentially enable a detailed dissection of cooperative interactions that are associated with particular structural or dynamic features of IDPs. Unbiased all-atom explicit-solvent MD simulations of IDPs have only recently become feasible due to the high computational costs of simulating a sufficient number of water molecules to accommodate extended structures and adequately sampling the large conformational space accessible to disordered states. Initial results obtained from long time-scale simulations on special purpose hardware²³ and using large-scale Replica Exchange simulations²⁴ have been promising.

The DNA-binding domain of the S. cerevisiae transcription factor GCN4, a regulator of protein biosynthesis, is the prototype of the basic leucine-zipper (bZip) domain with known homologues in birds (v-Jun) as well as mammals (Jun, Fos)²⁵. The isolated GCN4 bZip domain binds DNA as a homodimer of two α-helices²⁶. The helices form a coiled-coil dimerization interface in the C-terminal region, termed the leucine zipper, and diverge in the N-terminal basic region to make sequence-specific contacts in the major groove of the cognate DNA. In the absence of substrate, however, the basic region has been shown using circular dichroism (CD) ^27,28 and NMR ^27,29 to form a dynamic ensemble with significant residual helicity, while the leucine zipper maintains a well-ordered coiled-coil dimer interface.

In an effort to characterize the structure and dynamics of the partially disordered DNA-binding GCN4 bZip domain and obtain insight into its DNA binding mechanism we have performed multiple unbiased all-atom explicit-solvent MD simulations. By analyzing the agreement of back-calculated NMR chemical shifts, spin-relaxation orientational spectral density functions, and generalized order parameters, we were able to compare the accuracies of multiple MD trajectories, and identify the MD trajectory that is the most consistent with the experimental NMR measurements. Analysis of dynamically averaged semiempirical chemical shift predictions^30-32 is used to evaluate the populations of residual secondary structure elements and the populations of specific helix capping interactions that stabilize residual secondary structure elements. Analysis of calculated orientational spectral density functions indicates that the rotational diffusion of the GCN4 bZip domain occurs on timescales that are too fast relative to NMR measurements, making the comparison of simulated and experimental spectral density functions in the dynamic basic region difficult. We demonstrate that by calculating spectral density functions for our simulations using the leucine zipper as an internal molecular reference frame and correcting for rotational diffusion, simulated spectral density were more sensitive to the internal dynamics of the basic region and in better agreement with experiments. Similarly, we observe excellent agreement between experimental generalized order parameters and order parameters calculated using the leucine zipper as a molecular reference frame, and we examine the sensitivity of order parameters to different motions in the simulations. Finally, we conduct an analysis of the structural interactions, such as the presence of salt-bridges and helix capping hydrogen bonding interactions, that favor and disfavor helical conformations in the basic region, and consider the implications of the structure and dynamics of the apo form of the GCN4 bZip domain on its DNA binding mechanism. The structural couplings observed in our experimentally validated simulations support a mechanism where the binding of a preformed helical interface would induce folding in the remainder of the basic region.

Results and Discussion

We performed four 100 ns MD simulations of the DNA-binding bZip domain of GCN4 originating from different partially unfolded starting structures. The 56-residue construct we simulated consisted of the 25 residue N-terminal DNA-binding basic region (Lys1-Arg25), and the 31 residue C-terminal leucine zipper (Met26-Glu56). The basic region has previously been demonstrated to form a dynamic ensemble with significant residual helicity in solution by CD and NMR^27,29,33. To generate the starting structures for our simulations, the protein coordinates were taken from the crystal structure of the GCN4 bZip domain in complex with DNA (PDB code 1YSA)²⁶, where the protein is entirely helical, and were simulated without the DNA substrate for 50 ns in the NPT ensemble at 310K with the Amber99SB force field³⁴ and the TIP3P^35,36 water model. Harmonic position restraints of 0.5 kcal/mol/Ų were applied to the backbone heavy atoms of the leucine zipper region to prevent dimer dissociation. The basic region unfolds during this simulation and four structures with varying degrees of helicity were selected as starting points for 300 K production simulations. The four starting structures selected contained between 18% and 40% fractional helicity in the basic region, and are shown in SI Figure 1. These four structures were each re-solvated in larger water boxes, energy minimized, and equilibrated for 5 ns at 300 K before initiating 100 ns NVT production runs with the Amber99SB force field and the TIP3P water model without atomic position restraints. These four 100 ns production simulations, which were run with identical simulation parameters but different starting structures, are referred to as trajectories 1-4.

Residual Helical Structure in the Basic Region

In all four trajectories, the leucine zipper remained stable, but helical fragments of different lengths continuously formed and broke in the basic region. The amounts of helical structure in the basic region varied significantly among the four trajectories, illustrating that the helical populations of the basic region are not converged on the 100 ns timescale examined here. Each trajectory is therefore representative of a local sampling of phase space near the starting structure, rather than an equilibrated measure of the force field properties for this system. Trajectories 1, 2, 3, and 4 were initiated from structures in which 40%, 32%, 18%, and 28% of the basic region residues were in helical conformations, respectively, and the average helical content of the basic region throughout each simulation was 21%, 47%, 19%, and 26%, respectively. The per-residue fractional helicity observed in each trajectory is compared to the fractional helicity predicted from the experimentally measured chemical shifts in Figure 1. Trajectory 2, which has the most helical content of the trajectories (72% for the entire dimer) is in the closest agreement with helical populations predicted from the experimental chemical shifts, and is in the best agreement with estimates from CD of ∼75% helix³⁷. We note that a recent MD study of the GCN4 bZip domain which initiated apo simulations from the completely helical DNA bound form of structure reported a basic region which remained almost entirely helical in 50ns simulations, at odds with results obtained from NMR and CD³⁸, illustrating the importance of choosing appropriate starting structures when studying IDPs, as has previously been documented for globular proteins³⁹.

Figure 1.

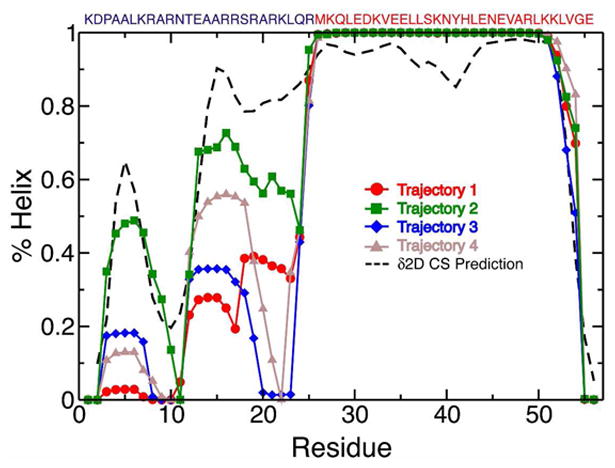
Fractional helicity for each residue of GCN4 bZip domain observed in four 100 ns MD trajectories initiated from starting structures with varying degrees of helicity. Helical conformations were assigned for each MD snapshot using the program STRIDE. Helix populations predicted from the experimental chemical shifts using the δ2D program are shown as a dotted line. The sequence of the GCN4 bZip domain is displayed above the graph with residues in the basic region colored blue and residues in the leucine zipper colored red.

Although the amount of helical content in the basic region of GCN4 varied substantially between trajectories, the residues involved in the formation of residual helical structure were consistent. Two regions of elevated helix population are observed; a cluster of residues from Ala4-Arg8 (henceforth termed H1), and a cluster of residues centered on Glu13-Arg19 (henceforth termed H2). Both clusters are in agreement with the locations of elevated helix content predicted from chemical shifts, were identified as regions with elevated helix content based on chemical shift temperature coefficients and spin relaxation data, and are flanked by potential helix-capping interactions (Asp2 and Pro3 proceed H1, and Asn11 and Thr12 proceed H2) In trajectory 2, and to a lesser extent in trajectory 1, substantial helical content is additionally observed in the “linker” region between H2 and the fully helical leucine zipper beginning and Met26, which is also predicted from the experimental chemical shift values.

The time course of helix formation and breaking is shown for each trajectory as the helical fraction of each residue averaged over 1 ns blocks in SI Figure 2. Energy landscapes comparing the conformational space explored by the basic region in each trajectory are plotted as a function of the number of basic region helical residues and basic region radius of gyration in SI Figure 3. These plots illustrate that these four independent trajectories, initiated from four different starting structures, explore substantially different regions of phase space. In what follows, by comparing the values of NMR chemical shifts and spin relaxation data calculated from these trajectories to experiments, we are able to gain insight into the discriminative power of these NMR measurements for assessing the accuracy of MD simulations of IDPs, and to identify the trajectory which produces a conformational distribution of GCN4 that is in the best agreement with the conformational properties observed in solution. We emphasize that we are comparing the properties of four independent unbiased and unrestrained simulations, and that the trajectories were not subject to any posteriori pruning or population reweighting.

Calculation of NMR Observables

Chemical Shifts

For each MD trajectory, we used SPARTA+⁴⁰ to compute the backbone chemical shifts of each frame (4.5ps spacing) and calculated the MD average of the Cα, C', H_N, and N chemical shift values for all nuclei for which an experimentally measured chemical shift was available. We found that the average chemical shifts of the leucine zipper did not vary substantially between trajectories, as the structural fluctuations of the coiled coil were minor in all trajectories on the timescales studied here. We observed significant variation in the average chemical shifts computed for the disordered basic region amongst the trajectories. The root mean square deviations (rmsd) of the average chemical shift predictions of each trajectory from the experimentally measured values are compared for the basic region residues in Table 1. Shift predictions were also repeated with Shiftx+⁴¹, and were consistent with the results obtained from Sparta+.

Table 1. Experimental and Predicted Chemical Shifts of the GCN4 basic region (residues Asp2-Arg25).

Trajectory1	Sparta+ CS Predictions2
	Cα	C'	HN	N
1	1.09	1.01	0.18	1.27
2	0.63	0.54	0.13	1.38
3	1.10	1.07	0.19	1.33
4	1.08	0.99	0.18	1.28

¹Four 100 ns MD simulations initiated from starting structures with varying degrees of helicity.

²RMSD's between experimental and average Sparta+ chemical shift predictions.

We observe that the calculated Cα, C', and H_N chemical shifts of the basic region are in substantially better agreement with experiment in trajectory 2, the most helical trajectory, compared to the other trajectories. The predicted N shifts of the basic region residues do not vary substantially between the trajectories and are in good agreement with experimental shifts compared to the average rmsd of N shift predictions in globular proteins. N shifts are particularly sensitive to side chain χ₁ angles, and the solvent exposed side chains of the basic region freely transition between rotamers in all of the trajectories, resulting in similar rotamer populations and similar average N chemical shifts and on the timescales examined here. Figure 2 displays a comparison of the differences between the MD averaged Sparta+ predictions (δ_MD) and the experimentally measured values (δ_Exp) of the basic region Cα, C', and H_N chemical shifts for each trajectory. The improved agreement with experiment is pronounced in the regions of elevated residual helical structure in trajectory 2. We note that larger deviations for Cα and C' are observed for Arg10 and neighboring residues. Analysis of the distributions of the shift predictions for these residues suggests that the simulations do not contain enough helical content in these regions to reproduce the experimental values.

Figure 2.

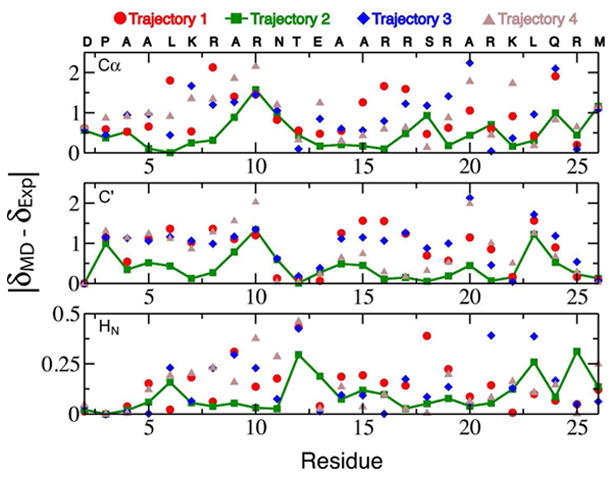
Deviations between the experimentally measured Cα, C', and H_N chemical shifts (δ_Exp) and the average Sparta+ chemical shift predictions (δ_MD) for the basic region residues of the GCN4 bZip domain from four 100 ns MD simulations initiated from starting structures with varying degrees of helicity.

Several C-capping hydrogen bonds in H1 are populated at levels of 0.2-0.3 in trajectory 2, but are either absent or weakly populated in trajectories 1, 3, and 4 (table 2). The MD averaged chemical shifts of the C' and H_N atoms from the residues participating in these hydrogen bonds calculated from trajectory 2 are in significantly better agreement with the experimental values compared to the trajectories lacking these interactions (Figure 3). This illustrates that in addition to being sensitive to presence of residual secondary structure elements, subsets of dynamically averaged chemical shift values are also useful reporters of the populations of the specific interactions that can stabilize secondary structure elements.

Table 2. Population of H1 C-capping hydrogen bonds.

Hydrogen Bond1	Trajectory2
	1	2	3	4
A5O-A9HN	0.00	0.29	0.02	0.04
L6O-R10HN	0.00	0.23	0.00	0.01
K7O-R10HN	0.00	0.28	0.10	0.01
K7O-N11HN	0.00	0.20	0.05	0.00

¹A hydrogen bond is defined for conformations where the distance between N and O is less than 3.5Å and the NHO angle is > 110°.

²Four 100 ns MD simulations initiated from starting structures with varying degrees of helicity.

Figure 3.

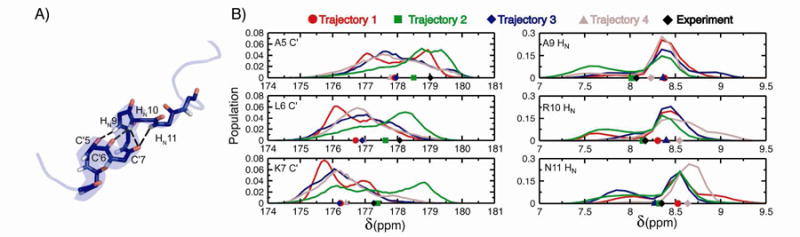
Populations of H1 helix stabilizing C-cap hydrogen bonds from chemical shifts. A) An illustrative conformation displaying hydrogen bond pairs formed by C-terminal residues of the partially populated H1 helix in MD simulations. B) Normalized distribution of Sparta+ predicted chemical shifts for the C' and H_N atoms involved in the hydrogen bonds observed in the MD trajectories. The average value of the shift predictions for trajectories 1, 2, 3, and 4 are displayed as a red circle, a green square, a blue diamond, and a brown triangle respectively. The experimentally measured value is shown as a black diamond.

We note that secondary H_N shifts have generally been considered the least sensitive of the backbone shifts for determining populations of helical structures⁴². The strong effects of helix capping i+3 or i+4 hydrogen bonds on H_N shift predictions observed here suggests that the relationship between the secondary H_N shift of a residue and its helical propensity could be complicated by the presence of hydrogen bonding interactions with the termini of neighboring partially populated helices. It is also interesting to speculate that certain protein sequences may confer a propensity for dynamic transient helix formation based on tuning the comparative energetics of helical, helix capping, and coil motifs.

It has previously been illustrated that dynamically averaged chemical shifts of disordered proteins are subject to a degree of degeneracy^20,43. For a given subset of chemical shifts, there may exist multiple conformational distributions that produce average chemical shifts that are in equally good agreement with experimental values. By simultaneously considering multiple chemical shift types that are variably sensitive to different conformational properties (Cα shifts which are more sensitive to ϕ/ψ dihedral angles, and C' and H_N shifts which are more sensitive to presence of hydrogen bonds) throughout the entire basic region, we gain increased confidence that the substantial improvements we observe in the prediction accuracy for trajectory 2 suggests that the conformational distribution of this trajectory most closely resembles the conformational distribution observed in solution. Additionally, close agreement with the secondary structure populations predicted from CD and the δ2D method and the excellent agreement with experimental spin relaxation data (vide infra), which are sensitive to substantially orthogonal conformational and dynamic features, strengthen this assertion.

Spectral Density Functions

Spectral density functions represent the frequency distribution of the motions of a given backbone amide bond vector. For each trajectory, we computed the autocorrelation functions (ACFs) of the amide bond vector orientations in the “laboratory” frame, without performing any alignment of the molecule²³. ACFs were subjected to a smoothing procedure (see methods), and were Fourier transformed to obtain orientational spectral density functions at specific frequencies (J(ω)) for comparison with experimentally measured values. A comparison of the experimental J(0), J(0.87ω_H), and J(ω_N) values and the simulated values computed from the unaligned trajectories are displayed in SI Figure 4. Simulated values of J(0) and J(0.87ω_H) showed a high correlation with experimental values for all trajectories (average correlation coefficients of r=0.94 and r=0.96, respectively) however simulated values of J(0) were lower than experimental values by between a factor three and a factor of eight amongst the trajectories, and simulated values of J(ω_N) showed a very poor correlation with experiment (average correlation coefficient r = −0.62). These discrepancies result from overall rotational tumbling occurring too quickly in the simulations. For a well ordered site in a macromolecule subject to limited conformational fluctuations, such as an amide bond vector in a stable helix, a local overall rotational correlation time, τ_m, can be estimated from the spectral density functions J(0) and J(ω_N) according to ${\mathrm{\tau }}_{\mathrm{m}}={\omega }_N^{-1}{[\{J(0)-J({\omega }_N)\}/J({\omega }_N)]}^{0.5}$. At 300 K the average value of τ_m in the coiled coil region in the apo form of GNC4 is estimated to be 18.9 ns from the experimental spectral densities²⁷. In trajectories 1, 2, 3, and 4 the average values of τ_m estimated from the spectral densities of the coiled coil region are 2.7, 6.3, 5.5, and 4.1 ns, respectively, illustrating that overall rotational tumbling observed in these simulations is too fast, as has been previously observed for the rotational diffusion of globular proteins ^44,45. This is likely due to limitations in current water models and deficiencies in the modeling of water-protein interactions with current popular force field and water model combinations^46,47,48,49.

To side-step deficiencies in the accuracy and the convergence of the rotational tumbling and enable a better comparison of the timescales and amplitudes of motion of the basic region observed in our simulations with experiments, we also computed spin relaxation values relative to an internal alignment frame, evoking the approximation of a separation of internal dynamics and overall tumbling that is frequently employed when considering the dynamics of globular proteins using the model free formalism^50,51. Such a separation of ‘internal’ dynamics and ‘global’ tumbling will not exist for the majority of intrinsically disordered proteins, which will not possess large regions of persistently stable structure that will have a dominant contribution to the rotational diffusion of the molecule. However, owing to the relative volume of the structured leucine zipper relative to the dynamic basic region, this approximation is reasonable for GCN4, and was employed in the analysis of the experimental relaxation data²⁷. For each trajectory, all frames were aligned based on the superposition of the backbone atoms of the leucine zipper. ACFs of amide bond vector orientations were computed in this aligned internal reference frame and were multiplied by an exponential decay with a correlation time of 18.9 ns to correct for rotational tumbling. The J(ω) values computed from the aligned reference frame using this approximation of isotropic tumbling are in significantly better agreement with experiment (Table 3, SI Figure 5) compared to these computed from the unaligned trajectories.

Table 3. Experimental and simulated S² and J(ω).

Trajectory	S2 (Aligned)	S2 (iRED)	J(0)	J(ωN)	J(0.87 ωH)
1	0.120	0.157	2.04	0.058	0.0052
2	0.068	0.090	1.37	0.057	0.0042
3	0.096	0.132	1.73	0.074	0.0059
4	0.095	0.152	1.40	0.062	0.0050

Rmsd's are shown for S² values computed using the structured coiled coil residues as an internal molecular reference frame (Aligned) and using the iRED approach. Rmsd's are shown for J(ω) values computed using the structured coiled coil residues as an internal molecular reference frame.

The J(ω) values computed from trajectory 2, the most helical trajectory, are in the best agreement with the experimental values, indicating that the trajectory that reproduces the populations of helical conformations in best agreement with the experimental chemical shifts and CD measurements also samples timescales of motion that are the closest to these observed experimentally from spin-relaxation, suggesting that the phase space explored in this trajectory is the most representative of conformational and dynamic properties observed in solution.

Comparison of simulated J(ω_N) and J(0.87ω_H) values to experiments seems to suggest that for all of the trajectories, the timescales of motion observed in the basic region generally appear to be too fast, particularly for residues closer to the N-terminus. These effects are particularly large for monomers that do not form any tertiary contacts in the simulations. We observed that in trajectory 2, one monomer which does not form any tertiary contacts undergoes motions with timescales that are very fast relative to experiments while the second monomer forms persistent tertiary contacts and undergoes motions with timescales that are comparable to the experimental values (SI Figure 6). However, no experimental evidence supports any of the tertiary contacts observed these simulations. Therefore, motions of the protein chain that displace water molecules may be occurring on timescales that are too fast, and could be fortuitously offset by the formation of too many or overly persistent hydrophobic contacts. These results are consistent with observations that popular MD force field and water models combinations similar to the one employed here produce rotational diffusion constants for globular proteins that are too large^44,45,49 and produce radii of gyration of unfolded proteins that are too small^24,46-48. It is interesting to note that a recently published 200μs simulation of an unfolded protein showed excellent agreement with experimentally measured J(0) and R₂ values using the TIP3P water model employed in this investigation while producing a radius of gyration that was too small relative to experimental values²³. It is possible that this agreement could potentially be the result of the same offsetting force field and water model deficiencies we hypothesize may be fortuitously cancelling here.

Order Parameters

Values of the generalized order parameters (S²) were computed for the trajectories aligned on the internal reference frame of leucine zipper in 18.9 ns blocks as described previously⁵². Experimental values of S² were determined using the same approximation of internal motion relative to the global tumbling of the internal molecular reference frame of the coiled coil²⁷. Experimental S² values at 300 K appear to be somewhat too large due to presence of transient higher molecular weight oligomeric species, suggested by the concentration dependence of experimentally measured R₂ values^27,53. To correct for this effect, experimental S² values were scaled by a factor of 0.92, so that the average coiled coil S² value was 0.87, the average coiled coil S² value observed in our simulations, and close to the value of 0.86 typically expected for residues in stable helices⁵⁴. The S² values computed for each trajectory are compared to the experimental values in Figure 4, and the rmsds from the experimental values are reported in table 3. Trajectory 2 again shows the closest agreement with the experimental values. With the exception of trajectory 4, which contains persistent tertiary contacts between residues 10-25 of the two monomers resulting in elevated S² values compared to experiment, the agreement with experiment is very good for all of the trajectories compared to the agreement seen in globular proteins using similar force fields⁵². To test if the excellent agreement with experimental values is primarily an artifact of the use of the molecular alignment frame, rather than the a reflection of the accuracy of the amplitudes of motion observed in the simulations, we also computed the of S² values using the isotropic reorientational eigenmode dynamics (iRED) method⁵⁵, which determines S² values based on the isotropically averaged covariance matrix of the amide bond vector orientations and therefore does not require a molecular alignment frame. The rmsd of simulated S² values computed by iRED are shown in table 2, and again trajectory 2 is in substantially better agreement with the experimental values. A comparison of the S² values computed by aligning the trajectories on the coiled-coil and computed by the iRED method is shown for each trajectory in SI figure 7. Analysis of the mode collectivities of the iRED eigenmodes compared to their eigenvalues does not suggest a complete separation of internal motions and overall tumbling, as would be expected from the fast tumbling timescales observed in these simulations (SI figure 8). Nevertheless, S² values computed by iRED neglecting the contribution of the 5 largest eigenmodes to the amplitudes of internal motions are in reasonable with experimental values and S² values computed with a molecular alignment frame.

Figure 4.

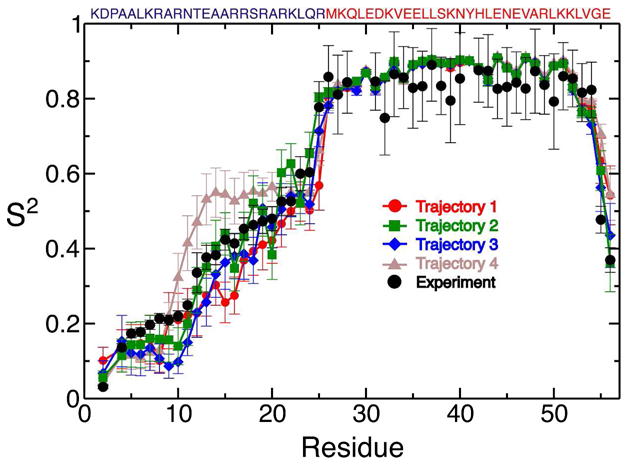
Comparison of experimental and simulated generalized order parameters (S²) from four 100 ns MD simulations initiated from starting structures with varying degrees of helicity. Simulated S² values were calculated after superposition of backbone atoms of the leucine zipper (residues 26-54). Error bars of the simulated S² values reflect the standard errors of the mean of each residue for five 18.9 ns analysis blocks. The sequence of the GCN4 bZip domain is displayed above the graph with residues in the basic region colored blue and residues in the leucine zipper colored red.

The S² values computed from trajectories 1, 2, and 3 are very similar even though the trajectories contain large differences in the populations of helical conformations in the basic region, illustrating that for this system S² values are not dominated by the population of helical conformations. The experimental order parameters exhibit a steep drop from Met26 to Gln24, which is reproduced in all of the trajectories examined here. We found that helical i+4 or 3₁₀-helical i+3 hydrogen bonds in the linker region between H2 and the stable coiled-coil exhibited a dynamic “flickering” behavior, where they would frequently break and reform. We observed this behavior in trajectories where helicity extends from the coiled-coil region into the basic region and in portions of trajectories where there is substantial (>90%) residual helicity in the linker region. Small fluctuations in the linker region can result in large angular displacements of the N-terminal residues of basic-region, resulting in very low S² values. The effects of these fluctuations appear to have a much larger effect on the computed S² and J(ω) values for the basic region residues than the helix populations of the more C-terminal residues.

Structural Determinants of Residual Helicity in the Basic Region

In order to identify the interactions that stabilize and destabilize the helical conformations in the basic region, we calculated the statistical associations of various structural features observed in the trajectories with the presence of helicity in H1 (Ala4-Arg8) and H2 (Glu13-Arg19) using phi coefficients. While trajectory 2, the most helical trajectory, samples a region of phase space that produces a distribution of conformations that is in the best agreement with experimental chemical shifts, spin relaxation data, and CD measurements, phi coefficients were calculated for structural interactions using all of the trajectories. This choice was made to provide better statistics of the structural interactions associated with non-helical conformations, which are sampled less frequently in trajectory 2. We note that while the population distributions of the conformations observed in Trajectories 1, 3, and 4 are not in agreement with experimental measurements, local associations between the presence of hydrogen bonds and salt-bridges and helical propensities remain informative. The previously observed N-capping interaction ³⁷ between the carboxyl group of Asp2 and the backbone amide of Ala5 was formed 77.0% of the time in the simulations, and showed a significant positive association with H1 helicity (ϕ=0.17). Conformations with the N-cap had a 24.2% helical propensity, while conformations without it had an 8.3% helical propensity. C-capping hydrogen bonds between carbonyl oxygen of Ala5 and the backbone amide of Ala9, the carbonyl oxygen of Leu6 and the backbone amide of Arg10, the carbonyl oxygen of Lys7 and the backbone amide of Arg10, and the carbonyl oxygen of Lys7 and the backbone amide Asn11 also showed significant positive association with H1 helicity (ϕ=0.24, ϕ=0.29, ϕ=0.34, and ϕ=0.28, respectively, calculated excluding conformations in which Ala10 participates in the helix). Conformations that formed any one of the four interactions had a 55.8% helical propensity, and those without any C-capping interactions had a 9.2% helical propensity. We also observed a helix destabilizing salt-bridge between the side chains of Asp2 and Arg10, which was formed 11.9% of time in the simulations. The presence of the salt-bridge showed a significant negative association with H1 helicity (ϕ=0.18). Conformations that formed the salt-bridge had a 0.6% helical propensity, and those without the salt-bridge had a 23.2% helical propensity. The side chain Arg10 competes with the amide proton of Ala5 for interaction with the carboxyl group of Asp2.

In H2, an N-capping interaction between the carboxyamide of Asn11 and the backbone amide of Glu14 was observed 68.5% of time in the simulations. This interaction did not however, show significant association with H2 helicity (ϕ=0.002). C-capping hydrogen bonds between the carbonyl oxygen of Arg16 and the backbone amide of Arg19, the carbonyl oxygen of Arg16 and the backbone amide of Ala20, the carbonyl oxygen of Arg17 and the backbone amide of Ala20, and the carbonyl oxygen of Arg17 and the backbone amide Arg21 also showed significant positive association with H2 helicity (ϕ=0.22, ϕ=0.30, ϕ=0.29, and ϕ=0.19, respectively, calculated excluding conformations in which helicity extends from the leucine zipper into H2). Conformations that formed any one of the four interactions had a 50.0% helical propensity, and those without any C-capping interactions had a 9.2% helical propensity. A helix-stabilizing salt bridge observed between the side chains of Glu13 and Arg16, which was formed 55.5% of the time in the simulations, was found to have a positive association with H2 helicity (ϕ=0.27). Conformations that formed the salt bridge had a 40.1% helical propensity, and those without the salt-bridge had a 16.0% helical propensity.

We also observed a positive association between helicity in H1 and helicity in H2 (ϕ=0.14), suggesting cooperativty in their formation. Conformations that are helical in H2 were 75% more likely to be helical in H1 (26.6% helical propensity in H1 with helix in H2 vs. 15.2% helical propensity in H1 without). Additionally, a significant positive association was observed between the H2-stabilizing Glu13-Arg16 salt bridge and the C-capping H1 interactions (ϕ=0.20). Conformations that form that salt bridge are approximately 2.5 time more likely to form at least one C-cap in H1 than those that do not (24.9% C-cap propensity with the salt bridge vs. 9.5% helical propensity without).

Insight into the Binding Mechanism of GCN4

Our analyses suggest that trajectory 2, the most helical of the four trajectories, is the most representative conformational ensemble of the apo form of the DNA-binding bZip domain of GCN4 in solution. Agreement with secondary structure populations predicted from CD and chemical shifts and the excellent agreement with structure based chemical shift predictions suggest that this trajectory contains an accurate representation of the populations of residual helical structure in the disordered basic region. Excellent reproduction of the generalized order parameters and reasonable agreement with experimental spectral densities suggests that the amplitudes and timescales of motion observed in this 100 ns trajectory are also reflective of the dynamics observed in solution.

To gain insight into the role of the structure and dynamics of the apo form of the GCN4 bZip domain in DNA binding we have mapped the fractional helicity observed in trajectory 2 onto crystal structure of the GCN4 bZip domain bound to DNA (PDB code 1YSA) in Figure 5. H2, which spans from Glu13-Arg19 and has the largest population of helical conformations in trajectory 2 (∼70% helical), forms the center of DNA-protein interface. Within H2, residues Asn11, Ala14, Ala15, Ser18, and Arg19 are highly conserved among bZip domains and form base-specific DNA interactions. Ala14 and Ala15 contact the 5-methyl groups of two thymine bases along the major groove of the DNA and create a hydrophobic pocket that accommodates the side chain of Asn11. This residue accepts a hydrogen bond from a cytosine and donates a hydrogen bond to a thymine, and is shielded from solvent by the side chains of Arg16, Arg17, and Ser18. Arg19 forms the boundary of the DNA binding site. The large residual helicity of the DNA binding interface in H2 in solution is suggestive of a preformed binding interface consistent with the conformational selection model of IDP binding: restriction of the basic-region conformations would lower the entropic penalty of the disorder-to-order transition associated with binding, and the preformed helical conformations would increase the probability of a productive encounter complex. Additionally, the salt-bridge that we observe between Glu13 and Arg16 in our simulations is formed in one of the monomers in the bound structure, illustrating that this H2 stabilizing interaction is compatible with the binding conformation. In support of this model, estimates of configurational entropy derived from the experimental order parameters agree with values derived from calorimetry ²⁷.

Figure 5.

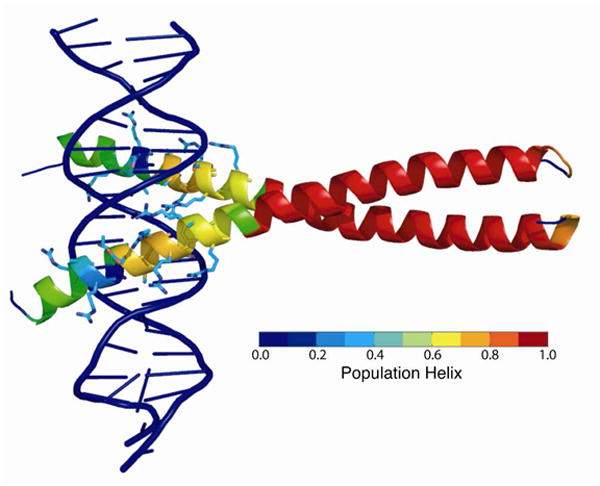
The fractional helicity of each residue observed in trajectory 2, the trajectory in the best agreement with experimental NMR data, is mapped onto the crystal structure of the GCN4 bZip domain bound to DNA (PDB code 1YSA) according to the color bar shown. Side chains are displayed for residues which make contacts with the DNA.

In contrast to H2, the residues in H1, Ala4-Arg8, are not conserved among bZip domains, and only Arg8 forms an interaction with the DNA. Deletion of the H1 N-cap has been found to decrease residual helicity and impede DNA-binding of the isolated basic region but not the full-length dimeric bZip domain of GCN4³⁷. This observation suggests that the coupling between H1 and H2 is bidirectional but does not affect H2 helicity significantly in the presence of the leucine zipper. Several bZip domains have been shown to be capable of binding DNA as unfolded monomers that subsequently dimerize by forming a leucine zipper on the DNA^56-58. A similar mode of binding has been proposed for GCN4 in vivo, given its relatively high (μM) dimerization constant and short half life ³⁷. If GCN4 indeed binds DNA as a monomer, residual helicty in H1 may positively contribute to binding by promoting helicity in H2. In the full-length bZip dimer, however, our simulations indicate that substrate binding may instead promote helicity in H1 via two distinct mechanisms. First, formation of DNA interactions by Arg10 should promote H1 helicity by abrogating interference of the Arg10-Asp2 salt bridge with the H1 N-cap. Second, the statistical association between helical conformations in the two sub-regions observed in the simulations suggests cooperative helix formation in the basic region in the dimer. Thus, stabilization of H2 upon binding to DNA could induce H1 folding. H1 may be associated with the recruitment of additional transcription factors by transcription-activation domains N-terminal to the bZip domain in the full-length pro-tein⁵⁹. Coupling of H1 folding to DNA binding via H2 would enforce sequential assembly of the transcription factor complex, which may be a primary purpose of intrinsic disorder in DNA-binding domains⁶⁰. Residual H1 helicity in the absence of DNA may reflect this coupling. The associated restriction of conformational space and pre-nucleation of helical conformations would be expected to contribute to the thermodynamics and kinetics of putative subsequent interactions, in analogy to the effects of H2 residual helicity on DNA binding.

Conclusions

In this investigation we carried out four 100 ns MD simulations of the partially disordered DNA binding bZip domain of the yeast transcription factor GCN4 originating from different starting structures with varying degrees of helicity in the basic region. In these simulations, we observed a stable leucine zipper coiled-coil dimerization interface and helical conformations forming and breaking in the basic region to varying extents. By analyzing the agreement of back-calculated NMR chemical shifts and spin-relaxation spectral density functions and order parameters we were able to compare the accuracies of multiple MD trajectories, and identify the MD trajectory that is the most consistent with the experimental NMR measurements.

Recent studies have demonstrated that dynamically averaged values of semiempirical NMR chemical shift prediction tools obtained from MD simulations of proteins which reflect conformational averaging can show improved agreements with experimental values compared to predictions from static structures^30-32. The results presented here illustrate that, in addition to providing estimates of the populations of secondary structure elements in disordered regions of proteins^42,61, dynamically averaged structure based chemical shift predictions can provide experimental support for the populations of specific interactions in disordered protein states.

The analysis of the simulated spin relaxation spectral density functions obtained form our simulations revealed several important insights regarding the use of spin-relaxation data for the validation of MD simulation of disordered proteins. It was clear that in our simulations utilizing the Amber99SB force field and the TIP3P water model, that the bZip domain of GCN4 tumbles too quickly, and that calculating the spectral density functions in an unaligned “laboratory” frame made it difficult to compare the effects of motions observed in the simulation to experimental measurements. We found that by calculating spectral density functions for our simulations using the leucine zipper as an internal molecular reference frame and correcting for rotational diffusion, simulated spectral density were more sensitive to the internal dynamics of the protein and in better agreement with experiments. The effect of rotational diffusion occurring on timescales that are too fast, which has previously been observed in globular proteins^44,45, is an important consideration when validating simulations of disordered protein states against NMR relaxation data. Until more optimal combinations of force fields and water models are found through a careful testing of the effects rotational diffusion⁴⁹, this approach presents a reasonable strategy for the study of partially disordered proteins.

We observed excellent agreement between experimental generalized order parameters and order parameters calculated using the leucine zipper as a molecular reference frame. We found however, that the simulated order parameters and spectral densities were not particularly sensitive to the local populations of secondary structure, but rather were dominated by the presence of tertiary contacts or motions in more distal hinge region that produced large angular displacements of the basic region relative the reference frame. These results illustrate that chemical shifts, which are sensitive to the populations of secondary structure elements, and spin relaxation data, which are sensitive to timescales and amplitudes of motion, can provide complimentary probes for the studying the structure and dynamics of IDPs.

Sampling and convergence remain significant problems in the study of IDPs by MD simulations, and indeed, even in simulations over two orders of magnitude longer than those examined here, difficulties in sampling were evident²³. In this investigation, we do not attempt to achieve convergence of the force field properties by the use of long time scale simulations or enhanced sampling techniques²⁴, and we are aware that these 100 ns trajectories represent a local sampling of phase space around the starting trajectories rather than a converged measure of the force field properties. We therefore, do not aim to provide insight into the accuracy of force field used in this investigation, but rather to generate trajectories that sample different regions of phase space and evaluate how well the different structural and dynamic properties of these trajectories agree with experimental measurements. By conducting a detailed analysis of the agreement of each trajectory with experimental data, we obtain considerable atomistic insight into the structure and dynamics of the GCN4 bZip domain. Achieving statistical convergence of sampling and overcoming force field deficiencies are likely to remain significant challenges for studying IDPs by MD simulation for some time. In investigations that aim to understand the behavior of specific IDPs, rather than those which aim to compare the properties of force fields, a comparison of multiple trajectories which explore different regions of phase space against experimental measurements could offer insight into the behavior of molecules that might not obtained in the evaluation of the properties a single longer trajectory.

Of the four trajectories we have examined in this investigation, the trajectory with the most helical content in the basic region (trajectory 2) showed the best agreement with experimental NMR measurements. This trajectory had ∼70% helical propensity in H2, which contains the residues that form the binding interface of the GCN4 bZip domain with DNA, suggesting that a preformed helical interface may be important for binding. By analyzing the structural features of the basic region that are associated with elevated helical propensity, we observed that separate sets of interactions are associated with helix-stabilizing and substrate interactions, suggesting that a preformed helical-interface is compatible with binding. Additionally, we observed cooperativity in the helix formation of H2 and H1, a less populated helical conformation that does not participate in the binding interface. This result, together with the observation that an H1 destabilizing salt bridge is incompatible with the bound conformation, suggest that an initial conformational selection event of H2 could induce folding in the rest of the basic region. It is important to note however, that while the presence of intrinsic dynamics in the apo form of a protein which sample a bound-like conformation may be consistent with a conformational selection model, it is not proof that a separate induced folding pathway is not the dominant pathway⁶². The relative importance of an initial conformational selection event compared to an alternative induced folding mechanism involving a non-specific encounter complex depends on the kinetics of the two pathways^15,16, which are not studied here.

Methods

Molecular Dynamics Simulations

An initial structure for simulations was obtained from the crystal structure of the bound form of the GCN4 bZip domain (PDB code 1YSA) ²⁶. This structure is missing the N-terminal Met224 in one of the monomers and the C-terminal Arg281 in the other. The two residues and the DNA substrate were removed from the structure in order to obtain a free symmetric dimer. Residues Lys225 to Glu280 were numbered 1 to 56. Hydrogens were added to the resulting structure using the Maestro program⁶³. Protonation states of ionizable groups under experimental conditions (pH 4.5) were assigned based on standard pK_a values, resulting in double protonation of His41. The protonated structure was solvated in an ortho-rhombic box of 39,291 TIP3P ^35,36 water molecules to accommodate a minimum water shell thickness of 1 nm. Sixteen chloride ions were added to the system to maintain electric neutrality. The protein was described by the AMBER ff99SB force field³⁴. The system was energy minimized and subsequently simulated for 50 ns in the NPT ensemble at 310 K with the Desmond program ⁶⁴, using periodic boundary conditions and a cut-off of 0.9 nm for both Particle-Mesh-Ewald ^65-67 and Lennard-Jones interactions. Harmonic position restraints of 0.5 kcal/mol/Ų were applied to the backbone heavy atoms of the leucine zipper (residues Met26 to Val54) to prevent rotational diffusion in the orthorhombic box. The SHAKE ⁶⁸ algorithm was applied for constraining vibrations of bonds involving hydrogen atoms. A RESPA integrator was used ⁶⁹, with a time step of 2 fs for bonded and short-range non-bonded interactions, and 6 fs for long-range electrostatics. Coordinate sets were saved every 5 ps. The unrestrained basic region was almost completely unfolded after 50 ns. Four structures with fractional helicities of 40%, 32%, 18%, and 28% in the basic region (residues Lys1-Arg25) were extracted from the last 10 ns of the simulation (SI Figure 1). The protein coordinates of these four structures were re-solvated in truncated octahedral boxes of 69,858, 69,843, 69,858 and 69,842 TIP3P water molecules, respectively, to accommodate potentially extended conformations of the basic region (corresponding to a water-box diameter of approximately 140 Å). Sixteen chloride ions were added to maintain electric neutrality. Each system was energy minimized and subsequently equilibrated to 300 K over 5 ns of simulation in the NPT ensemble with the Desmond program using periodic boundary conditions and a cut-off of 0.9 nm for both Particle-Mesh-Ewald and Lennard-Jones interactions, applying the SHAKE algorithm, and using a RESPA integrator with a time step of 2.5 fs for bonded and short-range non-bonded interactions and 7.5 fs for long-range electrostatics. Coordinate sets were saved every 1.005 ps. A structure with a box volume close to the average box volume over the last 4 ns of NPT equilibration was extracted from the last 1 ns of each equilibration simulation (volume and temperature reached their equilibrium values in less than 100 ps in all simulations). This structure was used as the starting structure for a 100 ns production run in the NVT ensemble, using identical simulation parameters without any positional restraints. Coordinate sets were saved every 4.5 ps in the production runs. These four 100 ns NVT production runs are referred to as trajectories 1-4.

Spectral Density Functions

Orientational spectral density functions were calculated by discrete Fourier transformation of simulated autocorrelation functions (ACFs) C(τ) of amide bond vector orientations according to

$$J(\omega )=\frac{2}{5}Re{\left[\underset{-\infty }{\overset{\infty }{\int }}C(\tau )exp(-i\omega \tau )d\tau \right]}_{.}$$ Eq. 1

ACFs for a given trajectory were calculated according to

$$C(\tau )=\langle P_2[\mu (t)\cdot \mu (t+\tau )]\rangle ,$$ Eq. 2

where P₂[x] is the second Legendre polynomial, μ is the relevant bond vector scaled to unit magnitude and angular brackets indicate averaging over time t⁷⁰. ACF s were calculated for lag times of up to 50ns in two frames of reference. In the “laboratory frame”, where no alignment was performed, ACFs were subjected to a smoothing procedure to ensure that they decayed smoothly to zero. For C(τ)>0.4 the simulated correlation function was left unchanged. The first local minimum of C(τ), C(τ)_min, was calculated, and if C(τ)_min was less than 0.05, it was replaced with a value of 0.05. In the interval C(τ)_min≤C(τ) ≤ 0.4 the simulated correlation function was fit as a single-exponential decay using a least-squares algorithm and subsequently replaced by a weighted average with the fit, such that the weight of the fit linearly increases from 0 to 1 as C(τ) decreases from 0.4 to C(τ)_min; for C(τ)<C(τ)_min the simulated correlation function was replaced by the extension of the single-exponential fit. In the “aligned” reference frame, MD snapshots were aligned based on the superposition of the backbone atoms of the leucine zipper (residues Met26-Val54 of both monomers). To correct for the effects of the rotational diffusion of the internal reference frame, all ACFs were multiplied by an exponential decay with a correlation time of 18.9 ns, and then subjected to the same fitting procedure that was applied to the unaligned ACFs. Smoothed autocorrelation functions for each monomer in each trajectory were individually Fourier-transformed into spectral density functions.

Order parameters

Simulated order parameters were calculated from

$$S^2=\frac{1}{2}\left(3\sum _{i=1}^3\sum _{j=1}^3{\langle {\mu }_i{\mu }_j\rangle }^2-1\right),$$ Eq. 3

in which μ₁, μ₂ and μ₃ are the x, y and z components of the relevant bond vector scaled to unit magnitude, μ, respectively⁷¹. Angular brackets indicate averaging over the snapshots in a given analysis block, after superposition of backbone heavy atoms of Met26-Val54 of both monomers to remove the effects of overall tumbling. Each 100 ns trajectory was analyzed in five 18.9 ns blocks, because the average local tumbling time in the leucine zipper is estimated to be approximately 18.9 ns at 300 K²⁷. Order parameters were also calculated using the isotropic reorientational eigenmode dynamics (iRED) approach⁵⁵. The average experimental S² value of amides in the coiled coil residues was 0.94 whereas values of ∼0.85 are expected in stable helices. The previously observed concentration dependence of the experimentally measured R₂ values suggests that this effect is likely caused by the presence of transient higher molecular weight oligomeric species^27,53. To correct for this effect, experimental S² values were scaled by a factor of .92, so that the average coiled coil S² value was 0.87, the average coiled coil S² value observed in our simulations. We stress that our conclusions for the dynamics of the basic region would remain identical if no scaling factor was applied.

Statistical Association Between Categorical Variables

Significance of statistical association was assessed at the 5% level (p < 0.05). Strength of association between two dichotomous categorical variables X and Y, (e.g. presence of a hydrogen-bond, presence of a salt-bridge, or presence of helicity) is expressed in terms of the phi statistic (ϕ), calculated according to:

$$\varphi =\sqrt{{\chi }^2/n},$$ Eq. 4

in which χ² is computed based on the null hypothesis that the two variables are independent and n is the total number of observations ⁷².

Abbreviations

NMR

nuclear magnetic resonance

MD

molecular dynamics

IDP

intrinsically disordered protein

bZip

basic leucine-zipper

CD

circular dichroism

H1

residual helix 1

H2

residual helix 2

δMD

average chemical shift prediction obtained from a MD trajectory

δExp

experimentally measured chemical shift

ACF

autocorrelation function

J(ω)

spectral density function at frequency ω

S²

generalized order parameter

iRED

isotropic reorientational eigenmode dynamics

τ_m

local overall rotational correlation time

ϕ

phi coefficient