Generalized Redistribute-to-the-Right Algorithm: Application to the Analysis of Censored Cost Data

Abstract

Medical cost estimation is a challenging task when censoring of data is present. Although researchers have proposed methods for estimating mean costs, these are often derived from theory and are not always easy to understand. We provide an alternative method, based on a replace-from-the-right algorithm, for estimating mean costs more efficiently. We show that our estimator is equivalent to an existing one that is based on the inverse probability weighting principle and semiparametric efficiency theory. We also propose an alternative method for estimating the survival function of costs, based on the redistribute-to-the-right algorithm, that was originally used for explaining the Kaplan–Meier estimator. We show that this second proposed estimator is equivalent to a simple weighted survival estimator of costs. Finally, we develop a more efficient survival estimator of costs, using the same redistribute-to-the-right principle. This estimator is naturally monotone, more efficient than some existing survival estimators, and has a quite small bias in many realistic settings. We conduct numerical studies to examine the finite sample property of the survival estimators for costs, and show that our new estimator has small mean squared errors when the sample size is not too large. We apply both existing and new estimators to a data example from a randomized cardiovascular clinical trial.

1. Introduction

High and rising health care costs in an environment of limited resources have sharpened the focus on economic evaluation of new treatments. Studies of cost-effectiveness usually aim at evaluating new treatments in the hope of finding an effective treatment that does not cause too much financial burden on society. In clinical trials and observational studies, survival time and health costs frequently are censored for administrative reasons, since not all patients can be observed until events such as death or disease relapse occur. Censoring poses a unique problem for cost estimation due to the “induced informative censoring” problem, first noted by Lin and colleagues (Lin et al. 1997). Traditional survival analysis methods assume that the censoring time is independent of the survival time (conditional on some covariates). However, the costs at censoring time are no longer independent of the total uncensored costs. For example, a healthier patient will accumulate costs more slowly, and therefore will have lower costs at the censoring time and at the potential event time (Lin 2003). Thus, many standard approaches for survival analysis, such as the Kaplan–Meier estimator (Kaplan and Meier 1958), or the Cox regression model (Cox 1972), are not valid for the analysis of cost data.

Many researchers have proposed methods for estimating mean medical costs. Most focus on restricted medical costs, that is, the costs accumulated within a time limit. Among them, Lin et al. (1997) proposed estimators via survival probability weighting using partitioned time intervals; Bang and Tsiatis (2000) proposed consistent estimators using the inverse probability weighting technique; and Zhao and Tian (2001) proposed a more efficient estimator. Later, Zhao et al. (2007) discovered some special conditions under which the estimators without using cost history and those using cost history become identical within each class.

Although many estimators for the mean costs have appeared in the literature, these often are deeply based in theory and therefore less accessible to practitioners. To address this situation, Zhao et al. (2011) established a mathematical equivalency between the BT estimator for the mean costs (Bang and Tsiatis 2000), and a replace-from-the-right (RR) algorithm (Pfeifer and Bang 2005). Thus, the BT estimator, which is based on the inverse probability weighting technique (Horvitz and Thompson 1952), has a more intuitive explanation from the point of the RR algorithm. Motivated by this idea, we propose a modified RR algorithm, the RRimp method, which utilizes cost history information and therefore is generally more efficient than the RR estimator. We provide a proof of the mathematical equivalence between the RRimp method and an existing estimator for the mean costs, the ZT estimator (Zhao and Tian 2001). The ZT estimator was derived from complicated theory. Therefore, the RRimp algorithm provides insight on how the ZT estimator works and eventually can help promote its application in practice.

Cost data are often highly skewed, with most patients incurring relatively small costs but a few accumulating huge costs. It is often desirable, therefore, to estimate the median and other quantiles of the costs. These quantities are readily available if we can estimate the survival function of costs. Using the original redistribute-to-the right algorithm (Efron 1967), which was used for explaining the Kaplan–Meier estimator, we propose an RR^S survival estimator for costs, and show that it is equivalent to a simple weighted (SW) survival estimator for costs (Zhao and Tsiatis 1997; Zhao et al. 2012), which uses the inverse probability weighting technique. We further extend this method to propose an RRimp^S survival estimator. We conduct simulation studies to compare this RRimp^S survival estimator with the RR^S survival estimator (or equivalent SW estimator), and with a more efficient ZT^S survival estimator (Zhao and Tsiatis 1997; Zhao et al. 2012). We discuss our findings in the Conclusion section.

2. Notation and Assumptions

For the ith individual in the study, i = 1, 2, . . . , n, we define T_i as the survival time from the beginning of the study until the occurrence of some event, for examples death or disease relapse. The censoring time for the ith individual is denoted as C_i. We can observe either the survival time or the censoring time, whichever is shorter; that is, we observe the follow-up time X_i = min(T_i, C_i) and the indicator variable Δ_i = I(T_i ≤ C_i). We define M_i(t) as the accumulated cost of patient i from time 0 to t. For some real applications, we observe only the total cost M_i = M_i(X_i). However, in other studies, we may know the entire cost history, M_i(t), 0 < t < X_i.

We assume that the censoring variable is independent of the survival time and cost accumulation process, a condition that is often satisfied in well-conducted clinical trials and in some observational studies where censoring occurs mainly for administrative reasons. Due to the presence of censoring, the marginal distribution of cost may be nowhere identifiable without making some parametric assumptions (Huang 2002). Hence we adopt an approach that focuses on the accumulated cost by a time limit L, where L is chosen such that a reasonable number of subjects are still being observed at that time. A consequence of applying such a restriction is that a survival time longer than L can be considered equivalently as having an event at time L, that is, $T_i^L=\min (T_i,L)$ (we still use T_i for notational convenience).

We consider the problem of estimating the mean cost, μ = E{M_i(T_i)}, and the survival function of cost, S(x) = Pr{M_i(T_i > x}, for costs accumulated to a time L. For reasons that become clear in the following, we also need to define the survival function for the event time as S^T(t) = Pr(T_i > t), and the survival function for the censoring time as K(t) = Pr(C_i > t).

3. Estimating the Mean Cost

3.1. Without Using Cost History: The BT Estimator and Its Equivalent RR Estimator

Bang and Tsiatis (2000) proposed a consistent estimator for the mean costs accumulated over time L with censored data, based on the inverse probability weighting technique:

$${\widehat{\mu }}_{BT}=\frac{1}{n}\sum _{i=1}^n\frac{{\Delta }_i{M}_i}{\widehat{K}\left(T_i\right)},$$ (1)

where M_i is the total observed cost for the ith individual, and K̂(T_i) is the Kaplan–Meier estimator for the survival function of the censoring time, K(t) = Pr(C_i > t). K(T_i) represents the probability that a subject is uncensored at T_i. The basic idea of the BT estimator is that each complete observation represents potential 1/K̂(T_i) observations that might be censored.

Even though the BT estimator is easy to obtain mathematically, for many a full understanding of its mechanism is not very intuitive. The replace-from-the-right (RR) estimator proposed by Pfeifer and Bang (2005), on the other hand, is more so. To explain the main idea of the RR method, first we note that in the absence of censoring, a mean cost estimator is simply the average of costs from all observations. When a subject is censored, we know that this subject lives longer than his/her censoring time, but we do not have information on his/her total cost. In the RR algorithm, we replace this subject's cost by an average of costs from those individuals who survived longer than this subject. Specifically, an RR estimator for the mean costs can be obtained by first arranging all the subjects from the shortest observed time to the longest. If some of these are equal, we put the event time before the (same) censored time. Since we focus on time-restricted cost estimation, we can assume that the individual with the longest observed time is uncensored. We then move from the right (the longest observation time) to the left (the shortest observation time). When we encounter the first censored observation, say, at time C_i, we replace its costs by the average of costs from all the observations to its right,

$$M_i^{RR}=\frac{{\sum }_{j=1}^{n}I(X_j>C_i)M_j}{{\sum }_{j=1}^{n}I(X_j>C_i)}.$$ (2)

We move to the left and repeat this process of replacing all the censored costs with the average of all upstream costs (some of which are real costs and some are replaced costs). The RR mean cost estimator is simply an average of all the costs from both complete observations and censored observations (replaced costs), that is,

$${\widehat{\mu }}_{RR}=\frac{1}{n}\sum _{i=1}^n\{{\Delta }_i{M}_i+(1-{\Delta }_i)M_i^{RR}\}.$$ (3)

Although the BT estimator (1) and the RR method (3) look quite different—the former is based on a well-known theory, and the latter makes intuitive sense—it is rather amazing that the two estimators in fact are mathematically equivalent (see Zhao et al. [2011] for a detailed proof).

Note that if we replace the costs M by the survival time T (restricted by time L), we also obtain an equivalency between the RR estimator for the mean (restricted) survival time, and a simple weighted estimator for the mean survival time,

$${\widehat{\mu }}^T=\frac{1}{n}\sum _{i=1}^n\frac{{\Delta }_i{T}_i}{\widehat{K}\left(T_i\right)}.$$

Since this simple weighted estimator has been shown to be equivalent to the area under the Kaplan–Meier survival curve (Satten and Datta 2001; Zhao and Tian 2001), we are providing an alternative and simpler way for obtaining the (restricted) area under the Kaplan–Meier survival curve using the RR algorithm.

3.2. Using the Cost History: the ZT Estimator and Its Equivalent RRimp Estimator

The BT estimator and its equivalent RR algorithm use only the total cost information from uncensored subjects. Hence, they are not very efficient. An improved estimator proposed by Zhao and Tian (2001) utilizes cost history information from both censored and uncensored observations. Therefore this ZT estimator is often more efficient. It has the following simplified form (Pfeifer and Bang, 2005):

$${\widehat{\mu }}_{ZT}=\frac{1}{n}\sum _{i=1}^n\frac{{\Delta }_i{M}_i}{\widehat{K}\left(T_i\right)}+\frac{1}{n}\sum _{i=1}^n\frac{(1-{\Delta }_i)\{M_i\left(C_i\right)-\overline{M\left(C_i\right)}\}}{\widehat{K}\left(C_i\right)},$$ (4)

where $\overline{M\left(C_i\right)}={\sum }_{j=1}^{n}I(X_j\ge C_i)M_j\left(C_i\right)∕{\sum }_{j=1}^{n}I(X_j\ge C_i)$, which is the average cumulative cost at time C_i of those subjects who are alive at C_i.

The ZT estimator consists of two terms. The first is the BT estimator. The second term is constructed using cost history information, which can be viewed as an adjustment term. The ZT estimator gains more efficiency through an adjustment made to the BT estimator using the difference of censored costs and the average accumulated costs at the same time point. Zhao and Tian (2001) established the large sample property for this estimator, and showed that the estimator is consistent and asymptotically normally distributed. Furthermore, Zhao et al. (2007) described the conditions under which this estimator is equivalent to the partitioned Bang and Tsiatis (2000) estimator (BTp), as well as to the two estimators of medical costs LinA/B proposed by Lin et al. (1997).

Since the BT estimator has an intuitive explanation through the RR algorithm, naturally one may wonder whether the ZT estimator has a similar intuitive explanation. Therefore we propose an RRimp algorithm, which makes intuitive sense, and later we show that it is equivalent to the ZT estimator. In contrast to the simple RR method, which depends only on the total costs from complete observations, the RRimp algorithm uses the cost history information from both censored and complete observations. Intuitively, for a censored subject i, we already know his/her accumulated cost before censoring M_i = M_i(C_i). Hence, we need only to estimate his/her cost beyond the censoring time point, M_i(T_i) – M_i(C_i). We propose to impute this cost using the average of all additional costs beyond the censoring point C_i from those subjects who survive longer. The detailed RRimp estimator can be described as follows. First, arrange all the subjects from the shortest to the longest follow-up time. If some of these are the same, we assume events happen shortly before censoring times. Since we focus on time-restricted (say, by L) cost estimation, we assume that the individual with the longest observed time (i.e., L) is uncensored. Starting from the right (the longest observed time) we move to the left. We first find the longest censoring time, denoted as C_i. We replace the cost for this observation by summation of his/her observed costs and the average additional accumulated costs from all subjects who have a longer survival time, that is,

$$M_i^{RRimp}=M_i+\frac{{\sum }_{j=1}^{n}I(X_j>C_i)\{M_j-M_j\left(C_i\right)\}}{{\sum }_{j=1}^{n}I(X_j>C_i)}.$$ (5)

We then move to the second longest censoring time and perform the same replacement procedure, using the replaced cost for the longest censoring time in calculating the average. We move to the left and repeat this process until we replace all the censored costs. The RRimp estimator is then obtained by an average of costs from all complete observations (real costs) and the censored observations (replaced costs), that is,

$${\widehat{\mu }}_{RRimp}=\frac{1}{n}\sum _{i=1}^n\left\{{\Delta }_i{M}_i+(1-{\Delta }_i)M_i^{RRimp}\right\}.$$ (6)

We illustrate this algorithm using a simple example. Suppose we observe the following data: follow-up time X = {1, 2, 3, 4, 5}, death indicator Δ = {1, 0, 1, 0, 1}, and their accumulated costs M_i(·) are shown in the figure that follows. Here the 2nd and 4th subjects are censored. In Step 1, we try to obtain the replacement cost for subject 4. Since subject 5 is the only one surviving longer than subject 4, the replacement cost for subject 4 is equal to the summation of the censored cost of subject 4 (= 60) and the additional cost of subject 5 beyond time C₄ (= 40 – 30), which is 70. Similarly, in Step 2 we try to obtain the replacement cost for subject 2 by adding the observed cost of subject 2 (= 50) and the average of additional costs after time C₂ for subject 3 (= 100 – 60, real costs), subject 4 (= 70 – 20, replaced costs) and subject 5 (= 40 – 10, real costs), which is equal to 90. Therefore, the mean cost estimated from the RRimp method gives an estimate of 62, as shown in the graph here.

Xi = 1	2	3	4	5
x	o	x	o	x
M1(·) = 10
M2(·) = 20	50
M3(·) = 30	60	100
M4(·) = 10	20	40	60
M5(·) = 5	10	20	30	40
Step 1: ($M_4^{RRimp}$)			70{= 60 + (40 – 30)}
Step 2: ($M_2^{RRimp}$)	90{= 50 + [(100 – 60) + (70 – 20) + (40 – 10)]/3}

$${\widehat{\mu }}_{RRimp}=(10+90+100+70+40)∕5=62.$$

Meanwhile, the ZT estimator of the mean cost obtained from the same data set is:

$$\begin{array}{cc}\hfill {\widehat{\mu }}_{ZT}=& \frac{1}{5}\sum _{i=1}^5\frac{{\Delta }_i{M}_i}{\widehat{K}\left(T_i\right)}+\frac{1}{5}\sum _{i=1}^5\frac{(1-{\Delta }_i)\{M_i\left(C_i\right)-\overline{M\left(C_i\right)}\}}{\widehat{K}\left(C_i\right)}\hfill \\ \hfill =& \frac{1}{5}\left(\frac{10}{1}+\frac{100}{3∕4}+\frac{40}{3∕8}\right)+\frac{1}{5}\left(\frac{50-35}{3∕4}+\frac{60-45}{3∕8}\right)\hfill \\ \hfill =& \frac{1}{5}(10+400∕3+320∕3)+\frac{1}{5}(20+40)\hfill \\ \hfill =& 50+12=62,\hfill \end{array}$$

where the Kaplan–Meier estimates for K(t) = Pr(C_i > t) are K̂(X_i) = (1, 3/4, 3/4, 3/8, 3/8), at X_i = {1, 2, 3, 4, 5}, and $\overline{M\left(C_i\right)}=\{35,45\}$, at C_i = {2, 4}, respectively. Hence, we obtain exactly the same estimate for the mean costs through both the ZT estimator and the RRimp method using this data set. In the appendix we provide mathematical proof of the equivalence between the ZT estimator and the RRimp estimator for any data set.

In summary, when censoring of data is present, we cannot observe full costs for every subject. If we have cost history information, we can replace the censored cost by supplementing what we can observe with the average of the additional accumulated costs from upstream observations. This RRimp method is mathematically equivalent to the ZT estimator, and, as demonstrated by simulations and examples in Zhao and Tian (2001), is generally more efficient than the BT estimator and its equivalent RR method.

4. Estimating Survival Functions for Costs

In addition to estimating the mean costs, we may want to estimate the survival function of costs in practice. The survival function can provide more information about costs, such as medians and quartiles, which are more robust to outliers. Motivated by the idea of the replace-from-the-right algorithm for estimating mean costs, we investigate how to use similar approaches to develop survival estimators for the costs. We show that a naive way of deriving the survival estimator based on the replace-from-the-right algorithm will result in a biased estimator. Instead, we propose a new RR^S estimator for the survival function of costs, based on the original redistribute-to-the-right idea from Efron (1967) for estimating the survival function of a failure time. Within this section only, when the context is clear, we use the same abbreviation “RR” to stand for redistribute-to-the-right. We show that the RR^S estimator is equivalent to a simple weighted (SW) survival estimator of costs, whose form was first described in the context of estimating quality-adjusted lifetime by Zhao and Tsiatis (1997). We also attempt to derive a survival estimator RRimp^S based on a modified RR algorithm that uses cost history information. We discuss the advantages and disadvantages of such an estimator.

4.1. The SW Estimator and Its Equivalent RR^S Estimator

Following the work of Zhao and Tsiatis (1997) and Zhao et al. (2012), a SW estimator for the survival function of costs can be obtained by:

$${\widehat{S}}_{SW}\left(x\right)=\frac{1}{n}\sum _{i=1}^n\frac{{\Delta }_i}{\widehat{K}\left(T_i\right)}I(M_i>x).$$ (7)

The large sample properties of this estimator, such as its consistency and asymptotic normality, were established by Zhao and Tsiatis (1997).

To construct an equivalent survival estimator, one is tempted to use the replacement costs at each censoring point and estimate the survival function for costs using the following formula:

$${\widehat{S}}_{naive}\left(x\right)=\frac{1}{n}\sum _{i=1}^n\left\{{\Delta }_{i}I(M_i>x)+(1-{\Delta }_i)I(M_i^{RR}>x)\right\}.$$ (8)

Unfortunately, if we use the empirical distribution function just shown to estimate the survival function for costs, treating the replaced costs as if they were the real costs, the estimated curve will be biased although the area under the curve, that is, the estimated mean costs, is unbiased. This is demonstrated in subsequent simulation studies.

In order to find an equivalent RR^S estimator, we rely on the original redistribute-tothe-right idea proposed by Efron (1967), used to explain the Kaplan–Meier estimator for survival time. For each censored subject, since we do not know the actual costs, we will find the contributions from observations that have longer follow-up time than this subject. Specifically, we first sort all subjects according to their observation times from the shortest (left) to the longest (right). For any tied observations, we assume the death event occurs a little earlier than the censored time. We also assume that the individual with the longest observed time is uncensored, since we focus on time-restricted cost estimation. Consider a censored observation i whose initial weight is set to be 1. We distribute its weight evenly to all the time points to its right. For example, if there are n_i such observations, then each one gets a weight of 1/n_i. Next we find the nearest censored observation to its right, and redistribute its weight again evenly to all the observations to its right. We repeat this process until we have redistributed the weight of the longest censoring time. Note that after redistribution the weights are nonzero only at those complete observations that are on the right side of the censored observation i. Denote the final weight at the jth complete event time as $W_j^{\left(i\right)}$, representing the contribution of a complete subject j to the censored subject i.

Due to censoring we often cannot evaluate the mark I(M_i > x). Instead we use the weighted sum

$$I{(M_i>x)}^{RR}=\sum _{j=1}^n{\Delta }_{j}I(T_j>X_i)W_j^{\left(i\right)}I(M_j>x)$$ (9)

as the replacement mark. As a result, the RR^S estimator for the survival function of costs is

$${\widehat{S}}_{RR}\left(x\right)=\frac{1}{n}\sum _{i=1}^n\left\{{\Delta }_{i}I(M_i>x)+(1-{\Delta }_i)I{(M_i>x)}^{RR}\right\}.$$ (10)

We illustrate this idea using a simple example. Assume we have data [X = {1, 2, 3, 4, 5}, Δ = {1, 0, 1, 0, 1}, M = {10, 20, 40, 30, 50}]. As shown in the following graph, we first find the weight $W_j^{\left(2\right)}$, that is, the contribution of complete observations to the censored observation 2. In Step 0, the censored observation 2 gets the weight of 1. In Step 1, we distribute its weight of 1 to all of the 3 observations to its right, so that each gets a weight of 1/3. Moving to the next censoring time, observation 4, we distribute its weight of 1/3 to the one observation to its right, making the weight at time 5 to be 2/3. Hence we have $W_3^{\left(2\right)}=1∕3$, and $W_5^{\left(2\right)}=2∕3$.

Xj =	1	2	3	4	5
	x	o	x	o	x
Step 0:	0	1	0	0	0
Step 1:	0	0	$\frac{1}{3}$	$\frac{1}{3}$	$\frac{1}{3}$
Step 2:	0	0	$\frac{1}{3}$	0	$\frac{2}{3}(=\frac{1}{3}+\frac{1}{3})$
$W_j^{\left(2\right)}$			$\frac{1}{3}$		$\frac{2}{3}$

It is easy to obtain the contributions of complete observations to the censored observation 4, in this case $W_5^{\left(4\right)}=1$. Hence the RR^S estimator is

$$\begin{array}{cc}\hfill {\widehat{S}}_{RR}\left(x\right)=& \frac{1}{5}\sum _{i=1}^5[{\Delta }_{i}I(M_i>x)+(1-{\Delta }_i)I{(M_i>x)}^{RR}]\hfill \\ \hfill =& \frac{1}{5}\{I(M_1>x)+I(M_3>x)+I(M_5>x)+I{(M_2>x)}^{RR}+I{(M_4>x)}^{RR}\}\hfill \\ \hfill =& \frac{1}{5}\left\{I(M_1>x)+I(M_3>x)+I(M_5>x)+\frac{1}{3}I(M_3>x)+\frac{2}{3}I(M_5>x)+I(M_5>x)\right\}\hfill \\ \hfill =& \frac{1}{5}\left\{I(M_1>x)+\frac{4}{3}I(M_3>x)+\frac{8}{3}I(M_5>x)\right\}.\hfill \end{array}$$

The simple weighted estimator for this example is

$$\begin{array}{cc}\hfill {\widehat{S}}_{SW}\left(x\right)=& \frac{1}{5}\sum _{i=1}^5\left\{\frac{{\Delta }_{i}I(M_i>x)}{\widehat{K}\left(T_i\right)}\right\}\hfill \\ \hfill =& \frac{1}{5}\left\{\frac{I(M_1>x)}{1}+\frac{I(M_3>x)}{3∕4}+\frac{1(M_5>x)}{3∕8}\right\}\hfill \\ \hfill =& \frac{1}{5}\left\{I(M_1>x)+\frac{4}{3}I(M_3>x)+\frac{8}{3}I(M_5>x)\right\}.\hfill \end{array}$$

It is clear that the RR^S estimator is equivalent to the SW survival estimator for costs in this example.

Remarks.

1. It is not difficult to show that the weight $W_j^{\left(i\right)}$ is related to the estimated conditional probability of an event occurring at X_j given that the subject is alive at X_i (discrete case). Thus, $W_j^{\left(i\right)}$ can be easily obtained as follows:

   $$W_j^{\left(i\right)}=\frac{1}{n{\widehat{S}}^T\left(C_i\right)\widehat{K}\left(T_j\right)},$$ (11)

   where Ŝ^T(x) is the Kaplan–Meier estimator for Pr(T > x), and K̂(x) is the Kaplan-Meier estimator for Pr(C > x).

2. We can show that this RR^S estimator (10) for the survival function of costs is mathematically equivalent to the SW estimator based on the similar proofs for mean cost estimators.

3. The weights $W_j^{\left(i\right)}$ are exactly the weights needed for obtaining the replaced costs for a censored observation i, in estimating the mean costs by the replace-from-the-right algorithm, that is,

   $$M_i^{RR}=\sum _{j=1}^n{\Delta }_{j}I(X_j>X_i)W_j^{\left(i\right)}{M}_j.$$

   Therefore, the replace-from-the-right algorithm for the mean cost estimator is a generalized version of the redistribute-to-the-right algorithm.
4. The replaced costs $M_i^{RRimp}$ from the RRimp estimator, however, are not equivalent to

   $$\sum _{j=1}^n{\Delta }_{j}I(X_j>X_i)W_j^{\left(i\right)}\{M_i+M_j-M_j\left(C_i\right)\},$$ (12)

   since $M_i^{RRimp}$ from (5) utilizes the cost information from censored observations beyond C_i while (12) does not.

4.2. RR Improved Survival Estimator for the Survival Function of Costs

As in the case of estimating the mean costs, the SW and its equivalent RR^S estimator for the survival function of costs are not efficient since they utilize only the costs from complete observations. Based on the principles of constructing the RR^S survival estimator and the RRimp estimator for mean costs, we propose an improved RR survival (RRimp^S) estimator, as shown next:

$${\widehat{S}}_{RRimp}\left(x\right)=\frac{1}{n}\sum _{i=1}^n{\{{\Delta }_{i}I(M_i>x)+(1-{\Delta }_i)I(M_i>x)}^{RRimp},$$ (13)

where

$$I{(M_i>x)}^{RRimp}=\sum _{j=1}^n{\Delta }_{j}I(T_j>X_i)W_j^{\left(i\right)}I(M_j^{\left(i\right)}>x)$$ (14)

is the new replacement mark, and $M_j^{\left(i\right)}=M_i+M_j-M_j\left(C_i\right)$ is the replacement cost, combining information from censored observation i and complete observation j.

For a censored subject i, if we observe M_i(C_i) > x, then we know for sure that M_i(T_i) > x. This information is not utilized in the SW estimator (7), or the equivalent RR^S estimator (4.3). However, it is captured in the RRimp^S estimator (13) and (14), since $M_j^{\left(i\right)}=M_i\left(C_i\right)+M_j-M_j\left(C_i\right)>x$ always holds under M_i(C_i) > x, and the sum of weights $W_j^{\left(i\right)}$ is 1, giving rise to I(M_i > x)^RRimp = 1.

Because $I(M_j^{\left(i\right)}>x)$ is monotone in x and the weights are nonnegative, this RRimp^S estimator is always monotone, which is a desirable property for a survival estimator. In contrast, an improved survival function estimator of costs, ZT^S, first developed by Zhao and Tsiatis (1997) in the context of quality-adjusted survival time, and later applied to cost estimation (Zhao et al. 2012), cannot be guaranteed to be monotone (Huang and Louis 1998). From subsequent simulation studies and the real example, we see that the RRimp^S estimator is also more efficient, in many practical situations, than both the SW estimator and the ZT^S estimator.

Unfortunately, unlike the SW and the ZT^S estimators, this RRimp^S estimator is not always consistent. An intuitive reason for this inconsistency is as follows. We replace I(M_j > x) by $I(M_j^{\left(i\right)}>x)$ in the RRimp^S estimator. Since M_j(C_i) and M_j – M_j(C_i) are dependent, while M_i(C_i) and M_j – M_j(C_i) are independent, the distribution of replaced cost $M_j^{\left(i\right)}=M_i\left(C_i\right)+M_j-M_j\left(C_i\right)$ is different from the distribution of the true cost M_j = M_j(C_i) + M_j – M_j(C_i). As a result, the RRimp^S estimator performs worse when there is a high correlation among costs accumulated in different periods. Nonetheless, the simulation studies show that the bias is quite small, even for the worst-case scenario with a high correlation.

5. Simulation Studies

We conduct simulation studies under several different settings to evaluate the survival function estimators for costs. We generate survival times using an exponential distribution T ~ exp(10), and a uniform distribution T ~ Unif(0, 15). The survival time is truncated at L = 10. We generate censoring times using a uniform distribution: C ~ Unif(0, 22), for light censoring (25%-30%), and Unif(0, 15), for heavy censoring (37%-44%). The sample size is set to be 100, and the number of simulations is 1000.

We consider U-shaped sample paths for the cost distribution, similar to the simulation settings of Lin et al. (1997), Bang and Tsiatis (2002), and Zhao et al. (2012). We partition the entire time period of 10 years into 10 equal intervals. Each individual's costs consist of initial diagnostic costs incurred at time 0, terminal costs incurred during the last year before the failure time, fixed annual costs, and random annual costs (which vary from year to year). The diagnostic costs, fixed annual costs, random annual costs, and terminal costs are generated using a log normal distribution with parameters (10, 0.245²), (6, 0.245²), (4, 0.245²), and (9, 0.632²), respectively. We estimate the survival function of costs using the SW/RR^S estimator, the ZT^S estimator from Zhao and Tsiatis (1997), and our RRimp^S estimator, under the four different simulation scenarios. We also examine the naive survival estimator of (8) for one of the settings.

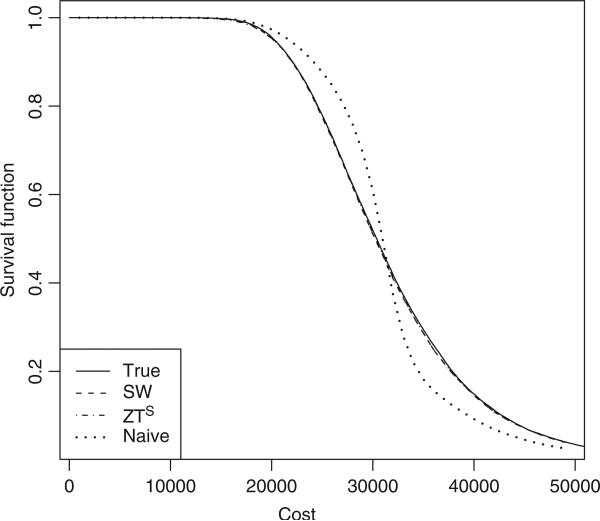
Figure 1 shows the true survival function for costs and the average of the survival curves from the 1000 simulations using different estimators, for the setting with heavy censoring and exponential survival time. As expected, the SW/RR^S estimator and the ZT^S estimator are both unbiased since they almost coincide with the true survival curve. However, the naive estimator, obtained by using the replacement costs as the true costs, is severely biased. We observe similar biases for the naive method under other scenarios.

Figure 1.

The mean of estimated survival estimators for costs based on 1000 replications with exponential survival time under heavy censoring: the solid curve is the true survival function; the dashed curve is the SW/RR^S estimator; the dot-dashed curve is the ZT^S estimator; the dotted curve is the naive estimator.

Figure 2 and Figure 3 display the mean and sample variances of different survival function estimators for costs based on 1000 replications, under four simulation scenarios. The SW/RR^S and ZT^S estimators are consistent as in Figure 1, since these almost coincide with the true survival curve. Although from a theoretical point of view the new proposed RRimp^S estimator is not always consistent, its average survival curves follow the true survival curves very well, for all the settings considered here. This indicates that the bias of the RRimp^S survival estimator is relatively small. In the plots of the sample variances, we find that the ZT^S estimator is more efficient than the SW/RR^S estimator. More importantly, our RRimp^S estimator outperforms both SW/RR^S and ZT^S estimators under all four of these scenarios, with more efficiency gain under heavy censoring. Hence, the RRimp^S survival function makes a significant improvement in efficiency. This improvement is achieved without sacrificing the monotonicity property, unlike in the case of the ZT^S estimator.

Figure 2.

The mean of estimated survival estimators for costs based on 1000 replications: the solid curve is for true survival function; the dashed curve is for SW/RR^S estimator; the dot-dashed curve is for ZT^S estimator; the dotted curve is for RRimp^S estimator. (a) Scenario with exponential survival time under light censoring. (b) Scenario with exponential survival time under heavy censoring. (c) Scenario with uniform survival time under light censoring. (d) Scenario with uniform survival time under heavy censoring.

Figure 3.

The sample variance of estimated survival estimators for costs based on 1000 replications: the solid curve is for SW/RR^S estimator; the dashed curve is for ZT^S estimator; the dotted curve is for RRimp^S estimator. (a) Scenario with exponential survival time under light censoring. (b) Scenario with exponential survival time under heavy censoring. (c) Scenario with uniform survival time under light censoring. (d) Scenario with uniform survival time under heavy censoring.

Since the RRimp^S survival estimator performs worse when there is a high correlation between costs accumulated in different periods, we design an extreme case in order to examine how biased the RRimp^S estimator could be. We generate the fixed annual costs using a log normal distribution with parameters (8, 0.245²), while setting the diagnostic costs, random annual costs, and terminal costs to be 0. All other parameters stay the same. Figure 4 displays the mean survival curves and the mean squared errors (MSE = variance + bias²), for the case with exponential survival time and heavy censoring, and for different sample sizes (n = 100, 400). We observe similar trends for other simulation settings. The bias for the RRimp^S estimator is noticeable now, albeit very small. The MSE for the RRimp^S estimator remains mostly the smallest among the three methods available, even when the sample size is as large as 400. In general, as the sample size gets larger, the variance becomes smaller but the bias stays the same. We expect the gain in terms of MSE for the RRimp^S estimator will be most prominent when the sample size is small, or when the censoring rate is high.

Figure 4.

The mean and MSE of estimated survival estimators for costs under the extreme case based on 1000 replications with exponential survival time under heavy censoring. (a) Mean of estimated survival estimators for costs with sample size 100. (b) MSE of estimated survival estimators for costs with sample size 100. (c) Mean of estimated survival estimators for costs with sample size 400. (d) MSE of estimated survival estimators for costs with sample size 400.

6. A Real Data Example: MADIT-II

The Multicenter Automatic Defibrillator Implantation Trial II (MADIT-II) was one of a series of studies designed to examine the potential survival benefit of a prophylactically implanted defibrillator in patients with a prior myocardial infarction and other selection criteria (Moss et al. 2002). Patients were recruited into the study over time and were randomized into either the implantable cardiac defibrillator (ICD) arm or the conventional therapy (CONV) arm, with a ratio of 2:1. After the trial was completed, it was shown that the risk of death in the ICD group was lower (hazard ratio = 0.69, pvalue = 0.016).

Given the huge costs associated with the defibrillator and the implantation process, a cost-effectiveness analysis was conducted based on patients from the u.s. centers, with 664 patients in the ICD arm and 431 in the CONV arm (Zwanziger et al. 2006). The follow-up time varied from 11 days to 55 months, and the average was 22 months. As in their original paper, we examine the costs accumulated over 3.5 years. The estimated survival function for medical costs for the ICD and CONV groups, based on SW/RR^S, ZT^S, and RRimp^S estimators, are shown in Figure 5. As mentioned earlier, the ZT^S estimator is not monotone, while both the SW/RR^S and the RRimp^S estimator are monotone. Our RRimp^S survival estimator for cost is also smoother than the SW/RR^S and ZT^S estimators. Figure 6 displays the standard errors of the estimators obtained by the bootstrap method. Similarly to the simulation studies, the standard errors of RRimp^S are mostly the smallest for different costs, and SW/RR^S are the largest. Therefore, our proposed RRimp^S method might be a good alternative for smooth and efficient estimation of the survival function of costs.

Figure 5.

Estimated survival function for medical costs for the MADIT-II study: (a) is for the ICD arm, and (b) is for the CONV arm.

Figure 6.

Standard errors (SEs) of the survival estimators for costs obtained by 200 bootstrap replications for the MADIT-II study: (a) SEs for the ICD arm, and (b) SEs for the CONV arm.

7. Conclusion

In this article we extend the research of Zhao et al. (2011), who provided a link between a theoretically justified mean cost estimator based on the inverse probability weighting techniques, that is, the BT estimator, and an intuitive replace-from-the-right estimator, the RR estimator. We propose a modified replace-from-the-right algorithm, the RRimp estimator, which utilizes the cost history process and therefore is generally more efficient than the RR estimator. We establish a mathematical equivalency between the RRimp estimator and an improved mean cost estimator, the ZT estimator. In doing so we provide an intuitive explanation for how the ZT estimator works, and thereby engender a better understanding of the theoretically derived mean cost estimators, the BT and ZT estimators. Meanwhile, this article also gives justification for the simple, intuition-based RR and RRimp estimators. Without the theoretical background for a full understanding of the BT and ZT estimators, some practitioners may hesitate to use these. With a facilitated interpretation of the RR and RRimp estimators, and an established equivalency between these estimators and the BT and ZT estimators, we believe the proposed estimators can become more accessible and useful to practitioners.

Deriving an intuitive estimator for the survival function of costs proves to be a tougher problem. We show that a naive method using the replaced cost as the true cost in an empirical survival function gives rise to a biased estimator. Resorting to the original redistribute-to-the-right idea (Efron 1967) derived for explaining the Kaplan–Meier estimator, we construct an RR^S survival estimator which can be shown to be equivalent to the SW survival estimator for costs. We also propose an RRimp^S survival estimator that has the desirable property of being monotone and is usually more efficient than the SW/RR^S survival estimator in many simulation studies and the real example we conducted. Unfortunately, this estimator is not always consistent. Judging from many simulations we conducted, the bias seems to be quite small however. It may be considered as an alternative survival estimator for costs in a real setting when cost history information is available, especially when the sample size is not very large or the censoring rate is high.

Both the replace-from-the-right and the redistribute-to-the-right algorithms can be viewed as special cases of imputation of missing data. Our work may motivate more research in the area of censored marked variables; quality-adjusted survival time and repeated events are two additional examples. Even though we demonstrated that the proposed RRimp^S estimator was more efficient than the SW estimator in realistic settings, we did not provide theoretical justifications. In our future research we will attempt to develop the standard error estimate of the RRimp^S estimator and to provide theoretical justification for its greater efficiency. We also aim to find a survival estimator for costs that is monotone, consistent, and efficient, if possible.

Appendix

Proof of the Equivalency of the ZT Estimator and the RRimp Method for Estimating the Mean Costs

Suppose we have observed the following survival and cost history data

$$[\{X_i,{\Delta }_i,M_i,M_i\left(t_j\right),j=1,\cdots ,J\},i=1,\cdots ,n],$$

where i denotes individuals, t_j(j = 1, , J) denotes the ordered distinctive censoring times. Let Y_j indicate the number of people who have observation times greater than t_j (i.e., $Y_j={\sum }_{i=1}^{n}I(X_i>t_j)$), and n_j represent the number of people who are censored at time t_j. If an event occurs at a censoring time t_j, we assume this event happens shortly before t_j. Therefore, the set {X_i = t_j} consists only of censored data.

First, for the subject i}who is censored at t_j (note that we allow multiple subjects who are censored at time t_j), define δM_i(t_j) as the difference between the observed cost at time t_j for the ith subject and the average accumulated cost at t_j for subjects who are still alive at t_j:

$$\delta M_i\left(t_j\right)=M_i\left(t_j\right)-\overline{M\left(t_j\right)}=M_i\left(t_j\right)-\frac{{\sum }_{i:X_i\ge t_j}{M}_i\left(t_j\right)}{Y_j+n_j}.$$

Define M*(t_j) as the sum of δM_i(t_j) over all subjects who are censored at t_j:

$$\begin{array}{cc}\hfill M^{\ast }\left(t_j\right)=& \sum _{i:X_i=t_j}\delta M_i\left(t_j\right)=\sum _{i:X_i=t_j}{M}_i\left(t_j\right)-n_j\overline{M\left(t_j\right)}\hfill \\ \hfill =& \sum _{i:X_i=t_j}{M}_i\left(t_j\right)-\frac{n_j}{Y_j+n_j}\sum _{i:X_i\ge t_j}{M}_i\left(t_j\right).\hfill \end{array}$$

Starting from the longest censoring time t_J, there are Y_J subjects who have complete costs and whose survival times are greater than t_J. Hence, the RRimp cost for the kth subject censored at t_J is

$$M_{J,k}^{RRimp}=M_k\left(t_J\right)+\frac{1}{Y_J}\sum _{i:X_i>t_J}\{M_i-M_i\left(t_J\right)\}.$$

Recall that the replacement cost from the RR method for the kth subject censored at time t_J is

$$M_J^{RR}=\frac{1}{Y_J}\sum _{i:X_i>t_J}{M}_i,$$

and thus, the sum of the differences between $M_{J,k}^{RRimp}$ (in RRimp method) and $M_J^{RR}$ (in RR method) at t_J is

$$\begin{array}{cc}\hfill \sum _{k:X_k=t_J}\left(M_{J,k}^{RRimp}-M_J^{RR}\right)=& \sum _{k:X_k=t_J}{M}_k\left(t_J\right)+\frac{n_J}{Y_J}\sum _{i:X_i>t_J}\{M_i-M_i\left(t_J\right)\}-\frac{n_J}{Y_J}\sum _{i:X_i>t_J}{M}_i\hfill \\ \hfill =& \sum _{i:X_i=t_J}{M}_i\left(t_J\right)-\frac{n_J}{Y_J}\sum _{i:X_i>t_J}{M}_i\left(t_J\right)\hfill \\ \hfill =& \left(1+\frac{n_J}{Y_J}\right)\sum _{i:X_i=t_J}{M}_i\left(t_J\right)-\frac{n_J}{Y_J}\sum _{i:X_i\ge t_J}{M}_i\left(t_J\right)\hfill \\ \hfill =& \left(1+\frac{n_J}{Y_J}\right)\left\{\sum _{i:X_i=t_J}{M}_i\left(t_J\right)-\frac{n_J}{Y_J+n_J}\sum _{i:X_i\ge t_J}{M}_i\left(t_J\right)\right\}\hfill \\ \hfill =& \left(1+\frac{n_J}{Y_J}\right)M^{\ast }\left(t_J\right).\hfill \end{array}$$ (A.1)

Now we move to the second longest censoring time t_J–1, where the number of subjects surviving longer than t_J–1 is Y_J–1. The RRimp cost for the kth censored subject at t_J– is

$$\begin{array}{cc}\hfill M_{J-1,k}^{RRimp}=& M_k\left(t_{J-1}\right)+\frac{1}{Y_{J-1}}\sum _{i:X_i>t_{J-1}}\{M_i-M_i\left(t_{J-1}\right)\}\hfill \\ \hfill =& M_k\left(t_{J-1}\right)+\frac{1}{Y_{J-1}}\left[\sum _{i:X_i>t_{J-1}}{\Delta }_i\{M_i-M_i\left(t_{J-1}\right)\}+\sum _{i:X_i=t_J}\left\{M_{J,i}^{RRimp}-M_i\left(t_{J-1}\right)\right\}\right]\hfill \\ \hfill =& M_k\left(t_{J-1}\right)+\frac{1}{Y_{J-1}}\left[\sum _{i:X_i>t_{J-1}}{\Delta }_i{M}_i-\sum _{i:X_i>t_{J-1}}{\Delta }_i{M}_i\left(t_{J-1}\right)-\sum _{i:X_i=t_J}{M}_i\left(t_{J-1}\right)+\sum _{i:X_i=t_J}{M}_i\left(t_J\right)+\frac{n_J}{Y_J}\sum _{i:X_i>t_J}{\Delta }_i\{M_i-M_i\left(t_J\right)\}\right]\hfill \\ \hfill =& M_k\left(t_{J-1}\right)+\frac{1}{Y_{J-1}}\left\{\sum _{i:X_i>t_J}{\Delta }_i{M}_i+\sum _{i:t_{J-1}<X_i\le t_J}{\Delta }_i{M}_i-\sum _{i:X_i>t_{J-1}}{M}_i\left(t_{J-1}\right)+\sum _{i:X_i=t_J}{M}_i\left(t_J\right)+\frac{n_J}{Y_J}\sum _{i:X_i>t_J}{\Delta }_i{M}_i-\frac{n_J}{Y_J}\sum _{i:X_i>t_J}{M}_i\left(t_J\right)\right\}\hfill \\ \hfill =& \frac{1}{Y_{J-1}}(1+\frac{n_J}{Y_J})\sum _{i:X_i>t_J}{\Delta }_i{M}_i+\frac{1}{Y_{J-1}}\sum _{i:t_{J-1}<X_i\le t_J}{\Delta }_i{M}_i+M_k\left(t_{J-1}\right)-\frac{1}{Y_{J-1}}\sum _{i:X_i>t_{J-1}}{M}_i\left(t_{J-1}\right)+\frac{1}{Y_{J-1}}\sum _{i:X_i=t_J}{M}_i\left(t_J\right)-\frac{n_J}{Y_J{Y}_{J-1}}\sum _{i:X_i>t_J}{M}_i\left(t_J\right),\hfill \end{array}$$

where the first two terms $\frac{1}{Y_{J-1}}(1+\frac{n_J}{Y_J}){\sum }_{i:X_i>t_J}{\Delta }_i{M}_i+\frac{1}{Y_{J-1}}{\sum }_{i:t_{J-1}<X_i\ge t_J}{\Delta }_i{M}_i=M_{J-1}^{RR}$ (Zhao et al. 2011). Thus, the sum of difference between $M_{J-1,k}^{RRimp}$ and $M_{J-1}^{RR}$ at t_J–1 is

$$\begin{array}{cc}\hfill \sum _{k:X_k=t_{J-1}}(M_{J-1,k}^{RRimp}-M_{J-1}^{RR})=& \sum _{i:X_i=t_{J-1}}{M}_i\left(t_{J-1}\right)-\frac{n_{J-1}}{Y_{J-1}}\sum _{i:X_i>t_{J-1}}{M}_i\left(t_{J-1}\right)+\frac{n_{J-1}}{Y_{J-1}}\sum _{i:X_i=t_J}{M}_i\left(t_J\right)-\frac{n_{J-1}{n}_J}{Y_{J-1}{Y}_J}\sum _{i:X_i>t_J}{M}_i\left(t_J\right)\hfill \\ \hfill =& \left(1+\frac{n_{J-1}}{Y_{J-1}}\right)\sum _{i:X_i=t_{J-1}}{M}_i\left(t_{J-1}\right)-\frac{n_{J-1}}{Y_{J-1}}\sum _{i:X_i\ge t_{J-1}}{M}_i\left(t_{J-1}\right)+\frac{n_{J-1}}{Y_{J-1}}\left(1+\frac{n_J}{Y_J}\right)\sum _{i:X_i=t_J}{M}_i\left(t_J\right)-\frac{n_{J-1}{n}_J}{Y_{j-1}{Y}_J}\sum _{i:X_i\ge t_J}{M}_i\left(t_J\right)\hfill \\ \hfill =& \left(1+\frac{n_{J-1}}{Y_{J-1}}\right)M^{\ast }\left(t_{J-1}\right)+\frac{n_{J-1}}{Y_{J-1}}\left(1+\frac{n_J}{Y_J}\right)M^{\ast }\left(t_J\right).\hfill \end{array}$$ (A.2)

Similarly, we have

$$\sum _{k:X_k=t_{J-2}}(M_{J-2,k}^{RRimp}-M_{J-2}^{RR})=\left(1+\frac{n_{J-2}}{Y_{J-2}}\right)M^{\ast }\left(t_{J-2}\right)+\frac{n_{J-2}}{Y_{J-2}}\left(1+\frac{n_{J-1}}{Y_{J-1}}\right)M^{\ast }\left(t_{J-1}\right)+\frac{n_{J-2}}{Y_{J-2}}\left(1+\frac{n_{J-1}}{Y_{J-1}}\right)\left(1+\frac{n_J}{Y_J}\right)M^{\ast }\left(t_J\right).$$ (A.3)

In (A.1), the contribution of M*(t_j) is $(1+\frac{n_J}{Y_J})$. In (A.2), its contribution is $\frac{n_{J-1}}{Y_{J-1}}(1+\frac{n_J}{Y_J})$. For (A.3), the contribution is $\frac{n_{J-2}}{Y_{J-2}}(1+\frac{n_{J-1}}{Y_{J-1}})(1+\frac{n_J}{Y_J})$. If we generalize the conclusion and sum up the equations from J to 1, we can find the contribution of M*(t_J) is

$$\left(1+\frac{n_J}{Y_J}\right)+\left(1+\frac{n_J}{Y_J}\right)\cdot \frac{n_{J-1}}{Y_{J-1}}+\cdots +\left(1+\frac{n_J}{Y_J}\right)\cdots \left(1+\frac{n_2}{Y_2}\right)\cdot \frac{n_1}{Y_1}=\prod _{j=1}^J\left(1+\frac{n_j}{Y_j}\right).$$

Similarly, the contribution of M*(t_j) is

$$\left(1+\frac{n_j}{Y_j}\right)+\left(1+\frac{n_j}{Y_j}\right)\cdot \frac{n_{j-1}}{Y_{j-1}}+\cdots +\left(1+\frac{n_j}{Y_j}\right)\cdots \left(1+\frac{n_2}{Y_2}\right)\cdot \frac{n_1}{Y_1}=\prod _{l=1}^j\left(1+\frac{n_l}{Y_l}\right).$$

Hence,

$$\begin{array}{cc}\hfill {\widehat{\mu }}_{RRimp}=& \frac{1}{n}\left\{\sum _{i=1}^n{\Delta }_i{M}_i+\sum _{k:X_k=t_J}{M}_{J,k}^{RRimp}+\sum _{k:X_k=t_{J-1}}{M}_{J-1,k}^{RRimp}+\cdots +\sum _{k:X_k=t_1}{M}_{1,k}^{RRimp}\right\}\hfill \\ \hfill =& \frac{1}{n}\left\{\sum _{i=1}^n{\Delta }_i{M}_i+\sum _{k:X_k=t_J}{M}_J^{RR}+\sum _{k:X_k=t_{J-1}}{M}_{J-1}^{RR}+\cdots +\sum _{k:X_k=t_1}{M}_1^{RR}\right\}+\frac{1}{n}\left\{\prod _{j=1}^J\left((1+\frac{n_j}{Y_j}\right)M^{\ast }\left(t_J\right)+\prod _{j=1}^{J-1}\left(1+\frac{n_j}{Y_j}\right)M^{\ast }\left(t_{J-1}\right)+\cdots +\left(1+\frac{n_1}{Y_1}\right)M^{\ast }\left(t_1\right)\right\}\hfill \\ \hfill =& {\widehat{\mu }}_{RR}+\frac{1}{n}\left\{\prod _{j=1}^J\left(1+\frac{n_j}{Y_j}\right)M^{\ast }\left(t_J\right)+\prod _{j=1}^{J-1}\left(1+\frac{n_j}{Y_j}\right)M^{\ast }\left(t_{J-1}\right)+\cdots +\left(1+\frac{n_1}{Y_1}\right)M^{\ast }\left(t_1\right)\right\},\hfill \end{array}$$

where ${\widehat{\mu }}_{RR}={\widehat{\mu }}_{BT}$ is already known, and $M^{\ast }\left(t_j\right)={\sum }_{i:X_i=t_j}[M_i\left(t_j\right)-\overline{M\left(t_j\right)}]$ according to its definition. It can also be shown that the Kaplan–Meier estimator for K(t_j) is

$$\widehat{K}\left(t_j\right)=\prod _{l=1}^j\frac{Y_l}{Y_l+n_l},$$

which means

$$\frac{1}{\widehat{K}\left(t_j\right)}=\frac{1}{{\prod }_{l=1}^j\frac{Y_l}{Y_l+n_l}}=\prod _{l=1}^j\left(1+\frac{n_l}{Y_l}\right).$$

Thus,

$$\begin{array}{cc}\hfill {\widehat{\mu }}_{RRimp}=& {\widehat{\mu }}_{BT}+\frac{1}{n}\left[\frac{{\sum }_{i:X_i=t_J}\{M_i\left(t_J\right)-\overline{M\left(t_J\right)}\}}{\widehat{K}\left(t_J\right)}+\frac{{\sum }_{i:X_i=t_{J-1}}\{M_i\left(t_{J-1}\right)-\overline{M\left(t_{J-1}\right)}\}}{\widehat{K}\left(t_{J-1}\right)}+\frac{{\sum }_{i:X_i=t_{J-2}}\{M_i\left(t_{J-2}\right)-\overline{M\left(t_{J-2}\right)}\}}{\widehat{K}\left(t_{J-2}\right)}+\cdots +\frac{{\sum }_{i:X_i{t}_1}\{M_i\left(t_1\right)-\overline{M\left(t_1\right)}\}}{\widehat{K}\left(t_1\right)}\right]\hfill \\ \hfill =& {\widehat{\mu }}_{BT}+\frac{1}{n}\sum _{i=1}^n\frac{(1-{\Delta }_i)\{M_i-\overline{M\left(C_i\right)}\}}{\widehat{K}\left(C_i\right)}\hfill \\ \hfill =& {\widehat{\mu }}_{ZT}.\hfill \end{array}$$

We have proved that the RRimp estimator is the same as the ZT estimator for estimating the mean cost.