Pseudo-Sibship Methods in the Case-Parents Design

Abstract

Recent evidence suggests that complex traits are likely determined by multiple loci, with each of which contributes a weak to moderate individual effect. Although extensive literature exists on multi-locus analysis of unrelated subjects, there are relatively fewer strategies for jointly analyzing multiple loci using family data. Here we address this issue by evaluating two pseudo-sibship methods: the 1:1 matching, which matches each affected offspring to the pseudo sibling formed by the alleles not transmitted to the affected offspring; the exhaustive matching, which matches each affected offspring to the pseudo siblings formed by all the other possible combinations of parental alleles. We prove that the two matching strategies use exactly and approximately the same amount of information from data under additive and multiplicative genetic models, respectively. Using numerical calculations under a variety of models and testing assumptions, we show that compared to the exhaustive matching, the 1:1 matching has comparable asymptotic power in detecting multiplicative / additive effects in single-locus analysis and main effects in multi-locus analysis, and it allows association testing of multiple linked loci. These results pave the way for many existing multi-locus analysis methods developed for the case-control (or matched case-control) design to be applied to case-parents data with minor modifications. As an example, with the 1:1 matching, we applied an L₁ regularized regression to a Crohn’s disease dataset. Using the multiple loci selected by our approach, we obtained an order-of-magnitude decrease in p-value and an 18.9% increase in prediction accuracy when comparing to using the most significant individual locus.

1. Introduction

It has long been recognized that spurious marker disease association can be introduced by population stratification in case-control studies [1]. When subjects are sampled from multiple populations that are different in both disease prevalence and allele frequencies, association analysis based on a case-control design might lead to false findings. As a result, population stratification is one of the most often cited explanations for the difficulties in replicating results of genetic association studies [2–4]. One way to avoid drawing erroneous conclusions on genetic associations is to use family-based designs, such as the case-parents design, in which both cases and their parents are genotyped [5]. The validity of this design stems from the fact that the hypothetical control formed by the nontransmitted alleles in a case-parents trio is from the same population as the case is.

When testing the association between a locus and a disease using case-parents data, modeling the genotype of an offspring conditioning on parental mating (genotypes) and the offspring being affected prevents spurious association caused by population stratification [6, 7]. The conditional approach is equivalent to matching the affected offspring to his or her three pseudo siblings formed by the other three combinations of parental alleles (hereafter 1:3 matching), and conditional logistic regressions can be used for statistical inference [6, 7]. Different tests based on the conditional logistic regression framework have been proposed, such as likelihood ratio tests (LRT) and score tests under a variety of assumptions about the true genetic model [6, 8, 9]. It has been shown that the well-known transmission disequilibrium test (TDT) [10, 11] is the score test of the conditional logistic regression using the 1:3 matching under multiplicative model [8]. Interestingly, as originally derived, the TDT is also a McNemar [12] type of test when matching each affected offspring to his or her pseudo sibling formed by the alleles that are not transmitted to the affected offspring (hereafter 1:1 matching). Other tests based on the 1:1 matching include such as the tests introduced by Terwilliger and Ott [11], and Wittkowski and Liu [13]. Obviously, using three pseudo siblings for each case utilizes more information from data than the 1:1 matching. Cordell and Clayton found that the 1:3 matching is more efficient than the 1:1 matching [14].

The 1:3 matching in a single-locus analysis is exhaustive in that each affected offspring is matched to all the other possible combinations of parental alleles. Generalized to L unlinked loci, the number of all pseudo offspring matched to an affected child then is 4^L-1 [14, 15]. In computation, this exponential growth can limit the number of loci to be jointly analyzed. For linked loci, additional computational complexity arises, as the transmission of parental alleles to offspring does not follow the Mendel’s law of independent assortment and all the possible offspring genotypes of a pair of parents do not occur with equal probabilities. Therefore the recombination fractions between SNPs are required to build conditional logistic regressions [14–16]. However, these recombination fractions are usually unknown and difficult to estimate. Thus, although the exhaustive matching maximizes information extracted from the case-parents data, it is difficult to be used in multi-locus association analysis. To avoid those complications, instead of the exhaustive matching, we can use the 1:1 matching.

In the literature, a number of multi-locus methods using the 1:1 matching have been proposed [17–30]. In those methods, a test statistic is first computed by comparing the transmitted alleles to the nontransmitted alleles, and then the statistical significance is assessed either by asymptotic theories or by a permutation procedure that randomly shuffles the “transmitted” and “nontransmitted” labels of each affected offspring and his or her pseudo sibling. In terms of haplotype phase, both haplotype-based [17–21, 23, 24] and genotype-based [22, 24–30] methods have been proposed. For genotype-based methods, both main effects [22, 24, 27] and gene-gene interaction have been tested [26]. Although the 1:1 matching is more straightforward to implement, computationally more tractable, and allows association testing of multiple linked SNPs, there is no doubt that it utilizes less information from data than the exhaustive matching. It is therefore important to know the efficiency of the 1:1 matching relative to that of the exhaustive matching. Especially, if the efficiency of the 1:1 matching is model- or test-dependent, it is critical to evaluate under what situations the 1:1 matching is efficient.

In this paper, we systematically investigate the relative efficiency of the two ways of creating pseudo controls: the 1:1 matching and the exhaustive matching. We prove that the two matching strategies use exactly and approximately the same amount of information from data under additive and multiplicative models, respectively. We also quantify the efficiency of the two matching strategies using statistical power computed from asymptotic LRTs under the conditional logistic regression framework. We compare the efficiency of the two matching strategies under different genetic models and testing models, in both one-locus analysis and two-locus analysis. As an illustration of using the 1:1 matching to conduct multi-locus analysis, we apply an L₁ regularized variable selection method to a Chron’s disease dataset, and compare its performance to using the most significant single locus.

2. Methods

2.1. The equivalence of the 1:1 matching and the exhaustive matching under additive genotype relative risks

Suppose we are testing the association between a disease and a single nucleotide polymorphism (SNP) with a risk allele ‘A’ and a normal allele ‘a’. For convenience, we use numerically coded genotypes based on the number of the “A” alleles and adopt the notations of trio types used in [9]. If we ignore the order of parents, there are six parental mating types and ten trio types, which are illustrated in the first two columns of Table 1. For a case-parents trio, let t ∈ {12,22,21,31,42,41,40,51,50,60} denote the trio type determined by the parental mating type and the genotype of the affected offspring, as shown in Table 1. When testing the association between a locus and a disease using the case-parents design, the approach conditioning on parental mating type and the case being affected is equivalent to the 1:3 matching, which matches each affected offspring to his or her three pseudo siblings [6, 7]. We use H_E (t) to denote the 1:3 matching set of numerically coded genotypes that comprises the genotype of the offspring and the other three combinations of parental alleles. Generalized to L unlinked SNPs, the set H_E (.) consists of 4^L genotypes. An alternative matching strategy matches each affected offspring to his or her pseudo-sibling constructed by the alleles that are not transmitted to the affected offspring, and we denote the 1:1 matching set by H₁(t). As an example, suppose the genotypes of the affected offspring, the father, and the mother are 2 (AA), 1 (Aa), and 1 (Aa), respectively, then t = 42, H₁(t) = {2,0} and H_E (t) = {2,0,1,1}, as shown in Figure 1.

Table 1.

Trio type, parental mating type, case type, and pseudo controls for case-parents data.

Trio type	Parental mating type	Case type	Pseudo controls
12	1: AA x AA	2: AA	AA, AA, AA
22	2: AA x Aa	2: AA	Aa, AA, Aa
21		1: Aa	AA, AA, Aa
31	3: AA x aa	1: Aa	Aa, Aa, Aa
42	4: Aa x Aa	2: AA	aa, Aa, Aa
41		1: Aa	Aa, AA, aa
40		0: aa	AA, Aa, Aa
51	5: Aa x aa	1: Aa	aa, Aa, aa
50		0: aa	Aa, Aa, aa
60	6: aa x aa	0: aa	aa, aa, aa

The first column shows the trio types, which are determined by parental mating types and case genotype. The second column shows the parental mating types, and if we ignore the order of parents there are 6 types in total, as shown from top to bottom. The third column shows the genotypes of the affected offspring; there are three types in total, AA, Aa and aa, which are represented by type 2, 1, and 0, respectively. The fourth column shows the genotypes of the pseudo siblings of the affected offspring under the 1:3 matching; the genotype in bold letters is that of the pseudo sibling of the affected offspring under the 1:1 matching.

Figure 1.

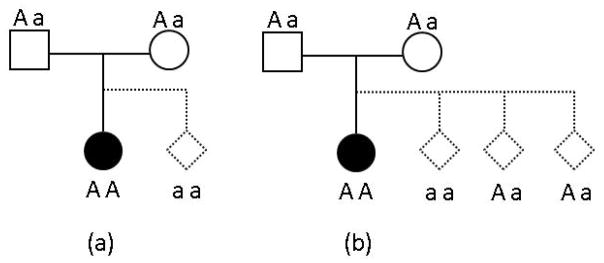
One (a) v.s. three (b) pseudo siblings for the affected offspring AA genotype, Aa father, and, Aa mother. The filled circles represent the genotypes of the affected offspring, and the dotted diamonds represent the genotypes of the pseudo siblings.

Let g_l, l=1,2,…,L be the number of copies of the risk allele at SNP l. We define the genotype relative risk (GRR) of genotype (g₁, g₂,…, g_L) as the relative risk of being affected for subjects with this genotype relative to subjects with genotype (0,0,…,0):

$$r_{g_1,g_2,\dots ,g_L}=\frac{Pr(D=1\mid g_1,g_2,\dots ,g_L)}{Pr(D=1\mid 0,0,\dots ,0)}.$$

Definition

We say the GRRs are additive if

$$r_{g_1,g_2,\dots ,g_L}=1+{\sum }_{l=1}^L{\gamma }_l{g}_l$$

where ${\gamma }_l=r_{0,0,\dots ,1,\dots ,0}-1=\frac{Pr(D=1\mid 0,0,\dots ,g_l=1,\dots ,0)-Pr(D=1\mid 0,0,\dots ,0)}{Pr(D=1\mid 0,0,\dots ,0)}$, for l = 1,…, L. For example, when L=1, r₀ = 1,r₁ = 1+γ₁,r₂ = 1+2γ₁.

Note that additive GRRs imply additive penetrances. We next show that additive GRRs implies the equivalence between the 1:1 matching and the exhaustive matching.

Theorem

Suppose the GRRs are additive, the 1:1 matching and the exhaustive matching use exactly the same amount of information from data. In other words, the likelihood functions of the 1:1 matching and the exhaustive matching are identical.

The proof for unlinked loci is provided in the Appendix. When loci are linked, if we also know recombination fractions among loci, we can use a weighted exhaustive matching, with the weights determined by recombination fractions. With the same method used in the Appendix and some additional notations, we can prove that the 1:1 matching and the weighted exhaustive matching use the same amount of information from data under additive GRRs. Here we focus only on unlinked loci for two reasons. First, this situation leads to the largest difference between the two matching strategies. Second, when SNPs are linked, using the exhaustive matching requires recombination fractions [14–16] that might not be easily estimated from case-parents data.

To make the results intuitive, consider the situation when L is 1. Let n_t denote the number of case-parents trios in trio type t, where t ∈ {12,22,21,31,42,41,40,51,50,60}. The likelihood functions under the exhaustive matching and under the 1:1 matching are

$$L_E(r_1,r_2)\propto {\left(\frac{r_2}{r_1+r_2}\right)}^{n_{22}}{\left(\frac{r_1}{r_1+r_2}\right)}^{n_{21}}{\left(\frac{r_2}{1+2r_1+r_2}\right)}^{n_{42}}{\left(\frac{2r_1}{1+2r_1+r_2}\right)}^{n_{41}}{\left(\frac{1}{1+2r_1+r_2}\right)}^{n_{40}}{\left(\frac{r_1}{1+r_1}\right)}^{n_{51}}{\left(\frac{1}{1+r_1}\right)}^{n_{50}},$$ (1)

and

$$L_1(r_1,r_2)\propto {\left(\frac{r_2}{r_1+r_2}\right)}^{n_{22}}{\left(\frac{r_1}{r_1+r_2}\right)}^{n_{21}}{\left(\frac{r_2}{1+r_2}\right)}^{n_{42}}{\left(\frac{1}{1+r_2}\right)}^{n_{40}}{\left(\frac{r_1}{1+r_1}\right)}^{n_{51}}{\left(\frac{1}{1+r_1}\right)}^{n_{50}},$$ (2)

respectively. Under the assumption of additive GRRs, i.e., 1+r₂ = 2r₁, both L_E and L₁ are proportional to

$${\left(\frac{2r_1-1}{3r_1-1}\right)}^{n_{22}}{\left(\frac{r_1}{3r_1-1}\right)}^{n_{21}}{\left(\frac{2r_1-1}{2r_1}\right)}^{n_{42}}{\left(\frac{1}{2r_1}\right)}^{n_{40}}{\left(\frac{r_1}{1+r_1}\right)}^{n_{51}}{\left(\frac{1}{1+r_1}\right)}^{n_{50}}.$$

Definition

We say GRRs are multiplicative if

$$r_{g_1,g_2,\dots ,g_L}={\prod }_{l=1}^L{(1+{\gamma }_l)}^{g_l}.$$

Corollary

When the marginal genetic effects are not large, the 1:1 matching and the exhaustive matching use approximately the same amount of information from data under multiplicative GRRs.

When the marginal genetic effects are not large, we can use the first-order Taylor expansion to approximate the GRRs and get rid of terms of higher orders. Hence, the result follows immediately. Therefore, the 1:1 matching and the exhaustive matching also use similar amount of information from data under multiplicative GRRs. When the frequency of the risk allele at a locus is small, the dominant model is close to the multiplicative model, implying the near equivalence between the two matching strategies under the dominant model. It is not clear how much power the 1:1 matching would lose under the recessive model. To quantify the relative efficiency of the 1:1 matching to that of the exhaustive matching, we use numerical comparisons under a variety of models and testing assumptions for both one-locus and two-locus analysis, as described next.

2.2. One-locus models and tests

2.2.1. Likelihood ratio tests for the association between a disease and a SNP

For testing the association between a SNP and a disease, the conditional likelihood function of conditioning on parental mating type and the case being affected is equivalent to the 1:3 matching likelihood function L_E (r₁,r₂), given in (1). An alternative matching method is the 1:1 matching, with the likelihood function, denoted by L₁(r₁,r₂), provide in (2). Based on the likelihood functions, we consider the following three types of likelihood ratio tests.

The first type of tests we study is two-degree-of-freedom tests. In this type of tests, we compare the maximized likelihood with parameters r₁ and r₂ to the likelihood under the null hypothesis r₁=r₂=1. We denote the resulted two-degree-freedom test with the 1:3 matching as “2df_E” and the test with the 1:1 matching as “2df₁”.

The second type of tests we study has one degree of freedom, which is obtained by placing restrictions on GRRs. We consider the following three commonly used restrictions:

• Multiplicative, for which $r_2=r_1^2$

• Recessive, for which r₁ = 1

• Dominant, for which r₂ = r₁

The likelihood ratio tests are constructed by comparing the maximized likelihood under each restriction to the likelihood under the null hypothesis r₁=r₂=1. In each of the above restricted models, only one parameter needs to be estimated, therefore the resulted likelihood ratio tests have only one degree of freedom. We denote the three tests with the 1:3 matching as “MUL_E”, “REC_E”, and “DOM_E”, respectively; and denote the three tests with the 1:1 matching as “MUL₁”, “REC₁”, and “DOM₁”, respectively. Because the TDT [10] is widely used, we also compute the power of the TDT.

The third type of tests we consider is the test of Hardy-Weinberg Equilibrium (HWE). Testing HWE in case-only data or case-control data has been used in fine-scale mapping [31–33]. It has also been used to provide information about the underlying disease models and thus to improve statistical power [34–36]. In case-only data or case-control data, testing HWE is equivalent to testing whether the underlying genotype penetrance is multiplicative, since HWE in affected subjects holds if and only if the disease model is multiplicative. In case-parents data, multiplicative GRRs imply independent transmission of alleles from parents to the affected offspring [9], that is, the transmission follows HWE. Therefore, we can conduct the HWE test for case-parents data by testing whether the GRRs are multiplicative. Under the null hypothesis of multiplicative GRRs, the likelihood functions using the 1:3 matching and the 1:1 matching are

$$\begin{array}{l}{L}_E(r)\propto {\left(\frac{r}{1+r}\right)}^{n_{22}}{\left(\frac{1}{1+r}\right)}^{n_{21}}{\left(\frac{r^2}{{(1+r)}^2}\right)}^{n_{42}}{\left(\frac{2r}{{(1+r)}^2}\right)}^{n_{41}}{\left(\frac{1}{{(1+r)}^2}\right)}^{n_{40}}{\left(\frac{r}{1+r}\right)}^{n_{51}}{\left(\frac{1}{1+r}\right)}^{n_{50}},\\ L_1(r)\propto {\left(\frac{r}{1+r}\right)}^{n_{22}}{\left(\frac{1}{1+r}\right)}^{n_{21}}{\left(\frac{r^2}{1+r^2}\right)}^{n_{42}}{\left(\frac{1}{1+r^2}\right)}^{n_{40}}{\left(\frac{r}{1+r}\right)}^{n_{51}}{\left(\frac{1}{1+r}\right)}^{n_{50}},\end{array}$$

respectively. For the 1:3 matching, we construct the likelihood ratio test by comparing the maximized L_E (r₁,r₂) to the maximized L_E (r), and we denoted the resulted test as “HWE_E”. Similarly, for 1:1 matching, we construct the likelihood ratio test “HWE₁” by comparing the maximized L₁(r₁,r₂) to the maximized L₁(r).

2.2.2. Power calculation

We have introduced nine likelihood ratio tests for both the 1:3 matching and the 1:1 matching. The efficiency depends not only on tests, but also on true genetic models. Here we consider four true genetic models: multiplicative, recessive, dominant, and additive. The definitions of the models have been discussed previously.

To compute the asymptotic power, we choose the number of trios to be 200, and fix the frequency of the risk allele ‘A’ to be 0.2. We assume that the trios are from a random mating population. For a given true genetic model, we first compute the expected numbers of different trio types. Using the expected numbers of trio types, for a given test, we then compute the non-centrality parameter using twice the log of the ratio of the likelihood maximized under the alternative hypothesis to the likelihood maximized under the null hypothesis [15]. As an example, to compute the power of the 2df_E test under a multiplicative model, we first compute the expected numbers of trio types under the multiplicative model; then compute the non-centrality parameter ncp = 2log(max L_E (r₁, r₂)/L_E (1,1)), where max L_E (r₁,r₂) is the likelihood maximized over the parameters r₁ and r₂; last, we compute the power using $Pr(X_2(\mathit{ncp})>{\chi }_{2,0.95}^2)$, where X₂ (ncp) is a chi-square-distributed random variable with two degrees of freedom and the non-centrality parameter ncp, and ${\chi }_{2,0.95}^2$ is the 95^th percentile of the chi-square distribution with two degrees of freedom.

2.3. Two-locus models

We use two-locus models as examples of multi-locus scenarios, since multi-locus models with more than two loci will result in complicated exhaustive matching. In the two-locus analysis, we consider both the 1:1 matching and the 1:15 (exhaustive) matching. We assume that the two SNPs are unlinked since this situation leads to the largest difference between the two matching strategies.

Two SNPs can jointly affect the risk of a disease in many different ways. Here we consider four types of true genetic models, including

• mul-mul, the model with multiplicative main effects at both SNPs and no interaction;

• dom-dom, the model with dominant main effects at both SNPs and no interaction;

• rec-rec, the model with recessive main effects at both SNPs and no interaction;

• gene-gene interaction, the model with multiplicative main effects and gene-gene interaction effect.

The GRRs of the four models are shown in Table 2.

Table 2.

The GRRs of four two-locus genetic models: multiplicative-multiplicative, dominant-dominant, recessive-recessive, and gene-gene interaction models, from top to bottom, respectively.

Genetic Model	SNP1	SNP2
		bb	Bb	BB
mul-mul	aa	1	λ	λ2
	Aa	λ	λ2	λ3
	AA	λ2	λ3	λ4
dom-dom	aa	1	λ	λ
	Aa	λ	λ2	λ2
	AA	λ	λ2	λ2
rec-rec	aa	1	1	λ
	Aa	1	1	λ
	AA	λ	λ	λ2
gene-gene interaction: test for main effects	Aa	1	λ	λ2
	Aa	λ	λ2	1.2λ3
	AA	λ2	1.2λ3	1.22λ4
gene-gene interaction: test for interaction	Aa	1	1.2	1.22
	Aa	1.2	1.22λ	1.23λ2
	AA	1.22	1.23λ2	1.24λ4

To test genetic association between the two loci and a disease, we consider the following conditional likelihood function

$$L_H(\alpha ,\beta ,\gamma )=\prod _{i=1}^n\frac{exp(\alpha g_{o,i}+\beta h_{o,i}+\gamma g_{o,i}{h}_{c,i})}{{\displaystyle \sum _{(g_{o,i}^{\prime },h_{o,i}^{\prime })\in \mathrm{H}(t_{i1},t_{i2})}}exp(\alpha g_{o,i}^{\prime }+\beta h_{o.i}^{\prime }+\gamma g_{o,i}^{\prime }{h}_{o,i}^{\prime })},$$

where H represents the 1:1 matching or the exhaustive matching; α, β, and γ denote the coefficients of the main effect at the first SNP, the main effect at the second SNP, and the interaction effect between the two SNPs, respectively; g_o,i and h_o,i are the numerically coded genotypes of the affected offspring in the ith case-parents trio at the first and the second SNPs, respectively; t_i1 and t_i2 are the trio types defined based upon the first and the second SNPs, respectively.

For the first three genetic models, namely mul-mul, dom-dom, and rec-rec, no interaction is assumed between the two loci. We test the main effect using LRTs similar to those described in the one-locus analysis. Specifically, we compare L_H (α, β,0) at its maximized value to L_H (0,0,0). For the gene-gene interaction model, in addition to testing the main effect, we also test the gene-gene interaction by comparing the maximized value of L_H (α,β,γ) to that of L_H (α, β,0). The computation of power of the LRTs under the four true genetic models are similar to what we use in the one-locus analysis, with 200 case-parents trios sampled from a random mating population with the risk allele frequencies at both SNPs being 0.2.

2.4. Application to real data

We conducted both single-locus and multi-locus analyses on a Caucasian-based case-parents dataset in which all offspring had Crohn’s disease. Crohn’s disease is an inflammatory bowel disease that affects about half a million people in North America [37]. Using a linkage analysis of nuclear families with inflammatory bowel disease patients, Rioux et al. [38] detected linkage signals at human chromosome 5q31. To narrow down the candidate region, they genotyped SNPs at 5q31 for 139 case-parents trios [39]. We used the publically available subset, i.e., 129 trios genotyped on 103 common SNPs, available from http://www.broadinstitute.org/archive/humgen/IBD5/haplodata.html (data downloaded on July 27, 2010). These 103 SNPs cover a 500-kb region at 5q31, and the linkage disequilibrium structure of the 103 SNPs was reported before [40]. In our analysis we excluded two trios with more than 40% missing genotypes, and analyzed the remaining 127 trios.

For the single-locus analysis of the data, we consider four types of tests, with each assuming a specific genetic model: 2df, the two-degree-freedom test; DOM, the dominant test; MUL, the multiplicative test; and REC, the recessive test. Each type is conducted with both the 1:1 matching and the 1:3 matching, so in total there are eight tests. All the eight tests are applied to each of the 103 SNPs of the Crohn’s disease dataset.

We also conduct the multi-locus analysis using the 1:1 matching. The exhaustive matching cannot be used, because the recombination fractions are unknown and cannot be accurately estimated, and there are 103 SNPs. In the Crohn’s disease data, the number of SNPs is close to the number of trios, which would create problems if we jointly analyze all the SNPs in a conditional logistic regression. This motivates us to use the Lasso regularization [41]. Another advantage of the Lasso regularization is that it shrinks estimates of regression coefficients toward zero by adding an L₁ penalty term, therefore it is especially suitable for selecting SNPs in genetic association analysis [42–45]. To realize Lasso regularization, we use the penalized R package, which provides L₁ regularized estimation for Cox proportional-hazards regression [46]. The reason why we choose this package is that Cox proportional-hazards regression can be used to fit conditional logistic regression by putting each matched case-control pair in a unique stratum [9]. In our analysis, we first impute missing genotype data using BEAGLE [47], as the penalized package requires complete data. Then with the genotype variable of each SNP being numerically coded to be 0, 1, or 2 according to the number of copies of the rare allele of the SNP, we use the leave-one-out cross-validation to choose the optimal tuning constant, which determines the degree of shrinkage of the regression coefficients. Following that we compute the coefficients of the conditional logistic regression for the SNPs chosen with the optimal tuning constant. And finally we compute the percentage of correctly predicted disease status. For comparison, we also compute the percentage of correctly predicted disease status using the most significant SNP.

3. Results

3.1. Results of one-locus models

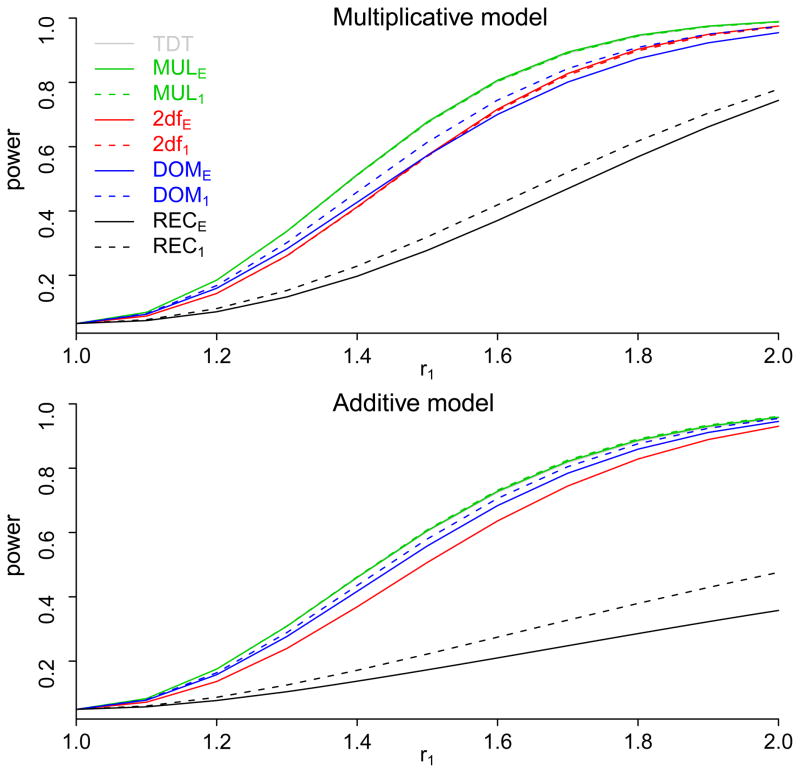
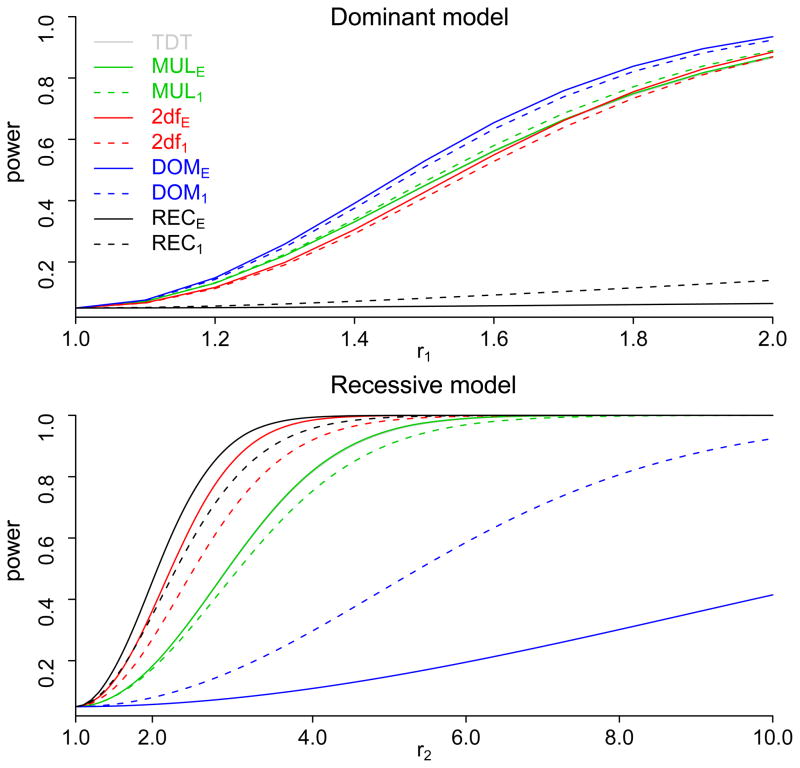
Figures 2 and 3 show the power of the TDT, and the four tests under four different one-locus genetic models for both the 1:1 matching and the 1:3 matching. The power of the TDT and MUL_E was nearly identical, and their power curves almost overlap to each other in Figures 2 and 3. This is not surprising, because the TDT is the score test and MUL_E is the likelihood ratio test of the same model. We also subtract the power of the 1:1 matching from that of the 1:3 matching, and summarize the differences in Table 3. Thus, positive values in Table 3 indicate that the 1:3 matching is more powerful than the 1:1 matching, and negative values indicate the opposite.

Figure 2.

The power of the nine tests: MUL, DOM, REC, and 2df tests for each of the two matching strategies, and the TDT test. Because the power curves of the TDT and MUL_E almost overlap to each other, it is hard to see the curves of the TDT on the plots. Upper panel: power curves when the true genetic model is multiplicative; lower panel: power curves when the true genetic model is additive.

Figure 3.

The power of the nine tests: MUL, DOM, REC, and 2df tests for each of the two matching strategies, and the TDT test. Because the power curves of the TDT and MUL_E almost overlap to each other, it is hard to see the curves of the TDT on the plots. Upper panel: power curves when the true genetic model is dominant; lower panel: power curves when the true genetic model is recessive.

Table 3.

Range of the power difference (in %) between the 1:3 matching and the 1:1 matching for four testing models (Multiplicative, Dominant, Recessive, 2df) and four true genetic models (Multiplicative, Dominant, Recessive, and Additive) in the single-locus analysis. A negative value means the 1:1 matching is more powerful, while a positive value means the 1:3 matching is more powerful.

Testing model	Multiplicative	Dominant	Recessive	2df
True model
Multiplicative	[0, 0.4]	[−4.5, 0]	[−5.1, 0.1]	[0, 0.5]
Dominant	[−2.2, 0]	[0, 2.1]	[−7.6, 0]	[0, 2.2]
Recessive	[0, 6.6]	[−51.9, 0]	[0, 15.0]	[0, 16.3]
Additive	[−0.4, 0]	[−2.2, 0]	[−11.2, 0]	[0, 0]

When the testing model agrees with the true model, as the 1:3 matching uses more information from data, naturally the 1:3 matching is always more powerful than the 1:1 matching. It is also more efficient under the two-degree-of-freedom test, for all true genetic models except the additive model. This exception is due to the fact that the likelihood functions L_E (r₁, r₂) and L₁(r₁,r₂) are identical under additive GRRs.

There are also many situations that the power of the 1:1 matching is comparable to or even greater than that of the 1:3 matching. For example, when the true model is additive, the two matching approaches have the same power under the two-degree-of-freedom test, and the 1:1 matching is more powerful under the other tests. When the true model is multiplicative, the 1:1 matching is also more powerful under dominant or the recessive test, and it is only slightly less powerful under the multiplicative or the two-degree-of-freedom test. Another situation where the 1:1 matching is superior is when the testing model is quite different from the true model. For example, when the testing model is dominant but the true model is recessive, as shown in Table 3 and the lower panel of Figure 3, the 1:1 matching outperformed the 1:3 matching with a maximum difference of 51.9% (recall that a negative value in Table 3 implies that the 1:1 matching is more powerful than the 1:3 matching). This demonstrates that the 1: 1 matching is more robust against the misspecification of genetic model.

For the multiplicative test, the 1:1 matching has comparable efficiency to the 1:3 matching for all genetic models, as also shown in Table 3. This is especially important, because when no prior information regarding the true genetic model is available, one often conducts tests with the multiplicative assumption to prevent substantial power loss due to model misspecification.

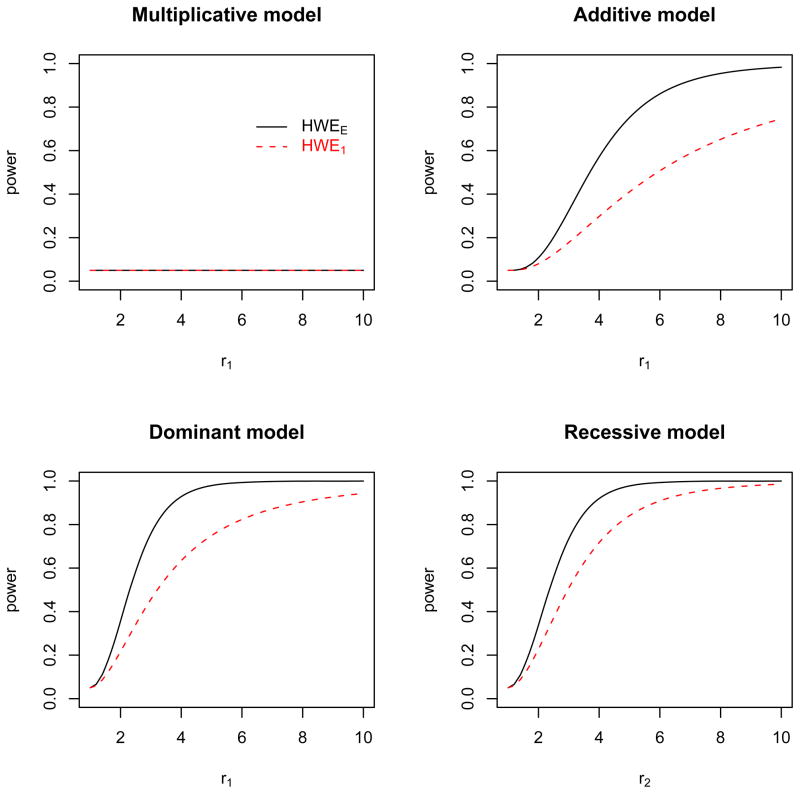
The results of the HWE test are shown in Figure 4. When the GRRs are multiplicative, the transmission of alleles from parents follows the HWE. As a result, the power of the HWE test is equal to the nominal p-value cutoff for both matching strategies. When the GRRs are additive, dominant, or recessive, the 1:3 matching is more powerful than the 1:1 matching. As those GRRs at a locus can be considered as allelic interactions, the result indicates that the 1:1 matching is less efficient in testing allelic interactions.

Figure 4.

The power of the HWE test for the 1:3 matching (solid line) and the 1:1 matching (dashed line) when the true genetic models are multiplicative, additive, dominant, and recessive, respectively.

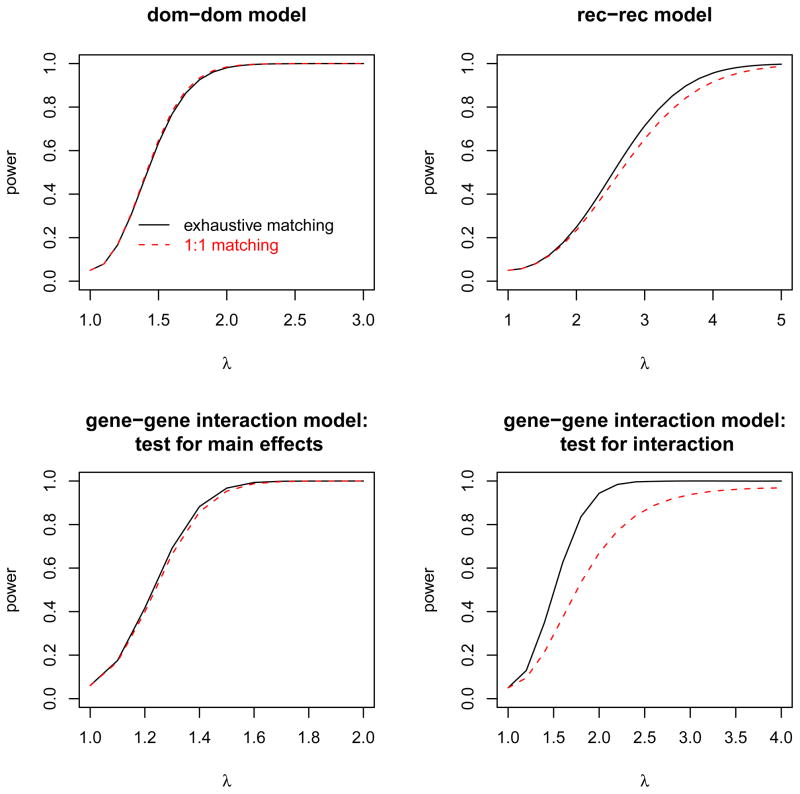
3.2. Results of two-locus models

The results of two-locus analysis are shown in Figure 5 and they are similar to those observed in the single-locus analysis. Recall that the main effects in our two-locus analysis are assumed to be multiplicative at both loci. When the testing model agrees with the true main effects, the exhaustive matching is expected to be more powerful than the 1:1 matching; however, we found that under the mul-mul model the difference in power between the two strategies is quite small, with the maximum difference being less than 0.7% (data not shown). This echoes what we found in the one-locus analysis, that is, for the multiplicative test, the 1:1 matching and the 1:3 matching have comparable efficiency. When the true main effects do not agree with the testing model, the relative efficiency of the 1:1 matching to the exhaustive matching is model dependent. The 1:1 matching is slightly more powerful in the dom-dom model (the upper left plot of Figure 5), but slightly less powerful in the rec-rec model (the upper right plot of Figure 5). For the gene-gene interaction models, we tested both main effects (shown in the lower left plot of Figure 5) and gene-gene interactions (show in the lower right plot of Figure 5). In detecting main effects, the 1:1 matching is as efficient as the exhaustive matching, with the maximum power reduction being less than 3%. In detecting gene-gene interactions, the 1:1 matching is not as efficient as the exhaustive matching, with the maximum loss being 30.2%.

Figure 5.

The power computed under two-locus models, for both the 1:1 matching (dashed line) and the exhaustive matching (solid line). The upper two plots show the power of detecting main effects computed under two main-effect-only models: dom-dom and rec-rec, respectively. The power of detecting main effects under the mul-mul model shows no noticeable difference between the 1:1 matching and the exhaustive matching; thus, the results are omitted. The lower plots show the power of detecting main effects and gene-gene interactions, respectively, under the gene-gene interaction model.

Intuitively, the exhaustive matching utilizes more information and thus should be more efficient than the 1:1 matching in both single-locus and multi-locus analysis. This is largely confirmed in the numerical comparisons above. First, a higher power in detecting main effect was observed with the exhaustive matching method when the true model was correctly specified. It seems that most of the time this gain in statistical power was minimal and hardly be appreciable in both single-locus and two-locus analysis. This might be partly due to the fact that not all pseudo-controls constructed under the exhaustive matching provide evidence for the true model. Some pseudo controls may represent the evidence against the true model, offsetting the statistical power in detecting an association. Second, we found that the exhaustive matching is much more powerful than the 1:1 matching in testing for interaction. By the way the 1:1 matching was constructed, it does not allow for other possible combinations of alleles at different loci except the ones passed from the parents; its power for detecting interaction is thus very much limited.

To summarize, the results of the one-locus and two-locus studies demonstrate that the 1:1 matching generally has comparable power to the exhaustive matching in detecting multiplicative / additive effects in single-locus analysis and main effects in multi-locus analysis, but not as efficient in detecting interactions, which agrees with our theoretical finding about the equivalence (near equivalence) between the 1:1 matching and the exhaustive matching under additive (multiplicative) GRRs.

3.3. Results of the Crohn’s disease dataset

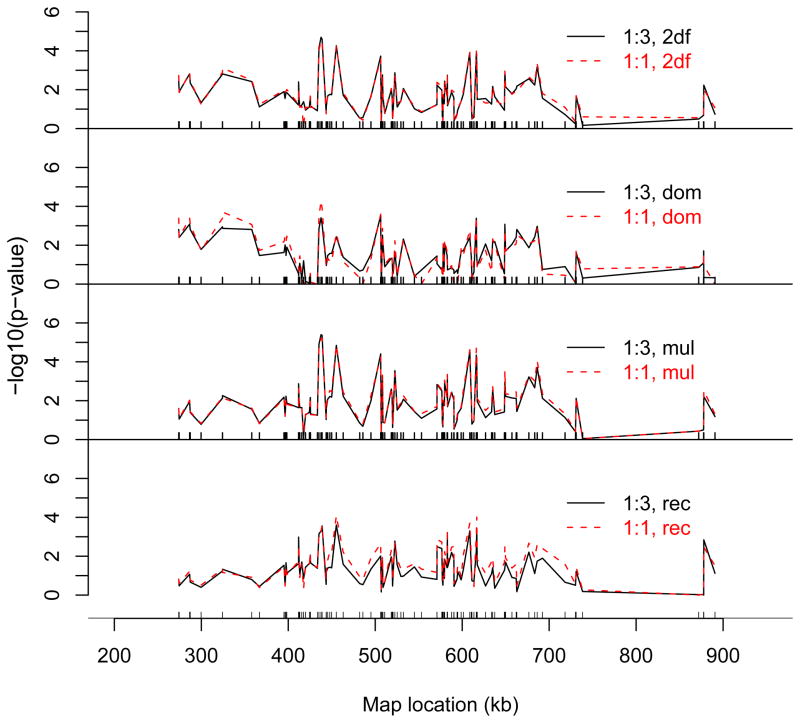
The p-values of the single-locus analysis of the Crohn’s disease dataset are shown in Figure 6. Among all tests, the two tests for the multiplicative effect show the highest significance for most SNPs. The difference in p-values between the 1:1 matching and the 1:3 matching is small for the two two-degree-of-freedom tests and for the two multiplicative tests. Because the two two-degree-freedom tests are exactly / approximately identical when the true model is additive / multiplicative, the results here suggest that additivity or multiplicity is a good approximation to the true genetic models of most SNPs.

Figure 6.

The p-values (on the −log10 scale) of the four single-locus tests for the Crohn’s disease data. The four tests are, from top to bottom, the 2df, DOM, MUL, and REC tests, respectively. Solid line: the 1:3 matching; dashed line: the 1:1 matching.

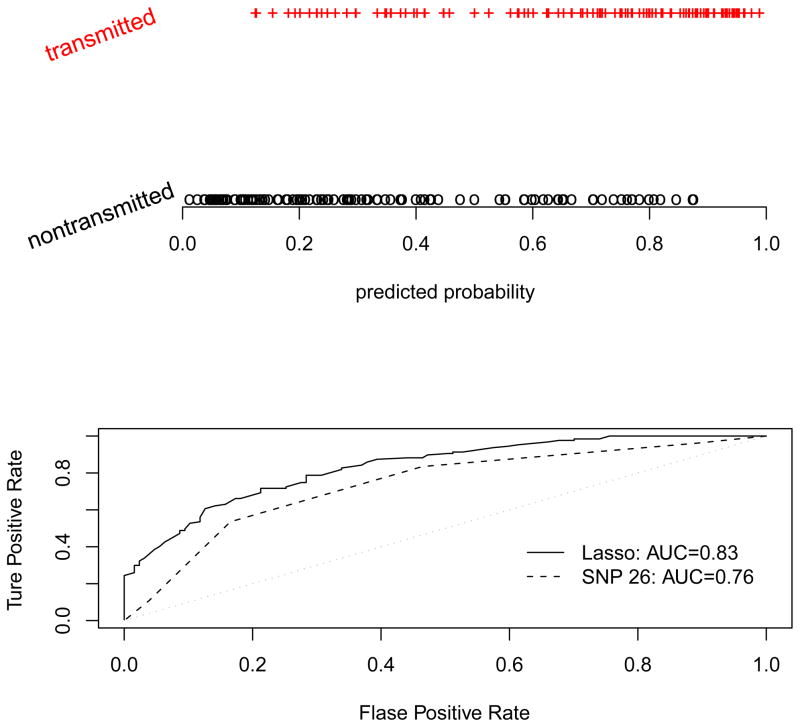
Given that the 1:1 matching is efficient in testing main genetic effects in multi-locus analysis, we use the 1:1 matching to search SNPs that are jointly associated with Crohn’s disease. In the multi-locus analysis, we first arbitrarily chose two values for the tuning constant, 1 and 20. The value 1 resulted in selecting 29 out of 103 SNPs, and the value 20 resulted in selecting two SNPs. Therefore, it is reasonable to believe that the optimal value of the tuning constant is between 1 and 20. Restricting the tuning constant to be in this range and using the leave-one-out cross-validation, we found the optimal value of the tuning constant is 3.48. This optimal value led to a conditional logistic regression with nine SNPs, with an overall p-value of 1.6×10⁻⁷. Using the final model with the nine selected SNPs, we computed the predicted probability that an offspring or a pseudo control is diseased, with the results shown in the upper plot of Figure 7. Using 0.5 as the cutoff to predict whether a child is diseased, the model with the nine selected SNPs correctly predicted 92 out of 127 affected offspring being diseased, that is, a 72.4% of correctness. As a comparison, we also computed the percentage of correctly predicted disease status using the most significant SNP. With missing genotypes imputed, the 26^th SNP has the smallest p-value (1.61×10⁻⁶ using 1:1 matching, 1.32×10⁻⁶ using 1:3 matching) and it provided the best predictability among all individual SNPs, but it only correctly predicted 68 of 127 affected offspring to be diseased, that is 53.5%. The receiver operating characteristic (ROC) curves and the areas under the ROC curves (AUC) are shown in the lower plot of Figure 7. Because we calculated the AUC using the data of the affected offspring and their pseudo sibs, the AUC values we obtained might overestimate what they would be if real case-control data are used. But the larger AUC of the multi-locus analysis nevertheless shows the benefit of using multi-locus analysis. These results demonstrate that the 1:1 matching enabled multiple-locus analysis provides an improved prediction of disease than the single-locus analysis.

Figure 7.

Upper panel: the predicted probabilities for the affected offspring (transmitted) and the pseudo siblings (nontransmitted) being diseased using the penalized multi-locus analysis under the 1:1 matching; lower panel: the receiver operating characteristic (ROC) curves and areas under the ROC (AUC) for SNP 26 selected by the single-locus analysis and for the nine SNPs selected by the penalized multi-locus analysis.

Although the nine selected markers show increased predictability for Crohn’s disease than the most significant SNP, we have to interpret the selected markers cautiously. It has been recently shown that untyped rare DNA variations can cause association between a disease and multiple common SNPs [48]. Thus, the selected SNPs might imply that multiple common and rare DNA variations at 5q31 are responsible for Crohn’s disease. Note that the region 5q31 has been replicated by several genome-wide association studies, such as [49, 50]. Thus, despite the uncertainty in interpreting the detected association based on the Crohn’s disease data, our results nevertheless demonstrate that the penalized multi-locus method based on the 1:1 matching can improve power in detecting association. In the future, we plan to evaluate the penalized method with large-scale genome-wide trio studies.

4. Discussion

To summarize, we compared the efficiency of the 1:1 matching to that of the exhaustive matching using both theoretical derivations and numerical computations. Our results show that 1) the two matching strategies use exactly / approximately the same amount of information under additive / multiplicative GRRs, and 2) the 1:1 matching is efficient in detecting main effects in multi-locus analysis. We illustrated the usefulness and efficiency of the 1:1 matching in multi-locus analysis by applying it to the Crohn’s disease data, and we improved the percentage of correctly predicted diseases status by more than 18.9% -- from 53.5% achieved by using the most significant SNP to 72.4% achieved by using the nine SNPs selected by the penalized method.

We studied the usefulness of the 1:1 matching in the case-parents design. With minor modifications, the same matching strategy can also be extended to general nuclear families with multiple affected and unaffected offspring. For a family with m affected offspring, it is reasonable to assume that the disease risk of a subject is independent of the genotypes of his siblings or parents, given the genotype of the subject. With this assumption, under a main-effect-only multi-locus model, the conditional likelihood function for this family then is

$$\frac{{\prod }_{j=1}^{m}exp({\beta }^T{g}_j)}{{\prod }_{j=1}^{m}exp({\beta }^T{g}_j)+{\prod }_{j=1}^{m}exp({\beta }^T{\overline{g}}_j)},$$

where g_j is the genotype vector for the jth affected offspring, ḡ_j is the genotype vector constructed by alleles not transmitted to the jth affected offspring, β is the vector of the coefficients of the main genetics effects in the conditional logistic regression. This way of creating matched data and constructing the likelihood function corresponds to a permutation test that permutes all siblings within a family, instead of individual siblings, in each permutation. As this permutation maintains the dependence of siblings within the same family [51], the matching we use here also preserves the dependence of siblings and leads to valid tests of association whether linkage presents or not. In addition, we may also include unaffected offspring in our modeling, by labeling the alleles of an unaffected offspring as “nontransmitted” and the alleles not transmitted to the unaffected offspring as “transmitted” [52]. This has to be used with caution, however, as incorporating the unaffected offspring may lead to either negligible gain in power or even reduced power when the penetrance is not high [53].

Here we showed that the 1:1 matching has comparable efficiency to the exhaustive matching in many situations. But we want to point out that our results do not indicate that one should always replace the exhaustive matching with the 1:1 matching. In fact, when testing the association between one locus and a disease, the exhaustive matching (the 1:3 matching) always uses the same or more information from data than does the 1:1 matching. For two unlinked loci, the exhaustive matching is also recommended, as the exhaustive matching (1:15) does not lead to substantially more computational cost than the 1:1 matching. It is when multiple loci are jointly analyzed, especially when the number of jointly analyzed loci is greater than two or when the loci are in linkage, the 1:1 matching provides an efficient, convenient, and easy-to-implement strategy to test main genetic effects. If gene-gene interaction effects are the focus of an analysis, the 1:1 matching is still valid, such as in [26]; however, it might be suboptimal in terms of power. It is clearly worthy of future research efforts to develop statistical methods that can efficiently capture interactions of multiple linked loci using family data.

Appendix

We can arbitrarily label one allele as the risk allele and the other one as the normal allele at each SNP, and define trio types at each SNP in the same ways as shown in Table 1. Let n_t1,t2,…,tL denote the number of trios with type t_l at SNP l for l=1,2,…,L, where

$$t_l\in \{12,22,21,31,42,41,40,51,50,60\}.$$

The contribution of n_t1,t2,…,tL to the exhaustive likelihood and the 1:1 matching likelihood are

$${\left(\frac{r_{g(t_1,t_2,\dots ,t_L)}}{{\displaystyle \sum _{g^{\prime }\in H_E(t_1,t_2,\dots ,t_L)}}{r}_{g^{\prime }}}\right)}^{n_{t_1,t_2,\dots ,t_L}}\text{and}{\left(\frac{r_{g(t_1,t_2,\dots ,t_L)}}{{\displaystyle \sum _{g^{\prime }\in H_1(t_1,t_2,\dots ,t_L)}}{r}_{g^{\prime }}}\right)}^{n_{t_1,t_2,\dots ,t_L}},$$

respectively, where g(t₁,t₂,…,t_L) is the genotype of the affected child in a case-parents trio with type (t₁,t₂,…,t_L), H₁ (t₁,t₂,…,t_L) denote the genotypes of the affected child and his or her pseudo-sibling under the 1:1 matching, and H_E(t₁,t₂,…,t_L) denote the 4^L genotypes of all possible siblings (including the affected child and the 4^L-1 pseudo-siblings) under the exhaustive matching. When the L loci are unlinked, the pseudo-sibship method implies that the 4^L genotypes in H_E (t₁,t₂,…,t_L) are equally likely.

Under the assumption of additive GRRs, the GRR of a genotype depends only on the number of the risk alleles at each SNP. Thus, for the 1:1 matching, the sum of the GRRs of the affected child and his or her pseudo-sibling is equal to the sum of the GRRs of the father and the mother. If we let n_l denote the number of risk alleles at SNP l in a pair of parents under trio type (t₁,t₂,…,t_L), we have

$$\sum _{g^{\prime }\in H_1(t_1,t_2,\dots ,t_L)}{r}_{g^{\prime }}=2+{\sum }_{l=1}^L{n}_l{\gamma }_l.$$

In the exhaustive matching, H_E (t₁,t₂,…,t_L) comprises of all the 4^L combinations of parental alleles. Thus, the sum of the risk alleles of the 4^L genotypes at SNP l is equal to (4^L/2)n_l. Thus,

$$\sum _{g^{\prime }\in H_E(t_1,t_2,\dots ,t_L)}{r}_{g^{\prime }}=4^L+{\sum }_{l=1}^L\frac{4^L}{2}{n}_l{\gamma }_l=\frac{4^L}{2}\sum _{g^{\prime }\in H_1(t_1,t_2,\dots ,t_L)}{r}_{g^{\prime }}.$$

As a result, we have

$${\left(\frac{r_{g(t_1,t_2,\dots ,t_L)}}{{\displaystyle \sum _{g^{\prime }\in H_E(t_1,t_2,\dots ,t_L)}}{r}_{g^{\prime }}}\right)}^{n_{t_1,t_2,\dots ,t_L}}={\left(\frac{2}{4^L}\right)}^{n_{t_1,t_2,\dots ,t_L}}{\left(\frac{r_{g(t_1,t_2,\dots ,t_L)}}{{\displaystyle \sum _{g^{\prime }\in H_1(t_1,t_2,\dots ,t_L)}}{r}_{g^{\prime }}}\right)}^{n_{t_1,t_2,\dots ,t_L}},$$

which proves that the likelihood functions for the 1:1 matching and the exhaustive matching are the same.