Abstract
GLIMMPSE is a free, web-based software tool that calculates power and sample size for the general linear multivariate model with Gaussian errors (http://glimmpse.SampleSizeShop.org/). GLIMMPSE provides a user-friendly interface for the computation of power and sample size. We consider models with fixed predictors, and models with fixed predictors and a single Gaussian covariate. Validation experiments demonstrate that GLIMMPSE matches the accuracy of previously published results, and performs well against simulations. We provide several online tutorials based on research in head and neck cancer. The tutorials demonstrate the use of GLIMMPSE to calculate power and sample size.
Keywords: power, multivariate linear models, Gaussian errors, Java, web
1. Introduction
1.1. Description of GLIMMPSE
GLIMMPSE is an open-source tool for calculating power and sample size for the general linear multivariate model (GLMM) with and without a Gaussian covariate. The software is free, accessible from a standard web browser, and requires no programming expertise. GLIMMPSE provides a step-by-step interface to allow scientists to produce accurate power calculations for common study designs with minimal time investment. In addition, GLIMMPSE can generate confidence intervals on power values for fixed designs.
GLIMMPSE supports two main types of linear models: designs with only fixed predictors, and designs with fixed predictors and a single Gaussian covariate (Sampson 1974; Gatsonis and Sampson 1989; Glueck and Muller 2003). The choice of study design determines the values of fixed predictors (such as drug dose or gender). In contrast, a Gaussian covariate will not be observed until data have been collected. Common designs with only fixed predictors include t tests, analysis of variance (ANOVA), and multivariate analysis of variance (MANOVA). Common designs with a covariate include analysis of covariance (ANCOVA), and multivariate analysis of covariance (MANCOVA). GLIMMPSE supports designs with unequal group sizes, and complex covariance structures.
Power computations in GLIMMPSE use exact results when available, and approximate results otherwise. Details about power calculations for the GLMM with Gaussian data and fixed predictors can be found in Muller and Peterson (1984), Muller and Barton (1989), Muller, Lavange, Ramey, and Ramey (1992), Muller and Stewart (2006), and Muller, Edwards, Simpson, and Taylor (2007). Details for fixed predictors with a single Gaussian covariate can be found in Glueck and Muller (2003). A summary of relevant power theory appears in Appendix A.
1.2. Why use this software?
Several software products calculate power for a variety of special cases of the GLMM. Among current products, the free SAS/IML module POWERLIB (Johnson, Muller, Slaughter, Gurka, Gribbin, and Simpson 2009; SAS Institute Inc. 2011b), the free desktop application Optimal Design (Raudenbush and Liu 2000), and the commercial product PASS (NCSS 2008) cover the greatest range of multivariate models. The SAS procedure PROC GLMPOWER (SAS Institute Inc. 2011b), and nQuery (Statistical Solutions 2008) compute power for univariate designs. Basagaña and Spiegelman (2010) describe free software (see http://www.hsph.harvard.edu/donna-spiegelman/software/optitxs/) for a range of epidemiologic studies. Zhang and Zhang (2012) list several R power and sample size modules for designing clinical and cluster randomized trials. Web-based power tools developed by Lenth (2009) and Schoenfeld (2007) provide power calculations for specific linear models such as t tests, ANOVA, and cross-over studies.
While existing power software products have strong points, all lack some abilities or features. For example, POWERLIB requires programming experience and familiarity with matrix algebra. In addition, commercial products can be prohibitively expensive for some research teams. With GLIMMPSE, we have attempted to combine the best features of existing power tools in a free, user-friendly product which is accessible through a standard web browser.
1.3. Advantages of the Java web services architecture
A web application provides many advantages over a traditional statistical module. Web browsers are freely available for most operating systems and are familiar to most users. The Java web services architecture (McGovern, Tyagi, Stevens, and Mathew 2003) provides additional benefits of modularity and scalability. In this context, modularity means that power calculations are encapsulated within a stand-alone code module. Thus, the user interface and application logic can be modified safely without affecting the statistical results. Modularity also allows for future interoperability of GLIMMPSE with platforms such as smart phones and tablets. Scalability in this context means that the software is robust to increasing user demand. As the number of users grows, continued fast response times can be maintained by adding server nodes with appropriate load balancing software. No code changes will be necessary.
1.4. Organization of the manuscript
The remainder of the manuscript has five sections. Section 2 contains the definitions and notations for the models, hypothesis tests, and power calculations. Section 3 describes the GLIMMPSE software. Section 4 summarizes the validation experiment for the GLIMMPSE power calculations and presents validation results. Section 5 lists online resources for the GLIMMPSE software, such as the user manual and step-by-step tutorials. Section 6 contains brief concluding remarks.
2. Models, hypothesis testing, and power
2.1. Models
The GLMM with Gaussian errors, fixed predictors, and a single Gaussian covariate will be referred to as the GLMM(F, g). The GLMM(F, g) is a regression model with N participants, (q − 1) fixed predictors, one Gaussian covariate, and p responses. Let Y (N × p) denote the matrix of outcome variables, where the rows [rowi (Y)]⊤, i ∈ {1, …, N}, are independent and identically distributed
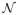 (0, Σy). The design matrix for fixed predictors is defined as F [N × (q − 1)], with BF [(q − 1) × p] representing unknown regression coefficients corresponding to fixed predictors. The design matrix for the Gaussian covariate is represented by g (N × 1), in which the rows [rowi (g)]⊤, i ∈ {1, …, N}, are independent and identically distributed
. Here Bg (1 × p) contains unknown regression coefficients corresponding to the Gaussian covariate. Define
. The matrix E (N × p) represents random Gaussian errors in the model, where the rows [rowi (E)]⊤, i ∈ {1, …, N} are independent and identically distributed
(0, Σy). The design matrix for fixed predictors is defined as F [N × (q − 1)], with BF [(q − 1) × p] representing unknown regression coefficients corresponding to fixed predictors. The design matrix for the Gaussian covariate is represented by g (N × 1), in which the rows [rowi (g)]⊤, i ∈ {1, …, N}, are independent and identically distributed
. Here Bg (1 × p) contains unknown regression coefficients corresponding to the Gaussian covariate. Define
. The matrix E (N × p) represents random Gaussian errors in the model, where the rows [rowi (E)]⊤, i ∈ {1, …, N} are independent and identically distributed
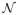 (0, Σe). The GLMM(F, g) is:
(0, Σe). The GLMM(F, g) is:
| (1) |
The covariance between Y and the Gaussian covariate is defined as Σyg (p × 1). It can be shown that:
| (2) |
The GLMM with fixed predictors only will be referred to as the GLMM(F). This can be considered a special case of the GLMM(F, g), with g = 0. In this case, Σe = Σy, and B (q × p) = BF.
GLIMMPSE requires that the design matrix for fixed predictors have full rank for both the GLMM(F, g) and the GLMM(F). A complete discussion of less than full rank coding and the equivalent full rank coding schemes appears in Muller and Fetterman (2002). Users are asked to specify the matrix of unique rows of X, known as the design essence matrix Es(X) (Muller and Stewart 2006, p. 218).
2.2. Hypothesis testing
For data analysis, the general linear hypothesis is stated as Θ = CBU, where C (a × q) is a matrix of between-participant contrasts, U (p × b) is a matrix of within-participant contrasts, and Θ (a × b) is a matrix of the observed values for the contrast results. The observed Θ is compared against a predetermined matrix of null values, known as Θ0 (a × b). Thus, the null and alternative hypotheses can be expressed as:
| (3) |
Under most experimental situations, there is no uniformly most powerful test for the GLMM (Muller and Stewart 2006). Brief descriptions of the univariate approach to repeated measures tests and three multivariate tests appear in Appendix A. More detail is available in Muller and Stewart (2006). Under the null hypothesis, the tests follow approximate central F distributions (see Appendix A). For data analysis, hypothesis testing procedures are identical for both the GLMM(F) and the GLMM(F, g).
2.3. Power analysis
Power is the probability of rejecting the null hypothesis. For the GLMM(F), Muller et al. (1992) suggested power approximations based on noncentral F distributions (see Appendix A). Glueck and Muller (2003) described power approximations for the GLMM(F, g). One can think of the random covariate values as having been sampled from a Gaussian distribution. Thus there are many possible realizations of the same experiment, and each realization may have a different power. The unconditional power is defined as the average of the possible power values (Gatsonis and Sampson 1989; Glueck and Muller 2003). The 100×k-th quantile power is the power value chosen so that power as small or smaller occurs in 100 × k percent of all possible realizations of the experiment. A summary of calculations for unconditional and quantile power is provided in Appendix A.
2.4. Inputs for power and sample size analysis
To perform a power calculation for the general linear hypothesis, the researcher must define the following: the Type I error rate (α), the full rank design essence matrix for fixed predictors, the contrast for between-participant effects, the contrast for within-participant effects, the null hypotheses, and the statistical test. GLIMMPSE allows the user to specify equal or unequal sizes for study subgroups.
In addition to the study design description, the scientist must specify values for the regression coefficients for all fixed predictors and the covariance structure. Regression coefficient values should reflect a scientifically meaningful difference. Values for the covariance are typically obtained from published results or pilot data. For the GLMM(F), the user must provide the covariance of the Gaussian errors for a single sampling unit (Σe). The Σe matrix is the covariance of Y conditional on the fixed predictors, assuming homoscedasticity across all values of the fixed predictors. For example, in an ANOVA design, Σe would contain the within-group variance. For the GLMM(F, g), the user must give the covariance of the outcomes for a single sampling unit (Σy), the variance of the Gaussian covariate ( ), and the covariance of the outcomes with the Gaussian covariate (Σyg). The Σy matrix is the covariance of Y conditional on the fixed predictors only, and excludes the effect of the Gaussian covariate. This is equivalent to the Σe matrix obtained when fitting a model with the same fixed predictors, but not including the Gaussian covariate.
2.5. Confidence limits for power
GLIMMPSE can produce confidence limits for power in GLMM(F) designs. When performing power calculations, Σe and B are often estimated from previous study data. If previous study data is used to estimate Σe and B, the matrices are not known with certainty. Therefore the calculated power values also have uncertainty. The confidence intervals produced by GLIMMPSE are based on theory developed by Taylor and Muller (1995) for univariate linear models, and Gribbin (2007) and Park (2007) for multivariate models. Confidence intervals are not currently available for GLMM(F, g) models.
To produce confidence intervals for power, the user must first specify which matrices are random: Σe only, or both Σe and B. In addition, the user must provide the sample size and rank of the design matrix for the data set used to produce the values for these matrices.
3. The GLIMMPSE software
3.1. Software architecture
GLIMMPSE is a web application built using a Java web services architecture (see Figure 1). The front-end user interface guides the user through the GLIMMPSE wizard to gather inputs for the power calculation. When the user completes the wizard, the user interface sends a JSON (Crockford 2012) formatted request to the power web service to perform the power calculations. The power service then calls the JavaStatistics library, where the power and sample size formulas are implemented. Once the power computation is complete, the power service returns JSON formatted results to the user interface for presentation. If requested, the wizard will also issue an HTTP GET request (W3C 1999) to the chart service to create a power curve image. Although not directly involved in power computation, the file web service handles requests from the user interface to save or upload a study design. More details on the web service communication layer are available on the GLIMMPSE documentation page at http://SampleSizeShop.org/documentation/glimmpse/. Version information for the software technologies used in GLIMMPSE is detailed in Appendix B.
Figure 1.
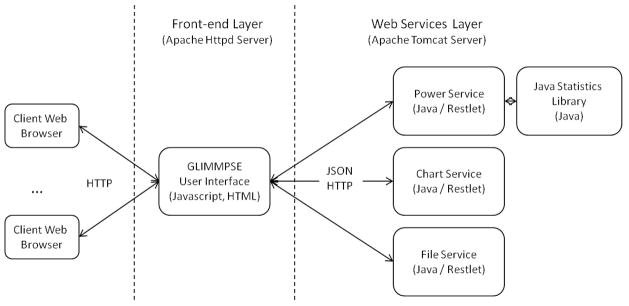
Overview of the GLIMMPSE architecture.
3.2. How to use GLIMMPSE
GLIMMPSE is accessed from a standard web browser via the URL: http://glimmpse.SampleSizeShop.org/
GLIMMPSE has been tested in Internet Explorer 8 (Microsoft 2010), Mozilla Firefox 3.6.16 (Mozilla 2011), and Safari 5.0.3 (Apple 2010).
GLIMMPSE offers two separate modes for entering study design information (see Figure 2). In Guided Mode, GLIMMPSE generates appropriate power based on user inputs describing independent and dependent variables, hypotheses, group means, and standard deviations. Users may optionally specify clustering or repeated measures. Matrix Mode is designed for individuals with advanced statistical training who prefer direct input of all matrices required for a power calculation. In either mode, users may save their study design information at any point to a JSON file. The user may later upload the saved study design to resume the power computation without loss of previously entered data.
Figure 2.
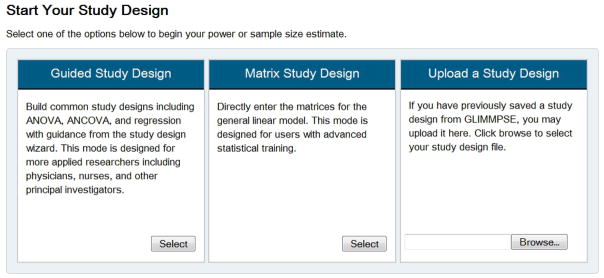
GLIMMPSE mode selection screen.
The user may define either a single power calculation, or perform multiple calculations in a single request. The user requests a list of power calculations by specifying multiple α levels, selecting several statistical tests, or defining multiple scale factors for the regression coefficients and covariance matrices. Scale factors are scalar multipliers applied to the matrices. They provide inflation or deflation factors to allow consideration of alternative values for regression coefficients and covariance matrices. In addition, the user may specify multiple target power values when solving for sample size, and may specify multiple per-group sample sizes when calculating power. For the GLMM(F, g), the user can select unconditional power, quantile power or both. For quantile power, the user may enter multiple quantiles.
The user may request confidence intervals for GLMM(F) designs. The Confidence Interval Options screen allows the user to specify if Σe or both Σe and B are random, and to enter information about the estimation data set. In addition, the user may specify tail probabilities for the confidence interval. Entering zero for the upper tail probability will produce a one-sided upper confidence interval, and entering zero for the lower tail probability will produce a one-sided lower confidence interval for power.
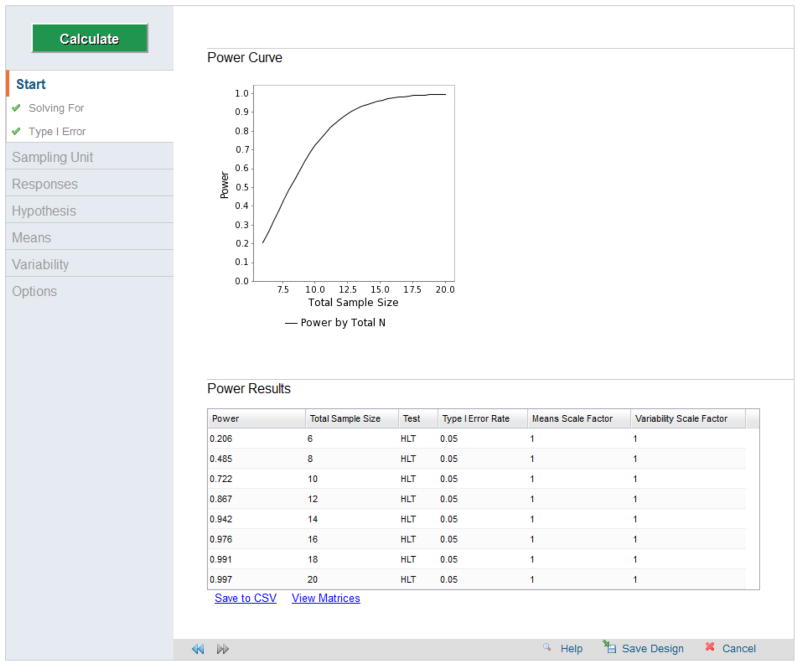
Power results are displayed in a table with each row representing an individual power calculation. Figure 3 shows example output from GLIMMPSE. Table 1 summarizes the information displayed for each power result. Each result contains both calculated and desired power values. When solving for power, these two values are the same. When solving for sample size, it may not be possible to achieve the exact power value specified by the user. In this case, the sample size is chosen so that the power of the experiment meets or exceeds the value chosen by the user. The sample size appears with both the nominal power, specified by the user, and the actual power, the power calculated for the sample size. The user may also request that a power curve be displayed, with power on the vertical axis and either the regression coefficient scale factor, covariance scale factor, or total sample size on the horizontal axis. For convenience, users may view the matrices used for the power calculations from the results screen. The user may save power results to a comma delimited file if they wish to import the data into other statistical packages. They may also save the power curve image to a JPEG file.
Figure 3.
GLIMMPSE results screen.
Table 1.
Information displayed for each power result.
| Column Name | Description |
|---|---|
| Test | Name of the statistical test |
| Actual Power | Calculated power |
| Confidence Interval | (Optional) Confidence limits on the calculated power result |
| Total Sample Size | Total number of research participants required to achieve the actual power |
| B-scale | Scale factor applied to the B or BF matrix |
| Σ-scale | Scale factor applied to the Σe matrix |
| Alpha | Type I error rate |
| Nominal Power | Desired power |
| Power Method | Indicates whether conditional, unconditional, or quantile power was used |
| Quantile | If the current power method is quantile power, this indicates the quantile chosen. Otherwise, this field is empty. |
4. Accuracy of power computations in GLIMMPSE
4.1. Validation Experiment
GLIMMPSE power calculations were validated against simulated and published power values for the general linear model (Glueck and Muller 2003; Johnson et al. 2009). The study designs used in the validation experiment are detailed in Appendix C. Two maximum absolute deviation (MAD) statistics were calculated. The first compared each GLIMMPSE power value to its corresponding published value. The other compared each GLIMMPSE power value to its corresponding simulated value. For designs with confidence intervals on power, MAD statistics were calculated comparing the GLIMMPSE upper and lower confidence limits to published upper and lower confidence limits.
Simulation techniques are described in Section 4.2 and a summary of accuracy results is presented in Section 4.3. Total CPU time is presented for GLIMMPSE calculations and simulations performed on an Intel i7-2600 quad core, 3.40 GHz processor with 8GB of RAM, running 64-bit Windows 7. Timing was assessed on power calculations directly from the JavaStatistics library. Therefore, timing results do not include HTTP processing time from the web interface. Full validation results and power values are available online at http://SampleSizeShop.org/documentation/glimmpse/validation-results/.
4.2. Simulation methods
For the GLMM(F), empirical powers were generated by defining α, a full rank X, C, U, B, Θ0 and Σe, and selecting a statistical test. We then simulated a random error matrix E (N × p), and formed the observed Y using Equation 1. From the observed Y and fixed X, we calculated Ŷ, B̂, Σ̂e, and Θ̂ using Equations 4 through 7 in Appendix A. The JavaStatistics library implementation of the required univariate or multivariate test was used to obtain a p value. This process was repeated for ten thousand replications, and we recorded the number of rejections of the null hypothesis at the specified α level. Empirical power was calculated as the proportion of rejections. We used ten thousand replications to ensure that the error in the estimation of power occurred at the second decimal.
For GLMM(F, g), we defined α, a full rank X, C, U, B, Θ0, , Σy, and Σyg and selected a statistical test. For both unconditional and quantile power, we used the two-level simulation technique described by Glueck and Muller (2003). In the first level, we generated one thousand realizations of the X matrix, assuming that the covariate was distributed . In the second level, we simulated one thousand random error matrices for each realization of X. We determined empirical power for each realization of X as described for the GLMM(F). The process yielded a list of one thousand empirical power values.
To find empirical unconditional power, we computed the average of the list of power values. For empirical quantile power, we first specified the quantile of interest, k. The empirical 100 × k-th quantile power is the k-th quantile of the list of power values. For example, empirical median power is the median of the thousand simulated power values.
4.3. Accuracy results
Accuracy results for the GLMM(F) are summarized in Table 2. The example study designs are described by number in Appendix C. The numbering scheme matches examples previously described by Johnson et al. (2009). Examples 1 through 4 are univariate GLMM(F) designs. Examples 5 through 9 are multivariate GLMM(F) designs. Published results were obtained using POWERLIB version 2.1 (Johnson et al. 2009). Power values calculated with GLIMMPSE matched POWERLIB results to six decimal places. For univariate designs, deviations from simulation occurred in the second or third decimal place. In the multivariate case, deviations from simulated values ranged from 0.045 to 0.232. Since power calculations for multivariate tests are approximate, some inaccuracy when compared to simulations is expected in multivariate designs. Example 9 uses two different power approximations for the same study design, denoted by MB and MEST. MB represents the approximation described by Muller and Barton (1989). MEST stands for the method described by Muller et al. (2007). Differences in accuracy between the MB approximation and the MEST approximation were similar to results previously described by Coffey and Muller (2003). By default, GLIMMPSE uses the more accurate approximation described by Muller et al. (2007).
Table 2.
Accuracy results for power values in GLMM(F) designs.
| Example | Mean Calculation CPU Time (sec.×10−4) | Mean Simulation CPU Time (sec.) | MAD for GLIMMPSE vs. POWERLIB (×10−7) | MAD for GLIMMPSE vs. Simulation |
|---|---|---|---|---|
| 1 | 4.1 | 0.17 | 9.5 | 0.010 |
| 2 | < 0.1 | 0.15 | 2.5 | 0.004 |
| 3 | 1.8 | 0.17 | 9.0 | 0.010 |
| 4 | < 0.1 | 0.18 | 9.5 | 0.006 |
| 5 | 1.1 | 0.32 | 9.7 | 0.070 |
| 6 | 1.9 | 0.81 | 9.6 | 0.120 |
| 7 | < 0.1 | 0.57 | 7.7 | 0.069 |
| 8 | 0.9 | 15.12 | 9.7 | 0.053 |
| 9 MB | < 0.1 | 0.61 | 6.6 | 0.232 |
| 9 MEST | < 0.1 | 0.61 | 8.5 | 0.045 |
Confidence intervals were produced for a univariate design in Example 4, and a multivariate design in Example 6. For the univariate case, the MAD between GLIMMPSE and POWER-LIB was 9.1 × 10−7 for the upper confidence limit, and 8.8 × 10−7 for the lower confidence limit. GLIMMPSE also matched POWERLIB confidence intervals to six decimal places in the multivariate case, with a MAD of 9.7×10−7 for the upper confidence limit and 9.5×10−7 for the lower confidence limit. The largest deviations from simulation for Example 6 occurred at sample sizes of 2 and 3, which also had the widest confidence intervals. All simulated powers for these examples fell within the calculated confidence limits.
Accuracy results for the GLMM(F, g) are summarized in Table 3. The example study designs are described by number in Appendix C. Examples 1 through 4 use the Hotelling-Lawley Trace. Examples 5 through 9 use the uncorrected univariate approach to repeated measures, Box, Geisser-Greenhouse, and Huynh-Feldt tests. Published results for the GLMM(F, g) using the Hotelling-Lawley Trace were obtained from Table II in Glueck and Muller (2003). The GLIMMPSE univariate approach to repeated measures results were verified against a table originally prepared by Glueck and Muller (2003) for journal submission, but which was removed from the final manuscript due to space constraints. The power values are presented in Tables 8–11 in Appendix C.
Table 3.
Accuracy results for power values in GLMM(F, g) designs.
| Example | Mean Calculation CPU Time (seconds) | Mean Simulation CPU Time (seconds) | MAD for GLIMMPSE vs. Published Values (×10−2) | MAD for GLIMMPSE vs. Simulation |
|---|---|---|---|---|
| 1 | 0.004 | 79.23 | 0.004 | 0.047 |
| 2 | 0.005 | 78.74 | 0.003 | 0.047 |
| 3 | 0.351 | 79.43 | 0.063 | 0.032 |
| 4 | 8.541 | 79.01 | 0.061 | 0.033 |
| 5 | < 0.001 | 93.59 | 7.300 | 0.095 |
| 6 | 0.002 | 93.63 | 7.300 | 0.094 |
| 7 | 0.692 | 93.66 | 7.300 | 0.071 |
| 8 | 2.811 | 93.69 | 7.300 | 0.072 |
For the Hotelling-Lawley Trace, GLIMMPSE matched Table II of Glueck and Muller (2003) to four decimal places. Numerical accuracy may be diminished in these designs due to dependence on numerical integration and bisection search in the determination of the noncentrality parameter. Deviations between GLIMMPSE and simulation for the Hotelling-Lawley Trace occurred in the second decimal place and were similar to those observed for multivariate GLMM(F) designs.
For the univariate approach to repeated measures, the deviation between GLIMMPSE and Tables 8–11 was 0.073 for all examples. Deviations from simulation ranged from 0.071 to 0.095. The power results in Tables 8–11 were based on the approximation methods described by Muller and Barton (1989). For these designs, GLIMMPSE powers were computed using the approximation methods of Muller et al. (2007). The difference explains the higher discrepancy between GLIMMPSE calculations and Tables 8–11, despite reasonable accuracy against simulation.
5. Additional resources for GLIMMPSE
5.1. The SampleSizeShop.org website
http://SampleSizeShop.org/ is a website dedicated to helping scientists and researchers calculate accurate sample size and power for their studies. The website includes educational resources about power and sample size methods, and provides access to the GLIMMPSE software. From http://SampleSizeShop.org/, users can access the GLIMMPSE user manual (http://SampleSizeShop.org/files/2012/08/GLIMMPSEUserManual_v2.0.0.pdf), documentation (http://SampleSizeShop.org/documentation/glimmpse/), and software downloads (http://SampleSizeShop.org/software-downloads/glimmpse/). In addition, step-by-step tutorials (http://SampleSizeShop.org/education/tutorials/) are available for the following study designs.
5.2. A study comparing cell proliferation markers in individuals with and without head and neck cancer
The Ki-67 value is a measure of cell proliferation (Seoane et al. 2010). In this study, researchers wish to compare Ki-67 values in individuals diagnosed with head and neck cancer to a reference value for healthy individuals. The tutorial demonstrates the use of GLIMMPSE to calculate power for a one-sample t test comparing mean Ki-67 values against a reference value. The tutorial is available at http://SampleSizeShop.org/files/2012/08/Tutorial1.pdf.
5.3. A phase II trial examining the effect of resveratrol on cell proliferation markers in individuals with head and neck cancer
Resveratrol is an antioxidant found in the skins of grapes and other fruits. In this phase II trial, researchers wish to examine the impact of resveratrol administration on Ki-67 values in a sample of individuals with head and neck cancer. The trial is a one sample design with a pre- and post-measurement. The primary hypothesis of interest is that Ki-67 values do not change in response to treatment with resveratrol. The tutorial demonstrates the use of GLIMMPSE to calculate power for a paired t test. The tutorial is available at http://SampleSizeShop.org/files/2012/08/Tutorial2.pdf.
5.4. A randomized trial examining the effect of resveratrol on cell proliferation markers in individuals with head and neck cancer
In this trial, researchers wish to examine the effect of resveratrol on Ki-67 values in individuals with head and neck cancer. Individuals are randomized to receive resveratrol or a placebo. Twice as many individuals receive resveratrol as receive the placebo. Measurements of Ki-67 values are obtained 6 months after treatment. The primary hypothesis of interest is that there is no difference in Ki-67 levels between the resveratrol and placebo groups. The tutorial demonstrates the use of GLIMMPSE to calculate power for a two-sample t test with unequal group sizes. The tutorial is available at http://SampleSizeShop.org/files/2012/08/Tutorial3.pdf.
5.5. A randomized trial examining the effect of resveratrol on cell proliferation markers in individuals with head and neck cancer allowing for unequal variance
The study in this tutorial is identical to the design described in Section 5.4, except that we allow for unequal variance between the resveratrol and placebo groups. The tutorial demonstrates how to use GLIMMPSE to calculate power for a two-sample t test with unequal variance. The tutorial is available at http://SampleSizeShop.org/files/2012/08/Tutorial4.pdf.
5.6. A randomized trial comparing the effects of resveratrol and a dietary supplement on cell proliferation markers in individuals with head and neck cancer
In this trial, researchers wish to compare the effects of placebo, resveratrol, and another dietary supplement on Ki-67 values in individuals with head and neck cancer. Individuals are randomized into three groups which receive resveratrol, the dietary supplement, or placebo. Equal numbers of participants are randomized to the three groups. Measurements of Ki-67 values are obtained 6 months after treatment. The primary hypothesis of interest is that there is no difference in Ki-67 values among the three groups. The tutorial demonstrates the use of GLIMMPSE to calculate power for a one-way analysis of variance. The tutorial is available at http://SampleSizeShop.org/files/2012/08/Tutorial5.pdf.
6. Concluding Remarks
GLIMMPSE provides power and sample size calculations for the general linear multivariate model through a convenient web interface. Great care was taken to make the results accessible to both statisticians and applied scientists.
To ensure software quality, GLIMMPSE developers followed software best practices. Unit testing demonstrated correct functionality and performance of each module. Integration testing verified interoperability among software components. In a complex, multi-tiered application such as GLIMMPSE, a careful and thorough development process is vital to a successful software release.
The accuracy of calculations in GLIMMPSE comes at some computational expense in the case of the GLMM(F, g). Less computationally expensive sample size methods for the GLMM(F, g) have been proposed by Shieh (2005) and Hsieh, Lavori, Cohen, and Feussner (2003). The methods described by Shieh (2005) depend on asymptotic theory and their performance in small samples is not known. Hsieh et al. (2003) suggested adjusting sample size based on variance inflation factors, but pointed out that sample sizes obtained with the technique can be unpredictable. The methods of Glueck and Muller (2003) provide a balance between computational complexity and accuracy for the GLMM(F, g).
Users can be assured of comparability to peer-reviewed published results, and equivalence to simulation results. All results from the validation experiments are clearly visible on the web-site. Open source code and publicly available unit testing results ensure that the underlying power calculations are transparent and demonstrably accurate.
Acknowledgments
GLIMMPSE extends an existing program called POWERLIB. Bercedis Peterson and Keith Muller wrote POWERLIB for SAS PROC MATRIX (Version 0) in 1983. In 1992, Lynette Keyes and Keith Muller converted POWERLIB to SAS/IML (Version 1). Keyes also created a new manual, based on the PROC MATRIX manual. Douglas Taylor wrote code for creating confidence limits for power values based on random estimates in 2001, which Keith Muller then used to enhance POWERLIB. In 2003, Jacqueline Johnson and Keith Muller created Version 2 of POWERLIB (Johnson et al. 2009). Additionally, James Slaughter greatly improved the _PROBF module, and Matthew Gurka conducted extensive tests. At the same time, the related manual was significantly revised from the previous version.
GLIMMPSE 2.0.0 extends POWERLIB to include the work of Glueck and Muller (2003). Development of GLIMMPSE 1.0.0 was funded by an American Recovery and Re-investment Act supplement (3K07CA088811-06S) for NCI grant K07CA088811. Both the parent grant and supplement were awarded to the University of Colorado Denver, (Deborah Glueck, PI). Additional funding was provided by NIDCR 1 R01 DE020832-01A1 to the University of Florida (Keith Muller, PI; Deborah Glueck, University of Colorado site PI). The funding from NCI allowed the development of the GLIMMPSE software. The additional funding from NIDCR permitted extensive architecture changes which will eventually support power for the general linear mixed model, as well as supporting beta testing and final software release activities.
Additional support for Dr. Muller was provided in part by NIH=NIDCR grants U54-DE019261, NIH=NCRR grant K30-RR022258, NIH=NHLBI grant R01-HL091005 and NIH=NIAAA grant R01-AA013458-01.
A portion of this paper was submitted to the University of Colorado Denver in partial fulfillment of the requirements for the Masters of Science in Biostatistics for Dr. Sarah M. Kreidler.
Disclosures: Dr. Muller has in the past been a paid consultant to SAS (aSAS Institute Inc. 2011a) Institute and NCSS (NCSS 2008). Dr. Muller’s wife worked for SAS for 5 years.
A. Statistical tests and power analysis
A.1. Tests for the general linear hypothesis
The statistical tests available in GLIMMPSE are described in detail by Muller and his coauthors (Muller and Peterson 1984; Muller and Barton 1989; Muller et al. 1992; Glueck and Muller 2003; Muller and Stewart 2006 ; Muller et al. 2007). Univariate tests for the general linear hypothesis include the uncorrected univariate approach to repeated measures, Box, Geisser-Greenhouse (GG), and Huynh-Feldt (HF) tests. Multivariate tests include the Hotelling-Lawley Trace, Pillai-Bartlett Trace, and the Wilks’ Lambda. Define r =rank(X) and νe = N − r. The tests are based on the following equations:
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
Tests are functions of Sh, Se, and St as summarized in Table 4. The calculations of multivariate power have been developed and programmed in terms of a generalization of a squared correlation coefficient, a measure of multivariate association. For more details about the measures of multivariate association, see Table 1 (Muller et al. 1992) and Table 3.2 (Muller and Stewart 2006, p. 71).
Table 4.
Tests for the GLMM.
| Name | Statistic | |
|---|---|---|
| Univariate Approach to Repeated Measures (REP) | tr(Sh)/tr(Se) | |
| Hotelling-Lawley Trace (HLT) |
|
|
| Pillai-Bartlett Trace (PB) | tr[Sh (Sh + Se)−1] | |
| Wilks’ Lambda (W) | |Se (Sh + Se)−1| |
A.2. Power analysis for the GLMM(F)
Let m indicate the statistical test. Let νn0 (m) and νd0 (m) be the numerator and denominator degrees of freedom under the null hypothesis. Let νna (m) and νda (m) be the numerator and denominator degrees of freedom under the alternative hypothesis. Let ωm be the noncentrality parameter for test m. The degrees of freedom for each test supported by GLIMMPSE are summarized in Table 5. The correction factors ε̂, ε̃ are defined in Table 6. The expected values E (ε̂) and E (ε̃) are defined in Muller and Barton (1989). Formulas for ωm for each test are summarized in Table 7.
Power analysis for the univariate and multivariate tests for GLMM(F) requires the following four steps (Muller et al. 1992; Gribbin 2007).
Specify α, Σe, X, B, C, U, and Θ0.
- With degrees of freedom defined in Table 5, obtain the critical value from an inverse central F distribution so that
(12) Calculate the non-centrality parameter ωm as defined in Table 7.
- With degrees of freedom defined in Table 5, compute power with a noncentral F distribution function so that
(13)
Define:
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
The approximations for the univariate approach to repeated measures are detailed in Muller and Barton (1989), Gribbin (2007), and Muller et al. (2007). By default, GLIMMPSE uses the approximation described by Muller et al. (2007) for the univariate approach to repeated measures. The distributions for the Hotelling-Lawley Trace, Pillai-Bartlett Trace, and Wilks’ Lambda are based on the approximations described by Muller et al. (1992), and Muller (1998). The GLIMMPSE default approximation methods follow the recommendations from the authors of POWERLIB (Johnson et al. 2009).
Table 5.
Degrees of freedom for central and noncentral F distributions.
| Test (m) | νn0 (m) | νd0 (m) | νna (m) | νda (m) |
|---|---|---|---|---|
| REP, uncorrected | ab | bve | abεn | bveεd |
| REP, GG | abE (ε̂) | bveE (ε̂) | abεn | bveεd |
| REP, HF | abE (ε̃) | bveE (ε̃) | abεn | bveεd |
| REP, Box | a | ve | abεn | bveεd |
| HLT | ab | g1 (ve, a, b) | ab | g1 (ve, a, b) |
| PB | abg4 (ve, a, b) | g2 (ve, a, b) | abg4 (ve, a, b) | g2 (ve, a, b) |
| W | ab | g3 (ve, a, b) | ab | g3 (ve, a, b) |
Table 6.
Correction for lack of sphericity for the univariate approach to repeated measures.
| Method | Correction Factor | |
|---|---|---|
| Box | 1/b | |
| Geisser-Greenhouse (GG) |
|
|
| Huynh-Feldt (HF) | ε̃ = Nbε̂ − 2/b (N − r − bε̂) |
Table 7.
Noncentrality parameters.
| Test (m) | ωm | |
|---|---|---|
| REP, uncorrected | tr(Δ) bεn/tr(Σ*) | |
| REP, GG | tr(Δ) bεn/tr(Σ*) | |
| REP, HF | tr(Δ) bεn/tr(Σ*) | |
| REP, Box | tr(Δ) bεn/tr(Σ*) | |
| HLT |
|
|
| PB | Ns · tr (Δ (veΣ* + Δ)−1)/[s − tr (Δ (veΣ* + Δ)−1)] | |
| W | Ng(1 − |veΣ* (veΣ* + Δ)−1|1/g)/|veΣ* (veΣ* + Δ)−1|1/g |
A.3. Power analysis for GLMM(F, g)
For GLMM(F, g), power calculations are available for the Hotelling-Lawley Trace and the univariate approach to repeated measures. Because g and hence X are random in this case, the noncentrality parameter under the alternative hypothesis is no longer fixed. As described by Glueck and Muller (2003), the distribution of the noncentrality parameter may be expressed exactly as a weighted sum of non-central χ2 random variables. The inverse of this distribution can either be obtained using a Satterthwaite style F approximation, or it can be determined exactly by using the method described by Davies (1980).
To calculate unconditional power, specify α, a full rank X, C, U, B, Θ0, , Σy, and Σyg, and calculate Σe as shown in Equation 2. Obtain the critical F under the null hypothesis as described for the GLMM(F). With hH,0, hH,1, hU,0 and hU,1 defined as in Equations A4 and A5 of Glueck and Muller (2003), the unconditional power formulas for the Hotelling-Lawley and the univariate tests are (H = HLT, U = REP)
| (24) |
| (25) |
For quantile power, specify the study design, calculate Σe and obtain the critical F under the null distribution. Specify the quantile of interest, k, and obtain the noncentrality parameter for test m, ωmk, such that Pr{ω < ωmk} = Fω (ωmk) = k. Once a value for the noncentrality parameter is determined, quantile power is obtained for the Hotelling-Lawley and the univariate tests as
| (26) |
| (27) |
B. Software technologies and version information
GLIMMPSE may be redistributed or modified under the terms of the GNU General Public License version 2 (Free Software Foundation 2010). All source code, Javadoc, and binary distributions are available for download from http://SampleSizeShop.org/software-downloads/glimmpse/.
The front-end user interface was built using the Google Web Toolkit version 2.4.0 (Google Inc. 2011) and HTML (W3C 1999). The user interface software is deployed to an Apache HTTPd web server version 2.2 (Apache Software Foundation 2010) in the standard htdocs directory. To allow the GLIMMPSE user interface to communicate with the web services layer, the Apache HTTPd modules mod_proxy, mod_proxy_httpd, and mod_rewrite were enabled, and a proxy redirect with the following syntax was added to the configuration file httpd.conf:
<Proxy *> Order deny,allow #Deny from all Allow from all </Proxy> RewriteEngine on ProxyRequests Off RewriteRule /file/(.*)$ http://tomcat-server-host:port/file/$1 [P] RewriteRule /chart/(.*)$ http://tomcat-server-host:port/chart/$1 [P] RewriteRule /power/(.*)$ http://tomcat-server-host:port/power/$1 [P] ProxyPassReverse / http://tomcat-server-host:port/
The power, chart, and file web services were built using the Java Development Kit (JDK) version 7 (ORACLE 2011), and Restlet version 2.0.10 (Noelios Technologies 2011). They are deployed within an Apache Tomcat server version 7.0 (Apache Software Foundation 2011).
The JavaStatistics library was developed using JDK version 7. Matrix operations and distribution functions were provided by the Apache Commons Math library version 3.0 (Apache Software Foundation 2012) and the JSC library (Bertie 2005).
C. GLIMMPSE validation experiment
C.1. Source code for the experiment
The validation experiment consists of a set of SAS files, SAS data sets, XML data files, and JUnit tests. Source code and instructions for running the experiment are available in the source distribution of the JavaStatistics library.
C.2. GLMM(F) Study designs used for validation of GLIMMPSE
GLIMMPSE power calculations for the GLMM(F) were compared against nine study design examples described by Johnson et al. (2009). Each study design is described in detail below. PDF files with all results and details are provided at http://SampleSizeShop.org/files/2012/12/FileName.pdf and in the supplements to this paper.
Example 1. Power for a two sample t test for several error variance values and mean differences
This study design includes two independent groups, and tests the hypothesis of no difference between the groups on a single outcome. Power was computed for a total sample size of 20, α=0.05, α2 ∈ {0.32,1.00,2.05}, and mean differences ∈{0, 0.05, 0.10, …, 2.5}. Full results are available at TestConditionalTwoSampleTTest.pdf.
Example 2. Power for a paired t test
The paired t test includes a single group of participants with pre- and post-measurements for a single outcome. The design tests the hypothesis of no difference between the two measures. Power is calculated for α = 0.05, total sample size of 10, and mean differences ∈ {0, 0.5, 0.10, …, 2.5}. The covariance of the errors is:
Full results are available at TestConditionalPairedTTest.pdf.
Example 3. Power for a two sample t test for various sample sizes and mean differences
This study design includes two independent groups, and tests the hypothesis of no difference between the groups on a single outcome. Power was computed for total sample sizes ∈ {3, 6, 9, …, 18}, α = 0.01, α2 = 0.068, and mean differences 2 {0, 0.05, 0.10, …, 0.75}. Full results are available at TestConditionalTwoSampleTTest3DPlot.pdf.
Example 4. Power and confidence limits for a univariate model
This example generates confidence limits for power for a two sample t test design. The hypothesis of no difference between the groups is tested. Two sided, lower and upper 95% confidence intervals are produced. The confidence limits were produced under the assumption that B was fixed and Σe was estimated from a data set with a sample size 24 and design matrix with a rank of 2. Power and confidence limits are produced for a total sample size of 12, α = 0.01, σ2 = 0.068, and mean differences ∈ {0, 0.01, 0.02, …, 0.75}. Full results are available at TestConditionalUnivariateWithConfidenceLimits.pdf.
Example 5. Power for a test of interaction in a multivariate model
This example tests for a time by treatment interaction in a design with four treatment groups and three repeated measures over time. Residual errors are assumed to have a compound symmetric structure with a variance of 1 at each time and a covariance of 0.4 between any pair of repeated measures. Power is calculated for α = 0.01, Σ-scale ∈ {1, 2}, B-scale ∈ {0, 0.5, …, 2.0}, and per-group sample sizes ∈ {5, 10}. Full results are available at TestConditionalMultivariateInteraction.pdf.
Example 6. Power and confidence limits for the univariate approach to repeated measures in a multivariate model
This example is based on a study of cerebral vessel tortuosity measured at four regions in the brain (Johnson et al. 2009). Fixed predictors include gender and five age groups, yielding a 10 × 10 identity matrix as the design essence matrix. Power is calculated for a test of no gender by region interaction, and two-sided 95% confidence limits are produced. The speculated B values are assumed known, and Σe is assumed to be estimated from a previous study with 21 participants and a design matrix rank of 1. The speculated means and variance values are listed below.
Power is calculated with α = 0.05/6, and with per-group sample sizes ∈ {2, 3, …, 10}. Mean differences ∈ {0.0016, 0.0032, …, 0.2} between males and females at the third region were tested at each sample size, producing a total of 2,259 power values. Full results are available in TestConditionalMultivariateWithConfidenceLimits.pdf.
Example 7. Power for a time by treatment interaction
The study design for this example includes two treatment groups, and five repeated measures over time. Power is calculated for the test of a time by treatment interaction, using an orthogonal polynomial contrast for equally spaced time measurements at 2, 4, 6, 8, and 10. This example demonstrates the use of the OrthogonalPolynomials class included in the JavaStatistics library. Power values are produced at ∈ = 0.05, with per-group sample sizes ∈ {10, 20, 40}. Residual errors are assumed to have a compound symmetric structure with a variance of 1.5 at each time and a covariance of 0.375 between any pair of repeated measures. Full results are available at TestConditionalOrthogonalPolynomial1Factor.pdf.
Example 8. Power for tests of polynomial trend for multiple between- and within-participant factors
This example calculates power for one, two, and three factor polynomial trends for both between-participant and within-participant effects. The design includes three between-participant effects (A, B, and C) and three within-participant effects (D, E, and F), each with three equally spaced levels. This example demonstrates the use of the one, two and three-way contrasts which can be produced by the OrthogonalPolynomials class included in the JavaStatistics library. Powers are produced for α = 0.05, per-group sample sizes of ∈ {2, 4, …, 12}, and B-scale values ∈ {9, 18, 27}. Factors are assumed to be independent with variances of 1 to 27. Full results are available at TestConditionalOrthogonalPolynomial3Factor.pdf.
Example 9. Power for a multivariate model with two within-participant factors
This example calculates power for a study design with two within-participant factors and no between-participant factors. Power is calculated for a test of two-way polynomial trends using contrasts produced by the OrthogonalPolynomials class included in the JavaStatistics library. Power is calculated for the corrected and uncorrected univariate approach to repeated measures tests at α = 0.04. The variance is adjusted with Σ-scale values ∈ {0.5, 1, 2}. The results mimic Table III from Coffey and Muller (2003), which compared the approximation methods described in Muller and Barton (1989), and a more recent method developed by Muller et al. (2007). Full results for the Muller and Barton (1989) approximation are available at TestConditionalOrthogonalPolynomial2FactorMB.pdf.
Full results for the Muller et al. (2007) approximation are available at TestConditionalOrthogonalPolynomial2FactorMEST.pdf.
C.3. GLMM(F, g) Study designs used for validation of GLIMMPSE
GLIMMPSE was validated against the theoretical example used to produce Table II of Glueck and Muller (2003). Tables 8 through 11 below show the results used for comparison with the univariate approach to repeated measures. The study design had three groups, and four repeated measures per participant. Power values were calculated with α = 0.05, and per-group sample sizes ∈ {5, 25,75}. A baseline covariate was included in the model, with Σg = [1], Σy = I4, and . The fixed portion of B was set to the following diagonal matrix.
| (28) |
B-scale factors matched the Δ values listed in Table II in Glueck and Muller (2003).
Table 8.
GLMM(F, g) power results for the uncorrected unvariate approach to repeated measures test.
| N | B-scale | Uncorrected | |||
|---|---|---|---|---|---|
| Median | Unconditional | ||||
|
| |||||
| Exact | Approximate | Exact | Approximate | ||
| 15 | 0.4997 | 0.257 | 0.257 | 0.251 | 0.251 |
| 0.8076 | 0.616 | 0.616 | 0.600 | 0.600 | |
| 1.0976 | 0.896 | 0.896 | 0.882 | 0.882 | |
| 75 | 0.1651 | 0.178 | 0.178 | 0.177 | 0.177 |
| 0.2623 | 0.406 | 0.406 | 0.403 | 0.403 | |
| 0.3508 | 0.674 | 0.674 | 0.671 | 0.670 | |
| 150 | 0.1142 | 0.175 | 0.175 | 0.174 | 0.174 |
| 0.1813 | 0.394 | 0.394 | 0.393 | 0.393 | |
| 0.2424 | 0.659 | 0.659 | 0.657 | 0.657 | |
Table 9.
GLMM(F, g) Power results for the Box test.
| N | B-scale | Uncorrected | |||
|---|---|---|---|---|---|
| Median | Unconditional | ||||
|
| |||||
| Exact | Approximate | Exact | Approximate | ||
| 15 | 0.4997 | 0.028 | 0.028 | 0.027 | 0.027 |
| 0.8076 | 0.162 | 0.162 | 0.154 | 0.154 | |
| 1.0976 | 0.475 | 0.475 | 0.454 | 0.454 | |
| 75 | 0.1651 | 0.023 | 0.023 | 0.023 | 0.023 |
| 0.2623 | 0.099 | 0.099 | 0.098 | 0.098 | |
| 0.3508 | 0.281 | 0.281 | 0.278 | 0.278 | |
| 150 | 0.1142 | 0.023 | 0.023 | 0.023 | 0.023 |
| 0.1813 | 0.098 | 0.098 | 0.097 | 0.097 | |
| 0.2424 | 0.275 | 0.275 | 0.273 | 0.273 | |
Table 10.
GLMM(F, g) power results for Geisser-Greenhouse test.
| N | B-scale | Uncorrected | |||
|---|---|---|---|---|---|
| Median | Unconditional | ||||
|
| |||||
| Exact | Approximate | Exact | Approximate | ||
| 15 | 0.4997 | 0.190 | 0.191 | 0.185 | 0.185 |
| 0.8076 | 0.526 | 0.527 | 0.510 | 0.510 | |
| 1.0976 | 0.847 | 0.848 | 0.830 | 0.830 | |
| 75 | 0.1651 | 0.152 | 0.152 | 0.151 | 0.151 |
| 0.2623 | 0.366 | 0.366 | 0.364 | 0.364 | |
| 0.3508 | 0.637 | 0.637 | 0.633 | 0.633 | |
| 150 | 0.1142 | 0.151 | 0.151 | 0.150 | 0.150 |
| 0.1813 | 0.359 | 0.359 | 0.356 | 0.356 | |
| 0.2424 | 0.625 | 0.625 | 0.623 | 0.623 | |
Table 11.
GLMM(F, g) power results for the Huynh-Feldt test.
| N | B-scale | Uncorrected | |||
|---|---|---|---|---|---|
| Median | Unconditional | ||||
|
| |||||
| Exact | Approximate | Exact | Approximate | ||
| 15 | 0.4997 | 0.257 | 0.257 | 0.251 | 0.251 |
| 0.8076 | 0.616 | 0.616 | 0.600 | 0.600 | |
| 1.0976 | 0.896 | 0.896 | 0.882 | 0.882 | |
| 75 | 0.1651 | 0.167 | 0.167 | 0.165 | 0.165 |
| 0.2623 | 0.388 | 0.388 | 0.385 | 0.385 | |
| 0.3508 | 0.658 | 0.658 | 0.654 | 0.654 | |
| 150 | 0.1142 | 0.158 | 0.158 | 0.157 | 0.157 |
| 0.1813 | 0.370 | 0.370 | 0.368 | 0.368 | |
| 0.2424 | 0.636 | 0.636 | 0.633 | 0.633 | |
The study design was used to test both quantile or unconditional power for the GLMM(F, g). Within each of these methods, the distribution of the noncentrality parameter can be calculated using either a Satterthwaite style approximation or an exact result using Davies’ algorithm (Davies 1980; Glueck and Muller 2003). The following combinations were tested:
Example 1
Median power for the Hotelling-Lawley Trace, using the Satterthwaite approximation. Full results are available at HotellingLawleyApproximateQuantileOutput.pdf.
Example 2
Median power for the Hotelling-Lawley Trace, using Davies’ algorithm (Davies 1980). Full results for approximate median power are available at HotellingLawleyExact QuantileOutput.pdf.
Example 3
Unconditional power for the Hotelling-Lawley Trace, using the Satterthwaite approximation. Full results for approximate unconditional power are available at Hotelling LawleyApproximateUnconditionalOutput.pdf.
Example 4
Unconditional power for the Hotelling-Lawley Trace, using Davies’ algorithm (Davies 1980). Full results for exact unconditional power are available at HotellingLawley ExactUnconditionalOutput.pdf.
Example 5
Median power for the uncorrected univariate approach to repeated measures, Box, Geisser-Greenhouse, and Huynh-Feldt tests, using the Satterthwaite approximation. Full results for approximate median power are available at UnirepApproximateQuantileOutput.pdf.
Example 6
Median power for the uncorrected univariate approach to repeated measures, Box, Geisser-Greenhouse, and Huynh-Feldt tests, using Davies’ algorithm (Davies 1980). Full results for approximate median power are available at UnirepExactQuantileOutput.pdf.
Example 7
Unconditional power for the uncorrected univariate approach to repeated measures, Box, Geisser-Greenhouse, and Huynh-Feldt tests, using the Satterthwaite approximation. Full results for approximate unconditional power are available at UnirepApproximateUnconditionalOutput.pdf.
Example 8
Unconditional power for the uncorrected univariate approach to repeated measures, Box, Geisser-Greenhouse, and Huynh-Feldt tests, using Davies’ algorithm (Davies 1980). Full results for exact unconditional power are available at UnirepExactUnconditionalOutput.pdf.
Contributor Information
Sarah M. Kreidler, University of Colorado Denver
Keith E. Muller, University of Florida
Gary K. Grunwald, University of Colorado Denver
Brandy M. Ringham, University of Colorado Denver
Zacchary T. Coker-Dukowitz, University of Florida
Uttara R. Sakhadeo, University of Florida
Anna E. Barón, University of Colorado Denver
Deborah H. Glueck, University of Colorado Denver
References
- Apache Software Foundation. Apache HTTP Server Version 2.2. Forest Hill: 2010. URL http://httpd.apache.org/ [Google Scholar]
- Apache Software Foundation. Apache Tomcat Version 7.0. Forest Hill: 2011. URL http://tomcat.apache.org/ [Google Scholar]
- Apache Software Foundation. Apache Commons Mathematics Library Version 3.0. Forest Hill: 2012. URL http://commons.apache.org/math/ [Google Scholar]
- Apple. Safari Version 5.0.3. Cupertino: 2010. URL http://www.apple.com/safari/ [Google Scholar]
- Basagaña X, Spiegelman D. Power and Sample Size Calculations for Longitudinal Studies Comparing Rates of Change with a Time-Varying Exposure. Statistics in Medicine. 2010;29(2):181–192. doi: 10.1002/sim.3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertie A. Java Statistical Classes Version 1.0. 2005 URL http://www.jsc.nildram.co.uk/
- Coffey CS, Muller KE. Properties of Internal Pilots with the Univariate Approach to Repeated Measures. Statistics in Medicine. 2003;22(15):2469–2485. doi: 10.1002/sim.1466. [DOI] [PubMed] [Google Scholar]
- Crockford D. JSON. 2012 URL http://www.json.org/
- Davies RB. Algorithm AS 155: The Distribution of a Linear Combination of χ2 Random Variables. Journal of the Royal Statistical Society C. 1980;29(3):323–333. [Google Scholar]
- Free Software Foundation. The GNU General Public License Version 2. 2010 URL http://www.gnu.org/licenses/gpl-2.0.html.
- Gatsonis C, Sampson AR. Multiple Correlation: Exact Power and Sample Size Calculations. Psychological Bulletin. 1989;106(3):516–524. doi: 10.1037/0033-2909.106.3.516. [DOI] [PubMed] [Google Scholar]
- Glueck DH, Muller KE. Adjusting Power for a Baseline Covariate in Linear Models. Statistics in Medicine. 2003;22:2535–2551. doi: 10.1002/sim.1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Google Inc. Google Web Toolkit Version 2.4.0. Mountainview: 2011. URL http://code.google.com/webtoolkit/ [Google Scholar]
- Gribbin MJ. PhD thesis. University of North Carolina; Chapel Hill: 2007. Better Power Methods for the Univariate Approach to Repeated Measures. [Google Scholar]
- Hsieh FY, Lavori PW, Cohen HJ, Feussner JR. An Overview of Variance Inflation Factors for Sample-Size Calculation. Evaluation & the Health Professions. 2003;26(3):239–257. doi: 10.1177/0163278703255230. [DOI] [PubMed] [Google Scholar]
- Johnson JL, Muller KE, Slaughter JC, Gurka MJ, Gribbin MJ, Simpson SL. POWERLIB: SAS/IML Software for Computing Power in Multivariate Linear Models. Journal of Statistical Software. 2009;30(5):1–27. doi: 10.18637/jss.v030.i05. URL http://www.jstatsoft.org/v30/i05/ [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenth RV. Russ Lenth’s Power and Sample Size Page. 2009 URL http://www.stat.uiowa.edu/~rlenth/Power/
- McGovern J, Tyagi S, Stevens M, Mathew S. Java Web Services Architecture. Morgan Kaufmann; San Francisco: 2003. [Google Scholar]
- Microsoft. Internet Explorer, Version 8. Redmond: 2010. URL http://www.microsoft.com/windows/internet-explorer/worldwide-sites.aspx. [Google Scholar]
- Mozilla. Firefox Web Browser, Version 3.6.12. Mountain View: 2011. URL http://www.mozilla.com/en-US/firefox/ [Google Scholar]
- Muller KE. A New F Approximation for the Pillai-Bartlett Trace Under H0. Journal of Computational and Graphical Statistics. 1998;7(1):131–137. [PMC free article] [PubMed] [Google Scholar]
- Muller KE, Barton CN. Approximate Power for Repeated-Measures ANOVA Lacking Sphericity. Journal of the American Statistical Association. 1989;84(406):549–555. [Google Scholar]
- Muller KE, Edwards LJ, Simpson SL, Taylor DJ. Statistical Tests with Accurate Size and Power for Balanced Linear Mixed Models. Statistics in Medicine. 2007;26(19):3639–3660. doi: 10.1002/sim.2827. [DOI] [PubMed] [Google Scholar]
- Muller KE, Fetterman BA. Regression and ANOVA: An Integrated Approach Using SAS Software. SAS Institute; Cary, NC: 2002. [Google Scholar]
- Muller KE, Lavange LM, Ramey SL, Ramey CT. Power Calculations for General Linear Multivariate Models Including Repeated Measures Applications. Journal of the American Statistical Association. 1992;87(420):1209–1226. doi: 10.1080/01621459.1992.10476281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller KE, Peterson BL. Practical Methods for Computing Power in Testing the Multivariate General Linear Hypothesis. Computational Statistics & Data Analysis. 1984;2:143–158. [Google Scholar]
- Muller KE, Stewart PW. Linear Model Theory: Univariate, Multivariate, and Mixed Models. John Wiley & Sons; Hoboken, New Jersey: 2006. [Google Scholar]
- NCSS. PASS Power Analysis and Sample Size. Kaysville: 2008. URL http://www.ncss.com/pass.html. [Google Scholar]
- Noelios Technologies. Restlet Version 2.0.10. Nanterre: 2011. URL http://www.restlet.org/ [Google Scholar]
- ORACLE. Java SE. Version 7. Redwood Shores: 2011. URL http://www.oracle.com/technetwork/java/javase/downloads/ [Google Scholar]
- Park S. PhD thesis. University of North Carolina; Chapel Hill: 2007. Accounting for Bias and Uncertainty in Power for Multivariate Gaussian Linear Models. [Google Scholar]
- Raudenbush SW, Liu X. Statistical Power and Optimal Design for Multisite Randomized Trials. Psychological Methods. 2000;5(2):199–213. doi: 10.1037/1082-989x.5.2.199. [DOI] [PubMed] [Google Scholar]
- Sampson AR. A Tale of Two Regressions. Journal of the American Statistical Association. 1974;69(347):682–689. [Google Scholar]
- SAS Institute Inc. SAS 9.2 Software. Cary: 2011a. URL http://www.sas.com/software/sas9/ [Google Scholar]
- SAS Institute Inc. SAS/IML 9.2 User’s Guide. SAS Institute Inc; Cary, NC: 2011b. URL http://www.sas.com/ [Google Scholar]
- Schoenfeld DA. Sample Size Calculators. 2007 URL http://hedwig.mgh.harvard.edu/sample_size/size.html.
- Seoane J, Pita-Fernández S, Gómez I, Vazquez I, López-Cedrún JL, Agustin DD, Varela-Centelles P. Proliferative Activity and Diagnostic Delay in Oral Cancer. Head & Neck. 2010;32(10):1377–1384. doi: 10.1002/hed.21338. [DOI] [PubMed] [Google Scholar]
- Shieh G. Power and Sample Size Calculations for Multivariate Linear Models With Random Explanatory Variables. Psychometrika. 2005;70(2):347–358. [Google Scholar]
- Statistical Solutions. nQuery Advisor, Sample Size and Power Calculation Software, Version 7.0. Saugus: 2008. URL http://www.statsol.ie/ [Google Scholar]
- Taylor DJ, Muller KE. Computing Confidence Bounds for Power and Sample Size of the General Linear Univariate Model. The American Statistician. 1995;49(1):43–47. doi: 10.1080/00031305.1995.10476111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- W3C. HTML 4.01 Specification. 1999 URL http://www.w3.org/TR/1999/REC-html401-19991224/
- Zhang E, Zhang HG. CRAN Task View: Clinical Trial Design, Monitoring, and Analysis. 2012 Version 2012-10-25, URL http://CRAN.R-project.org/view=ClinicalTrials.