An Imaging and Systems Modeling Approach to Fibril Breakage Enables Prediction of Amyloid Behavior

Abstract

Delineating the nanoscale properties and the dynamic assembly and disassembly behaviors of amyloid fibrils is key for technological applications that use the material properties of amyloid fibrils, as well as for developing treatments of amyloid-associated disease. However, quantitative mechanistic understanding of the complex processes involving these heterogeneous supramolecular systems presents challenges that have yet to be resolved. Here, we develop an approach that is capable of resolving the time dependence of fibril particle concentration, length distribution, and length and position dependence of fibril fragmentation rates using a generic mathematical framework combined with experimental data derived from atomic force microscopy analysis of fibril length distributions. By application to amyloid assembly of β₂-microglobulin in vitro under constant mechanical stirring, we present a full description of the fibril fragmentation and growth behavior, and demonstrate the predictive power of the approach in terms of the samples’ fibril dimensions, fibril load, and their efficiency to seed the growth of new amyloid fibrils. The approach developed offers opportunities to determine, quantify, and predict the course and the consequences of amyloid assembly.

Introduction

Amyloid fibrils represent a class of supramolecular particles self-assembled from a variety of naturally occurring or designed proteins or peptide sequences (1–5). These nanostructures are associated with numerous devastating human disorders, such as type II diabetes mellitus, Alzheimer’s and Parkinson’s diseases (1). Despite these assemblies being linked to disease, amyloid fibril nanostructures have favorable molecular and material properties that could be harnessed for technological applications. Nature has itself adopted amyloid structures for varied structural and functional roles to use their favorable properties for the benefit of living organisms (e.g. 6–8). If amyloid assembly and disassembly could be better understood in mechanistic terms, and controlled, the diseases that involve amyloid formation may be more effectively combated, and the molecular and material properties that amyloid fibrils possess could be harnessed as engineered high-performance bionanomaterials (3).

Amyloid fibrils share a common cross-beta core molecular architecture (5), with a highly ordered network of intermolecular hydrogen bonds that make them extremely stable structures (3). Despite having a width in the order of ∼10 nanometers, fibrils can grow up to several micrometers in length in vitro (9–12). A typical amyloid sample, independent of whether formed in vivo or in vitro is a highly heterogeneous mixture that contains monomers, small oligomers, and fibrillar species with a wide range of sizes. There are numerous studies showing that different species formed during amyloid assembly are potentially associated with the pathogenic properties connected to amyloid disease, such as the potential to cause membrane damage, cytotoxicity, and organ dysfunction (e.g. 13–17). In the case of amyloid fibrils, variations in fibril length distribution can lead to different biological responses, ranging from relatively inert material involving long and/or entangled fibril polymers to shorter, freely diffusing cytotoxic and/or propagating particles (12,18,19). The potential for short fibrillar particles to elicit cytotoxicity, to generate further cytotoxic species by disassembly, or to seed new amyloid growth and rapidly increase fibril load emphasizes the importance of mechanistic understanding of amyloid fibril assembly, disassembly, and their balance. Analyses of amyloid behavior therefore require the development of tools for the precise characterization of the species distributions of highly heterogeneous mixtures in intricate detail and how this varies with time, growth conditions, protein concentration, and solution environment.

Recent advances based on classical assembly theories (e.g. 20–22) have resulted in the development of mathematical models that are increasingly better at describing amyloid assembly reactions (23–26). These models, together with advances in experimental and computational studies (e.g. 24,27–31) have increased our understanding of the molecular mechanisms and nanoscale properties of amyloid assembly. In particular, secondary fibril fragmentation processes have been identified as a key mechanism in accelerating the formation of amyloid, in addition to primary nucleation and growth (23,25,31). Fibril fragmentation is also appreciated as a process of fundamental importance in creating small fibrillar species that can elicit enhanced seeding and cytotoxic potential (12,18). Although numerical and analytical solutions to models of amyloid assembly involving fibril breakage (23,25) have been proposed, experimental characterization of the mechanisms and rates of fibril fragmentation, and deconvolution of its effects from primary fibril elongation during their growth, remain challenging and unresolved. The challenges, thus far, have prevented systematic testing of the behavior of amyloid systems and the full characterization and prediction of the course of amyloid assembly.

Here, we describe a generic master equation-based mathematical framework, which we combine with experimental data obtained by tapping-mode atomic force microscopy (TM-AFM) imaging and image analysis capable of single fibril particle characterization, effectively bridging theory with experimental data of high informational content. We then apply our approach to the in vitro assembly of β₂-microglobulin (β₂m) fibrils, which allowed the determination of particle concentration and length distribution of fibrils as they break, and the rate of fibril fragmentation as a function of fibril length and breakage position. We demonstrate that deconvoluting these key molecular and mechanistic properties permits the predictive power to assess the assembly rate, the length distribution, the fibril load, and the seeding efficiency of amyloid fibril material. In summary, we show that our approach, involving systems modeling combined with TM-AFM image analysis of fibril length distributions during fibril breakage and fibril elongation experiments, together allow a full description of the amyloid fibrils’ fragmentation and growth behavior during amyloid assembly.

Materials and Methods

Generation and controlled fragmentation of β₂m fibril samples

In vitro-generated β₂m fibril samples were prepared using lyophilized recombinant wild-type monomeric β₂m as previously described (12) and as detailed in the Supporting Material. Fibril fragmentation was achieved by mechanical perturbation. All mechanical agitation experiments were performed using a method involving stirring of a 500 μl of fibril samples in 1.5-ml glass vials containing 3 × 8-mm polytetrafluoroethylene-coated magnetic stirring bars using a custom-made precision stirrer with accurate rpm readout (custom-built by the workshop of the School of Physics and Astronomy, University of Leeds). Stirring was performed at 1,000 rpm, 25°C, which generates turbulent flow in the sample that distribute the agitation action to prevent the alignment of fibrils and achieve fibril fragmentation on an experimentally accessible timescale. Such a stirring method also allows discrete samples to be taken at well-controlled time points of fragmentation and assembly so that the time course can be readily followed and analyzed.

TM-AFM imaging and quantitative image analysis

β₂m fibrils were deposited on mica by incubating freshly cleaved mica surface with 20 μL of a solution containing fibril sample diluted with sterile filtered and deionized water to 0.4 μM total monomer equivalent concentration of fibrils for 5 min at 25°C. Great care was taken to minimize additional mechanical perturbations through sample handling and pipetting. The mica surface was subsequently gently washed with 1 mL sterile-filtered deionized water and dried under a gentle stream of nitrogen gas. All TM-AFM height images were collected in air using a Dimension 3100 Scanning Probe Microscope (Veeco Instruments), a MPF-3D Atomic Force Microscope (Asylum Research), or a Bruker MultiMode 8 Scanning Probe Microscope (Bruker) using PPP-NCLR cantilever probes (Nanosensors, Neuchatel, Switzerland) with a nominal force constant of 48 N/m. Height images were collected at a resolution of 1024 × 1024 pixels over 10 × 10 μm surface area and processed using supplied software for each instrument to remove sample tilt and scanner bow. The length of individual fibril particles, L, was extracted and measured using automated scripts written in MATLAB (The MathWorks, Natick, MA). Because the efficiency of fibril deposition on surface substrate and successful measurement of length of individual fibrils depend on fibril length, the normalized length distribution of the fibrils in the bulk samples corrected for the length bias of surface imaging, P_c, was determined as previously described (12,32).

Fibril growth monitored by thioflavin T (ThT) fluorescence

Fibril growth reactions were monitored by ThT fluorescence in black flat-bottom uncoated 96-well plates using a BMG LABTECH FLUOStar Optima plate reader at 25°C as previously described (23). Fibril growth reactions were initiated manually and 10 μM ThT was used in each reaction with 100 μL total volume in each well.

Numerical modeling and analysis

Numerical modeling, image analysis, parameter estimation, and statistical analysis were carried out using scripts written in MATLAB (The MathWorks). The master equation approach and all equations used for data analysis are explained and justified in the Supporting Material. Numerical integrations of the master equation were solved for fibril species containing up to 20,000 monomeric units, and concentration errors introduced by truncation of larger species were <1%. Parameter estimation with the resulting time evolution of species distributions were performed by the maximum likelihood estimation (MLE) method described previously (32). Parameters were optimized using the simplex direct search algorithm. Model comparison were performed using the Akaike information criterion (AIC) as described previously (23) with the corrected AIC (AICc) scores calculated as AICc = 2 M − 2 ln($\mathcal{L}$) + 2M(M+1)/(N-M-1) where N is the number of data points and M is the number of fitted parameters and $\mathcal{L}$ is the maximized likelihood function from the MLE analysis of length distributions. Error analysis of the best-fit model was carried out using the Jackknife method performed on each of the fibril fragmentation time points.

Results

Construction of a generic framework for assembly models

To approach a full yet flexible description of the dynamic mechanism of amyloid assembly, vital for understanding and predicting amyloid formation both in vivo and in vitro, we use a master equation approach that can describe every possible forward and backward step involving every possible species in the assembly system. The master equation of assembly was setup and expressed as the following:

$$\frac{dc}{dt}=\mathbf{k}·\mathbf{c}$$ (1)

with the vector c representing the species distribution in the molar number concentration unit, and k, sometimes referred to as the kernel, representing a matrix capable of describing the mechanism of any assembly reaction (detailed in the Supporting Material). In terms of amyloid assembly, previous investigations have indicated that the fibrillar products are formed through mechanisms dominated by a forward templated growth reaction by monomer addition as well as a backward fibril fragmentation reaction (23,25). The matrix k for amyloid assembly can therefore be separated and expressed as k ≈ k_growth + k_frag. If the detailed species distribution, c, could be quantified for the assembly of fibrils under experimental conditions where growth or fragmentation each independently dominate, k representing the assembly and disassembly mechanism could be constructed and used to describe and to predict properties of amyloid assembly as well as the mechanical stability of amyloid fibrils toward fragmentation.

Fibril particle concentration and distribution

To bridge the previous theoretical framework (Eq. 1) with experimental data required to extract mechanistic information regarding amyloid fibril fragmentation and growth, we first developed an image analysis method that allowed us to determine the distribution of the particle number concentration (in molar units) for discrete fibril species of different length using TM-AFM. We then used this approach to characterize the fibril fragmentation and extension mechanisms of β₂m amyloid fibrils formed in vitro (12,33). β₂m amyloid assembly is involved in systemic dialysis-related amyloidosis (34) and an autosomal dominant, hereditary variant of systemic amyloidosis (35). In this study β₂m fibrils were formed from acid unfolded β₂m monomers at pH 2.0. The fibrils that result show all the typical physical, structural, and tinctorial characteristics of amyloid formed in vivo (33).

To resolve the molar particle concentration c_F of the sample containing long straight, unfragmented β₂m fibrils, which is inherently highly heterogeneous in length, three independent pieces of information were used. I), The fibril length distribution, P_c, of the fibril particles f in the β₂m fibril sample (Fig. 1, top row black line), which was measured using TM-AFM and single particle length, L, measurements, corrected for the length dependent imaging bias (32). II), The total monomer equivalent concentration of the sample c_1,tot, which in this case was 120 μM (determined before the start of the reaction using ultraviolet-absorbance). III) The mass per unit length of fibrils, which in the case of the β₂m fibrils employed here has been measured previously using scanning transmission electron microscopy and estimated to be 53 kDa/nm based on the modal value for the dominant fibril population (10). This value is equivalent to around 4.5 monomers per nm length: N_l = 4.5 nm⁻¹. Combining these three pieces of information, and assuming a negligible residual monomer concentration in the fibril sample (consistent with previous reports (36)), the molar fibril particle concentration for the fibril sample, c_F, was determined to be 2.7·10⁻⁸ M, using the following equation (detailed in the Supporting Material).

$$c_F=\frac{c_{1,tot}}{\sum _f{L}_f{N}_l{P}_c\left(L_f\right)}$$ (2)

The detailed species distribution of the sample, c = c(i) [M] (i =1,2,3,…monomer units), was then established using the length distribution by calculating the number of monomer units in each measured fibril using the known N_l (Eq. S2, in the Supporting Material) followed by MLE using a Weibull distribution model (32). The total fibril particle concentration c_F and the concentration of species of different length in the species distribution are key characteristics of the fibril sample that allow us to decipher the fragmentation behavior and the seeding potential of the fibrils. The molar concentration of fibril particles can also be used, for example, in comparing the cytotoxicity potential of amyloid samples on a per particle (molar) basis.

Figure 1.

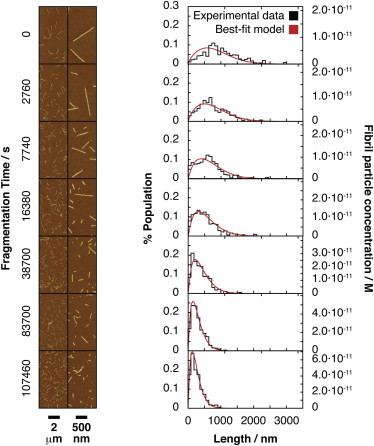
β₂m fibril fragmentation monitored by TM-AFM imaging. Typical AFM height images of the fibril samples as a function of fragmentation reaction time are shown in the left column with scale bars shown below the images. The left side images show half (5 × 10 μm) of 1024 × 1024 pixel, 10 × 10 μm images. The right side images show a 4×-magnified region on the same images. Normalized histograms of the length distribution of each fibril sample are shown in the right column, with the red lines indicating the best-fit time evolution of the length distributions as fragmentation proceeds according to kFrag resulting from model number 5 in Table S1. The fibril length distribution histograms are each constructed from 460 to 1200 individual fibril particles on 4–16 images. The scale corresponding to the fibril particle concentrations for each sample is shown to the right of the plots. To see this figure in color, go online.

Length and position dependence of fibril fragmentation

The characterization of the fibril species distribution and molar particle concentration allowed us to next characterize the mechanism of fibril fragmentation (Fig. 2 a) by extracting the matrix k_Frag (Eq. 1, and the Supporting Material) that describes how long straight β₂m fibrils in our sample are fragmented by mechanical perturbation. The rates of fibril breakage under the conditions employed, indicative of the fibrils’ stability toward fragmentation, were also determined. As previously described (12), the preformed long straight β₂m fibril sample (500 μl) was put into a 1.5 ml chromatography glass vial with a 3 × 8 mm polytetrafluoroethylene-coated magnetic stirring bar and subjected to turbulent agitation by stirring at a single constant speed of 1000 rpm (Materials and Methods). At different time points, up to 30 h, a small aliquot of the sample was taken out and immediately placed on freshly cleaved mica for analysis using TM-AFM (12). The resulting fibril length distributions are plotted in Fig. 1.

Figure 2.

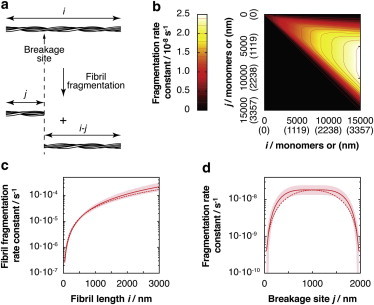
Length and position dependence of the best-fit fibril fragmentation model. (a) Schematic illustration of a fibril fragmentation reaction. (b) The fragmentation rate matrix k_Frag represented as a contour diagram, showing the first order fragmentation rate constants as a function of fibril length i, and position of breakage j, expressed as the number of monomers or nanometers in the brackets. (c) The fibril fragmentation rate constant as a function of fibril length for the best-fit fragmentation model. (d) Example of fragmentation rate constant as a function of breakage position for a fibril of 2000 nm in length for the best-fit fragmentation model. In (c) and (d), the shaded area indicates 95% confidence functional prediction bounds. The dotted red line in (c) and (d) shows the results obtained using the Hill model (37). To see this figure in color, go online.

To extract k_Frag that contains both length- and position-dependent rates information regarding the fibril fragmentation process, we fit numerical solutions of Eq. 1 to the time evolution of the fibril length distributions experimentally measured by single-particle TM-AFM imaging. We used two independent and parallel approaches to resolve k_Frag. In the first approach numerical solutions of Eq. 1 obtained using a series of k_Frag with increasing complexity (see the Supporting Material) were fit to the distribution data until the goodness of fit did not improve with a further increase in model complexity (Table S1, models 1–6). This approach lets the information content of the data dictate a model that can best describe the fibril fragmentation mechanism without the need to assume a mechanism a priori. We started with the simplest model that depicts the case where the microscopic fragmentation rate constants for breakage between each monomer is identical and is independent of length or position (Table S1, model 1). Notably, this is a frequently used assumption in existing amyloid assembly models (25). In this case, the overall fragmentation rate constant of a fibril of a given length, which is the sum of all microscopic fragmentation rate constants for all possible fragmentation sites between monomers in the fibril, is linearly dependent on fibril length because the number of fragmentation sites increases linearly with length. The calculated length distributions of such a fragmentation model, however, do not reproduce the measured fibril length distributions, resulting in the model approaching an exponential distribution that systemically deviates from the data after ∼5 h of fragmentation, especially for short fibril particles of a few hundred nm in length (Fig. S1). The complexity of k_Frag was then increased in a stepwise manner (detailed in the Supporting Material). The goodness of fit, corrected for the increased complexity of k_Frag in terms of the number of fitted parameters, was quantified using AIC with a lower AICc score indicating an overall better model (23). A total of 6 k_Frag, were tested in this manner until the AICc score stopped decreasing as model complexity increased (Table S1), indicating that the k_Frag with the lowest AICc score found is a likely description of the fibril fragmentation mechanism that has a complexity supported by the information content in the data. The best-fit (red lines in Fig. 1) k_Frag with the lowest AICc score is represented in Fig. 2 b as a contour diagram. The first order fibril fragmentation rate constant as a function of fibril length calculated from this best-fit model is plotted in Fig. 2 c; accordingly, the best fit k_Frag represents a fibril fragmentation mechanism where the breakage rate is dependent on fibril length in a nonlinear manner. For example, under the conditions employed, a fibril of 2 μm in length has an estimated fragmentation rate constant of 1.1·10⁻⁴s⁻¹ (log(k/s⁻¹) = −3.7 ± 0.2) corresponding to a half-life of ∼6300 s or <2 h. By contrast, a fibril of 200 nm in length has an estimated fragmentation rate constant that is almost two orders of magnitude lower at 2.9·10⁻⁶s⁻¹ (log(k/s⁻¹) = −5.5 ± 0.1) corresponding to a half-life of ∼240,000s or ∼66 h. The results also indicate a substantial dependence of fragmentation on position, with the highest microscopic fibril fragmentation rate constant displayed in the middle of fibrils. Illustrated by the microscopic fibril fragmentation rate constant as a function of the position of breakage for a 2 μm fibril (Fig. 2 d), the estimated microscopic fibril fragmentation rate constant in the middle of a 2 μm fibril is 1.8·10⁻⁸s⁻¹ (log(k/s⁻¹) = −7.7 ± 0.2), whereas a breakage of the same fibril resulting in a 200 nm and a 1800 nm fibril proceed with an estimated microscopic fibril fragmentation rate constant of 5.5·10⁻⁹s⁻¹ (log(k/s⁻¹) = −8.3 ± 0.2), >3 times less frequent.

In parallel, we tested a mechanistic model based on the spontaneous breakage of stiff rods as proposed by Hill (37). Fitting solutions of Eq. 1 obtained with a k_Frag that describes the Hill model (Table S1, model 7, and Fig. S1) to the distributions of fibril lengths did not result in a significantly better fit compared with the best-fit result obtained using the first approach as judged by the resulting AICc score (Table S1). The dashed lines in Fig. 2, c and d, show the length and position dependence of the fragmentation rate constants from the fit k_Frag using the Hill model, which displays a similar length and position dependence to the best-fit model. The deviation from the best-fit model may reflect the differences between the applied perturbations and the equilibrium assumptions of the model, and that the β₂m fibrils are not completely rigid as stiff rods but contain some degree of flexibility. Nevertheless, despite the overall worse fit to the data, this mechanism-dependent approach yielded a similar quantitative result in terms of the fragmentation rates compared with our parallel approach, confirming that the position- and length-dependent fragmentation mechanism and the fragmentation rate constants obtained are robust.

Determining the fibril elongation rate constant

The ability to determine the fibril concentration in molar terms further allows the second order fibril elongation rate constant free from contributions of secondary processes to be determined in molar units on a per fibril particle basis (Eq. S18). We seeded new monomer solutions of β₂m (12 μM) with small aliquots (2% w/w) of each of the β₂m fibril samples previously collected at different times of fibril fragmentation ((12), Fig. 3, Fig. S2). The molar fibril particle concentration of each of the seed samples was determined from their length distribution measured by TM-AFM imaging, single particle image analysis, and Eq. 2 as described previously. The reaction progress of the seeded reactions was monitored by ThT fluorescence (12,23) and the initial rate of fibril growth was plotted against the fibril particle concentration added (Fig. 3, a and b). Because β₂m fibril growth is described by a monomer addition process (23) and the initial rate of fibril growth is proportional to the initial fibril particle concentration with a proportionality constant of k⁺ (Eq. S18), k⁺ was quantified as the slope of the line fit to the data points in Fig. 3 b. Total linear least squares analysis (line in Fig. 3 b) yielded a k⁺ of 7.2·10⁴ M^-1s⁻¹ (log (k⁺/M⁻¹s⁻¹) = 4.9 ± 0.1) under the conditions employed here for β₂m fibril extension. This bimolecular reaction rate constant is ∼10⁵ times lower than the maximum diffusion-limited reaction rate constant based on estimates using the Smoluchowski collision frequency factor for collisions between spheres of similar dimensions to β₂m monomers undergoing diffusion, suggesting that approximately one in 10⁵ molecular collisions with the fibrils results in attachment at fibril ends. It is important to note that the determined value of k⁺ (by definition in Eq. S18) is defined on a per M average fibril particle basis. Assuming that extension competent sites operate independently, the rate constant on per site basis is k⁺/the average number of extension sites per fibril.

Figure 3.

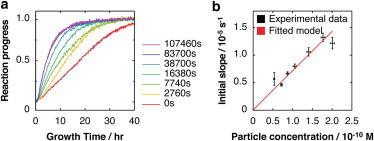
Determination of the second order fibril extension rate constant, k⁺. (a) Typical fibril growth reaction progress curves of reactions seeded by fibril samples taken from the fragmentation reaction shown in Fig. 1, monitored by ThT fluorescence. All curves are normalized to their upper baselines (unnormalized traces are shown in Fig S2). The times each sample was fragmented, before addition to excess monomer to stimulate fibril growth, are shown to the right. (b) Initial slope of the normalized reaction progress curves versus fibril seed particle concentration. The error bars indicate one standard error of four reaction replicates. The red line denotes a linear function fit to the data using a total least squares method. To see this figure in color, go online.

Predicting fibril length, concentration, extension, and breakage

To test the predictive power gained from the mechanistic analysis described previously and to demonstrate the ability of the approach developed to deconvolute the fragmentation and elongation rates of β₂m fibril samples of different length distributions, we performed a series of simulations to forecast the outcomes of independent experiments on independent fibril samples. First, we produced a new fibril sample of different length distribution compared with the previous sample (see the Supporting Material) for validating our predictions. We characterized the fibril length distribution of this sample as described previously (Fig. 4, top right, Fig. S3, left). We then simulated how fibril fragmentation would proceed and change the length distribution of this sample using the fragmentation model and rate parameters derived previously (note that the solution conditions, temperature, fragmentation conditions, and fibril morphology were identical to the previous sample). This enabled us to predict how the length distribution, as well as the molar particle concentration, evolves as a function of time (Fig. 4, left contour plot). To verify our predictions, we performed the fibril fragmentation experiment on the new sample and compared the experimentally measured length distributions at selected time points with our predictions (Fig. 4, right, Fig. S3). As shown in Fig. 4, the predicted length distributions follow closely the observed distributions at experimentally verified time points, demonstrating the ability of the model to predict the behavior of the new sample.

Figure 4.

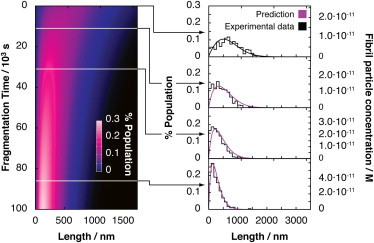
Prediction of the time evolution of changes in fibril length during fragmentation. Left contour diagram depicts predicted time evolution of the fibril length distribution of a fibril sample undergoing fibril fragmentation. Shown in the right column are purple lines indicating the corresponding predicted length distributions as fragmentation precedes compared with experimental validation data consisting of normalized histograms of the length distribution of the fibril sample at the same time points, determined by TM-AFM imaging and image analysis. The fibril length distribution histograms shown are each constructed from 390 to 1200 individual fibril particles on 4–10 images. The scale corresponding to the fibril particle concentrations for each sample is shown to the right of the plots. To see this figure in color, go online.

Because the previous analysis enables the particle concentration to be predicted and how this increases when fibrils fragment (Fig. S4), we next predicted the potential of the previous fibril sample to seed the formation of new fibrils and how this is enhanced by fibril fragmentation (12). We then verified our predictions experimentally by performing seeded fibril growth assays that mirror the simulations. Fig. 5 a (black +) and b show the experimental data of the seeding experiments, whereas Fig. 5 a (purple line) and c show the predicted initial fibril growth rate as a function of fragmentation time compared with the experimentally measured values. The results show that exploiting the known fibril fragmentation and fibril extension rates, and their associated kinetic constants on a fibril sample of known initial length distribution and particle concentration enables accurate and quantitative prediction of the reaction progress. This included the increase in the ability of fibril samples to seed the formation of new amyloid fibrils following fragmentation, and the associated time-dependent increase of fibril load.

Figure 5.

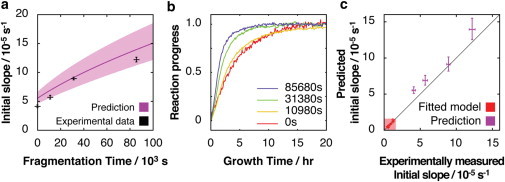
Prediction of the ability of a fibril sample to seed as fibril fragmentation proceeds. (a) Predicted (purple line) and measured (black cross) seeding efficiency characterized by the initial slope of seeded fibril growth using the fibril sample as a function of fragmentation time. The error bars on the measured data points indicate one standard error from six replicate reactions. The shaded area indicates 95% confidence functional prediction bounds. (b) Typical fibril growth reaction progress curves of reactions seeded by fibril samples taken from the fragmentation reaction shown in Fig. 4, monitored by ThT fluorescence. All curves are normalized to their upper baselines. The time each sample was fragmented before addition to excess monomer to stimulate fibril growth are shown in the inset. (c) Predicted initial slopes of seeded fibril growth compared with the measured initial slopes. The red shaded area contains data points used to calculate the fibril elongation rate constant (the same as shown in Fig. 3 b) to indicate predictive power at extrapolated seeding conditions. The error bars indicate one standard error. To see this figure in color, go online.

Finally, to test the predictive power of our fibril fragmentation and fibril growth models when applied simultaneously, we performed a simulation of a seeded fibril growth under agitation by combining the rate constants for the two processes in Eq. 1. A third independent sample formed under agitation was used as the initial seed to test the outcomes of this prediction versus the equivalent experimental data, yielding the progress of fibril length as a function of time. Because the modeling results enable the rate of fibril elongation to be compared with the rate of fibril fragmentation, an initial faster fibril growth is expected for this sample compared with the rate of breakage of short fibril seeds. As a consequence, the simulations predict a biphasic behavior wherein the average fibril length first increases, followed by a phase dominated by the fragmentation of long fibrils into progressively shorter particles. This results in a decelerating decrease in the average fibril length (Fig. 6, Fig. S5) that reaches steady state after ∼10⁹ s (∼30 years, compared with the ThT traces of seeded growth, which reached apparent steady state in <10 h). We then performed an experiment mirroring the simulated reaction and analyzed the average fibril length at selected times up to 86,400 s (Fig. 6, Fig. S6). The experimental results show, as predicted, a biphasic reaction in terms of fibril length, confirming that the separately characterized fibril fragmentation and growth models and associated kinetic parameters together can predict complex composite amyloid assembly processes.

Figure 6.

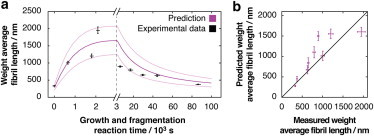
Prediction of a biphasic fibril growth reaction. (a) Predicted (purple) biphasic time evolution of the weight average fibril length of a seeded fibril reaction undergoing simultaneous fibril fragmentation and fibril growth. Measured weight average fibril lengths (each calculated from 310 to 2000 individual fibrils on 4–12 images) are shown as black crosses with error bars indicating one standard error. The shaded area indicates 95% confidence functional prediction bounds. (b) Predicted average fibril length compared with the measured average fibril length. Error bars indicate one standard error. To see this figure in color, go online.

Discussion

Recent advances in the experiments and theories of amyloid assembly mechanisms have resulted in a number of important developments in the field that have led to significantly more sophisticated models and mechanistic insights into the progress of amyloid assembly reactions (23–26,38,39). One key finding is that fibril fragmentation is now recognized as a critical process in accelerating fibril elongation, reducing the lag time of assembly, and enhancing seeding capacity (12,23,25). In addition, the recognition that fibril fragmentation produces particles that may have new biological properties has increased excitement in our quest to understand the mechanical properties of amyloid fibrils and their fragmentation processes (3,12,32,40). Here, we have characterized the mechanism of β₂m fibril fragmentation under mechanical perturbation through combined TM-AFM single particle image analysis, mathematical systems modeling, statistical distribution analysis, and model comparison. Using this approach, we have determined the molar fibril particle concentration and revealed how the rate of fibril fragmentation varies as a function of fibril length and breakage position. Together, these insights reveal the concentration of short amyloid fibrils and the rate of their formation by fibril fragmentation under a given set of experimental conditions. In our analysis, we show that the complex process of fibril fragmentation involves a set of nonequivalent rates with higher rates observed for symmetric breakages compared with asymmetric breakages for the same fibril. In addition, progressively higher rates of fragmentation were observed for longer fibrils than can be explained by the assumption of a linear increase in the number of fragmentation sites as fibrils grow in length (25). The results indicate that β₂m fibril fragmentation proceeds in a manner similar to a spontaneous fragmentation process predicted for rigid rods that has been previously described using statistical thermodynamic approaches (37).

In hemodialysis-related amyloidosis, β₂m amyloid deposits accumulate predominantly in the joints (34). In these areas, shear forces and mechanical stress may result in fibril fragmentation, possibly playing a role in accelerating the increase in fibril load of amyloid deposits in vivo. β₂m fibrils also fragment in the absence of additional mechanical perturbation when they grow beyond a few micrometers in length (32), which may reflect their limited stability toward breakage under thermal motion. Even though the stirring-induced turbulent flow applied here are unlikely to compare directly with the stresses likely encountered by β₂m amyloid deposits under physiological conditions, the approach presented here opens up a new opportunity to characterize the stability of β₂m amyloid fibrils toward breakage under varying types and degrees of mechanical stresses, including those that fibrillar assemblies are likely to encounter in vivo. Such situations may be mimicked by alterations in the stirring rate or the type of mechanical perturbation applied (e.g. 41,42). In other biological situations, fibril fragmentation may be caused by other factors, such as enzymatic action (43) and/or breakage due to fibril defects (27). For example, enzymatic processing by the chaperone machinery involving Hsp104 is known to fragment amyloid fibrils formed from the yeast prion protein Sup35 (43). This process is a key cellular mechanism that controls the generation of so-called prion propagons (31,40,44), which are seeds that can propagate prion phenotypes from mother to daughter cells. In the scenarios in which the predominant cause of fibril fragmentation is different from the mechanical perturbation performed here, it is possible that the breakage rates as a function of length and position may be different from the profile determined here for β₂m. This would result in distinct fibril size distributions and fibril particle concentrations that could reflect the different constructive or destructive biological roles of different amyloid assemblies in different cellular environments. Thus, the approach presented here, in which a full systems modeling and image analysis enables the dimensions of amyloid fibrils to be determined and predicted, will provide the means to compare fibril lengths, particle concentrations, and mechanisms of breakage for amyloid fibrils formed from other protein and peptide sequences, as well as mutations of these sequences and under different solution and physical environments. The application of the approach we present to other amyloid systems under varying mechanical, enzymatic, thermal, or other environmental conditions, therefore, could result in a new understanding of the different amyloid fibrils’ stability toward fragmentation under different stress conditions, and the consequences of this for disease-associated and biologically beneficial amyloid materials.

Amyloid fibrils have potentials as a new class of engineered nanomaterials due to their favorable physical properties (3). The fibrils’ stability toward breakage is also a key parameter that must be characterized and optimized for materials applications. The approach we have developed, therefore, will be useful toward nanomaterials research in determining and predicting the particle species distributions, particle concentrations, steady-state length distributions of fibrillar material, and how rapidly these materials break when subjected to mechanical perturbation. In essence, the approach developed here enables the fibril material’s stability toward breakage under specific conditions to be mapped, and its properties to be controlled in a predictive manner.

In terms of amyloid disease in general, the particle concentration and the physical dimensions of fibril particles impact on two vital disease-causing properties of amyloid: the ability to seed the production of new amyloid material via growth competent fibril ends, and to enhance the cytotoxic potential of amyloid either directly or via the production of fibril ends that increase the probability of fibril disassembly and the consequent release of toxic species (12,18). The ability of fragmented fibrillar particles to act as seeds of new amyloid (42) is dependent on the extent to which fibrils have been fragmented (12), with shorter fragmented fibrils being more effective in seeding for the same effective mass of seeds, due to the increased number of extension sites per mass of fibril material, compared with their longer counterparts (12). Here, we have demonstrated that the particle concentration information can be obtained by single particle analysis of AFM images. We show that particle concentration is a key quantitative factor for describing the seeded growth of amyloid fibrils, and it can be used as an excellent quantitative predictor of seeding efficiency. Short fibrils have also been shown to be more able to access cellular environments that are otherwise protected from large and entangled amyloid deposits (45–48), offering an explanation of why some amyloid fibrils may be infectious while others are not, and blurring the boundary between prions and nontransmissible amyloid. Short, fragmented amyloid fibrils may assert distinct cytotoxic properties depending on their dimensions. For example, short fibrils of β₂m, α-synuclein, and hen egg white lysozyme resulting from fibril fragmentation have been shown to possess a higher cytotoxic potential to different cell lines than longer fibrils of the same morphological type (12). Accordingly, small cytotoxic oligomeric assembly intermediates have been shown to be fibrillar in nature (49). Short fibrils of β₂m have also been shown to disrupt model lipid membranes, likely due to the presence of a larger number of disruptive surfaces at fibril ends (19,50). Indeed, short amyloid fibrils can act additionally as a reservoir of cytotoxic species, which can be shed from fibrillar ends (51). The ability our approach offers to measure and to predict changes in the amyloid populations, particle concentrations, and species distributions either in a forward direction (elongation growth) or in a backward direction (fibril fragmentation), as we have demonstrated for β₂m fibril growth and breakage, therefore, will be fundamental in understanding amyloid assembly, the use of amyloid as a nanomaterial, and amyloid-associated disease mechanisms. It will also be critical in developing therapeutic approaches to control the population of small cytotoxic and/or transmissible fibrillar fragments, for example by stabilizing monomeric precursors, preventing fibril elongation, or by reducing fibrils’ susceptibility to fragment.